Abstract
Single-phase fluid flow velocity maps in Ketton and Estaillades carbonate rock core plugs are computed at a pore scale, using the lattice Boltzmann method (LBM) simulations performed directly on three-dimensional (3D) X-ray micro-computed tomography (µCT) images (≤ 7 µm spatial resolution) of the core plugs. The simulations are then benchmarked on a voxel-by-voxel and pore-by-pore basis to quantitative, 3D spatially resolved magnetic resonance imaging (MRI) flow velocity maps, acquired at 35 µm isotropic spatial resolution for flow of water through the same rock samples. Co-registration of the 3D experimental and simulated velocity maps and coarse-graining of the simulation to the same resolution as the experimental data allowed the data to be directly compared. First, the results are demonstrated for Ketton limestone rock, for which good qualitative and quantitative agreement was found between the simulated and experimental velocity maps. The flow-carrying microstructural features in Ketton rock are mostly larger than the spatial resolution of the µCT images, so that the segmented images are an adequate representation of the pore space. Second, the flow data are presented for Estaillades limestone, which presents a more heterogeneous case with microstructural features below the spatial resolution of the µCT images. Still, many of the complex flow patterns were qualitatively reproduced by the LBM simulation in this rock, although in some pores, noticeable differences between the LBM and MRI velocity maps were observed. It was shown that 80% of the flow (fractional summed z-velocities within pores) in the Estaillades rock sample is carried by just 10% of the number of macropores, which is an indication of the high structural heterogeneity of the rock; in the more homogeneous Ketton rock, 50% of the flow is carried by 10% of the macropores. By analysing the 3D MRI velocity map, it was found that approximately one-third of the total flow rate through the Estaillades rock is carried by microporosity—a porosity that is not captured at the spatial resolution of the µCT image.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Digital rock (DR) physics is concerned with the computation of petrophysical properties of sedimentary rocks on the basis of high-resolution images of the pore space (Alpak et al. 2019; Andrä et al. 2013a, b; Blunt et al. 2013; Saxena et al. 2017a). The aim of DR technology is to complement and augment conventional, laboratory-based rock core analysis. A major focus of DR technology is to accurately simulate fluid flow behaviour within the pore space. One of the most powerful approaches for simulating single- and multi-phase flow directly on pore space images of rocks is the lattice Boltzmann method (LBM) (Alpak et al. 2019, 2018b; Benzi et al. 1992; Blunt et al. 2013; Chen and Doolen 1998; Coles et al. 1998). LBM simulation, which has originated from the lattice gas automata method (Hardy et al. 1973), belongs to a class of computational fluid dynamics (CFD) methods for simulating fluid flow. LBM is based on simulation of the collision and streaming of microscopic particles over a discrete lattice mesh, and evaluation of the macroscopic pressure gradient and velocity, from which the permeability of a porous material can be estimated; it can be shown that the averaged behaviour of the LBM simulation approximates the Navier–Stokes equation (Benzi et al. 1992; Chen and Doolen 1998). Compared to other, conventional CFD methods, the main advantages of LBM are that it is easy to code and is well-suited for parallel computing (Chen and Doolen 1998). Furthermore, LBM simulation enables flow to be directly simulated through complex geometries based on segmented digital images, such as the pore space images of porous rocks.
Before DR simulators, which are commonly based on the LBM approach, can be used as a predictive tool, it is necessary to validate their output against experimental data. A natural choice of method to benchmark flow simulations is flow-magnetic resonance imaging (flow MRI), because of its ability to quantitatively and non-invasively measure three-dimensional (3D) spatially resolved fluid flow fields in rocks (Karlsons et al. 2021; de Kort et al. 2019; Romanenko et al. 2012; Shukla et al. 2016). By looking at experimental spatially resolved flow velocity fields, it is possible to identify whether the microscopic flow phenomena, which will determine the core-scale petrophysical properties, are correctly simulated. Furthermore, spatially resolving flow properties provide fundamental insight into the degree of spatial heterogeneity and dispersion of the flow across the rock sample.
Some earlier studies have compared nuclear magnetic resonance (NMR) measurements to direct simulations of flow in porous materials (Bijeljic et al. 2013, 2011; Blunt et al. 2013; Lebon et al. 1997; Mantle et al. 2001; Manz et al. 1999; Sullivan et al. 2007; Yang et al. 2013). Many of these studies, however, have focused on investigating model porous systems (i.e. packed beds) (Lebon et al. 1997; Mantle et al. 2001; Manz et al. 1999; Sullivan et al. 2007; Yang et al. 2013). One of the advantages of using packed beds, which are typically comprised of mm-sized particles, is that the pore size of the system can be tuned so that it matches the spatial resolution that can be reached with the experimental device which is used to image the system. This then enables hydrodynamics and structure-flow correlations in such systems to be investigated at the pore scale. In such model systems, MRI has often been used because it is capable of routinely delivering 3D images at a spatial resolution of a few hundred microns. Although these spatial resolutions are sufficient to resolve the pore space in packed beds comprised of mm-sized particles, such spatial resolutions would be too coarse for adequately capturing pore-scale information in porous rocks. As a result, earlier studies, which compare flow simulations to magnetic resonance experiments in rocks, have utilized spatially unresolved NMR techniques, such as spatially unresolved NMR propagator measurements (Bijeljic et al. 2013, 2011; Blunt et al. 2013). Although 3D spatially resolved flow information in porous rocks has also been acquired using MRI, at a spatial resolution of ~ 1 mm (de Kort et al. 2018; Romanenko et al. 2012; Shukla et al. 2016), MRI flow images need to be acquired at higher spatial resolutions before they can be compared to pore-scale LBM simulations.
We have recently demonstrated the acquisition of a 3D spatially resolved fluid velocity map at a spatial resolution of 35 μm during water injection into a Ketton limestone plug (Karlsons et al. 2021). At this resolution, pore-scale features could be resolved. The work was based on the use of a combination of micro-MRI equipment in combination with data under-sampling and compressed sensing (CS)—a data acquisition strategy based on ideas from image compression theory (Karlsons et al. 2019; de Kort et al. 2018; Lustig et al. 2007). It was further shown that at such spatial resolutions additional insight into structure-flow relationships can be obtained by co-registering the flow velocity maps with X-ray micro-computed tomography (μCT) images of the grain space—co-registration of the MRI velocity maps with the μCT images makes it possible to correlate local flow velocities directly with the microstructure of the grain space. Furthermore, because flow simulations are often based on segmented X-ray μCT images (i.e. binarized X-ray µCT images partitioned into the pore and grain space phases), co-registration provides an opportunity to compare flow simulations to the MRI velocity fields on a voxel-by-voxel basis. X-ray μCT images of small rock plugs are acquired routinely at resolutions of ~ 1 μm, i.e. an order of magnitude higher than the currently accessible resolution with high-resolution flow MRI. The spatial resolution of the flow simulations will therefore also be higher than that of the high-resolution MRI velocity maps. However, because magnetic resonance determines an ensemble-average of the properties of individual molecules that carry NMR-active nuclei, the average fluid velocity of each voxel within the MRI velocity map is an accurate average velocity of all molecules contained within that voxel. So, despite the disparity in spatial resolution, quantitative, voxel-by-voxel comparisons can be made between experimentally acquired MRI velocity maps and (coarse-grained) µCT-image-based flow simulations.
However, flow simulations based on segmented X-ray μCT images do suffer from the resolution limit of that imaging method, which may lead to inaccurate results. In particular, for heterogeneous carbonate rocks, the smallest (micro)pores are still significantly smaller than the voxel size currently accessible with X-ray μCT. The areas in the rock where microporosity is present will have a lower average X-ray absorption because of the globally lower mass density of that area; however, a microporous area cannot be distinguished from a non-porous area with a lower mineral density because the X-ray absorption can be very similar. Using μCT, the only way to differentiate the regions of microporosity is to saturate the rock with a doped fluid (Lin et al. 2016). In the present work, co-registration of μCT and MRI images makes it possible to non-invasively differentiate between these two, because MRI is sensitive only to fluids and will therefore reveal only the fluid-saturated micropores, but not the areas of solid rock in which no fluid is located. The observation of fluid in micropores, however, may be limited by the fact that, in general, the NMR signal of fluid in smaller pores is known to disappear relatively fast due to the higher surface-to-volume ratio in those pores that enhances NMR signal decay (i.e. short transverse relaxation times).
In the context of DR physics, a key research question is to what extent these smaller pores actually contribute to the overall flow of fluid through the rock, and therefore to what extent a simulation of the flow field based on a μCT-derived pore space is accurate. Although in many cases the microporosity of the rock is not expected to carry significant flow, some regions of the microporous rocks (especially carbonates) can be connected only by microporosity in which case the contribution to flow by micropores can become significant (Blunt 2017). It has already been demonstrated (Bijeljic et al. 2018) via direct flow simulations in combination with mercury injection porosimetry and X-ray µCT differential imaging (Lin et al. 2016) with fluid doping that microporous regions can significantly contribute to the total permeability in heterogeneous carbonate rocks. In fact, Soulaine et al. (Soulaine et al. 2016) showed that even in a sandstone rock with only 2.6% microporosity (2% sub-voxel porosity), the microporosity can significantly influence the computed permeability values, because microporous regions often serve as bridges between macropores, hence influencing the flow behaviour in the rock. In this work, this question is addressed by comparing single-phase flow simulations, run on segmented 3D μCT images of Ketton and Estaillades limestone rock core plugs, with high-resolution MRI velocity maps that are capable of non-invasively capturing flow information in pore space. The MRI flow map provides an average fluid flow velocity for each voxel in the image. The results of the flow simulation will be directly compared to the MRI flow map by co-registration and coarse-graining of the simulation down to the same resolution as the flow MRI data.
This paper is structured as follows. In Sect. 2, the experimental details of high-resolution MRI flow velocity experiments and direct, pore-scale LBM simulations are given. Qualitative and quantitative comparison between the experimental and simulated velocity fields is reported in Sect. 3. First, in Sect. 3.1, the results are shown for the relatively homogeneous Ketton limestone rock. The analysis includes qualitative comparison of the two-dimensional (2D) velocity maps extracted from the 3D MRI and LBM datasets, and quantitative comparison between the data on a voxel-by-voxel and pore-by-pore basis. Then, in Sect. 3.2, a similar analysis is presented for the more heterogeneous Estaillades limestone rock. The contribution of microporosity to the total flow rate through the rock is also quantified.
2 Materials and Methods
2.1 Sample Preparation
A Ketton limestone core plug, 3.84 ± 0.01 mm in diameter and 11.10 ± 0.37 mm in length, and an Estaillades limestone core plug, 3.92 ± 0.02 mm in diameter and 12.65 ± 0.13 mm in length, were used in this study as representative samples of reservoir rocks; 3D sections of these rock samples are shown in Fig. 1. After drying the samples in an oven overnight at 70 ºC and acquiring µCT images, the rock samples were vacuum-saturated with deionized water. The gravimetric porosities (φg) of the water-saturated Ketton and Estaillades rock samples were determined to be φg = 21 ± 4% and φg = 25 ± 1%, respectively. Further properties of the samples are summarized in Table 1.
For flow MRI experiments, the rock samples were placed in an Adtech fluorinated ethylene propylene (FEP) heat shrink tubing which was connected to an inlet and outlet flow line. In the case of Estaillades rock, before placing the sample in the heat shrink tubing, two layers of Teflon tape with thickness of 75 µm were applied around the plug to minimize fluid by-passing through vugs on the surface of the rock during flow experiments. A constant flow rate of water at 0.03 ml min–1 was imposed using a Vindum VP-6 metering pump. This flow rate was chosen because it resulted in Stokes flow in the rock samples used and was still high enough for the pump to produce a stable flow. The flow rate and velocity-encoding parameters for the MRI experiments, as described below, were tuned simultaneously to optimize the quality of the resulting flow maps.
2.2 X-ray Micro-Computed Tomography
2.2.1 Ketton Rock
3D μCT data of the dried Ketton rock sample were acquired using a Bruker SkyScan 1172 µCT scanner (Bruker Micro-CT, Belgium) at an isotropic spatial resolution of 5.00 μm. Image acquisition was performed using a source voltage of 60 kV, a source current of 165 μA, and an Al (0.5 mm) filter. In total, 802 projection images were acquired by rotating the sample in angular increments of 0.25° over 200.5° with 10 scans per angular increment, yielding a total acquisition time of 11.4 h. Projection images were reconstructed using the NRecon package (Bruker) to give 2666 cross-sectional slices. To generate a 3D μCT image of the rock sample, all 2D cross-sectional slices were successively stacked in Avizo.
2.2.2 Estaillades Rock
The Estaillades sample was imaged using a Bruker SkyScan 2214 µCT scanner (Bruker Micro-CT, Belgium) at an isotropic spatial resolution of 3.00 μm. Imaging was performed using a source voltage of 90 kV and source current of 70 μA, with an Al (1 mm) filter. To image the entire sample, acquisitions were performed at 5 different scanning positions along the longest dimension of the sample. For each position, 3601 projections were acquired by rotating the sample in angular increments of 0.1° over 360° with 6 scans per angular increment, resulting in an acquisition time of 4.26 h. Thus, the total acquisition time was 21.3 h. Projection images from all 5 scanning positions were stitched together and reconstructed using the NRecon package (Bruker) to give 4319 cross-sectional slices. A 3D µCT image was generated by stacking the 2D cross-sectional slices.
2.3 Flow MRI
Phase-contrast MR velocimetry, otherwise known as flow velocity mapping, is used to directly and non-invasively measure fluid flow velocities in opaque porous media (Callaghan 2011; Gladden and Sederman 2013; Huang et al. 2017; Shukla et al. 2016). The underlying principle of velocity mapping is that the phase of the NMR signal can be made sensitive to translational motion; theoretical details of velocity mapping can be found elsewhere (Callaghan 2011; Gladden and Sederman 2013). In short, velocity mapping is an integration of a pulsed field gradient nuclear magnetic resonance experiment (PFG NMR) (Stejskal and Tanner 1965), which is used to encode fluid displacements (velocities), with an imaging experiment (i.e. a so-called k-space measurement), which is used to spatially resolve those displacements. Using velocity mapping a single, average, local velocity is spatially resolved in each voxel within an image.
In this work, MRI velocity maps were acquired on a 7.0 T vertical-bore magnet controlled by a Bruker BioSpin Avance III HD spectrometer. A Bruker Micro5 tri-axial magnetic field gradient system with a maximum gradient amplitude of 2.9 T m–1 was used to achieve the spatial resolution in the three orthogonal z-, x-, and y-directions. An 8-mm radio frequency (r.f.) saddle coil tuned to a resonance frequency of 299.84 MHz (1H) was used for spin excitation and signal detection. Flow velocities through the rock samples were measured along the superficial flow direction, here defined as the z-direction.
2.3.1 Ketton Rock
The main details of the MRI methods employed for the acquisition of velocity maps of Ketton rock are summarized below.
The under-sampled velocity maps of Ketton rock were acquired using a pulsed gradient spin echo-rapid acquisition with relaxation enhancement (PGSE-RARE) pulse sequence described in ref. (Karlsons et al. 2021). Under-sampling schemes for k-space acquisitions were generated using the µCT-based variable-density sampling approach with a k-space sampling fraction of 0.25 (Karlsons et al. 2019). The duration of the hard 90° excitation and 180° refocusing r.f. pulses were 6.0 μs and 12.0 μs, respectively. A RARE factor (\({N}_{\mathrm{RF}}\)) of \({N}_{\mathrm{RF}}\)= 8 with an echo spacing (\({t}_{\mathrm{e}})\) of \({t}_{\mathrm{e}}\) = 2.2 ms was used to acquire \({N}_{\mathrm{RF}}\) successive lines of k-space for each excitation pulse. To achieve velocity encoding, a pair of unipolar gradients \(\mathbf{g}\) of amplitude g = 2.0 T m–1 (\({\mathbf{g}}_{\mathrm{i}}\) = 4.0 T m–1) and duration of δ = 0.132 ms were used, separated by an observation time Δ = 4 ms. With 32 scans for signal averaging and a recycle delay (\({t}_{\mathrm{RD}})\) of 1.1 s, the acquisition time of the velocity map was 20 h. Velocities were encoded along the z-direction, i.e. along the superficial flow direction. Images under no-flow conditions were acquired to correct for the velocity offsets. The images were acquired with a field of view (FOV) of 13.5 mm × 4.5 mm × 4.5 mm and 384 voxels × 128 voxels × 128 voxels in the frequency- (z) and phase-encoding (x, y) directions, respectively, yielding a 3D velocity map with an isotropic resolution of 35.2 μm.
After acquisition, the under-sampled data were reconstructed using an in-house MATLAB toolbox, Object Oriented Mathematics for Inverse Problems (OOMFIP), for which the implementation was presented in (Benning et al. 2014). Further details of data reconstruction and image processing can be found in our earlier work (Karlsons et al. 2021).
2.3.2 Estaillades Rock
The under-sampled velocity maps of the Estaillades rock plug were acquired using the same PGSE-RARE pulse sequence that was used for flow MRI experiments in the case of Ketton rock. Under-sampling schemes were generated using the µCT-based variable-density sampling with a k-space sampling fraction of 0.3125. Hard 90° excitation and 180° refocusing r.f. pulses were used with durations of 6.6 μs and 13.2 μs, respectively. The number of echoes in the RARE echo train was \({N}_{\mathrm{RF}}\)= 8 with an echo spacing of \({t}_{\mathrm{e}}\) = 2.2 ms. The velocity imaging parameters were \({\mathbf{g}}_{\mathrm{i}}\) = 2.3 T m–1, δ = 0.132 ms, and Δ = 4 ms. Thirty-two scans were acquired for signal averaging with \({t}_{\mathrm{RD}}\) = 1.375 s, giving an acquisition time of 31.3 h. The velocity maps were acquired with a FOV of 13.5 mm × 4.5 mm × 4.5 mm and 384 voxels × 128 voxels × 128 voxels in the z-, x-, and y-directions, yielding a 3D velocity map with an isotropic resolution of 35.2 μm. The under-sampled velocity data of Estaillades rock were reconstructed using the OOMFIP package.
2.4 Direct Numerical Pore-Scale Flow Simulations
In this work, LBM simulations were performed directly on pore space µCT images of Ketton and Estaillades carbonate rocks. This section describes the details of image processing used to prepare the μCT data for use as the porous structure upon which the LBM simulations were performed, and the LBM simulations that were performed.
For a detailed description of the general theory of LBM, the reader is referred to (Benzi et al. 1992; Chen and Doolen 1998).
2.4.1 µCT Image Processing
In order to run LBM simulations, a binarized image that represents the structure of each rock sample is required. To achieve this, the acquired µCT intensity images of rocks were denoised, segmented into grain and pore spaces, and masked; for Ketton rock, the µCT image was first coarsened to 7.0 µm using a Lanczos filter (Duchon 1979) due to the data size limitations of the LBM code used (see Sect. 2.4.2.). First, the acquired 3D µCT images of rocks were denoised using a non-local mean filter (Buades et al. 2005). The denoised images were then binarized using the watershed-based segmentation algorithm (Beucher and Meyer 1993). Next, binary cylindrical masks were applied to the grain space images to ensure that the voxels belonging to the grains within the rock and regions outside the rock plug have the same binary intensity value (i.e. 1), thus guaranteeing that only the pore space has the other binary intensity value (i.e. 0). The pore space image is then obtained simply by computing the complement of the binary grain space image. Fluid flow simulations are performed on this pore space image, as described below.
For Estaillades rock, the binary mask was generated such that ~ 75 µm (one layer of Teflon tape) of the outer portions of the rock are radially removed from the rock plug in the final pore space image. Although this removes some sections of the rock matrix, it also partially accounts for the fact that some of the surface pores in the Estaillades sample were partly blocked by the Teflon tape during the flow experiment, so that the simulation is more structurally consistent with the experimentally acquired MRI data.
2.4.2 LBM Simulations
Two LBM algorithms were used in this work to simulate single-phase flow in rocks. In Ketton rock, the fluid flow was computed using an energy-based LBM (eLBM) simulator (Alpak et al. 2019, 2018a) which utilizes the multiple-relaxation-time (MRT) model as a momentum-balance solver. In Estaillades, the flow was simulated using an MRT-LBM algorithm (Alpak et al. 2018b) based on the same MRT solver.
Initially, the idea was to use eLBM for both rock samples as eLBM has a slightly more accurate way of representing the initial boundary conditions, hence had the possibility of giving more accurate velocities compared to MRT-LBM. However, for Estaillades rock significant stability issues with eLBM were observed, which is why it was necessary to use MRT-LBM for flow simulations in the Estaillades case. It is important to note that owing to its underlying multi-phase flow formulation and the use of (open) buffers to impose velocity boundary conditions, eLBM is relatively more random-access memory (RAM) intensive than MRT-LBM. Moreover, the velocity boundary condition is more sensitive to the underdiscretization of narrow throats in the digital rock images. Although an attempt was made to simulate flow in Estaillades rock using eLBM, which required coarsening of the Estaillades image to satisfy the eLBM’s memory requirements, it was observed that the resulting image contained a significant amount of underdiscretized narrow throats as well as some pore throats that were completely closed to flow due to coarsening. Consequently, significant stability issues with eLBM were observed, and the MRT-LBM code was utilized for flow simulations in Estaillades rock. The MRT-LBM code has a smaller memory footprint due to its underlying single-phase flow formulation. It requires less or no coarsening of the image (depending on the image size) because of its more compact and effective memory management. Moreover, the use of body-force boundary conditions to drive flow in MRT-LBM renders it significantly less sensitive to the presence of narrow throats in terms of stability of flow simulations.
2.4.2.1 eLBM
eLBM is a direct pore-scale visco-capillary flow simulator, which is based on the numerical solution of the Helmholtz free-energy-minimizing phase-field model (Alpak et al. 2019, 2018a). An MRT model is implemented in eLBM as the collision operator (relaxation term) to represent the particle collision processes. The distributed parallel general-purpose graphics processing unit (GPGPU) code implementation of the eLBM code enables pore-scale simulations to be efficiently run directly on large 3D µCT images of rocks. The implementation of the eLBM code is performed in Compute Unified Device Architecture (CUDA) programming language to take maximum advantage of accelerated computing multi-node GPGPUs. eLBM is, to our knowledge, the first industry-grade distributed parallel implementation of an energy-based LBM which takes advantage of multiple GPGPU nodes.
In eLBM, fluid is injected from the inlet buffer layer into the pore space with a constant prescribed velocity boundary condition. The outlet boundary condition is the gradient-free boundary to mimic the situation where the porous medium behaves in such a way that is larger than the simulated domain size (i.e. the fluids that are exiting the domain behave as if the domain is continued in a halo cell at the outlet). Loop boundary conditions are imposed on the surfaces of the domain that are perpendicular to the main flow direction (Alpak et al. 2018a). However, if the image naturally has solid walls at the outer surfaces of the domain that are normal to the main flow direction, the loop boundary condition implementation automatically reduces to the closed (no-flow) boundary conditions (i.e. the fluids cannot exit on one side and enter in the other side with no-slip boundary conditions on solid surfaces). In fact, for the velocity vector, the no-slip boundary condition is imposed on all fluid–solid boundaries including the no-flow boundaries on the external surfaces of the global domain. In this work, eLBM is run in single-phase mode by initializing the pore space with a single-phase fluid and injecting the same phase at the inlet. Therefore, a diffuse interface does not emerge in our simulations. In other words, eLBM can be seen as MRT-LBM (Alpak et al. 2018b) with constant velocity inlet and gradient-free outlet boundary conditions. Further details of eLBM are documented in references (Alpak et al. 2019, 2018a).
2.4.2.2 MRT-LBM
The MRT-LBM algorithm used in this work is based on the MRT model and a precise treatment of body force that drives the flow (Alpak et al. 2018b). The Boltzmann equation is discretized in space, velocity (momentum), and time coordinates using a 3D 19-velocity grid (D3Q19 scheme), which provides the optimal compromise between accuracy and computational efficiency. The conventional approach of representing particle collision (or relaxation towards an equilibrium state due to collision) is based on the single-relaxation time Bhatnagar–Gross–Krook (BGK) model (Bhatnagar et al. 1954), where a single relaxation time is employed to describe the relaxation processes. However, this model has several deficiencies, such as numerical instabilities at relatively high Reynolds numbers (Alpak et al. 2018b). In the MRT model (D’Humières et al. 2002), the velocity distribution function is transformed into moment space, where individual moments can be relaxed at individual rates. Overall, the MRT model has several advantages over the conventional single-relaxation time BGK model, and those include: (1) enhanced numerical stability, (2) independent bulk and shear viscosities, and (3) viscosity-independent, non-slip boundary conditions (Alpak et al. 2018b). The drawback of the MRT model is that it is slightly more computationally demanding compared to the BGK model. This minor hurdle is easily overcome through a GPGPU implementation of the MRT model for eLBM and MRT-LBM. Furthermore, similar to eLBM, the implementation of MRT-LBM code is performed in CUDA programming language to take maximum advantage of GPGPUs.
In MRT-LBM, fluid is driven by a body-force term by imposing a loop boundary condition on the inlet and outlet faces of the domain. The same body force is used for the fluid that leaves the domain at a given domain-boundary surface (e.g. the outlet face of the domain) and enters the domain at the opposite boundary surface (e.g. the inlet face of the domain). A precise treatment of body force is required to eliminate errors in velocity gradients. For the velocity vector, the zero-slip boundary condition is imposed on the surfaces between rock grains and fluid within the pore space. More information on MRT-LBM can be found in ref. (Alpak et al. 2018b).
2.4.2.3 Simulation Details
Simulations were performed on large 3D µCT images with a size of 1671 voxels × 643 voxels × 643 voxels (in the z, x, and y directions) at an isotropic spatial resolution of 7.0 µm for the Ketton rock plug, and 4279 voxels × 1500 voxels × 1500 voxels (in the z, x, and y directions) at an isotropic spatial resolution of 3.0 µm for the Estaillades rock plug. Experimental details of eLBM and MRT-LBM are given below.
A multi-relaxation-time algorithm was used in both MRT-LBM and eLBM (Alpak et al. 2019, 2018a, b). The relaxation time associated with the single-phase fluid was selected to model a fluid with a viscosity of 1.0 cp in the simulations, i.e. water. Assuming a density of 1.0, lattice spacing of 1.0, and lattice time step of 1.0 (all in lattice units), the relaxation time can be computed as 3.5 (Eq. 16 in (Alpak et al. 2019)). A body force of 1.0 × 10–5 in lattice units was used to drive the (initial) flow in the main flow direction in MRT-LBM. On the other hand, fluid flow was driven by a constant flow rate of 2.0 × 10–5 in lattice units into the inlet buffer in eLBM. Simulations were terminated after steady-state flow conditions were attained both in MRT-LBM and eLBM applications. Two criteria need to be satisfied to characterize the steady-state flow in this implementation: (1) the change in the mean velocity should be less than 1.0 × 10–7%, and (2) the change in the variance of the velocity field should be less than 1.0 × 10–7%. It was observed that the steady-state velocity field does not have a strong dependence on the boundary conditions and convergence criteria as long as reasonable values that do not violate the underlying assumptions of MRT-LBM and eLBM are used (Alpak et al. 2019, 2018a, b).
MRT-LBM and eLBM simulations were performed on a Linux based central processing unit-GPGPU (CPU-GPGPU) high-performance computing (HPC) cluster. All simulations were performed using eight cluster nodes each with two Tesla K80 GPGPU cards each. The technical specification of each CPU-GPGPU node is as follows: HP Proliant XL250a Gen9, 24 Cores—Intel(R) Haswell—Xeon(R) CPU E5-2680 v3 @ 2.50 GHz, 256 GB DRAM, 0.8 TB /scratch, 10 Gbps Ethernet, 56 Gbps Fully Non-Blocking FDR (FBB) Infiniband, 2 Tesla K80 GPGPU cards per node. It is important to note that each Tesla K80 card has ~ 5000 CUDA cores and 24 GB of RAM. Simulations utilized 100% of the GPGPU nodes’ processing potential. In other words, no two simultaneous simulation jobs were submitted to the same GPGPU nodes.
In order to be able to quantitatively compare the LBM and MRI velocity data, the velocities of the high-resolution LBM simulations were scaled such that the mean slice-by-slice flow rate of the LBM simulations was equal to the imposed flowrate of 0.03 ml min–1. The flow rate for each slice was calculated by multiplying the sum of all velocities within the slice with the cross-sectional area of each voxel. In the case of Estaillades rock, the high-resolution simulation data were first coarse-grained (Lanczos filter) to 6.0 µm spatial resolution for more efficient image registration and data manipulation. For all quantitative analysis, the simulated data were down-sampled to 35 µm spatial resolution (Lanczos filter) to enable direct comparison with the acquired MRI velocity data.
2.5 Image Co-Registration
Image co-registration was performed in Avizo using the “Register Images” module. The aim of the image co-registration was to spatially align MRI velocity maps and µCT-based LBM simulations in order to be able to qualitatively and quantitatively compare the flow fields of both methods. MRI intensity images, obtained by calculating the magnitude of complex-valued no-flow MRI datasets, and µCT greyscale intensity images, used to generate the pore space for simulations, were used as inputs for image registration. The main steps of image registration process are now discussed. First, the µCT intensity image (model image) was manually pre-aligned with the MRI intensity image (reference image). Next, the alignment of the model image relative to the reference image was optimized using rigid transformations with the normalized mutual information (Pluim et al. 2003; Studholme et al. 1999) as a metric for the goodness of image alignment. In the optimization procedure, the data were down-sampled, and the image registration was performed in steps at increasing spatial resolutions for more efficient image registration. Extensive direction and Quasi Newton optimizers were used for the co-registration of the coarse-resolution and the finest-resolution images, respectively. After the image co-registration process was completed, the resulting transformation of the µCT intensity image was applied to the LBM simulation. Last, the co-aligned µCT intensity image and LBM simulation were resampled onto the MRI data coordinate system using a Lanczos filter (Duchon 1979), which enables MRI flow maps and µCT-based images, including LBM simulations, to be visualized and compared on the same grid.
3 Results and Discussion
In this section, the LBM simulations and MRI velocity data for Ketton and Estaillades rock core plugs are compared. This includes a qualitative comparison of 2D slice images extracted from the 3D datasets and a quantitative voxel-by-voxel and more macroscopic, pore-by-pore comparison between the LBM and MRI data. First, this analysis was carried out for the Ketton limestone rock. Ketton rock represents a case where both methods, MRI and µCT, capture predominantly the macroporosity of the rock (i.e. large, intergranular pores). In the case of MRI, the information from the fluid in the micropores is not captured due to the rapid NMR signal decay (short transverse relaxation times) of the water molecules in the intragranular pores within the Ketton ooids. Second, the simulation and experimental data are compared for the Estaillades limestone rock, which has much more complex pore geometry and has more poorly connected rock structure than Ketton rock. In this case, MRI also reveals the flow information about fluids in the micropores due to the slower signal decay in the pores which enabled fluid information to be captured by MRI.
3.1 Ketton Rock
Figure 2 shows 2D (xy) slice images extracted from the 3D high-resolution LBM simulation at 7 µm spatial resolution and MRI velocity map at 35 µm spatial resolution, co-registered with the µCT structural image of the same Ketton rock sample. The images shown in Fig. 2 represent the velocity component in the superficial flow direction (z). Good agreement is observed between the LBM simulation and MRI velocity data. All characteristics of the flow behaviour present in the MRI flow maps in Ketton rock are reproduced by the LBM simulation. This includes the location of high-velocity flow channels and the occurrence and location of the regions with backflow (i.e. negative (z) velocities). As is evident from the difference map in Fig. 2, the magnitude of simulated velocities is also in good agreement with the acquired MRI velocities, although LBM seems to underestimate the magnitude of velocities in the high-velocity flow channels of the rock. This observation contradicts the results reported by Manz et al. (1999) who reported that LBM overpredicts large velocities in a beadpack composed of spherical beads, which could be due to a different LBM code used to simulate flow. Standard deviation calculated from the middle section of the 3D difference flow map is 0.37 mm s–1. Overall, both the simulated and MRI data show that the flow in Ketton rock is highly heterogeneous with the flow being carried by a few high-velocity flow channels.
Comparison between the LBM simulation and MRI velocity map in Ketton rock. Three different 2D slice images extracted from the 3D co-registered MRI and µCT dataset are shown. Good agreement is observed between the simulation and MRI experiment. The difference map (\(v_{z} \left( {{\text{MRI}}} \right) - v_{z} \left( {{\text{LBM}}} \right)\)) was obtained by calculating the difference between the MRI flow map and the coarse-grained LBM simulation. The velocity maps shown represent the velocity component in the superficial (z) flow direction. The images shown, from top to bottom, correspond to the position in the rock approximately 4.4 mm, 5.1 mm, and 5.7 mm from the inlet, respectively
To further investigate the agreement between the experimental and simulated flow data, more quantitative analysis was performed by comparing the velocity distributions and voxel-by-voxel velocities of the two datasets; the results of this analysis are shown in Figs. 3 and 4, respectively. Figure 3 shows that the (original) simulated (green dotted line) and experimental (black line) distributions of \({v}_{z}\) are significantly skewed and have a long positive tail, which extends far beyond the modal velocity of each distribution, and a considerable degree of backflow, which is represented by negative velocities. The experimental and simulated distributions also show that a significant amount of fluid in the pore space of Ketton rock is stagnant or near stagnant with velocities around \({v}_{z}\) = 0 mm s–1. In the velocity maps (Fig. 2), from which these distributions were extracted, indeed the fluid in the majority of pores is seen to be near stagnant. However, there also are noticeable differences between the two velocity distributions. In terms of the shape of the distributions, the two main discrepancies are the population of the modal velocity peak and the distribution of backflow. The location of the modal velocity peaks is also slightly different—the modal velocities of the MRI and simulated velocity distributions are \({v}_{z}\)≈ 0.08 mm s–1 and \({v}_{z}\) ≈ 0.02 mm s–1, respectively. MRI velocity measurements are, of course, affected by experimental noise, which can decrease the sharpness of the modal velocity peak and, in general, lead to broadening of the velocity distribution. The uncertainty in the MRI velocity measurements can be estimated from the intensity images since error in measured velocities is reciprocally proportional to the signal-to-noise ratio (SNR) of the images (Chang and Watson 1999; Shukla et al. 2016). Using this approach, it was estimated that in this case the noise-related velocity errors in pores fully saturated with water are on the order of 0.03 mm s–1, relative to the measured velocities. However, in the voxels at the edges of grains these errors can be as large as ~ 0.2 mm s–1 because of lower SNR due to partial volume effects. To investigate the effect of noise on the MRI measurements, the LBM velocity distribution was convoluted with a noise-related Gaussian distribution with a standard deviation of 0.15 mm s–1, the result of which is represented by the red dashed line in Fig. 3. (The standard deviation of 0.15 mm s–1 is the upper limit of the noise-related uncertainty in MRI velocity measurements.) It can be seen in Fig. 3 that there is now excellent agreement between the simulation and experimentally acquired data.
2D histogram showing voxel-by-voxel correlation between simulated and experimental velocities for single-phase flow in Ketton rock. Good agreement is observed between the two datasets. The white dashed line represents a reference line with a slope of unity. The black dots represent 100 voxels randomly picked from the data
Voxel-by-voxel comparison between the simulated and experimental velocity maps is shown in Fig. 4. Overall, good agreement is observed between the two datasets, as most voxels lie close to the straight reference line (white dashed line) with a slope of unity. Significant differences between the MRI and simulated velocities are observed for a relatively small number of voxels (note the logarithmic scale of the colour bar). It can be also seen in Fig. 4 that a number of voxels which represent stagnant or near-stagnant liquid in the LBM simulation exhibit a range of positive and negative velocities significantly greater than \({v}_{z}\) = 0 mm s–1 in the MRI velocity map. This can be partly explained by the experimental noise, especially at the pore–grain interfaces where noise can compromise the accuracy of the measured velocities due to partial volume effects, as was discussed above. Furthermore, an error is expected because the pore–grain interface phenomena occur at the molecular (ångström) scale, whilst the simulation model is constructed at the pore (micron) scale. The simulation model imposes zero velocity boundary condition at the pore–grain interface, whilst the precise location of this interface is inevitably affected by the voxel resolution, and so this may also lead to deviations in the velocity close to the interface assuming that experimental data is resolving/capturing a large portion of the physical phenomena in this neighbourhood. Because of the high voxel resolution in the simulation, the implications for the velocity field are largely a localized effect that does not propagate in the simulation.
The experimental and simulated velocity data were further analysed using a pore-scale approach, wherein velocity information was obtained for each individual pore in the images and then compared between the two datasets. To achieve this, a (combined) binarized structural image, which essentially represents the macropore network of the Ketton rock, was first generated from the individual binary masks of the MRI and LBM datasets by only selecting the voxels that are shared between the two datasets. This is done so that the same pores consisting of the same number of voxels can be later identified using pore labelling. The pore space of the structural image was then separated into individual, labelled pores using a Chamfer distance map and marker-based watershed algorithm (Beucher and Meyer 1993) in Avizo. The labelled structural image and each velocity dataset separately (MRI or LBM) were then used as inputs in the labelled pore analysis to extract and correlate the flow properties for individual pores. The results of this analysis are shown in Fig. 5. Figure 5a shows a pore-by-pore comparison between the simulated and experimental velocity data; the black dashed line in the plot represents a reference line with a slope of unity, whereas the blue line is a regression fit to the data. Although there is a good overall agreement between the two datasets, the general trend is that the LBM simulation slightly underpredicts large pore velocities, but overpredicts small and negative pore velocities; inspection of Figs. 2 and 4 also reveals a similar trend. This observation, however, cannot be fully explained by the experimental noise. In Fig. 5b, the fraction of the total flow, which is represented by the fractional summed z-velocities within pores (\({v}_{z}^{\mathrm{sum}}(i)/{v}_{z}^{\mathrm{sum},\mathrm{tot}}\)), is plotted as a function of the fraction of the number of those pores (\({N}_{\mathrm{p}}(i)/{N}_{p}^{\mathrm{tot}}\)) that carry this flow for both datasets. As can be seen, agreement between experiment and LBM simulation is excellent. An interesting aspect of the data shown in Fig. 5b is the indication that the flow field in Ketton rock exhibits significant heterogeneity on the pore scale with 10% of the pores carrying ≈ 50% of the flow. These results are consistent with the heterogeneity seen in the velocity fields in Fig. 2.
Pore scale comparison between the LBM simulation and MRI velocity map of the Ketton rock core plug. a Pore-by-pore correlation between the experimental and simulated mean z-velocities within a pore, \(v_{z}^{{\text{m}}}\). The black dashed line represents a reference line with a slope of unity, but the solid blue line represents the regression fit to the data. b The fractional summed z-velocities within pores with a summed z-velocity equal to or greater than (the parametric variable) \(i\), \(v_{z}^{{{\text{sum}}}} \left( i \right)/v_{z}^{{{\text{sum}},{\text{tot}}}}\), plotted as a function of the fraction of the number of pores, \(N_{{\text{p}}} \left( i \right)/N_{p}^{{{\text{tot}}}}\), carrying this flow for velocity data representing MRI ( ) and LBM (
) and LBM ( )
)
3.2 Estaillades Rock
3.2.1 Benchmarking of the LBM Simulation
To illustrate both the fluid-saturated microporous and macroporous regions in Estaillades rock, a magnetic resonance intensity image was co-registered with a µCT image of the rock; a 2D (xy) slice image of the co-registered MRI and µCT dataset is shown in Fig. 6, where the blue and green colour intensities represent the amount of water in the micropores and macropores of the rock, respectively. Figure 6 shows that microporosity occupies large regions of the rock, whereas only a few macropores can be identified in the rock structure; the latter are likely to carry most of the flow through the rock. It can also be seen that no water is present within the dense calcitic grains of the Estaillades formation.
2D (xy) slice image extracted from the 3D co-registered MRI intensity and µCT images of the Estaillades carbonate rock plug. The four red boxes labelled a–d represent a microporous grain, a non-porous calcitic grain, a mesh of medium-sized pores, and a large macropore, respectively. The MR signal intensity is proportional to the local water content in the rock
The flow MRI data of the Estaillades rock sample are now discussed, along with the comparison with the LBM flow simulations. Figure 7 shows 2D (xy) slice images of Estaillades rock obtained from the 3D LBM simulation at 6 µm spatial resolution and MRI velocity map at 35 µm spatial resolution, co-registered with the µCT dataset of the rock; the images represent the velocity component in the superficial flow direction (z). Considering the complex structure of the Estaillades formation, good qualitative agreement is observed (ignoring microporous regions) between the three image slices of the LBM and MRI datasets. Similarly to Ketton rock, it can be seen in both LBM and MRI data that the flow in Estaillades rock is highly heterogeneous with a few high-velocity flow channels. MRI flow maps also reveal that the fluid is stagnant or near-stagnant in the microporous regions of the rock (i.e. dark grey µCT image intensities). To further inspect the flow fields, four regions in Fig. 7 have been highlighted by red boxes. Region ‘a’ (top slice) represents a large pore where the LBM predicts the formation of a high velocity flow channel with \({v}_{z}\) ≳ 5 mm s–1 and a diameter extending to about half of the width of the pore, whereas MRI velocity map shows lower velocities in the same pore. Interestingly, the acquired MRI velocity map indicates that two relatively small high-velocity channels have formed in region ‘a’, instead of one, as predicted by LBM. In the other large pores in this image slice with significant flow, LBM tends to underestimate the flow velocity, as is evident from the difference map. Figure 7 region ‘b’ shows another high-velocity flow channel in the middle of a relatively large pore—in this case the LBM has accurately predicted the location and velocity of the flow field. In region ‘c’, a microporous rock grain can be seen. No flow information was obtained from this region using the LBM simulation, because the pore size was below the imaging resolution of X-ray µCT. However, using MRI, the average flow velocity can be accurately measured at voxel sizes much greater than the pore size of the fluid-saturated rocks (Romanenko et al. 2012; Shukla et al. 2016). In this case, the MRI flow map indicates that the microporous grain contains stagnant or near stagnant fluid. Lastly, region ‘d’ shows complex flow behaviour with adjacent positive and negative flow channels in a large macropore. This complex flow behaviour has been relatively accurately predicted by LBM, as good qualitative agreement in this region is observed between the MRI and LBM velocity data.
Comparison between the LBM simulation and MRI velocity map in Estaillades rock. Three different 2D slice images extracted from the 3D co-registered MRI and µCT dataset are shown. The difference map (\(v_{z} \left( {{\text{MRI}}} \right) - v_{z} \left( {{\text{LBM}}} \right)\)) was obtained by calculating the difference between the MRI flow map and the coarse-grained LBM simulation. The velocity maps shown represent the velocity component in the superficial (z) flow direction. Four regions, namely a, b, c, and d, have been highlighted by the red boxes which identify interesting flow patterns in the rock. The images shown, from top to bottom, correspond to the position in the rock approximately 2.4 mm, 6.3 mm, and 6.9 mm from the inlet, respectively
Visual inspection of Fig. 7 reveals that although in some of the pores, complex flow patterns are predicted well by the LBM simulation, in some pores, significant differences between the MRI and LBM data can be seen. To investigate these discrepancies in more detail, a more quantitative analysis similar to that carried out for the Ketton sample was performed on a pore-by-pore basis. This analysis was carried out for the macroporous regions of the rock that are shared between the binarized (structural) images of the MRI and LBM datasets. The results of this analysis are shown in Fig. 8; note that this analysis resulted in a large number of small pores (consisting of a few voxels); hence, for clarity, only pores with radius greater than 35 µm are shown. Figure 8a shows that there is a much greater scatter of the points and deviation from the reference line of slope unity relative the data observed for the Ketton sample (Fig. 5a). However, as with the Ketton data, the LBM simulation generally underestimates large pore velocities, but overestimates negative pore velocities. As can be seen in Fig. 8a, there is a large number of pores in the MRI velocity map with significant negative and positive mean pore z-velocities, \({v}_{z}^{\mathrm{m}}\), which have \({v}_{z}^{\mathrm{m}}\) ~ 0 mm s–1 in the LBM simulation. A close inspection of the LBM simulation shown in Fig. 7 also reveals a similar trend as the LBM simulation predicts more highly localized flow than is seen in the MRI velocity data. This observation is also supported by the plot shown in Fig. 8b, where, based on the LBM data, approximately 94% of the flow in the Estaillades rock is carried by just 10% of the pores. Similarly, data extracted from the acquired MRI velocity map indicate that the flow through the macroporous regions of the rock is highly heterogeneous with 10% of the pores carrying ≈ 80% of the flow (vs. ≈ 50% in Ketton rock).
Pore scale comparison between the LBM simulation and MRI velocity map of the macroporosity in the Estaillades rock core plug. a Pore-by-pore correlation between the experimental and simulated mean z-velocities within a pore, \(v_{z}^{{\text{m}}}\). The black dashed line represents a reference line with a slope of unity, but the solid blue line represents the regression fit to the data. b The fractional summed z-velocities within pores with a summed z-velocity equal to or greater than (the parametric variable) \(i\), \(v_{z}^{{{\text{sum}}}} \left( i \right)/v_{z}^{{{\text{sum}},{\text{tot}}}}\), plotted as a function of the fraction of the number of pores, \(N_{{\text{p}}} \left( i \right)/N_{p}^{{{\text{tot}}}}\), carrying this flow for velocity data representing MRI ( ) and LBM (
) and LBM ( )
)
There are several sources of error that may contribute to the error in the experimental and simulated velocity maps and lead to the discrepancies between the two datasets. As was already discussed in Sect. 3.1, one source of error is the experimental noise present in the MRI velocity data. In the flow MRI data of Estaillades, the noise-related velocity errors are estimated to be on the order of 0.06 mm s–1 and 0.2 mm s–1 for the macroporous and microporous regions (green and blue regions in Fig. 6), respectively. In the microporous regions of the rock, where the typical fluid velocities are < 1 mm s–1, the uncertainty of ~ 0.2 mm s–1 can significantly influence the accuracy of the measured velocity on a per-pixel basis. These errors are larger than those estimated from the MRI images of Ketton. One of the main sources of error in both the experiment and simulation is the partial volume effect, which increases with decreasing spatial resolution of the images (Shah et al. 2016; Tang et al. 1993). In terms of the LBM simulations, it has been demonstrated that the uncertainty in the computed single-phase flow properties increases with increasing voxel size (Saxena et al. 2018, 2017b) for a given rock type as limited by the typical pore throat size. Another limitation of the LBM simulation is that it is run on a segmented µCT image that represents only the connected pore space of the rock that can be resolved at the imaging resolution used, which can lead to further inconsistencies between the experiment and the simulation. These types of errors are expected to be greater in the case of Estaillades rock than in Ketton rock due to its smaller pore throat size-to-voxel size ratio (Ketton: 6, Estaillades: 5), lower connected porosity (connected φµCT; see Table 1), and its more complex rock geometry (Saxena et al. 2018, 2017b).
3.2.2 The Contribution of Microporosity to the Flow Through Estaillades Rock
The qualitative analysis of Fig. 7 indicated that the fluid-saturated micropores mainly exhibit low flow velocities. However, as is evident from Fig. 6, microporosity occupies a large proportion of the total porosity in Estaillades rock (in Fig. 7 only parts of microporous regions were displayed for clearer visualization of velocity maps). In fact, microporosity can constitute more than half of the total rock porosity in the Estaillades formation (Gao et al. 2019; Tanino and Blunt 2012). To investigate the extent to which these fluid-saturated micropores, which occupy a significant portion of the total porosity, affect the global flow rate, quantitative analysis was performed on the MRI velocity map with velocities encoded in the superficial flow direction (z). For this analysis, the flow rate, \({Q}_{z}\), for each axial (xy) image slice was calculated by summing the porosity-weighted z-velocities of each voxel within a given slice and then multiplying by the cross-sectional area of a single voxel. This analysis was performed for three separate images, namely the total porosity image, the macroporosity image, and the microporosity image. To generate an accurate value of \({Q}_{z}\) for each image slice, the velocity map was first multiplied by two masks, which were generated by manual thresholding of the MRI intensity image (Fig. 6). The first mask, which is binary, is needed to null the background noise and to separate the macroporous regions and the microporous regions; in the context of this analysis, the macroporous regions are defined as the regions with large and medium-sized pores that are coloured in green in Fig. 6 (i.e. ~ the pores that can be captured by µCT, as shown in Fig. 7), but the microporous regions, in the context of this study, are defined as regions with pore sizes well below image resolution—these are coloured in blue in Fig. 6. A second mask, which is not binary, aims to capture the fluid content per voxel and is computed by averaging multiple binary masks between the two threshold values corresponding to approximately the noise ceiling and a fully saturated pore. This mask is required to account for the partial volume effects in the microporous regions and at the grain boundaries, in order to make an accurate estimate of the flow rate, \({Q}_{z}\); with proper masking, this flow rate should be the same for each image slice along the superficial flow direction. The plot of \({Q}_{z}\) as a function of the position of the image slices for the three different porosity images in the middle region of the rock is shown in Fig. 9. It can be seen that although most of the flow goes through macropores, the microporous regions also noticeably contribute to the total flow rate through the Estaillades plug. For example, for the region of the rock from ~ 0.5 to 1.3 mm along the z-direction, the macroporous and microporous regions have approximately the same contribution to the total flow rate through the rock. The average contribution of microporosity to flow rate in this region of the rock was estimated to be 36 ± 5% relative to the average total \({Q}_{z}\) (the uncertainty was estimated by varying the manual segmentation threshold value by ± 10% relative to the chosen threshold). Given the significant flow through the micropores in Estaillades rock, it is not perhaps surprising to observe some discrepancies between the MRI and LBM velocity fields, since the LBM simulations were run on the macropore network of Estaillades rock. Note that in the MRI velocity image of Ketton, the macropore network alone (as shown in Fig. 2) accounted for the total \({Q}_{z}\) in the rock, so the contribution of micropores to the flow is expected to be minor. These results are somewhat similar with the previous findings reported by Bijeljic et al. (Bijeljic et al. 2018) who, based on the methodology of direct flow simulations, mercury injection capillary pressure (MICP) porosimetry, and differential X-ray imaging (30% KI dopant solution was used), demonstrated that microporosity in Ketton and Estaillades rocks contribute approximately 17 and 39%, respectively, to the overall computed permeabilities. (The micropores were defined as the pores with sizes below the imaging resolution of 5 µm.) This simple analysis indicates that microporosity plays an important role in the fluid flow and transport processes in microporous carbonate rocks.
Calculated flow rate, \(Q_{z}\), for each image slice in the middle region of the Estaillades rock plug. The black, blue, and green lines represent the total porosity ( ), macroporosity (
), macroporosity ( ), and microporosity (
), and microporosity ( ) of the rock. The red dashed line (
) of the rock. The red dashed line ( ) represents the flow rate, which was imposed during MRI experiments, i.e. at \(Q_{z}\) = 0.03 ml min–1
) represents the flow rate, which was imposed during MRI experiments, i.e. at \(Q_{z}\) = 0.03 ml min–1
4 Conclusions
In this work, high-resolution MR flow velocity imaging at 35 µm spatial resolution has been used to provide a robust benchmark of single-phase LBM simulations in two carbonate rocks, namely Ketton and Estaillades limestone. In order to be able to qualitatively and quantitatively compare the simulated and experimental velocity data, the velocity maps were co-registered with the high-resolution µCT structural images of the same rock core plugs.
First, the results were demonstrated for the simplest of the two cases—Ketton limestone rock, which is a relatively homogeneous carbonate sample with large macropores. Inspection of the velocity maps indicated that the LBM simulation used was able to accurately predict the location of high-velocity flow channels and backflow, and, in general, also the magnitude of the velocities. Excellent agreement between the MRI and LBM data was observed in various plots which quantitatively compare the two datasets. It was also observed that the LBM tends to underpredict large flow velocities in some of the pores.
Second, the experimental and simulated velocity maps for the more heterogeneous Estaillades rock were presented and analysed. Estaillades is a heterogeneous carbonate rock with a more complex rock microstructure and smaller pores than Ketton rock, hence presented a more challenging case for simulation. Comparison of the 2D visualizations extracted from the 3D co-registered velocity and structural images revealed that the LBM can reproduce many complex flow patterns in the Estaillades formation. However, in some pores noticeable differences between the MRI and LBM velocity maps were observed, which was also reflected in a quantitative comparison between the two datasets. Furthermore, it was demonstrated that the flow in Estaillades rock is highly heterogeneous with approximately 80% of the flow (i.e. the fractional summed z-velocities within pores) being carried by just 10% of the macropores; in the Ketton core plug ≈ 50% of the flow was carried by the same percentage of the pores in the rock. Analysis of the MRI velocity map revealed that approximately one third of the total flow rate through the Estaillades formation is carried by microporosity.
Future work will extend the use of the MR velocity imaging and simulation techniques used in this work to benchmark multi-phase flow simulations in rocks.
Availability of Data and Material
Available upon request.
References
Alpak, F.O., Berg, S., Zacharoudiou, I.: Prediction of fluid topology and relative permeability in imbibition in sandstone rock by direct numerical simulation. Adv. Water Resour. 122, 49–59 (2018a). https://doi.org/10.1016/j.advwatres.2018.09.001
Alpak, F.O., Gray, F., Saxena, N., Dietderich, J., Hofmann, R., Berg, S.: A distributed parallel multiple-relaxation-time lattice Boltzmann method on general-purpose graphics processing units for the rapid and scalable computation of absolute permeability from high-resolution 3D micro-CT images. Comput. Geosci. 22, 815–832 (2018b). https://doi.org/10.1007/s10596-018-9727-7
Alpak, F.O., Zacharoudiou, I., Berg, S., Dietderich, J., Saxena, N.: Direct simulation of pore-scale two-phase visco-capillary flow on large digital rock images using a phase-field lattice Boltzmann method on general-purpose graphics processing units. Comput. Geosci. (2019). https://doi.org/10.1007/s10596-019-9818-0
Andrä, H., Combaret, N., Dvorkin, J., Glatt, E., Han, J., Kabel, M., Keehm, Y., Krzikalla, F., Lee, M., Madonna, C., Marsh, M., Mukerji, T., Saenger, E.H., Sain, R., Saxena, N., Ricker, S., Wiegmann, A., Zhan, X.: Digital rock physics benchmarks-part I: imaging and segmentation. Comput. Geosci. 50, 25–32 (2013a). https://doi.org/10.1016/j.cageo.2012.09.005
Andrä, H., Combaret, N., Dvorkin, J., Glatt, E., Han, J., Kabel, M., Keehm, Y., Krzikalla, F., Lee, M., Madonna, C., Marsh, M., Mukerji, T., Saenger, E.H., Sain, R., Saxena, N., Ricker, S., Wiegmann, A., Zhan, X.: Digital rock physics benchmarks-part II: computing effective properties. Comput. Geosci. 50, 33–43 (2013b). https://doi.org/10.1016/j.cageo.2012.09.008
Benning, M., Gladden, L.F., Holland, D.J., Schönlieb, C.-B., Valkonen, T.: Phase reconstruction from velocity-encoded MRI measurements—a survey of sparsity-promoting variational approaches. J. Magn. Reson. 238, 26–43 (2014). https://doi.org/10.1016/j.jmr.2013.10.003
Benzi, R., Succi, S., Vergassola, M.: The lattice Boltzmann equation: theory and applications. Phys. Rep. 222, 145–197 (1992). https://doi.org/10.1016/0370-1573(92)90090-M
Beucher, S., Meyer, F.: The morphological approach to segmentation: The watershed transformation. In: Dougherty, E.R. (ed.) Mathematical Morphology in Image Processing, pp. 433–481. Marcel Dekker Inc., New York (1993)
Bhatnagar, P.L., Gross, E.P., Krook, M.: A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94, 511–525 (1954). https://doi.org/10.1109/ITCC.2003.1197559
Bijeljic, B., Mostaghimi, P., Blunt, M.J.: Signature of non-Fickian solute transport in complex heterogeneous porous media. Phys. Rev. Lett. 107, 204502 (2011). https://doi.org/10.1103/PhysRevLett.107.204502
Bijeljic, B., Raeini, A., Mostaghimi, P., Blunt, M.J.: Predictions of non-Fickian solute transport in different classes of porous media using direct simulation on pore-scale images. Phys Rev. E Stat. Nonlin. Soft Matter Phys. 87, 1–9 (2013). https://doi.org/10.1103/PhysRevE.87.013011
Bijeljic, B., Raeini, A.Q., Lin, Q., Blunt, M.J.: Multimodal Functions as Flow Signatures in Complex Porous Media. arXiv Prepr. (2018)
Blunt, M.J.: Multiphase Flow in Permeable Media: A Pore-Scale Perspective. Cambridge University Press, Cambridge (2017)
Blunt, M.J., Bijeljic, B., Dong, H., Gharbi, O., Iglauer, S., Mostaghimi, P., Paluszny, A., Pentland, C.: Pore-scale imaging and modelling. Adv. Water Resour. 51, 197–216 (2013). https://doi.org/10.1016/j.advwatres.2012.03.003
Buades, A., Coll, B., Morel, J.-M.: A non-local algorithm for image denoising. 2005 IEEE Comput Soc. Conf. Comput. vis. Pattern Recognit. 2, 60–65 (2005). https://doi.org/10.1109/CVPR.2005.38
Callaghan, P.: Translational Dynamics and Magnetic Resonance: Principles of Pulsed Gradient Spin Echo NMR. OUP, Oxford (2011)
Chang, C.T.P., Watson, A.T.: NMR Imaging of Flow Velocity in Porous Media. AIChE J. 45, 437–444 (1999). https://doi.org/10.1002/aic.690450302
Chen, S., Doolen, G.D.: Lattice Boltzmann Method. Annu. Rev. Fluid Mech. 30, 329–364 (1998). https://doi.org/10.4249/scholarpedia.9507
Coles, M., Hazlett, R., Spanne, P., Soll, W., Muegge, E., Jones, K.: Pore Level Imaging of Fluid Transport Using Synchrotron X-ray Microtomography. J. Pet. Sci. Eng. 19, 55–63 (1998). https://doi.org/10.1016/S0920-4105(97)00035-1
de Kort, D.W., Hertel, S.A., Appel, M., de Jong, H., Mantle, M.D., Sederman, A.J., Gladden, L.F.: Under-sampling and compressed sensing of 3D spatially-resolved displacement propagators in porous media using APGSTE-RARE MRI. Magn. Reson. Imaging. 56, 24–31 (2019). https://doi.org/10.1016/j.mri.2018.08.014
de Kort, D.W., Reci, A., Ramskill, N.P., Appel, M., de Jong, H., Mantle, M.D., Sederman, A.J., Gladden, L.F.: Acquisition of spatially-resolved displacement propagators using compressed sensing APGSTE-RARE MRI. J. Magn. Reson. 295, 45–56 (2018). https://doi.org/10.1016/j.jmr.2018.07.012
D’Humières, D., Ginzburg, I., Krafcyzk, M., Lallemand, P., Luo, L.-S.: Multiple-relaxation-time lattice Boltzmann models in three dimensions. Philos. Trans. Roy. Soc. Lond. Ser. A 360, 437–451 (2002)
Duchon, C.E.: Lanczos filtering in one and two dimensions. J. Appl. Meteorol. 18, 1016–1022 (1979). https://doi.org/10.1175/1520-0450(1979)018%3c1016:LFIOAT%3e2.0.CO;2
Gao, Y., Qaseminejad Raeini, A., Blunt, M.J., Bijeljic, B.: Pore occupancy, relative permeability and flow intermittency measurements using X-ray micro-tomography in a complex carbonate. Adv. Water Resour. 129, 56–69 (2019). https://doi.org/10.1016/j.advwatres.2019.04.007
Gladden, L.F., Sederman, A.J.: Recent advances in Flow MRI. J. Magn. Reson. 229, 2–11 (2013). https://doi.org/10.1016/j.jmr.2012.11.022
Hardy, J., Pomeau, Y., de Pazzis, O.: Time evolution of a two-dimensional classical lattice system. Phys. Rev. Lett. 31, 276–279 (1973)
Huang, L., Mikolajczyk, G., Küstermann, E., Wilhelm, M., Odenbach, S., Dreher, W.: Adapted MR velocimetry of slow liquid flow in porous media. J. Magn. Reson. 276, 103–112 (2017). https://doi.org/10.1016/j.jmr.2017.01.017
Karlsons, K., de Kort, D.W., Sederman, A.J., Mantle, M.D., de Jong, H., Appel, M., Gladden, L.F.: Identification of sampling patterns for high-resolution compressed sensing MRI of porous materials: ‘Learning’ from X-ray micro-computed tomography data. J. Microsc. 276, 63–81 (2019). https://doi.org/10.1111/jmi.12837
Karlsons, K., de Kort, D.W., Sederman, A.J., Mantle, M.D., Freeman, J.J., Appel, M., Gladden, L.F., Characterizing pore-scale structure-flow correlations in sedimentary rocks using magnetic resonance imaging. Phys. Rev. E 103, 023104 (2021). https://doi.org/10.1103/PhysRevE.103.023104
Lebon, L., Leblond, J., Hulin, J.P.: Experimental measurement of dispersion processes at short times using a pulsed field gradient NMR technique. Phys. Fluids. 9, 481–490 (1997). https://doi.org/10.1063/1.869208
Lin, Q., Al-khulaifi, Y., Blunt, M.J., Bijeljic, B.: Quantification of sub-resolution porosity in carbonate rocks by applying high-salinity contrast brine using X-ray microtomography differential imaging. Adv. Water Resour. 96, 306–322 (2016). https://doi.org/10.1016/j.advwatres.2016.08.002
Lustig, M., Donoho, D., Pauly, J.M.: Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 58, 1182–1195 (2007). https://doi.org/10.1002/mrm.21391
Mantle, M.D., Sederman, A.J., Gladden, L.F.: Single-and two-phase flow in fixed-bed reactors: MRI flow visualisation and lattice-Boltzmann simulations. Chem. Eng. Sci. 56, 523–529 (2001). https://doi.org/10.1016/S0009-2509(00)00256-6
Manz, B., Gladden, L.F., Warren, P.B.: Flow and dispersion in porous media: lattice-Boltzmann and NMR studies. AIChE J. 45, 1845–1854 (1999). https://doi.org/10.1002/aic.690450902
Pluim, J.P.W., Maintz, J.B.A., Viergever, M.A.: Mutual-information-based registration of medical images: a survey. IEEE Trans. Med. Imaging 22, 986–1004 (2003)
Romanenko, K., Xiao, D., Balcom, B.J.: Velocity field measurements in sedimentary rock cores by magnetization prepared 3D SPRITE. J. Magn. Reson. 223, 120–128 (2012). https://doi.org/10.1016/j.jmr.2012.08.004
Saxena, N., Hofmann, R., Alpak, F.O., Berg, S., Dietderich, J., Agarwal, U., Tandon, K., Hunter, S., Freeman, J., Wilson, O.B.: References and benchmarks for pore-scale flow simulated using micro-CT images of porous media and digital rocks. Adv. Water Resour. 109, 211–235 (2017a). https://doi.org/10.1016/j.advwatres.2017.09.007
Saxena, N., Hofmann, R., Alpak, F.O., Dietderich, J., Hunter, S., Day-Stirrat, R.J.: Effect of image segmentation and voxel size on micro-CT computed effective transport and elastic properties. Mar. Petrol. Geol. 86, 972–990 (2017b). https://doi.org/10.1016/j.marpetgeo.2017.07.004
Saxena, N., Hows, A., Hofmann, R., Alpak, O.F., Freeman, J., Hunter, S., Appel, M.: Imaging and computational considerations for image computed permeability: Operating envelope of digital rock physics. Adv. Water Resour. 116, 127–144 (2018). https://doi.org/10.1016/j.advwatres.2018.04.001
Shah, S.M., Gray, F., Crawshaw, J.P., Boek, E.S.: Micro-computed tomography pore-scale study of flow in porous media: effect of voxel resolution. Adv. Water Resour. 95, 276–287 (2016). https://doi.org/10.1016/j.advwatres.2015.07.012
Shukla, M.N., Vallatos, A., Phoenix, V.R., Holmes, W.M.: Accurate phase-shift velocimetry in rock. J. Magn. Reson. 267, 43–53 (2016). https://doi.org/10.1016/j.jmr.2016.04.006
Soulaine, C., Gjetvaj, F., Garing, C., Roman, S., Russian, A., Gouze, P., Tchelepi, H.A.: The impact of sub-resolution porosity of X-ray microtomography images on the permeability. Transp. Porous Media. 113, 227–243 (2016). https://doi.org/10.1007/s11242-016-0690-2
Stejskal, J.J., Tanner, J.E., Spin diffusion measurements: Spin echoes in the presence of a time‐dependent field gradient. J. Chem. Phys. 42, 288 (1965). https://doi.org/10.1063/1.1695690
Studholme, C., Hill, D.L.G., Hawkes, D.J.: An overlap invariant entropy measure of 3D medical image alignment. Pattern Recognit. 32, 71–86 (1999)
Sullivan, S.P., Sederman, A.J., Johns, M.L., Gladden, L.F.: Verification of shear-thinning LB simulations in complex geometries. J. Non-Newtonian Fluid Mech. 143, 59–63 (2007). https://doi.org/10.1016/j.jnnfm.2006.12.008
Tang, C., Blatter, D.D., Parker, D.L.: Accuracy of phase-contrast flow measurements in the presence of partial-volume effects. J. Magn. Reson. Imaging. 3, 377–385 (1993). https://doi.org/10.1002/jmri.1880030213
Tanino, Y., Blunt, M.J.: Capillary trapping in sandstones and carbonates: Dependence on pore structure. Water Resour. Res. 48, 1–13 (2012). https://doi.org/10.1029/2011WR011712
Yang, X., Scheibe, T.D., Richmond, M.C., Perkins, W.A., Vogt, S.J., Codd, S.L., Seymour, J.D., McKinley, M.I.: Direct numerical simulation of pore-scale flow in a bead pack: Comparison with magnetic resonance imaging observations. Adv. Water Resour. 54, 228–241 (2013). https://doi.org/10.1016/j.advwatres.2013.01.009
Acknowledgements
We also wish to thank Dr Daniel Markl (Cambridge University) for assistance with µCT acquisitions of the Ketton sample and Ab Coorn (Shell) for coring the Ketton and Estaillades samples and for acquiring the µCT image of the Estaillades sample.
Funding
This work was funded by Royal Dutch Shell plc.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Karlsons, K., de Kort, D.W., Alpak, F.O. et al. Integrating Pore-Scale Flow MRI and X-ray μCT for Validation of Numerical Flow Simulations in Porous Sedimentary Rocks. Transp Porous Med 143, 373–396 (2022). https://doi.org/10.1007/s11242-022-01770-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-022-01770-y



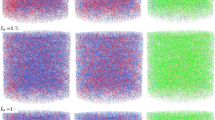




 ) and MRI velocity map (
) and MRI velocity map ( ) of Ketton rock. The velocity distribution of LBM convoluted with noise-related Gaussian distribution with standard deviation of 0.15 mm s–1 is also shown (
) of Ketton rock. The velocity distribution of LBM convoluted with noise-related Gaussian distribution with standard deviation of 0.15 mm s–1 is also shown ( )
)




