1 Introduction

Inertial forces and convective acceleration have a significant influence on the dissipation of mechanical energy in fluid flow regimes characterized by relatively high flow velocities. These forces induce nonlinear pressure responses that are not accounted for by the linear Darcy-equation (Darcy 1856). The second-order Forchheimer-equation is needed to explain these effects on the pressure gradient (Forchheimer 1901). Such flow conditions in porous media are relevant in many practical engineering problems. Particularly for the determination of the performance and the capacity of production wells and injection wells, i.e. in the petroleum industry (Huang and Ayoub 2008; Barree and Conway 2004), in groundwater wells utilized for domestic and irrigational purposes (Houben et al. 2018; Wen et al. 2011; van Lopik et al. 2019), and for groundwater heat pump applications (Gjengedal et al. 2021).

The inertial resistance factor β of the Forchheimer equation is a geometrical property that describes how the pore channel shape influence the nonlinear flow characteristics. It is challenging to determine this factor without performing field and laboratory tests. In-situ or experimental tests are therefore often routinely performed to determine well performances in the petroleum industry (Huang and Ayoub 2008). However, in many civil engineering projects there is limited time and funding available for detailed in-situ testing and laboratory tests, and many engineering projects therefore depend on empirical equations for prediction purposes. Most empirical equations used in soil engineering rely on soil characterization rather than on pore space characterization (van Lopik et al. 2019, 2017; Chapuis 2012). The Forchheimer equation is also frequently utilized in numerical modelling and computational fluid mechanics (Guo et al. 2019). Continuous use of these equations argues that further study on this topic is of scientific interest and is useful for many industries.

Convective acceleration occurs due to spatial variations of the flow channel geometry. This paper explores how geometrical properties of a pore channel induced convective acceleration and how this affects the inertial losses. Recent laboratory studies on 3D fabricated particle beds with predefined pore geometries enables more detailed and controlled analysis of the geometrical properties that are important for porous media flows (Huang, et al. 2013; Gjengedal et al. 2020). Gjengedal et al. (2020) has hypothesized that porous media flows exhibit similar behavioural traits to that of pipe flows in situations where the pipe channels are nonuniform, the so called minor losses approach in fluid mechanics. A method of comparison with the pipe flow equations is here presented, and the similarities between the porous media flows and pipe flows are further assessed.

2 Theory

The general Forchheimer equation corresponds to Eq. (1) for horizontally directed, one-phase, incompressible fluid flow in pore channels. Here the pressure dissipation ΔP (Pa) across the superficial length of the porous medium L (m) is proportional to a first-order viscous term and a second-order inertial term. The viscous resistance is proportional to the superficial velocity of the flow us (m/s), the viscosity of the fluid μ (Pa·s) and is inversely proportional to the permeability of the porous medium k (m2). The inertial resistance is proportional the inertial resistance factor β (m−1), the density ρ (kg/m3) of the fluid, and the superficial velocity squared. The superficial fluid velocity is here defined as the bulk fluid flow rate Q (m3/s) divided by the bulk cross-sectional area A (m2) of the porous media oriented perpendicular to the superficial flow direction.

$$\frac{\Delta P}{L} = \frac{\mu }{k} \cdot u_{s} + \beta \cdot \rho \cdot u_{s} \cdot \left| {u_{s} } \right| .$$
(1)

The permeability k and the inertial resistance factor β represent intrinsic geometrical properties that describe the size and shape of the porous media pore channels (Ruth and Ma 1992; Yazdchi and Luding 2012; Whitaker 1996; Gjengedal et al. 2020). These geometrical properties are typically represented by a diameter of the solids that surround the pores (Chukwudozie and Tyagi 2013; van Lopik et al. 2019). However, the permeability and the inertial resistance factor should be identified with respect to the shape and size of the pores within the pore matrix. A new semi-analytical approach is presented in detail by Gjengedal et al. (2020) and provides Eq. (2). This equation describes the fluid flow through a single pore in relation to the average flow velocity in the pore body region. The permeability and the inertial resistance factor are here represented by Eqs. (3) and (4), respectively.

$$\frac{\Delta P}{L} = \frac{{3 \cdot \pi \cdot \tau^{2} \cdot S^{2} }}{{k_{0} \cdot n^{3} }}\mu \cdot u_{s} + \frac{{C_{d} \cdot \tau^{3} \cdot S}}{{k_{0}^{2} \cdot n^{3} }} \cdot \rho \cdot u_{s}^{2} .$$
(2)
$$k = \frac{{k_{0} \cdot n^{3} }}{{3 \cdot \pi \cdot \tau^{2} \cdot S^{2} }} .$$
(3)
$$\beta = \frac{{C_{d} \cdot \tau^{3} \cdot S}}{{k_{0}^{2} \cdot n^{3} }} .$$
(4)

The geometry of the pore is described by the porosity n (m3/m3), the specific surface of the pore S (m2/m3), the tortuosity factor τ (-), and the pore body shape factor k0 (-). The dissipation coefficient Cd is not yet clearly defined in the porous media literature. It is suggested that the Cd depends on the constriction ratio and the streamlining shape of the pore channel, like the "minor loss" coefficient in the literature of fluid mechanics of pipes, Fig. 1 (Gjengedal et al. 2020).

Fig. 1
figure 1

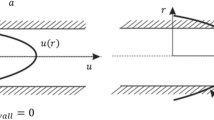
Flow obstructions: A A constricting pipe segment induce a "minor loss" effect in a pipe. B The same phenomenon occurs in porous media flows where the narrowing of the pore throat induces convective acceleration in the flow (Gjengedal et al. 2020)

Full size image

The concept of minor losses in pipes is an experimentally developed approach for determining the hydraulic loss contribution of various pipe components that have an obstructive effect on the flow, such as pipe bends, diffusers and flow controlling valves. These head loss components are termed "minor" because, in typical piping systems with long sections of pipes, they occur relatively infrequent in the pipeline and these losses are consequently minor compared to the head losses induced by the long straight pipe section itself (consequently the "major" losses). However, in piping systems with numerous turns, bends and valves over short distances, the minor losses can be far greater than the major losses. The corresponding equation for pipes is that of Eq. (5) (Çengel and Cimbala 2010).

$$h_{L} = \left( {f \cdot \frac{L}{D} + \sum K_{L} } \right) \cdot \frac{{V_{s}^{2} }}{2 \cdot g} .$$
(5)

The total losses of hydraulic head hL (m) through a pipe segment of length L (m), and diameter D (m) is a sum of two terms that are proportional to the average velocity squared Vs (m/s) and inversely proportional to the acceleration due to gravity g (m/s2). The liner term, represented by the Darcy-Weisbach friction factor component f, corresponds to the viscous friction in straight and uniform pipe channels. The second-order term, represented by the loss coefficient KL, express the minor losses of each individual obstructive component in the piping layout. The sum of these coefficients account for the total inertial losses that are induced by convective acceleration through the entire pipeline. An obstruction in the flow path of the fluid might e.g. be the contraction and expansion of the pipe channel geometry seen in Fig. 1.

Pipe manufacturers readily provide experimental data for the KL of various pipe components. The KL of a single pipe component is calculated from experimental data via Eq. (6) (Crane Company, 2009).

$$K_{L} = f_{T} \cdot \frac{L}{D}$$
(6)

The loss coefficient is treated as a product of an inertial resistance factor fT times the ratio of the length of the pipe segment L and the diameter D of the chosen representative pipe size within this segment. The smaller pipe size is typically selected as the reference size and the average flow velocity Vs in Eq. (5) is based on the flow velocity in the smaller pipe segment. The letter "T" infers that the inertial resistance factor fT represents turbulent flow conditions. Including Eq. (6) into Eq. (5) produces Eq. (7) with the addition of the Darcy-Weisbach friction factor for circular pipes (f = 64/Re). The hydraulic head is now represented in terms of the corresponding pressure differential ∆P (Pa), instead of heads.

$$\Delta P = \frac{64}{{{\text{Re}}}} \cdot \frac{L}{D} \cdot \frac{{\rho \cdot V_{s}^{2} }}{2} + f_{T} \cdot \frac{L}{D} \cdot \frac{{\rho \cdot V_{s}^{2} }}{2} .$$
(7)

The Reynolds number (Re) for pipe flow in Eq. (8) relate to the pipe diameter D (m), which is the scientific convention in pipe flow engineering problems.

$${\text{Re}} = \frac{{\rho \cdot V_{s} \cdot D}}{\mu } .$$
(8)

Equation (9) shows the pipe flow equation with the Reynolds number fully expressed. The linear term is now the famous Hagen–Poiseuille equation for circular pipes with a uniform circular pipe diameter.

$$\Delta P = \frac{32}{{D^{2} }} \cdot \mu \cdot V_{s} \cdot L + \frac{{f_{T} }}{D \cdot 2} \cdot L \cdot \rho \cdot V_{s}^{2} .$$
(9)

However, if a pipe has a nonuniform and non-circular geometry the characteristic shape of the pipe is not related to the diameter of the pipe alone. Therefore, to evaluate nonuniform pipe channels, the fundamental characteristic shape definition must be applied instead (Schiller 1923), corresponding to Eq. (10).

$$m_{{{\text{pipe}}}} = \frac{{{\text{volume}}\,{\text{of}}\,{\text{pipe}}}}{{{\text{surface}}\,{\text{area}}\,{\text{in}}\,{\text{pipe}}}} = \frac{{n_{{{\text{pipe}}}} }}{{S_{{{\text{pipe}}}} }} = \frac{{\pi \cdot \frac{{D^{2} }}{4} \cdot L}}{\pi \cdot D \cdot L} = \frac{D}{4} .$$
(10)

This necessitates a correction to the conventional loss coefficient KL of Eq. (6). It is evident from Eq. (10) that to utilize the pipe diameter D as the characteristic length unit must produce a loss coefficient four times greater than would otherwise occur should the mpipe unit be applied instead. This numerical difference is not obvious because it is imbedded in the experimentally derived KL value. The corrected pipe flow equation therefore becomes Eq. (11), where the characteristic length unit mpipe describes the shape of the pipe channel along the pipe length L.

$$\frac{\Delta P}{L} = \frac{2}{{m_{{{\text{pipe}}}}^{2} }} \cdot \mu \cdot V_{s} + \frac{{f_{T} }}{8} \cdot \frac{1}{{m_{{{\text{pipe}}}} }} \cdot \rho \cdot V_{s}^{2} .$$
(11)

Equation (2) for porous media and Eq. (11) for pipes display apparent similarities now that they are expressed in terms of a single pore channel and pipe channel. However, a direct comparison of Eqs. (2) and (11) necessitates that these two equations are organized in the same manner, where the fluid flow is evaluated from the same point of reference within the flow field in the pore channel and pipe channel.

Equation (2) must also be expressed by the characteristic length unit m in the most fundamental form through Eq. (12), and the average flow velocity must be expressing by Eq. (13). The letter "l" specifies that the average velocity Vl (m/s) is the velocity of the flow with respect to the "larger" channel opening within the pore, corresponding to the pore body region of the pore. This provides Eq. (14), which is more fitting for the problem at hand.

$$m = \frac{{{\text{porosity}}\,{\text{of}}\,{\text{the}}\,{\text{pore}}\,{\text{unit}}\,{\text{volume}}}}{{{\text{spesific}}\,{\text{surface}}\,{\text{of}}\,{\text{the}}\,{\text{pore}}\,{\text{unit}}\,{\text{volume}}}} = \frac{n}{S} .$$
(12)
$$V_{l} = \frac{\tau }{{k_{0} \cdot n}} \cdot u_{s} .$$
(13)
$$\frac{\Delta P}{L} = \frac{3 \cdot \pi \cdot \tau }{{m^{2} }} \cdot \mu \cdot V_{l} + C_{d} \cdot \frac{\tau }{m} \cdot \rho \cdot V_{l}^{2} .$$
(14)

The resemblance of the second-order terms of Eqs. (11) and (14) is now apparent. The comparison is particularly fitting in the special case with the tortuosity of the pore equal to unity (τ = 1.0). However, a direct comparison requires that a correction must be performed, to either one of Eq. (11) or Eq. (14), since the reference velocity for both equations is not yet the same. The reference velocity (Vs) in piping system is based on the velocity of the smaller pipe segment, while the reference velocity (Vl) in the pore channel is based on the fluid velocity in the pore body region of the pore. Gjengedal et al. (2020) therefore suggested that a correction should be performed on Eq. (14) for the inertial term according to Eq. (15), where the cross-sectional area ratio a (-) is applied in compliance with the conventions in fluid mechanics of pipes (Crane Company 2009; Idelchik 1994). The comparable porous media equation is therefore Eq. (16).

$$C_{d} = \frac{{C_{{K_{L} }} }}{{a^{2} }} , \quad {\text{where}}\quad a = \frac{{A_{{{\text{small}}}} }}{{A_{{{\text{large}}}} }} .$$
(15)
$$\frac{\Delta P}{L} = \frac{3 \cdot \pi \cdot \tau }{{m^{2} }} \cdot \mu \cdot V_{l} + C_{{K_{L} }} \cdot \frac{\tau }{m} \cdot \rho \cdot V_{s}^{2} .$$
(16)

The dissipation coefficient CKL of porous media is deemed similar to the inertial resistance factor fT for pipes and should therefore display similar behavioural traits with respect to the constriction ratio and the streamlining shape of the flow channel. Both factors should also display similar traits with respect to the flow characteristics that dominate in laminar and turbulent flow conditions. It is known that the minor loss coefficients of pipes display an increased numerical value in laminar fL flow conditions versus turbulent fT flow conditions, fL > fT (Idelchik 1994; Çengel and Cimbala 2010). The flow characteristics in Forchheimer flow is laminar, and it is therefore the laminar inertial resistance factor (fL) that should be similar to the dissipation coefficient CKL.

The suggested analogy for convective acceleration in porous media flows and laminar flow in nonuniform pipes can be verified through evaluating the legitimacy of Eq. (17) with published experimental data.

$$C_{K_{L} } = \frac{K_{L - {\text{laminar}} }}{2} \cdot \frac{m_{\text{pipe}} }{L}$$
(17)

3 Method

A comparison is performed on known CKL and fL coefficients derived from experimental data found in the literature. Two independent experimental works on different 3D fabricated porous media provide the CKL data (Huang et al. 2013; Gjengedal et al. 2020). These porous media were constructed by stacking spherical and octahedra particles in the predefined packing configurations shown in Fig. 2. These packing arrangements produce a pore in between the solids that correspond to the shape of the pores shown in Fig. 3. In the experiments of Huang et al. (2013) the spherical balls in the Samples T1–T4 were fabricated by gluing acrylic ball together in cubic containers. These balls were smooth, and the corresponding pore geometries in their experiments have a similar shape as shown in Fig. 3.

Fig. 2
figure 2

Ideal sketch of the 3D porous media testes by Huang et al. (2013) and Gjengedal et al. (2020). Huang et al. (2013) tested the cubical packing of spheres of T1 = 3.0 mm, T2 = 5.0 mm, T3 = 8.0 mm, and T4 = 10 mm diameters. Gjengedal et al. (2020) tested the cubic packing of spheres A3 = 1.0 mm diameter. And octahedrons of 1 mm diameter (B3, B6 and D) and octahedrons of 0.5 mm diameter (C1). Sketch is modified after Gjengedal et al. (2020)

Full size image
Fig. 3
figure 3

The sketch of the corresponding ideal pore shape and relative pore size of the porous media geometries in Fig. 2. The pore throat cross section is highlight in red. Sketch is modified after Gjengedal et al. (2020)

Full size image

Unlike the smooth acryl balls T1–T4, the Sample A–D particles of Gjengedal et al. (2020) are very rough due to the 3D printing technology employed in the fabrication. This caused the actual shape of the pores to be slightly different than the ideal and smooth configurations seen in Fig. 3. The rough samples have lower porosities, larger degree of contraction, and rougher surfaces than shown in the ideal sketches in Fig. 2. The estimated geometrical properties and the measured geometrical properties are reproduced in Table 1 for comparison, along with the calculated dissipation coefficient.

Table 1 The measured geometrical properties of the 3D porous media A3, B3, B6, C1, and D3 of Gjengedal et al. (2020) and the estimated geometrical properties of the 3D porous media T1, T2, T3, and T4 of Huang et al. (2013)
Full size table

The spherical particle configuration has the most severe constriction ratio of all the packing configurations. It is assumed that the smooth acrylic balls T1–T4 have the same area ratio as the ideal, a = 0.215, while the A3 sample has a much more severe constriction ratio of a = 0.128, due to the rough particle surface. Still, the A3 pore channel has a similar curved pore shape to that of T1–T4. Curved and rounded channels tend to reduce the "minor losses" observed in pipe flow experiments (Idelchik 1994; Crane Company 2009; Çengel and Cimbala 2010). This geometrical trait is reflected in the dissipation coefficient, which is lowest for the spherical samples A3 CKL ≈ 0.03 and T1–T4 CKL ≈ 0.033–0,048. Note that the T1–T4 and A3 samples have similar numerical CKL values, regardless of the particle roughness.

It is conventional in pipe flow experiments it to assign an angle of approach θ that describes the rate with which the contracting geometry changes towards the narrowest section of the flow channel (Crane Company 2009; Gibson 1910; Gibson 1911–1913). For these 3D geometries the narrowing does not occur evenly along the pore channels, and there will not be a single angle of approach that uniquely describes the rate of contraction. However, an apparent angle of approach θ* can be assigned based on the uniform angle that would result from an inscribed circle within the pore throat cross section and the pore body cross section. This angle allows for an intuitive comparison between the 3D sample types. The apparent angle of approach for A3 is approximately θ* ≈ 82° and for the T1–T4 samples the θ* ≈ 75°.

The octahedron Samples B, C and D are also fabricated with a rough surface and the actual shape of the pores are slightly different than the ideal and smooth configurations in Fig. 3. The ideal configuration of the B and C samples should produce the same area ratio of a = 0.500 regardless of the particle size. However, the C1 sample is relatively rougher than the B and D samples, which produce a more severe constriction ratio a = 0.290 than the B3 and B6 samples a ≈ 0.42. Consequently, the apparent angle of approach is more abrupt for the C1 θ* ≈ 71° than for B3 and B6 θ* ≈ 61°. A slightly higher dissipation coefficient of C1 CKL = 0.11 than the B3 and B6 samples CKL = 0.09 also arise.

The D3 sample has the least constricting area ratio a = 0.640 and the least abrupt apparent angle of approach θ* ≈ 38°. Yet, the channel pathway of sample D3 is offset by an interfixed octahedron particle and the pores have a tortuosity of τ = 1.2247. An alteration of the predominant flow direction tends to increase the "minor losses" observed in pipe flow experiments (Idelchik 1994; Crane Company 2009; Çengel and Cimbala 2010). Gjengedal et al. (2020) suggest that this trait is reflected in the D3 sample having the largest CKL = 0.13.

For comparison with pipe flow equations it is necessary to evaluate a pipe geometry that has similar geometric qualities to these pores. This is a pipe with a constricting segment along the flow channel and must consist of a contracting part and an expanding part, like the symmetrical half-cone pipe shown in Fig. 1A. Crane Company (2009) and Rennels and Hudson (2012) have summarized experimental data for the loss coefficients of such half-coned pipe segments and provide semi-empirical equations. The area ratio a and the angle of approach θ determine the shape and length of the pipe channel. The minor loss coefficients of pipes can be determined via Eq. (18–22). The minor losses depend on the flow direction through the half-cone, where Eq. (18–20) apply for the expanding cone segment (Rennels and Hudson 2012; Crane Company 2009).

$$\begin{array}{*{20}l} {K_{{L - {\text{exp}}}} = \alpha_{T} \cdot \left( {1 - \sqrt a^{2} } \right)^{2} ,} & {\begin{array}{*{20}l} {{\text{for}}} \\ {60^\circ < \theta < 180^\circ } \\ {0 < a < 1} \\ \end{array} } \\ \end{array}$$
(18)
$$\begin{array}{*{20}l} {K_{{L - {\text{exp}}}} = \alpha_{T} \cdot \left[ {1.366 \cdot {\text{sin}}\left\{ {\frac{{2\pi \left( {\theta - 15^\circ } \right)}}{180}} \right\}^{0.5} - 0.170 - 3.28 \cdot \left\{ {0.0625 - a^{4} } \right\}\sqrt {\frac{\theta - 20^\circ }{{40^\circ }}} } \right] \cdot \left( {1 - \sqrt a^{2} } \right)^{2} ,} & {\begin{array}{*{20}l} {{\text{for}}} \\ {20^\circ < \theta < 60^\circ } \\ {0 < a < 0.25} \\ \end{array} } \\ \end{array}$$
(19a)
$$\begin{array}{*{20}l} {K_{{L - {\text{exp}}}} = \alpha_{T} \cdot \left[ {1.366 \cdot {\text{sin}}\left\{ {\frac{{2\pi \left( {\theta - 15^\circ } \right)}}{180}} \right\}^{0.5} - 0.17} \right] \cdot \left( {1 - \sqrt a^{2} } \right)^{2} ,} & {\begin{array}{*{20}l} {{\text{for}}} \\ {20^\circ < \theta < 60^\circ } \\ {0.25 < a < 1} \\ \end{array} } \\ \end{array}$$
(19b)
$$K_{{L - {\text{exp}}}} = \alpha_{T} \cdot 8.3 \cdot \left( {{\text{tan}}\frac{\theta }{2}} \right)^{1,75} \cdot \left( {1 - \sqrt a^{2} } \right)^{2} ,\quad {\text{for}}\,0^\circ < \theta < 20^\circ \,0 < a < 1$$
(20)

Note that the equations are rendered in terms of the standardized area ratio a, while most pipe literature present these equations in terms of pipe diameter ratio, corresponding to the root of the standardized area ratio. Equation (21–22) apply for the contracting cone segment (Rennels and Hudson 2012).

$$\begin{array}{*{20}c} {K_{{L - {\text{con}}}} = \alpha_{T} \cdot 0.0696 \cdot {\text{sin}}\left( {\frac{\theta }{2}} \right) \cdot \left( {1 - \sqrt a^{5} } \right) \cdot \lambda^{2} + \left( {\lambda - 1} \right)^{2} ,} & {\begin{array}{*{20}c} {0^\circ < \theta^\circ < 180^\circ } \\ {0 < a < 1} \\ \end{array} } \\ \end{array}$$
(21)

where

$$\lambda = 1 + 0.622 \cdot \left( {\frac{\theta }{180}} \right)^{\frac{4}{5}} \cdot \left( {1 - 0.215 \cdot \sqrt a^{2} - 0.785 \cdot \sqrt a^{5} } \right)$$
(22)

The minor loss coefficients of Eqs. (18–22) are typically determined in fully developed turbulent flow conditions, where the inertial friction factor (fT) is independent of the Reynolds number and where the viscous contribution to the dissipation is negligible. However, in laminar flow conditions the minor loss coefficients show an increased numerical value (Idelchik 1994). A correction of the minor loss coefficient is typically applied by introducing the coefficient αL,T (-), which is close to unity for fully turbulent flow (αT ≈ 1.05) but is two for fully developed laminar flows (αL ≈ 2.0) (Çengel and Cimbala 2010). This phenomenon also occurs in porous media when the onset of turbulence is observed in experimental data. The data typically display a reduction in β of the Forchheimer equation as the flow velocity increases beyond the Forchheimer flow regime (Barree and Conway 2004; Fand et al. 1987; Skjetne and Auriault 1999).

Equations (18–20) are plotted in Fig. 4 and Eq. (21) in Fig. 5 and show the trends of the minor loss coefficients KL with respect to the contraction ratio and the angle of approach. The contraction losses and the expansion losses increase when the θ increase and when the a becomes progressively more constricting. The expansion losses are typically larger than the contraction losses for the same geometrical shape but are of similar magnitude for a0,5 > 0.60. This demonstrate that the direction of flow through a constricting pipe segment has an influence on the induced convective acceleration.

Fig. 4
figure 4

Minor loss coefficients for fluid flows in turbulent flow conditions (αT = 1.05) due to gradual and sudden expansion of a pipe. The values are calculated from Eq. (18–20). The data approximately compress into a single line for angles larger than 45° and larger angles are therefore not shown

Full size image
Fig. 5
figure 5

Minor loss coefficients for fluid flows in turbulent flow conditions (αT = 1.05) due to gradual contraction of a pipe. The values are calculated from Eq. (21)

Full size image

Equations (18–21) are used to calculate the corresponding dissipation coefficient CKL and the inertial resistance factor fL for these pipe geometries. The geometrical properties of a half-coned pipe segment: the pipe channel length Lpipe, the pipe channel volume npipe and the pipe channel internal surface area Spipe can be expressed by the diameter size of either one of the pipe entrances. The larger pipe size is here selected as the reference size (Alarge in Fig. 1) and calculated via Eq. (23, 24, and 25).

$$L_{{{\text{pipe}}}} = \frac{{\left( {D_{{{\text{large}}}} - a \cdot D_{{{\text{large}}}} } \right)}}{{2 \cdot {\text{tan}}\frac{\theta }{2}}} .$$
(23)
$$n_{{{\text{pipe}}}} = \left( {\left( {\frac{{D_{{{\text{large}}}} }}{2}} \right)^{2} + \frac{{D_{{{\text{large}}}} }}{2} \cdot \frac{{a \cdot D_{{{\text{large}}}} }}{2} + \left( {\frac{{a \cdot D_{{{\text{large}}}} }}{2}} \right)^{2} } \right) \cdot \frac{{\pi \cdot L_{{{\text{pipe}}}} }}{3} .$$
(24)
$$S_{{{\text{pipe}}}} = \frac{{\left( {D_{{{\text{large}}}} + a \cdot D_{{{\text{large}}}} } \right) \cdot \pi \cdot L_{{{\text{pipe}}}} }}{{2 \cdot {\text{cos}}\frac{\theta }{2}}} .$$
(25)

The numerical value of the pipe size Dlarge does not affect the outcome of the calculations, because the ratio of m/L in Eq. (17) render the outcome independent of the pipe size. The only geometrical variables that affect the outcome of Eq. (17) is the area ratio a and the angle of approach θ, which demonstrate that the inertial friction factors fL and fT are a function of the shape of the flow channel, but not the size of the flow channel.

If the contracting segment and the expanding segment of the pipe are not symmetrical the length units, L and m, must be calculated separately for both the contraction and the expansion segment of the channel. However, for a symmetrical half-cone pipe the angle of approach θ is equal in both segments. The comparable pipe flow expression then becomes the sum of the contraction loss and the expansion loss of the pipe, shown in Eq. (26).

$$C_{K_{L - {\text{pipe}}}} = \frac{{\alpha_{L} \cdot n_{\text{pipe}} }}{{S_{\text{pipe}} \cdot L_{\text{pipe}} \cdot 2}} \cdot \left( {K_{L - {\text{exp}}} + K_{L - {\text{con}}} } \right) $$
(26)

This equation is utilized to determine the pipe dissipation coefficients (CKL-pipe) for comparison with the porous media data.

4 Results

The CKL-exp due to expansion of a pipe is presented in Fig. 6 for the range of area ratios 0.01 < a < 0.98 and the range of angle of approaches 0° < θ < 170°. The figure demonstrates that a large angle of approach induces larger dissipation coefficients than smaller angles, in good agreement with the general behaviour of the minor loss coefficient (KL-exp). However, unlike the KL-exp data that plot almost equally for all angles above 45°, the CKL-exp provide individual curves for each individual angle of approach.

Fig. 6
figure 6

Dissipation coefficients CKL-exp due to gradual and sudden expansion of a half-cone pipe for laminar flow conditions (αL = 2.0). The values are obtained with the smaller flow channel as the reference velocity Vs. The data are calculated from the CKL-exp part of Eq. (26)

Full size image

The CKL-exp does not depend on the area ratio a in the same manner to that of KL-exp in Fig. 4. The CKL-exp display a peak value within the 0.2 < a < 0.3 range (slightly dependent on the angle of approach). When the area ratio approaches zero the dissipation coefficients trends towards a unique value depending on the angle of approach. On the other hand, the CKL-exp drops sharply towards zero when the area ratio increases and approach unity. In the special case with a = 1.0 the CKL-exp reaches a critical point and becomes zero. This demonstrate that the CKL-exp will always affect the fluid flow through the channel except when a = 1.0 and there is no change in the flow channel geometry.

The CKL-con due to contraction of a pipe is presented in Fig. 7 for the range 0.01 < a < 0.98 and the range of angle of approaches 0° < θ < 170°. The figure demonstrates that larger angles of approach induce larger dissipation coefficients than smaller angles, which is in good agreement with the minor loss coefficient KL-con. However, opposite to the KL-con data that have largest values at small area ratios, the CKL-con display a reversed trend where the peak values occur for relatively small constricting area ratios (0.6 < a < 0.7).

Fig. 7
figure 7

Dissipation coefficients CKL-con due to gradual and sudden contraction of a half-cone pipe for laminar flow conditions (αL = 2.0). The values are obtained with the smaller flow channel as the reference velocity Vs. The data are calculated from Eq. (26)

Full size image

The dissipation coefficients for the symmetrical half-cone pipe geometry are obtained by combining the data of Figs. 6 and 7. This is presented in Fig. 8, in addition to the dissipation coefficients of the T1, T2, T3, T4, A3, B3, B6, C1 and D3 samples. The combined effect of the CKL-exp data and the CKL-con data, produce a "bell-shaped" curve. Figure 8 demonstrates that a contracting and expanding pipe segment can obtain dissipation coefficients as high as CKL ≈ 0.2. The porous media dissipation coefficients plot within the same region as those of the calculated pipe data.

Fig. 8
figure 8

Dissipation coefficients CKL for symmetrically constricting half-cone pipe channels and dissipation coefficients of porous media samples T3, T4, A3, B3, B6, C1 and D3 in laminar flow conditions (αL = 2.0). The values are obtained with the smaller flow channel as the reference velocity Vs. The pipe values are calculated from Eq. (26)

Full size image

However, the porous media data plot differently than what the apparent angle of approach (θ*) would suggest. The CKL of T1, T2, T3, T4 with θ* ≈ 75°and A3 sample with θ* ≈ 82° is here shown to plot equal to a comparable pipe segment with θ° = 30–40°, arguably much lower than what would be expected. The opposite is observed for the octahedron samples C1, B3, and B6 whom all show higher CKL values than for comparable angle of approaches in pipes θ° = 85–95°. The differences are particularly profound for the D3 sample with θ* ≈ 38°, where the CKL is shown to plot equal to a pipe segment with θ° = 125°. The larger CKL value of C1 than for B3 and B6 is consistent with C1 (θ* ≈ 71°) having a more abrupt constriction ratio than the other two (θ* ≈ 61°). The same phenomenon occurs for the pipe data where larger θ° consistently produce larger CKL values for the same area ratio.

The data in Figs. 6, 7 and 8 are calculated with the smaller channel velocity Vs as the reference velocity. This point of reference visualizes how the angle of approach affect the CKL, more so than the area ratio. The data of Fig. 8 demonstrate this particularly well for very small angles of approach, e.g. θ° = 10°, which shows that the dissipation coefficient will be very small, e.g. CKL ≤ 0.001, regardless of the area ratio a.

The larger channel velocity Vl provides another point of reference that, in contrast to the Vs, visualize more clearly how the area ratio affect the magnitude of dissipation. The corresponding dissipation coefficient Cd calculated from Eqs. (17) and (26) for the symmetrically half-cone pipe segments is presented in Fig. 9 along with the corresponding porous media data.

Fig. 9
figure 9

Dissipation coefficients Cd for symmetrically constricting pipe channels and dissipation coefficients of porous media samples T1, T2, T3, T4, A3, B3, B6, C1, and D3 in laminar flow conditions (αL = 2.0). The values are obtained with the larger flow channel as the reference velocity Vl. The pipe data are calculated from Eq. 17 and Eq. (26) divided by the area ratio squared (a2)

Full size image

It is evident that the Cd values are much larger than the corresponding CKL values and Fig. 9 demonstrates more clearly how the constricting area ratio a influences the flow characteristics. For instance, even for very small angles of approach, e.g. 10°, Fig. 9 shows that the Cd will have a significant influence on the convective acceleration term if the area ratio is small enough, e.g. when a < 0.1. This is not as clear in the CKL data in Fig. 8 where the corresponding CKL values are very small. This effect is reflected in the porous media data, where the A3 sample now has the largest Cd and the D3 sample has the lowest Cd of all the samples, in good agreement with the data response of the experimental flow tests of Gjengedal et al. (2020) and Huang et al. (2013).

5 Discussion

The presented work compares pipe flow equations and porous media flow equations. It is demonstrated that the influence of convective acceleration in pipe channels and pore channels are comparable if their geometrical aspects are described precisely in the same manner, and from the same point of reference with regards to the fluid velocity in the channels. A contracting and expanding pipe segments obtain dissipation coefficients that plot within the same region as dissipation coefficients obtained from similar contracting and expanding porous media geometries. This is logical because both approaches deal with the same geometrical aspects, namely the expansion and contraction of a flow channel.

The comparison of the pipe flow data and the porous media data reveals some important geometrical characteristics and their influence on convective acceleration. From Fig. 8 it is shown that the dissipation coefficient CKL is only zero in the special case of a uniform flow channel geometry, when a = 1.0. This infers that the convective acceleration term can be ignored when the pore or pipe geometry is equal to a straight and uniform flow channel but must be accounted for in all other geometrical cases. For all other geometrical cases it can be expected that many relevant pore channel geometries in natural porous media will obtain dissipation coefficients lower than CKL < 0.2, as is observed for these pipe geometries in Fig. 8.

The rate of change in the geometry along the channel length governs the magnitude of convective acceleration that develops in the flow. The rate of change is here expressed as a function of the angle of approach θ and the area ratio a of the flow channel. The pipe data and the porous media data in Figs. 8 and 9 show dissipation coefficients CKL and Cd that have similar numerical values and trends with respect to the angle of approach θ and the area ratio a of the pipe flow channels. An abrupt constriction in pipes, with a large angle of approach θ induce more convective acceleration than does a gradual constriction where the angle of approach θ is small. The same trend occurs in the porous media data and can be observed by comparing the CKL data of C1 θ* ≈ 71° versus B3 and B6 θ* ≈ 61°. This is reasonable because the rate of change in the geometry will then be greater over shorter distances.

The T1–T4 and A3 samples achieve lower CKL values than the apparent angle of approach θ* would suggest when compared to the pipe CKL data. The opposite is seen in the C1, B3 and B6 samples with relatively higher CKL value than the pipe data. This indicate that the rounding of the channel geometry play an important role in reducing the numerical values of the CKL coefficient. These observations are in good agreement with the observed trends in other pipe flow experiments (Idelchik 1994; Crane Company 2009; Çengel and Cimbala 2010; Rennels and Hudson 2012). This implies that an abrupt and sharp change in the flow cross-sectional area induce more convective acceleration, than does a rounded and gradual change in the flow channel. This is a logical response because the rate of change in the geometry is greater over shorter distances for abrupt and sharp corners.

From Fig. 8 it can be expected that the most relevant straight, nonuniform flow channel geometries in natural porous media will obtain dissipation coefficients within the range 0 < CKL < 0.2. However, the influence of pore tortuosity is not directly accounted for in this study because the presented pipe data apply to straight pipes only. It is recognized from pipe flow experiments that an alteration of the predominant flow direction tends to increase the "minor losses" in pipe bends, even without contraction or expansion of the pipe channel (Crane Company 2009; Çengel and Cimbala 2010; Idelchik 1994). By comparing the D3 data with the pipe data in Fig. 8 it is evident that the CKL value of D3 is higher than the CKL of straight pipes with a similar angle of approach. The D3 angle θ* ≈ 38° is here shown to plot equal to a pipe segment with θ = 125°. This suggests that the induced convective acceleration in D3 originate from other sources than the contraction and expansion of the flow channel alone, and one such source might be the influence of the tortuosity. Further studies should evaluate this phenomenon by including a comparison with pipe bend data so that the influence of the tortuosity on the CKL can be accounted for.

An interesting characteristic can be observed in Eq. 26 with regards to the role of symmetry. If the pore channel is symmetrical the sum of the dissipation coefficients from the expanding and contracting segments will be independent of the direction of flow. However, if the pore channel is asymmetrical on either side of the obstruction, the sum of the dissipation coefficients will depend on the direction of flow because the sum of the two terms might be directionally dependant. This is shown in Eq. 26 where, for an asymmetrical pore channel, the length units L and m must be calculated separately for both the contraction and the expansion segment of the channel, which in turn will have different values of KL-exp and KL-con depending on the direction of flow. The resulting over-all effect on the dissipation coefficient CKL and Cd will thus be larger in one flow direction than in the other flow direction through the pore.

Naturally occurring pores are rarely symmetrical, e.g. since the pore geometry in soils is determined by the packing of irregular particle grains. The role of symmetry therefore has practical relevance in many engineering problems that deal with non-Darcy flow conductions, particularly with regards to well performance testing of pumping wells and injection wells. One relevant example is the Aquifer Thermal Energy Storage (ATES) system where a groundwater well can be used for both groundwater production and groundwater injection (Abuasbeh and Acuna 2018). If an ATES well is operated under non-Darcy flow conditions, it might have a different hydraulic capacity depending on the direction of flow, e.g. into or out from the well, and it is thus not necessarily reasonable to assign the same well capacity in pumping mode as in injection mode. Similarly, conducting a pumping test in a well is not necessarily the appropriate testing method for evaluating its injection capacity. This might play a role e.g. when old oil wells, originally used for oil production, will be used as CO2 injection wells in the future.

It is a scientific challenge to determine the shape of the pore channel in naturally occurring porous media. This requires extensive laboratory work, especially to evaluate the angle of approach θ* and the area ratio a of the flow channel, which arguably makes it challenging to utilize the CKL coefficient for prediction purposes or for comparison with other experimental data where these geometrical traits are unidentified. For practical applications it is probably more convenient to evaluate the combined influence of θ and a from the Cd data of Fig. 9 rather than the CKL of Fig. 8. Still, the presented results might serve as useful reference points for numerical modelling, especially when more experimental data becomes available for other pore geometries in the future. Consulting Eq. 2 to evaluate the geometry of the pore space in e.g. numerical models might therefore be useful from an interpretational point of view.

6 Conclusion

This work demonstrates that the influence of convective acceleration in nonuniform pore channels is analogues to convective acceleration in nonuniform pipe channels. The two phenomena are comparable if their geometrical characteristics are described precisely in the same manner, and from the same point of reference with regards to the fluid velocity in the channels. Studies on pipe geometries are consequently relevant for comparison with porous media studies. Data interpretation can then be improved as more experimental data and knowledge regarding the influence of the channel geometry become available from future studies and this will help our data interpretation and improve the predictability of porous media equations.

The presented results suggest that most nonuniform straight pipe flow channel geometries obtain dissipation coefficients within 0 < CKL < 0.2. These geometries are relevant for natural porous media and it is expected that most pore geometries will obtain values within this range. However, the dissipation coefficient is a function of the rate of change of the geometry along the channel length. The results show that the rate of change depends on:

  • The angle of approach θ and the area ratio a of the pore channel. The Cd data of Fig. 9 and the CKL of Fig. 8 demonstrate how these geometrical traits influence the magnitude of induced convective acceleration

  • The rounding of the pore channel geometry reduces the magnitude of induced convective acceleration

  • The tortuosity of a pore influences the CKL and increases the magnitude of induced convective acceleration

Further work should investigate the influence of other pore geometries and, especially the influence of the pore tortuosity. A comparison with pipe bend data might reveal the influence of the pore tortuosity on the CKL and Cd.