Abstract
Capillary number, understood as the ratio of viscous force to capillary force, is one of the most important parameters in enhanced oil recovery (EOR). It continues to attract the interest of scientists and engineers, because the nature and quantification of macroscopic capillary forces remain controversial. At least 41 different capillary numbers have been collected here from the literature. The ratio of viscous and capillary force enters crucially into capillary desaturation experiments. Although the ratio is length scale dependent, not all definitions of capillary number depend on length scale, indicating potential inconsistencies between various applications and publications. Recently, new numbers have appeared and the subject continues to be actively discussed. Therefore, a short review seems appropriate and pertinent.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A primary objective of enhanced oil recovery (EOR) methods is to extract original oil in place (OOIP) efficiently and economically from oil reservoirs (Lake 1989; Green and Willhite 2018). Despite many years of study, the best way to achieve this objective has remained one of the hottest research topics for petroleum engineers, geologists, chemical engineers and hydrologists.
Most EOR-methods attempt to increase the overall recovery efficiency  (defined in Eq. (23)) of the amount of oil or gas. As stated on the back cover of the textbook by Lake et al. (2014), the main theme in such attempts is the frequent reference to two fundamental principles: lowering the mobility ratio and increasing the capillary number. In this paper, the capillary number, defined as the quotient
(defined in Eq. (23)) of the amount of oil or gas. As stated on the back cover of the textbook by Lake et al. (2014), the main theme in such attempts is the frequent reference to two fundamental principles: lowering the mobility ratio and increasing the capillary number. In this paper, the capillary number, defined as the quotient
of viscous to capillary forces, will be the focus of interest. One of the most widely accepted expressions for capillary number is the ratio  of viscosity \(\mu \) times velocity
of viscosity \(\mu \) times velocity  to interfacial tension
to interfacial tension  . To mobilize the residual oil, this ratio must be increased by several orders of magnitude from the value \(10^{-6}\) it normally has in a waterflood, and the only realistic way to achieve this is by drastically lowering the interfacial tension
. To mobilize the residual oil, this ratio must be increased by several orders of magnitude from the value \(10^{-6}\) it normally has in a waterflood, and the only realistic way to achieve this is by drastically lowering the interfacial tension  . This is the most important reason for the popularity of surfactant EOR.
. This is the most important reason for the popularity of surfactant EOR.
 or purely with
or purely with  quantities. Its entries are Yes, No or Yo. An entry “Yes” is coloured
quantities. Its entries are Yes, No or Yo. An entry “Yes” is coloured  or
or  according to whether the number is purely
according to whether the number is purely  or
or  . An entry “Yo” indicates that the number is “almost pure”
. An entry “Yo” indicates that the number is “almost pure”Dullien (1992) and Hilfer and Øren (1996) noticed serious limitations of the capillary number  . Experiments indicate that the force balance and hence capillary number should depend on length scale, which is not the case for
. Experiments indicate that the force balance and hence capillary number should depend on length scale, which is not the case for  . In addition, the experimentally observed values of
. In addition, the experimentally observed values of  in capillary desaturation experiments are much too small, and Dullien (1992, p. 450) concludes “it is certainly peculiar that, when the viscous and capillary forces acting on a blob are equal, the capillary number, that is supposed to be equal to the ratio of viscous-to-capillary forces, is equal to \(2.2\times 10^{-3}\)”.
in capillary desaturation experiments are much too small, and Dullien (1992, p. 450) concludes “it is certainly peculiar that, when the viscous and capillary forces acting on a blob are equal, the capillary number, that is supposed to be equal to the ratio of viscous-to-capillary forces, is equal to \(2.2\times 10^{-3}\)”.
Given that  remains widely used, the main objective of this article is to review the various definitions of capillary numbers with respect to their importance for capillary desaturation curves. Let us recall that capillary desaturation curves play a crucial role in reservoir simulation and the planning of EOR-strategies. Our objective is therefore to review capillary numbers mainly with a view towards their use in capillary desaturation curves and their application in chemical EOR. Our definitions of recovery efficiencies, residual, remaining oil saturations and other important symbols are summarized in Appendix A. Definitions of capillary desaturation curves
remains widely used, the main objective of this article is to review the various definitions of capillary numbers with respect to their importance for capillary desaturation curves. Let us recall that capillary desaturation curves play a crucial role in reservoir simulation and the planning of EOR-strategies. Our objective is therefore to review capillary numbers mainly with a view towards their use in capillary desaturation curves and their application in chemical EOR. Our definitions of recovery efficiencies, residual, remaining oil saturations and other important symbols are summarized in Appendix A. Definitions of capillary desaturation curves  and capillary number correlations
and capillary number correlations  are given in Appendix B.
are given in Appendix B.
2 Capillary Numbers
It is now well accepted that the capillary number is a dimensionless group that quantifies the ratio of viscous force to capillary forces, as shown in Eq. (1). The problem of finding suitable definitions for the capillary number is identical to the problem of finding precise and, if possible, concise characterizations for the viscous and the capillary forces in Eq. (1). Lots of studies were devoted to this problem. Larson et al. (1981) summarized 14 correlating groups for the period from 1927 to 1979 and Taber (1980) summarized 17 correlating groups reported before 1979. According to our present survey, at least 41 different capillary number definitions or correlating groups have been reported. They are listed in Table 1. The first correlating group is reported to have been established in 1927 (Larson et al. 1981, Table 1). An early discussion of dimensionless groups can be found in (Leverett’s work 1939; 1941).
There are 41 numbers in this table. Most of them are mixed capillary numbers in the sense of Sect. 2.3. Many of them are closely related with each other or identical, such as \({{}^{8}\mathrm {Ca}}={{}^{23}\mathrm {Ca}}\). To appreciate the relation between various numbers it is necessary to consult the original references or the brief definition of symbols given in Tables 2 and 3. Note that for \({{}^{8}\mathrm {Ca}}\) the symbol K in Dombrowski and Brownell (1954) has dimensions of volumetric flow rate, not area. Many numbers contain quantities that appear to lack a clear definition or are otherwise difficult to access experimentally, such as the length of effective continuity behind front, the linear extent of trapped clusters, the mean length of an oil ganglion et cetera (see Table 3). Such numbers will be discussed in more detail in Sects. 2.3, 2.4, 2.5, 2.6 and 2.7. Other groups contain quantities that are not parameters of the problem, but elements of its solution, such as local microscopic or macroscopic pressure gradients. Although all of them have been used as capillary number correlations, they may not always be interpreted or intended as dimensionless groups expressing a force balance.
Some entries in Table 1 and numerous references contain or discuss gravity effects. For brevity, we limit the scope to viscous and capillary forces and do not discuss gravitational or centrifugal forces in this review. Similarly, we exclude drying (Yiotis et al. 2004) and diffusion–reaction problems (Kechagia et al. 2002) from the purview.
2.1 The Problem of Scale
While it is well accepted that the capillary number quantifies the ratio of viscous forces to capillary forces, it is rarely appreciated that this ratio depends on length scale. It should be emphasized that the length scales over which the two forces act need to be carefully checked in applications. Viscous and capillary forces on the pore scale differ from those on the laboratory scale and, again, from those on the field scale.
The upscaling problem from pore scale to laboratory scale is mathematically complicated by the emergence of measure valued functions (Hilfer 2018). This scientific fact is often overlooked by engineers in the field. Instead, it is generally assumed that the plateau region in conceptual pictures such as Hubbert (1957, Fig. 5, p. 35), Whitaker (1969, Fig. 3, p. 17), Bear (1972, Fig 1.3.1, p. 17), or Lake et al. (2014, Fig. 2.2, p. 21) exist. For convenience Figure 5 from Hubbert (1957, p. 35) is reproduced as Fig. 1. This assumption amounts to assuming that Eq. (57c) in Hilfer (2018) holds true. Precision measurements in Hilfer and Zauner (2011) and Hilfer and Lemmer (2015) tested such assumptions for natural and synthetic porous media. Figure 2 from Hilfer and Lemmer (2015) demonstrates that fluctuations are larger than commonly thought.
In this review a strict distinction between physical quantities on the pore scale and on the laboratory scale will be maintained. Pore scale quantities such as the interstitial phase velocity  , the interfacial tension
, the interfacial tension  or the contact angle
or the contact angle  are denoted in serif font and coloured blue. Laboratory scale quantities such as porosity
are denoted in serif font and coloured blue. Laboratory scale quantities such as porosity  , permeability
, permeability  or capillary pressure \({P_\mathrm {c}}\) are denoted in a boldface sans-serif font and coloured magenta. The only exceptions to this convention will be densities and viscosities. For densities and viscosities it is assumed that
or capillary pressure \({P_\mathrm {c}}\) are denoted in a boldface sans-serif font and coloured magenta. The only exceptions to this convention will be densities and viscosities. For densities and viscosities it is assumed that


holds, where  is the pore scale viscosity resp. density, and
is the pore scale viscosity resp. density, and  is the lab scale viscosity resp. density.
is the lab scale viscosity resp. density.
Conceptual figure 5 from Hubbert (1957, p.35) depicting the commonly expected behaviour of porosity as a smooth function of the volume of the averaging window
Four high precision measurements of porosity \(\phi (\ell )\) as a function of side length \(\ell \) obtained from four cubic averaging windows coloured black, blue, red and green (Hilfer and Lemmer 2015, Fig. 3). The sample is a cube of sidelength 15mm containing a pore space resembling that of Fontainebleau sandstone. The pore space is known with floating point precision. The porosity of the full sample is 0.134310101335984. The four averaging windows are disjoint for \(\ell <7.5\)mm. They overlap for \(\ell >7.5\)mm so that the decrease in fluctuations at large \(\ell \) is not significant. These data do not support the conceptual Fig. 1. For \(\ell <7.5\)mm the fluctuations are much larger than commonly thought
2.2 Microscopic Capillary Numbers
The most widely used capillary number is the microscopic capillary number. It is defined generically as

where  is the interstitial velocity and
is the interstitial velocity and  the pore scale viscosity of the displacing fluid. The capillary forces in this group are represented by the interfacial tension
the pore scale viscosity of the displacing fluid. The capillary forces in this group are represented by the interfacial tension  . The microscopic capillary number is identical or closely related as
. The microscopic capillary number is identical or closely related as

to the numbers \({{}^{1}\mathrm {Ca}}\), \({{}^{10}\mathrm {Ca}}\), \({{}^{12}\mathrm {Ca}}\), \({{}^{15}\mathrm {Ca}}\), \({{}^{16}\mathrm {Ca}}\), and as

to the numbers \({{}^{21}\mathrm {Ca}}\), \({{}^{24}\mathrm {Ca}}\) from Table 1.
2.3 Mixed Capillary Numbers
Mixed capillary numbers arise from microscopic capillary numbers by replacing  in eq. (3) with
in eq. (3) with  using Darcy’s law. The result is the number
using Darcy’s law. The result is the number

discussed already in Ojeda et al. (1953) (see also \({{}^{8}\mathrm {Ca}}\) in Dombrowski and Brownell (1954) or \({{}^{20}\mathrm {Ca}}\) in Stegemeier (1974)). The popular variant

discussed in Melrose and Brandner (1974) arises when the generalized Darcy law for two phase flow is used instead of Darcy’s law for single phase flow. While the replacement is convenient when  or \(k^r\) is known, its drawback is that the replacement mingles pore scale with Darcy scale. Inconsistencies can arise from this. As shown in Hilfer (1996, Eq. (6.51)) the replacement amounts to normalizing the macroscopic pressure using Darcy’s law instead of the capillary pressure function. This is tantamount to the hidden assumption that
or \(k^r\) is known, its drawback is that the replacement mingles pore scale with Darcy scale. Inconsistencies can arise from this. As shown in Hilfer (1996, Eq. (6.51)) the replacement amounts to normalizing the macroscopic pressure using Darcy’s law instead of the capillary pressure function. This is tantamount to the hidden assumption that
as discussed in Hilfer (1996, Sec.IV.C.2). While this assumption may hold for some processes and conditions it may fail for others (Hilfer 2020). For instance, in Fig. 8 the assumption holds for the leftmost points, and in Fig. 9 for points close to the vertical dashed line. For more examples see Hilfer (2020, Fig. 5). It follows that mixed capillary numbers do not give the correct force balance in EOR applications.
The great majority of capillary numbers in Table 1 are of mixed type. In column 4 of Table 1 the mixed numbers are listed with “No”.
An interesting type of mixed number was obtained in Armstrong et al. (2014, Eq. (7)). The development starts from the macroscopic numbers

and introduces an average cluster length defined in Armstrong et al. (2014, Eq. (4)). As discussed in Hilfer et al. (2015, Eq. (32)) the cluster length, the computed effective permeability and the computed capillary pressure are not experimental quantities, but computational pore scale quantities that depend on numerous parameters of the underlying computer algorithms.
2.4 Macroscopic Capillary Numbers
The macroscopic (or Darcy scale) capillary number is defined in Hilfer (1996, Eq. (6.54)) or Hilfer and Øren (1996, Eq. (50))

where  is the Darcy velocity of the displacing fluid
is the Darcy velocity of the displacing fluid  , \(\mu _i\) is its effective viscosity on the REV-scale,
, \(\mu _i\) is its effective viscosity on the REV-scale,  is the permeability, and
is the permeability, and

is the midpoint capillary pressure (see Anton and Hilfer (1999, Eq. (18)) for details). The midpoint capillary pressure \(P_\mathrm {b}\) has been expressed in Hilfer (1996, Eq. (6.70)) and Hilfer and Øren (1996, Eq. (66)) as

in terms of interfacial tension and the midpoint value of the empirical Leverett \(J\)-function correlation. Note that Eq. (10c) is not an “explanation” or “prediction” of \(P_\mathrm {b}\) based on interfacial tension. It is merely another way of writing Eq. (10b) by defining  . Both, \(P_\mathrm {b}\) as well as \(J_{\mathrm {b}}\), depend on
. Both, \(P_\mathrm {b}\) as well as \(J_{\mathrm {b}}\), depend on  as
as  or
or  . But these dependencies remain unknown.
. But these dependencies remain unknown.
The midpoint capillary pressure \(P_\mathrm {b}\) is extracted from the capillary pressure function \({P_\mathrm {c}}(S)\) for the process of interest. The function \({P_\mathrm {c}}(S)\) can be measured directly in the laboratory or estimated for larger scales from saturation profiles in hydrostatic gravitational equilibrium. Consider a porous column experiment. Let x denote position along the column and let \(x_0\) be a reference location at which the macroscopic pressure is the reference pressure  . Solving the equations of motion for two immiscible phases with \(\varrho _{\mathbbm {w}}>\varrho _{\mathbbm {o}}\) when all velocities and time derivatives vanish yields the well known result (Bear 1972)
. Solving the equations of motion for two immiscible phases with \(\varrho _{\mathbbm {w}}>\varrho _{\mathbbm {o}}\) when all velocities and time derivatives vanish yields the well known result (Bear 1972)


for pressure and saturation, where \(g\) is the acceleration of gravity. In this way \({P_\mathrm {c}}(S)\) and hence \(P_\mathrm {b}\) are obtained experimentally from measuring \(S(x)\) and inverting Eq. (11b).
The macroscopic capillary number  is identical with \({{}^{32}\mathrm {Ca}}\) and related as
is identical with \({{}^{32}\mathrm {Ca}}\) and related as

to the numbers \({{}^{7}\mathrm {Ca}}\) and \({{}^{36}\mathrm {Ca}}\). It was recently rediscovered in Andersen et al. (2017). The main difference between \({{}^{32}\mathrm {Ca}}\) and \({{}^{7}\mathrm {Ca}}\), apart from being inverted, is that \(P_\mathrm {b}\) is defined for all processes, while \(P_\mathrm {T}\) is only defined for primary drainage. The number

depends on scale, saturation and velocity. Quite different from previous expressions its definition involves relative permeability and capillary pressure. It may be called “localized macroscopic capillary number”, because it gives the local force balance between viscous and capillary forces within a macroscopically small but microscopically large region with saturation \(S\).
Another purely macroscopic number in Table 1 is

introduced in Yortsos and Fokas (1983) and discussed in Dong et al. (1998). Note that the symbol S in Yortsos and Fokas (1983) equals \(1-S\) in this paper. More seriously, the quantity \((d{P_\mathrm {c}}/d(1\!-\!S))_{\mathrm {ch}}\) can vanish in circumstances where the capillary forces do not vanish. This can occur e.g. for non-monotone \({P_\mathrm {c}}(S)\) functions such as those shown in Hilfer et al. (2012, Fig.1 and 2). Therefore, \((d{P_\mathrm {c}}/d(1\!-\!S))_{\mathrm {ch}}\) does not represent macroscopic capillary forces. This problem with \({{}^{27}\mathrm {Ca}}\) cannot be remedied easily.
2.5 Numbers Containing Contact Angle
A total of 13 capillary numbers in Table 1, namely \({{}^{4}\mathrm {Ca}}\), \({{}^{8}\mathrm {Ca}}\), \({{}^{9}\mathrm {Ca}}\), \({{}^{10}\mathrm {Ca}}\), \({{}^{11}\mathrm {Ca}}\), \({{}^{23}\mathrm {Ca}}\), \({{}^{17}\mathrm {Ca}}\), \({{}^{24}\mathrm {Ca}}\), \({{}^{30}\mathrm {Ca}}\), \({{}^{29}\mathrm {Ca}}\), \({{}^{31}\mathrm {Ca}}\), \({{}^{39}\mathrm {Ca}}\) and \({{}^{40}\mathrm {Ca}}\), contain a factor  , where
, where  is some contact angle on the pore scale. All of these numbers diverge or vanish for neutral wettability, i.e. when
is some contact angle on the pore scale. All of these numbers diverge or vanish for neutral wettability, i.e. when  .
.
The divergence of these 13 capillary numbers implies by virtue of the general relation (1), that the capillary forces vanish for  . Indeed, some text books (Dullien 1992, p.456) teach erroneously “that for neutral wettability (i.e.
. Indeed, some text books (Dullien 1992, p.456) teach erroneously “that for neutral wettability (i.e.  ) Eq. (5.3.83) predicts \(\mathrm {CA}_{\mathrm {imb}}=\infty \), because with a flat meniscus present the capillary forces are equal to zero—they don’t exist”. In this sentence the number \(\mathrm {CA}_{\mathrm {imb}}\) is \({{}^{31}\mathrm {Ca}}\) from Table 1. The sentence is erroneous, because the contact angle obeys Young’s equation (Rowlinson and Widom 1982, Eq. (1.21))
) Eq. (5.3.83) predicts \(\mathrm {CA}_{\mathrm {imb}}=\infty \), because with a flat meniscus present the capillary forces are equal to zero—they don’t exist”. In this sentence the number \(\mathrm {CA}_{\mathrm {imb}}\) is \({{}^{31}\mathrm {Ca}}\) from Table 1. The sentence is erroneous, because the contact angle obeys Young’s equation (Rowlinson and Widom 1982, Eq. (1.21))

where  are the surface tension of water, resp. oil, with the matrix and
are the surface tension of water, resp. oil, with the matrix and  . If
. If  and
and  , then
, then  vanishes. Thus, the capillary rise in a circular capillary of radius r
vanishes. Thus, the capillary rise in a circular capillary of radius r

vanishes. But that does not imply that “capillary forces are equal to zero”. Indeed  only means that the capillary forces pulling the meniscus upward are equal to the capillary forces pushing it downward.
only means that the capillary forces pulling the meniscus upward are equal to the capillary forces pushing it downward.
For this reason, it was emphasized in Hilfer (1996, p. 400), that the microscopic “capillary number is a measure of velocity in units of  , a characteristic velocity at which the coherence of the oil-water interface is destroyed by viscous forces”. The estimate
, a characteristic velocity at which the coherence of the oil-water interface is destroyed by viscous forces”. The estimate  m/s was given in Hilfer (1996, Table V) for the critical velocity.
m/s was given in Hilfer (1996, Table V) for the critical velocity.
In summary, capillary forces exist also for  , i.e. for neutral wetting
, i.e. for neutral wetting  and
and  . They vanish only for
. They vanish only for  . The balance of viscous and capillary forces on the pore scale is correctly quantified by
. The balance of viscous and capillary forces on the pore scale is correctly quantified by  . The capillary numbers \({{}^{4}\mathrm {Ca}}\), \({{}^{8}\mathrm {Ca}}\), \({{}^{10}\mathrm {Ca}}\), \({{}^{11}\mathrm {Ca}}\), \({{}^{17}\mathrm {Ca}}\), \({{}^{24}\mathrm {Ca}}\), \({{}^{30}\mathrm {Ca}}\), \({{}^{29}\mathrm {Ca}}\), \({{}^{31}\mathrm {Ca}}\),\({{}^{39}\mathrm {Ca}}\) and \({{}^{40}\mathrm {Ca}}\) do not give the correct balance of forces. In EOR applications such as Lashgari et al. (2016) or Alvarado and Manrique (2010, p.13) they should be used with special care.
. The capillary numbers \({{}^{4}\mathrm {Ca}}\), \({{}^{8}\mathrm {Ca}}\), \({{}^{10}\mathrm {Ca}}\), \({{}^{11}\mathrm {Ca}}\), \({{}^{17}\mathrm {Ca}}\), \({{}^{24}\mathrm {Ca}}\), \({{}^{30}\mathrm {Ca}}\), \({{}^{29}\mathrm {Ca}}\), \({{}^{31}\mathrm {Ca}}\),\({{}^{39}\mathrm {Ca}}\) and \({{}^{40}\mathrm {Ca}}\) do not give the correct balance of forces. In EOR applications such as Lashgari et al. (2016) or Alvarado and Manrique (2010, p.13) they should be used with special care.
2.6 Numbers Containing Viscosity Ratio
Among the definitions of \(\mathrm {Ca}\) in Table 1, the one proposed by Abrams (1975) is quite different from others because it incorporates the viscosity ratio. Abrams observed that multiplying the viscosity ratio as

seemed to decrease the scatter in the data points (Abrams 1975, Fig.3,4). The viscosity ratio is a key factor affecting the sweep efficiency \({E_\mathsf {V}}\).
Doorwar and Mohanty (2017) combined capillary number with other dimensionless scaling groups to predict recovery for unstable immiscible flows. Their so-called instability number reads

where  is the absolute permeability. The length \(D\) is called ”diameter” and seems to mean the diameter of the core, i.e. \(D\approx 2.5\)cm. It is unclear what \(D\) is for general EOR processes. Note also, that the exponent of the viscosity ratio is negative in \({{}^{38}\mathrm {Ca}}_{\mathbbm {w}}\) while it is positive in \({{}^{21}\mathrm {Ca}}_{\mathbbm {w}}\). If \({{}^{38}\mathrm {Ca}}\) can be regarded as a capillary number, then, at fixed and constant \(D\) and
is the absolute permeability. The length \(D\) is called ”diameter” and seems to mean the diameter of the core, i.e. \(D\approx 2.5\)cm. It is unclear what \(D\) is for general EOR processes. Note also, that the exponent of the viscosity ratio is negative in \({{}^{38}\mathrm {Ca}}_{\mathbbm {w}}\) while it is positive in \({{}^{21}\mathrm {Ca}}_{\mathbbm {w}}\). If \({{}^{38}\mathrm {Ca}}\) can be regarded as a capillary number, then, at fixed and constant \(D\) and  , Eqs. (18) and (17) are in conflict. We remind readers, however, that \({{}^{38}\mathrm {Ca}}\) was introduced not as a capillary number, but as an “instability number” in Doorwar and Mohanty (2017). More generally, any dependence of \(\mathrm {Ca}\) on viscosity ratio raises the question whether viscosity ratio influences not only sweep efficiency \({E_\mathsf {V}}\), where this influence is well established, but also displacement efficiency \({E_\mathsf {D}}\).
, Eqs. (18) and (17) are in conflict. We remind readers, however, that \({{}^{38}\mathrm {Ca}}\) was introduced not as a capillary number, but as an “instability number” in Doorwar and Mohanty (2017). More generally, any dependence of \(\mathrm {Ca}\) on viscosity ratio raises the question whether viscosity ratio influences not only sweep efficiency \({E_\mathsf {V}}\), where this influence is well established, but also displacement efficiency \({E_\mathsf {D}}\).
2.7 Dimensional Groups
Not all groups listed in Table 1 are dimensionless. The group \({{}^{9}\mathrm {Ca}}\) has dimensions of length and the group \({{}^{14}\mathrm {Ca}}\) has dimensions of (length)\(^{-2}\). These groups are listed in Table 1 because of their historical importance.
The ”interplay” between viscous and capillary forces “at the flood front” was discussed in great detail by Moore and Slobod (1955) in terms of the group \({{}^{9}\mathrm {Ca}}\), which led them to introduce the dimensionless group \({{}^{10}\mathrm {Ca}}\). They noticed important differences between drainage and imbibition based on their “Viscap concept” which they describe as a “capillary pressure-viscous force competition theory”. Because the pore size in laboratory core floods is the same as in reservoir floods they observe that “we generally cannot scale everything down in size”. They propose the dimensional group

as the correlating group for scaling. Here,  is the Darcy velocity of the displacing phase,
is the Darcy velocity of the displacing phase,  is the pore scale viscosity of the displacing phase,
is the pore scale viscosity of the displacing phase,  is the interfacial tension (IFT) between wetting and non-wetting phase, and
is the interfacial tension (IFT) between wetting and non-wetting phase, and  is the contact angle. The length \({L_{\mathrm {ec}}}\) in Moore and Slobod (1955) is not the “length of the flow path” but the “length of effective continuity of the oil phase behind the flood front”, or “ the distance over which pressure difference between the oil and the water phases is developed as a result of the phases flowing”.
is the contact angle. The length \({L_{\mathrm {ec}}}\) in Moore and Slobod (1955) is not the “length of the flow path” but the “length of effective continuity of the oil phase behind the flood front”, or “ the distance over which pressure difference between the oil and the water phases is developed as a result of the phases flowing”.
Moore and Slobod argue that \({L_{\mathrm {ec}}}\) is large for waterflooding of oil-wet systems, but small for water-wet systems, because in the latter case oil is discontinuous behind the front. Next, they claim that “\(L\) may be considered as an invariant, geometric property of the rock”. They then drop \(L\) “for simplicity”. In their words : “For simplicity, then, for water-wet systems \(L\) may be eliminated, and we then have the dimensionless group

as the scaling term for water-wet systems” (Moore and Slobod 1955, p. 5). If  is omitted from Eq. (20) and the Darcy velocity is replaced with the interstitial velocity
is omitted from Eq. (20) and the Darcy velocity is replaced with the interstitial velocity  , then Eq. (20) becomes the microscopic capillary number from Eq. (3).
, then Eq. (20) becomes the microscopic capillary number from Eq. (3).
The Taber group  is not a dimensionless group, but has dimensions of m\(^{-2}\). It has been influential in EOR, because Taber demonstrated the existence of a critical pressure gradient
is not a dimensionless group, but has dimensions of m\(^{-2}\). It has been influential in EOR, because Taber demonstrated the existence of a critical pressure gradient  m\(^{-2}\) for the mobilization of discontinuous oil in Berea sandstone Taber (1969). The critical gradient is then sometimes inserted into the condition \({{}^{6}\mathrm {Ca}}\approx 1\) to estimate the interfacial tension below which mobilization occurs from
m\(^{-2}\) for the mobilization of discontinuous oil in Berea sandstone Taber (1969). The critical gradient is then sometimes inserted into the condition \({{}^{6}\mathrm {Ca}}\approx 1\) to estimate the interfacial tension below which mobilization occurs from  for a sandstone of permeability
for a sandstone of permeability  . It should be clear that this can be misleading, because the
. It should be clear that this can be misleading, because the  mingles the pore scale and the Darcy scale.
mingles the pore scale and the Darcy scale.
2.8 Summary of Capillary Numbers
-
(1)
At least 41 different expressions for capillary number have been put forward in the literature.
-
(2)
The 41 capillary numbers fall into three categories: 5 macroscopic
 ’s, 12 microscopic
’s, 12 microscopic  ’s and 24 mixed \(\mathrm {Ca}\)’s. Macroscopic
’s and 24 mixed \(\mathrm {Ca}\)’s. Macroscopic  ’s contain only macroscopic quantities, microscopic
’s contain only macroscopic quantities, microscopic  ’s contain only microscopic quantities and mixed \(\mathrm {Ca}\)’s contain both kinds.
’s contain only microscopic quantities and mixed \(\mathrm {Ca}\)’s contain both kinds. -
(3)
Most \(\mathrm {Ca}\)’s are proposed for pore-matrix systems, and two for fracture-matrix systems.
-
(4)
Only two Ca’s incorporate the viscosity ratio, but in quite opposite dependencies.
-
(5)
Several definitions for \(\mathrm {Ca}\) were proposed only recently, indicating that \(\mathrm {Ca}\)-theory still needs to be developed, clarified and improved further.
3 Capillary Desaturation Curves
Capillary desaturation curves (CDCs), also known as capillary number correlations (CNCs), were defined in Eq. (28a). They correlate residual oil saturation \(ROS\) with capillary numbers. Accordingly, there are as many types of CDCs as there are capillary numbers, namely

where \(n=1,\dots ,41\) and the dots indicate other parameters. CDCs are among the most important curves in EOR (Lake 1989; Green and Willhite 2018), because the key issue in EOR is to reduce residual oil saturation \(ROS\) significantly and economically by various EOR methods and processes. Capillary desaturation curves enter as important input parameters into reservoir simulations (Youssef et al. 2013). In a numerical simulation the applicable capillary numbers will ensue automatically from correctly non-dimensionalizing the quantities in the mathematical model being simulated. A pore scale simulation will have pore scale numbers, while Darcy scale simulations will automatically exhibit the macroscopic capillary numbers. Mixed numbers will usually not arise.
3.1 Classic Microscopic and Mixed CDCs
To the best of our knowledge, one of the first CDCs was \(CDC_{10}\left( {{}^{10}\mathrm {Ca}}\right) \) in Moore and Slobod (1955, Fig.5a). It was replotted horizontally in Abrams (1975, Fig. 2) and the latter plot is reproduced here as Fig. 3. The curve is monotone decreasing. The viscosity ratio between displacing and displaced fluid is close to one. An immediate problem with Fig. 3 is that the capillary number \({{}^{10}\mathrm {Ca}}\) on the abscissa diverges for  . Note also, that the ordinate is oil saturation at breakthrough. Therefore, the saturations in Fig. 3 are expected to decrease further when more pore volumes are flooded through the sample. This expectation is confirmed in Abrams (1975, Fig. 5) (reproduced as Figure 10 in Sect. 3.3) showing the mixed \(CDC_{21}\left( {{}^{21}\mathrm {Ca}}\right) \) for seven reservoir rocks. The dash-dotted curve in Fig. 10 is for Berea sandstone.
. Note also, that the ordinate is oil saturation at breakthrough. Therefore, the saturations in Fig. 3 are expected to decrease further when more pore volumes are flooded through the sample. This expectation is confirmed in Abrams (1975, Fig. 5) (reproduced as Figure 10 in Sect. 3.3) showing the mixed \(CDC_{21}\left( {{}^{21}\mathrm {Ca}}\right) \) for seven reservoir rocks. The dash-dotted curve in Fig. 10 is for Berea sandstone.
\(CDC_{10}\left( {{}^{10}\mathrm {Ca}}\right) \) for Berea sandstone from Abrams (1975, Fig. 2). The ordinate is oil saturation at breakthrough. The abscissa becomes ill defined for contact angle 
\(CDC_{28}\left( {{}^{28}\mathrm {Ca}}\right) \) for Fontainebleau sandstone from Chatzis and Morrow (1984), Fig. 13
The influence of the continuity of the initial oil configuration on CDCs was investigated in Chatzis and Morrow (1984, Fig.13). Figure 4 shows \(CDC_{28}\left( {{}^{28}\mathrm {Ca}}\right) \), for Fontainebleau sandstone from Chatzis and Morrow (1984, Fig. 5). The solid lines in Fig. 4 represent floods with an initial oil configuration that is continuous throughout the sample. This is achieved by refilling the sample with oil after each flood. The dash-dotted line for initially discontinuous oil is obtained by increasing the flow rate or pressure drop without refilling the sample. It is seen that displacement of initially continuous oil is much easier than displacement of initially discontinuous oil. To achieve a given target \(ROS\) smaller capillary numbers are necessary for continuous oil than for discontinuous oil displacement.
Compilation of \(CDC_{20}\left( {{}^{20}\mathrm {Ca}}\right) \) for various experiments from Stegemeier (1977, Fig. 13) illustrating influence of wettability
Conceptual  from Lake (1989, Fig. 3–17, p. 70) to illustrate wettability effects
from Lake (1989, Fig. 3–17, p. 70) to illustrate wettability effects
Figure 5 from Stegemeier (1977, Fig. 13) collects the curves \(CDC_{8}\left( {{}^{8}\mathrm {Ca}}\right) \), \(CDC_{10}\left( {{}^{10}\mathrm {Ca}}\right) \), \(CDC_{15}\left( {{}^{15}\mathrm {Ca}}\right) \), \(CDC_{21}\left( {{}^{21}\mathrm {Ca}}\right) \), \(CDC_{16}\left( {{}^{16}\mathrm {Ca}}\right) \) and others into a single  plot. Of course, such a comparison is problematic, because the rock samples, the fluids and the EOR-processes are different in the various studies. Nevertheless, the summary shows common features. In many cases a plateau region, where \(ROS\) is nearly independent of \(\mathrm {Ca}\) is followed by a more or less gradual decrease. The two dashed curves show non-wetting phase residual oil saturation, while the solid curves show residuals for the wetting phase.
plot. Of course, such a comparison is problematic, because the rock samples, the fluids and the EOR-processes are different in the various studies. Nevertheless, the summary shows common features. In many cases a plateau region, where \(ROS\) is nearly independent of \(\mathrm {Ca}\) is followed by a more or less gradual decrease. The two dashed curves show non-wetting phase residual oil saturation, while the solid curves show residuals for the wetting phase.
The influence of wettability is depicted schematically in Fig. 6 from Lake (1989, Fig. 3-17) using standard microscopic  . The CDC labelled “Wetting phase” is a drainage curve, the curve labelled “Non-wetting phase” is an imbibition curve. As a rule, the plateau saturation for wetting CDCs is believed to fall below that for non-wetting CDCs Lake (1989). Experimental data that seem to confirm these EOR concepts are shown in Fig. 7 for various cores of uniform and mixed wettability. “WF” in the legend of Fig. 7 stands for waterflood, “SF” stands for surfactant flood. The cores are Berea outcrop sandstone. Compare the blue circles and the blue diamonds for uniformly water wet samples with the yellow triangles and magenta squares for two mixed wet cores. For uniformly water wet cores \(ROS\) remains constant, while for the mixed wet systems it decreases.
. The CDC labelled “Wetting phase” is a drainage curve, the curve labelled “Non-wetting phase” is an imbibition curve. As a rule, the plateau saturation for wetting CDCs is believed to fall below that for non-wetting CDCs Lake (1989). Experimental data that seem to confirm these EOR concepts are shown in Fig. 7 for various cores of uniform and mixed wettability. “WF” in the legend of Fig. 7 stands for waterflood, “SF” stands for surfactant flood. The cores are Berea outcrop sandstone. Compare the blue circles and the blue diamonds for uniformly water wet samples with the yellow triangles and magenta squares for two mixed wet cores. For uniformly water wet cores \(ROS\) remains constant, while for the mixed wet systems it decreases.
The CDCs discussed in this section are regarded as classic, because they are based on the widely used microscopic and mixed capillary numbers such as \({{}^{6}\mathrm {Ca}}\) and \({{}^{12}\mathrm {Ca}}\). Classic CDCs are usually measured on high permeability cores. Berea sandstones have values of  between 40 and 2500 mD (Chatzis and Morrow 1984). Examples for low permeability media are Bandera sandstones with
between 40 and 2500 mD (Chatzis and Morrow 1984). Examples for low permeability media are Bandera sandstones with  10mD in Moore and Slobod (1955),
10mD in Moore and Slobod (1955),  32 mD Abrams (1975) and a limestone with
32 mD Abrams (1975) and a limestone with  26 mD in Abrams (1975).
26 mD in Abrams (1975).
Experimental  from Abeysinghe et al. (2012, Fig. 9) for Berea outcrop sandstone
from Abeysinghe et al. (2012, Fig. 9) for Berea outcrop sandstone
The common features of classical CDCs exhibited above are :
-
(1)
The larger
 the lower is \(ROS\). In other words classical microscopic and mixed CDCs \(ROS=CDC(\mathrm {Ca})\) are monotone decreasing functions of \(\mathrm {Ca}\). Maximum oil recovery requires maximum \(\mathrm {Ca}\).
the lower is \(ROS\). In other words classical microscopic and mixed CDCs \(ROS=CDC(\mathrm {Ca})\) are monotone decreasing functions of \(\mathrm {Ca}\). Maximum oil recovery requires maximum \(\mathrm {Ca}\). -
(2)
At the highest values of
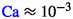 to
to 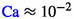 achieved to date in the laboratory residual oil often approaches zero. Classical CDCs are expected to approach zero, i.e.
achieved to date in the laboratory residual oil often approaches zero. Classical CDCs are expected to approach zero, i.e. 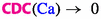 , for
, for 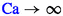 .
. -
(3)
There exists a breakpoint or critical capillary number \(\mathrm {Ca}_c\) such that \(ROS=CDC(\mathrm {Ca})\) is approximately constant for all \(\mathrm {Ca}<\mathrm {Ca}_c\). For many media the critical capillary number \(\mathrm {Ca}_c\) corresponds to the beginning of mobilization. For many porous media, such as sandstones, \(\mathrm {Ca}_c\approx 10^{-6}\dots 10^{-5}\).
-
(4)
Initially, continuous oil is displaced more easily than initially discontinuous oil.
-
(5)
CDCs for water-wet and oil-wet rocks are different. The breakpoint \(\mathrm {Ca}_c\) for the wetting phase is typically one or two decades above that for the non-wetting phase.
-
(6)
CDCs for mixed wet rocks seem not to show plateau where oil- and water-wet rocks exhibit their plateau saturation.
Macroscopic  for bead packs and Berea sandstone from Anton and Hilfer (1999, Fig.2)
for bead packs and Berea sandstone from Anton and Hilfer (1999, Fig.2)
3.2 Macroscopic CDCs
The macroscopic \(CDC_{32}\left( {{}^{32}\mathrm {Ca}}\right) \) based on \({{}^{32}\mathrm {Ca}}\) was computed for the first time in Anton and Hilfer (1999, Fig. 2) and it is reproduced here as Fig. 8. Desaturation data for bead packs from Morrow et al. (1988) are shown as symbols connected by a solid line (continuous oil) and as a dashed line (discontinuous oil). Desaturation data for Berea sandstone from Abrams (1975) are shown as stars in Fig. 8. Figure 8 shows lower values for \(ROS\) than Fig. 3 at breakthrough. Figure 8 also confirms the results for continuous versus discontinuous mode displacement seen in Fig. 4. The main result of Fig. 8 is the values of  on the abscissa. These are five decades larger than for classic CDCs. The breakpoint obeys
on the abscissa. These are five decades larger than for classic CDCs. The breakpoint obeys  . This confirms that
. This confirms that  is an accurate measure of viscous-to-capillary force balance during two phase flow in porous media, while
is an accurate measure of viscous-to-capillary force balance during two phase flow in porous media, while  is not.
is not.
Figure 9 shows a comparison of three capillary desaturation curves, the microscopic  (as tringles), the macroscopic
(as tringles), the macroscopic  (as circles), and the local macroscopic \(CDC_{36}\left( {{}^{36}\mathrm {Ca}}\right) \) (as pentagons), for the desaturation experiments on Dalton sandstone (sample 798) in Abrams (1975). The vertical dashed line at \(\mathrm {Ca}=1\) marks equality of viscous and capillary forces. Figure 9 directly visualizes the enormous shift by 7-8 decades. It also demonstrates that the global macroscopic CDC based on
(as circles), and the local macroscopic \(CDC_{36}\left( {{}^{36}\mathrm {Ca}}\right) \) (as pentagons), for the desaturation experiments on Dalton sandstone (sample 798) in Abrams (1975). The vertical dashed line at \(\mathrm {Ca}=1\) marks equality of viscous and capillary forces. Figure 9 directly visualizes the enormous shift by 7-8 decades. It also demonstrates that the global macroscopic CDC based on  can differ substantially from the local macroscopic CDC based on \({{}^{36}\mathrm {Ca}}\). This may have important consequences for EOR screening patterns.
can differ substantially from the local macroscopic CDC based on \({{}^{36}\mathrm {Ca}}\). This may have important consequences for EOR screening patterns.
Comparison of three CDCs for Dalton sandstone (sample 798) from Abrams (1975). The microscopic  is shown as tringles, the macroscopic \(CDC_{32}\left( {{}^{32}\mathrm {Ca}}\right) \) as circles, and the local macroscopic \(CDC_{36}\left( {{}^{36}\mathrm {Ca}}\right) \) as pentagons. The vertical dashed line at \(\mathrm {Ca}=1\) marks equality of viscous and capillary forces
is shown as tringles, the macroscopic \(CDC_{32}\left( {{}^{32}\mathrm {Ca}}\right) \) as circles, and the local macroscopic \(CDC_{36}\left( {{}^{36}\mathrm {Ca}}\right) \) as pentagons. The vertical dashed line at \(\mathrm {Ca}=1\) marks equality of viscous and capillary forces
The importance of macroscopic CDCs arises from :
-
(1)
Macroscopic CDCs are based purely on macroscopic quantities appearing in the generalized Darcy law and the capillary pressure saturation relation.
-
(2)
Macroscopic CDCs represent the balance of macroscopic viscous to macroscopic capillary forces correctly. Their breakpoint occurs at
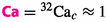 resp. \({{}^{36}\mathrm {Ca}}_c\approx 1\) while the breakpoint of microscopic and mixed CDCs occurs at \(\mathrm {Ca}\ll 1\).
resp. \({{}^{36}\mathrm {Ca}}_c\approx 1\) while the breakpoint of microscopic and mixed CDCs occurs at \(\mathrm {Ca}\ll 1\). -
(3)
Macroscopic CDCs depend on petrophysical properties of the reservoir rock while microscopic CDCs do not.
-
(4)
Macroscopic CDCs depend only on quantities that are measurable experimentally by standard methods and do not depend on mesoscopic cluster sizes, computational modelling or 3d image analysis of displacements.
-
(5)
Macroscopic CDCs suggest new and hitherto unexplored EOR methods and EOR processes.
\(CDC_{21}\left( {{}^{21}\mathrm {Ca}}\right) \) for various sandstones and one limestone from Abrams (1975, Fig. 5) illustrating the influence of viscosity contrast
\(CNC_{38}\left( {{}^{38}\mathrm {Ca}}\right) \) for various cores and floods summarized in Doorwar and Mohanty (2017, Fig. 10). Note the scale on the abscissa
3.3 Influence of Viscosity Ratio on CDCs
A thorough study of the influence of viscosity ratio on CDCs for six sandstone cores and one limestone was carried out in Abrams (1975) using 21 fluid pairs with different viscosities and interfacial tensions. A schematic summary of the highly fluctuating results is given in Abrams (1975, Fig. 5) and reproduced in Fig. 10. The factor  was introduced because it decreases the scatter in the data, albeit only very slightly. No theoretical justification was given for either the factor or the exponent 0.4. Recently, the factor
was introduced because it decreases the scatter in the data, albeit only very slightly. No theoretical justification was given for either the factor or the exponent 0.4. Recently, the factor  in Abrams (1975) was contradicted in Doorwar and Mohanty (2017). These authors multiply a factor \((\mu _{\mathbbm {w}}/\mu _{\mathbbm {o}})^{-2}\) and propose a theoretical basis for it. In Doorwar and Mohanty (2017) eight corefloods were conducted on a single Boise sandstone core. The brine permeability of the core was measured to be approximately 6 darcies, and the porosity was 29%. Tests showed good obvious trend of cumulative recovery with \({{}^{38}\mathrm {Ca}}\), as shown in Fig. 11 from Doorwar and Mohanty (2017). However, it is interesting that \({{}^{38}\mathrm {Ca}}\) in Fig. 11 is as large as \({{}^{38}\mathrm {Ca}}\approx 10^{10}\).
in Abrams (1975) was contradicted in Doorwar and Mohanty (2017). These authors multiply a factor \((\mu _{\mathbbm {w}}/\mu _{\mathbbm {o}})^{-2}\) and propose a theoretical basis for it. In Doorwar and Mohanty (2017) eight corefloods were conducted on a single Boise sandstone core. The brine permeability of the core was measured to be approximately 6 darcies, and the porosity was 29%. Tests showed good obvious trend of cumulative recovery with \({{}^{38}\mathrm {Ca}}\), as shown in Fig. 11 from Doorwar and Mohanty (2017). However, it is interesting that \({{}^{38}\mathrm {Ca}}\) in Fig. 11 is as large as \({{}^{38}\mathrm {Ca}}\approx 10^{10}\).
3.4 CDCs for Polymer Floods
In some classic microscopic \(CDC\) tests, polymers were used to increase the viscosity of the displacing phase. It is well accepted that polymers without surfactants cannot increase the microscopic capillary number  to reach the critical value \(\mathrm {Ca}_c\). Indeed, this would reduce \(ROS\) to a very low value, which is not observed. This is important for EOR, because polymers can increase the brine viscosity by at most two orders of magnitude due to the reservoir pressure gradient constraint. Therefore, it was believed for a long time that polymers cannot reduce \(ROS\) (Needham and Doe 1987; Lake 1989; Lake et al. 2014; Green and Willhite 2018).
to reach the critical value \(\mathrm {Ca}_c\). Indeed, this would reduce \(ROS\) to a very low value, which is not observed. This is important for EOR, because polymers can increase the brine viscosity by at most two orders of magnitude due to the reservoir pressure gradient constraint. Therefore, it was believed for a long time that polymers cannot reduce \(ROS\) (Needham and Doe 1987; Lake 1989; Lake et al. 2014; Green and Willhite 2018).
 (lower group of six decreasing curves) from polymer floods affected by viscoelasticity. from Wu et al. (2007)
(lower group of six decreasing curves) from polymer floods affected by viscoelasticity. from Wu et al. (2007)
However, some recent polymer flooding experiments produced CDCs that are different from previously observed CDCs. Figure 12 shows such a \(CDC\) polymer flooding reported in (Wu et al. 2007). In these experiments surfactants and alkali were used. The cores were flooded horizontally. In Figure 12, the upper group of curves shows the Oil Recovery Factor while the lower group shows \(ROS\). Figure 12 shows that the viscoelasticity of a HPAM polymer might play an important role in reducing \(ROS\) (Wu et al. 2007). Other studies also showed that the viscoelasticity of polymers seems to contribute to the reduction in \(ROS\) (Wang et al. 2007; Azad and Trivedi 2017; Wang et al. 2004, 2000).
Qi et al. (2017) reported a quite different polymer flooding CDC, as is shown in Figure 13. In these experiments, the cores were displaced vertically. Figure 13 shows that polymers without the addition of surfactants can reduce \(ROS\) to almost zero. They also attributed this to the viscoelasticity effect of HPAM to the ROS (Erincik et al. 2018). However, the extremely low ROS in their tests were also possibly caused by the gravity-stabilization effect (Adebayo et al. 2017; Hilfer 1996; Cinar et al. 2006; Schechter et al. 1994, 1991).
In another vertically placed flood test (Lu and Pope 2017), gravity-stable surfactant flooding without addition of the polymer (to control the mobility) achieved a very high recovery, which was not reported for horizontally placed core floods or field tests. In addition, this CDC (Figure 13) was obtained in a secondary recovery model at high initial oil saturation where oil was more continuously distributed. However, some cores were oriented vertically while others were horizontally oriented. This great difference should be given special attention.
A non-monotonic \(CNC\) was reported by Qi et al. (2014). It is shown in Fig. 14. In these experiments \(CNC_{12}\left( {{}^{12}\mathrm {Ca}}\right) \) was used. However, the three-layer long cores (4cm*4cm*30cm) used to get this CNC were quite different from typical short cores that are used in classic CDC tests. These core flooding tests were horizontally placed. The same physical model used was well shown in Hou et al. (2005). Note that in Fig. 14 the data points are not from a single core, but from different cores. It is interesting that the ROS is not further reduced when Ca goes higher than 10\({}^{-2}\). In addition, the minimum ROS does not go to zero. The Ca values in their tests went high to 10\({}^{-1}\), which were rarely reported. However, the ordinate in Figure 14 is not the actual residual oil saturation \(ROS\) but remaining oil saturation  due to insufficient sweep efficiency.
due to insufficient sweep efficiency.
Polymer flooding  with sharper decay from Qi et al. (2017)
with sharper decay from Qi et al. (2017)
Polymer flooding  from Qi et al. (2014)
from Qi et al. (2014)
Fracture \(CDC_{39}\left( {{}^{39}\mathrm {Ca}}\right) \) from AlQuaimi and Rossen (2018, Fig. 10)
3.5 Non-monotonic CDCs
The CDCs mentioned in Sect. 3.1 through 3.4 are generally based on core flooding tests. Numerous studies use other physical or numerical models to obtain CDC. These CDCs help to understand the flow in porous media at different scale and provide insights into displacement efficiency and sweep efficiency which are important for EOR.
Mai et al. (2009) and Mai and Kantzas (2009) found that waterflooding after primary production yields an improved viscous oil recovery at slower injection rates. This means lower improved oil recovery at higher  . Thus, a non-monotonic \(CNC\) can be obtained. Doorwar and Mohanty (2017) also reported lower breakthrough viscous oil recovery at higher Ca as defined in Eq. (3). See Fig. 7 on p. 25 in Doorwar and Mohanty (2017).
. Thus, a non-monotonic \(CNC\) can be obtained. Doorwar and Mohanty (2017) also reported lower breakthrough viscous oil recovery at higher Ca as defined in Eq. (3). See Fig. 7 on p. 25 in Doorwar and Mohanty (2017).
AlQuaimi and Rossen (2018) proposed the capillary number definition \({{}^{39}\mathrm {Ca}}\) for fractures that incorporated a geometrical characterization of the fracture. It is called fracture capillary number in this paper and the \(CDC_{39}\left( {{}^{39}\mathrm {Ca}}\right) \) is called fracture CDC. It seems that the CDCs based on \({{}^{39}\mathrm {Ca}}\) scatter less than the curves obtained for the conventional definition of the Ca, which can be seen in Fig. 15 from AlQuaimi and Rossen (2018). In addition, the values of \({{}^{39}\mathrm {Ca}}\) are much higher than values of the conventional Ca and their largest Ca values approach unity. It is worth mentioning that the models used for their \(CDC_{39}\left( {{}^{39}\mathrm {Ca}}\right) \) are different from the cores used for a typical CDC.
Chang et al. (2019) used the “complete” capillary number \({{}^{40}\mathrm {Ca}}\) which includes pore-scale characteristics of micromodels such as pore-throat diameter and micromodel depth. Their study concerns unstable drainage of brine by supercritical CO\({}_{2}\). Their most unusual observation is the non-monotonic increase of the CO\({}_{2}\) saturation for increasing \(\mathrm {Ca}\). This CNC (Fig. 6, p. 19) in Chang et al. (2019) is the opposite process of the CDC. Although transition from capillary fingering to viscous fingering during the unstable drainage process may help to account for their test results, the CNC is quite inconsistent with previous studies (Lenormand and Zarcone 1988).
A non-monotonic CNC for a 2-D network model was reported in Rodriguez de Castro et al. (2015). Their study showed that no plateau of ROS is observed when the Ca decreases. Figure 6 (p. 8525) and Figure 7 (p. 8526) in Rodriguez de Castro et al. (2015) show that the ROS was not only affected by the capillary number, but also by the viscosity ratio. It seems that a monotonic CDC is only possible when the displacing phase viscosity is larger than the displaced phase (viscosity ratio is larger than unity). In another test using the Hele-Shaw cell model, non-monotonic CNCs were obtained as well in Khosravian et al. (2015) (see Figure 4 (p. 1388) in Khosravian et al. (2015)). Interestingly, the non-monotonicity is very obvious when M is 0.22 (\( = 1 / 4.5 \)). However, some extent of non-monotonicity is also seen when viscosity ratio M is 1 (Figure 4, in Khosravian et al. (2015)). The non-monotonicity of CNC was also reported by other researchers. Zhao et al. (2016) studied impact of wettability on viscously unfavourable fluid-fluid displacement in disordered media by means of high-resolution imaging in microfluidic flow cells. Their study showed that even when the Ca (defined as  ) was the same, \({E_\mathsf {D}}\) and \({E_\mathsf {V}}\) can vary strongly regarding the Ca. The displacement efficiency can be seen in Fig. 3 (B) on p. 10253 from Zhao et al. (2016). Effect of Ca on \({E_\mathsf {V}}\) can be seen in Fig. 2 in this reference. Fig. 2 and Fig. 3 show obvious non-monotonicity of CNC. It is interesting that \({{}^{10}\mathrm {Ca}}\) was not used in Zhao et al. (2016), although the contact angles in their tests can be more easily fixed and obtained than in other tests.
) was the same, \({E_\mathsf {D}}\) and \({E_\mathsf {V}}\) can vary strongly regarding the Ca. The displacement efficiency can be seen in Fig. 3 (B) on p. 10253 from Zhao et al. (2016). Effect of Ca on \({E_\mathsf {V}}\) can be seen in Fig. 2 in this reference. Fig. 2 and Fig. 3 show obvious non-monotonicity of CNC. It is interesting that \({{}^{10}\mathrm {Ca}}\) was not used in Zhao et al. (2016), although the contact angles in their tests can be more easily fixed and obtained than in other tests.
Rabbani et al. (2018) also reported microfluidic tests that yield non-monotonic CNCs. These showed a gradual and monotonic variation of the pore sizes along the front path suppresses viscous fingering (Rabbani et al. 2018). The non-monotonicity was well seen in Fig. 2 and Fig. 3 in (Rabbani et al. 2018). With the same Ca (defined as  , the displacement efficiency (Fig. 3E in Rabbani et al. (2018)) or sweep efficiency (Fig. 2 in Rabbani et al. (2018)) varied. Their study showed that CNC is not only affected by Ca, but also by pore-size gradient. Since the viscosity ratio in their tests was kept constant, it is interesting that the flow does not follow a monotonic pattern, as would be expected. Since the models used in these tests can be regarded as homogeneous, the non-monotonicity of CNCs deserves further study. Note that all these non-monotonic CNCs were based on microscopic
, the displacement efficiency (Fig. 3E in Rabbani et al. (2018)) or sweep efficiency (Fig. 2 in Rabbani et al. (2018)) varied. Their study showed that CNC is not only affected by Ca, but also by pore-size gradient. Since the viscosity ratio in their tests was kept constant, it is interesting that the flow does not follow a monotonic pattern, as would be expected. Since the models used in these tests can be regarded as homogeneous, the non-monotonicity of CNCs deserves further study. Note that all these non-monotonic CNCs were based on microscopic  .
.
It is interesting that most CDCs from core flooding tests are monotonic (see e.g. Figs.5 and 6), while CDCs from micromodels can be monotonic (Zhang et al. 2011, Fig. 5) or non-monotonic (An et al. 2020, Fig. 4). It remains to be further investigated what major factors cause nonmonotonicity. Possible candidates are the two-dimensionality of micromodels or possibly insufficient scale separation (see e.g. Karadimitriou et al. 2013, Fig. 9). Other factors for the nonmonotonicity in micromodels may be associated with the flow regime crossover from capillary fingering to viscous fingering (An et al. 2020; Khosravian et al. 2015; Chen et al. 2017; Wang et al. 2013; Ferer et al. 2004), model inhomogeneity (Wang et al. 2013), solid surface wettability (Zhao et al. 2016), flow history (Krummel et al. 2013; Khosravian et al. 2015), and rock surface roughness (Glass et al. 2003; Chen et al. 2017).
4 The Use of Capillary Numbers in EOR
To illustrate the importance of \(\mathrm {Ca}\) and \(CDC\) for EOR, consider the mobilization of trapped oil. If for fixed and given initial oil saturation  the functions \(CDC_n\) are decreasing with \({{}^{n}\mathrm {Ca}}\), then different CDCs lead to very different EOR strategies. EOR strategies based on the traditional microscopic
the functions \(CDC_n\) are decreasing with \({{}^{n}\mathrm {Ca}}\), then different CDCs lead to very different EOR strategies. EOR strategies based on the traditional microscopic  would tend to increase the velocity or viscosity of the displacing fluid and to decrease the interfacial tension, but would predict recovery to be independent of length scale. EOR strategies based on the mixed
would tend to increase the velocity or viscosity of the displacing fluid and to decrease the interfacial tension, but would predict recovery to be independent of length scale. EOR strategies based on the mixed  would predict recovery to be independent of viscosity and to decrease with length scale because the pressure drops and hence the velocity decreases. EOR strategies based on the macroscopic
would predict recovery to be independent of viscosity and to decrease with length scale because the pressure drops and hence the velocity decreases. EOR strategies based on the macroscopic  , however, would predict recovery to increase with increasing length scale and viscosity, but to decrease with increasing permeability.
, however, would predict recovery to increase with increasing length scale and viscosity, but to decrease with increasing permeability.
Standard EOR techniques are based on the classical microscopic number  . Among different EOR techniques, chemical flooding is more closely related to the capillary number (Green and Willhite 2018) than other methods. Surfactants in chemical EOR serve to reduce the oil/water interfacial tension
. Among different EOR techniques, chemical flooding is more closely related to the capillary number (Green and Willhite 2018) than other methods. Surfactants in chemical EOR serve to reduce the oil/water interfacial tension  from typically around
from typically around  mN/m to 10\(^{-3}\) mN/m to reach sufficiently high capillary numbers (Guo et al. 2018, 2019). This is well accepted by many, if not all, petroleum engineers.
mN/m to 10\(^{-3}\) mN/m to reach sufficiently high capillary numbers (Guo et al. 2018, 2019). This is well accepted by many, if not all, petroleum engineers.
Microscopic CDCs also suggest that reduction in interfacial tension  has the same effect on ROS as increasing the viscosity \(\mu \) of the displacing phase by an equal percentage. It should be kept in mind, however, that \(\mu \) affects sweep efficiency as well as displacement efficiency, while this is not the case for
has the same effect on ROS as increasing the viscosity \(\mu \) of the displacing phase by an equal percentage. It should be kept in mind, however, that \(\mu \) affects sweep efficiency as well as displacement efficiency, while this is not the case for  . Laboratory tests (Zhang et al. 2010; Hou et al. 2005; Shen et al. 2009; Wang et al. 2010) and current chemical flooding practice (Guo et al. 2017, 2019) suggest that increasing viscosity has a higher effect on ROS, because it improves not only capillary number but also viscosity ratio. This seems especially true, when heterogeneity is taken into consideration. Heterogeneity effects have been well investigated in (Zhou et al. 1997) and (Hilfer and Helmig 2004).
. Laboratory tests (Zhang et al. 2010; Hou et al. 2005; Shen et al. 2009; Wang et al. 2010) and current chemical flooding practice (Guo et al. 2017, 2019) suggest that increasing viscosity has a higher effect on ROS, because it improves not only capillary number but also viscosity ratio. This seems especially true, when heterogeneity is taken into consideration. Heterogeneity effects have been well investigated in (Zhou et al. 1997) and (Hilfer and Helmig 2004).
5 Summary
-
1.
At least 41 different expressions for capillary number have been identified in the literature. The 41 capillary numbers fall into three categories: 5 macroscopic
 ’s, 12 microscopic
’s, 12 microscopic  ’s and 24 mixed \(\mathrm {Ca}\)’s. Macroscopic numbers contain only Darcy or field scale quantities, microscopic numbers contain only pore scale parameters, mixed numbers contain both.
’s and 24 mixed \(\mathrm {Ca}\)’s. Macroscopic numbers contain only Darcy or field scale quantities, microscopic numbers contain only pore scale parameters, mixed numbers contain both. -
2.
For macroscopic capillary numbers the accurate characterization of viscous and capillary forces is length scale dependent.
-
3.
Mixed capillary numbers containing contact angle have difficulty in describing neutral wettability.
-
4.
The most widely used classic definitions of \(\mathrm {Ca}\) in EOR are shown to be microscopic or mixed. They often contain the hidden assumption
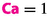 . This fact has been overlooked for a long time.
. This fact has been overlooked for a long time. -
5.
Different from microscopic and mixed capillary number, which are directly based on interfacial tension
 as a crucial parameter, macroscopic capillary numbers are based on macroscopic capillary pressure which is affected not only by fluid-fluid interfacial tension
as a crucial parameter, macroscopic capillary numbers are based on macroscopic capillary pressure which is affected not only by fluid-fluid interfacial tension  , but also by numerous other geometrical and physical parameters of the displacement.
, but also by numerous other geometrical and physical parameters of the displacement. -
6.
Classic capillary desaturation curves
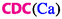 are mainly based on microscopic
are mainly based on microscopic  and mixed \(\mathrm {Ca}\)’s. Classic CDC’s are monotonic, and hence small residual oil saturation \(ROS\) requires large values of
and mixed \(\mathrm {Ca}\)’s. Classic CDC’s are monotonic, and hence small residual oil saturation \(ROS\) requires large values of  implying the use of surfactants in EOR to reduce interfacial tension
implying the use of surfactants in EOR to reduce interfacial tension  to ultra-low values and/or polymers to increase viscosity. This doctrine to reduce
to ultra-low values and/or polymers to increase viscosity. This doctrine to reduce  to ultra-low values is very widespread in chemical EOR.
to ultra-low values is very widespread in chemical EOR. -
7.
Different from classic
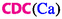 based on microscopic or mixed numbers, for macroscopic
based on microscopic or mixed numbers, for macroscopic 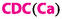 the transition from capillary force dominated flow to viscous force dominated flow happens at macroscopic
the transition from capillary force dominated flow to viscous force dominated flow happens at macroscopic 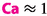 , which seems to be more reasonable.
, which seems to be more reasonable. -
8.
Non-monotonic \(CNC\)’s from many tests may reflect the importance of viscosity ratio and capillary number on
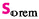 . A notable attempt to correlate them was made with \({{}^{38}\mathrm {Ca}}\). However, it remains to be investigated whether and how to use macroscopic capillary numbers to account for these non-monotonic \(CNC\)’s.
. A notable attempt to correlate them was made with \({{}^{38}\mathrm {Ca}}\). However, it remains to be investigated whether and how to use macroscopic capillary numbers to account for these non-monotonic \(CNC\)’s. -
9.
Macroscopic
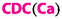 functions may call for alternative screening EOR strategies and new experiments.
functions may call for alternative screening EOR strategies and new experiments.
Change history
24 October 2022
Missing Open Access funding information has been added in the Funding Note.
References
Abeysinghe, K., Fjelde, I., Lohne, A.: Dependency of remaining oil saturation on wettability and capillary number. (paper SPE160883 presented at the SPE Saudi Arabia Section Technical Symposium and Exhibition held in Al-Khobar, Saudi Arabia, 8–11 April 2012) (2012)
Abrams, A.: The influence of fluid viscosity, interfacial tension, and flow velocity on residual oil left by waterflood. Soc. Petr. Eng. J. 15, 437 (1975)
Adebayo, A., Barri, A., Kamal, M.: Residual Saturation: an experimental study of effect of gravity and capillarity during vertical and horizontal flow. (paper SPE-187998-MS presented at the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition held in Dammam, Saudi Arabia, 24–27 April 2017) (2017)
AlQuaimi, B., Rossen, W.: Capillary Desaturation Curve for Residual Nonwetting Phase in Natural Fractures. SPE Journal, June, 788–802. (2018)
Alvarado, V., Manrique, E.: Enhanced Oil Recovery. Gulf Professional Publishing, Burlington (2010)
An, A., Erfani, H., Godinez-Briyuela, O., Niasar, V.: Transition From Viscous Fingering to Capillary Fingering: Application of GPU-Based Fully Implicit Dynamic Pore Network Modeling (2020) Water Resources Research, 56, e2020WR028149
Andersen, P., Standnes, D., Skjaeveland, S.: Waterflooding oil-saturated core samples—analytical solutions for steady-state capillary end effects and correction of residual saturation. J. Pet. Sci. Eng. 157, 364–379 (2017)
Anton, L., Hilfer, R.: Trapping and mobilization of residual fluid during capillary desaturation in porous media. Phys. Rev. E, 59, 6819 (1999). https://journals.aps.org/pre/abstract/10.1103/PhysRevE.59.6819
Armstrong, R., Georgiadis, A., Ott, H., Klemin, D., Berg, S.: Critical capillary number: desaturation studied with fast X-ray computed microtomography. Geophys. Res. Letts. 41, 1 (2014)
Arriola, A., Willhite, G., Green, D.: Trapping of Oil Drops in a Noncircular Pore Throat and Mobilization Upon Contact With a Surfactant. SPE J., February, 99–114 (1983)
Azad, M., Trivedi, J.: Quantification of the viscoelastic effects during polymer flooding: a critical review. (Review paper) (2017)
Bear, J.: Dynamics of fluids in porous media. Elsevier Publ. Co., New York (1972)
Chang, C., Kneafsey, T., Zhou, Q., Oostrom, M., Ju, Y.: Scaling the impacts of pore-scale characteristics on unstable supercritical CO2-water drainage using a complete capillary number. Int. J. Greenhouse Gas Control 86, 11–21 (2019)
Chatzis, I., Morrow, N.: Correlation of Capillary Number Relationships for Sandstone. SPE J., October, 555-562 (1984)
Chen, Y., Fang, S., Wu, D., Hu, R.: Visualizing and quantifying the crossover from capillary fingering to viscous fingering in a rough fracture. Water Resour. Res. 53, 7756–7772 (2017)
Cinar, Y., Jessen, K., Berenblyum, R., Juanes, R., Orr, F.: An Experimental and Numerical Investigation of Crossflow Effects in Two—Phase Displacements. SPE J., June, 216-226 (2006)
Dombrowski, H., Brownell, L.: Residual equilibrium saturation of porous media. Ind. Eng. Chem. 46, 1207 (1954)
Dong, M., Dullien, F., Zhou, J.: Characterization of waterflood saturation profile histories by the ‘complete’ capillary number. Transport Porous Media 31, 213–237 (1998)
Doorwar, S., Mohanty, K.: Viscous-fingering function for unstable immiscible flows. SPE J., February, 19–31. (2017)
Dullien, F.: Porous media—Fluid transport and pore structure. Academic Press, San Diego (1992)
Ehrlich, R., Hasiba, H., Raimondi, P.: Alkaline Waterflooding for Wettability Alteration—Evaluating a Potential Field Application. J. Petrol. Technol., December, 1335–1343 (1974)
Erincik, M., Qi, P., Balhoff, M., Pope, G.: New method to reduce residual oil saturation by polymer flooding. SPE J. 23, 1–13 (2018)
Ferer, M., Ji, C., Bromhal, G., Cook, J., Ahmadi, G., Smith, D.: Crossover from capillary fingering to viscous fingering for immiscible unstable flow: experiment and modeling. Phys. Rev. E 70, 016303 (2004)
Foster, W.: A low-tension waterflooding process. Journal of Petroleum Technology, February, 205–210 (1973)
Glass, R., Rajaram, H., Detwiler, R.: Immiscible displacements in rough-walled fractures: competition between roughening by random aperture variations and smoothing by in-plane curvature. Phys. Rev. E 68, 061110 (2003)
Green, D., Willhite, G.: Enhanced Oil Recovery. Society of Petroleum Engineers, Richardson (2018)
Guo, H., Dou, M., Hanqing, W., Wang, F., Yuanuan, G., Yu, Z., Li, Y.: Proper use of capillary number in chemical flooding. J. Chem. 2017, 1–11 (2017)
Guo, H., Li, Y., Kong, D., Ma, R., Li, B., Wang, F.: Lessons learned from Alkali/surfactant/polymer-flooding field tests in China. SPE Reserv. Eval. Eng. 22, 78–99 (2019)
Guo, H., Li, Y., Wang, F., Gu, Y.: Comparison of Strong Alkali and Weak Alkali ASP Flooding Field Tests in Daqing Oilfield. SPE Prod. Oper. 33, 353–362 (2018)
Hilfer, R.: Transport and relaxation phenomena in porous media. Advances in Chemical Physics, XCII, 299 (1996). https://www.wiley.com/en-af/Advances+in+Chemical+Physics%2C+Volume+92-p-9780470142042
Hilfer, R.: Multiscale local porosity theory, weak limits, and dielectric response in composite and porous media. J. Math. Phys. 59, 103511 (2018). https://doi.org/10.1063/1.5063466
Hilfer, R.: Capillary number correlations for two-phase flow in porous media. Phys. Rev. E 102, 053103 (2020). https://doi.org/10.1103/PhysRevE.102.053103
Hilfer, R., Armstrong, R., Berg, S., Georgiadis, A., Ott, H.: Capillary saturation and desaturation. Phys. Rev. E 92, 063023 (2015). https://doi.org/10.1103/PhysRevE.92.063023
Hilfer, R., Doster, F., Zegeling, P.: Nonmonotone saturation profiles for hydrostatic equilibrium in homogeneous media. Vadose Zone J., 11, vzj2012.0021 (2012). https://doi.org/10.2136/vzj2012.0021
Hilfer, R., Helmig, R.: Dimensional analysis and upscaling of two-phase flow in porous media with piecewise constant heterogeneities. Adv. Water Resour. 27, 1033 (2004). https://doi.org/10.1016/j.advwatres.2004.07.003
Hilfer, R., Lemmer, A.: Differential porosimetry and permeametry for random porous media. Phys. Rev. E 92, 013305 (2015). https://doi.org/10.1103/PhysRevE.92.013305
Hilfer, R., Øren, P.: Dimensional analysis of pore scale and field scale immiscible displacement. Transport Porous Media 22, 53 (1996). https://doi.org/10.1007/BF00974311
Hilfer, R., Zauner, T.: High precision synthetic computed tomography of reconstructed porous media. Phys. Rev. E 84, 062301 (2011). https://doi.org/10.1103/PhysRevE.84.062301
Hou, J., Liu, Z., Zhang, S., Yue, X., Yang, J.: The role of viscoelasticity of alkali/surfactant/polymer solutions in enhanced oil recovery. J. Pet. Sci. Eng. 47, 219–235 (2005)
Hubbert, M.: Darcy’s law and the field equations of the flow of underground fluids. Int. Assoc Sci. Hydrol. Bull. 2, 23–59 (1957)
Hughes, R., Blunt, M.: Network modeling of multiphase flow in fractures. Adv. Water Resour. 24, 409–421 (2001)
Jiang, Y.: Prediction of the relationship between capillary number and residual oil saturation. Pet. Geol. Oilf. Dev. Daq. 6, 63–66 (1987)
Karadimitriou, N., Musterd, M., Kleingeld, P., Kreutzer, M., Hassanizadeh, S., Joekar-Niasar, V.: On the fabrication of PDMS micromodels by rapid prototyping, and their use in two-phase flow studies. Water Resour. Res. 49, 2056–2067 (2013)
Kechagia, P., Tsimpanogiannis, I., Yortsos, Y., Lichtner, P.: On the upscaling of reaction-transport processes in porous media with fast or finite kinetics. Chem. Eng. Sci. 57, 2562–2577 (2002)
Khosravian, H., Joekar-Niasar, V., Shokri, N.: Effects of flow history on oil entrapment in porous media: an experimental study. AIChE J. 61, 1385–1390 (2015)
Krummel, A., Datta, S., Münster, S., Weitz, D.: Visualizing multiphase flow and trapped fluid configurations in a model three-dimensional porous medium. AIChE J. 59, 1022–1029 (2013)
Lake, L.: Enhanced Oil Recovery. Prentice Hall, Englewood Cliffs (1989)
Lake, L., Johns, R., Rossen, W., Pope, G.: Fundamentals of Enhanced Oil Recovery. Society of Petroleum Engineers, Richardson (2014)
Larson, R., Davis, H., Scriven, L.: Displacement of residual nonwetting fluid from porous media. Chem. Eng. Sci. 36, 75 (1981)
Lashgari, H., Xu, Y., Sepehrnoori, K.: Modeling dynamic wettability alteration effect based on contact angle. (paper SPE-179665-MS presented at the SPE Improved Oil Recovery Conference held in Tulsa, Oklahoma, USA, 11–13 April 2016) (2016)
Lefebvre duPrey, E.: Factors affecting liquid-liquid relative permeabilities of a consolidated porous medium. Soc. Petr. Eng. J., 13, 39 (1973)
Lenormand, R., Zarcone, C.: Physics of blob displacement in a two-dimensional porous medium. SPE Form. Eval. 3, 271–275 (1988)
Leverett, M.: Flow of oil-water mixtures through unconsolidated sands. Trans. AIME 132, 149–171 (1939)
Leverett, M.: Capillary behaviour in porous solids. Trans. AIME 142, 152–169 (1941)
Lu, J., Pope, G.: Optimization of gravity-stable surfactant flooding. SPE J. 22, 480–493 (2017)
Mai, A., Bryan, J., Goodarzi, N., Kantzas, A.: Insights into non-thermal recovery of heavy oil. J. Can. Pet. Technol. 48, 27–35 (2009)
Mai, A., Kantzas, A.: Heavy oil waterflooding: effects of flow rate and oil viscosity. J. Can. Pet. Technol. 48, 42–51 (2009)
McDonald, I., Dullien, F.: Correlating Tertiary Oil Recovery in Water-Wet Systems. SPE J., February, 7–9 (1976)
Melrose, J., Brandner, C.: Role of capillary forces in determing microscopic displacement efficiency for oil recovery by waterflooding. J. Can. Pet. Technol. 13, 64 (1974)
Moore, T., Slobod, R.: Displacement of oil by water-effect of wettability, rate, and viscosity on recovery. (paper 502-G presented at the 30th Annual Fall Meeting of the Petroleum Branch of the American Institute of Mining and Metallurgical Engineers, October 2–5, 1955, in New Orleans, Louisiana, USA) (1955)
Morrow, N.: Interplay of capillary, viscous and buoyamcy forces in the mobilization of residual oil. The Journal of Canadian Petroleum Technology, July-September, 35–46 (1979)
Morrow, N., Chatzis, I., Taber, J.: Entrapment and mobilization of residual oil in bead packs. SPE Reserv. Eng., 927 (1988)
Needham, R., Doe, P.: Polymer flooding review. J. Petrol. Technol. 39, 1503–1507 (1987)
Oh, S., Slattery, J.: Interfacial Tension Required for Significant Displacement of Residual Oil. SPE J., April, 83–96 (1979)
Ojeda, E., Preston, F., Calhoun, J.: Correlations of oil residuals following surfactant floods. Prod. Monthly 18, 20 (1953)
Perkins, F., Collins, R.: Scaling laws for laboratory flow models of oil reservoirs. Pet. Trans. AIME 219, 383 (1960)
Pope, G., Wu, W., Narayanaswamy, G., Delshad, M., Sharma, M., Wang, P.: Modeling relative permeability effects in gas-condensate reservoirs with a new trapping model. SPE Reserv. Eval. Eng. 3, 171–178 (2000)
Qi, L., Liu, Z., Yang, C., Yin, Y., Hou, J., Zhang, J., Shi, F.: Supplement and optimization of classical capillary number experimental curve for enhanced oil recovery by combination flooding. Sci. China Technol. Sci. 57, 2190–2203 (2014)
Qi, P., Ehrenfried, D., Koh, H., Balhoff, M.: Reduction of residual oil saturation in sandstone cores by use of viscoelastic polymers. SPE J. 22, 447–458 (2017)
Rabbani, H., Or, D., Liu, Y., Lai, C.-Y., Lu, N., Datta, S., Shokri, N.: Suppressing viscous fingering in structured porous media. Proc. Natl. Acad. Sci. USA 115, 4833–4838 (2018)
Rapaport, L.: Scaling laws for use in design and operation of water oil flow models. Trans. AIME 204, 143 (1955)
Rapaport, L., Leas, W.: Properties of linear water floods. Trans. AIME 198, 139–148 (1953)
Reed, K., Healy, R.: Some physicochecmical aspects of microemulsion flooding: a review. In: Shah, D., Schecheter, R. (eds.) Improved Oil Recovery by Surfactant and Polymer Flooding. Academic Press, New York (1977)
Rodriguez de Castro, A., Shokri, N., Karadimitriou, N., Oostrom, M., Joekar-Niasar, V.: Experimental study on nonmonotonicity of capillary desaturation curves in a 2-D pore network. Water Resour. Res. 51, 8517–8528 (2015)
Rowlinson, J., Widom, B.: Molecular Theory of Capillarity. Dover, Mineola (1982)
Rücker, M., Berg, S., Armstrong, R., Georgiadis, A., Ott, H., Schwing, A., Kersten, M.: From connected pathway flow to ganglion dynamics. Geophys. Res. Lett. 42, 3888–3894 (2015)
Saffman, P., Taylor, G.: The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. A 245, 312–325 (1958)
Schechter, D., Zhou, D., Orr, F.: Capillary Imbibition and Gravity Segregation in Low IFT Systems. (paper SPE 22594 presented at the 66th Annual Technical Conference and Exhibition of the Society of Petroleum Engineers held in Dallas, TX, October 6–9, 1991) (1991)
Schechter, D., Zhou, D., Orr, F.: Low IFT drainage and imbibition. J. Petrol. Sci. Eng. 11, 283–300 (1994)
Shen, P., Wang, J., Yuan, S., Zhong, T., Jiu, X.: Study of enhanced-oil-recovery mechanism of Alkali/Surfactant/Polymer flooding in porous media from experiments. SPE J. 14, 237–244 (2009)
Stegemeier, G.: Relationship of trapped oil saturation to petrophysical properties of porous media. (paper SPE 4754 prepared for the Improved Oil Recovery Symposium of the Society of Petroleum Engineers of the American Institute of Mining and Metallurgical Engineers, to be held in Tulsa, Oklahoma, April 22–24, 1974) (1974)
Stegemeier, G.: Mechanisms of Entrapment and Mobilization of Oil in Porous Media. In: Shah, D., Schecheter, R. (eds.) Improved Oil Recovery by Surfactant and Polymer Flooding. Academic Press, New York (1977)
Taber, J.: Dynamic and static forces required to remove a discontinuous oil phase from porous media containing both oil and water. Soc. Petr. Eng. J. 9, 3 (1969)
Taber, J.: Research on enhanced oil recovery: past, present and future. Pure Appl. Chem. 52, 1323–1347 (1980)
Wang, D., Cheng, J., Yang, Q., Gong, W., Li, Q.: Viscous-Elastic Polymer Can Increase Microscale Displacement Efficiency in Cores. (paper SPE 63227 presented at the 2000 SPE Annual Technical Conference and Exhibition held in Dallas, Texas, 1–4 October 2000) (2000)
Wang, D., Jiang, Y., Wang, Y., Gong, X., Wang, G.: Viscous-elastic polymer fluids rheology and its effect upon production equipment. SPE Production and Facilities, 19, 209-216. (paper SPE 77496 presented at the 2002 SPE Annual Technical Conference and Exhibition, San Antonio, Texas, 29 September—2 October, 2022) (2004)
Wang, D., Wang, G., Wu, W., Xia, H., Yin, H.: The Influence of Viscoelasticity on Displacement Efficiency—From Micro- to Macroscale. (paper SPE 109016 presented at the 2007 SPE Annual Technical Conference and Exhibition held in Anaheim, California, U.S.A., 11—14 November 2007) (2007)
Wang, Y., Zhang, C., Wei, N., Oostrom, M., Wietsma, T., Li, X., Bonneville, A.: Experimental study of crossover from capillary to viscous fingering for supercritical CO\(_2\)-Water displacement in a homogeneous pore network. Environ. Sci. Technol. 47, 212–218 (2013)
Wang, Y., Zhao, F., Bai, B., Zhang, J., Xiang, W., Li, X., Zhou, W.: Optimized Surfactant IFT and Polymer Viscosity for Surfactant-Polymer Flooding in Heterogeneous Formations. (paper SPE 127391 presented at the 2010 SPE Improved Oil Recovery Symposium held in Tulsa, Oklahoma, USA, 24–28 April 2010) (2010)
Whitaker, S.: Fluid motion in porous media. Ind. Eng. Chem. 61(12), 14 (1969)
Wu, W., Wang, D., Jiang, H.: Effect of the Visco-elasticity of Displacing Fluids on the Relationship of Capillary Number and Displacement Efficiency in Weak Oil-Wet cores. (paper SPE 109016 presented at the 2007 SPE Asia Pacific Oil & Gas Conference and Exhibition held in Jakarta, Indonesia, 30 October–1 November 2007) (2007)
Yiotis, A., Boudouvis, A., Stubos, A., Tsimpanogiannis, I., Yortsos, Y.: Effect of liquid films on the drying of porous media. AIChE J. 50, 2721–2737 (2004)
Yortsos, Y., Fokas, A.: An Analytical Solution for Linear Waterflood Including the Effects of Capillary Pressure. SPE Journal, February, 115–124 (1983)
Youssef, R.O.S., Peysson, Y., Bazin, B., Maire, E., Vizika, O.: Pore-scale to core-scale study of capillary desaturation curves using multi-scale 3d imaging. (paper SCA2013-027) (2013)
Zhang, C., Oostrom, M., Wietsma, T., Grate, J., Warner, M.: Influence of viscous and capillary forces on immiscible fluid displacement: pore-scale experimental study in a water-wet micromodel demonstrating viscous and capillary fingering. Energy Fuels 25, 3493–3505 (2011)
Zhang, H., Dong, M., Zhao, S.: Which one is more important in chemical flooding for enhanced court heavy oil recovery, lowering interfacial tension or reducing water mobility? Energy Fuels 24, 1829–1836 (2010)
Zhao, B., MacMinn, C., Juanes, R.: Wettability control on multiphase flow in patterned microfluidics. Proc. Natl. Acad. Sci. 113, 10251–10256 (2016)
Zhou, D., Fayers, F., Orr, F.: Scaling of multiphase flow in simple heterogeneous porous media (Vol. 12). (paper SPE27833 presented at the 9th Symposium on Improved Oil Recovery held In Tulsa, Oklahoma, 17–20 April 1994) (1997)
Acknowledgements
Financial support for this work from the China Natural Science Foundation (51834005), Science Foundation of China University of Petroleum, Beijing, (2462021XKBH008), the China Scholarship Council (201806440187), and Deutscher Akademischer Austauschdienst (91737128) is gratefully acknowledged.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Definition of Symbols
Recovery efficiencies are generally introduced by writing
The total recovery efficiency is then defined as

the (“microscopic”) displacement efficiency as

and the (“macroscopic”) volumetric displacement (or sweep) efficiency as

In this paper, we do not use the words microscopic and macroscopic in this way. Instead we use microscopic to mean “pore scale” and macroscopic to mean “Darcy scale” or “field scale” as discussed in subsection 2.1 of Sect. 2. The second equality in Eq. (23) identifies “amount” with “volume occupied”. And  ,
,  ,
,  denote remaining, missing and initial oil saturation. Efficiencies are pure numbers obeying \(0\le {E_\mathsf {R}},{E_\mathsf {D}},{E_\mathsf {V}}\le 1\), and the relation
denote remaining, missing and initial oil saturation. Efficiencies are pure numbers obeying \(0\le {E_\mathsf {R}},{E_\mathsf {D}},{E_\mathsf {V}}\le 1\), and the relation
holds by definition. Because the amount contacted cannot be measured as easily as the amount produced, the sweep efficiency remains somewhat ill defined.
Displacement efficiency \({E_\mathsf {D}}\) depends on many factors such as pore structure, pore distribution, microscopic heterogeneity, wettability and interfacial tension. It is generally believed that the sweep efficiency \({E_\mathsf {V}}\) is significantly affected, among other factors, by the mobility ratio between the displacing phase and the displaced phase (Lake 1989).
General EOR desaturation processes decrease the oil saturation  starting from an initial oil saturation
starting from an initial oil saturation  . If
. If  , then a process dependent residual oil saturation \(ROS\) is defined as
, then a process dependent residual oil saturation \(ROS\) is defined as

Equivalently, one has

where Eq. (23) has been used. In the literature the symbol  is often used for residual oil saturation instead of our symbol \(ROS\). Here, we prefer to define the symbol
is often used for residual oil saturation instead of our symbol \(ROS\). Here, we prefer to define the symbol  as the solution of the equation
as the solution of the equation

where  is the relative permeability function of oil, i.e.
is the relative permeability function of oil, i.e.  is a zero of
is a zero of  .
.
Let us now recall that the most significant parameter to affect or influence \(ROS\) (or  ), and hence \({E_\mathsf {D}}\), is capillary number
), and hence \({E_\mathsf {D}}\), is capillary number
Capillary forces are responsible, in part, for the inefficiency of the displacement of oil from petroleum reservoirs during water flooding. In this paper, the convention is used to call a function that relates  and other parameters of the EOR-process with residual oil saturation \(ROS\)
and other parameters of the EOR-process with residual oil saturation \(ROS\)

a capillary desaturation curve (CDC), while the function

is called a capillary number correlation (CNC). For  one finds \(CDC=CNC\). More generally, for
one finds \(CDC=CNC\). More generally, for  and
and  the \(CDC\)-functions and \(CNC\)-functions are related as
the \(CDC\)-functions and \(CNC\)-functions are related as

by virtue of Eq. (26). More precise definitions are given in Appendix B.
Definition of Capillary Desaturation Curves
An EOR process starting from an initial oil saturation  may depend on many parameters and conditions, but it always ends at some residual oil saturation \(ROS\). To define precisely the capillary desaturation function \(CDC\) in Eq. (28a) some standard mathematical notation is used, that may be unfamiliar to the reader. The notation
may depend on many parameters and conditions, but it always ends at some residual oil saturation \(ROS\). To define precisely the capillary desaturation function \(CDC\) in Eq. (28a) some standard mathematical notation is used, that may be unfamiliar to the reader. The notation
is used to denote a mapping f that maps the domain \(A\times B\) to a set C (called range of f), where \((a,b)\mapsto c=f(a,b)\) means that the element \((a,b)\in A\times B\) is mapped to the element \(c=f(a,b)\in C\). The symbol \(\times \) is the Cartesian product of sets. To define \(CDC\) one first introduces a mapping

that maps initial saturation and other parameters of the EOR process, the fluids, the rock, etc., to \(ROS\) called desaturation correlation. In Eq. (30) the set {EOR} stands for the set of parameters of the EOR desaturation process, such as number of pore volumes flooded, {fluids} stands for fluid parameters such as viscosities, interfacial tension, initial fluid configuration, etc., and {rocks} stands for reservoir parameters such as rock types, topological pore structure, pore geometry, surface roughness, wetting properties, etc. If the capillary number can be used to reduce the number of independent parameters in the desaturation correlation Eq. (30), then a simplified function

can be defined that has fewer arguments than \(DC\). It is called capillary number correlation (CNC) or capillary desaturation curve (CDC).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Guo, H., Song, K. & Hilfer, R. A Brief Review of Capillary Number and its Use in Capillary Desaturation Curves. Transp Porous Med 144, 3–31 (2022). https://doi.org/10.1007/s11242-021-01743-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-021-01743-7


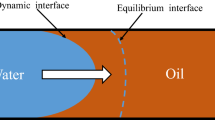


 ’s, 12 microscopic
’s, 12 microscopic  ’s and 24 mixed
’s and 24 mixed  ’s contain only macroscopic quantities, microscopic
’s contain only macroscopic quantities, microscopic  ’s contain only microscopic quantities and mixed
’s contain only microscopic quantities and mixed 




 the lower is
the lower is 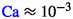 to
to 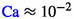 achieved to date in the laboratory residual oil often approaches zero. Classical CDCs are expected to approach zero, i.e.
achieved to date in the laboratory residual oil often approaches zero. Classical CDCs are expected to approach zero, i.e. 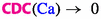 , for
, for 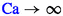 .
.

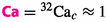 resp.
resp. 





 ’s, 12 microscopic
’s, 12 microscopic  ’s and 24 mixed
’s and 24 mixed 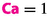 . This fact has been overlooked for a long time.
. This fact has been overlooked for a long time. as a crucial parameter, macroscopic capillary numbers are based on macroscopic capillary pressure which is affected not only by fluid-fluid interfacial tension
as a crucial parameter, macroscopic capillary numbers are based on macroscopic capillary pressure which is affected not only by fluid-fluid interfacial tension  , but also by numerous other geometrical and physical parameters of the displacement.
, but also by numerous other geometrical and physical parameters of the displacement.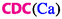 are mainly based on microscopic
are mainly based on microscopic  and mixed
and mixed  implying the use of surfactants in EOR to reduce interfacial tension
implying the use of surfactants in EOR to reduce interfacial tension  to ultra-low values and/or polymers to increase viscosity. This doctrine to reduce
to ultra-low values and/or polymers to increase viscosity. This doctrine to reduce  to ultra-low values is very widespread in chemical EOR.
to ultra-low values is very widespread in chemical EOR.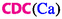 based on microscopic or mixed numbers, for macroscopic
based on microscopic or mixed numbers, for macroscopic 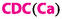 the transition from capillary force dominated flow to viscous force dominated flow happens at macroscopic
the transition from capillary force dominated flow to viscous force dominated flow happens at macroscopic 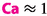 , which seems to be more reasonable.
, which seems to be more reasonable. . A notable attempt to correlate them was made with
. A notable attempt to correlate them was made with 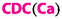 functions may call for alternative screening EOR strategies and new experiments.
functions may call for alternative screening EOR strategies and new experiments.