Abstract
Understanding the evolution of solute concentration gradients underpins the prediction of porous media processes limited by mass transfer. Here, we present the development of a mathematical model that describes the dissolution of spherical bubbles in two-dimensional regular pore networks. The model is solved numerically for lattices with up to 169 bubbles by evaluating the role of pore network connectivity, vacant lattice sites and the initial bubble size distribution. In dense lattices, diffusive shielding prolongs the average dissolution time of the lattice, and the strength of the phenomenon depends on the network connectivity. The extension of the final dissolution time relative to the unbounded (bulk) case follows the power-law function, \({B^k/\ell }\), where the constant \(\ell\) is the inter-bubble spacing, B is the number of bubbles, and the exponent k depends on the network connectivity. The solute concentration field is both the consequence and a factor affecting bubble dissolution or growth. The geometry of the pore network perturbs the inward propagation of the dissolution front and can generate vacant sites within the bubble lattice. This effect is enhanced by increasing the lattice size and decreasing the network connectivity, yielding strongly nonuniform solute concentration fields. Sparse bubble lattices experience decreased collective effects, but they feature a more complex evolution, because the solute concentration field is nonuniform from the outset.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Growth and dissolution of gas bubbles are phenomena commonly encountered in various industrial and environmental applications that involve porous media. Understanding the evolution of bubble clusters and the associated collective effects is paramount to the effective design of the following exemplary processes. The structural integrity of concrete during freeze-thaw cycles can be improved through the artificial entrainment of air bubbles (Mayercsik et al. 2016). Preventing bubble nucleation and growth within nanoporous electrodes used in electrochemical cells is key to preclude their mechanical failure (Kadyk et al. 2016). The nucleation of gas upon pressure depletion in producing oil reservoirs is a mechanism that can aid recovery by promoting the transport of reservoir fluids (Gao et al. 2021). The long-term effectiveness of carbon dioxide subsurface storage relies on trapping a buoyant plume by capillary forces to form isolated bubbles in the pores of the rocks that will eventually dissolve in the surrounding fluid (Krevor et al. 2015). In these examples, the porous medium not only defines the framework that confines the bubbles, but it controls their mobility and the transport of species between them.
The classical theory describing the dissolution of an isolated and stationary gas bubble in a quiescent liquid was presented by Epstein and Plesset (1950). Briefly, the driving force for the dissolution process is given by the difference between the bubble’s surface concentration and the solute concentration in the diffusion boundary layer that is formed in the liquid surrounding the bubble. The surface concentration is proportional to the bubble’s internal pressure, which accounts for surface curvature effects through the contribution of the Laplace pressure. For the case where the volume of ambient liquid is sufficiently large, Epstein and Plesset (1950) derived an analytical expression for the dissolution flux, which can be used to estimate the temporal evolution of the bubble radius (see Sect. 2). Extensions to this theory have been presented to describe the behaviour of a bubble attached at a flat surface (Enríquez et al. 2014; Peñas-López et al. 2015) or to account for confinement affects introduced by the presence lateral walls (Moreno Soto et al. 2020), as can be the case in some microfluidic devices.
When multiple bubbles are present in a quiescent liquid, collective effects appear as a result of the spatial and temporal evolution of the solute concentration field in the liquid surrounding the bubbles. Diffusive shielding is observed for neighbouring bubbles within close proximity (Weijs et al. 2012): a bubble is protected from dissolution as the local liquid concentration rises upon dissolution of the neighbouring bubble. When the difference between the sizes of two neighbouring bubbles (and hence their surface concentration) is sufficiently large, Ostwald ripening can occur (Ostwald 1897), a process where the larger bubble grows at the expense of the smaller bubble (Lifshitz and Slyozov 1961; Voorhees 1985; Schmelzer and Schweitzer 1987). Notably, a densely populated cluster of bubbles with initial uniform size can produce a characteristic dissolution pattern, where bubbles on the outer layer dissolve faster than those on the inner layers (Weijs et al. 2012; Laghezza et al. 2016). In such cases, the interplay between Ostwald ripening and diffusive shielding may give rise to situations where bubbles undergo periods of growth and dissolution alternately, and layers no longer dissolve regularly (Michelin et al. 2018; Vega-Martínez et al. 2020).
In contrast to the case of bubbles in bulk, collective effects of bubbles within porous media are relatively unexplored. The presence of the solid framework challenges the analysis of these systems by introducing at least two controlling effects on the dissolution process. First, the morphology of the pore space determines the gas-liquid interface curvature, meaning that an individual bubble can have more than one local curvature (Garing et al. 2017). It follows that the size of the bubble is no longer sufficient to predict the bubble’s dissolution rate and situations may arise where smaller bubbles grow at the expense of larger bubbles (Xu et al. 2017)—opposite to the classic Ostwald ripening. Moreover, it has been shown by means of experiments (Xu et al. 2017) and numerical models (Chalendar et al. 2018), that in porous media an equilibrium condition is possible where multiple bubbles coexist—opposite to the behaviour of bubbles in bulk liquid (Schmelzer and Schweitzer 1987). The second controlling effect has so-far received limited attention and is associated with the interplay between dissolution and transport fluxes in partially saturated porous media. In fact, the disconnected phase is expected to act as highly effective disperser by increasing the tortuosity of transport paths in the liquid phase, limiting the dissolution rate and affecting the solute concentration field beyond the characteristic length scale of a pore-body. Quantifying this effect remains very challenging, because it is difficult to probe experimentally at the required spatial and temporal resolution concentrations of chemical species “hidden” in porous media.
In this work we develop a pore network model to investigate the collective dissolution of bubbles in regular porous media. Compared to previous work that also used a pore-network model, in our formulation we explicitly account for the accumulation of solute in the pores, enabling us to analyse the spatial and temporal evolution of the solute concentration field. Our focus in this study is on lattices consisting of bubbles smaller than one pore body. Our aim is to unravel the interplay between the evolution of the bubble cluster and of the solute concentration field. We present the derivation of the mathematical model that includes material balances for both the bubbles and the solute in the liquid phase. The model is solved to investigate a range of situations, including networks with distinct connectivity as well as lattices with nonuniform bubble distributions (in terms of both size and location).
2 Dissolution of an Isolated Bubble
Consider the case of an isolated single-component gas bubble surrounded by a quiescent incompressible liquid in an unbounded domain. The internal pressure of the bubble, \(P_\mathrm{b}\), is contributed by the pressure of the liquid, \(P^0\), and the Laplace pressure, \(\Delta P\), which is inversely proportional to the bubble radius, R:
where \(\gamma\) is the interfacial tension. Assuming ideal gas behaviour, an expression is found that relates the mass density of the gas within the bubble ρb to the gas density at a planar interface \(\rho ^\mathrm{0}\):
where M is the gas molar mass, \(R_\mathrm{g}\) is the universal gas constant and T is the temperature. Depending on the concentration of gas in the liquid, mass transfer across the gas-liquid interface occurs according to the following mass balance:
where \(m_\text{ b }\) is the mass of gas in the bubble and J the outward diffusive mass flux of gas across the bubble interface. Assuming spherical symmetry and neglecting inertial effects due to the motion of the bubble interface, this diffusive flux can be described by the following expression (Epstein and Plesset 1950):
where D is the diffusion coefficient of the gas-liquid pair and t is time; \(C^0\) is the constant gas concentration in the liquid far from the bubble interface, while \(C_\mathrm{s}\) is the saturation concentration in equilibrium with the internal bubble pressure (i.e. the concentration at the interface). The latter is obtained from Henry’s law, such that \(C_\mathrm{s} = k_\mathrm{H} M P_\mathrm{b}\) and where \(k_\mathrm{H}\) is the Henry’s constant. Accordingly, \(f= C^0/C^0_\mathrm{s}\) refers to the degree of liquid saturation relative to the saturation concentration of a planar interface \(C^0_\mathrm{s} = k_\mathrm{H} M P^0\). Equation 4 is a good approximation to describe the evolution of solute concentration around a dissolving bubble, because the motion of the fluid caused by the motion of the bubble has a negligible effect in these conditions (Epstein and Plesset 1950).
Noting that \(m_\mathrm{b} = 4/3\pi {R}^3\rho _\mathrm{b}\) and upon substitution of Eqs. 4 and 2 into Eq. 3, one obtains the expression for the rate of change in the bubble radius.
The transient term, \(1/\sqrt{\pi D t}\), related to the time needed for the gas concentration profile in the boundary layer to develop, has been dropped from Eq. 4 because it is negligibly small compared to the dissolution time, as demonstrated experimentally in Duncan and Needham (2004). Equation 5 can be integrated to yield the final dissolution time \(t_\mathrm{d}^*(R=0)\) of a single isolated bubble of initial radius \(R^0\) in a gas-saturated liquid solution (\(f=1\)) (Duncan and Needham 2004):
We will use \(t_\mathrm{d}^*\) throughout this work as the reference to quantify effects associated with the presence of a pore-network and a lattice of bubbles. We note that an important consequence of Eqs. 1 and 5 is that a bubble can dissolve even if \(C^0>C^0_\mathrm{s}\) (i.e. \(f>1\)). In fact, the liquid saturation at which a bubble is in equilibrium with the surrounding liquid depends on its initial radius:
Accordingly, a bubble is expected to grow if \(f>f_\mathrm{eq}\) and dissolve if \(f<f_\mathrm{eq}\).
3 Pore Network Model for the Collective Dissolution of Bubbles
A pore-network model (PNM) is a computationally efficient framework to simulate flow and transport processes in porous media (Fatt 1956; Valvatne et al. 2005; Xiong et al. 2016). A PNM simplifies the void space of a given porous medium by a lattice of pore bodies connected by pore throats, describing them with simple geometries, e.g. spheres and cylinders, respectively. The connectivity and distribution of throat and pore sizes determine the macroscopic flow and transport properties of the network, which are simulated using fundamental mass and momentum balance equations. Direct modelling approaches, such as the lattice Boltzmann method or density functional modelling, are computationally less efficient compared to PNM, particularly for problems that necessitate locating and tracking interfaces between fluid phases in complex geometries (Blunt et al. 2013). Another notable feature of PNM is that they can be solved for relatively large systems (with physical length of several centimetres), enabling the study of upscaling behaviours in porous media over the range from the pore- to the continuum-scale (Held and Celia 2001). PNMs are being increasingly used to predict two-phase flow properties (e.g. capillary pressure or relative permeability curves) (Joekar-Niasar et al. 2008), and to simulate electrokinetic (Obliger et al. 2014; Gayon Lombardo et al. 2019) and reactive transport processes (Varloteaux et al. 2013; Mahmoodlu et al. 2020).
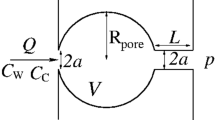
In this study, we develop and solve a PNM to simulate the collective dissolution of gas bubbles in regular pore networks partially filled with a quiescent liquid. We focus on a simple representation of the network, where spherical nodes and cylindrical edges represent the pore bodies and pore throats, respectively (Fig. 1). Unlike previous computational work on the evolution of bubbles in porous media (Xu et al. 2017; Chalendar et al. 2018), we solely consider bubbles that are smaller than one pore body (\(R<R_\mathrm{p}\) for \(t\ge 0\)), so as to ensure that they maintain a spherical shape throughout the dissolution process. This further implies that each bubble is immobile, its centre of mass coinciding with the centre of the pore body during the entire dissolution or growth process. This is an important simplification of our approach, because we neglect interactions between the bubble and the solid surface, which in turn lead to the formation of non-spherical bubbles that are characterised by a distribution of curvatures. However, the simplification allows us to reduce the numerical complexity of the problem and to explore relatively large networks of bubbles, while accounting explicitly for the inter-bubble transport of dissolved species. To this end, we consider two physical mechanisms which occur as a bubble dissolves in a pore body, namely i) mass exchange at the bubble/liquid interface and ii) diffusive transport of the dissolved gas between neighbouring pore bodies. We further assume isothermal conditions, ideal gas behaviour, and negligible inertial effects. At any given time, the concentration of the liquid within a pore body is assumed to be uniform. This assumption holds when
where \(t_\mathrm{diff}\) is a time scale for solute diffusion across a pore body of radius \(R_\mathrm{p}\). This condition is satisfied for the fluid pair considered in this study, namely nitrogen and water at ambient conditions (temperature of 298 K and absolute pressure of 101.325 kPa), because \(t_\mathrm{diff}/t_\mathrm{d}^*<0.1\) when \(R_\mathrm{p}\le 12\).
Basic elements of the pore network model developed in this study. (a) Two spherical pore bodies of radius \(R_{\mathrm {p}}\) are filled with a liquid of uniform solute concentration (\(C_{\mathrm {p},i}\) and \(C_{\mathrm {p},j}\), respectively). These are connected to other pore bodies through four cylindrical throats of length \(L_\mathrm {t}\) to form a larger pore network of connectivity, \(N_\mathrm{t} = 4\). Pore body i contains a spherical gas bubble of radius \(R_{i}\), density \(\rho _{i}\) and equilibrium surface concentration \(C_{\mathrm {s},i}\). (b) Drawings of the three pore connectivity structures considered in this study, namely \(N_\mathrm{t}=\{4,6,8\}\)
3.1 Material Balances
Consider a stationary gas bubble i of radius \(R_i\) within a pore body i of volume \(V_{\mathrm{p},i}\), which is connected to \(N_{\mathrm {t},i}\) pore bodies, as depicted in Fig. 1. We can write the following material balance for the solute in pore body i:
where \(m_\mathrm{d}=C_\mathrm{p}(V_\mathrm{p}-4\pi {R}^3/3)\) and \(m_\mathrm{b}=4\pi {R}^3\rho _\mathrm{b}/3\) are the mass of solute in the liquid and gas phase, respectively. The second term on the right-hand side of the equation refers to the mass transfer by solute diffusion between adjacent pore bodies and includes a summation over \(N_{\mathrm {t},i}\) pore body pairs (\(A_{\mathrm{t}}\) and \(L_{\mathrm{t}}\) are the cross-sectional area and length of the throat connecting two pore bodies). The rate of change in mass of solute in the liquid and gas phase is expressed as follows:
where the evolution of the bubble radius is given by Eq. 5 upon replacing \(C^0\) with \(C_\mathrm{p}\), i.e.:
In contrast to Eq. 5, where \(C^0\) is treated as a constant, the temporal evolution of dissolved solute concentration in pore i, \(C_{\mathrm{p,}i}\), is thus obtained by combining Eq. 10 with Eq. 9:
where \(\epsilon _i = (V_{\mathrm{p}} - 4\pi R_i^3/3)/ V_{\mathrm{p}}\) is the volume fraction of pore i occupied by the liquid phase.
3.2 Numerical Implementation
Equations 11 and 12 represent the system of coupled differential equations to be solved for the two variables \(C_{\mathrm{p},i}\) and \(R_i\) in a given pore body. For a network of P pore bodies, this set of equations has to be solved simultaneously for all pore bodies at each time step. To solve these equations numerically, we represent the pore network using graph theory and rewrite Eq. 12 in vector form:
where \(\dot{\mathbf {C}}_\mathrm{p}, \mathbf {\epsilon }, \mathbf {C_\mathrm{p}}\), \(\mathbf {R}\) and \(\dot{\mathbf {R}}\) are \((P\times 1)\) vectors that include the elements of \(\frac{\mathrm{d}C_{\mathrm{p},i}}{\mathrm{d}t}, \epsilon _i, C_{\mathrm{p},i}, R_{i}\) and \(\frac{\mathrm{d}R_{i}}{\mathrm{d}t}\), respectively. \(\mathcal {L}\) is a \((P\times P)\) Laplacian matrix defined as follows:
The resulting system of ordinary differential equations is solved using the ode45 solver in MATLAB with a relative error tolerance ‘RelTol’ \(= 10^{-8}\) and absolute error tolerances on the variables R and \(C_\mathrm{p}\) of \(10^{-4} \mu m\) and \(10^{-10}\)kg/m\(^3\). For the variable R the NonNegative option is additionally implemented. We consider regular pore-networks with uniform pore and throat dimensions (see Table 1). At \(t=0\), the concentration of the liquid phase is uniform throughout the network and takes a value corresponding to a saturation \(f=1\), i.e. \(C_\mathrm{p}(t=0)=C^0_\mathrm{p}=C^0_\mathrm{s}\). The simulation is initialised by populating the centre of the network with a lattice of bubbles with either uniform size, \(R^0\), or with an initial size distribution; the lattice may or may not contain vacant sites. For the calculations presented in this work the ratio pore body radius to initial bubble radius is chosen in the range \(2.5\le {R_\mathrm{p}}/R^0\le 12\), thereby ensuring that the condition \(R<R_\mathrm{p}\) is met for the duration of the simulation. An open boundary condition is imposed by setting the radius of the pore bodies in the outermost layer of the network to a value \(100\times {R}_\mathrm{p}\). The model was validated against the Epstein-Plesset equation (Eq. 5) for the case of a single bubble dissolution in a large pore body (\(R_\mathrm{p}/R^0 = 100\)). For all the simulations reported in this study, a negligible error (\(<10^{-10}\%\)) is observed in the material balance computed at each time step.
4 Results
We will first consider the case of a single, isolated bubble in a pore network and compare the numerical results to those obtained for an unconfined bubble. We will then present situations featuring regular arrangements of bubble lattices of different sizes within pore networks of different connectivity. These cases will be analysed in light of the evolving bubble size distribution and solute concentration field.
4.1 Dissolution of a Single Bubble in a Pore Network
Temporal evolution of the dimensionless bubble radius z (top row) and of the normalised concentration difference \(\Delta {c}\) (bottom row) for an isolated bubble in a liquid. (a) and (d): unconfined bubble, liquid at different initial saturation values, \(f^0\). (b) and (e): bubble in a pore network (\(N_\mathrm{t} = 6\) and \(R_\mathrm{p}/R^0=2.5\)), liquid at different initial saturation values, \(f^0\). (c) and (f): bubble in a pore network (\(N_\mathrm{t} = 6\), \(R_\mathrm{p}/R^0=\{1.2,2.5,4.2,12\}\)), liquid at initial saturation \(f^0=1\)
The evolution of the normalised bubble radius, \(z=R/R^0\), is plotted in Fig. 2 as a function of the normalised dissolution time, \(\tau =t_\mathrm {d}/t^*_\mathrm {d}\), in (a) the absence and in (b) the presence of a pore network surrounding the bubble (\(N_\mathrm {t}=6\)). In each plot, the different lines refer to simulations carried out for different values of the initial liquid saturation, \(f^0 = {C_\mathrm{p}^0}/{k_\mathrm{H} M_\mathrm{w} P^0}\) (above and below the so-called threshold saturation, \(f_\mathrm{eq}(R^0)=2.4\)). As expected, in both cases the bubble dissolves completely when \(f<f_\mathrm{eq}\) and it grows when \(f>f_\mathrm{eq}\). We note that the simulations with a pore network are limited to situations where \(z<R_\mathrm {p}/R^0\), because we do not consider in this study bubbles that grow beyond the size of a single pore body. In both cases, the dissolution curves indicate a characteristic acceleration, which originates from the increase in the Laplace pressure as the bubble radius decreases. The solute concentration in the liquid, \(C_\mathrm {p}\), is largely unaffected by the dissolution (or growth) of the bubble, because the volume of the liquid is much larger than the volume of the bubble. Accordingly, upon dissolution the normalised concentration difference, \(\Delta {c}=(C_\mathrm{s} - C_\mathrm{p})/| C_\mathrm{s}^0 - C_\mathrm{p}^0 |\), increases and mirrors the pattern outlined by the evolution of the bubble radius (Fig. 2d and e). The same applies for the growth curves, albeit the evolution of z (or \(\Delta {c}\)) is significantly slower. The main difference between the unbounded and the confined case is that the presence of the pore network extends the lifetime of the bubble, because solute transport can occur only through pore throats. For \(f^0 = 2.2\) and \(R_\mathrm{p}/R^0=2.5\), the dissolution time of the bubble in the network is up to 1.6 times larger than its unbounded counterpart. As one would expect, the effect of confinement reduces with increasing pore body size (Fig. 2c and f) and our simulations show that the effect becomes negligible beyond \(R_\mathrm{p}/R^0 = 12\). An analogous effect arising from a reduction in available mass transfer area has been reported for a bubble in contact with a non-permeable surface (Weijs and Lohse 2013; Peñas-López et al. 2015).
4.2 Dissolution of a Bubble Lattice in a Pore Network
The results discussed above are extended here to a situation where a dense cluster of 19 bubbles with uniform initial size is arranged in the centre of a regular pore network (\(N_\mathrm {t}=6\), \(R_\mathrm{p}/R^0=2.5\) and \(f^0=1\)). We use \(N_\mathrm{L}\) to denote the size of the lattice, i.e. in this case, the bubble cluster with two layers is denoted as \(N_\mathrm{L} = 2\). Figure 3a illustrates the initial arrangement of the 19 bubbles (\(\tau =0\)) and the spatial evolution of the normalised solute concentration field, \(c_\mathrm{p}= C_\mathrm{p}/C_\mathrm{p}^0\), at three distinct times (\(\tau =2, 3, 4.5\)). Upon dissolution, the solute plume expands radially, while the dissolution front propagates in the opposite direction, meaning that bubbles in the outermost layer of the original lattice dissolve first. The inward propagation of the dissolution front is the manifestation of the so-called diffusive shielding effect (Michelin et al. 2018), which sustains a larger solute concentration in the centre of the original bubble lattice and reduces the dissolution rate of bubbles located there. A closer inspection of Fig. 3a also reveals that bubbles in a given layer do not necessarily dissolve at the same time (see panel at \(\tau =3\), where the outermost layer of bubbles shows partial dissolution). These results demonstrate that despite having the same initial radius, the lifetime of each bubble depends strongly on its location relative to its neighbours. In Fig. 3b are shown four characteristic dissolution curves associated with this specific bubble lattice. It can be seen that depending on their location (indicated by the colour-coding), a bubble can undergo periods of dissolution and growth alternately, before dissolving completely. As anticipated above, the reason for this is the local development of the solute concentration in the pore network, as shown by the solute concentration curves for the same four pore bodies plotted in Fig. 3c. Here, \(\Delta {c}>0\) for a dissolving bubble, but \(\Delta {c}\) may also alternate between positive (dissolution) and negative (growth) values for bubbles located in the inner layers of the lattice experiencing diffusive shielding. We observe that the final dissolution time of the central bubble is approximately six times larger than the value observed for a single bubble in the same pore network. Collective effects can thus have a significant influence on the lifetime of a given bubble in the lattice.
Dissolution of \(B=19\) bubbles of equal initial radius (\(R^0=1~\mu\)m) arranged to form a hexagonal lattice in a regular pore network (\(N_\mathrm{t}=6\)) with initial liquid saturation, \(f^0=1\). (a) Evolution of the solute concentration field in the pore network at four different dimensionless times, \(t=\{0,2,3,4.5\}\) (the colour scale indicates the normalised solute concentration in each pore body and a black circle indicates the presence of a bubble). (b) Temporal evolution of the dimensionless bubble radius z and (c) of the normalised concentration difference \(\Delta {c}\) for four representative bubbles (the colour of each curve refers to the location of the bubble shown in the inset)
Evolution of the solute concentration field generated by the dissolution of a square lattice of \(B=121\) bubbles (\(R^0=1~\mu\)m) arranged in a regular pore network (\(R_\mathrm{p}/R^0=2.5\)) with (a) \(N_\mathrm {t}=4\) and (b) \(N_\mathrm {t}=8\) connections, and filled with liquid at initial saturation, \(f^0=1\). The colour scale indicates the normalised solute concentration in each pore body and a black circle indicates the presence of a bubble. The dimensionless time, \(\tau\), and the normalised average solute concentration in the network, \(\overline{c}_\mathrm {p}\), are given on top of each panel
4.3 Bubble Lattices in Pore Networks with Distinct Connectivity
The results presented above highlight the role of network connectivity in the dissolution process by controlling the rate at which the solute plume dissipates through the system. In the following, we examine the effect of connectivity in more detail by studying the spatial and temporal evolution of a square lattice of 121 bubbles with uniform initial size arranged in regular pore-networks (\(R_\mathrm{p}/R^0=2.5\) and \(f^0=1\)) with two different connectivity values, namely \(N_\mathrm {t}=4\) and \(N_\mathrm {t}=8\). Snapshots of the evolving solute concentration field in these two pore networks are presented in Fig. 4a (\(N_\mathrm {t}=4\)) and Fig. 4b (\(N_\mathrm {t}=8\)). Again, we observe that the solute plume expands radially as time progresses and the bubbles dissolve. However, in contrast with the previous case, the propagation of the dissolution front is less obvious, whereby some bubbles located in the inner layers of the original square lattice dissolve faster than some of those located in the outer layers, generating lattices with vacant sites. This characteristic dissolution pattern, referred to as “leap-frogging", has been reported previously for dense two-dimensional bubble lattices in bulk (Michelin et al. 2018). Here, the presence of the pore-network introduces an additional level of complexity, because the discrete connectivity of bubbles perturbs the shielding effect and leads to irregular dissolution patterns of the lattice. Bubbles act both as sources and sinks for dissolved species and network connectivity controls the rate at which a pore body can reach a saturation sufficient to reverse the dissolution process relative to the rate at which the solute can dissipate out of the pore-network. As a result of this competition, the pore-network with \(N_\mathrm {t}=4\) shows a slower solute dissipation and bubble dissolution rate than \(N_\mathrm {t}=8\) (at least a factor of two slower, as indicated by the evolution of the average solute concentration in Figure S1, Supporting Information). Most notably, the reduced number of connections in \(N_\mathrm {t}=4\) between pore bodies generates bubble lattices with more vacant sites as dissolution progresses, leading to a more heterogeneous solute concentration field, as compared to the case with \(N_\mathrm {t}=8\).
The temporal evolution of the dimensionless bubble radius z as a function of the dimensionless time, \(\tau\), for eight representative bubbles of a square lattice (\(R^0=1~\mu\)m, \(B=121\) and \(N_\mathrm {L}=5\)) arranged in a two-dimensional regular pore network (\(R_\mathrm {p}/R^0=2.5\)) with (a) \(N_\mathrm {t}=4\) and (b) \(N_\mathrm {t}=8\) connections and filled with a liquid a initial saturation, \(f^0=1\). The colour of each curve refers to the location of the bubble, as shown in Figure 5a and b (\(N_\mathrm {L}=5\))
Bi-dimensional maps of the bubbles’ order of dissolution are shown in Fig. 5 for the lattice with five layers described above (\(N_\mathrm {L}=5\)) in the two pore-networks (\(N_\mathrm {t}=4\) and \(N_\mathrm {t}=8\)), alongside results for three additional lattices, namely \(N_\mathrm {L}=3, 4\) and 6. It can be seen that increasing the lattice size and decreasing the network connectivity both lead to stronger perturbations in the propagation of the dissolution front. While for \(N_\mathrm {L}=3\), the two networks generate an almost identical order of dissolution, differences are readily apparent for larger lattices. Yet, the alternation of the order of dissolution between successive bubble layers (the “leap-frogging” effect (Michelin et al. 2018)) is the strongest for the network with \(N_\mathrm {t}=4\), while a pattern that approximates a uniform radial dissolution front is still observed for the largest lattice in the network with \(N_\mathrm {t}=8\). The reduced solute diffusivity through the network increases the lifetime of bubbles and provides the opportunity for the bubbles to grow, as shown by the \(z-t\) curves plotted in Fig. 6a (\(N_\mathrm {t}=4\)) and Fig. 6b (\(N_\mathrm {t}=8\)) for a selection of representative bubbles (their colour coding refers to the lattice with \(N_\mathrm {L}=5\) shown in Fig. 5). It can be seen that bubbles may experience significant growth (up to \(z\approx 2.1\) for \(N_\mathrm {t}=4\) and \(z\approx 1.4\) for \(N_\mathrm {t}=8\)) before dissolving completely. For the case with \(N_\mathrm {t}=4\), the largest bubble reaches a size \(z\approx {R}_\mathrm {p}/R_\mathrm {0}=2.5\), further indicating that for a large bubble lattice within a porous medium with low connectivity, it may be possible for bubbles to grow beyond the size of a single pore body.
5 Discussion
We have established that the dissolution behaviour of bubbles in pore networks is highly affected by the collective interaction between the bubbles and by the diffusive transport in the liquid surrounding them. The presence of the pore-network extends the lifetime of bubbles relative to the unbounded (bulk) case and the network connectivity determines the strength of this effect. Similar to the situation of a bubble lattice in an unbounded bulk liquid, our results show complete dissolution of bubbles. The reason for this behaviour is twofold. First, the volume fraction of the gas compared to the liquid is relatively small and we only consider here networks with an open boundary. Secondly, while we do consider the presence of a pore-network, in our model formulation we do not allow for interactions between a bubble and the solid surface. As such, the model cannot capture certain realistic scenarios, in which bubbles can grow beyond a pore body or feature multiple local curvatures, and in which a stable coexistence of multiple bubbles can be observed (Xu et al. 2017). Examples of such systems include the nucleation and growth of bubbles in oil fields operated below the bubble point (Gao et al. 2021) or the trapping of gas ganglia following the injection of CO\(_2\) for subsurface storage (Andrew et al. 2013). In these and other applications, the dissolution or growth of bubbles does not solely depend on their morphology, but also on the local spatial structure of the solute concentration field. The latter is largely determined by the distribution of local liquid/gas interface curvatures, which has been introduced in our model by considering bubbles of different sizes. The measurement of chemical concentration gradients in porous media remains an experimental challenge and pore-network models can go a long-way in addressing this problem. In this context, we envisage a future formulation of the model, where both effects (complex bubble morphology and local development of solute concentration) are explicitly accounted for. In the discussion that follows, we extend an available correlation for the final dissolution time of unbounded bubbles to bubbles in pore networks. Bubbles lattices of practical relevance are considered next, such as those that contain vacant sites and bubbles of initial varying size.
The maximum lifetime gain of a bubble, \(\tau _\mathrm {max}-1\), as a function of the number of bubble B in a square lattice arranged in a two-dimensional regular pore-network filled with liquid at initial saturation, \(f^0=1\) (\(R^0=1~\mu\)m, \(R_\mathrm {p}/R^0=2.5\), \(N_\mathrm {L}=\{0,1,2,3,4,5,6\}\). Square and circle markers refer to results obtained for a pore-network with \(N_\mathrm {t}=4\) and \(N_\mathrm {t}=8\) connections, respectively. The dashed curves are obtained upon fitting a power-law function, \(B^{k}/\ell\), to the simulation results, where the inter-bubble spacing, \(\ell = 7\). The solid line refers to the lifetime gain of a bubble in lattices of unbounded bubbles with an equivalent inter-bubble spacing of \(7 R^0\) (Michelin et al. 2018)
5.1 Lattice Size and Final Dissolution Time
As shown by Michelin et al. (2018) for two-dimensional lattice of bubbles suspended in a liquid, the maximum gain in the lifetime of a bubble scales as \({B}^{0.5}/\ell\), where B is the total number of bubbles in the lattice and \(\ell\) is the spacing between bubbles normalised by the initial radius. We extend here the analysis to pore networks containing a square lattice of bubbles and compute the final dissolution time relative to the value observed for a single unbounded bubble, \(\tau _\mathrm {max}-1\). The results are shown in Fig. 7 for lattices of different size B and for two pore networks (\(N_\mathrm {t}=4\) and \(N_\mathrm {t}=8\)). The results presented here are obtained for pore networks with \(\ell = 7\), thus are fitted to the power law: \(B^k/7\). We obtain \(k = {1.5}\) and \(k = {1.2}\) for \(N_\mathrm {t}=4\) and \(N_\mathrm {t}=8\), respectively, indicating that collective effects in a pore network produce a stronger increase in the lifetime of bubbles and that the strength of this effect is inversely proportional to the pore-network connectivity. In this context, the unbounded case (\(k= {0.5}\)) is equivalent to an infinite number of connections between bubbles and can thus be regarded as the theoretical lower limit for the final dissolution time.
5.2 Dissolution of Bubble Lattices with Vacant Sites
To analyse collective dissolution effects for bubble lattices with vacant sites, we consider a 6-connection pore-network (\(N_\mathrm {t}=6\)) in which \(B=19\) bubbles of uniform size are arranged, so as to cover an increasingly large domain area. Four examples of these arrangements are shown in Fig. 8a and are characterised by distinct values of the dimensionless parameter d, which represents the average distance between the bubbles and the lattice’s centroid:
where \(\{ x_\mathrm{c}, y_\mathrm{c} \}\) and \(\{ x_i, y_i \}\) are the coordinates of the centroid for the lattice and for bubble i, while \(L_\mathrm {t}\) is the pore-throat length. Accordingly, the smallest domain that can be generated in this pore-network is a lattice with two layers (\(N_\mathrm{L} = 2\)) and an average distance \(d=1.5\) (each bubble is separated from its neighbour by exactly one pore-throat length, top left panel in Fig. 8a). The average dissolution time of the lattice is computed as follows:
where \(t_{\mathrm{d},i}\) is the dissolution time of bubble i and \(t^*_\mathrm{d}(R^0_i)\) is the dissolution time of an unconfined bubble of size \(R^0_i\) in bulk.
(a) A selection of four lattices (\(B=19\), \(R^0=1\mu\)m ) of bubbles randomly arranged in a two-dimensional regular pore-network (\(N_\mathrm {t}=6\), \(R_\mathrm {p}/R^0=2.5\)). The four cases occupy an area equivalent to a dense lattice with \(N_\mathrm {L}=2\) (top left), 3 (top right), 4 (bottom left) and 4 (bottom right), and are characterised by distinct values of the dimensionless parameter d (see Eq. 15, values given on top of each panel). (b) The average dissolution time of bubble lattices with vacant sites but constant number of bubbles (\(B=19\)) as a function of d (initial liquid saturation, \(f^0= 1\). For each simulation, the whiskers represent the maximum and minimum lifetime of the bubble population. The horizontal dashed line represents the dimensionless dissolution time of an isolated bubble in the same pore-network (\(\tau \approx 1.5\)). The magenta line is an exponential function, \(\ln {\overline{\tau }} = \ln {7.05}-0.36d\), fitted to the simulation results obtained for \(d\le\)3.5
In Fig. 8b the average dissolution time, \(\overline{\tau }\) (solid markers), is plotted as a function of the average distance, d, for all the realisations, together with the maximum and minimum dissolution times for selected realisations plotted as the whiskers. It can be seen that denser lattices yield a larger average dissolution time, but also the largest spread among the maximum and minimum dissolution times within the lattice. Moreover, the decrease in average dissolution time follows an exponential decay up to \(d\approx 3.5\), as described by the function \(\ln {\overline{\tau }} = \ln {7.05}-0.36d\) (solid magenta line). Collective effects become negligible for \(d>6\), where \(\overline{\tau }\) approaches the value for a single bubble in a pore network (see Fig. 2c and f).
The evolution of a bubble lattice that contains vacant sites and an initial bubble size distribution (see Supporting Information, Section S2) becomes increasingly more complex, as indicated by one exemplar realisation depicted in Fig. 9. Here, we observe that the lattice no longer features a dissolution front that propagates by and large from the outer perimeter of the lattice to its center. This behaviour is also reflected in the evolution of solute concentration field, which is spatially nonuniform from the outset and evolves in a manner that may affect the position of the centre of mass of the solute plume. As quantified by the average bubble dissolution time (Fig. S2), collective effects are extended to lager values of the parameter d relative to a lattice with a uniform initial bubble size distribution, as a result of a larger spread of the local (bubble) dissolution time.
Evolution of the solute concentration field generated by the dissolution of a sparse hexagonal lattice of \(B=19\) bubbles with normally distributed initial radius (\(\overline{R}^0=1~\mu\)m) arranged in a regular pore network (\(R_\mathrm{p}/R^0=2.5\)) with \(N_\mathrm {t}=6\) connections, and filled with liquid at initial saturation, \(f^0=1\). This case corresponds to the schematic shown on the top right corner of Figure S2a (Supporting Information).The colour scale indicates the normalised solute concentration in each pore body and a black circle indicates the presence of a bubble. The dimensionless time, \(\tau\), is given on top of each panel
6 Conclusions
We have studied the collective dissolution of bubbles in regular pore networks partially saturated with a quiescent liquid. In our approach, we used a pore network model that accounts for mass exchange between the gaseous and liquid phase, and for the diffusive transport of the dissolved gas in the liquid phase. The latter plays a key role in controlling the evolution of bubble lattices, because the development of local concentrations in the liquid phase determines whether a bubble will grow or dissolve. Similar to previously reported observations of bubbles dissolving in bulk liquid, we observe diffusive shielding, a phenomenon that can extend the final dissolution time of bubble lattices. In a pore network, the strength of diffusive shielding depends on the connectivity of the network, in addition to the location of a bubble relative to its neighbours. We quantify this phenomenon and observe that the final dissolution time of a bubble lattice scales as \(B^k\), where B is the number of bubbles in the lattice and k is a parameter that depends on the network connectivity. Notably, the presence of the pore network perturbs the shielding effect, leading to irregular dissolution patterns of the lattice and to the generation of nonuniform solute concentration fields, even when the lattice is made of bubbles of uniform size. These effects are augmented for bubble lattices of practical relevance, such as those that contain vacant sites and bubbles of initial varying size, because the solute concentration field is nonuniform from the outset. While the focus in this study has been on regular pore networks featuring spherical bubbles, the presented approach is generally applicable and could be extended to account for irregularly shaped bubbles and networks with more complex geometries. In such heterogeneous porous media, the resultant saturation re-distribution of gas and liquid phases may extend beyond the characteristic length scale of a pore-body (Li et al. 2020). In this context, pore-network models offer an opportunity to study the complex interplay between dissolution and transport fluxes at the pore-scale for large bubble populations, enabling consistent upscaling to be performed.
References
Andrew, M., Bijeljic, C., Blunt, M.J.: Pore-scale imaging of geological carbon dioxide storage under in situ conditions. Geophys. Res. Lett. 40, 3915–3918 (2013)
Bell, I.H., Wronski, J., Quoilin, S., Lemort, V.: Pure and pseudo-pure fluid thermophysical property evaluation and the open-source thermophysical property library coolprop. Ind. Eng. Chem. Res. 53(6), 2498–2508 (2014)
Blunt, M.J., Bijeljic, B., Dong, H., Gharbi, O., Iglauer, S., Mostaghimi, P., Paluszny, A., Pentland, C.: Pore-scale imaging and modelling. Adv. Water Resour. 51, 197–216 (2013)
Cadogan, S.P., Maitland, G.C., Trusler, J.P.M.: Diffusion coefficients of CO\(_2\) and N\(_2\) in water at temperatures between 298.15 K and 423.15 K at pressures up to 45 MPa. J. Chem. Eng. Data 59(2), 519–525 (2014)
Chalendar, J.A.D., Garing, C., Benson, S.M.: Pore-scale modelling of Ostwald ripening. J. Fluid Mech. 835, 363–392 (2018)
Duncan, P.B., Needham, D.: Test of the Epstein-Plesset model for gas microparticle dissolution in aqueous media: effect of surface tension and gas undersaturation in solution. Langmuir 20(7), 2567–2578 (2004)
Enríquez, O.R., Sun, C., Lohse, D., Prosperetti, A., van der Meer, D.: The quasi-static growth of CO bubbles. J. Fluid Mech. 741(R1), 1–9 (2014)
Epstein, P.S., Plesset, M.S.: On the stability of gas bubbles in liquid-gas solutions. J. Chem. Phys. 18(11), 1505–1509 (1950)
Fatt, I.: The network model of porous media. Trans. AIME 207(1), 144–181 (1956)
Gao, Y., Georgiadis, A., Brussee, N., Coorn, A., van der Linde, H., Dietderich, J., Alpak, F.O., Eriksen, D., Mooijer-van denHeuvel, M., Appel, M., Sorop, T., Wilson, O.B., Berg, S.: Capillarity and phase-mobility of a hydrocarbon gas-liquid system. Oil Gas Sci. Technol. Rev. 76(43), 1–19 (2021)
Garing, C., de Chalendar, J.A., Voltolini, M., Ajo-Franklin, J.B., Benson, S.M.: Pore-scale capillary pressure analysis using multi-scale x-ray micromotography. Adv. Water Resour. 104, 223–241 (2017)
Gayon Lombardo, A., Simon, B.A., Taiwo, O., Neethling, S.J., Brandon, N.P.: A pore network model of porous electrodes in electrochemical devices. J. Energy Stor. 24(100736), 1–17 (2019)
Held, R.J., Celia, M.A.: Pore-scale modeling and upscaling of nonaqueous phase liquid mass transfer. Water Resour. Res. 37(3), 539–549 (2001)
Joekar-Niasar, V., Hassanizadeh, S.M., Leijnse, A.: Insights into the relationships among capillary pressure, saturation, interfacial area and relative permeability using pore-network modeling. Transp. Porous Media 74(2), 201–219 (2008)
Kadyk, T., Bruce, D., Eikerling, M.: How to enhance gas removal from porous electrodes? Sci. Rep. 6(38780), 1–14 (2016)
Krevor, S., Blunt, M.J., Benson, S.M., Pentland, C.H., Reynolds, C., Al-Menhali, A., Niu, B.: Capillary trapping for geologic carbon dioxide storage - From pore scale physics to field scale implications. Int. J. Greenhouse Gas Control 40, 221–237 (2015)
Laghezza, G., Dietrich, E., Yeomans, J.M., Ledesma-Aguilar, R., Kooij, E.S., Zandvliet, H.J., Lohse, D.: Collective and convective effects compete in patterns of dissolving surface droplets. Soft Matter 12(26), 5787–5796 (2016)
Li, Y., Garing, C., Benson, S.: A continuum-scale representation of Ostwald ripening in heterogeneous porous media. J. Fluid Mech. 889(A14), 1–26 (2020)
Lifshitz, I., Slyozov, V.V.: The Kinetics of Precipitation from Supersaturated Solid Solutions. J. Phys. Chem. Solids 19(1), 35–50 (1961)
Mahmoodlu, M.G., Raoof, A., Bultreys, T., Van Stappen, J., Cnudde, V.: Large-scale pore network and continuum simulations of solute longitudinal dispersivity of a saturated sand column. Adv. Water Resour. 144(103713), 1–9 (2020)
Mayercsik, N.P., Vandamme, M., Kurtis, K.E.: Assessing the efficiency of entrained air voids for freeze-thaw durability through modeling. Cem. Concr. Res. 88, 43–59 (2016)
Michelin, S., Guérin, E., Lauga, E.: Collective dissolution of microbubbles. Phys. Rev. Fluids 3(4), 1–35 (2018)
Moreno Soto, A., Lohse, D., van der Meer, D.: Diffusive growth of successive bubbles in confinement. J. Fluid Mech. 882(A6), 1–17 (2020)
Obliger, A., Jardat, M., Coelho, D., Bekri, S., Rotenberg, B.: Pore network model of electrokinetic transport through charged porous media. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 89(4), 1–10 (2014)
Ostwald, W.: Studien über die Bildung und Umwaldlung fester Körper. Phys. Chem. 22, 289–330 (1897)
Peñas-López, P., Parrales, M.A., Rodríguez-Rodríguez, J.: Dissolution of a CO\(_2\) spherical cap bubble adhered to a flat surface in air-saturated water. J. Fluid Mech. 775, 53–76 (2015)
Sander, R.: Compilation of Henry’s law constants (version 4.0) for water as solvent. Atmos. Chem. Phys. 15(8), 4399–4981 (2015)
Schmelzer, J., Schweitzer, F.: Ostwald Ripening of Bubbles in Liquid-Gas Solutions. J. Non-Equilib. Thermodyn. 12, 255–270 (1987)
Valvatne, P.H., Piri, M., Lopez, X., Blunt, M.J.: Predictive pore-scale modeling of single and multiphase flow. Transp. Porous Media 58(1–2), 23–41 (2005)
Varloteaux, C., Vu, M.T., Békri, S., Adler, P.M.: Reactive transport in porous media: Pore-network model approach compared to pore-scale model. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 87(2), 1–15 (2013)
Vega-Martínez, P., Rodríguez-Rodríguez, J., van der Meer, D.: Growth of a bubble cloud in CO\(_2\)-saturated water under microgravity. Soft Matter 16, 4728–4738 (2020)
Voorhees, P.W.: The Theory of Ostwald Ripening. J. Stat. Phys. 38, 231–252 (1985)
Weijs, J.H., Lohse, D.: Why surface nanobubbles live for hours. Phys. Rev. Lett. 110(5), 1–5 (2013)
Weijs, J.H., Seddon, J.R.T., Lohse, D.: Diffusive shielding stabilizes bulk nanobubble clusters. Chem. Phys. Chem. 13(8), 2197–2204 (2012)
Xiong, Q., Baychev, T.G., Jivkov, A.P.: Review of pore network modelling of porous media: experimental characterisations, network constructions and applications to reactive transport. J. Contam. Hydrol. 192, 101–117 (2016)
Xu, K., Bonnecaze, R., Balhoff, M.: Egalitarianism among bubbles in porous media: an ostwald ripening derived anticoarsening phenomenon. Phys. Rev. Lett. 119(26), 264502 (2017)
Acknowledgements
NJ is funded by the Marit Mohn Scholarship at the Department of Chemical Engineering, Imperial College London.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Joewondo, N., Garbin, V. & Pini, R. Nonuniform Collective Dissolution of Bubbles in Regular Pore Networks. Transp Porous Med 141, 649–666 (2022). https://doi.org/10.1007/s11242-021-01740-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-021-01740-w