Abstract
Flow in fractures is sensitive to their geometrical surface characteristics. The surface can undergo deformation if there is a change in stress. Natural fractures have complex geometries and rough surfaces which complicates the modelling of deformation and fluid flow. In this paper, we present a computational model that takes a digital image of a rough fracture surface and provides a stress–permeability relationship. The model is based on a first-principle contact mechanics approach at the continuum scale. Using this first principle approach, we investigate numerically the effect of fracture surface roughness and shifting of surfaces on the permeability evolution under applied stress and compare the results with laboratory experiments. A mudrock core fracture surface was digitalized using an optical microscope, and 2D cross sections through fracture surface profiles were taken for the modelling. Mechanical deformation is simulated with the contact mechanics based Virtual Element Method solver that we developed within the MATLAB Reservoir Simulation Toolbox platform. The permeability perpendicular to the fracture cross section is determined by solving the Stokes equation using the Finite Volume Method. A source of uncertainty in reproducing laboratory results is that the exact anchoring of the two opposite surfaces is difficult to determine while the stress–permeability relationship is sensitive to the exact positioning. We, therefore, investigate the sensitivity to a mismatch in two scenarios: First, we assess the stress–permeability of a fracture created using two opposing matched surfaces from the rock sample, consequently applying relative shear. Second, we assess the stress–permeability of fractures created by randomly selecting opposing surfaces from that sample. We find that a larger shift leads to a smaller drop in permeability due to applied stress, which is in line with a previous laboratory study. We also find that permeability tends to be higher in fractures with higher roughness within the investigated stress range. Finally, we provide empirical stress–permeability relationships for various relative shears and roughnesses for use in hydro-mechanical studies of fractured geological formations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The presence of fractures in subsurface rocks, e.g. sedimentary, metamorphic, and igneous rocks, often significantly enhances their permeability (Nelson 2001). Fractures occur naturally as pre-existing features in most rocks, but can also be artificially induced, e.g. by hydraulic fracturing to enhance fluid flow. Fractures can be beneficial in oil and gas development such as shale reservoirs (Economides and Martin 2007) or in geothermal energy production (Goldstein et al. 2011). However, they can be detrimental as they may potentially compromise the caprock integrity of geological carbon storage formations (Vilarrasa et al. 2011) or leading to early water breakthrough in water flooding for hydrocarbon recovery. Hence, understanding the fluid flow within fractures has long been of scientific interest (Zimmerman and Bodvarsson 1996).
Rocks deform under stress. Stresses vary substantially in the subsurface either due to tectonic stress or due to operations such as injection or production of fluids and the corresponding change of fluid pressure. Fractures are mechanically weaker, having lower stiffness, than the surrounding rock and hence they are particularly susceptible to stress changes. Subsequently, any change in fracture geometry will also impact the fracture hydraulic properties. Compaction and shear deformation in subsurface fractures alters the contact area and void space geometry. It is well known that chemical reactions, i.e. dissolution and precipitation, can alter the fracture aperture, connectivity and roughness (Laubach et al. 2019). These processes may have a significant impact on the overall fluid transport and permeability of subsurface geological formations (Zimmerman et al. 1993; Yeo et al. 1998). To understand this process, the relationship between deformation and permeability or stress and permeability are investigated both in experimental and numerical studies.
Fractures have rough surfaces. Although the roughness can vary, it is dependent on the host rock properties (Kim et al. 2013; Bandis et al. 1983), stress condition, type of fracture, mineralogy and presence of fluids. Figure 1 shows an example of such a rough fracture in a cylindrical mudstone. This fracture is a drilling-induced fracture, occurred during the core recovery process.
Characterizing surface roughness is a complicated process. There are over 18 parameters (Wang et al. 2016) proposed in the literature that can be used to describe the roughness, which can be subjectively classified into four categories: empirical, statistical, random field and fractal. Statistical methods offer relative simplicity (Zhou et al. 2015) when characterizing roughness. This includes the scale-independent root mean square of the heights, \(Z_{2}\) (Tse and Cruden 1979), peak asperity height and roughness average. This method lacks the subjectivity and is easy to implement into the numerical code. In addition, the joint roughness coefficient (JRC) (Barton and Choubey 1977) is a widely used empirical quantity (Kim et al. 2013) in geomechanics to characterize roughness. However, the traditional way of measuring JRC can be subjective and prone to overestimations (Wang et al. 2016; Grasselli and Egger 2003; Milne et al. 2009; Kim et al. 2013). This parameter alone can be estimated in at least four different ways, potentially varying by a factor of two (Kim et al. 2013) between the Maerz method (Maerz et al. 1990) and the manual procedure described in Barton and Choubey (1977).
Deformation of a fracture is a contact problem of two rough surfaces. It has been studied analytically as a flat surface contacting a nominally flat surface with spherically shaped asperities (Greenwood and Williamson 1966) as well as two rough surfaces in contact (Brown and Scholz 1985). Both studies provide a theoretical relationship between the applied normal stress and deformation of a fracture, given the surface topography and material elastic properties. A recent study (Brown and Scholz 1985) provides a general theory of contact, using assumptions such as that individual contacts do not interact elastically which implies that the deformation of a specific contacting surface is independent of forces of nearby surfaces. This theory showed that surface roughness plays a significant role in the deformation of two such surfaces. Despite exhibiting a good match with specific experimental data, this theory failed to match experimental data when the surfaces have domed-up shapes. Furthermore, the experimental data was limited to a small range of normal stress making the comparison difficult. Another analytical study (Liu et al. 2013) provides a stress–permeability relationship based on the two-part Hooke’s law, arguing that the true strain must be used instead of the engineering strain to calculate the deformation. This relationship was verified using data available in the literature.
Several studies investigated the permeability versus stress relationship of a rough fracture (Walsh 1981; Walsh et al. 2008; Koyama et al. 2009; Pyrak-Nolte and Morris 2000; Pyrak-Nolte and Nolte 2016). Walsh et al. (2008) investigated this problem numerically, using coupled flow and mechanical deformation on a 2D model. Realistic rough surface geometries were used based on the improvement of the existing spectral synthesis methods (Brown and Scholz 1985; Glover et al. 1998). Permeability was calculated parallel to the fracture based on the parallel plates approximation. Results were compared to experimental data, where the mismatch is seen between the model transmissibility and experimental one, and a good match if the fracture closure is compared. Pyrak-Nolte and Morris (2000) investigated a 3D fracture under normal stress and the relationship between fracture stiffness and fluid flow. However, the deformation of a 3D fracture is approximated assuming that fracture asperities are circular cylinders and the flow is modelled by conceptualizing fracture as a network of pipes.
Experimental studies (Huo et al. 2014; Ishibashi et al. 2015; Huo and Benson 2016; Bjørnara et al. 2018; Frash et al. 2017; Fang et al. 2018) on rough fractures from core samples provided important information to validate theoretical considerations and numerical models. Huo and Benson (2016) investigated relative permeability as a function of stress. Huo et al. (2014), looked at rough fractures within samples of Berea sandstone under various confining loads and measured permeability based on Darcy’s law. They used CT imaging to obtain apertures from the sample and compared measured with calculated permeability based on the parallel plates approximation. The calculated permeability was 2.6–4.9 times greater than the experimentally derived one. Ishibashi et al. (2015) used similar techniques on samples of granite and found that the permeability predicted using modelling was an order of magnitude higher than that measured in the laboratory. Many studies have been combined (Barton et al. 1985) into empirical relationships involving stress, closure and conductivity of a fracture. In this study, it was shown that the smooth joints in weaker formations tend to close more easily under normal stress.
A recent experimental study (Chen et al. 2017) was conducted on a series of flow tests on single fractured sandstone under various confining loads. The relationship between fracture geometric characteristic and permeability was investigated. An improved relationship that relates permeability or hydraulic aperture to the effective mechanical aperture, contact ratio and fractal dimension was proposed. Despite that the model showed better agreement with the experimental results than the Yeo model (Yeo 2001), it is based on sandstone samples with particular rock properties. For assessing caprock integrity in carbon and hydrogen storage projects, properties of hydraulic fractures in unconventional reservoirs or radioactive waste storage scenarios, this model needs to be extended to mudrocks. In addition, the study mostly focuses on the connecting joints geometric characteristic to the permeability, not on the stress-deformation-permeability process. Another experimental study (Zhou et al. 2015) investigated nonlinear flow in a rough fracture at low Reynolds numbers under compressive loading. A granite with a matched fracture surface, and a sandstone with an unmatched fracture surface were used for water flow tests, with the results fitting to the Forchheimer equation. Hydraulic aperture and hence permeability versus stress was obtained from laboratory studies, but the study mostly focused on the critical Reynolds number evolution during the stress load with the empirical equation proposed.
Rough fractures contact mechanics has recently been investigated by a Fourier transforms based numerical approach on a granodiorite fracture (Kling et al. 2018). Elastic and elastic-plastic contact deformation models were employed and the fracture closure versus stress relationship was investigated. This model showed improved results compared to the Barton-Bandis model (Barton et al. 1985) and reproduced experiments well. However, stress versus permeability was not investigated. And the proposed contact mechanics model works well for the rocks with Young’s modulus below 11 GPa (Kling et al. 2018), which is a limiting factor that needs further investigations.
Most studies which connect mechanics and flow in rough fractures calculate permeability based on a parallel plates approximation. Experimental evidence suggests that this approach tends to overestimate or show different permeability results. On the other hand, studies (Wang et al. 2016; Zou et al. 2017) which consider more sophisticated flow representations e.g. Lattice Boltzmann methods or Navier–Stokes between two rough surfaces, tend to focus mostly on fluid transport and lack the mechanical deformation. Besides, numerical 3D studies have to conceptualize the modelling, e.g. assuming that the fracture asperities have specific shapes such as cylindrical, or assuming that fracture surface can be simplified as a network of pipes (Pyrak-Nolte and Morris 2000; Pyrak-Nolte and Nolte 2016). The experimental studies described in the previous paragraphs, on the other hand, tend to focus mostly on the specific types of rock with fixed rock properties. Numerical modelling is free from this limitation and can provide stress–permeability relationships for various configurations.
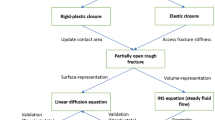
The purpose of this study is to present a computational model that simulates digital image based rough fracture deformation coupled to fluid flow and to analyze the corresponding stress–permeability relationship. The code used here is based on a first principle contact mechanics approach and avoids the assumptions needed in (semi-) analytical approaches or conceptualizations. We investigate a single Carmel mudrock (Kampman et al. 2014) sample numerically and experimentally, whose surface was digitized with a digital optical microscope (Keyence 2017; Phillips et al. 2021). The numerical investigation is based on a number of randomly selected cross sections used to build 2D models. We analyze laboratory and numerical stress–permeability relationships and the effects of the roughness and varying surfaces shifts.
2 Methods
Here, we introduce the methods used to model fracture mechanical deformation, permeability calculation and characterization of the surface roughness. In our analysis, we use an in-house developed simulator (Kubeyev et al. 2019) for fracture deformation based on the free and open-source reservoir simulation and development platform—MATLAB Reservoir Simulation Toolbox (MRST) (Lie 2014). In this study, we expanded it for hydro-mechanical modelling adding a Stokes flow solver and roughness characterization.
2.1 Mechanical Deformation
We summarize the method briefly here, based on a more detailed description in Kubeyev et al. (2019), and refer to it as interacting discrete continua (IDC). Discrete bodies are described by the static linear elasticity equations based on the momentum conservation
Hooke’s law
and the compatibility condition for strain
where \(\varvec{\sigma }\) denotes the Cauchy stress tensor, \(\varvec{f}\) the body force vector, \(\varvec{C}\) is the fourth order stiffness tensor, \(\varvec{\varepsilon }\) is the strain, and \(\varvec{u}\) the displacement vector.
Space is discretized using virtual elements (Andersen et al. 2016). Instead of solving the weak form of the linear elastic Eqs. (1)–(3) by determining the values for the local bilinear form
with explicit test functions \(\varvec{v}\) over the spatial domain \(\Omega _E\) of element E, VEM computes the approximate bilinear form
of test functions \(\varvec{v}\), for which only the projection \(\Pi ^\nabla\) onto linear polynomials (Gain et al. 2014) is known and a stabilization term \(s_E\) accounts for the additional terms. This provides flexibility when selecting test functions and hence geometries of the elements. Complex fracture surface geometries can be meshed much easier and contact points can be flexibly added compared to the conventional Finite Elements Methods (FEM).
The fracture is the void space in between rock masses. Here we consider a fracture that transects the 2D domain and hence, the rock is represented by two independent rock masses that interact over a rough surface when moved into contact through boundary conditions. When the discontinuity is introduced, the total potential energy (Wriggers 2006)
is not preserved. To preserve it, Lagrange multipliers (Papadopoulos and Solberg 1998) are added to the equation to solve the contact
where \(\Gamma _{c}\) is the contact area of two discrete bodies, \(\lambda _{N}\) is the Lagrange multiplier and g is the gap between bodies along the interface.
IDC (Kubeyev et al. 2019) provides three contact algorithms—contact detection and normal contact interaction as well as tangential interaction. Here, we focus on understanding compaction and postpone the investigation of fracture slip and shear to a future study. Hence, we make use of the first two and do not account for slip, friction or tangential interactions. For instance, consider we have two independent elastic bodies, where the first body is displaced towards the other because of the displacement boundary condition set on the former. Contact detection identifies if a penetration or contact happened. Penetration is defined as the state when the point in space is occupied by more than one body at the same time (Munjiza 2004). If that is the case, the contact is solved on the initial configuration and gap measurement between the bodies using the Lagrange multipliers. This ensures the prevention of penetration, loss of elastic strain energy and transferring the forces between bodies. Fracture deformation is modelled by a set of simulation steps solving these two contact algorithms sequently.
The identification of contact area and contact forces in the contact problem is nonlinear (Barber 2018). Identification of the contacting surface correctly on one hand and obtaining physically meaningful contact forces on the other hand needs to be achieved. For example, we model fracture compaction in this study. In one scenario, not enough contact surface identification may lead to penetration after solving the contact problem. However, the resulting contacting forces are correct in this scenario—being dilational and making both bodies compact. The contact problem is not solved correctly due to the penetration despite having correct contacting forces. In the opposite scenario, excessive contact surface identification will result in no-penetration after solving the contact problem, but the resultant contacting forces can be incorrect, being compactional (positive in geomechanics convention). Compactional contact forces make both bodies locally dilate at the specific places of excessive contact. Both scenarios are physically wrong and there is an optimal solution where the contact surface is correctly identified with the correct contacting forces calculated when solving a contact problem.
We address this issue algorithmically when the fracture deformation is modelled by the vector of small displacements boundary condition. Before reaching to the final solution, we check for any penetration and if any, we increase the contact surface accordingly. In addition, we ensure the absence of the compactional contacting forces in the solution. Hence, the process is iterative. This ensures the convergence of the contact problem, finding the optimal configuration where contact forces are correct and non-penetration condition holds.
We assume that discrete bodies behave linear-elastically, with no failure or fragmentation of the asperities. However, the presence of a discontinuity, i.e. a fracture, and solving for the contact problem between two discrete bodies leads to the nonlinearity in the fractured material behaviour. Thus, the fractured rock model is not linear elastic. Geomechanics convention of stress is used in this paper, where the positive stress is compactional.
2.2 Flow Part—Stokes Equation
We investigate fractures in 2D space, with the flux and permeability calculation perpendicular to the fracture cross section as shown in Fig. 2. This setting is appropriately represented by Stokes equation (Curle and Davies 1968; Richter et al. 2016) for the incompressible, Newtonian fluid in laminar flow through arbitrary cross sections, given by
with
where u is the velocity in m/s, P is the pressure perpendicular to the fracture cross section and parallel to the z in Pa, \(\mu\) is the dynamic viscosity in Pa\(\cdot\)sec. The no-flow boundary conditions at the fracture surface
translate to
We solve the Laplace Eq. (8) with its boundary conditions (9) using the incompressible single phase flow pressure solver of MRST Lie (2014) augmented with boundary conditions (9). We then calculate the permeability from the fluid velocity field using
In the finite volume discretization this yields
where \(k_{\bot }\) is the permeability of a fracture measured in the perpendicular direction to the fracture cross section in m\(^{2}\) then converted to mD, A is the flow area in m\(^{2}\). If the area is taken as the matrix and fracture area, then the permeability is \(k_{\bot }\), whereas if the flow area is taken only of the fracture then permeability is denoted as \(k_{f\bot }\). n is the number of grid cells, \(\Delta A_i\) is the area of a cell i and Q is the volumetric flow rate in m\(^{3}\)/sec. The pressure gradient is constant and set to \(\frac{{{\text{d}}P}}{{{\text{d}}z}} = 10000\,{\text{Pa }}{\mkern 1mu} {\text{m}}^{{ - 1}}\). The permeability \(k_{\bot }\) is not to be confused with the permeability from the matrix to fracture.
The deformation is modelled in a quasi-static manner by iteratively changing the value of the boundary conditions solving the contact problem as described in Sect. 2.1. At each simulation step, we then take the deformed fracture geometry and calculate permeability based on these Stokes equations. This way we obtain stress–permeability relationships.
Conventionally, fracture permeability in 2D numerical studies (Walsh et al. 2008; Paluszny and Matthai 2008; Kubeyev 2013) is calculated parallel to the planar fracture. In contrast, we calculate permeability in a different direction—perpendicular to the fracture cross section shown in Fig. 2. This is because the former method requires the need for artificial residual gaps such as the one employed by Walsh et al. (2008). We believe that these artificial gaps in a joint with the parallel direction calculation do not represent the correct values of permeability during deformation in this specific problem set because of the following reasons.
For example, consider a 2D fracture model where opposing surfaces of the fracture do not initially touch each other such as the main fracture shown in Fig. 2. Assume the permeability calculated in a parallel direction to the planar fracture, in contrast to the direction shown in the picture. Before the contact, there is a non-zero permeability as the voidage is open to flow. However, due to applied compaction normal to the fracture stress during the simulation, the fracture deforms and the first contact establishes itself. This contact along the fracture acts as the blockage for the flow in a 2D plane. Hence the permeability must be zero. However, it is modelled as non-zero where the artificial space is numerically placed to overcome this difficulty and proceed with further fracture deformation in the aforementioned study (Walsh et al. 2008). In reality, when these 2D surfaces are in contact, blocking the flow along the fracture, the flow will transpire in a third dimension making permeability of a rough fracture a 3D problem per se. We do not model 3D here, but to overcome these limitations, we calculate permeability in the perpendicular direction on many randomly picked 2D cross sections. Then we present results as the mean and the standard deviation of these cross sections. However, we emphasize that there are inherent differences between 2D and 3D modelling, and the former method may not be able to capture all properties of a 3D surface.
Calculating permeability in the parallel direction in 2D studies has the following disadvantages: the need for artificial gaps to let the area open for flow, otherwise, in case of any single contact, permeability becomes zero. Calculating permeability in the perpendicular direction does not have this disadvantage. However, the disadvantage of using either method to calculate permeability is that neither can fully account for flow tortuosity in the third dimension.
In addition to permeability, we calculate fracture transmissivity \(T_{f}\). This parameter is particularly useful for reservoir simulation studies when the fracture is embedded in a larger rock mass. The transmissivity is given by
where \(k_{f\bot }\) is fracture permeability calculated in the perpendicular direction, without considering flow in the rock matrix, \(a_{m}\) is the mechanical aperture of a fracture, taken as the arithmetic mean of mechanical apertures in a simulation model at each simulation step. In the analysis section we calculate a fit to the stress–fracture transmissivity curve using the following exponential formula and curve fitting procedure:
where \(\sigma\) is the normal stress at the boundary, \(\alpha\) is the scaling parameter that makes transmissivity and stress the same order of magnitude and a, b, c, d are the fitting parameters.
2.3 Equivalent Permeability
The permeability values obtained from the experimental work are not directly comparable to those computed from the simulation model. This is because the model has a rectangular shape and captures only a specific selected area in the surface. In contrast, the laboratory permeability values are of a fractured rock including the circular cross section of the core sample where the flow is in both, matrix and fracture. Schematically the difference is shown in Fig. 3, where the simulation model is a rectangle shown in red colour, and the experimental rock is a circle in dark yellow.
In order to compare the data obtained from the laboratory work to that of the numerical modeling results, we must take into account these differences. For a fractured core sample, the experimentally measured permeability \(k_\mathrm{ex}\) is related to the permeabilities of matrix \(k_{m}\) and fracture \(k_{f}\) (both in \(\mathrm m^{2}\)) due to Darcy’s law and mass conservation by
where, \(A_{m}\) and \(A_{f}\) are the flow area of the matrix and fracture in m\(^{2}\). Knowing the fracture length in the core L and the length of the numerical fracture sample l, we can relate the lab fracture flow area \(A_{f}\) to the numerical fracture flow area \(A_{f (n)}\) as follows:
This equation assumes that the average properties of the whole fracture are identical to those of the section used for the numerical analysis. In order to accommodate this, we randomly select many 2D cross sections from the whole 3D digital surface of the fracture in the fractured core and run our analysis on them.
The matrix permeability of mudrocks is typically on the order of \(10^{-21} - 10^{-19} \mathrm m^{2}\) (Busch and Amann-Hildenbrand 2013; Ross and Bustin 2009) and hence significantly smaller than the fracture permeability. It is therefore reasonable to assume \(k_{m}\) = 0, and the flow area of matrix and fracture of the core is equal to the cylindrical area, the equivalent permeability can be derived from Eq. (16) as
where L and l are in m, \(A_{f (n)}\) and \(A_{{{\text{cyl}}}}\) are in m\(^{2}\). Note that \(k_{f}\) and \(A_{f (n)}\) are not constant and changing with fracture deformation and thus are calculated in the numerical model at each simulation step. With the equations above, we make the experimental permeability directly comparable to the permeability measured from the numerical simulation. Besides, another benefit is that we keep the experimental permeability intact i.e. raw and free from the interpretations.
2.4 Barton-Bandis Model
In Sect. 3.1, we compare the experimental effective stress–permeability with the widely used Barton-Bandis empirical model, keeping the former intact i.e. raw and free from the interpretations. Barton et al. (1985) provide equations that couple normal stress, closure and conductivity of a fracture. It is an empirical model based on extensive research of natural fractures and relies on actual test data with functions later fitted to it. A minimum of two inputs in terms of JRC and joint wall compression strength (JCS) results in a stress–permeability relationship. A full model is presented in Appendix A. The equivalent and comparable permeability of the Barton-Bandis model to the lab core permeability is derived in a similar way as in Eqs. (16)–(18). This is done because the Barton-Bandis permeability is the fracture permeability and the experimental permeability is the core permeability of the fracture and matrix. In all our comparisons, we leave the experimental data untouched and avoid any interpretations or intervention to the raw data. Thus, we only modify the numerical and Barton-Bandis permeability and do it to have a legitimate comparison with the raw experimental data (see Appendix A).
2.5 Roughness Characterization
Roughness is used to describe the topology of a surface, referring to local departures from planarity (Bhushan 2000). We use the statistical method due to the simplicity (Zhou et al. 2015), mainly focusing on the root mean square \(Z_{2}\) of the heights proposed by Tse and Cruden (1979)
where Dx is the spacing between nodes in m which must be constant, \(y_{i+1} - y_{i}\) is the height difference between adjacent nodes in m and M is the number of height measurements. This formulation is scale-independent.
\(Z_{2}\) can be empirically related to the joint roughness coefficient (JRC), a widely used roughness characterization method. Usually, the latter is measured by comparing and mapping the surface of a fracture with typical roughness profile (Barton and Choubey 1977), with JRC’s typically ranging from 0 to 20. Here, we use the mapping
to calculate JRC from \(Z_{2}\) (Tse and Cruden 1979). Given the complexities of comparing JRC values from different studies, we primarily use \(Z_{2}\) for our analysis, but we also quote JRC for reference. As a fracture consists of two sides, we calculate the roughness parameters of both sides and present them as an arithmetic average. We acknowledge that one should use \(Z_{2}\) of the asperity of the fracture. However, this is not straightforward measurable in the laboratory. In addition, we calculate the peak asperity height \(R_{p}\)
and roughness average \(R_{a}\)
where n is the number of data items, \(y_{i}\) is the height of the fracture roughness surface and \(y_{a}\) is the height of the mean elevation plane. In contrast to \(Z_{2}\) and JRC, these are scale-dependent. As \(R_{\mathrm {p}}\) can sometimes identify an inward-looking fracture peak, we additionally calculate the maximum roughness \(R_{m}\):
for the two sides of the fracture respectively.
3 Laboratory Experiment
We conducted laboratory experiments to obtain the effective stress–permeability relationship for the Carmel mudrock sample shown in Fig. 1. The Carmel Formation is a caprock for a natural \(\mathrm CO_{2}\) reservoir cored near Green River, Utah. The formation has a thickness of 50 m and the storage complex consisting of three laterally gradational lithofacies: (1) interbedded, unfossiliferous red and grey shale and bedded gypsum, (2) red and grey claystone/siltstone, (3) fine-grained sandstone (Kampman et al. 2013). The core was taken from a depth of \(\sim\) 195 m, and a cylindrical sample with a diameter of 1 inch (2.54 cm) and a length of 2 inches (5.08 cm) has been plugged that contains a through-going fracture that splits the sample in two. The Carmel mudrock is rich in illite, quartz and hematite and details of the sample and origin have been provided previously (Phillips et al. 2020; Kampman et al. 2014).
A custom-designed permeameter at Heriot-Watt University was used to conduct permeability measurements on the sample. The sample was positioned in a Viton sleeve and placed in a flow chamber, which was then subjected to isotropic confinement (\(\sigma _{1}\) = \(\sigma _{2}\) = \(\sigma _{3}\)) using water as the confining fluid. Experiments were conducted using the steady-state method with nitrogen as the permeating gas, for effective stresses (\(\sigma '\)) ranging between 0.83 and 18.25 MPa. This stress is achieved by varying both confining pressure \(P_{c}\) and pore pressure \(P_{p}\) such that the effective stress is
The flow rate of the gas across the sample was calculated using the mass flow measured using a built-in mass flow controller (MFC), along with the density of gas calculated using an equation of state for nitrogen. During the experiment, the flow rates varied from \(6.74\cdot 10^{-8}\) to 3.58 \(\cdot 10^{-7}\) \(\mathrm m^{3}/s\). The average viscosity was \(1.84\cdot 10^{-5}\) Pa\(\cdot\)s. The pressure difference across the sample (\(\delta P\)) was calculated from upstream and downstream pressures measured from two pressure transducers. The permeability k of the sample at a given confining pressure was then calculated according to Darcy’s law. All tests were undertaken at a temperature of \(25\,{^\circ }\)C. The effective stress–permeability relationship obtained is shown in Fig. 4.
Figure 4 also shows an exponential fit to the experimental data
where \(\sigma '\) is the effective stress, and a, b, c, d are the fitting parameters equal to 0.5394, \(-2.958 \times 10^{-7}\), 0.04034, and \(-5.328 \times 10^{-8}\). The quality of the fit, i.e. root mean square error between the experimental data and the fit, is 0.0222, \(R^{2}\), the coefficient of determination, is 0.98 and the sum of square errors is 0.0074.
The laminar flow during the experiments is ensured by controlling the linearity of pressure differential versus flow rate relationship. The Reynolds number defined for a fracture (Zhou et al. 2015) is 11.7 at initial stress 0.83 MPa and 6.4 at the final stress 18.2 MPa.
3.1 Barton-Bandis Versus Experimental
In this subsection, we compare the Carmel core permeability obtained from the laboratory experiments in Fig. 4 with the equivalent permeability obtained from the Barton-Bandis empirical model. The comparison is made because the empirical model is widely used in stress–permeability studies. The Barton-Bandis model requires two inputs, JRC and JCS (Barton et al. 1985) and is designed for a range of JRCs (5–15) and JCSs (23–182) (Bandis et al. 1983). We use four JRCs = 5, 8, 11, 15 which represents the range that is found in the core sample (see Fig. 5). JCS is typically not available in the literature, hence, we use two JCSs = 50 and 182 in the analysis.
Figure 6a displays eight Barton-Bandis cases with varying JRC and JCS, where none of the curves can match the experimental data. There is a minimum of three orders of magnitude difference in the \(k_{f}\) value at the initial core permeability stress = 0.8 MPa between the model and the experiment, and it is as high as five orders of magnitude at the final experimental effective stress = 18.2 MPa. The shapes of the behaviour differ considerably, with the only Barton-Bandis case (JRC = 8, JCS = 50 MPa) has some degree of similarity in shape of the curve. To compare the permeability decline, we normalize the permeability by dividing it by the initial permeability at the lowest stress. Figure 6b shows the normalized permeability-stress relationship.
a Carmel mudstone 3D reconstruction of a bigger core part shown in Fig. 1. Arbitrary selected three cross sections of roughness profiles shown in red. Resolution is \( 2.25 \cdot 10^{{ - 6}} {\mkern 1mu} {\text{m}} \). b 100 randomly selected 2D cross sections from a 3D surface on the left. Cross sections have been flattened (see Sect. 4.3)
Being unable to match experimental data indicates the limitation of the empirical Barton-Bandis model. We hypothesize that the disparity is due to the fact that Barton-Bandis is based on initial fracture apertures of 0.1–0.6 mm (Bandis et al. 1983), with typically high initial equivalent permeability 4700–11000 mD as a result. This permeability is appreciably higher than the measured permeability 0.47 mD of the core (at the effective stress = 0.83 MPa) indicating that the fracture aperture of the core is orders of magnitudes smaller.
Unfortunately, the flow area or mean aperture of the laboratory fracture cannot be obtained from the core sample without the use of high resolution imaging techniques, such as micro-CT (Karpyn et al. 2007). However, the exponential fitting procedure (Zhang 2013) can be used to gain an insight into effective aperture and fracture permeability. The model relates the core permeability to the aperture
where d = 0.025 m is the core diameter, \(a_{c}\) is the critical aperture, and \(a_{0} = 5.1 \times 10^{-6}\) m is the initial aperture, \(\Delta a\) is the aperture change in m. Note that \(a_{0}\) is a fitting parameter, further fitting parameters are \(\beta\) = 0.84, \(\alpha\) = 0.1, \(a_{c} = 1 \times 10^{-7}\). Rock matrix permeability was not measured in the laboratory, hence we take Carmel Formation estimate as \(k_{m} = 0.000101\) mD (\(10^{-20}\) m\(^{2}\)) from the literature (Payne 2011; Ross and Bustin 2009) . The exponential fit using Eqs. (27)–(29), indicate the aperture of the rock sample is around 0.002–0.005 mm, which is orders of magnitude less than what Barton-Bandis is based on (0.1–0.6 mm). However, the empirical formulas presented in this study based on the numerical analysis, despite not matching absolute values, follow the rate of the decline of the experimental permeability well and hence could fill the gap.
4 Computational Modelling
For the analysis of the normal stress versus permeability relationship, we create a set of numerical 2D models based on transects from the rock sample. The fracture consists of interacting surfaces which are created by using height profiles generated from transects through the fracture surface measured by a microscope. Figure 7a shows a 3D reconstruction of a part of the fracture surface obtained from the Carmel mudstone sample (Fig. 1), with illustrative cross sections for height profiles indicated by red lines.
4.1 Initial Positioning of Two Interacting Surfaces
To create two opposing fracture surfaces we use two approaches. In all sections, except Sect. 5.6, we use the original 2D height profile on one side of the fracture and duplicate it for usage on the other side. This approach is adopted because the exact positional matching of two digitalized surfaces is not provided. The model with duplicated surface reflects a fully interlocked fracture that closes when any stress is applied. We then shift the duplicated profile, before the simulation, to the specified relative shift amount to represent mismatched fracture surfaces. We define the relative shift as the ratio between the shifted distance to the length of the profile. A similar approach has been used in previous studies (Zou et al. 2017; Koyama et al. 2009), however, they referred to it as shearing.
The shift that we use should not be confused with the tangential interaction of surfaces during slip, shear or friction, but rather the mismatching amount that may happen to the fracture surfaces without contact. In nature, this may represent a situation when fractures deform in two modes simultaneously, Mode 1 tensile opening, and then Mode 2 slip without the contact. What we model then is the normal compactional interaction of such shifted surfaces. As we do not include the process of tangential contact interactions (Kubeyev et al. 2019) that is related to shearing in our analysis we use the term shift to describe the offsetting (in the literature a.k.a. mismatching or un-correlating) of the fracture surfaces. The mismatching is found to play a dominant role in the flow nonlinearity compared to roughness during laboratory experiments (Zhou et al. 2015).
In Sect. 5.6 we create models by selecting two opposing height profiles randomly from two parts of the core sample (bigger and smaller parts in Fig. 1). First, in each part, we manually clean the noise at the fringes by selecting a subsection that cuts the noise out. Cleaned data is then used to sample randomly 100 curves within it using a built-in MATLAB function. Sampling is done by taking an equal amount of x- and y-sections, and again randomly selecting profiles within the combined set. Selected heights sections are used to create a rectangular shape numerical model, where the thickness of the rectangle varies with these heights. We perform the aforementioned procedure in both parts of the core sample. Selected surfaces are then placed as opposing Left and Right surfaces to the numerical model. In other sections of this study, we perform this procedure only on the bigger part of the core.
4.2 Infinitesimal Initial Gap
Initially, two bodies are placed at a random large gap between them as shown in Fig. 8a. Then, bodies are moved close to each other leaving an infinitesimal initial gap between them. Every initial model is verified during initialization for the possible overlap of the bodies using a contact detection algorithm.
In fracture modelling (Kim et al. 2004; Brown 1987; Yasuhara and Elsworth 2006; Koyama et al. 2009), a residual gap \(g_{r}\) is the small distance between fracture surfaces that is placed to avoid numerical difficulties related to solving ill-formed matrices. We set small \(g_{r} = \sqrt{ 1 \mathrm{nD} \cdot 12} = 1.088^{-10} \mathrm {m}\), where 1 nD (\(9.9\times 10^{-22}\) m\(^{2}\)) is the corresponding permeability of this residual gap. We ensure that the permeability in the fracture is much larger compared to the permeability of the residual gap, being at least nine orders of magnitude different. The approach does not affect convergence as it is the distance between separate bodies and not related to the computational mesh.
4.3 Normalization of Random Surfaces
The randomly selected profiles may have a high degree of inclination. To avoid the occurrence of tangential forces we ensure that the randomly picked rough surfaces are parallel. We therefore determine a straight line fit and rotate the height profile according to the angle of the straight line. To find the fit between the linear line and height profile we use an analytical approach to linear regression with a least square cost function, called normal equation (Weisstein 2011)
where \(\theta\) is the fitting parameter for the linear fit, X is the x-coordinates matrix, which includes a vector of ones and \(\mathbf {y}\). Randomly selected normalized profiles of the sample is shown in Fig. 7b.
4.4 Boundary Conditions
The mechanical boundary conditions are illustrated in Fig. 8a. Each model consists of two discrete bodies (Kubeyev et al. 2019): Left, coloured in blue and Right, coloured in yellow. The Right body’s right-hand-side faces have zero displacements boundary conditions in x and y direction. The Left body’s left faces have zero displacement boundary conditions in y-direction and a fixed displacement in x direction. The fixed displacement in x direction is a vector of displacement on the x axis taken as 1/1000 of the size of the smallest face in elements in the fracture roughness area. The top and bottom boundary conditions of both bodies are roller boundary conditions, i.e. fixed displacement perpendicular to the boundary \(u_{y}\) = 0 and free displacement in x direction. The inner boundary conditions of the separate bodies, i.e. the right boundary of the Left body and the left boundary of the Right body, are zero force if no contact has been detected. The two bodies are brought in contact by sequentially applying the displacement boundary condition of the Left body in iterative steps. At each simulation step, we report the resultant arithmetic average x component of the stress at the boundary of the Left body, i.e. the normal stress. The iterative procedure is continued until the normal stress \(\sigma _{x}^{\rm Boundary}\) reaches the specified stress (e.g. 25 MPa or 50 MPa) at the right boundary of the Right yellow body.
a An example of a simulation model with the mechanics boundary conditions. Blue and yellow colours indicate two discrete bodies Left and Right. The red line shows where the stress is measured. b Flow boundary conditions: no-flow around the fracture, pressure differential is in the perpendicular direction to the fracture, where we calculate the fluid velocity distribution and permeability. Note that the fracture is depicted as an ellipse for illustration purposes only
The flow boundary conditions of a fracture is shown in Fig. 8b and Eqs. (10) and (11), i.e. no-flow boundary condition around the fracture and pressure gradient perpendicular to the planar fracture 10000 \(\mathrm {Pa\,m}^{-1}\).
4.5 Simulation Set-Up
Long simulation time is a usual challenge in numerical studies. To reduce computation time, we coarsen selected surface profiles by sampling every 10th value. We verify that the coarsened model is not too different from the original by comparing roughness of the coarse and fine surfaces. The differences are 8 and 12 % in \(Z_{2}\) and JRC respectively. The final mesh resolution varies logarithmically through the grid, with a maximum 0.0016 m near the outer boundary, and \(2.25 \cdot 10^{-5}\) m in the contact area of the fracture.
The elastic parameters are chosen as the average representative values from the literature (Petrie et al. 2011; Petrie and Evans 2013): Young’s modulus is taken as 23 GPa and Poisson’s ratio = 0.31. These are isotropic with the plane strain used in all numerical models in this study.
5 Results and Discussion
In this section, we present the results of our work together with the analysis. First, we illustrate the deformation process for a specific fracture example. Second, we present the impact of the relative shift on the normal stress–permeability relationship and compare numerical results with the experimental ones. Then we investigate the sensitivity of the relationship to the variance of profile characteristics (roughnesses) in the sample. We then analyze the relationship for fractures created by pairing two uncorrelated random cross sections without shift.
5.1 Illustrative Numerical Example—Fracture Compaction
To illustrate the procedure, we present the fracture deformation process due to the applied series of normal stresses for one specific example. We take a cross section (parallel to the x-axis) from the rough surface of the rock sample shown in Fig. 7a. We create a numerical grid with the cross section (profile) being the Left body fracture surface. The Right fracture surface is created through duplication of the Left body’s profile with subsequent shift procedure. The profile has a roughness of \(Z_{2}\) = 0.194 (JRC 9.1) and a relative shift of 0.001. The maximum stress considered here is 25 MPa (maximum in laboratory data) and the permeability is calculated after every step.
(Top) Simulation of fracture compactional deformation—stress field \(\sigma _{x}\) in the model and colour bar of the stress field \(\sigma _{x}\). Fracture deformation can be observed from the increasing number of contacts (stress concentration) with increasing stress. (Bottom) Fluid velocity field in the fracture for various bounding stresses
The fracture surface deformation during simulation, contacting surface evolution and the fluid velocity distribution inside the fracture is shown in Fig. 9 for four boundary stresses. Fracture deformation can be observed from the increasing number of contacts (stress concentration) with increasing stress. At the small stress \(\sigma _{x}^{\rm Boundary}\) = 0.0025 MPa, only a small contact area at the lower side of the fracture has been established. There, the stress \(\sigma _{x}\) is much higher relative to the rest of the model. This implies a small amount of fracture closure, with the deformation localized in that region. Simulation at elevated boundary stress \(\sigma _{x}^{\rm Boundary}\) results in an increase in the number of contacting points. At \(\sigma _{x}^{\rm Boundary}\) = 0.29 MPa, there are already three main contacting sections. Consequently, at the final stress \(\sigma _{x}^{\rm Boundary}\) = 25 MPa, many points along the surface are in contact leading to an increase in the contact area and fracture closure (see upper right picture in Fig. 9). This also indicates that in the previous simulation step (at lower applied stress), the deformation in the contact areas was sufficient to allow new contacting areas to develop.
To illustrate the deformation and fluid velocity inside the fracture we zoom to a specific region of the fracture in Fig. 9. The four images in the lower part of the figure illustrate how fracture geometry changes and how the cross-sectional area of the fracture becomes smaller with increasing boundary stress \(\sigma _{x}^{\rm Boundary}\). When comparing the smallest (0.0025 MPa) and the highest stress \(\sigma _{x}^{\rm Boundary}\) (25 MPa), a significant deformation is seen with parts of the fracture fully closing at the final stress. The decrease in the fluid velocity is also obvious from the qualitative analysis of the distribution in the fracture.
5.2 Fracture Mismatch Analysis
We proceed with the analysis of mismatched fractures to understand the effect of the relative shift on the normal stress–permeability relationship. Analysing a single cross section would not be representative of the whole 2D surface. Thus, we select ten roughness curves from the 100 randomly selected profiles shown in Fig. 7b for the analysis of each specific shift. As we investigate four shifts with ten simulation cases each, we simulate 40 models in total. The selected 10 profiles exhibit mean roughness parameters of \(Z_{2}\) = 0.17 and JRC = 7.5.
We represent four relative shifts, the smallest 0.00025 that corresponds to the single-pixel dislocation and the other 3 represent the possible orders of magnitude in relative shift—0.001, 0.01 and 0.1. Figure 10a illustrates the fracture for the four shifts for a single realization.
a Example of 4 fractures with the different relative shifts of the surfaces, where heights define the fracture surface as described in Fig. 6a. Red and blue colours correspond to the Left and Right bodies. Permeability calculation starts from the first initial contact. b Normal stress–permeability \(k_{f\bot } \left( \sigma \right) \) relationships for 4 relative shifts. For each shift, the mean and the standard deviation of 10 different fracture realizations are shown with each realization represented by thin coloured curves
Results from all 40 simulations in terms of applied normal stress–permeability relationships at various mismatching shifts are shown in Fig. 10b. For each particular relative shift, we calculate the mean and standard deviation (std) of the permeability based on the 10 subcases and plot them as a black thick curve with the error bar correspondingly. The permeability calculated here is the fracture only permeability with no flow in the rock matrix assumed.
Several interesting trends can be identified in Fig. 10b. Firstly, the increase in the relative shift leads to a change in the shape of the curve, reducing the curvature within the range of the boundary stress \(\sigma _{x}^{\rm Boundary}\). The relationship becomes more gradual with the shift = 0.1 being almost linear. This aligns with the results from unidirectional flow tests performed on a rock fracture reproduction of a Permian sandstone using epoxy resin (Yeo et al. 1998). The sample was obtained without shear damage of two opposing surfaces of a fracture which is similar to our initial numerical set. This study showed an increase in permeability when the fracture is sheared, with a higher increase in the perpendicular direction than in the direction parallel to the shear. Second, in the stress range investigated, absolute values of permeability of the fracture increase with the increase in relative shift. Our results indicate the increase in the initial permeability from approximately 700 mD in the lowest shift (0.00025) to 4000 D in the highest shift (0.1)—a difference of four orders of magnitude.
To facilitate the analysis we normalize the mean permeability results by dividing the permeability at each stress by the initial permeability at the first contact (Fig. 11a). The normalized fracture permeability is shown on the left y-axis, whereas the absolute values on the log plot are shown on the right y-axis of the plot as dashed lines, both sharing the same boundary stress-x.
In the normalized plot, the permeability reduces more rapidly for small relative shifts. For example, there is a 88% reduction in the \(k_{f\bot }\) for the smallest shift model (0.00025) compared to 8% for the highest shift (0.1) at 5 MPa applied normal stress. For small shifts, the fracture tends to close easier even at relatively small applied stress. This is because for small shifts (less dislocated surfaces) the flow area is already small hence even at small stresses the deformation is sufficient to close the fracture and reduce the permeability significantly. After the initial sharp decline further increase in stress only marginally reduces the permeability.
a Fracture permeability \(k_{f\bot } \left( \sigma _{x} \right) \) relationships at various relative shifts, dimensionless fracture permeability on the left y-axis and actual fracture permeability on a log scale on the right y-axis. b Comparison of the laboratory poromechanics experiment obtained \(k_{\rm core} \left( \sigma ' \right) \) with the numerical equivalent permeability \(k_{eq\bot } \left( \sigma \right) \)
In contrast, for large shifts the contact area is typically smaller and the flow area is larger than in the small shift models. The deformation is mostly governed by several contacting asperities that act as a barrier for it. Thus, the permeability reduces more gradually over the specified stress range, as there is still a relatively large flow area and barriers restricting fracture closure. More stress is needed to close the fracture sufficiently to have a significant impact on the permeability decrease and for the shape of the stress permeability relationship to become more curved. Laboratory flow-stress tests carried out using a sandstone sample (Zhou et al. 2015) support the evidence that the relationship becomes more linear in fractures with larger mismatch length. While Zhou et al. (2015) presents results as hydraulic aperture versus stress, the results translate to a permeability versus stress with parallel plates approximation.
The large dislocation that can lead to the smaller contact area and larger flow area may also depend on the roughness and the self-similarity of the fracture surfaces. However, this is out of the scope of this work and needs an investigation in future studies.
Figure 11a also shows that the shift = 0.001 (blue curve) crosses the shift = 0.00025 (green curve) indicating that the higher shift permeability has a larger drop in permeability than the lower shift models. This may be related to the contact evolution, which we discuss in more detail in Sect. 5.6. There we provide examples from the three fracture cases. Note however, that the curves for absolute values of permeability do not cross as shown on the right.
5.3 Numerical Versus Laboratory Experiment
The comparison between the laboratory obtained core permeability versus effective stress and numerical modelling equivalent permeability versus normal stress-x is depicted in Fig. 11b for various shifts and for a specific shift in Fig. 12a. We added two shifts (0.0005 and 0.00075) simulation results to the existing 4 shifts. Usually, when comparing experimental versus modelling data, two things are considered: (1) comparing to what degree absolute values match and (2) comparing curve shapes which represent the type of behaviour or a function that can describe it. Matching absolute values is problematic because the lab experiment is carried out with interlocked (matched) surfaces of two parts of the sample, but the reference point to find the interlocked configuration for the numerical modelling was not available. Hence, models are generated by duplicating and shifting of the surface rendering the direct comparison impossible.
However, we compare curve shapes and qualitatively discuss the experimental versus numerical. It can be seen from Fig. 11b that the numerical stress–permeability curves with shift = 0.001 and 0.00075 behave similarly to the experimental data. Experimental data shows an onset of the power-law at \(\sim\) 1–3 MPa effective stress which is a linear decline on the log-log plot. Since the power-law behaviour does not manifest itself properly for shifts 0.01 and 0.1 and also the order of magnitude is substantially larger, we rule out larger shifts in the experimental data. The closest numerical model in terms of absolute values with shift = 0.00075 has the same shape of the curve: for stress less than 1 MPa the permeability is insensitive to stress. For larger stress, we observe a similar power-law decline in the experimental and numerical data.
There are additional differences between the experimental and numerical data. First, the laboratory experiment is done under coupled poromechanics settings where both fluid and mechanics affect each other. We do not model flow effect on the mechanics, we model mechanics deformation and at each simulation step calculate the flow velocity of the fluid inside the fracture. Hence, we compare the effective stress from the experiment against the applied boundary normal stress from the modelling. Second, there is a differentiation between the permeability measurements. In modelling, we calculate permeability in the perpendicular direction to the 2D cross section as discussed in Sect. 2.2. This fact yields an upper limit for permeability as tortuous flow paths are not accounted for. Equivalently, the permeability calculated along the fracture (in parallel to the cross section) is the lower limit as in 2D a single contact blocks the flow, and yields zero permeability. In contrast, the laboratory permeability is measured for a 3D fracture and expected to produce a value in between the two limits. Comparison of 2D numerical modelling against 3D laboratory data was performed before (Walsh et al. 2008).
5.4 Fracture Transmissivity \(T_{f}\) in Mismatched Fractures
We calculate numerical fracture transmissivity for the four presented shifts and show results in Fig. 12b as a function of normal stress. We perform numerical fitting on these shifts using power law, polynomial and exponential functions, where the best fit was obtained by using an exponential function provided in Eq. (15). The fitting curves resemble numerical results with the range of R-square of [0.9991 − 1], showing an excellent match. The only stress-transmissivity curve that deviates slightly at high stress is the one with the smallest shift of 0.00025. Fitting parameters for all shifts together with scaling coefficient used are presented in Table 1.
5.5 Effect of Roughness on \(k_{f\bot }\left( \sigma \right)\)
Here, we investigate the range of normal stress at the boundary versus permeability from the variation in roughness seen on the randomly picked cross sections of a fracture surface. For that, we calculate \(Z_{2}\) for all hundred cross sections, get the range of occurring roughness from the minimum \(Z_{2}\) = 0.12 to the maximum \(Z_{2}\) = 0.252 and group them into four bins. In each bin, we have a minimum of ten profiles. This yields models with a high roughness \(Z_{2}\) = [0.215 − 0.35], two intermediate \(Z_{2}\) = [0.186 − 0.215] and [0.153 − 0.186], and one range of models \(Z_{2}\) = [0.12 − 0.153] with low roughness. For instance, a noticeable difference in the roughness of the fractures can be seen in Fig. 13a where we show a representative profile for each bin. We set the small amount of mismatch (shift = 0.001) in all models.
a Four fractures with four different roughnesses with identical surfaces on both sides shifted relative to each other (shift = 0.001) and b normal stress at the boundary versus permeability relationship of the four bins of fractures roughness from Fig. 7 (log-log scale). coloured lines represent the simulation results of different fractures within each bin. The thick black line is the mean of all of the results within the bin and the error bars demonstrate one standard deviation
Results of the simulations are presented using a log-log scale in Fig. 13b with the mean and standard deviation, and the mean curves only are shown in Fig. 14a. Four mean curves demonstrate the initial sharp decline followed by a more gradual decrease of permeability with stress.
The more gradual decrease happens because during the deformation of the rough surfaces the amount of contacting area becomes larger making it more difficult to deform due to applied normal stress. Any additional contacting surfaces act as a bridge to restrict deformation. All models flatten out and exhibit a similar decline angle near the final higher stress 25 MPa. This process of closure was explained well (Jaeger et al. 2007) by the conceptual model of a mated fracture (Myer 2000). The model analyzed fractures as collinear ellipses, together with the earlier study (Sneddon and Lowengrub 1969) that provides the joint closure versus stress relationship. The framework indicates that at low stress, the area of contact is small with large compliance and hence small normal stiffness of the fracture (Jaeger et al. 2007). The small stiffness leads to a sharp decline in permeability at low stress. For higher stresses, the area of contact increases and compliance approaches zero with the fracture stiffness becoming infinitely large, hence the permeability decline reduces.
Figure 13b shows the higher roughness bin resulted in a higher standard deviation of the permeability curves. This is probably because, according to the roughness definition (Bhushan 2000), higher roughness means more local departures from the planarity. More local departures mean a higher probability of the initial contacts leaving the wider space for the fluid flow, and higher permeability.
Figure 14a illustrates that higher roughness fractures show typically higher initial permeability as well as the permeability after the applied stress. There is a 3.3 times difference in the initial \(k_{f\bot }\) between the highest and the lowest roughness fractures. The permeability stress relationship for lower roughnesses \(Z_{2}\) = [0.12 − 0.153] and \(Z_{2}\) = [0.153 − 0.186] generally show a steeper decline in the permeability at lower stress, compared to the rougher ones with larger \(Z_{2}\). We associate that with better matched surfaces at low stresses are more prone to close.
In contrast, high roughness surfaces \(Z_{2}\) = [0.215 − 0.35] show a more moderate initial decline in the permeability. The small wiggles seen on the maximum roughness curve in red at stress around 4 MPa stem from the averaging. Note that our sample does not cover the whole range of surface roughness characteristics observed in rocks.
In line with a previous study (Barton et al. 1985), we notice that smooth fractures tend to close easier than rougher ones, especially during initial deformation (lower stress). We also observe that the permeability drop \(k_\mathrm{init} / k_\mathrm{final}\) over the applied stress range is higher 6.8 and 6.6 in contrast to 6.1 for the two smoother and the roughest bins, respectively. The latter declines from an initial permeability 13670 mD at the first contact to 2239 mD during the deformation of a total stress 2.5 MPa, whereas for the smoothest bin it drops from 4150 to 610 mD.
We also calculate the fracture transmissivity for the four bins of fracture roughness \(Z_{2}\) and show results in Fig. 14b as a function of stress. The curve fitting to the numerical results was done using an exponential function, provided in Eq. (15). The fitting curves reveal a good match, with R-square of [0.9973\(-\)0.9986]. The three lowest roughness fitting curves (green, blue and black) tend to underestimate transmissivity at the final high stress (\(> 20\) MPa). Fitting parameters with scaling coefficient are presented in Table 2.
5.6 Uncorrelated Random Cross Sections \(k_{f\bot }\left( \sigma \right)\)
In this section, we analyze scenarios where the opposite Right fracture profile is taken from the second smaller half of the cylindrical Carmel sample (Fig. 1), and the bigger part is used to create the original Left body fracture profile as before. The procedure of creating a grid of the two distinct bodies is equivalent to the one described in Sect. 4. No shift is applied in this case since both sides are not identical such that a natural mismatch is present. We increase the range of applied final normal boundary stress to 50 MPa because the model with randomly unmatched surfaces is prone to be dominated by the individual peaks with large flow area, where the onset of the permeability stabilization is often not reached within the 25 MPa stress range.
Figure 15 shows the resulting stress–permeability relationships. Based on all realizations, we calculate the mean and standard deviation (std), shown as a thick black curve and error bars, having the initial mean of 6700 D, with the \({\text{std}}\) = 4700 D. The figure shows that for all 100 representations, the permeability decline is small. The \(k_\mathrm{init} / k_\mathrm{final}\) ratio here is \(\sim\) 1.3, smaller compared to \(\sim\) 6.5 in Sect. 5.5 for the stress of 25 MPa.
The mean curve in Fig. 15a indicate a moderate decline in the applied stress range of 50 MPa. The permeability decline starts at higher stress \(\sim\) 10 MPa compared to \(\sim\) 1 MPa in the Sect. 5.5. This onset of decline is similar to larger shifts (0.1 and 0.01) in Sect. 5.2.
Figure 15b shows the stress–permeability curves normalized by the permeability at zero stress. The mean drop in permeability is only to around 0.65 of the initial value. This is much smaller than the drop in lab experiments shown in Fig. 4, where the drop is 0.082 within the applied effective stress range of 18.3 MPa. The minimal normalized permeability is as low as 0.34, and the maximum is 0.86 in the most insensitive case.
Uncorrelated surfaces matching (Fig. 15a) cause a large spread in the initial permeability distribution 900–22600 D, minimum and maximum correspondingly. Final permeabilities have a range of 400–16700 D at the highest stress \(\sigma _{x}^\mathrm{Boundary}\) of 50 MPa. These fractures are already able to conduct a considerable amount of flow and the effect of stress is small.
Some cases have substantially steeper declines of permeability with respect to stress. For further analysis, we group the cases in two categories according to permeability drop, large and small. For instance, case 10 if compared with case 13 or case 23 has a much smaller permeability drop, even though the permeability of the first two cases are roughly the same (see Fig. 15a). The reason is as follows: the large permeability drop cases 13 and 23 tend to have a single contact place during deformation. Contact areas form a resistance to the deformation and the less contact areas are present in the fracture the more easy it is to deform, and hence the permeability drops more significantly for cases with single contact areas. The contacting surfaces are shown on the final grids of these cases in Fig. 16 where the stress concentration occur. Case 10 has a total of 17 contacts, illustrated as the areas with high-stress concentration. Cases 13 and 23 have 12 and 13 contacts respectively which makes it 1.4 times lower. In cases 13 and 23, because the contact is predominantly concentrated on a single place at the edge, the maximum x component of the stress tensor of the whole body is higher. The difference is \(-4 \times 10^{9}\) Pa and \(-1 \times 10^{9}\) Pa in case 13 and 10.
Statistics that relate roughness parameters \(Z_{2}\), \(\mathrm JRC\), \(R_{a}\), \(R_{m}\), \(R_{p}\) to the initial permeability and permeability reduction (\(\Delta\)Permeability = Initial\(-\)Final), are presented in Fig. 17, where 100 simulations results are grouped into 10 bins in histograms. All roughness parameters follow approximately a symmetric bell shaped. However, initial permeability and \(\Delta\)Permeability have a different non-symmetrical skewed type of distribution. Most of the occurrences in these parameters are concentrated in the smaller initial permeability and the total permeability reduction.
6 Conclusions
In this paper, we presented a computational model that inputs a digital image of the natural rough fracture and outputs the stress–permeability relationship of that fracture for use in hydro-mechanical studies. The model is based on contact mechanics using a first principle approach on the continuum scale for fracture deformation. The contact problem solution is exact, conserving the elastic strain energy. The model avoids the assumptions needed in (semi-) analytical approaches or conceptualizing the problem such as assuming that fracture asperities have specific shapes or geometries. Fracture permeability was calculated at each deformation step by using the Stokes equation perpendicular to the cross section of interest.
Topographical information pertaining to the rock surface was obtained using a digital optical microscope, which was then used to select random height profiles. These were used to create 2D models for the analysis of mechanical deformation and permeability.
We quantitatively assessed the impact of the fracture surface roughness, the shift of the surfaces and random surfaces on the permeability evolution under stress. We provided empirical stress versus fracture transmissivity relationships for various shifts and roughnesses based on the analysis of the numerical and laboratory experiments. Finally, we compared laboratory results against numerical simulations and the Barton-Bandis model. The numerical results compare well and therefore can aid in determining permeability in fractured systems under stress, especially in cases where experimental data is not available. Alongside the analysis, the following observations are noted:
-
Larger shift in a rough fracture results in a smaller drop in the permeability due to applied normal boundary stress, exhibiting a more gradual relationship. This agrees with the previous laboratory studies.
-
Permeability tends to be higher in models with higher roughness parameters \(Z_{2}\) and JRC, and this tendency generally holds throughout the deformation due to 25 MPa normal boundary stress.
-
Permeability in fractures with uncorrelated surfaces is relatively insensitive to the stresses below 50 MPa. On average, the drop in permeability is only 0.35 of the initial value.
-
The Barton-Bandis model shows substantially different stress–permeability relationships compared to laboratory tests. The disparity can be due to the fracture aperture in the Carmel core being much smaller than what the Barton-Bandis model is based on. In addition, the Barton-Bandis model is developed for granite, whereas a mudstone was used in this study.
References
Andersen, O., Nilsen, H.M., Raynaud, X.: On the use of the virtual element method for geomechanics on reservoir grids (2016), arXiv preprint arXiv:1606.09508
Bandis, S.C., Lumsden, A.C., Barton, N.R.: Fundamentals of rock joint deformation. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 20(6), 249–268 (1983). https://doi.org/10.1016/0148-9062(83)90595-8
Barber, J.R.: Contact Mechanics, vol. 250. Springer, New York (2018)
Barton, N., Bandis, S., Bakhtar, K.: Strength, deformation and conductivity coupling of rock joints, In: International journal of rock mechanics and mining sciences & geomechanics abstracts, Elsevier, Vol. 22, pp. 121–140 (1985). https://doi.org/10.1016/0148-9062(85)93227-9
Barton, N., Choubey, V.: The shear strength of rock joints in theory and practice. Rock Mech. 10(1–2), 1–54 (1977). https://doi.org/10.1007/bf01261801
Bhushan, B.: Surface Roughness Analysis and Measurement Techniques, pp. 79–150. CRC Press, Boca Raton (2000)
Bjørnara, T.I., Skurtveit, E., Sauvin, G.: Stress-dependent fracture permeability in core samples: an experimental and numerical study, In: 2nd International Discrete Fracture Network Engineering Conference, American Rock Mechanics Association (2018)
Brown, S.R.: Fluid flow through rock joints: the effect of surface roughness. J. Geophys. Res. Solid Earth 92(B2), 1337–1347 (1987). https://doi.org/10.1029/JB092iB02p01337
Brown, S.R., Scholz, C.H.: Closure of random elastic surfaces in contact. J. Geophys. Res. Solid Earth 90(B7), 5531–5545 (1985). https://doi.org/10.1029/JB090iB07p05531
Busch, A., Amann-Hildenbrand, A.: Predicting capillarity of mudrocks. Mar. Pet. Geol. 45, 208–223 (2013)
Chen, Y., Liang, W., Lian, H., Yang, J., Nguyen, V.P.: Experimental study on the effect of fracture geometric characteristics on the permeability in deformable rough-walled fractures. Int. J. Rock Mech. Min. Sci. 98, 121–140 (2017). https://doi.org/10.1016/j.ijrmms.2017.07.003
Curle, S., Davies, H.: Modern Fluid Dynamics, vol. 1. Van Nostrand, New York (1968)
Economides, M.J., Martin, T.: Modern Fracturing: Enhancing Natural Gas Production, 383–416 (2007)
Fang, Y., Elsworth, D., Ishibashi, T., Zhang, F.: Permeability evolution and frictional stability of fabricated fractures with specified roughness. J. Geophys. Res. Solid Earth 123(11), 9355–9375 (2018). https://doi.org/10.1029/2018jb016215
Frash, L.P., Carey, J.W., Ickes, T., Viswanathan, H.S.: Caprock integrity susceptibility to permeable fracture creation. Int. J. Greenh. Gas Control 64, 60–72 (2017). https://doi.org/10.1016/j.ijggc.2017.06.010
Gain, A.L., Talischi, C., Paulino, G.H.: On the virtual element method for three-dimensional linear elasticity problems on arbitrary polyhedral meshes. Comput. Methods Appl. Mech. Eng. 282, 132–160 (2014). https://doi.org/10.1016/j.cma.2014.05.005
Glover, P., Matsuki, K., Hikima, R., Hayashi, K.: Synthetic rough fractures in rocks. J. Geophys. Res. Solid Earth 103(B5), 9609–9620 (1998). https://doi.org/10.1029/97JB02836
Goldstein, B., Hiriart, G., Tester, J., Bertani, B., Bromley, R., Gutierrez-Negrin, L., Huenges, E., Ragnarsson, A., Mongillo, A., Muraoka, H.: Great expectations for geothermal energy to 2100. In: Proceedings 36th workshop on geothermal reservoir engineering (2011)
Grasselli, G., Egger, P.: Constitutive law for the shear strength of rock joints based on three-dimensional surface parameters. Int. J. Rock Mech. Min. Sci. 40(1), 25–40 (2003). https://doi.org/10.1016/s1365-1609(02)00101-6
Greenwood, J., Williamson, J.P.: Contact of nominally flat surfaces. In: Proceedings of the royal society of London. Series A. Mathematical and physical sciences 295(1442), 300–319 (1966). https://doi.org/10.1016/0043-1648(67)90287-6
Huo, D., Li, B., Benson, S.M.: Investigating aperture-based stress-dependent permeability and capillary pressure in rock fractures, In: SPE annual technical conference and exhibition, Society of Petroleum Engineers (2014). https://doi.org/10.2118/170819-MS
Huo, D., Benson, S.M.: Experimental investigation of stress-dependency of relative permeability in rock fractures. Transp. Porous Media 113(3), 567–590 (2016). https://doi.org/10.1007/s11242-016-0713-z
Ishibashi, T., Watanabe, N., Hirano, N., Okamoto, A., Tsuchiya, N.: Beyond-laboratory-scale prediction for channeling flows through subsurface rock fractures with heterogeneous aperture distributions revealed by laboratory evaluation. J. Geophys. Res. Solid Earth 120(1), 106–124 (2015). https://doi.org/10.1002/2014JB011555
Jaeger, J.C., Cook, N.G., Zimmerman, R.: Fundamentals of Rock Mechanics. John Wiley & Sons, Hoboken (2007)
Kampman, N., Maskell, A., Bickle, M., Evans, J., Schaller, M., Purser, G., Zhou, Z., Gattacceca, J., Peitre, E., Rochelle, C.: Scientific drilling and downhole fluid sampling of a natural co2 reservoir, green river, utah. Sci. Drill. 16, 33–43 (2013). https://doi.org/10.5194/sd-16-33-2013
Kampman, N., Bickle, M.J., Maskell, A., Chapman, H.J., Evans, J.P., Purser, G., Zhou, Z., Schaller, M.F., Gattacceca, J.C., Bertier, P., Chen, F., Turchyn, A.V., Assayag, N., Rochelle, C., Ballentine, C.J., Busch, A.: Drilling and sampling a natural co2 reservoir: implications for fluid flow and co2-fluid-rock reactions during co2 migration through the overburden. Chem. Geol. 369, 51–82 (2014). https://doi.org/10.1016/j.chemgeo.2013.11.015
Karpyn, Z., Grader, A., Halleck, P.: Visualization of fluid occupancy in a rough fracture using micro-tomography. J. Colloid Interface Sci. 307(1), 181–187 (2007). https://doi.org/10.1016/j.jcis.2006.10.082
Keyence: Digital microscope vhx-6000 user’s manual (2017)
Kim, H.-M., Inoue, J., Horii, H.: Flow analysis of jointed rock masses based on excavation-induced transmissivity change of rough joints. Int. J. Rock Mech. Min. Sci. 41(6), 959–974 (2004). https://doi.org/10.1016/j.ijrmms.2004.03.001
Kim, D.H., Gratchev, I., Balasubramaniam, A.: Determination of joint roughness coefficient (JRC) for slope stability analysis: a case study from the gold coast area. Australia. Landslides 10(5), 657–664 (2013). https://doi.org/10.1007/s10346-013-0410-8
Kling, T., Vogler, D., Pastewka, L., Amann, F., Blum, P.: Numerical simulations and validation of contact mechanics in a granodiorite fracture. Rock Mech. Rock Eng. 51(9), 2805–2824 (2018). https://doi.org/10.1007/s00603-018-1498-x
Koyama, T., Li, B., Jiang, Y., Jing, L.: Numerical modelling of fluid flow tests in a rock fracture with a special algorithm for contact areas. Comput. Geotech. 36(1–2), 291–303 (2009). https://doi.org/10.1016/j.compgeo.2008.02.010
Kubeyev, A., Maier, C., Doster, F.: Geomechanics numerical code for modelling contact in fractures and other discontinuities using virtual element method. In: 53rd U.S. rock mechanics/geomechanics symposium, American Rock Mechanics Association, ARMA, p. 13 (2019)
Kubeyev, A.: Impact of multi-set fracture pattern on the effective permeability of fractured porous media. J. Pet. Sci. Eng. 112, 161–169 (2013). https://doi.org/10.1016/j.petrol.2013.10.022
Laubach, S.E., Lander, R., Criscenti, L.J., Anovitz, L.M., Urai, J., Pollyea, R., Hooker, J.N., Narr, W., Evans, M.A., Kerisit, S.N., et al.: The role of chemistry in fracture pattern development and opportunities to advance interpretations of geological materials. Rev. Geophys. 57(3), 1065–1111 (2019). https://doi.org/10.1029/2019RG000671
Lie, K.-A.: An introduction to reservoir simulation using MATLAB: user guide for the Matlab Reservoir Simulation Toolbox (MRST). SINTEF ICT (2014). https://doi.org/10.1017/9781108591416.021
Liu, H.-H., Wei, M.-Y., Rutqvist, J.: Normal-stress dependence of fracture hydraulic properties including two-phase flow properties. Hydrogeo. J. 21(2), 371–382 (2013). https://doi.org/10.1007/s10040-012-0915-6
Maerz, N.H., Franklin, J.A., Bennett, C.P.: Joint roughness measurement using shadow profilometry. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 27(5), 329–343 (1990). https://doi.org/10.1016/0148-9062(90)92708-M
Milne, D., Hawkes, C., Hamilton, C.: A new tool for the field characterization of joint surfaces. In: Proc the 3rd CANUS rock mechanics symposium, Toronto (2009)
Munjiza, A.A.: The Combined Finite-Discrete Element Method. John Wiley & Sons, Hoboken (2004)
Myer, L.R.: Fractures as collections of cracks. Int. J. Rock Mech. Min. Sci. 37(1–2), 231–243 (2000). https://doi.org/10.1016/S1365-1609(99)00103-3
Nelson, R.: Geologic Analysis of Naturally Fractured Reservoirs. Elsevier, Amsterdam (2001)
Paluszny, A., Matthai, S.: Numerical simulation of geomechanic fracture networks: application to measuring effective permeability variability. In: The 42nd US rock mechanics symposium (USRMS), American Rock Mechanics Association (2008)
Papadopoulos, P., Solberg, J.: A Lagrange multiplier method for the finite element solution of frictionless contact problems. Math. Comput. Model. 28(4–8), 373–384 (1998). https://doi.org/10.1016/S0895-7177(98)00128-9
Payne, W.G.: Controls on porosity and permeability in the carmel formation: implications for carbon sequestration at gordon creek, utah, Ph.D. thesis, Citeseer (2011)
Petrie, E., Evans, J.: Modeling the significance of mechanical interfaces to fracture propagation and morphology-geomechanical models derived from outcrop analysis. In: Unconventional Resources Technology Conference, Society of Exploration Geophysicists, American Association of Petroleum, pp. 438–447 (2013) https://doi.org/10.1190/urtec2013-047
Petrie, E.S., Jeppson, T., Evans, J.P.: Use of wire line logs for estimation of strength variability in cap-rock lithologies (2011)
Phillips, T., Bultreys, T., Bisdom, K., Kampman, N., Van Offenwert, S., Mascini, A., Cnudde, V., Busch, A.: A systematic investigation into the control of roughness on the flow properties of 3d-printed fractures. Water Resour. Res. 57(4), ewrcr-25233 (2021). https://doi.org/10.1029/2020WR028671
Phillips, T., Kampman, N., Bisdom, K., Forbes Inskip, N.D., den Hartog, S.A., Cnudde, V., Busch, A.: Controls on the intrinsic flow properties of mudrock fractures: a review of their importance in subsurface storage. Earth-Sci. Rev. (2020). https://doi.org/10.3997/2214-4609.202021014
Pyrak-Nolte, L., Morris, J.: Single fractures under normal stress: the relation between fracture specific stiffness and fluid flow. Int. J. Rock Mech. Min. Sci. 37(1–2), 245–262 (2000). https://doi.org/10.1016/S1365-1609(99)00104-5
Pyrak-Nolte, L.J., Nolte, D.D.: Approaching a universal scaling relationship between fracture stiffness and fluid flow. Nat. Commun. 7(1), 1–6 (2016). https://doi.org/10.1038/ncomms10663(2016)
Richter, C., Kotz, F., Giselbrecht, S., Helmer, D., Rapp, B.E.: Numerics made easy: solving the navier-stokes equation for arbitrary channel cross-sections using microsoft excel. Biomed. Microdevices 18(3), 52 (2016). https://doi.org/10.1007/s10544-016-0070-2
Ross, D.J., Bustin, R.M.: The importance of shale composition and pore structure upon gas storage potential of shale gas reservoirs. Mar. pet. Geol. 26(6), 916–927 (2009). https://doi.org/10.1016/j.marpetgeo.2008.06.004
Sneddon, I., Lowengrub, M.: Crack problems in the classical theory of elasticity, New York, Vol. 29 (1969). https://doi.org/10.1002/zamm.19710510317
Tse, R., Cruden, D.: Estimating joint roughness coefficients. In: International journal of rock mechanics and mining sciences & geomechanics abstracts, Elsevier, Vol. 16, pp. 303–307 (1979). https://doi.org/10.1016/0148-9062(79)90241-9
Vilarrasa, V., Olivella, S., Carrera, J.: Geomechanical stability of the caprock during co2 sequestration in deep saline aquifers. Energy Procedia 4, 5306–5313 (2011). https://doi.org/10.1016/j.egypro.2011.02.511
Walsh, J.: Effect of pore pressure and confining pressure on fracture permeability, In: International journal of rock mechanics and mining sciences & geomechanics abstracts, Elsevier, Vol. 18, pp. 429–435 (1981). https://doi.org/10.1016/0148-9062(81)90006-1
Walsh, R., McDermott, C., Kolditz, O.: Numerical modeling of stress-permeability coupling in rough fractures. Hydrogeol. J. 16(4), 613 (2008). https://doi.org/10.1007/s10040-007-0254-1
Wang, M., Chen, Y.-F., Ma, G.-W., Zhou, J.-Q., Zhou, C.-B.: Influence of surface roughness on nonlinear flow behaviors in 3d self-affine rough fractures: lattice boltzmann simulations. Adv. Water Resour. 96, 373–388 (2016). https://doi.org/10.1016/j.advwatres.2016.08.006
Weisstein, E.W.: Normal equation (2011)
Wriggers, P.: Computational Contact Mechanics, 2nd edn. Springer, New York (2006)
Yasuhara, H., Elsworth, D.: A numerical model simulating reactive transport and evolution of fracture permeability. Int. J. Numer. Anal. Methods Geomech. 30(10), 1039–1062 (2006). https://doi.org/10.1002/nag.513
Yeo, W.: Effect of contact obstacles on fluid flow in rock fractures. Geosci. J. 5(2), 139–143 (2001). https://doi.org/10.1007/bf02910418
Yeo, I., De Freitas, M., Zimmerman, R.: Effect of shear displacement on the aperture and permeability of a rock fracture. Int. J. Rock Mech. Min. Sci. 35(8), 1051–1070 (1998). https://doi.org/10.1016/s0148-9062(98)00165-x
Zhang, C.-L.: Sealing of fractures in claystone. J. Rock Mech. Geotech. Eng. 5(3), 214–220 (2013). https://doi.org/10.1016/j.jrmge.2013.04.001
Zhou, J.-Q., Hu, S.-H., Fang, S., Chen, Y.-F., Zhou, C.-B.: Nonlinear flow behavior at low Reynolds numbers through rough-walled fractures subjected to normal compressive loading. Int. J. Rock Mech. Min. Sci. 80, 202–218 (2015). https://doi.org/10.1016/j.ijrmms.2015.09.027
Zimmerman, R.W., Bodvarsson, G.S.: Hydraulic conductivity of rock fractures. Transp. Porous Media 23(1), 1–30 (1996). https://doi.org/10.1007/bf00145263
Zimmerman, R.W., Chen, D.-W., Cook, N.G.: The effect of contact area on the permeability of fractures. J. Hydrol. (1993). https://doi.org/10.1016/0022-1694(92)90196-3
Zou, L., Jing, L., Cvetkovic, V.: Shear-enhanced nonlinear flow in rough-walled rock fractures. Int. J. Rock Mech. Min. Sci. 97, 33–45 (2017). https://doi.org/10.1016/j.ijrmms.2017.06.001
Acknowledgements
The authors gratefully acknowledge funding from ERANET Cofund ACT (Project no. 271497), European Commission, Research Council of Norway, the Rijksdienst voor Ondernemend Nederland, the Federal German Ministry for Economic Affairs and Energy (BMWI); and the Department for Business, Energy & Industrial Strategy, UK (BEIS) and funding from the European Union’s Horizon 2020 research and innovation programme, under grant agreement number 764531.
Author information
Authors and Affiliations
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A. Barton-Bandis Model
Appendix A. Barton-Bandis Model
Barton et al. (1985) provide equations that couple normal stress, closure and conductivity of a fracture. It is an empirical model based on extensive research of natural fractures and relies on actual test data with functions later fitted to it. A minimum of two inputs in terms of JRC and joint wall compression strength (JCS) results in a stress–permeability relationship. First, the initial mechanical aperture (mm) is defined as
where \(\sigma _{c}\) is the unconfined compressive strength (rock adjacent to fracture wall) in MPa. When the fracture is unaltered or unweathered JCS = \(\sigma _{c}\) can be taken in MPa Barton et al. (1985). Maximum possible closure (mm) is defined as
where A, B, C, D are coefficients estimated from the third loading cycle as specified in Barton et al. (1985). We take the values − 0.1032, − 0.0074, 1.135 and − 0.251 respectively, which correspond to the third loading cycle of a rock provided in the model (Bandis et al. 1983). The third cycle is the closest cycle in getting a single reproducible stress–permeability, however, probably more than three cycles are needed (Bandis et al. 1983). Initial normal stiffness (MPa/mm) is expressed as
The residual mechanical aperture (mm) can be calculated as the difference between the initial and joint closure
where \(\sigma\) is the applied normal stress in MPa, \(\Delta V_{J}\) is the joint closure in mm and \(E_{0m}\) is the initial mechanical aperture. Hydraulic aperture in mm
and the fracture permeability can be extracted using parallel plate approximation, after converting the hydraulic aperture from mm to m:
in m\(^{2}\) in SI units. Equations (A.1)–(A.6) can be used to obtain a normal stress–fracture permeability relationship by having at least two inputs: JRC and JCS.
We compare laboratory core plug permeability results to the Barton-Bandis model in Sect. 3.1. In Sect. 2.3 we derived an equivalent permeability from the numerical fracture permeability to be able to compare to the core permeability from the experiment. Similarly, here we derive the permeability of the Barton-Bandis model that is equivalent and comparable permeability to the laboratory core permeability. Alike Eq. (17), the relationship between the core fracture area and the Barton-Bandis fracture area can be provided with the fracture length being unknown in the Barton-Bandis model
where \(A_{f\left( B\right) }\) is the Barton-Bandis fracture flow area, \(l_{B}\) is the Barton-Bandis fracture length. Using the Barton-Bandis fracture area we get
Finally, using Eq. (18), Barton-Bandis equivalent permeability can be obtained to compare the Barton-Bandis derived stress–permeability to the experimental data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kubeyev, A., Forbes Inskip, N., Phillips, T. et al. Digital Image-Based Stress–Permeability Relationships of Rough Fractures Using Numerical Contact Mechanics and Stokes Equation. Transp Porous Med 141, 295–330 (2022). https://doi.org/10.1007/s11242-021-01719-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-021-01719-7