A Fractal Permeability Model for Gas Transport in the Dual-Porosity Media of the Coalbed Methane Reservoir

Abstract

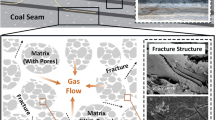
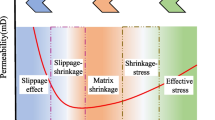
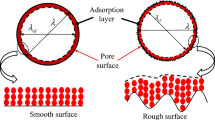
In the process of coalbed methane (CBM) exploitation, permeability is a key controlling parameter for gas transport in the CBM reservoirs. The CBM reservoir contains a large number of micropores and microfractures with complex structures. In order to accurately predict the gas permeability of the micropores and microfractures in CBM reservoirs, a fractal permeability model was developed in this work. This model considers the comprehensive effects of real gas, stress dependence, multiple gas flow mechanisms (e.g., slip flow, Knudsen diffusion and surface diffusion) and fractal characteristics (e.g., pore size distribution and flow path tortuosity) of micropores and microfractures on the gas permeability. Then, this fractal permeability model was verified by the reliable experimental data and other theoretical models. Finally, the sensitivity analysis is conducted to identify key factors to the permeability of CBM reservoir. The results showed that the fractal characteristics of the micropores and microfractures have significant effects on the permeability of CBM reservoir. Higher fractal dimension of micropores diameter and microfractures aperture represents the larger number of micropores and microfractures, resulting in a higher permeability. Higher tortuosity fractal dimension of micropores and microfractures means higher gas flow resistance, leading to the lower permeability. The multiple gas transport mechanisms coexist in micropores and microfractures of CBM reservoir. The permeability of slip flow and Knudsen diffusion both increases with the decrease in pore pressure. Surface diffusion is an important gas transport mechanisms in micropores, but it can be ignored in the microfractures. Knudsen diffusion plays a more obvious role in the lower pore pressure, which controls the gas transport in microfractures. And microfractures are beneficial to improve gas transport capacity of coalbed methane reservoir.

Appendices

Appendix A. Real Gas Effect

Under the high gas pressure condition in the CBM reservoir, the real gas effect significantly affects gas transport in micropores and microfractures. The effects of real gas on gas transport are characterized by gas compressibility factor and gas viscosity. The gas compressibility factor will change with the gas pressure and reservoir temperature, and it can be expressed as the function of the reduced gas pressure and reduced temperature (Loebenstein 1971):

$$Z = 1 + \frac{{p_{r} }}{{10.24T_{r} }}\left[ {\frac{2.16}{{T_{r} }}\left( {\frac{1}{{T_{r} }} + 1} \right) - 1} \right]$$

(A1)

where $Z$ is the real gas compressibility factor; $p_{r} = {p \mathord{\left/ {\vphantom {p {p_{c} }}} \right. \kern-\nulldelimiterspace} {p_{c} }}$ is the reduced gas pressure; $T_{r} = {T \mathord{\left/ {\vphantom {T {T_{c} }}} \right. \kern-\nulldelimiterspace} {T_{c} }}$ is the reduced temperature; $p$ is the gas pressure, MPa; $T$ is the temperature, K; $p_{c}$ is the critical pressure MPa; and $T_{c}$ is the critical temperature, K.

Similarly, gas viscosity can also be expressed as a function of the reduced gas pressure and reduced temperature (Jarrahiana and Heidaryan 2014):

$$\mu_{i} = \mu \left[ {1 + \frac{{A_{1} }}{{T_{r}^{5} }}\left( {\frac{{p_{r}^{4} }}{{T_{r}^{20} + p_{r}^{4} }}} \right) + A_{2} \left( {\frac{{p_{r} }}{{T_{r} }}} \right)^{2} + A_{3} \left( {\frac{{p_{r} }}{{T_{r} }}} \right)} \right]$$

(A2)

where $\mu$ is the gas viscosity under p = 1.01325 × 10⁵ Pa and T = 423 K; $\mu_{i}$ is the real gas viscosity, Pa s; and $A_{1}$, $A_{2}$ and $A_{3}$ are the three fitting constants, respectively.

Appendix B. Dynamic Diameter of Micropores

With the gas pressure decrease during the development of CBM, the effective stress will increase. The increase in effective stress will reduce the permeability, porosity, pore diameter and fracture aperture of CBM reservoir.

For the micropores, a power law relationship can describe the effect of effective stress on permeability and porosity (Dong et al. 2010):

$$k = k_{0} \left( {{{p_{e} } \mathord{\left/ {\vphantom {{p_{e} } {p_{0} }}} \right. \kern-\nulldelimiterspace} {p_{0} }}} \right)^{ - s}$$

(B1)

where $k$ is the permeability of micropores under the effective stress, m²; $k_{0}$ is the initial permeability of micropores, m²; $p_{0}$ is the atmospheric pressure, m²; $p_{e} = p^{\prime} - p$ is the effective stress, MPa; $p^{\prime}$ is the total stress, MPa; and $s$ is the permeability coefficient.

The relationship among the permeability, porosity, pore diameter and tortuosity can be expressed as (Civan et al. 2013):

$$k = \frac{{\phi_{p} d_{p}^{2} }}{32\tau }$$

(B2)

where $\tau$ is the tortuosity of micropores. Thus, the ratio of permeability to the initial permeability can be expressed as:

$$\frac{k}{{k_{0} }} = \frac{{\phi_{p} d_{p}^{2} }}{{\phi_{p0} d_{p0}^{2} }} = \left( {\frac{{p_{e} }}{{p_{0} }}} \right)^{ - s}$$

(B3)

where $\phi_{p0}$ and $d_{p0}$ are the initial porosity and diameter of micropores. Besides, the porosity is positively proportional to the third power of micropore diameter. Thus, the following equation can be obtained:

$$\frac{{d_{p}^{5} }}{{d_{p0}^{5} }} = \left( {\frac{{p_{e} }}{{p_{0} }}} \right)^{ - s}$$

(B4)

When considering the stress dependence effect, the dynamic diameter of micropores can be expressed as:

$$d_{p} = d_{p0} \left( {\frac{{p_{e} }}{{p_{0} }}} \right)^{{ - \frac{s}{5}}}$$

(B5)

Appendix C. Dynamic Aperture of Microfractures

For the microfractures network, the microfractures consist of the hard part and soft part, which follow different Hooke’s law (Liu et al. 2009; Chen et al. 2012). The hard part obeys the engineering strain based on Hooke’s law, and the soft part follows the natural strain based on Hook’s law. Thus, the stress–strain relationship of the hard part in microfractures can be expressed as:

$$d\sigma = K_{h} d\varepsilon_{h}$$

(C1)

where $\sigma$ is the stress of the microfractures, MPa; $K_{h}$ is the bulk modulus of the hard part, MPa; and $\varepsilon_{h}$ is the engineering strain of hard part, defined as:

$$d\varepsilon_{h} = - \frac{{dh_{h} }}{{h_{0,h} }}$$

(C2)

where $h_{h}$ is the fracture aperture of the hard part under the stress condition, m; $h_{0,h}$ is the initial aperture of the hard part, m.

For the soft part of the microfractures, the stress–strain relationship can be expressed as:

$$d\sigma = K_{s} d\varepsilon_{s}$$

(C3)

where $K_{s}$ is the bulk modulus of the soft part; $\varepsilon_{s}$ is the natural strain of soft part, defined as:

$$d\varepsilon_{s} = - \frac{{dh_{s} }}{{h_{s} }}$$

(C4)

where $h_{s}$ is the fracture aperture of the soft part.

Using the initial condition that $h_{h} = h_{0,h}$ and $h_{s} = h_{0,s}$ for $\sigma = 0$, the engineering strain of the hard part and the natural strain of the soft part can be integrated into:

$$h_{h} = h_{0,h} \left( {1 - \frac{\Delta \sigma }{{K_{h} }}} \right)$$

(C5)

$$h_{s} = h_{0,s} \exp \left( {\frac{\Delta \sigma }{{K_{s} }}} \right)$$

(C6)

The total aperture of the microfractures can be obtained as:

$$h_{f} = h_{h} + h_{s} = h_{0,h} \left( {1 - \frac{\Delta \sigma }{{K_{h} }}} \right) + h_{0,s} \exp \left( {\frac{\Delta \sigma }{{K_{s} }}} \right)$$

(C7)

$K_{h}$ is generally much larger than $K_{s}$, and the initial aperture of microfractures $h_{0} = h_{0,h} + h_{0,s}$. Thus, Eq. (C7) can be simplified into:

$$h_{f} = h_{0,h} + \left( {h_{0} - h_{0,h} } \right)\exp \left( {\frac{\Delta \sigma }{{K_{s} }}} \right)$$

(C8)