1 Introduction

For a porous medium, possibly containing fractures, the interplay between flow, thermal transport and deformation can be strong. In particular, cooling of the medium induces thermal stress that can lead to deformation and fracturing. Fractures deform and propagate as a result of the coupled dynamics. Coupled thermo-hydro-mechanical (THM) processes in the intact porous medium interact with flow and thermal transport in fractures as well as fracture deformation and propagation. Such coupled process–structure interaction is characteristic for a wide range of natural and engineered processes both in natural and manufactured materials. For example, the structural and functional performance of concrete structures—such as dams, bridges, nuclear and liquefied natural gas containers and cement sheaths of subsurface well-bore constructions—are affected by the time evolution of their properties under variable THM loads (Baroth 2019; Bois et al. 2012; Kogbara et al. 2013; Bouhjiti et al. 2018a, b; Lin et al. 2020). In the subsurface, THM processes interact with deformation and propagation of fractures in fluid injection operations (Siratovich et al. 2015; Gao and Ghassemi 2020; Wu et al. 2020). The coupled dynamics are also hypothesised to be crucial in heat transfer from the deep roots of geothermal systems by deepening natural convection through evolving fractures (Lister 1974; Bodvarsson 1982; Björnsson et al. 1982; Björnsson and Stefánsson 1987). Common to all of these applications is the limitation placed by tight coupling in the dynamics on the knowledge which can be gained from analysis of individual processes and mechanisms in isolation. This motivates development of simulation models that acknowledge the coupled nature of the physics.

Since it was established by Biot (1941), the theory of poroelasticity has successfully been applied to model coupled hydro-mechanical processes. The extension to thermo-poroelasticity (Coussy 2004) is also widely applied, including in geomechanics (Selvadurai and Suvorov 2017). More recently, models accounting for discontinuities in the form of fractures in poroelastic and thermo-poroelastic media have been developed. Typically, model development has focused either on deformation of pre-existing fractures or the mechanical fracturing of the materials. These models can be distinguished based on whether fractures are represented explicitly as discrete objects embedded in the porous medium or as part of the porous medium itself. The latter incorporate the effect of the extent to which a material is fractured by use of smeared or distributed representations. Such models include phase-field and damage approaches for fracture (de Borst and Verhoosel 2016) and continuum and multi-continuum approaches for flow models (Berre et al. 2019).

Approaches based on explicit representation of the fractures can further be distinguished by how the fractures are represented in discretisation, specifically, whether a conforming or non-conforming representation of the fractures is used in the grid (Berre et al. 2019). Non-conforming methods represent the fracture through an enriched representation. For poromechanics, combinations of the embedded discrete fracture method, extended finite element methods and/or embedded finite element methods have been applied (Ren et al. 2016; Cusini et al. 2020; Giovanardi et al. 2017). Such non-conforming approaches have also been expanded to include tensile fracture propagation based on extended finite element (Khoei et al. 2014) and embedded discrete fracture methods (Deb and Jenny 2020). Conforming methods use a representation in which the fractures coincide with matrix faces. Considering fractures that have a negligible aperture compared to the modelled domain, this representation can be combined with an approach in which fractures are modelled as lower-dimensional structures (Martin et al. 2005; Karimi-Fard et al. 2003) and discretised with elements of zero thickness (Király 1988; Boon et al. 2018; Flemisch et al. 2018; Berre et al. 2020). For poroelastic media with fractures, this allows for the application of standard finite element (Salimzadeh et al. 2017), finite volume (Ucar et al. 2018; Berge et al. 2020) and combined finite element/finite volume schemes (Garipov et al. 2016; Settgast et al. 2017; Garipov and Hui 2019), more recently also including fracture contact mechanics (Garipov et al. 2016; Gallyamov et al. 2018; Franceschini et al. 2020) and tensile fracture propagation (Settgast et al. 2017; Salimzadeh et al. 2017). Thermal effects on fracture deformation and propagation in poroelastic media are less studied, although some recent studies model deformation of existing fractures in thermo-poroelastic media (Salimzadeh et al. 2016, 2018a; Stefansson et al. 2021; Garipov and Hui 2019).

Motivated by the development of increasingly sophisticated THM models for fractured porous media, our goal in the present paper is to extend numerical modelling of THM to incorporate fracture propagation and to thereby contribute to bridging the gap between fracture mechanics models and coupled THM models for porous media. Specifically, we consider mathematical and numerical modelling of fracture deformation and propagation resulting from coupled THM-processes. Our focus is on convection-driven cooling in the subsurface, where forced or natural fluid convection induces thermo-poromechanical stress changes leading to fracture deformation and propagation. The dynamics are characterised by tight coupling between physical processes and strong interaction between the physical processes and the (evolving) geometry of the fracture network. Accordingly, our model and simulation approach are designed to faithfully represent these couplings, including fracture deformation and propagation.

The fractured thermo-poroelastic medium is represented using a discrete fracture–matrix model, where fractures are represented as lower-dimensional discontinuities in an otherwise continuous thermo-poroelastic medium. Deformation of existing fractures is modelled through contact mechanics relations based on a Coulomb friction criterion for slip along the fractures and a non-penetration condition (Hüeber et al. 2008; Berge et al. 2020). This is combined with a simple criterion for fracture propagation based on the mode I stress intensity factor, which we compute directly from the displacement jump in the vicinity of the fracture tip using a variant (Nejati et al. 2015) of the displacement correlation method (Chan et al. 1970). To adjust the grid to an arbitrary fracture propagation path is highly technical (Paluszny and Zimmerman 2011; Dang-Trung et al. 2020), and we instead make the assumption that fractures propagate along existing faces in the matrix grid. This constrains the numerical representation of an evolving fracture and makes it difficult to preserve reasonable fracture geometries for general propagation scenarios, in particular for three-dimensional problems. We therefore further limit ourselves to tensile fracturing, where the possible propagation path is easy to predict and the grid can be constructed to accommodate the propagation.

We discretise the model using a finite volume framework for fracture contact mechanics in thermo-poroelastic media (Stefansson et al. 2021). The finite volume approach combines the multi-point stress approximation method for Biot poroelasticity (Nordbotten 2016; Nordbotten and Keilegavlen 2021) with the multi-point flux approximation method for flow (Aavatsmark 2002). This combination has previously been applied for numerical modelling of fractured poroelastic media (Ucar et al. 2018) with a simplified model for deformation along fractures. The fracture contact mechanics discretisation builds on work by Berge et al. (2020), who formulated the contact conditions on the fracture using Lagrange multipliers representing the contact tractions (Wohlmuth 2011). Using this approach, the variational inequality representing the contact problem can be rewritten using complementary functions, and the resulting system of equations solved by a semi-smooth Newton method (Hüeber et al. 2008; Berge et al. 2020). Our model is implemented in the open-source simulator PorePy (Keilegavlen et al. 2021), which is designed for multiphysics problems in fractured porous media.

The PorePy implementation of mixed-dimensional flow and transport, contact mechanics and poromechanics has previously been tested and verified (Berge et al. 2020; Berre et al. 2020; Flemisch et al. 2018; Keilegavlen et al. 2021), and the complete thermo-poromechanical model is tested in Stefansson et al. (2021). Owing to the shared mathematical structure of thermal and poromechanical stresses and the modular design of the applied simulation framework, the existing testing of the poromechanical component covers the thermomechanical component as well. Herein, we assess the reliability of our simulation tool by tests that probe the approximations of both the onset of fracturing and the speed of fracture propagation. We then present two application-related simulations, both of which involve fracture propagation driven by convective cooling. The cases include, respectively, forced convection during production of geothermal energy and natural convection in vertical fractures in the presence of high thermal gradients. Taken together, the results show the importance of developing simulation tools that can accurately represent the tight couplings in THM processes and deal with deformation and propagation of fractures.

The paper is structured as follows. Section 2 presents the governing model equations for poroelastic media with deforming and propagating fractures, followed by discretisation schemes and numerical solution strategy in Sect. 3. Section 4 presents simulation results, before concluding remarks are given in Sect. 5.

2 Governing Equations

The conceptual model is based on explicit and conforming representation of fractures in the porous medium. Two modes of fracture deformation are considered: deformation with fixed transverse extension governed by contact mechanics relations and deformation through irreversible fracture propagation. We also impose conservation of mass and energy in matrix and fractures and momentum balance in the matrix.

2.1 Geometrical Representation of Fractured Porous Media

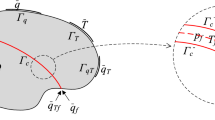
The model and its governing equations are posed in a mixed-dimensional framework arising from consideration of fractures as lower-dimensional objects. Hence, in a three-dimensional domain, fractures are represented as two-dimensional surfaces, and in a two-dimensional domain, as one-dimensional lines. In a \(D\)-dimensional domain, we denote the matrix subdomain by \(\Omega _{h}\); fractures are represented by subdomains \(\Omega _{l}\) of dimension \(D-1\). The matrix and fractures are connected by interfaces denoted by \(\Gamma _{j}\), with the subscript pair j, k used to indicate the two interfaces on either side of a fracture; see Fig. 1. The boundary of \(\Omega _{i}\) is denoted by \(\partial \Omega _{i}\), and its internal part corresponding to \(\Gamma _{j}\) by \(\partial _{j}\Omega _{i}\).

We also use subscripts i, h and l to identify the domain of the primary variables, which are displacement, pressure, temperature and contact traction (\({\varvec{u}}\), \(p\), \(T\) and \({\varvec{\lambda }}\)). Similarly, subscript j denotes the four interface variables defined in Sects. 2.2 and 2.6. The subscripts are suppressed when context allows, as are the subscripts f and s denoting fluid and solid, respectively.

To model fracture deformation, it is necessary to decompose a vector into its normal and tangential components relative to a fracture. The fracture normal is defined to equal the outwards normal \({\varvec{n}}_{h}\) on the j side, i.e. \({\varvec{n}}_{l} = {\varvec{n}}_{h} |_{\partial _{j}\Omega _{h}}\). A vector \({\varvec{\iota }}_l\) may now be decomposed as

$$\begin{aligned} \iota _{n} = {\varvec{\iota }}_l \cdot {\varvec{n}}_{l} {\text{ and }} {\varvec{\iota }}_{\tau } = {\varvec{\iota }}_l - i_{n} {\varvec{n}}_{l}, \end{aligned}$$
(1)

where subscripts n and \(\tau\) denote the normal and tangential direction, respectively.

2.2 Contact Mechanics for Fracture Slip and Opening

The contact mechanics relations are a traction balance between the two fracture surfaces and a nonpenetration condition, complemented by a Coulomb friction law governing the relative displacement when the surfaces are in contact. These relations are formulated in the displacement jump \([[{\varvec{u}} ]]\) and the contact traction \({\varvec{\lambda }}_{l}\). The higher-dimensional THM traction, \(\sigma _{h} \cdot {\varvec{n}}_{h}\), is balanced by the contact traction and the fracture pressure on the two interfaces:

$$\begin{aligned} \begin{aligned} ({\varvec{\lambda }}_{l}-p_{l} {\mathbf{I}} \cdot {\varvec{n}}_{l})|_{\Gamma _{j}}&= \sigma _{h} \cdot {\varvec{n}}_{h} |_{\partial_j \Omega _{h}} , \\ ({\varvec{\lambda }}_{l}-p_{l} {\mathbf{I}} \cdot {\varvec{n}}_{l})|_{\Gamma _{k}}&= - \sigma _{h} \cdot {\varvec{n}}_{h} |_{\partial_k \Omega _{h} }. \end{aligned} \end{aligned}$$
(2)

Here, the notation indicating that the variable is taken at the interface \(\Gamma _{j}\) or \(\Gamma _{k}\) should be interpreted as the extension and projection of this variable to the respective interface. The displacement jump over the fracture is defined as

$$\begin{aligned} \begin{aligned}{}[[ {\varvec{u}}_{l} ]] = {\varvec{u}}_{k} - {\varvec{u}}_{j}, \end{aligned} \end{aligned}$$
(3)

with \({\varvec{u}}_{j}\) and \({\varvec{u}}_{k}\) denoting displacement at \(\Gamma _{j}\) and \(\Gamma _{k}\), cf. Fig. 1. The gap function \(g\) is defined as the normal distance between the fracture surfaces when these are in mechanical contact. Following Stefansson et al. (2021), we set

$$\begin{aligned} \begin{aligned} g = \tan (\psi )||[[{\varvec{u}} ]] _{\tau }||, \end{aligned} \end{aligned}$$
(4)

with \(\psi\) denoting the dilation angle (Barton 1976), thus accounting for shear dilation of the fracture resulting from tangential displacement \([[{\varvec{u}} ]] _{\tau }\) of the rough fracture surfaces.

Given that fracture surface interpenetration and positive normal contact traction are prohibited, the following conditions have to be fulfilled:

$$\begin{aligned} \begin{array}{ r l } [[{\varvec{u}} ]] _n - g &{} \ge 0, \\ \lambda _{n} ([[{\varvec{u}} ]] _n-g) &{} = 0, \\ \lambda _{n} &{} \le 0. \end{array} \end{aligned}$$
(5)

Hence, when a fracture is mechanically open and there is no mechanical contact across the fracture, the normal contact force, \(\lambda _n\), is zero.

The friction law is imposed by enforcing

$$\begin{aligned} \begin{array}{ r l } ||{\varvec{\lambda }}_{\tau } || &{} \le -F\lambda _{n}, \\ ||{\varvec{\lambda }}_{\tau } || &{} < -F \lambda _{n} \rightarrow [[\dot{{\varvec{u}}}^{}]] _{\tau } = 0 ,\\ ||{\varvec{\lambda }}_{\tau } || &{} = -F \lambda _{n} \rightarrow \exists \,\zeta \in \mathbb {R^+}: [[\dot{{\varvec{u}}}^{}]] _{\tau } = \zeta {\varvec{\lambda }}_{\tau }, \end{array} \end{aligned}$$
(6)

where \(F\) and \([[\dot{{\varvec{u}}}^{}]] _{\tau }\) denote the friction coefficient and the tangential (shear) displacement increment, respectively. For simplicity, we consider a constant coefficient of friction in this work.

Fig. 1
figure 1

Left: A two-dimensional matrix domain \(\Omega _{h}\) and a one-dimensional fracture \(\Omega _{l}\) connected by interfaces, all gridded in a conforming way. Right: Local coordinate system at the tip of a two-dimensional fracture. The face of the tip cell is shown in purple and the interface cell centres on the j and k sides are shown as orange dots. The red propagation vector forms an angle \(\phi\) with \({\varvec{e}}_{\perp }\). The separation between fracture, interfaces and (to the left) matrix faces is for visualisation purposes only; in the model, all coincide geometrically

Full size image

2.3 Fracture Propagation

Fracture propagation occurs when the potential energy released by extension exceeds the energy required to separate the fracture surfaces by breaking atomic bonds (Griffith 1921). Using concepts of linear elastic fracture mechanics, we evaluate propagation based on computation of stress intensity factors (SIFs).

Referring to Fig. 1, the local geometry at a fracture tip is described using a coordinate system given by the orthogonal basis vectors \({\varvec{e}}_{\perp }\), \({\varvec{e}}_{n}\) and \({\varvec{e}}_{\parallel }\) (or \({\varvec{e}}_{\perp }\) and \({\varvec{e}}_{n}\) if \(D =2\)). We set \({\varvec{e}}_{n} ={\varvec{n}}_{l}\), and the tangential (\(\tau\)) vectors \({\varvec{e}}_{\perp }\) and \({\varvec{e}}_{\parallel }\) are, respectively, perpendicular and parallel to \(\partial \Omega _{l}\) at \(\partial \Omega _{l}\) (see Fig. 1). By use of a variant (Nejati et al. 2015) of the displacement correlation method (Richard et al. 2005), the components of the displacement jump in the local coordinate system give the three SIFs:

$$\begin{aligned} \begin{aligned} K_{\mathrm{I}}&= \sqrt{\frac{2\pi }{R_{\mathrm{d}}}}\bigg (\frac{\mu }{\kappa +1}[[{\varvec{u}} ]] _n\bigg ), \\ K_{\mathrm{II}}&= \sqrt{\frac{2\pi }{R_{\mathrm{d}}}}\bigg (\frac{\mu }{\kappa +1}[[{\varvec{u}} ]] _{\perp }\bigg ),\\ K_{\mathrm{III}}&= \sqrt{\frac{2\pi }{R_{\mathrm{d}}}}\bigg (\frac{\mu }{4}[[{\varvec{u}} ]] _{\parallel }\bigg ). \end{aligned} \end{aligned}$$
(7)

Here, \(\mu\) denotes the shear modulus and \(\kappa =3-4\nu\) the Kolosov constant, with \(\nu\) being the Poisson ratio. \(R_{\mathrm{d}}\) is the distance from the fracture tip to the point at which the displacement jump is evaluated. The three stress intensity factors are related to tensile (\(K_{\mathrm{I}}\)), shear (\(K_{\mathrm{II}}\)) and torsional (\(K_{\mathrm{III}}\)) forces.

As stated in the Introduction, we limit ourselves to purely tensile fracture, and ignore contributions from (\(K_{\mathrm{II}}\)) and (\(K_{\mathrm{III}}\)), which is only applicable if the stress around the fracture tip is symmetric (Salimzadeh et al. 2018b). With this assumption, a tip propagates if the computed mode I factor exceeds a critical value,

$$\begin{aligned} \begin{aligned} K_{\mathrm{I}} \ge K_{{\mathrm{c}}}, \end{aligned} \end{aligned}$$
(8)

and the propagation angle \(\phi\) illustrated in Fig. 1 is zero. Criteria for more sophisticated mixed-mode propagation, which can be highly relevant for subsurface applications, are reviewed by Richard et al. (2005).

2.4 Fracture Mass and Energy Balance

The thickness of a dimensionally reduced fracture is represented by the aperture, which changes as the domain deforms according to

$$\begin{aligned} a = a_{\mathrm{res}} + [[{\varvec{u}} ]] _n, \end{aligned}$$
(9)

where \(a_{\mathrm{res}}\) denotes the residual hydraulic aperture in the undeformed state, representing the effect of small-scale roughness of the two fracture surfaces. Assigning a nonzero value for \(a_{\mathrm{res}}\) ensures that the equation system does not degenerate. The tangential fracture permeability \({\mathcal{K}}_{l}\) is set to depend on aperture by the nonlinear relationship \({\mathcal{K}}_{l} =a^2/12\), which corresponds to setting the hydraulic aperture of the fracture equal to \(a\) (Zimmerman and Bodvarsson 1996).

On the assumption that the fractures are completely filled with fluid, the parameters of this subsection equal that of the fluid, as indicated by subscript f. We assume single-phase flow according to Darcy’s law:

$$\begin{aligned} \begin{aligned} {\varvec{v}} = -\frac{{\mathcal{K}}}{\eta } \left( \nabla p- \rho _{{\mathrm{f}}} {\varvec{g}} \right) , \end{aligned} \end{aligned}$$
(10)

where \(\eta\), \(\rho _{{\mathrm{f}}}\) and \({\varvec{g}}\) denote viscosity, density and the gravity acceleration. Note that the z-axis points upwards. The total heat flux may be split into continuum scale heat diffusion modelled by Fourier’s law and advection along the fluid flow field:

$$\begin{aligned} \begin{aligned} {\varvec{q}}&= -\kappa _{{\mathrm{f}}} \nabla T, \\ {\varvec{w}}&= \rho _{{\mathrm{f}}} c_{{\mathrm{f}}} T {\varvec{v}}, \end{aligned} \end{aligned}$$
(11)

where \(\kappa _{{\mathrm{f}}}\) and \(c_{{\mathrm{f}}}\) denote thermal conductivity and heat capacity, respectively.

We assume the density equation of state for the slightly compressible fluid to be (Coussy 2004)

$$\begin{aligned} \begin{aligned} \rho _{{\mathrm{f}}}&= \rho _{0} \exp \bigg [ {\frac{1}{K_{{\mathrm{f}}}}} (p-p_{0}) - \beta _{\mathrm{f}} (T-T_{0}) \bigg ], \end{aligned} \end{aligned}$$
(12)

with subscript 0 indicating a reference state. Following Stefansson et al. (2021) (see also Brun et al. 2018; Coussy 2004), balance of mass for a fracture \(\Omega _{l}\) reads

$$\begin{aligned} a\left( {\frac{1}{{K_{{{\rm f}}} }}\frac{{\partial p}}{{\partial t}} - \beta _{{{\rm f}}} \frac{{\partial T}}{{\partial t}}} \right) + \frac{{\partial a}}{{\partial t}} - \nabla \cdot \left( {a\frac{{\mathcal{K}}}{\eta }\left( {\nabla p - \rho{\varvec{g}}} \right)} \right) - \sum\limits_{{j \in {\hat{S}}_{l} }} {v_{j} } = aq_{p} . \end{aligned}$$
(13)

Here, the bulk modulus \(K_{{\mathrm{f}}}\) equals the inverse of the fluid compressibility, while \(\beta _{\mathrm{f}}\) and \(q_{p }\) denote the thermal expansion coefficient and a fluid source or sink term. The set \(\hat{S}_{l}\) contains the higher-dimensional interfaces of fracture l, i.e. the two fracture surfaces, and \(v_{j}\) is the fluid flux from matrix to fractures, which is further described in Sect. 2.6.

The internal energy is simplified to equal the enthalpy, given by

$$\begin{aligned} \begin{aligned} h_{\mathrm{f}}&= \rho _{\mathrm{f}} c_{\mathrm{f}} T . \end{aligned} \end{aligned}$$
(14)

Assuming local thermal equilibrium between fluid and solid, neglecting viscous dissipation and linearising (Stefansson et al. 2021), the energy balance is

$$\begin{aligned} \begin{aligned} c_{\mathrm{f}} \rho _{\mathrm{f}} T \frac{\partial a }{\partial {\textit{t}}} + c_{\mathrm{f}} a \frac{\partial \rho _{\mathrm{f}} T }{\partial {\textit{t}}} + \nabla \cdot \left[ a \left( c_{\mathrm{f}} \rho _{\mathrm{f}} T {\varvec{v}} - \kappa _{\mathrm{f}} \nabla T \right) \right] - \sum _{j \in \hat{S}_{l}}q_{j} + w_{j} = a q_{T }, \end{aligned} \end{aligned}$$
(15)

where we assume thermal sources and sinks to satisfy \(q_{T } = q_{p } c_{\mathrm{f}} \rho _{\mathrm{f}} T\). Expressions for the conductive and advective interface fluxes \(q_{j}\) and \(w_{j}\) are specified in Sect. 2.6.

2.5 Matrix Thermo-poroelasticity, Energy and Mass Balance

The following section presents the balance equations and constitutive relations for the matrix problem. The model resembles that of the previous section, with the addition of a momentum balance equation for the thermo-poroelastic medium, yielding three balance equations for \(\Omega _{h}\). For details on the derivations of the equations, we again refer to Coussy (2004), Brun et al. (2018) and Stefansson et al. (2021). We first define effective parameters (Cheng 2016) arising through the assumption of local thermal equilibrium:

$$\begin{aligned} \begin{aligned} {(\cdot )_e= \phi (\cdot )_f + (1-\phi )(\cdot )_s,} \end{aligned} \end{aligned}$$
(16)

with subscript s indicating the solid phase and \(\phi\) denoting porosity. While the resulting effective parameters are sufficiently accurate for the current study, they do not incorporate effects such as dispersion and the impact of the pore structure.

Neglecting inertial terms, the momentum balance is

$$\begin{aligned} \begin{aligned} \nabla \cdot \sigma = {{{\varvec{q}}}_{{\varvec{u}}}}, \end{aligned} \end{aligned}$$
(17)

with \({{\varvec{q}}}_{{\varvec{u}}}\) denoting body forces and the linearly thermo-poroelastic stress tensor related to the primary variables by an extended Hooke’s law

$$\begin{aligned} \begin{aligned} \sigma - \sigma _{0} = \mu\big (\nabla {\varvec{u}} + \nabla {\varvec{u}} ^T\big ) + \big(K_{{\mathrm{s}}}-2\mu/3\big) \text{tr}(\nabla {\varvec{u}}) {\mathbf{I}} - \alpha (p-p_{0}) {\mathbf{I}}- \beta _{\mathrm{s}} K_{{\mathrm{s}}} (T- T_{0}) {\mathbf{I}}, \end{aligned} \end{aligned}$$
(18)

with \(\alpha\) denoting the Biot coefficient. The mass balance equation reads

$$\begin{aligned} \begin{aligned} \left( \frac{\phi }{ K_{{\mathrm{f}}}}+\frac{\alpha -\phi }{K_{{\mathrm{f}}}}\right) \frac{\partial p}{\partial {\textit{t}}} + \alpha \frac{\partial (\nabla \cdot {\varvec{u}})}{\partial {\textit{t}}}-\beta _{e} \frac{\partial T}{\partial {\textit{t}}} - \nabla \cdot \left( \frac{{\mathcal{K}}}{\eta }\left( \nabla p-\rho {\varvec{g}} \right) \right) = q_{p}. \end{aligned} \end{aligned}$$
(19)

With the same assumptions as previously for the fluid description and assuming the solid energy to be \(\rho _{\mathrm{f}} c_{\mathrm{f}} T\), the energy balance is

$$\begin{aligned} \begin{aligned} \frac{\partial }{\partial {\textit{t}}} \left[ (\rho c)_eT \right] + \beta _{\mathrm{s}} K_{{\mathrm{s}}} T_{0} \frac{\partial (\nabla \cdot {\varvec{u}})}{\partial {\textit{t}}} + \nabla \cdot \left( c_{\mathrm{f}} \rho _{\mathrm{f}} T {\varvec{v}}- \kappa _{e} \nabla T \right) = q_{T}. \end{aligned} \end{aligned}$$
(20)

On \(\partial_j \Omega_h\), the following internal boundary conditions ensure coupling from \(\Omega _{h}\) to the interface variables on \(\Gamma _{j}\):

$$\begin{aligned} \begin{aligned} {\varvec{u}}_{h}&={\varvec{u}}_{j}, \\ {\varvec{v}}_{h} \cdot {\varvec{n}}_{h}&=v_{j}, \\ {\varvec{q}}_{h} \cdot {\varvec{n}}_{h}&=q_{j},\\ {\varvec{w}}_{h} \cdot {\varvec{n}}_{h}&=w_{j}. \end{aligned} \end{aligned}$$
(21)

The conservation equations are complemented by appropriate boundary conditions on the domain boundary. This applies to both the matrix and fracture domains.

2.6 Interface Fluxes Between Fractures and Matrix

Interface flux relations close the mixed-dimensional system of mass and energy balance equations (Martin et al. 2005; Jaffré et al. 2011):

$$\begin{aligned} \begin{aligned} v_{j}&= - \frac{{\mathcal{K}}_{j}}{\eta }\bigg ( \frac{2}{a_{l}} \left( p_{l} |_{\Gamma _{j}} - p_{h} |_{\partial_j \Omega _{h} } \right) -\rho _{{f,}l} {\varvec{g}} \cdot {\varvec{n}}_{h} \bigg ), \\ q_{j}&= - \kappa _{j} \frac{2}{a_{l}} ( T_{l} |_{\Gamma _{j}} - T_{h} |_{\partial_j \Omega _{h} }), \\ w_{j}&= \left\{ \begin{array}{ l l } v_{j} \rho _{{f,}h} c_{{f,}h} T_{h} &{}\quad {\text { if }} v_{j} >0 \\ v_{j} \rho _{{f,}l} c_{{f,}l} T_{l} &{}\quad {\text { if }} v_{j} \le 0 . \end{array} \right. \end{aligned} \end{aligned}$$
(22)

We set the normal permeability and thermal conductivity equal to their tangential counterparts, i.e. \({\mathcal{K}}_{j} ={\mathcal{K}}_{l}\) and \(\kappa _{j} =\kappa _{l}\).

3 Discretisation and Solution Strategy

Discretisation of the governing equations entails devising discrete representation of the conservation equations and of contact mechanics relations on existing fractures. Moreover, when the propagation criteria are met, the fracture geometry must be modified and the discretisations updated accordingly.

We make the following assumptions on the computational grid: grids for the subdomains \(\Omega _{h}\) and \(\Omega _{l}\) and the interface \(\Gamma _{j}\) are constructed so that faces on \(\partial _j\Omega _h\) match with cells in \(\Gamma _{j}\) and \(\Omega _{l}\). We make no assumptions on the cell types; for the simulations presented in Sect. 4, we mainly use Cartesian grids, as these are most easily fit to a known, straight propagation path, but also consider simplex cells for one simulation. While the framework allows for arbitrary fracture intersections, the current implementation does not cover formation of new intersections; that is, the merging of fracture subdomains. Thus, we only consider cases where fractures do not grow into each other.

3.1 Spatial Discretisation

Pressure and temperature are represented by their cell centre values in \(\Omega _{h}\) and \(\Omega _{l}\), as is the displacement in \(\Omega _{h}\) and contact force in \(\Omega _{l}\). The discrete primary variables on \(\Gamma\) are displacements, mass flux and advective and diffusive heat fluxes.

3.1.1 Contact Mechanics

The nonlinear contact mechanics problem is represented by an active set approach implemented as a semi-smooth Newton method following (Hüeber et al. 2008; Berge et al. 2020). The treatment of Eqs. (5) and (6) depends on whether the previous iterates were in an open, sticking or gliding state, with the states evaluated cell-wise in \(\Omega _{l}\). Equation (2) is discretised by relating the cell centre pressures and contact force in \(\Omega _{l}\) to the discrete traction on \(\Gamma\).

3.1.2 Discretisation of Balance Equations

For \(\Omega _{h}\), the stress term in (17) and the diffusive fluxes in (19) and (20) are all discretised with a family of finite volume multi-point approximations termed MPxA (Aavatsmark 2002; Nordbotten 2016; Nordbotten and Keilegavlen 2021). The methods construct discrete representations of the constitutive relations, Hooke’s, Darcy’s and Fourier’s law, in terms of the cell centre variables. These relations are used to enforce conservation of THM traction, mass and (diffusive) heat flux over the cell faces. For faces on the fracture surfaces, the discrete traction enters the contact mechanics discretisation described above. The full heat flux is given by the sum of the discrete Fourier’s law and the advective flux, where the latter is discretised by a single-point upstream method. For further information on the MPxA methods, we refer to Nordbotten and Keilegavlen (2021).

In \(\Omega _{l}\), Eqs. (13) and (15) are discretised analogously to the corresponding terms in \(\Omega _{h}\). Finally, fluxes over \(\Gamma\) are computed from discrete versions of the interface equations (22).

3.1.3 Solution of Nonlinear System

The discretised system of equations is solved by Newton’s method, with the terms from the contact conditions handled by a semi-smooth approach following (Hüeber et al. 2008; Berge et al. 2020). The termination criterion for the Newton iterations considers the residuals and updates of each of the primary variables \({\varvec{u}}_{h}\), \({\varvec{u}}_{j}\), \(p\) and \(T\). Within each nonlinear iteration, the linearised system illustrated in Fig. 2 is solved using a direct sparse solver (Davis 2004). While simple, this approach is memory intensive and puts practical constraints on mesh resolution, in particular for three-dimensional problems. A more scalable method would involve iterative solvers with block preconditioners for the THM components of the linear system (Both et al. 2019), with a tailored treatment of the contact conditions (Franceschini et al. 2019).

3.2 Solution Algorithm

The temporal derivatives are discretised by a backward Euler scheme, and the THM contact mechanics problem is solved monolithically, using implicit-in-time evaluation of all spatial derivatives. When the nonlinear solver has converged, we proceed to evaluation of fracture propagation. The solution algorithm is outlined in Fig. 3.

Stress intensity factors and the fracture propagation criterion are evaluated for each fracture tip face using Eqs. (7) and (8). The displacement jump is evaluated at the neighbouring cell of the tip face, i.e. \(R_{\mathrm{d}}\) is the distance between the centre of the tip face and the cell. The fracture is restricted to growth along faces of the matrix grid; no computation of the propagation length is performed. The geometrical update for each identified face now entails (1) duplicating the face for the matrix grid, (2) adding a lower-dimensional cell in the fracture grid and (3) adding one lower-dimensional cell for each of the two interfaces. The three new cells all coincide geometrically with the chosen face; see Fig. 2. Once new cells and faces have been added, connectivity information is updated both within subdomains and between the subdomains and the interface.

Variables are initialised in the new cells, and new apertures are set to \(a_{\mathrm{res}}\). This in effect adds mass to the system, cf. Eq. (12). To compensate, we prescribe an additional term on the right-hand side of Eq. (13) equal to \(-a_{\mathrm{res}}/dt\) in newly formed fracture cells in the subsequent time step, with dt denoting time-step size. Eq. (14) implies that no right-hand side term arises for the energy balance with the initialisation value \(T =0\).

Fig. 2
figure 2

Top: Illustration of the two-level block structure of the left-hand side of the system of linear equations arising from discretisation of the THM problem on a one-fracture domain. Equation numbers for each row are shown to the left. The markers shown to the right indicate primary variables, with the shape reflecting the subdomain or interface where they are defined, whereas the colours red, blue and black correspond to heat, mass and deformation, respectively. Bottom: Example grid and unknowns before (left) and after (right) propagation. One vertex (black circle) and the face along which propagation occurs are duplicated as part of the geometry update. The different types of domains are separated for illustration purposes. Figure adapted from Stefansson et al. (2021)

Full size image

Before the simulation proceeds to the next time step, all terms are rediscretised to account for modifications of the grids. This can be done locally, i.e. only for the faces and cells where the discretisation is affected by the grid update.

Fig. 3
figure 3

Solution algorithm with time loop to the final time \({\textit{t}} _{\mathrm{end}}\) and propagation evaluated at the end of each time step

Full size image

4 Simulation Results

The results presented in this section serve first to verify the computational approach and then to show application to two subsurface cases involving THM processes and fracture propagation. The PorePy toolbox (Keilegavlen et al. 2021) was used for all simulations, and run scripts for geometry and parameter setup, etc., are available on GitHub (Stefansson and Keilegavlen 2021). All parameters are homogeneous within each subdomain and those not specified in the text are listed in Table 1.

4.1 Verification

The verification of the computational approach entails first a test of the numerical stress intensity factors and next a convergence test of the fracture propagation speed.

4.1.1 Example 1: Stress Intensity Factors

To verify the SIF computation, we consider an analytical solution, first derived by Sneddon (1946), for a single crack in an infinite medium with uniform internal pressure on the fracture surfaces. Boundary conditions for the finite simulation domain are computed using the boundary element method following Keilegavlen et al. (2021), who also present a thorough convergence study for the aperture using PorePy. Herein, we compare the SIFs as computed by the displacement correlation method to the analytical solution

$$\begin{aligned} \begin{aligned} K_{{\mathrm{I}}, an}&= p_{\mathrm{f}} \sqrt{l \pi },\\ K_{{\mathrm{II}}, an}&=0. \end{aligned} \end{aligned}$$
(23)

Here, \(p_{\mathrm{f}}\) denotes the internal pressure on the fracture and l denotes fracture length.

Fig. 4
figure 4

Example 1: domain geometry (left) and close-up around the fracture showing the matrix mesh for the mesh with \(h=0.25\) (right). The blue box shows the location of the close-up

Full size image

We use a square domain of side length 50 m, \(l= {10}\) m and \(p_{\mathrm{f}} = 1 \times 10^{-4}\) Pa. We consider a sequence of four grids, the finest of which is shown in Fig. 4. To probe the method for different material parameters, we also use four different Poisson ratios. Based on displacement solutions on each grid, SIFs are estimated and the normalised \(L^2\) type errors are computed as

$$\begin{aligned} \begin{aligned} E_{{\mathrm{I}}}&= \frac{\left[ \sum _{j=1}^2\left( K_{{\mathrm{I}},j}-K_{{\mathrm{I}},an} \right) ^2\right] ^{1/2}}{2 K_{{\mathrm{I}},an}}, \\ E_{{\mathrm{II}}}&= \frac{\left[ \sum _{j=1}^2\left( K_{{\mathrm{II}},j}-K_{{\mathrm{II}},an} \right) ^2\right] ^{1/2}}{2 K_{{\mathrm{I}},an}}, \end{aligned} \end{aligned}$$
(24)

with the j index running over the two fracture tips.

Fig. 5
figure 5

Example 1: errors for \(K_{I}\) (left) and \(K_{II}\) (right) computed according to Eq. (24) for different values of the Poisson ratio \(\nu\) and different mesh sizes h

Full size image

The piecewise linear displacement representation of the stress discretisation does not capture the stress singularity at the fracture tips. Since the SIFs are computed from \([[{\varvec{u}} ]]\) in these cells at the tips, the method does not converge with mesh refinement. Rather, the results presented in Fig. 5 demonstrate robustness with respect to mesh size and the Poisson ratio \(\nu\). While we do not consider \(K_{II}\) in the subsequent simulations, we also present results demonstrating that the method indeed predicts tensile stresses (i.e. \(K_{II} \ll K_{I}\)) for this purely tensile problem.

The results of this test indicate that the numerical solution can be used to estimate \(K_{I}\) in tensile problems and thus form the basis of fracture growth evaluation.

4.1.2 Example 2: Propagation Speed

We now consider a test case designed to evaluate the simulated propagation speed of a fracture in a tensile regime of stable propagation. The unit square domain contains two horizontal fractures \(\Omega _{2}\) and \(\Omega _{3}\) extending 1/4 from the left and right boundary, respectively; see Fig. 6. The boundary conditions for fluid and heat are no-flow in the matrix and Dirichlet for the fractures, with zero values on the right and \(p = {5}\) mPa and \(T ={T_{0}-} {50}\) K on the left. Thus, cold fluid flows from left to right, entering the matrix at the right end of \(\Omega _{2}\). The domain is mechanically fixed at the top and bottom, and zero traction is imposed on the left and right boundaries. The forces driving propagation are the elevated pressure inside \(\Omega _{2}\) and cooling of the surrounding matrix.

Fig. 6
figure 6

Left: domain geometry used in Example 2. The grey lines indicate initial geometry, whereas the red line indicates the extension at the end of simulation. The blue box shows the location of the close-up to the right. Right: close-up around the fracture showing the matrix mesh for refinement \(h=1/128\)

Full size image

We use four temporal refinement levels and three spatial refinement levels in addition to a highly refined reference solution. The finest (non-reference) mesh and the final fracture geometry are illustrated in Fig. 6.

Figure 7 shows fracture size plotted against time for all refinement combinations. With one exception, discussed below, the results group according to spatial resolution. While the propagation speed is fairly constant across all mesh sizes, propagation onset occurs earlier for the coarser meshes. We attribute this offset to the SIFs being evaluated on the basis of \([[{\varvec{u}} ]]\)  at the centre of the fracture tip cell. The location of this cell centre is closer to the boundary for the coarser meshes, implying shorter travel time for the cooling front. As expected, the plot indicates convergence with mesh refinement.

The outlier is the smallest mesh size combined with the largest time step, for which the propagation speed is notably lower. The propagation speed is simply not resolved by the spatio-temporal discretisation, i.e. the propagation speed exceeds h/dt. In other words, given a spatial resolution, an upper bound on the time step must be honoured in the explicit type of propagation solution algorithm used herein.

Fig. 7
figure 7

Example 2: size of the propagating fracture \(\Omega _{2}\) versus time for 13 refinement combinations. Line colours and styles correspond to temporal and spatial discretisation size, respectively

Full size image
Table 1 Parameters for the simulation examples. For Example 1, only mechanical parameters are relevant
Full size table

4.2 Applications

We present two simulations that involve THM processes coupled with fracture propagation. The first case resembles geothermal energy production, with convection forced by fluid injection and production. The second case involves natural convection that takes place mainly inside fractures. In both cases, convection acts to alter thermal stresses and thereby cause fracture propagation.

4.2.1 Example 3: Thermal Fracturing and Forced Convection

We consider two immersed fractures in a cube-shaped domain of side length 1000 m, centred 1500 m below the surface. Each fracture contains one well, implemented as a source or sink term in a single cell, with injection in the leftmost fracture, \(\Omega _{2}\), and production in the rightmost fracture, \(\Omega _{3}\). The domain, fracture geometry and spatial mesh are shown in Fig. 8.

Fig. 8
figure 8

Example 3: fracture network geometry, well locations and spatial mesh (left) and close-up of fractures with mesh and well cells (right). The blue fracture cell in \(\Omega _{2}\) marks injection, whereas the red cell in \(\Omega _{3}\) indicates production

Full size image

The flow rate is 5 L s\(^{-1}\) for both wells, and the injection temperature is 30 K below the formation temperature. The anisotropic boundary tractions are based on lithostatic stress, with

$$\begin{aligned} \begin{aligned} \sigma _{xx} =0.6\rho _{\mathrm{s}} G z, \qquad \sigma _{yy} = 1.2 \rho _{\mathrm{s}} G z, \qquad \sigma _{zz} =\rho _{\mathrm{s}} G z. \end{aligned} \end{aligned}$$

This background stress implies that \(\Omega _{3}\), with normal vector \({\varvec{n}}_{3} =[1,0,0]^T\), is initially more favourably oriented for propagation than is \(\Omega _{2}\).

The Fig. 9 fracture size plot shows that \(\Omega _{2}\) grows at a steady speed after an initial phase of limited propagation. The growth is driven by elevated pressure due to injection and matrix cooling, which is most pronounced on the side of \(\Omega _{2}\) facing \(\Omega _{3}\) due to the advective component of the heat flow; cf. Fig. 10. Assuming that the thermal driving force dominates, which is reasonable given the relative size of injection pressure and background stresses, the relatively constant speed could be linked to the constant rate and temperature of injection.

The fracture \(\Omega _{3}\), where fluid is produced, does not propagate at all. Towards the end of the 2.5 year simulation, the magnitude of normal traction on \(\Omega _{3}\) has increased considerably relative to the initial value of approx. \(1 \times 10^{7}\) Pa, see Fig. 9. We attribute this to the contraction ensuing from matrix cooling surrounding \(\Omega _{2}\), which leads to a larger proportion of the compressive forces being supported by the non-cooled surroundings, including \(\Omega _{3}\).

Figure 9 also shows temperature and pressure in the two wells throughout the simulation. Most notably, injection pressure gradually declines. This increased injectivity in \(\Omega _{2}\) is caused by the combination of an increased aperture in the pre-existing part of the fracture, and the increase in the geometric extension of the fracture. Thus, fracture deformation caused by thermal and hydraulic stimulation strongly affects their (flow) properties, providing a clear example of the two-way process–structure interaction characteristic of fractured porous media.

This simulation indicates that long-term cooling during geothermal energy production may alter the stress state to a stage where fractures propagate. It is therefore important to develop simulation tools that can incorporate such changes to fracture geometry, in addition to handling multi-physics processes in the reservoir. Moreover, the injection pressure evolution shows the importance of capturing deformation of existing fractures in the same model.

Fig. 9
figure 9

Example 3: size of the two fractures vs. time (left) and pressure and temperature versus time in the injection well cells (right). Only the injection fracture \(\Omega _{2}\) grows

Full size image
Fig. 10
figure 10

Example 3: solution and fracture geometry at the end of the simulation. \(p\), \(a\) and \(\lambda _{n}\) are shown on the fractures, while \(T\) is shown both on the fractures and as contour lines indicating where the matrix is significantly cooled (10 K and 20 K below initial formation temperature). The blue rectangle indicates the initial shape of \(\Omega _{2}\)

Full size image

4.2.2 Example 4: Thermal Fracturing and Natural Convection

As a final example, we consider fracture propagation driven by cooling that is mainly caused by convection cells inside vertical fractures. The process, known as convective downward migration, has been proposed as a mechanism for transport of heat in the deep roots of volcanic geothermal systems (Lister 1974; Bodvarsson 1982). It is also predicted to have an important role in the source mechanism of hydrothermal activity in a more general perspective (Bodvarsson 1982; Axelsson 1985).

We consider five vertical fractures evenly spaced along the x direction and extending from the top boundary half-way through the cube-shaped domain with side length 400 m; see Fig. 11. The domain is centred 2800 m below the surface to mimic conditions within the earth’s crust where natural heat convection is likely to take place. Boundary and initial conditions are hydrostatic pressure and temperature according to a vertical gradient of − 0.15 K m\(^{-1}\) and upper boundary temperature 500 K, considered to represent a background temperature gradient close to the boundaries of geothermal areas. This value is estimated to be between − 0.10 and − 0.15 K m\(^{-1}\) within Iceland’s active zone of volcanism and rifting, where many high temperature systems exist (Ágústsson and Flóvenz 2005). The relatively large apertures required to permit convection cells within fractures have been reported, e.g. in New Zealand, Soultz in France and Cajon Pass site in USA (Massiot et al. 2017; Genter and Traineau 1996; Barton and Zoback 1992) and measurements from the Reykjanes geothermal field in Iceland suggest similar values (Keilegavlen et al. 2020). The boundary traction is the same as for the previous example, and the simulation time is 70 years. The results are displayed in Figs. 11, 12 and 13.

The vertical temperature gradient leads to instabilities in fluid density, which triggers convection cells inside the fracture; see Fig. 13. As shown by the temperature contour surfaces in Fig. 12, the resulting energy transport cools the rock surrounding the fractures to the point where propagation occurs at the lower end of the fractures. This change in fracture geometry, together with changes in aperture in the existing fracture due to contraction of the surrounding rock, again gives feedback to the fluid convection, as is evident from the difference in flow patterns between the solutions at the two different times reported in Fig. 13. As in Example 3, we see evidence of tight process–structure interaction, with the convection-induced cooling altering thermo-poromechanical stress sufficiently for the fractures to open and propagate.

Figure 11 displays size evolution for individual fractures. Propagation begins approximately half-way through the simulation, first for the fracture in the centre of the domain. Even after all fractures have started propagating, the central fractures \(\Omega _{3}\), \(\Omega _{4}\) and \(\Omega _{5}\) propagate significantly faster than the two outermost. This should be understood in the context of the compressive boundary conditions: the normal tractions on \(\Omega _{2}\) and \(\Omega _{6}\), respectively, are not relieved by the cooling of any fractures lying between them and the left and right boundary.

After onset, propagation continues until the end of the simulation, but not at all time steps for all propagating fractures, and certainly not along the entire propagation front. This is because the matrix surrounding the new part of a fracture must be cooled before the fracture proceeds and indicates that the fracture growth is stable, as in Example 2, and that the propagation speed is resolved in the temporal discretisation. An approximate downward propagation speed for fractures 3–5 is obtained by dividing the estimated slopes from Fig. 11 by the initial lateral fracture length 200 m, yielding \(\sim \,{2}\) m year\(^{-1}\). The setup for this test case is based on average properties in high temperature settings, and the results are in agreement with previous assessments of 0.3–3 m year\(^{-1}\) (Bodvarsson 1982). These results were obtained using a simple analytical relation to assess the temperature difference sufficient for thermal stress to outweigh the lithostatic force, with parameters and reservoir conditions similar to those used in the present simulation.

Fig. 11
figure 11

Example 4: initial geometry (left) and size of the five fractures versus time (right)

Full size image
Fig. 12
figure 12

Example 4: solution and fracture geometry at the end of the simulation. \(p\), \(a\) and \(\lambda _{n}\) are shown on the fractures, while \(T\) is shown both on the fractures and as contour surfaces indicating where the matrix is significantly cooled (7.5 K and 15 K below initial formation temperature)

Full size image
Fig. 13
figure 13

Example 4: flux fields and density distribution for two fractures. The top and bottom row correspond to just before propagation onset (\(t={{24}}\) year) and the end of simulation (\(t={70}\) year), respectively. The scaling of the arrows indicating flux direction and magnitude is a factor five larger for the top row, when fluxes are smaller due to smaller apertures. The red rectangles indicate initial fracture geometry

Full size image

5 Conclusion

While both numerical models for flow and heat transfer in fractured media and models for deformation of poroelastic media and fracture mechanics have been developed separately, models which combine these fields are more recent. In the current work, we present a novel numerical model that couples fracture contact mechanics and propagation with deformation, flow and heat transfer in fractured thermo-poroelastic media. The methodology is built on a multi-point finite-volume framework, combined with an active-set approach for fracture contact mechanics. Fracture propagation is based on stress intensity factors and computed using a variant of the displacement correlation method. In the numerical model, fractures are restricted to propagation which conforms to an existing grid. The numerical results show mesh convergence for computation of stress-intensity factors and fracture propagation speeds. Focusing on tensile fracture propagation, three-dimensional numerical test cases show how the model can be used to investigate fracture propagation caused by forced and natural convection, exemplified by long-term thermal reservoir stimulation due to cooling and convective downward migration of fractures. The simulations demonstrate the need for coupled models which account for both contact mechanics and fracture propagation as well as thermo-poroelasticity.