A Probability-Based Pore Network Model of Particle Jamming in Porous Media

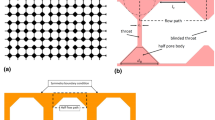
Abstract

Geometric straining of particles in porous media is of critical importance in a broad range of natural and industrial settings, such as contaminant transport in aquifers and the permeability decline due to pore plugging in oil reservoirs. Pore network modeling is a computationally efficient approach to simulate transport problems in porous media that has been used to simulate particle deposition and size exclusion. However, existing network models are unable to simulate particle jamming due to the simplification of geometry and the lack of capability for simulating particle–particle interactions. Here, we develop a novel pore network model for particle jamming in porous media. The jamming in pore throats is predicted by the probability of jamming, which is a function of pore/particle size ratio, particle concentration, and coefficient of friction (COF). A unified probability model is developed based on Discrete Element Method (DEM) simulations of particle jamming in porous media consisting of a single layer of spherical grains. The geometry is based on two packing extremes, those with grains arranged in a triangle and a square. The model is then implemented into the pore network model to predict jamming in porous media. This framework combines the efficiency of network modeling and the accuracy of direct simulations on particle jamming. We verify the model against CFD-DEM simulations. The results of network simulations show that the probability of jamming increases with COF. At low particle concentrations (C = 5%), the probability of jamming for large pore throats is small. There is a critical particle concentration (C = 9%) when the grain/particle size ratio is 10, above which jamming is self-reinforcing and the inlet face of the porous medium will be completely blocked (C = 11%). The effect of velocity on the probability of jamming is insignificant compared with the effects of particle concentration and pore/particle size ratio.

Article Highlights

• We propose a novel pore network model for particle jamming based on the probability.

• The pore network model has a higher computational efficiency, compared with other numerical models, such as CFD-DEM model.

• The pore network model can accurately predict the permeability changes of porous media during the jamming process.

Appendices

Appendix 1: Sensitivity analysis of particle properties

Mondal et al. (2016) found that Young’s modulus does not affect the simulation results of particle jamming. In this study, sensitivity analysis of particle properties, including Young’s modulus, Poisson’s ratio, and coefficient of restitution on jamming probability have been performed and the results are shown in Fig. 

Fig. 13

Sensitivity analysis of a Young’s modulus, b Poisson’s ratio, and c coefficient of restitution on jamming probability

13. The triangle packing structure is used, and the grain/particle size ratio is 10. The particle concentration is 5%, and coefficient of friction is 0.5. Figure 13 shows that these three properties do not have a significant effect on jamming probability.

Appendix 2: Derivation of Eq. 6

Given the probability of jamming, P₀, and the number of injected particles, N_in, the average number of particles goes through a pore throat is expected to be,

$$\overline{{N_{{{\text{out}}}} }} = \sum\limits_{k = 0}^{{N_{{{\text{in}} - 1}} }} {kP_{0} (1 - P_{0} )^{k} + N_{{{\text{in}}}} \left( {1 - P_{0} } \right)^{{{\text{N}}_{{{\text{in}}}} }} } .$$

(15)

Assume the first term on the right-hand side is,

$$y = \sum\limits_{k = 0}^{{N_{{{\text{in}} - 1}} }} {kP_{0} (1 - P_{0} )^{k} } .$$

(16)

Multiply Eq. 16 by (1 − P₀) we have

$$y\left( {1 - P_{0} } \right) = \sum\limits_{k = 0}^{{N_{{{\text{in}} - 1}} }} {kP_{0} \left( {1 - P_{0} } \right)^{k + 1} } .$$

(17)

So

$$\begin{aligned} y - y\left( {1 - P_{0} } \right) & = \sum\limits_{k = 0}^{{N_{{{\text{in}} - 1}} }} {kP_{0} \left( {1 - P_{0} } \right)^{k} } - \sum\limits_{k = 0}^{{N_{{{\text{in}} - 1}} }} {kP_{0} \left( {1 - P_{0} } \right)^{k + 1} } \\ & \Rightarrow yP_{0} = \sum\limits_{k = 1}^{{N_{{{\text{in}}}} }} {P_{0} \left( {1 - P_{0} } \right)^{k} - N_{{{\text{in}}}} } P_{0} \left( {1 - P_{0} } \right)^{{N_{{{\text{in}}}} }} \\ & \Rightarrow y = \frac{{1 - P_{0} }}{{P_{0} }}\left[ {1 - \left( {1 - P_{0} } \right)^{{N_{{{\text{in}}}} }} } \right] - N_{{{\text{in}}}} P_{0} \left( {1 - P_{0} } \right)^{{N_{{{\text{in}}}} }} \\ \end{aligned}$$

(18)

Substitute y back into Eq. 15, we have

$$\overline{{N_{{{\text{out}}}} }} = \frac{{1 - P_{0} }}{{P_{0} }}\left[ {1 - \left( {1 - P_{0} } \right)^{{N_{{{\text{in}}}} }} } \right]$$

(19)

Appendix 3: Derivation of Eq. 7

We performed sensitivity analysis on triangle packing structure (screen a) to understand the effect of particle concentration, grain/particle size ratio, and inflow velocity on the probability of jamming. Three velocities (10^–4 cm/s, 5 × 10^–4 cm/s, and 10^–3 cm/s) are used for each case. Figure 

Fig. 14

Probability of jamming as a function of particle concentration at D/d = 10 for different flow velocities. A COF of 0.5 was used

14 shows the jamming probability as a function of concentration and Fig. 15 shows jamming probability as a function of grain/particle size ratio.

The suspensions with higher particle concentrations and larger particles more easily jam and have a bigger probability of jamming. The probability of jamming decreases significantly around D/d = 10. The effect of velocity on the probability of jamming is insignificant compared with that of particle concentration and grain/particle size ratio (Figs. 14, 15). Therefore, in the following discussion, jamming is assumed to be independent of velocity, but is a function of concentration, friction, and pore throat geometry. We also assume that the effects of concentration, friction, and geometry on jamming are independent; therefore, the probability can be represented as

$$P_{0} \propto h_{1} \left( {D,d,etc} \right)h_{2} \left( C \right)h_{3} \left( f \right)$$

(20)

where h₁, h₂, and h₃ represent the effects of geometry, concentration, and friction on jamming, respectively. These effects will be studied individually.

We first investigate the effects of grain/particle size ratio and pore throat geometry on jamming. Both triangle and square packing structures are used. The simulation results are given in Fig. 16. Figure 16 shows that the probability of jamming increases with decreasing grain size (relative to the particle size). A plateau is found when the pore size is close to the particle size, which is referred to as P_0,max. More importantly, it shows that the same grain size with different pore geometry will result in different jamming probability. Jamming probability does not scale with grain/particle size ratio, since jamming always occurs at the constrictions (throats). The geometry and size of the throats would have a significant effect on jamming. Lafond et al. (2013) performed jamming experiments using a channel with a circular outlet. They found that the average number of particles discharged prior to jam can be scaled with the pore/particle size ratio, S_r. Pores in our case and in real porous media are often not circular. Here we defined an effective circle as the circle that has the same area as that of the constriction. Figure 17 shows the effective radius for triangle and square pores, respectively. This definition can also be used in more general cases where the pores are not a regular geometry.

Fig. 15

Probability of jamming as a function of grain/particle size ratio at C = 0.04 for different flow velocities. A COF of 0.5 was used

Fig. 16

Probability of jamming as a function of grain/particle size ratio for a triangle and b square packing structures

Fig. 17

Effective radius of the pore throat in a triangle and square packing structure

From Eq. 20, we can get

$$\frac{{P_{0} }}{{P_{o,\max } }} = \frac{{h_{1} \left( {S_{{\text{r}}} } \right)h_{1} \left( C \right)h_{1} \left( f \right)}}{{h_{1} \left( {S_{{\text{r}}} |P_{0} = P_{0,\max } } \right)h_{1} \left( C \right)h_{1} \left( f \right)}} = \frac{{h_{1} \left( {S_{{\text{r}}} } \right)}}{{h_{1} \left( {S_{{\text{r}}} |P_{0} = P_{0,\max } } \right)}}$$

(21)

As P₀ is at its plateau value, the effect of S_r on jamming probability is small and the value of h₁ is close to 1. Therefore,

$$h_{1} \left( {S_{{\text{r}}} } \right) = \frac{{P_{0} }}{{P_{0,\max } }}$$

(22)

The curve in Fig. 

Fig. 18

Normalized jamming probability as a function of pore/particle size ratio

18 is h₁, and it can be best fit by

$$h_{1} \left( {S_{{\text{r}}} } \right) = \frac{1}{{1 + e^{{6s_{{\text{r}}} - 13}} }}$$

(23)

Figure 19 shows the effect of the concentration on the jamming probability. As we assumed that each factor acts independently on jamming probability, h₂ is only a function of concentration. Therefore, we only study triangle packing structure. Figure 19a shows the jamming probability as a function of concentration. Again, a plateau is observed as concentration increases. Similarly, by normalizing the values by the plateau value, all curves collapse to a single curve (Fig. 19b), which is exactly h₂. Considering that jamming probability will be zero when particle concentration C is zero, we use the following equation to match the data in Fig. 19b,

$$h_{2} \left( C \right) = 1 - e^{ - 30C}$$

(24)

Fig. 19

a Jamming probability and b normalized jamming probability as a function of particle concentration

We also performed sensitivity analysis on the effect of friction. Figure 

Fig. 20

a Jamming probability and b normalized jamming probability as a function of friction coefficient

20a shows the probability of jamming as a function of COF at three different particle concentrations: C = 0.04, 0.08, and 0.15. The grain/particle size ratio is 10 (S_r = 3.2). In agreement with To et al. (2001), the probability of jamming increases with the COF in all cases. There are two mechanisms that contribute to the increase of jamming. First, the friction between particles and grains slow down the movement of particles. Particles accumulate around the constriction and form a local dense cluster. Second, friction reduces the number of particles that is required to form a “bridge” (To et al. 2001). As COF increases, the probability of jamming approaches a constant. Figure 20b shows that all three curves collapse on each other when P₀ is normalized by its peak value (at f = 1.5). We find that the effect of friction can be predicted well by an exponential function:

$$h_{3} \left( f \right) = 1 - e^{ - 3.33f} .$$

(25)

By combining Eqs. 23, 24, and 25, we can get a new model for the probability of jamming, which takes into account the effect of friction, concentration, pore size and geometry. When Sr < 1, size exclusion occurs so P₀ is 1. The new model is given by

$$P_{0} = C_{{{\text{st}}}} \frac{{\left( {1 - e^{ - 3.33f} } \right)\left( {1 - e^{ - 30C} } \right)}}{{1 + e^{{6S_{{\text{r}}} - 13}} }}.$$

(26)

where C_st is model constant. It is found that C_st = 0.6 gives the best match between model and DEM simulations.

Appendix 4: The criteria for determining the REV

Three screens with different size (Fig. 21) are used to perform sensitivity analysis and determine the REV. We inject a layer of particles with the same size, thickness and concentration into the screens, which means that the number of injected particles is proportional to the screen area. After the simulation, we count the number of particles remaining on the screen (Table 3). The number of remained particles are also proportional to the screen size. We find that increasing the screen size beyond 3 × 4 grains does not increase the accuracy of the simulation and is, therefore, an REV. We also performed similar test for the screen in Fig. 2b and found that 4 × 4 grains is a valid REV.

Table 3 Sensitivity analysis of screen area for triangular packing structure

Fig. 21

Screens with a 3 × 4, b 6 × 4, and c 6 × 8 grains