1 Introduction

Solute transport in porous media is relevant to a wide range of applications in contaminant hydrogeology, geothermal engineering, petroleum engineering, and a variety of chemical engineering systems (Whitaker 1967; Fried and Combarnous 1971; Balakotaiah et al. 1995; Coats and Smith 1964; Erfani et al. 2019, 2020, 2021). Transport in porous materials is controlled by two physical processes: advection and diffusion. Advection is the transport of a solute with the pore velocity (v) of the carrier fluid, and diffusion mechanism is due to the concentration gradient given by Fick’s law. The ratio of advection to diffusion is referred to as the dimensionless Péclet number, \(P_\mathrm{e}=\frac{vL}{D_m}\), where L denotes the characteristic transport length and \(D_m\) is the molecular diffusion coefficient. The pore scale Péclet number is defined based on the characteristic diameter of a pore (Hasan et al. 2019, 2020), while the field Péclet number is usually defined based on the distance between the injection point and the measurement location; as such the values of these two Péclet numbers are significantly different. In addition, due to the presence of the no-slip boundary on solid surfaces, tortuosity of the porous material and preferential pathways, a solute will also spread along the flow direction via fluctuations from the average velocity. These fluctuations can be quantified by the dispersion coefficient (D), which is defined statistically as \(D=\frac{1}{2}\frac{\partial \sigma ^2}{\partial t}\), where \(\sigma ^2\) represents the spatial variance of a solute plume relative to its center of mass, and t is time.

Depending on the application, two different transport scenarios can be considered: in some cases, the aim is to remove or reduce the concentration of resident solute from the system by injection of clean or low-concentration solution (e.g., low salinity water flooding, flushing of polluted soil). In other cases, the resident solute concentration increases with time (e.g., increase in surfactant concentration during surfactant flooding, increase in nutrient concentration during application of fertilizers to soil, increase in groundwater salinity during salt water intrusion). Here, the first scenario is referred to as the “unloading” process, while the second scenario is referred to as the “loading” process.

It has been reported in modeling and laboratory studies (e.g., Huang et al. 1995; Bromly and Hinz 2004; Zaheer et al. 2017) that the dispersion coefficient for the case of unloading (\(D^\mathrm{UL}\)) is larger than that for the case of loading (\(D^L\)), or at least that concentration-dependent dispersivity is (relatively) higher at low concentrations. However, there has not been any systematic study to demonstrate the quantitative difference between the \(D^\mathrm{UL}\) and \(D^L\) at different injection rates, and no clear explanation for this behavior has been provided (although it has been attributed to porous media heterogeneity (e.g., Huang et al. 1995)). Moreover, experimental and modeling studies have shown the critical influence of the sequence of heterogeneities along the principal direction of flow, in configurations of porous media. Berkowitz et al. (2009) demonstrated the importance of flow direction in the transport behavior of a conservative solute across an interface between coarse and fine glass beads packing. Specifically, they showed that a flow direction from coarse to fine porous media leads to delayed solute breakthrough and a more dispersed (skewed) breakthrough curve (BTC), relative to flow from fine to coarse porous media; these differences are diminished at higher flow rates. The effect of flow direction on solute transport across interfaces was elaborated further via modeling studies (Cortis and Zoia 2009; Appuhamillage et al. 2010; Alvarez-Ramirez et al. 2014; Afshari et al. 2018).

In the context of this literature, the main questions investigated in this paper are:

  • Are \(D^\mathrm{UL}\) and \(D^L\) different at the scale of a representative elementary volume (REV)?

  • How do the medium heterogeneity and flow conditions impact differences between \(D^\mathrm{UL}\) and \(D^L\)?

  • Does the macroscopic sequence of heterogeneity influence the differences between \(D^\mathrm{UL}\) and \(D^L\)?

To address these questions, solute transport experiments were visualized by optical microscopy in micromodels with homogeneous and heterogeneous patterns (Fig. 1). Resident concentration fields were visualized over time, which provided the temporal and spatial information required to address the above questions. The results of this study shed light on the reported phenomenon that contaminant remediation in aquifers requires far longer duration than that for aquifer contamination. Moreover, the insights provided here can assist in improving simulation of solute transport processes in geoscience and industrial applications, at various spatial scales.

This paper is organized as follows. First, experiments and data analysis are described. Results and discussion related to loading and unloading processes for homogeneous and heterogeneous micromodels at different Péclet numbers are then presented, and key outcomes of the analysis are summarized.

2 Materials and Methods

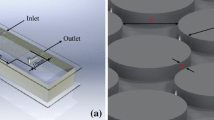
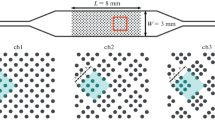
Microfluidic experiments were performed in polydimethylsiloxane (PDMS) micromodels with two homogeneous and heterogeneous designs (Fig. 1). Each micromodel was 3 cm long and 0.6 cm wide, filled with a distribution of solid cylinders to yield porosity values of 0.5 and 0.45 for the coarse and fine regions, respectively. The averaged entities of pore-scale experiments or models can be linked to continuum-scale theories if their system is larger than the representative elementary volume REV (Joekar-Niasar et al. 2008; Hasan et al. 2019). To ensure that the micromodel domain is statistically larger than the REV, porosity and permeability were calculated using the single-phase Navier–Stokes equation implemented in OpenFOAM\(^{\circledR }\) at different fields of view but with the same statistics for the solid cylinders (Godinez-Brizuela et al. 2017). The width of the micromodel was estimated to be 1.5 REV for the coarse pattern and 2 REV for the fine pattern considering both porosity and permeability variations. The permeabilities of the fine and coarse regions are approximately 23 and 42 Darcy, respectively.

The internal depth of the micromodel is uniform at 60 \(\mu\)m. The loading and unloading experiments were performed in both micromodels using clear water and a stable ink-water mixture (water-based blue colored, Ecoline). All loading and unloading experiments were performed with the same set of injection rates of q = 0.05, 0.1, 0.25, 0.5, and 1 mL h\(^{-1}\) under fully saturated conditions. For the heterogeneous micromodel pattern, different injection directions were also examined—namely coarse to fine (CtF) and fine to coarse (FtC). Note that the homogeneous micromodel had the same pattern as the coarse section of the heterogeneous model. It is noted that such a configuration is likely to occur in highly heterogeneous sedimentary rocks, where the fluid moves between zones with significantly different characteristics (permeability or porosity), or where the formation bedding is perpendicular to the main flow direction.

Fig. 1
figure 1

Homogeneous and heterogeneous micromodel designs. The homogeneous micromodel has the same design as the coarse section of the heterogeneous pattern. Arrows show the flow direction for coarse to fine (CtF), and fine to coarse (FtC) experiments

Full size image

The micromodels were fabricated following the procedure explained in detail in Karadimitriou et al. (2013). In this method, a silicon wafer (on which the negative pore space was imprinted by photolithography) was used as the mold on a PDMS slab. Then, a second flat PDMS slab was bonded to the patterned PDMS slab using the corona discharge technique. Elongated micromodels were visualized by an optical system of 4 digital cameras (Basler ACE 2), 3 beam splitters and a magnifying lens (SONY Sonnar, f1.8/135 mm) as well as a prism to direct light into the visualization setup. A detailed description of the experimental setup can be found in Karadimitriou et al. (2012). This setup was used formerly to investigate dispersion under unsaturated conditions (Karadimitriou et al. 2016, 2017), studying the role of saturation morphology on the dispersion coefficient during the loading process.

In each experiment, series of images were taken from the micromodel, which were later “stitched” together. The recorded intensity for each pixel was converted to the ink concentration using an exponential calibration equation, \(C_{i,j}=b\left( 1-e^{kI_{i,j}^{'}}\right)\), where \(I_{i,j}^{'}\) denotes the normalized intensity of the pixel i, j. The calibration coefficients, b and k, are determined from calibration experiments with known concentrations; details can be found in Karadimitriou et al. (2016). Temporal concentration profiles (BTCs) were estimated from the concentration averaged over a strip of pixels next to the outlet boundary.

The one-dimensional (macroscopic) advection-dispersion equation (ADE) reads as

$$\begin{aligned} \frac{\partial C}{\partial t}=D\frac{\partial ^2 C}{\partial x^2}-v\frac{\partial C}{\partial x} \end{aligned}$$
(1)

where v is the average pore velocity and D is the (longitudinal) coefficient of hydrodynamic dispersion in the principal (x) direction of flow. Throughout the analysis and discussion below, the dispersion coefficients for loading (\(D^L\)) and unloading (\(D^\mathrm{UL}\)), discussed in the Introduction, refer to dispersion estimated from Eq. 1.

Given that the width of the micromodel for the coarse domain is 1.5 REV and 2 REV for the fine domain, and the length is 5 times larger than width, an analytical solution of Eq. 1 was fitted to the temporal BTCs to obtain the dispersion coefficient and effective pore velocity. The analytical solution for the case of continuous injection of a solute, with concentration \(C_0\) [unit step injection, \(C(0,t)=C_0, t\ge 0\)] in an initially solute-free, semi-infinite porous medium \([C(x,0)=0, x>0]\), with zero concentration gradient at the outlet boundary \([\frac{\partial C(\infty ,t)}{\partial x}=0, t\ge 0]\), the solution to Eq. 1 reads as (Ogata and Banks 1961)

$$\begin{aligned} C(x,t)=\frac{1}{2}C_0\left[ \text{ erfc }\left( \frac{x-vt}{2\sqrt{Dt}}\right) + e^{xv/D}\text{ erfc }\left( \frac{x+vt}{2\sqrt{Dt}}\right) \right] \end{aligned}$$
(2)

Additionally, the temporal change in the average resident concentration for the entire domain was calculated, referred to hereafter as the resident concentration curve.

3 Results and Discussion

3.1 Homogeneous Model

As noted, this experiment focused on quantifying, at a small pore scale, possible differences between the time scales of loading and unloading processes, characterized in terms of \(D^L\) and \(D^\mathrm{UL}\). Several studies reported that the unloading process is significantly slower than loading (Huang et al. 1995; Bromly and Hinz 2004; Zaheer et al. 2017), although these various experiments were performed over much larger physical scales and with undefined (or at least not fully resolved) heterogeneity.

Figure 2 shows the average resident concentration versus time for the homogeneous sample for both loading and unloading experiments at different injection flow rates (ranging from 0.05 to 1 mL h\(^{-1}\)). The obtained resident concentration curves show that the curves are more skewed in the case of unloading, spanning longer time (maximum of 1000 s) compared to the loading experiments (maximum of 600 s) for the slowest case of 0.05 mL h\(^{-1}\). This indicates that \(D^\mathrm{UL}\) is larger than \(D^L\). The difference in transport time scale during loading versus unloading has impacted the spatial distribution of concentration as well. Since near the side walls, the pore velocity is smaller, the difference between the loading and unloading transport time scales would be larger. Thus, the spatial distributions of the concentration in loading versus unloading are very different (see insets in Fig. 2). As shown, flushing along the side boundaries of the micromodel is slower in the case of unloading relative to that of loading. A similar pattern of solute dispersion was observed by Sadeghi et al. (2020) in a 2D pore network.

Fig. 2
figure 2

Normalized average resident concentration (\(\left<\text{ C }\right>/\text{C}_0\)) over the entire domain for a loading (ink injection) and b unloading (clean water injection) experiments in the homogeneous model, for different flow rates, q (ranging from 0.05 to 1 mL h\(^{-1}\)). The curves appear smooth because measurements were made at time resolution of <1 s. Diamond and triangle symbols show the normalized average concentration of 0.5 for loading and unloading experiments, respectively. \(\left<\cdot \right>\) indicates the average of pixel-value concentrations

Full size image
Fig. 3
figure 3

Fitted dispersion coefficient versus effective pore velocity for loading and unloading experiments at different injection rates. The difference between the loading and unloading dispersion coefficients decreases as the injection rate (advection) increases. For loading, the range of variation with 90% confidence for the coefficient and exponent were calculated as \(\left[ 0, \,\, 8.066\times 10^{-3}\right]\) and \(\left[ 1.02, \,\,1.30 \right]\), respectively. For unloading, the range of variation with 90% confidence for the coefficient and exponent were calculated as \(\left[ 0.237\times 10^{-3}, \,\, 2.387\times 10^{-3}\right]\) and \(\left[ 0.86, \,\,1.09\right]\), respectively. (Note: pore-scale Pe values, shown on the upper horizontal axis, were calculated using a typical diffusion coefficient of \(D_m\approx 10^{-9}\) m\(^2\) s\(^{-1}\) and characteristic length of 60 \(\mu\)m.) Experiments for the lowest and highest rate were repeated and fairly similar results were obtained, as the variations are shown in the figure

Full size image

To obtain the dispersion coefficients and effective pore velocity for the loading and unloading scenarios, the 1D ADE (Eq. 2) was fitted to the obtained effluent BTCs (Appendix, Figs. 6 and 7). We of course recognize the inherent limitations in the 1D ADE characterization of the effluent concentration, but stress that our focus was on demonstrating the systematic differences between D values for loading and unloading, and their strong dependence on injection rate. Our analysis and conclusions regarding relative differences between loading and unloading can be considered valid given that the flow boundary effects are uniform and consistent in all experiments. Fig. 6 shows the BTCs and the fitted advection-dispersion curves for three sets of experiments. To ensure that the fitting procedure did not influence the trends in estimated parameter values, we also estimated the dispersion coefficient and mean velocity for the loading and unloading experiments using the method of time moments. Results of the method of time moments can be found in Fig. 8. As expected, the values obtained are slightly different, but the order of magnitudes does not change. Both approaches reflect consistently similar trends in dispersion versus velocity for loading and unloading scenarios.

The fitted curves show overall good agreement with the experimental data, while some deviations at the early- and late-time are visible, which imply some non-Fickian transport effects. These effects are considered secondary in the context of the focus of the current study. The relationships between the fitted dispersion coefficients and effective fluid velocities are shown in Fig. 3. Note that because one loading and one unloading experiment were carried out at each injection rate, the corresponding effective fluid velocity for each pair of experiments at a given injection rate should be the same. As a consequence, three parameters were fitted for each pair of loading and unloading experiments, namely a common average pore velocity, and either \(D^\mathrm{UL}\) or \(D^{L}\).

Fig. 3 shows that the differences between \(D^\mathrm{UL}\) and \(D^L\) decrease with an increase in the injection rate. Given that advection and diffusion are the two solute transport mechanisms in porous media, and given that increasing the rate of injection (i.e., advection) leads to smaller differences between \(D^\mathrm{UL}\) and \(D^L\), it can be concluded that diffusion is the main cause of the difference between \(D^\mathrm{UL}\) and \(D^L\). This becomes more visible if the pore-scale Péclet number is estimated on the basis of the pore-scale effective velocity, multiplied by the characteristic length (micromodel depth), and divided by the diffusion coefficient (\(D_m \approx 10^{-9}\) m2 s\(^{-1}\)) (Lee et al. 2004). The resulting value of the pore-scale Péclet number is approximately 1 for the smallest injection rate (0.05 mL h\(^{-1}\)) (refer to the secondary x-axis in Fig. 3). At this Péclet number—where advection and diffusion transport are comparable—the difference between the dispersion coefficients for the loading and unloading is seen to be significant. It can be hypothesized that the observed difference is due to counter-current advection and diffusion fluxes during unloading, while during loading, these two fluxes are in the same direction. The effect of such a phenomenon is more significant at smaller injection rates, where the magnitude of the advection and diffusion transport mechanisms are comparable. In former studies, it was proposed that diffusion process can be nonlinear. In this context, then, use of the linear Fick’s law will lead to a concentration-dependent diffusion coefficient (Bardow et al. 2005; Collins et al. 2019; Khalifi et al. 2020). The impact of such nonlinearity in diffusion on dispersion coefficients for loading and unloading, at larger time and physical scales, is not understood and requires further research.

Additionally, as seen in Fig. 3, there is a positive power law relation between the dispersion coefficient and pore velocity as reported in the literature (Babaei and Joekar-Niasar 2016; An et al. 2020; Bijeljic et al. 2006; Hasan et al. 2020). It should be noted that the precise nature of this power law dependence is at least partly a consequence of fitting the data with solution of the ADE, which assumes that the dispersive transport at the investigated experimental spatial and temporal scales is Fickian (Berkowitz et al. 2006, 2009).

3.2 Heterogeneous Model

Similar loading and unloading experiments under single-phase, fully saturated conditions were performed in a heterogeneous micromodel, examining the effect of flow direction, to explore the possible effect of the sequence of heterogeneity on dispersion. As for the case of the homogeneous model (previous section), Fig. 4 shows the obtained resident concentration curves at two injection rates of 0.05 and 1 mL h\(^{-1}\). The unloading experiments take longer time compared to the loading experiments, similar to the behavior in the homogeneous micromodels. Moreover, the physical heterogeneity (fine and coarse patterns) results in a more complicated spatial distribution of concentration.

The 1D ADE was fitted to the BTCs; the BTCs for the loading and unloading experiments for fine-to-coarse (FtC) and coarse-to-fine (CtF) directions, at the injection rates of 0.05 and 1 mL h\(^{-1}\), are shown in Fig. 7 (Appendix). Experiments performed under identical injection rates were fitted such that they share an identical, fitted effective pore velocity. Thus, five parameters were fitted for each injection rate, namely a common effective pore velocity, two \(D^{UL}\) for CtF and FtC experiments, and two \(D^L\) for CtF and FtC experiments at the same injection rate. As seen in Fig. 7, the fitting results using the (Fickian-based) ADE are not as satisfactory as for the heterogeneous experiments, which reflect the considerable non-Fickian effects. Note that application of other transport theories may improve the quality of the fits, but they include additional model parameters and complexity regarding parameter interactions with D; such an analysis of D using other methods is beyond the scope of the current study and is not expected to influence the key outcome that \(D^{UL}>D^L\). The fitting results are presented in Fig. 5. The differences between \(D^{UL}\) or \(D^L\) for each set of experiments again demonstrate a decrease between these coefficients with an increase in injection rate, similar to that for the homogeneous micromodel (Section 3.1).

Fig. 4
figure 4

Normalized average resident concentration (\(\left<\text{ C }\right>/\text{C}_0\)) over the entire domain of the heterogeneous micromodel for a Inection rate of 0.05 mL h \(^{-1}\) and b injection rate of 1 mL h \(^{-1}\). The figures show data for both fine to coarse (solid lines) and coarse to fine (dashed lines) flow directions during loading and unloading experiments. The curves appear smooth because measurements were made at time resolution of <1 s. Square and triangle symbols show the average resident concentration (over the whole micromodel) equal to 0.5 for the CtF and FtC directions, respectively. \(\left<\cdot \right>\) indicates the average of pixel-value concentrations

Full size image

With regard to the effect of flow direction, however, the results shown in Fig. 5 indicate little influence on transport behavior. For the loading experiments, the FtC flow direction appears to indicate slightly higher dispersion coefficients compared to the CtF case. The estimates for D were analyzed further by examining the four values for each pair of loading and unloading experiments separately, i.e., by fitting power-law functions for each (FtC, CtF) separately, for each of the loading and unloading experiments. The results of individual power-law function fits for each set of four points are presented in Table 1 (Appendix); it is seen that the differences in fitted slopes are relatively insignificant, particularly in light of the limited number of experiments and spread of the estimated dispersion and velocity coefficients.

Comparing this fine-coarse micromodel pattern to the homogeneous (coarse) micromodel pattern, one might expect that the structural and pore-space heterogeneities will amplify the difference between the \(D^{UL}\) and \(D^L\). However, as seen here, differences in dispersion coefficients and their power-law behavior relative to the velocity (see Fig. 5 and Table 1), for both loading and unloading processes, are not significant. This can be explained considering the constant depth of the micromodel, given that the permeability contrast between the fine and coarse sections in the micromodel is not significant. Thus, further investigations using variable-depth micromodels or larger contrasts between coarse and fine sections would provide further insight. Development of such micromodels may require a different manufacturing technique.

Fig. 5
figure 5

Fitted dispersion coefficient versus effective pore velocity for loading and unloading experiments in the heterogeneous model, for both fine-to-coarse and coarse-to-fine flow directions, at five different injection rates. For loading, the range of variation with 90% confidence for the coefficient and exponent were calculated as \(\left[ 0,\,\, 5.868\times 10^{-3}\right]\) and \(\left[ 0.63, \,\,1.51 \right]\), respectively. For unloading, the range of variation with 90% confidence for the coefficient and exponent were calculated as \(\left[ 0,\,\, 2.516\times 10^{-3}\right]\) and \(\left[ 0.56, \,\,1.23\right]\), respectively. (Note: pore-scale Pe numbers, shown on the upper horizontal axis, were calculated using a typical diffusion coefficient of \(D_m\approx 10^{-9}\) m\(^2\) s\(^{-1}\) and characteristic length of 60 \(\mu\)m.)

Full size image

4 Conclusion

Solute transport at the pore scale was examined, using PDMS micromodels, with a focus on loading and unloading of solute in fully saturated conditions. Experiments were conducted under different rates of fluid injection in both homogeneous and heterogeneous porous medium micromodels. It was shown that the effective dispersion coefficient is process-dependent, with loading processes exhibiting lower dispersion coefficient values relative to unloading processes. The differences between these coefficients decrease with a concurrent increase in the injection flow rate. It can be concluded that this behavior is due to counter-current advection and diffusion transport mechanisms during unloading, while in a loading process, both transport mechanisms act in the same direction. Additionally, a concentration-dependent diffusion process might also account for the observed phenomenon, but this requires further research to be established.

Using the heterogeneous (in the form of coarse and fine sections normal to flow direction) micromodel design, it was shown that the presence of heterogeneity in the porous medium increases the difference between the apparent loading and unloading dispersion coefficients. However, these experiments did not indicate significant differences between the coarse-to-fine and fine-to-coarse dispersion coefficients at a given injection rate. This might be due to the constant depth over the entire system, which controls the hydraulic conductance in coarse and fine regions. Thus, further investigations using variable-depth micromodels or larger contrasts between coarse and fine sections are required. Development of such micromodels may require a different manufacturing technique.

The obtained results shed light into the extent of a “cleaning period” required for contaminant removal from aquifers and may have important implications for field studies of contaminant and solute transport. Experiments and modeling studies at larger length and time scales are required to assess the phenomena reported here and to further investigate the mechanisms behind them.