1 Introduction

The Darcy–Bénard problem for free convection in a porous layer is being recognized as a classical problem of hydrodynamic stability. One must be aware that it is a coupled thermomechanical problem of fourth order in space. Its fourth-order nature involves mathematical challenges that enforce implicit restrictions on the standard physical modeling. The classical HRL onset problem was pioneered by Horton and Rogers (1945) and Lapwood (1948), who established the standard of searching for normal-mode solutions of this eigenvalue problem.

Unfortunately, it is very difficult to develop analytical solutions that are genuine fourth-order solutions without degeneracies. The method of normal modes will automatically give separable solutions, but it restricts the class of admissible boundary conditions. In essence, a fourth-order eigenvalue problem becomes degenerate in any spatial direction where the solution is taken to be of normal-mode type. This is because normal modes are eigenfunctions for the second-order Helmholtz equation. Solutions of a second-order eigenvalue problem cannot satisfy the four independent boundary conditions that a fourth-order problem, in general, will have. Alternatively, the easy way out of this dilemma is to select the four boundary conditions so that two of them are trivially satisfied, with the remaining two conditions setting the Helmholtz eigenvalue problem with its normal mode solutions.

Still, the Darcy–Bénard onset problem is the simplest of all thermomechanical eigenvalue problems. However, it is more complicated than its closest mathematical relative, which is the free vibration of elastic plates (Yu 1996). Thin elastic plates have only the transverse deflection as a variable for setting the biharmonic eigenvalue problem with homogeneous boundary conditions. There are three basic points that make the fourth-order Darcy–Bénard eigenvalue problem more perplexing, from both mathematical and physical viewpoints.

  1. (1)

    The Darcy–Bénard problem has two coupled eigenfunctions. These two are the perturbation temperature and the vertical velocity, in the simplest case. More generally, the vortex potential expressed by one scalar function takes the role of the single mechanical variable (Haugen and Tyvand 2003; Nygård and Tyvand 2011).

  2. (2)

    The vertical direction of the buoyancy force gives the Darcy–Bénard problem an inbuilt anisotropy with respect to directions, which the free elastic vibrations do not have. A striking result of this gravitational anisotropy is seen if we compare flow cells with thermal cells, which have exactly the same shape as the classical HRL problem where the entire solution is of normal-mode type. The thermal cells have the same vertical dependency as the flow cells, while they are mutually displaced by a quarter of a wavelength in the horizontal direction.

  3. (3)

    Generally, one cannot formulate all the boundary conditions in terms of one variable, so the problem has to be solved as a coupled thermomechanical problem. It is, of course, not satisfactory to let the mathematical convenience of normal modes overrule the general physics of a fourth-order problem.

Nield was first out to challenge the normal-mode paradigm of the Darcy–Bénard onset problem (Nield 1968). He extended the classical normal-mode type HRL solution (Horton and Rogers 1945; Lapwood 1948) by considering all possible combinations of Dirichlet or Neumann conditions for the perturbation temperature and the vertical velocity at the upper and lower boundaries of the horizontal porous layer. Since he kept the infinite extent horizontally, he did not change the normal-mode dependency in the horizontal direction. Then, Tyvand (2002) performed a similar extension of the HRL normal-mode solution in the horizontal direction, for a porous box. All possible combinations of Dirichlet and Neumann conditions at the lateral end-walls was considered, while the classical HRL conditions with normal-mode dependency were retained for the vertical direction. Later, Nield and Bejan (2010) showed tables condensing the results from Nield (1968) and Tyvand (2002). In fact, one of the problems defined in Tyvand (2002) was not analytically solvable because it was time-dependent. Finally, it was solved by Rees and Tyvand (2004), showing an onset mode that travels horizontally through the porous box.

Originally, the challenges of convection onset in finite porous enclosures were addressed by Wooding (1959). He showed how to solve the general onset problem for a vertical cylinder with normal-mode compatible conditions along the cylinder walls. The first one to challenge this normal-mode paradigm for finite porous bodies was Lyubimov (1975). He found that two-dimensional cavities with impermeable and conducting walls give a degenerate eigenvalue problem with a double set of eigenfunctions. Nilsen and Storesletten (1990) derived such solutions for an upright rectangular cavity, with symmetric and antisymmetric eigenfunctions representing the degeneracy. Rees and Lage (1996) later confirmed these findings. Moreover, Rees and Tyvand (2004) explained this degeneracy, by showing that a horizontal Fourier component can be separated out from the full fourth-order eigenvalue problem, thereby reducing the eigenvalue problem to a second-order problem. They demonstrated that the degeneracy of the problem involves an indeterminacy of the position of a convection cell wall. Still, any set of coupled eigenfunctions have the supposed quarter of a wavelength displacement between a thermal cell wall and its associated flow cell wall. The onset criterion for a given cavity in a given vertical temperature gradient is independent of the orientation of the cavity.

In the present paper, the nice analytical properties of the Dirichlet-type onset problem for two-dimensional cavities (Rees and Tyvand 2004) are lost as we replace the mechanical Dirichlet condition with a Neumann condition, bringing us back to a fourth-order thermomechanical problem without degeneracy. This problem will be solved numerically since closed-form analytical solutions are not available. The orientation of the cavity will necessarily affect the eigenvalue problem when no reduction to a second-order problem is possible.

The paper is organized with the following structure. Section 2 formulates the mathematical basis for the physical problem, including the proposal of a new scaling. In Sect. 3, the different families of boundary conditions are presented. Then, the eigenfunctions at marginal stability are presented in Sect. 4, where the solution methodology is described. Section 5 provides the main results for rectangular cavities, before Sect. 6 handles elliptical cavities. Finally, Sect. 7 discusses the implications of this article and provides some concluding remarks. In addition, “Appendix” presents an onset problem with impermeable walls that have given normal derivative for the temperature. We will show that these two problems have the same onset criterion because we relate it to our model with conducting and open walls.

2 Physical Problem with Mathematical Formulation

A horizontal porous cylinder is considered, with arbitrary cross section in the vertical x, z plane. The y axis is aligned with the axis of the horizontal cylinder, which has impermeable and insulating end-walls \(y=0\) and \(y=\Delta y\). When the ratio \(\Delta y/H\) is small enough, the onset mode is two-dimensional in the vertical cross-section plane. In Storesletten and Tveitereid (1991), a criterion \(\Delta y/H < 0.86\) was found for two-dimensional flow in a circular cavity, where H denotes the diameter. We will investigate the onset of two-dimensional convection in the vertical x, z plane of the cross section, where H denotes the geometric length scale. The unit normal vector pointing out of the boundary is \(\mathbf {n}\). The two-dimensional velocity vector \({\mathbf {v}}\) has Cartesian components (u, w). The temperature field is T(x, z, t), with t denoting time. There is an undisturbed motionless state with a uniform vertical temperature gradient \(-\beta\).

The gravitational acceleration g is written in vector form as \({\mathbf {g}}\). The porous medium is homogeneous and isotropic, with permeability K. The standard Darcy–Boussinesq equations for free thermal convection can be written

$$\begin{aligned} \nabla P +\frac{\mu }{K} {\mathbf {v}} + \rho _0 \alpha \,(T - T_0) {\mathbf {g}}&=0, \end{aligned}$$
(1)
$$\begin{aligned} \nabla \cdot {\mathbf {v}}&=0, \end{aligned}$$
(2)
$$\begin{aligned} (\rho c_{\mathrm{p}})_{\mathrm{m}}\frac{\partial T}{\partial t}+(\rho c_{\mathrm{p}})_{\mathrm{f}}\, {\mathbf {v}}\cdot \nabla T&= \lambda _{\mathrm{m}} \nabla ^2 T. \end{aligned}$$
(3)

In these equations, P is the dynamic pressure, \(\alpha\) is the coefficient of thermal expansion, \(\rho =\rho _0\) is the fluid density at the reference temperature \(T_0\), \(\mu\) is the dynamic viscosity of the saturating fluid, \(c_{\mathrm{p}}\) is the specific heat at constant pressure, and \(\lambda _{\mathrm{m}}\) is the thermal conductivity of the saturated porous medium. The subscript m refers to an average over the solid/fluid mixture, while the subscript f refers to the saturating fluid alone.

2.1 Dimensionless Equations

The conventional form of the equations is given by the substitutions

$$\begin{aligned} \frac{1}{H} (x, z)&= ({\hat{x}}, {\hat{z}}),\quad \frac{H}{\kappa _{\mathrm{m}} }(u, w) = ({\hat{u}},{\hat{w}}) = \hat{{\mathbf {v}}},\quad H\nabla = {\hat{\nabla }},\\ \frac{1}{\Delta T} (T - T_0)&= {\hat{T}},\quad \frac{K }{\mu \kappa _{\mathrm{m}}} (p - p_0) = {\hat{p}},\quad \frac{(\rho c_{\mathrm{p}})_{\mathrm{f}} \kappa _{\mathrm{m}} }{(\rho c_{\mathrm{p}})_{\mathrm{m}} H^2} t = {\hat{t}}, \end{aligned}$$
(4)

where \(\kappa _{\mathrm{m}} = \lambda _{\mathrm{m}}/(\rho _0 c_{\mathrm{p}})_{\mathrm{f}}\) is the thermal diffusivity of the saturated porous medium. We have introduced a temperature difference defined as \(\Delta T = \beta H\). This leads to the standard Darcy–Boussinesq equations

$$\begin{aligned} \hat{{\mathbf {v}}}+{\hat{\nabla }} {\hat{P}} - R {\hat{T}} \mathbf {k}&=0, \end{aligned}$$
(5)
$$\begin{aligned} {\hat{\nabla }}\cdot \hat{{\mathbf {v}}}&=0, \end{aligned}$$
(6)
$$\begin{aligned} \frac{\partial {\hat{T}}}{\partial {\hat{t}}} +\hat{{\mathbf {v}}} \cdot {\hat{\nabla }} {\hat{T}}&= {\hat{\nabla }}^2 {\hat{T}}. \end{aligned}$$
(7)

In Eq. (5), \(\mathbf {k}\) is the vertical unit vector. The Rayleigh number R is defined as

$$\begin{aligned} R =\frac{\rho _0 g \alpha K \beta H^2}{\mu \kappa _{\mathrm{m}} }. \end{aligned}$$
(8)

This standard dimensionless description is somewhat biased as it scales properly the temperature field but not the velocity field. Now we attempt a more balanced description, by applying the transformations

$$\begin{aligned} ({\hat{x}}, {\hat{z}}) = (x, z),\;\;({\hat{u}},{\hat{w}}) = (u,w) \sqrt{R},\;\;{\hat{T}} = T,\;\;{\hat{p}} = p \sqrt{R},\;\;{\hat{t}} = \frac{t}{\sqrt{R}}, \end{aligned}$$
(9)

whereby we redefine the dimensionless variables and remove the superscripts.

$$\begin{aligned} {\mathbf {v}}+\nabla P - \sqrt{R}\, T \mathbf {k}&=0, \end{aligned}$$
(10)
$$\begin{aligned} \nabla \cdot {\mathbf {v}}&=0, \end{aligned}$$
(11)
$$\begin{aligned} \sqrt{R} \frac{\partial T}{\partial t} + \sqrt{R}\,{\mathbf {v}} \cdot \nabla T&= \nabla ^2 T. \end{aligned}$$
(12)

These Darcy–Boussinesq equations encompass two driving mechanisms: first the buoyancy term in Darcy’s law and secondly the convective term in the heat equation. Instead of the traditional weighting of the order parameter R placed solely on buoyancy, our scaled equations put equal weight factors \(\sqrt{R}\) on the buoyancy term and the convective term. We get the nice balance of equally weighting the two intruding terms that couple the governing equations. Buoyancy intrudes thermally an otherwise mechanical force balance, while convective transport intrudes mechanically an otherwise thermal diffusion balance.

We have now presented two alternative sets of dimensionless equations for Darcy–Bénard convection. The first set is the standard version, which remains useful for reference. We introduced the second equation set (10)–(12) for improving our understanding of the mutual physical couplings between the thermal field and the flow field at convection onset.

The new unit for dimensionless velocity is

$$\begin{aligned} \frac{\kappa _{\mathrm{m}} \sqrt{R}}{H} = \sqrt{\frac{\rho _0 g \alpha \beta \kappa _{\mathrm{m}} K}{\mu }}, \end{aligned}$$
(13)

which means that we introduce a realistic buoyancy scaling of the velocity field, instead of a purely diffusive scaling linked to the layer thickness H. This buoyancy scaling involves the basic temperature gradient \(\beta\), without a length scale. There is thermomechanical balance as the thermal factor \(\sqrt{\kappa _{\mathrm{m}}}\) and flow factor \(\sqrt{K/\mu }\) contribute equally to the velocity scale. Below we will check whether the preferred eigenfunctions of convection onset will have a balance between the scaled amplitudes for vertical velocity and temperature perturbation.

It is easy to overlook the significance of physically scaled amplitudes in linear theory, but they enter the picture once we consider the ratio between the amplitudes for temperature and flow.

2.2 Basic Solution

A stationary basic solution of Eqs. (10)–(12) is given with subscript “b”

$$\begin{aligned} {\mathbf {v}}_\mathrm{b} = 0, \;\; \text {d} T_\mathrm{b}/\text {d}z = - 1,\;\; P_\mathrm{b} = - \frac{1}{2} \sqrt{R}\, z^2. \end{aligned}$$
(14)

This basic state of hydrostatic fluid has a linear temperature profile. The chosen boundary conditions for the porous cavity need to be consistent with this steady solution, with vertical gradients for temperature and pressure.

2.3 Linearized Two-Dimensional Perturbation Equations

In our stability analysis, we disturb the static state (14) with perturbed fields

$$\begin{aligned} {\mathbf {v}} = {\mathbf {v}}_\mathrm{b} + {\mathbf {v}},\;\; T = T_\mathrm{b}(z) + \theta ,\;\; P = P_\mathrm{b}(z) + p, \end{aligned}$$
(15)

with perturbations \({\mathbf {v}}, \theta , p\) that are functions of x, z and t. Linearizing Eqs. (10)–(12) and eliminating the pressure gives the coupled governing equations

$$\begin{aligned} \nabla ^2 w = \sqrt{R} \frac{\partial ^2\theta }{\partial x^2},\quad \sqrt{R}\left( \frac{\partial \theta }{\partial t} - w\right) = \nabla ^2 \theta . \end{aligned}$$
(16)

With zero divergence, the streamfunction \(\psi\) is introduced in Cartesian coordinates

$$\begin{aligned} (u, w) = \left( \frac{\partial \psi }{\partial z}, - \frac{\partial \psi }{\partial x}\right) . \end{aligned}$$
(17)

We rewrite the coupled equations (16)

$$\begin{aligned} \nabla ^2 \psi + \sqrt{R} \frac{\partial \theta }{\partial x} = 0,\quad \nabla ^2 \theta - \sqrt{R} \frac{\partial \psi }{\partial x} = 0, \end{aligned}$$
(18)

assuming that the onset of convection is non-oscillatory. The similarity of these two equations suggests a redefined streamfunction \(\Psi\)

$$\begin{aligned} \psi = i \Psi , \end{aligned}$$
(19)

where i denotes the imaginary unit. The real part of each eigenfunction has physical meaning. Now we establish a symmetric form of coupled equations

$$\begin{aligned} \nabla ^2 \Psi - i \sqrt{R} \frac{\partial \theta }{\partial x} = 0,\quad \nabla ^2 \theta - i \sqrt{R} \frac{\partial \Psi }{\partial x} = 0. \end{aligned}$$
(20)

The symmetry means that the governing equations are unchanged under the substitution \((\theta , \Psi ) \rightarrow (\Psi , \theta )\).

Whether this intrinsic symmetry of the coupled equations also simplifies the eigenvalue problem, depends on the boundary conditions. We will start with the simplest of all such cases.

2.4 Revisiting the Horton–Rogers–Lapwood (HRL) Problem

The thermal eigenfunction for the Horton–Rogers–Lapwood problem (Horton and Rogers 1945; Lapwood 1948) is

$$\begin{aligned} \theta (x,z) = e^{i k x} \sin (\pi z), \end{aligned}$$
(21)

satisfying the boundary conditions \(\theta (x,0) = \theta (x,1)=0\). Here k is the horizontal wave number. Since the boundary conditions for the flow are \(\Psi (x,0) = \Psi (x,1)=0\), the symmetry between the eigenfunctions \(\theta\) and \(\Psi\) is complete, which implies that these eigenfunctions are equal, at most differing by a constant of proportionality C, so that we have

$$\begin{aligned} \Psi (x,z) = C e^{i k x} \sin (\pi z), \end{aligned}$$
(22)

for the flow eigenfunction. Inserting these solutions into the governing equations decouples them into two identical Helmholtz-type equations

$$\begin{aligned} (\nabla ^2 + k \sqrt{R}) \theta = 0,\quad (\nabla ^2 + k \sqrt{R}) \Psi = 0 \end{aligned}$$
(23)

while the proportionality factor is \(C=1\). Equation (19) gives the factor of proportionality i between the physical eigenfunctions (\(\psi = i \theta\)), showing the horizontal phase shift between flow cells and thermal cells. The classical HRL dispersion relation follows immediately from Eq. (23)

$$\begin{aligned} k \sqrt{R} = \pi ^2 + k^2. \end{aligned}$$
(24)

With the square root of the Rayleigh number, this is a decoupled (and degenerate) second-order dispersion relation for the fourth-order eigenvalue problem.

We have a common unit amplitude for the temperature field and the streamfunction. The wave number k is the amplitude for each velocity component. Our version of the HRL problem is a properly scaled linearized problem. The maximum values for the vertical velocity w and temperature perturbation \(\theta\) occur at the center of a thermal cell, and their scaled amplitude ratio is \(\vert w \vert _\mathrm{max}/\vert \theta \vert _\mathrm{max} = k = \pi\) at the marginal state.

3 Thermomechanical Conditions Along the Cylinder Boundary

The boundary conditions for a general two-dimensional cylinder boundary involve a unit normal vector \(\mathbf {n}\) with arbitrary direction. The elementary HRL solution has a horizontal phase shift of a quarter of a wavelength between the eigenfunctions \(\theta\) and \(\psi\), and no mutual phase shift in the vertical direction. These simple phase relationships exist only when \(\mathbf {n}\) is either horizontal or vertical.

Our linearized set of coupled governing equations (23) are symmetric in the pair of eigenfunctions \((\theta , \Psi )\), and these equations are preserved under the substitution \((\theta , \Psi ) \rightarrow (\Psi ,\theta )\). Our choice of boundary conditions will decide whether this symmetry is maintained. We will only consider Dirichlet or Neumann-type conditions for the temperature and streamfunction. The temperature field is given the role of deciding the primary boundary condition, which means that the flow condition becomes a secondary condition which must be physically compatible with the chosen thermal condition.

3.1 DD Model: Dirichlet Conditions for \(\theta\) and \(\psi\)

The conditions of a thermally conducting and impermeable cylinder wall are

$$\begin{aligned} \theta = \Psi = 0, \;\hbox {at the boundary}, \end{aligned}$$
(25)

introducing \(\Psi = - i \psi\) as streamfunction. The identity \(\theta = \Psi\) leads to the uncoupled versions of Eq. (20)

$$\begin{aligned} \nabla ^2 \theta - i \sqrt{R} \frac{\partial \theta }{\partial x} = 0,\quad \nabla ^2 \Psi - i \sqrt{R} \frac{\partial \Psi }{\partial x} = 0. \end{aligned}$$
(26)

In Rees and Tyvand (2004), this model was explored, separating out a horizontal Fourier component

$$\begin{aligned} \theta = \Psi = e^{i k x} F(x,z), \end{aligned}$$
(27)

where the Helmholtz equation \(\nabla ^2 F + k^2 F = 0\) has the wavenumber k as eigenvalue. The critical Rayleigh number \(R = 4 k^2\) is greater than the classical value \(4 \pi ^2\). We are now interested in the ratio between the maximal amplitudes for vertical velocity and maximal perturbation temperature

$$\begin{aligned} \frac{\vert w \vert _\mathrm{max}}{\vert \theta \vert _\mathrm{max}} = k, \end{aligned}$$
(28)

which is the wave number eigenvalue. The decisive result for this DD model (Rees and Tyvand 2004) is the lowest wave number eigenvalue k for the Helmholtz equation. Its independence of the orientation of the cavity makes the critical Rayleigh number \(4 k^2\) independent of orientation. The lowest wave number k determines the periodic vertical cell walls.

3.2 DN Model: Dirichlet Condition for \(\theta\) and Neumann Condition for \(\psi\)

We will now give a physical description of our thermomechanical Dirichlet–Neumann (DN) model. It combines the thermal Dirichlet condition of zero perturbation temperature with the Neumann condition for the streamfunction with zero tangential velocity along the contour of the porous cavity.

The thermal Dirichlet condition \(\theta =0\) comes first in the developing of this DN model, and it implies that the temperature field has a strictly linear variation in the vertical direction. One way of approaching this limit under an externally given temperature gradient is to surround the porous cavity with a highly conductive metal grid along its contour, while the porous cavity itself and the saturating fluid have much smaller conductivities. It is important to have a woven metal grid of thin threads and not a solid metal layer surrounding the porous cavity, for leaving the cavity wall open to inflow and outflow.

We will give a physical description of the Neumann flow condition, which is \(\partial \psi /\partial n = 0\), where n is a local coordinate normal to the contour. It can be approximated fairly well by means of a porous medium of much higher permeability surrounding the porous cavity that we consider. Here, we take advantage of the thermal condition \(\theta =0\), since it removes buoyancy from any particle intruding the porous cavity from outside, ensuring that the flow condition is a purely mechanical condition. The essential absence of buoyancy in the surrounding fluid is important for its pressure distribution, which can be considered as hydrostatic with vanishing perturbation pressure \((p=0)\) along the contour of the porous cavity.

The thermal condition \((\theta =0)\) of a conducting boundary is shared with the DD model (Rees and Tyvand 2004). Buoyancy along the cylinder wall vanishes with zero perturbation temperature there. We need to reconsider Darcy’s law Eq. (10), where we introduce the pressure perturbation p and the temperature perturbation \(\theta\)

$$\begin{aligned} {\mathbf {v}}+\nabla p - \sqrt{R}\,\theta \mathbf {k}=0. \end{aligned}$$
(29)

We define a tangential unit vector \(\mathbf {\tau }\) along the cavity contour by \(\mathbf {\tau } = \mathbf {n} \times \mathbf {j}\), where \(\mathbf {j}\) is a unit vector perpendicular to the vertical x, z plane. We take the scalar product of Darcy’s law and \(\mathbf {\tau }\) and evaluate it along the cavity contour, giving

$$\begin{aligned} \mathbf {\tau } \cdot ({\mathbf {v}} + \nabla p) = \mathbf {\tau } \cdot {\mathbf {v}} = \mathbf {\tau } \cdot (\mathbf {\tau } \times \nabla \psi ) = \mathbf {j} (\mathbf {n} \cdot \nabla \psi ) = 0 \;\hbox {at the boundary}, \end{aligned}$$
(30)

where the buoyancy term is neglected because it is identically zero at this conducting boundary. The pressure perturbation is zero along the cavity contour, because of the approximately stagnant fluid outside the cavity, without buoyancy and with negligible pressure perturbation. Hereby we have the full boundary conditions for the DN model

$$\begin{aligned} \theta = \mathbf {n} \cdot \nabla \psi = 0 \;\;\hbox {at the boundary}, \end{aligned}$$
(31)

which includes the Neumann condition for the streamfunction along the open conducting boundary.

The boundary conditions of our DN model overlap with the open and conducting cylinder wall conditions studied by Barletta and Storesletten (2015).

3.3 ND Model: Neumann Condition for \(\theta\) and Dirichlet Condition for \(\psi\)

The ND problem is a counterpart to the present DN model, with interchanged Dirichlet and Neumann conditions for \(\theta\) and \(\psi\). The impermeable cylinder wall is assumed having a given normal derivative of temperature \(\mathbf {n} \cdot \nabla T_\mathrm{b} = - \mathbf {n} \cdot \mathbf {k}\) so that the perturbation temperature has zero normal derivative

$$\begin{aligned} \mathbf {n} \cdot \nabla \theta = \psi = 0, \;\hbox {at the boundary}. \end{aligned}$$
(32)

One illustrative computation for this ND model will be given in “Appendix”.

3.4 NN Model: Neumann Conditions for \(\theta\) and \(\psi\)

The case with Neumann conditions for both the temperature perturbation and the streamfunctions is of mathematical interest. It contrasts the DD model (Rees and Tyvand 2004), yet with the same symmetry between \(\theta\) and \(\Psi\). We omit calculations for this NN model, because it is physically artificial, at best. The buoyancy term in Darcy’s law will be nonzero along the boundary, which is inconsistent with an open-wall condition of zero tangential velocity.

4 Eigenfunctions at Marginal Stability

The coupled governing equations are

$$\begin{aligned} \nabla ^2 \theta - \sqrt{R} \frac{\partial \psi }{\partial x} = 0,\quad \nabla ^2 \psi + \sqrt{R} \frac{\partial \theta }{\partial x} = 0. \end{aligned}$$
(33)

The pressure eigenfunction p(x, z) obeys the Poisson equation

$$\begin{aligned} \nabla ^2 p = \sqrt{R} \frac{\partial \theta }{\partial z}, \end{aligned}$$
(34)

following from the divergence of Darcy’s law (5). The pressure perturbation will be computed after the temperature field has been determined. The DN model has the boundary conditions

$$\begin{aligned} \theta = \frac{\partial \psi }{\partial n} = 0, \;\hbox {at the boundary}, \end{aligned}$$
(35)

where \(\partial /\partial n = \mathbf {n} \cdot \nabla\). The pressure obeys a Dirichlet open-wall condition

$$\begin{aligned} p = 0,\;\hbox {at the boundary}. \end{aligned}$$
(36)

The dynamic condition of zero perturbation pressure (36) leads to the flow condition in (35). The perturbation isobars form closed cells inside the cavity.

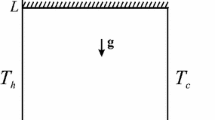
Figure 1 gives a definition sketch for the coupled thermomechanical eigenvalue problem with boundary conditions for \(\theta (x,z)\) and \(\psi (x,z)\). The associated problem for the pressure perturbation p(x, z) is sketched, taking the Rayleigh number R from the numerical solution for the eigenfunctions \(\theta (x,z)\) and \(\psi (x,z)\).

Fig. 1
figure 1

Sketch of the two-dimensional eigenvalue problem in the vertical plane, including streamfunction, thermal eigenfunction, and pressure eigenfunction. The governing equations and the homogeneous boundary conditions along the boundary of the cavity are given

Full size image

4.1 On Solving the Eigenvalue Problem

We will perform numerical calculations for different classes of geometries, using the commercial software Comsol Multiphysics. In each case, we make a choice of length unit, which enters the definition of the Rayleigh number. The present work is comparable with the DD model (Rees and Tyvand 2004). Our DN model differs from the DD model only by our Neumann boundary condition for the streamfunction. The DD model (Rees and Tyvand 2004) gives a critical Rayleigh number that is independent of the orientation of the cavity, while our DN model will have an onset criterion that depends on the orientation of a given cavity.

5 Rectangular Cavities

Our calculations start with rectangular cavities. We introduce a tilt angle \(\phi\) for the rectangle. It is the angle between the horizontal x axis and the side of the rectangle with dimensionless length L (aspect ratio). The other side of the rectangle has unit length, by definition.

5.1 The Analytical Solution

We have an analytical solution for a porous rectangle of unit height in the vertical direction, with horizontal extent L (the aspect ratio). Nield (1968) solved this problem for an infinite horizontal layer. A more general model (Barletta et al. 2015) with the parameters \(a_{1,2}\) and \(b_{1,2}\) includes the present boundary conditions as the parameter choices \(a_1 = a_2 = 0,b_1 = b_2 = \infty\) (with notation borrowed from Barletta et al. (2015)). The resulting dispersion relation from Barletta et al. (2015) is

$$\begin{aligned} (\eta ^2 - \chi ^2) \sinh \chi \sin \eta + 2 \chi \eta (1 - \cosh \chi \cos \eta ) = 0. \end{aligned}$$
(37)

The functional relationship between R and k is expressed by two auxiliary functions \(\eta (k,R)\) and \(\chi (k,R)\) defined as

$$\begin{aligned} \eta = \sqrt{k (\sqrt{R} - k)},\quad \chi = \sqrt{k (\sqrt{R} + k)}. \end{aligned}$$
(38)

Our dispersion relation follows Nield (1968) but is restricted to a discrete spectrum for the wavenumber k

$$\begin{aligned} k = k_n = n \frac{\pi }{L}, \end{aligned}$$
(39)

where n is a positive integer.

5.2 A Unit Square Cavity

Our numerical results for rectangular cavities start with the unit square (\(L=1\)). In Fig. 2, we display the preferred thermomechanical eigenfunctions for an upright square at marginal stability. Inserting \(k=\pi\) into the analytical dispersion relation (37), we check the Rayleigh number computed in Fig. 2, with good agreement. Figure 2 includes the associated isobars. Higher modes are not displayed because their shapes are similar to the preferred mode. There is zero perturbation pressure in the center of the square \((z=1/2)\), where the flow is vertical, and the temperature has a maximum.

Fig. 2
figure 2

Plots for the preferred thermomechanical eigenfunctions (left plot) and an isobar plot for the perturbation pressure (right plot) of an upright square. The isotherms are colored as red (positive) and blue (negative), with black contours. The associated streamlines are shown in yellow. Positive perturbation pressure shown in red color, while negative perturbation pressure is blue. The ratio \(|w|_\mathrm{max}/|\theta |_\mathrm{max}\) is 3.6066. The critical Rayleigh number is \(R = 22.946\)

Full size image
Fig. 3
figure 3

Plots for the eigenfunctions of a tilted square, where the tilt angle varies as follows: \(\phi =\pi /12\) (left), \(\phi =\pi /6\) (middle), \(\phi =\pi /4\) (right). The upper row shows the isotherms colored as red (positive) with black contours, and the associated streamlines are yellow lines. The lower row shows the isobars for the pressure perturbation. Only the preferred mode with the lowest Rayleigh number is displayed in each case. For the preferred eigenfunction, the ratio \(|w|_\mathrm{max}/|\theta |_\mathrm{max}\) is 3.6081 for \(\phi =\pi /12\), 3.6141 for \(\phi =\pi /6\), 3.6166 for \(\phi =\pi /4\)

Full size image

Figure 3 shows results for a tilted square, with the choices \(\phi =\pi /12\), \(\phi =\pi /6\) and \(\phi =\pi /4\) for the tilt angle. The upper row in Fig. 3 shows the isotherms and streamlines for these three slope angles, while the lower row shows the associated isobars for the same three tilt angles. Note that the cases \(\phi =\pi /3\) and \(\phi =5\pi /12\) are also represented in Fig. 3, because of the symmetry of the square. Analytical results are not available for the tilted square. The shape of the eigenfunctions changes very much with the tilt angle, while the variations in the critical Rayleigh number are small. The streamlines must be perpendicular to the sides of the square. The only exceptions are the streamlines that meet the four corners, making an angle of \(\pi /4\) with each of the sides that meet in a corner. Figure 3 shows that the preferred mode has only one flow cell, while there are two pressure cells in height. The strong buoyancy in the middle of the thermal cell corresponds to an opposing pressure force. The pressure gradient must force the fluid both into the porous cavity and out of it because there is no buoyancy at the conducting boundary where \(\theta =0\). It is interesting that the central dividing isobar with zero pressure is almost horizontal in all cases, and it should be exactly horizontal for the symmetric geometry of \(\phi =\pi /4\).

Figure 4 shows the Rayleigh number at marginal stability as a function of the tilt angle \(\phi\) for the four lowest modes of a porous square. We cover the full range \(0<\phi <\pi /2\) and observe the expected symmetry of \(R(\phi )\) number around \(\phi =\pi /4\). The three lowest eigenvalues show almost sinusoidal variation with the tilt angle, but we note that the second eigenvalue is exceptional with its local maximum for \(\phi =\pi /4\). The fourth eigenvalue for R has a different variation with two peaks that are displaced away from \(\phi =0\) and \(\phi =\pi /2\). In Fig. 4, the calculated Rayleigh numbers for \(\phi =0\) again show excellent agreement with the analytical results from the dispersion relation (37).

The ratio between the maximal vertical velocity and the maximal temperature is provided in Figs. 3 and 4. It varies only slightly with the tilt and is around 3.6. This ratio may be interpreted as a substitute for a wave number in a fourth-order problem that does not possess a wave number.

Fig. 4
figure 4

Plots for R (the Rayleigh number eigenvalues) of a tilted square as functions of the tilt angle (\(\phi\)). The four lowest eigenvalues are represented. The four values for \(\phi = 0\) are found analytically by inserting \(k=\pi , k = \pi /2, k = \pi /3\) and \(k=\pi /4\) in the dispersion relation (37)

Full size image
Fig. 5
figure 5

Plots for the preferred eigenfunctions of a tilted rectangle with aspect ratio \(L=3\). The following values of the slope angle \(\phi\) are represented: \(\pi /8\), \(\pi /4\), \(3 \pi /8\). Upper row shows isotherms colored as red (positive) and blue (negative), with black contours, and streamlines depicted in yellow. Lower row shows isobars

Full size image
Fig. 6
figure 6

Plots for the three lowest eigenfunctions of a tilted rectangle with aspect ratio \(L=3\), with tilt angle \(\phi = \pi /4\). Upper row shows isotherms colored as red (positive) and blue (negative), with black contours, and streamlines depicted in yellow. Lower row shows isobars

Full size image
Fig. 7
figure 7

Plots of the Rayleigh number (R) for a porous rectangle as a function of tilt angle with aspect ratio \(L=2\), \(L=3\) and \(L=10\), respectively

Full size image

5.3 Tilted Rectangular Cavities

The upright rectangular cavity (\(\phi =0\)) has already been studied analytically. We will now investigate how the marginal stability depends on the aspect ratio L and the tilt angle \(\phi\). We choose the unit length as the shorter side of the rectangle, without loss of generality, covering the entire range of variation for the tilt angle (\(0<\phi <\pi /2\)). By definition, we thus take \(L\ge 1\), so that the longer side of the rectangle has the aspect ratio as dimensionless length.

The upper row in Fig. 6 shows the isotherms and streamlines of the preferred eigenfunctions for an aspect ratio of \(L=3\). The displayed slope angles are \(\pi /8\), \(\pi /4\) and \(3\pi /8\). The lower row shows the associated isobars for the pressure perturbation. Figure 6 repeats the case \(L=3\) with a slope angle of \(\pi /4\), showing the three lowest eigenfunctions. The internal cell walls for second and third eigenfunction in Fig. 7 are interesting, as they are qualitatively different from the DD model (Rees and Tyvand 2004). These internal cell walls are not strictly vertical, neither for the flow nor for the isotherms. The DD model allows only internal cell walls that are exactly vertical. The flow cells in Fig. 6 have no recirculation, but the second and third eigenfunctions have internal cell walls separating domains of purely upwelling throughflow from the domains of purely downwelling throughflow. The pressure cells displayed in the lower rows of Figs. 5 and 6 show great variability of internal cell walls. This is because the eigenfunctions are non-separable spatially in the x and z directions.

Table 1 shows the ratio \(\vert w \vert _\mathrm{max}/\vert \theta \vert _\mathrm{max}\) as a function of the tilt angle for the preferred mode of a rectangle with \(L=3\). These values for a parameter similar to a wave number are smaller than those for \(L=1\).

Table 1 Ratio between \(|w|_\mathrm{max}\) and \(|\theta |_\mathrm{max}\) for the tilted rectangle with aspect ratio \(L=3\) for the preferred eigenfunction, as function of the tilt angle \(\phi\)
Full size table

Figure 7 shows the critical Rayleigh number as a function of the tilt angle \(\phi\) for \(L=2\), \(L=3\) and \(L=10\). We evaluate the dispersion relation \(R(k,L,\phi )\) given by Eq. (37) for \(k=\pi /L\) with zero tilt (\(\phi =0\)), and find

$$\begin{aligned} R(\pi /2,2,0) = 14.7939,~R(\pi /3,3,0) = 13.2479,~R(\pi /10,10,0) = 12.1128, \end{aligned}$$
(40)

in excellent agreement with the numerical values given in Fig. 8. With aspect ratio \(L=10\), the Rayleigh number is already close to the asymptotic limit \(R(0,\infty ,0) = 12\), derived by Nield (1968). Our results agree with his asymptotic limit for the preferred (critical) wave number \(k_c \rightarrow 0\) as \(L \rightarrow \infty\).

The same analytical dispersion relation (37) is valid for \(\phi =\pi /2\), but the definition of the Rayleigh number has to undergo the transformation \(R \rightarrow L^2 R\), since the shorter side of the rectangle is chosen as the length unit instead of the vertical side, which is a choice that we make in order to keep the Rayleigh number definition independent of the tilt angle. Evaluating the dispersion relation (37) under this transformation to make it fit with Fig. 8 gives the results for the critical Rayleigh number

$$\begin{aligned} 4 R\left( 2 \pi ,2,\frac{\pi }{2}\right) = 54.0937,~9 R\left( 3\pi ,3,\frac{\pi }{2}\right) = 13.2479, ~100 R\left( 10\pi ,2,\frac{\pi }{2}\right) = 1005.12, \end{aligned}$$
(41)

and again these analytical results are in excellent agreement with the numerical values given in Fig. 8.

Fig. 8
figure 8

Plots for the three lowest eigenfunctions of a compact porous circle with unity dimensionless radius. Upper row shows isotherms colored as red (positive) and blue (negative), with black contours, and streamlines depicted in yellow. Lower row shows isobars

Full size image
Fig. 9
figure 9

Plots for the preferred eigenfunctions of a porous ellipse (\(L=2\)). Left column shows isotherms colored as red (positive), with black contours, and streamlines depicted in yellow. Right column shows isobars. The ratio between \(|w|_\mathrm{max}\) and \(|\theta |_\mathrm{max}\) is 2.9112, 3.1109 and 3.3170, for \(R=17.07\), \(R=16.42\) and \(R=15.81\), respectively

Full size image

6 Elliptical Cross Sections

We will show some computations for elliptical cross sections.

6.1 The Circle

We start with the simplest case, which is the circle. The radius of the circle is the length unit, represented with dimension as H in the Rayleigh number (8). Its critical Rayleigh number is 6.7301. If we instead choose the diameter as the length scale, the critical Rayleigh number is redefined by multiplication by a factor 4, to become \(R=26.92\). Thereby, we can make a comparison with the classical result \(R=12\) from Nield (1968): It makes sense that the critical Rayleigh number will increase by a factor 2.24 (from 12 to 26.92) when an elliptical cavity changes its horizontal diameter from infinity to one, with vertical unity diameter.

Figure 8 shows the three lowest eigenfunctions for a porous circle, where the isotherms and streamlines are displayed in the upper row and the corresponding isobars in the lower row. We note that the second eigenfunction contains a slender recirculating cell of closed streamlines around the center of the circle. The third eigenfunction contains two such recirculating flow cells. Each closed flow cell ends in a stagnation point at the boundary, where the velocity is zero. At these stagnation points, the temperature perturbation is zero, and the isobar patterns show that the pressure gradient is also zero. It is consistent that there is no buoyancy force and no pressure force at these stagnation points. The preferred flow of the convection onset has no cell structure, only a throughflow which is vertical in the middle of the circle but must curve toward the circular boundary where the flow is perpendicular to the boundary of the cavity.

6.2 An Ellipse

We choose to compute the ellipse with the ratio \(L=2\) between the semi-axes. Figure 9 displays the preferred mode at the onset of convection, with the tilt angles \(\phi =0\), \(\phi =\pi /4\), \(\phi =\pi /2\). The variation of the critical Rayleigh number with the tilt angle is similar to the rectangle studied above. The upright ellipse (\(\phi =\pi /2\)) has a critical Rayleigh number of order 10 % lower than the lying ellipse (\(\phi =0\)).

These computations for the DN model are to be compared with “Appendix” where we have made the same computations for the ND model.

7 Discussion and Concluding Remarks

This paper deals with the fourth-order Darcy–Bénard eigenvalue problem, which is of basic interest in mathematical physics. We study the onset of thermal convection in two-dimensional porous cavities, where the cavity boundary is open to flow at hydrostatic pressure, while it is thermally conducting. With upright rectangles as the only exception, no closed-form analytical solutions are known. The eigenvalue problem is solved by the finite element method.

The present problem is complicated for all porous cavities, where the homogeneous boundary conditions are uniform along the contour of the cavity. This is because the problem is a genuinely fourth-order problem, where the variables cannot be separated in space. The only exception is the two-dimensional cavities with the double Dirichlet condition of zero perturbation temperature at an impermeable boundary (Rees and Tyvand 2004). It obeys the second-order Helmholtz equation after a horizontal Fourier component that takes care of the cell wall structure has been separated out.

For any curved cavity contour that does not obey the double Dirichlet condition, the temperature field and flow field will be coupled so strongly together that they form non-normal modes (Tyvand et al. 2019). Weak singularities may be identified for non-normal modes in rectangular cavities. The present non-normal modes with curved boundary will have no singularities, so they are uniformly valid solutions. In the absence of sharp corners, non-normal mode analytical solutions can possibly be developed in terms of power series, but they will converge slowly. In fact, this has already been demonstrated by Storesletten and Tveitereid (1991). Their fully 3D onset problem for a horizontal porous cylinder is of the non-normal mode type in the vertical plane. The convergence of their numerical method was sufficient for the critical Rayleigh number, but not for the cell pattern. This was revealed by their calculations for the 2D case, where they found that anti-symmetric modes have curved cell walls. It was disproved by the exact analytical solution by Rees and Tyvand (2004), who demonstrated that the 2D model with double Dirichlet conditions has strictly vertical cell walls between any two neighboring thermal cells or flow cells within the porous cavity.

The degeneracy of the 2D cavity problem with double Dirichlet condition is mathematically subtle. It represents a vulnerable physical modeling, where any 3D effect or Robin-type correction of a Dirichlet condition will ruin the degeneracy and turn both eigenfunctions into non-normal mode type. In an experiment for the onset of convection in porous cavities, one will, therefore, never see strictly vertical cell walls. The strong thermomechanical couplings of non-normal modes will overrule the mathematical degeneracy and make all internal cell walls curved unless they are lines of geometric symmetry.

The wavenumber parameter in normal mode solutions loosens the physical couplings between the eigenfunctions. The thermal field and the flow field can then be formulated more independently of one another, as some of the boundary conditions are trivially satisfied with normal modes. The non-normal modes of our present problem do not have a wavenumber parameter. It is an advantage to come up with alternative parameters for understanding the denser couplings of the non-separable thermomechanical fields. In the present paper, we suggest a new scaling of the Darcy–Boussinesq equations, where we introduce a buoyancy scale for the velocity. Thereby, we are able to make a physically relevant comparison between velocity amplitude and temperature amplitude.

While the appropriate scaling of velocity is a well-known theme for nonlinear convection, it seems to have been overlooked in the linear theory of convection onset. Our peculiar scaling lets the square root of the Rayleigh number represent both the buoyancy term in Darcy’s law, as well as the convective term in the heat equation. This scaling yields a balanced weighting of the two driving mechanisms for the linearized theory of convection onset. We test its relevance by computing the dimensionless amplitude ratio between the maximal vertical velocity versus the maximal perturbation temperature. This ratio equals the horizontal wavenumber in the DD model (Rees and Tyvand 2004).

The DD model and the present DN model represent two limiting cases for a two-dimensional porous cavity of permeability K, surrounded by a porous medium with a different permeability \(K_\mathrm{external}\). The DD model represents the asymptotic limit \(K_\mathrm{external}/K \rightarrow 0\), while the present model represents the asymptotic limit \(K_\mathrm{external}/K \rightarrow \infty\). In neither of these limiting cases, we need to consider the thermomechanical field outside the cavity. This is because the temperature field outside the cavity is annihilated due to the thermal Dirichlet condition, which removes the buoyancy of any fluid particle that passes through the contour of the cavity.

The classical result for a layer of infinite extent with the present set of boundary conditions was found by Nield (1968). The critical Rayleigh number is \(R_\mathrm{c}=12\), with zero wavenumber for the preferred mode. This shows that the preferred flow does not form closed recirculating cells because the open-wall condition promotes throughflow through the porous cavity, and we confirm that this is also true for finite cavities.

The enhanced physical realism in the present model compared with conventional models is best illustrated in the plots of flow cells versus thermal cells. A full fourth-order model with boundary conditions that are sufficiently rich physically and mathematically independent, will have curved cell walls for its onset modes, as illustrated in a recent paper (Tyvand et al. 2019). The flow cell structure is absent in the preferred throughflow mode, and there is only a single thermal cell and a double pressure cell. Nevertheless, curved cell walls are abundant in higher onset modes for our model, which we demonstrate for a circular cavity, included in Fig. 8.

We will now discuss how the critical Rayleigh number \(R_\mathrm{c}\) increases when a finite porous enclosure is obtained by gradually constricting starting from an unlimited horizontal layer. We keep the same vertical length scale, and we keep the present DN boundary conditions. Our model yields, \(R_\mathrm{c} = 12\), for an unlimited horizontal porous layer (Nield 1968). When we restrict the porous cavity to a square of unit height, the porous medium is stabilized so that the new onset criterion is, \(R_\mathrm{c} = 22.95\), which increases the critical Rayleigh number by a factor of 1.91 compared with the classical value of 12 found by Nield (1968). If we reduce the size of the cavity further and replace the unit square with a circle of unit diameter, the onset criterion is, \(R_\mathrm{c} = 26.92\), increasing the Rayleigh number by a factor of 2.24 compared with the criterion from Nield.

We make the following similar comparisons for the DD model (Rees and Tyvand 2004). One starts with a porous layer of infinite horizontal extent and constrict the flow domain gradually. The infinitely wide layer has a critical Rayleigh number, \(R_\mathrm{c} = 4 \pi ^2\) (Horton and Rogers 1945; Lapwood 1948). Accordingly, the value for a square is found to be \(R_\mathrm{c} = 8 \pi ^2\) (Nilsen and Storesletten 1990). It yields a remarkable stabilization by the exact factor of 2, slightly above the factor of 1.91 in our present DN model. Moreover, a circle has the critical Rayleigh number of \(R_\mathrm{c} = 92.53\) (Rees and Tyvand 2004; Storesletten and Tveitereid 1991). This onset criterion yields a stabilization by a factor 2.34, compared with the classical result of \(4 \pi ^2\). This is again close to the similar stabilization factor of 2.24 for the present DN model.

Finally, with the present paper, there is now a mature understanding of convection onset in two-dimensional porous cavities with Dirichlet or Neumann conditions.