Abstract
Turbulence transportation across permeable interfaces is investigated using direct numerical simulation, and the connection between the turbulent surface flow and the pore flow is explored. The porous media domain is constructed with an in-line arranged circular cylinder array. The effects of Reynolds number and porosity are also investigated by comparing cases with two Reynolds numbers (\(Re\approx 3000,6000\)) and two porosities (\(\varphi =0.5,0.8\)). It was found that the change of porosity leads to the variation of flow motions near the interface region, which further affect turbulence transportation below the interface. The turbulent kinetic energy (TKE) budget shows that turbulent diffusion and pressure transportation work as energy sink and source alternatively, which suggests a possible route for turbulence transferring into porous region. Further analysis on the spectral TKE budget reveals the role of modes of different wavelengths. A major finding is that mean convection not only affects the distribution of TKE in spatial space, but also in scale space. The permeability of the wall also have an major impact on the occurrence ratio between blow and suction events as well as their corresponding flow structures, which can be related to the change of the Kármán constant of the mean velocity profile.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Turbulent shear flows bounded by porous materials are encountered in various engineering applications such as transpiration cooling and additive manufacturing (3D printing). The success of additive manufacturing encourages the use of porous walls to achieve various flow control purposes. Understanding and manipulating the influence of the porous characteristics (e.g., morphology, topology) on turbulence owns strong significance in industry (Bottaro 2019), serving for drag reduction (Gómez-de Segura and García-Mayoral 2019; Li et al. 2020), enhanced heat transfer and mixing. Recent experiences show that as a high-fidelity numerical method, direct numerical simulation (DNS) enables microscopic visualization and analysis (Jin et al. 2015; Jin and Kuznetsov 2017; Chu et al. 2018, 2019, 2020; He et al. 2018; Wood et al. 2020) in porous media, which is hardly achievable within experiments in such confined and tortuous spaces.
Existing experiments provide information about the optically accessible areas. The modulation of turbulence by a permeable surface has been confirmed in experiments with different configurations, such as turbulent open channel flows over porous media composed of spheres. Suga et al. (2017) investigated spanwise turbulence structures over permeable walls by using particle image velocimetry (PIV) measurements. Three different kinds of anisotropic porous media are constructed to form a permeable bottom wall of a channel. Their wall permeability tensor is designed to own a larger wall-normal diagonal component (wall-normal permeability) than the other components and the spanwise turbulent structures are investigated. However, because of the difficulty in performing measurements inside the narrow and tortuous space, it is generally not easy to perform high-resolution measurement inside porous media (Kuwata and Suga 2016). Efstathiou and Luhar (2018) designed a boundary layer experiment over high-porosity foams (\(\varphi =0.97\)), where the friction Reynolds number upstream of the porous section was \(Re_{\tau }\approx 1960\). Mean statistics showed the presence of a substantial slip velocity at the porous interface (\(>30\%\) mean velocity). While the magnitude of the mean velocity deficit increased with average pore size, the slip velocity remained approximately constant. Terzis et al. (2019) examined experimentally the hydrodynamic interaction between a regular porous medium and an adjacent free-flow channel at low Reynolds numbers. In their study, the porous medium consisted of evenly spaced micro-structured rectangular pillars arranged in a uniform pattern, which enabled a direct measurement of the flow inside the porous structure. Guo et al. (2020) investigate the velocity distribution for a high Reynolds number above and the inside porous media. A visual flume test bench is built to simulate porous media as an accumulation of spherical glass beads. They found that the thickness of the transition layer in the porous-medium region is not sensitive to changes in the Reynolds number increases with the growing porosity.
Direct numerical simulation (DNS) exhibits an edge of observing and analyzing turbulent physics in a confined small space, such as turbulent flow inside a representative elementary volume (REV) of a porous medium (Chu et al. 2018, 2019; He et al. 2018). However, an adequate resolving of the smallest length scales of the flow in the interface region requires enormous computational resources. To limit the computational costs, appropriate modeling instead of direct resolving must be used in early years. Jimenez et al. (2001) belong to one of the pioneers to perform DNS with a special boundary condition: They identified no-slip boundary conditions for streamwise and spanwise velocities and set the wall-normal velocity for the permeable wall to be proportional to the local pressure fluctuations. The friction is increased by up to \(40\%\) over the walls, which was associated with the presence of large spanwise rollers.
Another approach is to describe the flow inside the porous structure with the volume-averaged Navier–Stokes (VANS) equations (Whitaker 2013) and to couple them with the Navier–Stokes equations used for the free flow. Breugem and Boersma (2005) are one of the first to utilize this method. They found a decrease in the peak value of the streamwise turbulence intensity normalized by the friction velocity at the permeable wall and an increase in the peak values of the spanwise and wall-normal ones. This can be explained by large scale spanwise rollers originated from Kelvin–Helmholtz instability near a highly permeable wall. This process exhibits a significant contribution to the Reynolds-shear stress and leads therefore to a large increase in the skin friction, which is supported by the recent research of (Manes et al. 2011; Kim et al. 2018, 2020). Rosti et al. (2018) explored the potential of drag reduction by porous materials. They systematically adjusted the permeability tensor on the walls of a turbulent channel flow via VANS-DNS coupling. The total drag could be either reduced or increased by more than 20\(\%\) through adjusting directional properties of the permeability. Configuring the permeability in the vertical direction lower than the one in the wall-parallel planes led to significant streaky turbulent structures (quasi 1-dimensional turbulence) and hence achieved a drag reduction. Recent studies achieved to resolve the porous media structures coupled with turbulent flows despite of its enormous computational costs. Kuwata and Suga (2016) used a Lattice-Boltzmann method (LBM) to resolve the porous structures coupled with turbulent flows. The porous media is composed with interconnected staggered cube arrays. The difference between a rough wall and a permeable wall is elucidated that turbulence is more isotropic near the porous wall due to the significant re-distribution effect of pressure fluctuation.
Despite numerous works have been conducted regarding flows over porous media, there are still a lot of open questions. The mechanism of turbulence transportation across the interface is still not fully understood, and the role of turbulent flow motions of different scales in the transportation process is rarely inspected. The current study is intended to explore the process of turbulence transportation in both spatial and spectral domain with the interface-resolved DNS, which provides an adequate resolution of the flow field between the porous structure and the free-flow. The purpose is to find the physical links between the geometrical feature of the porous media and the characteristics of the turbulence transfer process at the permeable interface, which helps the design of porous structures that generate specific flow properties. The turbulent statistics acquired here can be also used to support different levels of modeling like large-eddy-simulation (LES), Reynolds-averaged-Navier–Stokes (RANS) (Weihaupt et al. 2019; Yang et al. 2018, 2019) modelling or modal-based reduced order modeling (Wang et al. 2018, 2019a, 2019b). In the following, Sect. 2 will describe the numerical setup of the DNS cases. Section 3 introduces the basic statistics of the flow fields. Section 4 presents the TKE budget near the interface in both spatial and spectral domain, where the turbulence transportation process is thoroughly explored. Section 5 is devoted to the analysis of the instantaneous fluid exchanging motions at the interface, i.e., blow and suctions events, which explains the variation of mean statistics with porosity. A conclusive remark will be given in Sect. 6.
2 Numerical Method
2.1 Simulation Method
The three-dimensional incompressible Navier–Stokes equations, given by Eqn. 1 and Eqn. 2, are solved in non-dimensional form, where \(\Pi\) is the corresponding source term in the momentum equation to maintain a constant pressure gradient in the flow direction.
The spectral/hp element solver Nektar++ (Cantwell et al. 2011, 2015; Pandey et al. 2020) is used to numerically resolve the complex geometrical structures. The solver framework allows arbitrary-order spectral/hp element discretizations with hybrid shaped elements. Both modal and nodal polynomial functions are available for the high-order representation. The spectral-accurate discretization combined with meshing flexibility is optimal to deal with complex porous structures and to resolve the interface region. The time-stepping is treated with a second-order mixed implicit-explicit (IMEX) scheme. The fixed time step is defined with \(\Delta T/(h/U_b)=0.0005-0.001\), where h is the half width of free flow channel and \(U_b\) is the averaged bulk velocity in the channel flow. A total of 10 flow through time is used for developing the flow and another 5 flow through times to collect statistics.
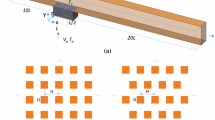
In the following discussion, the velocity components in the streamwise x-, wall normal y- and spanwise z-directions are denoted as u, v and w, respectively. Fig. 1 illustrates a two-dimensional \(x-y\) sketch of the simulation domain, where the dimensions are normalized by half height H of the computational domain. The domain size \(L_x \times L_y \times L_z\) is \(100 \times 20 \times 8\pi\), where the lower half \(-10< y < 0\) is the porous media domain and the upper half \(0< y < 10\) is the free-flow channel. The porous media layer consists of circular cylinders arranged in-line. The porous layer consists of 50 cylinder elements in streamwise direction and 5 elements in wall-normal direction, which gives 250 elements in total. The distance D between two cylinders is fixed at \(L_x/50=2\) in all cases. Two cylinder diameters \(D_c=1.6\) and \(D_c=1\) are given, corresponding to porosity \(\varphi =0.5\) and 0.8, respectively, which is defined by the ratio of the void volume \(V_{V}\) to the total volume \(V_{T}\) of the porous structure. A no-slip boundary condition is defined for all surfaces of the porous structure (e.g., on the surfaces of the circular cylinders) as well as for the upper wall (\(y=10\)) and for the lower wall (\(y=-10\)). Periodic boundary conditions are defined in x-direction between \(x=0\) and \(x=100\). The second pair of periodicity is defined in the spanwise direction \(z=0\) and \(z=8\pi\).
The geometry is discretized with full quadrilateral elements on the \(x-y\) plane with local refinement near the interface, as shown by an illustration in Fig. 2. The third direction (z-direction) is extended with a Fourier-based spectral method. High-order Lagrange polynomials through the modified base are applied within each elements. The numerical solver enables a flexible non-identical polynomial order based on the conforming elements, which offers enhanced meshing flexibility corresponding to different regimes according to prior knowledge. For instance, the polynomial orders of the elements in different mesh regions can be set as \(P=7\) in \(\Omega _1\), \(P=7\) in \(\Omega _2\) and \(P=3\) in \(\Omega _3\) (Fig. 2), corresponding to the channel, interface region and laminar porous media flow region.
2.2 Simulation Conditions
The characteristic parameters of the boundary layer for all simulation cases are summarized in Table 1. Four cases are introduced here covering two porosities and two Reynolds numbers. Cases with low and high porosity regions are differentiated with A and B in the case name, and the following number indicates the change of viscosity, hence the Reynolds number. The bulk Reynolds number in the channel flow is defined using the bulk averaged velocity \(U_b\), channel half height \(h=5\) and kinematic viscosity \(\nu\), i.e., \(Re=U_b h/\nu\). The Reynolds number based on friction velocity is defined as \(Re_\tau ^t = u_\tau ^t \delta ^t/\nu\) and \(Re_\tau ^p = u_\tau ^p \delta ^p/\nu\), where \(u_\tau\) is the friction velocity, i.e., \(u_\tau =\sqrt{\vert \tau _w \vert /\rho }\), and the superscripts t and p refer to the evaluation at the top wall and permeable wall of the channel, respectively. \(\delta ^t\) and \(\delta ^p\) denote the thickness of the boundary layers, and the border of them corresponds to the location of the maximum mean streamwise velocity.
An arbitrary instantaneous flow variable \(\phi\) can be decomposed as follows:
Equation 3 is Reynolds decomposition where the over bar \({\overline{\cdot }}\) denotes temporal average, i.e., \({{\overline{\phi }}}=1/T\int _{0}^T\phi \mathrm {d}t\), and the prime denotes the instantaneous turbulent fluctuation. Eqn. 4 is the double-averaging decomposition, where the brackets \(\langle \cdot \rangle\) indicate intrinsic spatial average on a wall-parallel plane, which is defined as \(\langle \phi \rangle =1/A_f \int _{A_f}\phi \mathrm {d}A\), \(A_f\) being the fluid occupied area, and \({{\tilde{\phi }}}={\overline{\phi }}-\langle {\overline{\phi }} \rangle\) is the form-induced fluctuation. The spatial averaging can also be carried out as \(\langle \phi \rangle _s=1/A_0 \int _{A_f}\phi \mathrm {d}A\), which is termed superficial area averaging, where \(A_0\) is the total area of fluid and solid.
From the time-averaged and \(x-z\) plane averaged momentum equation, the total shear stress can be written as:
where \(U=\langle {\overline{u}} \rangle\) is the mean streamwise velocity (Suga et al. 2020). At the top non-permeable wall, Eqn. 5 can be simplified as \(\tau _{xy}^t=\mu {\partial U} / {\partial y}\), which is identical with the canonical turbulent channel flow, and the friction velocity can be obtained with \(u_\tau ^t=\sqrt{\tau _{xy}^t}/\rho\) . Close to the permeable wall, and geometry of pores leads to spatial heterogeneity of time-averaged variables, so the dispersion stress \(\langle { {{\tilde{u}}} {{\tilde{v}}}}\rangle\) is non-zero. The total shear stress \(\tau _{xy}^p\) and friction velocity \(u_\tau ^p=\sqrt{\tau _{xy}^p}/\rho\) are measured at the crest height.
The non-dimensional mesh size in each direction \(\Delta x\), \(\Delta y\) and \(\Delta z\) is given in Table 2. The superscripts \((\cdot )^{p+}\) and \((\cdot )^{t+}\) represent variables scaled by \(\nu /u_\tau ^p\) and \(\nu /u_\tau ^t\), respectively. For instance, \(\Delta x^{t+}=\Delta x u_{\tau }^t/\nu\). The total mesh resolution ranges from \(98\times 10^6\) (case B1) to \(485\times 10^6\) for the high Reynolds number condition (case A2). On the top smooth side, the streamwise cell size ranges from \(6.3\le \Delta x^{t+}\le 9.0\), where the spanwise cell size is kept constant at \(\Delta x^{t+}=4.9\). This resolution is comparable with other DNS of channel flow (Lee and Moser 2019). On the porous media side, the spanwise resolution \(\Delta z^{p+}\) is decreased due to the higher \(u_{\tau }^p\) as given in Table 1. The resolution in the other directions \(\Delta x^{p+}\) and \(\Delta y^{p+}\) is, however, enhanced by local mesh refinement (Fig. 2), specially the streamwise one (\(2.2\le \Delta x^{p+}\le 3.5\)).
3 Basic Properties of the Flow Fields
3.1 Mean Statistics and Fluctuation
In this section, the mean statistics of different cases will be compared to understand the effect of interface characteristics and Reynolds number.
Fig. 3 shows the mean streamwise velocity U profiles, where \(U=\langle {{\overline{u}}} \rangle\). The inner-scaled \(U^+\) profiles of both sides are compared in Fig. 3a, which are normalized by friction velocities of the porous wall \(u_\tau ^p\) or top wall \(u_\tau ^t\), correspondingly. All the velocity profiles on the smooth top wall (dashed lines) follow the linear and log law fairly well regardless their difference in porosities and Reynolds numbers, which indicates a marginal influence of the porous media on this side. On the other hand, the velocity profiles above the permeable wall differ significantly from the canonical boundary layer profiles. The \(U^+\) profiles of the porous media side are much lower than the smooth wall side, owing to the increase in the friction velocity \(u_\tau ^p\). Moreover, the friction velocity \(u_\tau ^p\) shows an increase around \(32\%\) from low porosity cases (A1 and A2) to the high porosity ones (B1 and B2), resulting in a much lower magnitude of \(U^+\) for the latter.
It is also noted that the slope of the logarithmic region is severely changed for the permeable side. To illustrate this more clearly, Fig. 4 shows the log-law diagnose function, \(\Xi =(y+d)^+\mathrm {d}U^+/\mathrm {d}y^+\), whose constancy implies the presence of a logarithmic layer in the mean velocity profile (Pirozzoli 2014). The location of the zero-plane displacement, d, and the von Kármán constant \(\kappa\) of the wall-bounded flow is determined by fitting U(y) profile to the logarithmic law,
where B is the intercept of the logarithmic profile. The diagnose function \(\Xi\) above the smooth wall meet with the canonical value of \(1/\kappa =1/0.4\) in the region \(y^+\approx 50-100\) for the low porosity cases (A1 and A2), Fig. 4a. The logarithmic region for case B1 and B2 is not wide enough to execute the fitting process due to their very low Reynolds number. As to the permeable wall side, the fitted value of \(\kappa\) is 0.26 and 0.32 for cases A1 and A2, respectively, which is smaller than that of the impermeable wall. This result is consistent with previous works (Breugem and Boersma 2005; Kuwata and Suga 2016). In contrast, for cases B1 and B2, the value of \(\kappa\) is much higher than 0.4 for the smooth wall. This is rarely seen in previous studies, but can be related to the work of Kametani and Fukagata (2011) where they found that \(\kappa\) increases with the strength of suction on the wall. It is reasonable to infer that suction motion might dominate the momentum exchange at the interface for cases B1 and B2. This conjecture will be verified in the later discussion in Sect. 5.
The velocity profiles \(U^{t+}\) in the entire domain are shown in Fig. 3b, which are normalized by the friction velocity of the smooth wall side \(u_\tau ^t\). There are several important differences between the low and the high porosity cases. First, the thickness of the boundary layer is larger for walls with higher permeability, indicating a larger impact area in the channel. Second, the velocity within the porous media increases with porosity \(\varphi\). Third, the velocity in the vicinity of the interface is negative with a small value for cases A1 and A2, which is related to the recirculation region between the cylinders. In contrast, the velocity above the smaller cylinders (cases B1 and B2) is monotonic, indicating an absence of such a rotational region. This will be more clearly shown in the later discussion. Increasing the Reynolds number, the magnitude of the \(U^{t+}\) within the porous media is enhanced, which may indicate more active momentum exchange near the interface.
Mean streamwise velocity profiles U. a \(U^+\) profiles above the porous wall and smooth wall. The \(U^+\) profiles are normalized by the friction velocities of their respective side, i.e., \(u^p_\tau\) and \(u^t_\tau\); b \(U^{t+}\) profiles of the whole domain normalized by the friction velocity of the top wall \(u_{\tau }^t\)
The contours of the time averaged velocities \({\overline{u}}\) and \({\overline{v}}\) of the interface region are depicted in Fig. 5. A pair of counter-rotating vortices are observed between two circular cylinders in the low-porosity cases A1 and A2 (Fig. 5a, c), which is absent in the high-porosity cases (Fig. 5b, d). The recirculation induced by the vortices leads to the backflow near the interface of the U profile (Fig. 3b). The upper vortex is driven by the main stream velocity and restricted by the narrow void between cylinders, which results in a classical lid-driven cavity flow here. The upper and lower vortex are separated by the narrow throat between the cylinders, which blocks the convection from below. In comparison, the mean streamwise and vertical velocity within the porous media are higher in case B1 (Fig. 5b) and B2 (Fig. 5d). Between two neighbouring cylinders, a blow event (positive \({\overline{v}}\)) is followed by a suction event (negative \({\overline{v}}\)) in the downstream direction, which exchanges fluid between the interface and positions below the cylinder.
The wall normal variation of turbulent kinetic energy (TKE) and Reynolds shear stress, i.e., \(\langle \overline{u_i^{\prime }u_j^{\prime }} \rangle ^{t+}_s\), are depicted in Fig. 6, which are averaged in \(x-z\) plane and normalized by \(u_{\tau }^t\). Note that the subscript s denotes superficial area averaging (see definition in Sect. 2.2). For the cases studied, all the components of the TKE and the Reynolds shear stress are intensified on the porous media side compared to its counter part of the non-permeable wall, and the high porosity cases (B1, B2) have even higher magnitude than the lower ones. Increasing the Reynolds number results in a further increment of all four Reynolds stress components.
Despite sharing similar features above, the high and low porosity cases show clear differences at the interface and below. For cases A1 and A2, the TKE components approach zero quickly as moving from the permeable interface into the porous media domain, which suggests that disturbances in the free-flow result only in a marginal penetration into the porous media domain. In contrast, turbulent fluctuations are still relatively energetic below the interface for cases B1 and B2. The streamwise component \(\langle \overline{u^{\prime }u^{\prime }} \rangle ^{t+}_s\) shows a periodic distribution in the porous media domain due to the blockage of the cylinders, while the other two components show a smooth descending trend as moving toward the bottom wall. Nevertheless, the Reynolds shear stress \(\langle \overline{u^{\prime }v^{\prime }} \rangle ^{t+}_s\) becomes quite weak below the first row of cylinders for all the cases.
To show the spatial variation of TKE and Reynolds shear stress, contours of \(\overline{u^{\prime }u^{\prime }}\), \(\overline{v^{\prime }v^{\prime }}\), \(\overline{w^{\prime }w^{\prime }}\), \(\overline{u^{\prime }v^{\prime }}\) close to the permeable interface are depicted in Fig. 7. The magnitude of \(\overline{u^{\prime }u^{\prime }}\) fades quickly below the porous bed in all four cases. As for \(\overline{v^{\prime }v^{\prime }}\), \(\overline{w^{\prime }w^{\prime }}\), and \(\overline{u^{\prime }v^{\prime }}\), the momentum flux represented by these terms has a deeper impact region in the high porosity cases. A positive peak of the Reynolds shear stress \(\overline{u^{\prime }v^{\prime }}\) is observed at the impinging position B in all four cases, which differs from the negative Reynolds shear stress above the porous bed. For cases B1 and B2, an area of positive Reynolds shear stress reaches even below the first layer of cylinder. As will be discussed in Sect. 4, these positive \(\overline{u^{\prime }v^{\prime }}\) regions will enhance the energy exchange at the interface region.
Contours of the Reynolds stress components \(\overline{u_i^{\prime }u_j^{\prime } }\). Rows 1-4 are \(\overline{u^{\prime }u^{\prime }}\), \(\overline{v^{\prime }v^{\prime }}\), \(\overline{w^{\prime }w^{\prime }}\), and \(\overline{u^{\prime }v^{\prime }}\), respectively. Column a-d represent cases A1, B1, A2, and B2, respectively. The four positions A, B, C, and D in (c1) indicate the positions of the cylinder array gap, the impinging position (\(45^{\circ }\) upstream), the top of the cylinder, and the separation position (\(45^{\circ }\) downstream), respectively
3.2 Spectral Analysis of Turbulent Kinetic Energy
In addition to the one-point statistics, the porous media may also change the energetic scale in the free flow, which further influences the sustaining process of turbulence. Fig. 8 shows one-dimensional pre-multiplied spectra of turbulent kinetic energy \(k_x{\hat{q}}\)/\(k_z{\hat{q}}\) as a function of the streamwise/spanwise wave lengths \(\lambda _x, \lambda _z\) and wall distance \(y^{t+}\). Here, \({\hat{\cdot }}\) stands for the Fourier coefficients that have been transformed in x- or z-direction. The wave length \(\lambda _x\) and \(\lambda _z\) are normalized with the distance between two cylinders (pore unit length) D. The streamwise spectra are averaged in time and spanwise dimension, while spanwise spectra are averaged in time and streamwise dimension. The spectra above the non-permeable wall are superimposed (as solid lines) on the spectra above of permeable wall (color contour) for comparison.
A series of high-energy spikes are observed in the streamwise spectra of all cases, which are originated from the porous wall and reach as far as \(y^{t+}\approx 60\). The wave length of the spikes feature a series of harmonic waves with a maximal wave length of the pore unit length D, which indicates these spikes stand for the highly regulated fluctuation stemming from the porous units. In addition to the spikes, the remaining of the spectra represents the energy of ‘background’ turbulence. In cases A1 and A2, the peak of the ‘background’ spectra above the porous wall is \(\lambda _x^{t+}\approx 150\) in inner scale at \(y^{t+}\approx 20\), which is slightly smaller than \(\lambda _x^{t+}\approx 200\) of the smooth wall side. In case A2, with higher Reynolds number, there is a strong trend that the peak the ‘background turbulence’ spectra is synchronized with the porous unit spikes. The energy concentrates between \(\lambda _x\approx 2D\) or \(\lambda _x^{t+}\approx 400\) and \(\lambda _x\approx 0.2D\) or \(\lambda _x^{t+}\approx 40\). For the cases B1 and B2, the turbulent spectra also bias toward spikes at \(\lambda _x\approx 1\sim 2D\) obviously, especially for the high Reynolds number case B2. Moreover, energetic peaks at large scales \(\lambda _x\ge 10D\) are observed for spectra on both sides that correspond to shear instability eddies (Breugem and Boersma 2005). It appears that the periodic fluctuations originated from the permeable wall perform as an additional source in the energy cascade of turbulence. By introducing additional energetic modes into the spectra, the porous wall can efficiently biased the peak of streamwise spectra toward the pore unit length.
In contrast to the streamwise spectra, spanwise spectra are less affected by the periodic porous units. The spanwise spectra of cases A1 and A2 show basically identical pattern on the permeable and non-permeable side, with inner peaks at \(\lambda _z^{t+}\approx 100\) (\(\lambda _z/D\approx 1\) for case A1 and 0.5 for case A2). This is consistent with the value of a canonical wall-bounded flow (Wang et al. 2019a). In contrast, cases B1 and B2 biased from the spectra of a wall-bounded flow, with a considerable portion of energy residing at large scale modes \(\lambda _z/D \ge 5\). In the meantime, the inner-scaled energetic modes \(\lambda _z ^{t+}\approx 100\) (\(\lambda _z/D\approx 1.3\) for case B1 and 0.7 for case B2) remain strong till outer layer of the boundary layer (\(y^+>200\)).
The TKE spectra show the significant impact of porous media on scale energy, especially for the streamwise modes. This indicates that the coherent structures above the porous media can be quite different from those of a canonical wall-bounded flow in terms of length scale and evolution dynamics. Further effort is needed to shed light on this problem.
Pre-multiplied one-dimensional TKE spectra. Row 1: \(k_x{\widehat{q}}(\lambda _x)\); Row 2: \(k_z{\widehat{q}}(\lambda _z)\). Column a-d represents the cases A1, B1, A2, and B2, respectively. The color contours are the energy spectra from the porous media side, while the solid isolines representing spectra of the non-permeable side which are superimposed as a reference
4 Turbulent Kinetic Energy Budget
4.1 Profiles of TKE Budget Terms
In this section, the budget of TKE will be analyzed in detail to visualize the turbulence transport under the impact of the porous wall. Derived from the momentum equation, the Reynolds-averaged transport equation for the turbulence kinetic energy \({{\overline{q}}}=\overline{(u^{\prime 2}+v^{\prime 2}+w^{\prime 2})}/2\) can be written as:
with
The terms defined above in Eqn.(8) are convection C, turbulence production P, turbulent diffusion T, velocity-pressure-gradient \(\Pi\), viscous diffusion of turbulent kinetic energy \(D_\nu\) and turbulence dissipation \(\varepsilon\), respectively. To show the transportation of energy in the wall-normal direction, budget terms averaged in wall-parallel planes (superficial average \(\langle \cdot \rangle _s\)) are depicted in Fig. 9. Note that spatial-averaged budget terms shown here are originated from Eqn.(7), which only considers turbulent fluctuations and does not involve dispersion effect. Focus is set here on the permeable interface, since the energy budget over a non-permeable wall is well known. The behavior of production and dissipation is quite similar for all cases. The peak of production \(\langle P \rangle _s\) is slightly above the crest of the cylinders, while the peak of dissipation \(\langle \varepsilon \rangle _s\) is even closer to the permeable wall. For the low porosity cases (A1, A2), production ceases below the throats of the first layer of cylinders. In contrast, there is still active production below the first layer of cylinders in case of small cylinders (B1, B2). In addition, there is a negative \(\langle P \rangle _s\) peak slightly below the main positive peak in Fig. 9b and d, which corresponds to the strong positive Reynolds shear stress \(\overline{u'v'}\) at the up-front surface of the cylinders (Fig. 7b4, d4). The mean production then turns to be positive below the negative peak due to the contribution of lower surface of the small cylinders. A more detailed illustration of the spatial distribution of P will be given in the next subsection.
For the wall-normal transportation of TKE, the behavior of the large cylinder cases is similar to a non-permeable wall. As the strong mean vortex and fluctuation at the interface is confined in the cavity above the cylinder gap (Fig. 5a,c and 7a,c), the TKE flux can hardly reach below that. In contrast, the high porosity cases show active wall-normal transport in both the free flow and in the porous media region. Nearby the interface, turbulent and viscous diffusion transport TKE from the production peak both up to the free flow and down to the first layer of cylinders, while pressure transportation carries a large fraction of TKE from a high position (up to 1D above the crest height) into the porous domain, which is the similar to the low porosity cases. The mean convection \(\langle C \rangle _s\) carries a small portion of TKE from top half of cylinder to both directions. Below the first layer of cylinders, the turbulence produced at the lower surface of the cylinders is transported to the crest of the second row of cylinders through turbulent diffusion, then deeper inside the porous media by pressure transportation. This shows a clear picture that TKE is carried to the inside of porous domain by turbulent diffusion and pressure transportation alternatively.
4.2 Spatial Distribution of TKE Budget Terms
The profiles of spatial-averaged budget terms reveal the route of TKE transportation in wall-normal direction. To illustrate the transportation of turbulent fluctuation on the \(x-y\) plane, Fig. 10 shows contours of budget terms of TKE near the interface. For all the cases, the bulk of production P locates above the cylinder array, and mostly between the cylinders. Negative production areas are found attaching the up-front surfaces of the cylinders, which can be related to the positive Reynolds shear stress there (Fig. 7a4–d4). The high porosity cases have an additional positive region attaching the lower surface of the first layer of cylinders, in consistency with the observations made in Fig. 9b,d.
The second row of Fig. 10 shows complex spatial distributions of the mean convection C in the streamwise direction. In the high porosity cases B1 and B2, the energy is extracted from the upstream position of the cylinder to the downstream, and the streamwise length scale of the source/sink area is roughly the diameter of the cylinder D. There is also a strong source attaching the lower surface of the cylinders, which corresponds to a strong vertical mean velocity \({\overline{v}}\) and fluctuation \(\overline{v'v'}\) there (see Figs. 5b2, d2, and 7 b2, d2). For the cases A1 and A2, the structures of the convection C are smaller and weaker, suggesting a marginal impact on the energy flux.
The patterns of the turbulent diffusion term T (3rd row of Fig. 10) and the pressure transportation term \(\Pi\) (4th row of Fig. 10) are roughly the same with the production P and the convection C, but with different sign. For example, both T and \(\Pi\) have strong sinks locating between the cylinders and sources at the up-front surface of the cylinders, which are the opposite of P and C. For T in case B1 and B2, there is an additional sink attaching the lower surface of the cylinder, corresponding to the source area in P and C. These observations demonstrate that T and \(\Pi\) are re-distributing energy in space and smoothing out the non-homogeneity introduced by P and C, which is originated from the circular geometry of the cylinders.
The fifth row of Fig. 10 reflects that the gradient in wall-normal direction dominates the viscous diffusion term \(D_\nu\). In all four cases, a negative layer lies on top of the positive one surrounding the upper surface of the cylinders, which shows that the TKE is diffusing from the strong production area to the interface due to viscosity. The magnitude of \(D_\nu\) is relatively low compared with T and \(\Pi\), and its impact in the porous domain is negligible. The dissipation of energy \(\varepsilon\) in the last row of Fig. 10 is observed with its minimum on the top side of the cylinders, suggesting most TKE is dissipated above the interface before reaching inside the porous domain. The high porosity cases show larger dissipation below the interface, which proves indirectly that more energy is transported to the porous domain.
With the discussions above, it is clear that the high porosity cases enhance the exchange of energy between the free flow and porous media. This is realised in three folds. Firstly, the geometry of the small cylinders allows additional production peaks below the cylinders. Secondly, the mean convection enhances the vertical transport, which brings the energy at the interface to the inside of the porous domain. Thirdly, turbulent diffusion T and pressure transportation \(\Pi\) homogenize the energy distribution in the spatial space, which enables the TKE to be carried further to the porous domain.
4.3 Spectral Analysis of Energy Budget
The spatial transportation of TKE near the interface has been illustrated in previous subsections. The inter-scale energy transfer may also be affected by the porous wall. As shown in Sect. 3, the spanwise spectra are less effected by the periodic geometry of the porous wall. Therefore, it is more reasonable to conduct spectral TKE analysis in spanwise as the fluctuations are homogeneous in this direction without the influence of local energetic spikes. Following Mizuno (2016), Lee and Moser (2019), spectral analysis of the energy transport equation is conducted. The budget equation of the spectral TKE \({\widehat{q}}=\overline{\vert {\widehat{u}} \vert ^2+\vert {\widehat{v}} \vert ^2+\vert {\widehat{w}} \vert ^2 }/2\) is given by:
where
Spanwise spectral TKE budget for case A2. Rows 1-6 are \({\widehat{P}}\), \({\widehat{C}}\), \({\widehat{T}}\), \({\widehat{\Pi }}\), \({\widehat{D}}_\nu\), and \({\widehat{\varepsilon }}\), respectively. Columns a-d denote four streamwise locations A, B, C, and D, respectively, which are illustrated in Fig. 7. The area occupied by the cylinder is masked by gray patches
In the equations above, \({\hat{\cdot }}\) denotes the Fourier-transformed coefficient, the superscript \(^{*}\) denotes the complex conjugate and the overlines \({\overline{\cdot }}\) denote averaging in time. Fig. 11 shows pre-multiplied spanwise spectra of the turbulent kinetic energy budget, i.e., \({\widehat{P}}\), \({\widehat{C}}\), \({\widehat{T}}\), \({\widehat{\Pi }}\), \({\widehat{D}}_\nu\) and \({\widehat{\varepsilon }}\) at different streamwise locations for the case A2. Columns a-d denote four streamwise locations A, B, C, and D, respectively, which are illustrated in Fig. 7. The other cases are not shown here due to their similarity.
The most significant contribution of production \({\widehat{P}}\) comes from position B (Fig. 11b1), i.e., the upper-front surface of the cylinder. The peak of the \({\widehat{P}}\) locates at \(\lambda _z/D\,=\,0.6\) (\(\lambda _z^+\,=\,120\)) close to the surface, and the length scale of production mode increases with wall normal height y. The position of the peak and the growing trend are also shared by other three positions and agree with the observation in channel flows by Lee and Moser (2019). Note that at position A, where there is no solid surface below, the y-position of the peak is still similar with the other positions. On the other hand, the spectrum at position D is detached from the surface. This illustrates that the turbulence production process above the interface is mostly unchanged comparing to canonical channel flows (Mizuno 2016). However, differences can still be seen among different streamwise positions. At positions B and C, negative production modes are found at the large scale part (\(\lambda _z/D>1\)) close to the solid surface, resulting in a energy sink there. In other words, energy are extracted from the TKE to the mean flow through its interaction with structures of large spanwise scale.
The convection spectra \({\widehat{C}}\) reflect the change of scale energy due to spatial convection. At position A (Fig. 11a2), the modes are found to be mostly negative for \(y/D\,=\,0\sim 0.2\) and positive below, suggesting the TKE are convected to the porous domain at the gap. On the other hand, spectra \({\widehat{C}}\) at positions B and C show a complex scenario (Fig. 11b2 and c2) with positive and negative modes appearing at the same y-positions. It should be noted that these negative and positive patches in the convection spectra are caused by spatial convection rather than inter-scale energy transfer, referring to Eqn. (10). In fact, the modes of different signs indicate convection discriminate the structures by their scale. The negative patch at small scale modes at position B are losing energy to the downstream (position C), while the strong positive modes at position B are receiving energy from position C due to the re-circulation. At position D, the negative modes are detached from the solid wall with no significant positive mode around, suggesting the energy is mainly convected downstream.
Similar to the production spectra, the spectra of turbulent diffusion \({\widehat{T}}\) (Fig. 11a2–d2) also mimic those in channel flows. It can be observed from the spectra that mainly two roles are played by \({\widehat{T}}\). First, close to the fluid–solid interface (\(y/D\,=\,0\)), TKE is transported vertically from the sources in the production spectrum \({\widehat{P}}\) (e.g., positions A, B, D) or convection spectrum \({\widehat{C}}\) (e.g., position C) to lower and higher y-positions. Second, at higher positions (\(y/D>0\)), the recipient and donor modes almost balance at each y position, suggesting inter-scale energy transfer is the dominant transfer scheme there.
The pressure–strain interaction is another important mechanism for spatial transportation of energy. Compared to the other terms, the pressure spectra show almost no discrimination of signs on scale, suggesting that it is only affected by the spatial distribution of the TKE. At position A (Fig. 11a4), pressure transport changes sign alternatively as y decreases from \(y/D\,=\,0\), which delivers energy deeper below the interface. For position B, the pressure transportation spectrum in Fig. 11b4 counteracts the effect of convection to some extent, with an intensive negative patch around \(y/D\,=\,0\) and a positive layer attached to the surface of the cylinder. The spectrum at position C is mainly positive, corresponding to the negative modes at position B, which suggests that energy is brought downstream by pressure transportation. The spectrum at position D features only weak positive modes.
In the fifth row, the viscous diffusion spectra \({\widehat{D}}_\nu\) show only a small magnitude in all four locations with no distinction between different scales. Energy is transported from the flow toward the solid surface. In the last row, the peaks of the dissipation spectra \({\widehat{\varepsilon }}\) are seen at approximately \(\lambda _z/D\,=\,0.4\) or \(\lambda _z^+\,=\,80\) at \(y/D\approx 0\). This scale of the peak dissipation is smaller than that of the production and is consistent with the scale in channel flows (Lee and Moser 2019).
In summary, the observations above show that the spanwise scale of energy transfer, e.g., production scale and dissipation scale, persists despite the presence of a porous wall. In the meantime, the transportation terms \({{\widehat{C}}}\), \({{\widehat{T}}}\) and \({{\widehat{\Pi }}}\) are significantly complicated by the geometry of the porous wall. Besides the turbulent diffusion terms, the convection terms can also change the local scale energy. The importance of the pressure term should also be stressed as it plays an important role in the vertical transportation of energy.
5 Blow and Suction Events
Joint distribution of fluctuations \(u'\) and \(v'\) at different y positions. a \(y/D_c\,=\,-1\), b \(y/D_c\,=\,-0.5\), c \(y/D_c\,=\,0\), and d \(y/D_c\,=\,0.5\). The origin \(y\,=\,0\) is at the crest height, and \(D_c\) is the diameter of the cylinder. The color contours are shown for case A2 and solid isolines denote case B2. The levels the isolines are from \(3\times 10^{-4}\) to \(2.4\times 10^{-3}\) with a step of \(3\times 10^{-4}\)
5.1 Quadrant Analysis
One of the essential differences between a porous wall and a non-permeable wall is that, the permeable wall allows fluid exchange between both sides. Therefore, it is necessary to evaluate the behavior of such a mass transfer. The probability density functions (PDF) of the fluctuations, \(u'\) and \(v'\), at different \(y-\) (wall-normal) positions are shown in Fig. 12. The streamwise coordinate of the events is chosen to be in the middle of the cylinders, i.e., aligned with point A in Fig. 7. As defined in Wallace (2016), the combination of the fluctuations can be classified into four categories, \(Q_1\) (\(u'>0,\,v'>0\)), \(Q_2\) (\(u'>0,\,v'<0\)), \(Q_3\) (\(u'<0,\,v'<0\)), and \(Q_4\) (\(u'<0,\,v'>0\)), which is illustrated in Fig. 12a. The Reynolds number only has a marginal influence on the distribution; thus, only cases A2 and B2 are compared. Within the porous media (\(y/D_c=-1\), Fig. 12a), both A2 and B2, show large amounts of \(Q_2\) and \(Q_4\) events. Case B2 also exhibits quite a number of Q3 events. The most possible event for both cases is with positive \(v'\).
At the gap between two cylinders in the first layer (\(y/D_c=-0.5\), Fig. 12b), the PDF of case A2 exhibits a ‘tear drop’ shape, where the most probable event locates at \(v' >0\). This means a more frequent observation of blow events at the gap. The longer tail of \(v'>0\) also suggests the blow event can be intensive. The PDF of the case B2 also shows little skewness in the \(u'\) axis, but the most probable point poses a negative \(v'\), i.e., a suction event. This difference may explain the deviation of \(\kappa\) of the mean profiles. It is shown by Kametani and Fukagata (2011) that \(\kappa\) increases when there is a uniform suction on the wall and decreases when there is a blow. This is similar to the current observation. A ejection would bring the low speed flow from inside the porous domain to the free flow, which increase the velocity deficit between wall and center of the channel. The slope of U(y) thus increases, which corresponds to a decrease of \(\kappa\). In the opposite, the slope of U(y) decreases when the fluid near the wall is absorbed into the porous domain. The explanation for the preference of blow/suction events is still unveiled and need further investigation.
For positions at or above the interface (\(y/D_c=0,0.5\), Fig. 12c, d), the distribution of the two cases is similar showing a clear preference for Q2 and Q4 events. This is also close to the scenario of non-permeable wall turbulence, where sweep (Q4) and ejection (Q2) events are deemed essential for the turbulence production process in the near wall region (Kim et al. 1971).
5.2 Statistical Structure of Blow/Suction Events
In the last subsection, it has been established that the occurrence ratio between blow/suction events at the gap varies between different porosity cases. The flow structure associated with these events is hence of great interest since it is either inducing the events or enforced by them. The conditional averaged blow and suction events in case A2 and B2 are depicted in Figs. 13 and 14, respectively. The results for the low Reynolds number cases are quite similar, thus are not shown for simplicity. The conditional average is based on the net vertical mass flux \(M=\rho \int v'\mathrm {d}A_f\) at the gap between two cylinders in the first row (\(y/D_c=-0.5\)), and it is defined as a blow event when \(M>0\) and a suction event when \(M<0\). The flow field around the events is then averaged with the events aligned to the same point.
The statistical structures of the two cases shown here are similar. For both bases, it is observed that the influential area of blow/suction events can reach as far as the top wall. A blow event corresponds to a large scale Q2 motion above the interface, the extent of which exceeds 10D. On the other hand, a suction event is related to a large Q4 motion with a vortex structure following downstream. The blow and suction events appear alternatively streamwise, which forms very large scale circulations influencing both the free flow and the flow in the porous domain.
There are also differences between the two cases. The high porosity wall is subject to a larger influential extent and deeper penetration of the blow/suction events. In fact, the upper boundary layer is completely dominated by a fluctuation of Q2 and Q4 motion in case B2. In comparison, the upper boundary layer remains observable although severely invaded. Moreover, there is a clearer periodic pattern of large scale Q2/Q4 motion arranging in the streamwise direction for case B2, which may be related to large scale mode in the streamwise spectra (Fig. 8d1). In contrast, the border of Q2/Q4 event in case A2 cannot be defined so clearly.
6 Conclusions
Direct numerical simulations (DNS) are conducted for a turbulent channel flow over porous domain. By investigating four cases covering two Reynolds number up to \(Re\approx 6000\) and two porosity of \(\varphi =0.5\) and 0.8, the impact of Re and \(\varphi\) on transportation of turbulence across the interface is explored.
The porous domain with high or low porosity exhibits distinct features in both the free flow and porous media region. In comparison, the impact of Re on flow structures is not so prominent. The unsteady flow is observed deep inside the porous domain for the high-porosity cases, while turbulent fluctuations are not able to penetrate deep into the low-porosity porous media. This difference is partly attributed to the flow structures at the interface. For the low porosity cases, the first layer of cylindrical structures leads to a strong vortex occupying the cavity above the gap, which prevents turbulence convecting through. In the high porosity cases, the flow remains attached to the cylinders, leading to strong vertical convection around the cylinders which transport turbulence from the interface deep into the porous region.
More details about the spatial transport of turbulent kinematic energy (TKE) are revealed by budget analysis, which shows that the transport scheme of TKE is fundamentally changed for different porosity. The scenario in low porosity cases is quite close to that of a non-permeable wall, with the peaks of production and dissipation remain above the interface, and wall normal transportation ceased at \(y/D_c=-0.5\). In contrast, the high porosity media allows more TKE to be transported into the porous media region. Besides, a second production peak is observed adhere to the low surface of the cylinders. Below the first layer of cylinders, turbulent diffusion and pressure transportation work as energy sink and source alternatively, bringing considerable TKE downward.
The role of different scale modes is then revealed by the budget of spectral TKE. The spanwise wavelength peaks of production and dissipation spectra are similar to those of impermeable wall-bounded turbulence. Turbulent diffusion and viscous diffusion spectra above the cylinder surface are also similar to those of a canonical boundary layer. However, it is interesting to notice that mean convection can also vary the energy distribution among scales. The pressure transportation also exhibits a strong ability in spatial transportation, but has no contribution to inter-scale energy transfer. In general, the spanwise spectral TKE and its budget are only marginally effected by the porous media. On the other hand, the streamwise TKE spectra show a series of harmonic waves in the porous domain side with a main spike at \(\lambda _x/D=1\), owing to strong fluctuations induced by the porous media. For the low porosity cases, there is an additional peak at \(\lambda _x/D\approx 10\), which may be associated with the large-scale Q2/Q4 structure related to shear instability.
The change of statistics of turbulence by the porous wall is a reflection of its impact on the instantaneous behavior of the flow. The quadrant analysis of fluctuations at the gap between cylinders suggests blow events occur more frequently for low porosity cases, while suction events are more likely to happen in high porosity ones. This feature may be used to explain the difference of mean shear at the interface for different porosity cases and is also associated with the change of Kármán constant in the mean profile. Further investigation is needed in order to fully reveal the mechanism behind this phenomenon.
Abbreviations
- \({\overline{\cdot }}\) :
-
Time average
- \(\langle \cdot \rangle\) :
-
Intrinsic area average
- \(\langle \cdot \rangle _s\) :
-
Superficial area average
- \(\langle \cdot \rangle _{\mathrm {ca}}\) :
-
Conditional average
- \(\cdot '\) :
-
Instantaneous turbulent fluctuation
- \({{\tilde{\cdot }}}\) :
-
Form-induced fluctuation
- \({{\widehat{\cdot }}}\) :
-
Fourier transformation
- u, v, w :
-
Streamwise, wall-normal, and spanwise velocity
- x, y, z :
-
Streamwise, wall-normal, and spanwise direction
- \(P,C,T,\Pi ,D_\nu ,\varepsilon\) :
-
Production, convection, turbulent diffusion, velocity-pressure diffusion, viscous diffusion, and dissipation
- \(L_x,L_y,L_z\) :
-
Dimension of the computation domain
- \(\Delta x,\Delta y,\Delta z\) :
-
Spatial resolution of the computation domain
- H :
-
Half height of the computation domain
- h :
-
Half height of the free flow channel
- D :
-
Distance between cylinders
- \(D_c\) :
-
Diameter of the cylinders
- \(u_\tau ^p\),\(u_\tau ^t\) :
-
Friction velocities at permeable wall and top wall
- \(\cdot ^+\) :
-
Normalized by friction velocity and kinematic viscosity \(\nu\)
- \(\cdot ^{t+}\) :
-
Normalized by friction velocity of top wall and kinematic viscosity \(\nu\)
References
Beavers, G.S., Joseph, D.D.: Boundary conditions at a naturally permeable wall. J. Fluid Mech. 30, 197–207 (1967)
Bottaro, A.: Flow over natural or engineered surfaces: an adjoint homogenization perspective. J. Fluid Mech. 877, P1 (2019)
Breugem, W.P., Boersma, B.J.: Direct numerical simulations of turbulent flow over a permeable wall using a direct and a continuum approach. Phys. Fluids 17, 025103 (2005)
Cantwell, C.D., Sherwin, S.J., Kirby, R.M., Kelly, P.H.J.: From h to p efficiently: Strategy selection for operator evaluation on hexahedral and tetrahedral elements. Comput. Fluids 43, 23–28 (2011)
Cantwell, C.D., Moxey, D., Comerford, A., Bolis, A., Rocco, G., Mengaldo, G., De Grazia, D., Yakovlev, S., Lombard, J.-E., Ekelschot, D., et al.: Nektar++: an open-source spectral/hp element framework. Comput. Phys. Commun. 192, 205–219 (2015)
Chu, X., Weigand, B., Vaikuntanathan, V.: Flow turbulence topology in regular porous media: from macroscopic to microscopic scale with direct numerical simulation. Phys. Fluids 30, 065102 (2018)
Chu, X., Yang, G., Pandey, S., Weigand, B.: Direct numerical simulation of convective heat transfer in porous media. Int. J. Heat Mass Transfer 133, 11–20 (2019)
Chu, X., Wu, Y., Rist, U., Weigand, B.: Instability and transition in an elementary porous medium. Phys. Rev. Fluids 5, 044304 (2020)
Efstathiou, C., Luhar, M.: Mean turbulence statistics in boundary layers over high-porosity foams. J. Fluid Mech. 841, 351–379 (2018)
Gómez-de Segura, G., García-Mayoral, R.: Turbulent drag reduction by anisotropic permeable substrates-analysis and direct numerical simulations. J. Fluid Mech. 875, 124–172 (2019)
Guo, C., Li, Y., Nian, X., Xu, M., Liu, H., Wang, Y.: Experimental study on the slip velocity of turbulent flow over and within porous media. Phys. Fluids 32, 015111 (2020)
He, X., Apte, S., Schneider, K., Kadoch, B.: Angular multiscale statistics of turbulence in a porous bed. Phys. Rev. Fluids 3, 084501 (2018)
Jimenez, J., Uhlmann, M., Pinelli, A., Kawahara, G.: Turbulent shear flow over active and passive porous surfaces. J. Fluid Mech. 442, 89–117 (2001)
Jin, Y., Kuznetsov, A.V.: Turbulence modeling for flows in wall bounded porous media: an analysis based on direct numerical simulations. Phys. Fluids 29, 045102 (2017)
Jin, Y., Uth, M.-F., Kuznetsov, A.V., Herwig, H.: Numerical investigation of the possibility of macroscopic turbulence in porous media: a direct numerical simulation study. J. Fluid Mech. 766, 76–103 (2015)
Kametani, Y., Fukagata, K.: Direct numerical simulation of spatially developing turbulent boundary layers with uniform blowing or suction. J. Fluid Mech. 681, 154–172 (2011)
Kim, T., Blois, G., Best, J.L., Christensen, K.T.: Experimental evidence of amplitude modulation in permeable-wall turbulence. J. Fluid Mech. 887, A3 (2020)
Kim, H.T., Kline, S.J., Reynolds, W.C.: The production of turbulence near a smooth wall in a turbulent boundary layer. J. Fluid Mech. 50, 133–160 (1971)
Kim, T., Blois, G., Best, J.L., Christensen, K.T.: Experimental study of turbulent flow over and within cubically packed walls of spheres: Effects of topography, permeability and wall thickness. Int. J. Heat Fluid Flow 73, 16–29 (2018)
Kuwata, Y., Suga, K.: Transport mechanism of interface turbulence over porous and rough walls. Flow Turbulence Combust. 97, 1071–1093 (2016)
Lee, M., Moser, R.D.: Spectral analysis of the budget equation in turbulent channel flows at high reynolds number. J. Fluid Mech. 860, 886–938 (2019)
Li, Q., Pan, M., Zhou, Q., Dong, Y.: Turbulent drag modification in open channel flow over an anisotropic porous wall. Phys. Fluids 32, 015117 (2020)
Manes, C., Poggi, D., Ridolfi, L.: Turbulent boundary layers over permeable walls: scaling and near wall structure. J. Fluid Mech. 687, 141–170 (2011)
Mizuno, Y.: Spectra of energy transport in turbulent channel flows for moderate reynolds numbers. J. Fluid Mech. 805, 171–187 (2016)
Pandey, S., Chu, X., Weigand, B., Laurien, E., Schumacher, J.: Relaminarized and recovered turbulence under nonuniform body forces. Phys. Rev. Fluids 5, 104604 (2020)
Pirozzoli, S.: Revisiting the mixing-length hypothesis in the outer part of turbulent wall layers: mean flow and wall friction. J. Fluid Mech. 745, 378–397 (2014)
Rosti, M.E., Brandt, L., Pinelli, A.: Turbulent channel flow over an anisotropic porous wall-drag increase and reduction. J. Fluid Mech. 842, 381–394 (2018)
Suga, K., Nakagawa, Y., Kaneda, M.: Spanwise turbulence structure over permeable walls. J. Fluid Mech. 822, 186–201 (2017)
Suga, K., Okazaki, Y., Kuwata, Y.: Characteristics of turbulent square duct flows over porous media. J. Fluid Mech. 884, A7 (2020)
Terzis, A., Zarikos, I., Weishaupt, K., Yang, G., Chu, X., Helmig, R., Weigand, B.: Microscopic velocity field measurements inside a regular porous medium adjacent to a low reynolds number channel flow. Phys. Fluids 31, 042001 (2019)
Wallace, J.M.: Quadrant analysis in turbulence research: history and evolution. Ann. Rev. Fluid Mech. 48, 131–158 (2016)
Wang, W., Pan, C., Wang, J.: Quasi-bivariate variational mode decomposition as a tool of scale analysis in wall-bounded turbulence. Exp. Fluids 59, 1 (2018)
Wang, W., Pan, C., Wang, J.: Wall-normal variation of spanwise streak spacing in turbulent boundary layer with low-to-moderate Reynolds number. Entropy 21, 24 (2019a)
Wang, W., Pan, C., Wang, J.: Multi-component variational mode decomposition and its application on wall-bounded turbulence. Exp. Fluids 60, 95 (2019b)
Weishaupt, K., Terzis, A., Zarikos, I., Yang, G., de Winter, M., Helmig, R.: Model reduction for coupled free flow over porous media: a hybrid dimensional pore network model approach (2019). arXiv:1908.01771 [physics.comp-ph]
Whitaker, S.: The Method of Volume Averaging, vol. 13. Springer, Berlin (2013)
Wood, B.D., He, X., Apte, S.V.: Modeling turbulent flows in porous media. Annual Rev. Fluid Mech. 52, 171–203 (2020)
Yang, G., Coltman, E., Weishaupt, K., Terzis, A., Helmig, R., Weigand, B.: On the beavers-joseph interface condition for non-parallel coupled channel flow over a porous structure at high reynolds numbers. Transp. Porous Media 431–457 (2019)
Yang, G., Weigand, B., Terzis, A., Weishaupt, K., Helmig, R.: Numerical simulation of turbulent flow and heat transfer in a three-dimensional channel coupled with flow through porous structures. Transp. Porous Media 122, 145–167 (2018)
Acknowledgements
The study has been financially supported by Cluster of Excellence SimTech and project SFB1313 (Project No. 327154368) by Deutsche Forschungsgemeinschaft (German Research Foundation). The authors gratefully appreciate the access to the high-performance computing facility Hazel Hen at HLRS, Stuttgart of Germany. G. Y. kindly acknowledges the support of the Shanghai Pujiang Program (19PJ1405600).
Funding
Open Access funding enabled and organized by Projekt DEAL..
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chu, X., Wang, W., Yang, G. et al. Transport of Turbulence Across Permeable Interface in a Turbulent Channel Flow: Interface-Resolved Direct Numerical Simulation. Transp Porous Med 136, 165–189 (2021). https://doi.org/10.1007/s11242-020-01506-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-020-01506-w