Brine Formation and Mobilization in Submarine Hydrothermal Systems: Insights from a Novel Multiphase Hydrothermal Flow Model in the System H₂O–NaCl

Abstract

Numerical models have become indispensable tools for investigating submarine hydrothermal systems and for relating seafloor observations to physicochemical processes at depth. Particularly useful are multiphase models that account for phase separation phenomena, so that model predictions can be compared to observed variations in vent fluid salinity. Yet, the numerics of multiphase flow remain a challenge. Here we present a novel hydrothermal flow model for the system H₂O–NaCl able to resolve multiphase flow over the full range of pressure, temperature, and salinity variations that are relevant to submarine hydrothermal systems. The method is based on a 2-D finite volume scheme that uses a Newton–Raphson algorithm to couple the governing conservation equations and to treat the non-linearity of the fluid properties. The method uses pressure, specific fluid enthalpy, and bulk fluid salt content as primary variables, is not bounded to the Courant time step size, and allows for a direct control of how accurately mass and energy conservation is ensured. In a first application of this new model, we investigate brine formation and mobilization in hydrothermal systems driven by a transient basal temperature boundary condition—analogue to seawater circulation systems found at mid-ocean ridges. We find that basal heating results in the rapid formation of a stable brine layer that thermally insulates the driving heat source. While this brine layer is stable under steady-state conditions, it can be mobilized as a consequence of variations in heat input leading to brine entrainment and the venting of highly saline fluids.

1 Introduction

Hydrothermal venting at the ocean floor is a key mechanism of biogeochemical exchange between the solid earth and the global ocean. Fluid circulation through the young ocean floor sustains unique ecosystems (Boetius 2005), mobilizes metals from the crust to the ocean floor to form volcanogenic massive sulfide deposits (Hannington et al. 2011), and is a source of trace elements and isotopes that are now thought to play an important role in global scale biogeochemical ocean cycles (German et al. 2016). Much has been learned about these systems and their role in the Earth System from direct seafloor observations, water column measurements, ocean drilling, and geophysical imaging (Fornari et al. 2012; German and Seyfried 2014; Humphris et al. 1995). Yet, the inner workings of submarine hydrothermal system remain inaccessible to direct observations. Instead, the sub-seafloor hydro-geochemical regime needs to be indirectly inferred. Investigating systematic pattern in vent fluid chemistry and their spatial as well as temporal variations is one powerful approach (e.g., Butterfield and Massoth 1994; Mottl et al. 2011; Shanks 2001; Von Damm 2004). The chemistry of hundreds of vent fluid samples taken from hydrothermal systems located in diverse geological settings including fast spreading and slow spreading ridges as well as back-arc spreading centers has been published. The resulting dataset shows a spectacular diversity and complexity of vent fluid chemistry, yet some first-order features and trends are robust and clear. For example, vent fluid salinity often deviates from the seawater value pointing to phase separation and segregation phenomena at depth. When seawater is heated and intersects the two-phase boundary, it splits into a low salinity vapor and a higher salinity brine phase (Bischoff and Rosenbauer 1984; Driesner and Heinrich 2007). Segregation of these phases can result in the venting of fluids that have a higher or lower salinity than seawater. Observed vent fluid salinities vary between 5 and 200% of the seawater value (3.2 wt% NaCl). These salinity variations are particularly interesting in the context of metal mobilization and transport. Most metals, including iron (Fe), are chloro-complexing and tend to travel with the more saline fluid phase, implying that phase separation has a first-order effect on vent fluid chemistry (Butterfield et al. 1997; Jr. Seyfried et al. 1991; Von Damm 2004). Figure 1 illustrates this for a selection of vent fluid samples from the East Pacific Rise (EPR) and some selected slow spreading mid-ocean ridges.

Fig. 1

Plot of chloride versus total iron for various vent fluids in mid-ocean ridge settings: East Pacific Rise (Shanks, 2001; Von Damm, 2000, 2004), TAG (Edmonds et al., 1996), Snakepit (Von Damm, 1990), Lucky Strike (Charlou et al., 2000; Von Damm et al., 1998), Rainbow (Douville et al., 2002), Longqi (Ji et al., 2017), and Edmond/Kairei (Gallant and Von Damm, 2006; Kumagai et al., 2008)

Tracing salt within submarine hydrothermal systems is therefore a useful way of investigating metal transport within the oceanic crust and toward the seafloor. Yet, relating changes in vent fluid chemistry to hydrothermal processes at depth remains a challenge and requires numerical multiphase transport models as well as a reliable equation of state (EOS) that can establish links between hydrothermal flow observations and physicochemical processes at depth.

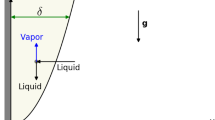
Some insights into brine formation and salt re-distribution within hydrothermal convection cells can be gained from exploring the EOS of seawater (Driesner and Heinrich 2007). Theoretical work on pure water (Jupp and Schultz 2000), later extended to salt water (Geiger 2005), has shown that the thermodynamic properties of (sea) water result in an upper temperature limit of approximately 400 °C in the upflow limb of submarine hydrothermal circulations cells (the exact value is a function of pressure and salinity). The critical point of seawater with 3.2 wt% NaCl is at 29.8 MPa and 407 °C. Consequently, boiling can occur at vent fields located at water depths shallower than ~ 3000 m. Such shallow boiling (and condensation) processes in combination with brine entrainment into the upflow zone are thought to be the reason for the high spatial and temporal variability in vent fluid salinities, which are, for example, observed at the East Pacific Rise vent field at 9°N located in ~ 2600 m water depth (Pester et al. 2014; Von Damm 2004; Von Damm et al. 1997). Boiling and entrainment processes are also likely to control vent fluid salinity at the ASHES vent field located in 1540 m water depth on the Juan de Fuca Ridge (JdFR), where chimneys just tens of meters apart show salinities below and above seawater (Butterfield et al. 1990). These ideas were tested and confirmed with numerical multiphase models by Coumou et al. (2009), who showed how the entrainment of brines formed in the upflow zone of relatively shallow hydrothermal systems can result in rapid and large fluctuations in vent fluid salinity.

If a fluid of seawater salinity is intersecting the two-phase boundary at pressures higher than the critical pressure of seawater, small amounts of a highly saline brine phase are condensing from the fluid phase thereby depleting it in NaCl. Note that we do not use the terms “subcritical” and “supercritical” phase separation here, which are often found in mid-ocean ridge literature, because they refer to the misleading concept of a fixed salt content. We rather follow Coumou et al. (2009) and refer to the physical processes of boiling and condensation. Brine condensation is likely to happen above the driving heat source of a circulation system. In most mid-ocean ridge settings, magmatic heat sources, e.g., the axial melt lens at fast spreading ridges or a gabbroic intrusion at slow spreading ridges, are located at hydrostatic pressures higher than the critical pressure of seawater and release their heat directly into the two-phase region. Within this region, the condensing dense brine phase will pool, while the less dense vapor phase will rise. This may result in a stable basal brine layer that insulates the heat source and through which heat transport is predominantly conductive.

Based on mass flux estimates and measured vent salinities at Main Endeavor Field, Fontaine and Wilcock (2006) estimated that a basal brine layer of ~ 100 m thickness should form within only 15 years. As this estimate was inconsistent with their calculated conductive heat balance, which required the brine layer to be thinner than 10 m to match the observed high heat flux, they argued that interfacial tension between fluid and solid phases will likely favor the segregation of vapor into the main fractures and brine into the smaller fissures. This would allow the vapor to flow efficiently through the system and to sustain large heat fluxes. Bischoff and Rosenbauer (1989) argued that double diffusion will break the stable stratification of the brine layer leading to internal convection, which mines the required heat from below. So far, the viability of both explanations remains questionable as neither has been tested in fluid dynamic simulations. A complementary explanation is lateral brine flow near the base of a circulation system. If brines move out of the two-phase region either by lateral migration or because heat supply is diminished, they would merge with the single-phase fluid flow above thus leading to the venting of highly saline fluids (Coumou et al. 2009). This process is likely to happen at the TAG hydrothermal mound on the Mid-Atlantic ridge, where stable brine venting (~ 125% of seawater salinity) has been documented to have occurred for more than a decade (Chiba et al. 2001). Long-term venting of brines is rare at intermediate to fast spreading ridges. Venting on the Northern Cleft segment of the JdFR is such an exception. Here repeated fluid sampling in the early 1990s documented persistent venting of high salinity fluids, which has been interpreted as interaction with a previously formed brine layer (Butterfield and Massoth 1994). At the Main Endeavor Field on the Juan de Fuca Ridge, vent fluid salinities have mostly been lower than seawater in the period 1984 to 2005 (Butterfield and Massoth 1994; Foustoukos et al. 2009; Lilley et al. 2003). Also at the East Pacific Rise at 9°50′N, low salinity venting occurred for more than 13 years since 1991 (Von Damm 2004). This predominance of lower-than-seawater salinity venting at intermediate to fast spreading ridges raises again the question what the fate of the complementary brine phase is. It continues to be an unresolved question whether brines are pooling at the base of circulation systems or brine venting occurs diffusively or/and highly diluted.

It is in this context that we are here investigating brine formation and mobilization in submarine hydrothermal systems using a newly developed two-dimensional hydrothermal modeling code. First, we present our numerical approach and explain our motives for developing a new code and how our approach differs from other existing simulators like CSMP++, MUFITS, TOUGH-NaCl and FISHES. Second, we show results of a suite of model calculations investigating a geometrically simple setup designed to approximate the conditions of a hydrothermal system at a mid-ocean spreading center with a basal heat source. For different pressure conditions, we study brine layer formation, its stability and effect on heat transfer as well as the conditions that result in the mobilization of the brine phase into the upflow zone.

2 Numerical Approach

2.1 Motivation for a New Thermohaline Code

Multiphase simulations of thermohaline flow in submarine hydrothermal systems continue to be numerically challenging and are still not routinely done. It requires an EOS that fully describes the fluid’s state and thermodynamic properties over sufficiently wide pressure (P), temperature (T), salinity (X) ranges, and a transport model able to handle multiphase flow and the strong non-linearity of the thermodynamic properties. Driesner and Heinrich (2007) and Driesner (2007) provide complete and realistic correlation formulae for phase stability relations and fluid properties at temperatures from 0 to 1000 °C, pressures from 0 to 5000 bar, and compositions from 0 to 1 weight fraction NaCl. The provided EOS improves upon earlier works (Palliser and McKibbin 1998a, b, c) in the correlation formulae in that the complete fluid state can be calculated as a function of PTX including a comprehensive set of thermodynamic properties. The CSMP++ porous media simulator (Geiger et al. 2006a, b; Weis et al. 2014) uses this EOS and has been used for submarine hydrothermal systems (Coumou et al. 2009; Gruen et al. 2012, 2014) and geothermal sites (Scott et al. 2016, 2017; Weis et al. 2012). Other existing simulators include NaCl-TOUGH2 (Kissling 2005b), which uses different correlation formulae (Palliser and McKibbin 1998a, b, c) and is an enhancement of TOUGH2 (Kipp Jr et al. 2008), which was originally developed for geothermal settings below 350 °C. Yet this code was only used once for modeling in a case study for the Taupo Volcanic Zone in New Zealand (Kissling 2005b). FISHES (for Fully Implicit Seafloor Hydrothermal Event Simulator) has been developed by Lewis and Lowell (2009), the thermodynamic properties are a synthesis of data and extrapolations from various studies (Anderko and Pitzer 1993; Archer 1992; Palliser and McKibbin 1998a, b, c; Tanger and Pitzer 1989), and it is appropriate/adequate for modeling two-phase problems at mid-ocean ridges (Choi and Lowell 2015; Han et al. 2013; Singh et al. 2013). Most recently, the reservoir simulator MUFITS has been adapted to resolve multiphase hydrothermal flow using the EOS by Driesner and Heinrich (2007) and was used to simulate brine formation in a volcanic setting (Afanasyev et al. 2018).

According to publications, the well-documented CSMP++ simulator appears to be the most frequently used code. Interestingly, the employed sequential method of solving the governing equation is different to the typically used coupled approaches implemented in other hydrothermal and geothermal simulators. MUFITS, TOUGH2, HYDROTHERM and FEHM all use a coupled numerical approach, where mass and energy conservation equations are solved simultaneously using an iterative scheme, which is often the Newton–Raphson method. It remains a question of active research to assess to strengths and limitations of sequential versus coupled approaches in terms of efficiency, stability, and accuracy. The reader can find further discussion on this in Ingebritsen et al. (2010), Vehling et al. (2018).

Coupled approaches should be better equipped for handling the strong non-linearities in the governing conservation equations and their strong couplings—and should theoretically be more efficient by allowing for larger time steps. In practice, the case is far from clear. For example, resolving the sharp phase boundaries and associated jumps in coefficients that occur over the relevant PTX ranges in the H₂O–NaCl system is a challenge in coupled approaches. Here the choice of the primary variables that define the thermodynamic state has to be done carefully. For the system H₂O–NaCl, correlation formulae are a function of pressure, temperature, and composition, but the energetic state is not always resolved. For example, saturations in the three-phase region where vapor, liquid, and halite coexist and for the pure water two-phase region cannot be calculated in PTX space (Figs. 2, 3). One possible solution is primary variable switching (Class et al. 2002; Wu and Forsyth 2001). However, if a phase boundary is crossed multiple times, and each crossing triggers a primary variable switch and associated variable initialization, convergence can be poor. In TOUGH-NaCl, this procedure leads to restrictions in the allowed phase state transitions (Kissling 2005b). For example, from single phase it is not allowed to have a direct transition to the three-phase coexisting region.

Fig. 2

Phase diagram of the system H₂O-NaCl in temperature–pressure composition coordinates with isolines for pressure and composition on surfaces

Fig. 3

adapted from Driesner (2013)

Isobaric cross sections of bulk spec. enthalpy versus fluid salt content within the PHX phase relation diagram. Colored bold lines show same phase region boundaries as shown in Fig. 2. Thin black lines are isotherms, crossing phase region boundaries. Dashed thin black lines are isotherms restricted to phase regions. a, b Red dots at the left border show spec enthalpy for boiling of pure water; boiling temperature is in a 311 °C and in b 366 °C. Temperatures of L + V + H regions are in blue. Yellow dots show spec. enthalpy of melting halite h_H and the corresponding melt h_L. Molten halite is part of phase region L. Figure design has been

Another option is to use a set of primary variables that always resolves the fluid state, e.g., pressure, specific enthalpy (H), and salinity. The downside is that the existing EOSs for the system H₂O–NaCl use PTX so that the thermodynamic state has to be determined with a costlier iterative scheme or with interpolations on look-up tables. In HYDROTHERM (Hayba and Ingebritsen 1994; Kipp Jr et al. 2008), this method has been shown to work well for the pure water two-phase region and also at difficult conditions around the critical point (22.06 MPa, 374.15 °C). Promising are also results obtained with MUFITS simulator which uses a PHX coupled scheme to resolve two-phase flow in the system H₂O–NaCl (Afanasyev et al. 2018).

In summary, the equation of state for the system H₂O–NaCl is reasonably well constrained, but progress needs to be made in simulating multiphase transport. We see a large utility and potential for a hydrothermal simulator that uses the coupled approach with primary variables of pressure, spec. enthalpy, and composition. Recently, we have presented a coupled pressure/enthalpy scheme simulating pure water multiphase flow (Vehling et al. 2018). This method uses a higher-order time differencing scheme (theta-time differencing) that leads to higher accuracy, larger time step sizes, and a better convergence of the Newton–Raphson iteration scheme. We here extend this method to the system H₂O–NaCl by adding an additional conservation equation and by translating the EOS of (Driesner 2007; Driesner and Heinrich 2007) from PTX to PHX space.

2.2 Model Assumptions and Governing Equations

We use an extension of the two-phase flow model and numerical approach presented in (Vehling et al. 2018), which is a pure water two-phase numerical code. We make again the following model assumptions:

• 1. capillary pressure effects are neglected

• 2. rock and fluid are in local thermodynamic equilibrium

• 3. rock enthalpy is related to temperature by a constant specific heat

• 4. the inertia energy terms are orders of magnitude smaller and hence can be neglected

• 5. we fully account for pressure–volume work and viscous dissipation.

To describe the H₂O–NaCl system, the conservation of mass of the combined H₂O–NaCl fluid (Eq. 1) and the conservation of energy (Eq. 2) is completed by salt mass conservation (Eq. 3):

$$\frac{{\partial \left( {\Phi \rho_{{\text{m}}} } \right)}}{\partial t} = - \nabla \cdot \left( {\sum\limits_{{{\text{f}} \in \{ {\text{l}},{\text{v}}\} }} {\rho_{{\text{f}}} {\vec{{\bf v}}}_{{\text{f}}} } } \right)$$

(1)

$$\begin{aligned} \frac{\partial E}{{\partial t}} = & \;\frac{\partial }{\partial t}\left( {\Phi \rho_{{\text{m}}} h} \right) + \rho_{{\text{r}}} c_{{{\text{pr}}}} \frac{\partial (T(1 - \Phi ))}{{\partial t}} \, \\ {\kern 1pt} = & \;\nabla \cdot K\nabla T - \nabla \cdot \left( {\sum\limits_{{{\text{f}} \in \{ {\text{l}},{\text{v}}\} }} {h_{{\text{f}}} \rho_{{\text{f}}} \vec{v}_{{\text{f}}} } } \right) + \sum\limits_{{{\text{f}} \in \{ {\text{l}},{\text{v}}\} }} {\frac{{\eta_{{\text{f}}} }}{{kk_{{{\text{rf}}}} }}} {\vec{{\bf v}}}_{{\text{f}}}^{2} + \frac{{\partial \left( {p\Phi } \right)}}{\partial t} + \sum\limits_{{{\text{f}} \in \{ {\text{l}},{\text{v}}\} }} {{\vec{{\bf v}}}_{{\text{f}}} \nabla p} \\ \end{aligned}$$

(2)

$$\frac{{\partial (\Phi \rho _{{\text{m}}} X)}}{{\partial t}} = \nabla \cdot \left( { - \sum\limits_{{{\text{f}} \in \{ {\text{l,v}},\} }} {\rho _{{\text{f}}} X_{{\text{f}}} {\vec{{\bf v}}}_{{\text{f}}} } } \right) + \nabla \cdot \left( {\sum\limits_{{{\text{f}} \in \{ {\text{l}},{\text{v}}\} }} {D\rho _{{\text{f}}} \nabla X_{{\text{f}}} } } \right)$$

(3)

All variables are summarized in Table 1. Subscripts l, v, h stand for liquid, vapor, and halite phase and f is either liquid or vapor. The third term on the RHS of Eq. (2) describes viscous dissipation, and the fourth and fifth terms contain the part of the pressure–volume work that is not accounted for in the specific enthalpy. We summarize these terms into the following expression, which is then back-substituted into Eq. (2):

$$\frac{{\partial \left( {\Phi p} \right)}}{\partial t} + \sum\limits_{{{\text{f}} = \{ {\text{l}},{\text{v}}\} }} {{\vec{{\bf v}}}_{{\text{f}}} \left( {\rho_{{\text{f}}} {\vec{{\bf g}}}} \right)} = - \sum\limits_{{{\text{f}} = \{ {\text{l}},{\text{v}}\} }} {{\vec{{\bf v}}}_{{\text{f}}} \left( {\nabla p - \rho_{{\text{f}}} {\vec{{\bf g}}}} \right)} + \left( {\frac{{\partial \left( {\Phi p} \right)}}{\partial t} + \sum\limits_{{{\text{f}} = \{ {\text{l}},{\text{v}}\} }} {{\vec{{\bf v}}}_{{\text{f}}} \nabla p} } \right)$$

(4)

Table 1 Variables

The fluid velocity trough a porous medium is described by Darcy’s law, where halite is treated as immobile phase, which is absent in advection terms.

$${\vec{{\bf v}}}_{{\text{f}}} = - k\frac{{k_{{r{\text{f}}}} }}{{\eta_{{\text{f}}} }}\left( {\nabla p - \rho_{{\text{f}}} {\vec{{\bf g}}}} \right)$$

(5)

The mean density ρ_m, mean specific enthalpy h, and mean salt mass fraction X are defined as follows, using X_h = 1:

$$\rho_{{\text{m}}} = S_{{\text{l}}} \rho_{{\text{l}}} + S_{{\text{v}}} \rho_{{\text{v}}} + S_{{\text{h}}} \rho_{{\text{h}}}$$

(6)

$$h = \frac{{S_{{\text{l}}} \rho_{{\text{l}}} h_{{\text{l}}} + S_{{\text{v}}} \rho_{{\text{v}}} h_{{\text{v}}} + S_{{\text{h}}} \rho_{{\text{h}}} h_{{\text{h}}} }}{{\rho_{{\text{m}}} }}$$

(7)

$$X = \frac{{S_{{\text{l}}} \rho_{{\text{l}}} X_{{\text{l}}} + S_{{\text{v}}} \rho_{{\text{v}}} X_{{\text{v}}} + S_{{\text{h}}} \rho_{{\text{h}}} X_{{\text{h}}} }}{{\rho_{{\text{m}}} }}$$

(8)

where by phase volumetric saturations adding themselves to one:

$$S_{{\text{l}}} + S_{{\text{v}}} + S_{{\text{h}}} = 1$$

(9)

2.3 Equation of State in the System H₂O–NaCl

We implemented the equation of state in the system H₂O–NaCl published by Driesner (2007), Driesner and Heinrich (2007), which is formulated for the pressure–temperature composition space (Fig. 2). In total, we find seven phase states. The black surface separates the single-phase region from the liquid + vapor (L + V) coexisting region. The red line (critical curve) following the crest of this surface indicates whether a single-phase fluid enters the two-phase region as vapor-like or liquid-like fluid. At pressures below the critical point of pure water (p_crit = 22.06 MPa, 374.15 °C), the critical curve is identical to the boiling curve of pure water. Here a single-phase fluid below the boiling temperature is always in a liquid state and would boil when heated to the two-phase boundary. At higher pressures, the critical curve moves to higher salt compositions, which implies that when a single-phase fluid with a salt content lower than the critical curve is heated until it hits the two-phase boundary, it would be a vapor-like fluid from which brine droplets are condensing.

Throughout this paper, we use the critical curve to distinguish between vapor- and liquid-like in the single-phase region at pressures higher than p_crit with vapor always having a lower density than a fluid on the critical curve for a given pressure. Therefore, a “vapor” is a fluid, which has a density below the density at the critical point of pure water (321.9 kg/m³), or a fluid having a higher temperature and a lower salt content than the critical curve at a given pressure.

The green surface marks the halite liquidus. In the liquid + halite (L + H) coexisting region, halite saturation increases linearly with increasing salt content, when temperature stays constant. The liquid, vapor, and halite coexisting surface (blue) forms the lower pressure boundary of the L + V region and the upper boundary of the V + H coexisting region. The dark yellow surface separates at low salinities the vapor region (single phase) from the V + H coexisting region.

We use a bisection method for the mapping between PTX and pressure, spec. enthalpy, and composition space (PHX). Special care must be taken in regions where the fluid state is not uniquely described in PTX space, which is the three-phase, pure water boiling, and halite melting regions. Within those regions, we make use of the constant temperature constraint for a given pressure, which allows solving directly for the unknown saturations. Figure 3 shows HX-slices for different pressures illustrating how the fluid state is uniquely described in PHX space. Pure water boiling below the critical pressure occurs at X = 0 between the specific enthalpies of vapor and liquid (Fig. 3a, b). If boiling occurs in the presence of salt (L + V region), the spec. enthalpies (and salt contents) of the vapor and liquid phases at a given temperature within the L + V region can be read off at the intersection of the respective isotherm with the phase region boundaries (bold lines). Note how the vapor phase can carry several wt% NaCl within the lower temperature range of the L + V region at higher pressures (Fig. 3c, d). At pressures lower than 39.015 MPa, the isothermal L + V + H coexisting field appears twice and the spec. enthalpies of each phase can be read off at the triangle corners (Fig. 3a, b, c). Within each (isothermal) lower temperature L + V + H region, an increase in bulk specific enthalpy results in the separation of liquid into vapor and halite, i.e., the liquid saturation decreases with halite and vapor saturations increasing. In the higher temperature L + V + H regions, vapor and halite are progressively forming a very high salinity liquid (> 85 wt% NaCl) with increasing bulk enthalpy. Finally, isothermal halite melting is resolved with saturations of solid and liquid halite varying between the yellow dots at X = 1.

We have implemented the EOS in MATLAB but for performance reasons use pre-computed 3-D look-up tables for the transport models. For this purpose, we mesh different phase fields in 3-D PHX space using an unstructured mesh of tetrahedral elements. In this way, we ensure that phase boundaries are well resolved and to not cross elements so that the interpolation scheme “knows” on which phase field it operates. Note that the EOS of Driesner and Heinrich (2007) does not include a parameterization of viscosity and we here use the one recently published by Klyukin et al. (2017).

2.4 Control Volume Method

As spatial discretization of the governing equations, we use a finite volume technique, in which a control volume (CV) is constructed around each node of an unstructured triangular finite element mesh (Fig. 4). This approach is equal to that used in Vehling et al. (2018) and has the advantage of being locally fluid mass, energy, and salt mass conserving. Mass and energy fluxes between two adjacent CVs are continuous when using temperature and pressure gradients obtained from corner nodes of the triangle elements. The same discretization is used in CSMP++ (Weis et al. 2014).

Fig. 4

Construction of the control volumes Ω_i from an unstructured finite element triangle mesh (black lines). The control volume boundary is composed of straight segments, and each element contains three segments

In the control finite volume method, fluxes are integrated over the boundary ∂Ω_i of each CV. For each control volume Ω_i, we obtain the integral formulations of Eqs. 1–3 by transforming the divergence of the flux terms into a line integral on ∂Ω_i using the divergence theorem.

$$\int\limits_{{\Omega_{i} }} {\frac{{\partial \left( {\Phi \rho_{{\text{m}}} } \right)}}{\partial t}{\text{d}}\Omega } = - \int\limits_{{\partial \Omega_{i} }} {\sum\limits_{{{\text{f}} \in {{\{ l,v\} }}}} {\rho_{{\text{f}}} {\vec{{\rm v}}}_{{\text{f}}} } \cdot {\vec{{\rm n}}}_{i} {\text{d}}} r$$

(10)

$$\int\limits_{{\Omega_{i} }} {\frac{\partial E}{{\partial t}}{\text{d}}\Omega } = \int\limits_{{\partial \Omega_{i} }} {\left( {K\nabla T - \sum\limits_{{{\text{f}} \in {{\{ l,v\} }}}} { - h_{{\text{f}}} \rho_{{\text{f}}} {\vec{{\rm v}}}_{{\text{f}}} } } \right) \cdot {\vec{{\rm n}}}_{i} {\text{d}}} r + \int\limits_{{\Omega_{i} }} {\left( {\frac{{\partial \left( {\Phi p} \right)}}{\partial t} + \sum\limits_{{{\text{f}} \in {{\{ l,v \} }}}} {{\vec{{\rm v}}}_{{\text{f}}} \left( {\rho_{{\text{f}}} {\vec{{\rm g}}}} \right)} } \right){\text{d}}\Omega }$$

(11)

$$\int\limits_{{\Omega_{i} }} {\frac{{\partial \left( {\Phi \rho_{{\text{m}}} X} \right)}}{\partial t}} {\text{d}}\Omega = \int\limits_{{\partial \Omega_{i} }} {\left( {\sum\limits_{{{\text{f}} \in {{\{\text{l,v}\} }}}} {D\rho_{{\text{f}}} \nabla X_{{\text{f}}} } - \sum\limits_{{{\text{f}} \in {{\{\text{l,v}\} }}}} {\rho_{{\text{f}}} X_{{\text{f}}} {\vec{{\bf v}}}_{{\text{f}}} } } \right) \cdot {\vec{{\bf n}}}_{i} {\text{d}}} r$$

(12)

where ${\vec{{\bf n}}}_{i}$ is the outward pointing unit normal vector field of the control volume boundary ∂Ω_i. To calculate gradients across the segments, we use the spatial derivatives of standard linear finite element shape functions N.

$$\nabla p(x) = \nabla \sum\limits_{j = 1}^{n} {N_{j} \left( x \right)p_{j} } = \sum\limits_{j = 1}^{n} {\nabla N_{j} (x)p_{j} }$$

(13)

$$\nabla T\left( x \right) = \nabla \sum\limits_{j = 1}^{n} {N_{j} \left( x \right)T_{j} } = \sum\limits_{j = 1}^{n} {\nabla N_{j} \left( x \right)T_{j} }$$

(14)

$$\nabla X\left( x \right) = \nabla \sum\limits_{j = 1}^{n} {N_{j} \left( x \right)X_{j} } = \sum\limits_{j = 1}^{n} {\nabla N_{j} \left( x \right)X_{j} }$$

(15)

where x is an arbitrary point of Ω, j is the index of each node and its corresponding shape function, and n is the total number of nodes in the mesh.

2.5 Numerical Discretization in Time

For the numerical time discretization, we use a variable combination of forward Euler method and backward Euler method, the so-called theta (θ)-method:

$$\frac{\partial u}{{\partial t}} = F\left( {u,x,t} \right)$$

(16)

$$\frac{{u^{t + \Delta t} - u^{t} }}{\Delta t} = \theta F\left( {u,x,t} \right)^{t + \Delta t} + \left( {1 - \theta } \right)F\left( {u,x,t} \right)^{t}$$

(17)

Based on our efficiency study in Vehling et al. (2018), we favor the Galerkin Method with θ = 2/3.

2.6 Newton–Raphson Scheme

The main numerical difficulty in solving the above system of equations is the strong coupling between the mass and energy conservation equations and the strong non-linearity of the fluid properties. While the equation coupling is treated in our scheme by computing pressure, mean specific fluid enthalpy, and bulk salt content simultaneously during a single solve of the matrix equation, the non-linearity in fluid properties (and states) is resolved by NR iterations. For this purpose, we write the equations for each control volume (or associated node) i in residual form:

$$R_{i} = - \int\limits_{{\partial \Omega_{i} }} {\sum\limits_{{{\text{f}} \in {{\{\text{l,v,s}\} }}}} {\rho_{{\text{f}}} {\vec{{\bf v}}}_{{\text{f}}} } \cdot {\vec{{\bf n}}}_{i} {\text{d}}} r - \int\limits_{{\Omega_{i} }} {\Phi \frac{{\partial \left( {\Phi \rho_{{\text{m}}} } \right)}}{\partial t}{\text{d}}\Omega }$$

(18)

$$G_{i} = \int\limits_{{\partial \Omega_{i} }} {\left( {K\nabla T - \sum\limits_{{{\text{f}} \in {{\{ \text{l,v}\} }}}} {h_{{\text{f}}} \rho_{{\text{f}}} {\vec{{\bf v}}}_{{\text{f}}} } } \right) \cdot {\vec{{\bf n}}}_{i} {\text{d}}} r + \int\limits_{{\Omega_{i} }} {\left( {\frac{{\partial \left( {\Phi p} \right)}}{\partial t} + \sum\limits_{{{\text{f}} \in {{\{ \text{l,v}\} }}}} {{\vec{{\bf v}}}_{{\text{f}}} \left( {\rho_{{\text{f}}} {\vec{{\bf g}}}} \right)} - \frac{\partial E}{{\partial t}}} \right){\text{d}}\Omega }$$

(19)

$$H_{i} = \int\limits_{{\partial \Omega_{i} }} {\left( {\sum\limits_{{{\text{f}} \in {{\{\text{l,v}\} }}}} {D\rho_{{\text{f}}} \nabla X_{{\text{f}}} } - \sum\limits_{{{\text{f}} \in {{\{ \text{l,v}\} }}}} {\rho_{{\text{f}}} X_{{\text{f}}} {\vec{{\bf v}}}_{{\text{f}}} } } \right) \cdot {\vec{{\bf n}}}_{i} {\text{d}}} r - \int\limits_{{\Omega_{i} }} {\frac{{\partial \left( {\Phi \rho_{{\text{m}}} X} \right)}}{\partial t}} {\text{d}}\Omega$$

(20)

Then, we create a linear system of equations by applying the Newton–Raphson procedure for every residua R_i, G_i and H_i:

$$\sum\limits_{j}^{n} {\frac{{\partial R_{i} }}{{\partial p_{j} }}\left( {p_{j}^{l + 1} - p_{j}^{l} } \right)} + \sum\limits_{j}^{n} {\frac{{\partial R_{i} }}{{\partial h_{j} }}\left( {h_{j}^{l + 1} - h_{j}^{l} } \right)} + \sum\limits_{j}^{n} {\frac{{\partial R_{i} }}{{\partial X_{j} }}\left( {X_{j}^{l + 1} - X_{j}^{l} } \right)} = - R_{i}^{l}$$

(21)

$$\sum\limits_{j}^{n} {\frac{{\partial G_{i} }}{{\partial p_{j} }}\left( {p_{j}^{l + 1} - p_{j}^{l} } \right)} + \sum\limits_{j}^{n} {\frac{{\partial G_{i} }}{{\partial h_{j} }}\left( {h_{j}^{l + 1} - h_{j}^{l} } \right)} + \sum\limits_{j}^{n} {\frac{{\partial G_{i} }}{{\partial X_{j} }}\left( {X_{j}^{l + 1} - X_{j}^{l} } \right)} = - G_{i}^{l}$$

(22)

$$\sum\limits_{j}^{n} {\frac{{\partial H_{i} }}{{\partial p_{j} }}\left( {p_{j}^{l + 1} - p_{j}^{l} } \right)} + \sum\limits_{j}^{n} {\frac{{\partial H_{i} }}{{\partial h_{j} }}\left( {h_{j}^{l + 1} - h_{j}^{l} } \right)} + \sum\limits_{j}^{n} {\frac{{\partial H_{i} }}{{\partial X_{j} }}\left( {X_{j}^{l + 1} - X_{j}^{l} } \right)} = - H_{i}^{l}$$

(23)

Here l + 1 refers to pressure, specific enthalpy, and salt composition after the next iteration step at time t + ∆t. Since each nodal residuum value depends only on the adjacent mesh nodes that are connected by the elements, all other derivatives are zero and the resulting matrix is sparse. Since we use an implicit numerical method, these derivatives have to be calculated every time before solving the linear system of equations.

2.7 Calculation Of Darcy Velocity at Segments

When modelling phase separation phenomena, fluid properties between two neighboring grid nodes can vary over orders of magnitudes, especially when different phases exist on nodes or when large gradients in salt content occur. Therefore, the density at the segment, which is used for calculating fluid flow directions $\left( {\nabla p - \rho_{{\text{f}}} {\vec{{\bf g}}}} \right)$, should account for salt content at the upwind node and also for the temperature gradient. Therefore, we calculate a density for each phase and for the nodes on both sides of the segment:

$$\rho_{{{\text{f}}1{\text{,seg}}}} = 0.5\rho_{{{\text{f}}1}} + 0.5\rho_{{\text{f}}} \left( {p_{2} ,T_{2} ,X_{1} } \right)$$

(24)

$$\rho_{{\text{f2,seg}}} = 0.5\rho_{{{\text{f2}}}} + 0.5\rho_{{\text{f}}} \left( {p_{1} ,T_{1} ,X_{2} } \right)$$

(25)

We use ρ_f1,seg for calculating fluid fluxes if node 1 is the upwind node and ρ_f2,seg if node 2 is the upwind node.

Often a vapor phase is flowing into a colder control volume without a vapor phase so that no vapor density can be calculated there. For avoiding extreme vapor velocities flowing into cold CV at pressure conditions below 22.7 MPa, we use the following equation for calculating the density of a vapor phase at a segment.

$$\begin{gathered} \rho_{{\text{v1,seg}}} = 0.5\rho_{{{\text{v1}}}} + 0.5\left( {w\rho \left( {p_{2} ,T_{2} ,X_{{{\text{cc}}}} } \right) + \left( {1 - w} \right)\rho_{{\text{v,boil}}} } \right) \hfill \\ \begin{array}{*{20}l} {w = 1} \hfill & {\forall T_{2} < T_{{{\text{boil}}}} - 15\;^\circ {\text{C }}} \hfill \\ {w = 0} \hfill & {\forall T_{2} > T_{{{\text{boil}}}} - 5\;^\circ {\text{C}}} \hfill \\ {w = \left( {T_{{{\text{boil}}}} - T_{2} - 5\;^\circ {\text{C}}} \right){/10}\;^\circ {\text{C }}} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} \hfill \\ \end{gathered}$$

(26)

Note that boiling temperature T_boil and vapor density ρ_v,_boil are a function of fluid pressure. X_cc is the salt content of a fluid at the critical curve (see Fig. 2) for a given pressure p_2.This formulation takes into account the high difference between liquid and vapor densities and leads to a better convergence of the Newton–Raphson scheme. In Fig. 5, we show a result of expression (26) for a pressure p₂ of 15 MPa.

Fig. 5

Vapor density at the segment as a function of downwind node temperature T₂ at a pressure p₂ of 15 MPa using expression (26). The upwind node has a temperature of T₁ = 350 °C, salt content of X₁ = 0 wt% NaCl and a vapor density of ρ_v1 = 87.2 kg/m³

When the phase exists at the upstream side, we calculate fluxes over the segment using the upstream weighting method for fluid enthalpy, viscosity, relative permeability, and salt content. The density that is multiplied with the fluid velocity is also upwind weighted. We prefer full upwind weighting, because we want to avoid numerical oscillations in salt composition. Additionally, when a phase does not exist at the downstream node, we save computing time by not creating synthetically downstream fluid properties.

2.8 Permeability and Relative Phase Permeability

When halite precipitates and fills up the pore space, rock permeability decreases. We have implemented the following function for the reduced permeability k_i, which is also used in TOUGH2 (Pruess et al. 2012):

$$k_{i} = k(1 - S_{{\text{h}}} )^{2}$$

(27)

We computed permeability at segments using a logarithmic average, as it can vary over orders of magnitudes:

$$k_{{{\text{seg}}}} = \exp \left( {\frac{{\ln \left( {k_{{i{\text{,up}}}} } \right) + \ln \left( {k_{{i{\text{,do}}}} } \right)}}{2}} \right)$$

(28)

When permeability gets very low due to a high halite saturation, convergence of the Newton–Raphson scheme can become slow, especially for finding a good pressure solution for mass conservation. Therefore, we define a halite saturation threshold S_{h max}, and if it is exceeded, we set the permeability k_seg to zero for all segments around this point. We then stop solving for mass and salt mass conservation at theses nodes, but still solve for energy conservation by heat conduction. In the presented examples, S_{h max} is set to 0.95. This value is lower than required for numerical stability, but it is a reasonable assumption for submarine hydrothermal systems that permeability drops to very low values at such high halite saturations.

When calculating relative permeability for liquid and vapor phase (k_rl and k_rv, resp.), we implemented a function in which the relative permeability is not additionally reduced by halite precipitation, because this is already accounted for in rock permeability (Eq. 27). Therefore, relative liquid permeability is a linear function from 0 to 1, when ${{S_{{\text{l}}} } \mathord{\left/ {\vphantom {{S_{{\text{l}}} } {\left( {1 - S_{{\text{h}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1 - S_{{\text{h}}} } \right)}}$ exceeds the residual liquid saturation S_rl:

$$\begin{gathered} \hfill k_{{{\text{rl}}}} = \frac{{{{S_{{\text{l}}} } \mathord{\left/ {\vphantom {{S_{{\text{l}}} } {\left( {1 - S_{{\text{h}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1 - S_{{\text{h}}} } \right)}} - S_{{r{\text{l}}}} }}{{1 - S_{{r{\text{l}}}} }} \, \forall {{S_{{\text{l}}} } \mathord{\left/ {\vphantom {{S_{{\text{l}}} } {\left( {1 - S_{{\text{h}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1 - S_{{\text{h}}} } \right)}} > S_{{{\text{rl}}}} \\ \hfill k_{{{\text{rl}}}} = 0 \, \forall {{S_{{\text{l}}} } \mathord{\left/ {\vphantom {{S_{{\text{l}}} } {\left( {1 - S_{{\text{h}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1 - S_{{\text{h}}} } \right)}} \le S_{{{\text{rl}}}} \\ \end{gathered}$$

(29)

$$k_{{{\text{rv}}}} = {{S_{{\text{v}}} } \mathord{\left/ {\vphantom {{S_{{\text{v}}} } {\left( {1 - S_{{\text{h}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1 - S_{{\text{h}}} } \right)}}$$

(30)

2.9 Calculating Fluid (Salt) Mass and Energy in Control Volume

When modelling phase separation phenomena, salt composition varies over orders of magnitudes between adjacent nodes. For calculating the salt mass stored in a CV, we only use fluid properties of the node associated with the CV. Using the area of the CV, we compute fluid (salt) mass and energy as follows:

$$\int\limits_{{\Omega_{i} }} {\Phi \rho_{{\text{m}}} d\Omega } = \Phi_{i} \rho_{{{\text{m}},i}} \Omega_{i}$$

(31)

$$\int\limits_{{\Omega_{i} }} {\left( {\Phi \rho_{{\text{m}}} h + (1 - \Phi )\rho_{{\text{r}}} c_{{p{\text{r}}}} T} \right)d\Omega } = \left( {\Phi_{i} \rho_{{{\text{m}},i}} h_{i} + (1 - \Phi_{i} )\rho_{{\text{r}}} c_{{p{\text{r}}}} T_{i} } \right)\Omega_{i}$$

(32)

$$\int\limits_{{\Omega_{i} }} {\Phi \rho_{{\text{m}}} Xd\Omega } = \Phi_{i} \rho_{{{\text{m}},i}} X_{i} \Omega_{i}$$

(33)

2.9.1 Convergence Criterion and Error Tracking

It is a challenging task to find good convergence criteria for the NR approach, when fluid properties and time step size vary over order of magnitudes. For the mass and salt mass conservation, we calculate an error of mass per square meter pore space over the time step ∆t in a CV of size Ω_i:

$$\left\| {R_{i} } \right\|_{{\text{a}}} : = \frac{\Delta t}{{\Omega_{i} \Phi_{i} }}R_{i} \, \left[ {\frac{{{\text{kg}}}}{{{\text{m}}^{2} }}} \right]$$

(34)

As density and salt content could become very small, we need a second criterion, where we normalize the error by density or, respectively, density and composition:

$$\left\| {R_{i} } \right\|_{b} : = \frac{{\left\| {R_{i} } \right\|_{a} }}{{\rho_{m,i} }}$$

(35)

$$\left\| {H_{i} } \right\|_{{\text{c}}} : = \frac{{\left\| {H_{i} } \right\|_{{\text{a}}} }}{{\rho_{{{\text{m}},i}} X_{i} }}$$

(36)

For energy conservation, we find that it is sufficient to work with an error displaying joule per square meter.

$$\left\| {G_{i} } \right\|_{{\text{d}}} = \frac{\Delta t}{{\Omega_{i} }}G_{i} \, \left[ {\frac{{\text{J}}}{{{\text{m}}^{2} }}} \right]$$

(37)

We use following magnitude of criteria:

$$\left\| {R_{i} } \right\|_{{\text{a}}} : = 1\frac{kg}{{m^{2} }} \, \left\| {H_{i} } \right\|_{{\text{a}}} : = \frac{{\left\| {R_{i} } \right\|_{1} }}{3} \, \left\| {R_{i} } \right\|_{{\text{b}}} : = 0.01 \, \left\| {H_{i} } \right\|_{{\text{c}}} : = 0.01 \, \left\| {G_{i} } \right\|_{{\text{d}}} : = 10^{5} \frac{{\text{J}}}{{{\text{m}}^{2} }} \,$$

(38)

To ensure strict mass, energy, and salt mass conservation, we save the residual errors R_i, G_i, and H_i and add them as source term for the next time step. Here we have to consider old and new time step sizes:

$$R_{{i,{\text{source}}}} = R_{i}^{{{\text{old}}}} \frac{{\Delta t^{{{\text{old}}}} }}{\Delta t} \, G_{{i,{\text{source}}}} = G_{i}^{{{\text{old}}}} \frac{{\Delta t^{{{\text{old}}}} }}{\Delta t} \, H_{{i{\text{,source}}}} = H_{i}^{{{\text{old}}}} \frac{{\Delta t^{{{\text{old}}}} }}{\Delta t}$$

(39)

2.9.2 Model Implementation and Limitations

The implemented Newton–Raphson method shows slower convergence, when the residual conserving functions R_i, G_i, and H_i have discontinuities, which can arise from CVs experiencing phase transitions or from discontinuities in the relative permeability functions. Additionally, convergence is reduced when derivatives of the residual functions with respect to primary variables of the same CV become relatively small or change sign. A combination of both problems occurs, for example, at the phase transition into the isothermal L + V + H region for G_i (energy conservation). Here, performance losses have to be accepted for code stabilization and convergence is achieved by reducing time step size and updating primary variables by reduced increments of the NR corrections until convergence.

For performance reasons, we use pre-computed look-up tables on unstructured tetrahedral meshes for all fluid properties and their derivatives. Over each tetrahedron, fluid properties vary linearly and derivatives have constant values. This simple discretization can potentially lead to convergence problems, and in some cases, it may well be better to use the original correlation functions to compute the derivatives. However, this is computationally costly as the correlation functions are in PTX formulations and iterative procedures are necessary to obtain them in PHX space.

Additionally, the correlation functions for vapor density and vapor enthalpy in Driesner (2007) show an unexpected “loop” very close to the critical point of water at very low salt content. The vapor densities show a peak of too high values and the vapor enthalpies a peak of too low values. As a preliminary workaround, we use a coarser mesh near this region in the PHX space, which effectively linearizes fluid properties over the width of a tetrahedron.

We have implemented the entire multiphase model in MATLAB building upon the highly efficient MILAMIN and MUTILS tools (Dabrowski et al. 2008). An alternative would have been to implement the scheme using one of the existing FV libraries and/or transport models such as PFLOTRAN (Hammond et al. 2014), OpenFOAM (Weller et al. 1998), or DUNE/pdelab (Bastian et al. 2010). We had opted for MATLAB because it provided us with the most flexibility and low-level control with regard to numerical implementation details. We hope that the presented details, especially on upwinding and phase weighting, will help with future 3D work on coupled multiphase hydrothermal flow models that may again be based on MATLAB or established FV libraries.

We tested our implementation against benchmarks and published results obtained by other codes. The respective benchmarks for pure water flow under single- and two-phase conditions have been presented in Vehling et al. (2018). Benchmarking of the saltwater case is less straightforward as the results strongly depended on the implemented EOS, which is unfortunately different among various published numerical models. We nevertheless show results of test cases used in previously published studies in "Appendix."

3 Simulation Results

3.1 Model Setup

We explore brine formation and mobilization in a simplified setup that mimics the situation at intermediate to fast spreading ridges, where hydrothermal circulation is mainly driven by heat released from a cooling axial melt lens (AML). The depth of the AML varies between 1 and 3 km beneath the seafloor and depends on magma supply as well as spreading rate (Morgan and Chen 1993; Theissen-Krah et al. 2011). The hydrostatic fluid pressure on top of the AML can therefore vary over tens of MPa between different ridge systems. We have performed numerical simulations for two different top pressure boundary conditions, 35 MPa and 20 MPa, in a domain of 3 km width and 1 km high. The grid has in total 6200 nodes and a refinement at the bottom center of 10 m node distance.

The sidewalls and the bottom domain boundaries are impermeable, and a fixed pressure boundary condition is used on top, which allows for free venting. Top inflow seawater temperature is 5 °C, and salt content is 3.2 wt%. The initial domain temperature is a linear function from top (5 °C) to the bottom (100 °C). At the bottom, we set a Gaussian-shaped temperature boundary condition with a maximum of 700 °C in the center and ~ 300 °C at the sides:

$$T_{{{\text{bot}}}} \left( x \right) = 300\;^\circ {\text{C}} + \Delta T \cdot \exp \left( { - \frac{{x^{2} }}{{2\sigma^{2} }}} \right)$$

(40)

Here σ is set to 450 m and x is the lateral coordinate in the interval from − 1500 to 1500 m. ∆T is 400 °C. In addition, we assume the bottom row of control volumes to be impermeable so that heat transfer here occurs by conduction only. After 900 years, ∆T is linearly reduced to 300 °C over a time span of 50 years to explore the response of a basal brine layer to long-term variations in heat supply (Fig. 6). Rock permeability is a function of depth z:

$$k\left( z \right) = k_{{{\text{top}}}} \cdot \exp (b \cdot z)$$

(41)

where k_top = 1.5 × 10^–14 m² and b = 0.0012. We use a porosity of Φ = 0.03, a rock heat capacity of c_pr = 880 J/(kg K), a rock thermal conductivity of K = 2 W/(m K), and a rock density of ρ_r = 2700 kg/m³. The residual saturation of the liquid phase S_lr is set to 0.3.

Fig. 6

Rock permeability and temperature boundary conditions

3.2 Simulation 1: High Pressure Conditions (35 Mpa On Top) Lead To Stable Brine Layer Formation

The temperature boundary condition results in rapid heating within a central area of 1000 m width bringing the fluid into the two-phase regime. Figure 7a shows the situation after 300 years of heating: a basal brine phase containing up to 75 wt% NaCl has formed and the low salinity vapor phase has merged with single-phase flow above, forming a large low salinity region (1–1.5% NaCl). As the salt signal travels at pore velocity and hence faster than the temperature signal, venting of low salinity cold fluids occurs. Figures 7b and 8a illustrate the stable quasi-steady-state situation for this setup at t = 900 years. A stable basal brine layer has formed with little internal flow. Above it, and largely separated from it, single-phase high-temperature flow occurs at seawater salinity. In between, a thin two-phase region exists (Fig. 8a).

Fig. 7

Simulation results for a top pressure of 35 MPa. Color plots of total salt content in the pore space in wt% NaCl and temperature contours in °C

Fig. 8

Scaled-up color plot of salt content and mass fluxes for a top pressure of 35 MPa. Black arrows display liquids of X < 10 wt% NaCl. Blue arrows display liquids of X > 10 wt% NaCl. Red arrows display vapor (see definition for vapor in Sect. 2.3). Note that vapor can have up to 10 wt% NaCl at pressures of 45 MPa (see starting point of large red arrow in b) at 45 m with ~ 5 wt% NaCl). Arrow lengths have same scale factor for all colors. White contour lines show isotherms in °C

The central brine layer forms progressively from the bottom up. Brine saturations increase and two-phase flow occurs until the pore space is completely filled with brine. “Gaps” in the brine layer that can occur due to changes in the convective pattern are filled up by lateral spreading of brines. Once the pore space is completely filled with brine, active phase separation moves higher up, where brine saturations then start to increase. After 300 years, the brine layer has its largest extension with a maximum height of 90 m. Due to this formation process, the brine salt content stays always very close to the liquid salt content side of the L + V coexisting surface (black surface in Fig. 2). No significant internal mixing of brines is observed, and single-phase flow above is separated from the stably stratified brine layer.

The top of the brine layer is equal to the 462 °C isotherm (Fig. 8). At this temperature, vapor salinity at the L + V coexisting surface is equal to the seawater salt content of 3.2 wt% NaCl at 44 MPa. This implies that 462 °C is also the maximum temperature within the single-phase circulation system and that recharging fluids never experiences phase separation once the system has reached this quasi-steady state. At this temperature, the brine phase has a salt content of 19 wt% NaCl and a density of 686 kg/m³, while the vapor phase has a density of 361 kg/m³. This factor ~ 2 density contrast is shown in Fig. 9 and leads to an interface, where vapor-like fluids are divided and kept separate from the brines below.

Fig. 9

Fluid density and bulk density at L + V coexisting region

Figure 8 shows that the brine density increases with depth, which is a consequence of the increasing salt content with increasing pressure. Internal brine flow is therefore very low. At the top interface, brines are weakly affected by the overlying flow and are slowly flowing toward the central upflow zone (Fig. 8a). Lighter brines can flow upwards leaving the brine layer, and heavier brines tend to flow very slowly downwards and then from the center toward the sides. The downward flowing brines become more saline and, as a result, very small amounts of vapor can form within the brine layer with saturation between 10^–4 and 10^–5.

The brine layer itself acts as a thermal boundary layer. Over the first 40 years, the total conductive heat flux into the domain decreases rapidly due to decreasing temperature gradients at the bottom. After 40 years, heat flux is further decreasing in concert with the increasing amount of salt accumulated in the basal brine layer (Fig. 10a). The formed low salinity vapor phase mixes with single-phase flow above and after ~ 250 years low salinity and low-temperature venting occur. The temperature signal, being buffered by the host rock, travels slower, and vent temperature only starts to increase after 500 years. After the basal brine layer has reached its maximum extend, phase separation becomes limited as the single-phase circulation systems is effectively decoupled. Consequently, vent fluid salinities return to seawater values after approximately 600 years. When the temperature boundary condition is reduced after 900 years, the down flowing recharge fluids can merge with the brines at a lower temperature, and therefore, no formation of heavy brines and low salinity vapor occurs anymore (Fig. 8b). Instead, we find a higher mass flux of brines at the interface toward the center in between x-coordinate 60 m and 200 m. Also, deeper brines with high salinity are mobilized toward the center. These brines are further merging with recharge fluids and a single-phase high salinity liquid of 5 to 10 wt% salt content forms that is sufficiently buoyant to rise. This merging process occurs over a very small temperature interval of 457–462 °C (T = 462 °C is temperature at critical curve at 44 MPa). At these temperatures, vapors have a relatively high salt content of 4 to 5 wt% (red arrows in Figs. 3c, d, 8b). Fluids of such high salinity do not reach the surface but rather mix with ambient seawater resulting in vent fluid salinities of only 3.5 wt%. Such mixing of ascending fluids is further amplified by the increasing permeability toward the seafloor.

Fig. 10

Simulation results for top pressure of 35 MPa. a Blue line: total power of conductive heat flow from bottom nodes into domain. Red line: Top power balance of inflow and outflow. Dark yellow line: bottom salt mass accumulation by considering halite and liquids with more than 10 wt% NaCl. Unit is tons of salt. Dashed black lines show the points in time pictured in Fig. 7. b Red line: maximum outflow temperature. Green line: salt content of fluid with maximal outflow temperature. After 900 years, the green line shows maximal salt content of outflow. Green dashed line show seawater salt content

This mobilization of the brine phase in response to a decreasing bottom temperature results in a shrinking of the basal thermal boundary layer so that the 462 °C isotherm stabilizes at a deeper level. As a consequence, the bottom heat flow starts to increase again after 950 years and reaches nearly the old level after 1100 years (Fig. 10a) highlighting the importance of brine formation and mobilization in modulating heat input into the hydrothermal system. We have repeated the numerical experiment with a reduced permeability k_top of 10^–14 m² and obtained the expected result of a 15-m-thicker basal brine layer. This confirms the arguments stated above that brine layer thickness is controlled by the balance between conductive heat flux from below and heat carried by the hydrothermal circulation system, which in turn is controlled by permeability.

3.3 Simulation 2: Mid-Pressure Conditions (20 Mpa on Top) Lead to A Brine Layer on Top of a Halite Zone

A reduction in the top pressure boundary condition results in a change in the stable phase assemblages and the dynamics of basal brine formation. In the mid-pressure set up, liquid–vapor separation is quickly followed by halite precipitation at the bottom. Here, at bottom pressures of 29 MPa, phase separation starts at temperatures of around 404 °C (Figs. 11, 12). The rising vapor phase has a very low salt content of only 0.1 wt% (at a temperature of 435°). Therefore, salt is rapidly accumulating at the bottom within the forming brine phase, whereas the rising vapor phase mixes with seawater resulting in a central upflow zone with salt contents of 0.3 to 1 wt% after 250 years, which is lower than in the high pressure case presented above (Fig. 11a). The basal brine phase has a salt content of up to 55 wt% and, upon further heating to a temperature of 476.4 °C, enters three-phase conditions where liquid, vapor, and halite coexist (Fig. 3c). During further heating, the fluid leaves the three-phase region and the brine phase becomes separated into vapor and halite (upon entering the V + H field, Fig. 3c). Above the V + H region, brines that formed during phase separation within heated recharge fluids are slowly flowing (no visible blue arrows) into the V + H region where the salt of the brine is deposited as halite (see Fig. 12a; dark red color at 100 m to 200 m). This process results in a clogging of the pore space, which progressively blocks the pathways for heat mining vapors.

Fig. 11

Simulation results for a top pressure of 20 MPa. Color plots of total salt content in pore space in wt% NaCl and temperature contours in °C

Fig. 12

Scaled-up color plot of total salt content and mass fluxes for a top pressure of 20 MPa. Black arrows display liquids of X < 10 wt% NaCl. Blue arrows display liquids of X > 10 wt% NaCl. Red arrows display vapor (see definition for vapor in Sect. 2.3). Arrow lengths have same scale factor for all colors. White contour lines show isotherms in °C

Figure 13 shows that the V + H region is continuously growing and halite saturation reach values > 90%. Also brine saturations in the overlying L + V region reach values of more than 95%. Compared to the high pressure simulation, the amount of salt accumulated in this basal boundary region is 3.5 times higher, and consequently, the salt content of venting fluids is substantially lower. After 900 years, a 20-m- to 30-m-thick brine layer has formed. This brine layer is less effectively separated from the overlying single-phase flow as it was in the high pressure experiment (Fig. 12b). The reason is that the layer is thinner and that the density contrast to the above single-phase fluid is smaller. At 400 °C, the low salinity single-phase liquids (black arrows) and the vapor phase have similar flow directions and form a thin two-phase flow region that connects overlying convection with the brine layer. Yet, the hot brines (> 400 °C) have a higher viscosity and a reduced buoyancy so that entrainment into the upflow zone is still very limited. Therefore, temperatures within the up flow zone never exceed 400 °C. Compared to the high pressure simulation, the total basal heat input is in steady state and 15% lower (Figs. 14a, 15).

Fig. 13

Simulation results for a top pressure of 20 MPa at central profiles from − 825 to − 1000 m depth after 250 yrs, 900 yrs and 1000 yrs. a, c, e Phase saturation with coexisting phase regions. b, d, f fluid temperature and total salt content of pore space

Fig.14

Simulation results for a top pressure of 20 MPa. a Blue line: total power of conductive heat flow from bottom into the domain. Red line: top power balance of inflow and outflow. Dark yellow line: bottom salt mass accumulation by considering liquids with more than 10 wt% NaCl, and halite. Unit is tons of pure salt. Dashed black lines show points of time pictured in Fig. 7. b Red line: maximum outflow temperature. Green line: salt content of fluid with maximal outflow temperature. After 900 years the green line shows maximal salt content of outflow. Green dashed line show seawater salt content

Fig. 15

a Total bottom heat input and b central [− 600 m, + 600 m] heat input comparison. Vertical dashed lines mark the change in the temperature boundary condition between 900 and 950 yrs

When the temperature boundary condition is reduced after 900 yrs, brines are mobilized into the upflow zone at a rate that is similar to the high pressure experiment. For the simulation time span between 950 and 1100 yrs, a comparison of Figs. 10 and 14 reveals the same decline of bottom salt mass for both simulations. The reduced heat flow from below results in the merging of recharge fluids with brines at colder temperatures under single-phase conditions. Here, also brines with 5 to 10% salt are sufficiently buoyant for feeding the up flow zone, whereas brines with higher salt contents have to be diluted before they can rise. Figure 14a shows that halite is constantly dissolved by diluted brines and that brine venting occurs for a longer period of time with respect to the high pressure experiment.

4 Discussion

We have presented a novel coupled scheme of solving the governing conservation equations of hydrothermal transport in the system H₂O–NaCl. This methodology is an extension of the pure water model recently presented by Vehling et al. (2018). A key ingredient of this methodology is the mapping of the PTX equation of state presented by Driesner and Heinrich (2007) into PHX space, which allows resolving isothermal phase transitions like pure water boiling and liquid–vapor–halite coexistence. The governing conservation equations are solved simultaneously and implicitly, which allows for larger-than-explicit time steps and for a direct control of the numerical error. However, quantifying the concrete strengths and limitations of this method requires an inter-code comparison with previous models that is beyond the scope of this paper.

Here we have presented a first application and investigate how brine formation and mobilization affect heat transport in a submarine hydrothermal system heated from below. We find that a basal internally stable stratified brine layer progressively forms with a maximum vertical extent that is controlled by a balance between basal heat input and hydrothermal heat transport. It is the vertical extent of this stable layer that controls heat transfer from a heat source below into the active circulation system above. The layer thickness is controlled by the stable phase assemblages (e.g., V + H versus V + L in the presented mid- and high pressure simulations above), the bottom temperature boundary condition, and the permeability within the flow zone. How different phase transitions affect heat input can be exemplified by comparing the mid- and high pressure simulations. The temperature boundary condition and permeability structure are the same in both simulations, yet the heat input is different (Fig. 15). Up to simulation time 150 yrs, the mid-pressure simulation has a 20% higher central heat flow because boiling occurs at lower temperatures and the formed vapor phase drives small-scale circulation, which results in a higher heat flux (Fig. 15b). This effect is reduced when brines and halite build up a conductive boundary layer. After 400 yrs, simulation 1 has a higher heat input because the recharge flow can be heated up to 462 °C (versus 400 °C in simulation 2) and hence has a higher enthalpy and can extract more heat from the conductive layer. Consequently, the layer is thinner and has a higher temperature gradient. When the simulations approach a steady state at about 800 yrs and after 1400 yrs, the mid-pressure simulation has an about 20% lower heat input.

Permeability directly controls the vigor of hydrothermal convection and thereby heat transport. The higher the permeability, the more effective heat transport becomes, and the thinner is the basal brine layer. This is exemplified by the predicted heat input of two models with different permeabilities shown (Fig. 16). Figure 16 further shows a comparison between a pure water model and simulation 1 for seawater. The predicted total basal heat input is about 25% higher in the pure water simulation. This shows the effectiveness of a basal brine layer in insulating the driving heat source. The progressive accumulation of a basal brine layer therefore reduces the conductive heat loss from the heat source.

Fig. 16

Blue lines: power of bottom heat flow. Dark yellow lines: total salt mass accumulation by considering liquids with more than 10 wt% NaCl

The total steady heat flux of our simulations integrated over 1 km along the ridge axis is 16 MW for the high pressure and 14 MW for the mid-pressure simulation. Theoretical calculations of total heat flux released by crustal accretion and cooling for fast spreading ridges of 10 cm/yr are in the range of 44 MW to 71 MW per 1 km ridge axis (Fontaine et al. 2017) depending on whether lower crustal hydrothermal cooling is taking into account. Our predicted values are substantially lower, which may be due to relatively low values of permeability and/or transient as well as 2-D versus 3-D effects. Hydrothermal fields with the highest heat fluxes like Main Field Endeavor (450 MW) and EPR 9°50′N (160 MW) (Lowell et al. 2013) are related to recent magmatic eruptions and a high melt input to the AML. Coming back to the paradox of sustaining high heat fluxes despite the rapid formation of a basal brine layer (Fontaine and Wilcock 2006), our results show that brines are not leaving the base by entrainment into the up flow zone, which again illustrates the problem of reconciling high heat fluxes with rapid brine formation. We find that brines with salt contents of more than ~ 10 wt% are significantly less buoyant than heated recharge flow so that they cannot be entrained and mobilized. Brines with a salt content of less than ~ 10 wt% can be partially mobilized but are rapidly diluted.

A possible solution to this conundrum is that brines are able to spread laterally. This requires a sufficient basal inclination and hot basal temperatures (within the two-phase region). A complementary possibility is that brines may be able to move to deeper crustal levels possibly along pathways newly formed by thermal cracking (Olive and Crone 2018). At T = 600 °C (the approximate temperature at the brittle–ductile transition) and 45 MPa, brines have a density of ~ 1200 kg/m³, a salinity of ~ 70 wt%, and a viscosity of ~ 2 × 10^–4 Pa·s (comparable to the viscosity of pure water at 150 °C and 45 MPa). They are therefore negatively buoyant and mobile providing good conditions for effective salt transport. This raises the interesting possibility of brine redistribution to lower crustal levels. One possibility is along-axis brine flow driven by undulation in melt lens location and shape. Such variations in AML properties are shown in Xu et al. (2014) for EPR (9°30´N–10°00´N) and in Canales et al. (2006) for the Juan de Fuca Ridge. Such along-axis brine flow may result in a “communication” between neighboring hydrothermal circulation cells. Another possibility is brine flow to deeper crustal levels perpendicular to the ridge axis. For example, the inferred thermal structure at the EPR at 9°N (Dunn et al. 2000) may provide suitable conditions for the downward migration of the brine phase along the steep lateral margins of the central hot region—consistent with the proposed hybrid hydrothermal circulation model for fast spreading ridges (Hasenclever et al. 2014). Axis perpendicular brine flow may also be related to off-axis melt lenses (OAML) close to the AML. Two mid-crustal OAMLs have been found within only 1.5 to 2.5 km lateral distance and at 200 m vertical distance from ridge axis at EPR 9°37.5′N to 9°57′N (Aghaei et al. 2017; Han et al. 2014). At the time of the seismic survey, these OAMLs had low melt fractions implicating that magma replenishment rates of the OAML are relatively low with respect to the AML. One of the discovered OAMLs has nevertheless appeared to have delivered the melts for extrusive eruptions. It is very likely that these OAML drive a hydrothermal circulation system with an independent up flow zone. Accumulation of an in situ forming brine phase plus possibly down flowing brines from the ridge axis may result in thermal insulation of OAMLs thereby helping to stabilize them despite a low melt supply. Testing these hypotheses requires robust multiphase hydrothermal flow models, and we hope that the presented methodology will help making multiphase flow models more accessible.

5 Conclusions

The presented modeling framework and its initial application to submarine hydrothermal systems illustrate the potential of coupled schemes in multiphase flow calculations. The benefits of this method are large time steps and an explicit error control in the mass and energy conservation over a time step. However, there are also some drawbacks that need to be addressed in future work. These include a review of the EOS and the corresponding derivatives in PHX space in order to improve the convergence behavior of coupled schemes and research into how iteration schemes can better handle isothermal phase boundaries, which are not buffered by the specific heat of the host rock.

The key findings of the application of the method to submarine hydrothermal systems heated from below are that (1) progressive brine formation limits conductive heat transfer from the driving heat source into the active circulation system, (2) the formation of a brine layer leads to the rapid decoupling of the basal two-phase flow region from an active single-phase convection cell above that feeds seafloor vent sites, and (3) variations in basal heat supply can result in the mobilization of the brine phase and the venting of highly saline fluids. The implications of these findings are that pure water simulations may provide misleading results on heat transfer in submarine hydrothermal systems as they cannot resolve brine formation. The results further re-confirm the paradox of how very high heat fluxes as observed, e.g., at the EPR at 9°N and at the JdF ridge can be sustained for a prolonged period of time given that a thick basal brine layer should rapidly insulate the driving heat source. These findings thereby illustrate the need for future integrated data modeling work to better constrain the role of brines in modulating mass and energy transport in submarine hydrothermal systems.

Appendix

1.1 Thermohaline Single-Phase Convection

First, we present two simple tests of a buoyancy-driven single-phase flow. These thermohaline convection tests were also used by Geiger et al. (2006b) and had been originally published in (Oldenburg and Pruess 1999). The comparison is particularly useful, as the Geiger et al. (2006b) model uses a very similar EOS. In these two tests, a fluid parcel of constant temperature and salinity is placed in the center of a 2D domain, first as a positively buoyant and secondly as a negatively buoyant anomaly (see Fig. 17). The top of the domain is kept at a constant pressure, and all other sides are closed (no flow). We use a regular mesh of 47 × 47 boxes, where each box is split into four triangles by adding an additional point in the box center. Compared to the mesh in Geiger et al. (2006b) with 4425 nodes, we get 4513 nodes for a similar spatial resolution. For test 1 (positive buoyancy), the initial parcel has a temperature of 300 °C and salinity of 10 wt% and for test 2 (negative buoyancy) a temperature of 250 °C and a salinity of 12 wt% (Table 2).

Fig. 17

Model domain with initial and boundary condition after Oldenburg and Pruess (1999)

Table 2 Model parameter for thermohaline test

Our results show good overall agreement with those in Geiger et al. (2006b). Differences are caused by different grids and mass transport schemes like upwind weighting of fluid properties. It should be noted that the numerical solutions of such compositional flows are known to suffer from a dependence on property weighting; especially, the second test of a negatively buoyant fluid is sensitive to this and the number of “falling drips” and their spacing are affected by grid resolution and segment density weighting, i.e., is model dependent (Figs. 18, 19).

Fig. 18

Test 1 after 2 yrs and 20 yrs simulation time. Lower panels show the velocity field

Fig. 19

Test 2 after 2 yrs and 20 yrs simulation time. Lower panels show the velocity field

1.2 One-Dimensional Multiphase Test with Fluid Extraction

The ability of the code to resolve two- and three-phase conditions is demonstrated in a 1-D test originally published by Kissling (2005a) and later also used by Lewis and Lowell (2009). A horizontal 1-D domain of 1000 m length is initially at constant pressure (p = 20 MPa), temperature (T = 350 °C), and salinity (X = 30 wt%). These conditions are kept constant at the left-hand boundary throughout the simulation. At the right-hand boundary, fluid is extracted at a rate of 0.0005 kg/(m²·s) until pressure is reaching almost zero after 4.8 × 10⁶ s simulation time. During this drawdown experiment, a fluid flowing from left to right undergoes a series of phase transitions (L → L + V → L + V + H → V + H). Relative permeability is set according to Eqs. 29 and 30, while halite is assumed to not have an effect on flow in order to be consistent with Kissling (2005a). Because Kissling (2005a) used a different EOS, namely the one of Palliser and McKibbin (1998c), where brine viscosity is much higher, we reduce rock permeability to 3.05·10^–15 for a qualitative comparison of our results. This modification results in very similar pressure profiles, but some differences remain due to differences in the phase densities and specific enthalpies (see also Lewis and Lowell 2009) (Table 3).

Table 3 Model parameters for test in "One-dimensional multiphase test with fluid extraction" section

Figure 20 shows our results when pressure at the right-hand boundary has reached 1 MPa after a simulation time of 4.793 × 10⁶ s. The reduction in pressure induces phase transitions from single-phase liquid to L + V, to L + V + H to V + H that cause a redistribution of salt and an accumulation of salt where halite is stable. The energy transport increases in the L + V + H region as a consequence of the increasing importance of vapor flow, which results in the strong temperature drop in the L + V + H region. While the pressure and the bulk salt concentration are relatively close to the solution presented Kissling (2005a), differences occur in the phase saturations. These differences result from a different EOS for salt water and possibly due to different numerical schemes. Note that TOUGH2 makes a switch in primary variables under two- and three-phase conditions. The test nevertheless shows the ability of our code to handle the continuous transitions between one-, two-, and three-phase fluid states.

Fig. 20

Results of a 1-D multiphase experiment originally presented by Kissling (2005a). Fluid is extracted at the right-hand boundary triggering a sequence of phase transitions. While the pressure and salt solutions are similar to the ones presented by Kissling (2005a), differences occur in the phase saturations—mainly as a result of differences in the used equation of state. Lower panel plot shows in addition the temperature solution and how phase transitions affect horizontal energy transport

1.3 One-Dimensional Vertical Salt Pipe

In this test case, originally performed in Kissling (2005a), we show that the code conserves mass for vertical counter flow of liquid and vapor. For the steady state of zero net mass flux, one can analytically calculate the pressure gradient for given fluid properties by setting the sum of vapor mass flux and liquid mass flux to zero and solving for the pressure gradient:

$$0 = - k\frac{{k_{{r{\text{l}}}} \rho_{{\text{l}}} }}{{\eta_{{\text{l}}} }}\left( {\frac{\partial p}{{\partial z}} - \rho_{{\text{l}}} {\vec{{\bf g}}}} \right) - k\frac{{k_{{r{\text{v}}}} \rho_{{\text{v}}} }}{{\eta_{{\text{v}}} }}\left( {\frac{\partial p}{{\partial z}} - \rho_{{\text{v}}} {\vec{{\bf g}}}} \right)$$

(42)

$$\frac{\partial p}{{\partial z}} = \frac{{{\vec{{\bf g}}}\left( {{{k_{{r{\text{l}}}} \rho_{{\text{l}}}^{{2}} } \mathord{\left/ {\vphantom {{k_{{r{\text{l}}}} \rho_{{\text{l}}}^{{2}} } {\eta_{{\text{l}}} + }}} \right. \kern-\nulldelimiterspace} {\eta_{{\text{l}}} + }}{{k_{{r{\text{v}}}} \rho_{{\text{v}}}^{2} } \mathord{\left/ {\vphantom {{k_{{r{\text{v}}}} \rho_{{\text{v}}}^{2} } {\eta_{{\text{v}}} }}} \right. \kern-\nulldelimiterspace} {\eta_{{\text{v}}} }}} \right)}}{{{{k_{{r{\text{l}}}} \rho_{{\text{l}}} } \mathord{\left/ {\vphantom {{k_{{r{\text{l}}}} \rho_{{\text{l}}} } {\eta_{{\text{l}}} + }}} \right. \kern-\nulldelimiterspace} {\eta_{{\text{l}}} + }}{{k_{{r{\text{v}}}} \rho_{{\text{v}}} } \mathord{\left/ {\vphantom {{k_{{r{\text{v}}}} \rho_{{\text{v}}} } {\eta_{{\text{v}}} }}} \right. \kern-\nulldelimiterspace} {\eta_{{\text{v}}} }}}}$$

(43)

The model setup is adopted from Kissling (2005a), where the simulation is performed on a grid of 100 m with a node spacing of 1 m. The top boundary has a fixed pressure (p = 60 MPa) and temperature (T = 600 °C). Additionally, liquid saturation is fixed to S_l = 0.5 here, which leads to a pressure gradient of − 6978 Pa/m by using linear relative phase permeability (k_rl = S_l, k_rv = S_v) and calculated fluid properties in Table 4. The mean salt composition is computed to X = 47.78 wt% NaCl. According to the pressure gradient, we fix pressure to 60.6987 MPa at the bottom, where also temperature is fixed to 600 °C. The initial domain conditions are T = 600 °C and p = 60 MPa. Rock properties are listed in Table 5. After a simulation time of approx. 8 × 10¹² s, the system is in steady state and the simulated results are in agreement with the analytical results, derived at top conditions (see Table 6). Differences are caused by slightly changing fluid properties within the domain due to pressure increase. Further comparison with results of those in Kissling (2005a) or in Lewis and Lowell (2009), where this test also has been performed, is not reasonable as fluid properties differ to much due to EOS; especially the lower liquid viscosity in this study leads to much higher pressure gradients and fluxes.

Table 4 Fluid Properties at T = 600 °C and p = 60 MPa compared to those in Kissling (2005a)

Table 5 Model parameters for test in "One-dimensional vertical salt pipe" section

Table 6 Analytical versus simulated results of test in "One-dimensional vertical salt pipe" section