Contact Angles in Two-Phase Flow Images

Abstract

In this work, we calculate contact angles in X-ray tomography images of two-phase flow in order to investigate the wettability. Triangulated surfaces, generated using the images, are smoothed to calculate the contact angles. As expected, the angles have a spread rather than being a constant value. We attempt to shed light on sources of the spread by addressing the overlooked mesh corrections prior to smoothing, poorly resolved image features, cluster-based analysis, and local variations of contact angles. We verify the smoothing algorithm by analytical examples with known contact angle and curvature. According to the analytical cases, point-wise and average contact angles, average mean curvature and surface area converge to the analytical values with increased voxel grid resolution. Analytical examples show that these parameters can reliably be calculated for fluid–fluid surfaces composed of roughly 3000 vertices or more equivalent to 1000 pixel². In an experimental image, by looking into individual interfaces and clusters, we show that contact angles are underestimated for wetting fluid clusters where the fluid–fluid surface is resolved with less than roughly 500 vertices. However, for the fluid–fluid surfaces with at least a few thousand vertices, the mean and standard deviation of angles converge to similar values. Further investigation of local variations of angles along three-phase lines for large clusters revealed that a source of angle variations is anomalies in the solid surface. However, in the places least influenced by such noise, we observed that angles tend to be larger when the line is convex and smaller when the line is concave. We believe this pattern may indicate the significance of line energy in the free energy of the two-phase flow systems.

Motivation

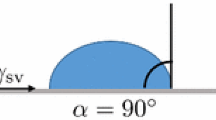
Wettability of a solid surface in contact with two fluids is traditionally defined by the angle the interface of the two fluids create with the solid. If the free energy associated with the solid–fluid and fluid–fluid interfaces depend only on interface areas, the contact angle $\theta$ will depend on the interfacial tensions between the two fluids ($\sigma _{21}$) and fluids with solid ($\sigma _{2s}, \sigma _{1s}$) through Young’s equation (1), (Young (1805) and Laplace (1806))

$$\begin{aligned} \cos \theta = \frac{ \sigma _{2s} - \sigma _{1s} }{ \sigma _{21}} \end{aligned}$$

(1)

The applicability of Eq. (1) is restricted to ideal smooth surfaces of a homogeneous solid material, and the corresponding contact angle is sometimes referred to as an intrinsic contact angle (Sun et al. 2020a). The effect of rough surfaces can be included in the surface tensions $\sigma _{1s}$ and $\sigma _{2s}$, with a resulting effective contact angle $\theta$. Even though the surfaces of glass beads in synthetic media are smoother than surfaces in natural porous media, the angles measured by means of micro-CT in the micron scale should be categorized as the effective angles. However, we expect the effective interfacial tensions to be fairly constant throughout the medium. We refer to Appendix 1 of reference (Berg et al. 2020), for further reading about sub-resolution roughness.

Accordingly, the contact angle is expected to be close to constant in a single material porous medium, such as sintered glass beads. Similarly, the mean curvature of fluid–fluid interfaces, $\kappa _{H,f}$, depends on the pressure difference, $P_c$, across the interface and the interfacial tension through Laplace’s equation,

$$\begin{aligned} \kappa _{H,f} = \frac{P_c}{2\sigma _{21}}, \end{aligned}$$

(2)

and hence, the fluid–fluid interfaces are expected to have constant curvature.

The contact angle, as an important means of measuring wettability Anderson (1986), influences fluid distribution in two-phase flow. It is also an important input parameter in pore scale simulations (Ramstad et al. 2019). With recent advances in micro-computed X-ray tomography, configurations of two fluids in complex three-dimensional porous media have been imaged (Berg et al. 2013; Schlüter et al. 2017). Therefore, one wishes to use a contact angle measured in situ from images in the simulations. Andrew et. al. (2014) measured contact angles manually, whereas Klise et al. (2016), Scanziani et. al. (2017) and AlRatrout et. al. (2017) performed automated measurements with different methodologies. However, the measured contact angles at multiple (thousands or tens of thousands) contact points in the X-ray images tend to show a wide distribution rather than a single value (AlRatrout et al. 2017, 2018a, b; Alhammadi et al. 2017). Mixed wetting, surface roughness, and advancing/receding contact angles are thought to be sources of the spread (AlRatrout et al. 2017, (2018a, b). However, a constant contact angle and surface curvature is also not expected if the free energy contains additional contributions related to the length of three-phase contact lines or surface curvatures (Khanamiri et al. 2018), predicted by Hadwiger’s characterization theorem (Hadwiger 1957).

User-biased image segmentation, the limited image resolution, and artifacts imposed by surface smoothing will contribute to a spread in the measured angles and local interface curvature. In order to answer questions related to the relative importance of surface roughness, advancing/receding angles, and additional free energy contributions for the contact angle and curvature variations, it is important to minimize and quantify these errors. The effect of advancing/receding angles was addressed by Mascini et al. (2020). They proposed an event-based approach where they investigated only receding contact angles in pore-filling events in the drainage process and observed a narrower distribution of the angles. In order to solve some of the mentioned issues, a number of averaging schemes have been proposed recently. For instance, Blunt et al. (2019) proposed a thermodynamic averaging scheme, which was updated later by including the dissipation (Akai et al. 2020; Berg et al. 2020). In this work, we do not investigate the thermodynamic approach where the efficiency of the displacement process is a major unknown.

In an number of recent works, integral geometry is used as an alternative to the direct angle measurement. Sun et al. (2020b) introduced this approach by linking local curvatures and topology of a cluster using the Gauss–Bonnet theorem. Blunt et al. (2020) and Sun et al. (2020a, c) elaborated on the methodology. These methods often require calculation of local curvatures which are typically products of surface smoothing, a common part shared between the direct measurement and the integral geometry methods. Addressing the sources of angle distribution in the direct method, in this work, can potentially be used in improving accuracy of the methods based on integral geometry.

Furthermore, our approach is entirely a mathematical solution to surface smoothing, without any assumptions based on the current understanding of a physical equilibrium, neither with any assumptions on the possible variables influencing the contact angles. We choose this approach in order to avoid smoothing artifacts possibly induced by such assumptions. The counterparts of our approach are for instance the work by Raeini et al. (2012) or smoothing by the Surface Evolver package. Raeini et al. (2012) ran two-phase flow simulation on the experimental images in order to correct the imaging artifacts where the simulated velocities were inconsistent with the physical model.

In this work, we present a method for extracting contact angles and curvatures from tomography images by smoothing triangulated surface representations of the solid–fluid and fluid–fluid interfaces (Khanamiri 2019). High resolution experimental data (Schlüter et al. 2016b) of sintered glass beads and simple fluids were investigated to minimize possibility of contact angle spread as a result of mixed wetting or other surface heterogeneities.

Triangular Mesh and Differential Geometry

In this section, a number of properties for a triangular mesh are introduced from differential geometry. The wire-frame in Fig. 1 shows 1-ring neighborhood $N_1( i )$ of vertex $x_i$. $N_1(i)$ is the triangular domain confined by the immediate neighbor vertices of $x_i$, for instance $x_j$. Unit normal vector of each triangular face, placed at centroid of the triangle, is calculated by cross product of two edges of the triangle. The cross products should be consistently clockwise or anti-clockwise to ensure all normal vectors pointing from one phase—fluid or solid—to another in the entire mesh. Unit normal vector for $x_i$ is calculated by Eq. (3),

$$\begin{aligned} \hat{n}(x_i) = \frac{\sum _{T_k \in N_1(i)} \hat{n}(T_k)}{|\sum _{T_k \in N_1(i)} \hat{n}(T_k) |}, \end{aligned}$$

(3)

where $T_k$ is a triangular face in $N_1(i)$, with unit normal vector $\hat{n}(T_k)$.

Fig. 1

1-ring neighborhood $N_1(i)$ of vertex $x_i$ with shaded Voronoi area

The shaded region in Fig. 1 is Voronoi area of $x_i$, which is a fraction of the area in the $N_1(i)$ neighborhood and defined by different methods. One simple method is to connect centroids of the triangles to midpoint of the edges. This results in a Voronoi area equals to one-third of the entire 1-ring neighborhood of the vertex, Desbrun et al. (1999), and can be calculated by,

$$\begin{aligned} A_{voronoi}(x_i)=\frac{1}{8}\sum _{j \in N_1(i)} (\cot \alpha _{ij}+\cot \beta _{ij}) {|x_i -x_j |}^2 \end{aligned}$$

(4)

where angles $\alpha _{ij}$ and $\beta _{ij}$ are the two angles opposite to the edge ij, as shown in Fig. 1. The definition by Meyer et al. (2003) is the same as Eq. (4) only when $\alpha _{ij}, \beta _{ij}$ and the angles at $x_i$ are nonobtuse. In case of obtuse angles, the portion of $A_\mathrm{voronoi}(x_i)$ from the edge ij in triangle $T_\alpha$ is $\hbox {area}(T_\alpha )/4$ if $T_\alpha$ is obtuse at $x_i$, and $\hbox {area}(T_\alpha )/2$ if $T_\alpha$ is obtuse in other angles. A visual inspection showed that the definition proposed by Meyer et al. (2003) ensures a robust smoothing in complex structures, whereas the method by Desbrun et al. (1999) can be unstable in neighborhoods with rapidly changing curvatures such as where two glass spheres are sintered.

Calculation of curvatures and smoothing a mesh requires finding Laplace–Beltrami operator, K for vertices. According to the derivation by Meyer et al. (2003),

$$\begin{aligned} K(x_i)=\frac{1}{2A_{{\rm voronoi}}(x_i)}\sum _{j \in N_1(i)}(\cot \alpha _{ij}+\cot \beta _{ij})(x_i-x_j). \end{aligned}$$

(5)

Equations (4) and (5) are known as cotangent discretization. For vertex $x_i$, $K(x_i)$ and the mean curvature $\kappa _H(x_i)$ are related by $K(x_i)=2\kappa _H(x_i)\hat{n}(x_i)$. Therefore, using dot product of two vectors, we have

$$\begin{aligned} \kappa _H(x_i)=\frac{1}{2}K(x_i).\hat{n}(x_i). \end{aligned}$$

(6)

For a mesh, say a fluid–fluid interface, the average mean curvature $\overline{\kappa _H}$ can be calculated using

$$\begin{aligned} \overline{\kappa _H}=\frac{ \sum _{i=1}^V \kappa _H(x_i)A_{{\rm voronoi}(x_i)}}{A}, \end{aligned}$$

(7)

where A is area of the interface and V is the number of vertices on the interface.

The contact angle of solid–fluid and fluid–fluid meshes on a vertex on the three-phase contact line $x_{i,3}$ can be calculated by

$$\begin{aligned} \theta (x_{i,3})=\arccos (\hat{n}_s(x_{i,3}).\hat{n}_f(x_{i,3})), \end{aligned}$$

(8)

where $\hat{n}_s$ and $\hat{n}_f$ are unit normal vectors of $x_{i,3}$ in the solid–fluid and fluid–fluid meshes, respectively.

Note that in the definition by Meyer et al. (2003), the sum of Voronoi areas for all vertices does not always add up to the total mesh area due to presence of the obtuse angles; and in order to obtain an accurate $\overline{\kappa _H}$, we should consider using correct mesh area in denominator of (7). Our calculations in geometries with known curvatures showed that this approach ensures correct result in calculating $\overline{\kappa _H}$ using Voronoi region definitions by both Meyer et al. (2003) and Desbrun et al. (1999). Since there is no fundamental and unified definition of Voronoi regions, the point-wise mean curvatures tend to depend on the choice of Voronoi region and are unreliable. However, $\overline{\kappa _H}$ obtained by integration in (7) is reliable as average mean curvature for a mesh. Furthermore, choice of Voronoi region does not have a large effect on point-wise contact angle calculation, as $\theta (x_i)$ in (8) is calculated using unit normal vectors which only weakly depend on the Voronoi region definition.

Mesh Generation

Segmented tomography images of fluids in porous media are volume data comprising voxels on a regular grid, and interfaces are defined on the voxel boundaries. A triangular mesh for the interfaces is created by defining triangles on each of the corresponding voxel boundaries. Every square face is symmetrically divided into four triangle faces as shown in Fig. 2. Using four triangles in the squares instead of two gives sufficient valence to all vertices for smoothing and curvature calculations. The resulting mesh will have a stair-case configuration with sharp edges and corners and must be smoothed in order to find contact angles and other related parameters such as curvatures.

Fig. 2

a Segmented tomography image with two different fluid voxels on top of two gray solid voxels, a triangular mesh grid defined on the square voxel boundaries. Blue and red are solid–fluid and fluid–fluid meshes, respectively. Green balls mark the three-phase contact vertices. The vectors are unit normal vectors for vertices

Note that when building a mesh for an interface (say fluid–fluid interface) from a segmented image, it is straightforward to identify the triangular faces and also the orientation of these faces, i.e., the normal vectors of the faces. The edges and vertices defining these faces are, however, not always to be shared between faces even when they have the same coordinates. This occurs when an interface, due to insufficient resolution, touches itself or another interface at a vertex or along an edge as shown in Fig. 3. These vertices and edges must be identified and duplicated into separate entities for each part of the interface. The vertices that must be duplicated are called nonorientable since, for a self-touching interface, the surface orientation is undefined at these points if the vertices are not duplicated. Nonorientable vertices tend to be abundant near the three-phase contact lines and in narrow parts of the pore space, and incorrect treatment of these vertices will lead to errors in contact angle and curvature calculations. These errors are especially severe for properties of the wetting fluid trapped in narrow regions forming pendular ring structures.

Fig. 3

a Simplified two-dimensional illustration of an interface in reality, b and in a mesh grid. Vertex in the marked poorly resolved part is nonorientable

Vertices in the mesh grid correspond to either a center or a corner of voxel boundaries in the voxel grid (see Fig. 2). The center vertices are always orientable, whereas the corner vertices can be nonorientable. Therefore, we use the correct orientation of center vertices in the 1-ring neighborhood of corner vertices to identify and correct the nonorientable ones.

Figure 4 shows examples of nonorientable vertices from experimental images—both far from and in the vicinity of three-phase contact line—and how they affect the mesh smoothing with and without corrections. Figure 4d–f shows the nonorientable vertices close to the three-phase contact line that, if not corrected, can be falsely classified as contact vertices where the contact angles are measured. As an example, in an experimental image with 232882 vertices on the three-phase contact line, 15181 vertices were nonorientable, and 8813 of nonorientable vertices were either on the three-phase line or incorrectly considered as a part of it before corrections.

Fig. 4

a-c solid–fluid mesh, in blue, where two solid grains are close: a five nonorientable vertices are marked on solid–fluid mesh before smoothing, vertices lie on the corners of pixels with corner–corner or edge–edge contact, b 10 iterations in smoothing without correction where the vertices are pinned avoiding proper smoothing, c 10 iterations in smoothing after duplicating vertices— green and red; d–f solid–fluid (blue) and fluid–fluid (red) in the vicinity of three-phase contact line: d three nonorientable vertices close to the contact line , e a few steps in iterations without corrections, f and with corrections. The corrections in (c) and (f) are done by duplicating the nonorientable vertices and assigning the correct neighbor vertices and triangles to each duplicate

Mesh Smoothing

The generated initial mesh has sharp edges and corners and must be smoothed in order to find contact angles and other related parameters such as curvatures. The vertices on the three-phase contact lines belong to both the solid–fluid and the fluid–fluid meshes which must be smoothed consistently through smoothing iterations. Different smoothing techniques have been proposed; for instance, Akai et al. (2019) fitted surfaces on triangular meshes; and AlRatrout et. al. (2017) changed positions of vertices by performing either Gaussian or curvature smoothing while keeping the global phase volumes approximately constant. Our approach is similar to the work by AlRatrout et al. (2017), in the sense that vertices are displaced to minimize the curvatures. However, weights of displacements and the way we use neighborhood of vertices are different in this work. Our methodology is mainly based on isotropic smoothing flow by Meyer et al. (2003). We displace the vertices along their unit normal vectors with mean curvature as the weight of disparagement. The constraint on the displacements is based on voxel length and imaging uncertainty as opposed to the phase volume constraint used by AlRatrout et al. (2017). Furthermore, we represent the surfaces by triangular cells whereas AlRatrout et al. (2017) used square cells. The details of smoothing are explained in this section.

In principle, smoothing a surface involves solving Laplace’s equation, $\nabla ^{2}f=0$ in general, or the Young–Laplace equation, $-2\kappa _H=\nabla .(\nabla f / |\nabla f |)=\hbox {const}$ in particular for fluid–fluid surfaces. Here f is the function expressing the surface. For the Laplace’s equation, smoothing is also equivalent to Euler–Lagrange equation, $\kappa _H=0$ used for surface area minimization (Meyer et al. 2003). In absence of a function, the surface is discretized and the Laplace’s equation is solved by a numerical method, e.g., finite difference. A 2-manifold—a mesh—is represented by vertices and discrete triangles rather than by an ordinary continuous surface. Generalization of Laplace’s equation from surfaces to manifolds is known as Laplace–Beltrami method which can be discretized using cotangent scheme in order to calculate Voronoi area (see Fig. 1), Laplace–Beltrami operator and mean curvature in Eqs. (4)–(6).

Smoothing is an iterative procedure where in each iteration, all vertices are displaced simultaneously after calculating the displacements. A vertex $x_i$ is displaced a distance $\varDelta x_i$ along the surface unit normal vector $\hat{n}(x_i)$ with $\kappa _H(x_i)$ as the weight of displacement. Smoothing the solid–fluid and the fluid–fluid meshes are performed in a similar manner, except for the vertices lying on the three-phase contact line.

$$\begin{aligned} x_{i,new} &= x_{i,previous} - \varDelta x_i \end{aligned}$$

(9)

$$\begin{aligned} \varDelta x_{i,s} &= t_s \kappa _{H,s}(x_{i,s}) \hat{n}_s(x_{i,s}) \nonumber \\ \varDelta x_{i,f} &= t_f (\kappa _{H,f}(x_{i,f}) - \overline{\kappa _{H,f}}) \hat{n}_f(x_{i,f}) \nonumber \\ \varDelta x_{i,3} &= t_s \kappa _{H,s}(x_{i,3}) \hat{n}_s(x_{i,3}) + t_f (\kappa _{H,f}(x_{i,3}) -\overline{\kappa _{H,f}}) \hat{n}_f(x_{i,3}) \end{aligned}$$

(10)

The average mean curvature for individual fluid–fluid surfaces, $\overline{\kappa _{H,f}}$ is updated for each iteration using Eq. (7). The coefficients $0<t_s<1$ and $0<t_f<1$ in (10) are tuning parameters used mainly to avoid too much displacement which can cause smoothing to diverge in meshes imitating complex porous structures. We start the smoothing with $t_s=0.15$ and $t_f=0.3$ and change the values in the iterations following a reward/penalty strategy, meaning that if for instance, solid–fluid mesh improves in one step $t_s$ is multiplied by 1.05, and if it worsens, $t_s$ is multiplied by 0.8 for the next step. Coefficient $t_f$ is tuned with the same rule. This procedure was fixed after several test runs, and there is no theoretical reason for the choice of values for the coefficients. One can perform the iterations with both different initial values and multipliers for $t_s$ and $t_f$ and obtain smooth meshes as long as the smoothing does not diverge.

The displacement of all vertices is subject to the following two constraints.

$$ \begin{aligned} |\varDelta x_i |= \min(|\varDelta x_i |, 0.2) \\ |x_i - x_{i,{\rm initial}} |< \sqrt{3} \end{aligned}$$

(11)

First constraint in (11) ensures that $x_i$ does not displace more than 0.2 voxel length at each iteration. The displacement is reduced to 0.2 voxel length, if it is larger than that. Second constraint ensures that $x_i$ does not move farther than $\sqrt{3}$ voxel length from its initial position. This value is the longest distance inside a voxel in the voxel grid. Maximum displacement of $\sqrt{3}$ is associated with the uncertainty in the experimental images such that $x_i$ could in reality be anywhere inside one voxel. In the images investigated, only a minor fraction of the vertices are moved a distance close to $\sqrt{3}$ in voxel length. For instance, after smoothing a tomography image, mean displacements of vertices in solid–fluid surfaces, fluid–fluid surfaces, and three-phase contact lines were approximately 0.30, 0.30, 0.52 voxel length, respectively; vertices displaced more than $0.95\sqrt{3}$ were only 0.20, 0.03, 0.02 percent of all vertices in those entities.

As mentioned earlier, for a smooth solid–fluid surface, mean curvatures are being minimized $\kappa _{H,s}(x_i) \rightarrow 0$. It should be noted that $\kappa _{H,s}(x_i)$ values are not becoming exactly zero because of the constraint in Eq. (11). The geometric implication is that for a solid–fluid surface throughout the iteration steps, the unit normal vectors of neighbor vertices align more parallel to each other once the surface is being smoothed, and their dot products approach unity. Therefore, we use $\tau _s$,

$$\begin{aligned} \tau _s = 1-\frac{1}{E_s} \sum _{i=1}^{V_s} \sum _{j \in N_1(i)} \hat{n}_s(x_i). \hat{n}_s(x_j) \rightarrow 0 \end{aligned}$$

(12)

as the target of smoothing for the solid–fluid mesh, where $V_s$ and $E_s$ are the number of vertices and edges in the solid–fluid mesh.

For a smooth fluid–fluid surface, the mean curvatures approach an unknown constant value $\kappa _{H,f}(x_i) \rightarrow \overline{\kappa _{H,f}}$. The standard deviation of $\kappa _{H,f}(x_i)$ should be locally minimized for each interface. Therefore, the target for the entire domain can be minimizing average of the standard deviations, std, for all fluid–fluid surfaces, and Eq. (13) serves as the target for smoothing the fluid–fluid mesh.

$$\begin{aligned} \tau _f=\frac{1}{M} \sum _{m=1}^M std(\kappa _{H,f}) \rightarrow 0 \end{aligned}$$

(13)

In Eq. (13), M is the number of fluid–fluid interfaces in the mesh grid.

We use $\tau$ and t variables to stop the iteration. Smoothing iterations continue as long as both $\tau _s$ and $\tau _f$ are reducing. If their minimum values are at the latest step, it means that they have not reached a minimum and smoothing is continued. The solid–fluid mesh often improves faster, and $\tau _s$ can reach a minimum before $\tau _f$. At this point, $\tau _f$ has not reached a minimum and the iterations must be continued. In these conditions, the quality of solid–fluid mesh may degrade as $\tau _s$ will start to increase. Therefore, the coefficient $t_s$ in Eq. (10) reduces automatically to keep the changes in the solid–fluid mesh to a minimum. The reason we do not immediately set $t_s=0$ is that the solid–fluid mesh in every iteration needs to be readjusted in the vicinity of the three-phase contact line when fluid–fluid mesh improves. With $t_s=0$ and a changing fluid–fluid mesh, the line will be pulled out of the solid–fluid mesh. Once $\tau _f$ has also passed a minimum and starts to increase, $t_f$ in Eq. (10) will automatically reduce. At last, when both $\tau _s$ and $\tau _f$ have passed minima, and one of the tuning coefficients is $t < 10^{-3}$, the smoothing stops after five more iterations, and the results of iteration with least $\tau _f$ is picked up as the final result. At the end, the number of iterations is approximately in the range of 50–100. Figure 5 shows variations of contact angle, $\tau _s$ and $\tau _f$, as smoothing progresses in an analytical model of a sphere–plane geometry explained in the next section.

Fig. 5

Evolution of mean contact angle $\theta _m, \tau _s$ and $\tau _f$ in smoothing a sphere–plane geometry with known analytical angle shown by the solid line. Error bars are standard deviations of $\theta$

In a smooth mesh grid, $\tau _s$ value is approximately in the order of $10^{-3}$ with variations between two steps in the order of $10^{-5}$; $\tau _f$ is approximately in the order of $10^{-2}$ with step variations in the order of $10^{-3}$. Smoothing several experimental images showed that although cotangent discretization smoothes surfaces, it is not convergent in the sense that despite the point-wise values of $\kappa _H$ become more uniform, they are not equal (Meyer et al. 2003; Xu 2013). Improvement slows down as smoothing progresses. The point-wise convergence may depend on the voxel grid resolution. In the next section, using analytical examples with known curvature and contact angles, we show that although point-wise $\kappa _H$ is not convergent, average mean curvatures $\overline{\kappa _H}$ and point-wise contact angles $\theta$ are convergent when grid resolution is sufficient.

Analytical Examples

We attempt to verify the smoothing algorithm and to investigate the limitations by examining two examples with known contact angle and curvature. We create synthetic voxel images of two different configurations simply by intersecting sphere–plane equations where the sphere radius and the distance between the plane and the sphere center are known. Figure 6 shows the two examples where the solid–fluid interfaces are simply represented by planes, and the fluid–fluid interfaces are part of a sphere. For these two configurations, analytical $\kappa _H$ and $\theta$ are constant. Images with different resolution were created by increasing number of the voxels representing the geometry.

Fig. 6

Smoothing two synthetic examples resolved by $87 \times 87 \times 87$ voxels where a an imaginary fluid droplet in red is in the form of a spherical cap resting on a planar solid surface in cyan, b an imaginary spherical droplet in red is intersected with two parallel solid planes in cyan both with the same distance from center of the sphere. The black dots mark the three-phase contact points on the smoothed meshes. All original voxel meshes are in gray

Figure 7 shows the calculated error $\varepsilon$ with respect to inverse of number of vertices in the fluid–fluid surface $1/V_f$. The grid resolution is higher at smaller $1/V_f$. Figure 7 shows that point-wise contact angles $\theta$ (Eq. (8)), average mean curvature $\overline{\kappa _{H,f}}$ (Eq. (7)), and interfacial area are converging as $1/V_f \rightarrow 0$, whereas point-wise mean curvatures $\kappa _{H,f}$ (Eq. (6)) are not converging.

Fig. 7

Mean % error $\overline{\varepsilon }$ for $\theta$ and $\kappa _{H,f}$, and % error $\varepsilon$ for interfacial mean curvature $\overline{\kappa _{H,f}}$ and area $A_f$ as a function of $1/V_f$, where $V_f$ is the number of vertices on the fluid–fluid surface. Grid resolution increases when $1/V_f \rightarrow 0$. The green dashed lines show $1/V_f=3.3\times 10^{-4}$, equivalent to $V_f=3000$. Note that the horizontal axes have a scale of $10^{-3}$

$V_f=148$ ($1/V_f=6.7\times 10^{-3}$) and $V_f=700$ ($1/V_f=1.4\times 10^{-3}$) for the spherical cap, $V_f=540$ ($1/V_f=1.8\times 10^{-3}$) and $V_f=2226$ ($1/V_f=4.4\times 10^{-4}$) for the cluster between two parallel planes have not yet captured the contact angles with an acceptable accuracy. Furthermore, $A_f$ and $\overline{\kappa _{H,f}}$, which is the inverse of radius for the complete sphere in these examples, can also be used as further discriminants to determine if the resolution was adequate in order to find $\theta$ and $\overline{\kappa _{H,f}}$. Overall, a fluid–fluid interface composed of roughly 3000 vertices or more and has roughly $\overline{\kappa _{H,f}} \le 0.01\,\hbox {pixel}^{-1}$ and $A_f \ge 10^3\,\hbox {pixel}^2$ could be reliable for computations. According to Fig. 7, both contact angle and average mean curvature are for the most part underestimated on poorly-resolved small interfaces.

Furthermore, for interfaces with sufficient resolution standard deviations of $\theta$ is roughly $1-2^\circ$; standard deviation of $\overline{\kappa _{H,f}}$ is in the order of $10^{-3}\,\hbox {pixel}^{-1}$.

Experimental Examples

In this section, we investigate dependency of contact angles on the size of fluid clusters in a 3D experimental X-ray tomography image published by Schlüter et al. (2016b). The two-phase flow experiments were performed with low flow rates at quasi-static equilibrium. The solid was composed of sintered glass beads with two different diameters; the fluids were brine and n-dodecane (Schlüter et al. 2016a). In this paper, we use an image from the early main imbibition with water saturation of 15.1 percent. Comparison of mean contact angles for individual fluid clusters revealed that the calculated contact angles for small clusters are smaller than those for large clusters. Figure 8 illustrates six examples. The large clusters (a)–(d) with several thousand vertices in the brine–dodecane interface have mean contact angles $\theta _m$ of $68^\circ$, $69^\circ$, $71^\circ$ and $74^\circ$; whereas smaller clusters with only a few hundred vertices have $\theta _m$ of $49^\circ$ and $31^\circ$. The cluster (f) in Fig. 8, has $\theta _m$ of $31^\circ$ which is even smaller than 49$^\circ$ for cluster (e). Cluster (f) is a droplet lying on the body of glass bead, while cluster (e) is one attempting to encircle the rim between two fused glass beads. We found that the small clusters of type (f) have often the least contact angles among the poorly resolved clusters. We believe this is a smoothing artifact. Smoothing without a constraint on the vertices displacement will eventually flattens a mesh. Displacement constraint of $\sqrt{3}$, Eq. (11), is a large degree of change for a small surface which stretches considerably to be close to a flat surface. This results in underestimation of both the contact angle and the curvature.

Figure 8 shows also number of three-phase contact lines $L_3$, and Euler characteristic $\chi$, of 2-manifold of the cluster surfaces. $\chi$ is calculated by Eq. (14),

$$\begin{aligned} \chi =V-E+F, \end{aligned}$$

(14)

where V, E, and F are number of vertices, edges, and triangle faces, respectively, on the entire surface of fluid cluster regardless of how fluid–fluid and solid–fluid interfaces cover the surface. This $\chi$ should not be mistaken with Euler characteristic of the cluster as a volume which is half the value of $\chi$. For clusters homeomorphic to a sphere and a torus $\chi$ is 2 and 0, respectively (see Fig. 8d, e). More complicated clusters will have $\chi$ values as negative even integers, as shown in Fig. 8a–c.

Fig. 8

Brine clusters with brine–dodecane interface in red and glass–brine in blue; number of vertices in fluid–fluid interface, $V_f$, Euler characteristic, $\chi$, mean contact angle, $\theta _m$, and number of separate three-phase contact lines, $L_3$, are listed in each figure

On the size-biased contact angles for poorly resolved small clusters, results also showed that very small clusters with a volume of only one or a few voxels have a contact angle of near or equal to zero, i.e., smoothing collapses both fluid–fluid and solid–fluid interfaces on a plane. Figure 9a shows $\theta _m$ reduces when size of the fluid–fluid, $V_f$ interface reduces. Although the number of three-phase contact vertices on the smaller interfaces is not large, prevalence of such interfaces will change the mean contact angle for the whole image. Figure 9d shows the histogram of angles for the whole image rises relatively sharply for angles close to zero. In the same figure, the blue histogram is drawn after eliminating contributions from interfaces with $V_f<500$. The changes between the two curves for angles roughly below $45^\circ$ is noticeable. In Fig. 9d, the blue curve (unfiltered) is result of measurement from 376,827 three-phase contact vertices $V_3$, with mean angle and standard deviation of $65^\circ$ and $17^\circ$, respectively. The red curve (filtered) includes 354,362 vertices, 94 percent of all vertices on the three-phase line, with mean angle and standard deviation of $68^\circ$ and $11^\circ$, respectively. Standard deviation of angles $\hbox {std}(\theta )$ for the individual interfaces with respect to $V_f$ and $V_3$ are illustrated in Fig. 9b, c. $\hbox {std}(\theta )$ of large clusters is roughly $10^\circ$, whereas it is nearly any value from 0 to $25^\circ$ for smaller ones. Lower $\hbox {std}(\theta )$ for a group of smaller clusters does not imply precise measurements. It only means the angles are closer to an average angle at vertices the experimental measurement is highly uncertain. As a rule of thumb and in order to be cautious, we recommend finding the mean angle from fluid clusters where the fluid–fluid interface has at least a few thousand vertices. This can be deducted from Fig. 9a, as well as from the analytical examples.

Fig. 9

a Mean contact angle $\theta _m$ as a function of number of vertices $V_f$ for individual fluid–fluid interfaces, b standard deviation of contact angles $\hbox {std}(\theta )$ versus $V_f$, c and versus number of vertices on three-phase contact lines $V_3$ for individual interfaces, d histogram of contact angles for the entire 3D image with all interfaces included (red) and interfaces with $V_f<500$ filtered out (blue). $\theta _m$ for entire image originally and after filtering is $65^\circ$ and $68^\circ$, respectively

It should be noted that because of high frequency of very small clusters ($V_f<100$) and for the sake of better visualization, those clusters are not presented in Fig. 9a–c. The trends remain the same with/without such clusters, most of which are a few voxels or even one in volume. Furthermore, the largest fluid–fluid interface with $V_f=1{,}602{,}085$ and $V_3 =168{,}510$ has $\theta _m=67^\circ$ and $\hbox {std}(\theta )=9^\circ$ which are similar to $\theta _m$ and $\hbox {std}(\theta )$ of large clusters and filtered results of the whole image. These high $V_f$ and $V_3$ are not presented in Fig. 9a–c, again for visualization purposes. The largest interface, which is the one separating the connected displacing and the connected displaced fluids, has $\theta _m$ value close to the mean angles of the well-resolved trapped clusters in Fig. 8.

Contact Angle Variations Along three-Phase Line

We showed that contact angle is best to be measured or averaged for the larger fluid–fluid interfaces where there is less measurement uncertainty compared with the smaller ones. In an example, the calculated $\theta$ for large clusters had similar values of $\theta _m \approx 68^\circ$ and $\hbox {std}(\theta ) \approx 10^\circ$. In this section, we investigate the local variations of contact angles along the three-phase lines. We show that 10 degrees standard deviation is partly random caused by imaging noise and partly a pattern that we believe is possibly related to the overlooked line energies.

We sort the $\theta$ values of the consecutive vertices along a three-phase line. In this way, angles resemble a time series, for which the auto-correlation function ACF can be calculated. Figure 10 shows the ACF, with 100 as number of the lag periods, for multiple lines on a single cluster. According to Fig. 10, ACF values are high for smaller values of lag, meaning that the variation of $\theta$ along the lines is smooth. We examine the hypothesis that whether or not the variations are related to the line curvature. Therefore, we calculate the angle $\psi$ created by the two edges neighboring each vertex on the three-phase lines. $\psi$ values are a measure of how much the line turns at a vertex and hence proportional to the line curvature. Figure 10 shows that lower $\theta$ values tend to occur when the three-phase line curvature is higher.

Fig. 10

ACF of $\theta$ values as a time series for three-phase lines of a cluster and variations of $\theta$ with rotation angles $\psi$—equivalent to the line curvature

The $\theta -\psi$ plots have a high degree of noise and may be affected by the imaging noise and the smoothing artifacts in poorly resolved features. We further investigate the variations by visualizing the original and smoothed solid surfaces and the color-coded $\theta$ values in Fig. 11. As shown in Fig. 11, $\theta$ is lower at and around kinks (high $\psi$) in the line. The kinks occur at surfaces with anomalies in the form of a small whole or a small lump of voxels on surface of the glass spheres. These features are certainly not resolved, and the resulted $\theta$ and $\psi$ values are not reliable.

Fig. 11

Color-coded—and size-coded—$\theta$ values along three-phase contact line viewed from inside the solid; the noise in the solid surface represented by the kinks in the line results in smaller $\theta$

However, further investigation of $\theta$ variations along the line, with least noisy image features, revealed $\theta$ values tend to be larger at the convex parts of the three-phase line and smaller in the concave parts (see Fig. 12). This can also be explained by the generalized Young’s equation Pethica (1977), Boruvka and Neumann (1977),

$$\begin{aligned} \cos \theta = \frac{\sigma _{2s}-\sigma _{1s}}{\sigma _{21}} - \frac{\gamma }{\sigma _{21}}\kappa , \end{aligned}$$

(15)

where $\gamma$ is the line tension and $\kappa$ is the signed line curvature. Convex parts of the line with $\kappa >0$ will have larger $\theta$, whereas concave parts with $\kappa <0$ will have smaller $\theta$. This pattern in the experimental images suggests that the likelihood of line energy playing a role in two-phase flow should not be ruled out. The variable contact angle correlating with line curvature hints that the free energy of the system should have an extra term for the line energy, in addition to contributions from the volumes and the surface areas.

Fig. 12

$\theta$—color-coded and size-coded—tends to be larger at convex parts of the three-phase line and smaller at the concave parts. This pattern was observed when the line neighborhood in the image was not noisy

In the following, we will estimate the line tension $\gamma$ based on the changes in contact angle along the three-phase contact line. Given the rotation angle $\psi$, in Fig. 10, at a vertex on a contact line, the line curvature at the vertex is

$$\begin{aligned} \kappa =\psi /\varDelta s, \end{aligned}$$

(16)

where $\varDelta s$ is the edge length between the two consecutive vertices. $\varDelta s$ is in the order of pixel length. Assuming effective average values for the tension terms in Eq. (15), one can construct the equation for two vertices on the convex and concave parts of a three-phase line.

$$ \begin{aligned} \cos \theta _{{\rm concave}} = \frac{\sigma _{2s}-\sigma _{1s}}{\sigma _{21}} - \frac{\gamma }{\sigma _{21}}\kappa _{{\rm concave}} \\ \cos \theta _{{\rm convex}} = \frac{\sigma _{2s}-\sigma _{1s}}{\sigma _{21}} - \frac{\gamma }{\sigma _{21}}\kappa _{{\rm convex}}. \end{aligned}$$

(17)

Subtracting the two equations in (17), we have

$$\begin{aligned} \gamma = \sigma _{12} \frac{\cos \theta _{{\rm concave}} - \cos \theta _{{\rm convex}}}{-\kappa _{{\rm concave}} + \kappa _{{\rm convex}}}. \end{aligned}$$

(18)

One can calculate $\gamma$ using a pair of vertices with known $\theta$ and $\kappa$ by mean of Eq. (18). Using five pairs of vertices, all on a single three-phase line, and an interfacial tension of $\sigma _{12}=36\times 10^{-3}\,\hbox {N/m}$, measured by Schlüter et al. (2017), the line tension was estimated from Eq. (18) as $\gamma \approx 8.7 \times 10^{-7}\,\hbox {N}$. Attempting the procedure on another line results in similar value of $\gamma \approx 9.3 \times 10^{-7}\,\hbox {N}$. These two values were calculated from the two lines shown in Fig. 12.

The calculated $\gamma$ is close to higher line tension values reported in the literature. Zhang et al. (2018) reported that the line tension of sessile droplets obtained from theories vary from $10^{-12}\,\hbox {N}$ to $10^{-10}\,\hbox {N}$ whereas experimental measurements vary from $10^{-12}\,\hbox {N}$ to over $10^{-5}\,\hbox {N}$, depending on the studied system (Zhang et al. 2018). Further, it has been debated that while the line tension at atomic scale is on the order of nN, gravitational effects at mm scales can add significant contributions to the line tension (Bruce et al. 2017). In our microscale measurements, it is possible that $\gamma$ is influenced by the sub-resolution surface roughness and wetting variations.

Now we can estimate the interfacial energy $F_{A_{12}}$ and the line energy $F_L$ for the fluid cluster for which the statistics is presented in Fig. 10.

$$\begin{aligned} \begin{aligned} F_{A_{12}} = \sigma _{12}A_{12} = 1.8 \times 10^{-8} J \\ F_L = \gamma L \approx 1.6 \times 10^{-8} J \end{aligned} \end{aligned}$$

(19)

The estimated line energy is nearly equal to the interfacial energy. The line energy will therefore influence the free energy of the two-fluid system in micro scale. The studied experimental system is composed of relatively large and smooth glass beads; thus, we can expect stronger effect in natural porous media such as sandstone rocks.

Summary

We calculated the contact angles and curvatures in X-ray tomography images of two-phase flow in porous material. Two analytical examples with known contact angles and curvatures were used to verify the mesh smoothing method. Analytical cases showed that average and point-wise contact angles, average mean curvature, and surface area converged with increased grid resolution. According to analytical examples, point-wise contact angles and average mean curvature for fluid–fluid surfaces resolved by 3000 vertices or more, equivalent to an area of $1000\,\hbox {pixel}^2$, could be calculated accurately. We addressed also the impact of poorly resolved small fluid clusters—which can often have high frequency in the experimental images—on the contact angle distribution and mean contact angle. We found that contact angles were underestimated for wetting fluid clusters where the fluid–fluid surface mesh was resolved with roughly less than 500 vertices. In addition, the cluster-based investigation showed that both mean and standard deviation of angles where the fluid–fluid surfaces had at least a few thousand vertices converge to similar values. We observed a standard deviation of approximately 10 degrees for large fluid clusters. Our investigation of the local variations of contact angles along the three-phase contact lines showed that a part of the variations is caused by measurement uncertainty. However, a part of variations represented a pattern in which contact angles tend to be larger at convex parts of the line and smaller at concave parts. This suggests that the free energy may have contributions from three-phase contact lines, in addition to the volumes and surfaces.