1 Introduction

Upscaling procedures are based on a bottom-up approach, where the analysis of flow and transport features at the pore scale is conducted through both physical (Narsilio et al. 2009; Tallakstad et al. 2009) and numerical models (Raeini et al. 2014b; Blunt 2001; Spanne et al. 1994; Porta et al. 2013). Laboratory experiments mostly investigate bulk quantities such as porosity, permeability, dispersion coefficients. Physical models to characterize the pore dynamics, and employ microfluidic devices (Li et al. 2017; Saleh et al. 1992), are therefore restricted to 2D geometries. Numerical models have been largely employed to investigate pore scale dynamics, both in real (Mostaghimi et al. 2013; Blunt et al. 2002; Adler et al. 1992) and in synthetic geometries (Ghassemi and Pak 2011; Koponen et al. 1998; de Anna et al. 2017; Khirevich et al. 2011; Matyka et al. 2008; Nabovati and Sousa 2007). The issue is also related to percolation theory, such that the percolation threshold and the universal exponents depend on the space dimension; a comparison between the conductivities of Sierpinski carpets (2D) and Menger sponges (3D) was performed in the past (Adler 1986; Lemaitre and Adler 1990), and significant differences between them were found.

One of the main sources of uncertainty in groundwater contamination studies lies in the modelling of boundaries. A viable way to enhance the reliability of the models employed in risk assessment studies is to enlarge the spatial and time domains accordingly, in order to lower the influence of the boundary conditions on the region of interest. Large-scale modelling of flow and transport in porous media is therefore drawing a considerable amount of attention. These models employ various levels of upscaling of the dynamics acting at pore (and subpore) scale (Raeini et al. 2014a; Ling et al. 2018).

Dimensional contraction is applied in almost all fields of physical analysis in order to exploit uniformity along one or more directions. Two-dimensional simulations of flow in porous media have been often preferred over 3D ones due to their lower computational burden, and this choice may become mandatory when a large number of simulations are to be carried out in order to obtain statistically significant figures for the quantity of interest (QoI). Dimensional contraction of physical phenomena can be usually carried out along directions which show negligible variations of QoIs. Yet, this hypothesis is seldom verified for the case of flow and transport in porous media and 2D models have been widely proposed and employed to simulate flow in both synthetic domains and in ones obtained as sections of 3D porous matrices. The validity of such models has been extensively questioned (Koponen et al. 1997; Goudarzi et al. 2018). Nevertheless, they still play a major role in the modelling community. Several works have pointed out that 2D models are likely to fail in reliably reproducing the flow field in 3D porous geometries (Mostaghimi et al. 2013; Koponen et al. 1997; Goudarzi et al. 2018; Knudsen et al. 2002; Saomoto and Katagiri 2015; Duda et al. 2011; Li et al. 2005). The threshold of validity of 2D approaches is arbitrary and much dependent on the purpose of the study.

In this paper we show to which extent a 2D numerical model can be employed for the REV assessment of a 3D domain, i.e. identify a representative scale for upscaling procedures of a synthetic 3D porous medium with comparable porosity. Contrasting predictions of REVs stemming from distinct statistical realizations (2D and 3D) of the same porous media reveal different flow dynamics. Moreover, incorrect REV estimations lead to inaccurate predictions of flow and transport features. To this purpose, we focus on the estimation of REV for several quantities of interest, such as porosity, permeability, mean velocity and velocity variance. We show that the REV obtained through the 2D model is much larger than the reference (3D) one: this reveals the profound difference between 2D and 3D flows through porous media. Both 2D and 3D simulations are carried out by means of a flexible, yet accurate numerical solver based on the Single Relaxation Time (SRT) Lattice Boltzmann Method (LBM) (Prestininzi et al. 2016) to determine the flow field in the porous media.

The structure of the paper is as follows: in Sect. 2 we briefly introduce the LBM, the algorithms adopted for the generation of the porous media and the scaling employed in the simulations; in Sect. 3 we present results and discussion of the 2D and 3D simulations; Sect. 4 is dedicated to conclusions, perspectives and recommendations, which are drawn based on the outcome of the study.

2 Methods

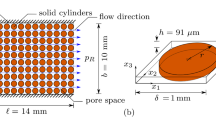
We consider porous media composed by randomly placed, equal, hard spheres and disks in 3D cubic, and 2D square domains, respectively. We employ the LBM as a numerical flow solver to reproduce the Darcy’s experiment numerically. Its ability to accurately predict flow paths, permeability, hydraulic conductivity is well documented in the literature (Zhang et al. 2000; Pan et al. 2001) and no further validation is here assumed to be needed. LBM simulations are employed to model flow in porous media, where packings are generated by means of a sphere packing generator program. Since the LB dynamics is inherently time-varying, a transient is necessary for the system to reach a steady state complying with constant boundary conditions. Steady state control is based on stationarity of the fluid velocity. Once the system has reached the steady state, it is analysed in terms of permeability, mean velocity and velocity variance.

Porosity can be estimated prior to the simulation, since it is a purely geometric parameter, independent of flow. Porosity \(\epsilon\) is defined as the ratio of the volume of voids to the total volume of the domain. The single phase creeping flow through a porous medium is described by the Darcy’s law (Bear 2013), and the permeability k is calculated as

$$\begin{aligned} k= \frac{\nu }{|g|} q , \end{aligned}$$
(1)

where \(q\) is the specific discharge, i.e. the mean velocity over the cross-sectional area open to flow, \(\nu\) is the kinematic viscosity of the fluid, |g| is the intensity of the driving force \(\mathbf {g}\) defined as \(\displaystyle \mathbf {g}=\frac{\mathbf {\nabla P}}{\rho }\) that is the ratio between the macroscopic pressure gradient \(\mathbf {\nabla P}\) and the density of the fluid \(\rho\). The REV investigation on the velocity field is carried out in terms of first and second-order statistics (mean and variance). The average value of the velocity magnitude \(\overline{|v|}\) in the void space is computed as

$$\begin{aligned} \overline{|v|}=\frac{1}{N_xN_yN_z}{\sum _{i=1}^{N_x} \sum _{j=1}^{N_y}\sum _{k=1}^{N_z}{{|\mathbf{v} |}_{ijk}}}, \end{aligned}$$
(2)

where

$$\begin{aligned} {|\mathbf{v} |}_{ijk}=\sqrt{{u}^2_{ijk}+{v}^2_{ijk}+{w}^2_{ijk}}, \end{aligned}$$
(3)

with u, v and w the flow velocity components and i, j and k stand for the discrete position along x, y and z directions, respectively.

The velocity variance \(\sigma ^2_v\) has a pivotal role in determining hydrodynamic dispersion, since it is related to the length scale over which the dispersion phenomenon occurs and to the dispersion coefficient D, in particular

$$\begin{aligned} D= L\frac{\sigma ^2_v}{|\mathbf{v} |} \end{aligned}$$
(4)

Dagan (2012), where L is the characteristic medium length and \(\sigma ^2_v\) is evaluated as

$$\begin{aligned} \sigma ^2_v=\frac{1}{N_xN_yN_z-1}{\sum _{i=1}^{N_x}\sum _{j=1}^{N_y}\sum _{k=1}^{N_z}{({|\mathbf{v} |}_{ijk}-\overline{|v|})^2}}. \end{aligned}$$
(5)

Two approaches are employed to estimate the REV for the aforementioned quantities. Both employ the evaluation of the generic quantity of interest \(\eta _m\) within each subvolume m, whose characteristic length scale is \(L_m\). Permeability \(k_m\) of the \(m^{th}\) subvolume is then evaluated by means of \(k_m =\displaystyle \frac{\nu }{|g|} q _m\), where only \(q\) depends on m, since both the viscosity and the driving force are kept constant. In this study, the point-centred cube geometry, for which all subvolumes progressively and symmetrically grow from the centre in all directions, is chosen since the results are not affected by boundary effects associated with the generation of the porous sample for randomly placed obstacles (Preller 2011). In the first approach, the REV estimation relies on a visual assessment and on a subjective judgment based on plotting the value of \(\eta _m\) against \(L_m\) and determining the REV value, estimated here as the minimum length scale \(L_m\) at which a stationary behaviour, also referred to as plateau (Costanza-Robinson et al. 2011). The second approach determines the REV value as the one inducing a given residual variability for the quantity \(\eta\) within the domain, i.e. it allows a quantification of the variability associated to the chosen REV. To this purpose, we employ two statistics, the Relative Error (RE) and the Convergence Criterion (CC). The first one, employed by (Li et al. 2009), compares the residual variation of a quantity \(\eta\) at step m with its mean value around m. It is defined as

$$\begin{aligned} RE_m=2\Big |\frac{\eta ^{m+1}-\eta ^{m-1}}{\eta ^{m+1}+\eta ^{m-1}}\Big |. \end{aligned}$$
(6)

The second statistics is a cumulative quantity that measures the variability of the quantity \(\eta\) up to the \(m^{th}\) step and is defined as

$$\begin{aligned} CC_m=\frac{\sigma _{\eta ,m}}{\overline{\eta }_m}, \end{aligned}$$
(7)

where the standard deviation \(\sigma _{\eta ,m}=\sqrt{\frac{1}{m-1}\sum _{i=1}^{m}(\eta _i-\overline{\eta _m})^2}\) and the mean value for the quantity \(\overline{\eta }_m=\frac{1}{m}\sum _{i=1}^{m}\eta _i\) are both evaluated for the truncated series up to the \(m^{th}\) subvolume. The quantitative approach sets a threshold value \(\gamma\), and determines the REV as the smallest domain size m for which each statistics falls below \(\gamma\). The RE values can show extensive fluctuations, irregular at times, even for large values of m, and therefore we here include the evaluation of the CC statistics, which, as a cumulative quantity, shows a smoother behaviour. The choice of a threshold for CC (or equivalently for RE) induces a variability due to a residual non-stationarity of order O(CC) (or O(RE)). It is clear that, while such source of uncertainty can be made arbitrarily small by setting a lower value for \(\gamma\), its choice needs to weigh the required accuracy of the whole study with the available computational resources.

2.1 Generation of numerical domains

2.1.1 3D domain

The 3D numerical specimen for the simulation is generated by means of a previously developed algorithm for hard-sphere packing generation and packing post-processing (Baranau and Tallarek 2014). The algorithms supported by the method for the packing generation (the Lubachevsky–Stillinger, Jodrey–Tory, and “force biased”) are able to generate a packing of spheres in a cubic box by specifying the box size, the number of spheres and their diameters as input parameters. At the beginning of the generation, the spheres are randomly located without overlapping in a box with periodic boundary conditions. During the packing generation, the spheres have uniform expansion and elastic collisions. Finally, a jammed packing with the highest jamming density is achieved, resulting in a steady configuration where any spheres’ motion is hindered (Donev 2006). The 3D specimen is described in terms of the coordinates of the centres of the spheres and their diameters. The packing is said to be monodisperse if all the spheres have the same diameter.

2.1.2 2D domain

The structure of a 2D domain for the simulation of porous media flows cannot be a packing structure, i.e. disks cannot be tangent, in order to let the fluid flow. Moreover, 2D domains can be seldom obtained by slicing a 3D packing, since such procedure introduces geometrical distortions (e.g. a slice of a monodisperse 3D specimen results in a 2D polydisperse one). Here, we employ an algorithm to generate the 2D specimen for the simulation where the following input parameters are specified: the total number of disks, the diameter, here equal for each disk, the minimum distance between two disks and the side length of the squared domain. The algorithm employs an iterative mechanism to add new disks until the coordinates for the total number of disks are generated.

2.2 The LBM solver

The Lattice Boltzmann Method describes the flow by means of a finite set of probability density functions \(f_i(\mathbf{x} ,t)\) which give the probability to find a fluid particle with a given particle velocity \(\mathbf{c} _i\), at a given position \(\mathbf{x}\) and at a given instant of time t. The probability density functions evolve according to the Lattice Boltzmann Equations (8), obtained by discretizing the Boltzmann kinetic equation with respect to space, time and particle velocity (Succi 2001). Thanks to its intrinsic simplicity, the LBM is particularly competitive for complex flows (e.g. flows in complex domains, multiphase flows, etc.). The Navier–Stokes equation can be obtained from the Lattice Boltzmann Equations by applying the Chapman-Enskog expansion (Succi 2001) and it is possible to show that the macroscopic quantities (fluid density and velocity), obtained as statistical moments of the probability density functions, are equivalent to those that one would obtain by solving the Navier–Stokes equations, under the condition that the Mach number of the flow (the ratio of the flow and the sound velocity) is small (Succi 2001). The Lattice Boltzmann Equations assume the form

$$\begin{aligned} f_{i}(\mathbf{x} +\mathbf{c} _{i}\Delta t, t+ \Delta t) - f_{i}{(\mathbf{x} ,t)}=-\frac{1}{\tau }[{f_{i}} (\mathbf{x} ,t)-f_i^{eq}(\mathbf{x} ,t)]+\Delta t F_i \quad i=0,...,Q-1 \end{aligned}$$
(8)

where Q is the number of discrete particle velocities. The LHS of Eq. 8 represents the streaming phase, while the RHS contains the Bhatnagar–Groos–Krook approximation of the collisional term and the forcing term. In Eq. (8), \(\displaystyle f_{i}^{eq}\) is the equilibrium distribution function; \(\tau\) is the relaxation time, which is related to the kinematic viscosity by \(\displaystyle \nu =c_s^2 (\tau - \frac{1}{2})\), with \(c_s={e_0}/{\sqrt{3}}\) the lattice speed of sound for the adopted velocity sets, defined in (Succi 2001). Finally, \(\Delta t\) is the time interval, defined in term of the grid spacing \(\Delta x\) as \(\displaystyle \Delta t=\frac{\Delta x}{e_0}\), once the characteristic particle velocity \(e_0\) is introduced; \(F_i\) are the components of the external forces along directions delineated by the lattice velocities as \(\displaystyle F_i=\frac{\omega _i \mathbf{g} \cdot \mathbf{c} _i}{c_s^2}\), where \(\mathbf{g}\) is the driving force for unit mass (Eq. 1), \(\omega _i\) are the weighting factors, see (Succi 2001) for their definition. The density \(\rho\) and the macroscopic velocity \(\mathbf{v}\) of the fluid are defined in terms of the particle distribution functions by

$$\begin{aligned} \rho= & {} \sum _{i=1}f_i(\mathbf{x} ,t); \end{aligned}$$
(9)
$$\begin{aligned} \mathbf{v}= & {} \frac{1}{\rho }\sum _{i=1}{} \mathbf{c} _i f_i(\mathbf{x} ,t). \end{aligned}$$
(10)

2.3 Setup of simulations

Firstly, the spatial domain is discretized by choosing the number of nodes corresponding to the reference length. If not further specified, the reference length is assumed to be the sphere/disk diameter D. The unit length in the discrete space is referred to as “lattice unit”, lu. Then, boundary conditions are assigned: the spheres/disks boundaries are modelled as no-slip impervious surfaces, by means of the bounce-back technique (Succi 2001); periodic conditions are imposed at all domain boundaries. Initial conditions are of fully saturated domain, at rest. An orthogonal coordinate system with coordinates (x, y, and z for the 3D case) is used. The flow motion is obtained by the application of an external mass force, aligned with the x direction. The relaxation time \(\tau\) plays an important role in the simulation setup, since it is strictly connected to the Reynolds number \(Re=\frac{U l}{\frac{1}{3}(\tau -\frac{1}{2})}\). The flow in the porous medium is characterised by \(Re\ll 1\). Then, we define l as a reference length for the void space and select it as a fraction of the disk/sphere’s diameter (e.g. \(l=D/5\)) and U as the reference velocity in the pore (\(U=10^{-5}\div U=10^{-4}\) lattice unit per time step of the simulation). The values of the kinematic viscosity and \(\tau\) can be obtained for a given value of the Reynolds number. It can be shown that with the assumed values of l, \(\tau\), U, the Knudsen number Kn, defined as the ratio of the mean free path \(\displaystyle \frac{\nu }{c_s}\) to the characteristic length scale l (Prestininzi et al. 2016), is small enough to ensure convergence of Eq. (8) to the correct hydrodynamic model (Montessori et al. 2015; Pazdniakou and Adler 2013).

3 Results and discussion

The estimation of the REV is carried out using the values of CC and RE for porosity, permeability, mean velocity and velocity variance. A threshold value of \(\gamma =0.15\) is used to identify the REV, i.e. we expect the quantity of interest to vary within \(15\%\) around the mean value in a specimen larger than the REV. For the purpose of this study, the choice of the threshold value is arbitrary and does not influence the outcome of the analysis. Although the choice of the threshold value clearly affects the REV estimation, it does not alter the results of this work, which is aimed at comparing REVs yielded by different models, obtained assuming the same threshold value. In each specific application, the value of \(\gamma\) reflects the level of accuracy that the modeller wants to achieve with respect to the QoIs. The generated 2D domain, whose main features are listed in Table 1, is shown in Fig. 1. Moreover, the autocorrelation function of the longitudinal velocity is calculated with the aim of ensuring that distances among disks do not induce long-range dependence in the flow field.

Table 1 Geometry and discretization of the 2D domain
Full size table

The increment \(L_{m+1}-L_m\) in the size of progressive subsections is 100 lu for the 2D case, so that each subsection encloses a meaningful number of disks in addition to the previous one. The outcome of the REV calculation for the 2D case using the first approach and the CC method is shown in Fig. 2. For the sake of clarity, it is appropriate to recall that, here, the first approach results in the calculation of the quantity within each subvolume (visual assessment). The blue lines in Fig. 2 reach a plateau after initially large oscillations, except for the permeability (panel [c]) which still significantly fluctuates for box sizes approaching the entire domain. The convergence of CC for permeability (panel [c]) is significantly slower compared to that of other quantities: if the threshold value for CC is set to 0.15 then the REV for permeability is larger than the entire domain. Red traces, that quantify such fluctuations, show decreasing monotonous behaviours, after an initial peak is reached and slight oscillations. Yet panel [c] shows that the permeability CC remains above the chosen threshold. Such value for the residual variation leads to the conclusion that a REV for permeability cannot be identified with \(\gamma =0.15\), i.e. the permeability REV is larger than the entire domain. This is consistent with previous studies (Mostaghimi et al. 2013), that have recognized that permeability generally requires larger REVs than other quantities, e.g. porosity, due to its slow convergence (Zhang et al. 2000; Costanza-Robinson et al. 2011).

The adopted threshold value entails a residual variability that, depending on the purpose of a specific application, could be considered too high to carry out robust investigations of flow and transport quantities. Despite being purposely large in this study, in order not to excessively constraint the allowed residual variation of different quantities, it leads to the conclusion that permeability REV estimation requires more than 333 disks (or equivalently 10000 lu).

Fig. 1
figure 1

2D porous matrix domain (10,000 × 10,000 lu2) to investigate the REV size of the main quantities of interest, with a close-up look at the squared section in the centre of the domain (500 × 500 lu2)

Full size image
Fig. 2
figure 2

2D case: assessing the REV size for bulk quantities: porosity (a), mean velocity (b), permeability (c), velocity variance (d) and their CC, versus domain size and number of diameters

Full size image

With reference to the behaviour of the mean velocity and its variance (left side plots in panel [b] and [d], respectively), it is evident that the 2D approach is prone to deceive the modeller by producing a “false” stationary plateau. Indeed both quantities seem to achieve a reasonably stable value between 20 and 60 diameters (or equivalently between 600 and 1800 lu), before dropping and then slowly growing again. In Fig. 3 we sampled to show how the permeability is heavily location and scale dependent.

Fig. 3
figure 3

Permeability variation within the domain. The value of permeability has been calculated at six distinct subdomains. The sizes of the subdomains are comparable to the ones commonly employed to discretize porous media for numerical simulations: 1000 × 1000 lu2 yellow square; 2000 × 2000 lu2 cyan square

Full size image
Fig. 4
figure 4

3D porous matrix made of hard spheres. The extent of such domain has been chosen on the REV assessment

Full size image

Figure 4 shows the 3D domain whose main features are listed in Table 2. The spheres’ centre coordinates are generated by means of the packing generation algorithm described in Sect. 2.1.1, whereas the spheres’ diameter is scaled to match the 2D porosity value within an approximation due to the spatial discretization.

Here, the increment \(L_{m+1}-L_m\) in the size of progressive subvolumes is 20 lu, in order to encompass a significant number of spheres at each step. The REV analysis for 3D specimen using the first approach and the CC method is shown in Fig. 5. The general trend of the graphs resembles that one of the 2D counterpart. With reference to Fig. 5, it is clear that the velocity variance is the quantity which requires the largest domain to attain stationarity. Such result does not contradict the previous observation that the permeability REV is the largest since, to the best of our knowledge, the analysis on velocity variance has never been performed yet. Besides, it has a lower convergence, compared to the mean velocity chart, as a matter of fact, this is expected for higher statistical moments, since the variance is the second-order statistical moment around the mean.

As a reference, the packing in Fig. 4, \(250 \times 250 \times 250\)\(lu^3\), is the estimated REV for a 15% residual variation for the velocity variance.

Table 2 Geometry and discretization of the 3D domain
Full size table
Fig. 5
figure 5

3D case: see Fig. 4 for detailed description. For the 3D case the velocity variance is the quantity requiring the largest REV (\(250 \times 250 \times 250 lu^3\) or equivalently 8 diameters)

Full size image
Fig. 6
figure 6

Quantitative approach for the REV estimation: Convergence Criterion and relative errors methods. The comparison of the considered quantities of interest between the 2D and 3D cases is illustrated in a semi-log plane

Full size image

It is supposed usually that simulations carried out for the 2D case can be helpful for any kind of prediction of quantities related to 3D flow and transport phenomena in porous media. The outcome of such procedure is that, in order to obtain reasonably accurate quantitative predictions (\(CC<15\%\)), numerical or physical models should employ a spatial domain larger than the one investigated, i.e. more than \(N=333\) disk diameters (or equivalently 10000 lu) for each direction (see Fig. 2, panel [c]). We would like to stress that this estimate is likely to be considered as a lower bound, since the assumed acceptable residual variation may be too large for robust predictions.

The comparison between the 2D and the 3D cases using both CC and RE methods (see Fig. 6) shows how the two specimens, which share a comparable porosity (the porosity difference being \(1.7\%\)), lead to consistently different estimates in both of REV sizes and therefore of effective parameters.

It is worth underlining that the aim of this work is to show that the REV obtained through the 2D model is much larger than the reference (3D) one, instead of comparing different quantitative methods. In particular, Fig. 6 highlights that porosity (panel [a]) and mean velocity (panel [b]), no matter what convergence criterion is chosen, require considerably smaller REV to attain stationarity, compared to permeability (panel [c]) and velocity variance (panel [d]). This reveals that a REV analysis is likely to benefit from the adoption of different threshold values for each QoIs. Such behaviour clearly shows the quantities of interest should drive the definition of the threshold necessary for the identification of the REV. In particular, the permeability and the velocity variance, once a threshold value is chosen, require a much higher REVs to converge, compared to porosity and mean velocity. With regard to CC graphs in panel [d], the number of diameters required to reach convergence for velocity variance REV in 2D is one order of magnitude higher than that needed in 3D (\(10^2\) vs \(10^1\), respectively). Using both methods (RE and CC) each graph in Fig. 6 (except for the geometric variable) shows that the 3D domain falls below the chosen threshold (0.15) within fewer number of diameters compared to 2D case. Even though the RE method gives different REV values than the CC method, they both lead to the same conclusion: the 2D REV is too large and cannot correctly characterize the corresponding 3D sample. With the aim of comparing REV values for these methods, we defined the variable

$$\begin{aligned} \alpha =\frac{REV_{2D}}{REV_{3D}} \end{aligned}$$
(11)

for the flow quantities (permeability, mean velocity and velocity variance). Its values are shown in Table 3, where the \(REV_{2D}\) and \(REV_{3D}\) are those associated to the minimum length scale in 2D and 3D corresponding to a residual variability of the QoI equal to \(\gamma\). When the value for CC (or RE) does not fall below the threshold value, the REV is considered to be greater than the sample size. Instead, when the value never grows above the threshold the value \(\alpha\) is not reported (any domain size would include the REV). The values of \(\alpha\) clearly point out that the 2D REV, if it exists (i.e. when it is smaller than the entire specimen), would be roughly 10 times larger than the 3D REV.

Table 3 \(\alpha\) values for the flow quantities (permeability, mean velocity and velocity variance) using the CC and RE statistics for the determination of REV, where \(\displaystyle \alpha ={REV_{2D}}/{REV_{3D}}\)
Full size table

It is worth highlighting that the conclusions of this study, though present in their embryonic and sparse forms in other studies (Mostaghimi et al. 2013; Zhang et al. 2000; Costanza-Robinson et al. 2011), are here robustly supported by a set of ad-hoc simulations. The recent availability of highly accurate numerical tools, such as the ones employed in this study, would encourage the contemporary scientific and technical community to tackle the study of pore scale dynamics in complex porous matrices. Due to the high computational burden required by the 3D simulations, the modeller would make do with a more affordable 2D representation, the search for a REV through 2D simulations, possibly leading to incorrect conclusions. There is the risk that such scenario would end up in the identification of the REV either as the largest domain computationally affordable, or as a smaller one, both solutions leading to a possibly large source of uncertainty stemming from the neglected residual variability.

Finally, we would like to point out that the outcome of this study not only applies to numerical models, but also to their physical counterparts. Indeed the resort to 2D lumped experiments resembling 3D flows may be exposed to the same sort of issues. This is nowadays even more compelling due to the widespread of microfluidics models, which offer the possibility to easily measure pore scale quantities, but are almost always 2D setups.

4 Summary and conclusions

In this study high resolution numerical simulations of pore scale flows are used to assess to which extent the properties of a 3D creeping flow through porous media can be represented by its 2D counterpart. To this purpose, we show that the estimation of the REV size for several quantities yields remarkably different values for the 2D and the 3D cases.

The adopted procedure consists in the generation of two monodispersed numerical specimens of comparable porosity, made of randomly placed disks (2D) and spheres (3D).

Then a creeping flow is simulated through both specimens, employing a numerical solver based on the SRT LBM.

The REV assessment is performed for several quantities, namely porosity, permeability, mean velocity and velocity variance. Each quantity is evaluated within a series of progressively growing subdomains in order to investigate their convergence behaviour.

Two criteria have been used in this study as quantitative approach for the REV estimation: Convergence Criterion and Relative Error statistics. They employ an acceptance threshold whose value depends on the acceptable residual variability of the quantity at hand. Both criteria lead to a REV estimation by the 2D model much larger than 3D one. The analysis so far conducted reveals to some extent the difference between 2D and 3D flows through porous media, at least for the monodispersed matrices cases analysed in this work.

Some conclusions are drawn. The great discrepancy in the flow field obtained in a 2D porous matrix and that in 3D one also reflects in peculiar patterns of the visual REV assessment (in this study the first approach) for some flow related quantities: they exhibit deceitful stationary plateaux, which are prone to support inaccurate estimates of the REV, when a quantification of the variability associated to the chosen REV is not performed (in this study the second approach).

The employment of 2D simulations (or experiments in 2D setups) in order to investigate 3D flow related quantities is seldom a correct choice: indeed a flow path through a 2D porous medium has a significantly lower number of geometrical degrees of freedom compared to the 3D one. This difference in tortuosity results in a REV for any flow related quantity which is much larger than the 3D counterpart. The situation is expected to be exacerbated in the more realistic cases of polydisperse media.

The 2D simulation employing domains encompassing the 2D REV can be even more computationally demanding than the 3D ones. In particular the ratio between the REV in the 2D and the 3D case has been evaluated for the flow quantities (permeability, mean velocity and velocity variance) for both statistics (CC and RE). Such values clearly point out that the 2D REV, when smaller than the investigated specimen , would roughly be 10 times larger than the 3D REV. Finally it is worth pointing out that the REV assessment is not only influenced by the spatial dimension (2D or 3D), but it is also dependent on the aim of the study, in other words on the investigated quantity of interest. In particular, in transport problems one would expect to obtain a larger REV for the velocity variance rather than a smaller one for the porosity REV if interested in pore structure analysis.