Predicting Resistivity and Permeability of Porous Media Using Minkowski Functionals

Abstract

Permeability and formation factor are important properties of a porous medium that only depend on pore space geometry, and it has been proposed that these transport properties may be predicted in terms of a set of geometric measures known as Minkowski functionals. The well-known Kozeny–Carman and Archie equations depend on porosity and surface area, which are closely related to two of these measures. The possibility of generalizations including the remaining Minkowski functionals is investigated in this paper. To this end, two-dimensional computer-generated pore spaces covering a wide range of Minkowski functional value combinations are generated. In general, due to Hadwiger’s theorem, any correlation based on any additive measurements cannot be expected to have more predictive power than those based on the Minkowski functionals. We conclude that the permeability and formation factor are not uniquely determined by the Minkowski functionals. Good correlations in terms of appropriately evaluated Minkowski functionals, where microporosity and surface roughness are ignored, can, however, be found. For a large class of random systems, these correlations predict permeability and formation factor with an accuracy of 40% and 20%, respectively.

1 Introduction

Permeability is the most important parameter for fluid transport through porous rocks and soils, such as aquifers and hydrocarbon reservoirs. The permeability in the subsurface is typically highly heterogeneous and may have several orders of magnitude in variation. The permeability is, however, not measurable by downhole logging tools and needs to be inferred from correlations based on a combination of logs. Tying all measured data to a set of underlying parameters will improve the credibility of these permeability estimates, and the effort to try to express the permeability in terms of a small number of underlying geometric properties goes back several decades, at least to the work of Kozeny (1927) and Carman (1937). The prediction of transport in porous structures from measures of the morphology and topology is an unsolved problem (Mecke 2000, p. 145). The so-called Kozeny–Carman equation remains to this day the most popular formulation. How this equation is expressed varies somewhat throughout the literature depending on which geometric parameters are considered known and how they are expressed in terms of each other. In the context of this paper, we will refer to a slightly generalized form of the original Kozeny formulation:

$$\begin{aligned} k = \frac{\phi ^3}{f \tau \sigma ^2}, \end{aligned}$$

(1)

where $\phi$ is porosity, $\sigma$ is the specific void space area, f is a factor that represents the shape of grains, and $\tau$ is the tortuosity which is the ratio of a typical flow path length to the sample length. The reasoning leading to (1) is based on bundle-of-tubes analogues, and the two parameters f and $\tau$ do not have any strict definition.

Electric resistivity is another important parameter that depends strongly on the pore space geometry, and resistivity measurements are used for inferring permeability (Archie 1942; Ogbe and Bassiouni 1978; Mohaghegh et al. 1997). In a porous material consisting of a non-conducting matrix and pores filled with a conducting fluid, such as brine-saturated sandstone, the resistivity will be proportional to the fluid resistivity. The proportionality constant, conventionally called “formation factor” F, only depends on pore space geometry. F is often expressed in terms of the Archie equation (Archie 1942, 1950):

$$\begin{aligned} F = \phi ^{-m}, \end{aligned}$$

(2)

where m is called the “cementation index” which may vary between rock types. The formation factor can also be expressed in terms of porosity and the electric tortuosity $\tau _e$

$$\begin{aligned} F = \frac{\tau _e}{\phi }. \end{aligned}$$

(3)

Note that (3) serves as the definition of $\tau _e$, and only expresses the fact that the current in a real medium has to travel through paths that are longer, more tortuous, than straight parallel tubes which would give $F = \frac{1}{\phi }$. Equation 3 has served as a starting point for developing correlations for F based on models for $\tau _e$. By comparing (2) and (3), we see that the Archie equation is consistent with describing the electric tortuosity as

$$\begin{aligned} \tau _e = \phi ^{-(m-1)}. \end{aligned}$$

(4)

The electric tortuosity is not the same as the (hydraulic) tortuosity that appears in the Kozeny–Carman equation (1), but, based on the idea that they both are representations of a common “intrinsic” pore space tortuosity, a number of expressions linking the two have been proposed. See Ghanbarian et al. (2013) for a fairly recent review.

Since permeability and formation factor only depend on pore space geometry, it is natural to propose that there should exist a small set of properly defined geometric measures that can, at least to very good approximation, be used for estimating these properties. The identification of these geometric measures remains an unsolved problem. In practice, f and $\tau$ in (1), and m in (2) often play the role of mere fudge–factors/fudge–functions for fitting experimental data, and more rigorous approaches are needed. Recently, it has been proposed (Lehmann et al. 2008; Mecke 2000; Mecke and Arns 2005; Vogel et al. 2010; Scholz et al. 2012, 2015; Liu et al. 2017; Armstrong et al. 2018) that permeability and formation factor may be estimated in terms of a set of geometric measures known as Minkowski functionals or intrinsic volumes. Two of these measures, $\phi$ and $\sigma$, are already represented in the Kozeny–Carman equation (1). In the present paper, we will investigate the predictive power of the full set of Minkowski functionals on the permeability and formation factor of two-dimensional computer-generated pore spaces.

2 Minkowski Functionals

The Minkowski functionals are integrals over geometrical sets, and they are also well defined for polyhedra with singular edges (Mecke 2000). In d-dimensions, there are $d+1$ functionals $W_0 \ldots W_d$, where $W_0$ is the hyper-volume and the rest are integrals over the $d-1$-dimensional bounding hyper-surface(s). A recent comprehensive overview of the application of Minkowski functionals for the characterization of porous media and porous media transport can be found in Armstrong et al. (2018). In two dimensions, the surface integrals are replaced by integrals over the pore space perimeter.

Our aim is to apply the Minkowski functionals for characterizing permeability and formation factor, which, for a representative elementary volume (REV) of a homogeneous medium, is independent of system size. The relevant quantities are then the specific functionals. Note also that what is relevant for the transport properties is the connected pore space. This implies that any isolated pores should be excluded from the calculation of the pore space functionals.

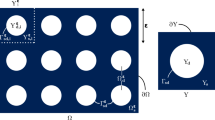
In the present paper, we will only be concerned with two-dimensional pore spaces, and the characteristic quantities are then (see Fig. 1) porosity

$$\begin{aligned} \phi = \frac{A_p}{A}, \end{aligned}$$

(5)

where $A_p$ is the connected pore space area and A is the total area, specific pore perimeter length

$$\begin{aligned} \sigma = \frac{1}{A} \int {\hbox {d}}L, \end{aligned}$$

(6)

where the integral runs over the connected pore space perimeter, and specific Euler characteristic

$$\begin{aligned} \chi _s = \frac{1}{A}\chi = \frac{1}{A}\frac{1}{2\pi }\int \frac{1}{R} {\hbox {d}}L, \end{aligned}$$

(7)

where R is the radius of curvature of the connected pore space perimeter. Note that (in 2D) $\chi$ for the connected pore space is equal to the number of grains (unconnected pores are counted as being part of the enclosing grains) since we have $\int \frac{1}{R} {\hbox {d}}L = -2\pi$ when we integrate along the perimeter of each single grain. The Euler characteristic is also a measure of topology, and for a connected periodic pore space, we have

$$\begin{aligned} \chi = -g, \end{aligned}$$

(8)

where g is the number of redundant connections, or, in an equivalent pore network, the number of links that can be broken keeping inlet and outlet connected.

Fig. 1

Example of a unit cell for a 2D periodic porous medium. Connected pore space in gray and grains in black. The specific Minkowski functionals that characterize the pore space are porosity, $\phi = \frac{\text {Area of gray}}{\mathrm {Total \,area}}$, specific pore perimeter length, $\sigma = \frac{\text {Length of red lines}}{\mathrm {Total \,area}}$, and specific Euler characteristic, $\chi _s = -\frac{\text {Number of grains}}{\mathrm {Total\, area}}$

2.1 Permeability and Hadwiger’s Characterization Theorem

The Minkowski functionals are especially useful for characterizing physical properties due to Hadwiger’s characterization theorem (Klain 1995), which states that certain valuations over geometric sets can be parameterized as a linear combination of the Minkowski functionals (Mecke 2000). Examples of such valuations are free energies in thermodynamics. Accordingly, claims have been made that it should be possible to estimate permeability from these functionals (Scholz et al. 2012, 2015). Minkowski functionals also correlate well with correct transport properties when reconstructing pore spaces (Schlüter and Vogel 2011; Mosser et al. 2017, 2018).¹

Permeability is not an additive quantity (as required by Hadwiger’s theorem), so the theorem is not directly applicable, but if the permeability is a function of a set of additive measures, then permeability is also a function of the Minkowski functionals since any additive property depends linearly on the functionals. Since permeability is not measurable by downhole logging tools, it needs to be inferred from correlations based on a combination of measurements. These measurable quantities are typically additive, and thus, if the permeability is a function of the Minkowski functionals, it should be possible to find good generally applicable correlations, while such correlations will be unobtainable if permeability cannot be determined based on these functionals.

Volumes with microporosity have a strong influence on the Minkowski functionals $\sigma$ and $\chi _s$, but do not contribute significantly to permeability (see Fig. 2). Also, surface roughness may change $\sigma$ without significantly affecting the permeability or formation factor. Based on these observations, we can conclude that the Minkowski functionals do not completely determine permeability and formation factor. We may, however, hope that a description of permeability and formation factor in terms of appropriately evaluated Minkowski functionals, where microporosity and surface roughness are ignored, will provide good approximations. The same level of accuracy would then also pertain to correlations based on additive measurements. The distinction between the porosity that is important for permeability and small-scale porosity that should be ignored, will, however, not always be as clear as in Fig. 2.

Fig. 2

Example of a connected pore space with grains in black (a). If we replace the dense grains with microporous grains (b), this microporosity will dominate in the evaluation of Minkowski functionals, but it will not change the permeability significantly

2.2 Dimensional Analysis

We may restrict the functional form of how permeability and formation factor may depend on the characteristic quantities for a two-dimensional pore space, $\phi \, [\cdot ]$, $\sigma \,[\hbox {m}^{-1}]$, and $\chi _s\, [\hbox {m}^{-2}]$, through dimensional analysis. Two dimensionless numbers can be formed

$$\begin{aligned} \phi \quad \text {and} \quad \lambda = -\frac{\sigma ^2}{\chi _s}, \end{aligned}$$

(9)

and permeability has dimension $\hbox {m}^{2}$, so the permeability may be expressed as

$$\begin{aligned} k(\phi ,\sigma ,\chi _s) = \frac{1}{\sigma ^2} K(\lambda ,\phi ), \end{aligned}$$

(10)

where K is an unknown dimensionless function. Note the similarity with the Kozeny–Carman equation (1), which can also be expressed in terms of $\sigma$ and a dimensionless permeability $K_{\text {KC}}$:

$$\begin{aligned} \begin{aligned} k_{\text {KC}}(\phi ,\sigma ,f,\tau )&= \frac{1}{\sigma ^2} K_{\text {KC}}(\phi ,f,\tau ) \\ K_{\text {KC}}(\phi ,f,\tau )&= \frac{\phi ^3}{f\tau }. \end{aligned} \end{aligned}$$

(11)

The formation factor is dimensionless, so we have

$$\begin{aligned} F(\phi ,\sigma ,\chi _s) = F(\lambda ,\phi ). \end{aligned}$$

(12)

We see that the Archie equation (2) is also expressed in terms of dimensionless numbers

$$\begin{aligned} F_{\text {A}}(m,\phi ) = \phi ^{-m}. \end{aligned}$$

(13)

We may investigate the viability of a description of permeability and formation factor in terms of the Minkowski functionals by generating multiple pore spaces with fixed values for the dimensionless numbers $\lambda$ and $\phi$, and compare the calculated permeability and formation factor with (10) and (12).

3 Generating Pore Spaces with Prescribed Minkowski Functionals

Most previous work on two-dimensional pore spaces has investigated synthetic models built from grains or sub-grains of equal shape (typically circles of a given size) (Gebart 1992; Koponen et al. 1996; Yazdchi et al. 2012; Ebrahimi Khabbazi et al. 2013; Matsumura and Jackson 2014; Scholz et al. 2015; Kundu et al. 2016; Liu et al. 2017; Zarandi et al. 2019). Our investigations indicate that the resulting pore spaces do not have sufficient coverage of the $(\phi ,\lambda )$ parameter space; therefore, we need to build models using differently shaped and sized sub-grains. We will also need to generate several pore spaces for each set of Minkowski functional values, which requires an algorithm that can generate pore spaces with prescribed Minkowski functionals.

The pore spaces are generated by filling an initially empty ($\phi =1$) spatial region with sub-grains of varying size and shape using a simple Metropolis-Monte-Carlo algorithm (MCMC), where an “energy” E is assigned to each specific configuration of grains (realization). This algorithm ideally creates realizations with probability

$$\begin{aligned} p \propto \exp ^{-E}. \end{aligned}$$

(14)

The current purpose of the MCMC algorithm is, however, not to generate any statistically correct ensembles, we just want to create reasonable pore spaces.

Prescribed values for the Minkowski functionals, $\phi _0$, $\sigma _0$, and $\chi _{s0}$, are enforced using simulated annealing, that is, by including a term

$$\begin{aligned} M = \left( w_0 (\phi - \phi _0)^2 + w_1 (\sigma - \sigma _0)^2 + w_2 (\chi _s - \chi _{s0})^2\right) / T \end{aligned}$$

(15)

in the MCMC energy and slowly reducing the annealing parameter T. $w_n$ are weights that may be tuned in order to improve convergence.

Periodic boundary conditions are applied in order to reduce edge effects both on the pore space itself and on the flow calculations.

The calculation of change in Minkowski functionals as a result of adding or removing a grain is local, and on a pixel representation (image), it amounts to recalculating the frequency of certain $2\times 2$-pixel configurations (Vogel et al. 2010). We have implemented a slightly modified version, taking into account the periodic boundary conditions, of the code found in the QuantIm library (Vogel 2017).

The MCMC energy term is based on the pixel representation

$$\begin{aligned} E = -a \sum _i (1-\delta _{0n_i}) + b \sum _i (1-n_i)n_i + M, \end{aligned}$$

(16)

where $n_i$ is the number of overlapping sub-grains at pixel i and a and b are tunable constants. The first term is important for porosity, while the second term governs the amount of sub-grain overlap.

The specified Minkowski functional values relate to the connected pore space only, and in the present work, we have selected to only generate pore spaces without any isolated pores. Isolated pores may be created when a sub-grain is added or removed (see Fig. 3), so a sub-grain should not be added or removed if this would create an isolated pore. The calculation of all energy terms used in the MCMC algorithm, including the Minkowski functionals, is local on the image so that the resulting algorithm should be very fast both in 2 and 3 dimensions. The connectivity check, however, requires non-local calculations. In our implementation, we first calculate the energy change, and the time-consuming connectivity check is performed only if the change should be accepted based on this. The non-local calculations substantially slow down the code and would especially do so in 3 dimensions. This is the main reason why our analysis presently is limited to 2D models. This is in contrast to pore space reconstruction algorithms, which can be based on the total pore space including isolated pores (Schlüter and Vogel 2011).

Fig. 3

In (a), three sub-grains have been placed forming a single grain, and the pore space is connected. Adding a fourth sub-grain may create an isolated pore (b). Removing the blue sub-grain in (c) will also create an isolated pore (d)

In order to enforce that the pixel representation has the correct Euler characteristic, an additional restriction is placed on where new sub-grains may be added; the distance between two grains must be at least one pixel (see Fig. 4).

Fig. 4

Two grains consisting of circular sub-grains (a) and the corresponding pixelized version (b). If grains are too close, the Euler characteristic (number of grains) will be different for the true and pixelized version

Based on the types of sub-grains used, we have generated four classes of models, with circular, square, triangular, and a mixture of sub-grain types, respectively.

3.1 Representative Elementary Volume

The concept of permeability belongs in a continuum theory for flow in porous media. The porous medium, which is highly heterogeneous on the pore scale, is replaced by a homogeneous medium at a larger scale. The scale at which the porous medium is homogeneous is related to the concept of a representative elementary volume (REV). Only REV-sized models should be used in the analysis, and hence, we are seeking a REV criterion based on the Minkowski functionals.

The size of a REV in two-dimensional models was discussed by Du and Ostoja-Starzewski (2006). In that paper, the REV characteristic length $L_{\text {REV}}$ was calculated for models built from equally sized non-overlapping disks using the disk diameter d as the characteristic small-scale length. As seen in Fig. 5, the resulting criterion for the REV size in terms of $\delta = L/d$ is strongly dependent on porosity. However, porosity is scale invariant, and a good criterion for determining the REV size should not depend strongly on it. While d might be a good measure for small-scale structure for low porosities, at high porosities the characteristic scale is related to the distance between particles, and thus, the REV criterion should be related to the number of particles in a REV-size box. Forming a length scale using the parameters $\sigma [\hbox {m}^{-1}]$, and $\chi _s[\hbox {m}^{-1}]$, a general REV criterion is

$$\begin{aligned} L > L_{\text {REV}} = \sigma ^{-2\alpha -1}(-\chi _s)^\alpha L_{\text {D REV}}, \end{aligned}$$

(17)

where $L_{\text {D REV}}$ is a dimensionless REV criterion. Varying $\alpha$ in equation (17), we have found that $\alpha = \frac{1}{2}$ gives the least dependency on porosity for the data in Du and Ostoja-Starzewski (2006), and consequently, we have the following approximate criterion for generating a REV-sized model (see Fig. 5):

$$\begin{aligned} L > L_{\text {REV}} = 130 \frac{\sqrt{-\chi _s}}{\sigma ^2}. \end{aligned}$$

(18)

However, using an anisotropy-based REV identification, it will be shown below that this criterion is not fully sufficient for identifying models that are smaller than a REV. Also, since the Minkowski-based criterion (18) is difficult to satisfy for some $(\lambda ,\phi )$-combinations given our system size ($2024\times 2024$ pixels), we have generated models using the relaxed criterion $L>1/3 L_{\text {REV}}$, and discarded non-REV models based on anisotropy as explained below.

Fig. 5

The size of a REV for models built from equally sized disks [based on the data in Du and Ostoja-Starzewski (2006)]. Red circles show the linear size $L_{\text {REV}}$ in units of disk diameter d, which gives a strong $\phi$-dependency. Black circles show $L_{\text {REV}}$ in units of $\frac{\sqrt{ -\chi _s}}{\sigma ^2}$, which is the combination of Minkowski functionals that gives the least $\phi$-dependency. In these units, all $L_{\text {REV}}<130$ indicated by the black line

The algorithms that we employ for generating synthetic pore spaces have no preferred directions and should ideally produce isotropic pore spaces. In practice, the permeability found by solving flow problems on any finite pore space will have different permeability in the x- and y-direction and nonzero cross-components. Based on the calculated permeability tensor, we estimate the isotropic infinite-size permeability as

$$\begin{aligned} k = \sqrt{k_1 k_2}, \end{aligned}$$

(19)

where $k_1$ and $k_2$ are the permeability eigenvalues (permeability in the two principal directions). Similarly, the isotropic formation factor estimate is

$$\begin{aligned} F = \frac{1}{2}(F_x+F_y). \end{aligned}$$

(20)

If a generated pore space has a high degree of anisotropy, the pore space is smaller than a REV, and we have discarded models with $k_1/k_2 > 1.25$ or $|F_x-F_y|/F > 0.25$. Out of 253 generated pore spaces with a linear size larger than $1/3L_{\text {REV}}$, 53 were discarded due to high anisotropy. Eighteen of these should actually be larger than $L_{\text {REV}}$, so the Minkowski-based criterion (18) is clearly not sufficient for defining the REV size.

We have also used the maximum anisotropy in groups of models with similar $\phi$ and $\lambda$ as a proxy for the accuracy of our permeability and formation factor estimates; the relative error in the estimate of the isotropic property (REV size) is deemed to be less than the maximum anisotropy in the finite size estimates:

$$\begin{aligned} \left| \frac{k - k_{\text {REV}}}{k_{\text {REV}}}\right| < \max \left( \frac{k_1- k_2}{k}\right) . \end{aligned}$$

(21)

If the difference in permeability between models is larger than the maximum anisotropy, the difference is deemed significant and cannot be attributed to the models being smaller than a REV.

4 Results

We have first generated a number of two-dimensional pore spaces by varying the allowed shapes and sizes of sub-grains and the parameters a and b in (16) without enforcing the Minkowski functionals (weights $w_n=0$ in (15)). We have then subsequently generated pore spaces using different shapes, sizes, and parameters while enforcing the Minkowski functional values. This produces sets of pore spaces that can be visually quite different but have the same characterization in terms of Minkowski functionals. The simulated parameter values are shown in Fig. 6. In total, 219 pore spaces were used in the analysis.

Fig. 6

The total coverage of parameter space by simulations. Simulations where the parameters a and b in (16) are specified without enforcing the Minkowski functionals in red, and simulations with specified values for the Minkowski functionals in blue. The dashed lines are $\lambda = 4\pi (1-\phi )$ and $\lambda = 12\sqrt{3}(1-\phi )$, which correspond to models with uniformly sized isolated circular and triangular grains, respectively (Eq. 27)

All pore spaces are generated as $2024\times 2024$-pixel pictures, and the permeabilities were calculated using the LIR solver for the stationary Stokes equation (Linden et al. 2015) implemented in the commercial GeoDict software (Math2Market 2018). The formation factors were calculated using a simple finite difference Laplace solver we have implemented in Python NumPy. Both solvers use periodic boundary conditions.

Examples of generated pore spaces are shown in Fig. 7. The models shown there are characterized by the same set of Minkowski functionals, but the model built from triangular grains has significantly different formation factor and permeability than the others. It will be shown below that this is a general trend. Note also that the three models all satisfy the REV criterion (18), while a visual inspection reveals that, except for the model built from circular grains, the pore spaces are clearly not of REV size, as they contain large grains spanning at least halfway across the model.

Fig. 7

Examples of pore spaces, solid phase in black. The models are characterized by the same set of Minkowski functionals: $\phi = {0.30}$, $\sigma =9.00 \times 10^{4}\hbox { m}^{-1}$, and $\chi _S = -1.35\times 10^{9}\hbox { m}^{-2}$. Going from left to right, the formation factors are $F = {8.9}$, $F = {12.1}$, and 11.2, and the corresponding permeabilities are $k = 1.2 \times 10^{-13}\hbox { m}^{2}$, $k = 5.7 \times 10^{-14}\hbox { m}^{2}$, and $1.2 \times 10^{-13}\hbox { m}^{2}$

4.1 Formation Factor

As can be seen from Fig. 8, the formation factor is mainly a function of porosity, as expected from the Archie equation (2). For a given porosity, larger $\lambda$ tends to give higher F.

Fig. 8

The formation factor as a function of $\phi$. The value of the second dimensionless parameter, $\lambda = -\frac{\sigma ^2}{\chi _S}$, is indicated by symbol size and color. The symbol shape indicates the subgrain shape

Pore spaces containing triangular sub-grains tend to have a different trend than the others, so trend analysis is performed on the 112 models with circular and square sub-grains only. We have fitted the data to the following trend function

$$\begin{aligned} F_{\text {pred}}(\phi ,\lambda ) = e^{\left( 1-\phi \right) \left( c_1 + c_2\phi +c_3\lambda + c_4\phi \lambda + c_5\lambda ^2 \right) } \phi ^{-\mu }, \end{aligned}$$

(22)

which is similar to the Archie equation (2) and has the correct end values $\frac{1}{F_{\text {pred}}(0,\lambda )} = 0$ and $F_{\text {pred}}(1,\lambda )=1$. The best-fit parameter values are:

• $\mu = {2.6}$

• $c_1={-1.7}$, $c_2={0.79}$, $c_3={-0.071}$, $c_4={0.31}$, $c_5={0.0015}.$

Fig. 9

Examples of formation factor as a function of porosity for a fixed $\lambda$. The marker shapes correspond to the shape of sub-grains, and models with a mixture of grain types are marked with a cross. Solid line is (22) globally fitted to pore spaces with circular and square sub-grains. The dashed lines are error estimates based on (21)

Examples of formation factor as a function of porosity for a fixed $\lambda$ are shown in Fig. 9. We see that the models built from triangular sub-grains tend to fall outside of the anisotropy-based error estimates (21). Thus, the difference is significant and cannot be attributed to the models being smaller than a REV.

Fig. 10

Relative distance of actual F from fitted predictor function (22) as a function of F. The marker shapes correspond to the shape of sub-grains, and models with a mixture of grain types are marked with a cross

The residual plot (Fig. 10) also shows a systematic trend for the triangle-based models, while the other models tend to spread within a $\pm \, 20\%$ range in a random pattern. Based on these observation, we conclude that the formation factor is not a function of the Minkowski functionals alone, but for pore spaces built from sufficiently smooth sub-grains, the functionals may be used to determine F with an accuracy of 20%.

For comparison, we have also fitted the data directly to the Archie equation (2) with a cementation index m that is a function of $\lambda$ and $\phi$:

$$\begin{aligned} F_{\text {pred}}(\phi ,\lambda ) = \phi ^{-(c_1 + c_2 \lambda + c_3 \lambda ^2 + c_4 \phi + c_5 \phi ^2 + c_6 \phi \lambda )}. \end{aligned}$$

(23)

With fit parameters $c_1={2.3}$, $c_2={-0.059}$, $c_3={0.00077}$, $c_4={-2.7}$, $c_5={2.6}$, and $c_6={0.25}$, the predictive power of (23) is insignificantly different from (22).

4.2 Permeability

As can be seen from Fig. 11, the dimensionless permeability $K = \sigma ^2 k$ is mainly a function of porosity, as may be expected based on the Kozeny–Carman picture (1). For a given porosity, larger $\lambda =\sigma ^2/\chi _s$ tends to give lower permeability.

Fig. 11

The dimensionless permeability $\sigma ^2 k$ as a function of $\phi$. The value of the second dimensionless parameter, $\lambda = -\frac{\sigma ^2}{\chi _S}$ is indicated by symbol size and color

In the same manner as for the formation factor, pore spaces containing triangular sub-grains tend to have a clearly different trend than the others, but in the case of permeability, each group of models has a different trend. We have fitted the data from 62 models with circular sub-grains to the following trend function

$$\begin{aligned} K_{\text {pred}}(\phi ,\lambda ) = e^{\left( c_1 +c_2\lambda + c_3\phi ^2 + c_4\phi ^2\lambda + c_5\lambda ^2 \right) } \phi ^{\alpha }, \end{aligned}$$

(24)

which is similar to (1) and consistent with $K(0,\lambda ) = 0$. The best-fit parameter values are:

• $\alpha = {3.1},$

• $c_1={-3.2}$, $c_2={-0.019}$, $c_3={1.8}$, $c_4={0.059}$, $c_5={-0.0026}.$

We see from Fig. 11 that $\sigma ^2 k$ remains finite as $\phi \rightarrow 1$ where the permeability tends to infinity. In this limit, we have $\sigma \rightarrow 0$ and $\chi _S\rightarrow 0$, and the system will contain isolated single grains. The limiting permeability value, $K_{\phi \rightarrow 1}$, depends on the details of the shape of these grains and is not well described by $\sigma$ and $\chi _S$. We have therefore excluded models with $\phi >0.85$ when fitting to (24).

Fig. 12

Examples of permeability as a function of porosity for a fixed $\lambda$. The marker shapes correspond to the shape of sub-grains, and models with a mixture of grain types are marked with a cross. Solid line is (24) globally fitted to pore spaces with circular sub-grains. The dashed lines are error estimates based on (21)

Fig. 13

Relative distance of actual K from fitted predictor function (24) as a function of K. The marker shapes correspond to the shape of sub-grains, and models with a mixture of grain types are marked with a cross

Examples of permeability as a function of porosity for a fixed $\lambda$ are shown in Fig. 12. We see that the models built from triangular and, to a lesser degree square, sub-grains fall outside of the anisotropy-based error estimates (21). Thus, the difference is significant and cannot be attributed to the models being smaller than a REV. The residual plot (Fig. 13) also shows a systematic trend for these models. The models with circular sub-grains tend to spread within a $\pm 20\%$ range in a random pattern, while the models with square and mixed sub-grain types are predicted by the trend within $\pm 40\%$. Based on these observation, we conclude that the permeability is not a function of the Minkowski functionals alone, but for pore spaces built from sufficiently smooth sub-grains the functionals may be used to determine k with an accuracy of 40%.

4.3 Describing Permeability in Terms of Electric Tortuosity

The electric tortuosity is defined by (3) as $\tau _e = \phi F$ and is a more readily measurable quantity than the Euler characteristic. Since the permeability cannot be fully determined using the Minkowski functionals, we have investigated whether a better predictor might be found using $\tau _e$ as an alternative to the dimensionless number $\lambda$.

The hydraulic tortuosity $\tau$ which appears in the Kozeny equation (1) is a different, albeit related, concept than the electric tortuosity $\tau _e$ (Ghanbarian et al. 2013; Berg and Held 2016). We have fitted the data from models with circular sub-grains to the following trend function

$$\begin{aligned} K_{\tau }(\phi ,\tau _e) = e^{\left( c_1 + c_2\phi ^2 + c_3\tau _e^2 \right) } \phi ^{\alpha }\tau _e^{-\beta }, \end{aligned}$$

(25)

which is consistent with equation (1) with

$$\begin{aligned} \tau = \tau _e^{\beta } \quad \text {and} \quad f = f(\phi ,\tau _e) = \phi ^{3-\alpha }e^{-\left( c_1 + c_2\phi ^2 + c_3\tau _e^2 \right) }. \end{aligned}$$

(26)

The best-fit parameter values are:

• $\alpha = {2.7}$, $\beta = {0.34},$

• $c_1={-3.3}$, $c_2={2.1}$, $c_3={-0.040}.$

Fig. 14

Relative distance of actual K from fitted $\phi$, $\sigma$, and $\tau _e$-based predictor function (25) as a function of K. The marker shapes correspond to the shape of sub-grains, and models with a mixture of grain types are marked with a cross

By comparing the residual plots in Figs. 13 and 14, we see that the use of $\tau _e$ instead of $\lambda$ in the pore space characterization brings the triangle-based models closer to the calculated trend. For the other models, the overall predictive power is reduced compared to (24). We conclude that for pore spaces built from sufficiently smooth sub-grains the parameter sets $\sigma$, $\phi$, and $\tau _e$ may be used to determine k with an accuracy of 45%.

Fig. 15

The dimensionless permeability $K=\sigma ^2 k$ of models with equally sized circular grains, compared with the fitted predictor function (24) (black line). Triangles are for a triangular lattice, squares for a square lattice, and circles for randomly distributed non-overlapping grains. Markers in green are this work, in blue from Fig. 6 in Gebart (1992), and in red from Fig. 2 in Yazdchi et al. (2011). The dotted lines are (28), added here to highlight the difference in permeability between the two lattices

4.4 Pore Spaces with Equally Sized and Shaped Grains

In models built using non–overlapping grains of equal size and shape, the dimensionless parameter $\lambda$ is a function of $\phi$, so that the two parameters cannot be varied independently. In particular, we have

(27)

Thus, for a given grain shape, K and F should, according to (10) and (12), be uniquely determined by porosity. We know that this is not the case, and the permeability is, for instance, dependent on lattice type for circular grains placed on a regular lattice (Gebart 1992). Thus, the validity of a Minkowski functional-based description is limited to classes of random models, especially when the porosity is close to the critical porosity where these regular models get jammed and, in 2D, permeability reach zero for nonzero $\phi$. An approximate expression for the permeability of a system consisting of equally sized circular grains on a regular lattice is (Gebart 1992)

(28)

In Fig. 15, we have plotted a number of numerically calculated permeabilities for circular grains on a regular lattice, and we see that (24) fails to give a good prediction for these systems. The prediction is much better for randomly distributed non-overlapping grains (green circles).

5 Conclusions

In order to investigate whether it is possible to derive good correlations for permeability an formation factor based on the Minkowski functionals, we have generated and analyzed two-dimensional computer-generated pore spaces covering a wide range of Minkowski functional value combinations. In general, due to Hadwiger’s theorem, any correlation based on any additive measurements cannot be expected to have more predictive power than those based on the Minkowski functionals.

Different surface roughness and microporosity will influence the functionals without significantly affecting the transport properties. However, also in the generated pore spaces, which do not contain micro porosity and rough surfaces, the Minkowski functionals do not determine permeability and formation factor uniquely.

Pore spaces with equally sized and shaped grains placed on a regular grid do not fall on the same trend as the random models, and models built using triangular sub-grains show a different trend than the others, possibly due to a different apparent surface roughness. Correlations that predict permeability and formation factor with an accuracy of 40% and 20%, respectively, for the other random models we have considered may, however, be found. Accuracy on the 40% level is considered very good in the context of predicting permeability from downhole measurements.

Permeability correlations where the Euler characteristic is replaced with the more readily measurable, and nonadditive, electric tortuosity may be found for a larger class of systems than the Minkowski functional-based correlations. The accuracy of these correlations is, however, found to be on the same level; we have derived a correlation accurate to 45%.