Abstract
To examine the need to incorporate in situ wettability measurements in direct numerical simulations, we compare waterflooding experiments in a mixed-wet carbonate from a producing reservoir and results of direct multiphase numerical simulations using the color-gradient lattice Boltzmann method. We study the experiments of Alhammadi et al. (Sci Rep 7(1):10753, 2017. https://doi.org/10.1038/s41598-017-10992-w) where the pore-scale distribution of remaining oil was imaged using micro-CT scanning. In the experiment, in situ contact angles were measured using an automated algorithm (AlRatrout et al. in Adv Water Resour 109:158–169, 2017. https://doi.org/10.1016/j.advwatres.2017.07.018), which indicated a mixed-wet state with spatially non-uniform angles. In our simulations, the pore structure was obtained from segmented images of the sample used in the experiment. Furthermore, in situ measured angles were also incorporated into our simulations using our previously developed wetting boundary condition (Akai et al. in Adv Water Resour 116(March):56–66, 2018. https://doi.org/10.1016/j.advwatres.2018.03.014). We designed six simulations with different contact angle assignments based on experimentally measured values. Both a constant contact angle based on the average value of the measured values and non-uniform contact angles informed by the measured values gave a good agreement for fluid pore occupancy between the simulation and the experiment. However, the constant contact angle assignment predicted 54% higher water effective permeability after waterflooding than that estimated for the experimental result, whereas the non-uniform contact angle assignment gave less than 1% relative error. This means that to correctly predict fluid conductivity in mixed-wet rocks, a spatially heterogeneous wettability state needs to be taken into account. The novelty of this work is to provide a direct pore-scale comparison between experiments and simulations employing experimentally measured contact angles, and to demonstrate how to use measured contact angle data to improve the predictability of direct numerical simulation, highlighting the difference between the contact angle required for the simulation of dynamic displacement process and the contact angle measured at equilibrium after waterflooding.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Multiphase flow in porous media has a wide range of applications including oil recovery, carbon storage and water flow in the unsaturated zone (Blunt 2017; Pruess and García 2002). To improve the predictive power of pore-scale models describing these phenomena, it is of great importance to implement realistic spatial information on wettability.
Recently, advances in imaging techniques have made it possible to directly observe contact angles on a pore-by-pore basis inside porous media. Andrew et al. (2014) measured in situ contact angles for a supercritical \(\hbox {CO}_2\)-brine-carbonate system at high temperatures and pressures. Khishvand et al. (2016) studied two- and three-phase flow experiments on Berea sandstone rock samples and measured contact angles based on micro-CT images. Furthermore, Alhammadi et al. (2017) conducted waterflooding experiments on carbonate rock samples saturated with crude oil taken from a producing hydrocarbon reservoir. The phase distributions were characterized with micro-CT imaging, and the in situ contact angles for three samples were measured using an automated algorithm (AlRatrout et al. 2017). The measured contact angles showed a wide distribution with values both above and below \(90^{\circ }\). Since the measurements of wettability were obtained on a pore-by-pore basis, it is of interest to determine how to incorporate this information in direct numerical simulation of two-phase flow.
Ramstad et al. (2012) conducted direct numerical simulations on micro-CT images of Berea and Bentheimer sandstone using the color-gradient lattice Boltzmann method. They computed the relative permeability for both steady-state and unsteady-state simulations. The results were compared with experimentally obtained relative permeabilities (Oak et al. 1990; Øren et al. 1998). Since the experiments were conducted on strongly water-wet outcrop sandstones, a good agreement with the experiment was obtained by assigning a constant contact angle of \(\theta =35^{\circ }\) in the simulations. Raeini et al. (2015) performed direct numerical simulations on micro-CT images of Berea sandstone using a volume-of-fluid-based finite-volume method. There was a good agreement in the capillary trapping curve between their simulations and published experimental measurements. This was achieved by assigning a constant contact angle of \(\theta =45^{\circ }\) in the simulations. Although there have been several other works on two-phase flow in 3D porous media using direct numerical simulation methods, most studies have assumed a constant contact angle (Pan et al. 2004; Li et al. 2005; Boek et al. 2017; Leclaire et al. 2017).
However, the experimental findings previously described strongly suggest that in natural crude oil and reservoir rock systems, it is common to have a wide range of contact angles as a result of wettability alteration caused by the sorption of surface active compounds to the solid surface. The degree of alteration depends on pore geometry, pore size, surface roughness and mineralogy (Buckley et al. 1998). Therefore, to better understand oil recovery from mixed-wet rocks, a spatial variation in contact angle should be taken into account.
Although several studies investigating a spatially heterogeneous wettability state using pore network modeling can be found in literature (McDougall and Sorbie 1995; Øren et al. 1998; Valvatne and Blunt 2004), there are few studies on direct numerical simulation of 3D porous media considering a distribution of contact angles from experimental measurements. There are several benefits of using direct numerical simulations, as opposed to network models. Direct simulation avoids uncertainty in pore network extraction and allows direct comparison of fluid distribution between experiments and simulations. Landry et al. (2014) investigated the impact of a mixed-wet state in a bead pack on relative permeability using two-phase lattice Boltzmann simulations. Using the approach of Hazlett et al. (1998), by altering the wettability of solid surfaces in contact with non-wetting phase after a drainage simulation, they calculated the decrease in non-wetting phase relative permeability as a result of the wettability alteration. In their work, a degree of wettability alteration was used as a variable in their sensitivity simulations. Jerauld et al. (2017) showed a comparison of steady-state relative permeability on a reservoir sandstone sample between experiments and simulations. The experiments were performed at reservoir temperatures and pressures after more than 3 weeks of aging in crude oil. They conducted three simulations with different wettability states assuming Gaussian distributions with different mean contact angles: \(\theta =45^{\circ } \pm 15^{\circ }\), \(\theta =90^{\circ } \pm 15^{\circ }\) and \(\theta =135^{\circ } \pm 15^{\circ }\). While the impact of wettability on relative permeability was modest, they concluded that the weakly oil-wet simulation (the simulation with \(\theta =135^{\circ } \pm 15^{\circ }\)) gave the best agreement with the relative permeability obtained from the experiments. In their work, although a range of the contact angle values was considered, their spatial distribution was not taken into account and the values were simply assumed: There was no independent measurement of contact angle.
In this paper, we show comparisons between waterflooding experiments in a mixed-wet carbonate from a producing reservoir (Alhammadi et al. 2017) and the results of direct numerical simulations using the color-gradient lattice Boltzmann method. We input spatially distributed experimentally measured contact angles (AlRatrout et al. 2017) in a direct numerical simulation on a 3D micro-CT image of a carbonate rock. The simulation results are compared to the experimental results in terms of local fluid configuration and fluid conductance (i.e., relative permeability). The key idea is to assign wettability information measured in the experiment to the numerical model. For this purpose, we design: (a) three simulations with the same contact angle for every pore, where the contact angle values represent an average for water-wet, weakly oil-wet and strongly oil-wet conditions, and (b) three simulations with different contact angles assigned to different pores informed by the measured values.
The paper is organized as follows: Firstly in Sect. 2, our direct numerical simulation method and the experimental data are described. Then in Sect. 2.3.4, the simulation results are compared with results obtained from waterflooding experiments on the same sample in terms of local fluid occupancy and water effective permeability. Conclusions are drawn in Sect. 3.
2 Materials and Methods
2.1 The Multiphase Lattice Boltzmann Method
Our 3D immiscible two-phase lattice Boltzmann, LB, method is constructed for a 3D 19 velocity (3D19V) lattice model based on the color-gradient approach proposed by Halliday et al. (2007). For the 3D19V lattice model, the lattice velocity, \({\mathbf {e}}_i\), is given as follows:
where \(c=\delta _{x}\)/\(\delta _{t}\) is the lattice speed with \(\delta _{x}\) being the lattice length and \(\delta _t\) the time step size. For simplicity, we set \(\delta _x=\delta _t=1\). We consider red and blue fluids whose particle distributions are \(f_i^r\) and \(f_i^b\), respectively. The total particle distribution of the fluid is given by \(f_i=f_i^r\)+\(f_i^b\). The macroscopic quantities of fluid density (\(\rho _k\)) and velocity (\({\mathbf {u}}\)) can be obtained from mass and momentum conservation expressed as
where \(\rho \) is the total fluid density given by \(\rho =\rho _r+\rho _b\). The total particle distribution (\(f_i\)) undergoes streaming and collision steps as follows:
where \(\varOmega _i({\mathbf {x}},t)\) and \(\phi _i\) are the collision operator and the body force term, respectively. The gravitational force can be inserted through \(\phi _i\). However, this is not considered in our simulations. The Bhatnagar–Gross–Krook (BGK) collision operator (Qian et al. 1992) is used as
where \(\tau \) is the single relaxation time (SRT) which determines the fluid viscosity of each phase and \(f_i^{\mathrm{eq}}\) is the equilibrium distribution function which is obtained by a second-order Taylor expansion of the Maxwell–Boltzmann distribution with respect to the local fluid velocity. The fluid interface is tracked using a color function \(\rho ^N\) defined as
The interfacial tension between two fluids is introduced as a spatially varying body force \({\mathbf {F}}\) based on the continuum surface force (CSF) model of Brackbill et al. (1992) which is given by
where \(\sigma \) is the interfacial tension and \(\kappa \) is the curvature of the interface. Then, the body force \({\mathbf {F}}\) is implemented through \(\phi _i\) in Eq. 4 using the scheme proposed by Guo et al. (2002). After the application of the body force, the total particle distribution is divided into \(f_i^r\) and \(f_i^b\) using the recoloring scheme proposed by Latva-Kokko and Rothman (2005) as follows:
where \(\beta \) is the segregation parameter which can take a value in (0, 1) and is fixed at 0.7 in our simulations, \(\omega _i\) is the weight coefficient for the 3D19V lattice model and \(\varphi \) is the angle between the color gradient and the lattice vector. A detailed description of our multiphase lattice Boltzmann model can be found in our previous study (Akai et al. 2018).
The no-slip boundary condition is implemented based on the full-way bounce back scheme at the solid boundary lattice nodes. In this scheme, the particle distributions at boundary lattice nodes are bounced back into flow domain instead of performing the collision step.
To properly model the wettability of the fluids, the wetting boundary condition described in Akai et al. (2018) is used. The basic idea of this boundary condition is to modify the direction of the interface normal vector at the boundary according to a specified contact angle. This method allows the accurate assignment of contact angle in arbitrary 3D geometries, with lower spurious currents than the commonly applied fictitious density boundary condition (Akai et al. 2018). For the inlet and outlet boundaries of a simulation domain, we use a constant velocity and a constant pressure boundary condition, respectively (Zou and He 1997).
2.2 Pore-Scale Waterflooding Experiments
Alhammadi et al. (2017) conducted three waterflooding experiments using three carbonate samples drilled from the same core plug and saturated with two types of crude oil (a light crude oil from the same reservoir and an Arabian medium crude oil that is relatively heavier). The sample was mainly composed of calcite (\(96.5 \pm 1.9\) weight %) with minor amounts of dolomite, kaolinite and quartz. The helium porosity and permeability measured on the core plug were 27.0% and 6.8 \(\times \)\(10^{-13}\)\(\hbox {m}^2\) (686 mD), respectively (Alhammadi et al. 2017). Through applying three aging protocols, three distinct wettability states were established after primary drainage. The distributions of initial oil after drainage and remaining oil after waterflooding were imaged with a micro-CT scanner at subsurface conditions. The in situ contact angles were measured at the three-phase contact line from the dot product of vectors representing the oil–brine interface and the brine–rock interface using the automated algorithm developed by AlRatrout et al. (2017). The measured contact angles had a wide distribution with different mean contact angles for the three samples.
In this paper, we focus on the waterflooding experiment of the most oil-wet rock, presented as sample 2 in Alhammadi et al. (2017, 2018). This core, of 4.75 mm diameter and 13.1 mm long, was first flooded with 20 pore volumes (PVs) of crude oil and then aged for 3 weeks. The aging was performed at 80 \(^{\circ }\)C and 10 MPa during which the sample was aged dynamically for 1 week [continuous supply of polar crude oil components (Fernø et al. 2010)], then statically for 2 weeks. Micro-CT images were acquired at the center of the sample with a resolution of 2 \(\upmu \hbox {m}/\mathrm{voxel}\) before and after 20 PVs of waterflooding at 80 \(^{\circ }\)C and 10 MPa. The images were taken 2 h after the end of waterflooding to avoid the movement of fluids during image acquisition. Three-phase segmentation (oil, brine and rock) was performed on an image volume with a size of 976 \(\times \) 1014 \(\times \) 601 \(\hbox {voxel}^3\), using a machine learning segmentation known as Trainable WEKA segmentation (Arganda-Carreras et al. 2017) to capture not only the amount of the remaining oil saturation, but also the shape of the remaining oil ganglia at the three-phase contact points at which contact angles were measured. A total of 1.41 million in situ contact angle measurements were made which indicated that the rock was mixed-wet with values both above and below \(90^{\circ }\). From these data, a cubic sub-volume consisting of 640 \(\times \) 640 \(\times \) 500 \(\hbox {voxel}^3\) (1.28 \(\times \) 1.28 \(\times \) 1.00 \(\hbox {mm}^3\)) was extracted for our simulations. The original raw micro-CT images and their three-phase segmented images before and after waterflooding are shown in Fig. 1.
Micro-CT images for the waterflooding experiment conducted on the aged sample. Here, the volume used for image analysis is shown. a Original raw gray-scale micro-CT images before waterflooding. b Three-phase segmented images before waterflooding. c Original raw gray-scale micro-CT images after waterflooding. d Three-phase segmented images after waterflooding. In a and c, oil, brine and rock are shown in black, dark gray and light gray, respectively. In b and d, oil, brine and rock are shown in red, blue and white, respectively. The black squares in c and d indicate the cubic sub-volume used for our simulation study
2.3 Pore Structures Used for the Simulations and Measured Contact Angles
2.3.1 Upscaling of Micro-CT Data
To save computational time, the three-phase segmented data of the sub-volume at 2 \(\upmu \hbox {m}/\mathrm{voxel}\) resolution were upscaled into a coarse grid system with a grid size of 5 \(\upmu \hbox {m}/\mathrm{voxel}\) using the following operation:
where \(L^{i,j,k}\) is the label of the grid block at (i, j, k) in the coarsened grid system and \(V^{i,j,k}_{\alpha }\) is the volume fraction of phase \(\alpha \) (s for solid, o for oil and w for water, respectively) in the grid block at (i, j, k). Based on the resultant label data, \(L^{i,j,k}\), consisting of 256 \(\times \) 256 \(\times \) 200 \(\hbox {voxel}^3\) (i.e., 1.28 \(\times \) 1.28 \(\times \) 1.00 \(\hbox {mm}^3\)), the void spaces were extracted. The label data, \(L^{i,j,k}\), were also used to compare experimentally measured local fluid occupancy after waterflooding to the simulated results. After removing isolated void spaces in the sub-volume, the connected void space had a porosity of 17.8%.
2.3.2 Partitioning of the Void Space into Individual Pore Regions
We partitioned the void space into pore regions (pores) for two reasons: firstly, to assign different contact angles to each pore region; and secondly to analyze the simulation results in terms of local fluid occupancy. The measured contact angles were available as 3D data points along three-phase contact lines observed in the experiments, whereas our simulation requires input of a contact angle for all grid voxels at solid and pore boundaries. We do not have sufficient experimental data to assign contact angles on a voxel-by-voxel basis, and in any event, this requires an unnecessarily detailed characterization of wettability. Instead, we assign a single contact angle to a pore region, but allow different pores to have different contact angles. This approach is conceptually similar to that adapted in pore network modeling (Blunt 2017). Moreover, our comparison between the simulation and experimental results will be made in terms of local fluid occupancy, i.e., we compare the fluid occupancy of each individual pore region.
The partitioning of the void space was performed using the separate object algorithm in Avizo\(^{\textregistered }\), a commercial image analysis software. The algorithm separates an object into several individual elements according to the distance map, which is the distance to the nearest solid. As a result, the void space was partitioned into 360 individual pore regions as shown in Fig. 2. The algorithm is similar to that described by other authors (for instance, Dong and Blunt 2009; Raeini et al. 2017).
2.3.3 Measured Contact Angles
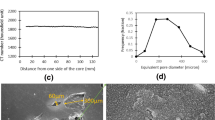
Several methods for the measurement of in situ contact angles using micro-CT images of rock samples have been proposed in the literature (e.g., Prodanovic et al. 2006; Andrew et al. 2014; Klise et al. 2016; Scanziani et al. 2017). In this work, we have used an automated algorithm by AlRatrout et al. (2017). This algorithm automatically measures contact angles along three-phase contact lines obtained from segmented micro-CT images by the dot product of two normal vectors of fluid–fluid and fluid–rock interfaces (Alhammadi et al. 2017). In total, 485,511 in situ measured contact angles through the water phase were available within the sub-volume (Fig. 3). The measured contact angles show a wide distribution with an average value of 107\(^\circ \), which is smaller than 141\(^\circ \) measured on a flat calcite mineral surface using the same crude oil and brine as in the flooding experiment (Alhammadi et al. 2017). The effective angle measured on the rough pore walls accounts for regions where a strong wettability alteration has taken place and portions of the surface that retain water after primary drainage, resulting in not only a single value but a range of contact angles both above and below 90\(^\circ \). The angles were measured based on the segmented images taken 2 h after the end of 20 PVs of waterflooding. These angles would represent effective contact angles on a rough surface in equilibrium once flow has stopped rather than dynamic contact angles to be used to simulate a displacement process, i.e., advancing and receding angles. In addition, when a three-phase contact line is pinned at sharp corners, various angles can be formed. Therefore, instead of using locally different angles for each pore, a mean contact angle for each individual pore region (\(\theta _p\)) was obtained by taking the average of the measured angles (Fig. 3b). In total, 322 pores out of 360 pores had more than 100 contact angle measurements, while 13 pores had no measured contact angles since—in the experiments—no three-phase contact line was detected within them: After waterflooding, they were entirely water or oil filled. If \(\theta _p\) of a pore was greater than 110\(^\circ \), which means most measured angles in the pore were greater than 90\(^\circ \), the pore was classified as oil-wet (OW). If \(\theta _p\) was smaller than 110\(^\circ \) and greater than 70\(^\circ \), the pore was classified as neutrally wet (NW). If \(\theta _p\) was smaller than 70\(^\circ \), the pore was classified as water-wet (WW). As a result, the 360 pores were divided into 5 WW pores, 212 NW pores, 130 OW pores, with 13 undefined pores. The contact angles for these undefined pores were assumed to be \(107 ^\circ \), which was the average of all the data points. As summarized in Table 1, 63% of the pore volume was in NW pores, 36% in OW pores with only a small contribution from WW and undefined regions. Based on this pore classification, we will discuss contact angles to be used in the simulations.
2.3.4 Simulation Conditions
The experimental sample had a helium porosity of 31.7%, while its segmented porosity based on the micro-CT images at a resolution of 2 \(\upmu \hbox {m}/\mathrm{voxel}\) was 20.4%. This implies that the sample has micro-porosity whose pore size is below the resolution of the micro-CT imaging. However, in this paper, we only consider resolvable macro-porosity: We assume that the micro-porosity remained water-filled in the experiments.
According to the images taken before waterflooding, the initial water saturation is estimated at 6% of which only a saturation of 1% is in the connected pore space. In this work, we assigned an initial water saturation of 1% in the locations where water was imaged in the experiments after primary drainage. In reality, more water was present in unresolved micro-porosity and it is likely that the water was connected, but through layers that were not resolved in the images. Higher-resolution imaging and simulations are required to assess the impact of this water and micro-porosity on the displacement behavior.
In the simulations, as in the experiments, the main flow direction was vertical, in the z direction. Ten lattice nodes as a buffer zone (0.05 mm) was attached to the inlet and outlet; therefore, the model used for the simulations consisted of 256 \(\times \) 256 \(\times \) 220 \(\hbox {voxel}^3\) at 5 \(\upmu \hbox {m}/\mathrm{voxel}\) (i.e., 1.28 \(\times \) 1.28 \(\times \) 1.10 \(\hbox {mm}^3\)). The pore structure used for the simulations is shown in Fig. 4. Water was injected from the inlet face at \(z=0\) mm with a constant velocity, while the outlet face at \(z=1.10\) mm had a constant pressure. We note that these boundary conditions imposed on the cropped sub-volume do not exactly reproduce the experimental waterflooding conditions since in the experiment the inlet and outlet faces of the sub-volume were neither a constant flow nor constant pressure condition. This uncertainty associated with boundary conditions could be reduced by increasing the size of a simulation domain.
We use the Darcy-scale capillary number defined as
where \(\mu _{w}\) is the viscosity of water, \(q_{w}\) is the Darcy velocity of injected water and \(\sigma \) is the interfacial tension between oil and water. Table 2 shows a comparison between experimental and simulation conditions. Similar to other studies using direct numerical simulations for waterflooding (Raeini et al. 2014b; Leclaire et al. 2017; Boek et al. 2017; Jerauld et al. 2017), our simulations were performed with Ca of order \(10^{-5}\), which is two orders of magnitude higher than the experimental value since computational time significantly increases as the capillary number decreases lower than \(10^{-5}\). Chatzis and Morrow (1984) reported that an average capillary number below which mobilization of residual oil occurs was \(Ca =3.8 \times 10^{-5}\) based on core flooding experiments on various sandstone cores. Later, Raeini et al. (2014a) showed that using direct numerical simulations on a single pore throat geometry, the threshold capillary number below which snapped-off droplets become trapped is \(Ca^\text {throat} = {\mu _w {\bar{u}}_\text {throat}}/{\sigma }= 9.3 \times 10^{-4}\), where \(Ca^\text {throat}\) is the pore-scale capillary number defined using the average velocity in a throat (\({\bar{u}}_\text {throat}\)). Assuming a cylindrical pore structure in which the maximum velocity at the center is two times higher than the average velocity, our Darcy-scale capillary number used for simulations can be translated to \(Ca^\text {throat}=2{\mu _{w}}{q_{w}}/{\phi \sigma } \approx 3 \times 10^{-4}\), where \(\phi \) is the porosity, \(20\%\) in our case. Since this capillary number is lower than the threshold capillary number reported in Raeini et al. (2014a), we assume the simulations and the experiment are comparable. Nevertheless because recent experimental work indicates in mixed-wet conditions dynamic effects can occur even for a capillary number of order \(10^{-6}\) (Zou et al. 2018), this assumption has to be further investigated.
Six simulations with different wettability states were conducted by assigning different contact angles to solid and pore boundary voxels belonging to each pore region. We employed our previously reported wetting boundary condition which accurately models the contact angle for 3D arbitrarily complex structures (Akai et al. 2018). As summarized in Table 3, a single value of the contact angle was assigned for all solid–fluid boundary nodes for cases 1–3 (constant contact angle cases). Cases 1 and 3 represent a uniformly water-wet and oil-wet rock, respectively. The contact angle of case 2 was 107\(^\circ \) based on the average of all 485,111 measured values. On the other hand, different contact angles were assigned for solid–fluid boundary nodes belonging to each pore for cases 4–6 (non-uniform contact angle cases). In case 4, the average contact angles for each pore were directly assigned. Since the measured contact angles were obtained from the fluid configuration at equilibrium after waterflooding, they can be different from the angles to be assigned for a simulation of a dynamic process. Furthermore, it is not evident that a single average value of contact angle, rather than a maximum, for instance, properly represents the critical value necessary to determine accurately the local capillary pressure for displacement. Therefore, two additional cases informed from the measured contact angles were prepared. In case 5, contact angles of 150\(^\circ \), 100\(^\circ \) and 30\(^\circ \) were assigned to OW, NW and WW pores, respectively. This case is designed to represent the correct threshold capillary pressures in a dynamic displacement process which is limited by the largest local contact angle in OW pores, see Fig. 3. In case 6, contact angles 150\(^\circ \), 80\(^\circ \) and 30\(^\circ \) were assigned to OW, NW and WW pores, respectively. Here, it is further assumed that the NW pores are effectively weakly water-wet.
2.4 Fluid Saturation During Waterflooding
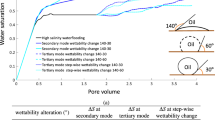
All the simulations were run for 10 PVs of water injection. The oil saturation as a function of pore volumes of water injected is shown in Fig. 5. As expected, a significant difference in oil recovery was observed for these six cases. The oil saturation from the experiment was 36% after 20 PVs of water injection. As shown in Fig. 5, case 1 (constant contact angle of \(\theta =30 ^\circ \)) shows a rapid decrease in the oil saturation and reaches a steady state after 3 PVs, whereas the other cases show a slow decrease in the oil saturation. Except for case 1, there are pore regions with contact angles greater than 90\(^\circ \). In these oil-wet regions, oil flows as a connected oil layer with low conductance in the corners of the pore spaces; therefore, production of oil continues long after water breakthrough. As shown in the figure, the average oil saturation of case 5 reached 36% after 8.4 PVs of water injection and then stabilized. This is consistent with the remaining oil saturation observed in the experiment.
Oil saturation as a function of pore volumes of water injected for the six simulation cases, see Table 3. The oil saturation of the same domain obtained from the experiment was 36% after 20 PVs of water injection, indicated by the dashed horizontal line
After 10 PVs of waterflooding, the simulations were continued while stopping water injection as in the experiment. After stopping water injection, the average fluid velocity within the simulation domain continued to decrease. We continued the simulations until the average fluid velocity became 10 times lower than the water velocity used for waterflooding. This equilibrium process was conducted to compare the simulation results with the experimental result which was imaged 2 h after the end of water injection. In fact, there was no appreciable change in the average fluid saturation between the end of 10 PVs of waterflooding and the equilibrium process. However, in oil-wet cases (case 2–6), we observed intermittent water pathways in the later part of waterflooding. This intermittent change in water phase connectivity could affect the water effective permeability which will be discussed in Sect. 2.7. Thus, the equilibrium simulations were continued to completely disconnect these unstable water pathways which did not exist in the experimentally obtained fluid distribution.
Fluid distributions obtained from the simulations at equilibrium following 10 PVs of waterflooding were compared to those obtained from the experiment. Figure 6 shows the average oil saturations in each slice perpendicular to the flow direction as a function of distance from the inlet. Cases 5 and 6 give a similar trend to that obtained from the experiment, especially in the region 0.15 mm \(\le z \le \) 0.65 mm. In all six cases, a considerable change in the oil saturation influenced by the boundary conditions can be seen for \(z<\) 0.15 mm and \(z>\) 0.95 mm. Therefore, the area of 0.15 mm \(\le z \le \) 0.95 mm was selected as an area of interest (AoI), which accounts for 80% of the entire simulation domain, for further quantitative comparisons between the experiment and simulations.
Oil saturation as a function of distance from the inlet after the equilibrium process following 10 PVs of waterflooding. Three cases with constant contact angle are shown in (a), while the other three cases with non-uniform contact angles are shown in (b). Here, the influence of the boundary conditions can be seen in the simulation results near the inlet and outlet. Therefore, an area of interest (AoI) was defined as shown by the black rectangles for further quantitative analyses
2.5 Local Fluid Occupancy Based on the Pore Size
The local fluid occupancy in the AoI was studied as a function of pore size. For each pore region, the number of oil-filled voxels at the initial conditions and after waterflooding was counted and summarized into histograms (Fig. 7) by sampling for every 5 -\(\upmu \)m increment of equivalent pore diameter, which is the diameter of the largest sphere that just can fit in each pore region. Note that these are pore volume weighted histograms and not pore number weighted. As shown in the figure, the fluid occupancy of each pore size is well predicted for cases 2, 3 and 5.
Histograms of fluid occupancy of the oil phase as a function of equivalent pore diameter. The simulation results from cases 1 to 6 are shown from a to f. Here, the black dashed line with cross marks shows the histogram of the oil saturation at the initial condition, while the black lines with black and red circles show the histograms of the oil saturation after waterflooding for the experimental and simulated results, respectively
Additionally, recovery factors from each pore region were evaluated (Fig. 8). In Fig. 8, the experiment shows greater recovery from the larger pores. This is expected for an oil-wet system, where water preferentially fills the larger pore spaces first, retaining oil in the narrower regions or as thin layers (Blunt 2017). This overall trend is captured in the simulations, except for case 1, where water-wet conditions were assumed. Here, recovery was greater from the smaller pores, which were preferentially filled with water, while oil was trapped in the larger pores. In case 6, we made the NW pores weakly water-wet. As a consequence, we see that the smaller pores see a higher recovery— they are preferentially filled with water. This is clearly inconsistent with the experimental trend: Case 5 where the NW pores had a contact angle above \(90^{\circ }\) provides a better match to the experiments.
To quantitatively compare the experiment and simulation the experiment and simulations, the pore volume weighted difference in recovery factor for each pore was evaluated, as shown in Table 4. It is defined as:
where \(N_b\) is the number of bins for the equivalent pore radius, \(\phi _{n}\) is the total pore volume of the pore regions belonging to the \(n-\hbox {th}\) bin and \(RF^{\mathrm{sim}}_n\) and \(RF^{\mathrm{exp}}_n\) are the RF of the \(n-\hbox {th}\) bin obtained from the simulation and experimental results, respectively. As shown in Table 4, cases 2 and 5 show the smallest error in recovery factors for each pore region. This means that the right amount of fluid was properly placed in the correct pore sizes in these cases.
2.6 Local Fluid Occupancy at the Sub-Pore Scale
We compared the local fluid occupancy between the experiment and simulations on a voxel-by-voxel basis using the following error index:
where \(N_p\) is the number of pore voxels within the AoI (1,849,485 voxels) and \(l_{i,j,k}^{\mathrm{sim}}\) and \(l_{i,j,k}^{\mathrm{exp}}\) are the labels defined at fluid voxels that take value 1 if the voxel is filled with oil and 0 if the voxel is filled with water, evaluated based on the simulated and experimentally obtained fluid distributions, respectively. The error index \(E_{\mathrm{local}}\) goes to 0 if the experimental and simulated results are perfectly matched, while it becomes 1 if the results are completely different. Table 4 summarizes the resultant error index. As expected, case 1 where water-wet conditions are assumed had the worst error index. The other cases showed 30–40% of error in the local fluid occupancy. Figure 9 visually compares the fluid distribution in the slice at \(z=0.45\) mm (the slice perpendicular to the flow direction) between the experiment and simulation for case 2 and 5 in which the best agreement was obtained for the recovery factors for each pore. As shown in Fig. 9, most pores are properly filled. However there was still disagreement with the experimental distribution, resulting in 31 and 35% of error in the local fluid occupancy, respectively.
Bultreys et al. (2018) showed the variation in local fluid occupancy in five repeated \(\mathrm{CO_2}\) drainage-imbibition experiments on a single Bentheimer sandstone sample conducted by Andrew et al. (2014). They observed that some pores are filled with a different fluid in the repeated experiments, although averaged statistical properties, such as the residual saturation, size distribution of trapped clusters and the occupancy as a function of pore size, as shown in Figs. 7 and 8, remained the same. The discrepancy was largest for pores of intermediate size. We therefore consider the observed error inevitable because of the unavoidable sensitivity of displacement to perturbations in the boundary and initial conditions. Considering this experimental uncertainty, we suggest that pore occupancy as a function of pore size is a more appropriate measure for comparison between the experiment and simulation, as observed in Figs. 7 and 8.
2.7 Fluid Conductance
The 3D distributions of the water phase after the equilibrium process following waterflooding are shown in Fig. 10. It can be seen that the water phase distribution obtained from case 5 is similar to that obtained from the experiment. The 3D phase distribution and its connectivity control the conductance of the phase (i.e., the relative permeability). Therefore, the 3D water phase distribution after waterflooding was evaluated in terms of fluid conductance. Since a relative permeability measurement was not available in the experiment, its water effective permeability after waterflooding was estimated by conducting single-phase LB simulations on the water phase obtained from the micro-CT images after waterflooding. For consistent comparison, single-phase LB simulations were also performed on the water phase obtained from the two-phase LB simulations for cases 1 to 6.
Comparison of the 3D water phase velocity distributions after waterflooding obtained from single-phase LB simulations on the water phase. a and b show the spatial distribution of the normalized fluid velocity, \(U_{\mathrm{abs}}/U_{\mathrm{avg}}\), for the experiment and simulation for case 5, respectively. c shows a histogram of the \(U_{\mathrm{abs}}/U_{\mathrm{avg}}\) sampled uniformly in 200 bins of \(\log (U_{\mathrm{abs}}/U_{\mathrm{avg}})\)
The comparison of water effective permeability after waterflooding is summarized in Table 4. Case 5 showed the best agreement with the computed water effective permeability of the experiment with only 0.7% difference. Note that if a constant contact angle \(\theta =107^{\mathrm{o}}\) (case 2) is used, which also had the best agreement in recovery factors for each pore and is a reasonable assumption when measured contact angles are not available, the water effective permeability was overestimated by 54% although the predicted water saturation was lower than that of the experiment. As discussed in the previous sections, in case 5, even though the voxel-by-voxel prediction of occupancy has an error of 35%, a proper placement of fluid in correct pore sizes as shown in Figs. 7, 8 and a proper representation of fluid connectivity result in an accurate prediction of the water effective permeability.
Moreover, we compare the simulated fluid velocity distributions between the experiment and simulation for case 5. Figure 11 shows the spatial distribution of the normalized fluid velocity, \(U_{\mathrm{abs}}/U_{\mathrm{avg}}\), where \(U_{\mathrm{abs}}\) is the magnitude of the computed fluid velocities at each voxel and \(U_{\mathrm{avg}}\) is the average value and a histogram of the \(U_{\mathrm{abs}}/U_{\mathrm{avg}}\) sampled uniformly in 200 bins of \(\log (U_{\mathrm{abs}}/U_{\mathrm{avg}})\) (Bijeljic et al. 2013). Although the experiment shows more channels with low fluid velocity than the simulation, the main flowing channels with higher velocity are well captured by the simulation.
3 Conclusions
We have performed direct numerical simulations on pore space images employing a direct assignment of local contact angle obtained from experimental measurements. As opposed to pore network models, use of direct numerical simulations allows direct comparison of fluid occupancy between experiments and simulations avoiding uncertainty in pore network extraction.
Six simulations with different contact angle assignments were performed. These cases were designed based on the experimentally measured values. We considered three cases with constant contact angles, and three cases where the contact angle varied across different pore regions in accordance with the experimentally measured values. Then, the local fluid occupancy of each pore region was analyzed for these simulation results and compared with that obtained from the experiment.
In the experiment, the larger pores showed greater local recovery, as they were preferentially filled first during waterflooding, with oil retained in the smaller pores and as layers. This is indicative of oil-wet or mixed-wet conditions.
Applying a constant contact angle of \(\theta =107^{\circ }\), which was the average value of the in situ measured angles, gave a good agreement in the local fluid occupancy based on the pore size. However, this case did not accurately predict the water effective permeability. This means that the spatial heterogeneity of the contact angle distribution observed in the experiment has to be taken into account to accurately predict fluid connectivity. However, directly applying pore-averaged measured values to each pore region did not improve the quality of the match. Applying a higher contact angle than the pore-averaged measured value for oil-wet pore regions improved the agreement between the experiment and simulations. In a process when non-wetting phase displaces wetting phase, it is locally the largest contact angle that determines the threshold capillary pressure at which one phase can advance and displace another. As a consequence, using contact angle values near the maximum observed within each pore provided the most accurate reproduction of the experimental results.
For the cases where the wetting boundary conditions of all solid and fluid boundaries were informed from the measured angles, but using near-maximum values in pores whose average contact angles indicated oil-wet behavior, the fluid occupancy for each pore region after waterflooding was reasonably well predicted. The simulated water effective permeability also gave a good agreement with the experimental result.
Overall, we have demonstrated how to use micro-CT image based experimentally measured contact angles in direct numerical simulations to improve the characterization of multiphase flow displacement in mixed-wet rocks. In particular, a spatially heterogeneous wettability state needs to be taken into account to obtain accurate predictions of fluid occupancy and flow properties.
References
Akai, T., Bijeljic, B., Blunt, M.J.: Wetting boundary condition for the color-gradient lattice Boltzmann method: validation with analytical and experimental data. Adv. Water Resour. 116(March), 56–66 (2018). https://doi.org/10.1016/j.advwatres.2018.03.014
Alhammadi, A., Alratrout, A., Bijeljic, B., Blunt, M.: X-ray micro-tomography datasets of mixed-wet carbonate reservoir rocks for in situ effective contact angle measurements. In: Digital Rocks Portal (2018). http://www.digitalrocksportal.org. Accessed 17 Nov 2018
Alhammadi, A.M., AlRatrout, A., Singh, K., Bijeljic, B., Blunt, M.J.: In situ characterization of mixed-wettability in a reservoir rock at subsurface conditions. Sci. Rep. 7(1), 10753 (2017). https://doi.org/10.1038/s41598-017-10992-w
AlRatrout, A., Raeini, A.Q., Bijeljic, B., Blunt, M.J.: Automatic measurement of contact angle in pore-space images. Adv. Water Resour. 109, 158–169 (2017). https://doi.org/10.1016/j.advwatres.2017.07.018
Andrew, M., Bijeljic, B., Blunt, M.J.: Pore-scale contact angle measurements at reservoir conditions using X-ray microtomography. Adv. Water Resour. 68, 24–31 (2014). https://doi.org/10.1016/j.advwatres.2014.02.014
Arganda-Carreras, I., Kaynig, V., Rueden, C., Eliceiri, K.W., Schindelin, J., Cardona, A., Sebastian Seung, H.: Trainable Weka Segmentation: a machine learning tool for microscopy pixel classification. Bioinformatics 33(15), 2424–2426 (2017). https://doi.org/10.1093/bioinformatics/btx180
Bijeljic, B., Raeini, A., Mostaghimi, P., Blunt, M.J.: Predictions of non-Fickian solute transport in different classes of porous media using direct simulation on pore-scale images. Phys. Rev. E 87(1), 013011 (2013). https://doi.org/10.1103/PhysRevE.87.013011
Blunt, M.J.: Multiphase Flow in Permeable Media: A Pore-Scale Perspective. Cambridge University Press, Cambridge (2017)
Boek, E.S., Zacharoudiou, I., Gray, F., Shah, S.M., Crawshaw, J.P., Yang, J.: Multiphase-flow and reactive-transport validation studies at the pore scale by use of lattice Boltzmann computer simulations. SPE J. 22(03), 0940–0949 (2017). https://doi.org/10.2118/170941-PA
Brackbill, J., Kothe, D., Zemach, C.: A continuum method for modeling surface tension. J. Comput. Phys. 100(2), 335–354 (1992). https://doi.org/10.1016/0021-9991(92)90240-Y
Buckley, J., Liu, Y., Monsterleet, S.: Mechanisms of wetting alteration by crude oils. SPE J. 3(01), 54–61 (1998). https://doi.org/10.2118/37230-PA
Bultreys, T., Lin, Q., Gao, Y., Raeini, A.Q., AlRatrout, A., Bijeljic, B., Blunt, M.J.: Validation of model predictions of pore-scale fluid distributions during two-phase flow. Phys. Rev. E 97(5), 053104 (2018). https://doi.org/10.1103/PhysRevE.97.053104
Chatzis, I., Morrow, N.R.: Correlation of capillary number relationships for sandstone. Soc. Pet. Eng. J. 24(05), 555–562 (1984). https://doi.org/10.2118/10114-PA
Dong, H., Blunt, M.J.: Pore-network extraction from micro-computerized-tomography images. Phys. Rev. E 80(3), 036307 (2009). https://doi.org/10.1103/PhysRevE.80.036307
Fernø, M.A., Torsvik, M., Haugland, S., Graue, A.: Dynamic laboratory wettability alteration. Energy Fuels 24(7), 3950–3958 (2010). https://doi.org/10.1021/ef1001716
Guo, Z., Zheng, C., Shi, B.: Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys. Rev. E 65(4), 046308 (2002). https://doi.org/10.1103/PhysRevE.65.046308
Halliday, I., Hollis, A.P., Care, C.M.: Lattice Boltzmann algorithm for continuum multicomponent flow. Phys. Rev. E 76(2), 026708 (2007). https://doi.org/10.1103/PhysRevE.76.026708
Hazlett, R., Chen, S., Soll, W.: Wettability and rate effects on immiscible displacement: lattice Boltzmann simulation in microtomographic images of reservoir rocks. J. Pet. Sci. Eng. 20(3–4), 167–175 (1998). https://doi.org/10.1016/S0920-4105(98)00017-5
Jerauld, G.R., Fredrich, J., Lane, N., Sheng, Q., Crouse, B., Freed, D.M., Fager, A., Xu, R.: Validation of a workflow for digitally measuring relative permeability. In: Abu Dhabi International Petroleum Exhibition & Conference, Society of Petroleum Engineers. https://doi.org/10.2118/188688-MS (2017)
Khishvand, M., Alizadeh, A., Piri, M.: In-situ characterization of wettability and pore-scale displacements during two- and three-phase flow in natural porous media. Adv. Water Resour. 97, 279–298 (2016). https://doi.org/10.1016/j.advwatres.2016.10.009
Klise, K.A., Moriarty, D., Yoon, H., Karpyn, Z.: Automated contact angle estimation for three-dimensional X-ray microtomography data. Adv. Water Resour. 95, 152–160 (2016). https://doi.org/10.1016/j.advwatres.2015.11.006
Landry, C.J., Karpyn, Z.T., Ayala, O.: Relative permeability of homogenous-wet and mixed-wet porous media as determined by pore-scale lattice Boltzmann modeling. Water Resour. Res. 50(5), 3672–3689 (2014). https://doi.org/10.1002/2013WR015148
Latva-Kokko, M., Rothman, D.H.: Diffusion properties of gradient-based lattice Boltzmann models of immiscible fluids. Phys. Rev. E 71(5), 056702 (2005). https://doi.org/10.1103/PhysRevE.71.056702
Leclaire, S., Parmigiani, A., Malaspinas, O., Chopard, B., Latt, J.: Generalized three-dimensional lattice Boltzmann color-gradient method for immiscible two-phase pore-scale imbibition and drainage in porous media. Phys. Rev. E 95(3), 033306 (2017). https://doi.org/10.1103/PhysRevE.95.033306
Li, H., Pan, C., Miller, C.T.: Pore-scale investigation of viscous coupling effects for two-phase flow in porous media. Phys. Rev. E 72(2), 026705 (2005). https://doi.org/10.1103/PhysRevE.72.026705
McDougall, S., Sorbie, K.: The impact of wettability on waterflooding: pore-scale simulation. SPE Reserv. Eng. 10(03), 208–213 (1995). https://doi.org/10.2118/25271-PA
Oak, M., Baker, L., Thomas, D.: Three-phase relative permeability of Berea sandstone. J. Pet. Technol. 42(08), 1054–1061 (1990). https://doi.org/10.2118/17370-PA
Øren, P.E., Bakke, S., Arntzen, O.: Extending predictive capabilities to network models. SPE J. 3(04), 324–336 (1998). https://doi.org/10.2118/52052-PA
Pan, C., Hilpert, M., Miller, C.T.: Lattice-Boltzmann simulation of two-phase flow in porous media. Water Resour. Res. 40(1), 1–14 (2004). https://doi.org/10.1029/2003WR002120
Prodanovic, M., Lindquist, W.B., Seright, S.R.: Residual fluid blobs and contact angle measurements from X-ray images of fluid displacement. In: XVI International Conference on Computational Methods in Water Resources, Copenhagen, Denmark (2006)
Pruess, K., García, J.: Multiphase flow dynamics during \(\text{ CO }_2\) disposal into saline aquifers. Environ. Geol. 42(2–3), 282–295 (2002). https://doi.org/10.1007/s00254-001-0498-3
Qian, Y.H., D’Humières, D., Lallemand, P.: Lattice BGK models for Navier–Stokes equation. EPL Europhys. Lett. 17(6), 479 (1992)
Raeini, A.Q., Bijeljic, B., Blunt, M.J.: Numerical modelling of sub-pore scale events in two-phase flow through porous media. Transp. Porous Med. 101(2), 191–213 (2014a). https://doi.org/10.1007/s11242-013-0239-6
Raeini, A.Q., Blunt, M.J., Bijeljic, B.: Direct simulations of two-phase flow on micro-CT images of porous media and upscaling of pore-scale forces. Adv. Water Resour. 74, 116–126 (2014b). https://doi.org/10.1016/j.advwatres.2014.08.012
Raeini, A.Q., Bijeljic, B., Blunt, M.J.: Modelling capillary trapping using finite-volume simulation of two-phase flow directly on micro-CT images. Adv. Water Resour. 83, 102–110 (2015). https://doi.org/10.1016/j.advwatres.2015.05.008
Raeini, A.Q., Bijeljic, B., Blunt, M.J.: Generalized network modeling: network extraction as a coarse-scale discretization of the void space of porous media. Phys. Rev. E 96(1), 013312 (2017). https://doi.org/10.1103/PhysRevE.96.013312
Ramstad, T., Idowu, N., Nardi, C., Øren, P.E.: Relative permeability calculations from two-phase flow simulations directly on digital images of porous rocks. Transp. Porous Media 94(2), 487–504 (2012). https://doi.org/10.1007/s11242-011-9877-8
Scanziani, A., Singh, K., Blunt, M.J., Guadagnini, A.: Automatic method for estimation of in situ effective contact angle from X-ray micro tomography images of two-phase flow in porous media. J. Colloid Interface Sci. 496, 51–59 (2017). https://doi.org/10.1016/j.jcis.2017.02.005
Valvatne, P.H., Blunt, M.J.: Predictive pore-scale modeling of two-phase flow in mixed wet media. Water Resour. Res. 40(7), 1–21 (2004). https://doi.org/10.1029/2003WR002627
Zou, Q., He, X.: On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys. Fluids 9(6), 1591–1598 (1997). https://doi.org/10.1063/1.869307
Zou, S., Armstrong, R.T., Arns, J.Y., Arns, C.H., Hussain, F.: Experimental and theoretical evidence for increased ganglion dynamics during fractional flow in mixed-wet porous media. Water Resour. Res. 54(5), 3277–3289 (2018). https://doi.org/10.1029/2017WR022433
Acknowledgements
We thank Japan Oil, Gas and Metals National Corporation (JOGMEC) for their financial support. We also thank Abu Dhabi National Oil Company (ADNOC) and ADNOC Onshore (previously known as Abu Dhabi Company for Onshore Petroleum Operations Ltd) for sharing the experimental data used in this work. Ahmed A. AlRatrout is acknowledged for preparing the experimentally measured contact angle data. Also, we thank anonymous reviewers for their constructive comments. The experimental data used here are available at Alhammadi et al. (2018).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Akai, T., Alhammadi, A.M., Blunt, M.J. et al. Modeling Oil Recovery in Mixed-Wet Rocks: Pore-Scale Comparison Between Experiment and Simulation. Transp Porous Med 127, 393–414 (2019). https://doi.org/10.1007/s11242-018-1198-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-018-1198-8