Abstract
This work addresses two continuing fallacies in the interpretation of percolation characteristics of porous solids. The first is that the first derivative (slope) of the intrusion characteristic of the non-wetting fluid or drainage characteristic of the wetting fluid corresponds to the void size distribution, and the second is that the sizes of all voids can be measured. The fallacies are illustrated with the aid of the PoreXpert® inverse modelling package. A new void analysis method is then described, which is an add-on to the inverse modelling package and addresses the second fallacy. It is applied to three widely contrasting and challenging porous media. The first comprises two fine-grain graphites for use in the next-generation nuclear reactors. Their larger void sizes were measured by mercury intrusion, and the smallest by using a grand canonical Monte Carlo interpretation of surface area measurement down to nanometre scale. The second application is to the mercury intrusion of a series of mixtures of ground calcium carbonate with powdered microporous calcium carbonate known as functionalised calcium carbonate (FCC). The third is the water retention/drainage characteristic of a soil sample which undergoes naturally occurring hydrophilic/hydrophobic transitions. The first-derivative approximation is shown to be reasonable in the interpretation of the mercury intrusion porosimetry of the two graphites, which differ only at low mercury intrusion pressures, but false for FCC and the transiently hydrophobic soil. The findings are supported by other experimental characterisations, in particular electron and atomic force microscopy.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
An unavoidable first step in modelling mercury porosimetry or water retention is to relate the pressure applied to the mercury, or the differential air pressure applied to the water saturated sample, to the sizes of the features intruded at that pressure. Traditionally, it is assumed that void features exposed to the non-wetting fluid (mercury displacing air or nominal vacuum, or air displacing water) are cylindrical, with diameter d. Then the features intruded at an applied pressure \(P_\mathrm {app}\) are calculated by the Laplace equation:
With respect to the mercury porosimetry in this work, we use the commonly accepted value of \(140^\circ \) for the contact angle \(\theta \) of mercury intruding sandstone against residual air, and \(0.48\, \mathrm {N\,m}^{-1}\) for the surface tension \(\gamma \), whereupon the numerator of Eq. (1) becomes \(1.47 \, \mathrm {N\,m}^{-1}\). The well-known uncertainties in these parameters (VanBrakel et al. 1981) are important but nevertheless more minor than the fallacies addressed below. With respect to water retention, we assumed that the water was fully wetting, so that the contact angle of the air intruding under increasing water suction was \(180^\circ \), with \(\gamma \) = \(0.075\, \mathrm {N\,m^{-1}}\). The uncertainties in the latter parameters will be discussed in an ensuing publication.
A pioneering approach to the interpretation of percolation characteristics, such as mercury intrusion or soil water retention, was to convert the differential pressure (i.e. applied pressure or suction) of the non-wetting fluid to pore-throat diameter via Eq. (1). Then networks of arbitrary geometry and connectivity could be computer-generated, and forward modelling of the percolation characteristics could be compared to experimental measurements (Chatzis and Dullien 1977; Levine et al. 1977). However, such trial-and-error forward modelling is time-consuming, and even if an acceptable fit is found, it is difficult to carry out a meaningful sensitivity analysis to quantify the arbitrariness of the mathematical network.
So the holy grail is an inverse model—going from the experimental percolation characteristic to the void structure which caused it. The simplest, and therefore pervasive, method of inverse modelling is to measure the first derivative, i.e. slope, of the intrusion curve and assume that it is proportional to the number of features at that size. The first error in this approach is that the slope is clearly proportional to the volume of pore throats at that size, not their number. The second is that for the use of Eq. (1) to be valid, all features must be fully exposed to the non-wetting fluid and all must be cylindrical, i.e. the porosity of the sample must comprise a bundle of capillary tubes. Such an approximation, criticised by Hunt et al. (2013), is shown in Fig. 1 for the void size distribution described in Sect. 3.1. It is correct only for a very limited range of porous materials, such as track etch membranes and zeolites. For the remainder, d has only a limited relationship to the actual sizes of the features intruded at the pressure \(P_\mathrm {app}\) related by Eq. (1), so we will refer to d as the nominal pore-throat diameter.
Capillary bundle approximation of void structure, following a uniform probability density (boxcar) function. Very narrow capillary tubes are shown dashed. The small scale bar shown at the base has length \(229\,\upmu \hbox {m}\). The tubes are shown on a regularly spaced Cartesian grid, so the porosity is lower than 0.26 as stated in Sect. 3.2
The enduring popularity of the first-derivative approach arises not because of its veracity but because, unlike true stochastic inverse modelling, it yields a single void size distribution. Despite the fundamental errors, it is in regular use for the interpretation of mercury intrusion of porous materials, the water retention of soil, and the porometry of filters and membranes. Sometimes the porosity of the sample is represented by a single tube—the effective hydraulic radius approximation. In many approaches, the capillary tubes are sinuous, with their degree of sinuosity being quantified as tortuosity. Soil water retention characteristics are also often interpreted by use of the equation proposed by Van Genuchten (1980), which imposes smoothness and asymptotes onto often wayward experimental results as illustrated in Fig. 7a, but which then results in non-orthogonal fitting parameters with no direct structural significance.
In addition, there are two secondary sources of error, which have been avoided in this work but may invalidate other studies. The first is that if the intruding non-wetting fluid is displacing a ‘defender’ fluid in the pores that cannot escape, then the void will not be intruded. In the case of mercury porosimetry, the sample is initially held in a vacuum so there is nothing to displace. With regard to water retention, some water does remain trapped within the soil matrix and is referred to as ‘immobile water’. For the current modelling, as with the Van Genuchten approach, immobile water is regarded as part of the solid immobile phase—an approximation which is reasonable for modelling properties such as permeability, but breaks down for other properties, for example, solute transport when the solute interacts with the immobile phase (Smedt and Wierenga 1979).
Another secondary source of error can arise from the size of the experimental samples and the model. For meaningful results, the samples must be at least as large as their representative elementary volume (REV). In the present study, IG graphite and FCC have been deliberately manufactured to be homogeneous at a scale of mm, so the 1 \(\mathrm {cm^3}\) samples studied are well above the respective REVs. With respect to soil, it was air-dried, sieved to \(\hbox {2}\,\hbox {mm}\) and repacked, so the 5 by 10 cm cores studied were also above the REVs of the homogenised samples.
With respect to the size of the model, if it is too small then void features become unrealistically accessible to the surface because there are few or no connecting throats between them and the surface (Larson and Morrow 1981). As detailed in the next section, in this work we model void structures with the inverse modelling package \(\hbox {PoreXpert}^{\textregistered }\) which generates infinitely repeating unit cells with periodic boundary conditions. The unit cells range from 0.1 to \(\hbox {6}\,\hbox {mm}\) cubes. One surface is exposed to the intruding fluid, so the periodic boundary conditions make the approximation an infinite sheet of thickness between 0.1 and \(\hbox {6}\,\hbox {mm}\), and there are up to 20, 25 or 30 features between the invading fluid and each void feature, depending on the size of the unit cell (the parameter \(\nu \) defined in the next section). So in terms of accessibility, in the context of the REVs, the representations are reasonable but not perfect.
We now firstly use the modelling package to exemplify the first-derivative fallacy, by showing that forward modelling of the same void size distribution, with different short-range size auto-correlations, can lead to very different simulated percolation characteristics. We then describe an improved method of estimating void sizes from percolation characteristics. The method involves identification of those void volumes that are likely to comprise clusters of smaller voids, and allocating the sizes of the clusters by assuming the same distribution as those voids that are not clusters.
In order to test the robustness of the new approach, we apply it to three different porous materials of current research interest, namely (i) graphite manufactured for next-generation Japanese nuclear reactor cores, (ii) microporous calcium carbonate being developed for delayed flavour and drug delivery and (iii) naturally occurring soil that is transiently hydrophobic, causing a reduction in fertility and increased risk of water run-off and flooding. For each material, we judge the validity, and if valid the accuracy, of conclusions based on the first-derivative approximation. All three materials present major challenges and are the subject of parallel studies, with citations given for those already published.
2 Methods, Materials and Experimental Characterisation
2.1 Void Network Modelling
\(\hbox {PoreXpert}^{\textregistered }\) is a void network simulation software which has been developed by the current authors and former co-workers, and made commercially available. It represents the void structure of a porous medium as a series of identical interconnected unit cells with periodic boundary conditions. Each unit cell of side length h comprises an array of \(\nu \times \nu \times \nu \) pores \(\left\{ \nu \in \mathbb {Z}\mid 5\le \nu \le 30\right\} ,\) equally spaced in a Cartesian cubic close-packed array. Void shapes are simplified to cubic ‘pores’, positioned with their centres at each node, connected by up to six cylindrical ‘throats’ in each Cartesian direction. The simplification of the void shapes does not greatly affect the percolation characteristics, which depend mainly on those other properties which are quantitatively matched to experiment, namely the volume, cross-sectional size and connectivity of the voids.
The characteristics of the unit cell are adjusted using an eight-dimensional Boltzmann-annealed amoeboid simplex, which moves around parameter space searching for an optimum void network that matches closely the sample’s porosity and minimises the discrepancy distance \(\delta \) between the experimentally derived and simulated percolation characteristics. \(\delta \) is quantified by normalising the range of the bounds of the parameter space on each axis (size and intrusion) to \(100\%\), measuring the closest distance from each simulated point to the experiment curve using these normalised scales, and averaging these distances. The optimisation is then the minimisation of \(\delta \) on varying five numerical parameters subject also to Boolean constraints.
Three of the numerical parameters comprise the skew and spread of the pore-throat size distribution (Matthews et al. 2010) and the connectivity of the network (Price et al. 2009). There is also the possibility of short-range throat/throat size auto-correlations, which are dealt with by ‘structure types’. In the present case, the structure type which best fits the experimental percolation characteristics of all three samples is ‘vertically banded’, i.e. the correlations cause planar layers of similarly sized throats within each unit cell parallel to the direction of non-wetting phase intrusion. The model can optimise its fit to the experimental percolation characteristic by choosing a correlation level \(\mathscr {C} \) within the range 0 (random) to 1 (fully correlated). Intermediate values (\( 0< \mathscr {C} < 1\)) correspond to overlapping size distributions between the parallel layers. The fifth parameter is termed ‘pore skew’ \(\mathscr {P} \) and compensates for inefficient packing on the regularly spaced Cartesian grid by bulking up pores with less than the maximum size up to (but not above) the maximum size. High values of \(\mathscr {P}\) produce a peak at the top of the void size distribution, which the new approach described here is then designed to eliminate. To minimise the peak, \(\mathscr {P}\) is kept as low as possible by sloping its parameter space hyper-surface. Additionally, there are three Boolean parameters—namely whether the network is fully connected, whether the experimental porosity is achieved and whether all the void features are separate in space without geometric overlap.
The void network resulting from this optimisation procedure is not unique, so a set of several stochastic realisations is generated which match the experimental intrusion characteristics. The most representative simulated structure for each sample is then found by choosing realisations for which none of the fitting parameters has a deviation from the mean of the set larger than the standard deviation \(\sigma \) of the set. If more than one sample meets that criterion, then the sample with the lowest discrepancy distance \(\delta \) is chosen. (The extent to which the resulting structure is fully representative of the experimental sample is discussed further in Sect. 3.2.)
Once a representative structure has been found, many properties of the porous materials can be simulated. With its predecessor Pore-Cor, PoreXpert has been used in previous studies to model the porous network and pore level properties of a range of materials other than those discussed here, for example, sandstones, catalysts, paper coatings and filters (Bodurtha et al. 2005; Gribble et al. 2011).
2.2 Nuclear Graphite
Samples of IG-110 and IG-430 graphite, also referred to as IG-11 and IG-43, were supplied by Toyo Tanso Ltd., Japan. IG-110 is a fine-grained, isotropic graphite which exhibits high thermal durability and strength, currently utilised in the Japanese high-temperature test reactor (HTTR) (Yan et al. 2013) and the Chinese high-temperature reactor-pebble bed modules (HTR-10) (Zhen et al. 2014). IG-430 is a comparable graphite, developed to display higher density, strength and thermal conductivity when compared with IG-110. Improved physical characteristics make it a suitable candidate for use in generation IV nuclear reactors. Table 1 shows some of the properties of the materials as listed by the manufacturers.
In a previous work (Jones et al. 2018), the samples have also been characterised by pycnometry (Table 2) and electron microscopy (Fig. 2). In that work it is described how for graphite, mercury intrusion gives very unreliable estimates of the lowest void sizes probed by the highest pressures of mercury. Therefore, grand canonical Monte Carlo (GCMC) interpretations of gas adsorption were used to construct the intrusion characteristic of the smallest voids, using the simulation software supplied and validated by the BELSORP surface area instrument manufacturers, MicrotracBEL, Japan (Miyahara et al. 2014). Such an intrusion characteristic was assumed equal to the cumulative pore volume distribution derived from the GCMC simulation, based on the correct assumption that all voids are accessible by the gas, so the shielding considerations discussed in Sect. 3.3 do not apply. The asymptote of the constructed intrusion characteristic at highest pressure was set according to the helium accessible porosity, expressed in Table 2 as open pore volume, measured with a Thermo Fisher Pycnomatic helium pycnometer. The sample envelope volumes were measured with a Micromeritics GeoPyc powder pycnometer, and the results combined with the known graphite crystal density to give the closed pore volumes shown in Table 2. The constructed combined percolation characteristics are shown in Fig. 3.
2.3 Minerals
Functionalised calcium carbonate (FCC) is produced by etching calcium carbonate particles and re-precipitating a modified surface structure with in situ or externally supplied CO\(_\mathrm {2}\) in the form of carbonic acid (Ridgway et al. 2004; Levy et al. 2015, 2017). Variations in the etching process produce a range of morphologies with recrystallised surfaces, consisting of incorporated hydroxyapatite (HAP) in the case of phosphoric acid, which are discretely separable dual porous systems with inter- and intra-particle porosity. FCCs are pharmaceutical grade analogues of MCCs (modified calcium carbonates), the latter being designed for the paper industry, particularly for coatings designed for inkjet printing (Ridgway et al. 2004). The type of FCC used in this work was OmyaPharm (2760/2), with a particle size distribution measured using a Malvern Master Sizer 2000 as shown in Fig. 4a. The morphology of the FCC was determined by scanning electron microscopy (Fig. 5).
Non-porous ground calcium carbonate (GCC), OmyaCarb 5, was also provided by Omya International AG (Oftringen, Switzerland). It is an Italian dry ground calcium carbonate prepared with a small amount of dry grinding aid. Its particle size distribution is shown in Fig. 4a, where it can be seen that its particle size distribution is wider than for FCC, but with the same weight-defined median value.
Mercury intrusion curves of the series of mixtures of OmyaPharm with GCC are shown in Fig. 6a. Their truncation (Fig. 6b) is justified in Sect. 4.2.
Mercury intrusion (3 to 100 \(\upmu \)m) and converted grand canonical Monte Carlo simulation (\(0.4\,\hbox {nm}\,\hbox {to} < 1\,\upmu \hbox {m}\)) combined to give a percolation curves covering the whole range of nominal pore-throat diameters from 0.4 nm to 100 \(\upmu \)m, compared with PoreXpert simulated percolation curves, for the two nuclear graphite samples, Jones et al. (2018)
FCC/GCC mixture intrusion curves, with pressures converted to nominal pore-throat diameters via Eq. (1). a Intrusion curves, b truncated intrusion curves. The ratios shown in the legend are mass percentages of each constituent. The closeness of fit of the model is illustrated by the fit (\(\mathsf{X}\)) to \(100\%\) FCC in (b)
2.4 Soil
The soil used in this work undergoes natural transitions between being hydrophilic or hydrophobic to ambient water. The sample is part of a much wider study of hydrophobicity in soils from nanoscale to field scale, currently being completed. The soil was randomly sourced from the National Botanic Garden of Wales, Carmarthenshire, at a depth of 5 to 10 cm. It was collected once when wettable and once when water repellent, with the wettability at the time of collection being determined by the water drop penetration time test (10 drops of 50 \(\upmu \)L distilled water). Bulk density samples were taken from the site during soil collection using a 100 cm3 core. The average bulk density for the site was determined from between 5 and 15 samples. Three replicate samples of both repellent and wettable soil were sieved to \(\hbox {2}\,\hbox {mm}\) and then packed in 4 mm increments into rings 19 mm deep \(\times \) 22 mm diameter to bulk densities as close as possible to the site’s field bulk density. The filled rings were then weighed, saturated from the bottom up by suction and weighed again to determine the saturated water content. They were then exposed to a range of differential pressures in the range \(1 \, \hbox {to}\, 1\,500 \, \hbox {kPa}\) in either pressure cells or on a tension table. At each of the corresponding matric potentials the gravimetric water content was determined, as shown in Fig. 7a.
Soil roughness was obtained with atomic force microscopy (AFM), using a Bruker BioScope Catalyst in PeakForce Tapping mode and with Bruker MPP-21200-10 probes. A total of eight regions per soil state were analysed, each region having an area of 25 \(\upmu \mathrm {m}^2\). Nanoscope analysis software calculated RMS roughness \(R_\mathrm{q}\) from topographical AFM data using the following relation:
where \(N'\) is the number of points in the scanned area and \(Z_i\) is the vertical displacement of the ith data point from the mean data plane (Fig. 7b) (Gazze et al. 2018).
Properties of the Botanic Garden repellent (BGR) and wettable (BGW) soil samples. a Water retention against differential pressure for three replicate samples, standard Van Genuchten fits and the water retention characteristics of PoreXpert representative structures generated as detailed in Sect. 2.1. b Surface nano-roughness calculated on \(25\,\upmu \mathrm {m}^2\) areas from AFM measurements. \(\hbox {BGW roughness}\,=\,39.4\,\pm \,13.3\,\hbox {nm}\); BGR roughness\(\,=\,34.8\,\pm \,12.7\) nm
3 Modelling and Interpretation
3.1 Inherent Problems
In using an inverse model to address the current weaknesses in interpretation, three inherent problems must be addressed, which result in the approaches described here being an imperfect but nevertheless substantial improvement. The first is that percolation characteristics only give information on the volumes and connectivity of the void network, but not the shapes of the voids, nor their spacing apart, nor the precise directions of the connections. So in the inverse model we use the simple void shape and spacing assumptions that are described in Sect. 2.1.
The second inherent problem is the size of the model with respect to the size of the sample, as discussed in Sect. 1. Ideally, the unit cells would be larger, but larger unit cells become ever more computationally intensive to generate and study with computation time and memory typically increasing as \(\nu ^3\) or \(\nu ^4\) according to the operations carried out or properties simulated.
The third inherent problem is that the inverse modelling, even with the simplifying assumptions, does not produce a unique void structure; there are an indeterminately large number of void networks which could produce the same percolation characteristics. To address this issue, we generate structures stochastically to produce a population which has definite bounds—one set of bounds being the range of nominal sizes of the voids, \(d_\mathrm {min}\) to \(d_\mathrm {max}\), determined by the range of experimental pressure or suction via Eq. (1). Ideally, we would produce enough stochastic generations to form a population that is statistically representative of the entire population of possible structures. However, in practice there is a trade-off between this inherent problem and that of computation time so we use \(\nu \) = 30 for the uniform probability density function (PDF) in the following section and the calcium carbonate mixtures, corresponding to unit cells with up to \(108\,000\) void features. Due to the complexity of modelling absolute permeability (Jones et al. 2018) and wettability (the subject of concurrent work), for the graphite samples \(\nu \) = 25 and for the soil samples \(\nu \) = 20, corresponding to unit cells with up to \(62\,500\) and \(32\,000\) void features, respectively. For all the simulations of real samples, we generate five stochastic generations, from which we select the most representative as described in Sect. 2.1.
3.2 The First-Derivative Fallacy
The first-derivative fallacy is illustrated by using PoreXpert to forward model the percolation characteristic of a uniform PDF (boxcar function) of throat sizes over the size range 0.7 to \(1\,422\,\upmu \hbox {m}\), i.e. equal numbers of throats at each of \(N = 500\) sizes logarithmically distributed within this size range, and none outside the size range. The precise number at each size depends on \(\nu \), and the connectivity \(\omega \) of the network arbitrarily set to an average of 3.366 throats per pore. In this case there are an average of 90.88 throats at each size. All \(27\,000\) pores were set to the largest size in the range, i.e. \(1\,422\,\upmu \hbox {m}\). The structures were generated to give an arbitrary porosity \({\varPhi }\) of 0.26. Generation of structures with \(\mathscr {C} > 0.7\) was impossible, because the correct porosity could not be achieved due to the inefficient packing of the void features on the regular Cartesian grid.
Figure 8 shows the results plotted in the form of mercury intrusion characteristics over the pressure range of 0.00103 to \(2.1\,\hbox {MPa}\), corresponding to the stated throat size range via Eq. (1). It can be seen that the simulated intrusion curve shapes vary from a sigmoid curve for \(\mathscr {C} = 0.0\) to an almost linear characteristic for \(\mathscr {C} = 0.7\). The corresponding slopes of the curves, shown dashed, are mostly centred around the same logarithmic mean pressure of \(0.047\,\hbox {MPa}\) (corresponding to a void size of \(31.5\,\upmu \hbox {m}\)), but have entirely different shapes, and would be erroneously interpreted as being caused by different distributions of void sizes. The structure which would be most correctly interpreted by taking its slope is that for the highest correlation level, \(\mathscr {C} = 0.7\)

The almost linear intrusion curve has a nearly constant slope that implies the correct, uniform PDF void size distribution. This is because taking the slope of the intrusion curve implies voids in the form of a capillary bundle; in the present case, those covering the size range are shown in Fig. 1. (In that figure, \({\varPhi } < 0.26\) because of the inefficient packing of the features on a regularly spaced Cartesian grid.) The structure with \(\mathscr {C} = 0.7\) most closely resembles a capillary bundle, because the throats are positioned in vertical bands mostly according to their size. However, it can be seen that with \(\mathscr {C} = 0.7\) there is a step in the simulated intrusion curve at low pressures. This can be understood by examining the unit cell intruded to \(15.7\%\) by volume (Fig. 9). It can be seen that the mercury has at that pressure percolated from the exposed top surface of the unit cell into the layers connected by the larger throats but has yet to percolate into those connected by smaller throats. The similarity of this structure to a capillary bundle cannot be seen in the figure, because the layered throats are masked by the large pores. Overall, the wide variation in the first derivatives of the intrusion curves, as shown in Fig. 8, all derived from the same void size distribution, underlines the invalidity of using the first derivative (slope) as a measure of void size distribution.
Percolation characteristics of a uniform PDF (boxcar function) of throat sizes over the size range 0.7 to \(1\,422\,\upmu \hbox {m}\), expressed as mercury intrusion curves, for various values of correlation level \(\mathscr {C}\) as defined in Sect. 2.1, and the slopes (first derivatives) of the intrusion curves
Unit cell of the uniform probability density throat size distribution with \(\mathscr {C} = 0.7\) (Sect. 2.1), and Cr = 2 Eq. (5). The solid phase is shown transparent, voids shown as solids, and clusters by a rendered pattern as shown in the detail. Most throats are hidden by their adjacent pores which are all of the same size. Mercury, intruded to \(15.7\%\) by volume into the top surface of the unit cell, is shown grey. It has intruded into the layers connected by the larger throats, which are the left-hand facing surface and right-hand obscured surface in the figure, but not yet into the central body of the unit cell interconnected by smaller throats. The very small scale bar at the base is of length \(2\,261\,\upmu \hbox {m}\)
It might be hoped that having forward modelled the mercury intrusion characteristic from the void size distribution, one could then use PoreXpert to inverse model the resulting intrusion curves to retrieve the original void size distribution. However, in this case that does not happen. Because of the effective coupling of the parameters (i.e. a change in one parameter can be compensated by a change in another to maintain convergence onto the experimental percolation characteristic), the partial parameter space of each individual parameter is not populated in a manner which is well-behaved. Also, the physical construction of the void networks causes the hyper-surfaces within the parameter space to be uneven, with false minima—which necessitates Boltzmann annealing of the simplex (Johnson et al. 2003). So because of the complexity of the convergence, there are two additional quasi-Bayesian constraints imposed on the simplex. Firstly, it starts with a typical relationship between the sizes of neighbouring pores and throats as measured directly (Wardlaw et al. 1987). Secondly, it learns from previous modelling attempts, which are for a range of natural and manufactured samples, none of which contain throats with sizes following a uniform PDF. The simplex then heads towards what it considers to be the most likely void size distribution, which is consequently not a uniform PDF.
3.3 The Void Size Identification Fallacy
A second major fallacy in the simplistic interpretation of percolation characteristics is that the sizes of all voids can be unambiguously identified. We refer to the pressure at which a void would be expected to fill with non-wetting fluid or the suction at which it would be expected to drain of wetting fluid as the size intrusion pressure \(P_\mathrm {size}\), since it depends only on the internal size of the void itself, not on the diameters of any throats connecting it to its neighbours within the void network. Every pore m within the network intrudes at a specific pressure or suction \(P_{\mathrm {app}}\) applied to the outside of the sample, approximated in the simulation as \(P_{\mathrm {app}}\) at the top surface only of the unit cell. The pressure at the pore throat of a particular pore, \(P_{\mathrm {pore throat},m}\), could equal \(P_{\mathrm {app}}\) if the pore throat is freely connected to the sample surface, or less than \(P_{\mathrm {app}}\) if the pore throat is shielded from the surface by other narrower pore throats. The shielding is more likely in a random network than in a correlated network, so that the shielding is a function of \(1/\mathscr {C}\), noting that there is an indefinite asymptote to the shielding function, namely \(f(1/\mathscr {C}) \xrightarrow [{\mathscr {C}}\rightarrow {1}]{} \geqslant 1 \). The inequality arises from the fact that even in a fully correlated network of a type such as vertically banded, there still may be some shielding when \(\mathscr {C} = 1\) due to the connectivity and tortuosity of the network, resulting in a shielding function greater than 1. Also, for other structure types, for example, a spherical locus of large throats and their associated pores surrounded at increasing radii by spherical shell loci of throats of successively decreasing size, there will still be significant shielding when \(\mathscr {C} = 1\). The shielding can also vary as the intrusion proceeds, so is also a function of the volume of non-wetting phase intruded \(V_{P_{\mathrm {app}}}^{\mathrm {intr}}\) at an external applied pressure \(P_{\mathrm {app}}\). As an example, the step in the intrusion curve for the uniform PDF for \(\mathscr {C} = 0.7\) (Fig. 8) is caused by high shielding for \(V_{P_{\mathrm {app}}}^{\mathrm {intr}} < 20\%\) and low shielding, i.e. \(f(1/\mathscr {C}) \simeq 1 \), for \(V_{P_{\mathrm {app}}}^{\mathrm {intr}} > 20\%\). In summary,
where the shielding function
Since by definition the pore throat must be smaller than the pore or void m to which it is connected, then \(P_{\mathrm {pore throat},m} \geqslant P_{\mathrm {size},m}\). Due to this inequality and that in Eq. (4), the relationship between \(P_{\mathrm {app}}\) and \(P_{\mathrm {size},m}\) cannot be determined analytically, and varies for each pore or void, depending on the size of the pore throat and its connectivity to the sample surface. Correspondingly, the size of pore or void m cannot be determined from \(P_\mathrm {app}\) via Eq. (1).
Fortunately, we are now in a position to apply further analyses to the data. The first is that we can forward model the percolation characteristic within a network generated by the inverse modelling of the same percolation characteristic. As \(P_{\mathrm {app}}\) is progressively increased during the simulation, we can record the local values \(P_{\mathrm {intr},m}\) at which every void is intruded during the percolation process. We assume there is a value of the threshold ‘cluster ratio’ Cr, assumed constant for all m, such that
above which a pore m can be identified as a cluster of voids. Figure 9 shows the unit cell for the uniform PDF with \(Cr = 2\). Since in that unit cell all pores have been set to the maximum size, then via Eq. (1), all \(P_{\mathrm {size},m}\) take a minimum value for all m, and so via Eq. 5 nearly all pores are actually clusters. Pores which are not clusters which have filled with mercury can be seen at the top of the unit cell, as shown in the enlarged detail.
This approach can be most readily understood when applied to a real sample. As an example, we use the \(50\%\,\hbox {FCC}\) mixture with GCC, for which the intrusion curve is shown in Fig. 6b. Figure 10 shows the representative unit cell for \(Cr = 1.5\). Figure 11a shows histograms of the total volumes of void features at each n of the \(N = 500\) feature sizes within the representative unit cell of the inverse model of the mercury intrusion of the \(50\%\) FCC mixture, with detail shown in Fig. 11b. The total volumes at each size are shown for throats

pores

and all clusters

with the distributions designated as \(\varTheta \), \(\varPi \) and \(X_\mathrm {all}\), respectively, with the total distribution \(\mathbb {T} = \varTheta + \varPi + X_\mathrm {all}\). The distribution of all clusters has an anomalously high value at the maximum size \(X' = X_\mathrm {all}(n\!=\!N)\), which we attribute to unresolved clusters. To calculate the volume of these unresolved clusters, a subset \(E = X_\mathrm {all}(0.9N<n<N\!-\!1)\)

is extrapolated with a second order polynomial in log–log space

to a point at the maximum size

shown in the enlargement box in Fig. 11b, which becomes \(X_\mathrm {max}=X_\mathrm {all}(n\!=\!N)\). The difference in volume between the extrapolated point and the anomalous point is then taken to be the volume of unresolved clusters, \(V^\mathrm {tot}_\mathrm {undiff} = X' - X_\mathrm {max}\). These are assumed to follow the same size distribution as the resolved clusters, \(X_\mathrm {undiff} = c.X_\mathrm {diff}\) where the constant c is set by the stated requirement that \(\mathrm {\Sigma } X_\mathrm {undiff} = V^\mathrm {tot}_\mathrm {undiff} \). The resulting resolved distributions are shown in Fig. 11c.
Top part of the unit cell model of a mixture of \(50\%\) FCC with GCC, showing clusters (rendered) for \(Cr = 1.5\), with an enlargement showing the some of the smaller detail. The unit cell has been intruded to \(6.2\%\) by volume with Hg (grey) in the z direction, i.e. from the top surface downwards in the figure
Application to \(50\%\) FCC mixture with GCC, with Cr = 1.5. a Calculation of cluster population. b Two successive enlargements of (a) above \(1\,\upmu \hbox {m}\). c Explicit void size distributions. d Cumulative volumes of all voids above \(2.7\,\upmu \hbox {m}\) for Cr = 1.4 to 5, confirming that Cr = 1.5
A second criterion follows from the observation that the void size and volume distribution is a sampling of the total distribution of the sample between the minimum and maximum applied mercury pressure or tension, via Eq. (1), or over a wider size range if two or more experimental techniques are combined. Although there may be a peak in the distribution at highest pressure or suction, since the size range is arbitrary with respect to the actual void size range within the sample, such a peak is sufficiently unlikely as to be discounted. Consequently the total void size distribution \(\mathbb {T}\) should be continuous and not have a peak at highest size. Intuitively, the cluster ratio Cr should be as large as possible while satisfying this criterion, since the greater the discrepancy between \(P_{\mathrm {app},m}\) and \(P_{\mathrm {size},m}\), the greater the probability that the size is a cluster.
It can be seen in Fig. 11d that for the \(50\%\) FCC mixture there are definite discontinuities in the distributions \(\mathbb {T}\) for cluster ratios Cr of 5, 3 and 2, but not for \(Cr = 1.5\). It can also be seen that there is a negligible difference between \(\mathbb {T}\) for Cr = 1.4 and 1.5. Hence, Cr = 1.5 was chosen, as used in the unit cell of Fig. 10 and the other graphs in Fig. 11.
4 Application to Experimental Samples
4.1 Nuclear Graphite
The first question we pose is whether the new pore analysis methodology is useful in elucidating the difference in void structure between the nuclear graphites IG-110 and IG-430. The difference between the materials is that IG-430 was produced by using pitch to produce coke for graphitisation, rather than petrol, giving the desired increase in tensile strength (Table 1). Examination of the materials by electron microscopy shows no evident difference (Fig. 2). However, subjecting them to mercury intrusion does show that IG-110 starts to intrude at a lower pressure than IG-430, and that there is significantly greater intrusion corresponding to pore-throat diameters in the range 3 to 100 \(\upmu \)m (Fig. 3). Figure 8 underlines the danger of misinterpreting the points of inflexion of a mercury intrusion curve. However, as can be seen in Fig. 3, in which the intrusion proceeds from right to left, the 3 to 100 \(\upmu \)m range occurs before the point of inflexion (i.e. at lower \(P_\mathrm {app}\) and higher nominal pore-throat diameter). So in this case, use of the first-derivative approximation, implying larger voids in the 3 to 100 \(\upmu \)m range for IG-110, should not be too bad an assumption if restricted to that size range.
The intrusion curves were modelled as described previously, and the simulated intrusion curves corresponding to the representative unit cells are shown in Fig. 3. A very useful feature of the inverse model is that it can intelligently bridge gaps in experimental percolation data. The lack of experimental data either side of 1 \(\upmu \)m in Fig. 3 simply results in greater differences between stochastic generations, since if the percolation characteristic is not defined, the simulated curve can vary freely in the undefined region without affecting \(\delta \).
It can be seen that the combined percolation characteristics cover more than 5 orders of magnitude of size. Convergence onto intrusion characteristics over such a wide size range proved demanding, to the extent that although the stochastic generation chosen for IG-430 is representative (with \(\delta = 0.8\%\)), that for IG-110 was selected only by minimum distance (\(\delta = 1.7\%\)). The simulations do pick up the difference in intrusion at low \(P_\mathrm {app}\), high nominal pore-throat diameter, although are not so close around the point of inflexion. The correlation levels of the resulting vertically banded structures are low (\(\mathscr {C}\) = 0.04 and 0.06 for IG-110 and IG-430, respectively), demonstrating very homogeneous, random arrangements of voids, as designed by the manufacturers.
For these samples, the cluster ratio Cr is found to be 10, following the procedure illustrated in Fig. 11d. Figure 13 shows intrusion by mercury to a pressure of \(0.135\,\hbox {MPa}\) causing intrusion to 8.1% of accessible void volume, equal to 1.01% of sample volume as arrowed in Fig. 3. It can be seen that at this pressure, intrusion has occurred exclusively in voids that are not clusters, i.e. not shown rendered in Fig. 13. Analysis of the void types (Fig. 12) reveals that whereas the pore-throat size distribution for the two samples are almost identical

, IG-110 contains a higher volume of pores

extending to larger sizes than IG-430

In this case there are no fully independent experimental data to support this void analysis. The void analysis follows that expected from the first-derivative approximation applied to the low \(P_\mathrm {app}\), high nominal pore-throat diameter section of the intrusion curve, and is compatible with the higher tensile strength of IG-430 (Table 1). However, the difference in void structure is too subtle either to show up on the electron micrographs (Fig. 2) or as a difference in open pore volume (Table 2).
Detail of representative unit cell of IG-110, with \(Cr = 10\), intruded with mercury (grey) to 8.1% of accessible void volume, equal to 1.02% of total sample volume, as arrowed in Fig. 3. Small scale bar top right is 137 \(\upmu \)m
4.2 Calcium Carbonate Mixtures
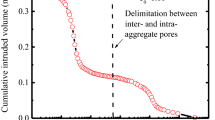
Secondly, we apply the new methodology to all the mixtures of FCC with GCC. It can be seen in Fig. 6b that there are two steps in their intrusion curves—one at around \(2\,\upmu \hbox {m}\), and the other around \(0.3\,\upmu \hbox {m}\), with the latter only being apparent for the higher ratios of FCC. Reference to Fig. 4a suggests that the main steps at around 2 \(\upmu \)m are due to mercury intruding the inter-particle space before intruding the intra-particle voidage, i.e. the dual distributions are discretely separable. This is confirmed by the fact that the \(100\%\) OmyaCarb 5 intrusion curve has the step at \(2\,\upmu \hbox {m}\), with no further intrusion at higher pressure (lower diameter). In order to model the intra-particle microporosity only, it is therefore valid to truncate the intrusion curves and model only the sections representing intrusion of the intra-particle microporosity (Fig. 6b). Such an approach has previously been used to separate flow and capillarity effects for the control of inkjet performance on paper coatings (Ridgway et al. 2004).
The standard reason to pack an active material with an inert one is in the design of packed bed reactors, where the active component of the mixture is a catalyst. Under these circumstances, the usual requirement is to keep the catalyst particles apart, suspended in an inert matrix which nevertheless allows flow of a fluid past the particles. If the active material is porous, this approach can be used to separate the inter- and intra-particle diffusion effects (Levy et al. 2015). Consequently, there are many studies of the likelihood of particles touching each other, for example, by Bezdek and Reid (2013).
In this present study, we ask the converse question, namely whether by packing FCC particles together we can create additional microporosity where the particles touch each other. Such a postulate would be supported by the slight step in the intrusion curves around \(0.3\,\upmu \)m (Fig. 6b) which increases with increasing FCC component. Alternatively, the FCC particles might have some particular features in their microporosity around \(0.3\,\upmu \)m. The final alternative possibility is that in the context of Fig. 8, the steps are merely the results of percolation through the interconnected void networks of the individual FCC particles, a phenomenon which becomes increasingly apparent as the percentage of FCC in the mixture increases.
In applying the methodology to experimental samples, one first has to bear in mind the non-uniqueness of inverse modelling structures, and the ease with which the amoeboid simplex can stochastically explore the wrong regions of the complex parameter space—or, in the vernacular, ‘minor garbage into the model, major garbage out’. So the first requirement is to ensure that the experimental data input to the model is as free as possible from artefacts. In this case, it is clear that the intra- plus inter-particles porosities derived from the mercury intrusion curves should follow a smooth monotonic curve. In fact, they do not, because of different particle packing efficiencies across the series of mixtures (Fig. 4b). On adding GCC, i.e. moving from right to left on the graph, the GCC initially fills in the inter-particle pores, giving lower porosity than expected, but at higher GCC (lower FCC) displaces the FCC particles giving a higher than expected porosity. An analogous effect can also be observed in the suspension rheology of such mixtures (Savarmand et al. 2008). These packing phenomena are not a feature that we wish to model, so they need to be eliminated by smoothing the sample porosities, as shown in Fig. 4b.
Following that correction, five stochastic simulations were carried out for each sample, and the representative structures chosen as described in Sect. 2.1. The example shown in Fig. 6b has a closeness of fit \(\delta = 1.1\%\), and can be seen to fit the slight step in the intrusion curve around \(0.3\,\upmu \hbox {m}\). Overall, for all the representative structures, \(\delta = 1.3\%\) with an absolute standard deviation of \(\pm 0.5\%\).
We then carry out a full analysis of all the void types across the samples, illustrated for 0, 50 and 100% FCC in Fig. 14a and b. It can be seen in Fig. 14b that there is no maximum in voidage at around \(0.3\,\upmu \hbox {m}\), i.e. in the middle of the logarithmic range shown. So the steps are explained by the third of the postulates above, namely percolation through the interconnected void networks of the individual FCC particles. The further enlargements in Fig. 14b confirm that as size decreases, nearly all the total voidage (\(\blacktriangleright \)) becomes made up of pore throats

Both these observations are corroborated by the micrographs (Fig. 5) which show no evidence of structure that would give rise to a local maximum in voidage around \(0.3\,\upmu \hbox {m}\) (a third of the scale bar of Fig. 5b), and which show that at that size and smaller, because of the laminar structure of the voidage, all the voidage comprises what are effectively pore throats. Neither conclusion could be drawn for the traditional, first-derivative, interpretation of the intrusion curves.
4.3 Hydrophobic Soil
In the case of soil, we ask whether the differences in water retention curves for Botanic Garden wettable (BGW) and repellent (BGR) soil shown in Fig. 7a represent a change in structure. There is a slight difference in porosity \({\varPhi }\) between the two samples, from \({\varPhi } = 0.380\) for wettable soil to 0.376 for repellent soil. This is likely to be due to the re-packing of the sample prior to the water retention experiment, but there could be a contribution from the change in wettability so in this case the change in porosity has not been corrected out. In order to model the curves, they must be plotted as percolation, i.e. intrusion of air, and the tensions converted to pore-throat sizes via Eq. (1), as shown in Fig. 15. Figure 16a and b shows that, as for the mineral samples, a cluster ratio of 1.5 is appropriate for both the wettable and hydrophobic soil samples. Figure 16c and d shows that the structure of the soil does not change significantly during a transition from a hydrophilic (shown blue) to hydrophobic (red) state and that when the whole size range is represented by using logarithmic scales, the differences become even more insignificant compared to the major difference in wettability of the two samples, which is the subject of a parallel study by Hallin et al. to be published.
The absence of a clear structural difference in the two wettability states is supported at core scale by the negligible change in porosity, although as explained above that cannot be deconvoluted from packing efficiency. At nanometre scale, the lack of structural difference is supported by the similar topographical roughness as measured by AFM, which shows no significant difference between the two states (t-test \(p\,\hbox {value} > 0.05\)) (Fig. 7b).
Botanic Garden soil: averaged water retention for three replicates of repellent (BGR) and wettable soil (BGW) expressed as normalised air intrusion versus nominal pore-throat diameter via Eq. (1), compared to fits corresponding to forward modelling of representative PoreXpert unit cells with vertically banded structure type
Application of the method to Botanic Garden soil. Cluster ratio comparison, for Cr from 1.4 to 5, for (a) wettable, (b) repellent soil. Comparison of all void types using cluster ratio \(Cr = 1.5\) for wettable soil (shown blue) and repellent (red), c linear axes, above \(250\,\upmu \hbox {m}\), d logarithmic axes over entire size range with enlargement at maximum void size
5 Discussion
A criticism of the new approach might be that it simply results in an another fitting parameter, in an inverse model which already has five numerical and three Boolean parameters. However, two factors work in its favour. The first is that the new methodology allows identification of the range of validity of the first-derivative approximation, as exemplified above. The second is that the additional parameter reduces, rather than increases, the artificiality of the void structure model. In order to make the computation tractable, the current model has void features positioned on a regularly spaced Cartesian grid. Thus, the smallest feature is as far away from its neighbour as the largest, and when features vary by many orders of magnitude in size, that is very far from realistic. The cluster ratio identifies clusters comprising voids which, since their total volume is that of the enclosing volume, must be touching each other, and such closely adjacent features include the smallest. Rather than being a feature of the material being studied, this compensating aspect of the cluster ratio makes it dependent mostly on the size range of the void features being modelled, and for the current samples it varies approximately as the cube of the number of orders of magnitude of the size range, i.e. \(Cr \varpropto \{\mathrm {log}_{10}(d_\mathrm {max}/d_\mathrm {min})\}^3\).
6 Conclusions
With the aid of a mathematically generated void network with a simple uniform probability density pore-throat size distribution, we have demonstrated that changes in the short-range pore-throat size auto-correlation factor \(\mathscr {C}\) can cause widely different simulated intrusion curves. In this context, it is clear that the traditional first-derivative interpretation of percolation characteristics measured by mercury intrusion, and analogously by porometry or water retention, can lead to false suppositions. We have identified an improved method of analysis which, with the aid of stochastic inverse modelling, allows a more realistic estimate of the sizes of voids within a porous material and identifies those voids within the estimate that are actually void clusters.
For the case of nuclear graphite, the improved method demonstrates that the traditional first-derivative approach is reasonable for the interpretation of changes in low-volume intrusion before the point of inflexion. However, for both microporous calcium carbonate and transiently hydrophobic soil, the method shows that the traditional interpretation of differences in percolation characteristics at higher intrusion volumes at or beyond any point of inflexion leads to false assumptions. The traditional approach interprets the changes as alterations in the void sizes, since those are the only characteristics yielded by the approach, whereas in fact the changes in percolation can be due to much more subtle effects, such as variability in short-range size auto-correlations.
Independent experimental evidence has been presented that supports, but does not prove, the new void structure analysis. Direct experimental confirmation could come from X-ray CT scanning, but the best resolution is typically 3 \(\upmu \)m, whereas a resolution of 0.1 \(\upmu \)m would be required to support the new findings. Focused ion beam ablation (FIB) could provide evidence for nuclear graphite, if ablation occurred over sufficient sample area precisely located in an electron microscope, and that will be the subject of a future study.
The method has been illustrated for three widely different samples, but could be applied to any porous material for which the capillary bundle approximation of porous structure is inappropriate. It is therefore applicable to nearly all naturally occurring meso- and macroporous materials and to nano-porous materials other than, for example, track etch membranes and zeolites.
References
Bezdek, K., Reid, S.: Contact graphs of unit sphere packings revisited. J. Geom. 104(1), 57–83 (2013)
Bodurtha, P., Matthews, G.P., Kettle, J.P., Roy, I.M.: Influence of anisotropy on the dynamic wetting and permeation of paper coatings. J. Colloid Interface Sci. 283, 171–189 (2005)
Chatzis, I., Dullien, F.: Modeling Pore Structure by 2-D and 3-D Networks with Application to Sandstones. J. Can. Pet. Technol. 16(1), 97–108 (1977). https://doi.org/10.2118/77-01-09
Gazze, S., Hallin, I., Quinn, G., Dudley, E., Matthews, G., Rees, P., Van Keulen, G., Doerr, S., Francis, L.: Organic matter identifies the nano-mechanical properties of native soil aggregates. Nanoscale 10, 520–525 (2018). https://doi.org/10.1039/C7NR07070E
Gribble, C.M., Matthews, G.P., Laudone, G.M., Turner, A., Ridgway, C.J., Schoelkopf, J., Gane, P.A.C.: Porometry, porosimetry, image analysis and void network modelling in the study of the pore-level properties of filters. Chem. Eng. Sci. 66(16), 3701–3709 (2011). https://doi.org/10.1016/j.ces.2011.05.013
Hunt, A.G., Ewing, R.P., Horton, R.: What’s wrong with soil physics? Soil Sci. Soc. Am. J. 77(6), 1877–1887 (2013). https://doi.org/10.2136/sssaj2013.01.0020
Johnson, A., Roy, I., Matthews, G., Patel, D.: An improved simulation of void structure, water retention and hydraulic conductivity in soil with the Pore-Cor three-dimensional network. Eur. J. Soil Sci. 54(3), 477–489 (2003). https://doi.org/10.1046/j.1365-2389.2003.00504.x
Jones, K.L., Laudone, G.M., Matthews, G.P.: A multi-technique experimental and modelling study of the porous structure of IG-110 and IG-430 nuclear graphite. Carbon 128, 1–11 (2018)
Larson, R., Morrow, N.: Effects of sample-size on capillary pressures in porous-media. Powder Technol. 30(2), 123–138 (1981). https://doi.org/10.1016/0032-5910(81)80005-8
Levine, S., Reed, P., Shutts, G., Neale, G.: Some aspects of wetting-dewetting of a porous-medium. Powder Technol. 17(2), 163–181 (1977). https://doi.org/10.1016/0032-5910(77)80041-7
Levy, C.L., Matthews, G.P., Laudone, G.M., Gribble, C.M., Turner, A., Ridgway, C.J., Gerard, D.E., Schoelkopf, J., Gane, P.A.C.: Diffusion and tortuosity in porous functionalized calcium carbonate. Ind. Eng. Chem. Res. 54(41), 9938–9947 (2015). https://doi.org/10.1021/acs.iecr.5b02362
Levy, C.L., Matthews, G.P., Laudone, G.M., Beckett, S., Turner, A., Schoelkopf, J., Gane, P.A.C.: Mechanism of adsorption of actives onto microporous functionalised calcium carbonate (FCC). Adsorpt. J. Int. Adsorpt. Soc. 23(4), 603–612 (2017). https://doi.org/10.1007/s10450-017-9880-7
Matthews, G.P., Laudone, G.M., Gregory, A.S., Bird, N.R.A., Matthews, A.G., Whalley, W.R.: Measurement and simulation of the effect of compaction on the pore structure and saturated hydraulic conductivity of grassland and arable soil. Water Resour. Res. 46(5), W05,501 (2010). https://doi.org/10.1029/2009WR007720
Miyahara, M.T., Numaguchi, R., Hiratsuka, T., Nakai, K., Tanaka, H.: Fluids in nanospaces: molecular simulation studies to find out key mechanisms for engineering. Adsorption 20(2), 213–223 (2014)
Price, J.C., Matthews, G.P., Quinlan, K., Sexton, J., Matthews, A.G.D.: A depth filtration model of straining within the void networks of stainless steel filters. AIChE J. 55(12), 3134–3144 (2009)
Ridgway, C.J., Gane, P.A.C., Schoelkopf, J.: Modified calcium carbonate coatings with rapid absorption and extensive liquid uptake capacity. Colloid Surface A 236(1–3), 91–102 (2004)
Savarmand, S., Carreau, P., Bertrand, F., Vidal, D.: (2008) Models for the rheology of clay-gcc coating colors. In: TAPPI 10th Advanced Coating Fundamentals Symposium (2008)
Smedt, F.D., Wierenga, P.: Mass transfer in porous media with immobile water. J. Hydrol. 41(1), 59–67 (1979). 10.1016/0022-1694(79)90105-7, http://www.sciencedirect.com/science/article/pii/0022169479901057
Van Genuchten, M.: A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 44(5), 892–898 (1980)
VanBrakel, J., Modry, S., Svata, M.: Mercury porosimetry–state of the art. Powder Technol. 29(1), 1–12 (1981). https://doi.org/10.1016/0032-5910(81)85001-2
Wardlaw, N., Li, Y., Forbes, D.: Pore-throat size correlation from capillary-pressure curves. Transp. Porous Media 2(6), 597–614 (1987)
Yan, X., Tachibana, Y., Ohashi, H., Sato, H., Tazawa, Y., Kunitomi, K.: A small modular reactor design for multiple energy applications: HTR50S. Nuclear Eng. Technol. 45(3), 401–414 (2013). https://doi.org/10.5516/NET.10.2012.070
Zhen, H., Zhengcao, L., Dongyue, C., Wei, M., Zhengjun, Z.: Co2 corrosion of IG-110 nuclear graphite studied by gas chromatography. J. Nucl. Sci. Technol. 51(4), 487–492 (2014). https://doi.org/10.1080/00223131.2013.877407
Acknowledgements
We thank EDF Energy as one of sponsors; nevertheless, the views expressed in this article are not necessarily their own. This work has been filed for a patent (IPO 1716322.1, October 2017).
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was supported by Omya International AG, EDF Energy and the Natural Environment Research Council (Grant Numbers NE/K004212/1 and NE/K004638/1). WRW is supported by the BBSRC Designing Future Wheat project (BB/P016855/1) and the BBSRC/NERC ASSIST project (NE/N018117/1).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Matthews, G.P., Levy, C.L., Laudone, G.M. et al. Improved Interpretation of Mercury Intrusion and Soil Water Retention Percolation Characteristics by Inverse Modelling and Void Cluster Analysis. Transp Porous Med 124, 631–653 (2018). https://doi.org/10.1007/s11242-018-1087-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-018-1087-1