Abstract
Reactive transport processes in a porous medium will often both cause changes to the pore structure, via precipitation and dissolution of biomass or minerals, and be affected by these changes, via changes to the material’s porosity and permeability. An understanding of the pore structure morphology and the changes to flow parameters during these processes is critical when modeling reactive transport. Commonly applied porosity–permeability relations in simulation models on the REV scale use a power-law relation, often with slight modifications, to describe such features; they are often used for modeling the effects of mineral precipitation and/or dissolution on permeability. To predict the reduction in permeability due to biomass growth, many different and often rather complex relations have been developed and published by a variety of authors. Some authors use exponential or simplified Kozeny–Carman relations. However, many of these relations do not lead to fundamentally different predictions of permeability alteration when compared to a simple power-law relation with a suitable exponent. Exceptions to this general trend are only few of the porosity–permeability relations developed for biomass clogging; these consider a residual permeability even when the pore space is completely filled with biomass. Other exceptions are relations that consider a critical porosity at which the porous medium becomes impermeable; this is often used when modeling the effect of mineral precipitation. This review first defines the scale on which porosity–permeability relations are typically used and aims at explaining why these relations are not unique. It shows the variety of existing approaches and concludes with their essential features.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Flow through porous media can be described and analyzed on different spatial scales. Usually, this flow occurs in the fluid-filled void space bounded by an impermeable solid matrix. Alterations in the pore surface structure or the pore morphology can occur through a whole variety of processes coupled to and interacting with the flow of fluids. Examples of such transforming processes are chemical reactions or microbiological activities. While changes in the pore surface properties, and thus the pore’s void space geometry, occur on the pore scale or even on the molecular scale, the scales of the application or of the engineering problem are typically much larger. Therefore, it is often appropriate, and required for the sake of computational feasibility, that the impacts of such morphology changes to the flow field be described by effective hydraulic properties. On top of that, effective (upscaled) parameters on larger scales require less pore geometry data, which is hard or, usually, impossible to collect in practical applications.
The permeability of a porous medium is one of these parameters and is used by modelers to represent the resistance to fluid flow in the porous medium on the scale of a representative elementary volume (REV), where an averaging concept is applied such that the individual pore geometry does not need to be resolved. The concept of using permeability avoids the need for a detailed description of the fluid–solid interface at the expense of losing information regarding pore-scale details. To integrate the alterations in the pore structure and morphology, a commonly employed method relates changes in the permeability to another effective REV-scale parameter, the porosity. The objective of this paper is to review the existing porosity–permeability relation concepts, to summarize their typical features, and to conclude with some recommendations focusing on systems with (bio-)geochemical pore space alterations.
The manuscript is organized as follows: We first provide in Sect. 2 a thorough definition of the scales of consideration; we introduce the REV scale, upon which the porosity–permeability relations are valid, and we introduce the parameters porosity and permeability. Further, we present an overview of the (bio-)geochemical processes changing the pore structure and morphology, and thus changes to the porosity and permeability. After that, we discuss the variety of published porosity–permeability relations grouped by the approach used to derive the relations, focusing mainly on (bio-)geochemically altered porous media and less on other geometry-modifying processes or the task of estimating permeability from porosity in general. In Sect. 4, we compare the relations presented in Sect. 3 by their targeted use, the form of the relation, and any special features. Finally, in Sects. 5 and 6 we summarize the lessons learned and give recommendations.
2 Fundamentals and Definitions
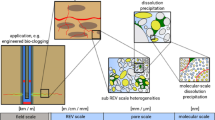
2.1 Scales of Consideration for Porous Media Processes
Interfaces between the solid matrix and the void space characterize the hydraulic properties of a porous medium. While the system behavior strongly depends on these interfaces at the small pore-specific spatial scale, the size of the overall porous media flow problem is often too large to consider each of these interfaces in detail. The representative elementary volume (REV) is a useful concept to characterize such spatial scale dependencies. This volume is the smallest volume at which a property does not change if the dimensions incrementally change (Bear 1988). Depending on that property, the required size of an REV may not be unique throughout the same porous medium. From one porous medium to another, or dependent on the overall dimensions of the problem, the REV size will typically vary between the millimeter and the meter range. Figure 1 shows a recursive view of a porous medium with a bioclogging process shown as an example. Each cutout represents a view of a different scale, from the molecular scale, past the pore scale and the REV scale, to the field scale (or scale of application). Of course, choosing the spatial dimension of a scale is often an arbitrary process and the transition from one scale to another will occur gradually. Nevertheless, this schematic helps understand that, with increasing scale dimensions, the resolution of details decreases and effective quantities are required to represent subscale effects. If it were possible to model at the microscale over any given length scale, these upscaling approaches would not be necessary, but as this is impossible, even with the most advanced computing systems available, problem simplification by upscaling is necessary.
For clarity, we need to define two characteristic REV-scale porous medium properties: porosity and permeability. The porosity, \(\phi \), is defined as the ratio of void space filled by fluid inside an REV to the bulk volume of the REV:
While this definition of porosity is simple and easy to understand, it blends many characteristics of the shape and morphology of the interfaces defined on the scales below the REV scale, i.e., the pore scale, to one parameter. These interfaces strongly affect and are affected by both the flow processes and the processes which are responsible for pore morphology alterations. Solid–fluid interfaces can be rigid even after alteration, for example, when minerals are precipitated. On the other hand, for example in the case of a biofilm growth in the pore space, the (pseudo)-solid–fluid interface is rather soft and to some degree flexible to adapt its shape according to the shear stresses applied by the fluid flow. Thus, it is evident that porosity as defined in Eq. (1) is not sufficient to uniquely characterize potential changes in hydraulic properties. Permeability \([\hbox {m}^{2}]\) (or hydraulic conductivity \([{{\hbox {m}}/{\hbox {s}}}]\)) is an effective quantity on the REV scale that considers the effect of resistance to flow from viscous effects on the pore scale. While permeability is an intrinsic property of the porous medium, the hydraulic conductivity of a porous medium is related to it via the viscosity of the fluid, thus representing a property of both the porous medium and the fluid.
2.2 Stokes Equation and Viscous Effects on the Pore Scale
Considering a flow domain on the pore scale allows us to describe the flow using mass and momentum balance equations. The mass balance equation for a fluid phase can be written as
where \(\rho \) is the fluid density, \({\mathbf {v}}\) the flow velocity vector, and q a source term. Furthermore, we neglect the nonlinear inertial term by assuming flow at very low Reynolds numbers in the porous medium and by assuming gravity, \(\rho {\mathbf {g}}\), to be the sole external force. With this simplification, we can write the vector-valued momentum balance equation as
Here, we introduce a matrix-valued momentum flux as
where p is fluid pressure, \({\mathbf {I}}\) the \(d \times d\) identity tensor, and \(\mathbf {\tau }\) the shear stress tensor. Using the deformation tensor \({\mathbf {D}} = \frac{1}{2} (\nabla {\mathbf {v}} + \nabla {\mathbf {v}}^T)\) as well as Newton’s law, the stress tensor is obtained (see also Truckenbrodt 1996) as
where \(\mu \) \([\hbox {kg}/\hbox {s\, m}]\) is the dynamic viscosity of the fluid. The porous medium exerts a resistance to the flow which is induced by a gradient in pressure or by gravitation. These viscous effects are expressed in the momentum balance Eq. (3) through the shear stress, as in Eq. (4). The no-slip condition at the walls of the pores defines the boundary conditions of the flow field. In a porous medium, where porosity, as in Eq. (1), changes on the REV scale, e.g., due to clogging, the boundaries of the flow domain on the pore scale need to be adjusted on the level of pore morphology changes such that the flow field will change accordingly.
When we give up on describing the exact flow field inside individual pores and instead use an averaged velocity vector on the REV scale, we can find an analogy to the Hagen–Poiseuille equation, a particular solution to the Navier–Stokes equation, e.g., in laminar pipe flow. Using the pipe diameter d, a cross-sectional averaged velocity, \(v_m\), and the gradient in hydraulic head, \(\nabla h\), it can be formulated as follows:
Here, \(g \rho d^2 / 32 \mu \) represents the viscous resistance to flow, and as shown, the velocity is proportional to the head gradient. On the REV scale in a porous medium, this viscous resistance term corresponds to the hydraulic conductivity, k, in \(\hbox {m}/\hbox {s}\).
2.3 Permeability and Porosity on the REV Scale
Permeability is a REV-scale property which relates REV-scale potential gradient and the resulting REV-scale fluid velocity in Darcy’s Law:
where K is the intrinsic permeability, \({\mathbf {g}}\) the gravitational acceleration, and \(\nicefrac {\varDelta p}{L}\) the pressure gradient.
However, the REV for permeability can be larger than the REV for porosity, as it needs to account for the connectivity and tortuosity of the pores (Mostaghimi et al. 2013). Permeability, as used in Darcy’s Law, can be obtained on the REV scale by upscaling the viscous effects as described by the (Navier–)Stokes equations formulated on the detailed pore geometry, obtained by imaging, on the pore scale. This is the only reliable way to estimate the permeability, as no explicit function can accurately correlate permeability to other REV-scale properties (Mostaghimi et al. 2013; Noiriel 2015). For porosity–permeability relations, we should assume that the REV has a size that allows a representative averaging for both properties. In general, as permeability can vary over orders of magnitude and, being a volume-averaged REV-scale property, it can be difficult to measure it reliably, especially when the sample sizes are small or the permeability is very low or heterogeneous (e.g., Lenormand and Fonta 2007; Lenormand and Bauget 2010; Egermann et al. 2005; Carles et al. 2007).
Early attempts to quantify permeabilities of different porous media focused on estimating techniques using constant, easily measurable properties, such as the porosity, the characteristic grain size, or the pore geometry of a given material. One of the first proposed relations is published in Hazen (1892), relating the hydraulic conductivity k in \(\hbox {cm}/\hbox {s}\) of a sand unit to the characteristic particle diameter \(d_{10}\) in \(\hbox {cm}\), the maximum diameter of the finest 10% of the grains in that sand:
where \(c_\mathrm {H}\) \([\hbox {1}/\hbox {s\, cm}]\) is an empirical coefficient. Typical values for \(c_\mathrm {H}\) are around 100, although many values from 1 to 1000 are available (Carrier 2003). The applicability of the Hazen relation is limited to a small range of characteristic particle diameters, 0.01 cm \(<d_{10}<\) 0.3 cm (Hazen 1892), which, together with the variability of \(c_\mathrm {H}\), make it unsuitable for general use.
A second widely used approach is the Kozeny–Carman equation, which was originally published in Kozeny (1927) and was later modified in Carman (1937) to calculate the pressure difference, \(\varDelta p\), required for fluid flow at the velocity, v, through a particle packing of the length, L. This equation is as follows:
where \(\varPhi _\mathrm {s}\) is the sphericity, a dimensionless particle geometry parameter, \(D_\mathrm {p}\) \([\hbox {m}]\) is the characteristic particle diameter, and \(\phi \) \([-]\) is the porosity. Equation (8) can be reformulated using Darcy’s Law, see Eq. (6), to estimate the permeability according to Kozeny and Carman, \(K_\mathrm {KC}\), in \(\hbox {m}^{2}\) directly:
Equation (9) can also be written as:
using parameters more relevant to natural porous media, tortuosity \(\tau \) and specific surface area S, rather than \(\varPhi _\mathrm {s}\) and \(D_\mathrm {p}\), (e.g., Gallo et al. 1998; MacQuarrie and Mayer 2005).
However, Mostaghimi et al. (2013) show that the Kozeny–Carman equation may significantly overestimate the permeability, especially for complex, tortuous, heterogeneous, or poorly connected porous media. For an analysis of dissolution, Poms et al. (2007) compare the Kozeny–Carman equation to permeabilities obtained from volume averaging and state that the difference between both permeability predictions will increase with the injection rate.
A third approach to estimating the permeability is derived from the Hagen–Poiseuille Law, which is valid for flow in small tubes and often used to calculate the flow through individual pore throats in a network of pores. The Hagen–Poiseuille Law can be derived from the Stokes equation, shown in Sect. 2.2, by assuming constant fluid density and a cylindrical geometry. It relates the pore radius, r, the viscosity of the fluid, \(\mu \), and the pressure gradient over the length of the pore, \(\nicefrac {\varDelta p}{L}\), to the flow rate, \(Q_\mathrm {HP}\), through that pore
Using Darcy’s Law (Eq. (6)) and a circular cross-sectional area, \(\pi r^2\), a representative permeability, \(K_\mathrm {HP}\) \([\hbox {m}^{2}]\), for the capillary can be calculated based on the Hagen–Poiseuille Law, which only depends on the radius, r \([\hbox {m}]\):
Similarly, for flow between smooth, parallel plates, the Cubic Law can be derived from the Stokes equation and applied to estimate the flow rate of the fluid between the plates \(Q_\mathrm {cubic}\) and the representative permeability \(K_\mathrm {cubic}\) \([\hbox {m}^{2}]\):
where a is the aperture between the plates and w the width of the plates. Using Darcy’s Law (Eq. (6)) \(K_\mathrm {cubic}\) can be calculated as:
The Cubic Law is often used to approximate the permeability of a fractured system with highly conductive fractures, where one can assume that most or all advective transport is concentrated in the fracture (e.g., Marsily 1986; Steefel and Lasaga 1994; Steefel and Lichtner 1994, 1998; Ellis and Peters 2016). For an application at larger scales having more than one fracture, it is convenient to extend Eq. (14) from a single, smooth fracture to multiple parallel fractures by including the fracture porosity \(\phi _\mathrm {f} = \nicefrac {a}{d}\), where d is the distance between the fractures (Steefel and Lasaga 1994):
The approaches discussed so far are intended to estimate the permeability of filters or particle packings (Eq. (7), (9)), for (a bundle of) capillary tubes (Eq. (12)), or for the gap between smooth, parallel plates (Eq. (14)). All of these cases assume a constant geometry and, as a result, a constant porosity and permeability.
However, in many cases where reactive transport processes like biological activities or chemical reactions are involved, significant alterations occur in the pore geometry and porosity due to mineral precipitation or dissolution, biofilm growth, or filtration of suspended particles. All such processes can thus result in changes to the permeability. The quantitative relation between the changes in porosity and the changes in permeability is specifically dependent on the individual changes to the pore space morphology. On the pore scale, only the pore geometry determines the resistance to fluid flow, see Sect. 2.2, while on REV scale, fluid flow is dependent on the upscaled parameter permeability, which integrates all the effects of sub-REV-scale geometries, see Sect. 2.3. While changes in permeability are usually correlated with porosity (e.g., Bear 1972), they may also be influenced by the changes of any other REV-scale parameter linked to pore geometry, such as the specific surface area (e.g., Golfier et al. 2002) or the tortuosity (e.g., Ives and Pienvichitr 1965). Modeling these highly coupled fluid flow and pore space altering processes on the REV scale crucially depends on a quantitatively correct method for describing the porosity–permeability relation. As pore morphology depends on the availability of flow components, which are in turn controlled by permeability, accurate relations for defining the changes to the permeability are imperative in understanding the flow processes.
2.4 Processes Modifying the Pore Space
There are many different processes modifying the porosity and permeability of a porous medium, including mechanical stress changes, sedimentation, filtration, diagenesis, swelling or shrinking, as well as biomass growth or decay and mineral precipitation or dissolution. This review focuses on biomass accumulation and mineral reactions, as both are included in countless reactive transport models in the following areas of study: nuclear waste storage site screening and behavior prediction (dissolution, precipitation) (e.g., Verma and Pruess 1988; Steefel and Lichtner 1994), hydrothermal system engineering (dissolution, precipitation), (e.g., Steefel and Lasaga 1994; Pandey et al. 2014), \(\hbox {CO}_2\) storage predictions (mainly dissolution, some precipitation), (e.g., Flukiger and Bernard 2009; Zhang et al. 2015), oil and gas reservoir acid or \(\hbox {CO}_2\) injection (dissolution), (e.g., Hoefner and Fogler 1988), microbially enhanced oil recovery (biomass growth), (e.g., Nielsen et al. 2014), or biomass-mediated remediation of subsurface contaminations (biomass growth) (e.g., Gogoi et al. 2003).
Mineral dissolution and precipitation for reactive transport modeling are discussed in detail in, e.g., Lasaga (1984) and Lichtner (1985); Steefel and Lasaga (1994) in the context of rock weathering or flow in hydrothermal systems, respectively. Mayer et al. (2002) also provide an overview of reactive transport modeling concepts focusing on the flexible integration of various possible kinetic rate equations for reactions with the examples of systems with biodegradation and acid mine drainage. Yeh and Tripathi (1989); Steefel et al. (2005) and, more recently, Steefel et al. (2015a) give an overview of reactive transport modeling in general. MacQuarrie and Mayer (2005) provide an overview of reactive transport modeling in fractured systems. Sahimi et al. (1990) give an overview on fluid-solid interactions for dissolution, migration of fines, flow of stable emulsions in porous media, and plugging of catalyst pellets. Thullner (2010) discusses bioclogging and summarizes the existing modeling approaches used in this field.
When modeling mineral reactions, kinetic rate laws are preferable over assuming a local chemical equilibrium. Assuming equilibrium reaction rates in these specific cases is only valid when supported by kinetic considerations (e.g., Steefel and Cappellen 1990; Steefel and Lasaga 1994). However, the upscaling of kinetics measured under ideal, well-mixed laboratory conditions to reactions in real, heterogeneous porous medium flow fields is not trivial (e.g., Steefel and Maher 2009; Steefel 2008). The prediction of biomass clogging, or more generally biomass distribution within a porous medium with reactive transport, is quite important in many environmental contexts where the reactions are at least partly catalyzed by the biomass (e.g., James 2003).
Mineral precipitation and biomass accumulation by growth or immobilization of suspended biomass reduce the pore space and should therefore decrease the permeability on the REV scale. On the other side, mineral dissolution and biomass decay or mobilization increase the pore space and should therefore decrease the permeability on the REV scale. However, not all pore space, or porosity on the REV scale, contributes to flow; the most obvious example of this being dead-end pores. The change in the effective porosity contributing to flow is difficult to estimate and will depend on the individual pore space altering process. However, a change in the overall porosity due to those processes can be quantified easily by updating the initial porosity \(\phi _0\) with the changes in volume fractions of the solids (e.g., biomass or minerals):
where \(\phi _i\) is the current and \(\phi _{i,0}\) the initial volume fraction of the solid i. The porosity can be directly calculated from the solid volume fractions (e.g., Steefel et al. 2015b; Steefel and Lasaga 1994; Steefel and Lichtner 1994; Civan 2001):
Mineral reactions and biomass accumulation induce changes in the porous medium’s morphology locally at the pore scale and depend, in terms of reaction or growth rates, on local values of concentration or concentration gradients. These dissolution or precipitation kinetics usually need to be determined experimentally for the given minerals and solutions of interest, but if the dissolution rate kinetics are known, the precipitation kinetics can be calculated from the dissolution kinetics using thermodynamic constraints, as discussed in, e.g., Lasaga (1984).
However, the concentration of a reactive species is also influenced by its advective and diffusive transport through the porous medium (e.g., Hoefner and Fogler 1988; Steefel and Lasaga 1994; Steefel and AC 1990; Steefel and Lichtner 1998; Mayer et al. 2002). This is one of the largest challenges for continuum-scale reactive transport models as it is not yet clear whether or not upscaled, macroscopic properties such as porosity, permeability, or averaged concentrations, can be used to effectively capture the hydrological and chemical dynamics exhibited locally at the pore scale (Steefel et al. 2005). In principle, the permeability of a porous medium is dependent on the complete history of the modifying process; the validity of replacing all of this knowledge with a simple relationship dependent on the change in pore volume still needs investigation (e.g., Bernabe et al. 2003; Golfier et al. 2004). However, for single pores, Li et al. (2008) show in their modeling study that for realistic field conditions there is a negligible discrepancy between the reaction rate determined by flux-weighted average at the pore outlet and the rate calculated assuming complete mixing. Only when advection and reaction rates are in a comparable order, Li et al. (2008) observe the development of concentration gradients within the pore, causing the simulation results for the well-mixed reactor model and the Hagen–Poiseuille flow model (see Eq. (11) to differ.
For both transport processes, advection and diffusion, dimensionless Damköhler numbers relating the reaction rate to the mass transport rates can be defined as:
and
Here, \(\mathrm {Da_I}\) and \(\mathrm {Da_{II}}\) are the Damköhler numbers with respect to advective and diffusive transport, k is the reaction rate constant, L the characteristic length scale, \(c_0\) the initial concentration, n the order of the reaction, \(\nicefrac {v}{\phi }\) the effective flow velocity, and \(D_\mathrm {pm}\) the effective diffusion coefficient in porous media. \(\mathrm {Da_{II}}\) is also sometimes referred to as the kinetic number Ki. For low injection rates, \(\mathrm {Da_I}\gg 1\), reactions are much faster than transport and the overall behavior of the system is transport-controlled, while for high injection rates, \(\mathrm {Da_I}\ll 1\), the overall system behavior is reaction-controlled (e.g., Daccord et al. 1993a).
Adding another descriptive dimensionless number, the Péclet number, \(\mathrm {Pe}\), relating the timescales of advection to those of diffusion,
or using both \(\mathrm {Da_I}\) and \(\mathrm {Da_{II}}=\mathrm {Da_I Pe}\), allows for an additional distinction of the system behavior. For low Pe, the system is limited by the advective transport of reactants or reaction products. For high Pe, the system can be either reaction-limited, when \(\mathrm {Da_{II}}\) is low, or mass transport- or diffusion-limited, when \(\mathrm {Da_{II}}\) is high, as discussed in, e.g., Daccord et al. (1993b). However, these dimensionless numbers need to be used with care as both the reaction rate and the flow velocity will change over space and time within a reactive system.
Mineral Dissolution For dissolution, the pattern of porosity increase depends on \(\mathrm {Da_I}\), \(\mathrm {Da_{II}}\) and Pe. This dependence is even more considerable for permeability. For very low Pe (high \(\mathrm {Da_I}\)), advection-controlled systems, complete dissolution is concentrated at the injection region while for very high Pe (low \(\mathrm {Da_I}\)) and low \(\mathrm {Da_{II}}\), i.e., reaction-controlled systems, dissolution occurs throughout the porous medium sample (e.g., Daccord et al. 1993a, b; Fredd and Fogler 1998; Golfier et al. 2004; Gouze and Luquot 2011; Hoefner and Fogler 1988; Kalia and Balakotaiah 2007; Luquot and Gouze 2009; Noiriel et al. 2005). For diffusion-limited systems, at high \(\mathrm {Da_{II}}\) and Pe, the local dissolution of a mineral leads to a focus of the flow to that location. This then leads to further dissolution in those regions, creating interconnected paths of high porosity and permeability (wormholes) (e.g., Carroll et al. 2013; Hao et al. 2013; Smith et al. 2013; Daccord et al. 1989, 1993a, b; Golfier et al. 2002, 2004; Poms et al. 2007; Hoefner and Fogler 1988; Fredd and Fogler 1998; Steefel and Maher 2009; Steefel 2008; Steefel and AC 1990; Kang et al. 2002; Kalia and Balakotaiah 2007; Ghommem et al. 2015; Ott and Oedai 2015). Such wormhole structures may even form for flow through nearly even fractures (Noiriel 2015). Preferential dissolution of a certain initial pore size may also change the two-phase flow properties, such as the capillary pressure–saturation relation as shown by (Rötting et al. 2015). However, when two separate fluid phases are present during dissolution, e.g., \(\hbox {CO}_2\) and brine as investigated in Ott and Oedai (2015), the formation of wormholes might be inhibited if the non-wetting phase is less reactive, as the non-wetting phase will preferentially occupy the large pore spaces within the wormholes, reducing or even preventing further dissolution by blocking the influx of further reactive wetting phase into the wormholes (Ott and Oedai 2015). But even in a uniform dissolution regime, the flow focuses during dissolution on preferential flow paths, decreasing the tortuosity (Menke et al. 2015). The dissolution patterns and their dependence on the flow rate at which the reactive fluid is injected has been studied intensively over many years (e.g., Daccord et al. 1989, 1993a, b; Golfier et al. 2002, 2004; Poms et al. 2007; Hoefner and Fogler 1988; Fredd and Fogler 1998; Steefel and AC 1990; Kang et al. 2002; Luhmann et al. 2014; Kalia and Balakotaiah 2007; Ghommem et al. 2015; Ott and Oedai 2015). Other parameters also influence the dissolution patterns, e.g., the initial permeability and porosity contrast within the porous medium or the distribution of reactive minerals (e.g., Carroll et al. 2013; Hao et al. 2013; Smith et al. 2013; Ellis and Peters 2016). The creation of wormholes by the injection of acid at an optimal rate into carbonate oil reservoirs is of particular interest as it allows for a significant increase in permeability with only the minimal amount of reactant necessary (e.g., Daccord et al. 1993a; Poms et al. 2007; Ghommem et al. 2015).
On the laboratory scale, Menke et al. (2016, 2017) both report that with increasing initial heterogeneity in carbonate rocks, the permeability will be more sensitive to changes in porosity, increasing faster than more homogeneous units. In a similar laboratory setup, Al-Khulaifi et al. (2017) report that the sensitivity of the permeability to changes in the porosity will change depending on the phase of dissolution. They report that in the early stages of dissolution the relationship will be very sensitive, giving way to a less sensitive phase. After this less sensitive phase has progressed, the dissolution will have advanced to focus in preferential flow paths, and the relationship will return to similar levels of sensitivity as in the beginning phase.
When dissolution and other processes occur simultaneously, porosity and permeability may even be anti-correlated on the laboratory experiments scale or at the REV scale. As examples, Garing et al. (2015), Luquot et al. (2014), Mangane et al. (2013) observe this phenomenon given a combination of dissolution and filtration of grains detached by dissolution at a downstream pore throat during the injection of a low-reactivity fluid into carbonate rocks. In these cases, a decrease in the permeability-controlling macroporosity and a large increase in the highly tortuous microporosity are reported.
Mineral Precipitation While mineral dissolution tends to result in stabilizing the flow and transport regime since both porosity and permeability increase, the opposite is true when minerals precipitate or biomass accumulates. With a reduction in permeability, the flow will either be reduced or, dependent on the boundary conditions for flow, bypass the region of reduced permeability; in either case the supply of reactants or nutrients declines and inhibits further reactions or growth. In the current literature, there are fewer studies available on the precipitation of minerals compared with those investigating only mineral dissolution.
Even for constant flow rates, the reaction rates usually decrease as the residence time reduces with the porosity. Thus, the \(\mathrm {Da_I}\) number decreases as well. Hence, systems with reductions in porosity and permeability often tend to inhibit themselves, at least locally, and their behavior ends up being less dependent on \(\mathrm {Da_I}\),\(\mathrm {Da_{II}}\) or Pe than for systems with dissolution. Precipitation of minerals may, for example, inhibit the formation of stable convective regimes in hydrothermal systems (Steefel and Lasaga 1994). Even when the initial permeability variations in such hydrothermal systems may have a huge influence in the long term, changes due to dissolution and precipitation may dominate (e.g., Bolton et al. 1999).
The shape of precipitated minerals can be influenced by the available host minerals. This may lead to different permeability changes for identical porosity reductions. Systems experiencing the development of pore-scale heterogeneity due to precipitation show a higher reduction in permeability when compared with those where precipitation occurs more uniformly (Noiriel et al. 2016). Noiriel et al. (2016) further observe that the permeability is mainly influenced by the narrowing or closing of pore throats, but for systems with an increase in surface roughness, this also reduced the permeability.
Biomass Accumulation Similar to mineral precipitation, biomass accumulation generally decreases permeability (e.g., Cunningham et al. 1990, 1991; Dupin et al. 2001a, b; Kim and Fogler 2000; Taylor and Jaff 1990b; Thullner et al. 2002; Thullner 2010; Vandevivere and Baveye 1992a, b; Vandevivere 1995; Vandevivere et al. 1995). Biomass growth in porous media may have a variety of different shapes: aggregates and colonies in the form of clumps, filaments, pearl necklaces, or thin surface layers, so-called biofilms, each of which will have a variety of surface structures (Characklis and Marshall 1990) itself. The impact of biomass clogging on permeability will be influenced by various factors. The total amount of biomass, the biomass structure, and the biomass distribution, as well as the nutrient supply, the flow shear stresses, and other environmental conditions and their history, will all influence the impacts of the clogging (e.g., Cunningham et al. 1990, 1991; Kim and Fogler 2000; Taylor and Jaff 1990b; Thullner et al. 2002; Thullner 2010; Vandevivere and Baveye 1992a, b; Vandevivere 1995; Vandevivere et al. 1995).
Minerals are rigid and solid, while biomass consists mainly of water and can have a residual biomass porosity or permeability (Thullner et al. 2002; Vandevivere 1995). Further, biomass consists of living cells, which require a substrate supply not only for their growth, but also for maintaining themselves. Without this minimum supply, the biomass will eventually decay, thereby loosing its mechanical strength, and the effects on the porosity and permeability might be reversed. In natural systems, additional inter-species competition, in the form of the production of antibiotics, or predation by eucaryotes for example, may additionally add to the dynamics of the biomass (Characklis and Marshall 1990). Also, an artificial injection of disinfectant, antibiotics, or similar substances will likely weaken the biomass and restore permeability (Dupin and McCarty 2000). Another particularity of biomass clogging is that even small numbers of cells, themselves insignificant for any influence on flow, may produce large amounts of extra-cellular polymeric substances (EPS) (Characklis and Marshall 1990; Thullner 2010; Vandevivere and Baveye 1992a) which can, despite their low cell numbers, have a significant impact on permeability (Vandevivere and Baveye 1992a). The physical properties of biomass aggregates or biofilms are, to a large extent, determined by the EPS (Characklis and Marshall 1990; Thullner 2010). Even small changes in the environmental conditions may result in significant changes to the EPS and therefore the biomass properties (Characklis and Marshall 1990; Thullner 2010).
Biomass accumulation in the form of a biofilm, a thin layer uniformly covering the solid surface, is the most commonly assumed form of growth in models accounting for bioclogging (Dupin and McCarty 2000). Because of the enormous specific surface area of porous media, even a thin biofilm can occupy a significant volume, causing a reduction in porosity and permeability. However, Vandevivere et al. (1995) show that permeability predictions based on porosity reduction by biofilms alone underestimates the observed permeability reductions. Using pore network models and assuming an impermeable biomass aggregate, (Dupin and McCarty 2000) shows that such aggregate growth induces a much greater permeability reduction per porosity reduction than when assuming growth as a biofilm, which is consistent with observations presented in Taylor and Jaff (1990a); Taylor et al. (1990).
Biomass accumulation can also lead to other processes, e.g., mineral dissolution or precipitation, when the biomass functions as a geochemical catalyst. As an example, the precipitation of carbonates can result from the metabolism of ureolytic microbes, providing both a source of inorganic carbon as well as the high pH conditions necessary for precipitation (e.g., Barkouki et al. 2011; Cuthbert et al. 2013; Ebigbo et al. 2012; Hommel et al. 2015; Mitchell et al. 2013; Paassen et al. 2010; Phillips et al. 2013b, a, 2015, 2016). Other mineral reactions may also involve biomass, for example, the (bio-)precipitation of hydroxides or oxides (Davis et al. 2007; Gadd and Pan 2016; Peng et al. 2007) or silica (Peng et al. 2007), along with many other minerals such as sulfides, sulfates, and phosphates (Bertrand et al. 2015; Gadd and Pan 2016).
Such combinations further increase the already complex interplay between hydrodynamic and (bio-)geochemical effects, not only by adding additional complexity within the (bio-)geochemical reactions themselves, but also by including the inherently different form of the porosity–permeability relation for biomass accumulation or minerals, as discussed above. A pore network study on biomass accumulation and mineral precipitation, as described in Qin and Hassanizadeh (2015), finds no unique relationship between the porosity reduction and the resulting permeability. Instead, Qin and Hassanizadeh (2015) observe that it is dependent on the initial biomass distribution and the operating conditions.
3 Porosity–Permeability Relations for (Bio-)geochemically Altered Porous Media
An approach for calculating the change in permeability due to changes in porosity should fulfill a few requirements: (i) the relationship should only rely on available parameters, (ii) it should consider the physical processes changing the porosity, (iii) it should fit experimental observations, and (iv) it must be able to be calculated at a reasonable computational expense.
On top of these requirements, Verma and Pruess (1988) conclude that the form of the porosity–permeability relationship should arise not only from the differences in pore system parameters, but also from the mechanisms that drive the changes in porosity. For example, If changes to the confining pressure are the primary source of porosity change, the pore body geometry may be much more affected than pore throat geometry as there is less matrix support. On the other hand, if mineral precipitation is the primary source of porosity change, pore throat geometry may be heavily affected, where pore body geometry may have minimal change (Verma and Pruess 1988).
Although originally developed to estimate the permeability for a constant porous medium, relations like the Kozeny–Carman Equation are used to estimate changes in permeability due to changes in porosity due to mineral precipitation or biofilm accumulation. With relations like the Kozeny–Carman equation (Eq. (9)), the change in permeability is calculated by relating the current permeability, K, based on the current porosity \(\phi \), to the initial or reference permeability, \(K_0\) , based on the reference porosity \(\phi _0\), (e.g., Schneider et al. 1996; Wijngaarden et al. 2011, 2013; Yasuhara et al. 2012; Steefel et al. 2015b; Xie et al. 2015; Pandey et al. 2014, 2015). This can be done as well with other porosity–permeability relationships, (e.g., Steefel et al. 2015b; Steefel and Lasaga 1994; Steefel and AC 1990; Bernabe et al. 2003; Civan 2001; Chadam et al. 1986; Luquot and Gouze 2009; Marshall 1958; Pape et al. 1999; Tsypkin and Woods 2005; Verma and Pruess 1988). These equations consequently follow the form:
The development of more complex porosity–permeability relations has been performed for application in a variety of study topics, see Sect. 2.4. Unfortunately, in all of these cases, no relation exists that can be used, without condition, in each (Bernabe et al. 2003). Even when relations are based on experimental setups, the effects of porosity change on permeability are largely affected by the process causing the change as well as the scale and dimensions of the experiment.
As most fields of study have either developed new relations, or have borrowed relations from similar studies, countless relations can be found in literature. Lai et al. (2014) and Thullner (2010) both include a listing of relevant relations for chemical dissolution processes and biomass accumulation, respectively, but these lists are not exhaustive. Civan (2001) uses and references a wide variety of experimental studies to show the capabilities of the porosity–permeability relation developed in Civan (1996, 2000). This chapter will analyze a series of different relations, comparing everything from their origin to their application.
Porosity–permeability relations have been developed from a large range of backgrounds, some are based on mathematical or geometrical considerations, others from an upscaling from pore-scale or pore network-scale simulations, and many more are simply to fit to empirical data. Mathematical or geometrical considerations usually require a simplification of the porous medium structure and often are rather complex, while relations used to fit experimental data are often simple exponential or power functions (e.g., Civan 2001).
An example of a simplification to the pore morphology used to derive a mathematical- or geometrical-based relation would be, using biomass growth as an example, assuming a uniformly distributed continuous biofilm, or the development of distinct individual Biomass colonies (e.g., Seki and Miyazaki 2001; Thullner et al. 2002). Similarly, considering mineral precipitation, minerals may be assumed to form a uniform layer (e.g., Steefel and Lasaga 1994; Li et al. 2008) or as distinct crystals. For mineral dissolution, the geometry change will depend, among other factors, see Sect. 2.4, on the initial distribution of the dissolving mineral (e.g., Carroll et al. 2013). However, as the effect of porosity change on permeability is strongly dependent on the relevant process and conditions, see Sect. 2.4, geometrical, upscaling, or empirical approaches to determine porosity–permeability relations should ideally result in similar or even identical relations for each set of given conditions.
In the following we present and discuss in detail the porosity–permeability relations published. We start with the classic Kozeny–Carman relation in various forms (Sect. 3.1), and relations derived from it (Sects. 3.2–3.5). We continue with exponential (Sect. 3.6), Cubic Law (Sect. 3.7) and the power law relations (Sect. 3.8) as well as relations derived from the Power Law (Sects. 3.9–3.11). Finally, we discuss a few complex relations that do not fit in any of the previous categories: the two porosity–permeability relations for biomass accumulation proposed by Seki and Miyazaki (2001) (Sect. 3.12) and Vandevivere (1995) (Sect. 3.13), the modified Fair–Hatch relation for mineral dissolution (Sect. 3.14), and another biomass relation based on upscaling from pore network modeling proposed by Thullner et al. (2002) (Sect. 3.15). For the widely used power-law and Verma–Pruess relations, we group the literature review into two categories, relations based on experimental investigations or specific forms of the relations used in modeling reactive transport.
3.1 Kozeny–Carman Relation
As mentioned above and in Sect. 2.3, the Kozeny–Carman equation was not originally developed to describe the permeability evolution of porous media undergoing alterations in pore morphology. Nonetheless, due to its age and ease of use, it is widely applied in models describing porosity and permeability changes due to mineral precipitation and biofilm accumulation. What specifically is used in these approaches follows the form outlined in (Eq. (21)), using the original form of the Kozeny–Carman relation discussed in Sect. 2.3 (Eq. (9)) (e.g., Schneider et al. 1996; Wijngaarden et al. 2011, 2013; Steefel et al. 2015b; Xie et al. 2015; Pandey et al. 2014, 2015). Negligible geometry changes are commonly assumed (\(\varPhi _\mathrm {s}\), \(D_\mathrm {p}\approx \text {constant}\)). This results in the following:
Here, \(K_0\) and \(\phi _0\) are the initial or reference values of K and \(\phi \) respectively. The only terms required to calculate the change in permeability are the starting and ending porosities. This can be seen as an advantage; no other calibration factors need to be determined; and no extensive geometrical corrections have been included. Schneider et al. (1996) uses this form of the Kozeny–Carman equation (22), but in some cases uses \(\phi ^5\) instead of \(\phi ^3\) depending on the rock type. In its original form, this equation does not allow for any special treatment of different grain sizes, textures, or (bio-)geochemical factors. Vandevivere (1995) states that at least one adjustable parameter, implicit or explicit, should be included in each relation to allot for the large diversity within porous media.
Another form of the original constant form Kozeny–Carman Equation can be used (Carman 1937), where the \((1-\phi )\) term is replaced with the specific surface, S, resulting in the following equation:
where \(S_0\) is the initial specific surface area. Here, both the porosity, \(\phi \), and the specific surface, S, change. In Equation 23, the specific surface area may also be expressed as the square of a characteristic length \(l_\mathrm {ch}\): \(S=l_\mathrm {ch}^2\) (e.g., Golfier et al. 2002). This second form (Eq. 23) is used often when deriving other relations (e.g., Taylor et al. 1990; Vandevivere 1995; Vandevivere et al. 1995; Martys et al. 1994), but is rarely directly used, as is done in Golfier et al. (2002). Amaefule et al. (1993) rearranged the Kozeny–Carman relation to:
where \(\gamma =\nicefrac {1}{S\sqrt{2\tau }}\) is a so-called flow unit parameter, accounting for the effects of the specific surface area S and the tortuosity \(\tau \). In the format of Eq. (21), it is almost identical to Eq. (22), except for the additional term \(\nicefrac {\gamma }{\gamma _0}\) describing surface area and tortuosity changes, which are neglected in Eq. (22):
However, Amaefule et al. (1993) aims to predict permeabilities in unexplored regions based on the values obtained at other locations, an application that falls out of the scope of this work.
3.2 Civan Relation
Expanding on the rearrangement of the Kozeny–Carman in Amaefule et al. (1993), Civan (1996) introduces an exponent \(\beta \) to the term \(\frac{\phi }{1-\phi }\) in Eq. (24) as an additional empirically determined parameter:
The motivation for the inclusion of \(\beta \) in Civan (1996) and the subsequent deviation from the Kozeny–Carman relation (Eq. (9)) is based on experimental data. Civan (2000) fits values for \(\gamma \) (4.1 and 5.82) and \(\beta \) (2.96 and 3.89) observing that for the investigated data sets \(\gamma \ne \nicefrac {1}{S\sqrt{2\tau }}\) as proposed in Amaefule et al. (1993) and \(\beta \ne 1\) as implied by the Kozeny–Carman relation (Eq. (9)). Civan (2000) shows that the parameters \(\gamma \) and \(\beta \) could be correlated with the coordination number, the number of pore throats connecting a pore body with its neighbors. This implies that, as long as the coordination number is constant, \(\gamma \) and \(\beta \) remain constant as well. For a permeability change this results in:
However, Civan (2000) also fits functions for \(\gamma \) and \(\beta \) in the case that the coordination number changes, e.g., for the data presented in Bhat and Kovscek (1999). The Civan relation is specifically intended to estimate the change in permeability during dissolution or precipitation (Civan 2001).
3.3 Marshall Relation
As a modification to the Kozeny–Carman relation (Eq. (9)), another relation, taking a similar approach, but including knowledge on pore size distribution, is developed in (Marshall 1958),
To develop this equation, the total grain size distribution is split into n sections each representing a different specific range of pore radii. The average grain size radius of each section, \(r_i\), is then used to describe the pore space geometry more specifically (Marshall 1958). When this equation is formatted according to Eq. (21)), the following equation results:
Here, the use of the original Marshall equation can be helpful in analyzing permeability from well studied porous units, but, especially when biomass growth or precipitation events have occurred, a full grain size analysis is impossible to measure without damaging the biomass or precipitate structures. Although this equation integrates more knowledge of the actual porous unit, it is less applicable to porous media changes than the Kozeny–Carman equation as the required \(r_i\) are difficult to obtain.
3.4 Taylor (Packing, Cut-and-Random-Rejoin) Relations
Using the second form of the Kozeny–Carman equation (Eq. (23)), Taylor et al. (1990) incorporate knowledge of packing geometry and biofilm growth to create the Taylor Packing relations. To develop the precise changes to geometry, Taylor et al. (1990) assume spherical grains of constant grain size and uniform packing configuration. A change in each sphere’s radius is then applied, representing the growth of a uniform, impermeable, and rigid biofilm. Depending on the packing of the grains, the porosity and the specific surface will then change according to the following equations:
These terms are functions of R, the original radius of the grains, and \(\psi \), the ratio of the biofilm thickness to the original radius of the grain. These terms are then placed into (Eq. (23)) to form a porosity–permeability relation. Different values for \(\alpha _m\) and m are provided for each of the packing configurations.
Following the development of the above Taylor Packing relations, Taylor et al. (1990) also develops another relation based on the work of Carman (1937); Childs and Collis-George (1950); Millington and Quirk (1961); Mualem (1976), where a “Cut-and-Random-Rejoin” model is used. Here, the grains of various radius are assumed to be distributed randomly throughout each plane of porous media. The overall conductance of the material depends on the connectivity of pore space between each of the planes and the geometry of their connections. The Hagen–Poiseuille equation, explained in Eq. (12), is then used to create a relationship between this pore size distribution and the permeability (Vandevivere et al. 1995).
When this model and the corresponding equation are applied to Eq. (23), and to the work of Millington and Quirk (1961), non-physical results occur. When applied to the format developed in Childs and Collis-George (1950); Mualem (1976), relations that provide plausible changes to permeability can be developed (Taylor et al. 1990; Vandevivere et al. 1995):
where \(\lambda \) represents the initial pore size distribution, \(r_\mathrm{min}\) and \(r_\mathrm{max}\) are the initial maximum and minimum pore radii, and the function \(I_3\) is defined in Taylor et al. (1990) as:
\(\lambda \) can range from zero to infinity, but usually ranges between 2 and 5. For example, when comparisons are made in Vandevivere et al. (1995), a value of \(\lambda = 3.98\) is used.
Both the Taylor Packing (Eq. (30)) and the Cut-and-Random-Rejoin (Eq. (31)) relations (Taylor et al. 1990), show the sizable weakness of a geometric approach. First, considerable assumptions related to the geometry are necessary. In the Taylor Packing relation (Eq. (30)), a comparison of these relations against experimental data is not even possible as the uniform packing configurations assumed cannot be physically created (Vandevivere 1995). Second, in all of the above relations, extensive knowledge of pore geometry is required; knowledge of these parameters at experiment scale or at field scale is very unlikely. Finally, when developing relations based strictly on geometrical approaches, the translation of these relations from the pore scale to the REV scale does not work, as the assumptions made are too unrealistic (Taylor et al. 1990; Vandevivere et al. 1995), leading to the conclusion made in Taylor and Jaff (1990a) refuting the use of their relations.
3.5 Ives–Pienvichitr Power Law Relation
While analyzing the deep filtration of a dilute suspension, Ives and Pienvichitr (1965) make modifications to the second form of the Kozeny–Carman equation (Eq. (23)). By simply assuming that the specific surface area term, S, is proportional to \(\phi ^{p}\), Ives and Pienvichitr (1965) simplify the Kozeny–Carman equation to the following Power Law:
Here, the fitting parameter, p, should change depending on the level of tortuosity. Okubo and Matsumoto (1979) fit \(p=0.5\) to data from a bioclogging experiment during artificial recharge. However, when a power-law relation is typically used, it is not formulated as is shown in (Eq. (33)) type, but in more general form, later explored in Sect. 3.8.
3.6 Exponential Relations
Exponential relations do not fit directly with power-law relations, and can also not be derived from the Kozeny–Carman relation. This makes them an alternative, usually experimentally based approach, to the porosity–permeability relation (Thullner 2010).
Garing et al. (2015) conduct dissolution experiments using carbonate rocks and deionized water as well as water containing \(\hbox {CO}_2\). For \(\hbox {CO}_2\)-containing water, Garing et al. (2015) observe a Power Law, see Sect. 3.8. For deionized water however, Garing et al. (2015) find a reduction of permeability by factors of up to seven, while at the same time the porosity increases by 9% from 0.42 to 0.458 during dissolution of carbonate rocks. Garing et al. (2015) attribute this to grain cements dissolving significantly faster than the grains themselves leading to clogging by straining of detached grains. This is observed for the low-reactivity deionized water, but not for water containing \(\hbox {CO}_2\). Similar results for low-reactivity fluids dissolving carbonates are observed in Luquot et al. (2014); Mangane et al. (2013). Garing et al. (2015) fit an exponential relation for permeability development during deionized water injection:
where fit values for the exponent \(\epsilon \) range from \(1.3 \times 10^{-3}\) to \(2.7 \times 10^{-2}\). However, as they do not relate the changes in permeability to those in porosity for this case.
When developing a model describing the reduction of permeability due to bacterial growth, Lappan and Fogler (1996) create the following equation:
where \(\epsilon \) is a fitting parameter (Lappan and Fogler 1996; Thullner 2010). When calibrating the relation to experimental data, \(\epsilon \), is assigned a value of 33.8.
Tsypkin and Woods (2005) develop a relation for the reduction of pore space due to salt precipitation in de-pressurized fractures. Although their model is originally developed for fractured rock reservoirs, their equations are based on the work of Battistelli et al. (1995); Verma and Pruess (1988), who develop both fractured rock and porous media relations:
with the fitting parameter, \(\epsilon \), describing the relative impact of evaporation and advection. While fitting their equation to data, Tsypkin and Woods (2005) recommend values of \(\epsilon \) ranging between 10 and 30.
Vandevivere and Baveye (1992b) fit a discontinuous exponential relation to the measured permeability reduction during bioclogging. With below 3% biomass volume per initial pore volume, they observe that the permeability is reduced by half for an increment of 1.6% of biomass volume, while above 3%, an increment of 0.6% of biomass volume is sufficient to achieve the same reduction. This results in \(\epsilon =43.3\) for biomass volumes below 3% and \(\epsilon =115.5\) above for the equation:
3.7 Cubic Law
The Cubic Law, or its modifications, already discussed in Sect. 2.3, can be used for fractured media when assuming that the fractures are highly permeable compared to the surrounding matrix and thus they determine the system’s effective permeability (Patir and Cheng 1978; Marsily 1986; Steefel and Lasaga 1994; Dobson et al. 2003; Ellis and Peters 2016). When the fracture aperture is modified, the updated permeability can be either directly calculated by Eqs. (14) or (15), which using Eq. (21) results in:
where \(a_0\) and a are the initial and the current aperture. For multiple parallel fractures, the relation using initial and current fracture porosities, \(\phi _\mathrm {f,0}\) and \(\phi _\mathrm {f,0}\), results in:
The Cubic Law assumes flow between smooth, parallel plates with a constant aperture. This assumption is questionable for real fractures, but its limitations can be mitigated by including a sequence of fractures with varying apertures or by considering wall roughness by replacing a in Eq. (38) with an effective hydrodynamic aperture, estimated from a and its variance (e.g., Noiriel et al. 2013; Patir and Cheng 1978).
A Cubic Law-based relation is used, for example, in Cuthbert et al. (2013) for microbially induced calcium carbonate precipitation, in Steefel and Lasaga (1994); Dobson et al. (2003) for dissolution and precipitation in a hydrothermal system, and in Noiriel et al. (2013) for dissolution of limestone. Fractures are the primary structures allowing for flow in each of these applications.
3.8 Power-Law Relations
As done in Ives and Pienvichitr (1965) (Sect. 3.5), the Kozeny–Carman relation (Eq. (23) can be simplified by assuming \(S\propto \phi ^p\). Instead of using explicitly using the expression \(3-2p\) as an exponent, as is done in Eq. (33), the exponent is simplified to \(\eta =3-2p\), and written as the following:
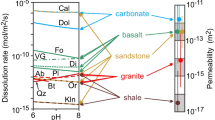
This Eq. (40) is widely used to describe permeability changes in experimental and modeling studies (Aharonov et al. 1998; Bear 1988; Bernabe et al. 2003; Carroll et al. 2013; Clement et al. 1996; Civan 2001; Coln et al. 2004; Doyen 1988; Garing et al. 2015; Hao et al. 2013; Luhmann et al. 2014; Luquot et al. 2014; Luquot and Gouze 2009; Menke et al. 2015; Noiriel et al. 2004, 2005; Pereira Nunes et al. 2016; Knapp and Civan 1988; Smith et al. 2013; Vandevivere et al. 1995; Zhang et al. 2015). It is convenient, as it requires only the porosity and provides \(\eta \) as a fitting factor. This fitting factor, \(\eta \), can either be calibrated from experimental data, or taken from the available process-specific literature. As discussed in Sect. 2.4, the value of \(\eta \) should be determined by the initial porous medium properties and the processes and conditions that cause the pore geometry to change. For example, Luquot et al. (2014) find that during dissolution, the initial porous medium structure determines the value of \(\eta \) which is linked to the hydraulic pore diameter change. Bernabe et al. (2003) develop a listing of different \(\eta \) values with regard to different processes. \(\eta \) between 2.5 and 3 are suggested for plastic compaction, \(\eta =8\) for mineral precipitation, \(\eta >= 10\) for chemical alteration, and \(\eta >= 20\) for mineral dissolution.
The most common form of the Power Law uses an \(\eta \) of 3 (Bear 1988). The Power Law with \(\eta =2\) is equal to the Cubic Law; see Eq. (38). Aharonov et al. (1998); Coln et al. (2004) postulate that any Power Law with exponents lower than 2 is not realistic, and that a value of \(\eta =2\) is often correct for units that have undergone natural diagenesis. According to Zhu et al. (1995), this Power Law works well for units with a higher original porosity, but after the porosity has been reduced past a pore connectivity threshold, \(\eta =3\) does not describe changes accurately.
In comparison to the basic Kozeny–Carman relation (Sect. 3.1), the power-law relation (Eq. (40)) includes the medium specific exponent \(\eta \) as a parameter, which makes it slightly more adaptive. It is both simple, easy to implement, and available for calibration to experimental data. For these reasons, it is widely used. Regardless of its advantages, it is often described as a shortcut and criticized for not accurately representing the complex processes that change pore structure.
3.8.1 Experimental Studies Using the Power Law
When modeling the dissolution experiment data presented in Smith et al. (2013), Carroll et al. (2013) and Hao et al. (2013) find that, for the investigated dissolution of carbonate rocks from the Weyburn–Midale formation by \(\hbox {CO}_2\), \(\eta \) depends on the heterogeneity of the mineral and pore space distribution. For the more homogeneous Marly dolostone they fit \(\eta =3\), while for the more heterogeneous Vuggy limestone, they fit an \(\eta \) between 6 and 8. The \(\eta \) values for those rocks are consistent with the developed dissolution patterns, with lower \(\eta \) being associated with more homogeneous dissolution and higher \(\eta \) with increasingly heterogeneous dissolution patterns up to the formation of wormholes. However, Smith et al. (2013) observe that for some experiments \(\eta \) changed with time as the dissolution progressed.
When investigating the pore space of sandstone units, Doyen (1988) measure the variable pore spaces and calibrate a value of \(\eta = 3.8\).
Garing et al. (2015) conduct dissolution experiments using carbonate rocks and both deionized water and water containing \(\hbox {CO}_2\). For water containing \(\hbox {CO}_2\), Garing et al. (2015) observe an increase in permeability, which they fit to a power-law relation with exponent \(\eta \) ranging between 4.87 and 23.72. However, for deionized water, Garing et al. (2015) observe a reduction in permeability by factors of up to seven while at the same time the porosity increases by 9% from 0.42 to 0.458 during dissolution of carbonate rocks.
Luhmann et al. (2014) dissolve dolomite with \(\hbox {CO}_2\)-charged brine at 100 \(^\circ \)C and 150 bar, observing power-law relation exponents in the range of \(1.93 \le \eta \le 9.03\). However, they observe a relatively small change in porosity where only 1.2 to 3.4% of the mass of each core is dissolved. Luhmann et al. (2014) then explain that through these experiments, it is not possible to determine the validity of the Power Law.
Dissolving limestone with \(\hbox {CO}_2\)-rich brine at a series of partial pressures of \(\hbox {CO}_2\) (\(\hbox {pCO}_2\)), Luquot et al. (2014) observe values of \(\eta \) ranging from -2.5 to 7.07. Values of \(\eta \) increase with an increase in \(\hbox {pCO}_2\), where \(\eta =-2.5\) corresponds to the low reactive \(\hbox {pCO}_2 = 0.034\hbox {MPa}\), and \(\eta =7.07\) corresponds to the \(\hbox {pCO}_2\) of \(3.4\hbox {MPa}\), showing an increase over two orders of magnitude.
Menke et al. (2015) combine experimental images and direct simulation in the investigation of the dissolution in a carbonate core due to \(\hbox {CO}_2\) saturated brine injection. Navier–Stokes equations are solved on the image voxels obtained by micro-CT imaging over time to determine the permeability. For a porosity increase from 17.2 to 32.0%, the permeability increases by almost 1.5 orders of magnitude during the dissolution. Menke et al. (2015) fit \(\eta =5.16\) for the overall experiment, although they also find that the increase in porosity and permeability is more rapid initially, meaning that \(\eta \) decreases over time. To further understand this same dissolution process, Menke et al. (2016) and Menke et al. (2017) report that the higher the initial heterogeneity within the rock’s pore structure is, the larger the fit \(\eta \) value will be. For two carbonate rock samples with increasing heterogeneity, an Estaillades Limestone with lower heterogeneity, and a Portland Limestone with higher heterogeneity, Menke et al. (2016) report a fit \(\eta \) ranging from \(\eta = 6.74\) to \(\eta = 7.52\) for the more homogeneous unit, and fit values ranging from \(\eta = 10.9\) to \(\eta = 11.0\) for the more heterogeneous unit. Following this experiment, Menke et al. (2017), find similar results with three more limestone rocks, again with varying heterogeneity. Menke et al. (2017) report \(\eta = 5.45\) to \(\eta = 6.93\) for the more homogeneous Ketton Limestone, \(\eta = 9.99\) to \(\eta = 13.4\) for the more heterogeneous Estaillades Limestone, and \(\eta = 16.2\) to \(\eta = 23.8\) for the most heterogeneous Portland Limestone. In another experiment investigating the dissolution of carbonate rock in \(\hbox {CO}_2\)-rich brine, Al-Khulaifi et al. (2017) report that the changes in permeability and porosity will change dependent on the dissolution phase. For three different samples of carbonate rock, a Silurian Dolomite Limestone, a Ketton Limestone, and a composite of the two, the fit \(\eta \) changes from a very high value at the beginning of the experiment to a lower intermediate value, and returns to a high value after the experiment had progressed. They argue that the fit \(\eta \) will therefore be dependent on the phase of the dissolution, as well as the initial heterogeneity of the rock’s pore structure. Al-Khulaifi et al. (2017) report \(\eta \) values ranging from 11.1 to 7.4 to 11.3 in the Silurian Dolomite Limestone, values ranging from 6.8 to 3.2 to 9.3 for the Ketton limestone, and 10.4 to 5.0 to 12.8 for the composite sample.
While experimentally investigating the effects of limestone dissolution, Noiriel et al. (2004, 2005) observe \(\eta = 13\) after some initial, dramatic permeability increase. Noiriel et al. (2005) report an \(\eta = 75\) for the initial period, during which high surface area micritic mold lodged in pore openings is dissolved.
During the development of a dissolution pore space model, Pereira Nunes et al. (2016) observe \(\eta = 4.4\) when solving the incompressible Navier–Stokes equations on geometries obtained from computer tomography images of samples during injection of \(\hbox {CO}_2\)-saturated brine. Pereira Nunes et al. (2016) find \(\eta = 4.5\) when using geometries obtained by reactive transport simulations instead.
Rötting et al. (2015) investigate the effect of carbonate dissolution in HCl solutions on the porosity, permeability, reactive surface area, and water retention curve. They observe \(5.5 \le \eta \le 23.2\) for coarse calcite cores, with one extreme value of \(\eta = 431\), and very high \(\eta \) values ranging from \(36.9 \le \eta \le 242\) for fine dolomite, for which the permeability increases by orders of magnitude during the experiment. Rötting et al. (2015) find that pores below a threshold diameter of 0.022 mm for calcite and 0.001 mm for dolomite are not significantly affected by dissolution which is limited to pores initially larger than the threshold diameter. This reduces the water retention or capillary pressure for high water saturations, while it remains unchanged for very low saturations.
3.8.2 Modeling Studies Using the Power Law
In order to better understand the pore geometry changes during subsurface steam injection, Bhat and Kovscek (1999) develop pore network models varying pore body and throat geometry, as well as the dissolution and precipitation processes. Using a network of sinusoidal pores, each with a pore body, a pore throat, and a level of connectivity, Z, Bhat and Kovscek (1999) vary the processes by which silica is dissolved and deposited. In order to fit their data to a relation, a simple Power Law is used (Eq. (40)). They find that, in general, as the connectivity Z decreases, the exponent increases, and that when the ratio of pore body radius to pore throat radius, \(\frac{R_{B}}{R_{T}}\), increases, the exponent increases. The exponents reported vary between 8 and 9. After comparing their results to experiment data in Koh et al. (1996), Bhat and Kovscek (1999) confirm that an exponent of 9 represents precipitation of silica in the narrow pore throats they studied.
Lichtner (1985) compare the effects of \(\eta =1,\, 2,\, 3,\) and 8, when modeling the precipitation of quartz in a hydrothermal system.
During an investigation into the changes in pore geometry given reactions in carbonate rock, Nogues et al. (2013) develop a series of pore network models. With a pore network geometry based on scans of representative carbonate rock formations, the model mainly focuses on variations in geochemistry. To describe the data collected from the model, Nogues et al. (2013) attempt to use a power-law relation (Eq. (40)), but focus on highlighting the drawbacks of this sort of relation, rather than identifying a specific component. They argue that the exponent should change, depending on geochemistry, flow rate, and initial porosity, eventually ranging from a value of 2 to 10. An exponent value of 6 is given for a high flow rate case (Nogues et al. 2013).
For modeling the effect of \(\hbox {CO}_2\) storage on the permeability of the sandstone reservoir, Zhang et al. (2015) use a Power Law with \(\eta = 11\) within their reactive transport model.
3.9 Clement Relation
During an investigation of microbial growth, Clement et al. (1996) develop the relation proposed in Taylor et al. (1990), developing their own relation linking permeability change to the change in porosity and maximum pore radius \(r_\mathrm {max}\):
Clement et al. (1996) simplify this relation by assuming that the change in the maximum pore radius can be expressed in terms of porosity \(\left( \nicefrac {r_\mathrm {max}}{r_\mathrm {max,0}}\right) ^m=\nicefrac {\phi }{\phi _0}\). Determining the empirical coefficient m to \(m=3\) results in a power-law relation with \(\eta \) = \(\nicefrac {19}{6}\). The relation developed in Clement et al. (1996) is identical to a Taylor Cut-and-Random-Rejoin relation with \(\lambda = 3\); see Sect. 3.4 (Clement et al. 1996; Thullner 2010).
3.10 Pape Relation
Based on measurements of fractal pore space geometry of sandstone, Pape et al. (1999) develop an empirically based relation, a combination of three Power Laws, to estimate the porosity for various formation rocks based on the porosity:
Here, each coefficient (\(A,\, B\), and C) should come from specific bore-log data collected while analyzing the sandstone. Noiriel et al. (2004) reference this as a linear combination of n Power Laws with exponents m and describe it more succinctly with the following equation:
As each coefficient \(A_m\) may change for each step in the pore geometry evolution, large amounts of calibration data are required in order to develop this relation.
3.11 Verma–Pruess Relation
A variation of the Power Law (Sect. 3.8) is the Verma–Pruess relation:
where \(\phi _\mathrm {crit}\) is the critical porosity at which the permeability becomes zero, and the exponent \(\eta \) is an empirical parameter as in Eq. (40).
Equation (44) is first introduced in Verma and Pruess (1988) as an expansion of the work presented in DO (1958) while investigating silica precipitation in porous media systems near nuclear waste storage sites. Verma and Pruess (1988) study the changes to a systems porosity and permeability for different confining pressures using a pore body and throat model. This model format claims significance as small reductions in porosity within a pore throat will result in a considerable decrease in pore connectivity, and therefore the series\(\text {'}\) permeability.
The primary addition to this model in comparison to the Power Law is the critical porosity, \(\phi _\mathrm {crit}\), which is used to describe the nonzero porosity threshold at which the permeability asymptotically approaches zero. The critical porosity describes that not all pore space is effective for flow (see Sect. 2.4). The idea is that only for \(\phi >\phi _\mathrm {crit}\), the pore space is connected and thus only the pore space exceeding this limit (\(\phi -\phi _\mathrm {crit}\)) contributes to flow, aiming at representing porous medium heterogeneities or disconnected pore space.
Summarizing the main features of the Verma–Pruess relation (Eq. (44)), we state that in comparison to the basic Power Law relation (Eq. (40)), the Verma–Pruess relation is not considerably more complicated. Although it remains simple, it does take a step to address the processes governing porosity–permeability relation with the addition of \(\phi _\mathrm {crit}\). A relation identical to the Verma–Pruess relation (Eq. (44)) is independently proposed by Martys et al. (1994) for scaling the permeability of overlapping or non-overlapping sphere packings.
3.11.1 Experimental Studies Using the Verma–Pruess Relation
Based on experimental data collected in sandstone units, Verma and Pruess (1988) state that \(\eta \) may range from 6 to less than 1 depending on the material and ranged during their tests from 1.98 to 0.73. Verma and Pruess (1988) also test variances in \(\phi _\mathrm {crit}\), estimating that the critical porosity should be around 0.8–0.9 of the original porosity.
In an experimental study, Bacci et al. (2011) measure both the porosity and the permeability of sandstone cores initially filled with saturated saline water during \(\hbox {CO}_2\) injection. They observe porosity reductions from 4 to 29% and permeability reductions from 30 to 86% and fit \(\phi _\mathrm {crit}\) and \(\eta \) to the measured reductions. Unfortunately, they do not provide the final fit values.
During an experimental exploration of dissolution in carbonate rocks, Luquot and Gouze (2009); Gouze and Luquot (2011) use a permeability–porosity relation based on the work of Martys et al. (1994) that looks like this:
which is identical to the relative Verma–Pruess relation (Eq. (44)), with an additional fitting parameter, \(\theta \). When this relation is formatted according to (Eq. (21)), or by setting \(\theta = \nicefrac {K_0}{\left( \phi _0-\phi _\mathrm {crit}\right) ^{\eta }}\), the Verma–Pruess relation, (Eq. (44)), is formed. During their calibration to experimental data, they find that the exponential parameter \(\eta \) varies from 0.24 to 1.24, and that the \(\phi _\mathrm {crit}\) value has an absolute value of 0.059. They also find that the value of \(\eta \) is controlled by the reactivity of the solution that first infiltrates the sample, linking the porosity–permeability relation with the Damköhler number for the dissolution reaction. Additionally, they highlight that their experiments are limited to short timescales and that for larger timescales, the porosity–permeability relation may deviate from the initial \(\eta \) to smaller exponents. However, they also observe that \(\eta \) may increase by up to a factor of six as soon as preferential flow paths connect within the sample.
Working with the data of Luquot and Gouze (2009), Gouze and Luquot (2011) investigate the effect an increase in hydraulic radius and a decrease in tortuosity will have on the overall \(\eta \). To this end, they define \(\eta = \xi + \zeta \), where \(\xi \) represents the contribution due to the change in hydraulic radius and \(\zeta \) the contribution due to the change in tortuosity.
Gouze and Luquot (2011) show that \(\xi \) and \(\zeta \) can be determined from the image data presented in Luquot and Gouze (2009). With this in mind, it can be concluded that the high \(\eta \) Luquot and Gouze (2009) observe for the intermediate Damköhler number is mainly caused by a high value of \(\xi \), or an increasing mean hydraulic radii in the sample.
In contrast, Gouze and Luquot (2011) find that for homogeneous dissolution, the permeability increase is only due to the decrease in tortuosity (\(\eta = \zeta \)).
While experimenting with silica injection induced precipitation, Xu et al. (2004) use a Verma–Pruess based relation. While fitting to experimental values, they find a range of parameters over a series of 18 simulations: \(\eta \) between 6 and 13 combined with a \(\phi _\mathrm {crit}\) between 88 and 94% of the initial porosity for the specific injection concentration of silica compared to an \(\eta \) between 4 and 5 combined with a \(\phi _\mathrm {crit}\) between 90 and 92% for a higher injected concentration. With such a large range of exponents, the results do not encourage the use of one form to fit all systems, even when the dynamics are similar. Xu et al. (2004) conclude that at lower relative values of \(\phi _\mathrm {crit}\), a larger value for \(\eta \) should be used.
3.11.2 Modeling Studies Using the Verma–Pruess Relation
When modeling biomass growth or microbially induced calcite precipitation in loose sand, Ebigbo et al. (2010) and Ebigbo et al. (2012) use \(\eta =3\) and estimate \(\phi _\mathrm {crit} =0\), meaning that a power-law relation could be used (Eq. (40)) in Ebigbo et al. (2010, 2012). Expanding on Ebigbo et al. (2012), Hommel et al. (2013) investigate microbially induced calcite precipitation in consolidated sandstone units. \(\eta \) is kept at 3, but in this case, the \(\phi _\mathrm {crit}\) is calibrated to a value of 0.108 for the consolidated rock, resulting in a true Verma–Pruess-type relation; see Eq. (44). However, for loose sand, Hommel et al. (2015) again use \(\phi _\mathrm {crit}=0\), resulting in a Power Law (Eq. (40)). Simulating Stokes flow thorough different random sphere packings, Martys et al. (1994) find a common \(\eta =4\), when using the appropriate \(\phi _\mathrm {crit}\). They find excellent agreement for the various porous media structures in both low and high porosity regimes.
3.12 Seki–Miyazaki Relation
Another criticism of Kozeny–Carman (Sect. 3.1) and Power Law relations (Sect. 3.8) is that, although they often work for coarse-textured material, they usually do not describe phenomena in fine-textured systems. Seki and Miyazaki (2001) explain this by splitting up the reduction mechanism into biofilms and biocolony clogging. According to Seki and Miyazaki (2001), biofilms grow more effectively with coarse-textured material given the additional specific surface area, while in fine-textured materials, microbial colonies perform the majority of the clogging. As these two processes cannot be described with the same model, Seki and Miyazaki (2001) develop a new model to measure both effects, based on experiments in Cunningham et al. (1991) and Vandevivere and Baveye (1992b). Seki and Miyazaki (2001) propose the following equation to calculate the decrease in permeability due to biomass clogging:
where \(\alpha \) is the biomass volume ratio, defined by the volume of biomass per pore volume of biomass-free medium (\(\alpha =\mathrm {\frac{\text {Biomass Volume}}{\text {Clean Pore Volume}}}\)). The factor \(\tau _\mathrm {s}\) is a shape factor describing the shape of grains without any developed microbial activity. Using \(\phi = \phi _0 -\alpha \phi _0\), (Eq. (46)) can be rewritten as:
which more prominently shows the impact of the updated porosity.
3.13 Vandevivere Relation
Another criticism of the basic Power Law relation (Sect. 3.8) in the context of biomass accumulation in porous media is that they only describe permeability reduction due to biofilm growth, and ignore any plugging phenomena (Thullner 2010; Vandevivere 1995). In order to include this process, the Vandevivere relation (Eq. (50)) is developed in Vandevivere (1995). Here, the effects of biofilm growth and plugging are calculated and superimposed according to a weighting function. The relation is composed of three components, a biofilm model, a plugging model, and a weighting function.
Biofilm Model In order to maintain simplicity in the biofilm model, Vandevivere (1995) assumes a system of straight capillary tubes, resulting in a Power Law with \(\eta =2\), see Eq. (40), (Thullner 2010; Vandevivere 1995; Vandevivere et al. 1995).
Plugging Model While developing the plugging model, Vandevivere (1995) acknowledges that the permeability of the system will be somewhere between the original unplugged permeability, \(K_0\), and the permeability of the system fully plugged by biomass, \(K_\mathrm {bio}\). The permeability would then depend on how much of the system is plugged and how much is not, which is expressed via the parameter relative porosity \(B = (1-\frac{\phi }{\phi _0})\) (Vandevivere 1995). A harmonic mean (Scheidegger 1957) of \(K_0\) and \(K_\mathrm {bio}\), shown below, is then used as the basis for the plugging model:
Weighting In order to handle the weighting, Vandevivere (1995) introduces a term F[B] based on the relative porosity B. When \(B=0\), the porous media is clean, and when \(B=1\), all pores have been filled. Vandevivere (1995) argues that as B increases, the slope of the weighting function should gradually become more negative, describing the increasing biofilm thickness. As the biofilm increases in thickness, the more likely it is for parts of the biofilm to detach and plug a downstream pore throat. This point, where biofilm begins to detach and form plugs, is called the critical point of B, or \(B_\mathrm {c}\). At this point, the equation will switch from favoring the biofilm model to the plugging model. This weighting function should always be decreasing and should resemble the second half of the normal distribution (Vandevivere 1995). As a description of this shape, the critical point \(B_\mathrm {c}\) is used, as confirmed in Characklis et al. (1987).
When these three equations, (Eqs. (40), (48), and (49)), are compiled to form the final relation, the following is developed:
Here, the relation depends on the values of \(B_\mathrm {c}\) and \(K_\mathrm {bio}\), both of which are porous medium and microbial species dependent, but can be chosen with simple assumptions, or be fit to experimental data. Vandevivere (1995) uses a value of 0.1 for \(B_\mathrm {c}\), which fits well to two diverging data sets. The value of \(K_\mathrm {bio}\) must be \(\ll K_0\), and as it is as expressed in the relations as a ratio, Vandevivere (1995) approximates it with a value of \(K_\mathrm {bio} = 2.5 \times 10^{-4} K_0\) (Thullner 2010; Vandevivere 1995).
3.14 Modified Fair–Hatch Relation
Used to describe the dissolution of minerals and the corresponding increase in porosity, the Fair–Hatch relation (Bear 1972) is expanded upon and modified in Chadam et al. (1986) using dimensional analysis (Gallo et al. 1998; Lai et al. 2014). The modified Fair–Hatch relation is shown below:
Here, \(E_1\) is a parameter and \(\phi _\mathrm {end}\) is the final porosity after complete dissolution of the soluble mineral. When used for biomass accumulation or precipitation, \(\phi _\mathrm {end}\) is the initial or reference porosity and, thus, \(\phi _\mathrm {end}=\phi _0\). In comparison to precipitation and biofilm clogging, other works have determined that the rate of permeability change should be higher during dissolution (Bernabe et al. 2003; Noiriel et al. 2004; Pereira Nunes et al. 2016).
3.15 Relations Upscaled from Pore-Scale and Pore Network-Scale Simulations
Pore-scale models, or microscale models, represent the processes that occur within one single pore alone. Pore network models use a system of interconnected pore-scale models where simulated changes in each pore result in a measurable behavior of the entire network (Thullner 2010). When a series of varied simulations are developed, pore network models can help to explain the processes on larger scales.
In the case of bioclogging, mineral precipitation, or dissolution, volume change in the pore space can be modeled easily at the pore scale after certain geometric assumptions are made. To calculate the flow parameters in the changed pore space, different equations can be used. The Navier–Stokes Equation can be solved within a discretized pore geometry in order to calculate flow parameters (Dupin et al. 2001b; Lee and Koplik 2001; Thullner 2010), or more commonly, the Hagen–Poiseuille Law (Eq. (11)) can be used (e.g., Kim and Fogler 2000; Nogues et al. 2013; Rege and Fogler 1987, 1991; Suchomel et al. 1998b). Pore network models have been developed during research on biologically induced porosity change (e.g., Dupin et al. 2001b; Qin and Hassanizadeh 2015; Suchomel et al. 1998a, b; Thullner et al. 2002), and some porosity–permeability relations have been developed from these upscaled pore-scale models (e.g., Dupin et al. 2001b; Suchomel et al. 1998a, b; Thullner et al. 2002). But such pore network models have also been used to study the effects of mineral precipitation and dissolution (e.g., Bhat and Kovscek 1999; Nogues et al. 2013), combined biomass growth and mineral precipitation (e.g., Qin and Hassanizadeh 2015), or filtration of particles (e.g., Kim and Fogler 2000; Lee and Koplik 2001; Rege and Fogler 1987, 1991; Sharma and Yortsos 1987a, b). However, in many cases, no actual porosity–permeability relations are derived, but the pore network models are used to investigate existing relations, e.g., the Power Law in case of Bhat and Kovscek (1999); Nogues et al. (2013) or simply observing the permeability decrease and its dependence on porosity reduction without parametrizing it as in Dupin et al. (2001b); Qin and Hassanizadeh (2015); Suchomel et al. (1998a, b).
3.15.1 Thullner Relation
Although most analytical functions used to fit numerical data in this field take the form of a Power Law, Thullner et al. (2002) argue that the numerical data will only fit a Power Law relation (Eq. (40)) for low permeabilities. They propose two porosity–permeability relations, one assuming the biomass forms distinct, separate plugging colonies and one assuming that biomass forms a biofilm that within each pore has a constant thickness. Both relations are based on stochastically generated pore networks of 50 by 50 pores. The pore length is kept constant at 1.5 mm. The radius of the pores is distributed lognormally with an average of 30 \(\mu \)m. For each relation model, three different simulation setups are developed where the standard deviation of the pore radius varied from 1/3, to 1/2, to 2/3. However, 50 pores might not be sufficient to form an REV, as the REV for permeability is larger than the REV for, e.g., porosity (Mostaghimi et al. 2013). For each of the three simulations setups, a set of 5000 realizations are created.
They prescribe the following constraints for the general porosity–permeability relation:
-
If the porosity is not reduced, the permeability is also not reduced. If the porosity is reduced to zero, the permeability is also reduced to zero.
-
The rate of permeability change to porosity change should be zero as the reduction in porosity approaches the biomass-free porosity.
-
The second derivative of the permeability with respect to porosity should be zero between initial and fully reduced porosities.
Colony Relation
Uniformly distributed random numbers between zero and the initial pore space volume \(V_\mathrm {init}\) are selected to represent the volume of biomass. With this clogging biomass added to each pore, the permeability and pore volume are calculated.
After all zero values of permeability are removed, the remaining set of permeability and porosity pairs are split into 100 equal intervals, where averages of their parameters are taken. The resulting three sets of 100 parameter porosity–permeability pairs are then plotted, and relation curves are fit to their results. Upon a review of these three sets, the observed change in permeability is heavily dependent on the standard deviation of the pore geometry distribution. The higher the heterogeneity of the pore geometry, the more effective the same amount of biomass is in decreasing the permeability (Thullner et al. 2002).
To fit the data and constraints outlined above, Thullner et al. (2002) present the following colony-based relation:
with two parameters, a weighting factor, a, and a critical porosity, \(\phi _\mathrm {crit}\), at which the permeability becomes zero, similarly to the Verma–Pruess relation from Sect. 3.11, with the same intent of accounting for the difference between total and effective porosity (Sect. 2.4). The weighting factor, a, is recommended to range between − 1.7 and − 1.9. Thullner (2010); Thullner et al. (2002) recommend to choose a value of \(\phi _\mathrm {crit}\) between 70 and 90% of the initial, biomass-free porosity. This relation is used in Nielsen et al. (2014) to modify the water-phase relative permeability while modeling microbially enhanced oil recovery.
Biofilm Relation:
The biomass is assumed to be initially distributed as a biofilm with a uniform thickness of 1 \(\mu \)m.
Within the simulation, constant rates of growth and decay are selected, along with biomass density and yield factors, and inflow substrate concentrations. These factors are selected to achieve the maximum reduction of permeability throughout the whole pore network, and to assure that the biomass should not grow preferentially in the vicinity of the inflow to the pore network. Factors to avoid biomass detachment by shear forces are implemented.
Similar to the colony model, Thullner et al. (2002) observe that clogging primarily depends on the heterogeneity of the pore geometry. The more homogeneous the pore network is, the more pore volume reduction is required to get the same reduction in permeability. To fit the data and constraints outlined above, Thullner et al. (2002) present the following biofilm based relation:
where \(\eta \) is an exponent used as a fitting parameter, \(\phi _\mathrm {crit}\) a critical porosity similar to Eq. (44) and (52), see also Sects. 3.11 and 2.4, and \(K_\mathrm {bio}\) the permeability of a system filled with biomass. While \(\phi _\mathrm {crit}\) is a threshold porosity, in this case, the permeability for \(\phi <=\phi _\mathrm {crit}\) is not equal to zero as for Eq. (52) and (44), but equal to the permeability of a fully plugged system \(K_\mathrm {bio}\), as also used in the Vandevivere relation (Eq. (50)). For the Thullner biofilm relation, values of \(\eta \) between 1.76 and 1.81, \(K_\mathrm {bio}\) between 1.5 and 2 orders of magnitude lower than the biomass-free permeability \(K_0\), and a relative decrease between 0.7 and 0.9 for \(\phi _\mathrm {crit}\) are recommended in Thullner (2010).
4 Comparison
A reduction in the porosity should also reduce the permeability of a porous medium following some, generally nonlinear, relation. In the other direction, an increase in the porosity should generally increase the permeability as well. We have seen in the previous section that many different approaches exist, motivated by analytical, mathematical, or geometrical derivations, as well as through homogenization approaches from the pore scale to the REV scale, by pore networks, or simply by empirical fittings to data. In this section, we compare these approaches to identify their common features and the different features they offer to adapt to specific requirements. The two main characteristic features of the relations are their degree of nonlinearity and their consideration of threshold values such as a critical porosity \(\phi _\mathrm {crit}\) or a residual permeability in fully biomass-clogged systems \(K_\mathrm {bio}\), see Fig. 2.
Main characteristic features of commonly applied porosity–permeability relations, visualized using variations of the power law, Eq. (40), and modifications of it, adding a critical porosity \(\phi _\mathrm {crit}\) or a residual permeability of the fully biomass-clogged system \(K_\mathrm {bio}\)
As the selection of a porosity–permeability relation should take into account the dominant pore space modifying process (Verma and Pruess 1988), the relations presented in Sect. 3 are as well compared based on their field of application, as summarized in Table 1, the main applications being biomass accumulation, mineral dissolution, and precipitation. Combinations thereof as well as relations proposed for other processes are summarized in Table 2. Most porosity–permeability relations used for chemical alterations of porous media, such as mineral dissolution or precipitation, use the Power Law, see Eq. (40), with varying exponents or slight adaptions, such as the Verma–Pruess relation, see Eq. (44). When only precipitation is considered, the Verma–Pruess relation is the most commonly used relation, while for dissolution only or for both precipitation and dissolution, most studies use the Power Law, see Tables 1 and 2 . In contrast, relations developed specifically for bioclogging are often rather complex, although simple power or exponential laws have also been fit to or used in modeling bioclogging.
Almost all relations predict a permeability reduction by a factor of two or more for a porosity reduction of 25% of the initial porosity, the exception being the Thullner colony relation, see Eq. (52), a relation requiring a porosity reduction of approximately 40% to achieve the same reduction in permeability. It has an exceptionally low permeability reduction for up to 60% porosity reduction. On the other side of this range, there are the power-law relations with large exponents, e.g., \(\eta >10\), or the exponential relation proposed in Lappan and Fogler (1996), see Eq. (35), which predict a permeability reduction by a factor of two for even less than 10% porosity reduction. Although exponential, the Lappan–Fogler relation is quite similar to a Power Law with an exponent of \(\eta = 13\). The bulk of porosity–permeability relations fall between the Kozeny–Carman relation, see Eq. (22), predicting a higher permeability for the same porosity reduction than most other relations, and the relation proposed in Tsypkin and Woods (2005), see Eq. (36) or a power-law relation with an exponent of \(\eta = 6\), predicting a lower permeability for the same porosity reduction than most other relations.
Relations with special characteristics are the Vandevivere (Eq. (50)) and the Thullner biofilm (Eq. (53)) relations. They both consider a nonzero residual permeability given a complete plugging of the porous medium. Additionally, the Vandevivere and the Thullner colony relation (Eq. (52)) are the only relations with an inflection point in their graphs, featuring a comparatively moderate decline in permeability for low porosity reductions which then change to the hyperbolic shape of the other porosity–permeability relations. This leads to the exceptionally low permeability reduction for up to 50-60% porosity reduction for Thullner colony relation. Other special porosity–permeability relations are the Verma–Pruess (Eq. (44)) and both the Thullner biofilm and Thullner colony (Eq. (52), (53)) relations, which consider a critical porosity below which the porous medium’s permeability is reduced to zero or, in case of the Thullner biofilm relation, a residual value. Both Thullner relations have terms which are of the same type as the Verma–Pruess relation (Eq. (44)); the Biofilm relation combining the Verma–Pruess-like term with a residual permeability (Eq. (53)) and the Colony relation consisting of a weighting between two Verma–Pruess-like terms with \(\eta =3\) and 2 (Eq. (52)).
All other relations reach \(K=0\) for \(\phi =0\) and, regardless of the complexity of their equation, behave similarly to Power Laws with suitable exponents (\(2\le \eta \le 13\)). Even Verma–Pruess relations can be approximated relatively well for the first 30-40% of porosity reduction by simply using a significantly higher \(\eta \). For example, the original Verma–Pruess relation with \(\eta =1.75\) and \(\phi _\mathrm {crit}=0.35\phi _0\) is very similar to a Power Law with \(\eta = 3\) up to about a 35% porosity reduction, see Fig. 4.
5 Lessons Learned
Power Laws: A Common Choice The Power Law (Eq. (40)) is often used to describe the effects of mineral precipitation and/or dissolution on permeability, but not exclusively. It is also used for other pore morphology altering processes, see Table 1. The Verma–Pruess (Eq. (44)) and similar relations, which are extensions of the Power Law considering a critical porosity, are often used when mineral precipitation is a dominating process. This appears to be a natural choice, as \(\phi _\mathrm {crit}\) has a higher influence for small porosities and for porosities decreasing during mineral precipitation, while for large and increasing porosities, e.g., dissolution processes, the relevance of \(\phi _\mathrm {crit}\) in the mathematical expression diminishes, see Figs. 2 and 4. Thus, in the latter case the Verma–Pruess relation reduces to a Power Law.
Biomass-Induced Porosity Reduction Involves More Complexity For predicting the reduction in permeability due to growth of biomass, many different, and often rather complex, relations have been developed and published by a number of authors. This probably reflects the variability and the complexity inherent to growth of biomass in porous media. It is dependent on a variety of processes and conditions, which result specifically from the investigated experimental setup: the microbiological species involved, the adaptability of biofilms or colonies to flow-induced shear stress, or other processes considered in a given setup. Exponential relations or relations based on the Kozeny–Carman equation are common, but less often used, see Tables 1 and 2 .
There is No Fundamentally Different Behavior Between Power Laws and More Complex Relations Most complex relations do not lead to fundamentally different permeability predictions when compared to simple power-law relations with a suitable exponent, see Fig. 3. Exceptions to this general trend are a few of the porosity–permeability relations developed for biomass clogging, the Vandevivere (1995) above 40% porosity reduction and, to a very small extent, the Thullner et al. (2002) Biofilm relation, which consider a residual permeability even when the pore space is completely filled with biomass. For high porosity reductions, the Verma–Pruess relation and both Thullner et al. (2002) biofilm and colony relations also deviate from a simple power-law relation that would match them for lower porosity reductions because they consider a critical porosity.
However, this is not surprising, as most of the complex relations contain a power-law term, \(\left( \nicefrac {\phi }{\phi _0}\right) ^\eta \), see the following relations: Kozeny–Carman (Eq. (22) or (23)), Civan (Eq. (27)), Taylor Cut-and-Random-Rejoin (Eq. (31)), Vandevivere (Eq. (50)), or modified Fair–Hatch (Eq. (51)). Also, the Cubic Law for fractured porous media is equal to a Power law with \(\eta =2\). The Thullner et al. (2002) biofilm and colony relations (Eq. (53) and (52)) contain a critical porosity term as well as the Verma–Pruess relation (Eq. (44)), \(\left( \nicefrac {\phi -\phi _\mathrm {crit}}{\phi _0-\phi _\mathrm {crit}}\right) ^\eta \), which, for \(\phi \gg \phi _\mathrm {crit}\), behaves similar to a power-law term, see Fig. 4. Only the Seki–Miyazaki relation (Eq. (47)) has neither a Verma–Pruess-type nor a power-law term, but regardless of this, it still is quite similar to a Power Law with \(\eta =3\), see Fig. 3. Only the Thullner et al. (2002) colony relation (Eq. (52)) is significantly different from the other relations.
6 Recommendations
Simple Power Laws are a Default First Choice Thus, the simple power-law relations can be regarded as a first choice when modeling transport through an evolving porous medium, as these relations are easy to implement and do not require any assumptions on the specific geometry change in the pore space. The only necessary parameter is the exponent \(\eta \), which can be fit to observations. In cases where a full clogging of the pore space with a residual nonzero permeability can be expected or observed, the Vandevivere (1995) (Eq. (50)) or the Thullner et al. (2002) biofilm (Eq. (53)) relation should be considered. We note here that a nonzero permeability at zero porosity obviously implies a phenomenological approach to a permeable biofilm. Similarly, those relations are also a good choice if a relation with an inflection point is required with a transition from low initial permeability reductions to stronger decline for higher porosity reductions. In cases where the permeability is reduced to zero before the porosity is, a critical porosity, as in the Verma and Pruess (1988) or the Thullner et al. (2002) biofilm and colony relations, should be considered. But even in such cases, a Power Law can be a good approximation as long as the case-specific expected minimum porosity is sufficiently higher than the critical porosity (\(\phi \gg \phi _\mathrm {crit}\)).
More Complex Laws are Only Justified Where Detailed Process Knowledge is Available We conclude that any knowledge about the details of the processes leading to the modification of the porous medium can justify the development of a specific porosity–permeability relation for the particular process under the conditions of interest. A rigorous derivation of consistent approaches, mathematical, geometrical, from the pore or pore network scale to the flow model’s scale of consideration, is desirable. This includes a thorough understanding of the processes on the pore scale with a specific consideration of precipitation or growth patterns, intermolecular forces, interactions between biofilms and flow fields. It is necessary to develop appropriate metrics to include the changes on the pore scale in effective measures on the REV scale. Eventually, this will most likely lead to similar curves to those shown in this review, but with more confidence in the predictability of porosity–permeability relations.
Inclusion of Sub-REV-Scale Information Results in More Accurate Relations Upscaling and homogenization of available sub-REV-scale information on the porosity and the resulting permeability change will probably result in more accurate porosity–permeability relations. While obtaining the relevant pore morphological properties of a porous medium used to be difficult, especially with a good resolution in both time and space, the recent advances in imaging methods (e.g., Blunt et al. 2013; Cnudde and Boone 2013; Wildenschild and Sheppard 2013) enable precise quantification of such parameters and their change, facilitating the development and use of more precise, process-specific relations to estimate the REV-scale permeability. Particularly, the combination of imaging and direct, pore-scale, or pore network modeling using the pore geometry obtained from the images, as done, e.g., in Pereira Nunes et al. (2016) or Menke et al. (2015), will enable to investigate porosity–permeability relations in much greater detail and to hopefully develop process-specific relations or verify previously developed relations and the parameters used. This increase in confidence in predicting permeability changes would be a great step forward for modeling flow and transport in (bio-)geochemically altered porous media. At some point, this might even enable an a priori choice of a suitable porosity–permeability relation depending on the processes and conditions.
References
Aharonov, E., Tenthorey, E., Scholz, C.H.: Precipitation sealing and diagenesis: 2. Theoretical analysis. J. Geophys. Res.: Solid Earth 103(B10), 23969–23981 (1998). https://doi.org/10.1029/98JB02230
Al-Khulaifi, Y., Lin, Q., Blunt, M.J., Bijeljic, B.: Reaction rates in chemically heterogeneous rock: coupled impact of structure and flow properties studied by X-ray microtomography. Environ. Sci. Technol. 51(7), 4108–4116 (2017). https://doi.org/10.1021/acs.est.6b06224
Amaefule, J.O., Altunbay, M., Tiab, D., Kersey, D.G., Keelan, D.K.: Enhanced reservoir description: using core and log data to identify hydraulic (flow) units and predict permeability in uncored intervals/wells. Soc. Pet. Eng. (1993). https://doi.org/10.2118/26436-MS
Bacci, G., Korre, A., Durucan, S.: Experimental investigation into salt precipitation during \(\text{ CO }_2\) injection in saline aquifers. Energy Procedia 4, 44504456 (2011). https://doi.org/10.1016/j.egypro.2011.02.399
Barkouki, T.H., Martinez, B.C., Mortensen, B.M., Weathers, T.S., De Jong, J.D., Ginn, T.R., Spycher, N.F., Smith, R.W., Fujita, Y.: Forward and inverse bio-geochemical modeling of microbially induced calcite precipitation in half-meter column experiments. Transp. Porous Media 90(1), 2339 (2011). https://doi.org/10.1007/s11242-011-9804-z
Battistelli, A., Calore, C., Pruess, K.: Analysis of salt effects on the depletion of fractured reservoir rocks. In: World Geothermal Congress Florence. Proceedings, pp. 1613–1618 (1995)
Bear, J.: Dynamics of Fluids in Porous Media. Elsevier, Amsterdam (1972)
Bear, J.: Dynamics of Fluids in Porous Media. Elsevier, Amsterdam (1988)
Bernabe, Y., Mok, U., Evans, B.: Permeability–porosity relationships in rocks subjected to various evolution processes. Pure Appl. Geophys. 160(5–6), 937960 (2003). https://doi.org/10.1007/PL00012574
Bertrand, J.C., Caumette, P., Lebaron, P., Matheron, R., Normand, P., Sime-Ngando, T.: Environmental Microbiology: Fundamentals and Applications. Springer, Berlin (2015)
Bhat, S.K., Kovscek, A.R.: Statistical network theory of silica deposition and dissolution in diatomite. In Situ 23(1), 2153 (1999)
Blunt, M.J., Bijeljic, B., Dong, H., Gharbi, O., Iglauer, S., Mostaghimi, P., Paluszny, A., Pentland, C.: Pore-scale imaging and modelling. Adv. Water Resour. 51(Supplement C), 197–216 (2013). https://doi.org/10.1016/j.advwatres.2012.03.003
Bolton, E.W., Lasaga, A.C., Rye, D.M.: Long-term flow/chemistry feedback in a porous medium with heterogenous permeability; kinetic control of dissolution and precipitation. Am. J. Sci. 299(1), 1–68 (1999). https://doi.org/10.2475/ajs.299.1.1
Carles, P., Egermann, P., Lenormand, R., Lombard, J.: Low permeability measurements using steady-state and transient methods. In: International Symposium of the Society of Core Analysts (2007)
Carman, P.C.: Fluid flow through granular beds. Trans. Inst. Chem. Eng. 15, 150166 (1937)
Carrier, W.D.: Goodbye, Hazen; Hello, Kozeny-Carman. J. Geotech. Geoenviron. Eng. 129(11), 1054–1056 (2003). https://doi.org/10.1061/(ASCE)1090-0241(2003)129:11(1054)
Carroll, S., Hao, Y., Smith, M., Sholokhova, Y.: Development of scaling parameters to describe \(\text{ CO }_2\)-rock interactions within Weyburn-Midale carbonate flow units. Int. J. Greenh. Gas Control 16(Supplement 1), S185–S193 (2013). https://doi.org/10.1016/j.ijggc.2012.12.026
Chadam, J., Hoff, D., Merino, E., Ortoleva, P., Sen, A.: Reactive infiltration instabilities. IMA J. Appl. Math. 36(3), 207 (1986)
Characklis, W., Cunningham, A., Escher, A., Crawford, D.: Biofilms in Porous media. In: Proceedings of the International Symposium of Biofouled Aquifers: Prevention and Restoration p 5778 (1987)
Characklis, W.G., Marshall, K.C.: Biofilms. Wiley, New York (1990)
Childs, E.C., Collis-George, N.: The permeability of porous materials. Proc. R. Soc. Lond. A 201(1066), 392405 (1950). https://doi.org/10.1098/rspa.1950.0068
Civan, F.: A multi-purpose formation damage model. Soc. Pet. Eng. (1996). https://doi.org/10.2118/31101-MS
Civan, F.: Predictability of porosity and permeability alterations by geochemical and geomechanical rock and fluid interactions. Soc. Pet. Eng. (2000). https://doi.org/10.2118/58746-MS
Civan, F.: Scale effect on porosity and permeability: kinetics, model, and correlation. AIChE J. 47(2), 271–287 (2001). https://doi.org/10.1002/aic.690470206
Clement, T.P., Hooker, B.S., Skeen, R.S.: Macroscopic models for predicting changes in saturated porous media properties caused by microbial growth. Ground Water 34(5), 934942 (1996). https://doi.org/10.1111/j.1745-6584.1996.tb02088.x
Cnudde, V., Boone, M.: High-resolution X-ray computed tomography in geosciences: a review of the current technology and applications. Earth-Science Reviews 123(Supplement C):1 – 17, https://doi.org/10.1016/j.earscirev.2013.04.003 (2013)
Coln, C.F., Oelkers, E.H., Schott, J.: Experimental investigation of the effect of dissolution on sandstone permeability, porosity, and reactive surface area1. Geochim. Cosmochim. Acta 68(4), 805817 (2004). https://doi.org/10.1016/j.gca.2003.06.002
Cunningham, AB., Bouwer, EJ., Characklis, WG.: Biofilms. Wiley, New York, chap Biofilms in Porous Media, pp. 697–732 (1990)
Cunningham, A.B., Characklis, W.G., Abedeen, F., Crawford, D.: Influence of biofilm accumulation on porous media hydrodynamics. Environ. Sci. Technol. 25, 13051311 (1991). https://doi.org/10.1021/es00019a013
Cuthbert, MO., McMillan, LA., Handley-Sidhu, S., Riley, MS., Tobler, DJ., Phoenix, VR.: A field and modeling study of fractured rock permeability reduction using microbially induced calcite precipitation. Environ. Sci. Technol. 47(23):13637–13643. https://doi.org/10.1021/es402601g (2013)
Daccord, G., Touboul, E., Lenormand, R.: Chemical dissolution of a porous medium: limits of the fractal behaviour. Geoderma 44(2), 159–165 (1989). https://doi.org/10.1016/0016-7061(89)90025-6
Daccord, G., Lenormand, R., Litard, O.: Chemical dissolution of a porous medium by a reactive fluidI: model for the wormholing phenomenon. Chem. Eng. Sci. 48(1), 169–178 (1993a). https://doi.org/10.1016/0009-2509(93)80293-Y
Daccord, G., Litard, O., Lenormand, R.: Chemical dissolution of a porous medium by a reactive fluidII: convection versus reaction, behavior diagram. Chem. Eng. Sci. 48(1), 179–186 (1993b). https://doi.org/10.1016/0009-2509(93)80294-Z
Davis, A.C., Patterson, B.M., Grassi, M.E., Robertson, B.S., Prommer, H., McKinley, A.J.: Effects of increasing acidity on metal(loid) bioprecipitation in groundwater: column studies. Environ. Sci. Technol. 41(20), 7131–7137 (2007). https://doi.org/10.1021/es071122v
Do, W.: Effect of applied pressure on the conductivity, porosity and permeability of sandstones. J. Pet. Technol. 10(11), 430–432 (1958). https://doi.org/10.2118/1081-G
Dobson, P.F., Kneafsey, T.J., Sonnenthal, E.L., Spycher, N., Apps, J.A.: Experimental and numerical simulation of dissolution and precipitation: implications for fracture sealing at Yucca Mountain, Nevada. J. Contam. Hydrol. 62, 459–476 (2003). https://doi.org/10.1016/S0169-7722(02)00155-9
Doyen, P.M.: Permeability, conductivity, and pore geometry of sandstone. J. Geophys. Res.: Solid Earth 93(B7), 77297740 (1988). https://doi.org/10.1029/JB093iB07p07729
Dupin, H.J., McCarty, P.L.: Impact of colony morphologies and disinfection on biological clogging in porous media. Environ. Sci. Technol. 34(8), 15131520 (2000). https://doi.org/10.1021/es990452f
Dupin, H.J., Kitanidis, P.K., McCarty, P.L.: Pore-scale modeling of biological clogging due to aggregate expansion: a material mechanics approach. Water Resour. Res. 37(12), 29652979 (2001a)
Dupin, H.J., Kitanidis, P.K., McCarty, P.L.: Simulations of two-dimensional modeling of biomass aggregate growth in network models. Water Resour. Res. 37(12), 29812994 (2001b)
Ebigbo, A., Helmig, R., Cunningham, A.B., Class, H., Gerlach, R.: Modelling biofilm growth in the presence of carbon dioxide and water flow in the subsurface. Adv. Water Resour. 33(7), 762781 (2010). https://doi.org/10.1016/j.advwatres.2010.04.004
Ebigbo, A., Phillips, A.J., Gerlach, R., Helmig, R., Cunningham, A.B., Class, H., Spangler, L.H.: Darcy-scale modeling of microbially induced carbonate mineral precipitation in sand columns. Water Resour. Res. 48(7), W07519 (2012). https://doi.org/10.1029/2011WR011714
Egermann, P., Lenormand, R., Longeron, D.G., Zarcone, C.: A fast and direct method of permeability measurements on drill cuttings. Soc. Pet. Eng. 8, 269–275 (2005). https://doi.org/10.2118/77563-PA
Ellis, B.R., Peters, C.A.: 3D mapping of calcite and a demonstration of its relevance to permeability evolution in reactive fractures. Adv. Water Resour. 95(Supplement C), 246–253 (2016). https://doi.org/10.1016/j.advwatres.2015.07.023
Flukiger, F., Bernard, D.: A new numerical model for pore scale dissolution of calcite due to \(\text{ CO }_2\) saturated water flow in 3D realistic geometry: principles and first results. Chem. Geol. 265(1), 171–180 (2009). https://doi.org/10.1016/j.chemgeo.2009.05.004
Fredd, C.N., Fogler, H.S.: Influence of transport and reaction on wormhole formation in porous media. AIChE J. 44(9), 1933–1949 (1998). https://doi.org/10.1002/aic.690440902
Gadd, G.M., Pan, X.: Biomineralization, bioremediation and biorecovery of toxic metals and radionuclides. Geomicrobiol J. 33(3–4), 175–178 (2016). https://doi.org/10.1080/01490451.2015.1087603
Gallo, Y.L., Bildstein, O., Brosse, E.: Coupled reaction-flow modeling of diagenetic changes in reservoir permeability, porosity and mineral compositions. J. Hydrol. 209(1), 366–388 (1998). https://doi.org/10.1016/S0022-1694(98)00183-8
Garing, C., Gouze, P., Kassab, M., Riva, M., Guadagnini, A.: Anti-correlated porosity–permeability changes during the dissolution of carbonate rocks: experimental evidences and modeling. Transp. Porous Media 107(2), 595–621 (2015). https://doi.org/10.1007/s11242-015-0456-2
Ghommem, M., Zhao, W., Dyer, S., Qiu, X., Brady, D.: Carbonate acidizing: modeling, analysis, and characterization of wormhole formation and propagation. J. Pet. Sci. Eng. 131(Supplement C), 18–33 (2015). https://doi.org/10.1016/j.petrol.2015.04.021
Gogoi, B., Dutta, N., Goswami, P., Mohan, T.K.: A case study of bioremediation of petroleum-hydrocarbon contaminated soil at a crude oil spill site. Adv. Environ. Res. 7(4), 767–782 (2003). https://doi.org/10.1016/S1093-0191(02)00029-1
Golfier, F., Zarcone, C., Bazin, B., Lenormand, R., Lasseux, D., Quintard, M.: On the ability of a Darcy-scale model to capture wormhole formation during the dissolution of a porous medium. J. Fluid Mech. 457, 213254 (2002). https://doi.org/10.1017/S0022112002007735
Golfier, F., Bazin, B., Lenormand, R., Quintard, M.: Core-scale description of porous media dissolution during acid injection—Part I: theoretical development. Comput. Appl. Math. 23, 173194 (2004)
Gouze, P., Luquot, L.: X-ray microtomography characterization of porosity, permeability and reactive surface changes during dissolution. J. Contam. Hydrol. 120–121, 45–55 (2011). https://doi.org/10.1016/j.jconhyd.2010.07.004
Hao, Y., Smith, M., Sholokhova, Y., Carroll, S.: \(\text{ CO }_{2}\)-induced dissolution of low permeability carbonates. Part II: numerical modeling of experiments. Adv. Water Resour. 62, 388–408 (2013). https://doi.org/10.1016/j.advwatres.2013.09.009
Hazen A (1892) Some physical properties of sands and gravels, with special reference to their use in filtration. In: 24th Annual Rep, Massachusetts State Board of Health Pub. Doc. No. 34:539556
Hoefner, M.L., Fogler, H.S.: Pore evolution and channel formation during flow and reaction in porous media. AIChE J. 34(1), 45–54 (1988)
Hommel, J., Cunningham, A.B., Helmig, R., Ebigbo, A., Class, H.: Numerical investigation of microbially induced calcite precipitation as a leakage mitigation technology. Energy Procedia 40C, 392–397 (2013). https://doi.org/10.1016/j.egypro.2013.08.045
Hommel, J., Lauchnor, E.G., Phillips, A.J., Gerlach, R., Cunningham, A.B., Helmig, R., Ebigbo, A., Class, H.: A revised model for microbially induced calcite precipitation: improvements and new insights based on recent experiments. Water Resour. Res. 51(5), 36953715 (2015). https://doi.org/10.1002/2014WR016503
Ives, K., Pienvichitr, V.: Kinetics of the filtration of dilute suspensions. Chem. Eng. Sci. 20(11), 965973 (1965). https://doi.org/10.1016/0009-2509(65)80094-X
James, A.B.C.R.S.H.: Subsurface biofilm barriers for the containment and remediation of contaminated groundwater. Bioremediat. J. 7(3–4), 151–164 (2003). https://doi.org/10.1080/713607982
Kalia, N., Balakotaiah, V.: Modeling and analysis of wormhole formation in reactive dissolution of carbonate rocks. Chem. Eng. Sci. 62(4), 919–928 (2007). https://doi.org/10.1016/j.ces.2006.10.021
Kang, Q., Zhang, D., Chen, S., He, X.: Lattice Boltzmann simulation of chemical dissolution in porous media. Phys. Rev. E 65(036), 318 (2002). https://doi.org/10.1103/PhysRevE.65.036318
Kim, D.S., Fogler, H.S.: Biomass evolution in porous media and its effects on permeability under starvation conditions. Biotechnol. Bioeng. 69(1), 4756 (2000)
Knapp, R., Civan, F.: Modeling growth and transport of microorganisms in porous media. IMACS, f 3, 676679 (1988)
Koh, CJ., Dagenais, PC., Larson, DC., Murer, AS.: Permeability damage in diatomite due to in-situ silica dissolution/precipitation. In: Proceedings of the SPE/DOE Tenth Symposium on Improved Oil Recovery (SPE 35394) (1996)
Kozeny, J.: Über kapillare Leitung des Wassers im Boden. Sitzungsber Akad Wiss Wien 136(2a), 271306 (1927)
Lai, K.H., Chen, J.S., Liu, C.W., Yang, S.Y.: Effect of permeability–porosity functions on simulated morphological evolution of a chemical dissolution front. Hydrol. Process. 28(1), 1624 (2014). https://doi.org/10.1002/hyp.9492
Lappan, R.E., Fogler, H.S.: Reduction of porous media permeability from in situ Leuconostoc mesenteroides growth and dextran production. Biotechnol. Bioeng. 50(1), 615 (1996)
Lasaga, A.C.: Chemical kinetics of water–rock interactions. J. Geophys. Res.: Solid Earth 89(B6), 4009–4025 (1984). https://doi.org/10.1029/JB089iB06p04009
Lee, J., Koplik, J.: Network model for deep bed filtration. Phys. Fluids 13(5), 1076 (2001)
Lenormand, R., Bauget, F., Ringot, G.: Permeability measurement on small rock samples (2010)
Lenormand, R., Fonta, O.: Advances in measuring porosity and permeability from drill cuttings. In: Society of Petroleum Engineers. https://doi.org/10.2118/111286-MS (2007)
Li, L., Steefel, C.I., Yang, L.: Scale dependence of mineral dissolution rates within single pores and fractures. Geochim. Cosmochim. Acta 72(2), 360377 (2008). https://doi.org/10.1016/j.gca.2007.10.027
Lichtner, P.C.: Continuum model for simultaneous chemical reactions and mass transport in hydrothermal systems. Geochim. Cosmochim. Acta 49(3), 779–800 (1985). https://doi.org/10.1016/0016-7037(85)90172-3
Luhmann, A.J., Kong, X.Z., Tutolo, B.M., Garapati, N., Bagley, B.C., Saar, M.O., Seyfried, W.E.: Experimental dissolution of dolomite by \(\text{ CO }_2\)-charged brine at 100C and 150bar: evolution of porosity, permeability, and reactive surface area. Chem. Geol. 380, 145–160 (2014). https://doi.org/10.1016/j.chemgeo.2014.05.001
Luquot, L., Gouze, P.: Experimental determination of porosity and permeability changes induced by injection of \(\text{ CO }_2\) into carbonate rocks. Chem. Geol. 265(12), 148159 (2009). https://doi.org/10.1016/j.chemgeo.2009.03.028
Luquot, L., Rodriguez, O., Gouze, P.: Experimental characterization of porosity structure and transport property changes in limestone undergoing different dissolution regimes. Transp. Porous Media 101(3), 507–532 (2014). https://doi.org/10.1007/s11242-013-0257-4
MacQuarrie, K.T.B., Mayer, K.U.: Reactive transport modeling in fractured rock: a state-of-the-science review. Earth Sci. Rev. 72(3–4), 189227 (2005). https://doi.org/10.1016/j.earscirev.2005.07.003
Mangane, P.O., Gouze, P., Luquot, L.: Permeability impairment of a limestone reservoir triggered by heterogeneous dissolution and particles migration during \(\text{ CO }_2\)-rich injection. Geophys. Res. Lett. 40(17), 4614–4619 (2013). https://doi.org/10.1002/grl.50595
Marshall, T.J.: A relation between permeability and size distribution of pores. J. Soil Sci. 9(1), 18 (1958). https://doi.org/10.1111/j.1365-2389.1958.tb01892.x
Marsily, G.D.: Quantitative Hydrogeology: Groundwater Hydrology for Engineers. Academic Press, San Diego (1986)
Martys, N.S., Torquato, S., Bentz, D.P.: Universal scaling of fluid permeability for sphere packings. Phys. Rev. E 50, 403–408 (1994). https://doi.org/10.1103/PhysRevE.50.403
Mayer, K.U., Frind, E.O., Blowes, D.W.: Multicomponent reactive transport modeling in variably saturated porous media using a generalized formulation for kinetically controlled reactions. Water Resour. Res. 38(9), 13-1–13-21 (2002). https://doi.org/10.1029/2001WR000862
Menke, H., Andrew, M., Blunt, M., Bijeljic, B.: Reservoir condition imaging of reactive transport in heterogeneous carbonates using fast synchrotron tomography: effect of initial pore structure and flow conditions. Chem. Geol. 428, 15–26 (2016). https://doi.org/10.1016/j.chemgeo.2016.02.030
Menke, H., Bijeljic, B., Blunt, M.: Dynamic reservoir-condition microtomography of reactive transport in complex carbonates: effect of initial pore structure and initial brine pH. Geochim. Cosmochim. Acta 204, 267–285 (2017). https://doi.org/10.1016/j.gca.2017.01.053
Menke, H.P., Bijeljic, B., Andrew, M.G., Blunt, M.J.: Dynamic three-dimensional pore-scale imaging of reaction in a carbonate at reservoir conditions. Environ. Sci. Technol. 49(7), 4407–4414 (2015). https://doi.org/10.1021/es505789f
Millington, R.J., Quirk, J.P.: Permeability of porous solids. Trans. Faraday Soc. 57(8), 12001207 (1961). https://doi.org/10.1039/tf9615701200
Mitchell, A.C., Phillips, A.J., Schultz, L., Parks, S., Spangler, L.H., Cunningham, A.B., Gerlach, R.: Microbial CaCO\(_3\) mineral formation and stability in an experimentally simulated high pressure saline aquifer with supercritical CO\(_2\). Int. J. Greenhouse Gas Control 15, 86–96 (2013). https://doi.org/10.1016/j.ijggc.2013.02.001
Mostaghimi, P., Blunt, M.J., Bijeljic, B.: Computations of absolute permeability on micro-CT images. Math. Geosci. 45(1), 103–125 (2013). https://doi.org/10.1007/s11004-012-9431-4
Mualem, Y.: A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 12(3), 513522 (1976). https://doi.org/10.1029/WR012i003p00513
Nielsen, S.M., Nesterov, I., Shapiro, A.A.: Simulations of microbial-enhanced oil recovery: adsorption and filtration. Transp. Porous Media 102(2), 227259 (2014). https://doi.org/10.1007/s11242-014-0273-z
Nogues, J.P., Fitts, J.P., Celia, M.A., Peters, C.A.: Permeability evolution due to dissolution and precipitation of carbonates using reactive transport modeling in pore networks. Water Resour. Res. 49(9), 60066021 (2013)
Noiriel, C.: Resolving time-dependent evolution of pore-scale structure, permeability and reactivity using X-ray microtomography. Rev. Mineral. Geochem. 80(1), 247–285 (2015). https://doi.org/10.2138/rmg.2015.80.08
Noiriel, C., Gouze, P., Bernard, D.: Investigation of porosity and permeability effects from microstructure changes during limestone dissolution. Geophys. Res. Lett. 31(24), L24603. https://doi.org/10.1029/2004GL021572 (2004)
Noiriel, C., Bernard, D., Gouze, P., Thibault, X.: Hydraulic properties and microgeometry evolution accompanying limestone dissolution by acidic water. Oil Gas Sci. Technol. 60(1), 177–192 (2005). https://doi.org/10.2516/ogst:2005011
Noiriel, C., Gouze, P., Mad, B.: 3D analysis of geometry and flow changes in a limestone fracture during dissolution. J. Hydrol. 486, 211–223 (2013). https://doi.org/10.1016/j.jhydrol.2013.01.035
Noiriel, C., Steefel, C.I., Yang, L., Bernard, D.: Effects of pore-scale precipitation on permeability and flow. Adv. Water Resour. 95(Supplement C), 125–137 (2016). https://doi.org/10.1016/j.advwatres.2015.11.013
Okubo, T., Matsumoto, J.: Effect of infiltration rate on biological clogging and water quality changes during artificial recharge. Water Resour. Res. 15(6), 15361542 (1979). https://doi.org/10.1029/WR015i006p01536
Ott, H., Oedai, S.: Wormhole formation and compact dissolution in single- and two-phase \(\text{ CO }_2\)-brine injections. Geophys. Res. Lett. 42(7), 2270–2276 (2015). https://doi.org/10.1002/2015GL063582
Pandey, S., Chaudhuri, A., Kelkar, S., Sandeep, V., Rajaram, H.: Investigation of permeability alteration of fractured limestone reservoir due to geothermal heat extraction using three-dimensional thermo-hydro-chemical (THC) model. Geothermics 51, 46–62 (2014). https://doi.org/10.1016/j.geothermics.2013.11.004
Pandey, S., Chaudhuri, A., Rajaram, H., Kelkar, S.: Fracture transmissivity evolution due to silica dissolution/precipitation during geothermal heat extraction. Geothermics 57, 111–126 (2015). https://doi.org/10.1016/j.geothermics.2015.06.011
Pape, H., Clauser, C., Iffland, J.: Permeability prediction based on fractal porespace geometry. Geophysics 64(5), 14471460 (1999). https://doi.org/10.1190/1.1444649
Patir, N., Cheng, H.S.: An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication. J. Lubr. Technol. 100(1), 12–17 (1978). https://doi.org/10.1115/1.3453103
Peng, X., Zhou, H., Yao, H., Li, J., Tang, S., Jiang, L., Wu, Z.: Microbe-related precipitation of iron and silica in the Edmond deep-sea hydrothermal vent field on the Central Indian Ridge. Chin. Sci. Bull. 52(23), 3233–3238 (2007). https://doi.org/10.1007/s11434-007-0523-3
Pereira Nunes, J.P., Blunt, M.J., Bijeljic, B.: Pore-scale simulation of carbonate dissolution in micro-CT images. J. Geophys. Res.: Solid Earth 121(2), 558576 (2016). https://doi.org/10.1002/2015JB012117
Phillips, A.J., Gerlach, R., Lauchnor, E.G., Mitchell, A.C., Cunningham, A.B., Spangler, L.H.: Engineered applications of ureolytic biomineralization: a review. Biofouling 29(6), 715733 (2013a). https://doi.org/10.1080/08927014.2013.796550
Phillips, A.J., Lauchnor, E.G., Eldring, J.J., Esposito, R., Mitchell, A.C., Gerlach, R., Cunningham, A.B., Spangler, L.H.: Potential CO\(_2\) leakage reduction through biofilm-induced calcium carbonate precipitation. Environ. Sci. Technol. 47, 142149 (2013b). https://doi.org/10.1021/es301294q
Phillips, A.J., Gerlach, R., Hiebert, R., Kirksey, J., Spangler, L.H., Esposito, R., Cunningham, A.B.: Biological influences in the subsurface: a method to seal fractures and reduce permeability with microbially-induced calcite precipitation. In: American Rock Mechanics Association 49th Annual Meeting Proceedings (2015)
Phillips, A.J., Cunningham, A.B., Gerlach, R., Hiebert, R., Hwang, C., Lomans, B.P., Westrich, J., Mantilla, C., Kirksey, J., Esposito, R., Spangler, L.: Fracture sealing with microbially-induced calcium carbonate precipitation: a field study. Environ. Sci. Technol. 50, 41114117 (2016). https://doi.org/10.1021/acs.est.5b05559
Poms, V., Bazin, B., Golfier, F., Zarcone, C., Lenormand, R., Quintard, M.: On the use of upscaling methods to describe acid injection in carbonates. In: Society of Petroleum Engineers https://doi.org/10.2118/71511-MS (2007)
Qin, C.Z., Hassanizadeh, S.M.: Pore-network modeling of solute transport and biofilm growth in porous media. Transp. Porous Media 110(3), 345–367 (2015). https://doi.org/10.1007/s11242-015-0546-1
Rege, S.D., Fogler, H.S.: Network model for straining dominated particle entrapment in porous media. Chem. Eng. Sci. 42(7), 15531564 (1987)
Rege, S.D., Fogler, H.S.: Development of radial models for formation damage in porous media. Chem. Eng. Commun. 108(1), 6783 (1991)
Rötting, T.S., Luquot, L., Carrera, J., Casalinuovo, D.J.: Changes in porosity, permeability, water retention curve and reactive surface area during carbonate rock dissolution. Chem. Geol. 403, 86–98 (2015). https://doi.org/10.1016/j.chemgeo.2015.03.008
Sahimi, M., Gavalas, G.R., Tsotsis, T.T.: Statistical and continuum models of fluid-solid reactions in porous media. Chem. Eng. Sci. 45(6), 1443–1502 (1990). https://doi.org/10.1016/0009-2509(90)80001-U
Scheidegger, A.E.: The physics of flow through porous media. Univ. of Toronto Pr., Toronto (1957)
Schneider, F., Potdevin, J., Wolf, S., Faille, I.: Mechanical and chemical compaction model for sedimentary basin simulators. Tectonophysics 263(1), 307–317 (1996). https://doi.org/10.1016/S0040-1951(96)00027-3
Seki, K., Miyazaki, T.: A mathematical model for biological clogging of uniform porous media. Water Resour. Res. 37(12), 29952999 (2001)
Sharma, M.M., Yortsos, Y.C.: A network model for deep bed filtration processes. AIChE J. 33(10), 16441653 (1987a)
Sharma, M.M., Yortsos, Y.C.: Fines migration in porous media. AIChE J. 33(10), 16541662 (1987b)
Smith, M.M., Sholokhova, Y., Hao, Y., Carroll, S.A.: \(\text{ CO }_{2}\)-induced dissolution of low permeability carbonates. Part I: characterization and experiments. Adv. Water Resour. 62, 370–387 (2013). https://doi.org/10.1016/j.advwatres.2013.09.008
Steefel, C., AC L.: Chemical modeling of aqueous systems II, American Chemical Society, Washington, chap evolution of dissolution patterns: permeability change due to coupled flow and reaction, pp. 212–225. https://doi.org/10.1021/bk-1990-0416.ch016 (1990)
Steefel, C., Depaolo, D., Lichtner, P.: Reactive transport modeling: an essential tool and a new research approach for the Earth sciences. Earth Planet. Sci. Lett. 240(3–4), 539558 (2005). https://doi.org/10.1016/j.epsl.2005.09.017
Steefel, C.I.: Geochemical Kinetics and Transport, pp. 545–589. Springer, New York (2008). https://doi.org/10.1007/978-0-387-73563-4_11
Steefel, C.I., Cappellen, P.V.: A new kinetic approach to modeling water-rock interaction: the role of nucleation, precursors, and Ostwald ripening. Geochim. Cosmochim. Acta 54(10), 2657–2677 (1990). https://doi.org/10.1016/0016-7037(90)90003-4
Steefel, C.I., Lasaga, A.C.: A coupled model for transport of multiple chemical species and kinetic precipitation/dissolution reactions with application to reactive flow in single phase hydrothermal systems. Am. J. Sci. 294(5), 529–592 (1994). https://doi.org/10.2475/ajs.294.5.529
Steefel, C.I., Lichtner, P.C.: Diffusion and reaction in rock matrix bordering a hyperalkaline fluid-filled fracture. Geochim. Cosmochim. Acta 58(17), 3595–3612 (1994). https://doi.org/10.1016/0016-7037(94)90152-X
Steefel, C.I., Lichtner, P.C.: Multicomponent reactive transport in discrete fractures: I. Controls on reaction front geometry. J. Hydrol. 209(1), 186–199 (1998). https://doi.org/10.1016/S0022-1694(98)00146-2
Steefel, C.I., Maher, K.: Fluid–rock interaction: a reactive transport approach. Rev. Mineral. Geochem. 70(1), 485532 (2009). https://doi.org/10.2138/rmg.2009.70.11
Steefel, C.I., Appelo, C.A.J., Arora, B., Jacques, D., Kalbacher, T., Kolditz, O., Lagneau, V., Lichtner, P.C., Mayer, K.U., Meeussen, J.C.L., Molins, S., Moulton, D., Shao, H., imnek, J., Spycher, N., Yabusaki, S.B., Yeh, G.T.: Reactive transport codes for subsurface environmental simulation. Comput. Geosci. 19(3), 445478 (2015a). https://doi.org/10.1007/s10596-014-9443-x
Steefel, C.I., Yabusaki, S.B., Mayer, K.U.: Reactive transport benchmarks for subsurface environmental simulation. Comput. Geosci. 19(3), 439443 (2015b). https://doi.org/10.1007/s10596-015-9499-2
Suchomel, B.J., Chen, B.M., Allen, M.B.: Macroscale properties of porous media from a network model of biofilm processes. Transp. Porous Media 31(1), 3966 (1998a)
Suchomel, B.J., Chen, B.M., Allen, M.B.: Network model of flow, transport and biofilm effects in porous media. Transp. Porous Media 30(1), 123 (1998b)
Taylor, S.W., Jaff, P.R.: Biofilm growth and the related changes in the physical properties of a porous medium: 1. Experimental investigation. Water Resources Research 26(9), 21532159 (1990a). https://doi.org/10.1029/WR026i009p02153
Taylor, S.W., Jaff, P.R.: Substrate and biomass transport in a porous-medium. Water Resour. Res. 26(9), 21812194 (1990b). https://doi.org/10.1029/WR026i009p02181
Taylor, S.W., Milly, P.C.D., Jaff, P.R.: Biofilm growth and the related changes in the physical properties of a porous medium: 2. Permeability. Water Resour. Res. 26(9), 21612169 (1990). https://doi.org/10.1029/WR026i009p02161
Thullner, M.: Comparison of bioclogging effects in saturated porous media within one- and two-dimensional flow systems. Ecol. Eng. 36(2), 176196 (2010). https://doi.org/10.1016/j.ecoleng.2008.12.037
Thullner, M., Zeyer, J., Kinzelbach, W.: Influence of microbial growth on hydraulic properties of pore networks. Transp. Porous Media 49(1), 99122 (2002). https://doi.org/10.1023/A:1016030112089
Truckenbrodt, E.: Fluidmechanik. Springer, Berlin (1996)
Tsypkin, G.G., Woods, A.W.: Precipitate formation in a porous rock through evaporation of saline water. J. Fluid Mech. 537, 3553 (2005). https://doi.org/10.1017/S0022112005005124
Vandevivere, P.: Bacterial clogging of porous media: a new modelling approach. Biofouling 8(4), 281291 (1995). https://doi.org/10.1080/08927019509378281
Vandevivere, P., Baveye, P.: Effect of bacterial extracellular polymers on the saturated hydraulic conductivity of sand columns. Appl. Environ. Microbiol. 58(5), 1690–8 (1992a)
Vandevivere, P., Baveye, P.: Relationship between transport of bacteria and their clogging efficiency in sand columns. Appl. Environ. Microbiol. 58(8), 2523–30 (1992b)
Vandevivere, P., Baveye, P., de Lozada, D.S., DeLeo, P.: Microbial clogging of saturated soils and aquifer materials: evaluation of mathematical models. Water Resour. Res. 31(9), 21732180 (1995). https://doi.org/10.1029/95WR01568
Verma, A., Pruess, K.: Thermohydrological conditions and silica redistribution near high-level nuclear wastes emplaced in saturated geological formations. J. Geophys. Res.: Solid Earth 93(B2), 11591173 (1988). https://doi.org/10.1029/JB093iB02p01159
van Paassen, L.A., Ghose, R., van der Linden, T.J.M., van der Star, W.R.L., van Loosdrecht, M.C.M.: Quantifying biomediated ground improvement by ureolysis: large-scale biogrout experiment. J. Geotech. Geoenviron. Eng. 136(12), 1721–1728 (2010). https://doi.org/10.1061/(ASCE)GT.1943-5606.0000382
van Wijngaarden, W.K., Vermolen, F.J., Meurs, G.A.M., Vuik, C.: Modelling biogrout: a new ground improvement method based on microbial-induced carbonate precipitation. Transp. Porous Media 87(2), 397420 (2011). https://doi.org/10.1007/s11242-010-9691-8
van Wijngaarden, W.K., Vermolen, F.J., Meurs, G.A.M., Vuik, C.: A mathematical model for Biogrout. Comput. Geosci. 17(3), 463478 (2013). https://doi.org/10.1007/s10596-012-9316-0
Wildenschild, D., Sheppard, A.P.: X-ray imaging and analysis techniques for quantifying pore-scale structure and processes in subsurface porous medium systems. Adv. Water Resour. 51(Supplement C), 217–246 (2013). https://doi.org/10.1016/j.advwatres.2012.07.018
Xie, M., Mayer, K.U., Claret, F., Alt-Epping, P., Jacques, D., Steefel, C., Chiaberge, C., Simunek, J.: Implementation and evaluation of permeability-porosity and tortuosity-porosity relationships linked to mineral dissolution-precipitation. Comput. Geosci. 19(3), 655671 (2015). https://doi.org/10.1007/s10596-014-9458-3
Xu, T., Ontoy, Y., Molling, P., Spycher, N., Parini, M., Pruess, K.: Reactive transport modeling of injection well scaling and acidizing at Tiwi field, Philippines. Geothermics 33(4), 477–491 (2004)
Yasuhara, H., Neupane, D., Hayashi, K., Okamura, M.: Experiments and predictions of physical properties of sand cemented by enzymatically-induced carbonate precipitation. Soils Found. 52(3), 539549 (2012). https://doi.org/10.1016/j.sandf.2012.05.011
Yeh, G.T., Tripathi, V.S.: A critical evaluation of recent developments in hydrogeochemical transport models of reactive multichemical components. Water Resour. Res. 25(1), 93108 (1989). https://doi.org/10.1029/WR025i001p00093
Zhang, L., Soong, Y., Dilmore, R., Lopano, C.: Numerical simulation of porosity and permeability evolution of Mount Simon sandstone under geological carbon sequestration conditions. Chem. Geol. 403, 112 (2015). https://doi.org/10.1016/j.chemgeo.2015.03.014
Zhu, W., David, C., Tf, Wong: Network modeling of permeability evolution during cementation and hot isostatic pressing. J. Geophys. Res.: Solid Earth 100(B8), 1545115464 (1995). https://doi.org/10.1029/95JB00958
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Hommel, J., Coltman, E. & Class, H. Porosity–Permeability Relations for Evolving Pore Space: A Review with a Focus on (Bio-)geochemically Altered Porous Media. Transp Porous Med 124, 589–629 (2018). https://doi.org/10.1007/s11242-018-1086-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-018-1086-2