Abstract
We undertake a formal derivation of a linear poro-thermo-elastic system within the framework of quasi-static deformation. This work is based upon the well-known derivation of the quasi-static poroelastic equations (also known as the Biot consolidation model) by homogenization of the fluid-structure interaction at the microscale. We now include energy, which is coupled to the fluid-structure model by using linear thermoelasticity, with the full system transformed to a Lagrangian coordinate system. The resulting upscaled system is similar to the linear poroelastic equations, but with an added conservation of energy equation, fully coupled to the momentum and mass conservation equations. In the end, we obtain a system of equations on the macroscale accounting for the effects of mechanical deformation, heat transfer, and fluid flow within a fully saturated porous material, wherein the coefficients can be explicitly defined in terms of the microstructure of the material. For the heat transfer we consider two different scaling regimes, one where the Péclet number is small, and another where it is unity. We also establish the symmetry and positivity for the homogenized coefficients.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The theory of consolidation of soils goes back to the work of Terzaghi (1944) and Biot (1941, 1972, 1977), and since then numerous authors have contributed to the field, extending the models to different situations and providing more rigorous results for the equations. Today, this field is better known as ‘poroelasticity’, and is of great importance in a range of different engineering disciplines, such as reservoir engineering and biomechanics. Notable contributions are Burridge and Keller (1981), where a formal upscaling leading to the quasi-static Biot-model was undertaken, and the book Sanchez-Palencia (1980) where a rigorous derivation can be found. In Clopeau et al. (2001) and Gilbert and Mikelić (2000) the rigorous derivation of a dynamic Biot-model corresponding to different choices of scalings of the microstructure is undertaken, and in Ferrin and Mikelić (2003) the case of an inviscid fluid filling the pore space is treated. In Lévy (1979) elastic wave propagation is considered. Additional cases and results can also be found in the references of these works.
The motivation for the present article is to better understand how thermal stresses in the solid structure of a porous medium are influenced by the forces exerted on the pore walls by the fluid. We consider a porous medium on the macroscopic scale such that the continuum hypothesis is valid, and derive the pointwise continuum model by upscaling the fluid-structure interaction at the microscopic scale where the complex geometry is resolved. We shall focus on a natural system, such as the subsurface, where flow velocity, mechanical strain, and temperature changes are small. This also allows for linearization of the constitutive laws of thermoelasticity, as well as linearization of the fluid-structure coupling conditions. Topics such as nonlinear deformation and high flow rates are beyond the scope of this article. Previously, the homogenization of a similar model problem was undertaken by Lee and Mei (1997), but with a different scaling, and with the fine-scale model defined in terms of Eulerian coordinates. This approach leads to relatively strict conditions on the allowable deformations. It also makes a direct comparison of models difficult. In Bringedal et al. (2016) a formal upscaling of non-isothermal reactive flow in porous media was undertaken, but the solid matrix was assumed rigid. In Eden and Muntean (2017) homogenization of a fully coupled thermoelasticity problem was undertaken, but not in the context of fluid-structure interaction. In the book Coussy (1995) there is also a section on linear thermo-poroelasticity, where the macroscale equations are derived using principles from continuum mechanics and thermodynamics. While finalizing this work, we have been made aware that a similar derivation has been undertaken simultaneously by the authors van Duijn et al. Their work is currently under review and exists as a preprint (Van Duijn et al. 2017).
Our microscale model consists of a fluid-structure interaction model, and energy conservation for both phases (the solid and fluid), where we scale the fluid-structure equations corresponding to the biphasic macroscopic behavior of the system (i.e., fluid pressure in balance with the normal forces coming from the solid matrix, and small viscous forces in the fluid). A rigorous study of this situation in the isothermal case can be found in Clopeau et al. (2001). Different scalings are of course possible, and for different values of the reference quantities, the homogenization process may result in vastly different macroscale models. A discussion around the characterization of the behavior of porous media according to the values of such reference quantities can be found in Auriault (1991). Regarding the energy conservation, we consider two different scaling regimes; one corresponding to a Péclet number of order one, giving a (nonlinear) convective term in the upscaled energy conservation equation, and one corresponding to a small Péclet number, resulting in no convective term, giving a fully linear upscaled system. Depending on the flow rate and the thermal conductive properties of the fluid, both may be relevant.
The upscaling procedure is done via the formal two-scale asymptotic expansion method of homogenization. This is a well-known technique for qualitatively assessing the structure of the upscaled equations. For a detailed explanation of this method we refer to the books Hornung (2012) and Cioranescu and Donato (2000). For an accurate physical model, the values of the homogenized coefficients should be confirmed by experiments, as the asymptotic expansion method only provides formulas for these in the case of simple microscale geometries. Our justification for the upscaled model comes from the similarity with the isothermal poroelastic equations, and the analogy to the thermoelasticity equations in mechanics.
2 The Pore-Scale Model
2.1 Notation
A short remark on the notation used in this article is in order. We denote by : the scalar product of two second-order tensors, i.e., \({{\mathrm{\mathbf {A}}}}: {{\mathrm{\mathbf {B}}}}= \sum _{i,j=1}^3A_{ij} B_{ij}\), and by \(\otimes \) the vector outer product, which given two vectors produce a second-order tensor, i.e., \((u \otimes v)_{ij} = u_iv_j\). Note also that we shall reserve the use of bold fonts for tensors of second order or more.
2.2 Presentation of the Equations
In this and the next section we present the governing equations to be used throughout the rest of this article. This will include a brief discussion of the constitutive relations of linear thermoelasticity for an anisotropic solid, relevant for the present work. For a detailed derivation of the equations of linear thermoelasticity, we refer to the book Silhavy (2013). We also mention Pabst (2005) where a more compact presentation is given.
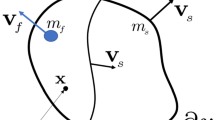
Our physical domain is \(\varOmega = (0,L)^3\), which consists of a solid skeleton, \(\varOmega _s\), and a fluid filled void space, \(\varOmega _f\), where the internal boundary between the solid and void parts is denoted by \(\varGamma \), i.e., in the reference configuration we have: \(\varOmega = \varOmega _s \cup \varOmega _f \cup \varGamma \) where \(\varOmega _s \cap \varOmega _f = \varnothing \), and \(\varGamma = \partial \varOmega _s \cap \partial \varOmega _f\). We let \(J = (0,T_{\text {end}}]\) be the time interval, where \(T_{\text {end}} > 0\) is the final time. We denote by \(x = (x_1,x_2,x_3)\) the coordinates of the reference configuration, and by t the time coordinate.
We let w be the displacement vector of the solid, defined on the reference configuration, and assume it can be decomposed as \(w(x,t) = \hat{w}(x,t) + w_0(t)\), where \(\hat{w}\) corresponds to the local deformation, and \(w_0\) corresponds to a rigid body motion. We let the v be the flow velocity of the fluid, defined on the current configuration, which we then can write as \(v(x+\hat{w},t) = \hat{v}(x+\hat{w},t) + \dfrac{\mathrm{d}w_0}{\mathrm{d}t}(t)\), using the reference coordinates.
Given a body force b, the linear momentum balance for an elastic solid is given by
where \(\rho _s\) is the solid density. In the non-isothermal case, the constitutive equation for the stress is
where \(T_s\) is the temperature distribution of the solid, and \({{\mathrm{\mathbf {F}}}}\) is the deformation gradient.
Denoting by \(c_s\) the specific heat capacity of the solid, the conservation of energy is given by
where \(h_s\) is the heat flux within the solid.
In the pore space, the flow is governed by the Navier–Stokes equations
with the mass conservation
where \(\rho _f\) is the fluid density, p is the fluid pressure, and \(\mu \) is the fluid viscosity.
Since there is no heat generation from dissipative effects in the fluid, we use a simple convection-diffusion equation for the energy conservation
where \(T_f\) is the temperature distribution of the fluid, \(c_f\) is the specific heat capacity of the fluid, and \(h_f\) is the heat flux within the fluid.
We now turn to the fluid-structure coupling conditions at the internal interface and denote by \(\nu \) the outward unit normal field of \(\varOmega _f\) (i.e., pointing into the solid).
By Newton’s third law we must have a balance of normal forces coming from both sides
where \(\mathbf {I}\) denotes the \(3 \times 3\) identity tensor.
The no-flow condition at the internal interface now takes the form
Finally, continuity of heat flux and continuity of temperature at the internal interface gives (due to our assumption of the two phases being in local thermodynamic equilibrium)
and
2.3 Constitutive Equations
We let \(({{\mathrm{\mathbf {F}}}}_0, \theta _0)\) denote the reference values of the deformation gradient and the temperature of the medium (considered here to be uniform, i.e., constant), and assume that for all \(t \in J\) the deviations from this reference state are small. Within this framework, a physical linearization of the constitutive equations is justified (see Pabst (2005) for more details). The deformation gradient \({{\mathrm{\mathbf {F}}}}\), however, is still a nonlinear measure of deformation; hence, we assume in addition that the displacement gradients, or more precisely the local deformations, \(\hat{w}\), are small such that \({{\mathrm{\mathbf {F}}}}\) can be considered approximately identity. This amounts to a geometric linearization of the kinematic measures, and consequently, the first Piola–Kirchoff stress and the Cauchy stress tensors coincide. The strains in the solid are therefore given by the symmetric gradient of the displacements, i.e., \({{\mathrm{\mathbf {e}}}}(w) = \frac{1}{2}(\nabla w + (\nabla w)^T)\). The constitutive equation for the stress, Eq. (2) then takes the form
which is a generalized Hooke’s law, extended to include thermal effects. The stiffness tensor of the material (or more precisely, the referential tensor of isothermal elasticities) is given by \({{\mathrm{\mathbf {C}}}}= (C_{ijkl})_{i,j,k,l = 1}^3\), which satisfies \(C_{ijkl} = C_{klij} = C_{jikl} = C_{ijlk}\), and the thermal stress tensor (or the referential coefficient of thermal stress) is \({{\mathrm{\mathbf {M}}}}= (M_{ij})_{i,j=1}^3\), satisfying \(M_{ij} = M_{ji}\). In order to have symmetric positive definite coefficients in the upscaled problem, the same must be true for \({{\mathrm{\mathbf {C}}}}\) and \({{\mathrm{\mathbf {M}}}}\), i.e.,
Further, we assume the heat fluxes within the solid and the fluid obey Fourier’s law of heat conduction, i.e.,
where \({{\mathrm{\mathbf {K}}}}_s = (K^s_{ij})_{i,j=1}^3\) and \({{\mathrm{\mathbf {K}}}}_f = (K^f_{ij})_{i,j=1}^3\) are the thermal conductivity tensors of the solid and fluid, respectively, which are assumed to be both symmetric and positive definite, i.e., \(K^{s,f}_{ij} = K^{s,f}_{ji}\), and \({{\mathrm{\mathbf {K}}}}_{s,f} {{\mathrm{\mathbf {x}}}}\cdot {{\mathrm{\mathbf {x}}}}> 0, \forall {{\mathrm{\mathbf {x}}}}\in \mathbb {R}^3 \setminus \{0\}\).
Within this completely linearized framework (physically and geometrically), the densities, \(\rho _s\) and \(\rho _f\), are constants taking the values of the reference densities. We assume in addition that the fluid viscosity, \(\mu \), is a constant.
We note that in a consistent linear theory, the material coefficients cannot depend on the current temperature, but only on the (uniform) reference temperature, \(\theta _0\).
2.4 The Domain
Before undertaking the scaling analysis, we provide a more detailed description of the domain, specifically that it is made up of a periodic repetition of a single pore, such that the geometry of the whole solid skeleton is determined by the geometry inside a singe microscopic cell. This is a valid assumption since we are modeling a fine grained porous media with microstructure on a scale much smaller than the continuum scale of interest. Thus, although the material is heterogenous on the microscale, it appears locally homogenous on the macroscale. We follow Allaire (1989) in this description.
Let l be a typical pore size, and let L be the size of the macroscale domain, and define as usual \(\varepsilon = l/L\). We let \(\varOmega ^\varepsilon = \frac{1}{L} \varOmega \) be the dimensionless domain, which now is \(\varOmega ^\varepsilon = (0,1)^3\), such that \(\varOmega _s^\varepsilon \) and \(\varOmega _f^\varepsilon \) are the corresponding dimensionless solid and void parts, respectively, and \(\varGamma ^\varepsilon \) is the corresponding dimensionless internal interface. We continue with the notation J for the time interval; keeping in mind time is now also dimensionless.
Let \(Y = (0,1)^3\) be the rescaled unit cube in \(\mathbb {R}^3\), consisting of a solid part, \(Y_s \subset \bar{Y}\), which is a closed subset of strictly positive measure, and a void space, \(Y_f = Y \setminus Y_s\), which is an open and connected subset of strictly positive measure. We let now \(\varGamma = \partial Y_s \cap \partial Y_f\) denote the internal interface of the unit pore cell, and assume the configuration is such that \(\varGamma \) is a smooth surface. We make a periodic repetition of \(Y_s\) over \(\mathbb {R}^3\), and set \(Y_{s,k}^\varepsilon = \varepsilon (Y_s + k)\), where \(k \in \mathbb {Z}^3\). Let \( K = \{ k \in \mathbb {Z}^3 : Y_{s,k}^\varepsilon \subset \bar{\varOmega }^\varepsilon \}\), such that \(\bar{\varOmega }_s^\varepsilon = \bigcup _{k\in K} Y_{s,k}^\varepsilon \) is the solid skeleton, and \(\varOmega _f^\varepsilon = \varOmega ^\varepsilon \setminus \varOmega _s^\varepsilon \) is the fluid filled void space. The fluid/solid internal interface can now be written \(\varGamma ^\varepsilon = \partial \varOmega _s^\varepsilon \setminus \partial \varOmega ^\varepsilon \). By construction, both \(\varOmega _s^\varepsilon \) and \(\varOmega _f^\varepsilon \) are now connected sets of strictly positive measure, and \(\varGamma ^\varepsilon \) is a smooth surface.

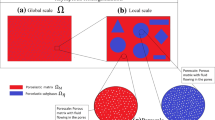
(Picture from Mikelić and Wheeler 2012)
Example of geometry inside unit cell.
The epsilon-superscript on \(\varOmega ^\varepsilon \) implies the implicit dependence of the domain on both length scales, l and L, but later when we impose the homogenization ansatz, we separate these two scales, and let the size of the domain become arbitrarily large (that is, we let \(\varepsilon \rightarrow 0\)). Then, behind each infinitesimal point x (seen from the macro scale) there is a pore cell with its own geometry which can only be seen by the fast variable y. When this scale separation is done, we shall denote the macro scale domain simply by \(\varOmega \), which is no longer possible to separate into solid and void parts because the porous structure is now seen as a single (fictitious) uniform material. An example of a pore cell geometry which satisfies the above assumptions is shown in Fig. 1.
2.5 Scaling Analysis
In this section, we introduce dimensionless variables and scale the system according to the quasi-static biphasic macroscale behavior (see Auriault (1991) for more details). In short, this means the fluid pressure should be of the same order as the normal stress coming from the elastic matrix and that the viscous forces are small.
The modeling of fluid and elastic solid structure interaction is in general challenging, since for an elastic solid Lagrangian coordinates are the preferred reference frame, while for the fluid it is the Eulerian one. Thus, when coupling the two processes at the mutual interface, one needs to take into account the movement of the interface itself, as seen in Sect. 2.2. For more details on this type of modeling we refer to Iliev et al. (2008). In the present work we shall avoid this difficulty by linearizing the fluid-structure coupling conditions, and thereby transform the fluid problem into Lagrangian coordinates based on the material deformation.
We let \(l = 10^{-5}\) m and \(L = 10\) m, which results in \(\varepsilon = l/L = 10^{-6}\). With a slight abuse of notation we write now the dimensional variables with a tilde, and the new dimensionless quantities in the same way as before
\(\begin{array}{llllll} \tilde{x} = Lx, &{} \quad \tilde{t} = \tau t, &{}\quad \tilde{\hat{w}} = l \hat{w}, &{}\quad \tilde{w}_0 = W_{\text {ref}} w_0, &{}\quad \tilde{\hat{v}} = V_{\text {ref}} v,&{} \\ \tilde{T_s} = T_{\text {diff}} T_s, &{}\quad \tilde{T_f} = T_{\text {diff}} T_f, &{}\quad \tilde{p} = P_{\text {ref}} p, &{}\quad \tilde{\mu } = \mu _{\text {ref}} \mu , &{} &{} \\ \tilde{{{\mathrm{\mathbf {C}}}}} = C_{\text {ref}} {{\mathrm{\mathbf {C}}}}, &{}\quad \tilde{{{\mathrm{\mathbf {M}}}}} = M_{\text {ref}} {{\mathrm{\mathbf {M}}}}, &{}\quad \tilde{{{\mathrm{\mathbf {K}}}}}_f = K_{\text {ref}}^f {{\mathrm{\mathbf {K}}}}_f, &{}\quad \tilde{{{\mathrm{\mathbf {K}}}}}_s = K_{\text {ref}}^s {{\mathrm{\mathbf {K}}}}_s, &{} &{} \\ \end{array}\)
where we choose the time scale, \(\tau = \frac{L}{V_{\text {ref}}}\), as the characteristic transport time. As we consider a system in equilibrium with only natural convection, we set \(\tau = 10^4\) s, which is the time it takes a fluid particle to traverse the distance L. This gives the reference velocity as \(V_{\text {ref}} = 10^{-3}\) m/s. This is a realistic value, as flow velocities coming from natural convection in a geological permeable layer can be as low as 1 m/year Wood and Hewett (1982). We let the size of the rigid displacements be \(W_{\text {ref}} = 1\) m, while the local deformation is no larger than the pore size. We set the characteristic temperature as the maximum difference between the reference temperature and the current temperature as \(T_{\text {diff}} = 10\) K. Linearizing the fluid/solid coupling conditions then amounts to discarding terms of \(\hat{w} \cdot \nabla v\) and \(\hat{w} \cdot \nabla T_f\) and higher order ones (this can be seen by expanding the fluid side about \(x + \hat{w} = x\)). Thus, since the spatial differential operators are acting with respect to the scale L, we are introducing errors of the order \( \varepsilon V_{\text {ref}} = 10^{-9}\) m/s and \(\varepsilon T_{\text {diff}}= 10^{-5}\) K, which we deem negligible.
The table below shows reference values for the coefficients, in the case of water and sandstone at room temperature (we note that some are only approximate, but good enough for our purposes, as we are only interested in identifying terms which differ by an order of \(\varepsilon \) or more) (Table 1).
The balance of contact forces at the interface, Eq. (7), in dimensionless variables reads
Due to the biphasic scaling regime, we have \(P_{\text {ref}} \sim C_{\text {ref}} \varepsilon \sim M_{\text {ref}} T_{\text {diff}} \sim 10^{5} N/m^2\). Dividing by this factor, we get \(\frac{V_{\text {ref}} \mu _{\text {ref}}}{L P_{\text {ref}}} \sim \mathcal {O}(\varepsilon ^2)\) in front of the viscous term. Thus, we can simplify the above equation and get the dimensionless form of Eq. (7) as
The momentum equation for the solid (1) in dimensionless form is
Multiplying with \(\frac{L}{P_{\text {ref}}}\), we get a new dimensionless body force (still denoted b) and the dimensionless constants \(\frac{\rho _s lL}{\tau ^2 P_{\text {ref}}} \sim \mathcal {O}(\varepsilon ^2) \) and \(\frac{\rho _s W_{\text {ref}} L}{\tau ^2 P_{\text {ref}}} \sim \mathcal {O}(\varepsilon ) \) multiplying the acceleration terms. Thus, we discard these and get the dimensionless form of Eq. (1) as
The dimensionless form of the momentum equation for the fluid, (4), is
Multiplying by \(\frac{L}{P_{\text {ref}}}\), we again get a new dimensionless body force (still denoted by b) and the dimensionless constants \(\frac{\rho _f L^2}{\tau ^2 P_{\text {ref}}} \sim \mathcal {O}(\varepsilon )\) and \(\frac{\rho _f W_{\text {ref}}L}{\tau ^2 P_{\text {ref}}} \sim \mathcal {O}(\varepsilon )\) multiplying the inertial terms. Multiplying the viscous term we have \( \frac{V_{\text {ref}} \mu _{\text {ref}}}{L P_{\text {ref}}} \sim \mathcal {O}(\varepsilon ^2)\). Thus, we discard the inertial terms and get the dimensionless form of Eq. (4) as
The mass conservation equation for the fluid, Eq. (5) and the no-flow condition at the boundary, Eq. (8), in dimensionless variables are
and
respectively.
We now turn to the energy conservation equations. The one for the fluid, Eq. (6), in dimensionless variables reads as
where \(\tau _D = \tau / \varepsilon \) is the characteristic heat diffusion time. Multiplying by \(\frac{L^2}{K_{\text {ref}}^f}\), we get the Péclet number in front of the convective term, which in this case is given by \(Pe = \frac{ c_f \rho _f V_\text {ref} L}{K_{\text {ref}}^f} \sim \frac{c_f \rho _f W_{\text {ref}} L}{\tau K^f_{\text {ref}}} \sim \mathcal {O}(1)\), meaning heat is transported within the fluid by convection and diffusion at an approximately equal rate. In the following, we shall also look at the case \(Pe = \mathcal {O}(\varepsilon )\), such that heat is mainly transported within the fluid through diffusion. This could be realized, e.g., in a system with a lower flow velocity or a fluid with a higher thermal conductivity. However, when we undertake the upscaling procedure, it will become clear that this choice can be seen just as a special case of the more general \(Pe \sim \mathcal {O}(1)\). In the concluding section we will however present the homogenized model corresponding to both choices of scaling. In front of the time derivative term, we get the dimensionless constant \(\frac{\rho _f c_f L^2}{\tau _D K_{\text {ref}}^f} \sim \mathcal {O}(\varepsilon )\). Thus, we discard this term and get the dimensionless form of Eq. (6) as
In the dissipative term of the energy conservation equation for the solid, Eq. (3), we neglect the contribution from the mechanical stress (which is second order in the gradient of w), and assume the heat generation from the thermal stress can be approximated by using a constant value for the temperature difference, i.e., \(-{{\mathrm{\mathbf {M}}}}(T_s - \theta _0) : {{\mathrm{\mathbf {e}}}}(\partial _t w) \approx -T_{\text {diff}} {{\mathrm{\mathbf {M}}}}: {{\mathrm{\mathbf {e}}}}(\partial _t w)\) (see, e.g., Kupradze et al. 1979). Thus, we get Eq. (3) in dimensionless variables as
We multiply by \(\frac{L^2}{K_{\text {ref}}^s}\), and get the dimensionless constants, \(\frac{\rho _s c_s L^2}{\tau _D K^s_{\text {ref}}} \sim \mathcal {O}(\varepsilon )\), multiplying the time derivative term, and \(\frac{M_{\text {ref}} l L}{\tau K^s_{\text {ref}}} \sim \mathcal {O}(1)\), multiplying the dissipative term. Thus, we discard the time derivative term and can write Eq. (24) as
The reference values of the thermal conductivities of the two phases can be regarded as approximately the same order (i.e., \(K_{\text {ref}}^f \sim K_{\text {ref}}^s\)), and we therefore write the dimensionless form of Eqs. (9) and (10) as
and
respectively.
2.6 The Complete Dimensionless Pore-Scale Model
For convenience, we summarize the dimensionless equations at the microscale below:
We impose periodic boundary conditions on the outer boundary (i.e., \(\partial \varOmega ^\varepsilon \)) and omit initial conditions since they are not important for the homogenization procedure. Note also that we have included an epsilon-superscript on the dependent variables to emphasize the implicit dependence on both the slow and fast scales.
Finally, we mention that the upscaling of Eqs. (28a) (without the thermal stress term), (28b), (28c), (28d), and (28e), leads to the quasi-static poroelastic equations as described in, e.g., Biot (1941) and Coussy (1995).
3 Two-Scale Asymptotic Expansions
3.1 Homogenization Ansatz
We now undertake the separation of scales and introduce the homogenization ansatz for the unknowns
Note that we now have an added dependence on the spatial variable \(y \in Y\), in which all terms of the above expansions are Y-periodic due to the scaling and the periodic arrangement of the porous structure. This is the key step in the two-scale asymptotic expansion method of homogenization. For a detailed review of this method and its applications to porous media, we refer to the books Hornung (2012) and Cioranescu and Donato (2000).
Since \(y = x/\varepsilon \), we reformulate the differential operators according to the chain rule, i.e., \(\nabla = \nabla _x + \varepsilon ^{-1} \nabla _y, \ \) and \( \ {{\mathrm{\mathbf {e}}}}(\cdot ) = {{\mathrm{\mathbf {e}}}}_x(\cdot ) + \varepsilon ^{-1} {{\mathrm{\mathbf {e}}}}_y(\cdot )\).
We now insert the asymptotic expansions into the governing equations and discard all therms of \(\mathcal {O}(\varepsilon )\) or higher. We furthermore assume that the governing equations of the last section are applicable in the product domain. We start with Eq. (28a) for the elastic solid structure
The conservation of momentum and mass for the fluid, Eqs. (28b) and (28c), yields
and
At the internal interface, continuity of contact forces and continuity of displacement velocity, Eqs. (28d) and (28e), gives
and
The energy conservation equations for the solid and fluid, Eqs. (28f) and (28g), yields
and
At the internal interface, continuity of energy and temperature, Eqs. (28h) and (28i), gives
and
It is evident from the above equations that at the lowest order, the displacement, pressure, and temperature has no y-dependence, so we write
However, as seen from Eqs. (30) and (31), at the lowest order, there is still a y-dependence in the fluid velocity.
3.2 The Flow
We now consider Eq. (30) at order \(\mathcal {O}(\varepsilon ^0)\), Eq. (31) at order \(\mathcal {O}(\varepsilon ^{-1})\), and the boundary condition, Eq. (33) at order \(\mathcal {O}(\varepsilon ^0)\), which gives the problem
Note that since \(\nabla _y v^0 = 0\) for \(y \in Y_f\), we have: \(\nabla _y \cdot 2{{\mathrm{\mathbf {e}}}}_y(v^0) = \varDelta _y v^0\). By defining \(q = v^0 - \partial _t w^0\), we can rewrite the above problem as
which is the well-known cell problem in the homogenization of the filtration through rigid porous media, see, e.g., Hornung (2012) pp. 16–18. By using the identities \(b = \sum _{j=1}^3 b_j e_j\), and \(\nabla _x p^0 = \sum _{j=1}^3 \dfrac{\partial p}{\partial x_j} e_j\), where \(b_j\) is the j’th component of the body force, and \(\{e_j\}_{j=1,2,3}\) the canonical basis of \(\mathbb {R}^3\), we can solve for q and \(p^1\) as follows
where \(\varLambda ^j\) and \(\varPi ^j\) (\(\varLambda ^j(y) \in \mathbb {R}^3, \varPi ^j(y) \in \mathbb {R}\)), are determined by the following cell problems (for \(j = 1,2,3\))
We integrate over \(Y_f\) and obtain the Darcy flux
where the effective coefficient, \({{\mathrm{\mathbf {K}}}}^H\), (known as the permeability tensor) is given by:
We get a similar expression for the average of \(v^0\)
It can be shown that the tensor \({{\mathrm{\mathbf {K}}}}^H\) is symmetric and positive definite. We refer to Mikelić (1994) for a proof.
By using the expressions for \(q^0\) and \(p^1\), we also obtain the following which will be useful later
3.3 Momentum Conservation
From Eqs. (29) and (32) at order \(\mathcal {O}(\varepsilon ^{-1})\) we obtain
Using the tensor outer product (denoted “\(\otimes \)”), we now make use of the following identity
such that we can use \(\dfrac{\partial w^0_i}{\partial x_j}\) as scalars in the expression for \(w^1\)
where the functions \(U^{ij}\), V, and W, (\(U^{ij}(y), V(y), W(y) \in \mathbb {R}^3\)), are determined by the following cell problems (for \(i,j = 1,2,3\))
and
and
We now continue with the solid at order \(\mathcal {O}(\varepsilon ^0)\), where we make use of the expression (46) from the last section. We thus obtain the following problem
Integrating the right hand side of the first equation over \(Y_s\), using also Eq. (42a), yields
Using the expression for \(w^1\), Eq. (48), we get for the left hand side
Putting the two sides together gives the upscaled momentum equation
where (for \(i,j,k,l, = 1,2,3\))
The effective tensors \({{\mathrm{\mathbf {A}}}}^H\) and \({{\mathrm{\mathbf {B}}}}^H\) are symmetric and positive definite. We refer to Sanchez-Palencia (1980) for a proof. That \(\mathbf {U}^H\) is symmetric and positive definite is shown the same way as for \({{\mathrm{\mathbf {B}}}}^H\), except that it now relies on the same properties for \({{\mathrm{\mathbf {M}}}}\).
3.4 Mass Conservation
In order to derive the upscaled mass conservation equation, we take terms of \(\mathcal {O}(\varepsilon ^0)\) from Eq. (31), together with \(\mathcal {O}(\varepsilon ^1)\) terms from the boundary condition (33), and obtain the following problem
Integrating the left hand side of the first equation over \(Y_f\), and using the expression for \(w^1\), Eq. (48), yields
where
Integrating the right hand side of (56a) over \(Y_f\), and using the expression for the average of \(v^0\), Eq. (45), yields
Putting the two sides together, we obtain the upscaled mass conservation equation
By testing with W in the cell problems (50) it is easily shown that \(G^H > 0\), i.e.,
The identification \(\mathbf {D}^H = {{\mathrm{\mathbf {B}}}}^H\) is shown by testing first with \(U^{ij}\) in the cell problem (50) to obtain
and on the other hand, by testing with W in cell problem (49)
Using this, we can rewrite Eq. (57) as
3.5 Energy Conservation
In this section we derive the upscaled energy conservation equation.
We consider the terms of order \(\mathcal {O}(\varepsilon ^{-1})\) from Eqs. (34), (35) and (36), and obtain the following problem
Using the identity \(\nabla _x T^0 = \sum _{j=1}^3 \dfrac{\partial T^0}{\partial x_j}e_j\), we can solve for \(T_f^1\) and \(T_s^1\) as
where \(\theta _f^j\) and \(\theta _s^j\) (\(\theta _f^j(y), \theta _s^j(y) \in \mathbb {R}\)) are determined by (for \(j = 1,2,3\))
By defining
due to the boundary condition, and using the properties of \({{\mathrm{\mathbf {K}}}}_s\) and \({{\mathrm{\mathbf {K}}}}_f\), we can write the more convenient problem
Continuing to the next order, \(\mathcal {O}(\varepsilon ^0)\), we obtain the problem
Integrating the first equation over \(Y_f\), and using the expressions for \(T_f^1\) and the average of \(v^0\), Eqs. (63) and (45), together with the boundary conditions (62d) and (39a) yields
Integrating the second equation over \(Y_s\), using also the expressions for \(T_s^1\) and \(w^1\), Eqs. (63) and (48), yields
Since the left hand sides of the two above equations are equal, we put them together and obtain the upscaled energy conservation equation
where (for \(i,j = 1,2,3\))
Again, some properties of the coefficients can be established. By testing with V in the cell problems (50) we obtain
The identification \(\mathbf {R}^H = - \,\mathbf {U}^H\) can also be shown by testing first with \(U^{ij}\) in the cell problem (50) to obtain
and then with V in the cell problem (49)
Further, we can also show \(N^H = -E^H\), by testing first with V in the cell problem (51)
and with W in the cell problem (51)
Lemma 1
\({{\mathrm{\varvec{\varTheta }}}}^H\) and \({{\mathrm{\varvec{\varXi }}}}^H\) are symmetric and positive definite.
Proof
Test with \(\theta ^i\) in the j’th cell problem (65), and by \(\theta ^j\) in the i’th problem to obtain
and
Thus, we can write \({{\mathrm{\varvec{\varTheta }}}}^H\) as:
and it follows that \({{\mathrm{\varvec{\varTheta }}}}^H\) is symmetric. For the positive definiteness, observe that for nonnegative \(\alpha _{1,2,3} \in \mathbb {R}\) not all equal to zero we have
That \({{\mathrm{\varvec{\varXi }}}}^H\) is symmetric and positive definite is shown in the same way. \(\square \)
We can now rewrite the upscaled energy conservation equation as
4 Summary
4.1 The Upscaled Quasi-static Thermo-poroelastic System
We now summarize the upscaled equations derived in the previous sections. We omit all superscripts in the variables, subscripts in the differential operators (with the understanding they are now all taken with respect to the slow variable x), and introduce a more familiar notation for the coefficients, similar to what is commonly used in the literature on the quasi-static poroelastic equations:
where \({{\mathrm{\varvec{\alpha }}}}\) is the Biot–Willis constant, \(c_0\) is the specific storage coefficient, and \({{\mathrm{\mathbf {A}}}}\) is the effective elastic moduli, containing the elastic coefficients of the porous medium.
Thus, we write the upscaled system as:
Compared to the linear poroelastic equations, we see that the stress in the momentum Eq. (72b) now has an additional linear dependency on the temperature of the medium, i.e., \({{\mathrm{\varvec{\sigma }}}}= {{\mathrm{\varvec{\sigma }}}}(w,p,T) = {{\mathrm{\mathbf {A}}}}{{\mathrm{\mathbf {e}}}}(w) - {{\mathrm{\varvec{\alpha }}}}p - {{\mathrm{\varvec{\beta }}}}T\). This is completely analogous to the linear thermoelastic equations in mechanics, see, e.g., Pabst (2005). The homogenized tensor \({{\mathrm{\varvec{\beta }}}}\) can be interpreted as an upscaled thermal stress coefficient, giving the induced thermal stress coming from a unit temperature gradient. In the mass conservation Eq. (72c) we see that the porosity (denoted by \(\eta \)) is also linearly dependent on the temperature, i.e., \(\eta = \eta (w,p,T) = c_0p - b_0 T + \nabla \cdot {{\mathrm{\varvec{\alpha }}}}w\). In other words, the amount of fluid that can be injected into an arbitrary fixed control volume is now given by: \(c_0p - b_0T\), where the homogenized coefficient \(b_0\) can be interpreted as a thermal expansion coefficient.
It remains to discuss the energy conservation Eq. (72d). If we had used the different scaling corresponding to a small Péclet number, i.e., \(Pe \sim \mathcal {O}(\varepsilon )\), the dimensionless energy conservation equation for the fluid at the microscale, Eq. (28g), would take the form:
Then, after separating the scales, the terms: \(\varepsilon (\frac{\partial T_f^\varepsilon }{\partial t} + \partial _t u^\varepsilon \cdot \nabla T_f^\varepsilon )\) give no contribution to the \(\mathcal {O}(\varepsilon ^{-1})\)-problem, and for the \(\mathcal {O}(\varepsilon ^{0})\)-problem, we only retain the term: \(\partial _t u^0 \cdot \nabla _y T^0\), which is evidently equal to zero. Thus, the upscaled energy conservation equation corresponding to a small Péclet number is:
and we have a fully linear upscaled system.
Denoting by: \(\xi = \xi (w,p,T) = a_0T - b_0p + \nabla \cdot {{\mathrm{\varvec{\beta }}}}w\), the energy present in some arbitrary control volume, we see from Eq. (72d) that the rate of change of energy present, \(\partial _t \xi \), is balanced by the net energy flux into the same control volume, either by conduction: \(- \nabla \cdot \left( {{\mathrm{\varvec{\varTheta }}}}\nabla T\right) \), or convection: \( ({{\mathrm{\varvec{\varXi }}}}\partial _t w + q_D) \cdot \nabla T\). We see also from Eq. (73) that in the case of a small Péclet number, the rate of change in energy present is balanced only by the conduction. The homogenized tensors \({{\mathrm{\varvec{\varTheta }}}}\) and \({{\mathrm{\varvec{\varXi }}}}\) can be interpreted as a kind of upscaled thermal conductivities, while \(a_0\) gives the energy present by a unit temperature rate of change.
An important property of the linear poroelastic equations is that the Biot–Willis coefficient appears both in front of the pressure term in the momentum Eq. (72b) (i.e., \({{\mathrm{\varvec{\alpha }}}}p\)), and in front of the volumetric term in the mass conservation Eq. (72c) (i.e., \(\nabla \cdot {{\mathrm{\varvec{\alpha }}}}w\)). As described in Coussy (1995) p. 75, a similar situation is expected with the temperature term in the momentum equation and the volumetric term in the energy equation. As we see from Eqs. (72b) and (72d), this is indeed the case, as the thermal stress coefficient, \({{\mathrm{\varvec{\beta }}}}\), appears in both places. Another interesting fact is the coefficient \(b_0\) which appear both in front of the temperature term in the mass conservation Eq. (72c) and in front of the pressure term in the energy Eq. (72d). This is indeed also the case in Coussy (1995), where they refer to the coefficient \(b_0\) as the “volumetric thermal dilation coefficient related to the porosity.”
In the article Lee and Mei (1997), the allowable deformations at the microscale are much smaller than the microscale length (i.e., l), which makes a direct comparison of our models difficult. However, we note that also here there is a linear dependency on temperature in the upscaled solid stress, and thus, Eq. (72c) matches that of Lee and Mei (1997). Our energy equations differ significantly, on the other hand, as in Lee and Mei (1997) there appears no pressure term.
4.2 Conclusions
We have presented a formal upscaling of the microscale thermal fluid-structure problem in porous media, leading to thermal Biot equations at the macroscale. This derivation gives a precise understanding of the coupling terms at the macroscale and forms a justification for heuristically derived models.
The most important limitation of the formal approach taken herein is the use of a perfectly periodic geometry. This limitation will not affect the applicability of the results to some human-made porous media, but will invalidate the approach for natural porous media. However, it has been shown for similar problems that the periodicity assumption can be relaxed, and we expect that these results would be possible to extend to the present setting. As such we expect the structure of the equations summarized in the preceding section to be valid also for non-periodic porous media, at least when there is some uniformity on the sizes of the solid grains.
All homogenization results are based on a series of “smallness” assumptions. We emphasize the important understanding that the results presented herein are based on \(\varepsilon \) being “small,” but not tending to zero. This distinction is important, since some of the parameters defined in the homogenization procedure (such as i.e., permeability) may depend on \(\varepsilon \), depending on the choice of characteristic macroscopic length scales. A further comment in this regard is that the Lagrangian formulation used herein implies that we only assume that the strain is small, and not that the displacement itself is small. Alternatively, if an Eulerian framework was used, it would be necessary to assume that the displacement is small relative to the microscale, which would preclude meaningful macroscopic deformations.
In this work we have chosen to a large extent to linearize the governing equations already at the microscale. This in part explains the linear structure of the majority of terms on the macroscale. Nonlinear constitutive relationships could be accommodated at the cost of technical and notational complexity, varying from relatively straight-forward (i.e., nonlinear constitutive laws for fluid density) to complex (nonlinear elastic or plastic constitutive laws for material deformation).
References
Allaire, G.: Homogenization of the Stokes flow in a connected porous medium. Asymptot. Anal. 2(3), 203–222 (1989)
Auriault, J.L.: Heterogeneous medium. Is an equivalent macroscopic description possible? Int. J. Eng. Sci. 29(7), 785–795 (1991)
Biot, M.A.: General theory of three-dimensional consolidation. J. Appl. Phys. 12(2), 155–164 (1941)
Biot, M.A.: Theory of finite deformations of porous solids. Indiana Univ. Math. J. 21(7), 597–620 (1972)
Biot, M.A.: Variational Lagrangian-thermodynamics of nonisothermal finite strain mechanics of porous solids and thermomolecular diffusion. Int. J. Solids Struct. 13(6), 579–597 (1977)
Bringedal, C., Berre, I., Pop, I.S., Radu, F.A.: Upscaling of non-isothermal reactive porous media flow with changing porosity. Transp. Porous Media 114(2), 371–393 (2016)
Burridge, R., Keller, J.B.: Poroelasticity equations derived from microstructure. J. Acoust. Soc. Am. 70(4), 1140–1146 (1981)
Cioranescu, D., Donato, P.: Introduction to Homogenization. Oxford University Press, Oxford (2000)
Clopeau, T., Ferrin, J.L., Gilbert, R.P., Mikelić, A.: Homogenizing the acoustic properties of the seabed, part II. Math. Comput. Model. 33(8–9), 821–841 (2001)
Coussy, O.: Mechanics of Porous Continua, pp. 71–108. Wiley, Hoboken (1995)
Eden, M., Muntean, A.: Homogenization of a fully coupled thermoelasticity problem for a highly heterogeneous medium with a priori known phase transformations. Math. Methods Appl. Sci. 40, 3955–3972 (2017)
Ferrin, J.L., Mikelić, A.: Homogenizing the acoustic properties of a porous matrix containing an incompressible inviscid fluid. Math. Methods Appl. Sci. 26(10), 831–859 (2003)
Gilbert, R.P., Mikelić, A.: Homogenizing the acoustic properties of the seabed: Part I. Nonlinear Anal. Theory Methods Appl. 40(1–8), 185–212 (2000)
Hornung, U.: Homogenization and porous media, vol. 6. Springer, Berlin (2012)
Iliev, O., Mikelić, A., Popov, P.: On upscaling certain flows in deformable porous media. Multiscale Model. Simul. 7(1), 93–123 (2008)
Kupradze, V.D., Gegelia, T.G., Basheleishvili, M.O., Burchuladze, T.V.: Three-dimensional problems of the mathematical theory of elasticity and thermoelasticity. Translated from the second Russian edition. Edited by VD Kupradze, North-Holland Series in Applied Mathematics and Mechanics (1979)
Lee, C.K., Mei, C.C.: Thermal consolidation in porous media by homogenization theory—I. Derivation of macroscale equations. Adv. Water Resour. 20(2), 127–144 (1997)
Lévy, T.: Propagation of waves in a fluid-saturated porous elastic solid. Int. J. Eng. Sci. 17(9), 1005–1014 (1979)
Mikelić, A.: Mathematical derivation of the Darcy-type law with memory effects, governing transient flow through porous medium. Glasnik Matematicki 29(49), 57–77 (1994)
Mikelić, A., Wheeler, M.F.: Theory of the dynamic Biot–Allard equations and their link to the quasi-static Biot system. J. Math. Phys. 53(12), 123, 702 (2012)
Pabst, W.: The linear theory of thermoelasticity from the viewpoint of rational thermomechanics. Ceram Silikaty 49(4), 242–251 (2005)
Sanchez-Palencia, E.: Non-homogeneous media and vibration theory. Lect. Notes Phys. 127, 158–190 (1980)
Silhavy, M.: The Mechanics and Thermodynamics of Continuous Media. Springer, Berlin (2013)
Terzaghi, K.: Theoretical Soil Mechanics. Chapman and Hali, Limited John Wiler and Sons Inc, New York (1944)
Van Duijn, C., Mikelic, A., Wheeler, M., Wick, T.: Thermoporoelasticity via homogenization I. Modeling and formal two-scale expansions. In: Working Paper or Preprint (2017). URL https://hal.archives-ouvertes.fr/hal-01650194
Wood, J.R., Hewett, T.A.: Fluid convection and mass transfer in porous sandstones? A theoretical model. Geochimica et Cosmochimica Acta 46(10), 1707–1713 (1982)
Acknowledgements
This work is partly supported by the Research Council of Norway Project 250223. The authors would like to thank the anonymous reviewers, Prof. Andro Mikelić, and Carina Bringedal for reading the manuscript and providing helpful comments, all of which contributed to the improvement of the paper. The authors also acknowledge the support from the University of Bergen.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Brun, M.K., Berre, I., Nordbotten, J.M. et al. Upscaling of the Coupling of Hydromechanical and Thermal Processes in a Quasi-static Poroelastic Medium. Transp Porous Med 124, 137–158 (2018). https://doi.org/10.1007/s11242-018-1056-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-018-1056-8