An Experimental and Numerical Study of Relative Permeability Estimates Using Spatially Resolved $T_1$-z NMR

Abstract

Relative permeability is a key characteristic describing flow properties of petroleum reservoirs, aquifers and water retention of soils. Various laboratory methods, typically categorised as steady-state, unsteady-state and centrifuge are used to measure relative permeability and may lead to different results. In recent years, 1D MRI, NMR $T_2$ and $T_1$ profiling have been applied for the characterisation of rock cores. It has been shown that spatially resolved NMR in conjunction with centrifuge technique may provide high-quality capillary pressure curves. Combining Burdine and Brooks–Corey models enables estimation of relative permeability from capillary pressure curves. This approach assumes a strong relationship between capillary pressure and relative permeability known to be complex. Here we compare a generalised approach of Green, which relies on saturation profiles set by various capillary drainage techniques, to a NMR relaxation approach. Comparisons are performed experimentally and numerically using three sandstone rocks to test the influence of rock morphology. The numerical part includes simulation of a centrifuge capillary drainage by applying morphological drainage transforms on high-resolution 3D tomograms. $T_1$ responses along the sample are simulated using a random walk technique. The NMR relaxation-based approach is then compared to LBM simulated relative permeability and to experiment. The study confirms the applicability of NMR relaxation methods for relative permeability estimation of water-wet rocks and validates a numerical approach against experiment.

1 Introduction

Simultaneous flow of immiscible fluids in porous media is described by a physical property called relative permeability. Relative permeability is essential for predicting movement of fluids in petroleum-bearing reservoirs and plays an important role in contaminant hydrology, nuclear waste storage and in soil science. The concept of relative permeability as a function of saturation or ’relative permeability curves’, and a laboratory method for measuring it were introduced by Hassler et al. (1936). Relative permeability techniques are typically classified into two types: steady-state (SST) and unsteady-state (USS) methods. Due to a specific pressure potential centrifuge methods (CM) are sometimes considered as a third type. The two methods (steady- and unsteady-state) in general do not provide identical relative permeability functions (Hussain et al. 2010).

Unsteady-state (USS) methods involve injection of a fluid to displace another fluid present in the core, e.g. Johnson–Bossler–Neumann (JBN) method (Johnson et al. 1959). The JBN method assumes negligible capillary pressure, which requires high flow rates to satisfy the condition. However, reservoir flow rates are generally very low and relative permeability may have a nontrivial dependence on flow rate. USS displacement methods are indirect since relative permeability is calculated from transient data.

In the multirate steady-state (SST) method, both wetting and non-wetting phases are injected into a core simultaneously. The pressure drop and saturations of fluids are measured once the equilibrium condition is established. Measurements are performed in steps with various flow rate ratios, and effective permeability for each phase is calculated as a function of wetting phase saturation using Darcy’s equation. SST measurements are affected by capillary-end effects (discontinuity at the outlet) requiring to maintain a proper balance between viscous and capillary forces.

The Centrifuge (CM) method for capillary pressure measurements was introduced by Hassler and Brunner (1945). Hagoort (1980) adopted the centrifuge technique to evaluate gas–oil relative permeability curves in unsteady-state conditions. In the limit of infinite mobility of invading phase, zero capillary pressure and constant centrifugal field, the analytical solution is available (Hirasaki et al. 1992). Fitting two-phase production data with any monotonic and smooth function of saturation, e.g. $k_\mathrm{r} = S^n$, provides relative permeability curves.

A combination of NMR and centrifuge techniques (CM-NMR) allows to obtain saturation profiles and a broad range of capillary pressure values, which in turn allows to reduce measurement time and improve the quality of constructed capillary pressure curves. Green (2009) proposed to use CM-NMR capillary pressure measurements to evaluate relative permeability using Burdine (1953) and either Brooks and Corey (1964) or van Genuchten (1980) models. Here we aim to compare this CM-NMR approach to NMR relaxation-based estimates proposed by AlGhamdi et al. (2013). We modified the latter for use with centrifuge (CM-NMR-$T_1$), which enables the acquisition of multiple data points in a single experiment similarly to Green et al. (2007). NMR longitudinal relaxation is used to avoid influence of internal gradients effects common in saturated sandstones.

In this work, reference experimental measurements of relative permeability were performed using steady-state (SST) flooding as well as using Corey–Burdine transform to capillary pressure data. CM-NMR-$T_1$ relative permeability curves of three sandstone rocks were simulated numerically and validated by $T_1$-z experiments. Simulations of a centrifuge capillary drainage are performed by applying morphological transforms on high-resolution 3D tomograms following (Arns et al. 2005b; Shikhov and Arns 2015). $T_1$ responses along the sample are simulated using the random walk technique on $\mu$-CT images (Arns et al. 2011). $T_1$ distributions obtained for individual slices along the core length at fully saturated and drained states are then used to estimate relative permeability (AlGhamdi et al. 2013). In addition we calculated effective permeability of two phases on CT image-based simulated drainage maps using the lattice Boltzmann method (LBM) (Ladd 1994; Arns 2004). Finally, we compare relative permeability derived from capillary pressure curves to those obtained using $T_1$-resolved NMR.

2 Relative Permeability Estimates Based on Capillary Pressure

2.1 Rock Samples and Their Digital Representations

2.1.1 Rock Samples

Three types of outcrop sandstones (Bentheimer, Castlegate and Leopard) are used for laboratory and numerical experiments. These rocks are composed of mainly quartz, feldspar and kaolinite. In addition, Castlegate and Leopard contain minor fractions of pore-lining muscovite and chlorite. The iron content of these sandstones varies from 0.03 $\hbox {wt}\%$ (Fe$_2$O$_3$) in Bentheimer to 0.42 $\hbox {wt}\%$ in Castlegate and 0.88 wt$\%$ in Leopard. Their porosity, permeability to brine, median throat diameter $d_{50}$ (MICP), basic mineral composition from XRD/XRF and volumetric magnetic susceptibility are summarised in Table 1.

Table 1 Petrophysical properties of sandstones

Fig. 1

Left Cross sections through the subsections of the segmented tomograms of a Bentheimer: 554 $\times$ 554 @ 2.888 $\upmu \hbox {m/voxel}$; b Castlegate: 476 $\times$ 476 @ 3.363 $\upmu \hbox {m/voxel}$; c Leopard: 744 $\times$ 744 @ 2.151 $\upmu \hbox {m/voxel}$ depicting an equal field of view, FOV $= 1.6 \hbox {mm} \times 1.6$ mm. Right Probability density distributions of covering radius for the pore space, clay region and merged grain phases of d Bentheimer, e Castlegate and f Leopard sandstone

Micro-CT images of the three samples were acquired on the ANU helical micro-CT system with $2048^2$ flatbed detector with sample diameters of 5 mm for Bentheimer (voxel size $\epsilon =2.888\,\upmu$m) and Castlegate ($\epsilon =3.363\,\upmu \hbox {m}$) and 3 mm for Leopard sandstone ($\epsilon =2.151\,\upmu \hbox {m}$). The sandstones were segmented in a standard way using an active contour method (Sheppard et al. 2004), see Fig. 1, where the phases are (1) void, populated with one or more fluids; (2) intermediate, partially resolved solid-void, attributed to clays, (3) solid, being quartz and feldspar. In the case of four-phase segmentation (Castlegate and Leopard), the two solid phases are a low intensity major phase (quartz and feldspar) and a high-intensity minor phase attenuated due to a presence of heavy minerals. To illustrate their relative morphology and heterogeneity we calculated the covering radius maps (Arns et al. 2005a), the respective covering radius distributions and report a range of image-based morphological statistics (Fig. 1; Table 2). We observe distinct morphological differences with Leopard exhibiting quite large pores, yet having a significant amount of smaller-scale resolved porosity. In particular, while similar in mean pore sizes and porosity, there are significant differences in critical diameter of percolation $l_\mathrm{c}$ (Arns et al. 2005a), which compare well to the median throat diameter $d_{50}$. Comparison with respective permeability values suggests that Leopard sandstone exhibits much higher tortuosity of flow pathways. Furthermore, the size of the clay regions from micro-CT images illustrates that clays are much more dispersed in Leopard given the comparably larger clay content.

Table 2 Morphological statistics of outcrop sandstones derived from the segmented $\upmu$-CT images

2.1.2 Experimental Procedures

The wettability of samples is controlled by cleaning cores in a soxhlet extractor with $50\%$:$50\%$ methanol–toluene mixture. Cores were then dried at $60\,^{\circ }\hbox {C}$ for 24 h. A desiccator connected to a vacuum pump is used to saturate dry samples with $2\%$ NaCl brine (Bentheimer) and $3\%$ NaCl brine for the other rocks. In centrifuge experiments, samples were drained in a Beckman L8-60 M/P ultracentrifuge for at least 24 h at a constant speed. The time required to produce about $99\%$ of mobile pore fluid at a given speed is used to set the wait time before ramping rotational speed (Hirasaki et al. 1992). It has been estimated that the requirement is met in 3 h for Bentheimer and Castlegate and in 12 h for Leopard. The accuracy of the determined saturation values is better than $\pm 0.02$ saturation units. The latter value accounts for random errors in determined displaced fluid weight, fluid density and temperature fluctuations of $\pm 1\,^{\circ }\mathrm{C}$. An additional error is associated with determination of sample’s volume $\pm 0.6\%$ (for the plug of about 1 in. long and 1 in. in diameter) is systematic and not included.

Fig. 2

Centrifuge drainage RPM-saturation maps simulated using micro-CT images of: a Bentheimer, image size 8979 $\times$ 1024 $\times$ 1024 voxels, voxel size $\epsilon =2.888\,\upmu \hbox {m}$; b Castlegate, image size 8064 $\times$ 960 $\times$ 960 voxels, voxel size $\epsilon =3.363\,\upmu \hbox {m}$); c Leopard, image size 12,225 $\times$ 900 $\times$ 900 voxels, voxel size $\epsilon =2.151\,\upmu \hbox {m}$)

2.1.3 Composite Images

Simulations of various capillary pressure techniques are performed on the segmented high-resolution ${\mu }$-CT images. Fully saturated state is simulated by assigning to the whole void space and a specified fraction of the intermediate phase physical properties of a fluid. The distributions of fluids are simulated using morphological transforms with appropriate boundary conditions to mimic one of a capillary drainage technique (Shikhov and Arns 2015). Physical dimensions of a Bentheimer cylindrical plug are 25.93 mm long and 26.57 mm across, while the composite $\mu$-CT image (8979 $\times$ 1024 $\times$ 1024 voxel at 2.888 ${\upmu }\hbox {m}$ resolution) has been composed from an original tomogram mirrored four times to represent equivalent length precisely, but being significantly narrower and square in cross-flow plane, 2.96 mm across. Dimensions of a Castlegate plug are 27.12 mm long and 24.42 mm across, while the $\mu$-CT composite image being mirrored once (8064 $\times$ 960 $\times$ 960 voxel at the voxel resolution of 3.363 ${\upmu }\hbox {m/voxel}$) accurately represents equivalent physical dimensions, in length, but only 3.23 mm across. A Leopard 1-in. core plug digital representation is composed from an original tomogram mirrored twice resulting in 12,225 $\times$ 900 $\times$ 900 voxel composite image. At the resolution of 2.151 ${\upmu }\hbox {m/voxel}$, the composite image length matches a core plug length of 26.35 mm, while the image width is 1.94 mm comparing to the plug diameter of 24.95 mm.

2.1.4 Simulated CM Drainage

Figure 2 shows simulated centrifuge drainage saturation maps of these three sandstones with the RPM colour scale up to 3000 rpm. The direction of invasion for the non-wetting phase is indicated by an arrow. The outlet side (bottom end) of the images is aligned to reflect a position of the cores in a centrifuge, where the position of outlet of outlet relative to axis of rotation is constant, while the position of inlet depends on core length. The three images exhibit a slight variation in length-to-width aspect ratios: 9:1 for Bentheimer (BH); 7.5:1 for Castlegate (CG); 12:1 for Castlegate (LP). Another factor influencing the quality of simulated centrifuge drainage is an ${\mu }$-CT image equivalent physical size. The cross sections of the simulated centrifuge saturation maps perpendicular to the invasion direction have side-length of (in $\hbox {mm}$ and expressed in a number of median pore throats): 2.96 $\hbox {mm}/75$ for Bentheimer; 3.23 $\hbox {mm}/130$ for Castlegate; 1.94 $\hbox {mm}/120$ for Leopard.

2.2 Capillary Pressure Transforms

Functions connecting capillary pressure and saturation of a wetting fluid in porous media are often used to predict fluid distributions in soils and clastic rocks. The power-law model connecting capillary pressure and partial saturation is commonly used. Originally proposed by Corey (1954) with the fixed exponent of two the model was generalised by Brooks and Corey (1964) who established that capillary pressure curves of different lithologies could be expressed by the following function of capillary pressure:

$$\begin{aligned} P_\mathrm{c\;BC} = P_\mathrm{e} \; S_\mathrm{e}^{-1/{\lambda }} , \end{aligned}$$

(1)

where $S_\mathrm{e} = (S - S_\mathrm{wi}) / (1 - S_\mathrm{wi})$ is normalised saturation, $S_\mathrm{wi}$ and S irreducible and actual saturation of a wetting fluid, and $P_\mathrm{e}$ entry pressure. The exponent $\lambda$ is lithology and wettability dependent and often referred to in the literature as Corey exponent as well as the model itself. The model has been proven theoretically by Li (2010) from fractal modelling of a porous medium. The validity of the Brooks and Corey (BC) model is limited by requirements of media homogeneity and the absence of fractures. Burdine (1953) proposed equations for two-phase relative permeability in the form of the following integral equations:

$$\begin{aligned} k_\mathrm{r\;w}= & {} (S_\mathrm{e})^2 \left[ \frac{\int _0^{S_\mathrm{e}} {\mathrm {d}}S_\mathrm{e}/P_\mathrm{c}^2\,}{\int _0^1 {\mathrm {d}}S_\mathrm{e}/P_\mathrm{c}^2}\right] , \end{aligned}$$

(2)

$$\begin{aligned} k_\mathrm{r\;nw}= & {} (1 - S_\mathrm{e})^2 \left[ \frac{\int _{S_\mathrm{e}}^1 {\mathrm {d}}S_\mathrm{e}/P_\mathrm{c}^2\,}{\int _0^1 {\mathrm {d}}S_\mathrm{e}/P_\mathrm{c}^2}\right] . \end{aligned}$$

(3)

If capillary pressure can be expressed as an analytic function of saturation these integrals can be calculated. In particular, by substituting Brooks and Corey model for capillary pressure, Eq. (1), into Burdine’s equations above a relative permeability function of saturation can be obtained:

$$\begin{aligned} k_\mathrm{r\;w}= & {} k^o_\mathrm{r\;w} \; (S_\mathrm{e})^{(2\;+\;3{\lambda })/{\lambda }} , \end{aligned}$$

(4)

$$\begin{aligned} k_\mathrm{r\;nw}= & {} k^o_\mathrm{r\;nw}\;[(1\;-\;S_\mathrm{w})\;/\;(1\;-S_\mathrm{wi})]^2 \; (1\; - \;S_\mathrm{e})^{(2\;+\;{\lambda })/{\lambda }} , \end{aligned}$$

(5)

where $k^o_\mathrm{r\;w}$ and $k^o_\mathrm{r\;nw}$ are relative permeability end points of wetting (w) and non-wetting (nw) phases. The exponent in Eq. (4), $n_\mathrm{w} = (2\;+\;3{\lambda })/{\lambda }$ can be used as a simple criterion for comparison of data obtained with different techniques. Corey-based capillary pressure curves approximate porous systems by a unimodal pore-throat distribution. This implies that Corey’s model ignores contributions to flow of pore-throat sizes significantly different from the mode of a distribution. We used common capillary pressure techniques (MICP and centrifuge) to validate digitised rock representations by comparing capillary pressure simulations on ${\mu }$-CT images to experiments (Shikhov and Arns 2015). We then fit the capillary pressure data with Corey’s power-law model to obtain estimates of relative permeability curves following the Burdine–Corey model.

2.3 Capillary Pressure Curves from Saturation Profiles

Capillary pressure curves can be obtained using one of capillary pressure techniques, e.g. centrifuge (CM) and MICP. In CM experiment, a single rotational speed provides a broad range of capillary pressures along the sample, which enables construction of a near complete capillary pressure curve if local saturation values are known. We simulated MICP and CM drainage experiments in 3D at the pore scale through morphological distance transforms using high-resolution $\mu$-CT images. The capillary pressure is realised by a structural element percolating from the core inlet towards outlet and re-labelling the union of these elements as an invading phase. The spherical shape of the structuring element (or ball) corresponds to perfect wetting conditions ($180^{\circ }$ contact angle), and the size of a ball (capillary radius) is determined by a local pressure potential, which in turn is a function of radial distance in centrifuge experiment (equation in the caption of Table 3) and constant throughout the sample in MICP measurements. The simulation procedure is described in detail in Shikhov and Arns (2015).

Table 3 Centrifuge drainage experimental parameters

Fig. 3

Left column Simulated saturation profiles from centrifuge drainage RPM-maps: a Bentheimer composite image, $8979 \times 1024 \times 1024$ voxels; c Castlegate composite image, $8064 \times 960 \times 960$ voxels; e Leopard composite image, $12,225 \times 900 \times 900$ voxels. Right column Comparison of simulated and experimental CM saturation profiles registered with frequency- and SPI NMR techniques for three rocks: b Bentheimer, d Castlegate, f Leopard

Simulated saturation profiles of centrifuged plugs represented by ${\mu }$-CT images (Fig. 3a, c, e) are compared to experimental profiles established using two NMR intensity profiling techniques, Fig. 3b, d, f. Clearly the agreement between the two different NMR experimental profiling techniques deteriorates with increasing heterogeneity. Leopard sandstone exhibits large pores (order 0.5 mm diameter), which if included at the boundary may result in only partial saturation of those. This in turn would change the normalisation of water saturation. Given the large pore size, a second explanation is that the inlet contains a significant amount of microporosity, which remains predominantly water saturated.

Simulated saturation profiles show that heterogeneity of wetting fluid saturation increases from Bentheimer through Castlegate to Leopard. One may notice spikes in saturation profiles at positions common for all centrifuge speeds. These artefacts are due to the symmetry planes introduced by mirroring the samples to generate long composite images.

Fig. 4

Left column Experimental mercury intrusion pore-aperture distributions and $T_1$ distributions of a Bentheimer, c Castlegate, e Leopard. Right column Comparison of simulated and experimental MICP and SST CM capillary pressure curves of b Bentheimer, d Castlegate, f Leopard

Figure 4b, d, f demonstrates a comparison of simulated capillary pressure curves versus experimental MICP and centrifuge drainage (CM) ones. Both ${\mu }$-CT saturation data and the Corey model have limited accuracy in a saturation region next to irreducible. Nevertheless, simulated and experimental MICP results are very close (Arns et al. 2005a). A common feature between simulated and experimental CM capillary pressure curves of all three rocks is a difference in irreducible saturation manifesting lack of resolution progressing with rock complexity (from Bentheimer to Leopard). The accuracy of simulated $P_\mathrm{c}$-curves is limited by low- and high-saturation end point effects which also affect capillary pressure data measured experimentally. The finite size of the samples, aspect ratio and discontinuities at inlet and outlet are the major contributors to the end point effect. Note, the draining phase in case of centrifuge experiment (CM) is air, while in flooding experiment the non-wetting phase is Soltrol 130. The difference in their viscous/capillary force ratio results in different residual saturations of wetting phase. From centrifuge air–water drainage, the residual water saturation is found to be $5.7\pm 1.2\%$ for Bentheimer, $11.1\pm 1.6\%$ for Castlegate and $19.7\pm 1.4\%$ for Leopard. The capillary pressure limits for these measurements are 50 psia for Bentheimer and 100 psia for Castlegate and Leopard. Figure 4a, c, e shows increase of microporosity fraction of total porespace (e.g. defined as part of MICP distributions below 3 $\upmu \hbox {m}$) from 5.3% for Bentheimer to 11.8% for Castlegate and 16.5% for Leopard which agree with CM drainage $S_\mathrm{w\;ir}$ values. Draining these rocks with Soltrol at a constant rate resulted in substantially higher residual values: $11.7\pm 1.0$, $16.8\pm 0.7$ and $29.1\pm 2.9\%$, respectively, see Table 4. Bentheimer sandstone is widely referred in literature with reported values of irreducible water saturation spread between 2 and $13\%$, e.g. Zhang et al. (1999).

2.4 Registration of Saturation Profiles with NMR

We compare saturation profiles of centrifuged cores simulated on $\mu$-CT images of three sandstone rocks following Shikhov and Arns (2015) to experimental profiles obtained using two 1D NMR imaging techniques. The first is frequency encode (or constant gradient) 1D NMR spin-density imaging. The second method which we applied to obtain spatially resolved saturation is single-point imaging (SPI) alternatively known as constant-time imaging (CTI), Emid and Creyghton (1985), which utilises phase encoding gradients to obtain spatial information. Time evolution of magnetisation is not an objective of such techniques. Instead, the strength of applied gradients becomes more important. Consequently, acquired images are free from factors typically affecting their quality, such as field inhomogeneity, chemical shift and susceptibility variations (Gravina and Cory 1994). The signal-to-noise ratio of the SPI experiment is much better than that of a spin-echo frequency-encoding experiment (Bogdan et al. 1995). We used a single-point imaging (SPI) sequence in a constant gradient variant. Detailed description of these techniques can be found elsewhere, e.g. Blümich (2000), Bogdan et al. (1995). The 1D frequency-encoding experiment is fast, but misses fast relaxation components in the observed signal associated with clay bound water due to relatively long spin-echo time required to acquire an image. SPI technique is free from this problem, however, time-consuming. Time can be a critical factor when dealing with centrifuged cores because of possible fluids redistribution and evaporation loss. We performed a series of NMR experiments (1D spin-density profiling using constant gradient and SPI techniques, $T_1$-z) for each core plug at a particular partial saturation set by centrifuge. The fluid loss due to evaporation over 6 h, required to complete these NMR experiments, was about 1 saturation unit (pore space fully occupied by fluids $=$ 100 saturation units). Figure 3b, d, f shows comparison plots of simulated and experimental saturation profiles for the three sandstones. Each plot contains four curves: the two solid lines are simulated profiles at two different rotational speeds selected to be close to experimental values; the two dashed lines are experimental profiles obtained with phase- and frequency-encoding NMR.

Simulated and experimental saturation profiles of Bentheimer show a good match (Fig. 3b): the slopes and positions of the saturation front between invading and defending fluids are reasonably close. However, this was achieved at different centrifugal capillary pressures set by rotational speed of 800–850 rpm (simulation) and 650 rpm (experiment). Noting as $\phi _\mu$ the microporosity of clay regions associated with intermediate phase in the tomographic image (voxels containing both, voids and solids), two saturation profiles are given for the numerical 800 rpm results. A slight shift to higher saturations for the simulations including microporosity is evident. Since the microporosity is not resolved, it is assumed that it stays $100\%$ water saturated.

Table 4 Experimental steady-steady and centrifuge drainage parameters

Castlegate simulated and experimental profiles, Fig. 3d, show excellent agreement (at 950 rpm simulated and at 800 rpm experimental). The slope of the saturation flonts is very well matched. The significant separation between the two NMR acquisition methods is due the difference in response of the clay phase as well as fast relaxation responses from irreducible saturation located in small crevices. The latter are not resolved in the numerical simulation, e.g. it is expected that the numerical simulation would underestimate this part. This is akin to MICP capillary pressure simulation versus experiment comparisons, where the MICP experiment is often utilised to judge the quality of the image acquisition with regard to resolution, Fig. 4b, d, f.

Leopard shows a good match between simulation and experiment at slightly shifted rotational speeds, e.g. 1100 rpm experimental versus 1300 rpm numerically Fig. 3f. Significant fluctuations are present due to the heterogeneity of the sample, which may be explained by the combination of large pores (see Fig. 1f) and reduced connectivity as expressed in the smaller critical diameter of percolation ($l_\mathrm{c}$) and higher tortuosity compared to the other sandstones (see Table 2).

2.5 Reference Drainage Relative Permeability (Experimental and Simulated)

Reference relative permeability data are obtained using SST coreflood experiments, Fig. 5a, c, e and LBM simulations, Fig. 5b, d, f, with extra reference data added where available (Hussain et al. 2014), Otiede et al. (2012). Coreflooding was performed on a pair of 2-in. long and 1-in. diameter sister-plugs for each of three sandstone rocks. The Corey fits to SST experimental data points are supplemented with $95\%$ confidence interval lines evaluated for fitting exponents. Total flow rate of SST relative permeability experiments was 3.5–5 mL/min for Bentheimer and Castlegate, and 0.25 mL/min for Leopard. Corresponding capillary numbers, $N_\mathrm{Ca}$, are between $10^{-6}$ and $10^{-5}$. Criteria of optimum parameters for coreflooding experiments have been extensively discussed for decades since the appropriate balance between high flow rate to suppress boundary effects, low flow rate to represent reservoir conditions, avoiding viscous instability, inflow end effects and maintaining core integrity is not a trivial task. One common criterion to estimate the lower bound of flow rate utilises a viscous and capillary forces ratio, ${\Delta }P_\mathrm{L}/P_\mathrm{d}$, where ${\Delta }P_\mathrm{L}$ is the pressure drop along the core length and $P_\mathrm{d}$ is characteristic capillary pressure (Huang and Honarpour 2004). We selected rates for our SST coreflooding experiments such that ${\Delta }P_\mathrm{L}/P_\mathrm{d}$ at $S_\mathrm{w\;ir}$ was almost constant for three rocks, 6.3 for Bentheimer, 6.5 for Castlegate and 6.4 for Leopard. Such values of ${\Delta }P_\mathrm{L}/P_\mathrm{d}$ promise reasonable suppression of capillary-end effect and at the same time limit production of clay particles from clay-rich Castlegate and Leopard.

There is a discrepancy in published literature regarding wetting fluid (water) end point $k_\mathrm{rw}^o$ of drainage relative permeability—in many cases the absolute water permeability point ($k_\mathrm{rw}=1 @ S_\mathrm{w} = 1)$ is included into the SST data set. This directly affects determination of a Corey exponent $n_\mathrm{w}$. In our opinion, at core scale, relative permeability at high water saturations (between the true end point $k_\mathrm{rw}=k_\mathrm{rw}^o$ and $k_\mathrm{rw}=1$) may be not defined as a static process in SST experiment. On Fig. 5 that region is plotted as a dashed line. That region may be related to USS experiments and locally determined properties in SST experiments.

Fig. 5

Reference relative permeability curves: experimental SST (left column) and simulated using LBM method in comparison with experiment (right column) of a, b Bentheimer; c, d Castlegate; e, f Leopard

A common numerical technique in computational fluid dynamics for porous media is the lattice Boltzmann method (LBM) (Chen et al. 1992), which has also been applied to calculate capillary pressure curves on extracted pore-networks (AlKharusi and Blunt 2008) or directly on segmented (solid-void labelled) high-resolution $\mu$-CT images (Arns 2004). It has been shown that for the case of slow displacement in systems where molecular free pass length is small comparing to characteristic physical length (low Mach and Knudsen numbers) the fluid can be treated as a continuous medium. This allows to use LBM method to recover the Navier–Stokes equation governing the single- and multiphase fluid flow (Ladd 1994). While LBM has proven to be a reliable technique for single- and multiphase flow simulation for the case of constant flow potential, it may be too complicated (and computationally prohibitive) to use LBM in the case of a centrifuge potential. Here to calculate effective permeability of stationary phases we used LBM implementation as D3Q19 scheme of velocity components with a single relaxation time collision operator (known as BGK after Bhatnagar–Gross–Knook), where the unknown variable of the scheme is Q-dimensional ($Q=19$) population (velocity) vector specified on the nodes of the D-dimensional ($D=3$) regular mesh (Arns 2004). Figure 5 shows comparison of simulated relative permeability using LBM to experimental SST flood measurements. Simulations show a good match to experiment, while for the case of Leopard, the wetting fluid curve demonstrates substantial scattering reflecting rock heterogeneity.

3 Relative Permeability by Spatially Resolved $T_1$-z NMR

3.1 Concept of Relative Permeability with Spatially Resolved NMR

NMR/MRI has long been used to obtain spatial information about fluids’ distribution within saturated porous materials. A good account on practical aspects and a review of MRI techniques applicable for petrophysical measurements is given in Mitchell et al. (2013). Chen and Balcom (2005), Green et al. (2007) proposed to apply a $T_1$-based SPRITE technique (single-point ramped imaging with $T_1$ enhancement) to determine fluid saturation along the length of a centrifuged rock core. Composite capillary curves were constructed in assumption of core homogeneity and known capillary pressure as a function of position. The application of centrifuge NMR-assisted registration techniques (CM-NMR) has been further expanded for relative permeability measurements by Green (2009). Alternatively, NMR may be utilised to estimate permeability of rocks using NMR-specific permeability-relaxation correlation, e.g. SDR equation (Kenyon et al. 1988):

$$\begin{aligned} k_{\mathrm{NMR}} = a\;T_\mathrm{1,2 LM}^b\;\phi ^c \; , \end{aligned}$$

(6)

where the prefactor a, exponents b and c are variables specific to formation and rock type. The exponents b and c are normally fixed to 2 and 4, respectively, while the default value of a in carbonates is accepted to be 0.1 and 4 in sandstones (Kenyon et al. 1988). This correlation is regarded as reliable for absolute permeability estimates in water bearing formations. AlGhamdi et al. (2013) proposed to use this correlation for relative permeability estimates in conditions where NMR $T_2$ relaxation responses from wetting and non-wetting phase can be measured separately. Then the ratio of a particular phase’ SDR effective permeability to absolute permeability is given by

$$\begin{aligned} k_\mathrm{r\;w/nw} = \frac{k_\mathrm{re\;w/nw}}{k_\mathrm{abs}} =\frac{a\;(T_\mathrm{2\,LM} (S_\mathrm{w/nw}))^2\;(\phi _\mathrm{w/nw})^4}{a\;(T_\mathrm{2\,LM}(S_\mathrm{w}=1))^2\;(\phi _\mathrm{tot})^4} , \end{aligned}$$

(7)

where indices w/nw stands for wetting/non-wetting phase. By eliminating a lithology-specific prefactor a and extending to both relaxation types (including $T_1$), the expression above may be written as:

$$\begin{aligned} k_\mathrm{r\;w/nw\;{\mathrm{NMR}}} = \left[ \frac{T_\mathrm{1,2\;LM} (S_\mathrm{w/nw})}{(T_\mathrm{1,2\;LM} (S_\mathrm{w}=1))}\right] ^2\;(S_\mathrm{w/nw})^4 \;. \end{aligned}$$

(8)

The NMR response is to be acquired from the whole core plug in multiple saturation steps. In the past, the approach was tested numerically with simulated NMR responses on uniformly drained (using morphological transforms) Bentheimer and Berea sandstones (AlGhamdi et al. 2013). Rocks were assumed to be perfectly water-wet (zero surface relaxivity to oil), and relaxation time of oil is saturation dependent due to change of internal gradient effect. Neither analytical nor experimental proof was given in that reference.

In this work we consider application of longitudinal relaxation to estimate relative permeability of the wetting phase only, since it has no sensitivity to oil saturation in strongly water-wet rocks. We compare experimentally and numerically the following steady-state and centrifuge-based approaches: (1) steady-state flood and corresponding simulation using LBM; (2) relative permeability obtained from capillary pressure curves (including 1D NMR saturation profiles) using Burdine transform; (3) NMR relaxation time relative permeability correlation, Eq. (8). NMR measurements were performed on fully saturated and centrifuge-drained sandstone core plugs using the 2 MHz low-field NMR system.

Use of $T_1$ and $T_2$ spatially resolved relaxation experiments has advantages and disadvantages. $T_1$-based experiments take much longer then $T_2$-based, approximately by a factor equal to the number of steps $\tau$ in $T_1$ Inversion Recovery ($T_1$-IR), typically 30–50. The standard $T_2$ technique (CPMG experiment) requires longer inter-scan time delays since it deposits more energy into the system than $T_1$-IR, which may partially offset CPMG time saving advantage over $T_1$-IR. Both experiments are, however, significantly shorter (20 min and 3 h) than centrifuge drainage experiments (24 h). Hürlimann (1998) demonstrated that depending on distribution of rock structural dimensions spins in certain parts of a pore space may relax following different relaxation regimes: in particular, free diffusion regime, which is echo time ($\tau _\mathrm{e}$) dependent and motionally averaging regime (independent on $\tau _\mathrm{e}$). Depending on rock morphology relaxation processes following these regimes may co-exist. Their ratio, however, strongly saturation dependent for air–water systems. For 1D imaging we typically use $\tau _\mathrm{e}=1.8$ ms, which means for structural length, $l_\mathrm{s}$ < 4 $\upmu \hbox {m}$ spins relaxing in a motionally averaging regime. For volumetric estimate of a pore fraction where relaxation occurs in motionally averaging regime the irreducible water saturation ($S_\mathrm{w\;irr}$) value can be employed, i.e. in a fully water saturation state the fraction of pore space relaxing in motionally averaged regime approximately equals to $S_\mathrm{w\;irr}$.

Table 1 shows that the magnetic susceptibility of the three rocks varies from weakly diamagnetic Bentheimer to paramagnetic Castlegate and Leopard, while the median pore-throat size decreases from Bentheimer to Leopard. This implies that effective and maximum gradients in these rocks are very different. Table 4 shows that irreducible water saturation of the three rocks also varies in a broad range, from ${\sim }5\%$ for Bentheimer to ${\sim }20\%$ for Leopard, i.e. fourfolds. In a fully water-saturated state, the motionally averaging regime is barely present in Bentheimer, while it is significant in Leopard. Consequently, application of CPMG-based techniques to these sandstones over the broad range of saturation states created by the centrifuge pressure potential complicates comparisons.

Fig. 6

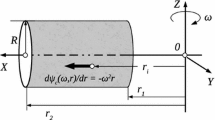
Diagram of a constant gradient (frequency encode) Inverse Recovery pulse sequence ($T_1$ 1D-resolved). The first interval $\tau$ stands for time-interval loop attenuating $T_1$ signal in one dimension. The second interval $\tau _\mathrm{e}$ is designed to provide sufficient delay to acquire 1D images in a second dimension

3.2 $T_1$ Inverse Recovery Experiment

In order to obtain the spatially resolved $T_1$ distributions, a modified Inversion Recovery pulse sequence was utilised (see Fig. 6). Instead of acquiring the free induction decay (FID) produced by the $90^\circ$ pulse, a $180^\circ$ pulse is applied after a period equal to $\tau _\mathrm{e}/2$ and induces an echo to be generated. The generated echo is utilised in combination with a read gradient to register the fluid distribution within the sample. In this implementation, a read gradient is switched on before the first $180^\circ$ pulse and switched off after the acquisition of the echo. Switching the gradient on 6–10 ms before starting the pulse sequence avoids having to wait for the gradient to stabilise, enabling considerably short $\tau$ and $\tau _\mathrm{e}$. Notice that only unwanted coherences would be spoiled during the recovery part of the experiment. For this pulse sequence, the acquired echo contains a distribution of frequencies that are linearly associated with different positions of the sample.

$$\begin{aligned} \omega = \gamma G z \;. \end{aligned}$$

(9)

The measured echo can be mathematically described as

$$\begin{aligned} M(t) = \int \rho (z) \left( 1-2\mathrm{e}^{-\tau /T_1}\right) \mathrm{e}^{-i(\gamma G z) t} \mathrm{d}z, \end{aligned}$$

(10)

where $T_1$ is the longitudinal relaxation time and $\rho (z)$ is proportional to distribution of fluid in the z direction. For a set value of $\tau$, $\rho (z)$ can be obtained from Eq. (10) via a Fourier transform. To determine the $T_1$ distribution of the fluid within the sample at different positions, the pulse sequence is performed for N values of recovery time $\tau$ and N distinct echoes are acquired. For a heterogeneous sample having a distribution of $T_1$ values, this procedure results in a 2D dataset and can be described as

$$\begin{aligned} M(\tau ,t) = \iint \rho (T_1,z) \left( 1-2\mathrm{e}^{-\tau /T_1}\right) \mathrm{e}^{-i(\gamma G z) t} \mathrm{d}T_1 \mathrm{d}z , \end{aligned}$$

(11)

from which the set of spatially resolved $T_1$ distributions can be obtained $\rho (T_1,z)$. Equation (11) is a combination of a Fourier transform with a Fredholm integral of the first kind and in order to obtain $\rho (T_1,z)$ the inversions must be performed separately. Since inverting the Fredholm integral involves a Tikhonov regularisation (Tikhonov and Arsenin 1977), the Fourier transform of each obtained echo must be performed first. Then, the Tikhonov-regularised nonnegative least squares are performed to each series of signal amplitudes obtained for the space positions, z. The Tikhonov regularisation must be optimised, and the smoothing parameter is chosen according to the analysis of the fitting residuals (Hansen 1992b, a).

3.3 Simulated Longitudinal Relaxation $T_1$ and $T_1$-z

NMR response was modelled using random walk technique on a regular lattice, which mimics molecular thermal random motion (self-diffusion) of fluid molecules (Bergman et al. 1995). In the context of NMR relaxation, this approach implies the use of the spin packets concept—each walker represents a volumetric ensemble of excitated spins. We used the implementation of a technique described in detail in Arns et al. (2005b), Arns and Melean (2009). Initial at time $t=0$, N walkers representing spin packets of a total strength $M_\mathrm{w}(0) = \Sigma _{n=0}^N M_\mathrm{w}^n(0)$ are randomly distributed in the 3D regular lattice of a pore phase of a segmented digitised image. At each time step i, the walkers are moved from their initial position to a neighbouring site on a lattice in one of six directions by $\epsilon = \sqrt{D_0 \; \tau _i}$, where $D_0$ is the bulk diffusion constant of the fluid. The attempt to invade a phase with different label which posess nonzero surface relaxivity $\rho _1$ would kill a walker with probability $\nu /6$, where $\nu$ is a random number drawn from normal distribution. Longitudinal relaxation in fluids saturating solid porous media is known to be a superposition of bulk and surface relaxation. Since these processes are independent, the resulting survival probability of a spin packet is a product of the individual survival probabilities due to each process over the given time step i: $S_i$ = $S_\mathrm{bulk} \cdot S_\mathrm{surf}$, where $S_\mathrm{bulk}$ = exp ($\tau _i$/$T_\mathrm{1,B}$) stands for survival probability describing bulk relaxation and survival term $S_\mathrm{surf}$ = $1 - \nu$ describes a surface relaxation process. The killing probability $\nu$ is related to the surface relaxivity $\rho _1$ via $T_1$ (Bergman et al. 1995; Arns and Melean 2009): $\nu = \rho _1 \epsilon / D_0 + O((\rho _1 \epsilon / D_0)^2)$. The survival probability due to surface relaxation process then $S_\mathrm{surf} = 1 - 6\rho _1 \tau _i/\epsilon$. Time-dependent strength of each walker at a time $t = \varSigma _i t_i$ is an initial magnetisation multiplied by survival probability at each time step. Thus, the evolution of summary strength of walkers over discrete space and time provides the simulated $T_1$ NMR signal attenuation; the resulting simulated magnetisation decay is a sum of all walkers strength at a given time step: $M_\mathrm{w}(t) = \varSigma _i M_\mathrm{w}^n(t_i) = M_\mathrm{w}(0) \varPi _i S_i$.

The $T_1$-z experiments are simulated by performing $T_1$ simulations on nearly cubic subsets of the composite $\mu$-CT images. The size of subsets along the drainage direction (z-axis) is selected to be equal to the resolution of the experimental. In $x-y$ plane, the subsets are selected to be a maximum square inscribed in the imperfect circular cross section of the image. Thus, the effect of gradient to encode the position in frequency encode $T_1$-z experiment was substituted by idealised representation of physically isolated volumetric subsets. For Bentheimer, simulations of spatially resolved NMR responses were performed on each of twelve 690 $\times$ 1024 $\times$ 1024 voxel slabs with appropriate offset, representing 12 partially resolved points along the image (equivalent MRI resolution is 1.99 mm/pt). For Castlegate seven 960 $\times$ 960 $\times$ 960 voxel slabs were used (equivalent MRI resolution is 3.23 mm/pt). For Leopard $T_1$-z, simulations performed using twelve 800 $\times$ 800 $\times$ 800 voxel slabs, so that the equivalent MRI resolution is 1.72 mm/pt.

3.4 Simulated and Experimental NMR Relaxation-Based Relative Permeability

Figures 7 and 8 depict the experimental and simulated $T_1$-z maps for each of three sandstone rocks centrifuged at four different speeds. $T_1$-z experiments were performed with the following parameters: 30 $\tau$ steps spaced logarithmically from 0.1 to 3000 ms, a relaxation delay value of $\tau _\mathrm{e} =$ 1.8 ms, constant gradient strength $G =$ 10 mT/m, and 32 scans with inter-scan time delay of 8 s.

Fig. 7

Experimental $T_1$-z maps of three sandstones centrifuged at different rotational speeds: Bentheimer, left column a, d, g, k: 400, 650, 750 and 950 rpm. Castlegate, middle column b, e, h, l: 500, 650, 850 and 950 rpm. Leopard, right column c, f, j, m: 500, 850, 1100 and 1600 rpm. The solid white line corresponds to $T_1$ logmean values along the core length; the dashed white line corresponds to logmean values taken from distributions truncated below 33 ms

Fig. 8

Simulated $T_1$-z maps of three sandstones centrifuged at various rotational speeds: Bentheimer, left column a, d, g, k: 600, 750, 1050 and 1350 rpm. Castlegate, middle column b, e, h, l: 750, 950, 1100 and 1500 rpm. Leopard, right column c, f, j, m: 950, 1500, 2000 and 3000 rpm. The solid white line corresponds to $T_1$ logmean values along the core length; the dashed white line corresponds to logmean values taken from distributions truncated below 33 ms

Experiments and simulations correspond to a steady-state centrifuge primary drainage, i.e. rocks are totally water-wet and equilibrium conditions at a particular rotational speed are established. The solid white line on the $T_1$-z maps (Fig. 7) indicates logmean of $T_1$ distributions along the core ($T_\mathrm{1\,LM}$) and the dashed line shows distributions truncated below the 33 ms cut-off value ($T_\mathrm{1\,LM,33}$) presumed separating irreducible and mobile fluids. Separation of these two lines is an indication of the immobile fluid. The experimental $T_1$-z maps in Fig. 7 show fluctuations of both $T_\mathrm{1\;LM}$ and $T_\mathrm{1\,LM,33}$ at low saturations. These fluctuations are likely associated with experimental noise and possible redistribution of fluids in a core after stopping the centrifuge. Figure 9 shows comparison plots of relative permeability curves calculated from $T_1$-resolved NMR responses on centrifuge-drained samples between simulation and experiment. In addition to simulations performed on a whole composite $\mu$-CT image, a data set is added where all spatially resolved $T_1$ distributions were calculated on the same 400$^3$ voxel subset to evaluate the influence of rock heterogeneity. The saturation of subsets was set stepwise (uniform capillary pressure within each subset).

Fig. 9

Left column Comparison of CM-$T_1$-z simulated and experimental relative permeability curves to experimental SST and simulated using LBM reference curves for a Bentheimer; c Castlegate; e Leopard. Right column the uniform data set (*) is replaced with experimental $T_1$ data calculated on distributions truncated below 33 ms cut-off

Experimental and simulated relative permeability curves of the water phase derived from $T_1$ distributions show a good match of corresponding Corey fit exponents, $n_\mathrm{w}$: 4.6 versus 4.9–5.0 for Bentheimer; 4.8 versus 4.9–5.0 for Castlegate and 5.3 versus 5.3–6.5 for Leopard. Experimental data (Fig. 7) exhibit an increasing degree of scattering with heterogeneity increase (Bentheimer $\rightarrow$ Castlegate $\rightarrow$ Leopard) towards the higher wetting fluid saturation. This may be explained by the nature of interpretation of NMR experiments: a fixed pore to throat aperture ratio is assumed. It is worth to recall that these rocks exhibit strongly different mean relaxation times which makes the approach sensitive to short-time component responses associated mainly with microporosity.

4 Discussion

4.1 Saturation Profiling Techniques

Corey exponents of water relative permeability, $n_\mathrm{w}$, obtained with different techniques are summarised in Table 5. The index (u) stands for “uniform set”—CM-NMR simulations were performed on composite images constructed by 14–17 identical relatively small $400^3$ voxel subsets; index (h) stands for “heterogeneous”—simulations carried out using whole composite images, better reflecting variations of rock morphology when present. Comparison of wetting phase relative permeability obtained using saturation profile information, including NMR-based approaches, reveals expected similarity between different techniques as well as sensitivity to image resolution for numerically simulated results.

Table 5 Summary of Corey saturation exponents $n_\mathrm{w}$

For Bentheimer sandstone Corey exponents obtained from profiling techniques are very close to each other: simulations performed on ${\mu }$-CT image resulted in $n_\mathrm{w}=3.86$ for profiling capillary pressure-based method (CM-Pc), $n_\mathrm{w}=3.90$ for the same technique performed experimentally using frequency-encoding NMR and $n_\mathrm{w}=4.05$ using NMR phase encoding technique. Our USS CM (Hagoort type) experiment provides $n_\mathrm{w}$ = 4.54 matching precisely the value $n_\mathrm{w}$ = 4.55 reported by Hagoort (1980). Other published data include Hagoort (1980) and Holt et al. (1996) with $n_\mathrm{w}$ = 4.02 and 4.01, respectively. Thus, exponent values fall approximately between 3.9 and 4.5. For Castlegate sandstone profiling techniques provide Corey exponents close to each other: simulations performed on ${\mu }$-CT image resulted in $n_\mathrm{w}=3.52$ for profiling method (CM-Pc), $n_\mathrm{w}=3.70$ for the same technique performed experimentally using frequency-encoding NMR and $n_\mathrm{w}=3.59$ using NMR phase encoding technique. For Leopard sandstone Corey exponents are: $n_\mathrm{w}=3.52$ for simulations performed on ${\mu }$-CT image using profiling method (CM-Pc), $n_\mathrm{w}=3.58$ for the same technique performed experimentally using frequency-encoding NMR and $n_\mathrm{w}=3.89$ using NMR phase encoding technique.

While various profiling techniques provide relative permeability exponents $n_\mathrm{w}$ close to each other for a specific type of rock, one may expect contrary to our observations that the exponent should be lower for Bentheimer and higher for Leopard reflecting rock heterogeneity. The explanation is likely associated with the spatial nature of data provided by profiling techniques: the spread of multiple points of locally determined relative permeability reflects complexity and heterogeneity of the porous system; however, the integration of these points for the whole plug is not a trivial task. We use running average and subsequent nonlinear least-square approach to minimise error of fitting function to produce a single curve; hydraulic conductance may dictate a complex mixture of linear and geometric averages. Numerical results are affected by resolution limits and accuracy of low-saturation region of capillary pressure curves. Consequently, various methods predict very similar relative permeability curves for Bentheimer sandstone where resolution is less critical. Centrifuge-profile estimates of relative permeability for Castlegate and Leopard leading to $n_\mathrm{w}$ around 3.5–3.7 should be regarded as inaccurate.

4.2 Relaxation-Based Estimates

By assuming that capillary pressure and relative permeability as function of saturation can be directly related to each other, Burdine–Corey model provides exponents $n_\mathrm{w}$ within a range restricted by values between 3 and 5. Based on the literature and data obtained with other methods we conclude that the values of Corey exponent $n_\mathrm{w}$ determined with experimental and simulated NMR (derived from the whole relaxation time distributions: 4.6–5.0 for Bentheimer, 4.8–5.0 for Castlegate and 5.3–6.5 for Leopard) are slightly exaggerated comparing to values from profiling techniques.

Consider two models used here to compare relative permeability estimates of water phase: Burdine–Corey power law, Eq. (4), and modified SDR NMR permeability correlation, Eq. (8). Ignoring relative permeability end points (by using $k^{o}_\mathrm{rw}=1$) we may express the equity of two models in the following form:

$$\begin{aligned} k_\mathrm{rw} = S_\mathrm{we}^{n_\mathrm{w}} = \frac{a(S_\mathrm{w})}{a(1)} \; \frac{T_\mathrm{1\;LM}(S_\mathrm{w})^2}{T_\mathrm{1\;LM}(1)^2}\;S_\mathrm{w}^{\;4} , \end{aligned}$$

(12)

$a(S_\mathrm{w})$ and a(1) are original prefactors of the SDR equation noting partial and full saturations, respectively. Essentially, we compare two power-law models as function of saturation, and relaxation time ratio is also expected to be a function of saturation:

$$\begin{aligned} k_\mathrm{rw} = S_\mathrm{we}^{n_\mathrm{w}} = S_\mathrm{we}^{n_{\mathrm{NMR}} + 4} . \end{aligned}$$

(13)

As discussed above, the Corey power-law model is a simplified representation of pore space and rather simplistically reflects contribution to flow from microchannels. Instead, the model provides an estimate of the distribution width of main macroflow channels. Narrow distribution of sizes leads to low values of water exponents $n_\mathrm{w}$ and broad distributions or inclusion of microporosity into data would lead to high values of exponent $n_\mathrm{w}$. This is exactly the case with CM-NMR technique. Both experimental and simulated $T_1$-z data contain signal contributions originating from microporosity. This, however, has no influence on acquired response from Bentheimer core.

Indeed, experimental $T_1$-z relative permeability agrees with other sources. Castlegate and especially Leopard sandstone which have larger contribution of short-time components (compare $T_\mathrm{2\,LM}$ 160 and 40 ms, respectively) in the total spectra, having microporosity response included. Therefore, it is not surprising that CM-NMR relative permeability estimated for these rocks corresponds to rocks with very broad pore-size distributions.

It can be useful to evaluate the relaxation saturation correlation (an NMR-specific part of correlation) outside the SDR equation, since the saturation term in Eq. (8) with exponent of 4 may obscure important dependencies. Furthermore, we can add for comparison relaxation data truncated below the standard cut-off of 33 ms to obtain CM-NMR data sets “free” from microporosity effects. The influence of short-time components of NMR response is also clear. For Bentheimer (see Fig. 10a) both fitting curves are very close, with $n_{\mathrm{NMR}}$ 0.97 and 0.82 for full and truncated by 33 ms cut-off distributions, respectively. Castlegate shows increasing separation with $n_{\mathrm{NMR}}$ 0.91 and 0.67 for full and truncated by 33 ms cut-off distributions (Fig. 10b).

Fig. 10

Squared logmean $T_1$ of full and reduced by 33 ms cut-off distributions simulated at different centrifuge drainage saturations for a Bentheimer; b Castlegate; c Leopard

Lastly, in the case of Leopard the two curves show significant separation having $n_{\mathrm{NMR}}$ 1.30 and 0.57 for full and truncated by 33 ms cut-off distributions (Fig. 10c). Interestingly, the heterogeneity of that rock strongly decreases the correlation of $T_\mathrm{1,\;LM,33}$ to saturation. These values provide a better relative permeability match to the rest of the data, Table 5. (h33) label stands for simulated data where $T_\mathrm{1,\;LM}$ have been calculated from distributions truncated by 33 ms cut-off. The assumption of $a^S$ = $a^1$ by AlGhamdi et al. (2013) means that correlation can be written in the form of Eq. (13). In this case for water-wet rocks SDR-based Eq. (12) cannot obtain $k_\mathrm{rw}$ values of systems with $n_\mathrm{w}$ $\le$ 4, while Burdine–Corey model has a range of exponents between 3 and 5. The assumption that the prefactors are the same for fully and partially saturated rock might be too strong.

5 Conclusions

This study demonstrates the applicability of NMR relaxation techniques for wetting phase relative permeability prediction. Results of $T_1$-z simulations are in good agreement with experiment confirming the accuracy of both numerical rock representations and the accuracy of NMR simulations. Figure 9a–f shows that scattering of experimentally obtained data points increases with increasing rock heterogeneity. This may be due to the increasing contribution of microporosity as captured by the MICP experimental pore-throat distributions, Fig. 4a, c, e, which suggests an increasing contribution to flow from microchannels (from Bentheimer to Leopard). Secondly, we demonstrated a reasonable match between capillary pressure models (Corey and Burdine models) and the SDR-based correlation. Comparison of relative permeabilities obtained with essentially non-destructive methods (NMR and $\mu$-CT based) yields reproducible results. The observations can be summarised as following:

• 1. Simulated NMR responses from three centrifuge-drained sandstone rocks of various morphology and mineral composition are in excellent agreement with experiment.

• 2. Saturation distributions may be improved by considering digital images of larger cross section.

• 3. NMR longitudinal relaxation accurately captures characteristic length of wetting phase in sufficiently homogeneous systems and is suitable for relative permeability estimates of wetting phase.

• 4. The NMR relative permeability predictions based on relaxation showed better agreement with experiment for rocks which exhibit increased clay content/microporosity. This could indicate that this method is applicable for a broader range of rocks.

The introduction of NMR saturation exponent allows calibration of the CM-$T_1$-z relative permeability method using data from other measurements.