1 Introduction

The number of injection wells in the USA is estimated to be above 500,000 (USEPA 2001; Lustgarten and Schmidt 2012). Without doubt, such fluid injections into the subsurface influence the stress state of respective rock formations. Highly sensitive seismometers can detect micro-earthquakes resulting from hydraulic fracturing operations, geothermal stimulations or wastewater injections. The created pathways are often a desired result to enhance the productivity of the reservoir exploitation, but they can also pose environmental risks.

For hydraulic fracturing operations, the concern has been raised that induced fractures could propagate through the overburden and connect the hydrocarbon-bearing formations with shallow groundwater aquifers. Such a contamination of underground sources for drinking water can usually be ruled out due to the distance between the shale formations and the aquifers that contain drinkable water (Zoback et al. 2010). A study by Fisher and Warpinski (2012) revealed that injection-induced seismicity is usually very confined. Only the presence of subvertical faults allows an upward migration of the seismicity. Besides the risk of contamination, the potential for reactivating faults and creating earthquakes can become crucial for the public perception of a project (Zoback et al. 2010; Leucht et al. 2010; Reith et al. 2013). This highlights the necessity to increase the knowledge base of coupled hydraulic and geomechanical modelling to better understand the relevant processes that lead to fault reactivation.

To ensure a broad applicability of a modelling approach designed for this purpose, the simulation code should cover multiphase flow in combination with the mechanical response of the rock formation. For this purpose, two simulators can be coupled, such as TOUGH2 and Code_Aster by Rohmer and Seyedi (2010) or TOUGH2 and FLAC3D by Rutqvist and Tsang (2002), Cappa and Rutqvist (2011). The latter combination has recently been expanded towards the modelling of fault reactivation by hydraulic fracturing (Rutqvist et al. 2013).

The aim of this study is to extend a given coupled multiphase flow and geomechanical approach towards the analysis of fault reactivation within a single software code, i.e. the open-source simulator DuMu\(^{{x}}\). We work along the hypothesis that this goal can be achieved by using a volume-based approach, which does not require to model the fault as a discrete surface but as a elements representing a fault zone instead. The modelling approach is then applied to a scenario setup presented in Rutqvist et al. (2013) to study the potential of fault reactivation by hydraulic fracturing operations.

2 Modelling Concept

2.1 Hydro-geomechanical Model

The modelling approach presented here uses the linear elastic two-phase model developed by Darcis (2013) consisting of two fluid phases and the rock as a third, solid phase. The mathematical description of this system is based on fundamental balance equations for the system’s mass and linear momentum, the total energy and the entropy. Some assumptions were made to simplify the derivation of the governing equations:

  • All participating solid materials are consolidated in a single solid phase s

  • Small deformations of the solid (application of small deformation theory valid)

  • Incompressible solid matrix and brine phase (Solid density \(\rho _{s}\) \(=\) const., brine density \(\rho _{w}\) \(=\) const.)

  • Isothermal conditions (solving the energy balance is not required)

  • Quasi-stationary conditions (inertia forces are neglected)

  • All the participating phases are immiscible within each other.

2.1.1 Governing Equations

In general, the mass balance for a fluid phase \(\alpha \) in its differential form can be written as

$$\begin{aligned} \frac{\partial \phi S_{\alpha } \rho _{\alpha }}{\partial t} + \mathrm {div}(\rho _{\alpha } \mathbf {v_{\alpha }}) = q_{\alpha } \end{aligned}$$
(1)

where \(\rho _{\alpha }\) represents the density, \(\mathbf {v_{\alpha }}\) is the velocity of phase \(\alpha \), \(\phi \) is the porosity, \(S_{\alpha }\) is the saturation and \(q_{\alpha }\) is the source/sink term of phase \(\alpha \).

The work presented here addresses a system with two fluid phases present and the solid as the porous medium. The mass balance of the solid phase is taken into account indirectly by expressing the effective porosity \(\phi _{\mathrm {eff}}\) as a function of the volumetric strain (the sum of elastic and plastic volumetric strain) \(\varepsilon _{v}\) and the initial porosity \(\phi _{\mathrm {0}}\):

$$\begin{aligned} \phi _{\mathrm {eff}} = 1 - (1 - \phi _{0}) e^{-\varepsilon _v} \end{aligned}$$
(2)

The effective permeability \(k_\mathrm {eff}\) was obtained from the an initial permeability \(k_\mathrm {0}\) with

$$\begin{aligned} k_{\mathrm {eff}} = k_{0} \left( \frac{\phi _{\mathrm {eff}}}{\phi _{0}} \right) ^n \end{aligned}$$
(3)

Both relations were developed by Chin et al. (1998) for petroleum reservoirs and assume isotropy and incompressible grains (Biot’s \(\alpha \) = 1) and have proven to be well suited for both elastic and plastic deformation (e.g. Cappa and Rutqvist 2011; Rutqvist et al. 2013). The power-law exponent n in Eq. 3 determines how strong porosity changes affect the permeability. It ranges from 3 up to 25 for consolidated geologic materials (Wong et al. 1997; David et al. 1994). Consistent with Cappa and Rutqvist (2011) and Rutqvist et al. (2013), we use a value of \(n=15\) for our simulations.

The fluid velocities of the respective phases \(\alpha \) relative to the solid are included in the form of the standard Darcy multiphase approach

$$\begin{aligned} \mathbf {v_{\alpha }} = -\frac{k_{\mathrm {r}\alpha }}{\mu _\alpha } \, \mathbf {K}_\mathrm {eff} \, (\mathrm {grad} \, p_\alpha - \rho _{\alpha } \,\mathbf {g}) \end{aligned}$$
(4)

with \(k_{\mathrm {r}\alpha }\) as the relative permeability (calculated after Brooks and Corey 1964), \(\mathbf {K}_\mathrm {eff}\) as the effective permeability tensor composed of the entries \(k_\mathrm {eff}\) (see Eq. 3), \(\mu _{\alpha }\) as the dynamic fluid viscosity and \(\mathrm {grad} \, p_\alpha \) as the pressure gradient of phase \(\alpha \). By inserting Eq. 4 into the mass balance equation (Eq. 1) and by replacing the porosity \(\phi \) by the effective porosity \(\phi _{\mathrm {eff}}\) from Eq. 2, we get

$$\begin{aligned}&\frac{\partial ( \phi _\mathrm {eff} \rho _\alpha S_\alpha )}{\partial t} - \,\mathrm {div} \left\{ \rho _\alpha \frac{k_{\mathrm {r}\alpha }}{\mu _\alpha } \, \mathbf {K}_\mathrm {eff} \, (\mathrm {grad} \, p_\alpha - \rho _{\alpha } \,\mathbf {g}) + \phi _\mathrm {eff} \, S_\alpha \, \rho _\alpha \frac{\partial \mathbf {u}}{\partial t} \right\} = q_\alpha \quad \end{aligned}$$
(5)

for the combined momentum and mass balance of the fluids (Darcis 2013). The third term in Eq. 5 with the displacement velocity \(\frac{\partial \mathbf {u}}{\partial t}\) takes the fluid flow due the displacement into account. We define the displacement to be negative in coordinate direction in agreement with the rock mechanics sign convention and thus the positive sign in Eq. 5.

For the solid phase, a quasi-static momentum balance is used as the time derivatives are assumed to be negligibly small:

$$\begin{aligned} \mathrm {div}\varvec{\sigma } - \rho _\mathrm {b} \mathbf {g} = 0. \end{aligned}$$
(6)

Here, \(\rho _\mathrm {b}\) represents the bulk density and \(\mathbf {g}\) is the vector of the gravitational acceleration. After Biot’s theory of poroelasticity (Biot 1941), which has been expanded to multiple phases by Lewis and Schrefler (1999), the effective pore pressure

$$\begin{aligned} p_\mathrm {eff} = S_{w}p_{w} + S_{n}p_{n} \end{aligned}$$
(7)

is taken into account by describing the stress of the solid phase with the effective stress tensor (assuming Biot’s \(\alpha \) = 1)

$$\begin{aligned} \varvec{\sigma ^{\prime }} = \varvec{\sigma } - p_\mathrm {eff}\,\mathbf {I} \end{aligned}$$
(8)

Equation 6 can be linearised by subtracting the initial state (subscript 0) for effective stress, effective pressure and the bulk density:

$$\begin{aligned} \Delta \varvec{\sigma }= & {} \varvec{\sigma } - \varvec{\sigma _0} = \varvec{\sigma ^{\prime }} - \varvec{\sigma _{0}^{\prime }} + \, (p_\mathrm {eff} - p_\mathrm {eff,0}) \,\mathbf {I} \end{aligned}$$
(9)
$$\begin{aligned}= & {} \Delta \varvec{\sigma ^{\prime }} + \, \Delta p_\mathrm {eff} \,\mathbf {I}\end{aligned}$$
(10)
$$\begin{aligned} \Delta \rho _\mathrm {b}= & {} \rho _\mathrm {b} - \rho _\mathrm {b,0} \end{aligned}$$
(11)

This gives

$$\begin{aligned} \mathrm {div}(\Delta \varvec{\sigma ^{\prime }} + \Delta p_\mathrm {eff}\,\mathbf {I}) - \Delta {\rho }_\mathrm {b} \mathbf {g} = 0. \end{aligned}$$
(12)

We assume small porosity changes (\(\Delta \phi \approx 0\), \(\Delta (1 - \phi ) \approx 0\)) and a constant solid density (\(\Delta \rho _{s} \approx 0\), see assumptions in Sect. 2.1). Furthermore, the initial saturation of the wetting phase \(S_{w}\) is equal to one and thus the change in saturation of the nonwetting phase \(\Delta S_{n}\) becomes \(S_{n}\), while \(\Delta S_{w}\) becomes \(-S_{n}\). Accordingly, the bulk density change reduces to

$$\begin{aligned} \Delta \rho _\mathrm {b}= & {} \Delta \phi (S_{w}\rho _{w} + S_{n}\rho _{n}) + \phi \Delta (S_{w}\rho _{w}+ S_{n}\rho _{n}) \end{aligned}$$
(13)
$$\begin{aligned}&+\Delta (1 - \phi )\rho _{s} + (1 - \phi ) \Delta \rho _{s} \end{aligned}$$
(14)
$$\begin{aligned}\approx & {} \phi S_{n}(\rho _{n} - \rho _{w}) \phantom {S_{n}\rho _{n}) + \phi \Delta (S_{w}\rho _{w}+ S_{n}\rho _{n}) } \end{aligned}$$
(15)

With these simplifications, we get

$$\begin{aligned} \mathrm {div}(\Delta \varvec{\sigma ^{\prime }} + \Delta p_\mathrm {eff}\,\mathbf {I}) - \phi \, S_{n} \,( \rho _{n} - \rho _{w}) \, \mathbf {g} = 0. \end{aligned}$$
(16)

for the momentum balance of the solid.

2.1.2 Constitutive Equations and Supplementary Constraints

To obtain a closed system, constitutive equations and constraints are required:

  • Linear elastic behaviour of the rock, i.e. the stress \(\varvec{\sigma }\) increases linearly and reversibly with the strain \(\varvec{\varepsilon }\) (according to Hooke’s law). Two independent elastic constants relate the stress and strain in an isotropic case. Here, we use the Lamé constant \(\lambda \) and the shear modulus G:

    $$\begin{aligned} \varvec{\sigma } = \lambda \, \mathrm {tr}[\varvec{\varepsilon }] + 2 \,G \, \varvec{\varepsilon } \end{aligned}$$
    (17)

  • The strain \(\varvec{\varepsilon }\) is derived from the displacement vector as follows

    $$\begin{aligned} \varvec{\varepsilon } = \frac{1}{2} (\mathrm {grad} \, \mathbf {u} + \mathrm {grad^{T}} \mathbf {u} ) \end{aligned}$$
    (18)

  • The sum of the fluid saturations adds up to one

    $$\begin{aligned} \varSigma _{\alpha } \, S_{\alpha } = 1 \end{aligned}$$
    (19)

  • The pressures are connected via the capillary pressure (calculated here according to the Brooks and Corey relation (Brooks and Corey 1964))

    $$\begin{aligned} p_{n} = p_{w} + p_{c}(S_{\alpha }) \end{aligned}$$
    (20)

2.2 Solution Procedure

For all simulations, the numerical toolbox DuMu\(^{{x}}\) (Flemisch et al. 2011; Becker et al. 2015) was used, which is based on the Distributed and Unified Numerics Environment DUNE (Bastian et al. 2008a, b). The system with two fluid phases and the solid as the porous medium with all equations described above was already implemented as the so-called el2p-model. The discretisation is described in detail by Darcis (2013), and thus, we will give only a short summary of important characteristics of the model.

Two different discretisation schemes are used for the two balance equations. While Eq. 5 is discretised with a vertex-centred finite volume scheme, the so-called box method (Helmig 1997), the standard Galerkin finite element method is used for the momentum balance of the solid (Eq. 6).

As reported by Darcis (2013), with this approach spurious pressure oscillations can be avoided. Kim (2010) also observed stability issues and suggested a staggered grid approach. A similar—quasi-staggered—effect is achieved here by the different weighting functions of the box and the standard Galerkin finite element method, allowing a nodal-based approach without explicitly using staggered grids.

In accordance with the model developed by Darcis (2013), on which this approach is based, all equations are solved fully coupled. Because of the constraints for pressure and saturation presented in 2.1.2 (Eqs. 19 and 20), we can reduce the system from five to three variables. Again, in agreement with Darcis (2013), we use the \(p_{w}-S_{n}\) formulation and solve the system for the primary variables \(\mathbf {u}\), \(p_{w}\) and \(S_{n}\).

Fig. 1
figure 1

The Mohr circle is a way to graphically illustrate the stress components acting on a plane inclined by an angle \(\beta \). The x-coordinate of each point on the circle represents the normal stress, while the y-coordinate is equal to the shear stress. The effective pressure shifts the Mohr circle to the left, as it reduces only the normal stresses (see Eq. 8). At the critical pressure \(p_{\mathrm {crit}}\), the failure curve, which is characterised by the cohesion \(S_{\mathrm {0}}\) and by the angle of internal friction \(\varphi \), and the Mohr circle touch each other at R\(^{\prime }_{1}\). If we assume that a plane with the orientation \(\beta _1\) exists, slip on this plane will happen (top). For a fault with a different orientation \(\beta _2\), a higher pressure shift \(p_{\mathrm {crit}}\) is needed until the effective stress state R\(^{\prime }_{2}\) on the Mohr circle reaches the failure curve

Full size image

2.2.1 Failure Evaluation

This work focuses on the effect of fault reactivation. To evaluate the potential for shear failure on a fault, the Mohr–Coulomb criterion is used. The failure curve is assumed to be linear and is then characterised by \(S_{\mathrm {0}}\), which accounts for the cohesive forces between the rock particles (Unit: Pa or \(\frac{\mathrm {N}}{\mathrm {m}^2}\)), that needs to be overcome before failure is initiated, and by \(\varphi \), which is the angle of internal friction and related to the coefficient of friction \(\mu _{\mathrm {frict}}\) by

$$\begin{aligned} \mathrm {tan} \varphi = \mu _{\mathrm {frict}}. \end{aligned}$$
(21)

One way to define the failure criterion is by a worst-case assumption: Failure occurs as soon as the Mohr circle (representing the effective stress state) touches the failure curve. More specifically, the point \(R_{1}^{\prime }\) where the Mohr circle touches the failure curve corresponds with a critical angle (see Fig. 1, top). One can assume that a plane inclined by this angle exists if no knowledge about fault or joint orientations is available. With that said, a critical pressure \(p_{\mathrm {crit}}\), for which the Mohr circle touches the failure curve, can be defined. This mathematically translates to

$$\begin{aligned} p_{\mathrm {crit}} = \sigma _{\mathrm {m}} - \frac{|\tau _{\mathrm {max}}| - S_{0} \, \mathrm {cos}\varphi }{\mathrm {sin}\varphi } \end{aligned}$$
(22)

as given in Jaeger et al. (2007). The mean principal stress \(\sigma _{\mathrm {m}}\) and the maximum shear stress \(\tau _{\mathrm {max}}\) are calculated from the principal stresses \(\sigma _1\) and \(\sigma _3\):

$$\begin{aligned} \sigma _{\mathrm {m}} = \frac{1}{2} (\sigma _1 + \sigma _3), \qquad \tau _{\mathrm {max}} = \frac{1}{2} (\sigma _1 - \sigma _3) \end{aligned}$$
(23)

Based on Eq. 22, a pressure margin between the critical pressure for shear slip \(p_{\mathrm {crit}}\) and the effective pressure \(p_{\mathrm {eff}}\) can be defined after Rutqvist and Tsang (2002).

$$\begin{aligned} p_{\mathrm {sm}} = p_{\mathrm {eff}} - p_{\mathrm {crit}} \end{aligned}$$
(24)

If data about fault or joint orientations are available, the normal stress \(\sigma (\beta _2)\) and shear stress \(\tau (\beta _2)\) of the stress state \(R_2\) can be calculated with the help of the dip angle \(\beta _2\) of the fault or joint (see Fig. 1, bottom):

$$\begin{aligned} \sigma (\beta _2) = \sigma _{\mathrm {m}} + \tau _{\mathrm {max}} \times \mathrm {cos}(2\beta _2), \qquad \tau (\beta _2) = \tau _{\mathrm {max}} \times \mathrm {sin}(2\beta _2) \end{aligned}$$
(25)

On the failure curve, the normal stress value \(\sigma _{\mathrm {fc}}\) corresponds with the same shear stress \(\tau (\beta _2)\):

$$\begin{aligned} \sigma _{\mathrm {fc}} = \frac{\tau (\beta _2) - S_{0}}{\mu _{\mathrm {frict}}} \end{aligned}$$
(26)

If \(\sigma (\beta _2)\) is reduced by \(p_{\mathrm {crit}}\) so far that it matches with the normal stress \(\sigma _{\mathrm {fc}}\) (i.e. the effective stress state R\(^{\prime }_{2}\) where touches the failure curve as illustrated by Fig. 1), failure will happen. Similar to the worst-case scenario, a pressure margin for shear slip \(p_{\mathrm {sm}}\) can be formulated:

$$\begin{aligned} p_{\mathrm {sm}} = \sigma _{\mathrm {fc}} - \sigma (\beta _2) \end{aligned}$$
(27)

In both cases, shear failure on the fault happens if \(p_{\mathrm {sm}}\) is greater than zero.

2.2.2 Fault Reactivation

Emerging technologies such as hydraulic fracturing, CO\(_2\) storage in the subsurface or geothermal stimulation have created a need to expand existing methods capable of modelling coupled multiphase flow and poro-mechanics towards the simulation of fracture initiation, growth and slip in general. Different approaches have been developed to achieve this goal: Phase-field models represent a fracture interface by describing the change from broken and the intact rock diffusely with an order parameter (Mikelic et al. 2015; Hofacker and Miehe 2013; Miehe et al. 2010). Other approaches depict faults as discrete surfaces by means of zero-thickness elements using a penalty method (Ferronato et al. 2008) or a Lagrange multiplier formulation (Jha and Juanes 2014).

If the focus is shifted from the modelling of discrete fractures and fault surfaces towards the simulation of fault zones and their potential reactivation, the way these structures are geometrically represented changes: Accounting for the fact that faults zones are complex features consisting of a fault core and a damage zone, Rutqvist et al. (2013) choose to model the fault not as a surface but as a fault zone instead, using a so-called ubiquitous joint model. A comparison between different fault modelling approaches by Cappa and Rutqvist (2011) revealed that both a zero-thickness interface and finite-thickness solid elements produce similar results. Thus, we choose to use the latter approach using finite- thickness elements for representing faults, as this fits well into our existing implementation and is also applicable to a variety of fault architectures ranging from single surfaces to complex fault zones (Cappa and Rutqvist 2011).

In a similar fashion, the description of the relevant physics during a slip event varies: It remains under discussion whether the coefficient of friction \(\mu _{\mathrm {frict}}\) is a function of the slip rate and a state variable (accounting average maturity of contact asperities) such as used by Jha and Juanes (2014) or the slip weakening is rate independent (Garagash and Germanovich 2012) and can be modelled by transferring no normal and shear stresses (Ferronato et al. 2008) or by a sudden reduction in the coefficient of friction (Cappa and Rutqvist 2011; Rutqvist et al. 2013).

We propose a different approach based on energetic considerations: During a shear slip event on a fault, previously built-up stress is released and transformed into seismic wave energy, thermal energy due to friction on the fault plane and energy required to cause fracture (Kanamori 2001). Thus, the shear stress on the fault plane is reduced. Following this, we can define the stress drop \(\Delta \sigma _{\mathrm {failure}}\) that denotes the difference in stress before and after a slip event. Generally, this \(\Delta \sigma _{\mathrm {failure}}\) is considered to range from 0.1 to 1 MPa. Such a confined range of values for the stress drop is not only assumed for large earthquakes (Aki 1972; Thatcher and Hanks 1973; Kanamori and Anderson 1975), but observational data indicate that this is also true for small events (Abercrombie and Leary 1993).

This leads to a new concept for modelling shear failure on an existing fault: If pressure margin \(p_{\mathrm {sm}}\) for shear failure is surpassed, slip on the fault reduces the stress by a value assumed to be constant. We assume that the energies, into which the elastic energy is transformed, are either dissipated or negligible for the stress redistribution, and thus, we consider them as not relevant for the phenomena described by our model. Accordingly, we propose to model shear failure simply as a sink of elastic energy. In the following, we will show that this can be modelled conceptually comparable to some of the approaches described above, as in either case a shear stress reduction is achieved by modifying the material properties.

2.2.3 The Maxwell Material as an Energetic/Phenomenological Equivalent

A purely elastic spring and a purely viscous damper in series (so-called Maxwell material) are introduced as a phenomenological equivalent of such an elastic energy sink description.

For such a structure, the stress on both the dashpot and the spring element is the same, but while the spring’s deformation is determined by its elastic modulus E according to Hooke’s law, the dashpot’s reaction to stress is that of a Newtonian fluid characterised by the dynamic viscosity \(\eta \). If this combination of a Hookean spring and a Newtonian dashpot is subjected to a constant strain \(\varepsilon _{\mathrm {0}}\), the time-dependent stress response will be

$$\begin{aligned} \sigma (t) = \sigma _{\mathrm {0}} \, \mathrm {exp} (-t \, E / \eta ) \end{aligned}$$
(28)

as presented in Roylance (2001). We can further calculate the portion of the strain stored reversibly in the spring with

$$\begin{aligned} \varepsilon _{\mathrm {rev}}(t) = \frac{\sigma (t)}{E} = \varepsilon _{\mathrm {0}} \, \mathrm {exp} (-t \, E / \eta ) \end{aligned}$$
(29)

and the irreversible strain of the dashpot, which is the remaining portion of the total strain \(\varepsilon _{\mathrm {0}}\), from

$$\begin{aligned} \varepsilon _{\mathrm {irr}}(t) = \varepsilon _{\mathrm {0}} \, (1 - \mathrm {exp} (-t \, E / \eta )). \end{aligned}$$
(30)

From Eq. 28, we can derive the so-called relaxation modulus

$$\begin{aligned} E_{\mathrm {rel}}(t) = \frac{\sigma (t)}{\varepsilon _{\mathrm {0}}} = \frac{\sigma _{0}}{\varepsilon _{\mathrm {0}}} \mathrm {exp} (-t \, E / \eta ). \end{aligned}$$
(31)

As initially only the spring is deformed and therefore \(\sigma _{0} = E \, \varepsilon _{0}\) is valid, this simplifies to

$$\begin{aligned} E_{\mathrm {rel}}(t) = E \, \mathrm {exp} (-t \, E / \eta ) \end{aligned}$$
(32)

after Roylance (2001).

From Eqs. 29 and 30 follows a time dependence of the reversible and the irreversible displacement: While the reversible strain decreases, the irreversible deformation increases with time. Energy-wise, elastic energy initially stored in the spring is shifted to the dashpot and transformed into heat. It becomes apparent that the Maxwell material behaves energetically similar to the effect of failure described in Sect. 2.2.2: in both cases, elastic energy is dissipated. Thus, we propose to use the Maxwell material as an energetic/phenomenological equivalent to shear failure.

2.3 Simplifications and Assumptions Used for the Shear Failure Process

  • In reality, shear failure would start where the critical pressure is surpassed first. But as we resolve the time discretely during the simulation despite its continuous character, it can happen that for the previous timestep, the critical margin for shear failure \(p_{\mathrm {sm}}\) was below zero for all elements, but is surpassed for several elements after the actual timestep. In order to avoid this, the time discretisation is refined the closer \(p_{\mathrm {sm}}\) gets to zero. This enables us to resolve the onset of fault reactivation and the cell where failure starts quite precisely.

  • For our example, the fault is represented by finite-thickness elements on quadrilateral grids. This means that slip and stress drop happen only in the direction of the coordinate axes and on planes spanned by the coordinate axes, respectively.

  • Once failure has been detected, the direction of maximal shear stress is determined. This gives the plane of shear failure, on which the shear stress is reduced.

  • The whole failure process is modelled within one timestep. This means parameters acting during the failure process such as the speed of the propagating slip are not resolved. Instead, only the effect on the stress field is modelled at the start and the end of a timestep.

  • Furthermore, we assume that the failure process is considerably faster than the flow processes. During the simulation, this is achieved by reducing the timestep length significantly if failure happens.

2.4 Modelling the Shear Failure Process

As already mentioned, this work focuses as a first step on the effect of shear failure; hence, the dissipation of elastic energy due to the visco-elastic behaviour during a slip event is limited to shear stress.

In detail, the pressure margin \(p_{\mathrm {sm}}\) (see Eq. 24) is evaluated at the centre of each element. If the value becomes positive, the stress has to drop on the fault plane with the maximum shear stress. But this desired shear stress reduction can not be achieved with the isotropic linear elastic relation between stress and strain (Eq. 17) used by the purely elastic model by Darcis (2013). Instead, we have to change the elastic constants for the respective direction, and thus, the material becomes anisotropic. For rocks, an orthorhombic symmetry is a reasonable choice (Fjar et al. 2008). In case of isotropy, stress and strain were related by Eq. 17, which is a simplification of relating both via the stiffness matrix \(\mathbf {C}\). For the linear elastic isotropic case, \(\mathbf {C}\) can be written as follows (using the Voigt notation)

$$\begin{aligned} \begin{bmatrix} \sigma _{x} \\ \sigma _{y} \\ \sigma _{z} \\ \tau _{yz} \\ \tau _{xz} \\ \tau _{xy} \\ \end{bmatrix} = \begin{pmatrix} 2 \, G + \lambda &{}\quad \lambda &{}\quad \lambda &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \lambda &{}\quad 2 \, G + \lambda &{}\quad \lambda &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \lambda &{}\quad \lambda &{}\quad 2 \, G + \lambda &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \; G \; &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \; G \; &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \; G \; \end{pmatrix} \begin{bmatrix} \varepsilon _{x} \\ \varepsilon _{y} \\ \varepsilon _{z} \\ \varGamma _{yz} \\ \varGamma _{xz} \\ \varGamma _{xy} \end{bmatrix} \end{aligned}$$
(33)

with \(\sigma \) denoting the normal stress, \(\tau \) the shear stress and \(\varepsilon \) and \(\varGamma \) normal and shear strain, respectively (compare Eq. 17). Additional independent entries are required for the orthorhombic case (Fjar et al. 2008):

$$\begin{aligned} \begin{bmatrix} \sigma _{x} \\ \sigma _{y} \\ \sigma _{z} \\ \tau _{yz} \\ \tau _{xz} \\ \tau _{xy} \\ \end{bmatrix} = \begin{pmatrix} C_{11} &{}\quad C_{12} &{}\quad C_{13} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ C_{12} &{}\quad C_{22} &{}\quad C_{23} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ C_{13} &{}\quad C_{23} &{}\quad C_{33} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad C_{44} &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad C_{55} &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad C_{66} \end{pmatrix} \begin{bmatrix} \varepsilon _{x} \\ \varepsilon _{y} \\ \varepsilon _{z} \\ \varGamma _{yz} \\ \varGamma _{xz} \\ \varGamma _{xy} \end{bmatrix} \end{aligned}$$
(34)

On closer inspection, one notices that the shear and normal components of stress and strain are now decoupled from each other, which allows us to choose different elastic moduli for shear and normal stresses. In the direction of the normal stresses, the rock still behaves elastic, and thus, we choose

$$\begin{aligned} C_{11}&= C_{22} = C_{33} = \lambda + 2 \, G \nonumber \\ C_{12}&= C_{13} = C_{23} = \lambda . \end{aligned}$$
(35)

Depending on the orientation of shear slip, one of the entries \(C_{44}\), \(C_{55}\) or \(C_{66}\) is modified in a way that it reproduces the constant stress drop, while the remaining entries stay elastic. The shear stress \(\tau \) on the failure plane is a product of the shear modulus G multiplied with the respective strain state \(\varGamma \)

$$\begin{aligned} \tau = \varGamma \times G \end{aligned}$$
(36)

The shear stress reduction can be achieved by reducing G in the same way the shear stress is reduced, so the ratio of stress before and after failure matches the ratio of the shear moduli

$$\begin{aligned} \frac{G_{\text {post-failure}}}{G_{\text {pre-failure}}} = \frac{\tau _{\text {post-failure}}}{\tau _{\text {pre-failure}}} = \frac{\tau _{\text {pre-failure}} - \Delta \sigma _{\text {failure}}}{\tau _{\text {pre-failure}}} \end{aligned}$$
(37)

or, solved for the reduced shear modulus \(G_{\mathrm {after}}\)

$$\begin{aligned} G_{\text {post-failure}} = \frac{\tau _{\text {pre-failure}} - \Delta \sigma _{\mathrm {failure}}}{\tau _{\text {pre-failure}}} \times {G_{\text {pre-failure}}} \end{aligned}$$
(38)

with \(\Delta \sigma _{\mathrm {failure}}\) as the constant stress drop. The approach becomes consistent with the theory of visco-elasticity if \(G_{\mathrm {after}}\) is not reduced directly as in Eq. 38, but by substituting of the Young’s modulus E with the relaxation modulus \(E_{\mathrm {rel}}\) of the Maxwell material (see Eq. 32). The viscosity \(\eta \) can then be chosen such that it reduces \(G_{\text {post-failure}}\) in the same way.

2.4.1 Calculation of Viscosity, Slip and Shear Dilation

While in the purely elastic case, E and the Poisson’s ratio \(\nu \) are used to calculate the bulk modulus B, the Lamé constant \(\lambda \) and the shear modulus G, Sharpe and Sharpe (2008) argue that B stays constant for visco-elastic materials in contrast to sometimes used, but physically incorrect assumption of a constant Poisson ratio. Accordingly, we can use B and the relaxation modulus \(G_{\text {post-failure}}\), to express \(E_{\mathrm {rel}}\) with

$$\begin{aligned} E_{\mathrm {rel}} = \frac{9 \times B \times G_{\text {post-failure}}}{3 \times B + G_{\text {post-failure}}} \end{aligned}$$
(39)

(Zoback 2010) and \(E_{\mathrm {rel}}\) can be used in turn to calculate the viscosity by reformulating Eq. 32

$$\begin{aligned} \eta = \frac{-\Delta t \times E}{\mathrm {ln}(E_{\mathrm {rel}} / E)} \end{aligned}$$
(40)

In summary, the shear modulus G decreases for a failing cell in the direction of the maximum shear stress. This is achieved by replacing Young’s modulus before failure E with the relaxation modulus \(E_{\mathrm {rel}}\). \(E_{\mathrm {rel}}\) in turn is dependent on the viscosity \(\eta \) which is chosen such that it reproduces the assigned shear stress drop \(\Delta \sigma _{\mathrm {failure}}\).

Vividly speaking, this means that the porous medium becomes “softer”, which will lead to a increased displacement after the timestep of failure has finished. This additional deformation results from the now active dashpot and represents the irreversible portion of the total displacement. Equivalent to the slip on a fault plane, this irreversible displacement persists as plastic deformation after the failure process is finished. We interpret the displacement in direction of the maximum effective normal stress as the slip and calculate an additional irreversible displacement normal to the fault plane from the dilation angle \(\gamma \) to account for deformation due to shear dilation. In a three-dimensional setup, the displacement in the remaining direction is assumed to be elastic and reversible.

For each timestep n, the irreversible displacement entry \(u_{\mathrm {irr}}\) in the slip direction is then determined from

$$\begin{aligned} u_{\mathrm {irr, slip}} = u_{\mathrm {after Failure}} - u_{\mathrm {before Failure}} \end{aligned}$$
(41)

while the irreversible displacement entry \(u_{\mathrm {irr}}\) resulting from shear dilation is calculated by

$$\begin{aligned} u_{\mathrm {irr, dilation}} = \mathrm {tan}(\gamma ) \times u_{\mathrm {irr, slip}}. \end{aligned}$$
(42)

Both are added to the respective components of irreversible displacement vector \(\mathbf {u}_{{\mathrm {irr}},j}\) of each node j and cumulatively summed up for each timestep n:

$$\begin{aligned} \mathbf {u}_{{\mathrm {irr,cum}},j}^{{n}} = \sum _{i=1, \ldots ,n} \mathbf {u}_{{\mathrm {irr}},j}^{{i}} \end{aligned}$$
(43)

Please note that \(\mathbf {u}_{{\mathrm {irr}},j}\) is only nonzero for the nodes of the element that just failed. Thus, only the entries of \(u_{\mathrm {irr,cum}}\) corresponding with those nodes and only in the direction of the slip change.

The calculation of the strain (see Eq. 18) is now based on the total displacement vector \(\mathbf {u}_\mathrm{tot}\) consisting of the contributions from elastic and irreversible plastic deformation.

$$\begin{aligned} \mathbf {u_{\mathrm {tot}}} = \mathbf {u_{\mathrm {}}} + \mathbf {u_{\mathrm {irr,cum}}}. \end{aligned}$$
(44)

2.4.2 Necessity of a Permanent Stress Drop

Up to this point, our model concept is composed of elements becoming alternately weaker as they fail one after another. But the stress is just consecutively redistributed between those elements, but not reduced as a failed element returns to a value very similar to its original stress state after failure is finished and the switch from visco-elastic back to elastic behaviour happens. But as discussed in Sect. 2.2.2, failure in fact decreases the stress by transforming it into other forms of energy. Consequently, the modelling concept, which up to now includes the switch between elastic and visco-elastic behaviour and the storage of the irreversible displacement, has to be expanded by a permanent stress drop to make the failure process truly “irreversible”. Accordingly, if a cell fails, the stress drop \(\Delta \sigma _{\mathrm {failure}}\) is stored. But in contrast to the already implemented constant stress drop used for the calculation of the viscosity, we use the actual stress drop \(\Delta \sigma _{\mathrm {actual}}\), which is the difference between the shear stress on the fault plane before and after the failure, to calculate the entries \(\Delta \sigma _{\mathrm {cum,j}}^{{n}}\) of cumulative stress change vector \(\mathrm {\Delta }\varvec{\sigma _{\mathrm {cum}}}\)

$$\begin{aligned} \Delta \sigma _{{\mathrm {cum}},j}^{{n}}&= \sum _{i = 1,\ldots ,n} \mathrm {\Delta }\sigma _{{\mathrm {actual}},i,j} \nonumber \\ \phantom {\mathrm {\Delta }\sigma _{{\mathrm {cum}},j}^{{n}}}&= \sum _{i = 1,\ldots ,n} \mathrm {\Delta }\sigma _{{\mathrm {pre\,failure}},i,j} - \sum _{i = 1,\ldots ,n} \mathrm {\Delta }\sigma _{{\mathrm {post\,failure}},i,j} \end{aligned}$$
(45)

for all timesteps n and each element j. In summary, \(\Delta \varvec{\sigma ^\prime }\) in Eq. 16, which depended originally only on the elastic displacement vector \(\mathbf {u}\), becomes a function of \(\mathbf {u_{\mathrm {tot}}}\).

3 Simulation Setup

The setup of this scenario is based on the study of Rutqvist et al. (2013) on fault reactivation during hydraulic fracturing operation, for which the coupled thermo-hydro-mechanical simulator TOUGH-FLAC (Rutqvist et al. 2002; Rutqvist 2011) was used. Assuming a fault zone which is intensively jointed oriented parallel to the fault plane, the fault was described with the ubiquitous joint model. The potential for shear failure was evaluated using the Mohr–Coulomb criterion and strain softening strength properties were assumed consistent with a slip-weakening fault model.

The two-dimensional domain is 2 km \(\times \) 2 km in size, located at a depth of 500–2500 m and discretised as illustrated by Fig. 2. It consists of the Marcellus play with a 30-m-thick gas-bearing shale layer in between other low-permeability formations. These formations could consist of grey shale or limestone and are assumed to have the same mechanical and hydraulic properties as the gas-bearing shale. A fault of 1 km length cuts through these layers with a dip angle of 80\(^{\circ }\). The fault is assumed to be initially impermeable, and a possible reactivation of this fault due to a fluid injection is the subject of this example.

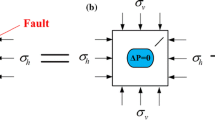
Similar to the scenario by Rutqvist et al. (2013), the initial pressure distribution in the system results from a hydrostatic pressure gradient (9.81 MPa/km) and an atmospheric pressure of 0.1 MPa at the surface. Except for the left boundary with Neumann no-flow conditions, the pressure at all other boundaries stays constant during the simulation. A static temperature distribution linearly increasing from 22.5 to \(72.5\,^{\circ }\mathrm{C}\) with depth is assigned. For the right and the top boundary, the stress normal to those boundaries is set to a constant value, while for the left and bottom boundary, zero normal displacement is imposed (see Fig. 3).

Fig. 2
figure 2

Discretisation for scenario 1: the domain of 2 km \(\times \) 2 km is refined around the fault zone, where the cells have a size of 1 m \(\times \) 1.25 m

Full size image
Fig. 3
figure 3

Model setup for scenario 1: an injection into a subvertical fault is studied with respect to a potential fault reactivation. Figure modified after Rutqvist et al. (2013)

Full size image

For the in situ stress field, the vertical stress is assumed to be the maximum principal stress corresponding with the significant depth of the domain, and the minimum principal stress is oriented horizontally and parallel to the injection well. In agreement with the assumptions of Rutqvist et al. (2013), the vertical stress gradient is calculated from the overburden density of 2700 kg/m\(^3\) based on the measured density of all formations overlying the Marcellus shale by Starr et al. (2011). A horizontal-over-vertical stress ratio of \(R = \sigma _{\mathrm {h}}/\sigma _{\mathrm {v}} = 0.6\) is used consistent with observations by Cipolla et al. (2010).

For the rock formations in the domain, a Young’s modulus of 30 GPa and a Poisson ratio of 0.2 are chosen. These values are derived from laboratory measurement of the Barnett Shale from Tutuncu et al. (2010), but Rutqvist et al. (2013) argue that due to lack of experimental data, these values can be used for the Marcellus shales as well. The fault’s Young’s modulus is set to a significantly lower value of 5 GPa, and zero cohesion was assigned. For the fault’s coefficient of friction, we assumed the same value of 0.6 as Rutqvist et al. (2013) used for the joints. For our fault description, we do not distinguish between joints and matrix within the faults zone. Furthermore, instead of setting a residual value for the coefficient of friction after the slip, this approach uses the constant stress drop to model the processes during fault reactivation.

For the rock matrix, an initial porosity of 0.01 and a permeability \(1 \times 10^{-19}\) m\(^2\) are used. The fault’s permeability is \(1 \times 10^{-16}\) m\(^2\) and has the same porosity. Both parameters depend on the elastic and plastic deformation resulting from deformation, slip and shear dilation as described in Sect. 2.4.1. The dilation angle was set to 10\(^{\circ }\). All the relevant material properties are listed in Table 1.

Table 1 Material properties of Scenario 1
Full size table

Derived from characteristic pump rates during hydraulic fracturing operations, Rutqvist et al. (2013) used an injection rate of \(Q=3.5\times 10^{-4}\) kg/s water into a 1.25 m\(^3\) numerical gridblock for the case of a relative permeable fault (k = 10\(^{-16}\) m\(^2\)). We applied this injection rate to six cells within the fault (see Fig. 4). For the temperature and pressure dependence of density and viscosity of water, the relations of Cooper and Dooley (2007) are used.

Fig. 4
figure 4

Illustration of the cells into which 3.5 \(\times \) 10\(^{-4}\) kg/s are injected

Full size image

4 Results and Discussion

The injection into the fault leads to a steady increase in pressure \(p_{{w}}\) and shear stress \(\tau _{{xy}}\) (see Fig. 5a, b). Correspondingly, the porosity \(\phi \) (Fig. 5c) and the permeability k (not shown) rise, too. After almost 2 h (simulation time t = 7070 s), the critical margin for shear failure is surpassed for the uppermost injection cell and failure is initiated. Shortly afterwards, at t = 8870.82 s, the injection is switched off. The resulting slip \(u_{\mathrm {irr}}\) and drop in shear stress is clearly visible in Fig. 5b, d). The slip occurs in y-direction accompanied by some dilation in the x-direction. After the slip event, pressure and porosity decrease.

Fig. 5
figure 5

Evolution of the pressure \(p_{{w}}\) (a), the shear stress \(\tau _{{xy}}\) (b), the porosity \(\phi \) (c) and the shear slip \(u_{\mathrm {irr}}\) (d) over time at \(x = 501\) m and \(z = -1497.5\) m

Full size image
Fig. 6
figure 6

Left evolution of the slip during the slip event. The top left corner of the failing cell (\(x = 501\) m, \(z = -1497.5\) m) is plotted. Right illustration of the slip and shear dilation of the failing cell during the slip event. The deformation of the grid is exaggerated

Full size image
Fig. 7
figure 7

Evolution of the pressure \(p_{{w}}\) (a), the shear stress \(\tau _{{xy}}\) (b), the porosity \(\phi \) (c) and the shear slip \(u_{\mathrm {irr}}\) (d) over time at \(x = 501\) m and \(z = -1497.5\) m

Full size image

A second set of plots shows the slip on the fault plane in detail (Fig. 6). While all other plots cover the example of a stress drop \(\sigma _{\mathrm {failure}}\) = 0.1 MPa, here the evolution of the slip is also shown for \(\sigma _{\mathrm {failure}}\) = 0.2 MPa. It becomes apparent that for the lower stress drop, two slip events shortly after another occurred, while \(\sigma _{\mathrm {failure}}\) = 0.2 MPa leads to only one event with about twice the displacement of the first failure on the fault. Fig. 6 also illustrates how the failing cell deforms: It is sheared in y-direction (consistent with the preset stress field), and some opening in x-direction resulting from the implemented shear dilation is observable.

Figure 7 provides details about the evolution of pressure, shear stress, porosity and permeability during the slip events. The shear deformation of the element decreases porosity and permeability slightly, but the resulting dilation then leads to an increase in porosity and permeability. While one might expect that a higher porosity results in a pressure drop, but the opposite is true due to water flowing into the cell facilitated by the increased permeability.

The described behaviour is plausible and comparable to the results of the corresponding scenario from Rutqvist et al. (2013). But naturally, the modelling of such a scenario contains a significant number of influential variables, which, if not specified exactly similar, hinder reproducibility. In our case, this is true for the injection parameters: While the mass rate per volume (in kg/(s m\(^3\))) was taken from Rutqvist et al. (2013), the exact location and number of the injection cells leave room for adjustments. We assume that this is the reason why the pressure at which fault reactivation occurs is similar (around 25 MPa in our case compared to around 26 MPa for the case with a fault’s permeability of \(1 \times 10^{-16}\) m\(^2\) in Rutqvist et al. (2013)), but the onset is different (2 vs. 3 h after the injection started). There is also discrepancy in the magnitude of the slip event: Both the rupture length (23.50 m) and the slip amount (\(-2.744\) mm) are much higher in case of Rutqvist et al. (2013) compared to only one cell failing with less than a tenth of a millimetre of slip. This might be attributed to the different injection setup, but the evaluation of the failure presumably plays also a role. During the development of the model, we noticed a significant dependence of the magnitude of fault reactivation on the temporal discretisation close to the exceedance of failure criterion. As mentioned in Sect. 2.3, we used a timestep refinement to appropriately resolve the onset of shear failure on the fault. Furthermore, Rutqvist et al. (2013) performed a parameter study on the impact of the residual friction angle. One outcome of this study was a range of stress drops from 2.5 up to 6 MPa depending on the residual friction angle. As visible in Fig. 5b, b), the shear stress in our case is well below these values, and thus, only a smaller stress drop is possible. Nonetheless, the correlation between stress drop and the resulting slip appears to be qualitatively comparable: The assigned stress drop of 0.1 and 0.2 MPa produces slips of 0.0062 and 0.0126 mm, while stress drops of 2.5 up to 6.0 MPa of Rutqvist et al. (2013) correspond with slips of 1.037 and 2.744 mm, respectively.

Our simulation also produces a rupture length different from the one presented in Rutqvist et al. (2013): While up to 23.50 m are reported by Rutqvist et al. (2013), just one element fails in our case and the rupture does not propagate into one of the neighbouring elements. Instead, the same element fails a second time. This behaviour is a result of the fact that in the current implementation of the model the element regains its full strength after failure has finished. We believe that once failure comes to a halt, only a partial regain in strength is more plausible due to some permanent damage caused by the rupturing. This could be achieved by making the elastic constants dependent on a damage variable. In this sense, Lyakhovsky and Ben-Zion (2008), Lyakhovsky et al. (2011) and Shalev and Lyakhovsky (2013) presented a model combining poro-elastic deformation and damage evolution with groundwater flow. The concept couples the rock properties with the damage variable, resulting in a strongly nonlinear stress–strain relationship. This could serve our purpose of a more plausible description of the failed element’s strength and would also allow some degradation of the elastic properties depending on the damage variable prior to the slip on the fault plane. Such an implementation would make an already failed element less likely to fail again and transfer stress to the neighbouring elements. A simple test where the shear modulus regained only 90 per cent of its original value leads to failure of a neighbouring element and, thus, indicates that this is a promising approach for further development of this model concept.

The combination of lower slip values, much more confined ruptures and smaller stress drops leads to even smaller earthquake magnitudes than the ones Rutqvist et al. (2013) observed for their simulation: From the seismic moment \(M_0\) (in N m) defined as

$$\begin{aligned} M_0 = G \times A \times d \end{aligned}$$
(46)

with the shear modulus G, the rupture area A and the mean slip d (Kanamori and Brodsky 2004), we can obtain the moment magnitude M of an earthquake

$$\begin{aligned} M = (\mathrm {log_{10} M_0}) / 1.5 - 6.07 \end{aligned}$$
(47)

after Kanamori and Brodsky (2004). Assuming a circular rupture patch with the diameter equal to the height of the failed cell (1.25 m), we get a moment magnitude of \(-3.3\) and \(-3.1\) for stress drops of 0.1 and 0.2 MPa, while Rutqvist et al. (2013) report magnitudes of 0.15 and 0.72 for 2.5 and 6.0 MPa, respectively.

5 Conclusions and Outlook

This paper introduces a numerical modelling concept to detect shear failure and resulting fault reactivation, where the slip event is represented by a visco-elastic proxy model. The aim of this study was to extend a given fully coupled multiphase flow and geomechanical approach towards the analysis of fault reactivation within the within the open-source simulator DuMu\(^{{x}}\). By evaluating failure based on the Mohr–Coulomb criterion and by using visco-elasticity as an equivalent to the shear stress reduction on the fault plane, this could be achieved. The approach was checked against a well-established scenario of fault reactivation due to hydraulic fracturing by Rutqvist et al. (2013), where a reduced coefficient of friction was used to model shear failure on the fault plane. Although the results do not match perfectly, the comparison demonstrates that our modelling approach is able to reproduce qualitatively the relevant characteristics such as slip and shear dilation as well as the feedback on the hydraulic properties. This supports the argument that both approaches model the dissipation of elastic energy during the slip event in conceptually comparable fashion, but are dependent on various influential parameters. Among these, the time discretisation close to the exceedance of the failure criterion and the corresponding onset of shear failure as well as the drop in the coefficient of friction or the shear stress need to be investigated in detail, preferably in the context of a benchmark study.

Future work should also apply the approach to multiphase examples, of which the implemented model is capable. For the sake of comparability, we choose the scenario of Rutqvist et al. (2013) over a multiphase injection scenario.

In addition, the main focus of the approach was on the modelling of shear failure on a fault, but a comprehensive approach must include tensile failure, too. Thus, such an expansion of the model towards a representation of tensile failure will be the subject of further research.