Abstract
The interactions between turbulent free flow and flow in a porous medium are of key interest in different fields, e.g., meteorology, agriculture, building physics, and aerospace engineering. Properly understanding the strongly coupled exchange processes between the two domains is crucial to describing these interactions. In (Mosthaf et al. in Water Resour Res 47(10):W10522, 2011. doi:10.1029/2011WR010685), a concept for coupling laminar compositional single-phase free flow to compositional two-phase porous-medium flow under non-isothermal conditions was presented. In this study, the existing coupling concept is first extended to turbulent free-flow conditions. This includes the interface conditions between a Reynolds-averaged Navier–Stokes free flow using algebraic turbulence models and a Darcy porous-medium flow. Second, eddy viscosity and boundary layer models for a rough interface are integrated into this model concept. Results from laboratory evaporation experiments are used for comparison of the developed model concept. A sensitivity analysis of the evaporation rate and porous-medium quantities on different model setups, boundary conditions, Beavers–Joseph coefficients, and roughness lengths is performed. Results demonstrate how including turbulence, either with eddy viscosity or boundary layer models, affects the evaporation rate. The model concept is able to predict early stage-I and intermediate to later stage-II evaporation rates. Sand-grain roughness concepts are successfully included into the model and show the desired qualitative effect.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A better understanding of the interactions between free flow and flow in porous media is critical for a variety of applications in different fields, like medical science (Chauhan et al. 2011), building physics (Defraeye et al. 2010), aerospace engineering (Dahmen et al. 2014), food processing (Verboven et al. 2006), and agriculture (Jambhekar et al. 2015; Fujimaki et al. 2006).
In many of these applications, the processes in the two domains are strongly coupled. Therefore, different modeling strategies for these problems exist. The most detailed, but also very time-consuming, method is a direct numerical simulation (DNS) of the entire problem. This one-domain approach is used, e.g., in Krafczyk et al. (2015), Hahn et al. (2002) and Breugem and Boersma (2005). In contrast to these one-domain models, in two-domain models a sharp interface separates the free-flow and the porous-medium domain and two different sets of equations are used to describe the processes in the two domains. Considering two different domains is desirable from a physical point of view. Because the free-flow processes act on smaller spatial and temporal scales than the porous-medium processes, the two-domain approach allows for the detailed modeling of the free flow while still applying simplifying assumptions to the porous medium (Dahmen et al. 2014; Mosthaf et al. 2014; Defraeye 2011). These different temporal and spatial scales also motivate different numerical treatments of the subdomains (Rybak et al. 2015; Arbogast et al. 2007). The effects of coupling turbulent free-flow models to Richards or Darcy–Forchheimer models have been both studied theoretically and applied to heat transfer and drying problems, see Defraeye et al. (2010), Dahmen et al. (2014), Lemos (2009) and Pedras and Lemos (2001).
It is critical to find a suitable coupling concept between the porous-medium and free-flow domains that is capable of properly describing the behavior at the interface. One option is to allow nonzero tangential velocities directly at the interface by replacing the no-slip boundary condition with a slip boundary condition, e.g., Beavers and Joseph (1967), Saffman (1971), Sahraoui and Kaviany (1992), and Nield (2009). However, these concepts neither account for turbulence, roughness, or saturation effects. The effects of roughness resulting from discrete obstacles on evaporation have been investigated previously, e.g., in Haghighi and Or (2015) and Sugita and Kishii (2002). Further, porous-medium surfaces are never perfectly smooth and thus the influence of roughness resulting from the matrix material needs to be analyzed. For heat transfer problems, this has been done by Kuznetsov and Becker (2004) and Kuznetsov (2004).
The coupling between the free-flow and porous-medium flow is extremely relevant to evaporation processes from bare soil surfaces. Evaporation from soil surfaces is a vital research subject in the past few years and has been investigated at the pore scale, e.g., (Shahraeeni et al. 2012; Assouline et al. 2010; Yiotis et al. 2007; Laurindo and Prat 1998; Suzuki and Maeda 1968), at the REV scale, e.g., (Trautz et al. 2015; Zhang et al. 2015; Mosthaf et al. 2014 and Schneider-Zapp et al. 2010), and at larger scales, e.g., (Vanderborght et al. 2010; Shukla and Mintz 1982 and Penman 1948).
Evaporation from bare soil surfaces is influenced by different processes and properties in both domains, as shown in Fig. 1. Although all of the processes shown in Fig. 1 are important, this study focuses on the influence of a turbulent free flow over a rough and permeable surface on the exchange processes. As mentioned above, aspects of roughness and turbulence have been partially investigated in other fields. However, previous studies do not combine models for turbulence and roughness to analyze the effects on coupled processes for all: mass, momentum, and energy transfer in both domains.
Other important aspects of these coupled processes have been studied by different groups. For example, the assumption of local thermodynamic equilibrium for phase transition and energy transfer has been questioned and analyzed, e.g., in Trautz et al. (2015), Nuske et al. (2014) and Smits et al. (2011). Haghighi et al. (2013), Shahraeeni and Or (2010) and Assouline et al. (2010) investigated how the development of wet soil pore patches together with the environmental conditions affects evaporation behavior. The effect of porous-medium parameters (e.g., permeability and porosity) on the evaporation rate has been analyzed numerically (Mosthaf et al. 2014; Ciocca et al. 2014) and experimentally (Shokri and Or 2011).
In this study, the coupled processes are considered by analyzing evaporation from a bare soil surface. During this evaporation process, two different stages are discerned (Lehmann et al. 2008; van Brakel 1980). The stage-I period is characterized by higher evaporation rates, constrained by the atmospheric demand. The stage-II period, in contrast, is characterized by a falling rate, followed by a constant rate period and limited by diffusive transport through the unsaturated soil (Shokri and Or 2011).
The objectives of this work are (i) to present a numerical model concept that considers turbulence and roughness and can be applied to various coupled porous-medium/free-flow applications, (ii) to analyze the sensitivity of parameters and processes that influence evaporation from rough and permeable surfaces induced by an adjacent turbulent free flow, and (iii) to demonstrate the applicability of the modeling approach by comparing simulation results to existing bench-scale evaporation experiments (Davarzani et al. 2014).
2 Models
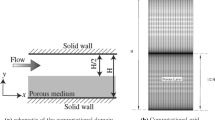
In this study, a REV-scale two-domain concept with a sharp interface between the porous-medium and the free-flow domain is used, as shown in Fig. 2. The transfer fluxes and state variables at the interface are model output. In contrast to other models, which use Richards equation (Defraeye 2011), consider only one-phase flow (Dahmen et al. 2014), do not include turbulence (Davarzani et al. 2014), or are more of theoretical nature (Discacciati and Quarteroni 2009; Lemos 2009; Rybak et al. 2015), this concept includes two fluids phases inside the porous medium and models non-isothermal component transfer with an adjacent turbulent, roughness-affected free flow.
In the following section, the models for the porous medium, the free flow, and the interface are presented in detail.
2.1 Porous Medium
Flow and transport in the porous medium is described using the extended Darcy’s law for multiphase flow, e.g., Helmig 1997; the following assumptions are applied: (i) local thermodynamic equilibrium, (ii) two mobile phases (here gas and liquid), consisting of two components (here air and water), (iii) rigid solid phase, (iv) creeping flow with \({\textit{Re}}<1\), (v) no turbulent/atmospheric pumping, (vi) Newtonian fluids, and (vii) Fickian diffusion:
The phases \(\alpha \) are the liquid phase (l) which is the wetting phase and the gas phase (g) which is the non-wetting phase here. The liquid and the gas phase pressures are related by the capillary pressure \(p_{\text {c}}\), with \(p_{\text {c}}=p_{\text {g}}-p_{\text {l}}\). In REV models, the capillary pressure is normally a function of saturation, see, e.g., van Genuchten (1980). Further, \(\varrho _\alpha \) is the fluid density, \(\nu _\alpha \) the kinematic viscosity of the fluid, and \(\varvec{{{v}}}_\alpha \) the fluid phase velocity. \({\mathbf {K}}\) is the intrinsic permeability tensor of the soil and \(k_{{\text {r}},\alpha }\) gives the relative permeability, as a function of the fluid and the fluid–fluid interactions. The gravity vector is denoted by \(\varvec{{{g}}}\).
The mass balance for the phase components is given by:
in which \(\kappa \) stands for the components water (w) and air (a). The porosity of the porous medium is given by \(\phi \), \(S_\alpha \) denotes the saturation of an REV with a fluid phase \(\alpha \). By definition the fluid phase saturations sum to one: \(S_{\text {l}} + S_{\text {g}} = 1\). The component mass fractions \(X^\kappa _\alpha \) are related by the supplementary condition: \(X^{\text {w}}_\alpha + X^{\text {g}}_\alpha = 1\). The partitioning processes are calculated with Raoult’s and Dalton’s law. The vector \(\varvec{{{j}}}^\kappa _{\alpha {\text {,pm,diff}}}\) contains the diffusive fluxes:
The effective porous-medium diffusion coefficient \(D^\kappa _{\alpha {\text {,pm}}}\) and the molecular diffusion coefficient \(D^\kappa _\alpha \) of a component \(\kappa \) in a phase \(\alpha \) are different due to the tortuosity \(\tau \) of the porous medium (Millington and Quirk 1961): \(D^\kappa _{\alpha {\text {,pm}}} = D^\kappa _\alpha \tau \phi S_\alpha \). Further, the molar density of a phase \(\varrho _{\alpha {\text {,mol}}}\), the molar mass of the component \(M^\kappa \), and the molar fraction \(x^\kappa _\alpha \) are needed to calculate the diffusive fluxes.
Because local thermodynamic equilibrium is assumed, the temperature T inside one local REV is the same for all phases. Thus, only one energy equation is needed:
Here, \(u^{\text {e}}_\alpha \) is the specific internal energy of a phase and \(h_\alpha \) is the specific phase enthalpy. In addition, the specific heat capacity \(c_{\text {s}}\) and the density of the solid material \(\varrho _{\text {s}}\) are needed. As for the diffusion coefficient, the effective thermal conductivity \(\lambda _{\text {pm}}\) is considered to be a mixture of water, air, and soil properties (e.g., the thermal conductivities of the fluid phases \(\lambda _\alpha \) and the solid material \(\lambda _{\text {s}}\)). For partially wet soils, it is a function of the phase contents and often derived experimentally, see, e.g., Smits et al. (2010).
2.2 Free Flow
The Navier–Stokes equations describe both laminar and turbulent free flow. As already discussed, simulating free flow and turbulence using DNS is theoretically possible, but computationally expensive. Therefore, turbulence is normally parametrized. In addition to the Navier–Stokes equations, the Reynolds-averaged Navier–Stokes (RANS) equations used for turbulence modeling are introduced. The following assumptions are made with respect to the free-flow models used in this work: (i) one fluid phase, consisting of two components, (ii) Newtonian fluid without dilatation, (iii) no gravitational forces, and (iv) Fickian diffusion.
2.2.1 Navier–Stokes
The single-phase free-flow mass balance is:
All properties are properties of the free-flowing gas phase; to highlight this, the index g is used.
The Navier–Stokes equation is used for the momentum balance. As previously mentioned, gravity is neglected for the free flow:
The shear stress tensor \({\varvec{\tau }}_{\text {g}}\), here neglecting dilatation effects, is represented by:
The mass balance for a component \(\kappa \) inside the gas phase is:
The diffusive component fluxes for the free flow read as:
Finally, the energy balance is given by:
This form of the energy balance equation includes the enthalpy transport by diffusive component fluxes; this means the enthalpy of a component \(h^\kappa \) times its diffusive flux \(\varvec{{{j}}}^\kappa _{\text {g,ff,diff}}\).
2.2.2 Reynolds-Averaged Navier–Stokes
For modeling the effects of turbulence on the exchange processes, different model concepts are available, as shown in Fig. 3. The Navier–Stokes equations can be transformed to the RANS equations by applying the Reynolds decomposition and a time averaging. For a detailed derivation of the RANS equations, the authors refer the reader to fluid dynamics textbooks, e.g., Wilcox (2006) and Pope (2006).
Turbulence can be modeled by using suitable closure concepts for the turbulent quantities resulting from the averaging process. General assumptions for the RANS equations using an eddy viscosity parametrization are: (i) Flow is incompressible to turbulent pressure fluctuations (which is valid up to a Mach number of 0.3), (ii) isotropic turbulence, and (iii) the Boussinesq assumption which states that the turbulent stresses can be modeled like viscous stresses.
In comparison with the Navier–Stokes equations, in the RANS equations the instantaneous values of the transported quantities are replaced by their time-averaged counterparts (indicated by a bar, like \(\bar{\varvec{{{v}}}}_{\text {g}}\)). Therefore, the mass balance is written as:
The RANS momentum balance is:
The turbulent shear stress tensor \(\bar{{\varvec{\tau }}}_{\text {g,t}}\) has an additional unknown, the eddy viscosity \(\nu _{\text {g,t}}\), which results from the averaging process:
In this work, the simplest group of closure equations for the eddy viscosity is used: the algebraic turbulence models, see Fig. 3. These models calculate the eddy viscosity based on algebraic relations between mean flow properties and geometrical information. The simplest example thereof is the Prandtl mixing length:
where \(l_{{\text {mix}}} = \kappa y\) is the mixing length, with the von Kármán constant \(\kappa =0.4\) and the orthogonal distance to the closest wall y. Here, \(\bar{u}_{{\text {g}}}\) denotes the main velocity component. The algebraic eddy viscosity models can be applied under the following assumptions: (i) There is an equilibrium between turbulent production and dissipation and (ii) the eddy viscosity can be formulated based on mean flow quantities and geometrical information.
We acknowledge that the algebraic turbulence models are only suitable for simple geometries and more comprehensive models are available in the literature, e.g., Wilcox (2006). However, here the focus is on the description of exchange processes for simple geometries, and therefore, algebraic turbulence models are appropriate. In this work, the following eddy viscosity models are used: Prandtl mixing length, the Hanna–van Driest modification (van Driest 1956; Hanna et al. 1981), and the Baldwin–Lomax model (Baldwin and Lomax 1978).
For the component mass balance, the eddy diffusivity \(D_{\text {g,t}}\) occurs as a new quantity, accounting for the enhanced turbulent mixing. The simplest way to obtain the eddy diffusivity is to use the Reynolds analogy with a turbulent Schmidt number \(Sc_{\text {t}} = 1\):
Now, the component mass balance can be formulated:
with the turbulent diffusive fluxes
For the energy balance, the eddy conductivity \(\lambda _{\text {g,t}}\) occurs as a new turbulent quantity, accounting for the enhanced exchange of energy. The Reynolds analogy using the turbulent Prandtl number \(Pr_{\text {t}} = 1\) can be used to convert the eddy viscosity to an eddy conductivity:
where \(c_{\text {p,g}}\) is the specific isobaric heat capacity. This leads to the RANS energy balance equation:
with the turbulent conductive fluxes:
2.3 Interface Conditions
Coupling conditions are needed at the interface between the free-flow and the porous-medium region, because different model concepts are used in the two subdomains. The interface conditions are based on those presented in Mosthaf et al. (2014). Here, two extensions will be made to this approach.
The first extension includes the eddy viscosity, eddy diffusivity, and eddy conductivity into the interface conditions for the sake of a consistent model concept. The second modification pertains to the energy balance and includes the enthalpy transported by the diffusive component fluxes in the free flow (\(\bar{h}_{{\text {g}}}^\kappa \bar{\varvec{{{j}}}}^\kappa _{{\text {g,ff,t,diff}}}\)).
Finally, the interface conditions for coupling single-phase turbulent free flow to two-phase porous-medium flow under non-isothermal and compositional conditions, based on the assumption of local thermodynamic equilibrium, are obtained. The equilibrium for the total mass flux states:
Here, \(\varvec{{{n}}}\) denotes the interface normal vector, pointing outside of the respective domain. Two coupling conditions have to be defined for coupling the momentum balances. The first condition balances the momentum tangential to the interface according to the Beavers–Joseph–Saffman condition (Beavers and Joseph 1967; Saffman 1971):
The limitations of this approach to laminar single-phase flow is emphasized here. However, as long as the viscous sublayer is above the porous medium, laminar conditions prevail at the interface. Further, DNS results by Hahn et al. (2002) indicate that in a specific range this condition is also valid for turbulent flow. The Beavers–Joseph coefficient \(\alpha _{{\text {BJ}}}\) is a dimensionless material parameter, and \(\varvec{{{t}}}_i\) denotes the ith linear independent interface tangential vector. The second condition balances momentum normal to the interface:
in which \({\mathbf {I}}\) is the identity matrix. For a phase component \(\kappa \), chemical equilibrium for the continuity of mass fractions,
and the continuity of component mass fluxes,
are imposed. The coupling conditions are completed by the thermal equilibrium for the continuity of temperature,
and the continuity of energy fluxes,
2.4 Roughness Parametrization
Sand-grain roughness may affect the boundary layer development which plays an important role for the diffusion-dominated transport near the interface. This section presents two concepts on how the sand-grain roughness of the porous medium can be included in coupled models. Both concepts were originally derived for roughness elements on an impermeable plate, and for both concepts, the determination of a characteristic sand-grain roughness length \(k_{{\text {s}}}\) is critical. A correlation with the sand-grain diameter is proposed in Schlichting and Gersten (1997) for roughness elements on an impermeable plate. Kuznetsov and Becker (2004) proposed a model which relates the sand-grain roughness to porous-medium properties.
2.4.1 Eddy Viscosity Models
The first sand-grain roughness parametrization builds upon the eddy viscosity concept. Cebeci (1978) wrote that the eddy viscosity can be modified for the sand-grain roughness parametrization as published by Rotta (1962) under the assumptions of aerodynamically smooth surfaces:
The wall friction velocity \(u^*\) is defined with the velocity gradient at the wall: \(u^* = \sqrt{\nu _{{\text {g}}} \partial \bar{u}_{{\text {g}}}/\partial y}\). The application range of this concepts is limited by the equivalent sand-grain roughness \(4.535 < k_{{\text {s}}}^+ < 2000\), which is obtained from a sand-grain roughness length \(k_{{\text {s}}}\) by: \(k_{{\text {s}}}^+ = k_{{\text {s}}} u^*/\nu \). This concept is also used by Kuznetsov and Becker (2004) to analyze how energy transfer is altered due to the sand-grain roughness parameter.
2.4.2 Boundary Layer Models
The second approach accounts for roughness only via the coupling conditions. Similar to Mosthaf et al. (2014) and Schneider-Zapp et al. (2010), the flow and transport is simulated under laminar conditions (Eqs. 4 and 5) and effects of turbulence are integrated through the boundary layer development and change in the coupling conditions. This approach is here within referred to as the BL model later on. It is assumed that (i) diffusion/conduction through the viscous sublayer is the limiting factor for mass/heat transfer, (ii) flow is fully mixed outside the viscous sublayer, and (iii) the starting point for the boundary layer development is known. In this case, the diffusive and conductive fluxes (Eqs. 17 and 20) as used in the interface conditions (Eqs. 25 and 27) are replaced by:
The mass fraction and temperature gradients are replaced by prescribed values at the edge of the boundary layer and the implicitly calculated values at the interface, as shown in Fig. 4.
The viscous sublayer thickness \(\delta _{{\text {v}}}\) can be calculated with the help of the characteristic dimensionless wall distance \(y^+\), the wall friction velocity \(u^*\), and the skin friction coefficient \(c_{{\text {f}}}\) or the Darcy friction factor f. All equations are given in White (2011).
For flow along smooth and rough plates, the skin friction coefficient \(c_{{\text {f}}}\) can be calculated by different empirical formulations. In this study, the formula presented in Truckenbrodt (2008) is used:
The second approach uses the Darcy friction factor f. Colebrook (1939) developed an empirical formulation for flow in pipes or ducts which was converted to an explicit formulation by Haaland (1983):
With the above-mentioned assumptions and concepts, the effects of roughness on the turbulent flow and hence on the exchange processes can be described.
2.5 Discretization and Numerical Framework
The presented model concept and its equations (Table 1) are implemented in the open-source simulator DuMu\(^\text {x}\) (Flemisch et al. 2011; Schwenck et al. 2015), which is based on the numerical toolbox DUNE (Bastian et al. 2008b, a). The code used in this paper is available on request to the corresponding author. The set of partial differential equations is discretized using the box method (Huber and Helmig 2000). More details on the implementation of the coupling concept can be found in Baber et al. (2012), whereas Fetzer (2012) provides more information on the implementation of the turbulence models. The monolithic system is solved by a fully implicit scheme using SuperLU (Demmel et al. 1999).
3 Results and Discussion
In this section, the experimental setup is introduced, followed by a presentation of the numerical setup. Afterward, simulation results are discussed, starting with different model setups and closing with a sensitivity analysis of the turbulence models and interface parameters.
3.1 Experiments
Experimental results are taken from Davarzani et al. (2014); please refer to this source for a detailed description of measurement devices, materials, and methods. Experimental data/results are available on request to the corresponding author. The wind tunnel/porous-medium experimental setup consists of a free-flow section and a sand box, as shown in Fig. 5. A detailed view on the sand box and the location of the sensors is shown in Fig. 6 and Table 2. The porous-medium properties are summarized in Table 3.
Setup of the wind tunnel experiment, after (Davarzani et al. 2014). Air flows from left to right. Dimensions are given in cm
Setup of the sand box and locations of the sensors, after (Davarzani et al. 2014). Dimensions are given in cm. Sensors 3 and 8 are used for comparison of porous-medium temperature and water saturation profiles
Experiments were run for three different wind velocities, as given in Table 4. A dimensionless analysis shows that turbulent flow conditions prevail and have to be accounted for by the model concept. With a hydraulic radius of \(d_{{\text {hy}}} = 4A/U = 0.134\,{\mathrm{m}}\), even for the smallest velocity the critical Reynolds number \(Re_{{\text {d,crit}}}\approx 2300\) is exceeded:
Measurements of free-flow and porous-medium state variables are used to determine initial and boundary conditions, as shown in Fig. 7 and Table 4. The mean values are taken as input parameters for the reference simulations. The evaporation rates are obtained from measuring changes in the sand box weight over the course of each experiment. For a better comparison of measured and simulated evaporation rates, the measured rates are post-processed by different floating time average intervals, as shown in Fig. 7. The 240-min-averaged evaporation rates are referred to as Experiment here within.
3.2 Reference Model Setup
The reference cases use the RANS equations (Eqs. 11–19) and 2-D model setup with the initial/boundary conditions described in Table 4 and Fig. 8. The reference discretization uses \(n_{\text {x}}=100\) and \(n_{\text {y}}=50\) cells, see Table 5 for more details.
The basic assumption, for the numerical modeling presented here, is to consider the experiment as a 2-D system. In reality, the flow is also influenced by the side walls and not only by the porous-medium surface. The hypothesis is that the exchange is driven by diffusion in the free flow near the porous-medium surface and is therefore mainly affected by the viscous sublayer evolving above the porous medium (e.g., Bird et al. 2007; Haghighi and Or 2013).
To reduce computational costs, only the lower half of the free-flow channel in the section downstream of the heater is modeled (see Figs. 5 and 8). Velocity, temperature, and humidity values are assumed to be constant over height. For a better definition of the setup, it would be important to have additional experimental measurements at the inlet position (e.g., vertical profiles of these values). For the reference cases, the surface of the porous medium is assumed to be smooth. This assumption will be loosened and discussed in the last section, in which the surface roughness parametrizations are analyzed. Measurements show that the soil remains saturated below 25 cm in the considered time frame. Therefore, only the upper 25 cm of the porous medium are modeled. No-flow boundary conditions are imposed at the porous-medium boundaries. The evaporation rates are calculated by evaluating the temporal derivative in the porous-medium domain.
For modeling turbulence, the Baldwin–Lomax model is used for the eddy viscosity, whereas the Reynolds analogy is applied for the eddy diffusivity and the eddy conductivity.
Evaporation rates for \(\bar{u}_{\text {g}}=1.22\,\mathrm{m}/\mathrm{s}\) and different numerical model setups, as shown in Fig. 8
Choice of Numerical Model Setup: To check the applicability of the above-mentioned simplifications and to assess the sensitivity of the system, three different setups are compared to the chosen reference case (see Fig. 8). The first considers a closed top (pipe) instead of only the lower half of the domain. The other setups are used to investigate the influence of the run length on the boundary layer development and its thickness. The evaporation rates for the setups are shown in Fig. 9. For the short setup, the evaporation rates are higher, because the boundary layer is not developed when passing over the porous medium. The other setups are more comparable in terms of evaporation rates; the reference and the pipe setup produce almost identical evaporation rates. The reference setup is selected for further study because of its numerical stability.
Grid Convergence: The computed evaporation rate is grid dependent, mainly caused by steep gradients in the surface normal direction. A grid convergence study is conducted separately in the x and y direction for the velocity of \(1.22\,\mathrm{m}/\mathrm{s}\), as shown in Fig. 10 and Table 5. It is acknowledged that for higher velocities, the reference discretization may not be enough to prove grid convergence. Nevertheless, it is a good compromise between accuracy and efficiency.
Evaporation rates for \(\bar{u}_{{\text {g}}}=0.55\,\mathrm{m}/\mathrm{s}\). The following curves are shown: experimental measurements, simulations neglecting turbulence (laminar), simulations including turbulence with constant free-flow boundary conditions (reference), and two cases for which the free-flow boundary conditions are varied over time according to measurements (\(\bar{u}_{{\text {g}}}\) and \(\bar{u}_{{\text {g}}},\bar{X}_{{\text {g}}}^{{\text {w}}},\bar{T}\)). a Evaporation rates. b Cumulative water mass loss
The resolution in x-direction affects the evaporation rate value during stage-I . This can be attributed to the fact that the grid points at the upper corner points of the porous medium are not coupled to the free flow and thus cannot contribute to the evaporation. For the y-direction, a lower resolution leads to a longer stage-I evaporation. In this case, porous-medium cells closer to the surface have larger volumes and thus contain water for a longer time.
3.3 Reference Cases
\(\bar{u}_{\text {g}}=0.55\) \(\mathrm{m}/\mathrm{s}\): For the lowest wind velocity, it can already be seen that the stage-I evaporation rates modeled using laminar flow are smaller than those including turbulence, as shown in Fig. 11a. In later stage-II , the evaporation rates for laminar and turbulent cases converge. This agrees with the fact that stage-II evaporation rates are limited by porous-medium properties rather than by atmospheric conditions. Especially in stage-II , which approximately starts after \(\sim \)3 days, simulation and experimental results fit well; as shown in Fig. 11b, the gradients of the water mass loss curves are very similar.
However, using the measured free-flow conditions as input parameters rather than a constant wind velocity, the evaporation rate shows more variability. The velocity variations lead to significant variations in the evaporation rate, as shown in Fig. 11a. Using the measured free-flow conditions in all three parameters (i.e., velocity, temperature, and water mass fraction) does not allow for the correct estimate of the evaporation rate. Nevertheless, variability in the free-flow conditions does not cause variability in stage-II evaporation rates. Furthermore, none of the resulting rate fluctuations are visible in the cumulative mass loss plot shown in Fig. 11b.
Evaporation rates for \(\bar{u}_{\text {g}}=1.22\,\mathrm{m}/\mathrm{s}\). The following curves are shown: experimental measurements, simulations neglecting turbulence (laminar), simulations including turbulence with constant free-flow boundary conditions (reference), and two cases for which the free-flow boundary conditions are varied over time according to measurements (\(\bar{u}_{{\text {g}}}\) and \(\bar{u}_{{\text {g}}},\bar{X}_{{\text {g}}}^{{\text {w}}},\bar{T}\)). a Evaporation rates. b Cumulative water mass loss
\(\bar{u}_{{\text {g}}}=1.22\) \(\mathrm{m}/\mathrm{s}\): Fig. 12a shows, as expected, that the difference between laminar and turbulent modeling becomes more significant at higher wind velocities. In this setup, the effect of the measured values, imposed as boundary conditions, is more pronounced and the fluctuations are less frequent with higher amplitudes. The fluctuations in the early stage-I evaporation rate can qualitatively be reproduced. Again, measured and simulated stage-I evaporation rates are in quite good agreement. For the simulations, the transition to stage-II is much sharper than in the experiment, because the REV concept cannot reproduce the pore-by-pore drying of the surface. Especially for larger wind velocities or larger distance between the evaporating pores, the evaporation rate may already drop during stage-I , see Shahraeeni et al. (2012). This behavior is observed here. The stage-II evaporation rates can be matched in a time-averaged sense. As before, varying the free-flow boundary conditions does not affect simulated stage-II evaporation rates. Therefore, other factors (e.g., errors in measurement, wrong averaging interval, non-homogeneous soil properties, heat transfer through the side walls of the soil box) have to be responsible for the measured fluctuations.
In the cumulative mass loss plot shown in Fig. 12b, the measured variations in the evaporation curves are visible as small kinks of the curve. From this plot, it can be seen that the transition to stage-II is predicted too early. At the end of the simulation, the predicted evaporation rate is underestimated by about 15 %. Although the laminar case strongly underestimates the stage-I evaporation, its final prediction of the water mass loss is almost comparable to the prediction of the turbulent case (with a difference of about 4 %).
Figure 13 shows vertical profiles above the porous medium. It can be seen how the boundary layers for temperature and water mass fraction are increasing while flowing along the porous medium. Further, it depicts the importance of the eddy viscosity and the fluid viscosity to flow and transport processes.
Evaporation rates for \(\bar{u}_{{\text {g}}}=3.65\,\mathrm{m}/\mathrm{s}\). The following curves are shown: experimental measurements, simulations neglecting turbulence (laminar), simulations including turbulence with constant free-flow boundary conditions (reference), and two cases for which the free-flow boundary conditions are varied over time according to measurements (\(\bar{u}_{{\text {g}}}\) and \(\bar{u}_{{\text {g}}},\bar{X}_{{\text {g}}}^{{\text {w}}},\bar{T}\)). a Evaporation rates. b Cumulative water mass loss
\(\bar{u}_{\text {g}}=3.65\) \(\mathrm{m}/\mathrm{s}\): For the highest wind velocity, the difference between the laminar and the turbulent case becomes most significant, reaching a difference of almost \(5\,{\mathrm{mm}}/\mathrm{d}\) during stage-I evaporation, as shown in Fig. 14a. The influence of measured free-flow properties on the simulated evaporation rate can hardly be evaluated, due to a rapidly decreasing stage-I evaporation rate and a very early drying out of the porous medium.
Figure 14b shows the cumulative mass loss with a different behavior than in the previous plots. First, higher evaporation rates lead to steeper gradients in the cumulative mass loss curves. Because of the steeper gradients, early stage-I evaporation rates seem to be approximated as good as for smaller wind velocity cases. However, this is difficult to deduce only by the evaporation rate plot (Fig. 14a). Second, simulated stage-II evaporation rates are higher than measured values. This, in contrast, can hardly be seen in the evaporation rate plot. It has to be remarked that the measured, porous medium controled, stage-II evaporation rates are much lower than for the previous velocities. But as the porous medium was the same for all experiments, the measured stage-II evaporation rates for the different velocities should be more or less equivalent (as it is for the simulations). Further, negative evaporation rates are observed for stage-II . This can be attributed to the averaging interval and experimental errors (e.g., scale resolution and sensitivity) as negative rates are observed in the original cumulative mass loss data set.
3.4 Porous-Medium Quantities
In this section, the effects of evaporation on the evolution of saturation and temperature are compared for simulations and experiments. For this comparison, data from sensor 3 and sensor 8 are used (Fig. 6; Table 2).
Temporal evolution of porous-medium properties for \(\bar{u}_{{\text {g}}}=1.22\,\mathrm{m}/\mathrm{s}\). The shown setups are: an isolated porous medium (reference) and a porous medium with constant temperature at the left, bottom, and right boundary (const. T). Red lines correspond to sensor 3 and blue lines to sensor 8. a Porous-medium temperature. b Water saturation
Temperature: The evolution of the porous-medium temperature for the two sensor locations is shown in Fig. 15a. Measurements are compared to the reference case with an isolated porous-medium sand box and a case in which the temperature is kept constant at the porous-medium boundaries. For the case of an isolated box, the simulated and measured temperature evolutions are quite different. This is due to the perfect isolation which means that there is no opportunity for the porous medium to compensate for the energy loss by evaporation, resulting in very low temperatures at the end of stage-I . After the porous medium is dried out, it is continuously supplied with energy from the free flow and finally reaches the free-flow temperature. This behavior cannot be seen in the measurements.
For the second setup with a constant temperature at the porous-medium boundaries, it is seen that (i) the temperature does not constantly decrease during stage-I , (ii) the porous-medium temperature is relatively more affected by the measured free-flow boundary conditions and the resulting fluctuations qualitatively match the observed behavior, and (iii) the porous-medium temperature does not approach the free-flow temperature toward the end of the simulation.
Of course, these two concepts are the extreme cases for the porous-medium boundary conditions. The prediction of the temperature evolution inside the porous medium is better when using a constant temperature around the porous medium. But this case drastically overestimates the stage-I evaporation rates compared to measurements; here the isolated case fits better (Fig. 16). This analysis shows that the heat loss has a strong influence on the temperature distribution. For future experiments and simulations, it is necessary to find a better way to quantify and account for these losses.
Saturation: Figure 15b shows the saturation evolution over time. The simulated saturation curves look similar to those from Davarzani et al. (2014). Also similar in both studies is that the near soil surface saturation evolution is better approximated than at deeper depths. The residual saturation is reached faster in simulations than in the measurements. Davarzani et al. (2014) concluded that this discrepancy in stage-II saturation distribution comes from overestimating the temperature variations in the porous medium. This is supported by the fact that a porous medium with constant temperature boundary conditions better approximates the measured temperature profiles and leads at least in the first days to a better match with measured saturations (Fig. 15b). Nevertheless, this effect is not large and it is assumed that other effects have to contribute, especially as in 7.5 cm depth, the shapes of the profiles are significantly different. Further possible factors are (i) linearizing the \(p_{\text {c}}\)–\(S_{\text {l}}\) curve at very low water saturation leads to an overestimation of liquid water flow (e.g., Ciocca et al. 2014; Mosthaf et al. 2014), (ii) relative permeability functions affect the flow behavior and saturation distribution during the evaporation process, (iii) different hydraulic properties around the sensors or with depth may affect the saturation measurements (Assouline 2006), and (iv) film and corner flow also have an influence as highlighted in a study on evaporation from pore networks (Laurindo and Prat 1998).
3.5 Turbulence Models
The evaluation of the influence of turbulence and turbulence models is structured in two parts: First, the influence of the eddy viscosity model is analyzed, and second, the impacts of eddy diffusivity and eddy conductivity models are investigated.
Eddy Viscosity Models: In Fig. 17, the evaporation rates for eddy viscosity models are compared. It can been seen that including an eddy viscosity model, hence including the turbulent momentum transport, but still using laminar mass/heat transport already leads to higher evaporation rates. This is caused by changes in the velocity profile and thus in the resulting boundary layer. The influence of turbulence is higher for the atmospheric controled stage-I evaporation rate. Compared to the laminar case, there is no difference in stage-II evaporation rates.
Evaporation rates for \(\bar{u}_{{\text {g}}}=1.22\,\mathrm{m}/\mathrm{s}\). The influences of neglecting turbulence (laminar), neglecting turbulence on mass and heat transport (laminar transport), and for different eddy viscosity models (all using the Reynolds analogy for mass and heat transport) are shown
The Prandtl mixing length model leads to higher evaporation rates, although the near-interface velocities are higher for the other two models. As already mentioned, near the interface the diffusive transport of water vapor is very important and the Prandtl model does not account for a dampening of the eddy viscosity inside the viscous sublayer and toward the interface. This results in much higher eddy diffusivities near the evaporating surface and thus keeps a higher atmospheric demand. The Baldwin–Lomax and Hanna–van Driest models are quite similar to each other, the latter with slightly higher evaporation rates, because of higher velocities close to the interface and a higher eddy diffusivity throughout the domain.
Eddy Diffusivity and Eddy Conductivity Models: Compared to the eddy viscosity models, the influence of the eddy diffusivity and eddy conductivity models is small, as shown in Fig. 18. The same models for eddy diffusivity and eddy conductivity are used on top of the Baldwin–Lomax model for the eddy viscosity. Using different turbulent Schmidt and Prandtl numbers (\(Sc_{{\text {t}}} = 0.63\), \(Pr_{{\text {t}}} = 0.85\)), instead of unity as for the Reynolds analogy, leads to the expected higher evaporation rates. Deissler’s model (Deissler 1954), which has the advantage of being independent of the eddy viscosity model, the Hanna–van Driest model, and the Reynolds analogy give almost the same results.
These results indicate that the choice of the eddy diffusivity and eddy conductivity model is of minor importance and the Reynolds analogy is a good first assumption for these kind of problems. Further, the hypothesis that stage-I evaporation rates are mainly affected by the laminar transport through the viscous sublayer, e.g., Haghighi and Or (2013), may be supported.
3.6 Interface Parameters
This section focuses on the influence of properties of the porous-medium/free-flow interface. Here the effect of the Beavers–Joseph coefficient and of the sand-grain roughness is studied. As explained above, different formulations to link the sand-grain roughness to soil properties exist, e.g., to relate the sand-grain roughness with the median grain size diameter or to use the Kozeny–Carman equation, see Kuznetsov and Becker (2004). Both values (\(d_{50}=k_{{\text {s}}}=0.52\,{\mathrm{mm}}\) and \(k_{{\text {s}}}=0.24\,{\mathrm{mm}}\)) are inside the range of values considered in this study. To show the influence of this parameter, the sand-grain roughness is varied over three orders of magnitude to numerically investigate its influence on the evaporation rates.
Beavers–Joseph Coefficient: Different studies pertaining to the sensitivity of evaporation rates on the Beavers–Joseph coefficient \(\alpha _{{\text {BJ}}}\) have been carried out for Stokes flow or laminar flow, e.g., Baber et al. (2012) and Davarzani et al. (2014). All conclude that the \(\alpha _{{\text {BJ}}}\) coefficient has little influence on the evaporation rate. However, in Fig. 19 an influence of the Beavers–Joseph coefficient on the evaporation rate is observed. The different observations may be explained by 0.1 as the lowest \(\alpha _{{\text {BJ}}}\) value in Baber et al. (2012) or by the plot type in Davarzani et al. (2014), because cumulative mass loss plots shadow effects occurring during stage-I . For turbulent conditions, the influence on the evaporation rate is small compared to the magnitude of variation in \(\alpha _{{\text {BJ}}}\). Nevertheless, the influence on the slip velocity is more noticeable, see Table 6. For high \(\alpha _{{\text {BJ}}}\) values, the influence on the slip velocity decreases as the no-slip condition is approached. For low \(\alpha _{{\text {BJ}}}\) values, the resulting slip velocities for laminar and turbulent models are both relatively high. The larger influence of \(\alpha _{{\text {BJ}}}\) on the evaporation rate for the laminar case is explained by a relatively stronger increase in the near-interface velocities and gradients. Further, in the laminar case, the velocity profile is affected over a larger height and the relative increase in velocity is higher compared to the turbulent case.
Roughness Via Eddy Viscosity Models: The sand-grain roughness is only used for the Hanna–van Driest turbulence model. For \(\bar{u}_{{\text {g}}}=1.22\,\mathrm{m}/\mathrm{s}\) and the lowest sand-grain roughness \(k_{{\text {s}}}=0.1\,{\mathrm{mm}}\), the critical value for enabling Eq. 30 is not reached. For \(k_{{\text {s}}}=1\,{\mathrm{mm}}\), the roughness parametrization becomes active, but no effect on the evaporation rate can be observed, Fig. 20. For the largest considered sand-grain roughness (i.e., 10 mm) the evaporation rate increases. This can be explained by looking at the viscous sublayer heights presented in Table 7. There it can be seen that for the largest roughness length, the viscous sublayer is smaller than the roughness and thus turbulent flow influences the processes at the interface, see, e.g., Schlichting and Gersten (1997).
For higher velocities, the critical roughness length, needed to see a response in the evaporation rates, becomes smaller. For \(\bar{u}_{{\text {g}}}=3.65\,{\mathrm{m}}/{\mathrm{s}}\) a value of \(k_{{\text {s}}}=1\,{\mathrm{mm}}\) is sufficient to increase the rates.
For both velocities, the results are qualitatively as expected: Larger roughness lengths or higher velocities lead to more turbulent transport near the soil surface and hence increase the exchange fluxes between the two domains. The question how the results quantitatively correspond to measured data for different kind of roughness lengths and types cannot be answered here and requires additional experiments.
Roughness Via Boundary Layer Models: The roughness parametrization with boundary layer models requires an additional parameter \(y^+\) to convert the dimensionless wall distance to a boundary layer thickness (see Eq. 31). We consider a value of \(y^+=10\) to represent the end of the viscous sublayer. A value of \(y^+=30\) marks the beginning of the logarithmic region. From Eqs. (31 and 33), it can be seen that the diffusive fluxes are inverse proportional to the \(y^+\) value. This can be observed in Fig. 21 that for \(y^+=10\) and hence the smaller boundary layer, the evaporation rate is about three times higher than for \(y^+=30\).
The application of these boundary layer models is only justified as long as a viscous sublayer is present. For aerodynamically rough surfaces, this is not the case. Table 7 shows that \(k_{{\text {s}}}=10\,{\mathrm{mm}}\) corresponds to the fully rough case for \(\bar{u}_{{\text {g}}}=1.22\,\mathrm{m}/\mathrm{s}\).
The two boundary layer models after Colebrook and White (CW, Eq. 35) and Truckenbrodt (Tr, Eq. 34) predict higher evaporation rates than the EV model. Nevertheless, both models produce quite different results. Although the CW model was developed to capture the entire range from smooth to aerodynamically rough surfaces, the evaporation rate by the CW model is almost 50 % higher than the rate simulated with the EV model. In contrast to CW model, the Tr model is restricted to aerodynamically rough surfaces. For the qualitative analysis performed here, it was assumed that the fully rough skin fiction value is an acceptable approximation for aerodynamically smooth surfaces. This is questioned by the difference in evaporation rate for the two roughness lengths.
4 Conclusion
In Sect. 2, a model concept for coupling turbulent free flow, using the RANS equations, and porous-medium flow, using extended Darcy’s law is presented. The results in Sect. 3 indicate that the effect of turbulence on the exchange behavior may be decisive, especially during stage-I evaporation. Therefore, simulation concepts for evaporation from bare soil surfaces have to properly account for turbulence effects.
Results show that a considerable amount of uncertainty in the simulated evaporation rate originates from the chosen model setup and the boundary conditions in both the free- and the porous-medium flow regions. This indicates that detailed measurements and well-defined experimental setups are required for bridging the gap between experiments and simulations. Possible sources of error in the presented numerical simulations are (i) the 2-D setup and parametrization of turbulence, (ii) the assumption of local thermodynamic equilibrium inside the porous medium, and (iii) the assumption of a constant inflow profile or effects resulting from the neglected heater section on the free flow.
Generally, the predicted stage-I evaporation rates are in good agreement with the experimental data. Fluctuations in the evaporation rate are partly reproduced by using measured free-flow boundary conditions. Also stage-II evaporation rates agree very well with the measured evaporation rates, except in the case of \(\bar{u}_{{\text {g}}}=3.65\,\mathrm{m}/\mathrm{s}\); here, the discrepancy is assumed to arise from the measurements.
However, the model is not able to predict the shape and time of the transition from stage-I to stage-II evaporation. The simulated transition between stage-I and stage-II is sharper than the measured transition in the experiments. Further, it was not possible to predict the cumulative evaporated water mass at the time the transition occurs. With respect to porous-medium saturation, it is observed that the extended multiphase Darcy’s law is not able to reproduce the measured saturation profiles. Similar to Davarzani et al. (2014) numerical and experimental saturations do not match well a few centimeters below the soil surface.
Differences in evaporation rate due to different turbulence models are rather small. Only the Prandtl mixing length model does not consider a dampening of the eddy viscosity toward the wall; therefore, the evaporation rates are higher, because the Reynolds analogy is used for the eddy diffusivity and conductivity. Different eddy diffusivity and eddy conductivity models have a small influence on the exchanged mass fluxes.
The Beavers–Joseph coefficient does affect slip velocities, but the effect on evaporation is small for the analyzed scale. For the same wind velocity, when using a laminar concept, the effect on the evaporation rates and near surface velocities is larger than when modeling the turbulence. Nevertheless, low \(\alpha _{{\text {BJ}}}\) values are needed to see any effect on the evaporation rates at all.
Including a roughness parametrization fulfills the expected qualitative behavior; higher surface roughness leads to higher evaporation rates. In contrast to the eddy viscosity model for roughness, the roughness parametrizations with boundary layer models introduce more parameters and thus more uncertainty. However, effects of the sand-grain roughness are only visible for high velocities or large grain sizes (e.g., gravel). A detailed quantitative comparison of the effect of roughness in models and experiments is still necessary.
Abbreviations
- \(\alpha _{\text {BJ}}\) :
-
Beavers Joseph coefficient
- \(\alpha _{\text {vg}}\) :
-
Van Genuchten parameter (\(1/\mathrm{Pa}\))
- \(\alpha \) :
-
Phase index: liquid (l) or gas (g)
- \(\delta _{\text {v}}\) :
-
Viscous sublayer thickness (m)
- \(\kappa \) :
-
Component index: water (w) or air (a)
- \(\kappa \) :
-
Von Kármán constant
- \(\lambda \) :
-
Thermal conductivity (\(\mathrm{W}/(\mathrm{m\, K})\))
- \(\lambda _{\text {pm}}\) :
-
Effective porous-medium thermal conductivity (\(\mathrm{W}/(\mathrm{m}\, \mathrm{K})\))
- \(\lambda _{\text {s}}\) :
-
Thermal conductivity of the solid material (\(\mathrm{W}/(\mathrm{m K})\))
- \(\lambda _{\text {t}}\) :
-
Eddy thermal conductivity (\(\mathrm{W}/(\mathrm{m\, K})\))
- \(\nu \) :
-
Kinematic viscosity (\(\mathrm{m}^2/\mathrm{s}\))
- \(\nu _{\text {t}}\) :
-
Kinematic eddy viscosity
- \(\phi \) :
-
Porosity
- \(\tau \) :
-
Tortuosity
- \({\bar{\tau }}_\text {t}\) :
-
Turbulent and laminar shear stress (\(\mathrm{kg}/\mathrm{s}^2 \mathrm{m}\))
- \({\tau }\) :
-
Shear stress (\(\mathrm{kg}/\mathrm{s}^2 \mathrm{m}\))
- \({\mathbf {I}}\) :
-
Identity matrix
- \({\mathbf {K}}\) :
-
Intrinsic permeability (\({\mathrm{m}^2}\))
- \(\varrho \) :
-
Mass density (\(\mathrm{kg}/\mathrm{m}^3\))
- \(\varrho _{\text {mol}}\) :
-
Molar density (\(\mathrm{mol}/\mathrm{m}^3\))
- \(\varrho _{\text {s}}\) :
-
Mass density of the solid material (\(\mathrm{kg}/\mathrm{m}^3\))
- \(\varvec{{{g}}}\) :
-
Gravity vector (\(\mathrm{m}/\mathrm{s}^2\))
- \(\varvec{{{n}}}\) :
-
Interface-normal vector
- \(\varvec{{{t}}}\) :
-
Interface-tangential vector
- \(\varvec{{{v}}}\) :
-
Velocity (\(\mathrm{m}/\mathrm{s}\))
- \(c_{\text {f}}\) :
-
Skin friction coefficient
- \(c_{\text {p}}\) :
-
Specific isobaric heat capacity (\(\mathrm{J}/\text {kg K}\))
- \(c_{\text {s}}\) :
-
Specific heat capacity of the solid material (\(\mathrm{J}/\text {kg K}\))
- D :
-
Molecular diffusion coefficient (\(\mathrm{m}^2/\mathrm{s}\))
- \(d_{\text {hy}}\) :
-
Hydraulic radius (m)
- \(D_{\text {pm}}\) :
-
Porous-medium diffusion coefficient (\(\mathrm{m}^2/\mathrm{s}\))
- \(D_{\text {t}}\) :
-
Eddy diffusivity (\(\mathrm{m}^2/\mathrm{s}\))
- f :
-
Darcy friction factor
- h :
-
Discretization width (mm)
- h :
-
Specific enthalpy (\(\mathrm{J}/\mathrm{kg}\))
- \(k_{\text {r}}\) :
-
Relative permeability
- \(k_{\text {s}}\) :
-
Sand-grain roughness (m)
- \(k_{\text {s}}^+\) :
-
Equivalent sand-grain roughness
- \(l_\text {mix}\) :
-
Mixing length (m)
- M :
-
Molar mass (\(\mathrm{kg}/\mathrm{mol}\))
- n :
-
Number of cells (in x- or y-direction)
- \(n_{\text {vg}}\) :
-
Van Genuchten parameter
- p :
-
Phase pressure (\(\mathrm{kg}/\mathrm{s}^2\mathrm{m}\))
- \(p_{\text {c}}\) :
-
Capillary pressure (\(\mathrm{kg}/\mathrm{s}^2 \mathrm{m}\))
- \(Pr_{\text {t}}\) :
-
Turbulent Prandtl number
- Re :
-
Reynolds number (length (x) or diameter (d) based)
- S :
-
Saturation
- \(Sc_{\text {t}}\) :
-
Turbulent Schmidt number
- T :
-
Temperature (K)
- u :
-
Velocity component in main flow direction (\(\mathrm{m}/\mathrm{s}\))
- \(u^*\) :
-
Wall friction velocity (\(\mathrm{m}/\mathrm{s}\))
- \(u^{\text {e}}\) :
-
Specific internal energy (\(\mathrm{J}/\mathrm{kg}\))
- X :
-
Mass fraction
- x :
-
Mole fraction
- y :
-
Wall distance/ y-coordinate (m)
- \(y^+\) :
-
Dimensionless wall distance
- BL:
-
Boundary layer
- ff:
-
Free flow
- if:
-
Interface
- pm:
-
Porous medium
References
Arbogast, T., Pencheva, G., Wheeler, M.F., Yotov, I.: A multiscale mortar mixed finite element method. Multiscale Model. Simul. 6(1), 319–346 (2007). doi:10.1137/060662587
Assouline, S.: Modeling the relationship between soil bulk density and the water retention curve. Vadose Zone J. 5(2), 554–563 (2006). doi:10.2136/vzj2005.0083
Assouline, S., Narkis, K., Or, D.: Evaporation from partially covered water surfaces. Water Resour. Res. 46(W10), 539 (2010). doi:10.1029/2010WR009121
Baber, K., Mosthaf, K., Flemisch, B., Helmig, R., Müthing, S., Wohlmuth, B.: Numerical scheme for coupling two-phase compositional porous-media flow and one-phase compositional free flow. IMA J. Appl. Math. 77(6), 887–909 (2012). doi:10.1093/imamat/hxs048
Baldwin, B.S., Lomax, H.: Thin layer approximation and algebraic model for separated turbulent flows. AIAA J. 78–257, 1–9 (1978). doi:10.2514/6.1978-257
Bastian, P., Blatt, M., Dedner, A., Engwer, C., Klöfkorn, R., Kornhuber, R., Ohlberger, M., Sander, O.: A generic grid interface for parallel and adaptive scientific computing. Part II: implementation and tests in DUNE. Computing 82(2–3), 121–138 (2008a). doi:10.1007/s00607-008-0004-9
Bastian, P., Blatt, M., Dedner, A., Engwer, C., Klöfkorn, R., Ohlberger, M., Sander, O.: A generic grid interface for parallel and adaptive scientific computing. Part I: abstract framework. Computing 82(2–3), 103–119 (2008b). doi:10.1007/s00607-008-0003-x
Beavers, G.S., Joseph, D.D.: Boundary conditions at a naturally permeable wall. J. Fluid Mech. 30(1), 197–207 (1967). doi:10.1017/S0022112067001375
Bird, R.B., Stewart, W.E., Lightfoot, E.N.: Transport Phenomena, 2nd edn. Wiley, New York (2007)
Breugem, W.P., Boersma, B.J.: Direct numerical simulations of turbulent flow over a permeable wall using a direct and a continuum approach. Phys. Fluids 17(2), 15 (2005). doi:10.1063/1.1835771
Cebeci, T.: Calculation of incompressible rough-wall boundary layer flows. AIAA J. 16(7), 730–735 (1978). doi:10.2514/3.7571
Chauhan, V.P., Stylianopoulos, T., Boucher, Y., Jain, R.K.: Delivery of molecular and nanoscale medicine to tumors: transport barriers and strategies. Ann. Rev. Chem. Biomol. Eng. 2, 281–298 (2011). doi:10.1146/annurev-chembioeng-061010-114300
Ciocca, F., Lunati, I., Parlange, M.B.: Effects of the water retention curve on evaporation from arid soils. Geophys. Res. Lett. 41, 3110–3116 (2014). doi:10.1002/2014GL059827
Colebrook, C.F.: Turbulent flow in pipes, with particular reference to the transition region between smooth and rough pipe laws. J. Inst. Civ. Eng. 11, 133–156 (1939). doi:10.1680/ijoti.1939.13150
Dahmen, W., Gotzen, T., Müller, S., Rom, M.: Numerical simulation of transpiration cooling through porous material. Int. J. Numer. Meth. Fluids 76(6), 331–365 (2014). doi:10.1002/fld.3935
Davarzani, H., Smits, K., Tolene, R.M., Illangasekare, T.: Study of the effect of wind speed on evaporation from soil through integrated modeling of the atmospheric boundary layer and shallow subsurface. Water Resour. Res. 50, 1–20 (2014). doi:10.1002/2013WR013952
de Lemos, M.J.S.: Turbulent flow around fluid–porous interfaces computed with a diffusion-jump model for \(k\) and \(\varepsilon \) transport equations. Transp. Porous Media 78, 331–346 (2009). doi:10.1007/s11242-009-9379-0
Defraeye T (2011) Convective heat and mass transfer at exterior building surfaces. PhD thesis, Katholieke Universiteit Leuven
Defraeye, T., Blocken, B., Carmeliet, J.: CFD analysis of convective heat transfer at the surfaces of a cube immersed in a turbulent boundary layer. Int. J. Heat Mass Transf. 53(1–3), 297–308 (2010). doi:10.1016/j.ijheatmasstransfer.2009.09.029
Deissler, R.G.: Analysis of turbulent heat transfer, mass transfer, and friction in smooth tubes at high Prandtl and Schmidt numbers. NACA Rep. 1210, 69–82 (1954)
Demmel, J.W., Eisenstat, S.C., Gilbert, J.R., Li, X.S., Liu, J.W.H.: A supernodal approach to sparse partial pivoting. SIAM J. Matrix Anal. Appl. 20(3), 720–755 (1999). doi:10.1137/S0895479895291765
Discacciati, M., Quarteroni, A.: Navier–Stokes/Darcy coupling: modeling, analysis, and numerical approximation. Revista Matemática Complutense 22(2), 315–426 (2009)
Fetzer, T.: Numerical analysis of the influence of turbulence on exchange processes between porous-medium and free flow. Diploma thesis, University of Stuttgart (2012)
Flemisch, B., Darcis, M., Erbertseder, K., Faigle, B., Lauser, A., Mosthaf, K., Müthing, S., Nuske, P., Tatomir, A., Wolff, M., Helmig, R.: DuMuX: DUNE for Multi-\(\{\)Phase, Component, Scale, Physics, \(\ldots \) \(\}\) Flow and Transport in Porous Media. Adv. Water Resour. 34(9), 1102–1112 (2011). doi:10.1016/j.advwatres.2011.03.007
Fujimaki, H., Shimano, T., Inoue, M., Nakane, K.: Effect of a salt crust on evaporation from a bare saline soil. Vadose Zone J. 5(4), 1246–1256 (2006). doi:10.2136/vzj2005.0144
Haaland, S.E.: Simple and explicit formulas for the friction factor in turbulent pipe flow. J. Fluids Eng. 105(1), 89–90 (1983). doi:10.1115/1.3240948
Haghighi, E., Or, D.: Evaporation from porous surfaces into turbulent airflows: coupling eddy characteristics with pore scale vapor diffusion. Water Resour. Res. 49(12), 8432–8442 (2013). doi:10.1002/2012WR013324
Haghighi, E., Or, D.: Interactions of bluff-body obstacles with turbulent airflows affecting evaporative fluxes from porous surfaces. J. Hydrol. 530, 103–116 (2015). doi:10.1016/j.jhydrol.2015.09.048
Haghighi, E., Shahraeeni, E., Lehmann, P., Or, D.: Evaporation rates across a convective air boundary layer are dominated by diffusion. Water Resour. Res. 49(3), 1602–1610 (2013). doi:10.1002/wrcr.20166
Hahn, S., Je, J., Choi, H.: Direct numerical simulation of turbulent channel flow with permeable walls. J. Fluid Mech. 450, 259–285 (2002). doi:10.1017/S0022112001006437
Hanna, O.T., Sandell, O.C., Mazet, P.R.: Heat and mass transfer in turbulent flow under conditions of drag reduction. AIChE J. 27(4), 693–697 (1981). doi:10.1002/aic.690270424
Helmig, R.: Multiphase Flow and Transport Processes in the Subsurface: A Contribution to the Modeling of Hydrosystems. Springer, Berlin (1997)
Huber, R., Helmig, R.: Node-centered finite volume discretizations for the numerical simulation of multiphase flow in heterogeneous porous media. Comput. Geosci. 4, 141–164 (2000). doi:10.1023/A:1011559916309
Jambhekar, V.A., Helmig, R., Schröder, N., Shokri, N.: Free-Flow–Porous-Media Coupling for Evaporation-Driven Transport and Precipitation of Salt in Soil. Transp. Porous Media. 110, 251–280 (2015). doi:10.1007/s11242-015-0516-7
Johansen, O.: Thermal conductivity of soils. Ph.D. Thesis, (CRREL draft transl. 637, 1977), Norwegian University of Science and Technology, Trondheim, Norway (1975)
Krafczyk, M., Kucher, K., Wang, Y., Geier, M.: DNS/LES studies of turbulent flows based on the cumulant lattice boltzmann approach. In: Nagel, W.E., Kröner, D.H., Resch, M.M. (eds) High Performance Computing in Science and Engineering’14, Springer International Publishing, pp 519–531. doi:10.1007/978-3-319-10810-0_34 (2015)
Kuznetsov, A.V.: Numerical modeling of turbulent flow in a composite porous/fluid duct utilizing a two-layer k-\(\varepsilon \) model to account for interface roughness. Int. J. Therm. Sci. 43(11), 1047–1056 (2004). doi:10.1016/j.ijthermalsci.2004.02.011
Kuznetsov, A.V., Becker, S.M.: Effect of the interface roughness on turbulent convective heat transfer in a composite porous/fluid duct. Int. Commun. Heat Mass Transf. 31(1), 11–20 (2004). doi:10.1016/S0735-1933(03)00197-0
Laurindo, J.B., Prat, M.: Numerical and experimental network study of evaporation in capillary porous media. Drying rates. Chem. Eng. Sci. 53(12), 2257–2269 (1998). doi:10.1016/S0009-2509(97)00348-5
Lehmann, P., Assouline, S., Or, D.: Characteristic lengths affecting evaporative drying of porous media. Phys. Rev. E 77(5), 056,309 (2008). doi:10.1103/PhysRevE.77.056309
Millington, R., Quirk, J.: Permeability of porous solids. Trans. Faraday Soc. 57, 1200–1207 (1961). doi:10.1039/TF9615701200
Mosthaf, K., Baber, K., Flemisch, B., Helmig, R., Leijnse, A., Rybak, I., Wohlmuth, B.: A coupling concept for two-phase compositional porous-medium and single-phase compositional free flow. Water Resour. Res. 47(10), W10522 (2011). doi:10.1029/2011WR010685
Mosthaf, K., Helmig, R., Or, D.: Modeling and analysis of evaporation processes from porous media on the REV scale. Water Resour. Res. 50, 1059–1079 (2014). doi:10.1002/2013WR014442
Nield, D.: The Beavers–Joseph boundary condition and related matters: a historical and critical note. Transp Porous Med 78, 537–540 (2009). doi:10.1007/s11242-009-9344-y
Nuske, P., Joekar-Niasar, V., Helmig, R.: Non-equilibrium in multiphase multicomponent flow in porous media: an evaporation example. Int. J. Heat Mass Transf. 74, 128–142 (2014). doi:10.1016/j.ijheatmasstransfer.2014.03.011
Pedras, M.H., de Lemos, M.J.: Macroscopic turbulence modeling for incompressible flow through undeformable porous media. Int. J. Heat Mass Transf. 44(6), 1081–1093 (2001). doi:10.1016/S0017-9310(00)00202-7
Penman, H.L.: Natural evaporation from open water, bare soil and grass. Proc. R Soc. Lond. A Math. Phys. Eng. Sci. 193(1032), 120–145 (1948). doi:10.1098/rspa.1948.0037
Pope, S.B.: Turbulent Flows, 4th edn. Cambridge University Press, Cambridge (2006)
Rotta, J.C.: Turbulent boundary layers in incompressible flow. Progr. Aerosp. Sci. 2, 1–219 (1962). doi:10.1016/0376-0421(62)90014-3
Rybak, I., Magiera, J., Helmig, R., Rohde, C.: Multirate time integration for coupled saturated/unsaturated porous medium and free flow systems. Comput. Geosci. 19(2), 299–309 (2015). doi:10.1007/s10596-015-9469-8
Saffman, P.: On the boundary condition at the surface of a porous medium. Stud. Appl. Math. L, 93–101 (1971). doi:10.1002/sapm197150293
Sahraoui, M., Kaviany, M.: Slip and no-slip velocity boundary conditions at interface of porous, plain media. Int. J. Heat Mass Transf. 35(4), 927–943 (1992). doi:10.1016/0017-9310(92)90258-T
Schlichting, H., Gersten, K.: Grenzschicht-Theorie, 9th edn. Springer, Berlin (1997)
Schneider-Zapp, K., Ippisch, O., Roth, K.: Numerical study of the evaporation process and parameter estimation analysis of an evaporation experiment. Hydrol. Earth Syst. Sci. 14(5), 765–781 (2010). doi:10.5194/hess-14-765-2010
Schwenck, N., Beck, M., Becker, B., Class, H., Fetzer, T., Flemisch, B., Grüninger, C., Hommel, J., Jambhekar, V., Kissinger, A., Koch, T., Schneider, M., Schröder, N., Seitz, G., Weishaupt, K.: DuMuX 2.8.0. doi:10.5281/zenodo.31611 (2015)
Shahraeeni, E., Or, D.: Thermo-evaporative fluxes from heterogeneous porous surfaces resolved by infrared thermography. Water Resour. Res. 46(9), W09,511 (2010). doi:10.1029/2009WR008455
Shahraeeni, E., Lehmann, P., Or, D.: Coupling of evaporative fluxes from drying porous surfaces with air boundary layer: characteristics of evaporation from discrete pores. Water Resour. Res. 48(9), W09525 (2012). doi:10.1029/2012WR011857
Shokri, N., Or, D.: What determines drying rates at the onset of diffusion controlled stage-2 evaporation from porous media? Water Resour. Res. (2011). doi:10.1029/2010WR010284
Shukla, J., Mintz, Y.: Influence of land-surface evapotranspiration on the earth’s climate. Science 215, 1498–1501 (1982). doi:10.1126/science.215.4539.1498
Smits, K.M., Sakaki, T., Limsuwat, A., Illangasekare, T.H.: Thermal conductivity of sands under varying moisture and porosity in drainage–wetting cycles. Vadose Zone J. 9(1), 172–180 (2010). doi:10.2136/vzj2009.0095
Smits, K.M., Cihan, A.C., Sakaki, T., Illangasekare, T.H.: Evaporation from soils under thermal boundary conditions: experimental and modeling investigation to compare equilibrium- and nonequilibrium-based approaches. Water Resour. Res. 47(5), W05540 (2011). doi:10.1029/2010WR009533
Sugita, F., Kishii, T.: Effect of roughness distribution on evaporation processes over non-homogeneous sand surfaces: a wind tunnel investigation. Hydrol. Process. 16(11), 2141–2153 (2002). doi:10.1002/hyp.1147
Suzuki, S., Maeda, S.: On the mechanism of drying of granular bed. J. Chem. Eng. Jpn. 1, 26–31 (1968). doi:10.1252/jcej.1.26
Trautz, A.C., Smits, K.M., Cihan, A.: Continuum-scale investigation of evaporation from bare soil under different boundary and initial conditions: An evaluation of nonequilibrium phase change. Water. Resour. Res. 51, 7630–7648 (2015). doi:10.1002/2014WR016504
Truckenbrodt, E.: Elementare Strömungsvorgänge dichteveränderlicher Fluide. In: Fluidmechanik, 4th edn, Klassiker der Technik, Springer, Berlin, pp. 1–111. doi:10.1007/978-3-540-79024-2_1 (2008)
van Brakel, J.: Advances in drying, vol 1, Hemisphere, Chap Mass transfer in convective drying, pp. 217–267 (1980)
van Driest, E.R.: On turbulent flow near a wall. AIAA J. 23(11), 1007–1011 (1956). doi:10.2514/8.3713
van Genuchten, M.T.: A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 44(5), 892–898 (1980). doi:10.2136/sssaj1980.03615995004400050002x
Vanderborght, J., Graf, A., Steenpass, C., Scharnagl, B., Prolingheuer, N., Herbst, M., Franssen, H.J.H., Vereecken, H.: Within-field variability of bare soil evaporation derived from eddy covariance measurements special section: patterns. Vadose Zone J. 9(4), 943–954 (2010). doi:10.2136/vzj2009.0159
Verboven, P., Flick, D., Nicolaï, B., Alvarez, G.: Modelling transport phenomena in refrigerated food bulks, packages and stacks: basics and advances. Int. J. Refrig 29(6), 985–997 (2006). doi:10.1016/j.ijrefrig.2005.12.010
White, F.M.: Fluid Mechanics, 7th edn. McGraw-Hill, Singapore (2011)
Wilcox, D.C.: Turbulence Modeling for CFD, 3rd edn. DCW Industries, La Cañada (2006)
Yiotis, A.G., Tsimpanogiannis, I.N., Stubos, A.K., Yortsos, Y.C.: Coupling between external and internal mass transfer during drying of a porous medium. Water Resour. Res. 43(W06403), 1–12 (2007). doi:10.1029/2006WR005558
Zhang, C., Li, L., Lockington, D.: A physically based surface resistance model for evaporation from bare soils. Water Resour. Res. 51, 1084–1111 (2015). doi:10.1002/2014WR015490
Acknowledgments
This work was supported by the German Research Foundation (DFG). Some of the authors are members of the International Research Training Group NUPUS funded by the German Research Foundation (DFG) and Netherlands Organization for Scientific Research (NWO). We thank the DFG for their support. Furthermore, we thank Hossein Davarzani and Ryan Tolene for their contributions to the experimental data and Bernd Flemisch and Christoph Grüninger for the helpful discussions and input.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Fetzer, T., Smits, K.M. & Helmig, R. Effect of Turbulence and Roughness on Coupled Porous-Medium/Free-Flow Exchange Processes. Transp Porous Med 114, 395–424 (2016). https://doi.org/10.1007/s11242-016-0654-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-016-0654-6