Simulation of Front Instabilities in Density-Driven Flow, Using a Reactive Transport Model for Biogrout Combined with a Randomly Distributed Permeability Field

Abstract

Biogrout is a method to strengthen granular soil, which is based on microbial-induced carbonate precipitation. To model the Biogrout process, a reactive transport model is used. Since high flow rates are undesirable for the Biogrout process, the model equations can be solved with a standard Galerkin finite element method. The Biogrout process involves the injection of dense fluids in the subsurface. In this paper, we present our reactive transport model for Biogrout and use it to simulate an experiment in which a pulse of a dense fluid is injected in a porous medium filled with water. In this experiment, front instabilities were observed in the form of fingers. The numerical simulations showed that the fingering phenomenon was less pronounced than in the experiment. By reducing the dispersion length and implementing a randomly distributed permeability field, the fingering phenomenon could be induced. Furthermore, the results of a case study to a Biogrout application are reported.

1 Introduction

The current research is done within the framework of Biogrout. It is investigated what the effects of buoyancy-driven flow and the associated fingering phenomenon can be on Biogrout.

Biogrout is a soil strengthening method, which is based on microbial-induced carbonate precipitation (MICP). Microorganisms are used to produce the solid calcium carbonate (${\mathrm {CaCO_3}}$), which strengthens the soil by connecting soil particles. The microorganisms are already present in the soil (Paassen et al. 2010) or injected into it (Whiffin et al. 2007). The microorganisms are supplied with urea ($\mathrm {CO(NH_2)_2}$) and calcium chloride ($\mathrm {CaCl_2}$). These substrates are injected into the soil and transported by water flow, induced by injection and extraction, to the desired location. Two reactions take place: a hydrolysis reaction and a precipitation reaction. The microbial enzyme urease provides the hydrolysis of urea, by which carbonate ($\mathrm {CO_3^{2-}}$) is produced. The hydrolysis reaction equation is given in Whiffin et al. (2007):

$$\begin{aligned} {\mathrm {CO(NH_2)_2 + 2 H{_{2}}O \mathop {\longrightarrow }\limits ^{bacteria} 2 NH_4^+ + CO_3^{2-}.}} \end{aligned}$$

(1)

In the presence of calcium ions (${\mathrm {Ca^{2+}}}$), the carbonate precipitates as calcium carbonate (${\mathrm {CaCO_3}}$):

$$\begin{aligned} {\mathrm {Ca^{2+}(aq) + CO_3^{2-}(aq) \rightarrow CaCO_3(s).}} \end{aligned}$$

(2)

Combining both reaction (1) and reaction (2) gives the overall reaction equation:

$$\begin{aligned} {\mathrm {CO(NH_2)_2(aq) + Ca^{2+}(aq) + 2 H{_{2}}O(l) \rightarrow 2 NH_4^+(aq) + CaCO_3(s).}} \end{aligned}$$

(3)

The by-product of these reactions is ammonium chloride (${\mathrm {NH{_{4}}Cl}}$), which is dissolved in water. As it is not desirable that the ammonium chloride stays in the soil, it should be removed. Therefore, the injection of substrates is followed by groundwater injection and extraction to rinse the remaining by-product solution.

The substrates and by-product of the reactions are dissolved in water, which increases the fluid density. For example, a 1 molar calcium chloride/urea solution has a density of $1.1\,\times \,10^{3}$ kg/m$^3$. If all the calcium chloride and urea of a 1 molar solution react, one ends up with a 2 molar ammonium chloride solution, which has a density of $1.03\,\times \,10^{3}$ kg/m$^3$. In a fresh groundwater environment, the dense fluid will move more easily downwards than upwards as a result of density differences. The forces of gravity and buoyancy can generate front instabilities in the form of fingers where a dense fluid is on top of a less dense fluid. In order to get the microorganisms and their substrates at the desired location and extract the by-product, it is important to examine the effect of fingering on the flow and transport. This will help to decide which concentrations and what flow rate should be used and where the injection and extraction wells should be positioned.

To examine the effect of buoyancy-driven flow and the associated fingering phenomenon, an experiment has been performed, in which a pulse of saline fluid is injected in a porous media flow cell, generating a two-dimensional flow field. The flow cell is filled with glass beads and saturated with water. The saline pulse is followed by a pulse of water. The experimental results are compared with the outcome of numerical simulations. Besides, a Biogrout case study is performed and reported.

A lot of research on fingering has already been done, both on viscous fingering (Saffman–Taylor instabilities) and instabilities caused by density differences; see, for example, Diersch and Kolditz (2002), Duijn et al. (2004), Farajzadeh et al. (2013), and Khosrokhavar et al. (2014). There are several approaches. One is the sharp interface approach in which the fluids are assumed to be immiscible (Chevalier et al. 2006; DiCarlo 2013). Another approach is the miscible fluid approach. If chemical reactions play a role (like in the Biogrout case), the miscible fluid approach should be taken, since the concentration can have a whole range of values and does not only have to be binary at the vicinity of a sharp interface; see, for example, de Wit (2004), Johannsen et al. (2006), Musuuza et al. (2009), Simmons et al. (2001), and Voss and Souza (1987).

The setup of the experiment and the case study is given in the Sects. 2 and 3. The reactive transport model for Biogrout, derived in Wijngaarden et al. (2011) and van Wijngaarden et al. (2013), is presented in Sect. 4. Section 5 contains the numerical methods that are used to solve the model equations, and Sect. 6 reports the results, including the effect of using a random porosity/permeability field to induce the fingering. In Sect. 7, some conclusions and discussion can be found.

2 Materials and Methods

To evaluate the effect of a buoyancy-driven flow on the distribution of injected solutes, a two-dimensional porous media flow cell experiment is performed. The flow cell constructed from a PVC frame with plexiglass front and back plates is 95 cm wide, 45 cm high, and 3 cm thick. The space is filled with glass beads, with a grain size ranging up to 200 $\upmu$m. A picture of some glass beads is shown in Fig. 1. Beside glass beads, also some crystals can be seen. These crystals result from the Biogrout experiment that is performed after the buoyancy-driven flow experiment that is reported here. One injection well, a hollow steel tube, is installed at the center of the flow cell, and two extraction wells are installed at mid-height about 12 cm from the side of the flow cell as shown in Fig. 2.

Fig. 1

A picture of some glass beads (spheres) that are used in the buoyancy-driven flow experiment

Fig. 2

Setup of the experiment. Injection well is denoted by $\varGamma _\mathrm{in}$ and the extraction wells by $\varGamma _\mathrm{out}$. The other boundaries ($\varGamma _\mathrm{closed}$) are closed

A solution of 0.5 M sodium chloride (NaCl) is prepared to which a bit of red food dye powder (Allura Red, E129) is added. The porous media flow cell is first filled with water and flushed for several hours. The flow rate at the injection and extraction wells is kept constant, where the injection flow rate is equal to the total extraction flow rate of about 300 mL/h. At a certain moment, the sodium chloride solution is injected for a period of 30 min after which tap water is injected again. The flow of the red sodium chloride solution is monitored using a Canon G7 compact camera at 10 min time-lapse intervals.

3 Case Study Setup

Since the scale of the experiment is quite small compared to practical applications, we also do a case study of an application of Biogrout, i.e., to create a cemented zone underneath a levee in order to prevent piping (Blauw et al. 2012, 2013). Piping is an important failure mechanism of levees in the Netherlands (van Beek et al. 2010). Piping starts with heave and cracking of the soft soil top layer at the land side of the levee. The cracks in the top soft soil layer allow for seepage via the permeable sand layer underneath the clay levee. If the water level difference between river and land side is large enough, sand grains may be transported along with the water flow. This will create a pipe underneath the levee, which becomes wider and wider as the process proceeds. Finally, this will lead to failure of the levee and to breakthrough.

One way of decreasing the risk of failure of the levee due to piping is to broaden the levee. This will decrease the pressure gradients in the sandy layer, which is the driving force for the process. This, however, is expensive and not always possible, for example, because of existing buildings close to the levee.

In those cases, Biogrout can be used to decrease the risk of failure due to piping. As it fixates the sand grains, it will prevent the creation of pipes, or block the propagation of pipes. While the Biogrouted sand will only have a minor decrease in permeability, the seepage water will flow through the fixated sand body. Hence, the water will not seek another way and herewith the risk of pipe formation is reduced.

Fig. 3

Configuration for the case study (cross section). The levee is shown as well as the desired location of the Biogrouted sand body. The location of the injection and extraction drains is indicated. The blue arrows display the seepage for a high water situation

Figure 3 shows the cross section of the configuration for the case study. It shows the levee and the desired location of the Biogrouted sand body. The blue arrows indicate the seepage. The Biogrouted sand and the top clay layer should be connected to prevent the formation of pipes in between. Therefore, the injection drain is located close to the top clay layer. The extraction drains are 2 m below the injection, since the dense fluid will tend to move downwards and since we assume that a Biogrouted sand body of 2 m depth provides a sufficient barrier for the pipes. The distance between the extraction drains is 2 m. This case study can be modeled through a 2D simulation, because of the symmetry. For our domain of computation $\varOmega$, we choose a depth of 6 m and a width of 4 m. We assume that these dimensions are large enough so that the numerical results are not affected by the location of the boundaries.

In the numerical simulation, the seepage is not taken into account. Therefore, we obtain a symmetrical situation. Because of this symmetry, we only calculate the part left to the injection drain and mirror the results. We take the mathematical model as described in Sect. 4.2 and the configuration as in Fig. 3. We position the origin of the coordinate system above the red circle in this figure, i.e., on the symmetry axes, at the bottom of the clay layer. Then, the coordinates of the centers of the extraction wells are ($\pm 1,-2.2$). The radius of the extraction drains is 0.1 m. The injection is placed under the clay layer of the dike. As a simplification, we use a part of the symmetry axis as the inflow boundary, namely the line segment between $z=-0.3$ m and $z=-0.1$ m. Hence, a line segment is used as the injection boundary rather than a semicircle.

As a flow rate, we choose $Q_\mathrm{in}=0.5\hbox { m}^3$ per day per running meter of the drain (for the whole domain). For comparison, this is twice as much as the flow rate in the porous media flow cell experiment. To prevent that the dense fluid will sink away, we choose a larger extraction flow rate, that is, $Q_\mathrm{out}=2 \hbox { m}^3$ per day per running meter of the drain for both the extraction drains. Since there are two extraction drains, the total extraction flow rate is eight times as large as the injection flow rate. The injection Darcy velocity $q_\mathrm{in}$ is calculated from the injection flow rate via $q_\mathrm{in}=Q_\mathrm{in}/A_\mathrm{in}$, in which $A_\mathrm{in}$ is the surface of the injection. In the same way, we have that the extraction Darcy velocity $q_\mathrm{out}$ equals $q_\mathrm{out}=Q_\mathrm{out}/A_\mathrm{out}$. The Biogrout liquids are injected for 12 hours, followed by the injection of water to rinse the soil. As the inflow concentration of urea and calcium, we choose $c_\mathrm{in}=0.5$ kmol/$\hbox { m}^3$. Afterward, water is injected which implies that $c_\mathrm{in}$ is given by $c_\mathrm{in}=0$ kmol/$\hbox { m}^3$ for $t>12$h. Since ammonium chloride is a reaction product, the injected concentration is equal to 0.

4 Mathematical Model

In this section, we describe the model equations that are used to simulate the experiment. The initial conditions and boundary conditions are given as well. This is done for the experiment as well as for the case study.

4.1 Model Equations, Initial and Boundary Conditions for the Simulation of the Experiment

In this subsection, we describe the mathematical model as well as the initial and boundary conditions that are used to simulate the experiment. This model is based on the reactive transport model for Biogrout as reported in Wijngaarden et al. (2011) and slightly adapted for this experiment.

We assume that the flow is incompressible and therefore divergence free. Hence, in the domain $\varOmega$, we have for time $t\ge 0$:

$$\begin{aligned} \nabla \cdot {\mathbf {q}}=0. \end{aligned}$$

(4)

Here, ${\mathbf {q}}$ (m/s) is the Darcy flow velocity.

For the relation between the Darcy flow velocity and the pressure, Darcy’s law is used (Zheng and Bennett 1995):

$$\begin{aligned} {\mathbf {q}}=-\frac{k}{\mu }(\nabla p +\rho _l g {\mathbf {e_z}}), \end{aligned}$$

(5)

in which k ($\hbox {m}^2$) is the intrinsic permeability, $\mu$ (Pa s) is the dynamic viscosity of the fluid, p (Pa) is the pressure, $\rho _l$ (kg/$\hbox {m}^3$) is the density of the fluid, and g ($\hbox {m/s}^2$) is the gravitational constant.

Fig. 4

Density of the sodium and chloride solution plotted against the concentration. Experimental values and a linear fit: $\rho _\mathrm{l}=1000 + 41C^{{\mathrm {Na}}^+}$

The pore water velocity relates to the Darcy flow velocity via

$$\begin{aligned} \mathbf {v}=\frac{\mathbf {q}}{\theta }, \end{aligned}$$

(6)

in which $\theta$ (1) is the porosity.

Substituting Eq. (5) into Eq. (4) gives a partial differential equation for the pressure:

$$\begin{aligned} \nabla \cdot \left( \frac{k}{\mu }(\nabla p +\rho _l g {\mathbf {e_z}})\right) =0, \quad \text { in } \varOmega . \end{aligned}$$

(7)

This is the Oberbeck–Boussinesq approximation; see, for example, Diersch and Kolditz (2002). The Oberbeck–Boussinesq approximation consists in neglecting all density dependencies, except for the crucial buoyancy term $\rho _l g$ in Eqs. (5) and (7).

We model the intrinsic permeability as a function of the porosity via the Kozeny–Carman relation (Bear 1972):

$$\begin{aligned} k=\frac{(d_\mathrm{m})^2}{180}\frac{\theta ^3}{(1-\theta )^2}. \end{aligned}$$

(8)

In this equation, $d_\mathrm{m}$ (m) is the mean particle size. We assume that the porosity is log-normally distributed $\theta \sim \log \mathcal {N}(\tilde{\mu },\sigma ^2)$, see Kosugi (1996) and Nimmo (2004).

Sodium chloride is dissolved in water. The resulting concentrations of sodium ($\mathrm {Na^+}$) and chloride ($\mathrm {Cl^-}$) are equal, because their relation in sodium chloride is 1:1. Since the concentrations of sodium and chloride are in the range of [0, 0.5], all sodium and chloride ions will dissolve. Hence, it is not necessary to use a crystal precipitation model like (Knabner et al. 1995). We used the experimental outcomes of (Weast 1980) to find a relation between the density of the fluid and the concentration of sodium (and chloride). In Fig. 4, we plotted the fluid density against the concentrations of sodium and chloride and constructed a linear fit. The (average) slope of this graph is 41 kg/kmol. For a zero concentration, the density equals 1000 kg/m$^3$. That gives the following relation for the density as a function of the sodium (and chloride) concentration:

$$\begin{aligned} \rho _l=1000+41 C^{\mathrm {Na}^+}, \end{aligned}$$

(9)

in which $C^{\mathrm {Na}^+}$ (kmol/m$^3$) is the concentration of sodium (which is equal to the chloride concentration).

The concentration of sodium is modeled by an advection–dispersion equation:

$$\begin{aligned} \displaystyle {\frac{\partial \left( \theta C^{{\mathrm {Na^+}}}\right) }{\partial t}=\nabla \left( \theta {\mathbf {D}} \cdot \nabla C^{{\mathrm {Na^+}}}\right) - \nabla \cdot ({\mathbf {q}} C^{{\mathrm {Na^+}}}), \quad \text { in } \varOmega }. \end{aligned}$$

(10)

In this equation, $\mathbf {D}$ ($\hbox {m}^2$/s) is the dispersion tensor, which coefficients equal $D_{ij}=(\alpha _\mathrm{L}-\alpha _\mathrm{T})\frac{v_iv_j}{|\mathbf {v}|}+\delta _{ij}\alpha _\mathrm{T}\sum _i \frac{v_i^2}{|\mathbf {v}|}+\delta _{ij} D_\mathrm{m}$, see Zheng and Bennett (1995). The constant $\alpha _\mathrm{L}$ (m) is the longitudinal dispersivity, $\alpha _\mathrm{T}$ (m) is the transverse dispersivity, and $D_\mathrm{m}$ ($\hbox {m}^2$/s) is the molecular diffusion coefficient. In this study, we choose smaller values for $\alpha _\mathrm{L}$ and $\alpha _\mathrm{T}$ then given in Gelhar et al. (1992), because the amount of dispersion is relatively small as indicated by the presence of the fingers and the sharp fronts in the experiment. A large value for the entries in the dispersion tensor would never show the observed fingering behavior. If dispersion would be more important, then the dependence of the dispersion lengths on the statistical distribution of the permeability can be incorporated. For more details and mathematical relations, we refer to Talon et al. (2003, 2004).

We assume that the dispersion tensors for sodium and chloride are equal. Furthermore, it is assumed that the porous medium is not charged. Together with similar initial and boundary conditions, we have that the sodium concentration and the chloride concentration are equal. Hence, we consider only one concentration, the sodium concentration. In this paper, we choose the longitudinal dispersivity equal to the transverse dispersivity, $\alpha _\mathrm{L}=\alpha _\mathrm{T}$. Usually, the transverse dispersivity is somewhat smaller than the longitudinal dispersivity as reported in Gelhar et al. (1992). We want the fronts as sharp as possible for the given mesh. A smaller dispersion length may lead to numerical instability, which is a result of the restriction on the mesh Péclet number in case of central differences, see van Kan et al. (2005). Hence, we choose equal dispersivities for this research.

The experiment is modeled in 2D with the configuration as shown in Fig. 2. The region is denoted by $\varOmega$, which is bounded by $\varGamma _{\text {closed}}$ and by the holes $\varGamma _{\text {in}}$ and $\varGamma _{\text {out}}$. The interfaces with $\varOmega$ and the injection and extraction wells are denoted by $\varGamma _{\text {in}}$ and $\varGamma _{\text {out}}$, respectively. The diameter of the injection and extraction wells is 0.02 m. The length of the domain is $L_x=0.95$ m, and the height is $L_z=0.45$ m.

Initially, the pores are filled with tap water, and hence, we have that $C^{{\mathrm {Na^+}}}(t=0,{\mathbf {x}})=0$ in $\varOmega$. In Table 1, the boundary conditions are given. Since the pressure should be prescribed somewhere to get a unique solution for the pressure, we choose to prescribe the pressure at the inflow. At the outflow boundaries, we prescribe the flow rate $q_\mathrm{out}$. The resulting injection flow rate will be twice as large as the extraction flow rate. Of course, there is no flow over the closed boundary. At the inflow boundary, we prescribe the mass flux. We assume an advective flux at the outflow boundary, and there is no flux over the closed boundary.

Table 1 Boundary conditions for the concentration and the flow

We use a mesh with more than three hundred thousand elements. We assign a value for the porosity to each element of this mesh. The values come from a log-normal distribution: $\theta \sim \log \mathcal {N}(\tilde{\mu },\sigma ^2)$. The mean M of this distribution equals $M=e^{\tilde{\mu }+\sigma ^2/2}$, and the variance V equals $V=(e^{\sigma ^2}-1)e^{2\tilde{\mu }+\sigma ^2}$. From the mean M and the variance V, one can calculate the $\tilde{\mu }$ and $\sigma ^2$ via $\tilde{\mu }=\log \left( \frac{M^2}{V+M^2}\right)$ and $\sigma ^2=\log \left( \frac{V+M^2}{M^2}\right)$. For each simulation, we use the same sampling from the standard normal distribution for reasons of reproducibility. Subsequently, the resulting sample for each element is multiplied by the standard deviation of the normal distribution, $\sigma$, and then shifted by the mean of this distribution, $\tilde{\mu }$. Finally, the exponential value is computed, which finally results into $\exp {(\tilde{\mu } + \sigma \mathcal {N}(0,1)}.$) The variation in porosity is shown in the left two figures of Fig. 5 for a $\log \mathcal {N}$(0.42, 0.001) distribution.

Fig. 5

Porosity in a region where fingers appear during the simulations. Left simulated porosity for the experiment. Middle zoom in of left figure. Right simulated porosity for the case study. The porosity is shown for a $\log {\mathcal {N}}(0.42,0.001)$ distribution

We calculate the intrinsic permeability k with the Kozeny–Carman relation (8). Since the permeability is a function of the porosity $\theta$ and the porosity varies from element to element, the permeability varies as well. The scale of variation for the chosen mesh is 1.1 mm, which is the square root of the total surface divided by the number of elements.

The values that have been assigned to the various constants are given in Table 2. The value of $q_\mathrm{out}$ has been chosen in such a way that the red area at time $t=0.5$ h in the simulation has the same magnitude as in the experiment. As a result, the pore water velocities at the inflow boundary are equal for all the simulations of the experiment.

Table 2 Values that are taken for the various constants

4.2 Model Equations, Initial and Boundary Conditions for the Case Study

In this case study, we try to create a cemented zone underneath a levee in order to prevent piping. Under the clay layer of the levee, the Biogrout substrates are injected for 12 hours, followed by water injection to rinse the soil. Extraction drains are placed a few meters below the injection drain. In order to do this case study, we use the model for Biogrout as derived in Wijngaarden et al. (2011) and van Wijngaarden et al. (2013). This model is based on the biochemical reaction Eq. (3).

The concentrations of urea, calcium ions, and ammonium ions are modeled with the advection–dispersion reaction equation:

$$\begin{aligned} \frac{\partial (\theta C^{i})}{\partial t}=\nabla \cdot (\theta {\mathbf {D}} \nabla C^{i}) - \nabla \cdot ({\mathbf {q}} C^{i}) + m_i \theta r_\mathrm{hp}. \end{aligned}$$

(11)

In this equation, $C^i$ is the concentration of species i, $i \in \{\hbox {urea}, {\mathrm {Ca^{2+}}}, {\mathrm {NH_4^+}}\}$, $\mathbf {D}$ is again the dispersion tensor with coefficients as in Sect. 4.1, $r_\mathrm{hp}$ is the rate of the overall Biogrout reaction (3), and $m_i$ is a constant that follows from the stoichiometry of the reaction. As urea and calcium are consumed in the same ratio, their values of $m_i$ are equal and negative: $m_\mathrm{urea}=m_{Ca^{2+}}=-1$. For the produced ammonium, we have $m_{\mathrm{NH}_4^+}=2$. The reaction rate $r_\mathrm{hp}$ is modeled with the following relation:

$$\begin{aligned} r_\mathrm{hp}=v_{\max }S^\mathrm{bac}\frac{C^\mathrm{urea}}{K_\mathrm{m,urea}+C^\mathrm{urea}}, \end{aligned}$$

(12)

in which $v_{\max }$ (kmol/$\mathrm{m}^3$/s) is the maximal microbial activity constant, $K_\mathrm{m,urea}$ (kmol/m$^3$) is the saturation constant of urea and calcium chloride, and $S^\mathrm{bac}$ (1) is the ratio of microorganisms (with respect to the injected concentration) that is fixated in the placement procedure prior to the injection of the cementation fluids.

Since it is assumed that calcium carbonate is not transported, there is only a reaction term in the differential equation for the time derivative of its concentration:

$$\begin{aligned} \frac{\partial C^{{\mathrm {CaCO_3}}}}{\partial t}= m_{{\mathrm {CaCO_3}}} \theta r_\mathrm{hp}. \end{aligned}$$

(13)

In this equation, $C^{{\mathrm {CaCO_3}}}$ is the concentration of calcium carbonate in mass per total volume rather than per liquid volume (kg/m$^3$), and $m_{{\mathrm {CaCO_3}}}$ (kg/kmol) is the molar mass of calcium carbonate which is used to convert from kilomoles into kilograms.

As illustrated in Fig. 1, the calcium carbonate crystals are formed in the pores. This causes a decrease in porosity where the increase in volume of calcium carbonate is equal to the decrease in pore space. Hence, the following differential equation holds:

$$\begin{aligned} \frac{\partial \theta }{\partial t} = -\frac{1}{\rho _{\mathrm{CaCO}_3}} \frac{\partial C^{\mathrm{CaCO}_3}}{\partial t}, \end{aligned}$$

(14)

in which $\rho _{\mathrm{CaCO}_3}$ (kg/m$^3$) is the density of calcium carbonate. In a homogenization procedure, this equation is obtained if only one pore is considered. In Noorden (2009), a level set formulation is used to describe the crystal boundary for more complex geometries, and a formal homogenization procedure is applied to obtain upscaled equations. Equation (14) is a compromise between generality and complexity in the modeling. From the above differential equation, the following relation between the porosity and the calcium carbonate content is derived:

$$\begin{aligned} \theta ({\mathbf {x}},t)=\theta ({\mathbf {x}},0)-\frac{C^{\mathrm{CaCO}_3} ({\mathbf {x}},t)-C^{\mathrm{CaCO}_3}({\mathbf {x}},0)}{\rho _{\mathrm{CaCO}_3}}. \end{aligned}$$

(15)

Note that the above relation is an averaged approach compared to the upscaling approaches by Bringedal et al. (2015), Noorden (2009) and van Noorden et al. (2010).

For the flow, we also use the Oberbeck–Boussinesq approximation; see Eqs. (4)–(7). However, since the liquid volume decreases due to the reaction and since a solid (calcium carbonate) is formed in the pore space, the right-hand side of Eq. (4) (and hence Eq. (7)) is not equal to zero. Instead, we have:

$$\begin{aligned} \nabla \cdot {\mathbf {q}} = K \theta r_\mathrm{hp}. \end{aligned}$$

(16)

The constant K ($\mathrm{m}^3$/kmol) has been defined as

$$\begin{aligned} K:=\left( \frac{m_{\mathrm{CaCO}_3}}{\rho _{\mathrm{CaCO}_3}}-(1-V_\mathrm{s}) \right) . \end{aligned}$$

(17)

As a result of the production of the solid calcium carbonate in the pores, there is less space available for the fluid. The decrease in pore space per unit of time is ${m_{\mathrm{CaCO}_3}}/{\rho _{\mathrm{CaCO}_3}} \theta r_\mathrm{hp}$. This process is partly canceled since the hydrolysis and precipitation reactions cause a decrease in liquid volume. The decrease in liquid volume per kmol reacted urea/calcium chloride equals $1-V_\mathrm{s}$. For more details, we refer to van Wijngaarden et al. (2013). In the absence of the reaction ($r_\mathrm{hp}=0$), this is again the Oberbeck–Boussinesq approximation. Substitution of Darcy’s law (5) gives the following partial differential equation for the pressure:

$$\begin{aligned} \nabla \cdot \left( -\frac{k}{\mu } (\nabla p + \rho _l g {\mathbf {e_z}})\right) = K \theta r_\mathrm{hp}. \end{aligned}$$

(18)

Again, we use the Kozeny–Carman relation (8) to model the intrinsic permeability as a function of the porosity. The porosity is again log-normally distributed, with mean $M=0.42$ and variance $V=0.001$. In the right plot of Fig. 5, a part of the porosity distribution in the domain of computation is shown. In this case study, urea, calcium chloride, and ammonium chloride are dissolved, rather that sodium chloride. Hence, the liquid density depends on these species. As a relation between the liquid density $\rho _l$ (kg/m$^3$), and the urea concentration [$C^\mathrm{urea}$ (kmol/m$^3$)], the concentration of calcium ions [$C^{{\mathrm {Ca^{2+}}}}$ (kmol/m$^3$)], and the ammonium concentration [$C^{{\mathrm {NH_4^+}}}$ (kmol/m$^3$)], we have:

$$\begin{aligned} \rho _l=1000+15.4996 C^\mathrm{urea}+86.7338 C^{\mathrm {Ca^{2+}}} + 15.8991 C^{\mathrm {NH_4^+}}. \end{aligned}$$

(19)

The values that have been assigned to the various parameters are partly given in Table 2. The used parameters that are not given in that table and the parameters that have another value as in the simulation of the experiment are given in Table 3.

Table 3 Values that are taken for the various constants in the case study

We use a mesh with almost two million elements. Since the porosity varies from element to element, the scale of variation (defined by the square root of the total surface divided by the number of elements) is 2.5 mm.

The boundary conditions for the flow and concentration in this case study are shown in Table 4. We have a no-flux condition on the top boundary and the symmetry boundary. At the injection boundary, we prescribe the flow rate and the mass flux. At the extraction boundary, we also prescribe the flow rate, and since the concentration is unknown beforehand, we assume an advective flux. At the bottom, right (and left) boundary, we assume hydrostatic pressure. We assume an advective flux in case of outflow over these boundaries and a zero mass flux in case of inflow, although we aimed at choosing the boundaries sufficiently far away such that the concentration at the boundary is (approximately) equal to zero. As an initial condition for the aqueous concentrations, we take $C^{\mathrm {urea}}=C^{\mathrm {Ca^{2+}}}=C^{\mathrm {NH_4^+}}=0\, \hbox {kmol/m}^3$, for all points in the domain of computation at time $t=0$ h. Initially, there is no calcium carbonate present in the domain: $C^{\mathrm {CaCO_3}}=0\hbox { kg/m}^3$, for all points in the domain of computation at time $t=0$ h. The partial differential equations for the concentrations of urea and calcium are equal (assuming that the dispersion coefficients are equal as well). Since the initial and boundary conditions are also similar, these concentrations are equal. We will only show some results for the urea concentration.

Table 4 Boundary conditions for the case study

5 Numerical Methods

In this section, we explain which numerical methods are used to solve the partial differential equations.

The partial differential equations are solved using the standard Galerkin finite element method, with triangular elements and linear functions of local basis.

Since high flow rates are not desirable in the Biogrout process, the advection is not dominant and an upwind/stabilization method is not necessary. Since an upwind method decrease the order of convergence, in our case the Standard Galerkin method is a better choice.

Of course, also other, mass conserving, methods could have been applied like the mixed finite element method (MFEM) or the finite volume (FV) method; see, for example, Kumar et al. (2013), Kumar et al. (2014), and Radu and Pop (2011), in which the convergence is studied as well. In Radu et al. (2013), the mixed finite element method is applied on a concrete carbonation model with a variable porosity. Since the finite element method is known to suffer from possible numerical mass conservation errors, we checked mass conservation for the time and mesh resolution that we used. We found numerically that the relative violation of the mass balance was as small as a few tenths of a percent over the entire simulation.

In order to derive the weak formulation of the differential equations, the partial differential equations are multiplied by a test function $\eta$ and integrated over the domain $\varOmega$. For the time integration, an implicit Euler scheme is used.

The Newton–Cotes quadrature rules are used for the calculation of the element matrices and vectors. From these element matrices and vectors, the large matrices and vector are built in MATLAB (R2013b_64). The MATLAB standard direct solver is used to solve the subsequent systems. As a time step, we choose $\Delta t=36$ s.

Most equations are coupled. We solve them decoupledly.

In order to simulate the experiment, the various partial differential equations are solved, and updates are done in the following order (in pseudocode):

• 1. $\rho _l^{n+1}:\;\rho _l^{n+1}=\rho (C^{\mathrm {Na^+,n}})$, according to Eq. (9);

• 2. $p^{n+1}:\;\nabla \cdot \left( \frac{k}{\mu }(\nabla p^{n+1} +\rho _l^{n+1} g \mathbf {e_z})\right) =0$, partial differential Eq. (7);

• 3. ${\mathbf {q}}^{n+1}$: $\mathbf {q^{n+1}}=-\frac{k}{\mu } (\nabla p^{n+1} + \rho _l^{n+1} g \mathbf {e_z})$, partial differential Eq. (5);

• 4. $C^{\mathrm {Na^+},n+1}{:}\;\left( \theta C^{\mathrm {Na^+},n+1}-\theta C^{\mathrm {Na^+},\,n}\right) /\Delta t{=}\nabla \cdot (\theta \mathbf {D^{n+1}} \nabla C^{\mathrm {Na^+},n+1}) - \nabla \cdot ({\mathbf {q}}^{n+1} C^{\mathrm {Na^+},n+1})$, partial differential Eq. (10).

The following list presents in pseudocode the order in which the equations are solved and the updates are done for the Biogrout case study:

• 1. $\rho _l^{n+1}:$ $\rho _l^{n+1}=\rho (C^{\mathrm {urea,n}},C^{\mathrm {Ca^{2+},n}},C^{\mathrm {NH_4^+,n}})$, according to Eq. (19);

• 2. $\theta ^{n+1}:$ $\theta ^{n+1}=\theta (\theta _0,C^{\mathrm{CaCO}_3,n})$, according to Eq. (15);

• 3. $k^{n+1}:\;k^{n+1}=k(\theta ^{n+1})$, according to Eq. (8);

• 4. $p^{n+1}:\;\nabla \cdot \left( \frac{k^{n+1}}{\mu }(\nabla p^{n+1} +\rho _l^{n+1} g \mathbf {e_z})\right) =K \theta ^{n+1} r_\mathrm{hp}^{n}$, partial differential Eq. (18);

• 5. ${\mathbf {q}}^{n+1}$: $\mathbf {q^{n+1}}=-\frac{k^{n+1}}{\mu } (\nabla p^{n+1} + \rho _l^{n+1} g \mathbf {e_z})$, partial differential equation (16);

• 6. $C^{urea,n+1}:$ $\left( \theta ^{n+1}C^{urea,n+1}-\theta ^nC^{urea,n}\right) /\Delta t=\nabla \cdot (\theta ^{n+1} \mathbf {D^{n+1}} \nabla C^{urea,n+1}) - \nabla \cdot ({\mathbf {q}}^{n+1} C^{urea,n+1}) - \theta r_\mathrm{hp}^{n+1}$, partial differential equation (11). Due to the reaction term, this partial differential equation is nonlinear in the urea concentration. Newton’s method is used to deal with that. In the Biogrout case, this method usually converges in three iterations.

• 7. $C^{NH_4^+,n+1}$: $\left( \theta ^{n+1}C^{NH_4^+,n+1}-\theta ^nC^{NH_4^+,n+1}\right) /\Delta t=\nabla \cdot (\theta ^{n+1} \mathbf {D^{n+1}} \nabla C^{NH_4^+,n+1}) - \nabla \cdot ({\mathbf {q}}^{n+1} C^{NH_4^+,n+1}) - \theta r_\mathrm{hp}^{n+1}$, partial differential equation (11). The values for $r_\mathrm{hp}^{n+1}$ follow from the last Newton iteration in the previous step;

• 8. $C^{\mathrm{CaCO}_3,n+1}$: $\left( C^{\mathrm {CaCO_3,n+1}}-C^{\mathrm {CaCO_3,n}}\right) /\Delta t= m_{\mathrm {CaCO_3}} \theta ^{n+1} r_\mathrm{hp}^{n+1}$, partial differential equation (13).

We also investigated the effect of inner iterations on the results. This was done by recalculating the density at each time step. If the difference between the previously calculated density was larger than some tolerance, the equations were solved with the updated density until the difference was smaller than some tolerance. Convergence was usually reached in one or two iterations. Figure 6 shows some results for the scheme for Biogrout, proposed above. The left plot of Fig. 6 shows the convergence behavior on a cross section for a two-dimensional Biogrout test case. In each refinement step, the time step size is divided by two and the mesh size is divided by $\sqrt{2}$, since the expected order of convergence is $\mathcal {O}(h^2+\Delta t)$, with h a measure for the mesh size and $\Delta t$ the size of the time step. Figure 6 shows a nice convergence behavior. In the right plot of this figure, the scheme without inner iterations is compared to the scheme with inner iterations. This is done for the coarsest and the finest simulation. It appears that the scheme with inner iterations only leads to small differences compared to the scheme that was proposed here. When using small time steps, there were no noticeable changes. Similar results were obtained for the other scheme, while investigating the effect of inner iterations on the results.

Fig. 6

Left Convergence of the Biogrout scheme without inner iterations. Right Scheme without inner iterations compared to the scheme with inner iterations

6 Results

6.1 Results of the Experiment and a Simulation with a Homogeneous Porous Medium

This section reports some results of the two-dimensional porous media flow cell experiment that has been performed. The experimental results are compared to the results of a simulation using a constant porosity and permeability. The left column of Fig. 7 shows some results of the flow cell experiment. The red fluid is the dense fluid. The color of the zones, where only water is present, ranges from white to yellow, depending on the daylight and the artificial light. The colors in between this background color and the red color correspond to a concentration between 0 and the injected concentration which is 0.5 kmol/m$^3$, but the exact relation is not known. At $t=0.5$ h, the injection of the dense fluid stops and the injection of water starts. This gives the red ring in the pictures for $t=1$ h, $t=2$ h, $t=3$ h, $t=4$ h and $t=5$ h. From $t=2$ h, fingers appear on roughly two locations: on the bottom of the ring and on the top of the ring where the heavy fluid is above the less dense fluid. In either case, fingers appear on positions where a dense fluid is on top of a less dense fluid. Note that the fingers on the bottom of the ring are larger.

Fig. 7

Some pictures of the experiment (left) and the numerical simulation with a homogeneous porous medium (right) at several times (from top to bottom $t=0.5$ h, $t=1$ h, $t=2$ h, $t=3$ h, $t=4$ h and $t=5$ h). In the simulation, the porosity $\theta$ equals $\theta =0.42$ and the intrinsic permeability k is $k=5.0\times 10^{-11}\hbox { m}^2$

The right column of Fig. 7 shows some results of a simulation of this experiment, using a porosity of $\theta =0.42$ and a permeability of $k=5.0\times 10^{-11}\hbox { m}^2$. As can be seen in the simulation, no fingers appear. Apparently, the numerical noise is not sufficient to trigger the fingering. Hence, in the next section, we will vary the porosity and permeability to trigger the fingering.

6.2 Numerical Results for an Inhomogeneous Porous Medium

In this section, we use an inhomogeneous porosity within our simulations. We assign a value for the porosity to every element of the mesh. The values come from a log-normal distribution: $\theta \sim \log \mathcal {N}(\tilde{\mu },\sigma ^2)$. We vary the mean porosity M and the variance V of this distribution and do several simulations. As the mean M we choose: $M=0.36$, $M=0.42$, and $M=0.49$. For the variance we choose: $V=0.0001$, $V=0.001$, and $V=0.005$. This results in nine different combinations. From the mean M and the variance V, one can calculate the $\tilde{\mu }$ and $\sigma ^2$ via $\tilde{\mu }=\log \left( \frac{M^2}{V+M^2}\right)$ and $\sigma ^2=\log (\frac{V+M^2}{M^2})$. The permeability that corresponds to a mean porosity of $M=0.36$ equals $k=2.5\times 10^{-11}\hbox { m}^2$, according to the Kozeny–Carman relation (8). The corresponding permeabilities of the means $M=0.42$ and $M=0.49$ are $k=5.0\times 10^{-11}\hbox { m}^2$ and $k=10\times 10^{-11}\hbox { m}^2$, respectively.

Fig. 8

Some pictures of the experiment (left) and the numerical simulation (right) at several times (from top to bottom $t=0.5$ h, $t=1$ h, $t=2$ h, $t=3$ h, $t=4$ h and $t=5$ h). In the numerical simulation, the medium is inhomogeneous with a mean porosity of $\theta =0.42$ and a variance of 0.001. This mean porosity corresponds to an intrinsic permeability of $k=5.0\times 10^{-11}\hbox { m}^2$

In the right column of Fig. 8, some results are shown for one of the simulations. In this simulation, the mean porosity is $M=0.42$ and the variance is $V=0.001$. In the numerical simulation with the homogeneous medium, of which the results are shown in Fig. 7, no fingers appear. In contrast to this simulation, we now see the same phenomenon as in the experiment in Fig. 8. Moreover, fingers start to appear at approximately the same time as in the experiment.

There are also some differences between modeling and the experiment. In the simulation, the fingers only appear on the bottom side of the ring, whereas in the experiment, also some small fingers appear at the bottom side of the top of the ring. Furthermore, the speed of the fingers in the experiment is larger than in the numerical simulation. From the results of the experiment, it can be seen that the layer close to the lowest boundary is more permeable than elsewhere. At time $t=4$ h, the red fluid reaches the bottom, and in one hour (at time $t=5$ h), it has already reached the left and right boundaries. Apparently, there is some space between the frame and the plexiglass.

Figure 9 shows the effect of the value of the variance. Since the random number generator is reset before every simulation, the values of the porosity are constructed from the same set of random numbers, as explained in Sect. 4. Hence, the fingers appear at the same location. The magnitude, however, depends on the value of the variance. A larger variance results in longer fingers.

Fig. 9

Concentration given at time $t=5\,\hbox {h}$. The mean porosity is $M=0.42$. The variance is $V=0.0001$ (left), $V=0.001$ (middle) and $V=0.005$ (right)

Figure 10 displays the effect of the variation in the mean M. Clearly, the value of the mean has a large effect on the fingering phenomenon. For a small mean, hardly any fingers arise. A larger mean results in more fingers, and clearly, the bottom is reached earlier. The effect of the mean value of the porosity on the density effect is explained below. Remember that the pore water velocity at the inlet is kept constant in the simulations.

The pore water velocity is determined by combining Eqs. (5), (6) and (8):

$$\begin{aligned} v_x= & {} -\frac{(d_\mathrm{m})^2}{180 \mu }\frac{\theta ^2}{(1-\theta )^2}\frac{\partial p}{\partial x}, \end{aligned}$$

(20)

$$\begin{aligned} v_z= & {} -\frac{(d_\mathrm{m})^2}{180 \mu }\frac{\theta ^2}{(1-\theta )^2}\frac{\partial p}{\partial z}-\frac{(d_\mathrm{m})^2}{180 \mu }\frac{\theta ^2}{(1-\theta )^2} \rho _l g. \end{aligned}$$

(21)

In case of a higher porosity, the term $\frac{\theta ^2}{(1-\theta )^2}$ is also larger. Now, remember that the pore water velocity at the inlet is constant. Hence, the increase in the porosity term in the first term at the right-hand side of Eqs. (20) and (21) is compensated by smaller pressure gradients in these terms. Now, let the ratio between the buoyancy term and the pressure gradient term in the right-hand side of Eq. (21) be a measure for the effect of the density differences. This ratio equals: $\rho _l g/\frac{\partial p}{\partial z}$. A higher porosity results in smaller pressure gradients, and therefore, the value of this ratio increases which indicates a larger effect of density differences.

Fig. 10

Concentration given at time $t=5\,\hbox {h}$. The variance is $V=0.001$. The mean porosity is $M=0.36$ (left), $M=0.42$ (middle) and $M=0.49$ (right)

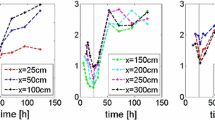
To quantify the effect of the porosity on the downward movement of the dense fluid, the lowest location of the front is plotted as a function of time in Fig. 11. For every time step, this location is determined by finding the smallest z value for which the concentration exceeds some threshold. As a threshold, we choose $C^\mathrm{threshold}=0.05$ kmol/m$^3$. Figure 11 displays some results for various values of the mean and the variance.

Fig. 11

Lowest position of the dense fluid as a function of time for various values of the mean and the variance. The mean porosity is $M=0.36$ (left), $M=0.42$ (middle), and $M=0.49$ (right)

Fig. 12

Concentration for an inflow concentration of $c_\mathrm{in}=1$ kmol/$\mathrm{m}^3$ (left column) and $c_\mathrm{in}=2$ kmol/$\hbox {m}^3$ (right column) at several times (from top to bottom $t=0.5$ h, $t=1$ h, $t=2$ h, $t=3$ h, $t=4$ h and $t=5$ h). The mean porosity is $M=0.42$, and the variance is $V=0.001$

This figure confirms the observations in Fig. 10: If the mean is larger, the dense fluid moves faster downwards. Furthermore, a larger variance results in larger fingers, as we concluded from Fig. 9. As a result, the dense fluid is earlier at the bottom of the domain. In our simulations, the variation in the mean has a larger effect on the fingering than the variation in the variance.

6.3 Variation in Substrate Concentration

In this section, we vary the inflow concentration of the dense fluid to investigate its effect. In the previous section, $c_\mathrm{in}=0.5$ kmol/m$^3$ has been used as an inflow concentration, like in the experiment. In this section, we choose $c_\mathrm{in}=1$ kmol/m$^3$ and $c_\mathrm{in}=2$ kmol/m$^3$. As a mean porosity, we set $M=0.42$, and for the variance, $V=0.001$ is chosen. Figure 12 shows the concentration at consecutive times for the various inflow concentrations. For these inflow concentrations, the flow is considerably affected by the density differences. A higher inflow concentration results into a heavier fluid. Therefore, the gravity component is larger, and hence, the dense fluid reaches the bottom earlier. Since the gravity component becomes more significant for a higher inflow concentration, the pressure term is relatively less important, and this results into a buoyancy-dominated flow. Since the bottom is earlier reached, there is less time for the formation of fingers. At the other hand, the density differences are larger, which is in favor of the formation of the fingers.

6.4 Case Study Simulations

In this section, we present the results of the case study simulations. We use the configuration, initial and boundary conditions as proposed in Sect. 4.2, combined with the heterogeneous porosity distribution. The aim was to construct a calcium carbonate wall as a barrier for the pipes. In order to prevent waste of materials, it is desirable that the urea (and calcium) are consumed rather than extracted. Besides that, it is necessary to remove the ammonium because of its impact on the environment.

6.4.1 Development of the Various Concentrations

Figure 13 shows how the concentrations of urea, calcium carbonate, and ammonium develop in the domain of computation. The concentration profiles are shown at several times. After 12 hours, the injection of the Biogrout substrates (in the top of the domain) was stopped and the water injection started. This causes a region around the injection well with zero urea concentration, which is visible in the plot of the urea (and calcium) concentration at time $t=13$ h. The urea is forced downward by injection/extraction and by the density differences. At time $t=13$ h, the large urea plume just started splitting in two large fingers. We see the same for the produced ammonium. In the right plot of Fig. 5, the initial porosity distribution is shown for this particular region.

At time $t=22$ h, in the same region small fingers arise, but also at the deepest location of the urea and ammonium front. At time $t=25$ h, these small fingers are increased.

At time $t=45$ h, the urea and calcium are consumed, and the calcium carbonate wall has his final shape. A barrier for the pipes has been formed. The plot of the ammonium concentration for this time shows that more and more fingers arise. Due to density differences, these fingers tend to flow down. On the other hand, the extraction (indicated by the white circles) pulls them upward.

Fig. 13

Results of the case study simulation with the heterogeneous porosity distribution for time $t=13\,\mathrm{h}$, $t=22\,\mathrm{h}$, $t=25\,\mathrm{h}$ and $t=45$ h. Presented are the urea concentration (left column), the calcium carbonate concentration (middle column), and the ammonium concentration (right column)

6.4.2 Extraction of Ammonium

In the left column of Fig. 14 is shown how the ammonium concentration evolves further in time. The heterogeneous porosity causes the ammonium plume to split into two parts (time $t=22$ h) and later on in multiple fingers that are being extracted (times $t=60$ h and $t=100$ h). On the symmetry axis $x=0$, the horizontal fluid velocity caused by the extraction drains is equal to zero, since the effect of one extraction well is canceled by the other. Closer to the extraction drain, the horizontal velocity in the direction of the drain increases. The splitting of the ammonium plume brings the ammonium closer to the extraction wells. After all the urea are consumed, the ammonium concentration decreases as a result of the extraction. Hence, the density difference with the surrounding water decreases, which makes it easier to extract the ammonium. After 100 h, only 4 mol ammonium is left in the domain and 121 mol ammonium was extracted.

6.4.3 Comparison with a Homogeneous Porosity Distribution

We repeated the same simulation for a homogeneous porosity. The ammonium concentration at several times is shown for this simulation in the right column of Fig. 14. In this case, only one plume is observed and no fingers appear. The ammonium plume moves downwards between the extraction wells. Although the flow rate of the extraction wells is eight times as large as the injection flow rate, only a part of the ammonium is extracted. After 100 h, only 50 mol is extracted, while 75 mol ammonium is still in the soil. In these simulations, the formation of fingers is advantageous for the removal of ammonium.

Fig. 14

Ammonium concentration at several times in the case study. The left column shows the results with the heterogeneous porosity distribution, and the right column displays the results for a homogeneous porosity

Figure 15 shows the distribution of the calcium carbonate for the simulation with the heterogeneous porosity distribution and the one with the homogeneous porosity. The aim was to create a calcium carbonate wall below the clay layer of at least 2 m length to decrease the risk on piping. The top 2 m of the calcium carbonate wall is similar for both simulations. Below these 2 m, the distribution of calcium carbonate is rather different. The fingers in the urea and ammonium plume in the simulation with the heterogeneous porosity are also visible in the calcium carbonate profile. Of course, this is not surprising, since calcium carbonate can only be formed where urea is present. In the simulation with the heterogeneous porosity, 6.22 kg of calcium carbonate was formed in the soil. In the simulation with the homogeneous porosity, the amount of extracted urea was a little lower and the amount of produced calcium carbonate was therefore a little higher: 6.25 kg.

Fig. 15

Final calcium carbonate concentration for the simulation with the heterogeneous porosity distribution (left) and the homogeneous porosity (right)

7 Discussion and Conclusions

In the experiment, fingers arise as expected where the dense fluid is on top of the less dense fluid. This happens particularly at the bottom side of the ring. But also at the bottom side of the top of the ring, small fingers come into being, which flow downwards, in opposite direction to the flow that is generated by injection and extraction. In the simulation, no fingers appeared in case of a homogeneous medium. When using a variable porosity according to a log-normal distribution, fingers developed in the numerical simulation. Fingers started to appear at approximately the same time as in the experiment. Several simulations were performed for various values of the mean porosity and variance. These simulations showed that a large variation in porosity (and hence permeability) results in larger fingers than a small variation, but this effect is not very large. The variation in the mean porosity has a much larger effect on the fingers as shown in Fig. 10. The reason is explained in Sect. 6.2.

In comparison with the experiment, the numerical simulations seem to underestimate the fingering phenomenon. Fingers only appear at the bottom side of the ring, while in the experiment also some small fingers appear at the inside of the top of the ring. Furthermore, the flow velocity of the fingers in the experiment is larger than in the numerical simulations.

The numerical simulation, in which the inflow concentration was varied, showed that the concentration has a large effect on the flow as shown in Fig. 12. Compared to the experiment and simulation with an inflow concentration of $c_\mathrm{in}=0.5$ kmol/$\hbox {m}^3$, the dense fluid moves downward more rapidly for a higher value for the inflow concentration.

The case study simulations showed that the fingering phenomenon has not necessarily a negative effect on the extraction of the ammonium. By the formation of fingers, the front is dispersed, which brings the dense fluid closer to the extraction drains, with the result that is was easier to extract most of the ammonium. On the other hand, while comparing the experimental results with the numerical simulations, it was concluded that the numerical simulations were underestimating the velocity of the fingers. If the velocity of the fingers would be higher than simulated in the case study, it is likely that more fingers escape from the vicinity of the extraction drains and that more ammonium is left in the soil.

Since the finite element method is known to suffer from possible numerical mass conservation errors, we checked mass conservation for the time and mesh resolution that we used. We found numerically that the relative violation of the mass balance was as small as a few tenths of a percent over the entire simulation.

We showed the results of simulations for only one particular drawing from the log-normal distribution. To get an idea of the bandwidth, the simulations should be repeated for a large number of (different) drawings from the same log-normal distribution. Further, the sensitivity of the parameters in the log-normal distribution should be investigated to be able to make a good prediction of the fluid transport.

The scale of porosity and permeability variation in the simulation of the experiment is 1.1 mm (Sects. 6.2 and 6.3) and 2.5 mm for the case study simulation (Sect. 6.4). The question is what this scale of variation is in practice.

In this article, the transverse dispersivity was chosen equal to the longitudinal dispersivity in order to get the front as sharp as possible for the given mesh. By using a finer mesh, it can be investigated what the effect is of a smaller transverse dispersivity.

In reality, a horizontal seepage flow is occurring from surface water toward drainage ditch. In the case study, the seepage flow is not taken into account during the injection of the Biogrout fluids. However, this flow influences the transport of the fluids and should really be taken into account, while designing an injection and extraction strategy for a real case.

Buoyancy-driven flow and associated fingers significantly affect the rate of salt extraction, which is required when applying Biogrout in practice. To reduce the density effect, one can use lower concentrations. However, this leads to a larger injected volume in order to reach a certain target amount of calcium carbonate. Also, the reaction rate should be adapted when using lower concentrations in order to prevent that all the calcium carbonate will precipitate close to the injection wells. Another option to mitigate fingering would be to increase the flow rate. This decreases the retention time, such that the dense fluid has less time to form fingers. A drawback of a lower retention time is that the reaction rate should be larger to get the same calcium carbonate production. Furthermore, high injection rates cause large pressure drops close to the injection well which can fracture the soil in its surroundings affecting the distribution of injected fluids. Finally, it is also possible to reduce the effect of density by gradually increasing the inflow concentration. In that case, there is no sharp front, and it is less likely that fingers come into being.

In laboratory and scale-up experiments of Biogrout, typically a concentration of 1 kmol/$\hbox {m}^3$ is used as an injection concentration for urea and calcium chloride (Harkes et al. 2010; van Paassen et al. 2009). The density of this fluid is $1.1 \times 10^3$ kg/$\hbox {m}^3$, which is even denser than the 2 kmol/$\hbox {m}^3$ sodium chloride solution that was used in the simulation described in Sect. 6.3, i.e., $1.08 \times 10^3$ kg/$\hbox {m}^3$. If all the urea and calcium chloride react, one ends up with a 2 kmol/$\hbox {m}^3$ ammonium chloride solution, which has a density of $1.03 \times 10^3$ kg/$\hbox {m}^3$. This density lies in between the density of the 0.5 kmol/$\hbox {m}^3$ and the 1 kmol/m$^3$ sodium chloride solution. According to our simulations, all these dense fluids easily sink away in the subsoil. By the formation of fingers, the dense fluid sinks even faster.

This paper clearly shows that it is important to take buoyancy-driven flow into account while simulating the Biogrout process. It is possible to simulate the fingering phenomenon by varying the porosity and the permeability and using a sufficiently fine mesh. In the simulations in this article, the formation of fingers is advantageous for the application of Biogrout, since the ammonium is extracted more easily.