Abstract
We consider a model problem for coupled surface–subsurface flow. The model consists of a nonlinear kinematic wave equation for the surface fluid’s height and a Brinkman model that governs fluid velocity and pressure for subsurface dynamics. For this coupled hyperbolic–elliptic model we establish the existence of weak solutions. The proof is based on a viscous approximation and the method of compensated compactness by virtue of appropriate energy estimates. To solve the coupled problem numerically, a finite volume method is applied. The numerical scheme is used to illustrate the influence of the Brinkman parameter on the coupled flow pattern for infiltration scenarios.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Coupled surface and subsurface flows appear in a wide range of environmental settings such as infiltration of overland flows during rainfalls and the interactions of rivers, lakes or wetlands with the vadose zone. The coupled flow system contains different sets of entities: fluid on the surface, and fluid and solid in the porous medium region. This requires a separate model for each flow domain and accurate coupling of these models at the fluid–porous interface. The choice of the subdomain model depends on the application and the flow regime.
There are several possible models for the surface flow, ranging from the (compressible or incompressible) Navier–Stokes/Euler equations (Temam 2001) to source terms at the fluid–porous interface that represent, e.g., the rainfall rate and act as boundary conditions for the subsurface model (Berninger et al. 2014). For creeping flows, the advective inertial forces are small in comparison with the viscous forces, and therefore, the nonlinear inertial terms in the incompressible Navier–Stokes equations can be neglected leading to the Stokes equations. For many applications, such as dynamics of rivers and oceans, the horizontal length scale is much larger than the vertical one, and in this case, the surface equations can be averaged over the depth, leading from the incompressible Euler equations to the shallow water equations (Vreugdenhil 2010). The dynamic wave equation describes one-dimensional shallow water waves, and the kinematic wave equation is an approximation of the dynamic wave model (Takahashi 2014). In this work, we will consider the kinematic wave equation to model the surface flow.
To describe fluid flows through porous media, Darcy’s law (Bear 1972; Darcy 1856; Helmig 1997) is usually applied. For the description of flows in porous medium systems with high porosity, the Brinkman (1947) extension of Darcy’s law is typically used.
The governing equations describing physical processes in the free flow and porous medium flow domains have been widely investigated, but a challenge arises in describing the transition between the two flow systems at the fluid–porous interface. It can be a sharp interface void of thermodynamic properties (Discacciati et al. 2002; Layton et al. 2003; Mosthaf et al. 2011), or a transition region of a positive thickness which can store and transport mass, momentum, and energy (Jackson et al. 2012). Correct specification of coupling conditions at the fluid–porous interface is essential for a complete and accurate mathematical description of flow and transport processes in compositional systems.
To couple the Stokes equations and Darcy’s law that describe fluid flows in single-phase coupled systems, the Beavers–Joseph velocity jump condition (1967) is typically applied in addition to the mass conservation and the balance of normal forces across the fluid–porous interface. Mathematical models and numerical algorithms for solving such coupled flow problems have been developed and analyzed during the last decade (Discacciati et al. 2002; Discacciati and Quarteroni 2009; Layton et al. 2003; Rivière and Yotov 2005; Cao et al. 2010; Layton et al. 2013; Rybak and Magiera 2014). Many applications, such as overland flow interactions with unsaturated groundwater aquifers, require multiphase physics in the subsurface. In this case, the porous medium model typically includes multiphase Darcy’s law (Helmig 1997) that represents flows of several fluids or Richards’ equation (1931) that describes movement of only water through saturated/unsaturated porous media. Coupling of subsurface flows described by the Richards equation and overland flows has been studied recently (Dawson 2008; Rybak et al. 2015; Kollet and Maxwell 2006; Sulis et al. 2010; Sochala et al. 2009; Berninger et al. 2014; Mosthaf et al. 2011).
Despite the wide variety of models for coupled surface–subsurface flow, there are comparably less rigorous results on the existence, uniqueness and regularity of solutions. This applies in particular for surface flows which are governed by hyperbolic systems of balance laws (shallow water or kinematic wave approximation). In this case, one has to take into account that the surface model allows for discontinuous weak solutions.
In this paper, we consider as a first step the coupling of the scalar kinematic wave equation with Brinkman’s equations. To couple these models, a sharp interface approach is applied, and coupling conditions based on the conservation of mass and the balance of forces at the interface are formulated. The main result is Theorem 6 that establishes the existence of a weak solution of the kinematic–Brinkman system. For the proof, we follow the idea of viscous regularization which is classical in the theory of hyperbolic conservation laws. The final existence proof relies then on the vanishing viscosity limit which is mastered by the theory of compensated compactness (Murat 1981). Finally, we introduce a finite volume scheme for the coupled system and present several numerical studies to validate the overall approach and to test different flow regimes.
The paper is organized as follows. In Sect. 2, the flow system of interest and the mathematical models including the corresponding interface conditions are described. In Sect. 3, the coupled model with viscous regularization is presented, the existence of a weak solution for such problem is proved (Theorem 5) and a priori estimates are obtained. The existence of a weak solution for the nonlinear case is proved in Sect. 4. The computational algorithm and numerical simulation results for the proposed model as well as comparison study of the considered model instance with some simplified cases are presented in Sect. 5. Finally, a conclusion is given, and possible extensions of this work are discussed.
2 The Mathematical Model
2.1 Geometry for the Coupled Model
For the coupled model, we consider a two-dimensional subsurface domain \({\varOmega }_{\mathrm {pm}} \subset \mathbb {R}^{2}\), which is assumed to be a unbounded domain between two parallel planes, i.e.,
for an (upward pointing) unit normal vector \(\mathbf {n} \in \mathbb {R}^{2}\) describing the slope, and a number \(a > 0\) defining the subsurface depth. Then, the upper plane forms the surface domain
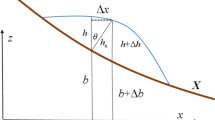
which serves also as the interface \({\varGamma }_{\mathrm {N}}\) between both domains, i.e., \({\varGamma }_{\mathrm {N}} = {\varOmega }_{\mathrm {ff}}\). However, for clarity we distinguish between them. The lower boundary of \({\varOmega }_{\mathrm {pm}}\) is denoted by \({\varGamma }_{\mathrm {D}}\). Figure 1 depicts the geometry of the system. The spatial coordinates of the subsurface are denoted by \(\mathbf {x}= (x_1, x_2) \in \mathbb {R}^2\), and on the surface by \(x \in \mathbb {R}\).
2.2 The Surface Model: Kinematic Wave Equation
The flow on the surface \({\varOmega }_{\mathrm {ff}}\) is described by the kinematic wave equation, which describes one-dimensional, hydrostatic water flow through an open channel, and can be seen as a further simplification of the shallow water equations.
Derivation of the Kinematic Wave Equation We assume that we have a one-dimensional flow of an incompressible fluid with constant density through an open channel with a fixed channel bed and a small bottom slope. The flow is assumed to vary gradually, such that hydrostatic pressure prevails and vertical acceleration can be neglected.
To derive the kinematic wave equation, we start with the nonconservative form of the shallow water equations in one space dimension
Here, h denotes the relative water height, v is the velocity, and \(z_b\) is the height of the bottom (with respect to a fixed datum). The gravitational acceleration is denoted by g, the bottom stress by \(\varvec{\tau }_b\) and the density of the water by \(\rho \). A source term f is included, which describes the water flow into and out of the ground. Next, we assume that the bottom stress \(\varvec{\tau }_b\) is proportional to the slope of hydraulic friction \(S_f\), i.e.,
Under the assumptions from above, Manning (1891) suggested the use of the following formula to describe the resistance effects for open channel flow:
where \(S_f\) denotes the slope of hydraulic friction, \(R > 0\) the hydraulic radius and \(C_{\mathrm {M}}>0\) the Manning coefficient—see Yen (2002) for a more recent reference on Manning’s formula. Now, if we assume that the flow is steady and uniform, we can neglect the local and convective acceleration (\(\partial _t v\), \(v \partial _x v\)) as well as the pressure force term (\(g \partial _x h\)) in the momentum Eq. (1)\(_{2}\). This gives the equilibrium of the gravitational force and the friction force, i.e.,
By applying Manning’s Eq. (2) for \(S_f\) and by assuming that the flow direction is fixed in the direction of the slope (\({\text {sign}}(v) > 0\), \({\text {sign}}(\partial _x z_b) < 0\), see Fig. 1), we get
Moreover, we assume that the hydraulic radius R is proportional to the water height h, that is \(R^{2/3} = C_{\mathrm {Ch}} \, h^{2/3}\), with \(C_{\mathrm {Ch}} >0\) depending on the channel. If we substitute the proportionality coefficient into Eq. (3), we can describe the velocity v in dependence of h, by
Inserting the velocity in the continuity Eq. (1)\(_{1}\) gives the kinematic wave equation
with the flux defined as
Remark 1
(Linear transport equation) If, instead of Manning’s formula, we assume that the slope of hydraulic friction is proportional to the velocity v, i.e., \(S_f = c_f v\) for \(c_f > 0\), then the kinematic wave equation becomes the linear transport equation
with constant velocity \(v = - \left( \tfrac{1}{c_f \rho } \partial _x z_b\right) >0\).
Surface Model Equation The kinematic wave Eq. (4) has (for \(f = 0\)) the form of a scalar conservation law. Hereafter, we ignore variations in the bottom topology and let the flow on the surface \({\varOmega }_{\mathrm {ff}} \cong \mathbb {R}\) be described by the initial value problem
for \(T > 0\). We make the following assumptions.
Assumption 1
The initial datum \(h_0:\mathbb {R}\rightarrow \mathbb {R}\) and the flux \(\phi :\mathbb {R}\rightarrow \mathbb {R}\) satisfy
For ease of notation, we further assume that \(\mathbf {n} = (0,1)^\top \). In this case, the subsurface coordinates are given by \(\mathbf {x}= (x_1, x_2) \in {\varOmega }_{\mathrm {pm}}\), with \(x_1 \in \mathbb {R}\), \(x_2 \in [0,a]\), and the surface coordinates are defined as \(x = x_1 \in \mathbb {R}\). Other domains with a different normal vector \(\mathbf {n}\) can be considered by adapting \(\phi \) according to the slope.
2.3 Subsurface Model: Brinkman’s Equations
To describe the subsurface fluid flow, we apply the steady-state Brinkman’s equations, which were first presented in Brinkman (1947) as a model to describe viscous flow of an incompressible fluid through a dense swarm of particles. Due to the coupling with the time-dependent surface model (5), we consider all variables of Brinkman’s equations as time dependent. The model is given by
where \(\mathbf {v}:{\varOmega }_{\mathrm {pm}} \times [0,T] \rightarrow \mathbb {R}^{2}\) is the fluid velocity, and \(p :{\varOmega }_{\mathrm {pm}} \times [0,T] \rightarrow \mathbb {R}\) the fluid pressure. The viscosity of the fluid is denoted by \(\mu > 0\). The Brinkman parameter \(M \ge 0\) is generally proportional to \(\tfrac{1}{\mu } K^{-1}\), where \(K^{-1} \ge 0\) denotes the inverse permeability. Actually, if the Brinkman parameter M is set to zero, one obtains the Stokes equations.
Brinkman’s equations are derived by considering the friction of the fluid on the particles, and sets of particles are combined to create a porous medium. Brinkman’s equations can describe fluid flow through a porous medium, which was done successfully in, for example, Iliev and Laptev (2004). Nonetheless, one has to keep in mind that, by the nature of the derivation, Brinkman’s equations yield reliable results only for porous media with a very high porosity, rigid swarms of particles or fibers in low concentration. There are different opinions about the porosity range in which Brinkman’s equations are applicable. Most commonly, it is assumed that Brinkman’s equations only hold for porous media with a porosity higher than 0.8 (or even 0.9) (Kim and Russel 1985; Lundgren 1972; Auriault 2009). However, for example in Martys et al. (1994) it is pointed out that they may be applicable in cases where the porosity goes down to 0.5.
It is possible to obtain Darcy’s law from Brinkman’s equations by taking the limit \(\mu \rightarrow 0\). However, this case is not covered by the analytical framework which is applied in this work, see Remark 5.
To complete the model, we impose Neumann boundary conditions
on \({\varGamma }_{\mathrm {N}} \times [0,T]\), with boundary value \(\mathbf {g}_{\mathrm {N}} :{\varGamma }_{\mathrm {N}} \times [0,T] \rightarrow \mathbb {R}^{2}\), where \(\partial _{\mathbf {n}}(\mathbf {v}, p)\) is given by
Additionally, we impose the Dirichlet boundary condition
2.4 Coupling Conditions
To get a closed model, we have to formulate coupling conditions. The model should fulfill the same conservation properties as the subsystems. To ensure the conservation of mass for an incompressible fluid, the normal component of the fluid velocity should be continuous across the boundary, i.e.,
The (vertical) fluid velocity \(\mathbf {v}\cdot \mathbf {n} = \mathbf {v}_{\mathrm {pm}} \cdot \mathbf {n}\) enters (5) as a right-hand side, i.e., we have
where \(\mathbf {v}\) is the velocity from the subsurface model (7). The surface flow system does not have any vertical velocity component, and therefore, the coupling condition is not as straightforward. Instead of the continuity of the velocity, we will assume that there is a global equilibrium of forces between the two subsystems at the interface, meaning that the forces along the interface sum to zero. Therefore, we assume that for each point of the interface, the surface flow pressure \(p = \mathbf {g}\rho h\) acts on the flow in the subsurface. Consequently, the surface flow pressure p enters the subsurface model (7) as the Neumann boundary condition
2.5 The Coupled Kinematic–Brinkman Model
To formulate the complete coupled model, consisting of the kinematic wave equation/scalar conservation law (5) and Brinkman’s system (7), we apply the coupling conditions (9), (10). For simplicity, we assume that \(\mathbf {g}\rho h(x,t) \mathbf {n} = (0,-1)^{\top }\), and obtain
The boundary condition \(\partial _{\mathbf {n}} (\mathbf {v}, p)(x,a,t) = -h(x,t) \mathbf {n}\) introduces a time dependency to the steady-state subsurface model. In the following we set

The weak formulation of the coupled model corresponds to the standard weak formulations of each subproblem. It reads as follows.
Definition 1
We call \(((v, p), h) \in (\mathrm {V}_0 \times \mathrm {P}_0) \times \mathrm {H}_0\) a weak solution of the Kinematic–Brinkman model (11) iff
holds for all \(\varphi \in C^{\infty }_{0}([0,T) \times \mathbb {R})\), and all \((\mathbf {w}, q) \in \mathrm {V}_0 \times \mathrm {P}_0\). Here ‘ : ’ denotes the Frobenius inner product.
Note that the normal velocities \(\mathbf {v}\cdot \mathbf {n}, \mathbf {w}\cdot \mathbf {n}\) in the weak solution are defined as the trace of functions in \((H^1({\varOmega }_{\mathrm {pm}}))^2\) on \( L^2({{\varGamma }_{\mathrm {N/D}}})\). To ease the notation we do not introduce a specific trace operator but use the same symbol. Let us note that the trace mapping from \((H^1({\varOmega }_{\mathrm {pm}}))^2\) to \( (L^2({{\varGamma }_{\mathrm {N/D}}}))^2\) is a linear continuous mapping such that there is in particular a constant \(C_{\mathrm {tr}} >0\) such that
for all \(\mathbf {w}\in (H^1({\varOmega }_{\mathrm {pm}}))^2\). Note that \({\varOmega }_{\mathrm {pm}}\) is a cylindric domain. It is the objective of this paper to show that a weak solution of the Kinematic–Brinkman model (11) exists.
3 A Regularized Kinematic–Brinkman Model
In this section, we consider a regularization of the coupled model (11). The regularization relies on mollification operators and a viscosity approximation for the surface model. We show in this section the existence and uniqueness of solutions for the regularized model and derive important a priori estimates. These will allow us in Sect. 4 to prove the existence of a weak solution of the Kinematic–Brinkman model (11) by sending the regularization parameter to zero.
3.1 Description of the Regularization
Let us introduce a regularization parameter \(\varepsilon \in (0,1]\) which will be arbitrary but fixed in this section. We search for the triple \(((\mathbf {v}^\varepsilon ,p^\varepsilon ),h^\varepsilon )\) such that
holds. Here, we added a linear diffusion term in the nonlinear conservation law to regularize the solution. By convolution of \(h_0\) we can obtain for each \(\varepsilon \in (0,1]\) a function \(h^\varepsilon _0\in C^\infty (\mathbb {R})\) that satisfies \(h^\varepsilon _0\in H^l(\mathbb {R})\) for any \(l\in \mathbb {N}\) and in particular for some \(\varepsilon \)-independent constant \(C_{\mathrm {mol}} > 0\)
To introduce a notion of weak solution for the regularized model (14), we define the following spaces

We note that \(\mathbf {v}\) in the homogeneous Dirichlet condition and the right side term of the weak formulation of the kinematic equation have to be understood in the trace sense which is well defined for the cylinder-type domain \({\varOmega }_{\mathrm {pm}} \).
Definition 2
A triple \(((\mathbf {v}^\varepsilon , p^\varepsilon ), h^\varepsilon ) \in (\mathrm {V}\times \mathrm {P}) \times \mathrm {H}\) is called weak solution of the coupled model (14) iff \(h^\varepsilon (\cdot ,0) = h^\varepsilon _0\) in \(\mathbb {R}\) and
holds for all \(t\in [0,T]\), all \(\varphi \in H^1(\mathbb {R}) \), and all \((\mathbf {w}, q) \in \{ \mathbf {w}\in (H^1({\varOmega }_{\mathrm {pm}}))^2\,|\, \mathbf {w}=0 \hbox { in }{\varGamma }_{\mathrm {D}} \} \times L^2({\varOmega }_{\mathrm {pm}})\).
Remark 2
In this contribution, we understand the term \(D^\varepsilon [h^\varepsilon ] :=\varepsilon \partial ^2_x h^\varepsilon \) in Eq. (14)\(_1\) as a purely artificial regularization of (11). We use it to establish the existence of smooth approximative solutions (see Theorem 4). Other regularization mechanisms could be chosen in a similar manner. Let us ignore the subsurface coupling for a moment and consider the equation
associated with the regularization
For the choice \(D^\varepsilon [h^\varepsilon ] :=\varepsilon \partial ^2_x h^\varepsilon \), the Cauchy problem for (19) admits a sequence of solutions \(\{h^\varepsilon \}_{\varepsilon >0}\) that converges a.e. to a classical entropy solution of (18) (see Dafermos 2010). The classical entropy solution is not the only weak solution of (18). Therefore, regularization terms which do not select an entropy solution in the limit \(\varepsilon \rightarrow 0\) are particularly interesting. It is well known that, e.g., the following choices (see Bertozzi et al. 1999; LeFloch and Rohde 2000; Duijn et al. 2007):
with \(\gamma > 0\) lead to convergence (at least in the sense of subsequences) toward weak solutions of (18) that are not entropy solutions. The last choice might be even physically relevant because then (19) describes the dynamics of a thin film on a plane where concentration peaks might occur at the film’s head. This requires a nonentropic solution concept in the limit \(\varepsilon \rightarrow 0\). Up to our knowledge, such thin film dynamics on porous beds (subsurfaces) has not been mathematically analyzed yet.
3.2 A Priori Estimates for Weak Solutions of the Regularized Model (14)
For the coupled model (14) it is possible to prove the following a priori estimate. The result is essential to provide global solvability of (14) for fixed \(\varepsilon >0\) and to get an \(\varepsilon \)-independent estimate.
Lemma 1
Let Assumption 1 be valid, and let \(\{((\mathbf {v}^\varepsilon , p^\varepsilon ), h^\varepsilon )\}_{\varepsilon \in (0,1]} \subset (\mathrm {V}\times \mathrm {P}) \times \mathrm {H}\) be a family of weak solutions of (14) in the sense of Definition 2. Then we have
for all \(t \in [0,T]\) and \(\varepsilon \in (0,1]\).
Proof
In the weak formulation (16) of the surface model, we choose \(\varphi (t) = h^\varepsilon (\cdot ,t) \) and obtain, for all \(t \in [0,T]\)
Here \(Q :\mathbb {R}\rightarrow \mathbb {R}\) is such that \(Q'(h) = \phi '(h) \, h\). Then the regularity of h and Assumption 1 imply \(Q(h(\cdot ,t)) \in L^1(\mathbb {R}) \cap L^\infty (\mathbb {R})\) a.e. Next, we consider the subsurface model. In the weak formulation (17) of the subsurface problem, we set \(\mathbf {w}= \mathbf {v}^\varepsilon \in \mathrm {V}\) and \(q = p^\varepsilon \in \mathrm {P}\). This yields
Addition of (20) and (21) results in
Integration with respect to time completes the proof if we take into account (15) for all \(\varepsilon \in (0,1]\). \(\square \)
3.3 Existence and Continuous-Dependence Estimates for Classical Solutions of the Uncoupled Kinematic Wave Equation
To prove the existence of a weak solution of the regularized coupled model (14) we will use a contraction argument that works only on the nonlinear kinematic wave equation for \(h^\varepsilon \). The following theorem is based on (Dafermos 2010, Theorem 5.3.1) and provides an estimate for solutions of regularized scalar conservation laws of the form
A function \(h^\varepsilon \in \mathrm {H}\) is called a weak solution of (23) iff \(h^\varepsilon (\cdot ,0) = h^\varepsilon _0\) in \(\mathbb {R}\) and
holds for all \(\varphi \in \mathrm {H}\).
Remark 3
For some given function \(f\in L^2(0,T;L^2(\mathbb {R})) \) there exists a unique weak solution of (23) (see, e.g., Serre 1999, Theorem 6.2.5).
We now assume slightly more regularity on f and get the following result.
Theorem 2
Let Assumption 1 be valid. Denote by \(h^\varepsilon _1, h^\varepsilon _2: \mathbb {R}\times [0,T]\rightarrow \mathbb {R}\) the unique weak solutions of (23) for the data
and
Then, \(h^\varepsilon _1, h^\varepsilon _2\) are classical solutions and we have in particular
Furthermore, there is a constant
such that for any \(t \in [0,T]\) it holds that
Proof
The existence of solutions of (23) can be found in, e.g., Serre (1999), for the regularity see Theorem 7.1.6. in Evans (2010) with the nonlinear flux as given function. In the following we omit for notational simplicity the dependency on \(\varepsilon \) and simply write \(h_{1/2}\), \(h_{1/2,0}\) instead of \(h^\varepsilon _{1,2}\), \(h^\varepsilon _{1/2,0}\). Let \((\eta ,q) \in (C^2(\mathbb {R}))^2\) be such that \(\eta ''>0\) and \(\eta '\phi '= q'\) hold. Then the classical solutions fulfill, for \(i=1,2\), the so-called entropy relation
where \(\psi \) is supposed to be an arbitrary nonnegative Lipschitz test function with compact support in \(\mathbb {R}\times [0,T)\). Taking the difference of the two entropy relations from (27) and making the (simplest) choice \(\eta (h) = \tfrac{h^2}{2}\) yield
Now, we apply the formula \(\tfrac{a^2 - b^2}{2} = \tfrac{(a-b)^2}{2} + b (a-b)\) and get
Considering the second term in the first integral, we obtain by the product rule
For the first term in Eq. (30) we can insert the partial differential Eq. (23) for \(h_2\), because it is a classical solution, and thus
For the second term in (30) we consider the weak formulation of (23) which reads, for \(i = 1,2\),
where \(\varphi \) is an arbitrary Lipschitz test function with compact support in \(\mathbb {R}\times [0,T)\). By choosing \(\varphi = \psi \, h_2\) and taking the difference of the weak formulations we obtain
Consequently, (29) now reads
where we used \(\varepsilon \psi \, (\partial _x h_1 - \partial _x h_2)^2 \ge 0\) and applied partial integration for the other \(\varepsilon \) terms. Next, we define
which are both of quadratic order in \((h_1 - h_2)\). Using this notation, inequality (32) can be written in the form
Now we fix \(t \in (0,T)\) and \(r > 0\) large enough. For any \(\delta > 0\) small enough and any \(\sigma \in (0,t]\) we choose the test function \(\psi (x,\tau ) = \zeta (x,\tau ) \, \omega (\tau )\), \(x \in \mathbb {R}\), \(\tau \ge 0\), with
Here, we set \(R(\tau ) :=r + s (t - \tau )\), where \(s = s({||}{h_{1/2}}{||}_{C^0(\mathbb {R}\times [0,T)})\) is the constant such that
This gives
Due to (34), the first term of the right-hand side is smaller than zero and therefore can be dropped. For the third term on the right-hand side we apply Young’s inequality and get
By taking the limit \(\delta \rightarrow 0\), Eq. (35) has the following form, for almost all \(\sigma \in (0,t)\),
Next, we consider the limit \(r \rightarrow \infty \) (and therefore \(R \rightarrow \infty \)). In this case, the last term in (36) vanishes because we have \(h_1, h_2 \in C([0,T];H^1(\mathbb {R}))\). Consequently, after applying Hölder’s inequality and estimating \(Z(h_1,h_2)\), \(\partial _x h_2\) we obtain
Next we define, for \( \tau \in [0,t]\),
Thus, inequality (37) can be written as
which holds true for all \(\sigma \in [0,t]\). Finally, applying the Gronwall type inequality from Lemma 2 below completes the proof. \(\square \)
The proof of Theorem 2 is based on the following Gronwall type inequality (from Dafermos 1979, Lemma 4.1).
Lemma 2
(Gronwall type inequality) If the functions \(g \in L^1([0,T])\) and \(\gamma \in L^\infty ([0,T])\) are nonnegative and satisfy for almost all \( s \in [0,T]\)
with nonnegative constants \(\alpha , B, C\), then it follows
3.4 Existence and Regularity Estimates for Weak Solutions of the Uncoupled Brinkman System
In the following we will consider the Brinkman system for given time-dependent Neumann boundary conditions \(\mathbf {g}_{\mathrm {N}} :\partial {\varOmega }_{\mathrm {pm}} \times (0,T)\rightarrow \mathbb {R}^2\) on \({\varGamma }_{\mathrm {N}} \) using the notation from (8) with \(\mathbf {n}\) defined as the outer unit normal of \( {\varGamma }_{\mathrm {N}} \). Thus, we have for some \(M \ge 0\) the time-parameterized problem
A weak solution of the Brinkman/Stokes Eq. (38) is defined in the following manner. Let \(\mathbf {g}_{\mathrm {N}} \in L^2(0,T;(H^{1/2}({\varGamma }_{\mathrm {N}} ))^2)\). A function \((\mathbf {v},p) \in \mathrm {V}\times \mathrm {P}\) is called a weak solution of the Brinkman problem (38) iff
holds for all \((\mathbf {w}, q) \in \bigl \{ \mathbf {w}\in (H^1({\varOmega }_{\mathrm {pm}}))^2 \,|\, \mathbf {w}=0 \hbox { a.e. in }{\varGamma }_{\mathrm {D}} \bigr \} \times L^2({\varOmega }_{\mathrm {pm}})\) and almost all \(t\in (0,T)\).
Remark 4
For \(\mathbf {g}_{\mathrm {N}} \in L^2(0,T; (H^{1/2}(\mathbb {R}))^2)\) there is a unique weak solution of (38). The proof relies on the coercivity of the weak form for the velocity system and the Babuska–Brezzi theorem for saddle point problems (see, e.g., Galdi 2011 for background on the Stokes system). For a weak solution we obtain for some constant \(C_{\mathrm {Br}}= C_{\mathrm {Br}}(\mu ,M,C_{\mathrm {tr}} ) > 0\) the bound
by setting \(\mathbf {w}=\mathbf {v}(\cdot ,t),\, q=p(\cdot ,t) \) for almost all \(t\in (0,T)\) in the weak formulation.
Weak solutions satisfy the following regularity statement.
Theorem 3
For \(k\in \mathbb {N}_0\) and a function \(\mathbf {g}_{\mathrm {N}} \in L^2(0,T;(H^{k+1/2}({\varGamma }_{\mathrm {N}} ))^2 )\) there is a constant \(C^k_{\mathrm {Br}} > 0\) such that for almost all \(t\in (0,T)\) the unique weak solution \((\mathbf {v}(\cdot ,t), p(\cdot ,t))\) of (38) satisfies
Proof
A proof of the shift regularity can be done following the regularity proofs in Galdi (2011), Chapter IV, which extend to the unbounded domain \({\varOmega }_{\mathrm {pm}}\).\(\square \)
Remark 5
Because \(C_{\mathrm {Br}} = {\text {O}}(\mu ^{-1})\), the a priori estimate (39) no longer holds in the limit \(\mu \rightarrow 0\). Note that Darcy’s law results as the formal limit problem of Brinkman’s model for \(\mu \rightarrow 0\). Consequently, the subsequent analysis is not applicable when Darcy’s law is used as the subsurface flow model.
3.5 The Coupling Scheme
To verify the existence of a solution of the regularized fully coupled problem (14), we apply an alternating, iterative approximation method. That means, we solve the subsurface system and thereafter use the newly obtained solution as a source for the surface model, which then serves again as input for the subsurface equations.
For arbitrary, but fixed \(\varepsilon \in (0,1]\), let the sequence \( \{ {((\mathbf {v}^{\varepsilon ,i}, p^{\varepsilon ,i}), h^{\varepsilon ,i})\}}_{i\in \mathbb {N}}\) for \(i \in \mathbb {N}\) be a sequence of iterative solutions of
To start the iterative method we set \(h^{\varepsilon ,0} \equiv h_0\). Note that we have changed the ordering of equations in (41), (42) in comparison with (14) to express the sequencing for each iteration.
By an iterative solution \(((\mathbf {v}^{\varepsilon ,i}, p^{\varepsilon ,i}), h^{\varepsilon ,i})\) for (41), (42), \( i \in \mathbb {N}\), we mean that \(h^{\varepsilon ,i}\) is a weak solution of (41) and that \((v^{\varepsilon ,i}, p^{\varepsilon ,i})\) is a weak solution of (42), i.e., it holds
for almost all \(t\in (0,T)\), all \(\varphi \in H^1(\mathbb {R}) \), and all \((\mathbf {w}, q) \in \{ \mathbf {w}\in (H^1({\varOmega }_{\mathrm {pm}}))^2)\,|\, \mathbf {w}=0 \hbox { in }{\varGamma }_{\mathrm {D}} \} \times L^2({\varOmega }_{\mathrm {pm}})\). The following remark discusses the existence and smoothness of iterative solutions.
Remark 6
-
(i)
The iteration is well posed in terms of weak solutions. Starting with \(h^{\varepsilon ,0}\equiv h^\varepsilon _0 \in L^2(0,T; H^1(\mathbb {R}))\) we get from Remark 4 and Theorem 3 with \(\mathbf {g}_N :=-{h}^{\varepsilon ,0} \, \mathbf {n} \) the unique existence of a weak solution \((\mathbf {v}^{\varepsilon ,1}, p^{\varepsilon ,1}) \in L^2(0,T; (H^2({\varOmega }_{\mathrm {pm}} ))^2) \times L^2(0,T; H^1({\varOmega }_{\mathrm {pm}}))\) of (41). In turn Remark 3 ensures the unique existence of a weak solution \(h^{\varepsilon ,1} \in L^2(0,T; H^1(\mathbb {R}))\) of (42) since the trace \(f :={\mathbf {v}}^{\varepsilon ,1} \cdot \mathbf {n}\) on \({\varGamma }_{\mathrm {N}}\) is even in \(L^2(0,T; H^1(\mathbb {R})) \). This closes the loop.
-
(ii)
To satisfy higher regularity of the solution suppose Assumption 1 is valid. Then we have \(h^{\varepsilon ,0} \equiv h^\varepsilon _0 \in L^2(0,T; H^2(\mathbb {R}))\) and trivially \( \partial _t h^{\varepsilon ,0} \in L^2(0,T; L^2(\mathbb {R}))\). We apply Theorem 3 for (38) with \(\mathbf {g}_{\mathrm {N}} :=-{h}^{\varepsilon ,0} \, \mathbf {n} \) and \(\partial _t \mathbf {g}_{\mathrm {N}} :=-\partial _t {h}^{\varepsilon ,0} \, \mathbf {n} \). This gives for the traces \( f :={\mathbf {v}}^{\varepsilon ,1} \cdot \mathbf {n}\in L^2(0,T;H^1(\mathbb {R}))\) and \(\partial _t f \in L^2(0,T;L^2(\mathbb {R}))\). We conclude with Theorem 2 that a weak solution \(h^{\varepsilon ,1} \in L^2(0,T; H^1(\mathbb {R}))\) of (42) exists which satisfies
$$\begin{aligned} h^{\varepsilon ,1} \in L^2(0,T;H^4(\mathbb {R})) \cap C([0,T];H^3(\mathbb {R})), ~ \partial _t h^{\varepsilon ,1} \in L^2(0,T;H^2). \end{aligned}$$This is also a classical solution of (42).
Our aim is to show that the sequence of iterative solutions \( \{((\mathbf {v}^i, p^i), h^i)\}_{i \in \mathbb {N}}\), obtained by the coupling scheme (41), (42), converges for \(i \rightarrow \infty \) to a weak solution of (14).
3.6 Local A Priori Estimates for the Iterative Solutions
The existence proof relies on certain a priori estimates for the iterative solutions. Note that these estimates hold only locally in time. Throughout this section, we assume that Assumption 1 holds such that all statements of Remark 6 apply.
Lemma 3
Let Assumption 1 be valid, and let \( {\{(( \mathbf {v}^{\varepsilon ,i}, p^{\varepsilon , i}), h^{\varepsilon , i})\}}_{i \in \mathbb {N}} \) be the family of iterative solutions of (41), (42). Then, for any fixed \(\beta \in (0,1)\) there exists a \(t_{\mathrm {max},1} > 0\) and \(C_{\mathrm {It}} = C_{\mathrm {It}}(\beta , M, \mu , T) > 0\) such that
and
hold for all \(t^* \in [0, t_{\mathrm {max},1}]\) and \(i\in \mathbb {N}\).
Proof
For the proof we skip the index \(\varepsilon \). Let \(((\mathbf {v}^i, p^i),h^i)\), \(i \in \mathbb {N}\) fixed, be an iterative solution of (41), (42). We multiply (42)\(_1\) (which holds in the classical sense, see Remark 6) with \( h^i\) and put \((\mathbf {w},q)=(\mathbf {v}^i, p^i) \) in the weak formulation for (41). Integrating (42) with respect to space in \(\mathbb {R}\) and some time interval \((0,t^*)\), \(t^* \in (0,T)\) arbitrary, yields
Next, we apply Young’s inequality for products. This gives, with freely choosable \(\gamma _1, \gamma _2 > 0\),
Application of the trace inequality (13) for \(\mathbf {v}^i\) and the estimate \({||}{\mathbf {v}^{i}}{||}_{H^1({\varOmega }_{\mathrm {pm}})} \!\le \! C_{\mathrm {Br}} {||}{h^{i-1}}{||}_{L^2(\mathbb {R})}\), from (40), for some \(C_{\mathrm {Br}} = C_{\mathrm {Br}}(M,\mu )>0\) give
By choosing \(\gamma _2 = \tfrac{C^{2}_{\mathrm {tr}}}{4 \min (M,\mu )}\), we obtain
for all \(t^* \in [0,T]\), and therefore, we can infer
with the choice \(\gamma _1 = \tfrac{1}{4}\), and the assumption that \(t^* < t_{\mathrm {max},1}\), with
Now, we can estimate the left-hand side of the last inequality by using a geometric series, which leads to
This a priori estimate can be substituted into (45). Therefore we obtain, for all \(t^* \le t_{\mathrm {max},1}\),
choosing now \(\gamma _1 = \tfrac{1}{2} C_{\mathrm {tr}} C_{\mathrm {Br}}\). This completes the proof with (15). \(\square \)
In the next step we consider higher-order derivatives of \(h^{\varepsilon , i}\).
Lemma 4
Let Assumption 1 be valid, and denote by \( {\{(( \mathbf {v}^{\varepsilon ,i}, p^{\varepsilon , i}), h^{\varepsilon , i})\}}_{i \in \mathbb {N}} \) the family of iterative solutions of (41), (42). Then, there exists a constant \(\widetilde{C}_{\mathrm {It}} = \widetilde{C}_{\mathrm {It}}(\varepsilon , C_{\mathrm {mol}}, \phi , \beta , M, \mu , T) > 0\) such that
hold for all \(t^* \in [0, t_{\mathrm {max},1}]\) with \(t_{\mathrm {max},1}\) from Lemma 3 and for all \(k\in \{1,2,3\}\).
Proof
The proof is given for the case \(k=1\). The cases \(k>1\) follow exactly along the same lines. For the estimate on the time derivative the latter is expressed by Eq. (42), which is satisfied classically, and then the estimate follows directly from the higher-order space estimates. In the proof we will consider classical derivatives of the unknowns \( \mathbf {v}^{\varepsilon ,i}, p^{\varepsilon , i}, h^{\varepsilon , i}\). These exist since the regularity of the iterative solutions hinges only on the regularity of the initial datum \(h^\varepsilon _0 \in C^\infty (\mathbb {R}) \cap H^l(\mathbb {R})\) for any \(l\in \mathbb {N}\) (see (15)). Arguing as in Remark 6(ii) gives the classical differentiability by Sobolev embedding.
We remark that the spatial subsurface coordinates are denoted by \(\mathbf {x}= (x_1, x_2) \in {\varOmega }_{\mathrm {pm}}\), and because we assumed \(\mathbf {n} = (0,1)^{\top }\), the surface coordinate \(x \in {\varOmega }_{\mathrm {ff}} \cong \mathbb {R}\) coincides with \(x_1\). Again we skip the index \(\varepsilon \) and define
Differentiating (41) with respect to \(x_1\) and (42) with respect to x yields
As in Lemma 3 we obtain for all \(t^* \in [0,T]\) to
The term \(S^i_1\) can be estimated using the methods used in the proof of Lemma 3, which yields
with \(\gamma _1, \gamma _2 > 0\) coming from Young’s inequality. For \(R^i_1 \) we observe
for an arbitrary \(\gamma _3 > 0\), coming again from Young’s inequality. Furthermore \(C_\phi = C_\phi ({||}{\phi '}{||}_{W^{1,\infty }(\mathbb {R})}) > 0\), see Assumption 1. Combining these estimates, with \(\gamma _1 = \tfrac{1}{2} C_{\mathrm {tr}} C_{\mathrm {Br}}\), \(\gamma _2 = \tfrac{C^{2}_{\mathrm {tr}}}{4 \min (M,\mu )}\), and \(\gamma _3 = \tfrac{\varepsilon }{2 C_{\phi }}\) gives
If \(t^* \le t_{\mathrm {max},1}\) we have shown in Lemma 3 for all \(i\in \mathbb {N}_0\) that
Therefore we get with \( g^i = \partial _x h^i\) and (15) the estimate
for all \(t^* \in [0, t_{\mathrm {max},1}]\), which completes the proof. \(\square \)
3.7 Existence of a Weak Solution for the Regularized Coupled Model (14)
The aim of this section is to show that the coupled model (14) has a weak solution in the sense of Definition 2. To this end we will use the coupling scheme (41), (42) to construct a sequence which will converge to a weak solution of (14). First, we will consider the properties of the coupling scheme.
Proposition 1
(Contraction property) We let Assumption 1 be valid and define \(H:= {||}{h_0}{||}_{L^2(\mathbb {R})} \). For a given \(\alpha \in (0,1)\), there exists a time \(t_{\mathrm {max}} (H) > 0\) such that the family of iterative solutions \({\{((\mathbf {v}^{\varepsilon ,i}, p^{\varepsilon ,i}), h^{\varepsilon ,i})\}}_{i \in \mathbb {N}} \) of (41), (42) satisfies
for all \(i \in \mathbb {N}\). The time \(t_{\mathrm {max}}(H)\) depends also on the fixed numbers \(\alpha , \varepsilon ,\mu , M,T\) and \(\beta , {C}_{\mathrm {It}}, \widetilde{C}_{\mathrm {It}}\) from Lemmas 3, 4.
Proof
We again skip the index \(\varepsilon \). We assume that \(t^* \in [0, t_{\mathrm {max},1}]\), with \(t_{\mathrm {max},1}\) from Lemmas 3 and 4. These Lemmas imply by Sobolev embedding, Eq. (15), and Assumption 1 that \(\{{||}{h^i(\cdot ,t^*)}{||}_{W^{1,\infty }(\mathbb {R})}\}_{i\in \mathbb {N}}\) is uniformly bounded for all \(t^* \in [0, t_{\mathrm {max},1}]\) by a constant that depends on all fixed parameters and H. Therefore we can conclude (see Theorem 2 for the definition of \(\theta \)) that there is a \(\bar{\theta }=\bar{\theta }(H) >0\) such that
for all \(i\in \mathbb {N}\).
Next, we choose \(t_{\mathrm {max},2}\) according to
where \(C_{\mathrm {Br}} > 0\) is the constant from Remark 4 and \(C_{\mathrm {tr}} > 0\) is the constant of the trace inequality (13). We define
and restrict \(t^*\) further to \(t^* \in [0, t_{\mathrm {max}}]\). From Theorem 2 for \( u_1 :=h^{i+1}\), \(u_2 :=h^i\), \(f_1 :=h^{i+1}(\cdot ,t)\), \(f_2 :=h^i(\cdot ,t)\) we conclude
where we used the bound for \(\theta \). Applying the trace inequality to the term on the right side gives
Now we apply again the \(H^1\)-estimate for solutions of the linear Brinkman problem to obtain
Finally, due to the choice of \(t_{\mathrm {max}}\) Eq. (50) and \(t^* < t_{\mathrm {max}}\), it follows that Eq. (49) holds. This completes the proof. \(\square \)
By applying the contractive property of Proposition 1 we are now able to prove the existence of a solution of the coupled model (14) on a short time interval.
Theorem 4
(Local existence) If Assumption 1 holds, there is, for all \(t^* \in (0, t_{\mathrm {max}})\), a weak solution \((( \mathbf {v}^\varepsilon , p^\varepsilon ),h^\varepsilon ) \in (\mathrm {V}\times \mathrm {P}) \times \mathrm {H}\) of the coupled model (14) in the sense of Definition 2. This weak solution satisfies in particular
Proof
As shown in Proposition 1 the sequence \(\{{h^i\}}_{i \in \mathbb {N}}\) (skipping the index \(\varepsilon \)) is contractive in the space \(C([0,t^*]; L^2(\mathbb {R}))\) provided \(0 < t^* < t_{\mathrm {max}}\). From Banach’s fixed-point theorem we conclude that there exists a unique \(h \in C([0,t^*]; L^2(\mathbb {R}))\) with
Furthermore the Lemmas 3 and 4 show (extracting appropriate subsequences from the family \({\{((\mathbf {v}^i,p^i), h^i )\}}_{i \in \mathbb {N}}\), which are denoted in the same way)
For the Brinkman–Stokes system we use Theorem 3 with \(k=2\), the above-mentioned Lemmas and the trace estimate to conclude that there are functions \((\mathbf {v},p) \in L^2(0,T;(H^4( {\varOmega }_{\mathrm {pm}}))^2)\times L^2(0,T; H^2( {\varOmega }_{\mathrm {pm}} )) \) with
Next, we note that any iterative solution \(((\mathbf {v}^i,p^i), h^i )\) satisfies the weak formulation (44). In the weak formulation we can shift the derivative on \(\phi (h^i)\) to the test function. Then we use (52) to pass to the limit in this term. In all of the other terms we can perform the limit in the weak formulation by (54), because they are linear in the unknowns. By the high spatial regularity of the limit function h we see that \(((\mathbf {v},p), h)\) is a weak solution of (14).\(\square \)
Actually, the argument of Theorem 4 can be extended to the time interval [0, T].
Theorem 5
(Global existence) Let Assumption 1 hold. For each \(\varepsilon \in (0,1]\) there exists a weak solution \(((\mathbf {v}^\varepsilon , p^\varepsilon ), h^\varepsilon ) \in (\mathrm {V}\times \mathrm {P}) \times \mathrm {H}\) of the coupled model (14) in [0, T] which satisfies in particular the estimate from Lemma 1.
Proof
From Theorem 4 we have the existence of a weak solution \(((\mathbf {v}^\varepsilon , p^\varepsilon ), h^\varepsilon )\) in the time interval \([0,t_\mathrm {max}]\). The number \(\bar{\theta }(H)\) in the proof of Proposition 1 depends only on \(H= {||}{h_0}{||}_{L^2(\mathbb {R})}\) (and the fixed values of \(\varepsilon ,\mu ,M,T,\beta ,\alpha \)) such that the existence interval \([0,t_\mathrm {max}]\) depends only on H. As the limit of iterative solutions we can bound \({||}{h^\varepsilon (\cdot ,t_\mathrm {max})}{||}_{L^2(\mathbb {R})}\) only by \(1 +(1-\beta )^{-1} H\) due to Lemma 3. However, Lemma 1 gives the improved bound \({||}{h^\varepsilon (\cdot ,t_\mathrm {max})}{||}_{L^2(\mathbb {R})}\le H\) for a weak solution component \(h^\varepsilon \). As a consequence we can repeat all arguments of Proposition 1 and Theorem 4 to extend the weak solution to \([0,2t_\mathrm {max}]\). Iteratively we achieve the existence on [0, T].\(\square \)
4 Existence of a Weak Solution for the Kinematic–Brinkman Model
According to Theorem 5, let
be a family of weak solutions of the regularized kinematic–Brinkman problem (14). We will show that the sequence in (55) converges (in an appropriate sense) to a triple of functions which constitute a weak solution of the original kinematic–Brinkman model (11).
Theorem 6
(Existence) Let Assumption 1 hold and additionally let the measure of the set \(\{ s \in \mathbb {R}~ : ~ \phi ''(s) = 0 \}\) be zero.
Then, there exists a subsequence of the family \(\{(( \mathbf {v}^{\varepsilon }, \quad p^{\varepsilon }), h^{\varepsilon })\}_{\varepsilon \in (0,1]}\), which is still denoted as \({ \{(( \mathbf {v}^{\varepsilon }, \, p^{\varepsilon }), h^{\varepsilon })\}}_{\varepsilon \in (0,1]}\), and functions \(h \in L^2( \mathbb {R}\times (0,T))\), \(\mathbf {v}\in \mathrm {V}_0\), and \(p \in \mathrm {P}_0\), such that
hold for \(\varepsilon \rightarrow 0\). Furthermore, \(((\mathbf {v},p),h)\) is a weak solution of (11).
To prove Theorem 6 we will rely on the a priori estimates from Lemma 1 and—what concerns the limit procedure for \(h^{\varepsilon }\)—on the Lemma of Murat (1981) in the \(L^p\)-framework (Schonbek 1982), and in particular we shall refer to the arguments used in Corli and Rohde (2012) and Lu (1989). Note that the additional regularity condition on \(\phi \) in Theorem 6 is needed in these papers.
To prepare the setting we introduce the entropy function \(\eta \in C^2(\mathbb {R})\) with associated entropy flux \( \psi \in C^2(\mathbb {R})\) for the hyperbolic Eq. (5), see Dafermos (2010). Precisely, that are functions that satisfy
and (for our context only) the global bounds
for all \(s \in \mathbb {R}\). Now we are in a position to establish the following compactness statement.
Lemma 5
(Murat) Let the assumptions of Theorem 6 be valid. Then for each open bounded set \(Q \subseteq \mathbb {R}\times (0,T)\) there is a compact set \(\mathscr {K} \subset W^{-1, 2}(Q)\) and a bounded set \(\mathscr {B} \subset \mathscr {M}(Q)\), where \(\mathscr {M}(Q)\) is the space of Radon measures on Q, such that
for each entropy function \(\eta \) that satisfies (56), (57).
Proof
A straightforward computation shows that it holds
We denote by \({\langle }{\cdot , \cdot }{\rangle }\) the duality product between \(W^{-1,2}(Q)\) and \(W^{1,2}_0(Q)\), and also between \(\mathscr {M}(Q)\) and \(C^{0}_{0}(Q)\). First, we will show that \(T^{\varepsilon }_{1} \subset \mathscr {K}\). For each \(\varphi \in W^{1,2}_{0}(Q)\) we have
The last line is a consequence of Lemma 1. By taking into account (15), we obtain for \(\varepsilon \rightarrow 0\)
and thus \(T^{\varepsilon }_{1} \subset \mathscr {K}\). Furthermore, with \(\widetilde{\varphi } \in C^{0}_{0}(Q)\) and again Proposition 1, we get
which implies \(T^{\varepsilon }_{2} \subset \mathscr {B}\). Finally, let \(Q_x\) be a compact interval in \(\mathbb {R}\) such that \(Q\subset Q_x \times (0,T) \) holds. We obtain for \(T^{\varepsilon }_{3}\)
Here we used Lemma 1 and the trace embedding (13) for the term \({||}{\mathbf {v}^{\varepsilon } \cdot \mathbf {n}}{||}_{L^2(\mathbb {R})}\). Altogether, we have \(T^{\varepsilon }_{3} \subset \mathscr {B}\) which concludes the proof. \(\square \)
With the compactness result of Lemma 5 we finalize the proof of Theorem 6.
Proof (of Theorem 6)
The family of norms \(\{{||}{h^\varepsilon }{||}_{L^2(\mathbb {R}\times (0,T))}\}\) is uniformly bounded because of Lemma 1. By Theorem 5 and the results in Lu (1989) and Murat (1981) we deduce that there is a function \(h\in L^r(\mathbb {R}\times (0,T)))\) with \(h^\varepsilon \rightarrow h\) in \(L_{\mathrm {loc}}^r( \mathbb {R}\times (0,T))\), for \(1\le r < 2\). Weak compactness in \(L^2( \mathbb {R}\times (0,T))\) implies (extracting a subsequence) \(h\in L^2( \mathbb {R}\times (0,T))\). Extracting another subsequence, the a priori estimate from Lemma 1 ensures the existence of functions \(\mathbf {v}, p\) with
We have proven the first part of Theorem 6, and it remains to verify that the triple \((h,\mathbf {v},p)\) is a weak solution of (11). First of all we note that the weak convergence of \(\{\mathbf {v}^\varepsilon \}_{\varepsilon \in (0,1]}\) implies by linearity and continuity of the trace mapping that the traces of \(\mathbf {v}^\varepsilon \) and \(\mathbf {v}\) on \({\varGamma }_N \times (0,T)\) satisfy
We consider now the following weak formulation for the viscous solution \(h^\varepsilon \), that is
Passing to the limit \(\varepsilon \rightarrow 0\) in (60) gives the desired condition (12)\(_{1}\) for h if we take into account the Lipschitz continuity of \(\phi \), the uniform \(L^2\)-boundedness of \(h^\varepsilon \), (15) and the weak convergence (59) in the linear boundary term. For the weak formulations for velocity \(\mathbf {v}\) and pressure p we note again that the Brinkman part is linear. Thus the weak convergence as stated in (58) suffices to pass to the limit \(\varepsilon \rightarrow 0\) and to obtain (12)\(_{2}\). \(\square \)
5 Numerical Experiments
In this section, results from numerical simulations for the coupled surface–subsurface model are presented and discussed. First, a discretization for the coupled model is introduced. Next, we make a qualitative comparison of the model for different parameters and fluxes, and examine the behavior of the discrete coupling algorithm for some test cases.
5.1 Discretization
For the discretization of the coupled model (11), we apply a finite volume scheme for each flow regime. For the surface flow we use an explicit Euler approximation for the time integration and upwinding for the flux. For the subsurface flow a two-dimensional scheme on staggered grids is applied, as described in, e.g., Rybak et al. (2015) for the Stokes equations. In both domains, matching, uniform and structured grids are used, with cell lengths \(\Delta x >0\) for the surface and \(\Delta x_1, \, \Delta x_2 > 0\) for the subsurface region. In all subsequent simulations, we consider a coupled domain depicted in Fig. 2.
Schematic depiction of the domain used in Sect. 5
Coupled Discretization To combine the surface and the subsurface flow on a discrete level, we couple the models at each time-step \(t_n = n \, \Delta t\), \(n \in \mathbb {N}\), \(\Delta t > 0\), and, if necessary, iterate for each time-step \(K_{\mathrm {It}}\)-times between the flow domains. Thus, a general, discrete coupling algorithm can be schematically written in the following form:

In spite of the robust performance of the numerical method for the presented experiments, the convergence analysis remains an open issue. In principle, the sequence of numerical approximations can be understood as the discrete analogon of the viscous approximations from Sect. 3. An \(L^2\)-contraction estimate for finite volume schemes has been proven in Jovanović and Rohde (2006), and the use of compensated compactness methods (Murat 1981) for numerical approximations is well established. This would be the basis to transfer the analysis of the continuous model to the discrete case.
Another interesting issue concerns the choice of the iteration number \(K_{\mathrm {It}}\) in Algorithm 1, which should be chosen such that the coupling error is of the same order as the discretization error. We are not aware of any rigorous analysis that attempts to answer this question (even for simplified situations). Our specific choice of \(K_{\mathrm {It}}\) in the numerical experiments is in fact just an ad-hoc decision. However, in Sect. 5.3 we investigate the influence of \(K_{\mathrm {It}}\) numerically for a test case.
5.2 Qualitative Comparison of the Models
In this section we qualitatively investigate the effects of choosing different surface and subsurface models. We make numerical computations using a finite volume discretization and Algorithm 1, and compare the results. To this end, we consider the coupled model (11). It is possible to achieve different models by setting the flux \(\phi \) and \(M \ge 0\). If we have \(\phi (h) = Vh\), as in Remark 1, we get the linear transport equation as the surface model with a velocity field \(V:{\varOmega }_{\mathrm {ff}} \rightarrow \mathbb {R}\). For \(\phi (h) = V{|}{h}{|}^{5/3}\) we obtain the kinematic wave equation as the surface model (Sect. 2.2). Likewise, if we set \(M = 0\) the Stokes equations are considered as the subsurface model, and in case \(M > 0\) one considers Brinkman’s equations.
For the numerical computations, we consider the domains \({\varOmega }_{\mathrm {ff}} = (-2, 10) \times \{3\}\) and \({\varOmega }_{\mathrm {pm}} = (0, 5) \times (0,3)\). The initial condition is chosen as
In each of the following numerical computations, the domains are discretized by regular meshes with width \(\Delta x = \Delta x_1 = 0.04\) and height \(\Delta x_2 = 0.04\). The time-step is \(\Delta t = 0.2\), and \(K_{\mathrm {It}} = 1\). The velocity \(V\) is chosen as \(V= 0.05\) for both the transport equation and the kinematic wave equation. For the case when Brinkman’s equations are considered, we assume \(M = 100\). At the interface \({\varGamma }\) we impose the coupling boundary conditions, and on \({\varGamma }_{\mathrm {D}} = \partial {\varOmega }_{\mathrm {pm}} \setminus {\varGamma }\) we impose the Dirichlet boundary condition \(\mathbf {v}= \mathbf {0}\).
The Linear Model Figure 3 shows the numerical solution at \(t = 80\) of the coupled model consisting of the linear transport equation and Stokes equations. It can be seen that the fluid on the surface flows through the subsurface from places with a higher water height to places with a lower water height. In comparison, it can be observed in Fig. 4 that the flow through a subsurface which is modeled by Brinkman’s equations is much slower. Evidently, this is due to the lower permeability of the porous medium, since the parameter M plays the role of the inverse permeability.
The Nonlinear Model The same behavior can be seen, if instead of the transport equation, the kinematic wave equation is considered—see Figs. 5 and 6. In contrast to the coupled models with the transport equation, we observe a much steeper slope of the water front. This is due to the strict convexity of the flux function \(\phi (h) = V{|}{h}{|}^{5/3}\) in the kinematic wave equation.
In Fig. 7 the effect of the Brinkman parameter M on the surface flow, modeled by the kinematic wave equation, is examined. The numerical experiments indicate that the coupling with Brinkman’s equations has a certain smoothing effect on the fluid height at the interface, which becomes more distinctive for lower M, i.e., higher permeability of the subsurface. In that case, more water moves through the subsurface to form an equilibrium, driven by pressure differences coming from the surface. However, outside of the interface the smoothing effect vanishes, which is why new shock waves are formed. Nonetheless, the flow exchange with the subsurface seems to reduce the occurrence of discontinuities in the fluid height at the interface.
5.3 The Influence of the Iteration Number
To study the influence of the number of iterations \(K_{\mathrm {It}} \in \mathbb {N}\) in Algorithm 1 we consider the case \(\phi (h) = Vh\), and \(M=0\). The domains are \({\varOmega }_{\mathrm {pm}} = [0, 12] \times [0, 3]\), \({\varOmega }_{\mathrm {ff}} = [-2, 15]\), and we make computations till \(T = 75\). The initial condition is given by \(h_0(x) = \chi _{x \le -1}(x)\). We fix \(\Delta x = \Delta x_1 = \Delta x_2 = 0.05\) and \(\Delta t \in \{0.25,\, 0.1,\, 0.05,\, 0.025\}\). For each number of iterations \(K_{\mathrm {It}} = 1,\ldots ,7\) we compute an approximative solution \(h^{K_{\mathrm {It}}}\) of the coupled problem (11) by applying Algorithm 1. Then, we calculate the difference of the solutions for subsequent number of iterations at T, i.e., the difference
and compute the \(L^2\)-norm of the difference. The result is depicted in Fig. 8. It can be seen that with each iteration the norm of the difference diminishes, until it stagnates when the discretization error (in time and space) dominates. Thus, the numerical stability of the algorithm, with respect to the number of coupling-iterations \(K_{\mathrm {It}}\), is provided.
5.4 Examination of the Mass Conservation
In this numerical test we want to investigate whether the discrete coupling algorithm is mass conservative. The surface and subsurface discretization by themselves are mass conservative, and thus mass loss/gain can only happen at the surface/interface. To measure it, we regard the sum of the surface water height, i.e.,
which is a measure of the total mass of the surface water.
For the numerical computations, we consider the domains \({\varOmega }_{\mathrm {ff}} = [0,10]\) and \({\varOmega }_{\mathrm {pm}} = [0,10] \times [0,5]\), discretized with mesh width \(\Delta x = \Delta x_1 = \Delta x_2 = 0.05\). The time-step size is \(\Delta t = 0.25\), and the iteration number is \(K_{\mathrm {It}} = 1\). For convenience we set \(V= 0\). We consider the initial data \(h_0(x) = \chi _{x \in [4.5, 5.5]}(x)\) and consequently have the initial mass \(\Sigma (0) = 0.1\).
The results of the computations are depicted in Fig. 9. In Fig. 9a, we see the evolution of the water height from \(t = 0\) to \(t = 250\), and in Fig. 9b, the mass difference with respect to the initial mass is plotted. The absolute mass difference averages \(5.6 \cdot 10^{-11}\), and therefore we can infer that the coupling algorithm is mass conservative.
Numerical computations for examining the mass conservation property of the discrete coupling algorithm. In a the approximative solution of the water height h is depicted, for some values of t. In b the difference between the initial mass \(\Sigma (0)\) and the mass \(\Sigma (t)\) at the time t is plotted. a Surface water height h. b Plot of the mass difference
6 Conclusion
In the paper, a coupled surface–subsurface model is considered. The subsurface is modeled by Brinkman’s equations in a two-dimensional unbounded domain. For the surface model a one-dimensional scalar conservation law, as a generalization of the kinematic wave equation, is applied. For this surface–subsurface model the existence of a weak solution is proven. This is done by introducing a regularized coupled model, and, via a fixed-point argument, proving the existence of a weak solution for it. Then, by applying the method of compensated compactness it is possible to show the existence for the original coupled model without regularization. In Sect. 5, an alternating, iterative numerical algorithm for the coupled model is presented and tested for different models.
Concerning the model, there are still some extensions possible. First, higher space dimensions should be considered, and instead of the steady-state Brinkman’s equations, a time-dependent subsurface model could be studied. Another issue of the model is that it cannot be expected that the water height h stays nonnegative. The model would have to be adapted to have an admissible solution set \(h \ge 0\), for example as it was done in Sochala et al. (2009), for a model that couples the kinematic wave equation and Richards’ equation. Finally, nontrivial bottom topology should be regarded, which would be a further step toward a realistic coupled surface–subsurface model.
References
Auriault, J.L.: On the domain of validity of Brinkman’s equation. Transp. Porous Media 79(2), 215–223 (2009)
Bear, J.: Dynamics of Fluids in Porous Media. Elsevier, New York (1972)
Beavers, G.S., Joseph, D.D.: Boundary conditions at a naturally permeable wall. J. Fluid Mech. 30, 197–207 (1967)
Berninger, H., Ohlberger, M., Sander, O., Smetana, K.: Unsaturated subsurface flow with surface water and nonlinear in- and outflow conditions. Math. Models Methods Appl. Sci. 24, 901–936 (2014)
Bertozzi, A., Münch, A., Shearer, M.: Undercompressive shocks in thin film flows. Phys. D 134(4), 431–464 (1999)
Brinkman, H.C.: A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl. Sci. Res. 1, 27–34 (1947)
Cao, Y., Gunzburger, M., Hua, F., Wang, X.: Coupled Stokes–Darcy model with Beavers–Joseph interface boundary condition. Commun. Math. Sci. 8(1), 1–25 (2010)
Corli, A., Rohde, C.: Singular limits for a parabolic-elliptic regularization of scalar conservation laws. J. Differ. Equ. 253(5), 1399–1421 (2012)
Dafermos, C.M.: The second law of thermodynamics and stability. Arch. Ration. Mech. Anal. 70(2), 167–179 (1979)
Dafermos, C.M.: Hyperbolic Conservation Laws in Continuum Physics, 3rd edn. Springer, Berlin (2010)
Darcy, H.: Les Fontaines Publiques de la Ville de Dijon. Dalmont, Paris (1856)
Dawson, C.: A continuous/discontinuous Galerkin framework for modeling coupled subsurface and surface water flow. Comput. Geosci. 12, 451–472 (2008)
Discacciati, M., Miglio, E., Quarteroni, A.: Mathematical and numerical models for coupling surface and groundwater flows. Appl. Numer. Math. 43, 57–74 (2002)
Discacciati, M., Quarteroni, A.: Navier–Stokes/Darcy coupling: modeling, analysis, and numerical approximation. Rev. Mat. Complut. 22(2), 315–426 (2009)
Evans, L.C.: Partial Differential Equations, 2nd edn. American Mathematical Society, Providence (2010)
Galdi, G.: An Introduction to the Mathematical Theory of the Navier–Stokes Equations. Springer, Berlin (2011)
Helmig, R.: Multiphase Flow and Transport Processes in the Subsurface: A Contribution to the Modeling of Hydrosystems. Springer, Berlin (1997)
Iliev, O., Laptev, V.: On numerical simulation of flow through oil filters. Comput. Vis. Sci. 6(2–3), 139–146 (2004)
Jackson, A.S., Rybak, I., Helmig, R., Gray, W.G., Miller, C.T.: Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 9. Transition region models. Adv. Water Res. 42, 71–90 (2012)
Jovanović, V., Rohde, C.: Error estimates for finite volume approximations of classical solutions for nonlinear systems of hyperbolic balance laws. SIAM J. Numer. Anal. 43(6), 2423–2449 (2006)
Kim, S., Russel, W.B.: Modelling of porous media by renormalization of the Stokes equations. J. Fluid Mech. 154, 269–286 (1985)
Kollet, S.J., Maxwell, R.M.: Integrated surface-groundwater flow modeling: a free-surface overland flow boundary condition in a parallel groundwater flow model. Adv. Water Res. 29, 945–958 (2006)
Layton, W., Schieweck, F., Yotov, I.: Coupling fluid flow with porous media flow. SIAM J. Numer. Anal. 40, 2195–2218 (2003)
Layton, W., Tran, H., Trenchea, C.: Analysis of long time stability and errors of two partitioned methods for uncoupling evolutionary groundwater - surface water flows. SIAM J. Numer. Anal. 51, 248–272 (2013)
LeFloch, P., Rohde, C.: High-order schemes, entropy inequalities, and nonclassical shocks. SIAM J. Numer. Anal. 37(6), 2023–2060 (2000)
Lu, Y.G.: Convergence of solutions to nonlinear dispersive equations without convexity conditions. Appl. Anal. 31(4), 239–246 (1989)
Lundgren, T.S.: Slow flow through stationary random beds and suspensions of spheres. J. Fluid Mech. 51, 273–299 (1972)
Manning, R.: On the flow of water in open channels and pipes. Trans. Inst. Civ. Eng. Irel. 20, 161–207 (1891)
Martys, N., Bentz, D.P., Garboczi, E.J.: Computer simulation study of the effective viscosity in Brinkman’s equation. Phys. Fluids (1994-present) 6(4), 1434–1439 (1994)
Mosthaf, K., Baber, K., Flemisch, B., Helmig, R., Leijnse, A., Rybak, I., Wohlmuth, B.: A coupling concept for two-phase compositional porous-medium and single-phase compositional free flow. Water Resour. Res. 47, W10,522 (2011)
Murat, F.: L’injection du cône positif de \(H^1\) dans \(W^{1,q}\) est compacte pour tout \(q<2\). J. Math. Pures Appl. (9) 60(3), 309–322 (1981)
Richards, L.A.: Capillary conduction of liquids through porous mediums. J. Appl. Phys. 1, 318–333 (1931)
Rivière, B., Yotov, I.: Locally conservative coupling of Stokes and Darcy flow. SIAM J. Numer. Anal. 42, 1959–1977 (2005)
Rybak, I., Magiera, J., Helmig, R., Rohde, C.: Multirate time integration for coupled saturated/unsaturated porous medium and free flow systems. Comput. Geosci. 19(2), 299–309 (2015)
Rybak, I., Magiera, J.: A multiple-time-step technique for coupled free flow and porous medium systems. J. Comput. Phys. 272, 327–342 (2014)
Schonbek, M.E.: Convergence of solutions to nonlinear dispersive equations. Commun. Partial Differ. Equ. 7(8), 959–1000 (1982)
Serre, D.: Systems of Conservation Laws 1: Hyperbolicity, Entropies. Cambridge University Press, Shock Waves (1999)
Sochala, P., Ern, A., Piperno, S.: Mass conservative BDF-discontinuous Galerkin/explicit finite volume schemes for coupling subsurface and overland flows. Comput. Methods Appl. Mech. Eng. 198, 2122–2136 (2009)
Sulis, M., Meyerhoff, S.B., Paniconi, C., Maxwell, R.M., Putti, M., Kollet, S.J.: A comparison of two physics-based numerical models for simulating surface water-groundwater interactions. Adv. Water Res. 33, 456–467 (2010)
Takahashi, T.: Debris Flow: Mechanics, Prediction and Countermeasures. CRC Press, Boca Raton (2014)
Temam, R.: Navier–Stokes Equations: Theory and Numerical Analysis. AMS (2001)
van Duijn, C.J., Peletier, L.A., Pop, I.S.: A new class of entropy solutions of the buckleyleverett equation. SIAM J. Math. Anal. 39(2), 507–536 (2007)
Vreugdenhil, C.B.: Numerical Methods for Shallow-Water Flow. Kluwer, Dordrecht (2010)
Yen, B.: Open channel flow resistance. J. Hydraul. Eng. 128(1), 20–39 (2002)
Author information
Authors and Affiliations
Corresponding author
Additional information
The authors would like to thank the German Research Foundation (DFG) for financial support of the project within the International Research Training Group 1398 Nonlinearities and Upscaling in Porous Media and the DFG grant RY 126/2-1.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Magiera, J., Rohde, C. & Rybak, I. A Hyperbolic–Elliptic Model Problem for Coupled Surface–Subsurface Flow. Transp Porous Med 114, 425–455 (2016). https://doi.org/10.1007/s11242-015-0548-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-015-0548-z