1 Introduction

In order to quantitatively describe the process of liquid moisture transfer in capillary-porous building materials and to assess the rising damp extent of shielding constructions, the dependence of liquid transfer coefficient on a material’s moisture content, that in turn depends on its capillary-porous structure properties, should be known. When evaluating this dependence using common methods, time-consuming and labor-consuming experiments should be carried out, as well as expensive tools and complex calculation procedures should be applied. The methods for evaluation of the dependence of liquid transfer coefficient upon material’s moisture content were given, among others by Freitag et al. (1995), Nikitsin et al. (2004), Roels and Carmeliet (2006), Bezpalko (2009), Gaffner (2011). The formulated models assume that capillary-porous structure of a sample is uniform and isotropic. However, not every building material meets such conditions; the exceptions can be ceramic wall products formed by means of plastic technology. Very complex movements of plastic mass made of loam in a mold contribute to the appearance of a stratification parallel to the press axis in molded band with a given profile. As a consequence, final product is of axial texture, which causes anisotropy of physical properties of the ceramic material.

The paper deals with the quantitative evaluation of the anisotropy of ceramic wall products made of plastic mass as influenced on capillary parameters and coefficient of capillary moisture transport. Measures characterizing the material’s ability to absorb liquids in a direction of a product’s molding and perpendicularly were experimentally determined, and then liquid transfer coefficient was calculated using these indicators and applying a simple, yet accurate and theoretically justified method developed by the Authors.

2 Theory and Experimental Methods

To understand the capillary transport of moisture in capillary-porous building materials, grounds of capillary theory discussed for a single cylindrical capillary can be quoted, which is described, among others in Janz (1997), Pogorzelski (1987), Żygadło and Piasta (1989). According to this theory, the capillary absorption process in vertical, cylindrical capillary made of hydrophilic material, can be approximately described by following dependence:

$$\begin{aligned} \tau =M_0 x^{2}, \end{aligned}$$
(1)

where \(\tau \) duration of capillary absorption since the moment of contact of lower sample surface with water (s), \(x\) distance traveled by water front in capillary during time \(\tau \) (height of capillary absorption) (m).

It follows from Eq. (1) that time \(\tau \), during which a water column in vertical cylindrical capillary rises up to the height \(x\), is proportional to the squared height. In this equation, the proportionality coefficient characterizes the ability of the capillary in question to resist the transfer, which can be described with the following formula:

$$\begin{aligned} M_0 =\frac{2\eta }{r_0 \sigma \cos \theta }, \end{aligned}$$
(2)

where \(\eta \) dynamic viscosity of water (Pa\(\cdot \)s), \(r_{0}\) mean capillary radius (m), \(\sigma \) water surface tension on liquid–gas interphase (N/m), \(\theta \) contact angle.

Equation (2) means that the penetration resistance increases along with the increase of dynamic viscosity of water and contact angle, as well as when surface tension and capillary radius decrease.

After some time, the process of capillary transport of moisture in a material disappears (internal friction and inertial forces tend to zero) and at the moment \(\tau =\tau _\mathrm{max}\) the capillary transfer forces compensate only the weight of water column of height \(x=h_\mathrm{max}\). The equilibrium prerequisite results in

$$\begin{aligned} h_\mathrm{max } =\frac{2\sigma \cos \theta }{r_0 \rho _\mathrm{w} g}, \end{aligned}$$
(3)

where \(\rho _\mathrm{w}\) density of liquid (kg/m\(^{3}\)), \(g\) gravitational acceleration (m/s\(^{2}\)).

Equation (1) is valid only for a unit capillary if the moisture transfer height \(x\) in a capillary is much lower than water column height in this capillary at the equilibrium \(h_\mathrm{max}\).

In a viewpoint of the obvious differences between the unit capillary and the real material, Eq. (1) cannot be directly applied to the quantitative description of the process of capillary moisture transfer in capillary-porous building materials without adopting any additional assumptions. However, this relationship can serve as a basis for developing the mathematical models for the quantitative description of the one-way water uptake process by dry samples from capillary-porous building materials.

It is known that at sufficiently high samples (homogeneous isotropic and unlimited half-space is considered in theoretical research) with one-way capillary water uptake and at the moment \(\tau \), the boundary between dry and moist part of the sample is fuzzy, and the humidity at the height of the sample varies from \(w_\mathrm{k } (\hbox {kg}/\hbox {m}^{3})\), which is observed at full capillary saturation, through initial value \(w_{0}\), that is equal to 0 for absolutely dry samples. Typically, this relationship is called the moisture profile \(w(x, \tau )\), and its typical form is represented on Fig. 1 as the solid line.

Fig. 1
figure 1

Typical moisture profile \(w(x,\tau )\) for a sample with unlimited height \(x=\infty \) at capillary water uptake (solid line) and replacing equivalent profile (dashed line)

Full size image

It should be noted that the capillary liquid transport does not take place through all open pores and capillaries of the material. Part of the open porosity, which is filled up with water during capillary saturation process, is related to as active porosity:

$$\begin{aligned} \varPhi _a =\frac{w_\mathrm{k} }{\rho _\mathrm{w} }. \end{aligned}$$
(4)

If active porosity of a given sample is visualized as a bunch of cylindrical capillaries with the same radius and parallel to axis of the sample, then analogously to Eq. (1), it can be written for applied geometric model:

$$\begin{aligned} \tau =Mx_\mathrm{e}^2 , \end{aligned}$$
(5)

where \(x_\mathrm{e}\) is the distance traveled by liquid meniscus during the uptake in narrow capillaries of the same radius for time \(\tau \). Moisture profile for the model sample is a rectangle, the area of which equals to \(w_\mathrm{k}\cdot x_\mathrm{e}\). To ensure the equivalence of the material sample with its model from a viewpoint of a liquid transport, area of the rectangle should be equal to the area under the solid line \(w(x, \tau )\) for tested sample:

$$\begin{aligned} w_\mathrm{k} x_\mathrm{e} =\int \limits _0^x {w(x,\tau )\mathrm{d}x}. \end{aligned}$$
(6)

Graphical illustration of this equation is presented on Fig. 1.

Therefore, if at the moment \(\tau \), the moisture profile \(w(x,\tau )\) is known, then equivalent limit \(x_\mathrm{e}\) between dry and moist fragment of the sample with moisture content \(w=w_\mathrm{k}\) can be calculated using Eq. (6). Then, Eq. (5) can be helpful in calculating the coefficient \(M (\hbox {s}/\hbox {m}^{2}\)) that characterizes the ability of the sample and its geometrical model to oppose the capillary water transfer.

If radius of the unit capillary \(r_{0}\) is replaced with equivalent radius \(r_\mathrm{e}\) in Eq. (2), following condition should be met:

$$\begin{aligned} M_0 =M, \end{aligned}$$
(7)

which serves for determining the equivalent radius value:

$$\begin{aligned} r_\mathrm{e} =\frac{2\eta }{\sigma \cdot \cos \theta \cdot M}. \end{aligned}$$
(8)

Because length of a tortuous distance \(l_\mathrm{k}\) traveled by a water molecule considerably exceeds the length of the segment \(l\) of the sample height in a direction of the axis \(x\), mean hydraulic (conditional) radius of the material \(r_\mathrm{k}\) should greatly surpass value \(r_\mathrm{e}\) in order to provide with a uniform moisture stream within the sample and its model. As it was reported by Nikitin and Backiel-Brzozowska (2008), the following dependence is valid:

$$\begin{aligned} r_\mathrm{k} =r_\mathrm{e} \xi ^{2}(w_\mathrm{k} ), \end{aligned}$$
(9)

where \(\xi (w_\mathrm{k})=l_\mathrm{k}/l\) is defined as the tortuosity of capillaries filled with water at the state of capillary saturation. According to Nikitsin and Backiel-Brzozowska (2013), tortuosity of capillaries \(\xi (w_\mathrm{k})\) can be evaluated from the formula:

$$\begin{aligned} \xi (w_\mathrm{k} )=\frac{\varPhi _a \left( {w_\mathrm{k} } \right) }{\left\{ {\frac{1}{2}+\sin \left[ {\frac{\arcsin \left( {2\varPhi _a \left( {w_\mathrm{k} } \right) -1} \right) }{3}} \right] } \right\} ^{2}}. \end{aligned}$$
(10)

Coefficient of capillary uptake resistance \(M (\hbox {s}/\hbox {m}^{2})\) along with water sorption coefficient \(A\) \((\hbox {kg}/(\hbox {m}^{2}\,\hbox {s}^{0.5})\)) and water penetration coefficient \(B (\hbox {m}/\hbox {s}^{0.5}\)) are connected with the following proportion:

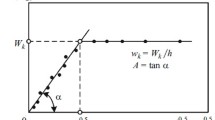
$$\begin{aligned} M=\left( {\frac{w_\mathrm{k} }{A}} \right) ^{2}=\frac{1}{B^{2}}. \end{aligned}$$
(11)

Descriptions of terms \(A\) and \(B\) have been presented in numerous researches, including ISO 9346:2007. Among indicators in Eq. (11), the issue can be solved in the simplest and most accurate way by determining the water sorption coefficient \(A\) and moisture content of the material at capillary moisture content \(w_\mathrm{k}\). To do this, performing special experiment makes possible to observe the changes in moisture weight \(m\) in the sample of height \(x=h\) and constant cross section area \(a\) during one-way capillary moisture uptake. Plot illustrating results of such experiment is presented on Fig. 2.

Fig. 2
figure 2

Determination of water sorption coefficient \(A\) and moisture of the material at capillary moisture saturation state \(w_\mathrm{k}\) on a basis of data upon a kinetics of one-way moisture uptake in sample of height \(h\) and constant cross section area \(a\) (experimental data marked with dots).

Full size image

Height of the tested sample \(h\) should be selected in such a way that rising moisture front could reach the upper part of the sample during convenient time \(\tau \), and its moisture content at that level was slightly deviated from value \(w_\mathrm{k}\). According to Fig. 1, it means that height of the sample \(h\) should be significantly lower than value \(x_\mathrm{e}\), which is dependent on time \(\tau \) and determined from the Eq. (6). It should be, however, taken into account that shortening the experiment duration at the expense of sample height reduction can result in lower accuracy of measured parameters.

Based on a spectrum of experimental data achieved by the Authors during determining the water sorption coefficient \(A\) for silicate product samples made of lime-sand and autoclaved cellular concrete (ACC) samples at commonly assumed height of the sample about 4–9 cm (or 23–25 cm for exceptional cases), about 5 cm high samples can be recommended. Then, according to Eq. (3), conditional radius of the capillary, in which moisture uptake is complete under ambient conditions, amounts to \(0.3\cdot 10^{-3}\,\hbox {m} (300\,\upmu \hbox {m})\). Such value also corresponds to the upper limit of the range measured using mercury porosimetry. Additional properties of the method for determining \(A\) and \(w_\mathrm{k}\) are presented, among others, in other publications (Janz 1997; Nikitsin et al. 2005).

Having determined the \(M\) coefficient applying equations presented in other works (Künzel 1995 and Nikitsin, Backiel-Brzozowska 2011), liquid transfer coefficient \(D_\mathrm{w}\), that is referred to as moisture diffusivity in PN-EN ISO 9346:2007, can be calculated. Empirical formula presented by Künzel (1995) and useful for calculating \(D_\mathrm{w}\) is very approximate, hence more accurate and theoretically justified formula proposed by Künzel (1995) and by Nikitsin and Backiel-Brzozowska (2012) will be applied here:

$$\begin{aligned} D_\mathrm{w} =\frac{2\xi ^{2}(w_\mathrm{k} )b(s)}{M\xi (w)}, \end{aligned}$$
(12)

in which \(\xi (w)\) is capillary tortuosity at real value of the moisture content of a material \(w\le w_\mathrm{k}\), while \(b(s)\) is dimensionless function dependent on the degree of active porosity saturation \(\varPhi _\mathrm{a}\) for the mobile liquid:

$$\begin{aligned} s=\frac{w}{w_\mathrm{k} }, \end{aligned}$$
(13)

At known value \(s\), function \(b(s)\) can be evaluated from the plot presented by Nikitsin and Backiel-Brzozowska (2012) or on a base of that plot approximation:

$$\begin{aligned} b(s)=5.034\cdot 10^{-2}\cdot s^{0.2405}+\frac{0.0259\cdot s}{1.027-s}. \end{aligned}$$
(14)

Tortuosity of capillaries \(\xi (w)\) is determined using Eq. (10) after replacing the active porosity \(\varPhi _\mathrm{a}\) with the product \(\varPhi _\mathrm{a}\cdot s\). This is the experimental procedure for determining parameters \(A\) and \(w_\mathrm{k}\) for ceramic building products and products made of other materials in two perpendicular directions, and thus the influence of anisotropy of products on the moisture diffusivity coefficient \(D_\mathrm{w}\) can be assessed after evaluating the latter parameter.

3 Experimental and Discussion

Material for comparative experiments consisted of random samples in a form of non-burned bricks made of plastic mass from Building Ceramics Lewkowo. Four rectangular prisms of dimensions about \(65\times 55\times 55\,\hbox {mm}\) were cut off from each semi-finished product (Fig. 3).

Fig. 3
figure 3

Cutting off the ceramic samples from non-burned brick

Full size image

Prepared samples were burned in electric furnace applying \(2 \,^{\circ }\hbox {C}/\hbox {min}\) warming rate up to the highest necessary temperature, in which material was stored for 2 hours and subsequently cooled along with the furnace. One part consisted of eight randomly selected samples was subject to \(850 \,^{\circ }\hbox {C}\), while the other (also eight samples) to 1,050 \(^{\circ }\hbox {C}\) of burning. Upper and lower burning temperature limits were set up on a basis of thermal properties of loam from Lewkowo Stare deposit. The loam characteristics are presented elsewhere (Backiel-Brzozowska 2004). Sand of 0.37 mm average granulation was used as leaning additive. Content of the sand was 15 % of dried loam.

Kinetics of the one-way capillary moisture transfer within samples in a direction of the product molding as well as perpendicularly to this direction was observed after determining the density of these samples. At first all samples were dried in temperature \(105 \,^{\circ }\hbox {C}\). Directly after cooling, lateral surfaces were insulated with paraffin and the initial masses of samples were set. Next samples were placed in the tray with the distilled water so that immersing them did not exceed 1 cm. Capillary pulling up occurred only through the bottom, unsecured surface of the sample. The change of mass of samples in the time was determined with the accuracy 0.01 g. Every measured value of the increase in mass was divided by the surface area of cross sections of the sample. The increase of the capillary moisture was illustrated in function of a square root of time. The kinetics of one-way moisture uptake for one of samples is shown in Fig. 2. Analogous results were achieved for remaining samples. Water sorption coefficient \(A\) and moisture content at capillary saturation state \(w_\mathrm{k}\) were determined as it is shown in Fig. 2 and capillary uptake resistance coefficient \(M\) was calculated using Eq. (11), while capillary tortuosity applying Eq. (10). Then data for 4 samples were averaged. Arithmetic mean values from results of measured and calculated parameters are presented in Table 1.

Table 1 Mean apparent density \(\rho _{0}\), sorption coefficient \(A\), capillary water uptake resistance \(M\), moisture content at capillary moisture saturation \(w_\mathrm{k}\), capillary tortuosity at saturation \(\xi (w_\mathrm{k})\), and partial saturation state \(\xi (0,5w_\mathrm{k})\) for four random ceramic brick samples
Full size table

Table 1 reveals that for considered samples, mean indicators of capillary uptake \(A\) and \(M\) most significantly depend on a direction the process runs to. In a direction perpendicular to the texture layers, samples are characterized by the lowest possible rate of capillary water transfer \(A\) and by the highest resistance of the uptake (coefficient \(M)\) as compared to those, for which capillary uptake process was observed in parallel direction to the texture layers (molding direction). This is typical for products with clear and stratified texture. The moisture of samples at the capillary saturation \(w_\mathrm{k}\), value of which decreases along with the burning temperature, varies less significantly, which is completely consistent with the existing knowledge. Direction of the moisture transport also affects the \(w_\mathrm{k }\)value. It was recorded that \(w_\mathrm{k}\) in the product’s molding direction exceeded values that were be determined for perpendicular direction. Because changes in \(w_\mathrm{k}\) occur within quite narrow range, oscillations of capillary tortuosity values \(\xi (w_\mathrm{k})\) are also slight. A comparison of mean values for \(w_\mathrm{k}\) determined for samples burned at temperatures \(850\) and 1,050 \(^{\circ }\hbox {C}\) has shown that for 0.05 level of significance the difference between these two mean values cannot be considered statistically significant, which means that with 0.95 probability \(w_\mathrm{k}\) does not depend on the direction of measurement.

Based on data from Table 1 and using Eq. (12) at saturation degrees of \(s=0.5\) and \(s=1\), moisture diffusivity \(D_\mathrm{w}\) was calculated, and then coefficient \(K_\mathrm{a}\) was determined, which allowed for evaluating how much the moisture diffusivity in the molding direction \(D_\mathrm{w\vert }\) exceeds this coefficient perpendicularly to the molding direction \(D_\mathrm{w-}\), hence anisotropy of ceramic products was characterized from a viewpoint of capillary moisture transport:

$$\begin{aligned} K_\mathrm{a}=D_\mathrm{w\Vert } / D_{\mathrm{w}^\bot }. \end{aligned}$$
(15)

The anisotropy coefficient \(K_{a}\) was evaluated both for \(850 \,^{\circ }\hbox {C}\) and 1,050 \(^{\circ }\hbox {C}\) temperatures, which was presented in Table 2. Coefficient \(K_{a}\) is a random value. Its variation can be characterized by the variation coefficient calculated as the ratio of the measurement error (standard deviation) to the average value of the measurement. In our experiment, the coefficient of variation is 0.139 for samples burned at \(850\,^{\circ }\hbox {C}\) and 0.095 for samples burned at 1,050  \(^{\circ }\hbox {C}\), respectively.

Table 2 Coefficient \(K_\mathrm{a}\) values at different degrees of capillary saturation \(s\) and burning temperature
Full size table

Table 2 shows that from a viewpoint of the capillary moisture transfer, anisotropy of building ceramics is very significant. At considered values of capillary saturation degrees, anisotropy coefficient \(K_\mathrm{a}\) is not changed in practice, and at the same time, elevating the burning temperature from 850 to 1,050 \( ^{\circ }\hbox {C}\) results in a double decrease of coefficient \(K_\mathrm{a}\). Such substantial difference can be accounted for the fact that large amounts of glassy phase are produced at 1,050  \(^{\circ }\hbox {C}\) and stratified texture of the ceramic product is blurred. Nevertheless, the layer texture of the sample remains also when it is burned at 1,050 \(^{\circ }\hbox {C}\), which is confirmed by considerable value of coefficient \(K_\mathrm{a}=3.791\). As it was proven by computer simulation results presented by Rahman Ali et al. (2005), ten-fold change in the moisture diffusivity coefficient \(D_\mathrm{w}\) results in that moisture content of a tested shielding construction exposed to weather conditions (taking into account rainfall) may be changed around two-fold. That difference for here tested ceramic building materials may reach even \(K_\mathrm{a}\approx 7.5\) (see Table 2).

Accepting that values of \(w_\mathrm{k}\) do not depend on direction of measurement, then the Eq. (15) in accordance with the Eq. (12) takes the following form

$$\begin{aligned} K_\mathrm{a} =\left( {{A_ \Vert }/A\bot } \right) ^{2}. \end{aligned}$$
(16)

As it has already been mention, the determination of water sorption coefficient for different capillary-porous materials is simple, it does not require a lot of work and gives accurate results.

The anisotropy discussed in this work should be considered for other building products characterized by a presence of the layered texture. For example, it is possible to rank raw materials from the upper decks of sedimentary rocks used as structural and finishing materials. To confirm the above-mentioned, we will use experimental data received by Roels (2000). The investigation of the water capillary transport was performed using a French layered oolitic limestone. 120 cube-shaped samples of size \(14\times 14\times 14\) mm cut from limestone plates of size \(180\times 216\times 14\) mm were investigated to evaluate main characteristics of the water capillary transport of the material. Values of the capillary moisture content \(w_\mathrm{k}\) and the water sorption coefficient \(A\) were obtained from imbibition experiments on oven dry samples performed parallel and perpendicular to the bedding. In the result, it turned out that the medium density of specimens was \(1660.5\,\hbox {kg}/\hbox {m}^{3}\), the saturation moisture was \(381.9\,\hbox {kg}/\hbox {m}^{3}\) (open porosity 38.19 %), and the capillary moisture \(w_\mathrm{k}=159.6\,\hbox {kg}/\hbox {m}^{3}\) (active porosity 15.96 %). In addition, the capillary moisture received by imbibition parallel and perpendicular to the bedding can be regarded as identical within the limits of the statistical error. However, values of the water sorption coefficient depend on direction in which capillary imbibition took place. The mean value of this coefficient parallel to the bedding was \(0.085\,\hbox {kg}/\hbox {m}^{2}\,\hbox {s}^{0.5 }\) and perpendicular to the bedding was \(0.054\,\hbox {kg}/\hbox {m}^{2}\,\hbox {s}^{0.5}\). In the considered case calculation according to the formula (15) including models (10), (11), (12), (13), and (14) showed the mean value of the anisotropy coefficient \(K_\mathrm{a}=2.478\).

Apart from that, after analyzing experimental data for 120 specimens, Roels (2000) divided specimens into two subgroups significantly different from each other in the character of microstructure and in values of the capillary moisture \(w_\mathrm{k}\) and water sorption coefficient \(A\). Texture of the first subgroup of samples (91 samples) can be considered as layered, because the value of the anisotropy coefficient \(K_\mathrm{a}=3.472\). In some individual samples of this subgroup (7 samples) the achieved values range from 6.868 to 85.21. For the second subgroup of samples (29 samples), cut from the central part of the limestone plate, it is possible to characterize the texture as chaotic, since calculated value of the anisotropy coefficient is close to 1 \((K_\mathrm{a}=0.91)\).

This way it was shown that materials from the upper decks of sedimentary rocks and building ceramics are characterized by a significant anisotropy in terms of water capillary absorption, which should be taken into consideration in construction and finishing works.

The Authors have also been interested in comparing the average conditional radius of capillaries, through which fluid transport is realized, with mean conditional radius of open porosity capillaries determined by means of mercury porosimetry. To do this, the porosimetric measurements of ceramic material samples burned at 850 and 1,050 \(^{\circ }\hbox {C}\) were performed. Mean value of two radii \(\bar{{r}}_\mathrm{k} =~0.104\,\upmu \hbox {m}\) was determined at burning temperature of \(850\,^{\circ }\hbox {C}\) as well as \(\bar{{r}}_\mathrm{k} =~0.150\,\upmu \hbox {m}\) at 1,050 \(^{\circ }\hbox {C}\), which corresponded to data from numerous publications, e.g., Cultrone et al. (2005), or Brylska and Hejmo (2003). In addition, calculations were made on a base of Eqs. (8), (9), and (10) and using data from (Janz 1997) by assuming the contact angle \(\theta =60\,^{\circ }, \sigma =0.07275\,\hbox {N}/\hbox {m}\), and dynamic viscosity \(\eta =0.001\,\hbox {Pa}\cdot \hbox {s}\) at \(20\,^{\circ }\hbox {C}\). Calculations revealed that conditional capillary radius in a molding direction \(r_\mathrm{k}=0.177\,\upmu \hbox {m}\) at \(850\,^{\circ }\hbox {C}\), while \(r_\mathrm{k}=0.110\,\upmu \hbox {m}\) at t = 1,050 \(^{\circ }\hbox {C}\), which are similar values to experimental data. However, in a direction perpendicular to molding, results appeared to be five times lower than empirical data amounting to \(r_\mathrm{k}=0.024\,\upmu \hbox {m}\) \((t=850\,^{\circ }\hbox {C})\) and \(r_\mathrm{k}=0.029\,\upmu \hbox {m}\) ( t \(=\) 1,050 \(^{\circ }\hbox {C})\). Such results could be elucidated by the fact that fine particles of material with the total weight of about 1 g are used during porosimetric tests and mercury is pumped in a direction of the weakest resistance, i.e., molding direction. Therefore, the results of mercury porosimetry can be used in some way to characterize the porous structure of the material in the molding direction, but it should not be applied in the perpendicular direction. Furthermore, mercury porosimetry does not give any information about the parameters of the active porosity, due to which the capillary moisture transport occurs, and which may be significantly less than the open porosity.

4 Summary

Results of theoretical and experimental studies provide a basis to conclude that the anisotropy of ceramic building products has a significant impact on the indicators characterizing the capillary moisture transfer process. The anisotropy coefficient defined as the ratio of the moisture diffusivity in a direction of product molding to the same coefficient, yet in perpendicular direction, can reach value of 7.5. Ignoring such explicit anisotropy of a product at calculating the moisture content of walls can lead to significant errors. When used for wall constructing, the ceramic building materials should be distributed in the compartments so that the liquid stream can travel perpendicularly to the direction of product molding.

Comparison of mean conditional radii of capillaries involved in liquid transport calculated using proposed equations with data from mercury porosimetry indicated that porosimetric data cannot be applied to characterize the porosity structure of ceramic building materials in a direction perpendicular to the product molding.