Pressure Transient Solutions for Vertically Slotted-Partially Penetrated Vertical Wells in Porous Media

Abstract

In this paper, we present semi-analytical pressure transient solutions for vertically slotted-limited entry or partially penetrated vertical wells. These solutions are needed for interpretation of the pressure transient tests conducted with the Wireline Formation Testing vertically slotted-packer configuration, and in wells with vertically slotted-liner completions. These slots have limited size openings and are vertically placed on a non-permeable cylindrical wellbore in a porous medium. The fluid from the formation is produced through these slots into the wellbore. Pressure transient solutions are not readily available for the uniform pressure boundary condition on the surface of the slots because such a condition creates a mixed boundary value problem, which is difficult to solve. Here we present exact pressure transient solutions obtained under the assumption that the pressure on the slot surface is uniform but a priori unknown, and the rest of the wellbore surface is non-permeable (no-flow condition). Furthermore, we generalize our solution for the case of multiple slots (open sections) on the wellbore for both well testing and Wireline formation tester packer modules. Our solutions are compared with the existing solutions. A new formula for obtaining the drawdown horizontal mobility is presented for anisotropic media.

1 Introduction

Pressure transient tests are conducted along the wellbore to obtain reservoir pressure and a discrete permeability (horizontal and vertical permeabilities) distribution with the wireline formation testers (WFT), shown in Fig. 1 (Kuchuk et al. 2010; Zimmerman et al. 1990). A wireline formation tester consists of a number of modules and allows an unlimited number of formation pressure measurements, formation testing, and multiple formation fluid sampling. The tool is capable of conducting interval pressure transient tests (IPTT) using the wireline conveyance systems.

Fig. 1

WFT Packer-Probe tool combination with the formation resistivity images along the wellbore: the FMI image (left) shows low-porosity stylolite streaks (white) separated and the FMI image (right) shows a multiple-fractured zone and a faulted zone at the bottom

Wireline Formation Testing (WFT) (Zimmerman et al. 1990; Kuchuk et al. 2010) tools are nowadays provided by several companies, and come with widely varying characteristics in terms of size, weight, pressure and temperature ratings, power requirements, measurement devices specifications, pumping power, etc. As we stated above, WFT tools offer these basic functions along the wellbore: (1) measure formation pressure via short pretests, (2) perform pressure transient tests, (3) perform single and multipoint interval (interference) tests, (4) make flow rate measurements, (5) take formation fluid samples and provide basic downhole fluid analysis, and (6) conduct stress tests. To perform all these functions, WFT tools have many modules that provide hydraulic and electrical powers, pressure gauge carries, sampling bottles and chambers, downhole fluid analyzer, and pumps for production/injection from the formation into the wellbore or visa versa. The conventional small-area sink probe (also sometimes referred to as the standard single probe) has been the main WFT producing and testing unit from the beginning, and has expanded and modified (dual-packer, guard probe, etc.) over the years.

For the purpose of pretests and pressure transient testing, the most important components of a WFT string are the probes or dual-packers (Fig. 1) through which the flow from the formation into the tool string takes place, and where both pressure and flow rate are recorded. Different types of probes and dual-packers exist and can be assembled in different ways. Beyond these essential elements, other modules also are necessary to perform the flow operations, such as pumps, power modules, sample chambers, etc. The packer module has two packer elements that are inflated to isolate about 1 m (3.3 ft) wellbore interval, as shown in Fig. 1. Because a large section of the sandface is open to flow between two packer elements, the production interval of the formation is several thousand times larger than that of conventional probes. Unlike the flow geometry of conventional probes, the radial symmetry about the wellbore axis is maintained with the dual-packer geometry during the flow in laterally anisotropic homogenous reservoirs, and is slightly distorted in vertically anisotropic systems. Therefore, the dual-packer module is very useful for conducting pressure transient tests in heterogeneous, layered, shaly, fractured, and vuggy formations. In these type of formations, it is not difficult to sustain the hydraulic isolation of the tested section from the rest of the wellbore, particularly in fractured and vuggy formations. As shown in Fig. 1, the dual-packer envelops a matrix, fracture and/or fault zone and is set against the borehole wall to hydraulically isolate the tested section, see for instance, Zeybek et al. (2002) for the details of packer-probe transient tests that are conducted across the fracture zones.

The dual-packer module is also very useful for WFT testing of unconsolidated formations and condensate reservoirs because the packer production area of the sandface several thousand times larger than the production area of conventional probes (Kuchuk et al. 2010). In other words, the wellbore pressure drop is very small during transient tests and sampling with the parker module compared to that of conventional probes even though production rate could be usually much higher for the parker module. It is well known that the sand production into the wellbore is extremely sensitive to the pressure drop during WFT testing and sampling of unconsolidated formations. Condensate reservoirs are also extremely sensitive to the pressure change. If the wellbore pressure drops below the dewpoint during testing and sampling, liquid condenses from gas and form a condensate bank, which highly complicates both testing and sampling.

In some respects, a dual-packer pressure transient test resembles a small scale DST-type test, although the radius of investigation of a dual-packer pressure transient test is not more than a few tens of feet (10–50 ft). A longer production time will increase the radius of investigation very little because a spherical flow is established in the vicinity of the wellbore due to a small-length production interval, unless the formation is thin. The dual-packer module with one or two probes is also very useful for permeability profiling along the wellbore, particularly in layered reservoirs. For instance, as shown in Fig. 1, the FMI image (left) shows three low-porosity stylolite streaks (white) separated by dark very permeable intervals. The top stylolite streak is particularly patchy. Usually, the stylolite intervals may be thinner than 1 ft, therefore, conventional probes are not suitable to test these stylolite zones. The same figure also shows the FMI image (right), where a multiple-fractured zone and a faulted zone at the bottom can be observed. Again conventional probes are not suitable to test these fractured and faulted zones.

The recently introduced vertically slotted-packer probe (Saturn¹ 3D radial packer module), as shown in Fig. 2, provides a new type of 4-Dimensional pressure transient test data. As shown in Fig. 3, the packer has four rectangular slots with a height of 188 mm (0.6168 ft) and a width of 74.5 mm (0.2444 ft). The tips of each slot are slightly oval-shaped. The four slot packer module is circumferentially equally spaced over the cylindrical surface of the packer element (see Fig. 2). In addition to 4-D pressure transient tests, the slotted-packer module allows us to obtain reliable pressure profiles and fluid samples in difficult reservoir and well conditions, such as low-permeability and unconsolidated formations, heavy oil and near-critical fluids, and rugose boreholes (Wireline-Schlumberger 2012).

Fig. 2

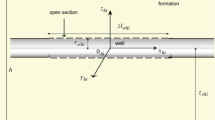
Schematic of the vertically slotted-packer module: a Vertical flow position of probes. b Flow distribution in the formation through four slots, after Wireline-Schlumberger (2012)

Fig. 3

Schematic of the vertically slotted-packer module with its dimensions, where the origin the coordinate system is on the well axis at $\left\{ x=r_{w}, y= 0, z=0 \right\}$ which corresponds to the center of the probe

Recently Al-Otaibi et al. (2012) and Flores de Dios et al. (2012) presented two papers on the applications of the slotted-packer module. The first paper dealt with downhole fluid sampling and transient tests in low mobility carbonate formations. They used a commercial numerical simulator and an analytical model (Kuchuk 1994; Wilkinson and Hammond 1990), which is a transient solution for a partially penetrated well to interpret tests. Of course, this solution does not accurately model the early time behavior of the slotted-packer module. The Flores de Dios et al. (2012) paper mainly dealt with taking downhole fluid samples using the slotted packer module in a heavy-oil unconsolidated-sandstone reservoir ($\approx 8^{\circ }$ API).

The testing, solutions, and interpretation of 2D and 3D interval pressure transient tests (IPTT) with the dual-packer module and with one- or two-probe combination (Fig. 1) were given by Pop et al. (1993), Kuchuk (1994, 1998), Kuchuk and Onur (2003), Onur et al. (2004a, b), Onur and Kuchuk (1999), Kuchuk et al. (2010). Solutions and interpretation models are not available for the 4D IPTTs conducted with the vertically slotted-packer tool, as shown in Fig. 2. With appropriate solutions, slotted-packer 4D IPTTs may provide an estimation of permeabilities in the $x$, $y$, and $z$ directions.

The earlier solutions for the pressure transient behavior of partially penetrated wells (Odeh 1968; Hantush 1957; Nisle 1958; Brons and Marting 1961) used the line source approximation to derive the finite-length uniform-flux line source solution, from which the wellbore pressure was approximated at the middle point of the open section of the well. The second set of solutions is based on either finite uniform-flux line source approximations with an appropriate equivalent-pressure point (Gringarten and Ramey 1975) or uniform-flux pressure-averaged approximations (Streltsova-Adams 1979; Yildiz and Bassiouni 1990; Kuchuk and Wilkinson 1991; Kuchuk 1994; Wilkinson and Hammond 1990; Ozkan and Raghavan 1991; Biryukov and Kuchuk 2012). The third set of solutions is based on the uniform-pressure boundary condition, whioch is the true wellbore condition, on the surface of the open interval given by Papatzacos (1987a, b), in which they used the prolate spherical coordinates to solve the pressure diffusion equation for partially penetrated wells.. Although it is an exact infinite-conductivity solution, the partially penetration geometry can only be mapped approximately to a prolate spheroid.

Recently Biryukov and Kuchuk (2012) presented exact pressure transient solutions obtained under the assumption that the pressure on the open surface is uniform but a priori unknown, and the rest of the wellbore surface is non-permeable (no-flow condition). Furthermore, they generalize their solution for the case of multiple production sections on the wellbore for both well testing and wireline formation tester packer modules. They compared their solutions with the middle point, equivalent-pressure point, and pressure-averaging solutions given in the petroleum literature. In addition to the recent Biryukov and Kuchuk (2012) paper, a few other papers were also published on selectively perforated and/or completed wells, i.e., wells with multiple production slots (ring slots along the wellbore), specially Spivak and Horne (1983), Larsen (1993), Yildiz and Cinar (1998), Tang et al. (2000), Yildiz (2002a, b, 2004, 2006a, b). The Spivak and Horne (1983) vertically slotted-liner solution, which is obtained from the uniform-flux solution, is somewhat similar to the solutions given in this paper. However, there are some fundamental differences, such as where to evaluate the pressure over the sandface, because it changes for these types of slot-line solutions when the effects of the bottom and top boundary are felt in the wellbore. Furthermore, we consider anisotropic media, while the Spivak and Horne (1983) solution is for isotropic systems. They considered both ring and vertical slots along the wellbore.

In this paper, we develop “exact” solutions to boundary value problems for the slotted-packer module with uniform pressure and uniform-flux inner boundary conditions on the cylindrical surface of a well in a three-dimensional porous medium internally bounded by an impermeable cylindrical wellbore. These solutions are also extended to formations that are bounded by no-flow top and bottom boundaries.

2 Mathematical Model

Let us consider pressure diffusion of a single-phase constant viscosity and slightly compressible fluid in a three-dimensional infinite anisotropic non-deformable homogeneous porous medium bounded by $- \infty <x<\infty$, $- \infty <y<\infty$, and $- \infty <z<\infty$, in which there are no sinks and/or sources. The permeabilities of the media in the principle directions are denoted by $k_{x}$, $k_{y}$, and $k_z$. It is assumed that fluid viscosity $\mu$, porosity $\phi$, and total compressibility $c_t$ are pressure- and time-invariant and uniform throughout the reservoir. In this paper, we assume that the principle axes of the permeability tensor coincide with the principle axes of the coordinate system we use. If this is not the case, for a given formation, we can always find a new coordinate system whose axes coincide with the permeability tensor. However, for deviated wells in formations with horizontal layers, or vertical, deviated, or horizontal wells in tilted formations, the coordinate transformation is complicated (Besson 1990; Onur et al. 2004a, 2011).

Single-phase pressure diffusion in an anisotropic homogeneous porous medium (shown in Fig. 3), defined above, can be described by the following partial differential equation (Muskat 1937)

$$\begin{aligned} \lambda _{x} \frac{\partial ^2\mathcal{P}}{\partial x^2}+ \lambda _{y} \frac{\partial ^2\mathcal{P}}{\partial y^2}+ \lambda _{z} \frac{\partial ^2\mathcal{P}}{\partial z^2}= \varphi \frac{\partial \mathcal{P}}{\partial t}, \, \, -\infty <x,y,z<\infty , \,\, t>0, \end{aligned}$$

(1)

subject to the initial condition

$$\begin{aligned} \mathcal{P}(\mathbf {x}, t)= h(\mathbf {x}) \, \,\, \, -\infty <x,y,z<\infty \,, \, \, \, t=0, \end{aligned}$$

(2)

and the outer boundary condition

$$\begin{aligned} \mathcal{P}(\mathbf {x},t) = 0, \, \, x,y,z \rightarrow \pm \infty , \, \, t>0, \end{aligned}$$

(3)

where the spatial position vector is $\mathbf {x}= x \mathrm{{ \mathbf i}} + y \mathrm{{ \mathbf j}} + z \mathrm{{ \mathbf k}}$ and $r = \mid \!\mathbf {x}\!\mid = \sqrt{ x^2+y^2 +z^2 }$, $\mathrm{{ \mathbf i}}$, $\mathrm{{ \mathbf j}}$, and $\mathrm{{ \mathbf k}}$ are the unit vectors in the $x$, $y$, and $z$ directions, respectively. $\mathcal{P}(\mathbf {x},t) = p_0(\mathbf {x}, 0)-p(\mathbf {x}, t)$, $h(\mathbf {x}) = p_0-p(\mathbf {x}, 0)$, $p(\mathbf {x}, 0)$ is the initial pressure distribution imposed at $t\le 0$. For most of our problems, without a loss of generality, $p_0(\mathbf {x}, 0) \equiv p_0$, thus $h(\mathbf {x}) = 0$, where $p_0$ is the initial reservoir pressure. For the MBVPs considered here, we also assume the medium to be transversely anisotropic ($k_x=k_y=k_h$ and $k_z=k_v$), i.e., the permeability varies very little directionally in the horizontal plane, which is reasonable for spatial scales of well testing and wireline formation testers.

The inner boundary conditions of Eq. 1 for the pressure transient problems we considered are of the mixed type. In a mixed boundary value problem (MBVP), we have both the Neumann and Dirichlet boundary conditions imposed on the inner boundary surface. For instance, as shown in Fig. 3, the boundary condition at the open (producing) section of the inner boundary $\partial \varOmega _1$, for which the total volumetric flow rate $q$ is specified, can be written as

$$\begin{aligned} - \iint \limits _{\partial \varOmega _1} \left\{ {\varvec{n}}\cdot {\varvec{T}}\; \mathrm{grad}\left[ \mathcal{P}(\mathbf {x},t) \right] \right\} \mathrm{d}S= q(t) \qquad \mathrm{on} \;\; \partial \varOmega _1, \quad t>0, \end{aligned}$$

(4)

where ${{\varvec{n}}}$ is the outer normal vector to the surface $\partial \varOmega _1$, ${\varvec{T}}$ is the mobility tensor, $q$ is the total flux outwards from the surface $\partial \varOmega _1$, and for the no-flow section of the inner boundary

$$\begin{aligned} \left\{ {\varvec{n}}\cdot {\varvec{T}}\; \mathrm{grad}\left[ \mathcal{P}(\mathbf {x},t) \right] \right\} = 0 \quad \mathrm{on} \;\; \partial \varOmega _2, \quad t>0. \end{aligned}$$

(5)

Furthermore, we also require the pressure (potential) at the open surface $\partial \varOmega _1$ to be uniform (independent of $\mathbf {x}$), which implies that

$$\begin{aligned} \mathcal{P}(\mathbf {x}, t) =\mathcal{P}_{wu} (t) \quad \mathrm{on} \;\; \partial \varOmega _1, \quad t>0. \end{aligned}$$

(6)

The inner boundary conditions specified by Eqs. 4–6 over the surfaces $\partial \varOmega _1$ and $\partial \varOmega _2$ create a mixed boundary value problem.

In this paper, we will present solutions for the constant sandface flow rate ($q_{sf}$). If the flow rate varies, then wellbore pressure at any time can be written from the convolution integral (Muskat 1937), which is Duhamel’s superposition principle, as

$$\begin{aligned} p_w(t)=p_o -\int \limits _0^t q_{sf} \left( \tau \right) \, g_w\left( t-\tau \right) \,\mathrm{d}\tau \end{aligned}$$

(7)

and in the Laplace domain

$$\begin{aligned} \bar{p}_w(s) = \frac{p_o}{s} - \bar{q}_{sf}(s) \bar{g}_w(s), \end{aligned}$$

(8)

where $t$ is time and $g_w$ is the impulse response at the wellbore. If the flow rate is constant at the surface, the wellbore pressure, including skin and storage effects in the Laplace domain, can be written from Eq. 8 (see pages 60–66 of Kuchuk et al. (2010) for the details) as

$$\begin{aligned} \bar{p}_{w}( s)= \frac{p_o}{s} - \frac{q {g}_w(s)}{s\left[ 1+Cs\bar{g}_w(s) \right] }. \end{aligned}$$

(9)

Equation 9 in terms of the dimensionless wellbore impulse response can be written as

$$\begin{aligned} \bar{p}_{wD} (s)= \frac{ \bar{g}_{wD} (s)}{1+C_Ds\bar{g}_{wD} (s)}, \end{aligned}$$

(10)

and in terms of the dimensionless pressure and skin ($S$) as

$$\begin{aligned} \bar{p}_{wD} (s_D)= \frac{ s \bar{p}_{D} (s) +S}{s\left\{ 1+C_D s \left[ s \bar{p}_{D} (s) +S \right] \right\} }, \end{aligned}$$

(11)

where

$$\begin{aligned} p_{wD} = \frac{4 \pi k_h l_w \varDelta p_w }{q \mu }\;, \;\;\; t_D = \frac{k_h t}{\phi \mu c_t r_w^2}\;, \;\;\; C_D = \frac{C}{2 \pi \phi c_t h r^2_w}, \end{aligned}$$

(12)

$C$ is the wellbore storage coefficient, $S$ is the skin factor, and $s$ is the Laplace transform variable that is related to the dimensionless time $t_D$. The above equations in this section provide a general framework for interpreting simultaneously measured pressure data with an arbitrarily varying flow rate as a function of time for both pressure transient well and wireline formation testing. The dimensionless $p_D$s for the formation pressure with the inner boundary conditions of Eq. 1 will be presented in the following sections. If the flow rate is variable at the sandface or surface, the convolution integral given by Eq. 7 and its Laplace transform given by Eqs. 8 should be used to obtain the wellbore pressure. Therefore, to simplify the below derivations, we will assume everywhere that total flow rate $q(t)\equiv q$ is independent of time.

3 Pressure Transient Solutions for Vertical Multiple Slots (Openings) on a Partially Penetrated Well

In the following subsection, we first obtain solutions for a vertical single slot on a partially penetrated well in an unbounded porous medium. Then the solutions will be generalized for both vertically bounded systems and multiple slots, as shown Fig. 3.

3.1 Single-Slot Solution

Consider one of the vertical slots, as shown in Fig. 3, with a thickness (height) of $2l_w$ and a width of $2b$ on a partially penetrated well in an unbounded porous medium. The flow rate $q$ through the slot from the formation into the wellbore is assumed to be constant. The slot surface is equipotential, i.e., is under uniform but a priori unknown pressure change $\mathcal{P}_{wu}(t)=p_0(t)-p_{wu}(t)$, where subscripts $w$ and $u$ denote wellbore and uniform pressure, respectively. The reservoir is assumed to be infinite in all directions (solutions for the reservoir bounded in the vertical direction $z$ will be presented in the next section), with porosity $\phi$ and permeability equal to $k_h$ in horizontal and $k_v$ in vertical directions. The fluid viscosity $\mu$ and total compressibility $c_t$ are constant. Using the mathematical model described above, the single-slot partially penetrated well pressure transient problem can be formulated as

$$\begin{aligned}&\lambda _{h} \frac{1}{r}\frac{\partial }{\partial r}r \frac{\partial \mathcal{P}}{\partial r}+\lambda _{h}\frac{1}{r^2}\frac{\partial ^2\mathcal{P}}{\partial \theta ^2}+ \lambda _{v} \frac{\partial ^2 \mathcal{P}}{\partial z^2} = \varphi \frac{\partial \mathcal{P}}{\partial t},\end{aligned}$$

(13)

$$\begin{aligned}&\mathcal{P}(r,\theta ,z,0)=0,\end{aligned}$$

(14)

$$\begin{aligned}&\mathcal{P}(r_w,z,\theta ,t)=\mathcal{P}_{wu}(t),~\mathrm{for}~ \left| z\right| < l_w~\text{ and }~\left| r_w\theta \right| <b, \end{aligned}$$

(15)

$$\begin{aligned}&\frac{\partial \mathcal{P}}{\partial r}(r_w,\theta ,z,t)=0, ~\mathrm{for}~ \left| z\right| \ge l_w~\text{ or }~\left| r_w\theta \right| \ge b, \end{aligned}$$

(16)

$$\begin{aligned}&\mathcal{P}(r,z,\theta ,t)\rightarrow 0 ~\mathrm{as}~\sqrt{r^2+z^2}\rightarrow \infty , \end{aligned}$$

(17)

$$\begin{aligned}&r_w \lambda _{h} \int _{-b/r_w}^{b/r_w}\int _{-l_w}^{l_w} \frac{\partial \mathcal{P}}{\partial r}(r_w,\theta ,z,t) \mathrm{d}z \mathrm{d}\theta = -q, \end{aligned}$$

(18)

where mobilities are defined as $\lambda _{h} = \frac{k_{h}}{\mu }$ and $\lambda _{v} = \frac{k_{v}}{\mu }$, and $\varphi = \phi c_t$. Due to symmetry about the horizontal and vertical planes, we will further treat the problem only in the domain $\{\theta \ge 0,~z\ge 0\}$. Let us define the following dimensionless variables as

$$\begin{aligned} p_{D}\!=\!\frac{4k_h \pi l_w \mathcal{P}}{q \mu };~~ p_{Dwu}\!=\!\frac{4k_h \pi l_w}{q \mu }\mathcal{P}_{wu};~~ b_D\!=\!\frac{b}{r_w};~~ r_D\!=\!\frac{r}{r_w};~~ z_D=\frac{z}{l_w};~~\nu ^2\!=\!\frac{k_v}{k_h}\frac{r_w^2}{l_w^2},\nonumber \\ \end{aligned}$$

(19)

and $t_D$ is defined in Eq. 12. Then the mathematical model given above can be written in dimensionless form as

$$\begin{aligned}&\frac{1}{r_D} \frac{\partial }{\partial r_D}r_D\frac{\partial p_{D}}{\partial r_D}+\frac{1}{r_D^2}\frac{\partial ^2\mathcal{P}}{\partial \theta ^2}+\nu ^2\frac{\partial ^2 p_{D}}{\partial z_D^2} = \frac{\partial p_{D}}{\partial t_D}, \end{aligned}$$

(20)

$$\begin{aligned}&p_{D}(r_D,\theta ,z_D,0)=0, \end{aligned}$$

(21)

$$\begin{aligned}&p_{D}(1,\theta ,z_D,t_D)=p_{Dwu}(t_D), ~\mathrm{for}~ 0\le z_D<1~\text{ and }~~ 0\le \theta <b_D, \end{aligned}$$

(22)

$$\begin{aligned}&\frac{\partial p_{D}}{\partial r_D}(1,\theta ,z_D,t_D)=0, ~\mathrm{for}~ z_D\ge 1~\text{ or }~\theta \ge b_D,\end{aligned}$$

(23)

$$\begin{aligned}&p_D(r_D,\theta ,z_D,t_D)\rightarrow 0 ~\mathrm{as}~\sqrt{r_D^2+z_D^2}\rightarrow \infty , \end{aligned}$$

(24)

$$\begin{aligned}&\frac{1}{\pi }\int _0^{b_D}\int _0^1\frac{\partial p_{D}}{\partial r_D}(1,\theta ,z_D,t_D) \mathrm{d}z_D= -1. \end{aligned}$$

(25)

Equations 22 and 25 can be further rewritten in the following form

$$\begin{aligned} \frac{\partial p_{D}}{\partial r_D}(1,\theta ,z_D,t_D)=-q_D(\theta ,z_D,t_D), ~\mathrm{for}~ 0\le z_D<1~\text{ and }~~ 0\le \theta <b_D, \end{aligned}$$

(26)

where the function $q_D(\theta ,z_D,t_D)$ is a priori unknown and will be specified later. Using the boundary conditions given by Eqs. 23 and 26, the solution to Eq. 20 can be written as

$$\begin{aligned} p_D(r_D,\theta ,z_D,t_D)=\int _{0}^{t_D}\int _{0}^{1}\int _{0}^{b_D} q_D(\psi ,u,\tau ) \mathrm{G}(r_D,\theta ,\psi ,z_D,u,t_D-\tau ) \mathrm{d}u \mathrm{d}\psi \mathrm{d}\tau , \end{aligned}$$

(27)

where $\mathrm{G}$ is a Green’s function for the corresponding problem which can be expressed as

$$\begin{aligned} \mathrm{G}(r_D,\theta ,\psi ,z_D,u,t_D) =\varTheta (r_D,\theta ,\psi ,t_D)Z(z_D,u,t_D), \end{aligned}$$

(28)

with

$$\begin{aligned}&\varTheta (r_D,\theta ,\psi ,t_D)={\mathcal {L}^{-1}}\left\{ \frac{1}{\sqrt{s}} \sum _{n=0}^{\infty }\left( 1-\frac{\delta _{0n}}{2}\right) \frac{2\mathrm{K}_n(r_D\sqrt{s})\cos (n\theta )\cos (n\psi )}{\mathrm{K}_{n+1}(\sqrt{s})+\mathrm{K}_{n-1}(\sqrt{s})}\right\} , \end{aligned}$$

(29)

$$\begin{aligned}&\mathrm{Z}(z_D,u,t_D)=\frac{2e^{-(z_D-u)^2/(4\nu ^2t_D)}}{\sqrt{\pi t_D}\nu }. \end{aligned}$$

(30)

where

$$\begin{aligned} \delta _{ij} = \left\{ \begin{array}{ll} 1 &{} \text{ when } i=j,\\ 0 &{} \text{ when } i\ne j. \end{array} \right. \end{aligned}$$

(31)

Now let us assume that the slot flux density $q_D(\theta ,u,\tau )$ can be expressed as

$$\begin{aligned} q_D(\theta ,u,\tau )=\frac{1}{\pi }\sum _{i=0}^\infty \sum _{j=0}^\infty c_{ij}(t) \frac{(-1)^iT_{2i}(\theta /b_D)}{\sqrt{b_D^2-\theta ^2}}\frac{T_{2j}(z_D)}{\sqrt{1-z_D^2}}, \end{aligned}$$

(32)

where $T$ is the Chebychev polynomial and the time functions $c_{ij}$ will be determined later. The factor $\frac{1}{\sqrt{b_D^2-\theta ^2}\sqrt{1-z_D^2}}$ reflects the main singularity of the flux density near the slot tips —its divergence—and insures fast convergence of the series.

Substituting $q_D$ in this form into Eq. 27, we can obtain the following expression for the dimensionless reservoir pressure:

$$\begin{aligned} p_D(r_D,\theta ,z_D,t_D)=\sum _{i=0}^\infty \sum _{j=0}^\infty \int _{0}^{t_D}c_{ij}(\tau )\varTheta _{2i}(r_D,\theta ,t_D-\tau ) \mathrm{Z}_{2j}(z_D,t_D-\tau ) \mathrm{d}\tau , \end{aligned}$$

(33)

where

$$\begin{aligned}&\varTheta _{2i}(r_D,\theta ,t_D)={\mathcal {L}^{-1}}\left\{ \frac{1}{\sqrt{s}} \sum _{n=0}^{\infty }\left( 1-\frac{\delta _{0n}}{2}\right) \frac{2\mathrm{K}_n(r_D\sqrt{s})\mathrm{J}_{2i}(n b_D) \cos (n\theta )}{\mathrm{K}_{n+1}(\sqrt{s}) +\mathrm{K}_{n-1}(\sqrt{s})}\right\} ,\end{aligned}$$

(34)

$$\begin{aligned}&\hbox {Z}_{2j}(z_D,u,t_D)=\frac{1}{\sqrt{\pi t_D}\nu }\int _0^\pi e^{-(z_D-\cos \eta )^2/(4\nu ^2t_D)}\cos (2j \eta ) \mathrm{d}\eta . \end{aligned}$$

(35)

Although these functions seem complicated, we will show in Appendix 1 how they can be easily evaluated. It should be observed that the function $p_D(r_D,\theta ,z_D,t_D)$ satisfies the boundary condition defined by Eq. 23. The unknown functions $c_{ij}(t_D)$ and the uniform wellbore pressure $p_{Dwu}(t_D)$ can be obtained from the boundary conditions specified by Eqs. 22 and 25, implying that

$$\begin{aligned} \begin{aligned}&\sum _{i=0}^\infty \sum _{j=0}^\infty \int _{0}^{t_D}c_{ij}(\tau ) \varTheta _{2i}(1,\theta ,t_D-\tau ) \mathrm{Z}_{2j}(z_D,t_D-\tau ) \mathrm{d}\tau =p_{Dwu}(t_D)\\&\qquad \text{ for }~0\le z_D<1~\text{ and }~0\le \theta <b_D, \end{aligned} \end{aligned}$$

(36)

$$\begin{aligned} \displaystyle c_{00}(t_D)=1. \end{aligned}$$

(37)

To solve this system of integral equations efficiently, we must use a finite number of unknown functions $c_{ij}(t_D)$, and discretize Eq. 37 on a set of collocation points. Due to the nature of the basis functions we used to expand $q_D(\theta ,z_D,t_D)$, we suggest to take a set of Chebyshev nodes $z_{Dm}=\cos \left[ \frac{\pi }{2M}\left( 0.5+m\right) \right] ,~m=0,...,M-1$ and $\theta _{k}=b_{Dw}\cos \left[ \frac{\pi }{2K}\left( 0.5+k\right) \right] ,~k=0,...,K-1$. Furthermore, we also discretize Eq. 37 on a uniform time grid $t_{Dv}=v\varDelta t,~v=0,1,...$ assuming that within each interval $[t_{Dv},~t_{D(v+1)}]$, the functions $c_{ij}(t_D)$ are constant and equal to some value $c_{ij}^v$ and $p_{Dwu}(t_D)=p_{Dwu}^v$. Finally, the system of integral equations given by Eqs. 37 and 37 will be reduced to the following system of linear algebraic equations:

$$\begin{aligned}&\sum _{i=0}^{K-1}\sum _{j=0}^{M-1}\sum _{v=0}^Vc_{ij}^vF_{ijmk}^{V-v}=p_{Dwu}^V, \end{aligned}$$

(38)

$$\begin{aligned}&\qquad c_{00}^V=1, \end{aligned}$$

(39)

where

$$\begin{aligned} F_{ijmk}^{V}=\int _{t_{DV}}^{t_{D(V+1)}}\varTheta _{2i}(1,\theta _k,\tau ) \mathrm{Z}_{2j}(z_{Dm},\tau ) \mathrm{d}\tau . \end{aligned}$$

(40)

A technique for the fast and accurate evaluation of the matrix $F_{ijkm}^V$ is given in Appendix 1. Due to the singular nature of $q_D$ expansion, to obtain high accuracy, only a small number of equations must be considered. $K$ and $M$, chosen from the interval 15 to 30 (depending on the value of $\nu$), provide at least 3-4 digits precision for the slot dimensionless pressure $p_{Dwu}$. Also, Eq. 38 is valid only for a uniform time grid, which for some cases might be regarded as a limitation, that is why we propose to adapt it to a time grid with a variable step size. In particular, the following 4-point time scheme is found to be stable and computationally efficient. Consider a sequence of time “subgrids” in the form: $t_{Dv_d}=v2^d,~v=0,~1,~2,~3,~4;~d=d_0,~d_0+1,d_0+2,...,d_{\max }$, and let $v_d$ denote $v$-th point on $d$-th subgrid, then our time scheme can be formalized as follows: First iteration:

$$\begin{aligned} \sum _{i=0}^{K-1}\sum _{j=0}^{M-1}\sum _{v=0}^Vc_{ij}^{v_{d_0}} F_{ijmk}^{(V-v)_{d_0}}=p_{Dwu}^{V_{d_0}},~~c_{00}^{V_{d_0}}=1, V=0, 1, 2, 3, \end{aligned}$$

(41)

d+1-th iteration ($d_0\ll d\ll d_{\max }-1)$:

$$\begin{aligned}&c_{ij}^{0_{d+1}}=\frac{c_{ij}^{0_{d}}+c_{ij}^{1_{d}}}{2}, ~c_{ij}^{1_{d+1}}=\frac{c_{ij}^{2_{d}}+c_{ij}^{3_{d}}}{2},\end{aligned}$$

(42)

$$\begin{aligned}&F_{ijmk}^{0_{d+1}}=F_{ijmk}^{0_{d}}+F_{ijmk}^{1_{d}}, ~F_{ijmk}^{1_{d+1}}=F_{ijmk}^{2_{d}}+F_{ijmk}^{3_{d}},\end{aligned}$$

(43)

$$\begin{aligned}&\sum _{i=0}^{K-1}\sum _{j=0}^{M-1}\sum _{v=0}^Vc_{ij}^{v_{d+1}} F_{ijmk}^{(V-v)_{d+1}}=p_{Dwu}^{V_{d+1}},~~c_{00}^{V_{d+1}}=1, ~V=2,~3. \end{aligned}$$

(44)

Note that here we assume that $v_{d}+1\equiv (v+1)_d$ in the definition of $F_{ijmk}^{V}$ (see Eq. 40). This procedure allows us to obtain the pressure change $p_{Dwu}(t)$ and the coefficients $c_\textit{ij}(t)$ on the gridpoints covering time range $2^{d_0}< t_D <2^{d_{\max }+2}.$ Also in order to avoid missing near wellbore diffusion effects we need $t_{Dmin}=2^{d_0}$ to be much less then $\max \left\{ 1,l_{Dw}\right\}$. We suggest to chose $d_0=-10$ (and thus $t_{Dmin}\approx 10^{-3}$) or less if earlier time data is required. The pressure and $c_\textit{ij}$ values outside the time grid points can be obtained by simple logarthimic interpolation. We can also substitute obtained coefficients $c_{ij}(t)$ into Eq. 33 and easily obtain pressure (and its derivative) at any point of the reservoir.

3.1.1 Pressure-Averaged Uniform-Flux Solution

Next we present a simplified solution based on the assumption that the flux density is uniform on the slot. In this case, the mixed boundary value problem remains the same, except that Eq. 15 should be replaced with

$$\begin{aligned} 4\lambda _{h}b l_w \frac{\partial \mathcal{P}}{\partial r}(r_w,\theta ,z,t) = -q~\mathrm{for}~ \left| z\right| < l_w~\text{ and }~\left| r_w\theta \right| <b, \end{aligned}$$

(45)

which can be rewritten in dimensionless form as

$$\begin{aligned} \frac{\partial p_D}{\partial r_D}(1,\theta ,z_D,t) = -\frac{\pi }{b_D}~\mathrm{for}~ \left| z_D\right| < 1~\text{ and }~\left| \theta \right| <b_D. \end{aligned}$$

(46)

Because Eq. 27 is valid for any flux density distribution, we can use it directly to obtain the pressure response

$$\begin{aligned} p_D(r_D,\theta ,z_D,t_D)=\frac{\pi }{b_D}\int _{0}^{t_D}\int _{0}^{1}\int _{0}^{b_D} \mathrm{G}(r_D,\theta ,\psi ,z_D,u,t_D-\tau ) \mathrm{d}u \mathrm{d}\psi \mathrm{d}\tau . \end{aligned}$$

(47)

Performing integration in the above equation yields

$$\begin{aligned} p_D(r_D,\theta ,z_D,t_D)=\frac{\pi }{b_D}\int _{0}^{t_D} \varTheta _{q}(r_D,\theta ,\tau )Z_{q}(z_D,\tau ) \mathrm{d}\tau , \end{aligned}$$

(48)

where

$$\begin{aligned} \varTheta _{q}(r_D,\theta ,t_D)={\mathcal {L}^{-1}}\left\{ \frac{1}{\sqrt{s}} \sum _{n=0}^\infty \left( 1-\frac{\delta _{0n}}{2}\right) \frac{2\mathrm{K}_{n}(r_D\sqrt{s})\cos (n\theta )}{\mathrm{K}_{n+1}(\sqrt{s})+\mathrm{K}_{n-1}(\sqrt{s})} \frac{\sin (nb_D)}{n}\right\} , \end{aligned}$$

(49)

and

$$\begin{aligned} Z_{q}(z_D,\tau )=2\left[ \mathrm{erf} \left( \frac{1+z_D}{2\nu \sqrt{\tau }}\right) +\mathrm{erf} \left( \frac{1-z_D}{2\nu \sqrt{\tau }}\right) \right] . \end{aligned}$$

(50)

Now we can obtain the dimensionless wellbore pressure by taking the average value of Eq. 48 over the slot surface, which is equal to

$$\begin{aligned} p_{Dwa}(t_D)=\frac{1}{b_D^2}\int _{0}^{t_D} \hat{\varTheta }_{q}(\tau )\hat{Z}_{q}(\tau )\mathrm{d}\tau , \end{aligned}$$

(51)

with

$$\begin{aligned} \hat{\varTheta }_{q}(t_D)={\mathcal {L}^{-1}}\left\{ \frac{1}{\sqrt{s}}\sum _{n=0}^\infty \left( 1-\frac{\delta _{0n}}{2}\right) \frac{2\mathrm{K}_{n}(\sqrt{s})}{\mathrm{K}_{n+1}(\sqrt{s})+\mathrm{K}_{n-1}(\sqrt{s})}\frac{\sin ^2(nb_D)}{n^2}\right\} , \end{aligned}$$

(52)

and

$$\begin{aligned} \hat{Z}_{q}(\tau )=2\mathrm{erf}\left( \frac{1}{\nu \sqrt{\tau }}\right) +2\frac{\nu \sqrt{\tau }}{\sqrt{\pi }}\left( e^{-1/{\nu ^2\tau }}-1\right) . \end{aligned}$$

(53)

3.2 Single-Slot Solution in a Vertically Bounded Medium

The solution methodology presented above for the infinite 3D reservoir unbounded in the $z$ direction can be extended to the finite formation thickness case shown in Fig. 3. If we consider a reservoir with a thickness $h$ and a distance $z_{w}$ from the middle point of the slot to the bottom of the formation, then the dimensionless form of MBVP defined by Eqs. 13–18 will remain the same with an additional boundary condition (no-flow at the bottom and top boundaries), which can be written as

$$\begin{aligned} \frac{\partial \mathcal{P}}{\partial z}(r_w,\theta ,-z_w,t)=\frac{\partial \mathcal{P}}{\partial z}(r_w,\theta ,h-z_w,t)=0, \end{aligned}$$

(54)

or in dimensionless form as

$$\begin{aligned} \frac{\partial p_{D}}{\partial z_D}(1,\theta ,-z_{Dw},t_D)=\frac{\partial p_{D}}{\partial z_D}(1,\theta ,h_D-z_{Dw},t_D)=0, \end{aligned}$$

(55)

where

$$\begin{aligned} h_{D}=\frac{h}{l_w}\;\;\text{ and }\;\;~z_{Dw}=\frac{z_{w}}{l_w}. \end{aligned}$$

(56)

Again we replace Eqs. 22 and 25 with the equivalent form

$$\begin{aligned} \frac{\partial p_{D}}{\partial r_D}(1,\theta ,z_D,t_D)=-q_D(\theta ,z_D,t_D), ~\mathrm{for}~ \left| z_D\right| <1~\text{ and }~~ 0\le \theta <b_D, \end{aligned}$$

(57)

where the function $q_D(\theta ,z_D,t_D)$ is unknown and will be specified later. Using the method of images, we can bring this problem back into the infinite domain by adding a set of slots with their middle points being positioned at $z_D=\pm 2l h_D,~l=1,2,\ldots , \infty$ with the same flux density distribution as on the original slot, and at $z_D=\pm 2l h_D-2z_{Dw},~l=0,1,2,\ldots , \infty$ with the inverse flux density distribution $q_D(\theta ,-z_D,t_D)$. Then the solution to the correponding boundary-value problem can be written as

$$\begin{aligned} p_D(r_D,\theta ,z_D,t_D)=\int _{0}^{t_D}\int _{-1}^{1}\int _{0}^{b_D} q_D(\psi ,u,\tau ) \mathrm{G}_h(r_D,\theta ,\psi ,z_D,u,t_D-\tau ) \mathrm{d}u \mathrm{d}\psi \mathrm{d}\tau , \end{aligned}$$

(58)

where $\mathrm{G}_h$ is a Green’s function for the corresponding problem, which can be expressed as

$$\begin{aligned} \mathrm{G}_h(r_D,\theta ,\psi ,z_D,u,t_D)=\varTheta (r_D,\theta ,\psi ,t_D) \left[ Z(z_D,u,t_D)/2+Z_h(z_D,u,t_D)\right] , \end{aligned}$$

(59)

with $\varTheta (r_D,\theta ,\psi ,t_D)$ and $Z(z_D,u,t_D)$ being defined by Eqs. 29–30 and

$$\begin{aligned} \mathrm{Z}_h(z_D,u,t_D)&= \frac{e^{-\frac{(z_D-u+2z_{Dw})^2}{4\nu ^2t_D}}}{\sqrt{\pi t_D}\nu } +\sum _{l=1}^\infty \left[ \frac{e^{-\frac{(z_D-u-2lh_D)^2}{4\nu ^2t_D}}}{\sqrt{\pi t_D}\nu }+ \frac{e^{-\frac{(z_D-u+2lh_D)^2}{4\nu ^2t_D}}}{\sqrt{\pi t_D}\nu } \right. \nonumber \\&+\left. \frac{(-1)^l e^{-\frac{(z_D-u+2z_{Dw}-2lh_D)^2}{4\nu ^2t_D}}}{\sqrt{\pi t_D}\nu }+\frac{(-1)^l e^{-\frac{(z_D-u+2z_{Dw}+2lh_D)^2}{4\nu ^2t_D}}}{\sqrt{\pi t_D}\nu } \right] . \end{aligned}$$

(60)

As in the unbounded case, let us assume that the flux density $q_D(\theta ,z_D,t_D)$ can be expanded in terms of Chebyshev polynomials as (note that since $q_D$ is no longer an even function of $z_D$ we must include both even and odd Chebyshev Polynomials)

$$\begin{aligned} q_D(\theta ,u,\tau )=\frac{1}{\pi }\sum _{i=0}^\infty \sum _{j=0}^\infty c_{ij}(t) \frac{(-1)^iT_{2i}(\theta /b_D)}{\sqrt{b_D^2-\theta ^2}}\frac{T_{j}(z_D)}{\sqrt{1-z_D^2}}, \end{aligned}$$

(61)

then we obtain the following expression for the dimensionless pressure distribution in the reservoir:

$$\begin{aligned} p_D(r_D,\theta ,z_D,t_D)&= \sum _{i=0}^\infty \sum _{j=0}^\infty \int _{0}^{t_D}c_{ij}(\tau )\varTheta _{2i}(r_D,\theta ,t_D-\tau )\nonumber \\&\times \left[ \mathrm{Z}_{j}(z_D,t_D-\tau )+\mathrm{Z}_{hj}(z_D,t_D-\tau )\right] \mathrm{d}\tau , \end{aligned}$$

(62)

with $\varTheta _{2i}$ and $Z_j$ being defined by Eqs. 34–35 and

$$\begin{aligned} \mathrm{Z}_{hj}(z_D,t_D)=\int _0^\pi \mathrm{Z}_{h}(z_D,\cos (\eta ),t_D)\cos (j\eta )\mathrm{d}\eta . \end{aligned}$$

(63)

As in the previous case, a method is given in Appendix 1 for the efficient computation of $\mathrm{Z}_{hj}$. Finally, to determine unknown functions $c_{ij}(t_D)$ and $p_{Dw}(t_D)$, we need to solve the following system of integral equations:

$$\begin{aligned}&\sum _{i=0}^\infty \sum _{j=0}^\infty \int _{0}^{t_D}c_{ij}(\tau ) \varTheta _{2i}(1,\theta ,t_D-\tau ) \mathrm{Z}_{hj}(z_D,t_D-\tau ) \mathrm{d}\tau \nonumber \\&\qquad =p_{Dwu}(t_D) ~ \text{ for }~\left| z_D\right| <1~\text{ and }~0\le \theta <b_D, \end{aligned}$$

(64)

$$\begin{aligned} c_{00}(t_D)=1, \end{aligned}$$

(65)

which can be treated in the same way as we proposed in the vertically unbounded case.

3.2.1 Pressure-Averaged Uniform-Flux Solution

Let us also present a simplified solution based on the assumption that the flux density is uniform on the slot (see Eqs. 45 and  46). The pressure response can be easily obtained from Eq. 58 as

$$\begin{aligned} p_D(r_D,\theta ,z_D,t_D)=\frac{\pi }{b_D}\int _{0}^{t_D}\int _{0}^{1}\int _{0}^{b_D} \mathrm{G}_{\mathrm{h}}(r_D,\theta ,\psi ,z_D,u,t_D-\tau ) \mathrm{d}u \mathrm{d}\psi \mathrm{d}\tau . \end{aligned}$$

(66)

Performing integration in the above equation yields

$$\begin{aligned} p_D(r_D,\theta ,z_D,t_D)=\frac{\pi }{b_D}\int _{0}^{t_D} \varTheta _{q}(r_D,\theta ,\tau )Z_{qh}(z_D,\tau ) \mathrm{d}\tau , \end{aligned}$$

(67)

where $\varTheta _{q}$ is defined by Eq. 49 and

$$\begin{aligned} Z_{qh}(z_D,\tau )&= \sum _{i=-\infty }^\infty \left[ \mathrm{erf}\left( \frac{1+z_D+2i h_D}{2\nu \sqrt{\tau }}\right) +\mathrm{erf}\left( \frac{1-(z_D+2i h_D)}{2\nu \sqrt{\tau }}\right) \right. \nonumber \\&\left. +\mathrm{erf}\left( \frac{1+z_D+2z_{Dw}+2i h_D}{2\nu \sqrt{\tau }}\right) +\mathrm{erf}\left( \frac{1-(z_D+2z_{Dw}+2i h_D)}{2\nu \sqrt{\tau }}\right) \right] .\nonumber \\ \end{aligned}$$

(68)

Now we can estimate the dimensionless wellbore pressure by taking the average value of Eq. 67 over the slot surface, which is equal to

$$\begin{aligned} p_{Dwa}(t_D)=\frac{1}{b_D^2}\int _{0}^{t_D} \hat{\varTheta }_{q}(\tau )\hat{Z}_{qh}(\tau ) \mathrm{d}\tau , \end{aligned}$$

(69)

with $\hat{\varTheta }_{q}$ defined by Eq. 52 and

$$\begin{aligned} \hat{Z}_{qh}(\tau )=W(\tau ,0,h_D)+W(\tau ,z_{Dw}, h_D), \end{aligned}$$

(70)

where

$$\begin{aligned} W(\tau ,x,h_D) \!&= \! \sum _{i=-\infty }^\infty \left( \nu \sqrt{\frac{\tau }{\pi }}\left[ e^{-\frac{(x+i h_D+1)^2}{\nu ^2\tau }}+e^{-\frac{(x+i h_D-1)^2}{\nu ^2\tau }}\!-\!2e^{-\frac{(x+i h_D)^2}{\nu ^2\tau }}\right] \!+\! (x+i h_D+1)\right. \nonumber \\&\times \left. \mathrm{erf}\left( \frac{x+i h_D+1}{\nu \sqrt{\tau }}\right) +(x+i h_D-1)\mathrm{erf}\left( \frac{x+i h_D-1}{\nu \sqrt{\tau }}\right) \right. \nonumber \\&\left. -2(x+i h_D)\mathrm{erf}\left( \frac{x+i h_D}{\nu \sqrt{\tau }}\right) \right) . \end{aligned}$$

(71)

3.3 Solutions for Vertical Multiple Slots

Another generalization is to consider a number of same slots symmetrically placed on the wellbore, as shown in Fig. 3. In this case the mixed boundary value problem will remain the same, as given by Eqs. 13–17, and 54 with an additional inner boundary condition

$$\begin{aligned} \frac{\partial \mathcal{P}}{\partial \theta }\left( r_w,-\frac{\pi }{N_o},z,t\right) =\frac{\partial \mathcal{P}}{\partial \theta }\left( r_w,\frac{\pi }{N_o},z,t\right) =0. \end{aligned}$$

(72)

which defines the symmetry with respect to variable $\theta$ due to ${N_o}$ symmetrically placed slots. The boundary condition on the total flowrate Eq. 18 should be also replaced with

$$\begin{aligned} r_w \lambda _{h} \int _{-b/r_w}^{b/r_w}\int _{-l_w}^{l_w} \frac{\partial \mathcal{P}}{\partial r}(r_w,\theta ,z,t) \mathrm{d}z \mathrm{d}\theta = -q/N_o. \end{aligned}$$

(73)

Using the same dimensionless variables as before (Eqs. 19 and 56), these equations can be written in dimensionless form as

$$\begin{aligned}&\frac{\partial p_D}{\partial \theta }\left( 1,-\frac{\pi }{N_o},z_D,t_D\right) =\frac{\partial p_D}{\partial \theta }\left( 1,\frac{\pi }{N_o},z_D,t_D\right) =0, \end{aligned}$$

(74)

$$\begin{aligned}&\frac{1}{2\pi }\int _0^{b_D}\int _{-1}^1\frac{\partial p_{D}}{\partial r_D}(1,\theta ,z_D,t_D) \mathrm{d}z_D= -1/N_o. \end{aligned}$$

(75)

As in the previous cases,we assume that the flux density on each slot is expressed in terms of a series of Chebyshev polynomials as

$$\begin{aligned} q_D(\theta ,u,\tau )=\frac{1}{\pi }\sum _{i=0}^\infty \sum _{j=0}^\infty c_{ij}(t) \frac{(-1)^iT_{2i}(\theta /b_D)}{\sqrt{b_D^2-\theta ^2}}\frac{T_{j}(z_D)}{\sqrt{1-z_D^2}}, \end{aligned}$$

(76)

then the solution for the dimensionless pressure $p_D$ can be obtained in the following form

$$\begin{aligned} p_D(r_D,\theta ,z_D,t_D)=\int _{0}^{t_D}\int _{-1}^{1}\int _{0}^{b_D} q_D(\psi ,u,\tau ) \mathrm{G}_{hN_o}(r_D,\theta ,\psi ,z_D,u,t_D-\tau ) \mathrm{d}u \mathrm{d}\psi \mathrm{d}\tau , \end{aligned}$$

(77)

where $\mathrm{G}_{hN_o}$ is a Green’s function for the corresponding problem, which can be expressed as

$$\begin{aligned} \mathrm{G}_{hN_o}(r_D,\theta ,\psi ,z_D,u,t_D) =\varTheta _{N_o}(r_D,\theta ,\psi ,t_D)\left[ Z(z_D,u,t_D) /2+Z_h(z_D,u,t_D)\right] , \end{aligned}$$

(78)

with

$$\begin{aligned} \varTheta _{N_o}(r_D,\theta ,\psi ,t_D)={\mathcal {L}^{-1}}\left\{ \frac{1}{\sqrt{s}}\sum _{n=0}^\infty \left( 1-\frac{\delta _{0n}}{2}\right) \frac{2\mathrm{K}_{nN_o}(r_D\sqrt{s})\cos (nN_o\theta )\cos (nN_o\psi )}{\mathrm{K}_{nN_o+1}(\sqrt{s})+\mathrm{K}_{nN_o-1}(\sqrt{s})}\right\} , \nonumber \\ \end{aligned}$$

(79)

and $Z(z_D,u,t_D)$ and $Z_h(z_D,u,t_D)$ being defined by Eqs. 30 and 60, respectively. The substitution of $q_D$ given by Eq. 76 in Eq. 77 yields

$$\begin{aligned} p_D(r_D,\theta ,z_D,t_D)&= \sum _{i=0}^\infty \sum _{j=0}^\infty \int _{0}^{t_D}c_{ij}(\tau )\varTheta _{N_o2i}(r_D,\theta ,t_D-\tau ) \left[ \mathrm{Z}_{j}(z_D,t_D-\tau )\right. \nonumber \\&\left. +\,\mathrm{Z}_{hj}(z_D,t_D-\tau )\right] \mathrm{d}\tau , \end{aligned}$$

(80)

where

$$\begin{aligned} \varTheta _{N_o2i}(r_D,\theta ,t_D)={\mathcal {L}^{-1}}\left\{ \frac{1}{\sqrt{s}} \sum _{n=0}^\infty \left( 1-\frac{\delta _{0n}}{2}\right) \frac{2\mathrm{K}_{nN_o}(r_D\sqrt{s})\mathrm{J}_{2i}(nN_o b_D)\cos (nN_o\psi )}{\mathrm{K}_{nN_o+1}(\sqrt{s}) +\mathrm{K}_{nN_o-1}(\sqrt{s})}\right\} . \nonumber \\ \end{aligned}$$

(81)

Finally, the unknown functions $c_{ij}(t_D)$ and $p_{Dw}(t_D)$ can be determined by solving the following system of integral equations:

$$\begin{aligned}&\sum _{i=0}^\infty \sum _{j=0}^\infty \int _{0}^{t_D}c_{ij}(\tau ) \varTheta _{N_o2i}(1,\theta ,t_D-\tau ) \mathrm{Z}_{hj}(z_D,t_D-\tau ) \mathrm{d}\tau \nonumber \\&\quad =p_{Dwu}(t_D) ~ \text{ for }~\left| z_D\right| <1~\text{ and }~0\le \theta <b_D, \end{aligned}$$

(82)

$$\begin{aligned} c_{00}(t_D)=1. \end{aligned}$$

(83)

The solution of this system can be obtained by using the same technique as in previous cases.

3.3.1 Pressure-Averaged Uniform-Flux Solution

Next we present an approximate solution based on the assumption that the flux density is uniform on the slots. In this case, the mixed boundary value problem remains the same, except that Eqs. 15 and 73 should be replaced with

$$\begin{aligned} 4\lambda _{h}b l_w \frac{\partial \mathcal{P}}{\partial r}(r_w,\theta ,z,t) = -q/N_0~\mathrm{for}~ \left| z\right| < l_w~\text{ and }~\left| r_w\theta \right| <b, \end{aligned}$$

(84)

which can be rewritten in dimensionless form as

$$\begin{aligned} \frac{\partial p_D}{\partial r_D}(1,\theta ,z_D,t) = -\frac{\pi }{b_DN_0}~\mathrm{for}~ \left| z_D\right| < 1~\text{ and }~\left| \theta \right| <b_D. \end{aligned}$$

(85)

Again, since Eq. 77 is valid for any flux density distribution, we can use it to directly obtain the pressure response as

$$\begin{aligned} p_D(r_D,\theta ,z_D,t_D)=\frac{\pi }{b_D N_0}\int _{0}^{t_D}\int _{-1}^{1}\int _{0}^{b_D} \mathrm{G}_{hN_o}(r_D,\theta ,\psi ,z_D,u,t_D-\tau ) \mathrm{d}u \mathrm{d}\psi \mathrm{d}\tau . \end{aligned}$$

(86)

Performing integration in the above equation yields

$$\begin{aligned} p_D(r_D,\theta ,z_D,t_D)=\frac{\pi }{b_DN_0}\int _{0}^{t_D} \varTheta _{qN_0}(r_D,\theta ,\tau )Z_{qh}(z_D,\tau ) \mathrm{d}\tau , \end{aligned}$$

(87)

where

$$\begin{aligned} \varTheta _{qN_o}(r_D,\theta ,t_D)={\mathcal {L}^{-1}}\left\{ \frac{1}{\sqrt{s}} \sum _{n=0}^\infty \left( 1-\frac{\delta _{0n}}{2}\right) \frac{2\mathrm{K}_{nN_o}(r_D\sqrt{s})\cos (nN_o\theta )}{\mathrm{K}_{nN_o+1}(\sqrt{s})+\mathrm{K}_{nN_o-1}(\sqrt{s})} \frac{\sin (nN_ob_D)}{nN_0}\right\} , \end{aligned}$$

(88)

and $Z_{qh}$ is defined by Eq. 68.

Now we can obtain the dimensionless wellbore pressure by taking the average value of Eq. 87 over the slot surface, which is equal to

$$\begin{aligned} p_{Dwa}(t_D)=\frac{1}{b_D^2}\int _{0}^{t_D} \hat{\varTheta }_{qN_0}(\tau )\hat{Z}_{qh}(\tau ) \mathrm{d}\tau , \end{aligned}$$

(89)

with

$$\begin{aligned} \hat{\varTheta }_{qN_o}(t_D)={\mathcal {L}^{-1}}\left\{ \frac{1}{\sqrt{s}}\sum _{n=0}^\infty \left( 1-\frac{\delta _{0n}}{2}\right) \frac{2\mathrm{K}_{nN_o}(\sqrt{s})}{\mathrm{K}_{nN_o+1}(\sqrt{s})+\mathrm{K}_{nN_o-1}(\sqrt{s})}\frac{\sin ^2(nN_ob_D)}{n^2N_0^2}\right\} , \end{aligned}$$

(90)

and $\hat{Z}_{qh}$ defined by Eq. 70.

3.4 Vertical Slot Solutions in 3D Anisotropic Porous Media

In this section, we generalize the solution proposed above to the case of $k_x\ne k_y$ ($\lambda _y\ne \lambda _x$), i.e., the permeabilities in the $x$ and $y$ directions are different. Here we assume that $\lambda _y>\lambda _x$. If it is not the case, we can always rotate the coordinate system in the horizontal plane and interchange the $x$ and $y$ axis. Let us denote $\chi =\sqrt{\lambda _x/\lambda _y}$, make a coordinate transformation $y\rightarrow y'=y/\chi$, and introduce the elliptical coordinates in the horizontal plane

$$\begin{aligned}&x/r_w=a~\cosh \xi \cos \theta , \end{aligned}$$

(91)

$$\begin{aligned}&y'/r_w=a~\sinh \xi \sin \theta , \end{aligned}$$

(92)

with $a^2=1-\chi ^2$, then we can write the corresponding boundary-value problem as

$$\begin{aligned}&\frac{2\lambda _{x}}{r_w^2 a^2(\cosh (2\xi )-\cos (2\theta ))}\left( \frac{\partial ^2\mathcal{P}}{\partial \xi ^2}+\frac{\partial ^2\mathcal{P}}{\partial \theta ^2}\right) + \lambda _{v} \frac{\partial ^2 \mathcal{P}}{\partial z^2} = \varphi \frac{\partial \mathcal{P}}{\partial t}, \end{aligned}$$

(93)

$$\begin{aligned}&\mathcal{P}(\xi ,\theta ,z,0)=0,\end{aligned}$$

(94)

$$\begin{aligned}&\mathcal{P}(\xi _w,z,\theta ,t)=\mathcal{P}_{wu}(t),~\mathrm{for}~ \left| z\right| < l_w~\text{ and }~\theta \in \bigcup _p\varLambda _p, \end{aligned}$$

(95)

$$\begin{aligned}&\frac{\partial \mathcal{P}}{\partial \xi }(\xi _w,\theta ,z,t)=0, ~\mathrm{for}~ \left| z\right| \ge l_w~\text{ or }~\theta \notin \bigcup _p\varLambda _p, \end{aligned}$$

(96)

$$\begin{aligned}&\mathcal{P}(\xi ,z,\theta ,t)\rightarrow 0 ~\mathrm{as}~\xi \rightarrow \infty ,\end{aligned}$$

(97)

$$\begin{aligned}&\frac{\partial \mathcal{P}}{\partial z}(\xi _w,\theta ,-z_w,t)=\frac{\partial \mathcal{P}}{\partial z}(\xi _w,\theta ,h-z_w,t)=0, \end{aligned}$$

(98)

$$\begin{aligned}&r_w \sqrt{\lambda _x\lambda _y} \sum _p\int _{\varLambda _p}\int _{-l_w}^{l_w} \frac{\partial \mathcal{P}}{\partial \xi }(\xi _w,\theta ,z,t) \mathrm{d}z \mathrm{d}\theta = -q, \end{aligned}$$

(99)

where $\xi _w= {{\mathrm{{arctanh}}}}(\chi )$ and $\varLambda _p=\{\theta :\left| \theta -\theta _p\right| \le b/r_w=b_D\}$ with $\theta _p$ being the angular coordinate of the center of the $p$-th slot, as shown in Fig. 3. Note that in this case we do not have symmetry any more with respect to $\theta$ due to anisotropy in the $x-y$ (horizontal) plane. Using the dimensionless variables introduced earlier in Eq. 19 and 56 (except that due to horizontal anisotropy $k_h$ should be replaced with $k_x$), the mixed boundary value problem in a 3D anisotropic porous medium can be written as

$$\begin{aligned}&\frac{2}{a^2(\cosh (2\xi )-\cos (2\theta ))}\left( \frac{\partial ^2p_{D}}{\partial \xi ^2}+\frac{\partial ^2p_{D}}{\partial \theta ^2}\right) + \nu ^2 \frac{\partial ^2 p_{D}}{\partial z_D^2} = \frac{\partial p_{D}}{\partial t_D}, \end{aligned}$$

(100)

$$\begin{aligned}&p_{D}(\xi ,\theta ,z_D,0)=0,\end{aligned}$$

(101)

$$\begin{aligned}&p_{D}(\xi _w,z_D,\theta ,t_D)=p_{Dwu}(t),~\mathrm{for}~ \left| z_D\right| < 1~\text{ and }~\theta \in \bigcup _p\varLambda _p, \end{aligned}$$

(102)

$$\begin{aligned}&\frac{\partial p_{D}}{\partial \xi }(\xi _w,\theta ,z_D,t_D)=0, ~\mathrm{for}~ \left| z_D\right| \ge 1~\text{ or }~\theta \notin \bigcup _p\varLambda _p, \end{aligned}$$

(103)

$$\begin{aligned}&p_{D}(\xi ,z_D,\theta ,t_D)\rightarrow 0 ~\mathrm{as}~\xi \rightarrow \infty , \end{aligned}$$

(104)

$$\begin{aligned}&\frac{\partial p_{D}}{\partial z_D}(\xi _w,\theta ,-z_{Dw},t_D) =\frac{\partial p_{D}}{\partial z_D}(\xi _w,\theta ,h_D-z_{Dw},t_D)=0, \end{aligned}$$

(105)

$$\begin{aligned}&\frac{1}{4\pi \chi }\sum _p\int _{\varLambda _p}\int _{-1}^{1} \frac{\partial p_{D}}{\partial \xi }(\xi _w,\theta ,z_D,t_D) \mathrm{d}z_D \mathrm{d}\theta = -1. \end{aligned}$$

(106)

As in previous cases, we assume that on the $p$-th slot the flux density $q_D(\theta ,z_D,t_D)$ can be expanded in terms of the Chebyshev polynomials as

$$\begin{aligned} q^p_D(\theta ,z_D,t_D)=\frac{\chi }{\pi }\sum _{i=0}^\infty \sum _{j=0}^\infty c_{ij}^p(t_D) \frac{(-1)^{[i/2]}T_{i}([\theta -\theta _p]/b_D)}{\sqrt{b_D^2-(\theta -\theta _p)^2}}\frac{T_{j}(z_D)}{\sqrt{1-z_D^2}}, \end{aligned}$$

(107)

then the corresponding pressure drop induced by such a flux density distribution can be written as

$$\begin{aligned} p_D^p(\xi ,\theta ,z_D,t_D)=\int _{0}^{t_D}\int _{-1}^{1}\int _{-b_D}^{b_D} q_D^p(\psi ,u,\tau ) \mathrm{G}^p_h(\xi ,\theta ,\psi ,z_D,u,t_D-\tau ) \mathrm{d}u \mathrm{d}\psi \mathrm{d}\tau , \end{aligned}$$

(108)

where

$$\begin{aligned} \mathrm{G}_h^p(\xi ,\theta ,\psi ,z_D,u,t_D) =\varTheta ^p(\xi ,\theta ,\psi ,t_D)\left[ Z(z_D,u,t_D) /2+Z_h(z_D,u,t_D)\right] . \end{aligned}$$

(109)

and

$$\begin{aligned} \varTheta ^p(\xi ,\theta ,\psi ,t_D)&= \frac{1}{\chi } {\mathcal {L}^{-1}} \left\{ \sum _{r=0}^{\infty }\frac{{{\mathrm{{Mc}}}}_r(\xi ,-a^2s/4)}{{{\mathrm{{Mc}}}}'_r(\xi _w,-a^2s/4)}{{\mathrm{{ce}}}}_r(\theta ,-a^2s/4) {{\mathrm{{ce}}}}_r(\psi ,-a^2s/4)\right. \nonumber \\&\left. +\sum _{r=1}^{\infty }\frac{{{\mathrm{{Ms}}}}_r(\xi ,-a^2s/4)}{{{\mathrm{{Ms}}}}'_r(\xi _w,-a^2s/4)}{{\mathrm{{se}}}}_r(\theta ,-a^2s/4) {{\mathrm{{se}}}}_r(\psi ,-a^2s/4)\right\} , \end{aligned}$$

(110)

${{\mathrm{{ce}}}}_n$ and ${{\mathrm{{se}}}}_n$ are being normalized angular even and odd Mathieu functions, and ${{\mathrm{{Mc}}}}_n$ and ${{\mathrm{{Ms}}}}_n$ are radial even and odd Mathieu functions of the third kind. Expanding Mathieu functions over sines and cosines we can rewrite the last expression as

$$\begin{aligned} \varTheta ^p(\xi ,\theta ,\psi ,t_D)= {\mathcal {L}^{-1}}\left\{ \sum _{n=0}^{\infty }Fc_n(\xi ,\theta ,a^2s/4)\cos (n\psi )+\sum _{n=1}^{\infty }Fs_n(\xi ,\theta ,a^2s/4)\sin (n\psi )\right\} , \end{aligned}$$

(111)

where

$$\begin{aligned}&Fc_{2n+\gamma }(\xi ,\theta ,a^2s/4)=\sum _{r=0}^{\infty } \frac{{{\mathrm{{Mc}}}}_{2r+\gamma }(\xi ,-a^2s/4)}{{{\mathrm{{Mc}}}}'_{2r+\gamma } (\xi _w,-a^2s/4)}A^{2r+\gamma }_{2n+\gamma }{{\mathrm{{ce}}}}_{2r+\gamma } (\theta ,-a^2s/4),~\gamma =0,~1,\end{aligned}$$

(112)

$$\begin{aligned}&Fs_{2n+\gamma }(\xi ,\theta ,a^2s/4)=\sum _{r=0}^{\infty } \frac{{{\mathrm{{Ms}}}}_{2r+\gamma }(\xi ,-a^2s/4)}{{{\mathrm{{Ms}}}}'_{2r+\gamma }(\xi _w,-a^2s/4)} B^{2r+\gamma }_{2n+\gamma }{{\mathrm{{se}}}}_{2r+\gamma }(\theta ,-a^2s/4),~\gamma =0,~1 \end{aligned}$$

(113)

and $A^{2r+\gamma }_{2n+\gamma }$ and $B^{2r+\gamma }_{2n+\gamma }$ are corresponding expansion coefficients. The substitution of $q_D^p$ given by Eq. 107 in Eq. 108 yields

$$\begin{aligned} p_D^p(r_D,\theta ,z_D,t_D)&= \sum _{i=0}^\infty \sum _{j=0}^\infty \int _{0}^{t_D}c_{ij}^p(t_D)\varTheta _{i}^p(\xi ,\theta ,t_D-\tau ) \left[ \mathrm{Z}_{j}(z_D,t_D-\tau )\right. \nonumber \\&\quad \left. +\,\mathrm{Z}_{hj}(z_D,t_D-\tau )\right] \mathrm{d}\tau , \end{aligned}$$

(114)

where

$$\begin{aligned}&\varTheta _{2i}^p(\xi ,\theta ,t_D)\nonumber \\&\quad ={\mathcal {L}^{-1}}\left\{ \sum _{n=0}^{\infty } \left[ Fc_n(\xi ,\theta ,a^2s/4)\cos (n\theta _p)+Fs_n(\xi ,\theta ,a^2s/4) \sin (n\theta _p)\right] \mathrm{J}_{2i}(nb_D)\right\} , \end{aligned}$$

(115)

$$\begin{aligned}&\varTheta _{2i+1}^p(\xi ,\theta ,t_D)\nonumber \\&\quad ={\mathcal {L}^{-1}}\left\{ \sum _{n=1}^{\infty } \left[ Fs_n(\xi ,\theta ,a^2s/4)\cos (n\theta _p) -Fc_n(\xi ,\theta ,a^2s/4)\sin (n\theta _p)\right] \mathrm{J}_{2i+1}(nb_D)\right\} . \end{aligned}$$

(116)

Finally the unknown coefficients $c_{ij}(t_D)$ and $p_{Dwu}$ can be obtained by solving the following system of integral equations:

$$\begin{aligned}&\sum _p\sum _{i=0}^\infty \sum _{j=0}^\infty \int _{0}^{t_D}c^p_{ij}(\tau ) \varTheta ^p_{i}(\xi _w,\theta ,t_D-\tau ) \mathrm{Z}_{hj}(z_D,t_D-\tau ) \mathrm{d}\tau =p_{Dwu}(t_D)\nonumber \\&\qquad \text{ for }~\left| z_D\right| <1~\text{ and }~\theta \in \bigcup _p\varLambda _p, \end{aligned}$$

(117)

$$\begin{aligned} \sum _p c^p_{00}(t_D)=1, \end{aligned}$$

(118)

which can be treated in the same way as we suggested previously. The only difficulty that might arise is the summation of the series in $\varTheta _i^p$; we proposed one possible approach to solving this problem in Appendix 1. Now let us simplify the function $\varTheta _i^p$ and the system of equations given by Eqs. 117 and 118 for a few particular cases.

3.5 One Slot with its Center Positioned at $\theta =0,\pi$

In this case, due to the obvious symmetry with respect to $\pm \theta$, we should consider only even Chebyshev polynomials in flux density expansion given by Eq. 107. Thus, the only non-zero coefficients are $c^1_{2ij}$, and the function $\varTheta _{2i}^1$ smplifies to

$$\begin{aligned} \varTheta _{2i}^1(\xi ,\theta ,t_D)={\mathcal {L}^{-1}}\left\{ \sum _{n=0}^{\infty }Fc_n(\xi ,\theta ,a^2s/4)\mathrm{J}_{2i}(nb_D)\right\} , \end{aligned}$$

(119)

and the system of integral equations to be solved becomes

$$\begin{aligned}&\sum _{i=0}^{\infty }\sum _{j=0}^\infty \int _{0}^{t_D}c^1_{2ij}(\tau ) \varTheta ^1_{2i}(\xi _w,\theta ,t_D-\tau ) \mathrm{Z}_{hj}(z_D,t_D-\tau ) \mathrm{d}\tau =p_{Dwu}(t_D)\nonumber \\&\quad \text{ for }~\left| z_D\right| <1~\text{ and }~\theta \in [0,b_D], \end{aligned}$$

(120)

$$\begin{aligned} c^1_{00}(t_D)=1. \end{aligned}$$

(121)

3.5.1 One Slot with its Center Positioned at $\theta =\pm \frac{\pi }{2}$

Here, due to the obvious symmetry around $\theta =\pm \pi /2$, we should consider only the even Chebyshev polynomials in flux density expansion Eq. 107, thus the only non-zero coefficients are $c^1_{2ij}$ and the function $\varTheta _{2i}^1$ simplifies to

$$\begin{aligned}&\varTheta _{2i}^1(\xi ,\theta ,t_D)\nonumber \\&\quad ={\mathcal {L}^{-1}}\left\{ \sum _{n=0}^{\infty }(\!-\!1)^n \left[ Fc_{2n}\left( \xi ,\theta ,\frac{a^2s}{4}\right) \mathrm{J}_{2i}(2nb_D)\pm Fs_{2n+1}\left( \xi ,\theta ,\frac{a^2s}{4}\right) \mathrm{J}_{2i}([2n\!+\!1]b_D)\right] \right\} ,\nonumber \\ \end{aligned}$$

(122)

and the system of integral equations to be solved becomes

$$\begin{aligned}&\sum _{i=0}^\infty \sum _{j=0}^\infty \int _{0}^{t_D}c^1_{2ij}(\tau ) \varTheta ^1_{2i}(\xi _w,\theta ,t_D-\tau ) \mathrm{Z}_{hj}(z_D,t_D-\tau ) \mathrm{d}\tau =p_{Dwu}(t_D)\nonumber \\&\quad \text{ for }~\left| z_D\right| <1~\text{ and }~\theta \in [\pm \frac{\pi }{2}, \pm \frac{\pi }{2}+b_D], \end{aligned}$$

(123)

$$\begin{aligned} c^1_{00}(t_D)=1. \end{aligned}$$

(124)

3.5.2 Two Slots with Centers Positioned at $\theta =0$ and $\theta =\pi$

Here, we can consider only one half of the problem in the domain $-\pi /2\le \theta \le \pi /2$, and take only the symmetric part of $\varTheta ^1_{2i}$:

$$\begin{aligned} \varTheta _{s2i}^1(\xi ,\theta ,t_D)={\mathcal {L}^{-1}}\left\{ \sum _{n=0}^{\infty } Fc_{2n}(\xi ,\theta ,a^2s/4)\mathrm{J}_{2i}(2nb_D)\right\} , \end{aligned}$$

(125)

thus the system of integral equations to be solved becomes

$$\begin{aligned}&\sum _{i=0}^\infty \sum _{j=0}^\infty \int _{0}^{t_D}c^1_{2ij}(\tau ) \varTheta ^1_{s2i}(\xi _w,\theta ,t_D-\tau ) \mathrm{Z}_{hj}(z_D,t_D-\tau ) \mathrm{d}\tau =p_{Dwu}(t_D)\nonumber \\&\quad \text{ for }~\left| z_D\right| <1~\text{ and }~\theta \in [0,b_D]{,} \end{aligned}$$

(126)

$$\begin{aligned} c^1_{00}(t_D)=\frac{1}{2}. \end{aligned}$$

(127)

3.5.3 Two Slots with Centers Positioned at $\theta =\pm \frac{\pi }{2}$

As in the previous case, we can consider only one half of the problem in the domain $0 \le \theta \le \pi$, and thus take only the symmetric part of $\varTheta ^1_{2i}$:

$$\begin{aligned} \varTheta _{s2i}^1(\xi ,\theta ,t_D)={\mathcal {L}^{-1}}\left\{ \sum _{n=0}^{\infty } (-1)^nFc_{2n}(\xi ,\theta ,a^2s/4)\mathrm{J}_{2i}(2nb_D)\right\} , \end{aligned}$$

(128)

and the system of integral equations to be solved becomes

$$\begin{aligned}&\sum _{i=0}^\infty \sum _{j=0}^\infty \int _{0}^{t_D}c^1_{2ij}(\tau ) \varTheta ^1_{s2i}(\xi _w,\theta ,t_D-\tau ) \mathrm{Z}_{hj}(z_D,t_D-\tau ) \mathrm{d}\tau =p_{Dwu}(t_D)\nonumber \\&\quad \text{ for }~\left| z_D\right| <1~\text{ and }~\theta \in [\frac{\pi }{2},\frac{\pi }{2}+b_D]{,}\end{aligned}$$

(129)

$$\begin{aligned}&\quad c^1_{00}(t_D)=\frac{1}{2}. \end{aligned}$$

(130)

3.5.4 Four Slots with Centers Placed at $\theta =0$, $\theta =\pi$, and $\theta =\pm \frac{\pi }{2}$

This is a combination of two previous cases. Again, it is enough to consider only two slots with $\theta _1=0$ and $\theta _2=\pi /2$ and to take the symmetrical parts of the corresponding functions:

$$\begin{aligned}&\varTheta _{s2i}^1(\xi ,\theta ,t_D)={\mathcal {L}^{-1}} \left\{ \sum _{n=0}^{\infty }Fc_{2n}(\xi ,\theta ,a^2s/4) \mathrm{J}_{2i}(2nb_D)\right\} ,\end{aligned}$$

(131)

$$\begin{aligned}&\varTheta _{s2i}^2(\xi ,\theta ,t_D)={\mathcal {L}^{-1}} \left\{ \sum _{n=0}^{\infty }(-1)^nFc_{2n}(\xi ,\theta ,a^2s/4) \mathrm{J}_{2i}(2nb_D)\right\} . \end{aligned}$$

(132)

Then the system of integral equations takes the following form:

$$\begin{aligned}&\sum _{p=1}^2\sum _{i=0}^\infty \sum _{j=0}^\infty \int _{0}^{t_D}c^p_{2ij}(\tau ) \varTheta ^p_{s2i}(\xi _w,\theta ,t_D-\tau ) \mathrm{Z}_{hj}(z_D,t_D-\tau ) \mathrm{d}\tau =p_{Dwu}(t_D)\nonumber \\&\qquad \text{ for }~\left| z_D\right| <1~\text{ and }~\theta \in [0,b_D] \bigcup [\pi /2-b_D,\pi /2], \end{aligned}$$

(133)

$$\begin{aligned} c^1_{00}(t_D)+c^2_{00}(t_D)=\frac{1}{2}. \end{aligned}$$

(134)

4 Results

First, we compare our solution with the vertically slotted-liner solution given by Spivak and Horne (1983), shown in Fig. 4, where the slots are parallel to each other in the $x$ direction. The Spivak and Horne (1983) dimensionless pressure values at $r_D= 1$ were obtained from their Fig. 6 by digitizing the plot. As can be seen from Fig. 4, the Spivak and Horne (1983) solution is somewhat inaccurate, particularly at early times.

Fig. 4

Comparison of dimensionless pressures obtained from Spivak and Horne (1983) and our solutions for 3- and 6-slot cases

Figure 5 presents the comparison of our solutions with the solutions given by Onur (2012), Biryukov and Kuchuk (2012), and Hegeman (2012). For this case, an infinite reservoir vertically bounded from the top and bottom is used to generate the wellbore pressure data with the input model parameters that are given in Table 1. Our dimensionless pressure values were obtained by solving the system of integral equations given by Eqs. 82 and  83. The difference between our analytical and the Hegeman (2012) numerical solutions for a 4-slot packer module is about 3 %, which is remarkably good. The difference between the Biryukov and Kuchuk (2012) uniform pressure solution for the partially penetrated packer with a totally open area and our solution for a 4-slot packer module is about 12 %. It should also be noticed that there is about a 4 % difference between the Onur (2012) and Biryukov and Kuchuk (2012) solutions due to the treatment of the uniform pressure condition over the open interval.

Fig. 5

Comparison of pressures changes obtained from Onur (2012) and Biryukov and Kuchuk (2012) for partially penetrated packer solutions, and Hegeman (2012) and our solutions for a 4-slot packer module

Table 1 Formation and fluid properties for the 4-slot packer module example

In Fig. 6, we present the comparison of the dimensionless uniform ($p_{Dwu}$ from Eqs. 82 and  83) and averaged ($p_{Dwa}$ from Eq. 51) pressures of a 4-slot packer module with a wellbore radius $(r_w)$ of 0.396 ft for various $k_v/k_h$ values as a function of dimensionless time. As can be observed from this figure, the differences between two pressures are small (less than 12 %) and change with time. For large times, the difference becomes a geometrical steady-state skin (does not change as a function of dimensionless time) when the system reaches spherical flow regime. This can be seen clearly in Fig. 7, which compares the derivatives of the uniform-and averaged-pressure solutions, when the derivatives exhibit a -1/2-slope spherical flow regimes, their derivatives become identical. For small times, the difference approaches zero because both the uniform pressure and averaged-pressure solutions become the same ($t_{D} \rightarrow 0\;\;p_{D}=\sqrt{\pi t_{D}}$) and exhibit identical linear flow regimes.

Fig. 6

Uniform ($p_{Dwu}$) and averaged ($p_{Dwa}$) dimensionless pressures of a 4-slot packer module with a wellbore radius ($r_w)$ of 0.396 ft for various $k_v/k_h$ values

Fig. 7

Comparison of derivatives of uniform- and averaged-pressures of a 4-slot packer module with a wellbore radius ($r_w)$ of 0.396 ft for various $k_v/k_h$ values

Figure 8 presents derivatives for various anisotropy ratios, $k_v/k_h = 0.01, \; 0.1, \; 1, \;10, \; \text{ and } \; 100$, for a 4-slot packer module in a vertically bounded reservoir, where the wellbore radius is ($r_w = 0.396\hbox { ft}$). For every anisotropy ratio case, the derivative clearly exhibits a 1/2-slope linear flow regime at very early times. As we explain in the previous paragraph, the flow becomes linear in any flow systems that is internally bounded by a regular surface (cylinder, ellipse, line, sphere, etc.) as $t_{D} \rightarrow 0$ [see Page 48 of Kucuk (1978)].

Fig. 8

Derivatives for a 4-slot packer module in a vertically bounded reservoir with wellbore radius ($r_w)$ of 0.396 ft for various $k_v/k_h$ values

As shown in Fig. 8, all derivatives go through a maximum after which they exhibit -1/2-slope spherical flow regimes, which yields the spherical permeability $k_s =\left( {k_h ^2k_v } \right) ^{1/3}$. After the spherical flow regimes, the derivatives lead up to the radial flow regime, which yields the horizontal permeability $k_h$. The start and end of the spherical flow regimes, and the start of the radial flow regime are quite different for various $k_v/k_h$ values. As can be seen from Fig. 8, the duration of the spherical flow regime of the $k_v/k_h = 100$ case is very short, because due to a very high vertical permeability compared to the horizontal permeability, the effect of the no-flow top and bottom boundaries is observed at early times.

Figure 9 compares the derivatives for a 4-slot packer module in a vertically bounded reservoir for various wellbore radii and $k_v/k_h$ values. The derivatives are almost the same at early times and slightly different during spherical flow regimes, where the effect of the wellbore radius becomes a steady-state pressure drop (geometrical skin) at late times.

Fig. 9

Comparison of derivatives for a 4-slot packer module in a vertically bounded reservoir for various wellbore radii and $k_v/k_h$ values

4.1 Drawdown Mobility

During pretests or normal drawdown tests, the stabilized (spherical steady-state) drawdown pressure drop from the formation pressure can be considered as an indicator of a formation mobility. Under some simple assumptions regarding pretest, it is possible to relate the drawdown pressure to the formation mobility. Of course, if we know the skin factor then the drawdown formation mobility becomes an estimate, rather than an indicator, provided that there is no gas evolution around the slotted-packer.

For the 4-slot packer module, it is difficult to obtain a simple expression for the steady-state solution from the solutions given above. However, we can fit the dimensionless steady-state pressure to a second degree polynomial equation ($a+bx+cx^2$) as a function of the natural logarithm of $k_v/k_h$ values for a given wellbore radius, as shown Fig. 10. For this plot, $r_w = 0.396\hbox { ft}$. Thus, the dimensionless state-state pressure can be written as

$$\begin{aligned} p_{Dss} = a+b \ln \left( \frac{k_v}{k_h}\right) +c \left[ \ln \left( \frac{k_v}{k_h}\right) \right] ^2. \end{aligned}$$

(135)

Table 2 presents the polynomial coefficients of Eq. 135 for the 4-slot packer module for various wellbore radii. Equation 135 is an excellent fit for the dimensionless state-state pressure, as shown Fig. 10; the absolute relative error between the actual dimensionless pressure and the estimated one from Eq. 135 is less then 0.5 % for $k_v/k_h \le 1$ (i.e., horizontal permeability is greater than the vertical one) and less then 3 % for $k_v/k_h >1$ (i.e., vertical permeability is greater than the horizontal one). It is well know that for most formations, the horizontal permeability is greater than the vertical permeability.

Fig. 10

Dimensionless pressure as a function of the natural logarithm of values of $k_v/k_h$ for a wellbore radius ($r_w)$ of 0.396 ft

Table 2 The polynomial coefficients of Eq. 135 for the 4-slot packer for various wellbore radii

Using the definition of the wellbore dimensionless pressure given by Eq. 12 and the dimensionless steady-state pressure given by Eq. 135, the drawdown horizontal mobility ($k_h/\mu$) for anisotropic media can be written as

$$\begin{aligned} k_h/\mu = \frac{ q\, p_{Dss} }{4 \pi l_w \varDelta p_w }, \end{aligned}$$

(136)

where $p_{Dss}$ is given by Eq. 135, the steady-state pressure is defined as $\varDelta p_w= p_o-p_w$, $p_o$ is the initial formation pressure measured by the slotted-packer module before the drawdown period or obtained from the buildup test, $q$ is the flow rate may vary between 0.1 and 50 cm$^3$/s depending on formation parameters. To obtain $k_h/\mu$ from Eq. 136 we have to assume a reasonable $k_v/k_h$ value or is combined with the buildup spherical permeability.

A typical pretest sequence is: a drawdown test followed by a buildup test. During the drawdown test, mostly mud filtrate perhaps with a little volume of oil is produced from the 4-slot packer module, and the produced volume is normally small. The pressure at the packer interval reaches quickly a spherical steady-state condition, unless the permeability formation is very low.

5 Conclusions

In this work, we have considered mixed boundary value problems for pressure transient diffusion in porous media arising in connection with the pressure transient behavior of formation tests conducted with the Wireline Formation Testing (WFT) vertically slotted-packer configuration in a vertical well. The solutions in this paper are essentially based on the idea of introducing an unknown flux density function on the open section (slot) of the wellbore, and its expansion in terms of singular basis functions. These functions reduce the mixed boundary value problem to a system of linear algebraic equations of modest size, which is easy to solve numerically. Such solutions also prove to be accurate, numerically stable. It is shown that the existing analytical solution is somewhat inaccurate. The anisotropy ratio ($k_v/k_h$) significantly affects the pressure transient behavior of the slot packer module. The wellbore radius also affects the pressure transient behavior the system. Finally, we have given a formula to obtain the drawdown horizontal mobility ($k_h/\mu$) for anisotropic media.

Appendix 1

In this section we present an efficient way to evaluate the functions $Z_j$, $Z_{jh}$ and $\varTheta _{2i}$. $Z_j$ can be easily evaluated by passing into Laplace domain

$$\begin{aligned} \mathrm{Z}_{j}(z_D,u,t_D)&= \frac{2}{\sqrt{\pi t_D}\nu }\int _0^\pi e^{-(z_D-\cos \eta )^2/(4\nu ^2t_D)}\cos (j \eta ) \mathrm{d}\eta \nonumber \\&= \frac{2}{\sqrt{\pi t_D}\nu }{\mathcal {L}^{-1}}\left( \int _0^\pi \frac{\cos (j\eta )\mathrm{d}\eta }{s+(z_D-\cos \eta )^2},\frac{1}{4\nu ^2t_D}\right) \nonumber \\&= \frac{2}{\sqrt{\pi t_D}\nu }{\mathcal {L}^{-1}}\left( \frac{1}{2i\sqrt{s}}\int _0^\pi \frac{\cos (j\eta )\mathrm{d}\eta }{(z_D+i\sqrt{s}-\cos \eta )}\right. \nonumber \\&\left. -\frac{\cos (j\eta )\mathrm{d}\eta }{(z_D-i\sqrt{s}-\cos \eta )},\frac{1}{4\nu ^2t_D}\right) \nonumber \\&= \frac{2}{\sqrt{\pi t_D}\nu } Im {\mathcal {L}^{-1}}\left( \frac{1}{\sqrt{s}}\int _0^\pi \frac{\cos (j\eta )\mathrm{d}\eta }{(z_D+i\sqrt{s}-\cos \eta )},\frac{1}{4\nu ^2t_D}\right) . \end{aligned}$$

(137)

The last integral can be evaluated using the following result from Prudnikov et al. (1981)

$$\begin{aligned} \int _0^\pi \frac{\cos (j\eta )\mathrm{d}\eta }{a+\cos \eta }=\left\{ \begin{array}{l} \frac{\pi }{\sqrt{1-a^2}}\left( \sqrt{1-a^2}-a\right) ^j~\text{ if }~|a| \le 1,\\ \frac{\pi }{\sqrt{a^2-1}}\left( \sqrt{a^2-1}-a\right) ^j~ \text{ if }~|a|>1. \end{array}\right. \end{aligned}$$

(138)

In the same way, the Laplace transform is useful when evaluating $Z_{jh}$. The Laplace transform of $Z_h$ can be written as follows (see Erdelyi (1954))

$$\begin{aligned} L\left[ \mathrm{Z}_h(z_D,u,t_D)\right]&= \sum _{l=0}^\infty \frac{(-1)^l e^{-(z_D-u+2z_{Dw}+2lh_D)\sqrt{s/\nu ^2}}}{\sqrt{s}\nu } +\sum _{l=1}^\infty \left[ \frac{e^{-(2lh_D+u-z_D)\sqrt{s/\nu ^2}}}{\sqrt{s}\nu }\right. \nonumber \\&+\frac{e^{-(z_D-u+2lh_D)\sqrt{s/\nu ^2}}}{\sqrt{s}\nu }+\left. \frac{(-1)^l e^{-(2lh_D-z_D+u-2z_{Dw})\sqrt{s/\nu ^2}}}{\sqrt{s}\nu } \right] . \end{aligned}$$

(139)

The infinite summation can now easily be performed, we then obtain

$$\begin{aligned} L\left[ \mathrm{Z}_h(z_D,u,t_D)\right]&= \frac{e^{-(z_D-u+2z_{Dw}) \sqrt{s/\nu ^2}}}{\sqrt{s}\nu (1+e^{-2h_D\sqrt{s/\nu ^2}})} +\frac{e^{-(2h_D+u-z_D)\sqrt{s/\nu ^2}}}{\sqrt{s}\nu (1-e^{-2h_D \sqrt{s/\nu ^2}})}\nonumber \\&+\frac{e^{-(z_D-u+2h_D)\sqrt{s/\nu ^2}}}{{\sqrt{s}\nu (1-e^{-2h_D \sqrt{s/\nu ^2}})}}+\frac{e^{-(2h_D-z_D+u-2z_{Dw})\sqrt{s/\nu ^2}}}{{\sqrt{s}\nu (1+e^{-2h_D\sqrt{s/\nu ^2}})}}, \end{aligned}$$

(140)

and consequently we get the following expression for the Laplace transform of $Z_{hj}$

$$\begin{aligned} L\left[ \mathrm{Z}_{hj}(z_D,t_D)\right]&= \frac{\pi e^{-(z_D+2z_{Dw})\sqrt{s/\nu ^2}}(-1)^j\mathrm{I}_j(\sqrt{s/\nu ^2})}{2\sqrt{2s}\left( 1-e^{-2h_D\sqrt{s/\nu ^2}}\right) } +\frac{\pi e^{-(2h_D-z_D)\sqrt{s/\nu ^2}}(-1)^j\mathrm{I}_j\left( \sqrt{s/\nu ^2}\right) }{2\sqrt{2s}\left( 1-e^{-2h_D\sqrt{s/\nu ^2}}\right) }\nonumber \\&\!+\frac{\pi e^{-(z_D+2h_D)\sqrt{s/\nu ^2}}\mathrm{I}_j \left( \sqrt{s/\nu ^2}\right) }{{2\sqrt{2s}\left( 1\!-\!e^{-2h_D\sqrt{s/\nu ^2}}\right) }}\!+\!\frac{\pi e^{-(2h_D-z_D-2z_{Dw})\sqrt{s/\nu ^2}}\mathrm{I}_j\left( \sqrt{s/\nu ^2}\right) }{{2\sqrt{2s}\left( 1\!-\!e^{-2h_D\sqrt{s/\nu ^2}}\right) }}, \nonumber \\ \end{aligned}$$

(141)

where $\mathrm{I}_j$ is the Modified Bessel function of the First kind.

Now let us consider the function $\varTheta _{2i}(1,\theta ,t_D)$. It can be seen that the series terms in the Laplace domain in Eq. 34 are slowly convergent for $r_D=1$, but from Abramowitz and Stegun (1972) we can find that

$$\begin{aligned} \frac{2\mathrm{K}_{\mathrm{n}}(\sqrt{s})}{\mathrm{K}_{\mathrm{n}-1}(\sqrt{s}) +\mathrm{K}_{\mathrm{n}+1}(\sqrt{s})} =-\frac{{\mathrm{K}_\mathrm{n}}(\sqrt{s})}{{\mathrm{K}'_\mathrm{n}}(\sqrt{s})}\sim \frac{\sqrt{s}}{\sqrt{s+n^2}} \end{aligned}$$

(142)

for large $n$. Thus, we can rewrite Eq. 34 for $r_D=1$ as

$$\begin{aligned} \varTheta _{2i}(1,\theta ,t_D)&= {\mathcal {L}^{-1}}\left\{ \frac{1}{\sqrt{s}}\sum _{n=0} \left( 1-\frac{\delta _{0n}}{2}\right) \left[ \frac{2{\mathrm{K}}_n(\sqrt{s}) \mathrm{J}_{2i}(n b_D)\cos (n\theta )}{\mathrm{K}_{n+1}(\sqrt{s}) +\mathrm{K}_{n-1}(\sqrt{s})}-\frac{\sqrt{s}\cos n\theta }{\sqrt{s+n^2}}\right] \right\} \nonumber \\&+ \frac{1}{\sqrt{\pi t_D}}\sum _{n=-\infty }^{\infty }e^{-n^2t_D} \mathrm{J}_{2i}(n b_D)\cos (n\theta ). \end{aligned}$$

(143)

Now the first sum converges very fast (about 50 terms is enough to obtain 4-5 digits precision), while the second has a very high convergence rate for $t_D\ge 1$, due to the presence of the exponential term. The convergence rate, however, slows down rapidly for $t_D<1$, we, therefore, propose to rewrite it in the following form:

$$\begin{aligned}&\sum _{n=-\infty }^{\infty }\frac{e^{-n^2t_D}}{\sqrt{\pi t_D}}\mathrm{J}_{2i}(n b_D)\cos (n\theta )\nonumber \\&\qquad =(-1)^i \int _0^\pi \sum _{n=-\infty }^\infty \frac{e^{-n^2t_D}}{\pi \sqrt{\pi t_D}}\cos (n[b_D\cos \alpha +\theta ]) \cos (2i\alpha ) \mathrm{d}\alpha \nonumber \\&\qquad =\frac{(-1)^i}{\sqrt{\pi }t_D}\sum _{n=-\infty }^{\infty } \int _0^\pi e^{-\frac{(2\pi n/b_D+\theta /b_D+\cos \alpha )^2}{4t_D/b_D^2}} \cos (2i\alpha ) \mathrm{d}\alpha . \end{aligned}$$

(144)

Note that here we used the Poisson summation formula. The last integral and summation can be easily evaluated exactly by the same way as we described for $Z_j$ and $Z_{hj}$ above. A similar technique without any significant changes can be also applied to evaluation of the function $\varTheta _{N_02i}$. It can also be shown that for large $n$

$$\begin{aligned} Fc_n\left( \xi _w,\theta ,\frac{a^2s}{4}\right)&\rightarrow \frac{2\sqrt{2} \mathrm{K}_{\mathrm{n}}\left( \sqrt{\frac{sa^2}{2}\sinh 2\xi _w}\right) \cos n\theta }{\sqrt{sa^2\sinh 2}\xi _w\left[ {\mathrm{K}_{\mathrm{n}-1}} \left( \sqrt{\frac{sa^2}{2}\sinh 2\xi _w}\right) +{\mathrm{K}_{\mathrm{n}+1}}\left( \sqrt{\frac{sa^2}{2}\sinh 2\xi _w}\right) \right] }\nonumber \\&\rightarrow \frac{\cos n\theta }{\sqrt{\frac{sa^2}{2}\sinh 2\xi _w+n^2}}, \end{aligned}$$

(145)

and

$$\begin{aligned} Fs_n\left( \xi _w,\theta ,\frac{a^2s}{4}\right)&\rightarrow \frac{2\sqrt{2} {\mathrm{K}_\mathrm{n}}\left( \sqrt{\frac{sa^2}{2}\sinh 2\xi _w}\right) \sin n\theta }{\sqrt{sa^2\sinh 2}\xi _w\left[ {\mathrm{K}_{\mathrm{n}-1}} \left( \sqrt{\frac{sa^2}{2}\sinh 2\xi _w}\right) +{\mathrm{K}_{\mathrm{n}+1}}\left( \sqrt{\frac{sa^2}{2}\sinh 2\xi _w}\right) \right] }\nonumber \\&\rightarrow \frac{\sin n\theta }{\sqrt{\frac{sa^2}{2}\sinh 2\xi _w+n^2}}. \end{aligned}$$

(146)

Thus, the series in Eqs. 115–116 can be rewritten as

$$\begin{aligned} \varTheta _{2i}^p(\xi ,\theta ,t_D)&= {\mathcal {L}^{-1}}\Bigg \{ \sum _{n=0} \Bigg [Fc_n\left( \xi ,\theta ,\frac{a^2s}{4}\right) \cos (n\theta _p)+Fs_n\left( \xi ,\theta , \frac{a^2s}{4}\right) \sin (n\theta _p)\nonumber \\&-\left( 1-\frac{\delta _{0n}}{2}\right) \frac{\cos [n(\theta -\theta _p)]}{\sqrt{\frac{sa^2}{2} \sinh 2\xi _w+n^2}}\Bigg ]\times {\mathrm{J}}_{2i}(nb_D) \Bigg \}\nonumber \\&+\frac{\sqrt{2}}{\sqrt{a^2\pi \sinh 2\xi _w t_D}}\sum _{n=-\infty }^{\infty }e^{-\frac{2n^2t_D}{a^2\sinh 2\xi _w}}{\mathrm{J}}_{2i}(n b_D)\cos [n(\theta -\theta _p)],\end{aligned}$$

(147)

$$\begin{aligned} \varTheta _{2i+1}^p(\xi ,\theta ,t_D)&= {\mathcal {L}^{-1}}\Bigg \{\sum _{n=1}\Bigg [Fs_n\left( \xi ,\theta ,\frac{a^2s}{4}\right) \cos (n\theta _p)-Fc_n\left( \xi ,\theta ,\frac{a^2s}{4}\right) \sin (n\theta _p)\nonumber \\&-\frac{\sin [n(\theta -\theta _p)]}{\sqrt{\frac{sa^2}{2}\sinh 2\xi _w+n^2}} \Bigg ] \times {\mathrm{J}}_{2i+1}(nb_D)\Bigg \}\nonumber \\&+\frac{\sqrt{2}}{\sqrt{a^2\pi \sinh 2\xi _w t_D}}\sum _{n=-\infty }^{\infty }e^{-\frac{2n^2t_D}{a^2\sinh 2\xi _w}}{\mathrm{J}}_{2i+1}(n b_D)\sin [n(\theta -\theta _p)].\nonumber \\ \end{aligned}$$

(148)

The last series in Eq. 147 has the same form as in the horizontally isotropic case, while the one in Eq. 148 can be rewritten as

$$\begin{aligned}&\frac{\sqrt{2}}{\sqrt{a^2\pi \sinh 2\xi _w t_D}}\sum _{n=-\infty }^{\infty }e^{-\frac{2n^2t_D}{a^2\sinh 2\xi _w}}{\mathrm{J}}_{2i+1}(n b_D)\sin [n(\theta -\theta _p)]\nonumber \\&\quad =(-1)^i\int _0^\pi \sum _{n=-\infty }^\infty \frac{\sqrt{2}e^{-\frac{2n^2t_D}{a^2\sinh 2\xi _w}}}{\pi \sqrt{a^2\pi \sinh 2\xi _w t_D}}\cos (n[b_D\cos \alpha +\theta -\theta _p])\cos [(2i+1)\alpha ] \mathrm{d}\alpha \nonumber \\&\quad =\frac{(-1)^i}{\sqrt{\pi } t_D}\sum _{n=-\infty }^{\infty } \int _0^\pi e^{-\frac{(2\pi n/b_D+[\theta -\theta _p]/b_D+\cos \alpha )^2}{4t_D/(a^2b_D^2\cosh \xi _w\sinh \xi _w)}}\cos [(2i+1)\alpha ] \mathrm{d}\alpha , \end{aligned}$$

(149)

which can be summed up in the same way as we proposed for $Z_j$ and $Z_{hj}$. The last point on which we want to focus is the computation of integrals in Eq. 40. On every subinterval $[t_1, t_2]$ the functions $\varTheta _i^{(p)}(1,\theta ,t_D)$, $Z_j(z_D,t_D)$ and $Z_{hj}(z_D,t_D)$ can be approximated as follows

$$\begin{aligned}&\displaystyle \varTheta _i^{(p)}(1,\theta ,t_D) = \frac{A_i(\theta )}{t^{1/2}}+\frac{B_j(\theta )}{t_D^{[i/2]+1}},\end{aligned}$$

(150)

$$\begin{aligned}&\displaystyle Z_j(z_D,t_D) = C_j(z_D)+\frac{D_j(z_D)}{t_D^{[j/2]+1/2}}, \end{aligned}$$

(151)

$$\begin{aligned}&\displaystyle Z_{hj}(z_D,t_D) = \left[ \frac{E_j(z_D)}{t_D^{1/2}}+\frac{F_j(z_D)}{t_D^{[j/2]}}\right] e^{-\frac{{\mathrm{min}} (2z_{Dw}+z_D-1,2h_D-2z_{Dw}-1)^2}{4\nu ^2t_D}}. \end{aligned}$$

(152)

We suggest computing the coefficients by a simple 2-point interpolation. Now the integral given in Eq. 40 can be written as

$$\begin{aligned} \int _{a_1}^{a_2}\tau ^{-\alpha }e^{-\beta /\tau } \mathrm{d}\tau =\int _{1/a_2}^{1/a_1}u^{\alpha -2}e^{-\beta u} \mathrm{d}u=\frac{e^{-\beta /a_2}}{a_2^{\alpha -1}}\int _1^{a_2/a_1}v^{\alpha -2}e^{-\frac{\beta }{a_2}(v-1)}\mathrm{d}v . \end{aligned}$$

(153)

Although the last integral can be expressed in terms of incomplete gamma functions, one can see that for a 4-step time scheme we proposed above, $a_2/a_1$ can take only the following values: $2, 1.5,\; \text{ and }\; 4/3$. Thus, this integral is a function of only one variable $\frac{\beta }{a_2}$ (while $a_2/a_1$ and $\alpha$ constitute only a finite set of parameters) and, therefore, can easily be approximated in a wide range using, for example, cubic splines for moderate values of $\frac{\beta }{a_2}$ and some simple asymptotic approximations for very small and very big values.