1 Introduction

Modelling of crack propagation behaviour correctly is important in many soil and biomedical engineering problems. Understanding of the fracture mechanism in porous materials is of great importance in oil recovery and intervertebral disc herniation. Prediction of fractures may enhance the oil recovery rates or give more insight in the treatment of intervertebral disc herniation. Last three decades numerical models are being developed for this purpose. Boone and Ingraffea (1990) developed an hydraulic fracturing model using the finite element method (FEM) for poroelastic materials. A cohesive zone description was used for the fracture process and the fluid flow in the fracture was solved using a finite difference method. In their work, the cohesive zone elements that model the crack were inserted in the finite element mesh beforehand, which requires an a priori knowledge of the fracture path. Secchi et al. (2007) used the finite element method to model a cohesive fracture as well, but included an adaptive remeshing method in order to accommodate for fracture propagation in arbitrary directions. This method was successfully applied to simulate a propagating crack in arbitrary directions and was even extended to three-dimensional situations (Secchi and Schrefler 2012). Unfortunately, the remeshing algorithm is computationally inefficient and may give rise to incorrect results in the case of non-linear behaviour of the bulk material.

An alternative technique to model arbitrary crack growth, irrespective of the structure of the underlying finite element mesh, is the use of the partition-of-unity property of finite element shape functions (Melenk and Babuška 1996). Belytschko and Black (1999), Dolbow et al. (2000) used this property to model a propagating crack in a solid material following linear elastic fracture mechanics. The crack is modelled as a discontinuity which is incorporated in the finite element method by enhancing existing nodes by additional degrees of freedom and is commonly referred to as the extended finite element method (X-FEM). Wells and Sluys (2001) incorporated a cohesive zone model in X-FEM to model fracture propagation in arbitrary directions in a solid. The strength of X-FEM is that a fracture can grow in any direction and at any time without the need of remeshing.

Recently, partition of unity method has also been used to model fracture propagation in porous materials. Borst et al. (2006) investigated shear banding in a porous material. A discontinuous description was used for both solid and fluid phase. Fluid flow is described by Darcy’s law with a constant permeability and a pressure gradient defined by the pressure difference on both sides of the crack. A continuous pressure description over the fracture was presented in (Réthoré et al. 2007). In their latter work the fluid flow is related to crack opening and a viscous Couette flow profile in the crack. However, no crack propagation was considered. Kraaijeveld and Huyghe (2011) extended this work towards ionized porous materials and considered propagating cracks. Pure mode-iand mode-iifractures were described with a continuous and discontinuous pressure, respectively.

In this contribution we enhance the aforementioned models to accommodate for crack nucleation similar to (Remmers et al. 2003), mixed-mode crack growth and propagation in an orthotropic material. We use the model to study the effect of the direction of crack growth in saturated porous media as a function of permeability. The porous material is described by the standard Biot equations and the fluid flow in the material is included by Darcy’s law. The partition of unity method in combination with the cohesive zone approach is used to introduce a crack. The crack is described by a strong discontinuity in the displacement field while the pressure field is considered to be continuous across the fracture. Fluid flow from the crack into the formation is accounted for. The tangential fluid flow is described with lubrication theory.

In the next paragraph the kinematic relations are described. We then present the momentum and mass balance equations in Sect. 3 and describe the discretization and numerical implementation in Sect. 4. The constitutive equations are given in Sect. 5. Finally, we show the performance of the numerical model in Sect. 6 and give some concluding remarks in Sect. 7.

2 Kinematic Relations

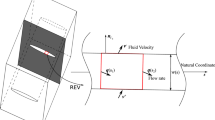
Consider a body \( \varOmega \) that is crossed by a discontinuity \(\varGamma _\mathrm{d}\), as shown in Fig. 1. The discontinuity divides the body in two domains, \(\varOmega ^+\) and \( \varOmega ^-\). The vector \(\mathbf{n}_{\text {d}}\) is defined as the normal of the discontinuity surface \(\varGamma _\mathrm{d}\) pointing into domain \(\varOmega ^+\). The total displacement field of the solid skeleton can, at any time \(t\), be described by a regular displacement field \(\hat{\mathbf{u}}(\mathbf{x},t)\) and an additional displacement field \(\tilde{\mathbf{u}}(\mathbf{x},t)\) (Belytschko and Black 1999; Moës et al. 1999; Remmers et al. 2008)

$$\begin{aligned} \mathbf{u}(\mathbf{x},t) = \hat{\mathbf{u}}(\mathbf{x},t)+\mathcal {H}_{\varGamma _\mathrm{d}}( \mathbf{x}) \tilde{\mathbf{u}}(\mathbf{x},t), \end{aligned}$$
(1)

where \(\mathbf{x}\) is the position of a material point in the domain \(\varOmega \) and \(\mathcal {H}_{\varGamma _\mathrm{d}}\) is the Heaviside step function, which is defined as

$$\begin{aligned} \mathcal {H}_{\varGamma _\mathrm{d}} = \left\{ \begin{array}{l l} 1 &{} \quad \text{ if } \quad \mathbf{x} \in \varOmega ^+ \\ 0 &{} \quad \text{ if } \quad \mathbf{x} \in \varOmega ^- . \end{array} \right. \end{aligned}$$
(2)

The strain field \(\varvec{\epsilon }\) results from differentiating the displacement field (1) with respect to material point \(\mathbf{x}\) with the assumption of small strain theory

$$\begin{aligned} \varvec{\epsilon }(\mathbf{x},t) = \nabla ^s\hat{\mathbf{u}}(\mathbf{x},t) +\mathcal {H}_{\varGamma _\mathrm{d}}\nabla ^s\tilde{\mathbf{u}}(\mathbf{x},t),\quad \mathbf{x}\notin \varGamma _\mathrm{d}. \end{aligned}$$
(3)

Here, \(\nabla ^s\) is the symmetric part of the differential operator

$$\begin{aligned} \nabla ^s \mathbf{u} = \frac{1}{2}(\nabla \mathbf{u}+(\nabla \mathbf{u})^T). \end{aligned}$$
(4)

The strain is not defined at the discontinuity surface \(\varGamma _\mathrm{d}\). Here, the opening of the discontinuity is the governing kinematic quantity, which is equal to the jump in the displacement field

$$\begin{aligned}{}[\mathbf{u} (\mathbf{x},t)]_\mathrm{d} = \tilde{\mathbf{u}}(\mathbf{x},t) , \quad \mathbf{x} \in \varGamma _\mathrm{d} . \end{aligned}$$
(5)
Fig. 1
figure 1

The body \(\varOmega \) crossed by discontinuity \(\varGamma _\mathrm{d}\). The body is completed with the boundary conditions

Full size image

The pressure field contains a weak discontinuity over the fracture. The gradient of this pressure difference quantifies the interaction of fluid flow between the fracture and the formation. By enhancing the pressure field with a signed distance function, as was used by Réthoré et al. (2007), the gradient near a discontinuity is taken into account in a natural way

$$\begin{aligned} p(\mathbf{x},t) = \hat{p}(\mathbf{x},t) + \mathcal {D}_{\varGamma _\mathrm{d}}(\mathbf{x})\tilde{p}(\mathbf{x},t) , \end{aligned}$$
(6)

where the distance function \(\mathcal {D}_{\varGamma _\mathrm{d}}(\mathbf{x})\) is defined as

$$\begin{aligned} \mathcal {D}_{\varGamma _\mathrm{d}}(\mathbf{x}) = |( \mathbf{x} - \mathbf{x}_{\varGamma _\mathrm{d}}) \cdot \mathbf{n}_\mathrm{d}| \, \quad \mathbf{x} \in \varOmega . \end{aligned}$$
(7)

Here, \(\mathbf{x}_{\varGamma _\mathrm{d}}\) is the coordinate of the nearest point on the discontinuity and \(\mathbf{n}_\mathrm{d}\) is the corresponding normal vector. The pressure gradient follows from the spatial derivative of the pressure field (6)

$$\begin{aligned} \nabla p(\mathbf{x}) = \nabla \hat{p}(\mathbf{x}) + \mathcal {D}_{\varGamma _\mathrm{d}}(\mathbf{x})\nabla \tilde{p}(\mathbf{x}) + \nabla \mathcal {D}_{\varGamma _\mathrm{d}}(\mathbf{x}) \tilde{p}(\mathbf{x}), \end{aligned}$$
(8)

where the gradient of the distance function \(\mathcal {D}_{\varGamma _\mathrm{d}}\)

$$\begin{aligned} \nabla { \mathcal {D}}_{\varGamma _\mathrm{d}}( \mathbf{x}) = \left\{ \begin{array}{l l} \mathbf{n}_\mathrm{d} &{} \quad \text {if} \quad \mathbf{x} \in \varOmega ^+ \\ -\mathbf{n}_\mathrm{d} &{} \quad \text {if} \quad \mathbf{x} \in \varOmega ^- \text {.} \end{array} \right. \end{aligned}$$
(9)

3 Balance Equations

The system is described by two balance equations: the balance of linear momentum and the mass balance. In the following, the weak form of both balance equations will be derived for both the bulk material and the interface.

The porous solid skeleton is considered to be fully saturated with a fluid. We assume that there is no mass transfer between the two constituents. The process is isothermal and gravity, inertia and convection are neglected. With these assumptions the linear momentum balance reads

$$\begin{aligned} \nabla \cdot \varvec{\sigma } = \mathbf{0} , \end{aligned}$$
(10)

where \(\varvec{\sigma }\) is the total stress which is decomposed in Terzaghi’s effective stress \(\varvec{\sigma _\mathrm{e}}\) and the hydrostatic pressure \(p\) (Terzaghi 1943)

$$\begin{aligned} \varvec{\sigma } = \varvec{\sigma _{ \mathrm e}} - p \mathbf{I}\, \text {.} \end{aligned}$$
(11)

In this equation \(\mathbf{I}\) is the unit matrix. The effective stress \(\varvec{\sigma _\mathrm{e}}\) is related to the strains \(\varvec{\epsilon }\) which have been defined in (3) by means of the constitutive law. In rate form, this reads

$$\begin{aligned} \dot{\varvec{\sigma _\mathrm{e}}}=\mathbf{C}\dot{\varvec{\epsilon }} . \end{aligned}$$
(12)

The momentum balance is completed with the following boundary conditions, see Fig. 1.

$$\begin{aligned} \begin{aligned}&\varvec{\sigma } \cdot \mathbf{n}_{\varGamma } = \mathbf{t}_\mathrm{p}(\mathbf{x},t), \quad \quad&\mathbf{x} \in \varGamma _t ,\\&\mathbf{u}(\mathbf{x},t) = \mathbf{u}_\mathrm{p}(\mathbf{x},t), \quad \quad&\mathbf{x} \in \varGamma _u ,\\ \end{aligned} \end{aligned}$$
(13)

with \(\varGamma _t \cup \varGamma _u = \varGamma , \varGamma _t \cap \varGamma _u = \emptyset \).

Under equal assumptions as made for the momentum balance, and assuming the fluid to be incompressible, the mass balance is written as

$$\begin{aligned} \nabla \cdot \mathbf{v}_\mathrm{s} + \nabla \cdot \mathbf{q} = 0 , \end{aligned}$$
(14)

where \(\mathbf{v}_\mathrm{s}\) is the deformation velocity of the solid skeleton and \(\mathbf{q}\) is the seepage flux, which is related to the pressure gradient by means of Darcy’s law: Darcy’s relation is assumed to hold for the fluid flow in the bulk material (Biot 1941)

$$\begin{aligned} \mathbf{q} = - \varvec{K} \cdot \nabla p , \end{aligned}$$
(15)

where \(\varvec{K}\) is the permeability tensor, which is assumed to be constant in time and space (Kraaijeveld and Huyghe 2011). In the case of an isotropic material, the permeability is equal to \( \varvec{K} = K \varvec{I}\). The mass balance is completed with the following boundary conditions, see Fig. 1.

$$\begin{aligned} \begin{aligned}&\mathbf{q}(\mathbf{x},t) \cdot \mathbf{n}_\varGamma = q_\mathrm{p}, \quad \quad&\mathbf{x} \in \varGamma _q \text {,} \\&p(\mathbf{x},t) = p_\mathrm{p}, \quad \quad&\mathbf{x} \in \varGamma _p \text {,} \end{aligned} \end{aligned}$$
(16)

with \(\varGamma _q \cup \varGamma _p = \varGamma , \varGamma _q \cap \varGamma _p = \emptyset \).

In accordance with the cohesive zone approach, the softening of the material is governed by a traction acting on the discontinuity surface. This traction is coupled to the hydrostatic pressure in the crack. Assuming continuity of stress from the formation to the fracture we can write the local momentum balance as

$$\begin{aligned} \varvec{\sigma } \cdot \mathbf{n}_\mathrm{d} = \mathbf{t}_\mathrm{d} - p_\mathrm{d} \mathbf{n}_\mathrm{d} , \end{aligned}$$
(17)

where \(p_\mathrm{d}\) is the hydrostatic pressure in the discontinuity

$$\begin{aligned} p_\mathrm{d} = p(\mathbf{x} \in \varGamma _\text {d} ) \end{aligned}$$
(18)

Mass balance is described by an equilibrium of fluid exchange between the formation and the fracture, the opening rate of the fracture and the tangential fluid flow in the fracture. This is written as

$$\begin{aligned} \mathbf{q}^+_{\varGamma _\mathrm{d}} \cdot \mathbf{n}_\mathrm{d} - \mathbf{q}^-_{\varGamma _\mathrm{d}} \cdot \mathbf{n}_\mathrm{d} = - [\dot{\mathbf{u}}]_n + u_n \frac{\partial }{\partial s} \left( k_\text {d} \frac{\partial p_\text {d} }{\partial s} \right) , \end{aligned}$$
(19)

with \(\mathbf{q}^+_{\varGamma _\mathrm{d}}\) and \(\mathbf{q}^-_{\varGamma _\mathrm{d}}\) being the fluid flow from the fracture into formation for the fracture lip of the \(\varOmega ^+\) and the \(\varOmega ^-\) domain, respectively, \([\dot{\mathbf{u}}]_n\) denotes the time derivative of the normal opening of the fracture and \(k_\text {d}\) being the permeability in the fracture. The latter is given by Witherspoon et al. (1980):

$$\begin{aligned} k_\text {d} = \frac{u_n^2}{12 \mu } \text {,} \end{aligned}$$
(20)

where \(\mu \) is the viscosity of the fluid. For the derivation of this equilibrium equation, we refer to Irzal et al. (2013). In Eq. (19) we used, under the assumption of small deformations, that the normal vector of the two fracture lips is in opposite direction.

The weak form of the balance equation is obtained by multiplying Eqs.(10) and (14) with an admissible displacement and pressure field, \( \varvec{\eta } \) and \(\zeta \), respectively. These admissible fields have the same form as the original fields

$$\begin{aligned} \varvec{\eta } = \hat{\varvec{\eta }} + \mathcal {H}_{\varGamma _\mathrm{d}} \tilde{\varvec{\eta }} ,\qquad \zeta = \hat{\zeta } + \mathcal {D}_{\varGamma _\mathrm{d}} \tilde{\zeta } . \end{aligned}$$
(21)

Substituting the variations into Eqs.(10) and (14), Applying Gauss theorem, using the symmetry of the Cauchy stress tensor, introducing the internal boundary \(\varGamma _\mathrm{d}\) and the corresponding admissible displacement jump and using the boundary conditions at the external boundaries \(\varGamma _{t}\) and \(\varGamma _{q}\) gives

$$\begin{aligned}&\in t _\varOmega \nabla \hat{\varvec{\eta }} : \varvec{\sigma } \text {d}\varOmega + \int _\varOmega \mathcal {H}_{\varGamma _\mathrm{d}} \nabla \tilde{\varvec{\eta }} : \varvec{\sigma } \text {d}\varOmega \nonumber \\&\quad = \int _{\varGamma _t} \hat{\varvec{\eta }} \cdot \mathbf{t}_\mathrm{p} \text {d}\varGamma _t + \int _{\varGamma _t} \mathcal {H}_{\varGamma _\mathrm{d}} \tilde{\varvec{\eta }} \cdot \mathbf{t}_\mathrm{p} \text {d}\varGamma _t - \int _{\varGamma _\mathrm{d}} \tilde{\mathbf {\eta }} \cdot ( \varvec{\sigma } \cdot \mathbf{n}_\mathrm{d} ) \text {d}\varGamma _\mathrm{d} \end{aligned}$$
(22)

and

$$\begin{aligned}&- \int _{\varOmega } \hat{\zeta } \nabla \cdot \mathbf {v}_\mathrm{s } \text {d}\varOmega - \int _{\varOmega } \mathcal {D}_{\varGamma _\mathrm{d}} \tilde{\zeta } \nabla \cdot \mathbf {v}_\mathrm{s } \text {d}\varOmega + \int _{\varOmega } \nabla (\hat{\zeta }) \cdot \mathbf {q} \text {d}\varOmega + \int _{\varOmega } \nabla ( \mathcal {D}_{\varGamma _\mathrm{d}} \tilde{\zeta } ) \cdot \mathbf {q} \text {d}\varOmega \nonumber \\&\quad \quad = \int _{\varGamma _q} \hat{\zeta } q_\mathrm{p} \text {d}\varGamma _q+ \int _{\varGamma _q} \mathcal {D}_{\varGamma _\mathrm{d}} \tilde{\zeta } q_\mathrm{p} \text {d}\varGamma _q - \int _{\varGamma _\mathrm{d}} \hat{\zeta } \mathbf {q}^+_{\varGamma _\mathrm{d}} \cdot \mathbf {n}_\mathrm{d} \text {d}\varGamma + \int _{\varGamma _\mathrm{d}} \hat{\zeta } \mathbf {q}^-_{\varGamma _\mathrm{d}} \cdot \mathbf {n}_\mathrm{d} \text {d}\varGamma . \end{aligned}$$
(23)

In these equations, \(\mathbf{t}_\mathrm{p} \) and \(\mathbf{q}_\mathrm{p}\) are the prescribed traction and prescribed fluid outflow boundary conditions, respectively (Fig. 1) and \(\varGamma _\mathrm{d}\) represents the integral over the internal boundary of the discontinuity. The terms \( \varvec{\sigma } \cdot \mathbf{n}_\mathrm{d} \) , \(\mathbf {q}^+_{\varGamma _\mathrm{d}} \cdot \mathbf {n}_\mathrm{d}\) and \(\mathbf {q}^-_{\varGamma _\mathrm{d}} \cdot \mathbf {n}_\mathrm{d} \) are given by the balance Equations at the discontinuity (17) and (19). By taking one of the admissible variations \(\delta \hat{\varvec{\eta }}, \delta \tilde{\varvec{\eta }}, \delta \hat{\zeta }\) and \(\delta \tilde{\zeta }\) at the time, the weak form of equilibrium can be separated into four sets of equations. A detailed description is given in (Réthoré et al. 2007; Wells and Sluys 2001).

4 Discretization and Numerical Implementation

The spatial discretization of the system of equations is based on the partition-of-unity property of finite element shape functions (Melenk and Babuška 1996). Using this property, the fracture is included in the FEM by adding an additional degree of freedom to the finite element nodes surrounding the fracture (Fig. 2). These additional degrees of freedom have the form of the additional terms in the field Eqs. (1) and (6) for the displacement and the pressure, respectively. The time discretization is performed using an implicit Euler time scheme. The resulting system is non-linear and is therefore solved with a Newton–Raphson iterative procedure. A detailed derivation and description is given in (Irzal et al. 2013; Kraaijeveld and Huyghe 2011; Réthoré et al. 2007)

Fig. 2
figure 2

A two-dimensional finite element mesh crossed by a discontinuity is represented by the black line. The black nodes surrounding the discontinuity are enhanced with additional degrees of freedom. The grey elements therefore contain additional terms in the stiffness matrix and the force vector

Full size image

The numerical implementation is based on and described in detail in the work of Remmers (2006) and Remmers et al. (2008). The most important aspects will be recaptured in this section. In addition, the new implementations of the nucleation of cracks and the propagation of cracks in transverse isotropic materials are introduced. Consider a finite element domain crossed by a discontinuity as shown in Fig. 2. A structured mesh containing four nodal elements is used in this work. Additional degrees of freedom are added to the black nodes which are crossed by the discontinuity. It is assumed that the discontinuity within an element is a straight line, always ends at an element edge, and is referred to as a cohesive segment. The numerical integration is performed by the standard Gauss integration. However, only using the original integration points is not sufficient any more since the discontinuity can cross an element at an arbitrary location. To acquire sufficient integration points at each side of the discontinuity, an integration method (Fig. 3) introduced by Wells and Sluys (2001), is used. Two integration points per element are located at the discontinuity to integrate the discretized local balance equations.

Fig. 3
figure 3

Numerical integration of a quadrilateral element crossed by a discontinuity

Full size image

To govern the propagation of a fracture, a fracture criterion is needed to determine the moment and the direction of propagation. The stress state at the crack tip is estimated based on the average stress in the vicinity of the tip. The averaging is calculated with a Gaussian weighting function (Jirásek 1998). The average stress \(\varvec{\sigma }_{\text {av}}\) at the crack tip is then the weighted sum of the stress in the integration points near the crack tip

$$\begin{aligned} \varvec{\sigma }_{\text {av}} = \sum _{i=1}^{\text {n}_{\text {int}}} \frac{w_i}{w_{\text {tot}}} \varvec{\sigma }_{\text {e,}i} \quad \text {with} \quad w_{\text {tot}} = \sum _{j=1}^{\text {n}_{\text {int}}} w_{j} \text {.} \end{aligned}$$
(24)

Here \(n_{\text {int}}\) is the number of integration points in the domain, \(\varvec{\sigma }_{\text {e,}i}\) is the current effective stress state in integration point \(i\) which has a weight factor \(w_{i}\) defined as

$$\begin{aligned} w_{i} = \frac{(2 \pi )^{-\frac{3}{2}}}{l_{a}^3} \mathrm{e}^{\frac{-r^2_i}{2l_{a}^2}} \text {,} \end{aligned}$$
(25)

with \(r_i\) being the distance between the crack tip and the integration point \(n_i\), and \(l_a\) being a length scale parameter defining how fast the weight factor decays as a function of the distance between the integration points and the crack tip. As was proposed by Remmers et al. (2008) the average stress surrounding the crack tip is used to determine both the moment and the direction of propagation. From this average stress, an equivalent traction \(t_{\text {eq}}\) at the crack tip is calculated (Camacho and Ortiz 1996)

$$\begin{aligned} t_{\text {eq}} (\theta ) = \sqrt{\langle {t_{{\text {n}}} } \rangle ^{2} + \frac{1}{\beta }t_{{\text {s}}}^{2} } \quad {\text {with}} \quad \left\langle {t_{{\text {n}}} } \right\rangle = \left\{ {\begin{array}{ll} 0 &{}\quad {{\text {if}} \quad t_{{\text {n}}} \le 0}\\ {t_{{\text {n}}} }&{}\quad {{\text {if}} \quad t_{{\text {n}}} > 0}\\ \end{array} {\text {,}}} \right. \end{aligned}$$
(26)

where \(\beta \) is a scaling factor for the shear stress, \(t_n\) and \(t_s\) are the normal and shear traction, respectively

$$\begin{aligned}&t_n = \mathbf{n}^T \varvec{\sigma _{\text {av}}} \mathbf{n}&t_s = \mathbf{s}^T \varvec{\sigma _{\text {av}}} \mathbf{n} \text {.} \end{aligned}$$
(27)

Here \(\mathbf{n}\) is the normal vector and \(\mathbf{s}\) is the tangent vector to an axis \(\eta \) which is rotated by an angle \(\theta \) with respect to the x-axis (Fig. 4). If the maximum equivalent traction exceeds the ultimate strength \(\tau _{\text {ult}}\) of the material the fracture is extended in the direction of angle \(\theta \) through one element.

Fig. 4
figure 4

Schematic representation of a material with at the crack tip the global \(x\)–\(y\) coordinate system and the local coordinate system, described with a normal unit vector \(\mathbf{n}\) and a tangential unit vector \(\mathbf{s}\)

Full size image

The disadvantage of using an average stress in the fracture criterion is that the crack propagation can be slightly delayed due to the averaging of the stress. The advantage is that the direction of propagation is more reliable since it is based on a global stress state. However, the initial traction in the discontinuity will also be underestimated (Remmers et al. 2008). To avoid this two different length scale parameters \(l_{a}\) are used, see Eq. (25). The moment and direction of fracture propagation are determined by a length scale parameter which is typically three times the element length (Wells and Sluys 2001), while the initial tractions are calculated with one-forth of this length scale.

The average stress criterion based on the equivalent traction in Eq. (26) is also used to determine the moment of fracture nucleation. Instead of calculating this criterion in each integration, which would be computationally inefficient, an additional checkpoint is added in the centre of each element (Fig. 5). Once the equivalent traction in one of the checkpoints exceeds the nucleation criterion a discontinuity is added. The cohesive segment is assumed to be straight and crosses the checkpoint under the angle \(\theta \) with respect to the x-axis. The cohesive zone of the nucleated crack must have a length of at least 1 element. The numerical implementation of this restriction is illustrated in Fig. 5 with three examples. If the nucleation criterion is exceeded in multiple checkpoints at the same time, nucleations occurs in the checkpoint with the highest equivalent traction.

Fig. 5
figure 5

Three different locations of nucleation checkpoints with corresponding cohesive zones

Full size image

4.1 Fracture Propagation in an Orthotropic Material

The structure of an orthotropic material induces anisotropic fracture properties. We assume the strongest direction of the orthotropic material as a fibre direction. Following Yu et al. (2002) we can define a directional depended ultimate strength as

$$\begin{aligned} \tau _{\text {ult}}(\alpha ) = \tau _{\text {min}} + ( \tau _{\text {max}} - \tau _{\text {min}})\cos (\alpha )^2 \text {,} \end{aligned}$$
(28)

here \(\alpha \) is the angle between the fibres and normal \(\mathbf{n}\) of the fracture, \(\tau _{\text {max}}\) is the ultimate strength in the fibre direction and \(\tau _{\text {min}}\) is the ultimate strength perpendicular to the fibre direction (Fig. 6). To determine if the equivalent traction (26) at angle \(\theta \) exceeds the fracture criterion it is necessary to express Equation (28) in terms of \(\theta \)

$$\begin{aligned} \tau _{\text {ult}}(\theta ) = \tau _\mathrm{min} + ( \tau _\mathrm{max} - \tau _\mathrm{min})\cos \left( \theta + \frac{1}{2} \pi - \theta _\mathrm{f} \right) ^2 \text {.} \end{aligned}$$
(29)

In the orthotropic material a fracture propagates or initiates if

$$\begin{aligned} \frac{t_{\text {eq}}(\theta )}{ \tau _{\text {ult}}(\theta )} > 1 \text {.} \end{aligned}$$
(30)
Fig. 6
figure 6

Schematic representation of a fracture under an angle \(\theta \) in an orthotropic isotropic material. The strength of the material defined by a fibre direction \(\theta _\mathrm{f}\). The angle \(\alpha \) is the angle between the fibre direction and the normal \(\mathbf{n}\) of the fracture

Full size image

5 Constitutive Equations

The mathematical formulation of the balance equations are completed by constitutive behaviour for the bulk material and the fracture. The constitutive relation for an orthotropic bulk material is also given.

5.1 Mechanical Behaviour of the Orthotropic Bulk

In the remainder of the paper we consider a special orthotropic material; a transverse isotropic material. Transverse isotropy is a common form of anisotropy in rock formations but is also present in many biological materials (Abousleiman et al. 1996; Weiss et al. 1996). A transverse isotropic material is an orthotropic material with one axis of material rotational symmetry. We assume that the strength of the transverse isotropic material is highest in the direction of the axis of rotational symmetry. Defining this direction again as the fibre direction, the isotropic relationships for the effective stress are replace by

$$\begin{aligned} \begin{pmatrix} \sigma _{11} \\ \sigma _{22} \\ \sigma _{12} \end{pmatrix} = \mathbf{C} \begin{pmatrix} \epsilon _{11} \\ \epsilon _{22} \\ \gamma _{12} \end{pmatrix} \text {,} \end{aligned}$$
(31)

where the stress components \(\sigma \) and the strain components \(\epsilon \) are defined in a local coordinate system \((1,2)\), as shown in Fig. 6. The [\(3\times 3\)] stiffness matrix \(\mathbf{C}\) is defined as

$$\begin{aligned} \mathbf{C} = \begin{pmatrix} \frac{E_{11}^2(1-\nu _{23})}{E_{11}(1-\nu _{23})-2E_{22}\nu _{12}^2} &{} \frac{E_{11} E_{22} \nu _{12}}{E_{11}(1-\nu _{23})-2E_{22}\nu _{12}^2} &{} 0 \\ \frac{E_{11} E_{22} \nu _{12}}{E_{11}(1-\nu _{23})-2E_{22}\nu _{12}^2} &{} \frac{E_{22}(E_{11}-E_{22} \nu _{12}^2)}{(1+\nu _{23})[E_{11}(1-\nu _{23})-2E_{22}\nu _{12}^2]} &{} 0 \\ 0 &{} 0 &{} G_{12} \\ \end{pmatrix} \text {.} \end{aligned}$$
(32)

In this equation, \(E_{11}\) and \(E_{22}\) are Young’s moduli, \(\nu _{12}\) and \(\nu _{23}\) are the Poisson’s ratios representing the compressive strain in the direction of the second subscript due to a tensile stress in the direction of the first subscript, and \(G_{12}\) is the shear modulus in the 1–2 plane. Here, based on symmetry, the following identity was used

$$\begin{aligned} \frac{\nu _{12}}{E_{11}} = \frac{\nu _{21}}{E_{22}} \text {.} \end{aligned}$$
(33)

The permeability is also a parameter depending on direction in an orthotropic material (Abousleiman et al. 1996). We also describe the fluid flow in an orthotropic material by Darcy’s law Eq. (15), with the permeability tensor \(\varvec{K}\) being defined as

$$\begin{aligned} \varvec{K} = \begin{pmatrix} K_{1}&{}0 \\ 0&{}K_{2} \end{pmatrix} \end{aligned}$$
(34)

where \(K_1\) and \(K_2\) are the permeabilities in the direction of the subscript.

5.2 Mechanical Behaviour in the Fracture

The constitutive mechanical behaviour at the discontinuity is given by a relation between the traction at the interface and the displacement jump \(\mathbf{u}_\mathrm{d}\) across the discontinuity (Irzal et al. 2013)

$$\begin{aligned} \mathbf{t}_\mathrm{d} = \mathbf{t}_\mathrm{d}(\mathbf{u}_\mathrm{d},\kappa ) \text {.} \end{aligned}$$
(35)

Here \(\kappa \) is a history parameter that is equal to the largest displacement jump reached. The relation between the traction \(\mathbf{t}_\mathrm{d}\) and the displacement jump \(\mathbf{u}_\mathrm{d}\) can be any phenomenological relation, see e.g. Shet and Chandra (2002), and is referred to as a cohesive law.

The initial normal and shear tractions, respectively written as \(t_{\mathrm{n}_0}\) and \(t_{\mathrm{n}_0}\), are taken to be equal to the normal and shear traction at the moment of propagation (27) in order to avoid sudden jumps in the stress. Based on the work of Camacho and Ortiz (1996) a distinction is made between normal and shear softening behaviour. If the initial normal traction is positive the discontinuity is assumed to open as a cleavage crack. The normal and shear tractions decay linearly to zero from their initial values as a function of the normal opening of the crack (Fig. 7)

$$\begin{aligned}&t_\mathrm{n} = t_{\mathrm{n}_0} \left( 1 - \frac{v_\mathrm{n}}{v_{\mathrm{n}_\mathrm{cr}}} \right)&t_\mathrm{s} = t_{\mathrm{s}_0} \left( 1 - \frac{v_\mathrm{n}}{v_{\mathrm{n}_\mathrm{cr}}} \right) \mathrm{sgn}(v_\mathrm{s}) \text {.} \end{aligned}$$
(36)

Here \(v_\mathrm{n}\) and \(v_\mathrm{s}\) are respectively the normal and sliding the displacement, \(\mathrm {sgn}(\cdot )\) is the signum function.

Fig. 7
figure 7

The normalized tractions across the discontinuity as a function of the displacement jump in: a a cleavage crack and b a shear crack

Full size image

The parameter \(v_{\mathrm{n}_\mathrm{cr}}\) is the length of the fully developed traction-free crack. This parameter depends on the fracture toughness \(\mathcal {G}_\mathrm{c}\), which is the area under the softening curve, and the initial normal traction \(t_{\mathrm{n}_0}\)

$$\begin{aligned} v_{\mathrm{n}_\mathrm{cr}} = \frac{2\mathcal {G}_\mathrm{n}}{t_{\mathrm{n}_0}} \text {.} \end{aligned}$$
(37)

The traction-separation relations for unloading and shear opening are described in detail in (Camacho and Ortiz 1996). Self-contact of the fracture is simulated by using a penalty stiffness method.

It is necessary to perform a linearisation on Eq. (35) in order to use the tangential stiffness matrix in an incremental iterative solution

$$\begin{aligned} \Delta \mathbf{t}_\mathrm{d} = \mathbf{T} \Delta \mathbf{u}_\mathrm{d} \text {.} \end{aligned}$$
(38)

6 Examples

In the first two examples, the accuracy of the model for an isotropic and a transverse isotropic material is analysed in an unconfined compression test. An analytical solution is available for both problems. In the last two examples the performance of the numerical model is investigated by simulating fracture propagation in a transverse isotropic material and by a mixed-mode fracture problem. All examples are two dimensional in a plane strain setting. The mesh consists of quadrilateral elements with bilinear shape functions for both the displacement and the pressure. This interpolation order means we violate the Babuška-Brezzi condition (Brezzi 1974). However, no adverse effects of the violation have been observed in the numerical results.

6.1 Unconfined Compression

The accuracy of the poroelastic model is tested by considering the Mandel–Cryer benchmark (Cryer 1963; Mandel 1953). In the Mandel–Cryer problem an infinitesimal long plate, considered under plane strain conditions, is rigged compressed by a force of \(F\) = 0.1 N (Fig. 8). The specimen dimension is taken as \(a=1\) mm. The material parameters are given in Table 1. The squared elements have a size of 0.05 mm and the time step is 150 s. Free drainage is assumed at the lateral sides of the specimen. Due to the drainage a pore pressure decrease occurs, leading to a loss of stiffness at the sides. To compensate for this loss, the pore pressure rises in the undrained centre of the specimen. This non-monotonic pressure response characterizes the Mandel–Cryer problem. The normalized pore pressure across the specimen in the x-direction is shown in Fig. 9. The numerical pore pressure is consistent with the analytical solution.

Fig. 8
figure 8

Scheme and result of the Mandel Cryer benchmark

Full size image
Fig. 9
figure 9

Normalized pressure \( \frac{5\text {a}}{F}p\) over the sample in x-direction, where \(x=0\) is in the centre. The numbers drawn in the line indicate the time in seconds. Analytical solution from Mandel (1953)

Full size image
Table 1 Model parameters used in the isotropic Mandel–Cryer benchmark
Full size table

The isotropic solution for the Mandel–Cryer problem was extended to transverse isotropic materials by Abousleiman et al. (1996). This analytical solution is used to determine the accuracy of the numerical model for a transverse isotropic material. The benchmark problem is similar than that in the isotropic case (Fig. 8). The transverse isotropic material has a higher stiffness in the vertical direction \((\theta _\mathrm{f} = 90^\circ )\). The material parameters are given in Table 2. The anisotropic permeability has no influence on the analytical solution. Therefore, we consider the permeability also isotropic in this example. The numerical result for the anisotropic Mandel–Cryer problem is also consistent with the analytical solution (Fig. 10).

Fig. 10
figure 10

Normalized pressure \( \frac{5\text {a}}{F}p\) over the sample in x-direction, where \(\hbox {x}=0\) is in the centre. The numbers drawn in the line indicate the time in seconds. Analytical solution from Abousleiman et al. (1996)

Full size image
Table 2 Model parameters used in the anisotropic Mandel–Cryer benchmark
Full size table

6.2 Fracture Propagation in a Transverse Isotropic Material

To illustrate the performance of the numerical model for a fracture propagating in a transverse isotropic material a mode ifracture is considered (Fig. 11). Free drainage (\(p\) = 0) is assumed at the sides of the specimen. An initial fracture with a length of 5.0 mm is created in the centre and the anisotropic stiffness taken as \(\theta _\mathrm{f} = 70^\circ \). The top and bottom surface are pulled with a constant velocity \(v=5.0\mathrm{e}^{-6}\frac{\text {mm}}{\text {s}}\) in vertical direction while the displacement in horizontal direction is constrained. The element length is 0.20 mm and a time step of 50 s is used. The average stress is scaled by parameter \(l_{a}\) = 0.6 mm. An overview of the material parameters are given in Table 3.

Fig. 11
figure 11

A rectangular plate of porous material with an initial crack. The material is transverse isotropic with \(\theta _\mathrm{f} = 70^\circ \)

Full size image
Table 3 Model parameters used in the anisotropic Mode 1 fracture simulation
Full size table

A small influence of the transversal permeability can be seen in the pressure distribution before propagation occurs (Fig. 12a). The pressure gradient is aligned with the direction of the low permeability. Using the adapted propagation criterion (29) for anisotropic materials, the crack grows parallel to the anisotropic stiffness (Fig. 12b). This is a result of the values for \(\tau _{\text {max}}\) and \(\tau _{\text {min}}\) but does represent the propagation of a fracture in a transverse isotropic material.

Fig. 12
figure 12

Visualization of the pressure distribution. The displacements are amplified by a factor 10. a Pressure distribution at \(t\) = 500 s, b pressure distribution at \(t\) = 2,000 s

Full size image

6.3 Mixed-Mode Fracture

The performance of the numerical model is analysed considering a mixed-mode fracture in a L-shaped porous material (Fig. 13). This type of problem has been investigated experimentally by Winkler (2001) in a concrete material and was successfully reproduced using solid mechanics X-FEM (Dumstorff and Meschke 2007; Unger et al. 2007). In this example we consider a soft porous material with a Young’s modulus of 90.0 MPa and a permeability of 7.5\(\mathrm{e}^{-3} \frac{\text {mm}^4}{\text {Ns}}\). The time step is 300 s and the element length is 10.0 mm. The average stress parameter is taken as \(l_{a}\) = 30.0 mm. Further material parameters are given in Table 4. The specimen is constrained in both directions at the bottom surface. At the right surface free drainage is prescribed while the other surfaces are impervious. There is no initial crack present in the material so the nucleation point will be determined numerically. A velocity \(U=2.5\mathrm{e}^{-4}\) \(\frac{\text {mm}}{\text {s}}\) is prescribed at a distance of 30 mm of the boundary at the middle surface.

Fig. 13
figure 13

Schematic representation of the L-shaped fracture problem

Full size image
Table 4 Material properties L-shaped mixed-mode test
Full size table

The early pressure distribution can be seen in Fig. 14a. The prescribed displacement induces a positive pressure near the loading point. At the middle surface a negative pressure arises due to extension. This leads to fluid flow towards this region (Fig. 15). Fracture nucleation takes place, as expected, at the central corner and results in a negative pressure surrounding the fracture (Fig. 14b). The negative pressure is generated by the triaxial stress state near the fracture tip Anderson (2005). This stress is first taken up by the fluid resulting in negative pore pressure. The pressure profiles at two later time points can be seen in Figs. 14c, d. The low pressure surrounding the fracture leads to fluid flow from the formation into the fracture (Fig. 16). Immediately after fracture nucleation occurred, closing of the fracture took place. This is a result of the initial traction present in the nucleated fracture. To prevent this, the initial traction in the element at the mesh border is neglected.

Fig. 14
figure 14

Pressure distribution of the L-shaped mixed-mode fracture. a \(t\) = 17,100 s, b \(t\) = 29,700 s, c \(t\) = 54,000 s, d \(t\) = 150,000 s

Full size image
Fig. 15
figure 15

Flow (\(\frac{\text {mm}}{\text {s}}\)) distribution of the L-shaped mixed-mode fracture at \(t\) = 17,100 s. a Flow in x-direction, b flow in y-direction

Full size image
Fig. 16
figure 16

Flow (\(\frac{\text {mm}}{\text {s}}\)) distribution of the L-shaped mixed-mode fracture at \(t\) = 42,300 s. a Flow in x-direction, b flow in y-direction

Full size image

To further investigate the performance of numerical model the same simulation is repeated with two different permeabilities. Permeability values of \( 7.5\mathrm{e}^{-2} \; \frac{\text {mm}^4}{\text {Ns}}\) and \( 7.5 \; \frac{\text {mm}^4}{\text {Ns}}\) are used. The permeability has an influence on the moment of fracture nucleation, on the fracture propagation velocity and on the fracture pattern (Fig. 17). The higher the permeability, the earlier a fracture nucleates. This phenomenon is a consolidation effect. The tensile stress near the nucleation point is initially carried by the fluid pressure. This results in a negative pressure and a fluid flow towards this point (Figs. 14a and 15). There is a stress transfer from the fluid towards the solid skeleton as fluid flow progresses. Since the fluid flow is linearly depended on the permeability there is a faster stress transfer in a more permeable material. The fracture criterion is therefore exceeded earlier. For the same reason the fracture propagates faster in a highly permeable material.

Fig. 17
figure 17

Crack path for 3 different permeability values at \(t\) = 60,000 s. The graph is zoomed in at the grey box shown in Fig. 13

Full size image

We hypothesize that the bending of the crack is also correlated with the consolidation theory. The right part of the sample is in compression and fluid is squeezed out of this area resulting a slower tensile stress transfer. This effect is strengthened in case of a lower permeability. Therefore, the fracture propagates downwards because the right side of the material compressed.

7 Conclusion

We have extended two-dimensional numerical formulation for fracture propagation in porous materials to model nucleation in orthotropic materials. A fracture can grow in arbitrary directions by exploiting the partition-of-unity property of finite element shape functions. The direction of propagation is based on an average stress criterion surrounding the crack tip. This criterion is adapted for a orthotropic material by considering the directional stiffness of the material. The exchange of fluid between the formation and the fracture is accounted for. The tangential fluid flow in the fracture is included by the lubrication theory. The accuracy of the numerical model is investigated using the Mandel–Cryer Benchmark for both isotropic and transverse isotropic materials. The results show good consistency with the analytical solution.

In the transverse isotropic mode ifracture problem we successfully showed a propagating fracture in an anisotropic material. The pressure distribution is depending on the anisotropic permeability and the fracture direction is aligned with the highest strength direction of the material. The L-shaped problem demonstrates the possibility to use a poroelastic partition of unity-based cohesive zone model to simulate crack nucleation and subsequent mixed-mode growth in porous materials. The fracture path and propagation velocity were found to depend on the permeability of the bulk material. It shows the capability of our numerical model to respond to a change in a material parameter. Experimental validation and quantification of this phenomenon remains to be demonstrated.