1 Introduction

Mass transport of solutes in disordered porous media is of interest in many areas of science and engineering. Examples include remediation of contaminated groundwater (Tang et al. 1981; Grathwohl 1998), tracer studies in oil recovery (Whitaker 1967), radioactive waste disposal (Yu and Neretnieks 1997; Bourg et al. 2003), development of modern chemical catalysts (Wakao and Smith 1962; Carberry 2001), etc. Most applications require further understanding the effects of pore space changes, e.g., due to various physical, chemical, thermal and mechanical processes, on the transport properties. Progress can be achieved by development of physically based and microstructure-informed models suitable for analyses of such effects. Important initial requirement is that such models be able to predict measurable transport properties at a macro-scale (engineering, geological) from measurable pore space characteristics describing structures at a meso-scale (tens of inter-pore distances).

Pore network models are amongst the appealing approaches that have been used to model transport properties in porous structures. Such models have been applied to single-phase transport problems involving residual saturation and capillary pressure, as well as to relative permeability, multi-phase flow or mass transfer problems, dispersion, etc. (Blunt et al. 2002; Gao et al. 2012; Joekar-Niasar et al. 2008; Blunt 2001; Reeves and Celia 1996).

Pore network models contain a set of sites and a set of bonds connecting some of the sites. Mathematically, this is a graph embedded in appropriate Euclidean space—2D for planar and 3D for spatial network models. The bonds are pathways for mass transport, while sites are bond junctions directing transport according to (dynamic) equilibrium. The success of such models depends on the way they represent the real pore space in terms of its geometrical and topological characteristics. In most cases, the sites are considered as pores and the bonds are considered as throats, collectively representing the real pore space.

For some applications, such as multi-phase flow, it may be necessary to pay specific attention to the local morphology of the throats (Gao et al. 2012; Payatakes et al. 1973; Man and Jing 1999; Fenwick and Blunt 1998; Hui and Blunt 2000). For others, such as longer-scale permeability or diffusivity predictions, the throats could be considered as straight channels with locally averaged cross sections (De Josselin de Jong 1958). In the latter case, the variability in throat morphologies becomes of secondary importance. The transport is controlled predominantly by the spatial positions of pores, and the connectedness of the pore set via throats with different permittivities.

Pore network models have to reflect basic geometric properties of the porous media, such as porosity and size distributions of pores and throats. This has been demonstrated and discussed in a number of works, e.g., (Meyers et al. 2001; Dillard and Blunt 2000; Blunt et al. 1992; Ioannidis and Chatzis 1993; Paterson et al. 1996; Pereira et al. 1996). In addition, the models have to reflect basic topological properties, such as average pore coordination number and pores coordination spectrum. The effect of the average pore coordination on transport coefficients has been demonstrated in a number of works (Chatzis and Dullien 1977; Wilkinson and Willemsen 1983; Meyers and Liapis 1999). The spectrum represents the relative numbers of pores coordinated by different numbers of throats. This poses a stronger constraint on the construction of a pore network than the average pore coordination number. The effect of different spectra with the same average pore coordination number on transport has also been demonstrated (Jivkov et al. 2013).

For a number of porous media, the geometrical and topological properties of the pore space can be determined by analysis of 3D images, obtained e.g., with synchrotron X-ray computed micro- tomography (Al-Raoush and Willson 2005; Dong and Blunt 2009). This applies to media with pore sizes substantially larger than 100 nm, such as sandstone and limestone, where the throats can be resolved and coordination spectra as well as the average pore coordination numbers can be calculated. In such cases, topologically representative networks can be constructed by a selection of a regular basis of pores and throats connecting neighbouring pores, and subsequent elimination of throats to achieve the topological constraints. This has been illustrated for average coordination number in simple bases, such as cubic lattice, e.g., (Dixit et al. 1998, 2000; Raoof and Hassanizadeh 2010), as well as for full coordination spectra in a bi-regular lattice (Jivkov et al. 2013). A limitation of such constructions is that potential correlations between sizes of pores and adjacent throats are not accounted for.

When statistical geometry (size) and topology (connections) data are available, a regular pore network can be constructed relatively easily by calculating an appropriate length scale. The length scale refers to the distance between the centres of neighbouring lattice sites. If the pores are assigned to the sites, the length scale has the meaning of average inter-pore distance in the real medium. If the pores are assigned to the bonds of the lattice, connecting neighbouring sites, the length scale has the meaning of pore length in the real medium. The latter intepretation is used in the current work, as the experimental evidence is for elongated nearly cylindrical pores.

For micro- and meso-porosity, e.g., below 100 nm, the smallest pore radii detected by focused ion beam nanotomography (FIB-nt) are around 5 nm (Keller et al. 2011). The pore sizes below 5nm can be obtained from \(\hbox {N}_{2}\) adsorption analysis (NAGRA 2002). The resolution of the experimental techniques is not sufficient to identify throats, if such exist in the same sense as for macro-porosity. For pore network construction, this means that connectivity data for a “standard” elimination-based construction are not available or is partially available as a large number of connections are below the experimental resolution. In such cases, the length scale of a network model based on the available data is not calculable without additional assumptions.

One possibility is to assume that spherical pores of sizes dictated by the measured distribution are located at every network site and their cumulative volume determines the measured porosity. This allows for the calculation of a length scale, but the connectivity between neighbouring pores needs to be controlled differently. For example, introducing a throat diffusivity calculated from the sizes of the connected pores and the size of the solute molecules yields a specific network topology and diffusivity emerging from there (Xiong et al. 2014). The approach was shown to provide insights into the structure control of diffusivity and the results correlated well with experimentally measured diffusion coefficients (Xiong et al. 2014). However, it is not sufficient to explain the variability in reported experimental measurements of diffusion coefficients or observed anisotropic transport in a number of porous media. The development of a more realistic model for media with partially resolvable pore space characteristics needs to reflect additional experimental observations and introduce a length scale that provides a constraint to the model rather than being determined from total porosity and location of pores in all lattice sites.

The aim of this work is to develop a methodology for pore network construction for media with known porosity, but partially known pore size distribution and topological properties. Opalinus clay is selected as a model material to illustrate the application of the new model. It exhibits very low permeability and the principal mass transport mechanism is diffusion (Kohler et al. 1996). Opalinus clay has large specific surface area, high ion-exchange capacity, and sorption affinity for organic and inorganic ions, and is considered as the main candidate in the decontamination and treatment of heavy metal ions (Aytas et al. 2009), and as potential backfill material in the disposal of radioactive nuclear wastes (Boult et al. 1998).

Sorption of diffusing species changes the pore space in Opalinus clay and may have a significant beneficial impact on the long-term diffusivity (Wang et al. 2005). The macroscopic diffusivity of the system with and without sorption is different (Korichi et al. 2010). The latter is usually referred to as the effective diffusivity of the medium, \(D_\mathrm{e}\), and depends on the pore space structure alone. The former is referred to as the apparent diffusivity, \(D_\mathrm{a}\), and depends on the sorption kinetics in addition to the pore space structure. In this work only effective diffusivity is analysed, the apparent diffusivity can be studied similarly to our previous work (Xiong et al. 2014). In view of the role of clay as a barrier to radionuclide transport, the focus here is on the diffusion of Tritiated water molecules, HTO.

The network construction proposed in this work is very different from our previous study and reflects a recent report on the geometry and topology of Opalinus pore system (Keller et al. 2011). Since the observable data are insufficient to establish rigorously a length scale, a parametric study of the length scale effect on the transport properties is performed. Further, the experimentally observed pore space anisotropy is incorporated to calculate a diffusivity tensor to the degree allowed by the model topological structure. The results are in good agreement with experimentally measured diffusion coefficients, and the methodology can be used to determine model length scales using such experimental diffusion coefficients.

2 Material and Methods

2.1 Experimental Data

Opalinus clay displays pore sizes ranging from 1 to 100 nm which dominate its transport properties (Marschall et al. 2005). In addition, Opalinus clay is anisotropic due to preferred orientation (or texture) of clay minerals attained during sedimentation and compaction (Wenk et al. 2008). Experiments indicated anisotropic diffusion of solute species with fast diffusion parallel and slow diffusion perpendicular to the bedding plane. The 3D pore size distribution data of Opalinus clay used in this work are obtained by focused ion beam (FIB) nano-tomography and \(\hbox {N}_{2}\) adsorption analysis (Keller et al. 2011).

The pore space resolved by FIB-nt consisted of a large number of disconnected pores located predominantly within the fine-grained clay mineral matrix. These larger pores were elongated in the bedding plane, had approximately cylindrical shapes with radii \(>\)10 nm and occupied approximately 1.7 vol% of the sample. Thus the volume density (porosity) of the larger (observable) pores is \(\theta _{o} = 0.017\). Further, the observable pores by FIB-nt were largely isolated and did not provide a percolating network through the sample. \(\hbox {N}_{2}\) adsorption analysis gave a total physical porosity of around 10.4 vol%, of which 8.7 vol% were attributed to pores with un-resolvable sizes \(<\)10 nm. Thus the volume density (porosity) of the smaller (un-resolvable) pores is \(\theta _{u} = 0.087\).

These results strongly suggest that the fine-grained clay matrix contains an extensive pore network with comparatively small pore radii. Thus, the pore space analysed by FIB-nt is considered as part of the effective “flow relevant” porosity that surrounds the clay mineral particles and is interconnected by small pores with radii \(<\)10 nm, which cannot be resolved by FIB-nt. Our interpretation of this results is given in Fig. 1a as cumulative pore volume versus pore radius, revealing total porosity of the sample \(\theta = 0.104\). Pore connectivity information is not available from the experiments. It is described that the pore radii in the distribution are determined by assumed a cylindrical pore shape (Keller et al. 2011). This allows us to use the radii for the construction explained in Sect. 2.3.

Fig. 1
figure 1

Pore size distribution in Opalinus clay: a Cumulative pore volume fraction versus pore size distribution determined by FIB-nt and \(\hbox {N}_{2}\) adsorption analyses, interpreted from (Keller et al. 2011); b cumulative distribution of larger pore sizes, obtained from the experimental data and used for selecting pore population by a generator of uniformly distributed random numbers as illustrated; c cumulative distribution of smaller pore sizes with assumed probability density from (a)

Full size image

For the construction, pore radii are selected from the experimental pore size distribution using a generator of uniformly distributed random numbers, \(0 \le p < 1\). This requires the use of the cumulative distribution function, \(F(r)\), which gives the probability of finding a pore of radius smaller than \(r\). The cumulative probability function is constructed from the experimental data using the expression \(F(r) = 1 - v / v_\mathrm{max}\), where \(v\) is the volume fraction for a given radius \(r\) in Fig. 1a and \(v_{max}\) is the volume fraction for all large pores (1.7 %) or small pores (8.7 %). This expression ensures that when a uniformly distributed random number, \(p\), is selected, the corresponding pore size \(r=F^{-1}(p)\) belongs to the measured distribution and the accumulated volume of such selections equals \(v\) (Meyer and Klobes 1999).

The experimental distribution from Fig. 1a is split into cumulative probability of larger and smaller pores shown in Fig. 1(b) and Fig. 1(c), respectively. This is required to make independent generations of the two pore systems. For a given uniformly distributed random number \(p\), the pore size could be determined numerically by linear interpolation between experimental points as illustrated in Fig. 1(b) and Fig. 1(c).

The specific details are as follows:

$$\begin{aligned} r=\left\{ {{\begin{array}{l@{\quad }l} {r_{i-1} } &{} {p=F\left( {r_{i-1} } \right) },\\ {ar_i +\left( {1-a} \right) r_{i-1} } &{} {F\left( {r_{i-1} } \right) <p<F\left( {r_i } \right) ,a=\frac{p-F\left( {r_{i-1} } \right) }{F\left( {r_i } \right) -F\left( {r_{i-1} } \right) }}, \\ {r_i } &{} {p=F\left( {r_i } \right) }, \\ \end{array} }} \right. \end{aligned}$$
(1)

where \(r_{i}-_{1}<r_{i}\) and \(F(r_{i}-_{1})<F(r_{i})\). This process ensures that any collection of generated pore sizes belongs to the experimental distribution.

2.2 Previous Modelling and Present Approach

While there has been little effort on network modelling of Opalinus clay, a number of studies on network modelling of anisotropic media have been reported. The classical approach is to distribute a wide range of correlated pore and throat size distributions over a known structured medium (Knackstedt et al. 2001). One shortcoming of this is that only the sizes of the pores and throats exhibit heterogeneity; the underlying topology does not.

Another approach is to use packing algorithms. Many packing algorithms, such as sphere-packing algorithm (Thane 2006), are able to create heterogeneous grain packing with a wide distribution of grain sizes. Pore-network model construction for these packing is typically done via Delaunay tessellation (DT) of the grain centres. Using this approach a two-scale unstructured pore network model for multi-phase problems has been recently proposed (Mehmani and Prodanović 2014). The macro-network is constructed by Delaunay tessellation of the grain centres. However, this could generate many distorted pores when many small grains touch a large grain. The method is also based on the assumption that there exists a network that is representative of the clay voids and the scaling factor \(b\) is known based on measurements which may be difficult to obtain.

A multi-scale approach to simulate geometrical and transport properties of clay pore structure has also been reported recently (Tyagi et al. 2013). First, the clay micro-structure including grains, micropores and nanopores is generated. The micropores are assigned to segments of the grain boundaries and the nanopores are assigned to the interlayer. Then the homogenisation-based techniques are used to up-scale the transport coefficients. The homogenised macro-scale models are only valid, if scale separation exists. For micropores generation, it is not possible to force the desired correlation functions. As it is clear that the larger the variance in pore size distribution, the finer the grid that needs to be used. And the information for nanopores is difficult to obtain from experimental techniques.

In this work, we maintain the view that regular networks can still be used to generate models which represent anisotropic and heterogeneous media. The advantage of regular networks is that the influence of meso-scale averaged parameters, such as averaged inter-pore distances, can be studied, in representative topologies. Such effects cannot be easily analysed with unstructured networks, e.g., build from Voronoi tessellations around randomly distributed in pore space.

Our strategy consists of the following three main steps:

  • Selection of appropriate topological basis for network construction, representing the average neighbourhood in a pore system;

  • Allocation of larger pores in line with their relative porosity and size distribution in a preferred direction; and

  • Allocation of smaller pores according to their relative porosity and size distribution in domains and directions not occupied by larger pores.

With this construction strategy, we explore the effect of different length scales in the bedding and out-of-bedding directions, where the bedding direction may be occupied solely by larger pores or complemented by smaller pores, and the out-of-bedding direction may be occupied exclusively by smaller pores or complemented by a small fraction of larger pores.

2.3 Pore Network Topology

Pore networks can be constructed directly from reconstructed 3D-images of porous samples (Piri and Blunt 2005). Such a construction uses the locations and radii of the pores and throats and results in an irregular network specific to the imaged sample. The irregular pore network is useful for validating the physics behind flow simulations with 4D imaging of mass transport through the sample.

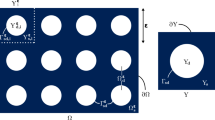
In the absence of data for connectivity and throat sizes, direct construction of irregular network is not possible. One remedy is to construct a network based on a regular cellular complex which represents the spatial distribution of pores in an average sense, i.e., to perform a prior “geometric homogenisation” of the medium. In a previous work (Jivkov et al. 2013) we have proposed a complex of compactly packed truncated octahedral cells, Fig. 2a, considering that a cell of this shape represents the average neighbourhood of a pore in a material. This complex represents the physical space. It is reduced to a mathematical graph by placing sites (graph nodes) at the centres of all cells and bonds (graph edges) between neighbouring sites as illustrated in Fig. 2b.

Fig. 2
figure 2

Cellular complex as basis for network construction: a fragment illustrating compact tessellation of a porous medium into cells, with each cell representing the average pore neighbourhood; and b cell neighbourhood illustrating graph elements to which experimental pore system information is mapped

Full size image

If a microstructure to graph mapping assumes that pores mapped to sites and throats are mapped to some bonds, then the maximum pore coordination offered by this topology is 14. This is a mapping, suitable for pore systems containing predominantly spherical pores with connectivity and throat size statistics obtained from experimental data (Jivkov et al. 2013). It is also suitable for pore systems with only pore size distribution available from experimental techniques. In this case, the throats are volume-less but they are assigned a notional cross section area to assist the description of local diffusion and sorption. The notional area is based on the sizes of the neighbouring pores (Xiong et al. 2014).

If a microstructure to graph mapping assumes that pores mapped to some bonds and the sites are considered as pore junctions, then the maximum pore coordination offered by this topology is 26. This mapping is suitable for the experimental data for clay described in Sect. 2.1. In both cases, the bonds act as mass conduits between discrete spatial positions and the transport through the graph is governed by bond conductivity coefficients and mass conservation at sites.

It is worth noting, that the graph construction is a partial construction of a complex dual to the primal (physical) of Fig. 2a, where nodes, edges, faces and cells of the dual complex correspond to cells, faces, edges and nodes of the primal complex (Grady and Polimeni 2010). From here, the sites inherit integral properties of the primal cell, such as material volume and total mass of diffusing species in the cell. The bonds inherit integral properties of the primal cell faces, such as area and total flux through area. This allows us to consider the sites as bond junctions, possibly smeared in the physical cell but requiring mass conservation. Further a bond could represent a single pore, a number of pores of different cross section collectively describing the flux, or no pores.

Hence in a mathematical graph representing a pore system, sites are substituted with nodes, while bonds are substituted by one, a number of, or no edges. The geometrical structure of such a graph is most conveniently described by the so-called incidence matrix \(\underline{\underline{\mathbf{A}}}\) of dimensions \(\hbox {E} \times \hbox {N}\), where E is the number of edges and N is the number of nodes. An element of this matrix, \(a_{en}\), can be either \(-\)1, +1, or 0, if node \(n\) is the first, second or not incident of edge \(e\). The particular assignment of first and second node does not affect the subsequent analysis, but the presence of only two non-zero elements per row with opposite signs is essential.

Considering a primal complex of fixed number of cells, the columns N of the incidence matrix are fixed to this number. The number of rows, E, can grow as new edges (pores) which are added to the system. The value of this representation is that the incidence matrix describes not only the topological structure of the system, which can be used for connectivity analysis, but is also the boundary operator for the set of nodes, i.e., describes the derivative of a (discrete) function defined on the nodes (Grady and Polimeni 2010).

Specifically, a concentration field over the graph nodes can be written as a vector C of dimension N and the gradient of this field is given by the matrix product \({\underline{\underline{\mathbf{A}}}}\) C, which is a field over the edges written as a vector \(\underline{\nabla \mathbf{C}}\) of dimension E. It is equally important that the transpose of the incidence matrix is the boundary operator for the set of edges, i.e. describes the derivative of a (discrete) function defined over the edges. Specifically, a flux field over the graph edges can be written as a vector J of dimension E and the gradient of this field is given by \(\underline{\underline{\mathbf{A}}}^{\mathbf{T}}\) J, which is a field over the nodes written as vector \(\underline{\nabla {\mathbf{J}}}\) of dimension N. These considerations will be used in Sect. 3 to formulate the boundary value problems for pore systems.

2.4 Assignment of Larger Pores

Larger pores are assigned to available bonds (graph edges) with radii selected by the process shown in Fig. 1b. An available bond is a bond with no previously assigned pore, and only one large pore can be assigned to a bond. With the accepted cylindrical pore shape each assignment increments the pore volume by (\(\pi r^{2}L)\), where \(r\) and \(L\) are the selected radius and the particular bond length, respectively. The lengths of the two types of bonds are: \(L_{1}=S\) for bonds normal to square faces, and \(L_{2}=S\surd 3/2\) for bonds normal to hexagonal faces. \(S\) is the distance between two parallel square boundaries in the truncated octahedron cell, Fig. 2. In this case, \(S\) is referred to be the characteristic (unknown) length scale. Then the volume of a pore network with N cells (later N graph nodes) is \(N\,S^{3}/2\), i.e., the cell volume is \(V_{c}=S^{3}/2\). The assignment of larger pores terminates when their accumulated volume fraction, \(\Sigma (\pi r^{2}L) / (N\,S^{3}/2)\), attains the experimental value (1.7 % in our case). As the number of pores per volume is unknown, the length scale \(S\) cannot be determined directly. Only indirect information, such as pore shape, surface area and observed connectivity can be used for estimating the length scale.

The range of length scales can be determined as follows: firstly, for a given length scale, the volume fraction of the larger pores (1.7 %) must be achieved. However, the accumulated volume fraction may not be attained even when all available bonds are assigned pores for a sufficiently large length scale. This sets an absolute upper limit to the length scale, \(S_\mathrm{MAX}\), notably dependent on our topology. For \(S < S_\mathrm{MAX}\), the resulting graphs are analysed for connectivity, a process described briefly in Sect. 3.2.

Secondly, the model must satisfy the experimental observation that the larger pores form a disconnected or at least not percolating pore system. Therefore in the work, a length scale \(S\) is accepted as realistic if the graphs are not percolating through the complex. This sets a realistic upper limit, \(S_\mathrm{max}\), to the length scale based on the observation that larger pores form a non-percolating system. Results are presented in Sect. 4. The effect of how close the larger pore system is to percolation is also discussed in Sect. 4.

In order to ensure that the shapes of the assigned pores are elongated, a lower limit to the length scale can be derived. For sufficiently small \(S\), the pores will cease to be elongated in the bond directions, indicating non-realistic length. Parametric study of the lower limit has not been performed, but it is assumed that \(S_\mathrm{min} = 100\,\hbox {nm}\), which ensures that more than 95% of the shorter pores of length \(L_{2}\) are elongated in the bond direction (see Fig. 1b).

After selecting a suitable \(S\), the assignment of larger pores is constrained in order to simulate the preferred orientation observed experimentally. The assignment of pores to bonds is spatially random in the selected direction. The maximum number of pores in a direction equals the number of bonds in this direction. In order to describe the fraction of bonds allowing pore assignment, a conditional probability \(f\,(0\le f \le 1)\) is used. This defines the maximum number of pores in a direction as \(f\) times the number of bonds in that direction. In the limits, for \(f = 1\) all bonds in a direction are available for assignment of larger pores, and for \(f = 0\) no larger pores are placed in this direction. For different directions, we can have different values of \(f\).

In this work, all bonds in the bedding direction are available for larger pore assignment. This is illustrated in Fig. 3a for bonds exclusively in (1, 0, 0) direction, and in Fig. 3b for bonds exclusively in (1, 1, 1). The directions are relative to a coordinate system aligned with the normal vectors to the square faces of the primal complex. The examples are from disconnected pore systems for clarity. The cases shown in Fig. 3 are the two principally different structures that can be analysed for transport anisotropy with the proposed network topology.

Fig. 3
figure 3

Limiting configurations of observable pores: a exclusive assignment in (1, 0, 0) direction; and b exclusive assignment in (1, 1, 1) direction

Full size image

Specifically, a conditional probability \(f\) in the system of Fig. 3a is (1, 0, 0). All the larger pores are assigned in the first principal direction which is assumed to be the bedding direction of the clay in Fig. 3a. A concentration gradient along (1, 0, 0) in this system will generate diffusion along the bedding direction of the clay, which is expected to provide the largest macroscopic diffusion coefficient, denoted by \(D_{1}\). A concentration gradient along (0, 1, 0) or (0, 0, 1) in the system of Fig. 3a will generate diffusion perpendicular to the bedding direction of the clay, which is expected to provide a smaller macroscopic diffusion coefficient, denoted by \(D_{3}\).

A concentration gradient along (1, 0, 0), (0, 1, 0) or (0, 0, 1) in the system of Fig. 3b will generate diffusion inclined to the bedding direction of the clay, which is expected to provide an intermediate macroscopic diffusion coefficient, denoted by \(D_{2}\). The calculation of this coefficient can be used to derive a diffusivity tensor for continuum modelling of diffusion in porous media.

2.5 Assignment of Smaller Pores

The mapping of smaller pores is performed for length scales within the acceptable limits determined by larger pores. Smaller pores, with radii selected by the process from Fig. 1c, are assigned to bonds not already occupied by larger pores. The smaller pores are also assumed to be of cylindrical shape and each new pore assignment increments the pore volume according to selected radius and bond length. The process terminates when the total pore volume fraction, from larger and smaller pores, attains the experimental porosity, 10.4 % in our case. Notably, more than one smaller pore can be assigned to any bond not occupied by a larger pore, i.e., multiple edges between two nodes in the corresponding graph can be introduced.

The assignment of smaller pores uses a random selection of bonds from the list of available bonds after the first step, i.e., the smaller pores are randomly distributed in space. The pore network after assigning larger pores and smaller pores is show in Fig. 4. Note that the cross sections of smaller pores are scaled-up in order to improve the illustration. In Fig. 4a, the network is constructed with equal length scales in the bedding and out-of bedding directions and allowance for smaller pores at available bonds in the bedding direction. In Fig. 4b, the network is constructed with smaller length scale in the out-of-bedding direction and smaller pores are not allowed in the bedding direction. The two figures make an illustration of the some of the options analysed below.

Fig. 4
figure 4

Pore network model with larger pores (red) and smaller pores (green): a large and small pores in (1, 0, 0) and small pores in all other directions—equal length scale for bedding and out-of-bedding; and b large pores in (1, 0, 0) direction and small pores in all other directions—smaller length scale in out-of-bedding directions

Full size image

3 Theory and Calculation

3.1 Pore Diffusivities and Graph Metric

The diffusion in the constructed model is driven by the concentration gradient along the cylindrical pores. For a pore with radius \(R_\mathrm{e}\), connecting nodes \(n\) and \(m\), the mass flow of diffusing species, \(J_\mathrm{e}\,[\hbox {kg/s}]\), is described by the Fick’s first law

$$\begin{aligned} J_e =-D_\mathrm{e} A_\mathrm{e} \Delta C_\mathrm{nm} /L_\mathrm{e}, \end{aligned}$$
(2)

where \(D_\mathrm{e} [\hbox {m}^{2}/\hbox {s}]\) is the pore diffusivity, \(A_\mathrm{e}= \pi R_\mathrm{e}^{2} [\hbox {m}^{2}]\) is the pore cross section area, \(L_\mathrm{e}\,[\hbox {m}]\) is the pore length, and \(\Delta C_\mathrm{nm}=C_\mathrm{n}- C_\mathrm{m}\,[\hbox {kg/m}^{3}]\) is the concentration difference between nodes. Further, the restriction to diffusion due to steric hindrance at the entrance to the pore and frictional resistance within the pore is accounted for. Following (Bryntesson 2002) the effective pore diffusivity of species of radius \(r_{0}\) is defined by

$$\begin{aligned} D_\mathrm{e} =D_0 \left( {1-\frac{r_0 }{R_\mathrm{e} }} \right) ^{4} \end{aligned}$$
(3)

where \(D_{0}\) is the free molecular diffusion coefficient of the species in the medium filling the pore system. Specifically for this work, the Opalinus clay is considered fully saturated with water to reflect repository conditions, and the diffusing contaminant is HTO, a neutral species. The free molecular diffusion coefficients of the diffusing species calculated with the Einstein-Stokes equation at room temperature is: \(D_{0} = 2.24\times 10^{-9}\hbox { m}^{2}/\hbox {s}\) (Baeyens 2010).

The concentration differences or gradients in the edges, \(\Delta C_\mathrm{nm }=C_\mathrm{n}- C_\mathrm{m}\), are given by the application of the discrete boundary operator on the graph nodes, i.e., the matrix A, and the discrete field of nodal concentrations, i.e., the vector C. Thus, Eq. (2) defines a discrete field of edge flows, a vector J, where each component is the edge gradient scaled by an edge weight given by \(W_\mathrm{e}=D_\mathrm{e} A_\mathrm{e} / L_\mathrm{e}\,[\hbox {m}^{3}/\hbox {s}]\). Clearly, the weight of an edge depends on the assigned pore radius, selected length scale and radius of diffusing species via Eq. (3).

For convenience of expression the edge weights are arranged in a diagonal matrix, \(\underline{\underline{\mathbf{W}}}\), of dimensions \(\hbox {E} \times \hbox {E}\), where the element in row and column \(e\) is the weight of edge \(e\). This matrix defines a metric on the graph corresponding to the diffusion problem. Thus, the discrete flow field is given by \(\underline{\mathbf{J}}= -\underline{\underline{{\mathbf{W}}}} \underline{\underline{\mathbf{A}}} \underline{\mathbf{C}}\).

It is worth noting that, although in this work we use constant edge weights for the graph metric, in principle the weights can incorporate any non-linearity of physical significance, e.g., changes of cross section due to sorption or dissolution. Further, the graph representation allows for easy addition or removal of edges, either dynamically or by using a static incidence matrix and controlling the elements of the graph metric.

3.2 Structural Analysis of Graphs

The graph generated during the first step of pore system mapping, Sect. 2.3, represents the system of larger (observable) pores. It is described by an incidence matrix \(\underline{\underline{\mathbf{A}}}_{\mathbf{1}}\), with N columns given by the number of nodes (cells) and \(\hbox {E}_{{1}}\) rows given by the number of assigned pores to specific bonds, i.e., graph edges. In general, this graph is a union of disconnected components, which may be isolated nodes, or connected sub-graphs. An in-house code is used to segment the formed graph into all disconnected components. The code uses an iteration and recursion over the incidence matrix \(\underline{\underline{\mathbf{A}}}_{\mathbf{1}}\). For a given node \(n\), not belonging to a segmented component, the elements in column \(n\) are inspected. If all elements are zero, the node is isolated and forms a separate component. A non-zero element \((\pm 1)\) in a row \(e\) indicates an edge incident to node \(n\). The second non-zero element in the row \(e\) is in a column, say \(m\), corresponding to the node \(m\). This node is included in the connected component containing node \(n\) and its column is inspected similarly to node \(n\). The recursive process terminates with a node that has no neighbours outside the segmented component. Notably, the nodes included in this component are excluded from further inspection by column-wise iteration.

The set of disconnected components derived by this procedure is further analysed for system-scale connectedness or percolation. When one or more of these components are percolating through the cell complex the construction violates the requirement imposed by the experimental observations. This is used in conjunction with graph constructions with increasing length scales to obtain an upper limit to the length scale. It should be noted that this limit is dependent on the probability weights for assignments of larger pores in different directions as shown in Sect. 4.

The full graph of the system is then obtained by performing the second step of mapping smaller pores to unoccupied bonds. As already mentioned in Sect. 2.3, a number of pores are allowed to be mapped to a bond as necessary for achieving the experimental porosity. It is emphasised that these are represented by separate edges in the graph having individual weights. Physically this means that a number of small pores are allowed to cross a face of the primal (physical) cell complex, providing collectively the mass flow between the adjacent nodes but with individual resistances to diffusion. The full incidence matrix \(\underline{\underline{{\mathbf{A}}}}\) of the system contains as many rows as are the individual edges and describes simultaneously the geometric structure of the graph and the boundary operator over nodes.

3.3 Problem Formulations and Solution

The mass diffusion through the constructed graph is governed by mass conservation at nodes, i.e., the rate of change of diffusing species mass at the nodes equals the resultant mass flows through the nodes. For this, we recall that a node in the graph inherits the volume of the primal (physical) cell \(V_\mathrm{c}\), hence the rate of change of species mass at the graph nodes is given by \(V_\mathrm{c}d\mathbf{C}/{\mathrm{d}t}\), where C is the discrete field of concentrations at nodes. The resultant mass flows through the nodes are the algebraic sums of the flows through adjacent edges, which is the divergence of the flow field, \(\underline{\underline{\mathbf{J}}}= -\underline{\underline{\mathbf{W}}}\,\underline{\underline{\mathbf{A}}}\,\underline{\mathbf{C}}\), or otherwise the boundary operator over the edges of the graph given by \(\underline{\underline{\mathbf{A}}}^{\mathbf{T}}\). Thus the process of mass diffusion through a weighted graph G with boundary nodes \(\partial \hbox {G}\), representing a pore system, is formulated by

$$\begin{aligned}&V_\mathrm{c} \frac{d\underline{\mathbf{C}}}{\mathrm{d}t}=-\underline{\underline{\mathbf{A}}}^{\mathbf{T}} \underline{\underline{\mathbf{W}}}\,\underline{\underline{\mathbf{A}}}\, \underline{{\mathbf{C}}}\quad \hbox {on G}, \end{aligned}$$
(4)
$$\begin{aligned} \mathbf{C}=\mathbf{C}^{0}\quad \hbox {on G for }t= 0, \end{aligned}$$
(5)
$$\begin{aligned} \underline{\underline{\varvec{{\upalpha }}}}\,\mathbf{C}+\underline{\underline{\varvec{{\upbeta }}}}\,\underline{\underline{\mathbf{A}}}^{\mathbf{T}} \underline{\mathbf{J}}=\underline{\mathbf{B}}\quad \hbox {on }\partial \hbox {G for }t> 0, \end{aligned}$$
(6)

where Eqs. (5) and (6) represent the initial and boundary conditions, respectively. Specifically in Eq. (6) \(\underline{\underline{{\varvec{\upalpha }}}}\) and \(\underline{\underline{{\varvec{\upbeta }}}}\) are diagonal matrices allowing for essential, natural and film (mixed) boundary conditions to be written compactly. A node \(n\) with prescribed essential condition alone, e.g., \(C=C_\mathrm{n}\), will have \(\alpha _\mathrm{nn} = 1, \beta _\mathrm{nn} = 0\) and \(B_\mathrm{n}=C_\mathrm{n}\). A node \(n\) with prescribed natural condition alone, e.g., \(J=J_\mathrm{n}\), will have \(\alpha _\mathrm{nn} = 0, \beta _\mathrm{nn} = 1\) and \(B_\mathrm{n}=J_\mathrm{n}\). Finally, a node \(n\) with prescribed mixed condition will have the appropriate linear combination with \(0 < \alpha _\mathrm{nn} < 1\) and \(0 < \beta _\mathrm{nn} < 0\) and corresponding \(B_\mathrm{n}\).

The formulation of flow via Eqs. (4)–(6) may appear similar to the finite differences method. However, we emphasise on the rather different approach for arriving at this formulation. In the first place the approach helps realising the intrinsic relation between the topological structure of the pore space and the transport, both described via the incidence matrix. Secondly, it allows for clearer mapping of real pore system characteristics to graph properties. In particular, the realisation that the network is partially dual to the physical space provides flexibility for the meanings attached to nodes and edges. Thus a node, inheriting volume from the physical cell, can be considered as a container for mass exchange. Further, the flow through a face of the physical cell can be associated by a number of edges as required by the pore system characteristics.

Problems formulated by Eqs. (4)–(6) are solved by an in-house code, using efficient algorithms (C++ boost library) to take advantage of the sparse nature of the incidence matrix. The code is typically an order of magnitude faster than commercial finite element packages; this was checked against the widely used Abaqus.

For the simulations and results presented in Sect. 4, we use a network occupying the region \((0 \le X_{1} \le 20S_{1}, 0 \le X_{2} \le 20S_{2}, 0 \le X_{3} \le 20S_{3})\) with respect to a coordinate system \((X_{1}, X_{2}, X_{3})\) normal to the square faces of the unit cell. Here, \(S_{1}, S_{2}, S_{3}\), are the distances between cell centres in the three coordinate directions. This network contains \(N_{g} = 14{,}859\) nodes and \(E_{g} = 110{,}860\) bonds. The size is sufficiently large to reduce the effect of the random spatial distribution of pore sizes on the calculated macroscopic diffusivity of the system to less than one order of magnitude. This has been confirmed by a series of random spatial distributions for which the analyses provided nearly identical results.

The initial conditions for all simulations are \(\mathbf{C}^{0} = \mathbf{0}\), see Eq. (6). The boundary conditions reflect a particular experimental setup where concentrations \(C_{0}\) and \(C_{1}\) are prescribed on two opposite boundaries, while the remaining four boundaries do not permit flux. For bedding direction (1, 0, 0), see Sect. 2.3, the calculation of the macroscopic diffusivity \(D_{1}\) uses simulations with \(B_{n}=C_{0}\) for nodes \(n\) on plane \(X_{1} = 0, B_{n}=C_{1}\) for nodes \(n\) on plane \(X_{1} = 20S_{1}\), and \(B_{n} = 0\) for nodes \(n\) on planes \(X_{2} = 0, X_{2} = 20S_{2}, X_{3} = 0, X_{3} = 20S_{3}\). For the same bedding direction, the calculation of the macroscopic diffusivity \(D_{3}\) uses simulations with \(B_{n}=C_{0}\) for nodes \(n\) on plane \(X_{2} = 0, B_{n}=C_{1}\) for nodes \(n\) on plane \(X_{2} = 20S_{2}\), and \(B_{n} = 0\) for nodes \(n\) on planes \(X_{1} = 0, X_{1} = 20S_{1}, X_{3} = 0, X_{3} = 20S_{3}\).

For bedding direction (1, 1, 1), see Sect. 2.3, the calculation of the macroscopic diffusivity \(D_{2}\) uses simulations with \(B_{n}=C_{0}\) for nodes \(n\) on plane \(X_{1} = 0, B_{n}=C_{1}\) for nodes \(n\) on plane \(X_{1} = 20\,S_{1}\), and \(B_{n} = 0\) for nodes \(n\) on planes \(X_{2} = 0, X_{2} = 20\,S_{2}, X_{3} = 0, X_{3} = 20\,S_{3}\). In all simulations \(C_{0} = 1\) and \(C_{1} = 0\) have been used, since we are interested in the calculation of steady-state macroscopic diffusion coefficients. These have been calculated at steady-state from the total mass flow across a boundary with prescribed concentrations, the physical area of this boundary and the distance to the opposite boundary according to the macroscopic version of Fick’s law; Eq. (2).

4 Results and Discussion

Geometrical, topological and transport parameters for various pore systems to graph mappings have been analysed. For each mapping with given parameters, analyses for 10 random spatial distributions of pores have been performed and the reported results are the averaged values of these analyses. For the given size of the lattice, the results from 10 different realisations were within 10% from the average values reported.

To check additionally our constructions we have used the experimental BET surface area \(20-21\hbox {m}^{2}/\hbox {g}\) (Keller et al. 2011) and have calculated the corresponding theoretical surface area. In parallel, we have calculated the surface area for all pores in the pore network model. The ratio of theoretical surface area to model surface area is around 0.95 and was found practically independent of the model length scale.

4.1 Determination of Principal Length Scale

The geometrical properties are the limits of the unknown principal length scale. Since we assumed that each bond can be assigned a single larger (observable) pore with radius from distribution in Fig. 1(a), the absolute upper limit, \(S_\mathrm{MAX}\), for the length scale can be determined. The value of \(S_\mathrm{MAX}\) can be obtained when all available bonds are assigned with pores but the accumulated pore volume is less than the experimentally measured. This limit depends on whether the set of larger pores is entirely in the preferred direction, \(f = 0\), or some deviation from this ideal texture is allowed, \(f > 0\). We choose to call \(f\) the measure of disorder. Recall that \(f\) is the fraction of bonds outside the preferred direction permitting pore assignment.

The analyses for the unknown principal length scale are performed with the assumption for equal length scales in the three directions, i.e., \(S_{1}=S_{2}=S_{3}\). The results for the absolute upper limit of the length scale are given in Fig. 5a. They show how the selected topology for pore system mapping and specific disorder constrain the lengths that could be analysed by the proposed method. Although these limits are not used further for the clay analysed, they indicate that the range of length scale even when the observable pore system is allowed to percolate. It should be noted that for the given distribution of larger pore sizes, Fig. 1b, \(S_\mathrm{MAX}\) grows to approximately 1400 nm when all bonds are permitted larger pores, i.e., for \(f = 1\).

With the restriction for a non-percolating system, applicable to the clay modelled here, the realistic upper limit, \(S_\mathrm{max}\), of the length scale is given in Fig. 5b. These results show that the realistic upper limit of length scale is increasing when the disorder \(f\) increases. When the disorder \(f\) increases to 0.3 (practically after assignment of pores to 30 % of the bonds outside of the preferred orientation is permitted), it yields a saturation of the realistic upper limit of the length scale to the value of 500 nm. For the ideal texture, \(f = 0\), the realistic upper limit is 400 nm.

As already mentioned in Sect. 2.4 we have selected a lower limit \(S_\mathrm{min} = 100\hbox \mathrm{nm}\), to ensure that more than 95 % of the assigned large pores are elongated on their respective bonds independent of bond orientation. The subsequent analyses are performed on graphs constructed with length scales \(S_\mathrm{min} \le S \le S_\mathrm{max}\).

Fig. 5
figure 5

Upper limits of graph length scale dictated by graph topology, larger pore size distribution and texture: a the absolute upper limit, \(S_\mathrm{MAX}\), determined from the condition of achievable prescribed pore volume fraction; b the realistic upper limit, \(S_\mathrm{max}\), determined from the condition for non-percolating system of larger pores. Parameter \(f\) is the fraction of bonds outside preferred direction permitting pore assignment and measures the disorder, i.e., the deviation from ideally textured medium with all pores aligned with preferred direction

Full size image

Smaller pores obeying the distribution given in Fig. 1c are assigned to bonds not occupied by larger pores. For both pore sets, the growth in pore number scales with the square of the length scale. The fraction of bonds in the preferred direction occupied by large pores varies between 5 % for \(S_\mathrm{min}\) and approaches 100 % for \(S_\mathrm{max}\) (as expected from Fig. 5b). The smaller pores occupying the remaining bonds grow from approximately one pore per available bond for \(S_\mathrm{min}\), to nearly 18 pores per bond for \(S_\mathrm{max}\). It is worth emphasising again that the smaller pores have no preferred orientation, so that within the length scale interval analysed they are assigned with equal probability to unoccupied bonds in the preferred direction and in the remaining six directions of our topology.

4.2 Effective Diffusivity of Systems with Equal Length Scales

Macroscopic (graph-wide) diffusion coefficients are calculated according to the parameters and procedures described in Sect. 3. Systems with length scales within the acceptable limits and with different deviations from ideal texture, measured by \(f\), have been analysed.

The results for the diffusion coefficient \(D_{1}\), obtained for concentration gradient along the preferred direction, are shown in Fig. 6. Figure 6a shows that an increasing deviation from ideal texture yields a monotonic reduction of the emergent diffusivity. This is understandable as for any given length scale and porosity, the total volume of larger pores is the same irrespective of the assignment direction of larger pores. So the assignment of larger pores outside the preferred orientation reduces the number of larger pores in the direction of the concentration gradient. Further, Fig. 6b shows that an increasing length scale yields a monotonic increase of the emergent diffusivity, most notable for the system with ideal texture, \(f = 0\).

These results indicate how significant is the control of the smaller pores on the emergent diffusivity induced by the complementary connectivity. Consider the case of ideal texture and recall that at \(S_\mathrm{min}\) only 5 % of the bonds in preferred direction are assigned larger pores, while the smaller pores are approximately one per available bond. At the same time at \(S_\mathrm{max}\) nearly 100 % of the bonds in the preferred orientation are assigned larger pores. Yet the difference in the emergent diffusion coefficients is less than two times. This difference decreases even further when the larger pore system deviates from ideal texture, to approach 1.5 for systems with larger pores permitted on 50 % of the bonds in the non-preferred orientation. Hence, the effect of the small pores diminishes, when the system of larger pores approaches percolation.

Fig. 6
figure 6

Macroscopic diffusivity in the clay bedding direction: a as a function of pore system deviation from ideal texture at different length scales; and b as a function of pore system principal length scale at different deviations from ideal texture. The macroscopic diffusivity is normalised with the free molecular diffusion coefficient \(D_{0} = 2.24\times 10^{-9}\hbox { m}^{2}/\hbox {s}\)

Full size image

The results of our simulations, obtained with different length scales and textures, are in the range \(D_{1}/ D_{0} = 0.022{-}0.044\). Hence, with \(D_{0} = 2.24\times 10^{-9}\hbox {m}^{2}/\hbox {s}\), the predicted effective diffusion coefficients are in the range \(D_{1} = 4.5\times 10^{-11}\) to \(9.7\times 10^{-11}\hbox { m}^{2}/\hbox {s}\). Reported experimentally obtained values for HTO diffusion in Opalinus clay are \(D_{1} = 5.5\times 10^{-11}\hbox { m}^{2}/\hbox {s}\) (Baeyens 2010) and \(D_{1} = 3.1\times 10^{-11}\) to \(8.0\times 10^{-11}\hbox { m}^{2}/\hbox {s}\) (Van Loon et al. 2004; Wang et al. 2005). Clearly, the model predictions can cover nearly the entire range of reported experimental values. Some very small measured diffusivities fall outside of the predicted range, which may be due to differences in the pore systems in these experiments and the one modelled here. One possible reason for the smaller measured diffusivities is that in the experiments the samples were partially saturated unlike the model assumption. Another possible reason is that clay mineralogical heterogeneity yields different length scale out of the bedding direction. This is explored further in Sect. 4.4.

The results for the diffusion coefficient \(D_{3}\), obtained for concentration gradient perpendicular to bedding direction (1, 0, 0), are shown in Fig. 7. They are scaled with the diffusion coefficient in the bedding direction calculated for the corresponding length scale and texture case. In general the effect of increasing disorder (deviation from ideal texture), shown in Fig 7a, as well as of increasing length scale, shown in Fig. 7b, on the diffusivity perpendicular to the bedding direction is opposite to their effects on the diffusivity parallel to the bedding direction. The results in Fig. 8a show that the increasing disorder of the larger pores produces more isotropic response as the ratio of perpendicular to parallel diffusivities approaches one. In particular, if 50 % of the bonds outside the bedding direction permit larger pore assignment, the system is approximately isotropic. For highly disordered large pores, the effect of length scale on the anisotropy diminishes as seen in Fig. 7b.

Fig. 7
figure 7

Macroscopic diffusivity perpendicular to the clay bedding direction: a as a function of pore system deviation from ideal texture at different length scales; and b as a function of pore system length scale at different deviations from ideal texture. The macroscopic diffusivity is normalised with the corresponding diffusivity in the bedding direction

Full size image

From the results presented in Figs. 6 and 7, the predicted macroscopic diffusivity perpendicular to bedding direction is in the range \(D_{3} = 2.0\times 10^{-11}\) to \(6.4\times 10^{-11}\hbox { m}^{2}/\hbox {s}\) for different length scales and textures. Experimentally obtained values for this diffusivity were \(D_{3} = 1.0\times 10^{-11}\) to \(2.3\times 10^{-11}\) (Van Loon et al. 2003; Wang et al. 2005). The model is slightly over-predicting the experimental values, which could be attributed to differences of pore size distribution between the Opalinus clay used in (Van Loon et al. 2004) and the imaged Opalinus clay that formed the basis of the model.

A possible cause for the higher model predictions is our assumption that the smaller pores are fully disordered, i.e., they are allowed to occupy with equal probability available bonds in all network directions. If the smaller pores also had the preferred orientation of the larger pores, the ratio between the perpendicular and the parallel diffusivity coefficients would decrease.

Another cause for the discrepancy is that the model with equal length scales uses only the pore size distribution in different directions to achieve anisotropy. This means that the model used above simulates pore constrictivity but does not represent tortuosity differences, because the path length in all directions is practically the same. Such observation supports the need to consider different length scales in the out-of-bedding directions, which is presented in Sect. 4.4.

4.3 Approach to Calculating a Diffusivity Tensor

The results for the diffusion coefficient \(D_{2}\), obtained for concentration gradient inclined to the bedding direction, i.e., a gradient in (1, 0, 0) and bedding in (1, 1, 1), are shown in Fig. 8. As in Fig. 7, they are scaled with the diffusion coefficient in the bedding direction calculated for the corresponding length scale and texture case. The effects of larger pore disorder and length scale on emergent inclined diffusivity are similar to those on the emergent perpendicular diffusivity. For all configurations studied, \(D_{3} < D_{2} < D_{1}\), which is expected in view of the graph structure and gradient applied. The particular values found for the inclined diffusivity from Figs. 6 and 7 are in the range \(D_{3} = 2.2\times 10^{-11}\) to \(7.4\times 10^{-11}\hbox { m}^{2}/\hbox {s}\). Introduction of preferred orientation of smaller pores will have similar effect on the inclined diffusivity as on the perpendicular diffusivity, but it is expected that the coefficient will remain between the two values measured in the perpendicular and the parallel directions.

Fig. 8
figure 8

Macroscopic diffusivity inclined to the clay bedding direction: a as a function of pore system deviation from ideal texture at different length scales; and b as a function of pore system length scale at different deviations from ideal texture. The macroscopic diffusivity is normalised with the corresponding diffusivity in the bedding direction

Full size image

For a single preferred orientation of larger pores and disorder in all other orientations, the anisotropic diffusivity tensor of the porous continuum, with components \(d_{ij}\), can have only two principal values, \(d_\mathrm{max }\) and \(d_\mathrm{min}\). For bedding in the (1, 0, 0) graph direction, \(d_\mathrm{max}=D_{1}\), but \(d_\mathrm{min}\) does not equal \(D_{3}\) determined above, as this is affected by the allowed transport directions in the graph. With respect to the coordinate system with unit vectors (1, 0, 0), (0, 1, 0) and (0, 0, 1), the continuum diffusivity tensor will have components \(d_{11}=D_{1}\), \(d_{22}=d_{33}=D_{3}\) and unknown \(d_{ij}=d\) for \(i \ne j\). The diffusivity in direction (1, 1, 1) in this case should equal \((D_{1} + 2d) / \surd 3\), but this must equal the diffusivity measured in (1, 0, 0) for preferred orientation (1, 1, 1), which is \(D_{2}\). From here, the out of diagonal coefficient can be determined as \(d = (\surd 3D_{2}- D_{1}) / 2\). The results presented in Figs. 6, 7, and 8 can be used to calculate this coefficient and the smaller principal value of the continuum diffusivity tensor if required.

4.4 Effective Diffusivity of Systems with Different Length Scales

In order to achieve variation in tortuosity, the effects of different length scales in different directions are studied. As the path lengthening (tortuosity) is smaller in the direction parallel to the bedding from experimental investigation (Van Loon et al. 2004), we investigate networks with larger length scale in the bedding direction and smaller length scales in the directions perpendicular to bedding. This is more physically realistic than the case with equal lengths, as it assigns shorter lengths for smaller pores, which occupy predominantly the out-of-bedding directions. Thus, the tortuosity for smaller length scale is larger than that for larger length scale for the same physical distance.

We have investigated two length scales in the bedding direction, \(S_{1} = 100, 150\,\hbox {nm}\), for which the system of large pores is clearly not percolating as in experimental observations. For each of these, the secondary length scale has been varied between 10 and 100 nm, i.e., \(S_{2}=S_{3} = 10{-}100\,\hbox {nm}\). Further, cases where smaller pores are and are not present in the bedding direction have been simulated.

The effective diffusivities parallel and perpendicular to the bedding direction for above cases are shown in Fig. 9. The value of \(D_{1}\) increases rapidly as the length scale perpendicular to the bedding direction increases, Fig. 9a. The largest value of \(D_{1}\) is predicted when \(S_{1 }/ S_{2,3}= 2\). After that, the macroscopic diffusivity \(D_{1}\) decreases gradually. The reason why \(D_{1}\) reaches a maximum at \(S_{1 }/ S_{2,3 }= 2\) can be explained as follows. The total volume of the model is decreasing as the length scale out of bedding direction reduces. For the given porosity and pore size distribution, the decreasing volume leads to decreasing number of larger pores in the bedding direction. When the ratio of \(S_{1}\) to \(S_{2,3}\) equals 2, the number of larger pores in the bedding direction per unit volume reaches the largest value. This is shown in Fig. 10, which describes the relationship between the number of larger pores per unit volume and the length scale out of bedding direction.

Fig. 9
figure 9

Macroscopic diffusivity for different length scales: a parallel to the clay bedding direction; b perpendicular to the clay bedding direction. The value with dash line is for only larger pores in the bedding direction. \(S_{1}\) is the length scale in the bedding direction and \(S_{2,3}\) is the length scale perpendicular to the bedding direction

Full size image

Figure 9a also shows that the macroscopic diffusivity \(D_{1}\) with smaller pores allowed in the bedding direction is larger than the value of \(D_{1}\) with only larger pores in the bedding direction. This shows that the effect of smaller pores in the bedding direction, which reduce diffusion path lengths, can be quite significant. The predicted effective diffusion coefficients \(D_{1}\) are in the range from 0 to \(7.52\times 10^{-11}\hbox { m}^{2}/\hbox {s}\) in Fig. 10a. Clearly, the introduction of a secondary length scale, principally measuring heterogeneity in clay mineralogy, provides a wider range of calculable \(D_{1}\) than the single length scale method (Fig. 6). Therefore, it offers one explanation for differences in experimentally measured diffusion coefficients.

Fig. 10
figure 10

The number of larger pores per unit volume for different length scales. \(p\) is the number of larger pores per unit volume. The value with dashed line is for only larger pores in the bedding direction. \(S_{1}\) is the length scale in the bedding direction and \(S_{2,3}\) is the length scale perpendicular to the bedding direction

Full size image

Figure 9b shows the relationship between macroscopic diffusivity perpendicular to the bedding direction \(D_{3}\) and length scales. The predicted effective diffusion coefficients increase as the length scale perpendicular to the bedding direction increases. This is due to the fact that the path is less tortuous for the same physical distance and the number of smaller pores is increasing when the length scale \(S_{2,3}\) increases. The macroscopic diffusivity \(D_{3}\) with allowed smaller pores in the bedding direction is smaller than the value of \(D_{3}\) for only larger pores in the bedding direction. This is contrary to the effect on diffusivity \(D_{1}\) and is clearly emerging from the larger number of smaller pores in directions perpendicular to bedding, required for a given porosity and length scale.

The results of our simulations, obtained with different length scales and textures, are in the range \(D_{3} = 0{-}4.82\times 10^{-11}\hbox { m}^{2}/\hbox {s}\). The ratios of \(D_{3}\)–\(D_{1}\) cover a wider range than for the case of equal length scales. From Fig. 9, it can be derived that when \(S_{1} = 100\,\hbox {nm}\) and \(S_{2,3}= 50\,\hbox {nm}, D_{1} = 5.1\times 10^{-11}\hbox { m}^{2}/\hbox {s}\) and \(D_{3} = 1.3\times 10^{-11}\hbox { m}^{2}/\hbox {s}\). These values and the ratio of \(D_{3}/ D_{1}\) are closest to the experimental data (Van Loon et al. 2004; Joseph et al. 2013).

5 Conclusions

An effective methodology for analysis of mass transport through media with partially known geometrical and topological pore system characteristics has been developed. Large class of porous media fall into this category, particularly micro- and meso-porous materials, because the existing experimental techniques do not allow for complete quantitative analysis of their pore systems.

Based on a topology, representing an average pore neighbourhood, real pore systems have been represented with weighted mathematical graphs by appropriate mapping of the experimentally available quantitative and qualitative information. The benefits of such formulation are in the clarity of the mapping process and in the ability to perform efficiently concurrent analyses of the topological structure and of the transport coefficients of the pore network. The results of this work have been obtained with both our in-house code, based on discrete exterior calculus (analysis on graphs), and the commercial finite element software Abaqus. While the outcomes were identical, the analysis on graphs approach has been one order of magnitude faster than the finite element solver.

The model has been applied to Opalinus clay using reported experimental pore size distributions of resolvable and “hidden” porosity. Further, qualitative information about preferred orientation and connectivity of observable pores have been used to calculate bounds for the model length scale, which cannot be determined otherwise with the available experimental data. The length scale effects on the topological and the transport properties of the pore network have been analysed. Calculated diffusion coefficients are in a very good agreement with reported macroscopic experimental data, particularly when clay heterogeneity is simulated via different length scales in bedding and perpendicular directions.

Due to the increased number of transport directions, seven compared to three in networks based on cubic lattices, the model can be used to derive more realistic macroscopic diffusivity tensors for continuum-based modelling, e.g., in finite element codes.