Linear and Nonlinear Analyses of the Onset of Buoyancy-Induced Instability in an Unbounded Porous Medium Saturated by Miscible Fluids

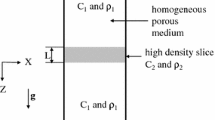
Abstract

This study analyzes the stability of an initially sharp interface between two miscible fluids in a porous medium. Linear stability equations are first derived using the similarity variable of the basic state, and then transformed into a system of ordinary differential equations using a spectral expansion with and without quasi-steady-state approximation (QSSA). These transformed equations are solved using the eigenanalysis and initial value problem approach. The initial growth rate analysis shows that initially the system is unconditionally stable. The stability characteristics obtained under the present QSSA are quantitatively same as those obtained without the QSSA. To support these theoretical results, numerical simulations are conducted using the Fourier-spectral method. The results of theoretical linear stability analyses and the numerical simulations validate to each other.

Appendices

Appendix 1

The complementary solution of Eq. (3.16) is

$$\begin{aligned} w_1&= \frac{a^{*}}{2}\left[ -\exp \left( {a^{*}\zeta } \right) \mathop \int \limits _{-\infty }^\zeta {\exp \left( {-a^{*}\xi } \right) \sum _{n=0}^\infty {A_n \left( \tau \right) \phi _n \left( \xi \right) } \mathrm{d}\xi }+\exp \left( {-a^{*}\zeta } \right) \right. \nonumber \\&\left. \mathop \int \limits _{-\infty }^\zeta {\exp \left( {a^{*}\xi } \right) \sum _{n=0}^\infty {A_n \left( \tau \right) \phi _n \left( \xi \right) } \mathrm{d}\xi } \right] +B_1 \exp \left( {a^{*}\zeta } \right) +B_2 \exp \left( {-a^{*}\zeta } \right) .\qquad \end{aligned}$$

(7.1)

Using the properties of definite integral, we have

$$\begin{aligned} \mathop \int \limits _{-\infty }^\zeta {f\left( \xi \right) \mathrm{d}\xi } =\mathop \int \limits _{-\infty }^\infty {f\left( \xi \right) \mathrm{d}\xi +} \int \limits _\infty ^\zeta {f\left( \xi \right) \mathrm{d}\xi } =\mathop \int \limits _{-\infty }^\infty {f\left( \xi \right) \mathrm{d}\xi -} \mathop \int \limits _\zeta ^\infty {f\left( \xi \right) \mathrm{d}\xi } , \end{aligned}$$

(7.2)

where $f\left( \xi \right) =\exp \left( {-a^{*}\xi } \right) \sum _{n=0}^\infty {A_n \left( \tau \right) \phi _n \left( \xi \right) }$. On combining Eqs. (7.1) and (7.2), we can write the complete solution of Eq. (3.16) as

$$\begin{aligned} w_1&= \frac{a^{*}}{2}\left[ \exp \left( {a^{*}\zeta } \right) \mathop \int \limits _\zeta ^\infty {\exp \left( {-a^{*}\xi } \right) \sum _{n=0}^\infty {A_n \left( \tau \right) \phi _n \left( \xi \right) } \mathrm{d}\xi }+\exp \left( {-a^{*}\zeta } \right) \right. \nonumber \\&\left. \mathop \int \limits _{-\infty }^\zeta {\exp \left( {a^{*}\xi } \right) \sum _{n=0}^\infty {A_n \left( \tau \right) \phi _n \left( \xi \right) } \mathrm{d}\xi } \right] -\frac{a^{*}}{2}\exp \left( {a^{*}\zeta } \right) \mathop \int \limits _{-\infty }^\infty \exp \left( {-a^{*}\xi } \right) \nonumber \\&\sum _{n=0}^\infty {A_n \left( \tau \right) \phi _n \left( \xi \right) } \mathrm{d}\xi +B_1 \exp \left( {a^{*}\zeta } \right) +B_2 \exp \left( {-a^{*}\zeta } \right) . \end{aligned}$$

(7.3)

On using the first boundary condition, $w_1 \rightarrow 0$ as $\zeta \rightarrow \infty$, into Eq. (7.3) we have

$$\begin{aligned} B_1 =\frac{a^{*}}{2}\left[ {\mathop \int \limits _{-\infty }^\infty {\exp \left( {-a^{*}\xi } \right) \sum _{n=0}^\infty {A_n \left( \tau \right) \phi _n \left( \xi \right) } \mathrm{d}\xi } } \right] , \end{aligned}$$

(7.4)

and the second boundary condition,$w_1 \rightarrow 0$ as $\zeta \rightarrow \hbox { }-\infty$, gives

$$\begin{aligned} B_2 =0. \end{aligned}$$

(7.5)

In writing Eqs. (7.4) and (7.5), we have used the following results:

$$\begin{aligned} \mathop {\hbox {lim}}\limits _{\zeta \rightarrow \infty } \exp \left( {-a^{*}\zeta } \right) =0,\quad \mathop {\hbox {lim}}\limits _{\zeta \rightarrow -\infty } \exp \left( {a^{*}\zeta } \right) =0 \; \hbox {and}\; \mathop \int \limits _\zeta ^\zeta {f\left( \xi \right) \mathrm{d}\xi } =0, \end{aligned}$$

(7.6)

where $a^{*}$ has a finite value. On putting the values of $B_1$ and $B_2$ in Eq. (7.3), the solution for $w_1$ is Eq. (3.17).

Appendix 2

By discretizing Eqs. (3.32), (3.33), and (3.35a) using central difference formulations, we obtained the following relation:

$$\begin{aligned} \mathbf{Gw}=\mathbf{0}, \end{aligned}$$

(8.1)

where

$$\begin{aligned}&\displaystyle G_{1,1} = C_1 , \quad G_{1,2} =B_1 +D_1 , \quad G_{1,3} =A_1 +E_1,\end{aligned}$$

(8.2)

$$\begin{aligned}&\displaystyle G_{2,1} =B_2 , \quad G_{2,2} =A_2 +C_2 , \quad G_{2,3} =D_2 , \quad G_{2,4} =E_2 ,\end{aligned}$$

(8.3)

$$\begin{aligned}&\displaystyle G_{i,i-2} =A_i , \quad G_{i,i-1} =B_i , \quad G_{i,i} =C_i , \quad G_{i,i+1} =D_i,\nonumber \\&\displaystyle G_{i,i+2} =E_i ,\; \hbox {for} \; i=3,\ldots ,n-2,\end{aligned}$$

(8.4)

$$\begin{aligned}&\displaystyle G_{n-1,n-3} =A_{n-1} , \quad G_{n-1,n-2} =B_{n-2} , \quad G_{n-1,n-1} =C_{n-1} , \quad G_{n-1,n} =D_{n-1} ,\qquad \quad \end{aligned}$$

(8.5)

$$\begin{aligned}&\displaystyle G_{n,n\!-\!2} =A_n , \quad G_{n,n\!-\!1} \!=\!B_n , \quad G_{n,n} \!=\!C_n \!-\!E_n,\qquad \end{aligned}$$

(8.6)

$$\begin{aligned}&\displaystyle \mathbf{w}=\left[ {w_1 ,w_2 ,\ldots w_{n-1} ,w_n } \right] ^{T},\end{aligned}$$

(8.7)

$$\begin{aligned}&\displaystyle A_i =\left\{ {1-\frac{\zeta _i }{4}h} \right\} ,\end{aligned}$$

(8.8)

$$\begin{aligned}&\displaystyle B_i =\left\{ {-4+\frac{\zeta _i }{2}h^{2}-\left( {2a^{*2}+\sigma ^{*}\tau } \right) h^{2}+a^{*2}\frac{\zeta _i }{4}h^{3}} \right\} ,\end{aligned}$$

(8.9)

$$\begin{aligned}&\displaystyle C_i \left\{ 6+2\left( {2a^{*2}+\sigma ^{*}\tau } \right) h^{2}+a^{*4}h^{4}+a^{*2}\sigma ^{*}\tau h^{4}\right. \nonumber \\&\displaystyle \left. -a^{*2} Ra^{*}h^{4}\frac{1}{2\sqrt{\pi }}\exp \left( {-\frac{\zeta _i^2 }{4}} \right) \right\} ,\end{aligned}$$

(8.10)

$$\begin{aligned}&\displaystyle D_i =\left\{ {-4-\frac{\zeta _i }{2}h-\left( {2a^{*2}+\sigma ^{*}\tau } \right) h^{2}-a^{*2}\frac{\zeta _i }{4}h^{3}} \right\} ,\end{aligned}$$

(8.11)

$$\begin{aligned}&\displaystyle E_i =\left\{ {1+\frac{\zeta _i }{4}h} \right\} . \end{aligned}$$

(8.12)

Here, $w_i$ is the vertical velocity disturbance at $\zeta =\zeta _i$ and $h\left( {=\zeta _{i+1} -\zeta _i } \right)$ is the fixed step size. We obtained neutral stability condition for a given $a^{*}$ by finding $Ra^{*}$ that makes the $\det \left( \mathbf{G} \right) =0$ under $\sigma ^{*}=0$.