1 Introduction

Unsteady flow in porous media can arise from unsteady boundary conditions or unsteady pressure gradients. Such flows can be found in many fields of environmental, technical, and even bio-mechanical background. Some examples are mass transfer between the turbulent atmospheric boundary layer and a forest (e.g., Finnigan 2000), at the soil or snow/atmosphere interface (e.g., Bowling et al. 2011; Maier et al. 2011), and between a turbulent or wavy water stream and a plant canopy (e.g., Lowe et al. 2005). Blood flow through organs can also be regarded as unsteady flow through a porous media (e.g., Fan and Wang 2011). So far, a unique description of these flow problems cannot be found in the literature, and different concepts on how to treat unsteady porous media flow exist.

For steady porous media flows, it is generally accepted and confirmed by numerous experimental results that the pressure drop (or hydraulic gradient) on a scale considerably larger than the pore scale can be represented by two terms, a linear and a quadratic one in the space-averaged velocity. For low Reynolds numbers based on pore diameter, the pressure drop increases linearly with the flow velocity, as it is dominated by viscous forces (creeping flow). This regime (\({\textit{Re}}_{\mathrm{pore}}<1\)) is called the Darcy regime, as it was first discussed by Darcy (1857). At larger pore Reynolds numbers, the quadratic term first gains weight in the force balance, and then, at \({\textit{Re}}_{\mathrm{pore}}>300\), the flow becomes turbulent. For the non-linear regime, Forchheimer (1901) proposed a quadratic correction to the relation between pressure drop and macroscopic flow velocity. The resulting expression can be derived either by a dimensional analysis or by rigorous averaging of the Navier–Stokes equations over a representative elementary volume; see Whitaker (1986, 1996).

For unsteady porous media flow, a number of experiments have shown that a phase shift between pressure drop and superficial velocity can exist (Laushey and Popat 1968; Burcharth and Andersen 1995; Hall et al. 1995; Gu and Wang 1991). This phase shift results from the inertia of the accelerated fluid, which must be represented by an unsteady term. The resulting equation can be written as

$$\begin{aligned} \varvec{\nabla }p = a \varvec{u}+ b \varvec{u}|\varvec{u}| + c\, \partial _t\varvec{u}. \end{aligned}$$
(1)

The coefficients \(a, b\) and \(c\) representing the linear and quadratic parts of the interaction force and the inertia term due to flow acceleration. If \(b=0\), the expression reduces to what is called unsteady Darcy equation. The standard Darcy equation can be obtained with \(b=c=0\). Note, that \(a\) needs to be formulated as a tensor in the general case of anisotropic materials which is omitted here for the sake of simplicity. Attempts have been made to determine the coefficients \(a, b\), and \(c\) from experiments (Gu and Wang 1991; Hall et al. 1995; Burcharth and Andersen 1995; Lowe et al. 2005). However, a full agreement between experimental results and behavior predicted by Eq. (1) with fitted coefficients has not yet been achieved.

Whitaker (1986, 1996) proposed using the volume-averaged Navier Stokes equations (VANS) to predict flow in porous media. By volume-averaging the momentum equation over a representative control volume, he derived a superficial averaged form of the Navier–Stokes equations. The interaction term at the pore/grain interface is closed by the steady-state Darcy and Forchheimer approximations. Under the condition of unidirectional flow through isotropic, homogeneous material, this equation can be written with a structure identical to that of Eq. (1). This approach has been adopted by several authors because it offers a mathematically sound framework for applications, in which strong changes in material properties such as porosity and permeability are present. Examples are the investigations of turbulent flow/porous media interaction by Breugem et al. (2006), the study of instabilities in Poiseuille flow over a porous layer (Hill and Straughan 2008; Tilton and Cortelezzi 2008) and analysis of bioheat transport (Fan and Wang 2011). A similar formulation was used by Kuznetsov and Nield (2006), Wang (2008) and Habibi et al. (2011) to directly derive an analytical solution for unsteady flow in a porous channel.

Another way to derive an unsteady Darcy equation in the form of (1) was presented by Rajagopal (2007) within the context of mixture theory. He also discussed possible implications of the unsteadiness of the flow field, suggesting consideration of a virtual mass term if inertial nonlinearities cannot be neglected. This term was proposed by Sollitt and Cross (1972) to account for the inhomogeneity of the flow field surrounding individual structures in the porous material during transient flow. It results in a larger time scale in unsteady porous media flow, compared to the VANS approach with steady-state closure. To the authors’ best knowledge, a systematic comparison and assessment of the different formulations of the unsteady Darcy equation has not been done so far.

In this paper, we investigate the time scale \(\tau =\frac{c}{a}\) in Eq. (1) for unsteady porous media flow. First, we summarize the resulting forms of the unsteady Darcy equation from the VANS and the virtual mass approaches (Sect. 2). Then, we propose an alternative expression for the time scale in unsteady porous media flow by volume-averaging the equation of the kinetic energy (Sect. 3). Finally, we use fully resolved direct numerical simulation (DNS) of the flow in the pore space to verify this expression (Sect. 4). By keeping the Reynolds number small, the flow remains linear, and the non-linear Forchheimer term can be neglected. The time scales obtained from the simulation results are compared to those obtained by the VANS, the virtual mass and our new kinetic energy approaches.

2 Unsteady Porous Media Flow

In this section, we briefly recall two related forms of the unsteady Darcy equation, obtained by the VANS approach with steady state closure and the virtual mass approach. Both are obtained by volume-averaging of the Navier–Stokes equations for incompressible flow of a Newtonian fluid through a porous medium

$$\begin{aligned} \rho \partial _t\varvec{u}+ \rho \varvec{u}\varvec{\cdot }\varvec{\nabla }\varvec{u}&= -\varvec{\nabla }{p} + \rho \varvec{g}+ \mu \varvec{\nabla }^2\varvec{u}, \end{aligned}$$
(2)
$$\begin{aligned} \mathrm{div}\varvec{u}&= 0, \end{aligned}$$
(3)

where \(\varvec{u}\) denotes the (Eulerian) velocity field. The gravitational force \(\varvec{g}\) will be dropped in the subsequent sections, as it could be lumped together with the pressure term. The convective operator is defined as usual, i.e., \(\varvec{u}\varvec{\cdot }\varvec{\nabla }\varvec{u}:= \sum _{i=1}^d u_i\,\partial _{x_i}\varvec{u}\). We present these and all following equations in dimensional form as at this stage of derivation, the reference scales are not yet determined.

For consistency with the prior work of Whitaker (1986), we denote the fluid phase by \(\beta \) and the solid phase by \(\sigma \). The total control volume is denoted by \(V\), and \({V_\beta }\) denotes the volume occupied by the fluid. On the fluid-solid interface \(A_{\beta \sigma }\), we define the normal vector \(\mathbf {n}_{\beta \sigma }\).

The superficial average of any physical quantity \(\varphi \) that is associated with the fluid phase \(\beta \) is defined by

$$\begin{aligned} {\left\langle {\varphi } \right\rangle }_\mathrm{s} = \frac{1}{|V|} \int _{{V_\beta }} \varphi ~\mathrm{d}x. \end{aligned}$$
(4)

We also introduce the intrinsic average

$$\begin{aligned} {\left\langle {\varphi } \right\rangle }_\mathrm{i} = \frac{1}{|{V_\beta }|} \int _{{V_\beta }} \varphi ~\mathrm{d}x, \end{aligned}$$
(5)

which is related to the superficial average by \({\left\langle {\varphi } \right\rangle }_\mathrm{s} = \epsilon {\left\langle {\varphi } \right\rangle }_\mathrm{i}\), where the ratio of the volumes \(\epsilon = |{V_\beta }|/|V|\) denotes the porosity. Let us recall that we can decompose any physical quantity \(\varphi = {\left\langle {\varphi } \right\rangle }_\mathrm{i} + \widetilde{\varphi }\) into its intrinsic average \({\left\langle {\varphi } \right\rangle }_\mathrm{i}\) and a fluctuation \(\widetilde{\varphi }\) (Whitaker 1986).

2.1 Steady and Unsteady form of the Darcy Equation

Using the above notation, we can write Darcy’s law as the proportional relation between the superficial velocity \({\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\) and the applied intrinsic pressure gradient \(\varvec{\nabla }{{\left\langle {p} \right\rangle }_\mathrm{i}}\). In vectorial form, this relation reads as

$$\begin{aligned} {\left\langle {\varvec{u}} \right\rangle }_\mathrm{s} = -\frac{K_D}{\mu } \varvec{\nabla }{{\left\langle {p} \right\rangle }_\mathrm{i}}, \end{aligned}$$
(6)

where \(K_D\) denotes Darcy’s permeability, which can be experimentally determined by applying a constant pressure gradient and measuring the flow rate \(Q = A\cdot {\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\) through a given cross-sectional area \(A\). Therefore, \(K_D\) is commonly identified as the permeability obtained under steady flow conditions. \(K_D\) needs to be formulated as a tensor in the general case. However, we restrict ourselves here to uniform flow in a homogeneous, isotropic material and, hence, use a scalar permeability \(K_D\).

When investigating unsteady porous media flow at low Reynolds numbers, the situation is less clear. In the general unsteady case, the permeability, if defined as above, is not necessarily constant over time. A common model for this type of flow is given in the form of the unsteady Darcy equation

$$\begin{aligned} \tau \partial _t{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s} + {\left\langle {\varvec{u}} \right\rangle }_\mathrm{s} = -\frac{K}{\mu } \varvec{\nabla }{\left\langle {p} \right\rangle }_\mathrm{i}, \end{aligned}$$
(7)

where \(\tau \) represents a time-scale and \(K\) a permeability (e.g., Burcharth and Andersen 1995; Kuznetsov and Nield 2006; Rajagopal 2007; Sollitt and Cross 1972).

The aim of this paper is to assess the validity of the unsteady Darcy Eq. (7) with constant coefficients. This can be transformed into the question of whether the permeability and the time constant can be treated as time-independent in the general unsteady case. Furthermore, we address the question of how these values can be determined. To achieve this aim, we first discuss two well-known approaches for deriving the unsteady Darcy equation, which are based on the volume-averaging of the Navier–Stokes Eq. (2). In Sect. 3, we shall derive and discuss an alternative way based on the volume-averaging of the kinetic energy equation. In our discussion, we consider that we have a control volume \(V\) with periodic boundary conditions on \(\partial {V}\). This assumption is reasonable for homogeneous porous media in regions far from the boundaries, where the control volume \(V\) ideally repeats itself. Furthermore, we restrict ourselves to unidirectional flow through this representative elementary volume (REV). Finally, we assume a small Reynolds number and uniform macroscopic flow.

2.2 Volume-Averaging of the Momentum Equation

Whitaker (1996) developed the following formulation by volume-averaging the Navier–Stokes Eq. (2):

$$\begin{aligned}&\rho \partial _t{\left\langle {\varvec{u}} \right\rangle }_\mathrm{i} + \rho {\left\langle {\varvec{u}} \right\rangle }_\mathrm{i} \mathrm{div}{\left\langle {\varvec{u}} \right\rangle }_\mathrm{i} + \underbrace{\rho \epsilon ^{-1}\mathrm{div}{\left\langle {\tilde{\varvec{u}}\tilde{\varvec{u}}} \right\rangle }_\mathrm{s}}_{\text {volume filter}} \nonumber \\&\qquad = -\varvec{\nabla }{\left\langle {p} \right\rangle }_\mathrm{i} + \underbrace{\mu \varvec{\nabla }^2{\left\langle {\varvec{u}} \right\rangle }_\mathrm{i}}_{\text {Brinkman correction}}+\underbrace{\frac{1}{|{V_\beta }|}\int _{A_{\beta \sigma }}\varvec{n}_{\beta \sigma }\cdot \left( -\tilde{p}\varvec{I}+\mu \varvec{\nabla }\tilde{\varvec{u}}\right) ~\mathrm{d}A}_{\text {surface filter}}. \end{aligned}$$
(8)

The surface filter represents the drag due to surface forces at the fluid-solid interface. It is identical to what Rajagopal (2007) referred to as an interaction term.

For a homogeneous and periodic REV, the second and third terms on the left-hand side vanish, as does the Brinkman correction. The equation then reduces to

$$\begin{aligned} \begin{aligned}&\rho \partial _t{\left\langle {\varvec{u}} \right\rangle }_\mathrm{i} = -\varvec{\nabla }{\left\langle {p} \right\rangle }_\mathrm{i} +\underbrace{\frac{1}{|{V_\beta }|}\int _{A_{\beta \sigma }}\varvec{n}_{\beta \sigma }\cdot \left( -\tilde{p}\varvec{I}+\mu \varvec{\nabla }\tilde{\varvec{u}}\right) ~\mathrm{d}A}_{\text {surface filter}}. \end{aligned} \end{aligned}$$
(9)

In the steady state, the surface filter can be replaced by the Forchheimer approximation

$$\begin{aligned} \frac{1}{|{V_\beta }|}\int _{A_{\beta \sigma }}\varvec{n}_{\beta \sigma }\cdot \left( -\tilde{p}\varvec{I}+\mu \varvec{\nabla }\tilde{\varvec{u}}\right) ~dA = -\frac{\mu }{K_D}(1 + F|{\left\langle {\varvec{u}} \right\rangle }_\mathrm{i}|) {\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}, \end{aligned}$$
(10)

cf. Whitaker (1996). Additionally, if the Reynolds number is sufficiently small, the term \(F|{\left\langle {\varvec{u}} \right\rangle }_\mathrm{i}|\) vanishes and the steady Darcy Eq. (6) is obtained.

For unsteady flow it has been proposed by several authors to use closure (10) with constant coefficients for the interaction term although its possible time dependence has been discussed (Rajagopal 2007). Inserted in Eq. (9) we arrive at the following expression:

$$\begin{aligned} \frac{K_{\text {D}}}{\nu \epsilon }\partial _t{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s} + {\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}= -\frac{K_{\text {D}}}{\mu } \varvec{\nabla }{\left\langle {p} \right\rangle }_\mathrm{i}, \end{aligned}$$
(11)

where \(\mu =\rho \nu \). By comparing it with the unsteady Darcy Eq. (7), we can identify the time constant obtained by this approach as

$$\begin{aligned} \tau _\mathrm{vans} = \frac{K_{\text {D}}}{\nu \epsilon }. \end{aligned}$$
(12)

The above form of the unsteady Darcy equation relies on the assumption that the steady-state approximation (10) can be used in the unsteady case (here denoted as VANS with steady state closure). The time dependence of the interaction term and its closure (10) is being examined in the following sections of this paper. The next section describes a method that is intended to take this time dependence into account, the virtual mass approach. In addition, we shall demonstrate by DNS in Sect. 4.5, that the steady state closure can not be used in the considered unsteady flow situations.

2.3 Virtual Mass Approach

It has been emphasized in the literature (e.g., Laushey and Popat 1968; Burcharth and Andersen 1995; Hall et al. 1995; Gu and Wang 1991) that, due to inertial effects, the time constant in Eq. (7) needs special attention. Using the analogy to unsteady flow around a single obstacle, a virtual mass coefficient was introduced by, e.g., Sollitt and Cross (1972) to compensate for the volume of fluid to be accelerated in the vicinity of the obstacle.

To take these effects into account, a virtual mass force per unit volume can be added to the closure of the interaction term in Eq. (10). For small Reynolds numbers—neglecting the Forchheimer term—this results in

$$\begin{aligned} \frac{1}{|{V_\beta }|}\int _{A_{\beta \sigma }}\varvec{n}_{\beta \sigma }\cdot \left( -\tilde{p}\varvec{I}+\mu \varvec{\nabla }\tilde{\varvec{u}}\right) ~\mathrm{d}A = -\frac{\mu }{K_D} {\left\langle {\varvec{u}} \right\rangle }_\mathrm{s} - \rho \, C_{\text {vm}}\frac{1-\epsilon }{\epsilon }\partial _t{\left\langle {\varvec{u}} \right\rangle }_\mathrm{i}. \end{aligned}$$
(13)

Here, \(C_{\text {vm}}\) is the virtual mass coefficient, yet to be determined. In this way, we obtain

$$\begin{aligned} \frac{K_{D}}{\nu \epsilon }\left[ 1+C_{\text {vm}}\frac{1-\epsilon }{\epsilon }\right] \partial _t{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s} + {\left\langle {\varvec{u}} \right\rangle }_\mathrm{s} = -\frac{K_{D}}{\mu }\varvec{\nabla }{\left\langle {p} \right\rangle }_\mathrm{i}. \end{aligned}$$
(14)

Thus, the time constant derived by this approach is given by:

$$\begin{aligned} \tau _{\text {vm}} = \frac{K_D}{\nu \epsilon }\left[ 1+C_{\text {vm}}\frac{1-\epsilon }{\epsilon }\right] , \end{aligned}$$
(15)

where \(C_{\text {vm}}\) is an empirical coefficient. Lowe et al. (2008) determined \(C_{\text {vm}}\) by fitting measured data for the phase and amplitude of the flow in a canopy (porous media) with the model equation. They also compared estimates for \(C_{\text {vm}}\) from the literature, which are in the range of \(0.5\le C_{\text {vm}}\le 2.0\).

One interpretation of the constant \(C_\text {vm}\) is that it models flow inhomogeneities on the pore scale. Hence, the success of the virtual mass approach relies on the knowledge of \(C_\text {vm}\) for a certain flow situation, which needs to be determined in experiments. In Sect. 4.8, we numerically investigate the influence of the choice of \(C_\text {vm}\) and compare the results for different values of \(C_\text {vm}\) with DNS.

3 A New Approach to Determine the Time Constant in Unsteady Porous Media Flow

To understand the nature of the virtual mass term, we now derive an alternative possibility to define a time constant for the unsteady Darcy model (7), which is based on the conservation of kinetic energy. The resulting form of the unsteady Darcy equation is in agreement with the virtual mass approach in the sense that we correct the time constant by a factor greater than one, which depends only on the pore-structure and the microscale-velocity. In our derivation, we need to make a number of assumptions and approximations, which we support by our DNS from Sect. 4.

3.1 Volume-Averaging of the Energy Equation

We start deriving an equation of the form of Eq. (7) by the use of the kinetic energy equation. Keeping in mind that \(\partial _t(\varvec{u}\varvec{\cdot }\varvec{u}) = 2\varvec{u}\varvec{\cdot }\partial _t\varvec{u}\), we can multiply the momentum part of the incompressible Navier–Stokes Eq. (2) by the velocity \(\varvec{u}\) to obtain an equation for the kinetic energy of the flow (without a gravity term):

$$\begin{aligned} \frac{\rho }{2} \partial _t(\varvec{u}\varvec{\cdot }\varvec{u}) + \rho \varvec{u}\varvec{\cdot }(\varvec{u}\varvec{\cdot }\varvec{\nabla }\varvec{u}) - \mu \varvec{u}\varvec{\cdot }\varvec{\nabla }^2\varvec{u}= - \varvec{u}\varvec{\cdot }\varvec{\nabla }{p}. \end{aligned}$$
(16)

Volume-averaging the equation now yields

$$\begin{aligned} \frac{\rho }{2} \partial _t{\left\langle {\varvec{u}\varvec{\cdot }\varvec{u}} \right\rangle }_\mathrm{s} + \rho {\left\langle {\varvec{u}\varvec{\cdot }(\varvec{u}\varvec{\cdot }\varvec{\nabla }\varvec{u})} \right\rangle }_\mathrm{s} - \mu {\left\langle {\varvec{u}\varvec{\cdot }\varvec{\nabla }^2\varvec{u}} \right\rangle }_\mathrm{s} = - {\left\langle {\varvec{u}\varvec{\cdot }\varvec{\nabla }{p}} \right\rangle }_\mathrm{s}, \end{aligned}$$
(17)

which can be regarded as the energy equation analogon to Eq. (8). Let us again consider an REV with periodic boundary conditions on \(\partial {V}\) in uniform flow conditions. We will first demonstrate that the second term on the left-hand side (advective term) vanishes and then reformulate the other terms. After applying the Gauß theorem to the advective term, we find that

$$\begin{aligned} {\left\langle {\varvec{u}\varvec{\cdot }(\varvec{u}\varvec{\cdot }\varvec{\nabla }\varvec{u})} \right\rangle }_\mathrm{s}&= \frac{1}{2|V|}\int \limits _{\partial {V}} \varvec{u}\varvec{\cdot }\varvec{n}|\varvec{u}|^2\,ds - \frac{1}{2}{\left\langle {\mathrm{div}(\varvec{u}) |\varvec{u}|^2} \right\rangle }_\mathrm{s}. \end{aligned}$$
(18)

The surface integral vanishes under periodic boundary conditions, and, due to incompressibility, we have \(\mathrm{div}(\varvec{u})=0\). Hence, the advective term does not contribute to the kinetic energy balance.

Let us proceed by considering the term \({\left\langle {\varvec{u}\varvec{\cdot }\varvec{\nabla }{p}} \right\rangle }_\mathrm{s}\). We can decompose \(p = {\left\langle {p} \right\rangle }_\mathrm{i} + \tilde{p}\) into a mean part \({\left\langle {p} \right\rangle }_\mathrm{i}\) and a fluctuation \(\tilde{p}\). Here, \({\left\langle {p} \right\rangle }_\mathrm{i}\) is the averaged pressure over the fluid phase of the averaging volume, and \(\varvec{\nabla }{{\left\langle {p} \right\rangle }_\mathrm{i}}\) is the pressure gradient driving the flow. In our case, the pressure gradient is taken as constant over the whole averaging volume, so we get

$$\begin{aligned} {\left\langle {\varvec{u}\varvec{\cdot }\varvec{\nabla }{p}} \right\rangle }_\mathrm{s}&= {\left\langle {\varvec{u}\varvec{\cdot }\varvec{\nabla }{\left\langle {p} \right\rangle }_\mathrm{i}} \right\rangle }_\mathrm{s} + {\left\langle {\varvec{u}\varvec{\cdot }\varvec{\nabla }{\tilde{p}}} \right\rangle }_\mathrm{s} \end{aligned}$$
(19)
$$\begin{aligned}&= {\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\varvec{\cdot }\varvec{\nabla }{\left\langle {p} \right\rangle }_\mathrm{i} + \frac{1}{|V|}\int _{\partial {V}}\varvec{u}\varvec{\cdot }\varvec{n}\,\tilde{p}\,ds - {\left\langle {\mathrm{div}(\varvec{u})\varvec{\cdot }\varvec{\nabla }{\tilde{p}}} \right\rangle }_\mathrm{s}. \end{aligned}$$
(20)

The last term is zero due to incompressibility. Since we assume periodicity, the surface integral also vanishes.

Let us now consider the viscous term in (17). Via integration by parts, it can be decomposed into two contributions, representing the diffusion and the pseudo-dissipation of the kinetic energy, respectively (e.g., Pope 2000):

$$\begin{aligned} \mu {\left\langle {\varvec{u}\varvec{\cdot }\varvec{\nabla }^2\varvec{u}} \right\rangle }_\mathrm{s} = \frac{\mu }{2}{\left\langle {\varvec{\nabla }^2(\varvec{u}\varvec{\cdot }\varvec{u})} \right\rangle }_\mathrm{s} - \mu {\left\langle {\varvec{\nabla }\varvec{u}: \varvec{\nabla }\varvec{u}} \right\rangle }_\mathrm{s}, \end{aligned}$$
(21)

where \({\mathbf {A} : \mathbf {B}} := \sum _{i,j} A_{ij} B_{ij}\) denotes the Frobenius inner product. The volume integral of the diffusion of kinetic energy \(\tfrac{\mu }{2}{\left\langle {\varvec{\nabla }^2(\varvec{u}\varvec{\cdot }\varvec{u})} \right\rangle }_\mathrm{s}\) vanishes in the case of a periodic domain. Moreover, it can be shown that for incompressible flow in periodic domains, the pseudo-dissipation \(\mu {\left\langle {\varvec{\nabla }\varvec{u}: \varvec{\nabla }\varvec{u}} \right\rangle }_\mathrm{s}\) equals the dissipation of kinetic energy \(2\mu {\left\langle {\varvec{s}: \varvec{s}} \right\rangle }_\mathrm{s}\), where \(\varvec{s}:= \tfrac{1}{2}(\varvec{\nabla }\varvec{u}+ (\varvec{\nabla }\varvec{u})^T)\) is the symmetric part of the velocity gradient. Altogether, we can write (17) as

$$\begin{aligned} \frac{\rho }{2} \partial _t{\left\langle {\varvec{u}\varvec{\cdot }\varvec{u}} \right\rangle }_\mathrm{s} + 2\mu {\left\langle {\varvec{s}: \varvec{s}} \right\rangle }_\mathrm{s}= - {\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\varvec{\cdot }\varvec{\nabla }{\left\langle {p} \right\rangle }_\mathrm{i}. \end{aligned}$$
(22)

This is the balance of the pore scale kinetic energy for a homogeneous and periodic REV under uniform macroscopic flow conditions. The rate of change of kinetic energy on the pore scale (first term) is obtained by the balance of its dissipation (second term) and the power input by the pressure gradient (right hand side). If the unsteady Darcy equation with constant coefficients (7) was a good model for unsteady flow in porous media, it should be possible to bring both into a comparable form. In order to do so, we need to introduce some approximations.

First, we show that, for the steady state, the volume-integrated dissipation of kinetic energy is related to the permeability and viscosity.

This is done by rewriting the unsteady Darcy equation (7) in the energy form by multiplying it by \({\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\):

$$\begin{aligned} \frac{\tau }{2}\,\partial _t({\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\varvec{\cdot }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}) + {\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\varvec{\cdot }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s} = - \frac{K}{\mu }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\varvec{\cdot }\varvec{\nabla }{\left\langle {p} \right\rangle }_\mathrm{i}. \end{aligned}$$
(23)

Note that \(\tau \) and \(K\) do not necessarily have to be constant in the unsteady case. However, for the steady state, i.e., \(\partial _t(\,\cdot \,)=0\), we find by comparing Eq. (22) with Eq. (23) that

$$\begin{aligned} 2\mu {\left\langle {\varvec{s}: \varvec{s}} \right\rangle }_\mathrm{s}= \mu {\left\langle {\varvec{\nabla }\varvec{u}: \varvec{\nabla }\varvec{u}} \right\rangle }_\mathrm{s} = \frac{\mu }{K}{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\varvec{\cdot }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}. \end{aligned}$$
(24)

This shows that the steady state dissipation of the kinetic energy on the pore scale can be expressed by the viscosity, the classical Darcy permeability (\(K=K_D\)) and the square of the superficial velocity. In order to use Eq. (24) as a closure for the unsteady case, we have to assume that \(K=( {\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\varvec{\cdot }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s})/2{\left\langle {\varvec{s}: \varvec{s}} \right\rangle }_\mathrm{s}\) does not depart much from its steady state value. We investigate this question using DNS in Sect. 4.5.

Second, to determine whether Eq. (23) can be taken as a good approximation of Eq. (22), we approximate the unsteady term of the latter by

$$\begin{aligned} \frac{\rho }{2}\partial _t{\left\langle {\varvec{u}\varvec{\cdot }\varvec{u}} \right\rangle }_\mathrm{s} = \frac{\rho }{2}\partial _t\left( \frac{{\left\langle {\varvec{u}\varvec{\cdot }\varvec{u}} \right\rangle }_\mathrm{s}}{{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\varvec{\cdot }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}}{{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\varvec{\cdot }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}}\right) \approx \frac{\rho }{2}\frac{{\left\langle {\varvec{u}\varvec{\cdot }\varvec{u}} \right\rangle }_\mathrm{s}}{{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\varvec{\cdot }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}} \partial _t\left( {{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\varvec{\cdot }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}}\right) . \end{aligned}$$
(25)

Here, we point out that we neglect the fact that \(\frac{{\left\langle {\varvec{u}\varvec{\cdot }\varvec{u}} \right\rangle }_\mathrm{s}}{{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\varvec{\cdot }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}}\) is, in general, time-dependent. However, as we see from our DNS results in Sect. 4.7, this assumption is reasonable, since it does not substantially depart from its steady state, even if sudden changes in the flow occur. The following form of the energy equation is now obtained by substituting Eqs. (24) and (25) in Eq. (22):

$$\begin{aligned} \frac{\rho }{2}\frac{{\left\langle {\varvec{u}\varvec{\cdot }\varvec{u}} \right\rangle }_\mathrm{s}}{{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\varvec{\cdot }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}} \partial _t\left( {{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\varvec{\cdot }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}}\right) + \frac{\mu }{K_{\text {D}}}{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\varvec{\cdot }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s} = - {\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\varvec{\cdot }\varvec{\nabla }{\left\langle {p} \right\rangle }_\mathrm{i}. \end{aligned}$$
(26)

In the case of a homogeneous and isotropic medium, \({\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\) and \(\varvec{\nabla }{\left\langle {p} \right\rangle }_\mathrm{i}\) are parallel, which implies that Eq. (26) can be divided by \(|{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}|\) and brought into a form corresponding to equation (7):

$$\begin{aligned} \tau _\text {en}\partial _t{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s} + {\left\langle {\varvec{u}} \right\rangle }_\mathrm{s} = -\frac{K_{\text {D}}}{\mu } \varvec{\nabla }{\left\langle {p} \right\rangle }_\mathrm{i}, \end{aligned}$$
(27)

with the coefficient \(\tau _\text {en}\) being proportional to the ratio of the intrinsic averaged kinetic energy in the pore space versus the kinetic energy of the intrinsic velocity. This leads us to our main result, which is an explicit representation of the time-scale in unsteady porous media flow:

$$\begin{aligned} \tau _\text {en} = \frac{K_{\text {D}}}{\nu }\frac{{\left\langle {\varvec{u}\varvec{\cdot }\varvec{u}} \right\rangle }_\mathrm{s}}{{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\varvec{\cdot }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}}= \frac{K_{\text {D}}}{\epsilon \,\nu }\frac{{\left\langle {\varvec{u}\varvec{\cdot }\varvec{u}} \right\rangle }_\mathrm{i}}{{\left\langle {\varvec{u}} \right\rangle }_\mathrm{i}\varvec{\cdot }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{i}}. \end{aligned}$$
(28)

Note that Eq. (27) with (28) can be used only if both approximations (24) and (25) are accurate enough and do not depart too much from their limits in steady flow. We will address this question by DNS in Sect. 4.

The time-coefficient \(\tau _\text {en}\) given by Eq. (28) has an interesting property, which we would like to comment on: as a consequence of the Cauchy–Schwarz inequality, it holds that \({\left\langle {\varvec{u}\varvec{\cdot }\varvec{u}} \right\rangle }_\mathrm{i} \ge {\left\langle {\varvec{u}} \right\rangle }_\mathrm{i}\varvec{\cdot }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{i}\), which readily implies that

$$\begin{aligned} \tau _\text {en} \ge \tau _\mathrm{vans}. \end{aligned}$$
(29)

Hence, the VANS approach with steady state closure is the lower limit for our time-coefficient, which is in line with the observations that led to the virtual mass approach. In particular, if the intrinsic averaged kinetic energy in the pore space is in balance with the kinetic energy of the intrinsic velocity, then the pore-scale effects are negligible, and the VANS approach with steady state closure leads to a reasonable approximation for unsteady porous media flow.

3.2 Summary of the Different Approaches

The coefficients derived by the kinetic energy approach differ from those derived by the VANS approach with steady state closure or the virtual mass correction. In each derivation, several assumptions have to be made to obtain the unsteady form of Darcy’s equation. All approaches are exact in the steady state limit and \(K=K_D\) is the permeability.

In the VANS approach, the interaction term is replaced by the steady-state approximation \(\frac{\mu }{K_D}{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\), and a constant permeability is being assumed. In the virtual mass approach, an additional virtual mass force is added rendering the interaction term time depending. This virtual mass force can be absorbed into the coefficient in front of the time derivative giving a modified time constant.

In contrast, our approach incorporates permeability by approximating the interaction term \(2\mu {\left\langle {\varvec{s}: \varvec{s}} \right\rangle }_\mathrm{s}\) with \(\frac{\mu }{K}{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\cdot {\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\). In the steady limit we then find, by comparison with the Darcy equation, that the expression

$$\begin{aligned} K = \frac{{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\cdot {\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}}{2{\left\langle {\varvec{s}:\varvec{s}} \right\rangle }_\mathrm{s}} = \frac{{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\cdot {\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}}{{\left\langle {\varvec{\nabla }\varvec{u}:\varvec{\nabla }\varvec{u}} \right\rangle }_\mathrm{s}}, \end{aligned}$$
(30)

which relates the superficial velocity to the volume averaged dissipation of kinetic energy, can indeed be identified with the classical Darcy permeability \(K_\text {D}\). In order to arrive at the unsteady Darcy equation we have to assume that \(K\) as defined by Eq. (30) does not depart much from its steady state.

We summarize in Table 1 the time-scales resulting from the different approaches.

Table 1 Different choices for the time-scale in Eq. (7). For practical computations, we propose using the steady-state value \(\tau _\text {en}\) of the time-scale of the energy-approach
Full size table

The time scales obtained from the different derivations represent different physical quantities. All time scales have been derived under the assumptions described in the previous sections. The main assumption, which is common to all approaches, is the one that the coefficients in the unsteady Darcy equation remain constant w.r.t. time in unsteady flow. This is equivalent with assuming self-similar velocity profiles during flow acceleration.

We present here a simple argument that self-similar velocity profiles cannot be expected during flow acceleration. The argument results from the fact that it takes a certain time for the effect of the viscosity to propagate from the solid surface to the core of the flow. This time can be estimated by the viscous time scale in the pore space \(\tau _\mathrm{visc}=D^2/\nu \), \(D\) being a grain diameter. If this time is much smaller than the time scale of the flow acceleration, e.g., \(\tau _\mathrm{vans}\), then self-similar profiles can be expected during flow acceleration. However, if the viscous time scale is much larger than \(\tau _\mathrm{vans}\), then self-similar velocity profiles can not be expected. The flow acceleration is effectuated by the pressure gradient which is irrotational. The unsteady velocity profile shapes therefore depart from the steady state ones by the viscous effect. To compare \(\tau _\mathrm{vans}\) with \(\tau _\mathrm{visc}\), we use the Kozeny–Carman equation (Kozeny 1927) to estimate the permeability \(K=D^2 \epsilon ^3 /(180 (1-\epsilon )^2)\). For \(\epsilon <0.5\), we have \(K<D^2/180\) and find \(\tau _\mathrm{vans}\ll \tau _\mathrm{visc}\). This renders self-similar velocity profiles very unlikely during flow acceleration.

Concluding, the accuracy of Eq. (7) and its applicability to unsteady flow in porous media depends on how far the individual terms deviate from their steady state approximations during flow acceleration. We will investigate this issue in the next section using highly resolved numerical simulations of unsteady low-Reynolds number flow in various porous media.

4 Numerical Results

In the following, we present numerical studies to support the assumptions we made in the derivation of the unsteady Darcy Eq. (27) and its coefficients. Therefore, we compute highly resolved solutions of the full Navier–Stokes Eqs. (2) through different configurations of porous media with increasing complexity. In all simulations, the Reynolds numbers, based on pore velocity and pore length scale, are kept on the order of \(10^{-3}\), which is small enough to ensure that the Forchheimer terms can be neglected.

Before we describe the setup of the simulations, and discuss their results, let us first describe the benchmark problem used throughout this section.

4.1 Benchmark Problem

For all three test cases, heavy side functions are applied to the \(x\)-component of the pressure gradient to drive the flow:

$$\begin{aligned} \varvec{\nabla }{\left\langle {p(t)} \right\rangle }_\mathrm{i}=p_{x}\mathbf {e}_x\cdot {\left\{ \begin{array}{ll} 0 &{} \qquad t < 0,\\ 1 &{} \qquad 0 \le t \le t_1, \\ 2 &{} \qquad t > t_1, \end{array}\right. } \end{aligned}$$
(31)

Here, \(\mathbf {e}_x\) denotes the unit vector in \(x\)-direction, \(p_{x}\) is the constant pressure gradient and \(t_1\) is chosen in such a way that the flow first reaches its steady state and then develops again once \(p_{x}\) is doubled.

The analytical solution of the unsteady Darcy Eq. (7) is given by

$$\begin{aligned} {\left\langle {\mathbf {u}(t)} \right\rangle }_\mathrm{s}=p_{x}\mathbf {e}_x\cdot \frac{K}{\mu }\cdot {\left\{ \begin{array}{ll} 0 &{} \qquad t < 0,\\ \exp (-t/\tau )-1 &{} \qquad 0 \le t < t_1, \\ \exp (-(t-t_1)/\tau )-2 &{} \qquad t > t_1. \end{array}\right. } \end{aligned}$$
(32)

In this equation, the permeability \(K\) is measured from the steady state of the DNS results, which is reached after a sufficient time. The only unknown in this solution is now the time constant \(\tau \), which gives us a quality measure to determine the accuracy of the different approaches for this benchmark problem. Let us point out that, in the case of the energy approach, we take \(\tau \) as the steady-state value \(\tau _\text {en}\).

4.2 Simulation Setup

The full Navier–Stokes Eqs. (2) for an incompressible Newtonian fluid are solved by a finite volume method on a Cartesian grid (Manhart 2004), where the pore space is represented by an immersed boundary method (Peller et al. 2006; Peller 2010). For the spatial discretization we use a second-order central scheme, and we advance in time by a low-storage third-order Runge–Kutta method (Williamson 1980). The solver code is well validated in various flow configurations, including laminar and turbulent flows; cf., e.g., Breuer et al. (2009); Hokpunna and Manhart (2010); Peller (2010). To ensure accurate and reliable results, we conduct a refinement study for each simulation.

In the following, we denote by \(D\) the cylinder diameter and sphere diameter in the two- and three-dimensional cases, respectively, and the channel height in the one-dimensional case. The Reynolds number is then, in all cases, computed by \({\textit{Re}}= {\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\cdot \mathbf {e}_xD/\nu \). We furthermore introduce the pore spacing as \(H\), and we define the blockage ratio as \(B = D/H\).

A channel flow at a low Reynolds number can be understood as a prototype for a porous media flow, with \(\epsilon =1\). Thus, we start with a straight one-dimensional channel with solid walls.

In our DNS of the channel flow, we consider a Reynolds number of \({\textit{Re}}= 3.35 \times 10^{-3}\). Periodic boundary conditions are applied in stream- and span-wise directions, such that the flow repeats itself periodically.

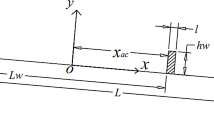
To increase flow complexity, we consider a two-dimensional flow through an array of regularly placed cylinders. Although, we use this as an idealized configuration to assess our theoretical findings, one could imagine real configurations in which such a geometry could serve as a good model, e.g., a tube bundle in a heat exchanger or an array of plants or a forest. We simulate a box containing one cylinder as indicated in Fig. 1. By using periodic boundary conditions in the directions perpendicular to the cylinder axes, we actually simulate an infinite array of cylinders.

Fig. 1
figure 1

Two-dimensional simulation. Arrangement of cylinders (2D) and computational box containing one cylinder (left) and streamline plot of flow at low Reynolds number (right)

Full size image

The Reynolds number in the two-dimensional case has been adjusted to \({\textit{Re}}= 1.55 \times 10^{-4}\). The grid has a resolution of \(480\) cells per cylinder diameter \(D\). The blockage ratio is \(B = 0.75\), and the porosity can be computed as \(\epsilon = 0.5582\). In Fig. 1 (right), streamlines of the steady state flow are plotted. In the lateral gaps between the cylinders, high steady-state velocities can be observed. Upstream and downstream of the cylinder, the flow reverses and forms a backflow region. The flow field is symmetrical about the two symmetry planes of the cylinder, which is a result of the geometry and the low Reynolds number.

Our three-dimensional simulations are performed on two different configurations.

The first one is a sphere-pack in which the spheres are arranged on a uniform grid with a porosity of \(\epsilon =0.73\), and the blockage ratio is given by \(B=0.8\). The simulation domain is the three-dimensional extension of the one shown in Fig. 1 (left). The Reynolds number is set to \({\textit{Re}}= 8.45\times 10^{-5}\), and we resolve one sphere diameter with \(192\) grid cells.

The second configuration is the flow through a dense sphere-pack in hexagonal close packing (cf. Fig. 2, left), which results in a porosity of \(\epsilon =0.26\). Periodic boundary conditions are applied in all directions, such that the flow and geometry repeat themselves in space. The Reynolds number is \(1.25\times 10^{-6}\), where we resolve one sphere diameter with \(400\) grid cells. These resolutions are required to compute the dissipation rate with reasonable accuracy during postprocessing since no effort has been made to specially treat the cells cut by the sphere surface, where the maximum dissipation occurs. In Fig. 2 we plot streamlines for the steady flow field. Unlike in the two-dimensional case, in which the cylinders are arranged on a regular lattice, we can not see any backflow regions.

Fig. 2
figure 2

Three-dimensional simulation of a dense sphere pack. Arrangement of spheres (3D) (left) and streamlines (right)

Full size image

We assessed the proper grid resolution by a systematic grid study. For the different cases, we simulated the flows with different resolutions. We measured the values of superficial velocity \({\left\langle {u} \right\rangle }_\mathrm{s}\), dissipation \(2\mu {\left\langle {\varvec{s}: \varvec{s}} \right\rangle }_\mathrm{s}\) and the factor \(\frac{{\left\langle {\varvec{u}\varvec{\cdot }\varvec{u}} \right\rangle }_\mathrm{s}}{{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\varvec{\cdot }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}}\) at fixed times in steady-state, and we took the results from the finest resolutions as references to calculate the relative errors. Figure 3 illustrates the changes of the relative errors with respect to the number of grid points per \(D\) (in channel case \(2H\)) in log-log plots. We can see that the superficial velocity \({\left\langle {u} \right\rangle }_\mathrm{s}\) and the factor \(\frac{{\left\langle {\varvec{u}\varvec{\cdot }\varvec{u}} \right\rangle }_\mathrm{s}}{{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\varvec{\cdot }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}}\) have a second order convergence with respect to grid spacing. The dissipation has only first order convergence. This can be explained by the post-processing from which we computed the dissipation. We did not pay special attention to treating the velocity gradients at the surface of the spheres/cylinders in the calculation of the dissipation. In the channel flow, not using the Immersed Boundary Method, the dissipation converges with second order as well. In the reference solutions, we used \(800\) grid cells along the channel hight for the channel case, \(480\) grid cells per diameter for the cylinder case and \(192\) grid cells per diameter for the sphere array case. Note that the difference between the second finest grids and reference solutions in the superficial velocity is less than \(0.1\,\%\) in all cases and that the one in the dissipation is around \(1\,\%\), which essentially implies that the errors in the reference solutions are even smaller.

Fig. 3
figure 3

Relative error of superficial velocity, dissipation and ratio between integrated kinetic energy in the pore space and that of the superficial velocity

Full size image

4.3 Velocity Profiles During Flow Acceleration

In this section, we examine velocity profiles during flow acceleration. In Fig. 4 we show velocity profiles at different instances in time for the channel flow (left) and for the flow in the cylinder array (right). The latter is positioned in the smallest gap between two cylinders where the velocity is largest. Note that the profiles are normalized by their instantaneous maximum values. The plots clearly show the deformation of the profile shapes w.r.t. time. In the channel flow, a parabolic profile is obtained at late times. However, at very short times, the flow is essentially a constant profile from which a parabolic profile slowly develops. The change in the profile shape can be interpreted as the interaction of pressure gradient and viscosity. While pressure gradient accelerates the flow uniformly over the channel width, the viscosity slows down the flow from the wall. As both processes act with different time scales, a deformation of the profile is being obtained during the flow acceleration.

Fig. 4
figure 4

Velocity profiles at different times during flow acceleration. Channel flow (left) and flow in a cylinder array between two cylinders (right)

Full size image

The deformation of the velocity profile in the flow through the cylinder array is even more pronounced. Two peaks at the cylinders’ walls develop at short times that disappear at late times. At short times the flow is accelerated by the pressure field while the viscosity acts more slowly. Therefore, the flow field tends to be irrotational at very short timesFootnote 1 which explains the two peaks. At late times the profiles tend towards a profile similar to a parabola due to the influence of the viscosity.

The change in the shape of the velocity profiles let us speculate that flow quantities such as interaction term or dissipation might hardly be linearly dependent on superficial velocity during flow acceleration. We will have a closer look on the relation between superficial velocity and interaction term or dissipation, respectively, in Sects. 4.5 and 4.6.

4.4 Superficial Velocity

In this numerical experiment, we study the development of the superficial velocity in the \(x\)-direction, \({\left\langle {u(t)} \right\rangle }_\mathrm{s} := {\left\langle {\mathbf {u}(t)} \right\rangle }_\mathrm{s}\cdot \mathbf {e}_x\), after applying the pressure gradient jumps. In particular, we compare the exact solutions obtained for the time constants from the VANS and energy approaches with the DNS results. We do not include the virtual mass approach here since, in the two- and three-dimensional cases, it would yield the same results as the energy approach for a properly tuned constant \(C_\text {vm}\).

For the different configurations, we measure the permeability \(K\) from the steady-state DNS results. We compute \(\tau _\mathrm{vans}\) by Eq. (12) and \(\tau _\text {en}\) as defined in Eq. (28), and compare the analytic solutions obtained with the respective time constants to the DNS results.

In Fig. 5, we plot the solutions \({\left\langle {u(t)} \right\rangle }_\mathrm{s}\) obtained by the different approaches as a function of time. The time constant \(\tau _\mathrm{vans}\) is, in all cases, smaller than \(\tau _\text {en}\), and does not represent the unsteadiness correctly for this particular example. For the two- and three-dimensional arrangements, the discrepancy is even larger. In the case of a hexagonal sphere-pack with lower porosity \(\epsilon =0.26\), we observe the most significant deviation of the VANS approach with steady state closure from the DNS results. However, in all experiments, we see that the analytical solution (32) of the unsteady Darcy equation closely follows the DNS solution, if the time constant is determined by the energy approach, Eq. (28).

Fig. 5
figure 5

Comparison of DNS results with analytical solutions using \(\tau _{\mathrm{vans}}\) and \(\tau _{\text {en}}\)

Full size image

4.5 Interaction Term

If we neglect the Forchheimer terms in Eq. (10), we obtain the approximation

$$\begin{aligned} \frac{1}{|{V_\beta }|}\int \limits _{A_{\beta \sigma }}\varvec{n}_{\beta \sigma }\cdot \left( -\tilde{p}\varvec{I}+\mu \varvec{\nabla }\tilde{\varvec{u}}\right) ~dA = -\frac{\mu }{K_D}{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}, \end{aligned}$$

which is used in the derivation of the VANS model of unsteady porous media flow. While this is undisputed in the steady state, the velocity profiles in Sect. 4.3 pose a question regarding the validity of this assumption for unsteady porous media flow. Hence, we compare the surface filter (interaction term) obtained by DNS with its steady state approximation, Eq. (10). In all simulations, we observe that, in the steady state, the ratio between interaction term and closure approaches unity, which is consistent with the theory for steady Darcy flow. However, in the unsteady regime, we observe a large discrepancy between the actual interaction term and its closure.

For the different cases, we inspect the approximation of the interaction term by plotting it as a function of its closure (Figure 6). Here, the diagonal represents the steady-state solution. During the transient phase, large deviations can be observed in which the interaction term is consistently larger than its approximation, thus slowing down the acceleration of the flow compared to the VANS approach with closure (10).

Fig. 6
figure 6

Variation of the surface filter \(|\frac{1}{|{V_\beta }|}\int _{A_{\beta \sigma }}\varvec{n}_{\beta \sigma }\cdot \left( -\tilde{p}\varvec{I}+\mu \varvec{\nabla }\tilde{\varvec{u}}\right) ~dA|\) with \(\frac{\mu }{K_D}|{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}|\)

Full size image

From the observations made in our experiments, we conclude that the steady-state approximation of the interaction term leads to an insufficient representation of the physics in the cases under investigation. This is in line with observations from Sect. 4.3

4.6 Dissipation of the Kinetic Energy

In our derivation using the volume-averaged kinetic energy equation, we introduced the approximation

$$\begin{aligned} 2\mu {\left\langle {\varvec{s}: \varvec{s}} \right\rangle }_\mathrm{s}= \frac{\mu }{K}{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\varvec{\cdot }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}, \end{aligned}$$
(33)

which is accurate in the steady state. We inspect the quality of the approximation during the transient simulations. In Fig. 7 we observe that the dissipation correlates well with its approximation during flow acceleration. Obviously, the dissipation is less sensitive to the deformations of the velocity profile shapes than the interaction term (mainly wall shear stress). There is a small underprediction of the dissipation, visible as a systematic deviation of the dissipation from its approximation, which is also present for large values, i.e., for large times in the steady state. It is a result of an inconsistency in determining the dissipation by post-processing, which converges by first order, see Section 4.2. Thus, the approximation of the dissipation of kinetic energy seems to be more reasonable than that of the surface filter by their respective steady-state counterparts.

Fig. 7
figure 7

Variation of the dissipation \(2\mu {\left\langle {\varvec{s}: \varvec{s}} \right\rangle }_\mathrm{s}\) with \(\frac{\mu }{K_D}{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\varvec{\cdot }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\)

Full size image

4.7 Time-Scale

In the derivation of the unsteady Darcy equation, we made a second approximation by assuming in Eq. (25) that

$$\begin{aligned} \partial _t\frac{{\left\langle {\varvec{u}\varvec{\cdot }\varvec{u}} \right\rangle }_\mathrm{i}}{{\left\langle {\varvec{u}} \right\rangle }_\mathrm{i}\varvec{\cdot }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{i}}\approx 0. \end{aligned}$$
(34)

The purpose of this section is to assess whether this assumption is justified or not.

In Fig. 8, we plot the time dependence of the factor \(\frac{{\left\langle {\varvec{u}\varvec{\cdot }\varvec{u}} \right\rangle }_\mathrm{i}}{{\left\langle {\varvec{u}} \right\rangle }_\mathrm{i}\varvec{\cdot }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{i}}\). When the flow starts from rest, we assume the lower limit \(\tau = \tau _\text {vans}\). However, as the flow develops, our time scale quickly relaxes towards its steady-state value, \(\tau \rightarrow \tau _\text {en}\).

Fig. 8
figure 8

Temporal variation of \(\frac{{\left\langle {\varvec{u}\varvec{\cdot }\varvec{u}} \right\rangle }_\mathrm{s}}{{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}\varvec{\cdot }{\left\langle {\varvec{u}} \right\rangle }_\mathrm{s}}\) from DNS

Full size image

At the second step change in pressure, the departure from its steady-state value remains, in all cases, below \(10\,\%\) and then rapidly readjusts to its steady-state value. Hence, in the case of developed flow through porous media, our examples support the assumption that the time scale can be taken as a constant value.

As we can see in Fig. 8, the steady state obtained in the DNS results for the channel flow is at around \(\tau _\text {en}=1.2\,\tau _\text {vans}\). The analytical solution for steady flow in a channel is a parabolic velocity profile (Batchelor 1967). From this, we obtain \(\tau _\text {en}=1.2\,\tau _\text {vans}\). This value is in perfect agreement with our numerical results.

For the two-dimensional cylinder array, the steady state is at about \(\tau _\text {en}=1.787\,\tau _\text {vans}\) which is even larger than for the channel flow. The largest time scale ratio of our experiments is reached for the hexagonal sphere-pack at a value of \(2.747\). As shown in Sect. 4.4, the VANS approach with steady-state closure leads to a significant deviation from the actual flow dynamics in this case, whereas the energy approach can accurately represent the unsteadiness of the flow.

4.8 Comparison with the Virtual Mass Approach

To assess the dependency of the time constant on the porosity, we conducted several runs with different porosities for the two-dimensional configuration. Here, the size of the cylinder is kept the same, and the domain size (i.e., the distance between the cylinders) is adjusted such that different porosities are obtained. A resolution of \(120\) grid cells per diameter is maintained by this procedure.

For each porosity, we determined an empirical time constant \(\tau _\text {dns}\) by fitting the analytical solution of the unsteady Darcy Eq. (32) to the DNS data of \({\left\langle {u(t)} \right\rangle }_\mathrm{s}\). Those values compare well with those obtained by the energy approach \(\tau _{\text {en}}\). Both are, however, larger than the time scales obtained by the VANS approach with steady-state closure \(\tau _{\text {vans}}\). The form of the virtual mass time constant (15) implies that

$$\begin{aligned} \frac{\tau _{\text {vm}}}{\tau _{\text {vans}}} = 1+\frac{C_{\text {vm}}(1-\epsilon )}{\epsilon } \ge 1. \end{aligned}$$
(35)

We compare the obtained DNS values with \(\tau _\text {vm}/\tau _\text {vans}\) in Fig. 9 for different coefficients \(C_{\text {vm}}\). The tendency of the virtual mass term is correct in the sense that it increases with decreasing porosity. However, its slope differs from the slope of the values obtained by DNS. It is not possible to match all the DNS values with one single virtual mass coefficient. From equation (35), it can be inferred that the limiting behavior toward \(\epsilon \rightarrow 1\) is not accurately captured if \(C_\text {vm}\) is taken independently of the porosity \(\epsilon \). We included \(\tau _{en}\) in figure 9 for completeness, as it shows good agreement with \(\tau _\text {dns}\).

Fig. 9
figure 9

Time scales from DNS \(\tau _\text {dns}/\tau _\text {vans}\) compared to \(\tau _\text {en}/\tau _\text {vans}\) and the virtual mass approach \(\tau _\text {vm}/\tau _\text {vans}\) for different virtual mass coefficients \(C_\text {vm}\) as a function of porosity \(\epsilon \)

Full size image

5 Conclusions

To investigate unsteady flow in porous media, we focused on the applicability of the unsteady form of Darcy’s equation and its time scale. Our direct numerical simulations of transient flow in the pore space support the use of the unsteady form of Darcy’s equation with constant coefficients, although velocity profile shapes have been found not to be self-similar during flow acceleration. The simulations, however, show that the volume-averaged Navier–Stokes system with a steady-state closure for the interaction term underpredicts the time scale in the unsteady Darcy equation. Motivated by these observations, we reviewed existing approaches and presented an alternative way to define a time scale.

We derived the unsteady form of Darcy’s equation by starting with the equation of the kinetic energy of the flow in the pore space. The interaction term here represents the dissipation of kinetic energy, which was approximated by its steady-state value using the classical permeability. We demonstrated that this assumption is well suited in all of our simulations of various configurations, as the dissipation remains very closely proportional to the square of the superficial velocity during the transient phase. The energy approach leads to a different time scale that is proportional to the ratio of the integrated kinetic energy in the pore space to that of the intrinsic velocity. This ratio can be rather large ranging from a value of \(1.2\) for plain channel flow to \(2.75\) for a dense sphere pack with hexagonal packing. Our time scale is well in accordance with those evaluated by direct numerical simulation of transient flow in the respective configurations.

The virtual mass approach is qualitatively in line with the findings of this study in that it increases the time scale in the unsteady Darcy equation. However, the dependence of the virtual mass term with porosity cannot be obtained with a constant virtual mass coefficient. We suggest using the time scale obtained by the energy equation approach because it establishes a well-defined quantity. The use of model reduction techniques that allow to determine this quantity without the need for direct numerical simulations is a subject of future research.