1 Introduction

Flow through porous media and the associated heat transfer is of essential importance in view of diversified engineering applications, which includes nuclear waste disposal, exploration of uranium ore, nuclear reactor, and electronic cooling to name a few. The fundamentals of flow physics in porous media turn out to be an important issue in the context of convective heat transfer analysis in many practical relevance. A few of such common practical applications, apart from those previously mentioned areas are the energy storage system, heat pipes, and electronic cooling even the flow of fluid through physiological system. The analysis of convective heat transfer in any system is fundamentally involved with the transport phenomena of fluid through that system. The dynamics of flow through porous media invoke complexity owing to the presence of solid matrix. In one side the complex nature of the flow through porous media along with its widespread practical applications on the other extreme compelled many researchers to consider and deeply involved with the transport phenomena of heat and fluid in porous media in a comprehensive way (Nield et al. 2003b, 2004a; Nield and Kuznetsov 2009; Haji-Sheikh and Vafai 2004; Sundaravadivelu and Tso 2003).

An important feature of the flow through porous media is essentially the internal heat generation because of the presence of the solid matrix, and thus, the analysis of the heat transport through porous channels or ducts owing to the fact of the internal heat generation has been the area of fundamental research to the research community since last few decades (Lee and Vafai 1999; Hooman and Gorji-Bandpy 2004; Kim and Kim 2001; Hooman and Gurgenci 2007a, b; Nield and Kuznetsov 2009).

The internal heat generation because of the effect of viscous dissipation in the course of flow through porous media acts as a source term, and this effect is manifested as a significant rise in temperature in the flow field due to the conversion of the kinetic energy of the fluid molecule to the thermal energy. Despite the importance of the reflective effect of viscous heating on the thermal transport analysis of heat, a good number of earlier studies as reported in the literature have been carried out in an analytical framework without considering the effect of viscous dissipation in the analysis (Kim and Kim 2001; Haji-Sheikh and Vafai 2004; Lee and Vafai 1999). On the contrary, due to the presence of solid matrix, the effect of viscous dissipation in porous media flow becomes more pronounced compared to that of the non-porous media flow and, indeed, demand for the consideration of this term while forced convective heat transfer is studied. A closer look on the literature, on the other hand, reveals that many researchers have considered the effects of viscous dissipation in the analysis of forced convective heat transfer in porous media (Hung and Tso 2008, 2009; Hooman et al. 2007; Haji-Sheikh et al. 2004, 2005). In view of the stringent role of viscous dissipation effect on the alteration of overall heat balance in the flow of fluid through porous media, this effect had appeared as an important term to be considered while modeling the transport equation of thermal energy to assess the convective heat transfer rate properly. The fact is that the proper modeling of the viscous dissipation term in the energy equation became an important task to the theoretical research community in order to assess the convective heat transfer rate in porous media flow. However, a careful review of the literature explores that a number of researchers have investigated the indisputable role of the effect of viscous dissipation on the alteration of heat balance in the porous media flow and in doing so, they have considered this term through proper modeling of energy equation while studying the thermal transport of convective heat transfer in porous media flow (Nield 2000; Bejan 2004; Nield and Bejan 2006). A few number of different models as available in the literature have considered the viscous dissipation term in the thermal energy equation in different way though the sole objective of different model has been on shielding the effect of dissipation in the overall energy balance in the flow field (Nield 2000; Al-Hadhrami et al. 2003). Nevertheless, the focal objective of different model has been on addressing the effect of viscous dissipation properly encompassing two individual effects: one is the internal heating inside the porous media and other is the fluid frictional heating at the wall.

A detail review of the literature on the analysis of forced convective heat transfer in porous media taking into consideration of the effect of viscous dissipation includes both the thermally developing and developed flow. Nield et al. (2002, 2003a, 2004b) investigated the thermal development of forced convection in porous media for the flow through parallel plate channel considering different thermal boundary conditions such as constant heat flux and constant wall temperature. Following the Greatz methodology, the forced convection flow of rarefied gas in a hyper-porous medium has been investigated by Nield and Kuznetsov (2009). On the other hand, a review on the literatures also indicates that a number of researchers have also considered the effect of heat generation on fully developed flow through saturated porous duct (Barletta 1996; Hooman and Ranjbarkani 2003; Nield et al. 2003b; Hung and Tso 2009; Hooman and Gurgenci 2007b).

In a recent work, using an analytical formalism, Ghazian et al. (2011) investigated the effect of viscous dissipation on the fully developed forced convective heat transfer. The study considered Couette flow between two parallel plates channel partially filled with porous media, and reported the effect of viscous dissipation on the temperature profile and Nusselt numbers in a comprehensive way. Very recently, following an analytical formalism, Prakash et al. (2012) investigated the effect of heat generation on the forced convection heat transfer characteristics in a porous duct considering Brinkman–Forchheimer model.

It is important to mention here that the review of the literature pertinent to the analysis of forced convective heat transfer in porous media as reported above reveals that no work, so far, has been reported till date considering the analysis of limiting forced convective heat transfer through porous media between two asymmetrically heated parallel plates, albeit a few number of studies on limiting forced convective heat transfer analysis in the absence of porous media are available in the literature (Repaka and Satyamurty 2010; Kumar and Satyamurty 2011; Mondal and Mukherjee 2012a, b). In another study, the analysis of forced convection between two asymmetrically heated parallel in the absence of porous media has been presented in a comprehensive way (Nield 2004). The study considered different velocity profile in order to obtain the closed-form expression of the Nusselt number at both the plates of the channel for both constant wall temperature and constant heat flux boundary conditions. However, the study revealed that the Nusselt number is independent of the asymmetrical wall heating for the symmetric nature of the velocity about the channel centreline.

Internal heat generation in porous media is an important issue because of the presence of the solid matrix, and thus the transport physics of heat through porous media, particularly, in the limiting condition is essentially a matter of concern, and required to be concentrated by researchers in order to delineate the important features of heat transfer characteristics. Accordingly, in the present study, an effort has been made to probe the characteristics of the limiting forced convective heat transfer in a porous channel.

The motivation of the present study stems from the earlier reported work on limiting forced convective heat transfer in non-porous duct studied by Repaka and Satyamurty (2010), while the present study focuses on the forced convective heat transfer characteristics in the limiting condition in the presence of saturated porous media between two asymmetrically heated parallel plates, aiming toward the exploration of the individual effect of viscous dissipation, internal heat generation, and the effect of porosity on the thermal transport characteristics of heat in a comprehensive way.

The present paper is organized in five sections: In Sect. 2, discussion is made about the problem taken up for the study and describes the analysis part in detail following the introduction part. Section 3 is committed to the results and discussion, while in Sect. 4 the principal conclusions are summarized.

2 Mathematical Formulation of the Problem and the Governing Equations

Fig. 1
figure 1

Schematic to the problem, \(H\) is the half gap length between two plates. Temperature \(T_{1 }\) and \(T_{2}\) represent the temperature of lower and upper plate, respectively

Full size image

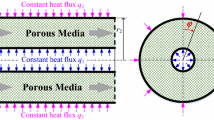
In the present analysis, a steady flow of incompressible and Newtonian fluid between two parallel plates channel filled with porous media is considered. It is assumed that the fluid is flowing along x direction and flow is unidirectional. The channel height is 2H, and the length of the channel is L, where length of the channel \(L\gg 2H\). The coordinate system is attached at the center line of the channel as shown in Fig. 1. The plates of the channel are kept at different constant temperatures. The lower plate and upper plate temperature are \(T_{1}\) and \(T_{2}\), respectively. In addition to the above, a few more assumptions are considered in the present study and are given below:

  • Thermo-physical properties are constant;

  • no slip boundary condition is considered for both hydrodynamically and thermally;

  • axial conduction in wall as well as in fluid is neglected.

Based on the consideration of the above assumptions, we arrive at the following governing transport equations of heat and fluid, are the continuity, momentum, and the thermal energy equation.

Continuity equation

$$\begin{aligned} \frac{\mathrm{d}\bar{{u}}}{\mathrm{d}\bar{{x}}}=0. \end{aligned}$$
(1)

The Brinkman momentum equation in the direction of flow reduces to

$$\begin{aligned} \mu _\mathrm{eff} \frac{\mathrm{d}^{2}\bar{{u}}}{\mathrm{d}\bar{{y}}^{2}}-\frac{\mu _\mathrm{f} }{K_\mathrm{p} }\bar{{u}}+\lambda =0. \end{aligned}$$
(2)

In Eq. (2), the term \(\lambda \) is the negative of applied pressure gradient, \(\mu _\mathrm{f}\) is the fluid viscosity, \(\mu _\mathrm{eff}\) is the effective viscosity of the porous medium, \(K_\mathrm{p}\) is the permeability of the porous medium, and \(\rho \) is the density of the fluid being considered in the present analysis.

The thermal energy equation is written as

$$\begin{aligned} \rho C_p \bar{{u}}\frac{\partial \bar{{T}}}{\partial \bar{{x}}}=k\frac{\partial ^{2}T}{\partial \bar{{y}}^{2}}+\bar{{Q}}+\phi . \end{aligned}$$
(3)

In the above equation, \(k\) is the thermal conductivity, \(C_p\) is the specific heat capacity of the fluid at constant pressure, and the term \(\phi \) includes the viscous dissipation effect. Equation (3) is subject to the boundary conditions of constant wall temperature \(\left. {\bar{{T}}}\right| _{\bar{{y}}=-H} =T_1 \) and \(\left. {\bar{{T}}} \right| _{\bar{{y}}=H} =T_2 \). In order to cast the above set of governing transport equations into non-dimensional framework, a few non-dimensional variables are defined, and those are \(\hat{{x}}=\frac{\bar{{x}}}{H};\;\hat{{y}}=\frac{\bar{{y}}}{H};\;\hat{{u}}=\frac{\bar{{u}}}{{\lambda H^{2}}/{\mu _\mathrm{f} }}\); and \(\theta =\frac{\left( {T-\bar{{T}}}\right) }{\left( {T_\mathrm{in} -\bar{{T}}} \right) }\), where \(T_\mathrm{in}\) is the inlet fluid temperature and \(\bar{{T}}=\frac{\left( {T_1 +T_2 } \right) }{2}\) is the average wall surface temperature. However, with the aid of these non-dimensional variables, the governing transport equations can be written as:

Continuity equation

$$\begin{aligned} \frac{\mathrm{d}\hat{{u}}}{\mathrm{d}\hat{{x}}}=0. \end{aligned}$$
(4)

Momentum equation

$$\begin{aligned} \frac{1}{\varepsilon }\frac{\mathrm{d}^{2}\hat{{u}}}{\mathrm{d}\hat{{y}}^{2}}-\frac{\hat{{u}}}{\mathrm{Da}}+1=0. \end{aligned}$$
(5)

In order to arrived at Eq. (5), we define the non-dimensional term \(\varepsilon =\frac{\mu _\mathrm{f} }{\mu _\mathrm{eff} }\) is the porosity of the porous medium, \(\mathrm{Da}=\frac{K_\mathrm{p} }{H^{2}}\) is the Darcy number. The solution of Eq. (5), with the standard no slip boundary condition \(\hat{{u}}({\pm 1})=0\), and the symmetry condition \({\mathrm{d}\hat{{u}}(0)}/{\mathrm{d}\hat{{y}}=0}\), gives the velocity distribution in the porous media flow field. The velocity distribution obtained from the solution of Eq. (5) is written as:

$$\begin{aligned} \hat{{u}}({\hat{{y}}})=\mathrm{Da}\left[ {1-\frac{\cosh \beta \hat{{y}}}{\cosh \beta }} \right] . \end{aligned}$$
(6)

The above velocity profile is obtained from the solution of Eq. (5). However, the velocity can be further re-written into non-dimensional form, and in order to do so, the mean velocity of fluid is evaluated as \(u_\mathrm{m} =\frac{\int _{-1}^1 {\bar{{u}}(\bar{{y}})w\bar{{y}}\mathrm{d}\bar{{y}}} }{\int _{-1}^1 {\bar{{y}}w\mathrm{d}\bar{{y}}} }\), where \(w\) is the width of the channel. Thus, the mean velocity of the fluid obtained as:

$$\begin{aligned} u_\mathrm{m} =\frac{\lambda H^{2}}{\mu _\mathrm{f}}\mathrm{Da}\left[ {1-\frac{\tanh \beta }{\beta }} \right] . \end{aligned}$$
(7)

The non-dimensional velocity distribution, therefore, can be written as

$$\begin{aligned} \tilde{u}=\frac{\bar{{u}}}{u_\mathrm{m} }=\frac{\left[ {1-\frac{\cosh \beta \hat{{y}}}{\cosh \beta }} \right] }{\left[ {1-\frac{\tanh \beta }{\beta }} \right] }. \end{aligned}$$
(8)

However, with the above non-dimensional velocity distribution [Eq. (8)] and temperature, \(\theta =\frac{\left( {T-\bar{{T}}} \right) }{\left( {T_\mathrm{in} -\bar{{T}}} \right) }\), next, attempt has been taken to cast the thermal energy equation as given in Eq. (3) into the dimensionless form. Before going for the non-dimensionalization of the energy equation, first objective is to pay attention on the viscous dissipation term \(\phi \) in the energy equation. In order to do so, the model developed by Al-Hadhrami et al. (2003) is considered in the present analysis. The model includes the viscous dissipation effect in the energy equation taking into consideration of two individual effects, and suggested that the internal heating related to the power required to drag the fluid through porous medium and the fluid frictional heating due to dissipative effect should remain in the viscous dissipation term. Thus, the viscous dissipation term in the dimensional form takes the form given below

$$\begin{aligned} \phi =\frac{\mu _\mathrm{f} \bar{{u}}^{2}}{K_\mathrm{p} }+\mu _\mathrm{eff} \left( {\frac{\mathrm{d}\bar{{u}}}{\mathrm{d}\bar{{y}}}} \right) ^{2}. \end{aligned}$$
(9)

The first term in Eq. (9) relates the internal heating arises owing to power required to drag the fluid through porous medium, while the second term is the contribution of fluid frictional heating. In the present analysis, an attempt has been taken to investigate the heat transfer characteristics in the limiting condition, more precisely in the conduction limit, and In order to obtain the same, the thermal energy equation excluding the convection term is solved, while the effect of viscous dissipation and internal heat generation have been included in the model. However, the dimensional energy equation, very pertinent to the problem considered in the present study takes the form given below

$$\begin{aligned} k\frac{\partial ^{2}\bar{{T}}}{\partial \bar{{x}}^{2}}+\bar{{Q}}+\frac{\mu _\mathrm{f} \bar{{u}}^{2}}{K_\mathrm{p} }+\mu _\mathrm{eff} \left( {\frac{\mathrm{d}\bar{{u}}}{\mathrm{d}\bar{{y}}}} \right) ^{2}=0. \end{aligned}$$
(10)

In the non-dimensional form, Eq. (10) can be expressed as:

$$\begin{aligned} \frac{\mathrm{d}^{2}\theta }{\mathrm{d}^{2}\hat{{y}}^{2}}+Q+\mathrm{Br}\left[ {\frac{\tilde{u}^{2}}{\mathrm{Da}}+\frac{1}{\varepsilon }\left( {\frac{\mathrm{d}\tilde{u}}{\mathrm{d}\hat{{y}}}} \right) ^{2}} \right] =0. \end{aligned}$$
(11)

In the above equation, \(\mathrm{Br}=\frac{\mu _\mathrm{f} u_\mathrm{m}^2 }{k\left( {T_\mathrm{in} -\bar{{T}}} \right) }\), is the Brinkman number, which includes the effect of viscous dissipation in non-dimensional form, and \(Q=\frac{\bar{{Q}}H^{2}}{k\left( {T_\mathrm{in} -\bar{{T}}} \right) }\), is the non-dimensional volumetric heat generation that takes care of the contribution of internal heat generation. In order to solve the above equation [Eq. (11)] subject to the boundary condition of different but constant wall temperatures, a parameter is defined, which takes care of the unequal wall heating and symbolize by the degree of asymmetrical wall heating \(A=\frac{\left( {T_2 -T_\mathrm{in} } \right) }{\left( {T_1 -T_\mathrm{in} } \right) }\).

However, Eq. (11) is subject to the following boundary conditions written in non-dimensional form:

$$\begin{aligned} \left. \theta \right| _{\hat{{y}}=-1}&= \frac{\left( {T_1 -\bar{{T}}} \right) }{\left( {T_\mathrm{in} -\bar{{T}}} \right) }=-S\end{aligned}$$
(12a)
$$\begin{aligned} \left. \theta \right| _{\hat{{y}}=1}&= \frac{\left( {T_2 -\bar{{T}}} \right) }{\left( {T_\mathrm{in} -\bar{{T}}} \right) }=S \end{aligned}$$
(12b)
$$\begin{aligned}&\hbox {where the term}\,S=\frac{\left( {1-A} \right) }{\left( {1+A} \right) }. \end{aligned}$$
(13)

The solution of Eq. (11) with the aid of the above set of boundary conditions [Eq. (12a, b)] yields the temperature profile in non-dimensional form. Thus, the non-dimensional temperature profile obtained in the conduction limit can be expressed as:

$$\begin{aligned} \theta&= C_1 \hat{{y}}+C_2 -Q\frac{\hat{{y}}^{2}}{2}-\frac{\mathrm{Br}}{R_1{\cdot }\mathrm{Da}}\left[ {\frac{\hat{{y}}^{2}}{2}+\frac{\hat{{y}}^{2}}{4\cosh ^{2}\beta }+\frac{\cosh \left( {2\beta } \right) \hat{{y}}}{8\beta ^{2}\cosh ^{2}\beta }-\frac{2\cosh \left( {2\beta } \right) \hat{{y}}}{\beta ^{2}\cosh \beta }} \right] \nonumber \\&-\frac{R_2 }{\varepsilon }\left[ \frac{\hat{{y}}^{2}}{2}-\frac{\cosh \left( {2\beta } \right) \hat{{y}}}{8\beta ^{2}} \right] . \end{aligned}$$
(14)

In Eq. (14), \(C_1\) and \(C_2\) are constants, and evaluated using the boundary conditions as given in Eq. (12a, b). Moreover, the expressions of two different terms \(R_1\) and \(R_2\) as appeared in Eq. (14), along with the expression of the constants \(C_1\) and \(C_2\) are given below.

$$\begin{aligned}&\displaystyle R_1 =\left[ {1-\frac{\tanh \beta }{\beta }} \right] ^{2}\end{aligned}$$
(15a)
$$\begin{aligned}&\displaystyle R_2 =\frac{\mathrm{Br}{\cdot }\beta ^{4}}{\left[ {\cosh ^{2}\beta \left( {\beta -\tanh \beta } \right) ^{2}} \right] }\end{aligned}$$
(15b)
$$\begin{aligned}&\displaystyle C_1 = S\end{aligned}$$
(15c)
$$\begin{aligned}&\displaystyle C_2 = \frac{Q}{2}+\frac{\mathrm{Br}}{2{\cdot }R_1{\cdot }\mathrm{Da}}\left[ {1+\frac{1}{2\cosh ^{2}\beta }+\frac{\cosh \left( {2\beta } \right) }{4\beta ^{2}\cosh ^{2}\beta }-\frac{4}{\beta ^{2}}} \right] +\frac{R_2 }{2\varepsilon }\left[ {\frac{1}{2}-\frac{\cosh \left( {2\beta } \right) }{4\beta ^{2}}} \right] . \nonumber \\ \end{aligned}$$
(15d)

On plugging the values of the above constants into the expression of the dimensionless temperature profile as given in Eq. (14) yields the final and closed-form expression of the same. The final form of the temperature profile obtained in the limiting condition is reduced as follows:

$$\begin{aligned} \theta&= \frac{\left( {1-A} \right) }{\left( {1+A} \right) }\hat{{y}}+Q\left[ {\frac{1}{2}-\frac{\hat{{y}}^{2}}{2}} \right] -\frac{\mathrm{Br}}{R_1{\cdot }\mathrm{Da}}\left[ {\begin{array}{l} \left\{ {\frac{1}{2}-\frac{\hat{{y}}^{2}}{2}} \right\} +\frac{1}{2\cosh ^{2}\beta }\left\{ {\frac{1}{2}-\frac{\hat{{y}}^{2}}{2}} \right\} \\ +\frac{1}{4\beta ^{2}\cosh ^{2}\beta }\left\{ {\frac{\cosh \left( {2\beta } \right) }{2}-\frac{\cosh \left( {2\beta } \right) \hat{{y}}}{2}} \right\} \\ -\frac{2}{\beta ^{2}}\left\{ {1-\frac{\cosh \beta \hat{{y}}}{\cosh \beta }} \right\} \\ \end{array}} \right] \nonumber \\&+\,\frac{R_2 }{2\varepsilon }\left[ {\left\{ {\frac{1}{2}-\frac{\hat{{y}}^{2}}{2}} \right\} -\frac{1}{2\beta ^{2}}\left\{ {\frac{\cosh \left( {2\beta } \right) }{2}-\frac{\cosh \left( {2\beta } \right) \hat{{y}}}{2}} \right\} } \right] . \end{aligned}$$
(16)

In order to obtain an insight regarding the convective heat transfer characteristics, the physical quantity of interest is the Nusselt number at both the plates. The focal objective of the present study is to explore the thermal transport characteristics of heat, more specifically the limiting heat transfer characteristics in porous media flow between two asymmetrically heated parallel plates. To delineate the same, next task is to obtain the expression of Nusselt number in the limiting condition at both the plates. In case of fully developed flow, the usual practice of evaluating the closed-form expression of Nusselt number is to define the mean temperature of the fluid in the flow field. The mean temperature in dimensional form, pertinent to the problem considered in the present analysis can be expressed as

$$\begin{aligned} T_\mathrm{m} =\frac{\int \nolimits _{-H}^{H} {\bar{{u}}Tw \mathrm{d}\bar{{y}}} }{\int \nolimits _{-H}^{H} {\bar{{u}}w\mathrm{d}\bar{{y}}} }. \end{aligned}$$
(17)

However, the expression of mean temperature in non-dimensional form is given by

$$\begin{aligned} \theta _\mathrm{m} =\frac{\left( {T_\mathrm{m} -\bar{{T}}} \right) }{\left( {T_\mathrm{in} -\bar{{T}}} \right) }=\frac{\int \nolimits _{-1}^1 {\tilde{u}\theta \mathrm{d}\hat{{y}}} }{\int \nolimits _{-1}^1 {\tilde{u}\mathrm{d}\hat{{y}}} }=\frac{I_\mathrm{NR} }{I_\mathrm{DR} }. \end{aligned}$$
(18)

In the above expression the term \(I_\mathrm{NR}\) can be further expressed as

$$\begin{aligned} I_\mathrm{NR} =\left( {I_1 +I_2 +I_3 +I_4 +I_5 -I_6 -I_7 +I_8 +I_9 -I_{10} +I_{11} } \right) , \end{aligned}$$
(19)

where each of the term \(I_1\)–\(I_{11}\) along with \(I_\mathrm{DR}\) as appeared in the expression of the non-dimensional bulk mean temperature are function of the porosity of the porous media, and their expressions are given below

$$\begin{aligned} I_1&= \frac{R_2 }{R_1^{1/2} }\left[ 0 \right] \end{aligned}$$
(20a)
$$\begin{aligned} I_2&= \frac{Q}{R_1^{1/2} }\left[ {\frac{2}{3}-\frac{2}{\beta ^{2}}+\frac{2\tanh \beta }{\beta ^{2}}} \right] \end{aligned}$$
(20b)
$$\begin{aligned} I_3&= \frac{\mathrm{Br}}{R_1^{3/2}{\cdot }\mathrm{Da}}\left[ {\frac{2}{3}-\frac{2}{\beta ^{2}}+\frac{2\tanh \beta }{\beta ^{2}}} \right] \end{aligned}$$
(20c)
$$\begin{aligned} I_4&= \frac{\mathrm{Br}}{2R_1^{3/2}{\cdot }\mathrm{Da}{\cdot }\cosh ^{2}\beta }\left[ {\frac{2}{3}-\frac{2}{\beta ^{2}}+\frac{2\tanh \beta }{\beta ^{2}}} \right] \end{aligned}$$
(20d)
$$\begin{aligned} I_5&= \frac{\mathrm{Br}}{4R_1^{3/2}{\cdot }\mathrm{Da}{\cdot }\cosh ^{2}\beta }\left[ {\cosh \left( {2\beta } \right) \left( {1-\frac{\tanh \beta }{\beta }} \right) } \right] \end{aligned}$$
(20e)
$$\begin{aligned} I_6&= \frac{\mathrm{Br}}{8R_1^{3/2} {\cdot }\mathrm{Da}{\cdot }\beta ^{2}{\cdot }\cosh ^{2}\beta }\left[ {\frac{\sinh \left( {2\beta } \right) }{\beta }-\left( {\frac{3\sinh \beta +\sinh \left( {3\beta } \right) }{3\beta }} \right) } \right] \end{aligned}$$
(20f)
$$\begin{aligned} I_7&= \frac{2\mathrm{Br}}{R_1^{3/2} {\cdot }\mathrm{Da}{\cdot }\beta ^{2}}\left[ {2-\frac{2\tanh \beta }{\beta }} \right] \end{aligned}$$
(20g)
$$\begin{aligned} I_8&= \frac{2\mathrm{Br}}{R_1^{3/2} {\cdot }\mathrm{Da}{\cdot }\beta ^{2}}\left[ {\frac{2\tanh \beta }{\beta }-\left( {\frac{\beta +\cosh \beta {\cdot }\sinh \beta }{\beta {\cdot }\cosh ^{2}\beta }} \right) } \right] \end{aligned}$$
(20h)
$$\begin{aligned} I_9&= \frac{R_2 }{2\varepsilon {\cdot }R_1^{1/2} }\left[ {\frac{2}{3}-\frac{2}{\beta ^{2}}+\frac{2\tanh \beta }{\beta ^{2}}} \right] \end{aligned}$$
(20i)
$$\begin{aligned} I_{10}&= \frac{R_2 }{4\varepsilon {\cdot }\beta ^{2}{\cdot }R_1^{1/2} }\left[ {\cosh \left( {2\beta } \right) \left( {1-\frac{\tanh \beta }{\beta }} \right) } \right] \end{aligned}$$
(20j)
$$\begin{aligned} I_{11}&= \frac{R_2 }{8\varepsilon {\cdot }\beta ^{2}{\cdot }R_1^{1/2} }\left[ {\frac{\sinh \left( {2\beta } \right) }{\beta }-\left( {\frac{3\sinh \beta +\sinh \left( {3\beta } \right) }{3\beta }} \right) } \right] \end{aligned}$$
(20k)
$$\begin{aligned} I_\mathrm{DR}&= \frac{2}{R_1^{1/2} }\left[ {1-\frac{\tanh \beta }{\beta }} \right] . \end{aligned}$$
(20l)

Having established the expression of non-dimensional mean temperature, the next objective is to proceed toward the evaluation of the explicit expression of Nusselt number at both the plates. In order to do so, the local heat transfer in the conduction limit at the lower plate of the channel is calculated, and is expressed as:

$$\begin{aligned} q_1 =h_1 \left( {T_1 -T_\mathrm{m} } \right) =-k\left. {\frac{\partial T}{\partial \bar{{y}}}} \right| _{y=-H} \end{aligned}$$
(21)

\(h_1,\) the convective heat transfer coefficient, is related to other parameters as

$$\begin{aligned} \mathrm{Nu}_1 =\frac{h_1 H}{k}=\left[ {1/{\left( {\theta _\mathrm{m} -\theta _1 } \right) }} \right] \left. {\left( {\frac{\partial \theta }{\partial \hat{{y}}}} \right) } \right| _{\hat{{y}}=-1}. \end{aligned}$$
(22)

Similarly, the limiting Nusselt number at the upper plate of the channel is expressed as

$$\begin{aligned} \mathrm{Nu}_2 =\frac{h_2 H}{k}=\left[ {1/{\left( {\theta _2 -\theta _\mathrm{m} } \right) }} \right] \left. {\left( {\frac{\partial \theta }{\partial \hat{{y}}}} \right) } \right| _{\hat{{y}}=1}, \end{aligned}$$
(23)

where \(\theta _\mathrm{m}\) is the dimensionless mean temperature in the conduction limit, and \(\theta _1, \theta _2\) are the non-dimensional temperature at the lower and upper plates of the channel, respectively. Equation (14), in conjunction with Eq. (21) establishes an explicit expression for the limiting Nusselt number at the lower plate of the channel, giving quantitative relation among the different physical parameters governing the thermo-fluidic transport. It is given as

$$\begin{aligned} \mathrm{Nu}_1 \!=\!\frac{\frac{\left( {1-A} \right) }{\left( {1+A} \right) }\!+\!\left[ {Q\!+\!\frac{\mathrm{Br}}{R_1 {\cdot }\mathrm{Da}}\left\{ {1\!+\!\frac{1}{2\cosh ^{2}\beta }} \right\} \!+\!\frac{R_2 }{2\varepsilon }} \right] \!-\!\frac{\sinh \beta }{\beta }\left[ {\frac{R_2 \cosh \beta }{2\varepsilon }\!-\!\frac{\mathrm{Br}}{2R_1 {\cdot }\mathrm{Da}{\cdot }\cosh \beta }\!+\!\frac{2\mathrm{Br}}{R_1 {\cdot }\mathrm{Da}{\cdot }\cosh \beta }} \right] }{\frac{\left( {1-\beta } \right) }{\left( {1+\beta } \right) }\!+\!\theta _\mathrm{m}}.\nonumber \\ \end{aligned}$$
(24a)

Proceeding similarly, the expression of limiting Nusselt number at the upper plate of the channel is established as follows:

$$\begin{aligned} \mathrm{Nu}_2 =\frac{\frac{\left( {1-\beta } \right) }{\left( {1+\beta } \right) }-\left[ {Q+\frac{\mathrm{Br}}{R_1 {\cdot }\mathrm{Da}}\left\{ {1+\frac{1}{2\cosh ^{2}\beta }} \right\} +\frac{R_2 }{2\varepsilon }} \right] +\frac{\sinh \beta }{\beta }\left[ {\frac{R_2 \cosh \beta }{2\varepsilon }+\frac{3\mathrm{Br}}{2R_1 {\cdot }\mathrm{Da}{\cdot }\cosh \beta }} \right] }{\frac{\left( {1-\beta } \right) }{\left( {1+\beta } \right) }-\theta _\mathrm{m}}.\nonumber \\ \end{aligned}$$
(24b)

In the expression of both the Nusselt numbers, the expression of bulk mean temperature \(\theta _\mathrm{m}\) is evaluated using Eqs. (18)–(20). Based on the expression of Nusselt number obtained at unequal constant wall temperatures as mentioned above [Eq.  (24a, b)], the convective heat transfer characteristics in the limiting case in a viscous dissipative flow through saturated porous channel is discussed in the next section.

3 Results and Discussion

The effect of viscous dissipation is an important issue in the context of forced convective heat transfer analysis through porous media. Viscous dissipation effect in the flow field is manifested on the heat transfer characteristics through the momentous alteration in the overall heat balance, and is best described by the use of the Brinkman number. The effect of viscous dissipation acts as a source of heating in the flow field, which in effect stimulates the fluid temperature. The primary focus of the present study is to explore the heat transfer characteristics in the conduction limit for the flow of Newtonian fluid between two asymmetrically heated parallel plates filled with saturated porous media as mentioned before. Accordingly, in the present section, an effort has been made to delineate the thermal transport characteristics of heat in a saturated porous media including the prominent effect of viscous heating, porosity of the media, and the internal heat generation in the analysis. In order to do so, an analytical formalism has been presented in Sect. 2 of the present study to obtain the closed-form expression of the dimensionless temperature profile and in the following the explicit expressions of limiting Nusselt numbers at both the plates. However, the graphical representation of the dimensionless temperature profile and the Nusselt number for different cases have been presented here highlighting the individual effect of the viscous dissipation, porosity of the media, and the volumetric heat generation in a comprehensive way.

Fig. 2
figure 2

Dimensionless temperature profile for different values of Br, obtained at Da = 0.01, \(\varepsilon =0.7\), and \(Q=0\) a, c \(A=0.5\), b, d \(A=-0.5\). The behavior of the temperature profile is shown for each of positive and negative Br. The temperature profile for non-zero values of Br changes about the same obtained at Br = 0. Positive values of Br increases the frictional heating and the fluid temperature increases, while negative values of Br does the reverse

Full size image

The present study aims at finding out the profound effect of viscous dissipation effects on the temperature profile, and consequently the variation of the Nusselt numbers. The relative strength of heat generation due to viscous dissipation to the heat supplied to the fluid is measured by Brinkman number Br. The prime interest of the present study, on the other hand, lies in finding out the influencial role of the viscous dissipation effect on the temperature profile, and consequently the variation of Nusselt numbers in the conduction limit. Figure 2a–d shows the variation of dimensionless temperature for two different degrees of asymmetrical wall heating \(A=0.5\) and \(-0.5\), respectively. It is important to observe from the above figures that different values of Brinkman number \(\mathrm{Br}=0, {\pm }0.01, {\pm }0.1, {\pm }0.5\), and \({\pm }1\) have been considered in delineating the role of viscous dissipation effect on the variation of temperature profile in the flow field. Both the figures as presented above correspond to the porosity of the porous media \(\varepsilon =0.7\) and Darcy number \(\mathrm{Da}=0.01\), while no volumetric heat generation has been considered in obtaining Fig. 2a–d. Positive values of Br represent a case of wall heating, and resemble the situation of heat transfer to the fluid across the wall, while the negative values of Br represent the wall cooling case. It is apparent from Fig. 2a, d that the positive values of Br increases the fluid temperature, while the negative values of Br does the reverse for both the cases of degree of asymmetrical wall heating considered. However, the alteration of fluid temperature with Br as reflected in Fig. 2a–d is in compliance with the cases of wall heating and cooling related to the positive and negative Br, respectively. It is noteworthy that the temperature profile for Br = 0 exhibits a linear trend disregarding the effect of degree of asymmetry parameters considered in the present study, which represents the conduction profile in the thermal entrance region. For given Br and other parameters, a small difference in temperature profile that one may observe on closely looking into above figures is attributable to the different degrees of asymmetrical wall heating considered. Interestingly, one may observe from the above figures that the temperature profile for any non-zero values of Br changes in a symmetrical way about the same obtained at Br = 0. However, the variation of temperature profile as depicted in Fig. 2a, d shows similarity with the published results reported by Repaka and Satyamurty (2010) and Mondal and Mukherjee (2012b). It is important to mention in this context here that the choices of Br are rather arbitrary, considered in the present study in order to show viscous dissipation effects on the temperature profiles owing to the presence of intense sold matrix in the flow field of a porous channel. However, the typical values for Br are small and of the order of \(10^{-2}\) or often smaller, which are applicable in plenty of physical situations. Considering some practical values of \(\mathrm{Br}={\pm }0.01, 0.1\) and in view of physically realistic conditions, an attempt has been made to show the variation of temperature profile in a viscous dissipative flow through porous channel as one can see from Fig. 2c, d.

Fig. 3
figure 3

The influence of porosity \(\varepsilon \) on the variation of \(\theta \) for two different cases of asymmetric wall heating: a \(A=0.5\) and b \(A=-0.5\). The other parameters as considered in obtaining theses figures are Da = 0.01, \(Q=0\), and Br = \({\pm }0.5\). The dimensionless temperature \(\theta \) increases for decreasing \(\varepsilon \) for both the values of Br owing to fact of the presence of intense solid matrix for the lower values of \(\varepsilon \)

Full size image

Next, an attempt has been made to see the effect of porosity on the variation of the dimensionless temperature profile in the flow field as obtained in the conduction limit. In order to do so, the graphical representation of the dimensionless temperature has been illustrated to show the variation of temperature for different values of porosity \(\varepsilon =0.3\), 0.5, 0.7, and 1.0 considered in the present study. Figure 3a, b shows the variation of temperature in the flow field for different values of \(\varepsilon \) obtained without considering the effect of volumetric heat generation. Two different values of \(\mathrm{Br}={\pm }0.5\) have been considered in delineating the effect of porosity on the limiting temperature profile as envisaged from Fig. 3a, b. Figure 3a corresponds to the degree of asymmetry parameter \(A=0.5\), while Fig. 3b corresponds to \(A=-0.5\). One may see that the temperature for positive Br increases even for all values of porosity considered disregarding the effect of asymmetrical wall heating, while the reverse holds true for the negative value of Br. In order to delve deep into the functionality of the porosity on the variation of the temperature, which in essence predicts the thermal transport characteristics of heat, four different values of porosity have been considered as mentioned before. It is very interesting to observe that for the smaller value of porosity, i.e., for the cases of higher effective viscosity of the porous media, the temperature of the fluid becomes higher than that of the same obtained at higher value of porosity, i.e., for the cases of comparable viscosity of the fluid and the porous media. This is attributable to the presence of intense solid matrix in the flow field for the cases of smaller values of porosity of the media. The presence of the intense solid matrix in the flow field owing to smaller value of porosity of the media imparts more heat to the fluid, essentially arises the fluid temperature because of the fact of the intense fluid friction in a flow through porous channel.

In addition to the effect of viscous dissipation, there could be many other situations where the generation of internal heating is of essential importance in view of its impact on the drastic alteration in the thermal transport characteristics of heat following the changes in the overall heat balance in the flow field. This effect essentially becomes an important factor and thus, required to be considered in the analysis of forced convective heat transfer, specific to the cases of fluid having large Prandtl number Pr (Hooman and Gurgenci 2007b). Figure 4a, b depicts the distribution of non-dimensional temperature in the flow field for different values of dimensionless volumetric heat generation \(Q=1\), 10, 20, and 50, respectively. Two different values of Brinkman number \(\mathrm{Br}={\pm }0.5\) have been considered in delineating the effect of volumetric heat generation on the distribution of temperature in the flow field as apparent from Fig. 4a, b. Both the figures as presented above correspond to the value of porosity \(\varepsilon =0.7\) and \(\mathrm{Da}=0.01\). Specific to the case of positive Br, the higher value of \(Q\) increases the fluid temperature, which is expected. It is important to mention here that the consideration of the volumetric heat generation in the thermal energy equation acts like an adding effect in increasing the temperature in the flow field and that is what getting is reflected on the variation of temperature for positive Br as one may observe in Fig. 4a, b. On the contrary, it is noteworthy to observe an interesting role of volumetric heat generation on the variation of dimensionless temperature for negative Br. Specific to the case of negative value of Br and for a given degree of asymmetrical wall heating, the presence of large amount of volumetric heat generation prohibits the degree of wall cooling as one can see from Fig. 4a, b.

Fig. 4
figure 4

The influence of \(Q\) on the variation of \(\theta \) for two different cases of asymmetric wall heating: a \(A=0.5\) and b \(A=-0.5\). The other parameters as considered in obtaining theses figures are Da = 0.01, \(\varepsilon =0.7\), and Br = \({\pm }0.5\). The dimensionless temperature \(\theta \) increases for increasing \(Q\) for the positive values of Br. Increasing \(Q\) increases the dimensionless fluid temperature \(\theta \)

Full size image

As mentioned earlier that the negative values of Br represent the wall cooling case, and corroborate the situation of heat transfer from the fluid to the wall. The consideration of negative values of Br, therefore, behaves like an opposing effect in increasing the fluid temperature in the flow field. Conversely, the higher values of volumetric heat generation \(Q\) will increase the fluid temperature, no matter whether the positive or negative values of Br are being considered in the analysis to explore the underlying transport physics of heat. The physical explanation of having an interesting behavior on the variation in temperature with \(Q\) for negative Br stems from the fact of the rich interplay between two effects mentioned above. The competition between two effects, i.e., the increment of fluid temperature by \(Q\) and the decrement of the same by the negative Br will eventually lead to the overall temperature in the flow field as reflected in Fig. 4a, b. The gross consequence of this effect, however, one may observe from the above figures that the temperature profile obtained for any particular \(Q\) and a given degree of asymmetry parameter do not changes symmetrically for any particular value of positive and negative Br, which holds true for the other cases as one may see from Figs. 2 and 3 on closely looking into them.

Fig. 5
figure 5

The influence of \(\varepsilon \) on the variation of \(\mathrm{Nu}_{1\mathrm{c}} \) for two different cases of asymmetric wall heating: a \(A=0.5\) and b \(A=-0.5\). The variation of \(\mathrm{Nu}_{1\mathrm{c}}\) obtained at Da = 0.01, \(Q=0\). The variation of Nusselt number shows discontinuity in behavior and at the point of discontinuity, an equilibrium in energy is reached

Full size image

Having established the influential role of different performance indexing parameters of forced convection heat transfer on the variation of the non-dimensional temperature in the flow field in a porous channel, next, an effort has been rewarded to see the individual effect of those parameter on the limiting heat transfer characteristics. In order to have an insight about the heat transfer rate in forced convection through porous channel, the physical quantity of interest is the Nusselt number, and more precisely is the parametric variation of Nusselt number in different cases as considered in the present study. Figure 5a, b shows the variation of limiting Nusselt number on the lower plate of the channel \(\mathrm{Nu}_{1\mathrm{c}}\) versus Br for different values of porosity of the media considered in the present study. Two different degrees of asymmetrical wall heating \(A={\pm }0.5\) have been considered in delineating the variation of Nusselt number as can be seen from Fig. 5a, b. A constant value of \(\mathrm{Da}=0.01\) along with a case of no volumetric heat generation has been considered in obtaining the above two figures.

It is important to observe from the figures presented above that the variation of \(\mathrm{Nu}_{1\mathrm{c}}\) is not continuous, rather a point of discontinuity exists in the variation for all the cases of \(\varepsilon \) considered in the present study. The point of discontinuity is referred as the point of singularity, and at this point of singularity, the variation of \(\mathrm{Nu}_{1\mathrm{c}}\) shows an unbounded swing owing to the presence of an equilibrium state of energy. The existence of point of singularity as seen on the variation of \(\mathrm{Nu}_{1\mathrm{c}}\) shows similarity with the published results as available in the literature (Aydin and Avci 2006; Repaka and Satyamurty 2010; Mondal and Mukherjee 2012b). At the point of singularity, the local equilibrium between the heat supplied by the wall and the heat generated due to the viscous dissipation effect is attained and thus, an unstable state is induced, which incurs the unbounded swing as observed in above figures.

However, from the onset of point of singularity and with the increasing value of Br in the positive direction \((\mathrm{Br}> 0)\), Nusselt number decreases because of the decrease in the driving potential of the heat transfer, and finally reaches at different asymptotic values as \(\mathrm{Br}\rightarrow \infty \) for all the cases of porosity and degree of asymmetry parameter taken into consideration. As explained earlier that the negative value of \(\mathrm{Br}(\mathrm{Br}<0)\) represents the wall cooling problem, and is applied to weaken the bulk temperature of the fluid. However, the viscous dissipation effect increases the temperature of the fluid and alters the heat balance, thus essentially becomes an important factor in determining the heat transfer rate in convective heat transfer analysis. Therefore, with the increasing value of Br in the negative direction, the bulk fluid temperature increases, and different asymptotes appear as \(\mathrm{Br}\rightarrow -\infty \) for different asymmetry parameters considered. A precise look on the above figures do reveal that the onset of the point of singularity alters with the alteration in degree of asymmetry parameter, which is as expected. An important observation from the figures presented above may be highlighted that the effect of porosity does not have significant role to play in regard to the alteration of point of singularity considerably. This is because of the fact that the contribution of heat generation due to the effective viscosity of the porous media (effect of porosity) is not violent to alter the heat balance in the flow field drastically for any given degree of asymmetrical wall heating. The increasing value of \(\varepsilon \) heats up the fluid less in comparison to the lower value of the same and, thereby, increases the driving temperature difference of the heat transfer and consequently, Nusselt number increases, which one can clearly notice from Fig. 5a, b.

Fig. 6
figure 6

The influence of Da on the variation of \(\mathrm{Nu}_{1\mathrm{c}} \) for two different cases of asymmetric wall heating: a \(A=0.5\) and b \(A=-0.5\). The variation of \(\mathrm{Nu}_{1\mathrm{c}}\) obtained at \(\varepsilon =0.7\), \(Q=0\). The variation of Nusselt number shows discontinuity in behavior (point of singularity) and at the point of discontinuity, an equilibrium in energy is reached. The alteration in Da changes the location of the onset of the point of singularity owing to the alteration in heat balance in flow field for both the cases of asymmetrical wall heating

Full size image

Figure 6a, b depicts the variation of \(\mathrm{Nu}_{1\mathrm{c}} \) with Br as obtained for different values of Darcy number \(\mathrm{Da}=0.01\), 0.1, and 10, respectively. The value of porosity \(\varepsilon =0.7\) and no volumetric heat generation has been considered in obtaining the figures presented above. Figure 6a, b corresponds to degree of asymmetrical wall heating \(A=0.5\) and \(-0.5\), respectively. The primary objective of the representation of the variation of \(\mathrm{Nu}_{1\mathrm{c}}\) for different Darcy number \(\mathrm{Da},\) is to explore the thermal transport characteristics of heat in presence of solid matrix in the flow field, and to obtain the quantitative estimates about the influential role of some important features in regard to the forced convective heat transfer in a porous channels. The variation of \(\mathrm{Nu}_{1\mathrm{c}}\) shows a point of discontinuity in its behavior owing to the fact of the local equilibrium in energy and maintains a constant value as Br goes to infinity in either direction. However, the significant effect of the Darcy number Da is reflected on the variation of \(\mathrm{Nu}_{1\mathrm{c}}\) as one may find on closely looking into Fig. 6a, b. It is important to mention here that the decreasing value of permeability of the media heats up the fluid more following the contribution of the viscous heating, arising out of the dragging of fluid through solid matrix present in porous channel. This, essentially, increases the driving temperature difference of the heat transfer for a given value of asymmetry parameter \(A\) and other parameters considered, thus the heat transfer rate increases as reflected in Fig. 6a, b. In order to delve deep into the effects of the permeability of the porous media on the heat transfer characteristics, three different values of Da have been used as mentioned earlier. A closer look on the above figures do reveals that the location of the onset of the point of singularity on the variation of \(\mathrm{Nu}_{1\mathrm{c}}\) alters as Da changes. This, however, can be explained from the perspective of the influential role of Da on the heat transfer characteristics. Actually, the changes in permeability of the porous media alter the overall heat balance in the flow field following the significant rise in fluid heating owing to viscous dissipation effect. However, the gross effect of this fact is reflected on the heat transfer rate and thus, the onset of the point of singularity changes for a given value of asymmetrical wall heating and other parameters as envisaged from Fig. 6a, b.

Fig. 7
figure 7

The influence of volumetric heat generation \(Q\) on the variation of \(\mathrm{Nu}_{1\mathrm{c}} \) for two different cases of asymmetric wall heating: a \(A=0.5\) and b \(A=-0.5\). The variation of \(\mathrm{Nu}_{1\mathrm{c}}\) obtained at \(\varepsilon =0.7\), Da = 0.01. The variation of Nusselt number shows discontinuity in behavior (point of singularity) and at the point of discontinuity, an equilibrium in energy is reached. The alteration in \(Q\) changes the location of the onset of the point of singularity because of the rise in heat in the flow field for both the cases of \(A=-0.5\)

Full size image

A comprehensive investigation has been made to look at the influential role of the individual effect of porosity \(\varepsilon \), Darcy number Da on the convective heat transfer characteristics in a porous channel as discussed before. Next, an effort has been made to address the effect of the volumetric heat generation on the heat transfer characteristics in a focused way. To do that, Fig. 7a, b has been depicted with the objective of delineating the effect of volumetric heat generation \(Q\) on the thermal transport characteristics of heat, more precisely to see what effect does the volumetric heat generation have on the variation of \(\mathrm{Nu}_{1\mathrm{c}}\)? Figure 7a, b corresponds to the degrees of asymmetrical wall heating \(A=0.5\) and \(-0.5\), respectively, while the other parameter like \(\mathrm{Da}=0.01\) and \(\varepsilon =0.7\) has been considered in obtaining those figures. As expected, satisfying the requirement of equilibrium state of energy, the variations of \(\mathrm{Nu}_{1\mathrm{c}}\) versus Br show unbounded swing for different values of \(Q\) even for all the cases of asymmetrical wall heating considered. However, a precise look on the above figures indicates that, with the increasing value of \(Q\), the onset of point of singularity shifts toward the negative value of Br for all the cases of degree of asymmetry parameters considered. This, however, may be explained from the energy balance in the flow field and can be argued mathematically on closely looking into the closed-form expression of the Nusselt number as given in Eq. (24a).

3.1 Thermodynamic Analysis of the Onset of Point of Singularity on the Variation of Nusselt Numbers

Interestingly, one can find the appearance of the point of discontinuity on the variation of the Nusselt number for different parameters as considered in the present study. The discontinuity appears on the variation is the outcome of the local equilibrium of energy as explained before. Convective heat transfer is characterized by the thermodynamic irreversibility, which arises due to two different effects: one is the viscous dissipation in the fluid, and other is the heat flow due to finite temperature difference. Irreversibility associated with any thermodynamic process can be evaluated through entropy generation function (Degroot and Mazur 1984). In the second law analysis, fluid friction irreversibility arises as a result of viscous heating is of essential importance, and irreversible energy conversion from frictional heating of viscous dissipation into the fluid has an important bearing on the temperature field of the fluid. In the present study, the total entropy generation corresponds to two individual effects: one is the heat transfer due to finite temperature difference, and the other is due to dissipative effects. The volumetric rate of entropy generation, which arises out of two effects can be expressed as

$$\begin{aligned} \dot{{S}^{\prime \prime \prime }}={\dot{S}}^{\prime \prime \prime }_\mathrm{gen,cond} +{\dot{S}}^{\prime \prime \prime }_\mathrm{gen,visc} =\frac{k\left( {\nabla T} \right) ^{2}}{T^{2}}+\frac{\mu }{T}\phi . \end{aligned}$$
(25)

First term on the right side of the above equation is attributable the heat transfer due to finite temperature difference, and the second term is the viscous dissipation term. The relative order of magnitude of above two terms is expressed by

$$\begin{aligned} \sim \frac{{\dot{S}}^{\prime \prime \prime }_\mathrm{gen,cond} }{{\dot{S}}^{\prime \prime \prime }_\mathrm{gen,visc} }=\frac{\mathrm{Br}}{\Delta T}. \end{aligned}$$
(26)

There may be many such cases, where the irreversibility associated to the effect of viscous heating for the analysis of forced convective heat transfer may not be ignored even for the small values of \(\mathrm{Br}(\mathrm{Br}\ll 1)\). In order to have a higher heat transfer rate for any given temperature difference, it is customary that the irreversibility associated with the process required to be minimized, which, however, can be done by minimizing the irreversibility due to fluid friction of viscous dissipation. In the present study, two different degrees of asymmetrical wall heating have been considered in investigating the variation of both the Nusselt numbers as evident from the figures presented above. The irreversibility associated with the heat transfer for two different values of asymmetry parameter, however, leads the irreversibility to be minimized as a result of frictional heating of viscous dissipation in order to obtain the maximum possible heat transfer for a given degree of wall heating. The gross effect is essentially reflected on the variation of \(\mathrm{Nu}_{1\mathrm{c}}\) for different degrees of asymmetrical wall heating, which one can clearly notice from the fact that the onset of the point of singularity alters with the variation in degrees of asymmetrical wall heating as portrayed in Figs. 6 and 7.

4 Conclusions

In the present work, a comprehensive discussion has been made in regard to the significant role of the effect of viscous heating, effect of porosity, effect of volumetric heat generation, and the degree of asymmetrical wall heating on the limiting convective heat transfer characteristics in a parallel plates channel filled with saturated porous media. Following an analytical formalism, the closed-form solution for the temperature distribution in the flow field is presented, which in turn devise the explicit expression of the Nusselt numbers at both the plates. In the analysis, a few assumptions like negligible axial conduction and negligible convective term have been made only to attain a situation of obtaining the analytical solutions of the temperature profile in the limiting condition. The key role of different performance indexing parameters of forced convection heat transfer in a porous channel has been identified, emphasizing their individual effect on the heat transfer characteristics in a comprehensive way. The influential role of viscous dissipation, permeability of the media, and the volumetric heat generation are found to be of essential importance in the limiting heat transfer characteristics when both the plates of the channel are kept at unequal constant temperatures. The present analysis can be extended further in different direction by relaxing some of the assumptions made in the study. However, the following conclusions can be outlined from the investigation made in the present study.

  • The dimensionless temperature in the limiting condition shows the usual trend of increasing fluid temperature for positive Br and a decreasing trend for the negative values of Br for all the cases of parametric studies as considered in the present analysis.

  • Specific to the cases of the smaller value of porosity, the temperature of the fluid becomes higher than that of the same obtained at higher value of porosity this is attributable to the presence of concentrated solid matrix for the cases of smaller values of porosity of the media. The presence of the concentrated solid matrix imparts more heat to the fluid, arising out of the effect of viscous dissipation in a flow through porous channel.

  • The consideration of volumetric heat generation in the thermal energy equation acts like an adding effect in increasing the temperature in the fluid. The higher value of \(Q\) increases the fluid temperature for the positive Br and, which is expected. Specific to the case of negative value of Br and for a given degree of asymmetrical wall heating, the presence of large amount of volumetric heat generation prohibits the degree of wall cooling.

  • The parametric variation of \(\mathrm{Nu}_{1\mathrm{c}}\) versus Br is not continuous; rather a point of discontinuity exists on the variation \(\mathrm{Nu}_{1\mathrm{c}}\) for all the cases of parametric variations as considered in the study. At the point of singularity, the variation of \(\mathrm{Nu}_{1\mathrm{c}}\) shows an unbounded swing owing to the presence of equilibrium state of energy. The onset of the point of singularity alters with the alteration in degree of asymmetry parameter although the effect of porosity does not have significant role to play in regard to the alteration of point of singularity considerably.

  • The changes in permeability of the porous media alter the overall heat balance in the flow filed. This is because of the significant rise in fluid heating due to the viscous dissipation effect. The gross effect of the alteration in permeability of the porous media is reflected on the variation of \(\mathrm{Nu}_{1\mathrm{c}}\) as it changes the onset of the point of singularity for a given value of asymmetrical wall heating and other parameters considered.

  • The variation of \(\mathrm{Nu}_{1\mathrm{c}}\) versus Br shows unbounded swing for different values of \(Q\) considered. The increasing value of \(Q\), shifts the onset of point of singularity toward the negative value of Br for all the cases of degree of asymmetry parameters considered. This is because of the alteration in energy balance in the flow field, and can be argued mathematically on closely looking into the expression of the Nusselt number.