Flow Modeling of Well Test Analysis for Porous–Vuggy Carbonate Reservoirs

Abstract

Porous–vuggy carbonate reservoirs consist of both matrix and vug systems. This paper represents the first study of flow issues within a porous–vuggy carbonate reservoir that does not introduce a fracture system. The physical properties of matrix and vug systems are quite different in that vugs are dispersed throughout a reservoir. Assuming spherical vugs, symmetrically distributed pressure, centrifugal flow of fluids and considering media that is directly connected with wellbore as the matrix system, we established and solved a model of well testing and rate decline analysis for porous–vuggy carbonate reservoirs, which consists of a dual porosity flow behavior. Standard log–log type curves are drawn up by numerical simulation and the characteristics of type curves are analyzed thoroughly. Numerical simulations showed that concave type curves are dominated by interporosity flow factor, external boundary conditions, and are the typical response of porous–vuggy carbonate reservoirs. Field data interpretation from Tahe oilfield of China were successfully made and some useful reservoir parameters (e.g., permeability and interporosity flow factor) are obtained from well test interpretation.

1 Introduction

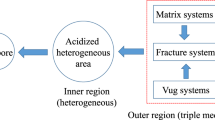
Carbonate reservoirs have complex structures and have generated great scientific interest and significant challenges (Rawnsley et al. 2007; Sarma and Aziz 2006; Bahrami et al. 2008; Popov et al. 2009; Gua and Chalaturnyk 2010). Carbonate reservoirs can be composed of matrix and fracture systems while others are composed of matrix, fracture, and vug systems. Owing to the existence of fractures and vugs, reservoirs have multiple porosity properties. Reservoirs composed of matrix and fracture systems are called “matrix–fracture dual porosity reservoirs” (Warren and Root 1963; Al-Ghamdi and Ershaghi 1996). Reservoirs composed of matrix, fracture, and vug systems are called “matrix–fracture–vug triple porosity reservoirs” (Liu et al. 2003; Camacho-Velázquez et al. 2006). Matrix–fracture dual–porosity and matrix–fracture–vug triple-porosity reservoirs are the most commonly studied (Lai et al. 1983; Rasmussen and Civan 2003; Wu et al. 2004, 2007; Wu et al. 2011; Camacho-Velázquez et al. 2006; Corbett et al. 2010, for example). However, reservoirs mainly composed of matrix and vug systems, like porous–vuggy carbonate reservoirs in Tahe oilfield of China, do exist. This paper seeks to model matrix–vug dual-porosity reservoirs without introducing a fracture system.

The flow problem of oil in porous media reservoirs is a complicated inverse problem in carbonate reservoirs because of their elusive flow behaviors (Corbett et al. 2010, 2012). Fracture and vug development differs across reservoirs (Abdassah and Ershaghi 1986; Mai and Kantzas 2007); each reservoir has a distinct set of fluid transport behaviors. Well testing analysis is the “eye” for discerning the elusive flow behavior in invisible reservoirs. Therefore, a vital research task is to establish well test models that evaluate reservoir properties.

The flow problem in carbonate reservoirs has been well researched: (i) theory and applications on dual porosity flow model for well test analysis of fractured reservoirs (Al-Ghamdi and Ershaghi 1996; Bourdet and Gringarten 1980; Braester 1984; Bui et al. 2000; Izadi and Yildiz 2007; Lai et al. 1983; Liu et al. 2003; Jalali and Ershaghi 1987; Rasmussen and Civan 2003; Wijesinghe and Culham 1984; Wijesinghe and Kececioglu 1985) and (ii) theory and applications on triple porosity flow model for well test analysis of fractured–vuggy reservoirs (Bai and Roegiers 1997; Camacho-Velázquez et al. 2006; Nie et al. 2011, 2012a; Pulido et al. 2006; Veling 2002; Wu et al. 2004, 2007; Wu et al. 2011). Both the medium connected to the wellbore and the interporosity of fluid from the matrix or vug systems into the fracture system were considered as the fracture system. Pseudo-steady interporosity flow characteristics were commonly assumed by considering arbitrarily shaped matrix blocks and vugs (Camacho-Velázquez et al. 2006; Wu et al. 2004, 2007; Wu et al. 2011). Unsteady interporosity manner was assumed by considering spherical shaped matrix blocks and vugs (Nie et al. 2011, 2012a). It is hard to distinguish the difference between separate vug and connected vug systems by using well test analysis. Hence, vug dispersal in carbonate rock was assumed in the flow model. In this study, we will adopt these assumptions for the convenient mathematical description of fluid flow in vugs. The objective of this study is to investigate a flow model of pressure- and rate-transient analysis for porous–vuggy carbonate reservoirs. Only single-phase flow behavior will be considered in the model because a semi-analytical method can adopt to solve the mathematical model. Multiphase flow models are hard to solve by using semi-analytical methods and are usually solved by using numerical methods. The single-phase flow model researched in this study is, in theory, suitable for oil-saturated reservoirs. It can also be applied to water producing oil reservoirs in engineering practices. Nie et al. (2012b) discussed the applicability of a single-phase flow to water-producing reservoirs in detail and, therefore, are not discussed here. The paper is structured as follows: Sect. 2 introduces model assumptions on physical properties; Sect. 3 establishs and solves the mathematical model, Sect. 4 plots the type curves and analyzes the pressure- and rate-transient characteristics; Sect. 5 discusses the relationship and comparability with earlier numerical studies; and Sect. 6 validates the provided model using real field data. The standard type curves and successful well test interpretation in this article demonstrate that the model can be used for real case studies.

2 Physical Modeling

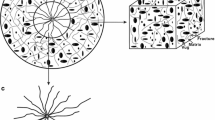
The carbonate reservoir in Tahe oilfield of China is an example of a reservoir that is composed of vug and matrix systems. Figure 1 shows a rock core cross-section and a well-imaging logging of a well in Tahe oilfield. This kind of carbonate reservoir is called a porous–vuggy carbonate reservoir.

Fig. 1

Rock core cross-section and well-imaging logging of Tahe oilfield

Figures 2 and 3 show the physical modeling scheme of porous–vuggy carbonate reservoirs. Vug and matrix systems are relatively independent in physical properties. Vugs are uniformly dispersed in a reservoir and the media directly connected with a wellbore is the matrix system. Therefore, during well production, fluid flow through a matrix system into the wellbore and interporosity flow from vug system to matrix system are assumed. The fluid flow in porous–vuggy carbonate reservoirs displays a dual porosity flow behavior (see Fig. 4).

Fig. 2

Porous–vuggy reservoir scheme

Fig. 3

Conceptual model of porous–vuggy reservoir

Fig. 4

Flow scheme of porous–vuggy reservoir

The following simplifying assumptions are made: the system is assumed homogeneous and isotropic with constant physical property parameters, such as, permeability and porosity, which means the property parameters are the same at every point and any direction and do not change with time. All vugs are spherical with radius of $r_{1}$ (see Fig. 3), and thus the radius ($r_{1}$) is equivalent to the average radius of all vugs. Fluid flows from the center of a vug to matrix and then flows through matrix into wellbore. An unsteady interporosity flow (vug pressure not only relates to time, $t$, but also to radial spherical coordinate, $r$, causing a pressure drop in vug) is considered. The pressure distribution in a vug is spherically symmetric (Nie et al. 2011, 2012a).

Physical model assumptions are as follows:

• (1) A single well production at a constant rate or at a constant wellbore pressure in porous–vuggy type carbonate reservoirs; the external boundary of the reservoir may be infinite or closed or at constant pressure for constant rate production; and for constant wellbore pressure production we only consider the closed external boundary (Blasingame et al. 1991; Doublet and Blasingame 1994; Marhaendrajana and Blasingame 2001).

• (2) Total compressibility (rock and fluid) is low and a constant.

• (3) Isothermal and Darcy flow, ignoring the impact of gravity and capillary forces.

• (4) When the well is first put in production, fluid is sourced from the wellbore before significant inflow from the formation occurs (wellbore storage). The wellbore storage effect is only considered for the constant rate case.

• (5) Skin effect. The wellbore formation could be damaged due to drilling and completion operations. An additional pressure drop with well production is where the “skin” is the reflection of the additional pressure drop considered for both constant rate production and constant wellbore pressure production.

• (6) At time $t=0$, pressure is uniformly distributed in a reservoir, equal to initial pressure ($p_\mathrm{i}$).

3 Mathematical Modeling

3.1 Establishment of Mathematical Model

 

• (1) Governing differential equations

Governing equation of matrix system in radial cylindrical coordinate system

$$\begin{aligned} \frac{\partial ^{2}p_\mathrm{m} }{\partial r_\mathrm{m} ^{2}}+\frac{1}{r_\mathrm{m} }\frac{\partial p_\mathrm{m} }{\partial r_\mathrm{m} }+\frac{\mu }{k_\mathrm{m} }q_\mathrm{v} =\frac{\mu \phi _\mathrm{m} C_\mathrm{{mt}} }{k_\mathrm{m} }\frac{\partial p_\mathrm{m} }{\partial t} \end{aligned}$$

(1)

where $p_\mathrm{m}$ is matrix pressure (Pa), $r_\mathrm{m}$ is radial cylindrical coordinate of matrix system (m), $k_\mathrm{m}$ is matrix permeability ($\text{ m}^{2}$), $\mu$ is oil viscosity (Pa s), $\phi _\mathrm{m}$ is matrix porosity (fraction), $C_\mathrm{mt}$ is the total compressibility of the matrix system ($\text{ Pa}^{-1})$, $t$ is production time (s), $q_\mathrm{v}$ is the interporosity flow volume in unit time from unit volume (vug $\text{ s}^{-1}\,(\text{ m}^{3}/\text{ s}/\text{ m}^{3}))$, the subscript “m” represents matrix, the subscript “v” represents vug, the subscript “t” represents total.

Governing equation of vug system in radial spherical coordinate system

$$\begin{aligned} \frac{\partial ^{2}p_\mathrm{v} }{\partial r_\mathrm{v} ^{2}}+\frac{2}{r_\mathrm{v} }\frac{\partial p_\mathrm{v} }{\partial r_\mathrm{v} }=\frac{\mu \phi _\mathrm{v} C_\mathrm{{vt}} }{k_\mathrm{v} }\frac{\partial p_\mathrm{v} }{\partial t} {(0<r_\mathrm{v} <r_1 )} \end{aligned}$$

(2)

where $p_\mathrm{v}$ is vug pressure (Pa), $r_\mathrm{v}$ is radial spherical coordinate of vug system (m), $k_\mathrm{v}$ is vug permeability ($\text{ m}^{2})$, $\mu$ is oil viscosity ($\text{ Pa} \text{ s}$), $\phi _\mathrm{v}$ is vug porosity (fraction), $C_\mathrm{vt}$ is the total compressibility of vug system ($\text{ Pa}^{-1}$).

• (2) Interporosity flow equations

Fluid flows from the center of a vug to matrix. By Darcy’s law, the flow velocity at spherical surface ($r_\mathrm{v}=r_\mathrm{1}$) of a vug is

$$\begin{aligned} v=-\frac{k_\mathrm{v} }{\mu }\left.\left(\frac{\partial p_\mathrm{v} }{\partial r_\mathrm{v} }\right)\right|_{r_\mathrm{v}= r_{1}} \end{aligned}$$

(3)

where $v$ is flow velocity (m/s), $r_\mathrm{1}$ is the radius of spherical vug (m).

Because the outflow volume in unit time from unit volume vug is $q_\mathrm{v}$, the velocity at a spherical surface is equal to the surface area of a spherical vug divided by the outflow volume of fluid from a vug in unit time, that is

$$\begin{aligned} v={\left(\frac{4}{3}\pi r_1 ^{3}q_\mathrm{v} \right)}\Big /{\left(4\pi r_1 ^{2}\right)}=\frac{1}{3}r_1 q_\mathrm{v} \end{aligned}$$

(4)

Combining Eq. 3 with Eq. 4, where the interporosity flow volume in unit time from unit volume vug is

$$\begin{aligned} q_\mathrm{v} =-\frac{3}{r_1 }\frac{k_\mathrm{v} }{\mu }\left.\left(\frac{\partial p_\mathrm{v} }{\partial r_\mathrm{v} }\right)\right|_{r_\mathrm{v} \,=\, r_{1}} \end{aligned}$$

(5)

• (3) Inner boundary conditions.

• (i) Well production at constant rate:

• (a) Considering the wellbore storage and skin effect using the real wellbore radius

In the physical model, the media directly connected with the wellbore is considered as the matrix system, therefore the rate of oil flow from the matrix system into the wellbore can be calculated using

$$\begin{aligned} q_\mathrm{w} =\frac{2\pi k_\mathrm{m} h}{\mu }\left.\left[r_\mathrm{m} \frac{\partial p_\mathrm{m} (t)}{\partial r_\mathrm{m} }\right]\right|_{r_\mathrm{m}=r{_\mathrm{w}}} \end{aligned}$$

(6)

where $h$ is formation thickness (m), $q_\mathrm{w}$ is rate of oil flow from the matrix system into the wellbore (${\text{ m}}^{3}/{\text{ s}}), r_\mathrm{w}$ is the radius of wellbore (m).

The oil rate at the wellhead is affected by the wellbore storage effect while oil volume changes with the change of pressure in the wellbore. The rate of change in oil volume with the change of pressure in the wellbore is the wellbore storage coefficient:

$$\begin{aligned} C_\mathrm{s} =\frac{{\text{ d}}V}{{\text{ d}}p_\mathrm{w} }=\frac{{\text{ d}}V}{{\text{ d}}t}\cdot \frac{{\text{ d}}t}{{\text{ d}}p_\mathrm{w}} \end{aligned}$$

(7)

where $C_\mathrm{s}$ is the wellbore storage coefficient (${\text{ m}}^{3}/{\text{ Pa}}$), $V$ is oil volume in wellbore ($\text{ m}^{3}), p_\mathrm{w}$ is the wellbore pressure (Pa).

Equation 7 can be transformed:

$$\begin{aligned} \frac{{\text{ d}}V}{{\text{ d}}t}=C_\mathrm{s} \cdot \frac{{\text{ d}}p_\mathrm{w} }{{\text{ d}}t}=q_\mathrm{s} =q_\mathrm{w} -qB \end{aligned}$$

(8)

where $q_\mathrm{s}$ is oil-change rate caused by the wellbore storage effect ($\text{ m}^{3}/\text{ s}$), $q$ is oil rate at wellhead ($\text{ m}^{3}/\text{ s}$), $B$ is oil volume factor ($\text{ m}^{3}/\text{ m}^{3}$).

Combining Eqs. 6 and 8, the inner boundary condition considering the wellbore storage effect can be got by (Agarwal et al. 1970; Bourdet 2003)

$$\begin{aligned} C_\mathrm{s} \frac{\text{ d}p_\mathrm{w} }{\text{ d}t}=\frac{2\pi k_\mathrm{m} h}{\mu }\left.\left[r_\mathrm{m} \frac{\partial p_\mathrm{m} (t)}{\partial r_\mathrm{m} }\right]\right|_{r_\mathrm{m} = r_\mathrm{w}} -qB \end{aligned}$$

(9)

It is worth noting that the rate $q$ is a constant and the ($\text{ d}p_\mathrm{w}/\text{ d}t$) is a function of time in Eq. 9.

When considering the skin effect, the wellbore pressure ($p_\mathrm{w}$) can be expressed by

$$\begin{aligned} p_\mathrm{w} =\left.\left(p_\mathrm{m} -Sr\frac{\partial p_\mathrm{m} }{\partial r}\right)\right|_{r= r_\mathrm{w}} \end{aligned}$$

(10)

where $S$ is the skin factor, dimensionless.

• (b) Considering the wellbore storage and skin effect using the effective wellbore radius

The effective wellbore radius $r_\mathrm{wa}$ is defined as (Agarwal et al. 1970; Chaudhry 2004)

$$\begin{aligned} r_\mathrm{{wa}} =r_\mathrm{w} \text{ e}^{-S} \end{aligned}$$

(11)

where $r_\mathrm{wa}$ is the effective wellbore radius (m).

If $S$ is positive, the effective wellbore radius is smaller than $r_\mathrm{w}$. If $S$ is negative, the effective wellbore radius is larger than $r_\mathrm{w}$. The real wellbore radius can only deal with positive skins, while the effective wellbore radius can deal with both positive skins and negative skins. For an effective wellbore radius model, the rate of oil flow from the matrix system into the wellbore can be calculated using

$$\begin{aligned} q_\mathrm{w} =\frac{2\pi k_\mathrm{m} h}{\mu }\left.\left(r_\mathrm{m} \frac{\partial p_\mathrm{m} }{\partial r_\mathrm{m} }\right)\right|_{r_\mathrm{m}= r_\mathrm{wa}} \end{aligned}$$

(12)

Combining Eqs. 8 and 12, the inner boundary conditions considering the wellbore storage and skin effect at constant rate production can be expressed by

$$\begin{aligned} C_\mathrm{s} \frac{\text{ d}p_\mathrm{w} }{\text{ d}t}=\frac{2\pi k_\mathrm{m} h}{\mu }\left(r_\mathrm{m} \frac{\partial p_\mathrm{m} }{\partial r_\mathrm{m} }\right)\left| {_{r_\mathrm{m}=}}{_{r_\mathrm{wa}}} \right.-qB \end{aligned}$$

(13)

In this article, Eqs. 11 and 13 are employed in the flow modeling for well test analysis.

• (ii) Well production at constant wellbore pressure:

The matrix pressure at the effective wellbore radius ($r_\mathrm{m}=r_\mathrm{wa}$) is equal to the wellbore pressure ($p_\mathrm{w}$):

$$\begin{aligned}&p_\mathrm{m} \left| {_{r_\mathrm{m}=}}{_{r_\mathrm{wa}}} \right.=p_\mathrm{w} \end{aligned}$$

(14)

$$\begin{aligned}&q=\frac{2\pi k_\mathrm{m} h}{\mu B}\left(r_\mathrm{m} \frac{\partial p_\mathrm{m} }{\partial r_\mathrm{m} }\right)\left| {_{r_\mathrm{wa}}} \right. \end{aligned}$$

(15)

In the physical model, the centrifugal flow from the center of a spherical vug to matrix is considered. The vug center is equivalent to an impermeable point, which meets the Neumann-boundary condition. Therefore, at the center of a vug:

$$\begin{aligned} \frac{\partial p_\mathrm{v} }{\partial r_\mathrm{v} }\left| {_{r_\mathrm{v}=}}{_{0}} \right.=0 \end{aligned}$$

(16)

• (4) External boundary conditions

Infinite reservoir

$$\begin{aligned} \mathop {\lim }\limits _{_{r_\mathrm{m} \rightarrow \infty }} p_\mathrm{m} =p_\mathrm{i} \text{(infinite)} \end{aligned}$$

(17)

where $p_\mathrm{i}$ is initial reservoir pressure (Pa).

Constant pressure boundary

$$\begin{aligned} p_\mathrm{m} \left| {_{r_\mathrm{m}=}}{_{R_\mathrm{e}}} \right.=p_\mathrm{i} \; \text{(constant} \text{ pressure)} \end{aligned}$$

(18)

where $R_\mathrm{e}$ is radial distance of external boundary (m).

Closed boundary

$$\begin{aligned} \frac{\partial p_\mathrm{m} }{\partial r_\mathrm{m} }\left| {_{r_\mathrm{m}=}}{_{R_\mathrm{e}}} \right.=0 \text{(closed)} \end{aligned}$$

(19)

At the spherical surface of a vug, vug pressure equals matrix pressure

$$\begin{aligned} p_\mathrm{v} (r_\mathrm{v} ,t)\left| {_{r_\mathrm{v}=}}{_{r_{1}}} \right.=p_\mathrm{m} \end{aligned}$$

(20)

• (5) Initial conditions

$$\begin{aligned} p_\mathrm{m} \left| {_{t=0} } \right.=p_\mathrm{v} \left| {_{t=0}} \right.=p_\mathrm{i} \end{aligned}$$

(21)

It is worth noting that the variable units in the mathematical model are standard SI units. If a set of mixing units is used for the variables, coefficients could be produced in the equations. For example, if “MPa” is used for pressure, “cm/s” is used for velocity, “$\upmu \text{ m}^{2}$” is used for permeability, “mPa s” is used for viscosity, and “cm” for radius, a coefficient of 0.1 on the right side of Eq. 3 will be produced, that is:

$$\begin{aligned} v=-\frac{0.1k_\mathrm{v} }{\mu }\left(\frac{\partial p_\mathrm{v} }{\partial r_\mathrm{v} }\right)\left| {_{r_\mathrm{v}=}}{_{r_{1}}} \right. \end{aligned}$$

(22)

3.2 Dimensionless Mathematical Model

3.2.1 Dimensionless Definitions

The dimensionless mathematical model is relatively easier to solve than the mathematical model with dimensions. In order to obtain the dimensionless mathematical model, we must define a group of dimensionless parameters first and then substitute them into the mathematical model with dimensions. Definitions of the dimensionless parameters are as follows:

• Skin factor $S=2\pi k_\mathrm{m} h\Delta p_\mathrm{s} /(qB\mu )$, where $\Delta p_\mathrm{s}$ is additional pressure drop.

• Dimensionless radius of matrix system based on effective radius $r_\mathrm{{mD}} =r_\mathrm{m} /(r_\mathrm{w} \text{ e}^{-S})$.

• Dimensionless radius of external boundary $R_\mathrm{{eD}} =R_\mathrm{e} /(r_\mathrm{w} \text{ e}^{-S})$.

• Dimensionless radius of vug system $r_\mathrm{{vD}} =r_\mathrm{v} /r_1$.

• Dimensionless time $t_\mathrm{D} =k_\mathrm{m} t/[\mu r_\mathrm{w} ^{2}(\phi _\mathrm{m} C_\mathrm{{mt}} +\phi _\mathrm{v} C_\mathrm{{vt}} )]$.

• Spherical geometric shape factor of a vug (De Swaan 1976; Rangel-German and Kovscek 2005) $\alpha _\mathrm{v} =15/r_1 ^{2}$.

• Interporosity flow factor of vug system to matrix system $\lambda _\mathrm{{vm}} =\alpha _\mathrm{v} r_\mathrm{w} ^{2}k_\mathrm{v} /k_\mathrm{m} =15r_\mathrm{w} ^{2}k_\mathrm{v} /(k_\mathrm{m} r_1 ^{2})$;

• Fluid storage capacitance coefficient of matrix system $\omega _\mathrm{m} =\phi _\mathrm{m} C_\mathrm{{mt}} /(\phi _\mathrm{m} C_\mathrm{{mt}} +\phi _\mathrm{v} C_\mathrm{{vt}} )$.

• Fluid storage capacitance coefficient of vug system $\omega _\mathrm{v} =\phi _\mathrm{v} C_\mathrm{{vt}} /(\phi _\mathrm{m} C_\mathrm{{mt}} +\phi _\mathrm{v} C_\mathrm{{vt}} )$.

For constant rate production

• Dimensionless pressure of matrix system $p_\mathrm{{mD}} =2\pi k_\mathrm{m} h(p_\mathrm{i} -p_\mathrm{m} )/(qB\mu )$.

• Dimensionless pressure of vug system $p_\mathrm{{vD}} =2\pi k_\mathrm{m} h(p_\mathrm{i} -p_\mathrm{v} )/(qB\mu )$.

• Dimensionless wellbore pressure $p_\mathrm{{wD}} =2\pi k_\mathrm{m} h(p_\mathrm{i} -p_\mathrm{w} )/(qB\mu )$.

• Dimensionless wellbore storage coefficient $C_\mathrm{D} =C_\mathrm{s} /[2\pi hr_\mathrm{w} ^{2}(\phi _\mathrm{m} C_\mathrm{{mt}} +\phi _\mathrm{v} C_\mathrm{{vt}} )]$.

For constant wellbore pressure production

• Dimensionless pressure of matrix system $p_\mathrm{{mD}} =(p_\mathrm{i} -p_\mathrm{m} )/(p_\mathrm{i} -p_\mathrm{w} )$.

• Dimensionless pressure of vug system $p_\mathrm{{vD}} =(p_\mathrm{i} -p_\mathrm{v} )/(p_\mathrm{i} -p_\mathrm{w} )$.

• Decline curve dimensionless time of Blasingame (Blasingame et al. 1991; Doublet and Blasingame 1994; Marhaendrajana and Blasingame 2001) $t_\mathrm{{Dd}} =t_\mathrm{D} /[(R_\mathrm{{eD}}^\mathrm{2} -1)(\ln (R_\mathrm{{eD}} )-0.5)/2]$.

• Dimensionless rate $q_\mathrm{D} =qB\mu /[2\pi k_\mathrm{m} h(p_\mathrm{i} -p_\mathrm{w} )]$.

• Decline curve dimensionless rate of Blasingame $q_\mathrm{{Dd}} =q_\mathrm{D} [\ln (R_\mathrm{{eD}})-0.5]$.

• Dimensionless rate integral function of Blasingame $q_\mathrm{{Ddi}} =\frac{1}{t_\mathrm{{Dd}} }\int _0^{t_\mathrm{{Dd}} } {q_\mathrm{{Dd}} (\tau )\text{ d}\tau }$.

• Dimensionless rate integral derivative function of Blasingame ${q}^{\prime }_\mathrm{{Ddi}} =-\frac{\text{ d}q_\mathrm{{Ddi}} }{\text{ d}\ln t_\mathrm{{Dd}} }=-t_\mathrm{{Dd}} \frac{\text{ d}q_\mathrm{{Ddi}} }{\text{ d}t_\mathrm{{Dd}} }$.

There are three key dimensionless parameters which represent the porous–vuggy carbonate reservoir with dual-porosity properties—the interporosity flow factor of vug system to matrix system ($\lambda _\mathrm{vm}$), the fluid storage capacitance coefficient of matrix system ($\omega _\mathrm{m}$) and the fluid storage capacitance coefficient of vug system ($\omega _\mathrm{v}$). The definition of $\lambda _\mathrm{vm}$ includes the ratio of vug permeability ($k_\mathrm{v}$) to matrix permeability ($k_\mathrm{m}$), hence it exhibits the relative flow ability in vug and matrix systems. If pore-volume of the matrix system is $V_\mathrm{m}$, pore-volume of the vug system is $V_\mathrm{v}$, and bulk volume of the reservoir is $V$, and accordingly the porosity of the matrix system is defined as $\phi _\mathrm{m} =V_\mathrm{m}/V$ and the porosity of the vug system is defined as $\phi _\mathrm{v} =V_\mathrm{v} /V$.

Substitute the definitions of porosity into the definitions of the fluid storage capacitance coefficient:

$$\begin{aligned}&\omega _\mathrm{m} =V_\mathrm{m} C_\mathrm{{mt}} /(V_\mathrm{m} C_\mathrm{{mt}} +V_\mathrm{v} C_\mathrm{{vt}} )\end{aligned}$$

(23)

$$\begin{aligned}&\omega _\mathrm{v} =V_\mathrm{v} C_\mathrm{{vt}} /(V_\mathrm{m} C_\mathrm{{mt}} +V_\mathrm{v} C_\mathrm{{vt}} )\end{aligned}$$

(24)

$$\begin{aligned}&\omega _\mathrm{m} +\omega _\mathrm{v} =1 \end{aligned}$$

(25)

Therefore it can be seen from Eqs. 23–25 that the fluid storage capacitance coefficients exhibit the relative volume relationship of the vug system to the matrix system. If the pore-volume of vug system is larger than that of matrix system, the fluid storage capacitance of vug system will be larger than that of matrix system ($\omega _\mathrm{v} > \omega _\mathrm{m}$), which means the reserves of fluid stored in the vug system is larger than the reserves of fluid stored in the matrix system.

3.2.2 Dimensionless Mathematical Model in Real Space

The dimensionless models will be derived in the following:

• (1) Governing differential equations

Substitute Eq. 5 into Eq. 1:

$$\begin{aligned} \frac{\partial ^{2}p_\mathrm{m} }{\partial r_\mathrm{m} ^{2}}+\frac{1}{r_\mathrm{m} }\frac{\partial p_\mathrm{m} }{\partial r_\mathrm{m} }-\frac{3}{r_1 }\frac{\mu }{k_\mathrm{m} }\frac{k_\mathrm{v} }{\mu }\left.\left(\frac{\partial p_\mathrm{v} }{\partial r_\mathrm{v} }\right)\right|_{r_\mathrm{v}=r_{1}}=\frac{\mu \phi _\mathrm{m} C_\mathrm{{mt}} }{k_\mathrm{m} }\frac{\partial p_\mathrm{m} }{\partial t} \end{aligned}$$

(26)

Change the above definitions of dimensionless radius, dimensionless time and dimensionless pressure:

$$\begin{aligned}&r_\mathrm{m} =r_\mathrm{{mD}} \cdot (r_\mathrm{w} \text{ e}^{-S})\end{aligned}$$

(27)

$$\begin{aligned}&r_\mathrm{v} =r_\mathrm{{vD}} \cdot r_\mathrm{1}\end{aligned}$$

(28)

$$\begin{aligned}&t=t_\mathrm{D} \cdot [\mu r_\mathrm{w} ^{2}(\phi _\mathrm{m} C_\mathrm{{mt}} +\phi _\mathrm{v} C_\mathrm{{vt}} )]/k_\mathrm{m} \end{aligned}$$

(29)

• (i) Well production at constant rate:

  $$\begin{aligned}&p_\mathrm{m} =p_\mathrm{i} -p_\mathrm{{mD}} \cdot (qB\mu )/2\pi k_\mathrm{m} h\end{aligned}$$

  (30)
  $$\begin{aligned}&p_\mathrm{v} =p_\mathrm{i} -p_\mathrm{{vD}} \cdot (qB\mu )/2\pi k_\mathrm{m} h \end{aligned}$$

  (31)

• (ii) Well production at constant wellbore pressure:

  $$\begin{aligned}&p_\mathrm{m} =p_\mathrm{i} -p_\mathrm{{mD}} \cdot (p_\mathrm{i} -p_\mathrm{w})\end{aligned}$$

  (32)
  $$\begin{aligned}&p_\mathrm{v} =p_\mathrm{i} -p_\mathrm{{vD}} \cdot (p_\mathrm{i} -p_\mathrm{w} ) \end{aligned}$$

  (33)

Substitute Eqs. 27–33 into Eqs. 26 and Eq. 2, respectively:

$$\begin{aligned}&\frac{\partial ^{2}p_\mathrm{{mD}} }{\partial r_\mathrm{{mD}}^\mathrm{2} }+\frac{1}{r_\mathrm{{mD}} }\frac{\partial p_\mathrm{{mD}} }{\partial r_\mathrm{{mD}} }-\frac{1}{5}\lambda _\mathrm{{vm}} \text{ e}^{-2S}\left(\frac{\partial p_\mathrm{{vD}} }{\partial r_\mathrm{{vD}} }\right)\left| {_\mathrm{r_\mathrm{{vD}} =1} } \right.=\omega _\mathrm{m} \text{ e}^{-2S}\frac{\partial p_\mathrm{{mD}} }{\partial t_\mathrm{D} }\end{aligned}$$

(34)

$$\begin{aligned}&\frac{\partial ^{2}p_\mathrm{{vD}} }{\partial r_\mathrm{{vD}} ^{2}}+\frac{2}{r_\mathrm{{vD}} }\frac{\partial p_\mathrm{{vD}} }{\partial r_\mathrm{{vD}} }=\frac{15\omega _\mathrm{v} }{\lambda _\mathrm{v} }\frac{\partial p_\mathrm{{vD}} }{\partial t_\mathrm{D} } \quad \quad {(0<r_\mathrm{{vD}} <1)} \end{aligned}$$

(35)

Equation 34 is the dimensionless governing equation of matrix system in a radial cylindrical coordinate system. Equation 35 is the dimensionless governing equation of vug system in a radial spherical coordinate system. Although the definitions of dimensionless pressure are different for constant rate production and constant wellbore pressure production, the dimensionless governing equations are the same.

• (2) Inner-boundary conditions

Change the above definitions of dimensionless wellbore storage coefficient:

$$\begin{aligned} C_\mathrm{s} =C_\mathrm{D} \cdot [2\pi hr_\mathrm{w} ^{2}(\phi _\mathrm{m} C_\mathrm{{mt}} +\phi _\mathrm{v} C_\mathrm{{vt}} )] \end{aligned}$$

(36)

Substitute Eqs. 27, 30, and 36 into Eq. 13 for constant rate production:

$$\begin{aligned} \left(C_\mathrm{D} \frac{\text{ d}p_\mathrm{{mD}} }{\text{ d}t_\mathrm{D} }-r_\mathrm{{mD}} \frac{\partial p_\mathrm{{mD}} }{\partial r_\mathrm{{mD}} }\right)\left| {_{r_\mathrm{mD}=}}{_{1}} \right.=1 \end{aligned}$$

(37)

Change the above definitions of dimensionless rate for constant wellbore pressure production:

$$\begin{aligned} q=q_\mathrm{D} \cdot [2\pi k_\mathrm{m} h(p_\mathrm{i} -p_\mathrm{w})]/(B\mu ) \end{aligned}$$

(38)

Substitute Eqs. 27, 31, and 38 into Eqs. 14 and 15, respectively, for constant wellbore pressure production:

$$\begin{aligned}&p_\mathrm{{mD}} =1\end{aligned}$$

(39)

$$\begin{aligned}&q_\mathrm{D} =-\left.\left(\frac{\partial p_\mathrm{{mD}} }{\partial r_\mathrm{{mD}} }\right)\right|_{r_\mathrm{mD}={1}} \end{aligned}$$

(40)

Substitute Eqs. 28 and 31 into Eq. 16:

$$\begin{aligned} \frac{\partial p_\mathrm{{vD}} }{\partial r_\mathrm{{vD}} }\left| {_{r_\mathrm{vD}=}}{_{0}} \right.=0 \end{aligned}$$

(41)

By the same method, the dimensionless equations for external boundary conditions and initial conditions can be easily obtained:

• (3) External-boundary conditions

Infinite reservoir

$$\begin{aligned} \mathop {\lim }\limits _{_{r_\mathrm{mD} \rightarrow \infty }} p_\mathrm{{mD}} =0 \text{(infinite)} \end{aligned}$$

(42)

Constant pressure boundary

$$\begin{aligned} p_\mathrm{mD} \left|{_{r_\mathrm{mD}=}}{_\mathrm{R_\mathrm{eD}}} \right.=0\; \text{(constant} \text{ pressure)} \end{aligned}$$

(43)

Closed boundary

$$\begin{aligned} \frac{\partial p_\mathrm{{mD}} }{\partial r_\mathrm{{mD}} }\left| {_{r_\mathrm{mD}=}}{_{R_\mathrm{eD}}} \right.=0\; \text{(closed)} \end{aligned}$$

(44)

At the spherical surface of a vug, vug pressure equals matrix pressure

$$\begin{aligned} p_\mathrm{{vD}} (r_\mathrm{{vD}} ,t_\mathrm{D} )\left| {_{r_\mathrm{vD}=}}{_{r_{1\mathrm{D}}}} \right.=p_\mathrm{{mD}} \end{aligned}$$

(45)

• (4) Initial conditions

$$\begin{aligned} p_\mathrm{{mD}} \left| {_{t_\mathrm{D} =0} } \right.=p_\mathrm{{vD}} \left| {_{t_\mathrm{D} =0} } \right.=0 \end{aligned}$$

(46)

3.2.3 Dimensionless Mathematical Model in Laplace Space

Introduce the Laplace transform based on $t_\mathrm{D}$, that is

$$\begin{aligned} L[p_\mathrm{D} (r_\mathrm{D} ,t_\mathrm{D} )]=\overline{p} (r_\mathrm{D} ,z)=\int \limits _0^\infty {p_\mathrm{D} (r_\mathrm{D} ,t_\mathrm{D} )} \text{ e}^{-zt_\mathrm{D} }\text{ d}t_\mathrm{D} \end{aligned}$$

(47)

Transform the Laplace to Eqs. 34, 35, 37, 39–46 and the dimensionless mathematical model in Laplace space becomes:

• (1) Governing differential equations

Governing equation of matrix system in radial cylindrical coordinate system

$$\begin{aligned} \frac{\partial ^{2}\overline{p} _\mathrm{{mD}} }{\partial r_\mathrm{{mD}}^\mathrm{2} }+\frac{1}{r_\mathrm{{mD}} }\frac{\partial \overline{p} _\mathrm{{mD}} }{\partial r_\mathrm{{mD}} }-\frac{1}{5}\lambda _\mathrm{{vm}} \text{ e}^{-2S}(\frac{\partial \overline{p} _\mathrm{{vD}} }{\partial r_\mathrm{{vD}} })\left| {_{r_\mathrm{vD} =}}{_{1}} \right.=z\omega _\mathrm{m} \text{ e}^{-2S}\overline{p} _\mathrm{{mD}} \end{aligned}$$

(48)

Governing equation of vug system in radial spherical coordinate system

$$\begin{aligned} \frac{\partial ^{2}\overline{p} _\mathrm{{vD}} }{\partial r_\mathrm{{vD}} ^{2}}+\frac{2}{r_\mathrm{{vD}} }\frac{\partial \overline{p} _\mathrm{{vD}} }{\partial r_\mathrm{{vD}} }=\frac{15z\omega _\mathrm{v} }{\lambda _\mathrm{v} }\overline{p} _\mathrm{{vD}} \quad \quad {(0<r_\mathrm{{vD}} <1)} \end{aligned}$$

(49)

• (2) Inner boundary conditions

Well production at constant rate

$$\begin{aligned} \left(zC_\mathrm{D} \overline{p} _\mathrm{{mD}} -r_\mathrm{{mD}} \frac{\partial \overline{p} _\mathrm{{mD}} }{\partial r_\mathrm{{mD}} }\right)\left| {_\mathrm{r_\mathrm{{mD}} =1} } \right.=\frac{1}{z} \end{aligned}$$

(50)

Well production at constant wellbore pressure

$$\begin{aligned}&\overline{p} _\mathrm{{mD}} =\frac{1}{z}\end{aligned}$$

(51)

$$\begin{aligned}&\overline{q} _\mathrm{D} =-\left(\frac{\partial \overline{p} _\mathrm{{mD}} }{\partial r_\mathrm{{mD}} }\right)\left| {_{r_\mathrm{mD} =1}} \right.\end{aligned}$$

(52)

$$\begin{aligned}&\overline{q} _\mathrm{{Dd}} =\overline{q} _\mathrm{D} [\ln (r_\mathrm{{eD}} )-0.5] \end{aligned}$$

(53)

At the center of vug

$$\begin{aligned} \frac{\partial \overline{p} _\mathrm{{vD}} }{\partial r_\mathrm{{vD}} }\left| {_{r_\mathrm{vD} =0}} \right.=0 \end{aligned}$$

(54)

• (3) External-boundary conditions

Infinite reservoir

$$\begin{aligned} \mathop {\lim }\limits _{_{r_\mathrm{{mD}} \rightarrow \infty }} \overline{p} _\mathrm{{mD}} =0\; \text{(infinite)} \end{aligned}$$

(55)

Constant pressure boundary

$$\begin{aligned} \overline{p} _\mathrm{{mD}} \left| {_{r_\mathrm{mD} =\mathrm{R}_\mathrm{eD}}} \right.=0\; \text{(constant} \text{ pressure)} \end{aligned}$$

(56)

Closed boundary

$$\begin{aligned} \frac{\partial \overline{p} _\mathrm{{mD}} }{\partial r_\mathrm{{mD}} }\left| {_{r_\mathrm{mD} =R_\mathrm{eD}}} \right.=0\; \text{(closed)} \end{aligned}$$

(57)

At the spherical surface of a vug, vug pressure equals matrix pressure

$$\begin{aligned} \overline{p} _\mathrm{vD} (r_\mathrm{{vD}} ,t_\mathrm{D} )\left| {_{r_\mathrm{vD} =r_{1\mathrm{D}}}} \right.=\overline{p} _\mathrm{mD} \end{aligned}$$

(58)

3.3 Solution to Dimensionless Mathematical Model

First, we derive the solution to the partial differential flow equation of vug system under its definite conditions, Eqs. 49, 54, and 58. The general solution of Eq. 49 is

$$\begin{aligned}&\bar{{p}}_\mathrm{{vD}} =(A_\mathrm{v} \text{ e}^{\sigma _\mathrm{v} r_\mathrm{{vD}} }+B_\mathrm{v} \text{ e}^{-\sigma _\mathrm{v} r_\mathrm{{vD}} })/r_\mathrm{{vD}}\end{aligned}$$

(59)

$$\begin{aligned}&\sigma _\mathrm{v} =\sqrt{15\omega _\mathrm{v} z/\lambda _\mathrm{v} } \end{aligned}$$

(60)

Substitute the general solution Eq. 59 into Eqs. 54 and 58:

$$\begin{aligned}&A_\mathrm{v} =\frac{1}{\text{ e}^{\sigma _\mathrm{v} }-\text{ e}^{-\sigma _\mathrm{v} }}\bar{{p}}_\mathrm{{mD}}\end{aligned}$$

(61)

$$\begin{aligned}&B_\mathrm{v} =-\frac{1}{\text{ e}^{\sigma _\mathrm{v} }-\text{ e}^{-\sigma _\mathrm{v} }}\bar{{p}}_\mathrm{{mD}} \end{aligned}$$

(62)

The solution of Eq. 49 in Laplace space is obtained through

$$\begin{aligned} \bar{{p}}_\mathrm{{vD}} =\frac{\bar{{p}}_\mathrm{{mD}} }{r_\mathrm{{vD}} }\frac{\text{ e}^{\sigma _\mathrm{v} r_\mathrm{{vD}} }-\text{ e}^{-\sigma _\mathrm{v} r_\mathrm{{vD}} }}{\text{ e}^{\sigma _\mathrm{v} }-\text{ e}^{-\sigma _\mathrm{v} }} \end{aligned}$$

(63)

Taking the derivative of Eq. 63 with respect to $r_\mathrm{vD}$

$$\begin{aligned} \frac{\text{ d}\overline{p} _\mathrm{{vD}} }{\text{ d}r_\mathrm{{vD}} }\left| {_{r_\mathrm{vD} =1}} \right.=[\sigma _\mathrm{v} \text{ cth}(\sigma _\mathrm{v} )-1]\bar{{p}}_\mathrm{{mD}} \end{aligned}$$

(64)

where hyperbolic cotangent function $\text{ cth}(\sigma _\mathrm{v} )={(\text{ e}^{\sigma _\mathrm{v} }+\text{ e}^{-\sigma _\mathrm{v} })}/{(\text{ e}^{\sigma _\mathrm{v} }-\text{ e}^{-\sigma _\mathrm{v} })}$.

Substitute Eq. 64 into the governing equation of matrix system Eq. 48

$$\begin{aligned}&\frac{\text{ d}^{2}\overline{p} _\mathrm{{mD}} }{\text{ d}r_\mathrm{{mD}} ^{2}}+\frac{1}{r_\mathrm{{mD}} }\frac{\text{ d}\overline{p} _\mathrm{{mD}} }{\text{ d}r_\mathrm{{mD}} }-f(z)\overline{p} _\mathrm{{mD}} =0\end{aligned}$$

(65)

$$\begin{aligned}&f(z)=\frac{1}{5}\lambda _\mathrm{{vm}} \text{ e}^{-2S}[\sigma _\mathrm{v} \text{ cth}(\sigma _\mathrm{v} )-1]+z\omega _\mathrm{m} \text{ e}^{-2S} \end{aligned}$$

(66)

The general solution of Eq. 65 is

$$\begin{aligned} \overline{p} _\mathrm{{mD}} =A_\mathrm{m} \text{ I}_0 (r_\mathrm{{mD}} \sqrt{f(z)})+B_\mathrm{m} \text{ K}_0 (r_\mathrm{{mD}} \sqrt{f(z)}) \end{aligned}$$

(67)

At the wall of the effective wellbore, $r_\mathrm{m}=r_\mathrm{w}\text{ e}^{-S},\,r_\mathrm{mD}=1,\, p_\mathrm{m}=p_\mathrm{w},\,p_\mathrm{mD}=p_\mathrm{wD}$, so Eq. 67 becomes

$$\begin{aligned} {I}_0 (\sqrt{f(z)})A_\mathrm{m} +\text{ K}_0 (\sqrt{f(z)})B_\mathrm{m} -\overline{p} _\mathrm{{wD}} =0 \end{aligned}$$

(68)

Substitute the general solution Eq. 67 into the constant rate production condition Eq. 50:

$$\begin{aligned} \sqrt{f(z)}{I}_1 (\sqrt{f(z)})A_\mathrm{m} -\sqrt{f(z)}{K}_1 (\sqrt{f(z)})B_\mathrm{m} -zC_\mathrm{D} \overline{p} _\mathrm{{wD}} =-\frac{1}{z} \end{aligned}$$

(69)

Substitute the general solution Eq. 67 into the constant wellbore pressure production condition Eqs. 51–52:

$$\begin{aligned}&{I}_\mathrm{0} (\sqrt{f(z)})A_\mathrm{m} +{K}_\mathrm{0} (\sqrt{f(z)})B_\mathrm{m} =\frac{1}{z}\end{aligned}$$

(70)

$$\begin{aligned}&\sqrt{f(z)}{I}_1 (\sqrt{f(z)}{I}_\mathrm{1} (\sqrt{f(z)})A_\mathrm{m} -\sqrt{f(z)}{K}_1 (\sqrt{f(z)})B_\mathrm{m} +\overline{q} _\mathrm{D} =0 \end{aligned}$$

(71)

Substitute the general solution Eq. 67 into the external boundary conditions Eqs. 55–57:

$$\begin{aligned}&\mathop {\lim }\limits _{_{{r_\mathrm{mD}} \rightarrow \infty }} {I}_0 (r_\mathrm{{mD}} \sqrt{f(z)})A_\mathrm{m} +\mathop {\lim }\limits _{_{{r_\mathrm{mD}} \rightarrow \infty }} {K}_0 (r_\mathrm{{mD}} \sqrt{f(z)})B_\mathrm{m} =0\end{aligned}$$

(72)

$$\begin{aligned}&{I}_0 (R_\mathrm{{eD}} \sqrt{f(z)})A_\mathrm{m} +{K}_0 (R_\mathrm{{eD}} \sqrt{f(z)})B_\mathrm{m} =0\end{aligned}$$

(73)

$$\begin{aligned}&{I}_1 (R_\mathrm{{eD}} \sqrt{f(z)})A_\mathrm{m} -{K}_1 (R_\mathrm{{eD}} \sqrt{f(z)})B_\mathrm{m} =0 \end{aligned}$$

(74)

For constant rate production, from Eqs. 68–69 and Eqs. 72, 73, or 74, there are three unknown numbers ($A_\mathrm{m},\,B_\mathrm{m},\,\overline{p} _\mathrm{{wD}}$) and three equations, the solutions for the model in Laplace space can be easily obtained using linear algebra, such as a Gauss–Jordan reduction. For constant wellbore pressure production, from the Eqs. 70–71 and 74, there are three unknown numbers ($A_\mathrm{m},\,B_\mathrm{m},\,\overline{q} _\mathrm{D}$) and three equations, the solutions for the model in Laplace space can be similarly obtained.

In real space, the dimensionless bottomhole pressure ($p_\mathrm{wD}$) and the derivative ($\text{ d}p_\mathrm{wD}/\text{ d}t_\mathrm{D}$) can be obtained using Stehfest numerical inversion (Stehfest 1970) to convert $\overline{p} _\mathrm{{WD}} (u$) back to $p_\mathrm{{WD}} (t_\mathrm{D}$):

$$\begin{aligned} p_\mathrm{WD} (t_\mathrm{D} )=u\cdot \sum _{i=1}^{N} {V_i } \cdot \overline{p} _\mathrm{{WD}} (i\cdot u) \end{aligned}$$

(75)

where the transform parameter $u$ is defined in calculations as

$$\begin{aligned} u=\ln (2)/t \end{aligned}$$

(76)

The weighting coefficients $V_{i}$ are given by

$$\begin{aligned} V_i =(-1)^{i+N/2}\cdot \sum _{k=\left[\frac{i+1}{2}\right]}^{\min (i,N/2)} {\frac{k^{N/2}(2k)!}{(N/2-k)!k!(k-1)!(i-k)!(2k-i)!}}\nonumber \\ \end{aligned}$$

(77)

where $N$ must be an even number and $i$ and $k$ are integers.

According to Stehfest (1970), accuracy can be improved by increasing $N$. However, the value of $N$ is limited by roundoff error. Double-precision results can be obtained by using “$N=18$” (Moench and Ogata 1981).

The derivative function in Laplace space is calculated by

$$\begin{aligned}&L\left[\frac{\text{ d}p_\mathrm{{WD}} (t_\mathrm{D} )}{\text{ d}t_\mathrm{D} }\right]=u\cdot L[p_\mathrm{{WD}} (t_\mathrm{D} )]-p_\mathrm{{WD}} (t_\mathrm{D} )\left| {_\mathrm{t_\mathrm{D} =0} } \right.=u\cdot \overline{p} _\mathrm{{WD}}\end{aligned}$$

(78)

$$\begin{aligned}&\frac{\text{ d}p_\mathrm{{WD}} (t_\mathrm{D} )}{\text{ d}t_\mathrm{D} }={p}^{\prime }_\mathrm{{WD}} =u^{2}\cdot \sum _\mathrm{i=1}^N {V_i } \cdot \overline{p} _\mathrm{{WD}} (i\cdot u) \end{aligned}$$

(79)

The numerical values for $p_\mathrm{{WD}} (t_\mathrm{D} /C_\mathrm{D}$) and (${p}^{\prime }_\mathrm{{WD}} \cdot t_\mathrm{D} /C_\mathrm{D}$) can be calculated by creating known values of $t_\mathrm{D} /C_\mathrm{D}$ and substituting them into Eqs. 75–79. This enables the standard bi-logarithmic type curves of well test analysis of $p_\mathrm{{WD}} (t_\mathrm{D} /C_\mathrm{D}$) and (${p}^{\prime }_\mathrm{{WD}} \cdot t_\mathrm{D} /C_\mathrm{D}$) vs. $t_\mathrm{D} /C_\mathrm{D}$ (Nie et al. 2012c) to be easily plotted. The standard bi-logarithmic type curves of rate decline analysis (Blasingame et al. 1991; Doublet and Blasingame 1994; Marhaendrajana and Blasingame 2001) for $q_\mathrm{Dd} ,\,q_\mathrm{Ddi}$ and $q^{\prime }_\mathrm{Ddi}$ vs. $t_\mathrm{Dd}$ is similarly obtained.

4 Type Curves

4.1 Type Curves of Pressure-Transient Analysis

4.1.1 Basic Concept About Type Curves

Well testing has been used for decades to determine essential formation properties and to assess wellbore conditions. In addition, type curves plotted according to flow models have been used for well test analyses (Bourdet 2003; Chaudhry 2004; Ezekwe 2010; Onur and Reynolds 1988). Ezekwe (2010) described type curves as graphic plots of theoretical solutions to flow equations under specific initial conditions, boundary conditions and geometry of the interpretation model representing a reservoir–well system; type curves also provide a continuous solution that incorporates the effects of the various flow stages that control pressure behavior. The pressure profiles usually look identical, while the derivative curves for each situation are unique. Pressure derivative curves represent the shapes that can occur with different reservoir properties and geometries. If a constant rate of well production is initiated, pressure transients will radiate from the well and travel toward the external boundaries of the reservoir. The pressure transients will go through several different processes as they travel. These processes are called flow stages or flow regimes. The flow stages depend on elapsed time and distance from the wellbore, and have characteristic pressure distributions in the reservoir. Type curves are a plot of pressure transients and rate transients against elapsed time, and are used to recognize flow stages.

Since type curves reflect the properties of a reservoir, different reservoirs have different type curves. One objective of flow model research is to calculate type curves for a variety of reservoirs and observe the theoretical flow characteristics calculated from these curves. While, the objective of well test analyses is to learn about the flow characteristics of a reservoir by observing the real type curves obtained through well-testing (see Figs. 13,  14) and to obtain property parameters by comparing of real curves with theoretical curves. Of course, well test analysis is not an omnipotent method that can generate information about all the properties of a reservoir. For example, the well test analysis using the flow model presented in this article can only obtain the following parameters: wellbore storage coefficient ($C_\mathrm{s}$), skin factor ($S$), effective permeability of matrix system ($k_\mathrm{m}$), storage capacitance coefficients of matrix and vug systems $(\omega _\mathrm{m}$ and $\omega _\mathrm{v})$, interporosity flow factor of fluid flow from vug system to matrix system ($\lambda _\mathrm{vm}$), and the ratio of the vug permeability to the quadratic radius of vug ($k_\mathrm{v}/r_\mathrm{1}^{2}$). Although the vug permeability cannot be obtained directly from well test analyses, it can be indirectly calculated. If the average radius of vugs is ascertained by measuring directly the diameter of vugs from rock cores, calculating the diameter of vugs from the pictures of well-imaging logging, scanning electron microscope, or CT techniques (Computed Tomography), the average permeability of a vug system ($k_\mathrm{v}$) can be calculated by substituting the radius ($r_\mathrm{1}$) into the ratio ($k_\mathrm{v}/r_\mathrm{1}^{2}$).

4.1.2 Flow Stage Recognition

Figures 5, 6, 7, 8, 9, 10, 11 contain the type curves of pressure-transient analysis for a porous–vuggy carbonate reservoir. Figure 5 shows the complete transient flow process of well production at a constant rate in a porous–vuggy carbonate reservoir under different external boundaries. It can be divided into six flow stages:

Fig. 5

Constant rate production type curves under different boundaries

Fig. 6

Constant rate production type curves based on ($t_\mathrm{D} /C_\mathrm{D}$) affected by $C_\mathrm{D}$

Fig. 7

Constant rate production type curves based on $t_\mathrm{D}$ affected by $C_\mathrm{D}$

Fig. 8

Constant rate production type curves affected by $S$

Fig. 9

Constant rate production type curves affected by $\lambda _\mathrm{vm}$

Fig. 10

Constant rate production type curves affected by $\omega _\mathrm{m}$

Fig. 11

Constant rate production type curves affected by $R_\mathrm{eD}$

• Stage I Pure wellbore storage stage. In this stage, the production is dominated by the fluid initially stored in the wellbore and formation fluid does not start flowing. Curves for pressure and derivative of pressure are on an upward sloping line with a slope of 1. In this stage, the type curves are controlled by dimensionless wellbore storage coefficient ($C_\mathrm{D}$).

• Stage II Skin effect stage. The formation fluid near the wellbore (a damaged zone probably caused by drilling and completion operations) participates in flowing. The shape of the derivative curve looks like a “hump”. In this stage, the type curves are controlled by skin factor ($S$).

• Stage III Matrix system radial flow stage (first radial flow). Production is mainly dominated by a depletion of the matrix system. In theory, for radial flow, slope of the pressure derivative curves will be zero and the derivative curves will converge to the “0.5 line”, which means the logarithmic value of the pressure derivative is 0.5. However, because the influence of interporosity flow, the pressure derivative curves in the radial flow stage shown in Fig. 5 is not horizontal and slightly inclined. After the wellbore storage and skin effect stages, the fluid in the matrix system radially flows into the wellbore and the pressure of the matrix system drops, the interporosity flow of fluid in vugs into the matrix would immediately follow because the vugs are embedded in the matrix. Therefore, the duration of the matrix system radial flow stage is very short and hard to observe, just like the real well-testing curves (see Figs. 17, 18).

• Stage IV Interporosity flow stage of vug system to matrix system. Production is dominated by the depletion of both the matrix and vug systems. The pressure derivative curve is concave, which is a reflection of the interporosity flow of vug to matrix. The dimensionless pressure (including the term ($p_\mathrm{i}-p_\mathrm{w})$) curve directly reflects wellbore pressure depletion, and the dimensionless pressure derivative curve directly reflects rate of wellbore pressure depletion. Physical processes that occur during this interporosity flow stage are: wellbore pressure depletion is retarded due to fluid supplement from vug to matrix system, which makes the rate of wellbore pressure depletion decrease and the value of pressure derivative decrease accordingly; however, the fluid supplement from the vug to matrix system is retarded with the pressure depletion of the vug system. When the rate of fluid supplement cannot support the rate of pressure depletion of the matrix system, the rate of wellbore pressure depletion increases and the value of the pressure derivative increases accordingly. Therefore, the interporosity flow stage can be divided into two flow periods, the decreasing period of the rate of wellbore pressure depletion and the increasing period of the rate of wellbore pressure depletion. In the first period the wellbore pressure derivative curve goes down, while in the second period the wellbore pressure derivative curve goes up, causing the wellbore pressure derivative curve to be concave, instead of convex. The concavity reflects the change in the rate of wellbore pressure depletion caused by the interporosity of fluid from vug to matrix system and shows that the porous–vuggy reservoir is a dual porosity system. A fracture–matrix dual-porosity reservoir model may produce a similar concavity (Nie et al. 2012a) because the type curves of the different models are calculated by using similar dimensionless parameters; however, the real curves of well-testing for different dual-porosity reservoirs differ greatly because the value of the parameters with units differs greatly. For example, the matrix permeability of a matrix–vug reservoir is much less than the fracture permeability of a matrix–fracture reservoir. The concave shape of our example well differs greatly from that of the example well in Nie et al. (2012a). In this stage, the type curves are controlled by the interporosity flow factor of vug system to matrix system ($\lambda _\mathrm{vm}$) and fluid storage capacitance coefficients ($\omega _\mathrm{m}$ and $\omega _\mathrm{v}$).

• Stage V Whole radial flow stage of matrix system and vug system (second radial flow). The production is dominated by the depletion of both matrix and vug systems. The interporosity flow of vug to matrix has stopped. The pressures between matrix and vug system have gone up to a state of dynamic balance and the depletion of matrix and vug systems are concurrent and synchronous. The derivative curve also converges to the “0.5 line”.

• Stage VI External boundary response stage. The pressure wave has spread to the external boundary. Different external boundaries yield different curve shapes. For a constant pressure boundary: pressure depletion of the reservoir caused by well production is suddenly supplemented, which makes the rate of wellbore pressure depletion swiftly decrease and the value of the pressure derivative decrease accordingly; the transient flow would ultimately become a steady-state flow when the wellbore pressure becomes a constant; the pressure derivative curve goes down and the pressure curve becomes horizontal during the steady-state flow period. For a closed boundary: pressure depletion of the reservoir without the peripheral energy supplement is aggravated, which makes the rate of wellbore pressure depletion swiftly increase and the value of the pressure derivative increase accordingly; the transient flow would ultimately become pseudo-steady-state flow when the wellbore pressure derivative becomes a constant; the pressure curve and its derivative curve tilt up and converge to a straight line with unit slope in a pseudo-steady-state flow period. In this stage, the type curves are controlled by the dimensionless radius of external boundary ($R_\mathrm{eD}$).

Please note that the duration of the matrix system radial flow stage and whole radial flow stage are controlled indirectly by the parameters $\lambda _\mathrm{vm}$ and $R_\mathrm{eD}$. Parameter sensitivity analyses will exhibit how each particular stage is controlled by different parameters.

4.1.3 Parameter Sensitivity Analysis

Type curves are sensitive to model parameters. Different values of a parameter will cause the curve to shift of at various stages.

Figure 6 shows the sensitivity of type curves to the dimensionless wellbore storage coefficient ($C_\mathrm{D}$). It seems that $C_\mathrm{D}$ influences the interporosity flow stage heavily. In fact, it only influences the early wellbore storage stage because the axis of abscissas is ($t_\mathrm{D} /C_\mathrm{D}$). ($t_\mathrm{D} /C_\mathrm{D}$) is used to ensure that the type curves based on ($t_\mathrm{D} /C_\mathrm{D}$) will cross the origin of coordinates ($10^{-2},\, 10^{-2}$). In order to observe how the wellbore storage coefficient influences the early wellbore storage stage, we plotted the type curves based on ($t_\mathrm{D}$) by setting $C_\mathrm{D}$ as 1 and 10, see Fig. 7. The starting time of well production is zero, and, for “$C_\mathrm{D}=1$” and “$C_\mathrm{D}=10$”, the starting times of skin effect are $t_\mathrm{1}$ and ${t}^{\prime }_\mathrm{1}$, respectively, the starting times of interporosity flow are $t_\mathrm{2}$ and ${t}^{\prime }_\mathrm{2}$, respectively, and the starting times of whole radial flow are $t_\mathrm{3}$ and ${t}^{\prime }_\mathrm{3}$, respectively. Therefore, for “$C_\mathrm{D}=1$” and “$C_\mathrm{D}=10$”, the durations of the pure wellbore storage effect are $t_\mathrm{1}$ and ${t}^{\prime }_\mathrm{1}$, respectively, the duration of the skin effect and early radial flow stages are $(t_\mathrm{2} -t_\mathrm{1}$) and $({t}^{\prime }_\mathrm{2} -{t}^{\prime }_\mathrm{1}$), respectively, and the duration of the interporosity flow stage are $(t_\mathrm{3} -t_\mathrm{2}$) and $({t}^{\prime }_\mathrm{3} -{t}^{\prime }_\mathrm{2}$), respectively. The following relationships can be obtained:

$$\begin{aligned} t_1 <{t}^{\prime }_1 ,(t_\mathrm{2} -t_\mathrm{1} )=({t}^{\prime }_\mathrm{2} -{t}^{\prime }_\mathrm{1} ),(t_\mathrm{3} -t_\mathrm{2} )=({t}^{\prime }_\mathrm{3} -{t}^{\prime }_\mathrm{2} ) \end{aligned}$$

(80)

Equation 8 shows that as $C_\mathrm{D}$ increases, the duration of the pure wellbore storage effect is prolonged and the duration of the other flow stages are not altered. In a word, the parameter $C_\mathrm{D}$ directly influences the duration of the pure wellbore storage stage and indirectly influences the start time of the other flow stages.

Figure 8 shows the sensitivity of type curves to skin factor ($S$). Skin factor influences pressure transients positively. Since a higher dimensionless pressure curve means a greater pressure drop and skin factor is the reflection of an additional pressure drop near a wellbore, a larger $S$ leads to a higher value for the dimensionless pressure curve.

Figure 9 shows the sensitivity of type curves to the interporosity flow factor of vug to matrix system ($\lambda _\mathrm{vm}$). According to the definition, $\lambda _\mathrm{{vm}} =1.5 \left(\frac{r_\mathrm{w} }{r_1 }\right)^{2}\cdot \frac{k_\mathrm{v} }{k_\mathrm{m} }$, vug permeability, matrix permeability, and the radius of spherical vug ($r_\mathrm{1}$) are contained in $\lambda _\mathrm{vm}$. Therefore, we analyzed the influence of $\lambda _\mathrm{vm}$ upon type curves and did not analyze the influence of $r_\mathrm{1},\,k_\mathrm{v}$ and $k_\mathrm{m}$. $\lambda _\mathrm{vm}$ represents the start time of interporosity flow of a vug system to a matrix system. As $\lambda _\mathrm{vm}$ increases, start time of interporosity begins earleir, finish time of matrix radial flow ends earlier, and start time of whole radial flow begins later.

According to the definitions of the two fluid-storage capacitance coefficients ($\omega _\mathrm{m}$ and $\omega _\mathrm{v}$), they are related such that $\omega _\mathrm{m} +\omega _\mathrm{v} =1$; therefore we only analyze the influence of $\omega _\mathrm{m}$. Figure 10 shows the sensitivity of type curves to fluid-storage capacitance coefficients of matrix system ($\omega _\mathrm{m}$). As $\omega _\mathrm{v}$ decreases, concavity deepens and broadens, and the duration of interporosity flow extends.

The parameter $\lambda _\mathrm{vm}$ influences the start time of interporosity flow stage and the parameter $\omega _\mathrm{m}$ influences the duration of interporosity flow stage.

Figure 11 shows the sensitivity of type curves to the dimensionless radius of external boundary ($R_\mathrm{eD}$). As $R_\mathrm{eD}$ increases, start time of the external boundary response moves forward and the duration of whole radial flow extends.

4.2 Type Curves of Rate-Transient Analysis

Figures (12–14) show the type curve characteristics associated with a declining rate response for well production in a porous–vuggy carbonate reservoir. The type curve characteristics display the typical response pattern found in fluid flow for well production at constant wellbore pressure. Flow stages are also recognized by their distinct type curves.

Fig. 12

Constant wellbore pressure production type curves under closed boundary

Fig. 13

Constant wellbore pressure production type curves affected by $\lambda _\mathrm{vm}$

Fig. 14

Constant wellbore pressure production type curves affected by $\omega _\mathrm{m}$

Four flow stages can be recognized in Fig. 12:

• Stage I Radial flow stage of the matrix system.

• Stage II Interporosity flow stage of vug to matrix system. The curve of dimensionless rate integral derivative function is concave, which reflects interporosity flow from vug to matrix.

• Stage III Whole radial flow stage of matrix and vug system. The interporosity flow of vug to matrix has stopped, and pressures between matrix and vug have gone up to a state of dynamic balance. The curves of decline curve dimensionless rate, dimensionless rate integral function and dimensionless rate integral derivative function are on a downward sloping line.

• Stage IV External-boundary response stage. The curves of dimensionless rate and its derivative curves converge to a straight line with a negative unit slope. The transient flow would ultimately enter into pseudo-steady-state flow.

Type curves that are affected by the two main parameters ($\lambda _\mathrm{vm}$ and $\omega _\mathrm{m}$) are plotted. It can be seen that $\lambda _\mathrm{vm}$ and $\omega _\mathrm{m}$ have different influences on rate transients. A greater $\lambda _\mathrm{vm}$ leads to a higher location of “concavity” and a greater $\omega _\mathrm{m}$ leads to a shallower “concavity”.

5 Comparisons with Earlier Numerical Studies

Earlier numerical models were well studied to simulate flow and transport processes in carbonate reservoirs (Corbett et al. 2010, 2012; Wu et al. 2004, 2011; Wu and Pruess 1988). The first step of the numerical methodology is building a conceptual geological model representative of a certain carbonate characteristic (e.g., fractures or vuggy matrix) from outcrop data, rock core data, and wireline logs. The second step is establishing a set of partial differential equations in a 3-D system according to the conceptual geological model. The third step is simulating well production for a wide range of possible parameters using finite difference or finite-volume simulator. The fourth step is analyzing the numerical pressure transients. The last is matching the numerical results with field data to estimate property parameters. Wu et al. (2004, 2007, 2011)) examined their numerical solutions using analytical solutions of single-phase flow by ignoring wellbore storage and skin effects (note that their numerical models did not consider the wellbore storage and skin effects). Numerical method can be used to study both multiple- and single-phase flows, however, analytical method for unsaturated reservoirs is more convenient than numerical method in real applications.

The conceptual geological models for carbonate reservoirs include dual-, triple-, and quadruple-continuum models. One type of dual-continuum model assumes that cubic matrix blocks are embedded in a network of interconnected fractures (Warren and Root 1963), and considers global flow and transport in the formation occurring only through the fracture system, and treats matrix blocks as spatially distributed sinks or sources to the fracture system and the interporosity flow between the fracture and matrix systems as a pseudo-steady state. This type of dual-continuum model only discretizes the grid of fracture system. The other type of dual-continuum model incorporates additional matrix–matrix interactions and considers global flow occurring not only between fractures but also between cubic matrix blocks. This type of dual-continuum model discretizes the grid of both fracture and matrix systems. One type of triple-continuum model, by introducing small fractures as an additional continuum, considers global flow occurring not only between large fractures but also between small fractures and employs pseudo-steady-state interporosity flow assumption between cubic matrix blocks and fractures. This type of triple-continuum model needs to discretize the grid of both large fracture and small fracture systems. The other type of triple-continuum model, by introducing vugs as an additional continuum, considers global flow occurring not only between fractures but also between vugs and employs pseudo-steady-state interporosity flow assumption between matrix and vugs. This type of triple-continuum model need to discretize the grid of both vug and fracture systems. Note that, this additional continuum of vug system assumes all the vugs are connected and deals with the isolated vugs as additional sinks or sources of the matrix system. Quadruple-continuum models introduce vugs and small fractures, as additional continua between large fracture and matrix systems. These quadruple-continuum models still use the pseudo-steady-state interporosity flow assumption between different continua. Carbonate reservoirs could be different combination of matrix (M), large fractures (F), small fractures (f), and vugs (V). Dual-continuum models can be used to evaluate interactions along F–M connections. Triple-continuum models can be used to evaluate interactions along F–f–M or F–V–M connections. Quadruple-continuum models can be used to evaluate interactions along F–f–V–M connections. Different conceptual geological models can be used to evaluate different combinations and produce different “Geotype” curves (Corbett et al. 2012).

Based on rock core data and wireline logs, the conceptual geological model of M–V connections is firstly proposed in this paper. The provided semi-analytical method in this paper is the special study on the conceptual geological model of porous–vuggy carbonate reservoirs. It is inconvenient to compare our solutions with the earlier numerical solutions because of different conceptual geological models. The differences of our conceptual model with earlier conceptual models are: (1) fractures in earlier conceptual models are considered as a necessary continuum, in contrast, no fractures are involved in our conceptual model; (2) vugs in earlier conceptual models are deemed as a continuum, in contrast, vugs in our conceptual model are assumed as being uniformly dispersed, instead of being connected; and (3) the interporosity flow between vugs and matrix is considered as being unsteady in our conceptual model, instead of pseudo-steady. The derived type curves in this paper would be a family of “Geotype” curves for carbonate reservoirs. Our conceptual model can be used to evaluate interactions along M–V connections. In the following we will validate our conceptual model using real field data.

6 Field Data Interpretation

There is pressure buildup during well testing of the porous–vuggy carbonate reservoir in the Tahe oilfield of China (see Fig. 15). The curve of wellbore pressure ($p_\mathrm{ws}$) with shutting-down time ($\Delta t$) is shown in Fig. 16. Formation and well parameters are shown in Table 1.

Fig. 15

Rock core cross-section at example well

Fig. 16

Buildup pressure curve with shutting-down time

Table 1 Formation and well parameters

When matching test data against type curves, we plotted the bi-logarithmic testing curves of the wellbore pressure difference ($\Delta p$) vs. the shutting-down time ($\Delta t$), see Fig. 17. The $\Delta p$ is the difference of wellbore pressure ($p_\mathrm{ws}$) at any time after shutting-down with wellbore pressure ($p_\mathrm{wsi}$) at initial shutting-down ($\Delta t=0$), that is, $\Delta p (\Delta \text{ t})=p_\mathrm{ws}(\Delta \text{ t}$) - $p_\mathrm{wsi}$. Figure 17 is the typical pressure response of a porous–vuggy carbonate reservoir. The pressure derivative curve is fluctuant. In fact, many well testing data are irregular (Carnegie et al. 2009; Setiawan et al. 2011; Wu et al. 2007) possibly due to unidentifiable noise. Therefore, we smoothed the pressure derivative curve using a General least-squares smoothing technique (McDonald et al. 2009; Nisbet et al. 2009). Savitzky and Golay (1964) researched the least-squares procedures usefulness for smoothing data. This technique has since been validated for use as a smoothing algorithm (Gorry 1991; Green et al. 1985) and is often used to smooth pressure derivatives derived from well-testing (Lane et al. 1991; Pirard and Bocock 1986; Von Schroeter et al. 2004). Figure 18 shows the smoothed derivative curve, which is concave. We made a well test interpretation using the researched model of this article. The matching curves of well test interpretation are shown in Fig. 18. Well test interpretation results are shown in Table 2. Four flow stages can be observed in Fig. 18: Stage I, pure wellbore storage stage; Stage II, skin effect stage; Stage III, interporosity flow stage of vug to matrix system, the pressure- derivative curve is concave; Stage IV, whole radial flow stage of matrix and vug system, the pressure derivative curve has a zero slope. Matrix system radial flow stage (the first radial flow stage) is not observed because there is an early interporosity time ($\lambda _\mathrm{vm}=5.2\times 10^{-5}$) according to interpretation results. The fluid storage capacitance coefficient of matrix system ($\omega _\mathrm{m}$) is 0.08 and the fluid storage capacitance coefficient of vug system ($\omega _\mathrm{v}$) is 0.92, which implies 92 % fluid reserves are stored in vugs. The wellbore storage coefficient ($C_\mathrm{s}$) is $4.1 \times 10^{-5 }\text{ m}^{3}$/Pa, which means the oil volume in wellbore would increase by $4.1 \times 10^{-5}\,\text{ m}^{3}$ if the wellbore pressure decreases 1 Pa. The effective permeability of matrix ($k_\mathrm{m}$) is $1.13 \times 10^{-14}\text{ m}^{2}$. However, the effective permeability of vug ($k_\mathrm{v}$) and the average radius of spherical vugs ($r_\mathrm{1}$) cannot be ascertained by using well test analysis. We can only calculate the ratio of $k_\mathrm{v}$ to ($r_\mathrm{1})^{2}$ by substituting $k_\mathrm{m}$ and $r_\mathrm{w}$ into the definition of $\lambda _\mathrm{vm}$, with a resulting ratio of $6.95\times 10^{-18}$. The skin factor ($S$) is 0.38, which indicates slight formation damage near the wellbore. The formation damage could be removed by using acidizing operation. In sum, the matching effect is desirable and the interpretation results are credible.

Fig. 17

Matching curves of well testing interpretations

Fig. 18

Matching curves of well testing interpretations

Table 2 Well test interpretation results

7 Conclusions

This research has established and solved the flow modeling of well test analysis for porous–vuggy carbonate reservoirs, and described the standard type curves. The following conclusions can be drawn:

• (1) Concave type curves are the typical response of fluid flow in porous–vuggy carbonate reservoirs and show a dual porosity flow behavior.

• (2) Type curves are dominated by interporosity flow factor, external-boundary conditions and fluid-storage capacitance coefficient. Each parameters has a different influence on type curves.

• (3) The flow process at constant rate production can be divided into six flow stages and flow process at constant wellbore pressure production can be divided into four flow stages.

• (4) Successful field data interpretation validated the provided model and demonstrated that this model could be applied to real case studies.