Abstract
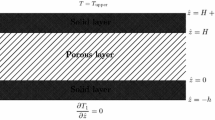
We consider convection in a uniform fluid-saturated porous layer which is bounded by conducting plates and heated from below. The primary aim is to determine the identity of the postcritical convection planform as a function of the thicknesses and conductivities of the bounding plates relative to that of the porous layer. This work complements and extends an early paper by Riahi (J Fluid Mech 129:153–171, 1983) who considered a situation where the porous layer is bounded by infinitely thick conducting media. We present regions in parameter space wherein convection in the form of rolls is unstable and within which cells with square planform form the preferred pattern.
Similar content being viewed by others
Abbreviations
- \({{\mathcal A}}\) :
-
Arbitrary constant
- A, B, C:
-
Roll amplitudes
- c1, c2, c3:
-
Constants in amplitude equations
- c.c.:
-
Complex conjugate
- C :
-
Heat capacity
- d :
-
Conductivity ratio
- f, g:
-
Functions in weakly nonlinear theory
- \({\mathcal F}\) :
-
Dispersion relation
- \({{\bar g}}\) :
-
Gravity
- h :
-
Height of sublayer
- k :
-
Disturbance wavenumber
- K :
-
Permeability
- p :
-
Pressure
- Ra :
-
Darcy–Rayleigh number
- t :
-
Time
- T :
-
Dimensional temperature
- u, v:
-
Horizontal velocities
- w :
-
Vertical velocity
- x, y:
-
Horizontal coordinates
- z :
-
Vertical coordinate
- α :
-
Disturbance wavenumber
- β :
-
Expansion coefficient
- γ :
-
Equal to d/δ
- δ :
-
Sublayer thickness ratio
- ΔT :
-
Reference temperature drop
- \({\epsilon}\) :
-
Small quantity
- θ :
-
Temperature
- Θ:
-
Disturbance temperature
- κ :
-
Thermal diffusivity ratio
- λ :
-
Function of Ra and α
- μ :
-
Dynamic viscosity
- ρ :
-
Density
- σ :
-
Function of Ra and α
- τ :
-
Slow time scale
- \({\phi}\) :
-
Relative orientation of two rolls
- Ω :
-
Coupling coefficient
- c:
-
Critical conditions
- f:
-
Fluid
- m :
-
Iteration number
- ref:
-
Reference value
- 1, 2, 3, …:
-
Context-dependent meanings
- \({\hat {}}\) :
-
Dimensional quantity
- \({\bar {}}\) :
-
Reduced disturbance
- ′:
-
Derivative with respect to z
References
Genç, G., Rees, D.A.S.: Onset of convection in horizontally partitioned porous layers. Phys. Fluids (2011)
Horton C.W., Rogers F.T.: Convection currents in a porous medium. J. Appl. Phys. 16, 367–370 (1945)
Lapwood E.R.: Convection of a fluid in a porous medium. Proc. Camb. Philos. Soc. 44, 508–521 (1948)
Masuoka T., Katsuhara T., Nakazono Y., Isozaki S.: Onset of convection and flow patterns in a porous layer of two different media. Heat Transf. Japan. Res. 7, 39–52 (1979)
McKibbin R., O’Sullivan M.J.: Onset of convection in a layered porous medium heated from below. J. Fluid Mech. 96, 375–393 (1980)
McKibbin R., O’Sullivan M.J.: Heat transfer in a layered porous medium heated from below. J. Fluid Mech. 111, 141–173 (1981)
McKibbin R., Tyvand P.A.: Thermal convection in a porous medium composed of alternating thick and thin layers. Int. J. Heat Mass Transf. 26, 761–780 (1983)
Mojtabi A., Rees D.A.S.: The effect of conducting bounding plates on the onset of Horton-Rogers-Lapwood convection. Int. J. Heat Mass Transf. 54(3), 293–301 (2011)
Newell A.C., Whitehead J.A.: Finite bandwidth, finite amplitude convection. J. Fluid Mech. 38, 279–303 (1969)
Nguyen-Quang T., Guichard F., Nguyen T.H.: Spatial pattern formation of motile microorganisms: from gravititactic bioconvection to protozoan culture dynamics. In: Vafai, K. (eds) Porous Media: Applications Biological Systems and Technology, pp. 535–567. CRC Press, Boca Raton (2010)
Nield D.A., Bejan A.: Convection in Porous Media, 3rd edn. Springer, New York (2006)
Pop I., Ingham D.B.: Convective Heat Transfer: Mathematical and Computational Modeling of Viscous Fluids and Porous Media. Pergamon, Oxford (2001)
Postelnicu, A.P.: Thermal stability of two fluid porous layers separated by a thermal barrier. In: Proceedings of the 3rd Baltic Heat Transfer Conference, Gdansk, Poland, pp. 443–450 (1999)
Rana R., Horne R.N., Cheng P.: Natural convection in a multi-layered geothermal reservoir. ASME J. Heat Transf. 101, 411–416 (1979)
Rees D.A.S.: The stability of Darcy–Bénard convection. In: Vafai, K. (eds) Handbook of Porous Media, pp. 521–558. Marcel Dekker, New York (2000)
Rees, D.A.S.: Stability analysis of Darcy-Bénard convection. In: Lecture notes for the Summer School on Porous Medium Flows, Neptun, Constanţa, Romania, 25–29 June 2001
Rees, D.A.S., Genç, G.: The onset of convection in porous layers with multiple horizontal partitions. Int. J. Heat Mass Transf. (2011) (to appear)
Rees D.A.S., Riley D.S.: The effects of boundary imperfections on convection in a saturated porous layer: non-resonant wavelength excitation. Proc. R. Soc. Lond. A 421, 303–339 (1989a)
Rees D.A.S., Riley D.S.: The effects of boundary imperfections on convection in a saturated porous layer: near-resonant wavelength excitation. J. Fluid Mech. 199, 133–154 (1989b)
Rees D.A.S., Riley D.S.: The three-dimensional stability of finite-amplitude convection in a layered porous medium heated from below. J. Fluid Mech. 211, 437–461 (1990)
Rees D.A.S., Selim A., Ennis-King J.P.: The instability of unsteady boundary layers in porous media. In: Vadász, P. (eds) Emerging Topics in Heat and Mass Transfer in Porous Media, pp. 85–110. Springer, New York (2008)
Riahi N.: Nonlinear convection in a porous layer with finite conducting boundaries. J. Fluid Mech. 129, 153–171 (1983)
Tyvand P.A.: Onset of Rayleigh-Bénard convection in porous bodies. In: Ingham, D.B., Pop, I. (eds) Transport Phenomena in Porous Media II, pp. 82–112. Elsevier, New York (2002)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Rees, D.A.S., Mojtabi, A. The Effect of Conducting Boundaries on Weakly Nonlinear Darcy–Bénard Convection. Transp Porous Med 88, 45–63 (2011). https://doi.org/10.1007/s11242-011-9722-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11242-011-9722-0