Minimizing cache usage with fixed-priority and earliest deadline first scheduling

Abstract

Cache partitioning is a technique to reduce interference among tasks running on the processors with shared caches. To make this technique effective, cache segments should be allocated to tasks that will benefit the most from having their data and instructions stored in the cache. The requests for cached data and instructions can be retrieved faster from the cache memory instead of fetching them from the main memory, thereby reducing overall execution time. The existing partitioning schemes for real-time systems divide the available cache among the tasks to guarantee their schedulability as the sole and primary optimization criterion. However, it is also preferable, particularly in systems with power constraints or mixed criticalities where low- and high-criticality workloads are executing alongside, to reduce the total cache usage for real-time tasks. Cache minimization as part of design space exploration can also help in achieving optimal system performance and resource utilization in embedded systems. In this paper, we develop optimization algorithms for cache partitioning that, besides ensuring schedulability, also minimize cache usage. We consider both preemptive and non-preemptive scheduling policies on single-processor systems with fixed- and dynamic-priority scheduling algorithms (Rate Monotonic (RM) and Earliest Deadline First (EDF), respectively). For preemptive scheduling, we formulate the problem as an integer quadratically constrained program and propose an efficient heuristic achieving near-optimal solutions. For non-preemptive scheduling, we combine linear and binary search techniques with different fixed-priority schedulability tests and Quick Processor-demand Analysis (QPA) for EDF. Our experiments based on synthetic task sets with parameters from real-world embedded applications show that the proposed heuristic: (i) achieves an average optimality gap of 0.79% within 0.1× run time of a mathematical programming solver and (ii) reduces average cache usage by 39.15% compared to existing cache partitioning approaches. Besides, we find that for large task sets with high utilization, non-preemptive scheduling can use less cache than preemptive to guarantee schedulability.

1 Introduction

Cache partitioning is a well-known technique to reduce inter-task interference among tasks running concurrently on processors with shared last-level caches. With cache partitioning in preemptively scheduled systems, the preempting task will not evict the cached memory blocks of the preempted task if both tasks use separate cache partitions. The technique can be implemented using specific hardware extensions (e.g., Intel’s Cache Allocation Technology (Intel 2015) or ARM’s Lockdown by master (Limited 2008)) (Gracioli et al. 2015) or in software by exploiting address mapping between main memory and cache lines (e.g., cache coloring) (Kim et al. 2013; Ye et al. 2014; Mancuso et al. 2013; Kloda et al. 2019). However, if the task’s working set does not fit into the task’s private cache partition, the task will see an increased number of cache misses and, consequently, increased execution time. To mitigate this problem, various optimization methods are employed to allocate cache partitions of sufficient size to satisfy tasks’ timing constraints.

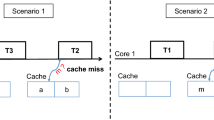
Cache partitioning optimization methods for real-time systems focus on finding the cache partitioning under the assumption that all available cache segments can be allocated to the tasks. Despite the wealth of the literature, reducing cache usage is not part of the optimization criteria. However, for a variety of reasons, unrestrained cache usage might be of concern to embedded engineers. Multilevel caches often consume about half of the processor energy (Hennessy and Patterson 2019; Zhang et al. 2003; Wang et al. 2011), and choosing the processors with a last-level cache size fitting the application requirements or appropriately selecting its size can largely reduce power dissipation. A smaller cache is more energy efficient and suitable for applications with a small working set, while a larger cache can benefit a wider range of applications but at the cost of increased energy consumption and potential energy waste for certain applications (Zhang et al. 2003). Moreover, by limiting the size of the cache allocated to hard real-time tasks, the remaining partitions can be used to improve the quality of service of the best-effort applications. In the context of partitioned multi-core systems where the task-to-core allocation is decided earlier in the design process, the cache partitioning problem boils down to minimizing the cache usage on each core while ensuring its schedulability (see Example 1.1). When a task-to-core allocation is not given, the cache minimization can be used as a sub-procedure in the task and cache co-allocation method (Xu et al. 2019; Sun et al. 2023b; Shen et al. 2022).

Fig. 1

Last-level cache dimensioning in a multicore mixed-criticality system

Example 1.1

Consider a multicore mixed-criticality system from Fig. 1 where three real-time operating systems (RTOS$_1$, RTOS$_2$, and RTOS$_3$) are running alongside a general purpose operating system (GPOS$_1$). Each operating system runs a set of tasks on a dedicated core. The tasks are statically allocated to the cores and do not migrate from one core to another due to certification restrictions (e.g., ensuring isolation among tasks with different criticality levels (Ernst and Di Natale 2016)) or interoperability issues (e.g., missing libraries). The processor has an L2 cache shared among all cores reducing the performance gap between the processor and main memory. Cache partitioning is used to avoid inter-core interference (i.e., tasks running on different cores access the shared cache simultaneously and evict their cached blocks) and intra-core interference (i.e., preempting task evicts the cached blocks from the preempted tasks on the same core). Finding a minimal size of cache partition for each real-time operating system is crucial for determining a maximal size of cache partition that can be allocated to the general-purpose operating system. The partitioning method can either assign cache partitions on a per-task basis (each task can have a private L2 cache partition, e.g., Kim et al. (2013)) or on a per-core basis (each core can have a private L2 cache partition but the tasks running on the same core cannot be assigned different sub-partitions, e.g., Kloda et al. (2019)). In the former case, we propose a cache minimization for single-core preemptive systems where each task can have a private cache partition, and in the latter case for non-preemptive systems where all tasks execute non-preemptively using the same cache partition without incurring cache-related preemption delays.

An apparent solution at hand for minimizing the cache usage is to invoke iteratively one of the standard cache partitioning methods by decreasing (increasing) cache size at each step until the system becomes unschedulable (schedulable). Several cache allocation methods are easily amenable to this approach or can terminate earlier when schedulability is guaranteed, and there is no need for further reduction in system utilization (e.g., gradient descent for minimizing system utilization (Kirk 1989) discussed in Sect. 5.1.5). In this research, we also report such methods and outline the required modifications. On the other hand, some methods use remaining cache segments to allow faster convergence (e.g., branch-and-bound (Altmeyer et al. 2016)), and specific approaches must be proposed. Moreover, restarting the search for each cache size without any knowledge of the previous iterations might not be particularly efficient, and certain proprieties of the schedulability tests, in particular, sustainability as suggested by Altmeyer et al. (2016), can be exploited to skip the redundant tests when going from one cache partition size to another.

The paper builds upon and extends the RTNS 2023 paper Minimizing Cache Usage for Real-time Systems (Sun et al. 2023a). Several new contributions are made compared to the original paper. First, we extend the original paper by adding preemptive and non-preemptive versions of EDF scheduling policy to all cache usage minimization techniques in Sect. 5. Second, we integrate the Quick Processor-demand Analysis (QPA) into cache minimization methods by leveraging the sustainability of the test in Sect. 5.2.2. Third, we evaluate the proposed techniques using a wider range of parameters and different task set generation methods in Sect. 6.

2 Cache partitioning methods

Cache partitioning is a technique to assign portions of the cache to either tasks or cores to reduce interference (both intra- or inter-core) and increase the predictability of the system. There are two ways of performing cache partitioning in modern processors: (i) index-based, where partitions are formed by an aggregation of associative sets in the cache (thus, each set or a group of sets is individually assigned to a task or core and all memory allocation for this task or core is mapped to the assigned set(s)) and (ii) way-based, where partitions are formed by an aggregation of individual cache ways (the number of partitions, in this case, is limited by the number of ways (Gracioli et al. 2015)).

Index-based cache partitioning can be implemented using specific hardware extensions (Srikantaiah et al. 2008) or by software within the operating system by relying on specific processor features, such as virtual memory (to implement cache coloring for instance) (Kim et al. 2013; Kloda et al. 2019; Gracioli and Fröhlich 2013). Way-based techniques have the advantage of not demanding changes in the cache organization and isolating the requests for the different partitions from each other (no contention for cache ways in the cores). However, an important drawback of the way-based methods is the limited number of partitions and granularity of allocations due to the associativity of the cache (Gracioli et al. 2015). If one increases the associativity (to have more cache partitions), then the cache will have bigger access time and will demand more space to store the tags. Thus, increasing the associativity of a cache is not always feasible or efficient (Gracioli et al. 2015).

For index-based methods implemented in software, such as cache coloring, there are also two implementation choices: (i) to assign partitions to tasks, or (ii) to assign partitions to cores. The former demands the operating system to be aware of the cache partitions and somehow implement the assignment of partitions to tasks in its memory allocator (Gracioli and Fröhlich 2013). The latter is very useful, for instance, in hypervisor-based systems, where the hypervisor is responsible for assigning partitions to cores, despite the operating systems and the number of tasks running on top of it, providing cache partitioning to operating systems that do not support it (Gracioli et al. 2019).

We note that several changes to the microarchitecture have been proposed for more flexible cache partitioning in real-time and mixed-criticality systems (Lesage et al. 2012; Farshchi et al. 2018). Recently, several works have integrated cache partitioning with hypervisors and state-of-the-art platforms to provide memory isolation in mixed-critically applications (Gracioli et al. 2019; Cinque et al. 2022; Martins and Pinto 2023; Kloda et al. 2023).

3 Related work

We review different cache partitioning techniques and discuss how these techniques can be adapted to minimize cache usage in real-time systems. In single-core systems, the allocation of cache segments to different real-time tasks can reduce the preemption cost related to the cache (Kirk 1989; Kirk et al. 1991; Kim et al. 2013). In one of the earliest works, Kirk (1989) attempts to minimize task set utilization by allocating the cache segments to the tasks for which it would yield the highest decrease in the total utilization (i.e., gradient descent). Although the main objective is to minimize the utilization, the method can be easily modified for the purpose of cache minimization to stop when the schedulability is guaranteed by the utilization bound. Plazar et al. (2009) formulate an integer linear problem to allocate cache partitions minimizing the total length of tasks’ worst-case execution times that can be easily replaced with utilization. Zhang et al. (2022) also employ integer linear programming to minimize task set utilization through the allocation of different types of memories to tasks running on an embedded microcontroller. Sasinowski and Strosnider (1993) apply dynamic programming to minimize task set utilization. The algorithm adds tasks one by one, looking for the cache allocation minimizing the utilization of the current subset of tasks for every possible number of segments. This is done by combining the previous allocations with the allocations of the task that has just been added. (e.g., the minimal utilization for six tasks using two segments can be found as the sum of minimal utilizations of five previous tasks using, respectively, zero, one or two segments and the sixth task using two, one or zero segments, respectively). Considering every possible number of segments is not efficient for finding the minimal cache usage. However, the algorithm can be modified for this purpose as shown in Sect. 5.1.5. Bui et al. (2008) propose a genetic algorithm to solve the cache to task allocation problem for multiprocessor platforms. While all the methods mentioned above consider utilization as minimization criteria, Altmeyer et al. (2016) show that this might not be optimal with respect to schedulability. To find the optimal cache partitioning in this respect, the authors propose a branch-and-bound search combined with exact response time analysis. The proposed search technique cannot be directly applied to minimize the cache usage as at each step it tries to allocate all remaining cache segments in order to accelerate the convergence. We report the required modifications in Sect. 5.1.4.

An alternative approach to the problem of shared cache is to allow the tasks to use the entire cache and take into account the cache-related preemption delays (CRPD) (Altmeyer et al. 2012; Bastoni et al. 2010; Cavicchio et al. 2015). Minimizing the cache usage for such systems would involve a different optimization problem (Guo et al. 2020, 2017) where the inter-task cache interference can be characterized using the concept of an interference matrix. This approach may lead to better schedulability performance and more efficient cache usage. However, adding cache effect to schedulability analysis (Busquets-Mataix et al. 1996a, b; Tomiyama and Dutt 2000; Altmeyer and Burguière 2009; Altmeyer et al. 2011; Lunniss et al. 2013; Zhang et al. 2017, 2020) is not widely supported by the static program analysis tools. For instance, aiT WCET Analyzer, as of the time of writing, supports this feature only for three targets, namely, LEON2, e200, and e300 .¹

The reconfigurable cache architectures (Albonesi 1999; Yang et al. 2002, 2001) have been proposed to to reduce cache energy dissipation by adjusting cache capacity. During periods of low cache activity, a portion of cache ways or sets can be temporally disabled (during more cache-intensive periods the full cache capacity is restored). Chen et al. (2013) leverage such resizeable cache architecture and use cache partitioning to minimize the energy consumption of multiprocessors by solving a mixed integer linear programming problem.

While our work targets single-core, the cache-cognizant scheduling policies have been proposed for global multi-core systems. These policies dispatch a new task for execution if there is an idle processor and a sufficient number of cache segments (each task has a constant and predefined cache requirement) (Guan et al. 2009). Other cache-aware scheduling policies can promote the execution of tasks sharing a common working set (Calandrino and Anderson 2008) or preempt the tasks running on the remote cores using the same cache partition as the preempting task (Ward et al. 2013). For cache-agnostic global schedulers, Xiao et al. (2020) propose the schedulability analysis that accounts for cache interference. In multi-core systems, other shared resources, like memory bandwidth, may also degrade the system’s predictability. Several works propose coordinated cache and bandwidth co-allocation (Paolieri et al. 2011; Suzuki et al. 2013; Xu et al. 2019). Although we do not consider memory bandwidth in our analysis, different solutions can be used alongside to mitigate the interference due to DRAM bank sharing (e.g., bank partitioning (Pan and Mueller 2018; Cheng et al. 2017; Yun et al. 2014), software bandwidth regulators (Yun et al. 2013; Kritikakou et al. 2014; Zuepke et al. 2023) or segmented execution models (Pellizzoni et al. 2011; Durrieu et al. 2014)). If the task-to-core mapping is not given as assumed in this work, various task and cache co-allocation methods can be applied (Sun et al. 2023b; Guo et al. 2020; Xiao et al. 2022; Xu et al. 2019).

4 System model

We consider a system with n tasks scheduled by a preemptive or non-preemptive scheduler on a single-core platform. Additionally, under preemptive scheduling, each task can be assigned a private cache partition, and under the non-preemptive one, all the tasks share one single cache partition.

The cache has a size of S and is divided into m equally-sized separate segments. Each task can be assigned an arbitrary number of cache segments for its individual use. The set of segments owned by a task is its partition (Sasinowski and Strosnider 1993). Under the preemptive scheduling policy, the cache partitions cannot be shared among different tasks as it might lead to inter-task cache eviction resulting in cache-related preemption delays. This constraint is not necessary under non-preemptive policies, thereby we can consider that all tasks share all assigned segments. If task $\tau _i$ is assigned k cache segments, its worst-case execution time (WCET, i.e., the longest task execution time when running stand-alone) is given by $C_{i,k}$. Additionally, we denote by $C_{i,0}$ task $\tau _i$’s worst-case execution time with zero cache partition. We assume the monotonicity of the execution times with respect to the number of cache segments: by assigning more cache segments to the tasks, their worst-case execution time will not increase. We acknowledge that the execution times might not be necessarily monotonic, but the impact of these effects is limited (Altmeyer et al. 2016), and smaller partitions can be used instead. Several previous works consider similar memory models (Altmeyer et al. 2016; Bui et al. 2008; Kirk et al. 1991; Plazar et al. 2009).

Each task $\tau _i$ gives rise to a potentially infinite sequence of identical jobs (instances) released sporadically after the minimum inter-arrival time or period $T_i$. Each job released by task $\tau _i$ is characterized by a relative deadline $D_i$ assumed to be less than or equal to the task period (i.e., constrained deadlines): $D_i \le T_i$, and its worst-case execution time that depends on the number of cache segments assigned to the task. All the above parameters are positive integers. We will also use $U_{i,k}=C_{i,k}/T_i$ to refer to the task $\tau _i$ utilization when executing with k cache segments at its disposal. Additionally, we use $U=\sum _{i=1}^n{U_{i,0}}$ to denote the task set base utilization (i.e., the sum of task utilization without using cache).

In this work, we consider both fixed and dynamic priority scheduling algorithms. We select the Earliest Deadline First (EDF) scheduling (Liu and Layland 1973) as a dynamic priority scheduler. If the tasks are scheduled by a fixed-priority scheduler, we make the following assumptions. Each task is assigned a unique priority and tasks are indexed in decreasing priority order ($\tau _1$ has the highest priority and $\tau _n$ has the lowest priority). In this work, in particular, we assume Rate Monotonic (RM) (Liu and Layland 1973) assignment rule where task priorities are inversely proportional to task periods. The worst-case response time $R_i$ of task $\tau _i$ is defined as the longest time from the release of a job of the task until its completion. If the worst-case response time is less than or equal to the task $\tau _i$ deadline ($R_i \le D_i$), we say that task $\tau _i$ is schedulable. Likewise, we say that a task set is schedulable if all its tasks are schedulable.

5 Minimizing cache usage

We look for a cache-to-task assignment for which all n tasks are schedulable, and a minimal number of cache segments is used. We consider preemptive and non-preemptive scheduling under fixed-priority and EDF policies.

5.1 Preemptive scheduling

The cache partitioning problem for preemptive scheduling can be shown NP-hard by reduction to the knapsack problem (Bui et al. 2008). We propose four methods to minimize cache usage under preemptive scheduling. To verify the schedulability of fixed-priority systems, we will use utilization bound test (Liu and Layland 1973) with linear and response time analysis (RTA) (Joseph and Pandya 1986; Audsley et al. 1991) with pseudo-polynomial time complexity in the number of tasks. For EDF scheduling, we will use utilization bound test (Liu and Layland 1973) with linear and processor demand analysis (Baruah et al. 1990a, b) with exponential time complexity in the number of tasks.

5.1.1 Background on schedulability analysis

We present state-of-the-art techniques for verifying the schedulability of preemptive systems with implicit and constrained deadlines under fixed-priority and EDF scheduling policies.

In preemptive fixed-priority systems, a system running n tasks with implicit deadlines (i.e., $\forall \tau _i \in \tau : D_i=T_i$) is schedulable under RM policy if the task set utilization does not exceed the utilization bound $U(n)=n (2^{1/n} - 1)$ (Liu and Layland 1973). The exact schedulability condition, applicable also to constrained deadlines (i.e., $\forall \tau _i \in \tau : D_i \le T_i$) and other priority assignments, can be guaranteed using the RTA. In this approach, the worst-case response time $R_i$ of task $\tau _i$ can be computed by a fixed-point iteration of the following formula:

$$\begin{aligned} R_i = C_i + \sum _{j=1}^{i-1} \Bigg \lceil \dfrac{R_i}{T_j} \Bigg \rceil \cdot C_j, \end{aligned}$$

(1)

and can be solved using:

$$\begin{aligned} {\left\{ \begin{array}{ll} R_i^{(0)} &{}= C_{i} \\ R_i^{(\ell )} &{}= C_{i} + \sum _{j=1}^{i-1} \Bigg \lceil \dfrac{R_{i}^{(\ell -1)}}{T_j} \Bigg \rceil \cdot C_{j} \end{array}\right. } \end{aligned}$$

The upper bounds to the response time with lower time complexity have been proposed in (Davis and Burns 2008; Baruah 2011; Bini et al. 2015; Nguyen et al. 2015).

EDF-schedulability of task sets with implicit deadlines can be verified through the processor utilization factor. Every task set with total utilization $U \le 1$ is schedulable under EDF on a single processor (Liu and Layland 1973). Exact EDF-schedulability tests for task sets with constrained deadlines can be performed by processor demand analysis (Baruah et al. 1990a, b). It calculates the processor demand (i.e., the workload that must be executed in a given time interval) of a task set at every absolute deadline to check if the processor demand does not exceed available processor time. Processor demand h(t) of tasks $\tau$ in time interval of length $t>0$ is given by:

$$\begin{aligned} h(t) = \sum _{i=1}^n \max \left\{ 0, \left\lfloor \dfrac{t-D_i}{T_i} \right\rfloor + 1 \right\} C_i \end{aligned}$$

(2)

The task set $\tau$ is schedulable under preemptive EDF if and only if:

$$\begin{aligned} \forall t>0 \;: \; h(t) \, \le \, t \end{aligned}$$

(3)

The value of t can be bounded by:

$$\begin{aligned} L = {\left\{ \begin{array}{ll} \min \{L_a,L_b \} \; \text { if } \hspace{0.1cm} U < 1\\ L_b \hspace{1.5cm} \; \text { if } \hspace{0.1cm} U = 1. \end{array}\right. } \end{aligned}$$

(4)

where (Ripoll et al. 1996):

$$\begin{aligned} L_a&= \dfrac{\sum _{i=1}^n(T_i-D_i) \cdot U_i}{1-U} \end{aligned}$$

(5)

$$\begin{aligned} L_{b}&= \sum _{j=1}^{i} \Bigg \lceil \dfrac{L_{b}}{T_j} \Bigg \rceil \cdot C_{j} \end{aligned}$$

(6)

Condition (3) must hold for each t corresponding to a task absolute deadline in time interval [0, L]. In this paper, we use Quick Processor-demand Analysis (QPA) (Zhang et al. 2003) which is a fast and simple schedulability test for EDF that verifies the above condition. QPA iterates over the values of the processor demand function h(t) in intervals of decreasing length t. By doing so and using the fact that demand bound function h(t) is monotonically non-decreasing, it is possible to safely skip testing for some of the preceding deadlines (i.e., if $h(t_y) = t_x < t_y$ then all deadlines in time intervals of $[t_x,t_y]$ are met because for any $t_x \le t< t_y: h(t)<h(t_x)$). Such an approach, on average, effectively reduces the number of time instances that need to be examined.

5.1.2 Mathematical programming

For each task $\tau _i$ with $i=1,\ldots ,n$, we define a variable $C_i$ that represents its worst-case execution time. For each $k=0,1,\ldots ,m$, we introduce the binary variables $x_{i,k}$ which take on value 1 if and only if task $\tau _i$ is assigned k cache segments and 0 otherwise:

$$\begin{aligned} \forall i=1,\ldots ,n: \; C_i = \sum _{k=0}^{m} x_{i,k} \cdot C_{i,k} \end{aligned}$$

(7)

We additionally require that each task $\tau _i$ has exactly one variable $x_{i,k}$ for all $k=0,1,\ldots ,m$ that is equal to 1:

$$\begin{aligned} \forall i=1,\ldots ,n: \; \sum _{k=0}^{m} x_{i,k} = 1 \end{aligned}$$

(8)

Our objective function is to minimize the total cache usage:

$$\begin{aligned} {\textbf {minimize }} \sum _{i=1}^{n} \sum _{k=0}^{m} x_{i,k} \cdot k \end{aligned}$$

(9)

Now, we add constraints to ensure the system’s schedulability under FP and EDF.

FP systems. For FP systems, we ensure the schedulability using the response time analysis formulation proposed by Baruah and Ekberg (2021) and by Davare et al. (2007). We introduce ${\hat{R}}_i$ as the upper bound of task $\tau _i$’s worst-case response time (i.e., ${\hat{R}}_i \ge R_i$). All tasks are schedulable if we can find such values of ${\hat{R}}_i$ for all $i=1,\ldots ,n$ that are less than or equal to their respective deadlines:

$$\begin{aligned} \forall i=1,\ldots ,n: {\hat{R}}_i \le D_i \end{aligned}$$

(10)

The variable ${\hat{R}}_i$ upper bounds the task $\tau _i$’s worst-case response time if the following constraints are satisfied:

$$\begin{aligned} \forall i=1,\ldots ,n: \; C_i + \sum _{j=1}^{i-1} Z_{i,j} \cdot C_j \le {\hat{R}}_i \end{aligned}$$

(11)

where $Z_{i,j}$ is an integer that upper bounds the number of times a higher-priority task $\tau _j$ can preempt task $\tau _i$ during its worst-case response time, and thus, it must satisfy another constraint:

$$\begin{aligned} \forall i=1,\ldots ,n, j=1,\ldots ,i-1: \; Z_{i,j} \cdot T_j \ge {\hat{R}}_i \end{aligned}$$

(12)

Since Formula (11) is a quadratic constraint, the mathematical model for FP is an integer quadratically constrained program (IQCP), where the objective function is formulated by Formula (9), and the constraints are formulated by Formulas (7), (8) and (10-12).

EDF systems. For EDF system, we check whether the demand bound function h(t) is upper bounded by each time instance $t \in {\mathcal {M}}$:

$$\begin{aligned} \forall t \in {\mathcal {M}}: h(t) = \sum _{i=1}^n \max \left\{ 0, \left\lfloor \dfrac{t-D_i}{T_i} \right\rfloor + 1 \right\} C_i \le t, \end{aligned}$$

(13)

where (Hermant and George 2007)

$$\begin{aligned} {\mathcal {M}} = \bigcup _{i=1}^n \left\{ d_{i,j} = D_i + (j-1)\cdot T_i \; | \; 1 \le j \le \Bigg \lceil \dfrac{L-D_i}{T_i} \Bigg \rceil \right\} , \end{aligned}$$

(14)

$$L = \left\{ {\begin{array}{*{20}l} {\min \left\{ {L_{a} = \frac{{\sum\limits_{{i = 1}}^{n} {(T_{i} - D_{i} )} \cdot U_{{i,0}} }}{{1 - U}},H} \right\}\;{\text{ if }}U} \hfill & 1 \hfill \\ {H\;{\text{ if }}U = 1,} \hfill & {} \hfill \\ \end{array} } \right.{\text{ }}$$

and $H=lcm\{ \, T_i \, | \, 1 \le i \le n \}$ is the hyper-period of the task set.

Since all the constraints (i.e., (7), (8), and (13)) are linear functions, the mathematical model for EDF scheduling policy is an integer linear program (ILP).

5.1.3 Guided local search

The Guided local search (GLS) proposed in this paper is an iterative local search algorithm that utilizes problem-specific knowledge to guide the search direction and tabu search mechanism to avoid revisiting duplicate solutions. The procedures of GLS are outlined in Algorithm 1.

The search starts from an initial solution s, where all the tasks are allocated with the maximal number of segments m (line 1). If the initial solution is not schedulable, we stop the algorithm since the task set cannot be feasible with fewer cache segments (lines 2–3). Otherwise, we continue the algorithm to do the iterative search (lines 5-10). The iterative search is divided into two phases (i.e., decrease phase and increase phase) depending on the schedulability of the current solution. In the decrease phase (lines 5–6), the current solution s is schedulable, and in each step, one task is selected to decrease its cache partition. As a result, the solution moves from schedulable to unschedulable gradually. Once the solution crosses the schedulability boundary, the algorithm enters the increase phase (lines 7-8), where the current solution increases its cache partition, moving back to schedulable. Whenever the algorithm visits a new solution, its schedulability is checked, and the best-so-far solution $s^*$ will be updated by s if the latter uses less cache and is schedulable (line 9). The algorithm terminates when the number of schedulability checks $\eta$ reaches its upper limit $\eta _{max}$, which is a parameter defined by the user.

The schedulability of each solution is checked by the RTA for FP and QPA for EDF scheduling policy. Both tests are sustainable with respect to the worst-case execution times (i.e., schedulability is preserved when task parameters are “easier”) (Baruah and Chakraborty 2006). This means that the tests can be repeated only for tasks or intervals where a deadline miss has been detected. Hence, during the increase phase, the schedulability can be verified, in the case of RTA, only for the tasks that were unschedualble, and, in the case of QPA, for the time intervals that were unschedulable or have not been checked in the previous unschedulable solution. For instance, if the QPA test fails at time instant $t_x$, then if we increase cache partitions, we can resume the test from $t_x$ (i.e., it is not necessary to restart the test from L). Likewise, if the RTA fails when checking task $\tau _x$ (we assume that the tasks are checked in the decreasing priority order) and we increase cache partitions, we can skip the test for tasks $\tau _1,\ldots ,\tau _{x-1}$ and run the tests for the remaining tasks.

Algorithm 1

Guided local search

Now, we explain the details of the neighborhood structure, task selection rule, and the tabu mechanism used in the GLS.

• Neighborhood structure defines the solutions that can be reached by the current solution in one local search step. In the decrease (increase) phase of the GLS, the neighborhood structure is defined as the n solutions, in each of which one task is selected to decrease (increase) its cache partition to the least number of segments that increase (decreases) the task’s WCET by one step. For clarity, we illustrate this with an example. Suppose we have a task set consisting of two tasks pca ($\tau _1$) and stitch ($\tau _2$), whose benchmarked WCET profiles are given in Fig. 5. The current cache partition of the two tasks is $\{1024, 512\}$ KB, and we assume it to be schedulable. Then, the two neighborhood solutions obtained by decreasing the cache partitions of task $\tau _1$ and $\tau _2$ are $\{512, 512\}$ and $\{1024, 256\}$, respectively.

• Task selection rule determines which task is selected to decrease (increase) its cache partition and move the solution to the corresponding neighborhood. In the decrease (increase) phase, we select the task with the maximal (minimal) value of $\delta _i = {\downarrow }s_i / {\uparrow }U_i$ ($\delta _i = {\uparrow }s_i / {\downarrow }U_i$), where ${\downarrow }s_i$ (${\uparrow }s_i$) denotes task $\tau _i$’s cache decrease (increase) size and ${\uparrow }U_i$ (${\downarrow }U_i$) denotes the resulted utilization increase (decrease). The intuition behind it is to decrease the most (increase the least) cache usage with the least increase (most decrease) of total utilization. We use the same example task set as before to illustrate the task selection rule. Suppose the utilization increase of the two tasks are ${\uparrow }U_1{=}0.5$ and ${\uparrow }U_2{=}0.2$. The decrease of their cache partitions can be calculated as ${\downarrow }s_1{=}1024{-}512{=}512$ and ${\downarrow }s_2{=}512{-}256{=}256$. Then, we have $\delta _1 {=} 512{/}0.5{=}1024$ and $\delta _2 {=} 256{/}0.2{=}1280$. In this case, we will select task $\tau _2$ to decrease its cache partition since $\delta _2 > \delta _1$.

• Tabu mechanism is used to avoid the search visiting duplicated solutions. In the GLS, whenever a new solution is visited, we use a hash function to map the solution into an integer and save it to a visit history. Meanwhile, at each step of the local search, we move the current solution to a neighborhood only if it has not been visited in the history. If all the neighborhood solutions have already been visited, we restart the search by re-initializing the current solution as a random solution to escape the local optima.

5.1.4 Branch-and-bound

We propose a branch-and-bound (B &B) algorithm inspired by Altmeyer et al. (2016). Our branching strategy consists of allocating the cache to one task at a time. The initial node of the B &B generates all possible cache partitions for the first task, creating a branch for each partition. The algorithm then expands these branches by generating all possible cache partitions for the current task in the current node. A solution is considered valid when the cache partition of all tasks has been specified and the resulting task set is schedulable.

To reduce the number of partial solutions to be explored, we propose a pruning strategy that checks the schedulability of each partial solution under an optimistic assumption that each not yet specified task partition equals the current remaining cache segments. If the task set is not schedulable under this assumption, the current partial solution is pruned. Additionally, once a valid solution is found, we update the available cache to be one segment lower than the best-so-far cache usage $m^*$ to further improve the pruning efficiency. The algorithm terminates if an optimal solution has been found or an upper limit of schedulability test invocations $\eta _{max}$ has been reached.

The property of the sustainability (Burns and Baruah 2008) of the schedulability test together with the assumption that the execution times are monotonically non-increasing with the number of cache segments is exploited to reduce the number of test invocations (Altmeyer et al. 2016). If tasks from $\tau _1$ to $\tau _{i-1}$ are deemed schedulable under cache allocation $s^{(i-1)}$, then they will remain schedulable under any cache allocation with greater or equal cache partitions. Moreover, for fixed-priority scheduling, as tasks $\tau _1$-$\tau _{i-1}$ response times do not depend on lower-priority tasks $\tau _{i}$-$\tau _n$, tasks $\tau _1$-$\tau _{i-1}$ do not have to be tested when branching adds a new partition for task $\tau _i$. In the case of EDF scheduling, we use the same technique as in GLS to avoid unnecessary computation by resuming the schedulability test from $t_x$ (i.e., the time instant where the previous test fails) if the task set was previously unschedulable, and now each task has a larger or equal task allocation.

Algorithm 2

Cache usage minimization using B &B

The detailed procedures of the proposed B &B can be found in Algorithm 2. It defines a recursive function minimize_cache, which takes a partial solution $s^{(i-1)}$ containing the cache partitions of the first $i-1$ tasks as input and outputs the best-so-far solution $s^*$ with its cache usage $m^*$. Lines 2-3 check whether the upper limit of the schedulability test invocations has been reached. Lines 4-7 check if the current solution is a complete solution containing the cache partitioning of all tasks. For a complete solution, it checks its schedulability and updates the best-so-far cache usage if it is schedulable. In line 6, $\sum s^{(n)}$ computes the total number of cache segments used by solution $s^{(n)}$. Line 8 updates the number of remaining cache segments $m'$ according to the current best-so-far solution. Lines 9-10 implement the pruning strategy to discard the partial solution if it cannot be schedulable even with the optimistic assumption. Lines 11-15 implement the branching strategy starting from the first task with the least cache partition. The function next_corner_point($\tau _i$) gives the next cache partition size for which the worst-case execution time of task $\tau _i$ drops (see Example 5.1). In lines 17–18, the algorithm initializes $s^*, s^{(0)}$ and invokes the recursive function to minimize cache usage.

Fig. 2

Execution time vs cache size for sift-vga

Example 5.1

Fig. 2 shows the execution time of sift-vga program from the CortexSuite benchmarks (Thomas et al. 2014) (see Sect. 6.1 for more details) as a function of cache size partition size ranging from 0 to 512 KB with a step of 32 KB. The original curve (blue color) is comprised of 17 points. It can be easily seen that many of these points are redundant. Indeed, the execution time does not decrease continuously, but stays at a constant level until a certain point when it falls down as the cache partition becomes large enough to hold the next important data structure (Bienia et al. 2008). The corner points leading to a decrease in execution time are marked in red in Fig. 2.

5.1.5 Dynamic programming

We present a dynamic programming (DP) based on Sasinowski and Strosnider (1993) to minimize cache usage. Similar to Sasinowski and Strosnider (1993), we define $M_{i,k}$ as the minimum utilization of tasks $\tau _1,..., \tau _i$ if there are k cache segments available to them:

$$\begin{aligned} M_{i,k} = \min \limits _{0 \le s_i \le k}{\sum _{j=1}^i{U_{j,s_j}}} \end{aligned}$$

(15)

where $s_i$ denotes the number of cache segments allocated to task $\tau _i$. We also define $P_{i,k}$ to be the number of segments to allocate to $\tau _i$ to get $M_{i,k}$. The key observation in Sasinowski and Strosnider (1993) is the following recurrence relation:

$$\begin{aligned} M_{i,k} = \min \limits _{0 \le s_i \le k}{(U_{i,s_i} + M_{i-1, k-s_i})} \end{aligned}$$

(16)

which provides a simple way to compute $M_{i,k}$ for all tasks and cache sizes in an iterative manner starting from $i=1,k=0$ towards $i=n,k=m$. However, unlike Sasinowski and Strosnider (1993), our algorithm does not need to enumerate all the $M_{i,k}$ values since it is designed to minimize cache usage while ensuring schedulability. For this purpose, we present Algorithm 2, which includes an early stopping criterion in lines 5–10. The early stopping criterion checks the schedulability using utilization bound ($U(n)=n (2^{1/n} - 1)$ for RM and $U(n)=1$ for EDF) (Liu and Layland 1973) and outputs the first cache partitioning solution that results in a schedulable task set. Additionally, we have reversed the inner and outer loop for faster convergence.

Algorithm 3

Cache usage minimization using DP

5.2 Non-preemptive scheduling

We apply two basic search strategies, linear and binary search, to find the minimal number of cache segments that guarantee the system’s schedulability. The advantage of a non-preemptive policy is that the tasks executing non-preemptively can share the same partition without any interference. Hence, the problem is less complex than in the fully preemptive scheduling as there are only $m+1$ different cache partitionings to consider. In Sect. 5.2.2, we apply linear search to FP using RTA, and to EDF using utilization-based test and QPA. In Sect. 5.2.3, we apply binary search to FP.

5.2.1 Background on schedulability analysis

We start by outlining the schedulability analysis for non-preemptive fixed-priority (RTA) and EDF scheduling (utilization-based test and processor demand criterion).

The response time analysis for non-preemptive fixed-priority scheduling was proposed by Bril et al. (2006); Davis et al. (2007). In non-preemptive scheduling, every job executes from its start uninterruptedly until completion. The priority-inversion might happen when a higher-priority job must wait for the completion of a lower-priority job released before. The longest lower-priority blocking time that task $\tau _i$ can experience is given by the longest worst-case execution time among all low-priority tasks:

$$\begin{aligned} B_{i} = \max _{j>i} C_{j} \end{aligned}$$

(17)

The schedulability analysis of fixed-priority non-preemptive systems requires checking multiple jobs of the same task (Davis et al. 2007). It might be the case that the second, third, or later job has larger response time than the first job. This anomaly is known as self-pushing: while the job under analysis is executing, it blocks all higher-priority jobs released after the start of its execution; consequently, the next job will experience their accumulated interference. Therefore, the analysis of task $\tau _i$ must check all its jobs released within i-level busy-period defined as the longest time interval during which the jobs with priorities equal to i or higher are pending:

$$\begin{aligned} L_{i} = B_{i} + \sum _{j=1}^{i} \Bigg \lceil \dfrac{L_{i}}{T_j} \Bigg \rceil \cdot C_{j} \end{aligned}$$

(18)

The above relation can be solved by fixed-point iteration. The i-level busy-period length can be found by solving the following iteration:

$$\begin{aligned} {\left\{ \begin{array}{ll} L_i^{(0)} &{}= B_{i} + C_{i} \\ L_i^{(\ell )} &{}= B_{i} + \sum _{j=1}^{i} \Bigg \lceil \dfrac{L_{i}^{(\ell -1)}}{T_j} \Bigg \rceil \cdot C_{j} \end{array}\right. } \end{aligned}$$

We should check the schedulability of each task $\tau _i$ instance within time interval $[0,L_i]$. The l-th job of task $\tau _i$ can start its execution when there are no other pending tasks. Its starting time must fulfill the following relation that can be solved by fixed-point iteration:

$$\begin{aligned} s_{i,l} = B_i + (l-1) \cdot C_{i} + \sum _{j=1}^{i-1} \Bigg \lceil \dfrac{s_{i,l}}{T_j} \Bigg \rceil \cdot C_j \end{aligned}$$

(19)

The starting time $s_{i,l}$ of the l-th job of task $\tau _i$ can be found iteratively:

$$\begin{aligned} {\left\{ \begin{array}{ll} s_{i,l}^{(0)} &{}= B_i + (l-1) \cdot C_{i}\\ s_{i,l}^{(\ell )} &{}= B_i + (l-1) \cdot C_{i} + \sum _{j=1}^{i-1} \Bigg \lceil \dfrac{s_{i,l}^{(\ell -1)}}{T_j} \Bigg \rceil \cdot C_j \end{array}\right. } \end{aligned}$$

(20)

The worst-case response time $R_{i,l}$ of l-th job of task $\tau _i$ is $C_i$ time units after its start:

$$\begin{aligned} R_{i,l} = s_{i,l} + C_i \end{aligned}$$

(21)

The task $\tau _i$ worst-case response time $R_i$ is the maximum worst-case response time of its jobs:

$$\begin{aligned} R_{i} = \max _{l} R_{i,l} \end{aligned}$$

(22)

We recap two schedulability conditions for tasks with implicit and constrained deadlines scheduled by non-preemptive EDF upon a single processing unit.

The first condition applies to tasks with implicit deadlines (i.e., $\forall \tau _i \in \tau : D_i=T_i$) and has polynomial time complexity in the number of tasks. As non-preemptive EDF can be considered a special case of resource sharing in preemptive EDF (Davis 2014), the following schedulability conditions hold (Baker 1990, 1991). Given the tasks indexed by increasing periods, their jobs are schedulable by non-preemptive EDF if:

$$\begin{aligned} \forall 1 \le j \le n \;: \; \sum _{i=1}^j \dfrac{C_i}{T_i} + \dfrac{B_j}{T_j} \hspace{0.25cm} \text { where } \hspace{0.25cm} B_j = \max \left\{ C_i \;| \; T_i > T_j \right\} \end{aligned}$$

(23)

The second condition applies to tasks with constrained deadlines (i.e., $\forall \tau _i \in \tau : D_i \le T_i$) and has exponential time complexity in the number of tasks. George et al. (1996) and Baruah and Chakraborty (2006) extend the schedulability test for preemptive EDF (see Sect. 5.1) to the non-preemptive case by introducing a revised blocking factor:

$$\begin{aligned} b(t) = \max \{ \, C_i \, | \, D_i > t \, \} \end{aligned}$$

(24)

into the following condition:

$$\begin{aligned} \forall t > 0 \,: \, b(t) + h(t) \, \le \, t \end{aligned}$$

(25)

5.2.2 Linear search

In linear search, we check every number of cache segments in ascending order until we find one for which all tasks are schedulable.

FP systems We apply the schedulability test for each task in decreasing priority order If the test fails for a given number of cache segments, we assign an additional segment and repeat the test. However, it is not necessary to resume the schedulability test from the first task if the test is sustainable with respect to the WCETs (Altmeyer et al. 2016). All tasks that were previously proved schedulable will also be schedulable with one more cache segment. Their response times depend on the task WCETs, which by adding more cache segments, will decrease or remain unchanged. Hence, the response times cannot increase, and each task deemed schedulable with a given number of cache segments will remain schedulable with more cache segments (the response time analysis sustainability with respect to execution times and their monotonicity with respect to the cache partition size). In the worst case, the linear search method invokes $n+m$ times the schedulability tests. Algorithm 4 shows the linear search approach for cache minimization.

Algorithm 4

Cache usage minimization using linear search

Example 5.2

Consider six tasks, $\tau _1$, $\tau _2$, $\tau _3$, $\tau _4$, $\tau _5$ and $\tau _6$ ordered in decreasing priority order and running non-preemptively on a single core that shares the last-level cache with other cores. Using cache partitioning, we want to minimize the number of cache segments used by the tasks. We assume that we can verify their schedulability using a schedulability test which is sustainable with respect to the tasks’ execution times. We apply linear search based cache minimization given in Algorithm 4. Figure 3 shows the successive iterations of the algorithm.

Fig. 3

Example of cache usage minimization based on the linear search for non-preemptive scheduling

The algorithm starts with the highest-priority task $\tau _1$ and checks its schedulability with no cache segments. As the test fails, we repeat it by increasing the number of cache segments by one until $\tau _1$ becomes schedulable. As task $\tau _1$ can be schedulable with two segments, we move then to the next task, $\tau _2$, and check its schedulability assuming two cache segments. Because the schedulability test fails, we increase the cache partition size to three cache segments. This time we do not have to rerun the schedulability test for task $\tau _1$ as it has already been deemed schedulable with two segments so will also be schedulable with three or more segments as we assume that the schedulability test is sustainable with respect to the execution times and the execution times are monotonically non-increasing with the number of cache segments. We, therefore, run the schedulability test only for task $\tau _2$. As the test fails for three segments, we repeat it again for $\tau _2$ only with four cache segments. Since the test is successful for $\tau _2$, we check $\tau _3$ with four cache segments which is also schedulable. The test fails at the next task, $\tau _4$, and then we increase the total cache partition size to five segments and retake the schedulability test for $\tau _4$ with five segments. The task is schedulable and we proceed to tasks $\tau _5$ and $\tau _6$, which are also schedulable. We can conclude that we need at least five cache segments to guarantee the schedulability of the task set.

We can further improve the cache minimization procedure by observing that the tasks’ execution times do not decrease at every cache segment (see Example 5.1). If task $\tau _i$ is not schedulable with k cache segments under non-preemptive scheduling, and (i) its worst-case execution time, (ii) worst-case execution time of all higher-priority interfering tasks, and (iii) maximal worst-case execution time among all lower-priority tasks are the same with $k+1$ cache segments as with k cache segments, then task $\tau _i$ cannot be made schedulable on $k+1$ cache segments. This means that we can skip the schedulability test for $\tau _i$ with $k+1$ cache segments and keep increasing the size of the cache partition as long as there is no change in any worst-case execution time of the previously mentioned tasks.

EDF systems We will incorporate two schedulability tests for non-preemptive EDF, utilization-based test (sufficient condition for tasks with implicit deadlines) and QPA (exact schedulability test applicable also to tasks with constrained deadlines).

To determine the EDF-schedulability of non-preemptive tasks with implicit deadlines, we need to verify Formula (23) for each $j \in \{1,\ldots ,n\}$. A task set using the minimum number of cache segments must meet all these conditions. We begin by checking the conditions starting from $j=1$ and $k=0$ (i.e., no cache). If the j-th condition is not fulfilled, we incrementally add a new cache segment until the condition can be met. Since the worst-case execution times are monotonically non-increasing with respect to the cache partition size, all blocking and utilization factors, $B_i$ and $U_{i,k}$, are also monotonically non-increasing. Hence, if we add a new cache segment to “fix” j-th condition, all previously checked conditions $1,\ldots ,j{-}1$ remain valid and do not have to be verified again. The procedure is detailed in Algorithm 5.

Algorithm 5

Cache usage minimization for NP-EDF with implicit deadlines

For tasks with constrained deadlines, our approach is based on Quick Processor-demand Analysis (QPA) (Zhang et al. 2003). The test verifies a sufficient and necessary schedulability condition. We modify QPA by incrementing the number of cache segments allocated to the tasks at each failure point when the schedulability cannot be guaranteed.

The QPA has been also applied to non-preemptive EDF (Zhang and Burns 2013). It follows the same principle and takes into account the blocking factor b(t). While the blocking factor is a non-increasing function of t, it has been proved that the value of $h(t) + b(t)$ is its non-decreasing function (Zhang and Burns 2013). Therefore, it is safe to skip the deadlines lower than the currently calculated processor demand even if the blocking factor at these deadlines might increase. The blocking factor is recalculated at each iteration. The study interval is naturally decomposed into two sub-intervals: $[D_1,D_n-1]$ with blocking (i.e., $b(t)>0$) and $[D_n,L]$ with no blocking (i.e., $b(t)=0$). As it is more likely for a deadline miss, also due to the blocking, to occur in the first interval (Zhang and Burns 2009), Zhang and Burns (2013) show that it is more effective to start by checking schedulability within the first interval. If an overflow is found, the system is unschedulable. Otherwise, if there is no overflow in the first interval, the schedulability within the second interval is checked.

Our cache minimization procedure extends QPA (Zhang and Burns 2013) and its detailed description can be found in Algorithm 6. It starts by sorting the tasks in a non-decreasing order of relative deadlines and finding the maximal number of cache segments k for which the task set utilization will not exceed 1 (line 1). Then, the schedulability is checked, first, in time intervals of $[D_1,D_n-1]$ (line 3), and then in time intervals of $[D_n,L]$ (line 5). The schedulability test is combined with cache minimization and is based on function minimize_cache, which takes a time interval $[t_1,t_2]$, the initial number of cache segments allocated to tasks $\tau$, and outputs the minimal number of cache segments k needed to ensure schedulability of tasks $\tau$ in the time interval $[t_1,t_2]$. Whenever the schedulability test fails (line 12), the number of cache segments k allocated to tasks is increased. The function next_corner_point($\tau ,i$) gives the next cache partition size for which the worst-case execution time of at least one task $\{\tau _j \, | \, D_j\ge D_i\}$ drops (see Example 5.1). As the worst-case execution times are monotonically non-increasing with respect to the cache partition size, all previously checked intervals remain schedulable and it is not necessary to repeat their tests. Function latest_deadline($\tau ,t$) calculates the latest absolute deadline occurring before time instant t ($\max \{d_j \, | \, \forall \tau _j \in \tau , \, d_j < t\}$, see Zhang and Burns (2009)).

Algorithm 6

Cache usage minimization for NP-EDF with constrained deadlines

5.2.3 Binary search

The second strategy is based on the binary search and is applied to FP. For each single task, we look for a minimum number of cache segments ensuring its schedulability. This number cannot be less than any minimum number of segments for which previously tested tasks were schedulable. The method starts with half of the available cache segments and checks the first task schedulability. In case of the test success (failure), the segments’ numbers greater (less) than the tested number are discarded. The search continues on the remaining number of cache segments from its middle number and repeats the same procedure until the number of segments cannot be decreased anymore. Then, the search is applied for the next task in the decreasing priority order. Like in the linear search, we do not need to test again the tasks that were already deemed schedulable if the test is sustainable with respect to the worst-case execution times. We do neither consider the segments’ numbers that were too small to ensure the schedulability of the previous tasks. The total number of schedulability test invocations is upper bounded by $n\log m$. Algorithm 7 outlines the binary search-based cache minimization.

Algorithm 7

Cache usage minimization using binary search

Example 5.3

Consider the three first tasks, $\tau _1$, $\tau _2$ and $\tau _3$, from Example 5.2. We use binary search approach to find the minimal number of cache segments that guarantees the task set schedulability under a non-preemptive scheduling policy. We assume that there are $m=6$ cache segments available. Algorithm 7 starts with task $\tau _1$, $k_{min}=0$, and $k_{max}=6$. It first checks $\tau _1$’s schedulability with $k=3$ segments. As the task is schedulable, we set $k_{max}=2$ and repeat the test for $k=1$ segment. As task $\tau _1$ is not schedulable with one segment, we set $k_{min}=2$. We repeat the test with $k=2$ segments and, since the test is successful, we set $k_{max}=1$ which ends the iteration for task $\tau _1$. We move to task $\tau _2$. First, we reinitialize $k_{max}=6$, and then check $\tau _2$’s schedulability with $k=4$ segments. As the test is successful, we set $k_{max}=3$ and repeat the test for $k=2$. Task $\tau _2$ is not schedulable with $k=2$ cache segments so we set $k_{min}=3$ and retry for $k=3$ segments which is again unschedulable and therefore we set $k_{min}=4$ and move to the next task, $\tau _3$, as $k_{min} > k_{max}$ terminates the inner loop. The algorithm in like manner checks the schedulability of task $\tau _3$ with $k=5$, $k_{min}=4$, $k_{max}=6$ (schedulable) and then with $k=4$, $k_{min}=4$, $k_{max}=5$ (schedulable). Hence, the tasks need at least $k_{min}=4$ cache segments to guarantee their schedulability.

The overall search time complexity depends on the schedulability test. The response time analysis (NP-RTA) giving sufficient and necessary schedulability conditions (Davis et al. 2007) has pseudo-polynomial time complexity. The polynomial-time complexity can be achieved by sufficient but not necessary schedulability tests. For instance, we can test the schedulability of each task with one single problem interval of length $D_i{-}C_i$ (Equation (16) in Davis et al. (2007), denoted by NP-SINGLE) and upper bound task $\tau _i$’s latest starting $\hat{s_i}$:

$$\begin{aligned} \hat{s_i} = \max \{B_i,C_i\} + \sum _{j=1}^{i-1} \Bigg \lceil \dfrac{D_i-C_i}{T_j} \Bigg \rceil \cdot C_j \end{aligned}$$

(26)

If $\hat{s_i}\le D_i-C_i$, we can conclude that any job of task $\tau _i$ can start early enough to finish its execution before its deadline. Another approach worth considering is the use of the hyperbolic utilization bound (NP-HYPER) derived by Theorem 9 in Brüggen et al. (2015). Note that while the first two tests can skip tasks that are already deemed schedulable, the utilization bound must be recalculated by adding utilization factors of all tasks when increasing the cache size.

Intuitively, the binary search will outperform linear search if there are many cache partitions and relatively few tasks. We can compare both search techniques by assuming that for each task binary search results in at most $\lfloor \log (m+1) \rfloor +1$ test invocations. Figure 4 illustrates the worst-case complexity comparison between both search techniques.

Fig. 4

Worst-case complexity comparison for linear and binary search

6 Evaluation setup

6.1 Benchmark profiles

To evaluate the proposed cache minimization approaches, we performed experiments on benchmark applications executing under different cache partition sizes. We used Cachegrind (Seward et al. 2008), which is an open-source cache profiler tool, to run the benchmarks and collect cache-related values (e.g., cache miss ratio). We modified Cachegrind to support arbitrary cache sizes (by default, it must be power of two). While the values obtained from Cachegrind cannot be interpreted as worst-case execution time upper bounds, the tool helps us understand the relation between partition size and execution speed.

Fig. 5

Execution time vs cache size for CortexSuite

We consider a set of applications from the CortexSuite benchmark suite (Thomas et al. 2014) for computer vision and machine learning. We assume a two-level set-associative cache hierarchy with Least Recently Used (LRU) eviction policy and line size of 64 B at both levels. Level L1 is split into L1d (for data) and L1i (for instructions), both with a fixed size of 32 KB and 4 ways. Level L2 of 16 ways is shared by instructions and data. We vary the L2 cache size from 0 up to 2 MB, with steps of 32 KB. We ran 20 benchmarks and collected the number of cache misses (for L1 and L2), the number of data references, and the number of executed instructions. Then, assuming the characteristic of ARM Cortex A8 (Hennessy and Patterson 2011) (2 instructions per cycle, 1 cycle for L1 hit, 11 cycles for L1 miss, and 60 cycles for L2 miss), we got the execution times for each benchmark and for each cache partition size. Figure 5 shows a sample of the obtained profiles. Similar trends have been observed in Bienia et al. (2008) for PARSEC benchmark suite and in Hennessy and Patterson (2017) for SPEC2000 programs. The above simulation technique is similar to several works in real-time systems literature (Lesage et al. 2015; Mancuso et al. 2013; Kwon et al. 2021; Sun et al. 2023b). Nevertheless, the proposed cache usage optimization techniques can be used with any WCET analysis tool or measurement methodology.

6.2 Task set generation

Based on the benchmark profiles, we randomly generate task sets with different parameters: (i) task set size $n \in \{16, 32, 64\}$, (ii) available cache size $S \in \{1, 2, 4\}$ MB, (iii) cache segment size $dS \in \{32, 128, 512\}$ KB, and (iv) task set base utilization U ranging in [0.7, 1.6] with a step of 0.1. For each parameter combination, we consider two scenarios, i.e., implicit deadlines and constrained deadlines. For each scenario, we randomly generate 20 task sets to evaluate the developed cache minimization methods for the FP and EDF scheduling policies. The generation procedures for the implicit- and constrained- deadline task sets are summarized as follows.

Implicit deadlines We generate implicit-deadline task sets in three steps. First, we generate task periods $T_i$ by uniformly sampling from [10, 000, 100, 000]. Second, we generate the base utilization $U_i$ of each task $\tau _i$ using UUnifast (Bini and Buttazzo 2005) such that the total base utilization of the task set equals the target base utilization (i.e., $U = \sum _{i=1}^n{U_i}$). Finally, we randomly sample n benchmark profiles and calculate each task’s WCETs when using different numbers of cache segments according to the sampled profile.

Constrained deadlines For the constrained deadline scenario, we follow the same procedures as above to generate task periods, utilizations and WCETs. Then, we use the method in Singh (2023) to generate task deadlines. Specifically, we define the ratio $\delta _i = C_{i,0} / D_i$ as the density of task $\tau _i$ and then use DRS (Griffin et al. 2020), an extended version of UUnifast, to generate each task’s density such that the total task density $\sum _{i=1}^n{C_i / D_i} = 1.25 \cdot U$. Note that the task’s base utilization $U_{i,0}$ is set as the lower bound of $\delta _i$ to ensure that $D_i \le T_i$. Finally, the task deadline $D_i$ is calculated as $\lfloor C_{i,0}/\delta _i\rfloor$.

In addition to the above two scenarios, we consider a special case for the preemptive EDF scheduling policy, where the task periods are harmonic numbers. This is because the ILP for preemptive EDF cannot scale well with the generic task periods considered in the above two scenarios, which results in a very large L in (13) (sometimes even larger than $2^{64}$). Therefore, we generate additional task sets with harmonic periods to upper-bound the busy interval (for a harmonic-period task set, L is no larger than the largest task period, i.e., $L \le T_{max}$) and evaluate the effectiveness of the developed ILP method. Specifically, the harmonic task periods are randomly sampled from $\{8,000, 16,000, 32,000, 64,000, 128,000\}$ in our experiments, and the task deadlines are generated using the same procedures as above (i.e., constrained deadlines).

6.3 Experimental settings

In this paper, all the experiments are conducted on a workstation equipped with Intel Xeon Silver 4216 CPU running Linux. The proposed cache minimization algorithms are implemented in Python 3.10, and the mathematical programs (i.e., the IQCP for FP and the ILP for EDF) are solved by a mathematical programming solver Gurobi 9.5.2 (Gurobi Optimization, LLC 2022) with Python API. To complete the experiments within a reasonable time, we set a run time limit of 3600 s for the solver.

We run each comparison algorithm on each generated task set to evaluate its cache usage and schedulability. The cache usage of a test algorithm is considered the maximum cache available in the system if the task set is deemed unschedulable by the algorithm.

7 Evaluation results

This section reports our experimental results and observations. First, we give an overview of the comparison results in Sect. 7.1. Then, we present the detailed evaluation results under different parameter settings in Sect. 7.2-7.4. Additionally, we evaluate the effectiveness of the ILP for preemptive EDF on the task sets with harmonic periods and constrained deadlines in Sect. 7.5.

We compare the performance of the proposed cache minimization techniques for FP and EDF scheduling algorithms on the generated task sets in terms of their cache usage, schedulability ratio, and running time. For the cache minimization techniques, we use the mathematical programming methods (i.e., IQCP and ILP), guided local search (GLS in Algorithm 1), branch-and-bound (B &B in Algorithm 2), dynamic programming (DP in Algorithm 3), and the search techniques for non-preemptive scheduling: RTA applied to FP (NP-RTA in Algorithm 4), utilization-based test (NP-U in Algorithm 5) and QPA (NP-QPA in Algorithm 6) both for EDF. We note that the mathematical programming is only evaluated in scenarios FP and EDF (harmonic) since it is not scalable in EDF (constrained) with a generic period range, and DP achieves the optimal solutions of EDF (implicit) efficiently.

7.1 Overall comparison

Table 1 Overall comparison results

Table 1 summarizes the average results of cache minimization techniques over all generated task sets under different scheduling policies and scenarios. Our main observations are as follows.

Preemptivity The non-preemptive cache partitioning methods save more cache than the preemptive algorithms in all scenarios, except for the ones with constrained deadlines (EDF constrained and EDF harmonic) and have an order of magnitude lower runtime. The preemptive methods can save more cache in constrained-deadlines scenarios when the non-preemptive methods have less slack to tolerate priority-inversion.

Scheduling algorithms EDF achieves better shcedulability ratio than FP (as shown in many previous studies (Buttazzo 2005)) and allows for better cache usage.

Methods The average optimality gap of the cache usage achieved by the proposed GLS is smaller than 2% under the FP scheduling policy. GLS achieves the best average cache usage among all cache minimization algorithms proposed for preemptive task sets under both the FP policy and the EDF policy with constrained deadlines.

7.2 Cache usage for variable n

Table 2 summarizes the average results of cache minimization techniques over all generated task sets under different scheduling policies and scenarios for $n=16,32,64$ with $dS=32$ and $S=4096$ KB. The detailed results are presented in Fig. 6a–l.

Table 2 Comparison results for variable n

Fig. 6

Cache usage for $dS=32$ KB, $S=4096$ KB, and variable n

The results support the following observations. First, the proposed GLS outperforms DP and B &B and achieves near-optimal cache usage compared to IQCP, which demonstrates the effectiveness of GLS. For implicit deadlines, EDF significantly outperforms other approaches. The cache usage of the preemptive (resp., non-preemptive) approaches increases (resp., decreases) with the increase of n. We also note that the non-preemptive approach NP-RTA uses more (resp., less) cache than preemptive approaches for small (resp., large) utilization. These observations are explained as follows. First, non-preemptive tasks share the available cache as one single partition, leading to consistent WCET reduction regardless of the number of tasks. However, preemptive tasks need to divide the available cache into private partitions to avoid inter-task cache eviction, resulting in decreasing WCET reduction as n increases. Second, preemptive task sets are easily schedulable at low utilization, but non-preemptive scheduling can lead to unschedulability even at low utilization (the utilization bound drops to 0). As a result, the preemptive approach uses less cache when utilization is low, but non-preemptive is more efficient at higher utilization levels due to larger WCET reduction.

7.3 Cache usage for variable dS

Table 3 Comparison results for variable dS

Fig. 7

Cache usage for $n=16, S=2048$ KB, and variable dS

Table 3 summarizes the average results of cache minimization techniques for three cache segment sizes, $dS=32, 64$ and 128 KB, with $n=16$, and $S=2048$ KB. The detailed results are in Figs. 7a–l. The results of the experiment show that: (i) The cache usage of all algorithms increases with the increase of dS; (ii) The performance of B &B improves as dS increases. The reason for (i) is that dS represents the granularity of the cache segments, and as dS increases, precision in cache partitioning is lost. For (ii), it suggests that B &B can benefit more from smaller m compared with GLS. This is because B &B enumerates all possible cache allocation options without the knowledge guidance used in GLS. As a result, B &B can achieve a good performance for a coarse-grained cache partitioning but performs worse for a finer granularity.

7.4 Schedulability ratio for variable S

Table 4 Comparison results for variable S

Fig. 8

Schedulability ratios for $n=32$, $ds=32$ KB, and variable S

Table 4 summarizes the average results of cache minimization techniques for three cache sizes, $S=1,2$ and 4 MB, with $n=32$, and $dS=32$ KB. Figure 8a–l present the detailed results. The schedulability results show a similar trend as in cache usage: (i) GLS performs near-optimally compared to IQCP and outperforms other preemptive cache minimization methods; (ii) The non-preemptive method performs better than the preemptive ones for high utilization. Additionally, the schedulability ratio of the preemptive methods improves with increasing cache size, however, the non-preemptive method does not see further improvements beyond a cache size of 2048 KB. This is because non-preemptive tasks can share all available cache and our benchmarking experiments have shown that their WCETs do not improve with more than 2048 KB of cache.

7.5 Evaluation of ILP on harmonic task sets

Due to the scalability issues, we evaluate the mathematical programming for EDF (i.e., the number of points to check in Equation (14) grows exponentially with periods) using harmonic periods that result in lower hyperperiod length. Table 5 resumes our findings.

Table 5 Comparison results for task sets with harmonic periods and constrained deadlines under preemptive EDF scheduling policy

8 Conclusions and future work

In this paper, we presented a comprehensive study of cache partitioning methods to minimize cache usage for real-time systems. We proposed efficient solutions for both preemptive and non-preemptive scheduling scenarios under FP and EDF algorithms. For preemptive scheduling, we formulated the problem as an integer quadratically constrained program and proposed an efficient guided local search heuristic, a branch-and-bound search, and an efficient dynamic programming algorithm. For non-preemptive scheduling, we developed linear and binary searches coupled with different schedulability analyses (RTA for FP and QPA for EDF). We evaluated the proposed methods using real-world benchmarks and found that our heuristic achieved an average optimality gap of 0.79%, with run time that was 0.1x that of a mathematical programming solver. Furthermore, our results indicated that non-preemptive cache minimization methods can save more cache usage than preemptive methods for large task sets with high utilization.

In future work, we plan to investigate the potential benefits of combining non-preemptive and preemptive scheduling to further improve our cache usage minimization algorithm.