Partial-order reduction in reachability-based response-time analyses of limited-preemptive DAG tasks

Abstract

Response-time analysis (RTA) has been a means to evaluate the temporal correctness of real-time systems since the 1970 s. While early analyses were successful in capturing the exact upper bound on the worst-case response-time (WCRT) of systems with relatively simple computing platforms and task activation models, nowadays we see that most existing RTAs either become pessimistic or do not scale well as systems become more complex (e.g., parallel tasks running on a multicore platform). To make a trade-off between accuracy and scalability, recently, a new reachability-based RTA, called schedule-abstraction graph (SAG), has been proposed. The analysis is at least three orders of magnitude faster than other exact RTAs based on UPPAAL. However, it still has a fundamental limitation in scalability as it suffers from state-space explosion when there are large uncertainties in the timing parameters of the input jobs (e.g., large release jitters or execution-time variations). This could impede its applicability to large industrial use cases, or to be integrated with automated tools that explore alternative design choices. In this paper, we improve the scalability of the SAG analysis by introducing partial-order reduction rules that avoid combinatorial exploration of all possible scheduling decisions. We include systems with dependent and independent task execution models (i.e., with and without precedence constraint). Our empirical evaluations show that the proposed solution is able to reduce the runtime by five orders of magnitude and the number of explored states by 98% in comparison to the original SAG analysis. These achievements come only at a negligible cost of an over-estimation of 0.1% on the actual WCRT. We applied our solution on an automotive case study showing that it is able to scale to realistic systems made of hundreds of tasks for which the original analysis fails to finish.

1 Introduction

Guaranteeing temporal correctness of real-time systems is typically done via a response-time analysis (RTA) whose goal is to determine the worst-case response time (WCRT) of a set of input jobs scheduled by a given scheduling policy on a computing resource. A real-time system is said to be schedulable if the WCRT of each job is smaller than its deadline. It is know that most variations of the RTA problem for periodic tasks scheduled by a job-level fixed-priority (JLFP) policy such as fixed-priority (FP) or earliest-deadline first (EDF) are NP-hard even for a uniprocessor platform (Ekberg 2020).

1.1 Related work

Known exact WCRT analyses fall into two general categories: (i) fixed-point iteration-based analyses (Audsley et al. 1993; Davis et al. 2007) that have pseudo-polynomial time complexity and (ii) reachability-based analysis (RBA) (Guan et al. 2007; Sun and Lipari 2016a; Nasri and Brandenburg 2017; Nasri et al. 2018, 2019; Yalcinkaya et al. 2019a; Nogd et al. 2020; Nelissen et al. 2022).

Fixed-point iteration-based analyses are typically faster than RBAs, however, they are exact only in special cases, e.g., when analyzing sporadic (or periodic) tasks scheduled by the FP or EDF scheduling policies on a uniprocessor platform (Baruah et al. 1990; Jeffay et al. 1991; Audsley et al. 1993; Davis et al. 2007). RBAs, on the other hand, are often exact in more general cases, e.g., preemptive (Guan et al. 2007) or non-preemptive (Yalcinkaya et al. 2019a) periodic and sporadic tasks scheduled by global FP policies. However, a majority of them are known to have very poor scalability w.r.t. the number of tasks, processors, or task parameters such as period values (Guan et al. 2007; Sun and Lipari 2016a; Yalcinkaya et al. 2019a).

Recently, a new reachability-based RTA, called schedule-abstraction graph (SAG), has been proposed (Nasri and Brandenburg 2017; Nasri et al. 2018, 2019; Nogd et al. 2020; Srinivasan et al. 2021; Nelissen et al. 2022). It surpasses the scalability limitations of the timed-automata based RBAs by at least three orders of magnitude (Yalcinkaya et al. 2019a; Nasri et al. 2019). However, as we will show in Sect. 3, this analysis still suffers from state-space explosion when there are large uncertainties in the timing parameters of the input tasks or jobs, e.g., large release jitter or execution-time variations.

1.2 Schedule-abstraction graph

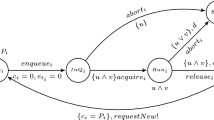
SAG explores the space of possible decisions that a JLFP scheduler can take when dispatching a set of jobs on processing resources. This decision space is explored by building a graph whose vertices represent the state of the resource (e.g., processor) after the execution of a set of jobs and whose edges represent possible scheduling decisions that evolve the system states. SAG has been designed for non-preemptive jobs (Nasri and Brandenburg 2017; Nasri et al. 2018, 2019; Nogd et al. 2020), hence, a scheduling decision is to determine “a next job that can possibly be dispatched” after a system state. An example job set along with its schedule are provided in Fig. 1a, b, respectively. The graph made by the SAG for this job set is shown in Fig. 1c. While building the graph, the response time of each job dispatched on an edge is tracked. Hence, when the graph is fully constructed, the method outputs the smallest and largest response time of each job in all scenarios (edges) that involve that job.

To defer the state-space explosion, Nasri and Brandenburg (2017) have introduced two main techniques: (i) powerful interval-based abstractions to aggregate similar system states (or equivalently, schedules that have a similar impact on the final system state), and (ii) state-merging rules to combine system states whose future can be explored together. These techniques allowed their solution to be at least 3000 times faster than other exact RBAs based on generic formal verification tools such as UPPAAL (Yalcinkaya et al. 2019a), and to scale to large system sizes.

1.3 Current limitation of SAG

Despite the current success in scalability, the schedule-abstraction-based analysis still faces one big fundamental limitation: each edge can only account for a single scheduling decision (i.e., dispatching of one job) (Nasri and Brandenburg 2017; Nasri et al. 2018, 2019; Nogd et al. 2020; Nelissen et al. 2022). As a result, as soon as there are large uncertainties in the release time or execution time of the jobs in the input job set, the number of states generated by the SAG grows exponentially because the analysis will try to explore all (valid) combinations of ordering between jobs. This may impede applicability of SAG to large industrial use cases.

1.4 This paper

The goal of our work is to improve scalability of the schedule-abstraction-based analysis by introducing partial-order reduction (POR) rules that allow combining multiple scheduling decisions on one edge and hence avoiding combinatorial exploration of all possible orderings between jobs in cases where there are large uncertainties.

As our goal is to demonstrate how to apply POR on SAG-based analyses, in this work we will focus on two simpler (yet NP-hard) schedulability analysis problems: analyzing a set of non-preemptive jobs (i) with and (ii) without precedence constraint relations scheduled by a work-conserving JLFP scheduling policy on a uniprocessor platform. These jobs could be generated from limited-preemptive periodic tasks with fixed-preemption points, periodic DAG tasks, or any other tasks with predictable arrival patterns (e.g., bursty) or precedence constraint relations.

A recent survey on industrial real-time systems shows that more than 80% of real-time systems have periodic activities, about 40% of them include single-core platforms (Akesson et al. 2020, 2021), and about 65% of them use a non-preemptive and/or cooperative execution model. The findings of this survey show that the two problems we consider in our work are not only relevant now but also in the next ten years as indicated by over 30% of industrial practitioners that filled-in the survey.

We show that (for non-preemptive sequential jobs), our solution is able to reduce the runtime of the SAG analysis by five orders of magnitude and the number of explored states by 98%, while remaining an exact schedulability analysis. This achievement comes at a negligible cost of an over-estimation of only 0.1% on the actual WCRT. We have the same achievements for limited-preemptive periodic tasks with fixed-preemption points (see Sect. 6.3.1) and tasks whose segments has an arbitrary precedence constraint modeled by a directed-acyclic graph (DAG) (see Sect. 6.3.2). However, since the original SAG analysis could not analyze most of these task sets within a respectable time budget, we currently do not have an estimation of the speed-up of our new analysis w.r.t. the original SAG for these cases. Our empirical experiments, however, conclude that our new analysis scales really well w.r.t. the number of jobs to analyze even in the presence of many precedence constraints.

Furthermore, we applied our solution to a large case study from an automotive use case with more than 710 runnables and tens of thousands of jobs per hyperperiod. This shows that our solution is suitable to be used as an exact schedulability analysis in industrial-grade design-space exploration tools.

1.5 Extended version

This paper builds upon and extends the paper “Partial-Order Reduction for Schedule-Abstraction-based Response-Time Analyses of Non-Preemptive Tasks” (Ranjha et al., 2022) by extending the POR solution to job sets with inter-job dependencies (i.e., precedence constraints), hence making the solution applicable to (i) limited-preemptive tasks with fixed-preemption points, (ii) DAG tasks, where the precedence constraints can be modeled as a directed-acyclic graph, and (iii) job sets with arbitrary precedence constraints. We have also extended the experimental evaluations of both the original and extended version of the contribution and added a thorough analysis of the related work.

2 System model and assumptions

2.1 Job and system model

We consider the problem of scheduling a finite set of non-preemptive jobs $\mathcal {J}$ on a uniprocessor platform. A job $J_i = ( [r_i^{min}, r_i^{max} ], [C_i^{min}, C_i^{max} ], d_i, p_i )$ is characterized by its earliest release time $r_i^{min}$, a.k.a. arrival time (Audsley et al. 1993), latest release time $r_i^{max}$, best-case execution time (BCET) $C_i^{min}$, worst-case execution time (WCET) $C_i^{max}$, absolute deadline $d_i$, and priority $p_i$. We assume that the job timing parameters are integer multiples of the system clock.

Job $J_i$ non-deterministically releases at a time instant $r_i \in [r_i^{min}, r_i^{max} ]$ and executes for an a priori unknown amount of time $C_i \in [C_i^{min}, C_i^{max} ]$. Because of this uncertainty, we say that $J_i$ is possibly released at time t if $r_i^{min} \le t < r_i^{max}$ and certainly released if $t \ge r_i^{max}$.

In the first part of this paper, we assume jobs are independent from each other. In that case, we say a job is ready at time t if it is released but did not start executing before t. In Sect. 5, we extend the analysis to jobs with precedence constraints. In that case, a job $J_i$ has a (potentially empty) set $pred (J_i)$ of predecessors. Then, $J_i$ is ready at time t if and only if it is released, did not start executing yet, and all the jobs in its set of predecessors have already completed their execution.

Because we assume that every job $J_i$ is non-preemptive, a job $J_i$ that starts executing at time t, finishes its execution by time $t + C_i$ while continuously occupying the processor during the interval $[t, t + C_i )$. Let $f_i$ denote the finish time of $J_i$. Once $J_i$ finishes its execution by $f_i$, the processor becomes available again and the next job may start. The response time of $J_i$ is the length of the interval between its earliest release time $r_i^{min}$ and its finish time $f_i$, i.e, $f_i - r_i^{min}$. Following Audsley’s definition Audsley et al. (1993), we assume that the deadline of a job is set based on the arrival time and hence is not affected by the release jitter.

Priorities are integer numbers. A smaller value indicates a higher priority, namely, if $p_i < p_j$, then the job $J_i$ has a higher priority than the job $J_j$. Priority ties are broken arbitrarily but consistently, i.e., we assume that the “<” operator implicitly uses this tie-breaking rule. The priority of a job is assigned by a job-level fixed-priority (JLFP) scheduling policy. For example, under EDF, a job’s priority is its absolute deadline.

We use $\langle ~\rangle$ to refer to an ordered set (or a sequence) and $\{~\}$ to refer to a non-ordered set. Neither contains repeated items. We use $\max _0\{X\}$ over a set of positive integers X to indicate that the maximum of an empty set is 0. Namely, if $X \ne \emptyset$ then $\max _0\{X\} = \max \{X\}$, otherwise, $\max _0\{X\} = 0$

2.2 Scheduler model

We consider all non-preemptive job-level fixed-priority (JLFP) scheduling policies. Despite the original schedule-abstraction graph (Nasri and Brandenburg 2017) supporting both work-conserving and non-work-conserving scheduling policies, we only focus on work-conserving policies in this paper, i.e., policies that do not leave the processor idle as long as there is a ready job in the system. These policies can be found in most real-time operating systems (RTOSes) and are widely used in industry (Akesson et al. 2021).

Like the original analysis, we solely focus on schedulers that are priority-driven and deterministic, i.e., schedulers that only schedule a job if it is the highest-priority ready job in the system and always produce the same schedule for a given execution scenario, where an execution scenario is defined as a mapping of the jobs to release times and execution times as follows.

Definition 1

(Nasri and Brandenburg 2017) An execution scenario $\gamma = ( C, R )$ for a set of jobs $\mathcal {J} = \{J_1, J_2, \ldots , J_m \}$ is a sequence of execution times $C = \langle C_1, C_2, \ldots , C_m\rangle$ and release times $R = \langle r_1, r_2, \ldots , r_m \rangle$ such that, $\forall J_i \in \mathcal {J}$, $C_i \in [C_i^{min}, C_i^{max} ]$ and $r_i \in [r_i^{min}, r_i^{max} ]$

We consider a set of jobs $\mathcal {J}$ to be schedulable under a given scheduling policy A if there exists no execution scenario of $\mathcal {J}$ that results in a deadline miss when scheduled by A.

2.3 From periodic tasks to job sets

As mentioned earlier, the input to schedule-abstraction graph is a job set which could be resulted from any arbitrary arrival model. Since one of most prevalent workload arrival patterns in industrial applications is periodic activation (present in 80% of industrial systems according to Akesson et al. (2020, 2021)), we explain how one can obtain a job set from a set of synchronous periodic tasks.

It is known that the arrival pattern of a set of periodic tasks repeats after a hyperperiod, where the hyperperiod, denoted by H, is the least-common multiple of the periods of the tasks. Thus, in order to ensure a safe analysis, the job set should include all task instances (jobs) that each periodic task releases within the interval [0, H].

Let T be the period, $C^{min}$ and $C^{max}$ be the BCET and WCET, D be the deadline (assuming $D \le T$), P be the priority, and $\sigma$ be the release jitter of a task $\tau$. This task will generate $m = H / T$ jobs in the interval [0, H), where the $k^{\text {th}}$ job ($1\le k \le m$) of this task is characterized as follows: $J = ([(k-1)\cdot T, (k-1)\cdot T + \sigma ], [C^{min}, C^{max}], (k-1)\cdot T + D, P)$. Following Audsley’s definitions, we consider that the job’s absolute deadline is at $(k-1)\cdot T + D$, and hence, a job that is released later due to release jitter does not get a longer (deferred) deadline. When the scheduling policy is fixed-priority policy, the job inherits priority of its task and when it is EDF, the job’s priority is equal to its absolute deadline, i.e., $(k-1)\cdot T + D$.

Because we assumed a constrained-deadline model, if the job set is schedulable, there will be no carry-out workload at time H that could possibly impact the execution of the job set in the next hyperperiod. It is important to note that the schedule-abstraction graph analysis explores all possible execution scenarios that can be generated from any release time (within the given arrival interval) of each job in the observation window. Hence, if the job set is schedulable, there is no need to assume that the release time of the jobs in one hyperperiod must be identical to the release time of the jobs in other hyperperiod. The analysis itself will take care of the release jitter.

If a task has more than one execution segment (e.g., in case of limited-preemptive tasks with fixed-preemption point), then for each segment of each task instance, one separate job will be created. These jobs, share the same arrival interval ($[r^{min}, r^{max}]$), however, a precedence constraint must be added between them to ensure that a later segment never starts before its predecessors complete. Later in Sect. 5, we will explain how to introduce precedence constraint between jobs.

3 Motivation

Fig. 1

An example showing the difference between the original SAG analysis (Nasri and Brandenburg 2017) and our new POR-based SAG analysis. a An example job set with release jitter. b Visual representation of release intervals and deadlines. c SAG constructed by the analysis of Nasri and Brandenburg (2017). d SAG constructed by our POR-based analysis for the same system

When a given job set has timing uncertainties, e.g., due to release jitter or execution time variation, the exact release or execution times of the jobs are not known. Since an online JLFP scheduler takes its decisions by looking at the released jobs in the ready queue when the processor is available, multiple schedules might be generated depending on the release order of jobs and the completion time of already running jobs (called execution scenarios).

The current SAG analysis (Nasri and Brandenburg 2017) processes one scheduling decision at a time as can be seen on the labels of the edges in Fig. 1c. It starts from an idle system (state $v_1$) and looks for all next possible scheduling decisions. In our example, $J_1$ has no release jitter and is released at time 0. Since it is the first and only job in the ready queue in $v_1$, it will always be dispatched before other jobs under a work-conserving scheduling policy, hence, there is only one edge from $v_1$ to $v_2$.

However, due to the non-deterministic execution time of $J_1$, the processor may become available for other jobs at any time from 7 to 13 (note that 7 is the BCET and 13 the WCET of $J_1$). The SAG abstracts these uncertainties in an uncertainty interval $[A_1^{min}(v_2), A_1^{max}(v_2)] = [7, 13]$ on state $v_2$ which means that the processor may possibly be available for other jobs at time 7 and will certainly be available at time 13.

Representing a system state using an uncertainty interval allows SAG to fairly reduce the number of states needed to keep track of different schedules. However, it also forces the analysis to work with uncertainties. Namely, now to decide how $v_2$ will change after the next scheduling decision, SAG must consider any job that can be dispatched next in this state. In our example, due to the release jitter, either $J_2$, $J_3$, or $J_5$ can be dispatched next (or can be released next), after which any of the two remaining jobs can be dispatched. For example, if $J_5$ is released at time 5 and $J_2$ and $J_3$ are released at time 9 and 8, respectively, and the execution time of $J_1$ is 7, then the scheduler will dispatch job $J_5$, then job $J_3$, and finally job $J_2$. Alternatively, we could see a scenario in which $J_2$ is dispatched first (e.g., when it is released at time 6). The SAG captures all these scenarios in the graph by adding out-going edges to the states for each possible scheduling decision. After building the graph, the smallest and largest observed finish time of a job (on any edge with the label of that job) is reported as the BCRT and WCRT of the job, respectively.

It becomes clear from the above discussion that, when there are large uncertainties in the timing parameters, the analysis will face a state-space explosion due to the combinatorial increase in the number of possible orderings between jobs. Our key observation to improve the performance of the SAG analysis is that the exploration of many of these job execution orderings is not relevant to asserting the schedulability of the job set, as none of these orderings may lead to a deadline miss.

For example, the graph in Fig. 1c, has 10 nodes and 14 edges. Yet, none of the possible job execution orderings of $J_2$, $J_3$, and $J_5$ considered in the graph may lead to a deadline miss. Ideally, we would want to skip over these three jobs without exploring every individual job execution ordering. By avoiding the exploration of such scenarios, we could get a performance gain in the analysis and have a much smaller graph like the one shown in Fig. 1d.

4 Partial-order reduction (POR)

Our key idea is to identify subsets of jobs for which the combinatorial exploration of all orderings is irrelevant to the schedulability of the job set. Exploring these combinations is irrelevant when (i) all scenarios lead to the same system state and (ii) none of the jobs observe a deadline miss. Dispatching such jobs can be considered in a single step (that combines all those scheduling decisions), which further defers the state-space explosion. The POR technique proposed in this work allows us to identify such job orderings and treat them as a batch of scheduling decisions on a single edge in the SAG.

Figure 1d shows the SAG constructed using our proposed POR technique, where $J_2$, $J_3$, and $J_5$ are combined and assigned to a single edge, removing the need to enumerate all possible scenarios between these jobs and shrinking the resulting SAG. Note that the interval recorded in $v_9$ in Fig. 1c is the same as the interval recorded in $v_3$ in Fig. 1d, even though the latter did not explore all different scenarios.

As shown earlier, when expanding a state $v_p$, the original SAG analysis (Nasri and Brandenburg 2017) simply adds a new vertex (state) for each job that is a direct successor of $v_p$.

Definition 2

(Nasri et al. 2019) Let $\mathcal {J}^P$ be the set of jobs already dispatched until reaching state $v_p$. A job $J_j \in \mathcal {J} {\setminus } \mathcal {J}^P$ is a direct successor for path P ending in vertex $v_p$ iff there exists an execution scenario in which job $J_j$ is dispatched after state $v_p$ and before any other job.

In this work, we use POR to determine whether a set of future (i.e., not yet dispatched) jobs can be “reduced” to a single edge that encompasses all orderings of the original jobs without explicitly exploring all these orderings. We call the candidate job set $\mathcal {J}^S$ considered for a reduction to a single edge the candidate reduction set. If the candidate reduction set meets the conditions for a safe POR (as will be defined in Definition 5), it is added to the graph using a single edge and vertex. Otherwise, the graph is expanded with a new vertex for each direct successor as per the original SAG.

4.1 Problem definition

An important property of the original schedulability analysis of Nasri and Brandenburg (2017) is that it is both an exact schedulability and an exact response-time analysis.

Definition 3

An analysis is an exact schedulability analysis iff (i) for all job sets that are deemed schedulable by the analysis, there is no execution scenario that may result in a deadline miss, and (ii) for all job sets deemed unschedulable by the analysis, there is at least one execution scenario that results in a deadline miss.

Definition 4

An analysis is an exact response-time analysis iff (i) there is no execution scenario such that any job has a response-time smaller than the best-case response time (BCRT) or larger than the WCRT returned by the analysis for that job, and (ii) for each job, there must be an execution scenario where the job experiences a response time equal to the computed BCRT and another where it experiences the computed WCRT.

However, since the goal of POR is to eliminate the need to explore excessive job execution orderings, we need to make a trade-off between the exactness of the analysis and its scalability. In this work, we propose an exact schedulability analysis that returns safe but not tight response-time bounds (i.e., the lower bound reported by our solution might be smaller than the actual BCRT of a job and the upper bound reported by our solution might be larger than the actual WCRT of the job) in exchange for a reduced state-space. That is, we present an analysis that satisfies both conditions (i) and (ii) of Definition 3 but only condition (i) of Definition 4.

Thus, we define a safe partial-order reduction as follows.

Definition 5

A POR of a set of jobs $\mathcal {J}^S$ is safe iff it maintains both conditions of Definition 3 (i.e., provide an exact schedulability analysis) and satisfies condition (i) in Definition 4 (i.e., derives safe bounds on the response time).

The key to having a safe POR is that the jobs in the reduction set do not affect the response time of the jobs that are not contained in the reduction set. Therefore, we define a safe reduction set as follows.

Definition 6

Given a system state $v_p$, a set of jobs is a safe reduction set (denoted by $\mathcal {J}^M(v_p)$) iff there is no other job in $\mathcal {J} \setminus (\mathcal {J}^M(v_p) \cup \mathcal {J}^P)$ that can start executing before all jobs in $\mathcal {J}^M(v_p)$ finish their execution.

For simplicity, we omit to specify the state in the notation and simply denote a safe reduction set by $\mathcal {J\,}^M$ when it is apparent from the context which state is being referred to. We will discuss how to compute $\mathcal {J\,}^M$ in detail in Sect. 4.4.

Having defined the criteria that should hold for a safe POR with a safe reduction set, we are ready to formally introduce our problem as follows:

Problem 1

Given a system state $v_p$, find a safe reduction set $\mathcal {J\,}^M$ that satisfies the conditions of Definitions 5 and 6.

4.2 Overview of the solution

Fig. 2

An overview of the partial-order reduction before exploring a state $v_p$: from the initial candidate reduction set to constructing a safe reduction set

This section provides an overview of our solution for partial-order reduction (shown in Fig. 2). As mentioned earlier, the key idea is to construct a safe reduction set $\mathcal {J\,}^M$ before letting the original SAG analysis explore a state $v_p$. If we find such a safe reduction set, then we add all jobs in $\mathcal {J\,}^M$ on one single edge that evolves state $v_p$ to the next system state (as shown in the example in Fig. 1d). Otherwise, we let the original SAG analysis explore all the possible states reachable from state $v_p$. In that case, one outgoing edge per potential direct successor job of state $v_p$ will be added to $v_p$. These two outcomes are shown on the right side of Fig. 2. A more formal explanation of this process will be presented in Sect. 4.9 (Algorithm 4), after we put all pieces of the analysis together.

There are various ways to find out which jobs could form a safe reduction set. However, the method used to form one such set must have low computational complexity, as otherwise, it increases, instead of decreasing, the overhead of building the SAG. To have an efficient solution, we follow a greedy iterative approach (shown on the left side of Fig. 2, and later formalized in Algorithm 4). We first form an initial candidate job set (Step 1) and then repeatedly expand it to include any job that may interfere with the execution of the jobs in the candidate set (Steps 2–5). An interfering job is one that can potentially execute between two jobs in the candidate set.

We now describe each step of the analysis shown in Fig. 2. Since jobs that satisfy the conditions of Definition 2 (according to the original SAG analysis) have a chance to be direct successors of the state $v_p$, we start by an initial candidate reduction set $\mathcal {J\,}^S$ that is obtained by adding jobs that the original SAG analysis would naturally consider as direct successors of $v_p$ (note that at this stage, we do not add anything to the graph). Figure 3a shows an example of an initial candidate reduction set $\mathcal {J\,}^S= \{J_1, J_2\}$. Both $J_1$ and $J_2$ have a chance to be dispatched after state $v_p$ before any other job such as $J_3$ or $J_4$. The job $J_3$ does not belong to the initial $\mathcal {J\,}^S$ because it cannot be dispatched before $J_1$ since $J_1$ is certainly released by time 8 and has a higher-priority than $J_3$.

In Step 2, we check if there are jobs not part of the candidate set $\mathcal {J\,}^S$ that could potentially interfere with jobs in $\mathcal {J\,}^S$. In the example shown in Fig. 3a, $J_3$ could interfere with $\mathcal {J\,}^S$ because in some execution scenarios like the one shown in Fig. 3b, it could execute before $J_2$ (which is in $\mathcal {J\,}^S$). Later in Sect. 4.4, we will discuss how to identify such interfering jobs using the two main properties of the underlying scheduling policy: its work-conserving and JLFP properties (Sects. 4.4.1 and 4.4.2).

Fig. 3

a An example of an initial candidate reduction set $\mathcal {J\,}^S= \{J_1, J_2\}$, b an execution scenario in which $J_3$ interferes with $\mathcal {J\,}^S$

If no other job that does not belong to $\mathcal {J\,}^S$ could interfere with $\mathcal {J\,}^S$, then in Step 6, we check if the jobs in $\mathcal {J\,}^S$ can have a deadline miss. We assert schedulability of these jobs by obtaining a lower and an upper bound on the response-time of each job. These bounds will later be used by Algorithm 1 (line 6) to form a new state after applying POR on the jobs in $\mathcal {J\,}^S$. Algorithm 1 in turn calls Algorithms 2 and 3 (introduced in Sect. 4.8).

To limit the overhead of POR, we limit the complexity of Step 6 in Fig. 2 to a polynomial complexity (w.r.t. the number of jobs in $\mathcal {J\,}^S$). We do so by designing two polynomial-time methods to obtain the response-time bounds of the jobs in $\mathcal {J\,}^S$ (Sect. 4.6). One of them derives the response-time bounds using a fixed-point iteration method (Eqs. (6) and (7)) and the other uses a priority-agnostic simulation-based method (Algorithms 2 and 3).

In the rest of this section, we formally describe the solution and provide more details for each of the steps mentioned before.

4.3 Graph generation using partial-order reduction

We integrate the partial-order reduction step in the design of the schedule-abstraction graph by introducing Algorithm 1. The output of this algorithm is a complete SAG that is built using POR whenever it could be applied. Algorithm 1 is based on the SAG construction algorithm of Nasri et al. (2019), with the addition of POR at lines 4–8.

We first create a safe reduction set $\mathcal {J\,}^M$ at line 4 (using Algorithm 4 which will be presented later in Sect. 4.9). If $\mathcal {J\,}^M$ is not empty (line 5), Algorithm 1 applies POR. It computes a lower and upper bound, denoted by $\overline{EFT}$ and $\overline{LFT}$, respectively, on the finish time of all jobs in $\mathcal {J\,}^M$ using Algorithms 2 and 3 introduced later in Sect. 4.4. A new vertex $v_k$ is then created using $\overline{EFT}$ and $\overline{LFT}$ as bounds on the earliest and latest time by which the processor may become available after executing all jobs in $\mathcal {J\,}^M$. Vertex $v_k$ is then added to the graph at line 7.

If Algorithm 4 returns an empty set $\mathcal {J\,}^M$ (i.e., no safe reduction set could be found), we continue with the original SAG analysis by applying the same expansion phase as in Nasri et al. (2019).

After the expansion phase (whether it uses POR or not), the algorithm is identical to the original SAG analysis as it applies the same merge phase introduced in Nasri et al. (2019) (lines 13–16) for every newly added vertex. Nasri and Brandenburg (2017) checks two conditions to merge two vertices $v_p$ and $v_k$: (i) the core-availability intervals of these two states must intersect, i.e., $[A_1^{min}(v_p), A_1^{max}(v_p)] ~\cap ~ [A_1^{min}(v_k), A_1^{max}(v_k)] \ne \emptyset$ and (ii) the set of jobs dispatched on a path from $v_1$ to $v_p$ must be the same as the set of jobs dispatched on a path from $v_1$ to $v_k$.

Fig. 4

Example of a schedule-abstraction graph with POR after the addition of states $v_9$ and $v_{10}$. a the SAG before merging $v_6$ and $v_9$, b the SAG after merging $v_6$ and $v_9$

However, when POR is applied, the number of jobs on the edges can vary depending on the number of jobs in the safe-reduction sets. As a result, going through all yet-to-be-expanded states might not be the most efficient way to check condition (ii) of the merge rules of the original SAG analysis. In order to improve the runtime of this step (basically, the runtime of the while-loop in lines 13–16), we keep the list of yet-to-be-expanded states sorted (in a non-decreasing order) according to the number of jobs on a path from $v_1$ to each state in the list. When checking for possible merge opportunities of a state $v_k$, we only compare it against states that encompass the same number of dispatched jobs (namely, they have the same number of jobs on the path from $v_1$ to those states) because otherwise Condition (ii) of the merge rule would obviously not hold. For example, after the creation of $v_9$ and $v_{10}$ in the example in Fig. 4a, the only other state that could be a candidate to be merged with $v_9$ is $v_6$. In this example, $v_{10}$ cannot be merged with any other state since there is no other state that encompasses four dispatch events. Figure 4b shows the resulting SAG after merging $v_6$ and $v_9$.

To increase the chance of state merging, while expanding the graph, we prioritize the states that encompass fewer dispatch events over others. Hence, as it can be seen on the vertex indices in the example in Fig. 4a, after states $v_1$ to $v_8$ have been created, the expansion phase has happened for $v_7$ and $v_8$ (but not for $v_5$ and $v_6$ which encompass a larger number of dispatch events (i.e., 5 and 3, respectively).

4.4 Constructing a safe reduction set

This section focuses on the construction of a safe reduction set. According to Definition 6, a candidate reduction set $\mathcal {J\,}^S$ is a safe reduction set iff there is no other job $J_x \in \mathcal {J} {\setminus } (\mathcal {J\,}^M(v_p) \cup \mathcal {J}^P)$ that may start to execute before the jobs in $\mathcal {J}^S$ complete. An interfering job for candidate reduction set $\mathcal {J}^S$ is thus defined as follows.

Definition 7

A job $J_x \in \mathcal {J} \setminus (\mathcal {J}^S\cup \mathcal {J}^P)$ is an interfering job for $\mathcal {J}^S$ iff $J_x$ can execute before any of the jobs in $\mathcal {J}^S$.

The conditions under which a job $J_x$ can interfere with $\mathcal {J}^S$ depend on the scheduling policy used for the job set under analysis. Since this work analyses work-conserving JLFP scheduling algorithms, the interference conditions relate to the work-conserving and priority-driven properties of the scheduling algorithm.

4.4.1 Work-conserving interference condition

Let $J_x \in \mathcal {J}\setminus (\mathcal {J}^S\cup \mathcal {J}^P)$ be a job that neither belongs to the set of already-dispatched jobs ($\mathcal {J}^P$) nor the candidate reduction set $\mathcal {J}^S$. The job $J_x$ can execute between two jobs in $\mathcal {J}^S$ if $J_x$ is released before the end of an idle interval between the execution of two jobs in $\mathcal {J}^S$. Consider the example in Fig. 5, where $\mathcal {J}^S= \{J_1, J_2\}$ and $J_x$ is $J_3$. In a scenario where $J_1$ is released at 6 and $J_2$ at 12, it is possible for a low-priority job such as $J_3$ to be dispatched between the two higher-priority jobs in $\mathcal {J}^S$, i.e., at time 11. This chance is provided for $J_3$ because it is released before (or at) the end of an idle interval.

In order to find out whether a job $J_x$ may start to execute within an idle interval between the execution of two jobs in $\mathcal {J}^S$, we need to determine when idle intervals may happen. To do so, we compute two bounds: (i) the earliest time by which an idle interval may start prior to the execution of a job $J_i \in \mathcal {J}^S$, and (ii) the latest time by which such idle interval may end. Lemma 1 below computes a bound for the latter.

Lemma 1

The latest idle interval before the execution of $J_i \in \mathcal {J}^S$ cannot end later than $r_i^{max}$.

Proof

By contradiction. Suppose that there could be an idle interval before the execution of $J_i \in \mathcal {J}^S$ that ends at $r_i^{max} + 1$. Then, it means that the processor remains idle until $r_i^{max} + 1$ even though $J_i$ is certainly released. This contradicts the assumption that the scheduling policy is work-conserving, as a work-conserving scheduling policy never keeps the processor idle when there is a ready job.

To determine whether there is a potential idle interval ending at $r_i^{max}$, we must compute when that idle interval may start. To do so, we first define the set of jobs in $\mathcal {J}^S$ that are certainly released before time t as

$$\begin{aligned} \mathcal {C}(t, v_p) = \{ J_j \in \mathcal {J}^S\mid r_j^{max} < t\} \end{aligned}$$

(1)

Now, let $\overline{EFT}(\mathcal {C}(t, v_p), v_p)$ be a lower bound on the finish time of all jobs in $\mathcal {C}(t, v_p)$. If $\overline{EFT}(\mathcal {C}(t, v_p), v_p)$ is strictly smaller than t, then there may be an idle interval starting at $\overline{EFT}(\mathcal {C}(t, v_p), v_p)$ and ending by t. Otherwise, there cannot be any idle interval immediately before t.

Therefore, based on the above discussion, we define the set of jobs in $\mathcal {J}^S$ before which an idle interval may exist as

$$\begin{aligned} \mathcal {J}^\delta = \{J_i \mid J_i \in \mathcal {J}^S~\wedge ~ \overline{EFT}(\mathcal {C}(r_i^{max}, v_p), v_p) < r_i^{max}\} \end{aligned}$$

(2)

Fig. 5

An example where $J_3$ interferes with a candidate reduction set $\mathcal {J}^S= \{J_1, J_2\}$ because $J_3$ releases before the end of an idle time in $\mathcal {J}^S$

We formally prove the above properties in the two following lemmas.

Lemma 2

Let $J_i$ be a job in $\mathcal {J}^S$ that is released at $r_i^{max}$. If there is an idle interval just before the execution of $J_i$ starts, then $\overline{EFT}(\mathcal {C}(r_i^{max}, v_p), v_p)$ is a lower bound on the start time of that idle interval.

Proof

Since by Eq. (1), all jobs in $\mathcal {C}(r_i^{max}, v_p)$ must have been released strictly before $r_i^{max}$, if there is an idle interval before $J_i$ starts to execute, then all the jobs in $\mathcal {C}(r_i^{max}, v_p)$ must have completed their execution by $r_i^{max}$ (by the work-conserving property).

Now, by contradiction, suppose that there is an idle interval that starts before $\overline{EFT}(\mathcal {C}(r_i^{max}, v_p), v_p)$. This means that the jobs in $\mathcal {C}(r_i^{max}, v_p)$ can finish before $\overline{EFT}(\mathcal {C}(r_i^{max}, v_p), v_p)$. This contradicts the fact that $\overline{EFT}(\mathcal {C}(r_i^{max}, v_p), v_p)$ is the EFT of the set of jobs $\mathcal {C}(r_i^{max}, v_p)$ as proven in Lemma 6.

Lemma 3

If $\mathcal {J}^\delta = \emptyset$, there exists no execution scenario such that there is an idle interval between the execution of two jobs in $\mathcal {J}^S(v_p)$ scheduled after $v_p$.

Proof

If $\mathcal {J\,}^\delta = \emptyset$ it means that for each $J_i \in \mathcal {J\,}^S$, $\overline{EFT}(\mathcal {C}(r_i^{max}, v_p), v_p) \ge r_i^{max}$. Since by definition, $\overline{EFT}(\mathcal {C}(r_i^{max}, v_p), v_p)$ is a lower bound on the finish time of $\mathcal {C}(r_i^{max}, v_p)$, the idle interval ending with $r_i^{max}$ is empty for each $r_i^{max}$. Hence, there is no idle interval between any two arbitrary jobs in $\mathcal {J\,}^S$.

For instance, given a candidate reduction set $\mathcal {J\,}^S= \{J_1, J_2\}$ as in the example of Fig. 5, $\mathcal {C}(r_1^{max}, v_p) = \mathcal {C}(8, v_p) = \emptyset$ and $\mathcal {C}(r_2^{max}, v_p) =\mathcal {C}(12, v_p) = \{J_1\}$. In this example, the earliest finish time of $J_1$ is at time 8 which happens when it is released at time 6, the processor becomes available at time 7 (note that $A_1^{min} = 7$), and $J_1$ has one unit of execution time (Sect. 4.5 will explain how to obtain $\overline{EFT}$). Finally, from Eq. (2), we get $\mathcal {J\,}^\delta = \{J_2\}$.

Now that we know when idle intervals between jobs in $\mathcal {J\,}^S$ may end, we can formulate the condition that should hold for a job to be able to interfere with the jobs in $\mathcal {J}^S$ due to the work-conserving property of the scheduling algorithm.

Lemma 4

If a job $J_x \in \mathcal {J}\setminus (\mathcal {J}^S\cup \mathcal {J}^P)$ can execute in an idle interval between two jobs in $\mathcal {J}^S$, then

$$\begin{aligned} \mathcal {J}^\delta \ne \emptyset \wedge r_x^{min} < \delta _{M}(v_p), \end{aligned}$$

(3)

where $\delta _{M}(v_p) = \max \{r_j^{max} \mid J_j \in \mathcal {J}^\delta \}$.

Proof

If $\mathcal {J}^\delta \ne \emptyset$, $\delta _{M}(v_p)$ is the latest end of an idle interval ending before the execution of the last job in $\mathcal {J}^S$. $J_x$ is released before $\delta _{M}(v_p)$, so $J_x$ will be a ready job at some idle instant before $\delta _{M}(v_p)$. As the scheduler is work-conserving it will not leave the processor idle when there is a ready job, and hence will schedule $J_x$. Thus, $J_x$ can execute between two jobs in $\mathcal {J}^S$ and interferes with $\mathcal {J}^S$.

Fig. 6

An example where $J_3$ interferes with a candidate reduction set $\mathcal {J}^S= \{J_1, J_2, J_4\}$ because $J_3$ releases before a lower-priority job in $\mathcal {J}^S$ starts (in this case, $J_4$)

Going back to the example in Fig. 5 with $\mathcal {J}^S= \{J_1, J_2\}$, we see that for the job $J_3$, the condition Eq. (3) is ‘true’ because $\mathcal {J}^\delta = \{J_2\}$, $\delta _{M}(v_p) = 12$, and $r_3^{min} = 11 < 12$.

4.4.2 Priority-driven interference condition

A job $J_x \in \mathcal {J}\setminus (\mathcal {J}^S\cup \mathcal {J}^P)$ can execute between two arbitrary jobs in $\mathcal {J}^S$ if it has a higher priority than a job $J_l \in \mathcal {J}^S$ and is released before $J_l$ started to execute. Figure 6 shows an example of a higher-priority job (namely $J_3$) interfering with $\mathcal {J}^S= \{J_1, J_2, J_4\}$ because it is released before the time at which a lower-priority job in $\mathcal {J}^S$ (i.e., $J_4$) has started executing.

Let $\mathcal {J}^{high}$ be the set containing all the jobs not in $\mathcal {J}^S$ that have a higher priority than at least one job in $\mathcal {J}^S$, formally

$$\begin{aligned} \mathcal {J}^{high} = \{ J_x \mid J_x \in \mathcal {J}\setminus (\mathcal {J}^S\cup \mathcal {J}^P) ~\wedge ~ \exists J_l \in \mathcal {J}^S, p_x < p_l \} \end{aligned}$$

(4)

Then, Lemma 5 provides a sufficient condition under which there is no interfering job for a candidate reduction set $\mathcal {J\,}^S$.

Lemma 5

Let $\widehat{LST}_i(\mathcal {J\,}^S, v_p)$ be an upper bound on the start time of any job $J_i \in \mathcal {J\,}^S$. If there exists no $J_x \in \mathcal {J}{\setminus } (\mathcal {J\,}^S\cup \mathcal {J\,}^P)$ such that Eq. (3) holds and $\forall J_y \in \mathcal {J\,}^{high}$, $\forall J_l \in \mathcal {J\,}^S$ such that $p_y < p_l$ we have $r_y^{min} > \widehat{LST}_l(\mathcal {J\,}^S, v_p)$, then there exists no interfering job for $\mathcal {J\,}^S$ and $\mathcal {J\,}^S$ is a safe reduction set.

Proof

Under a non-preemptive work-conserving JLFP policy, a job $J_x \in \mathcal {J}{\setminus } (\mathcal {J\,}^S\cup \mathcal {J\,}^P)$ can only start its execution before a job $J_i \in \mathcal {J\,}^S$ iff: (i) $J_x$ has a higher priority than $J_i$ and $J_x$ is possibly released before $J_i$ starts executing or (ii) if the processor is idle before the start of $J_i$, and $J_x$ possibly releases before or during this idle time interval.

Lemma 4 proves that Eq. (3) must hold if $J_x$ interferes with $\mathcal {J\,}^S$ by executing in an idle interval. Since by the lemma’s assumption, Eq. (3) does not hold for any job $J_x \in \mathcal {J} {\setminus } (\mathcal {J\,}^S\cup \mathcal {J\,}^P)$, no job respects condition (ii). Therefore, if the claim does not hold, then there must be a set of jobs $\mathcal {J\,}^I$ not in $\mathcal {J\,}^S$ (i.e., $\mathcal {J\,}^I \cap \mathcal {J\,}^S= \emptyset$) that satisfies condition (i). That is, for all $J_x \in \mathcal {J\,}^I$, there exists $J_l \in \mathcal {J\,}^S$ such that $p_x < p_l$ and $J_x$ is released before $J_l$ starts executing.

By assumption, $\widehat{LST}_l(\mathcal {J\,}^S, v_p)$ is an upper bound on the start time of any job $J_l \in \mathcal {J\,}^S$ when no job interferes with $\mathcal {J\,}^S$. Hence, for the jobs in $\mathcal {J\,}^I$ to interfere with $\mathcal {J\,}^S$, there must be at least one job $J_y \in \mathcal {J\,}^I$ and a job $J_l \in \mathcal {J\,}^S$ such that $p_y < p_l$ and $J_y$ is released before or at $\widehat{LST}_l(\mathcal {J\,}^S, v_p)$ (from condition (i)). This contradicts the lemma’s assumption that $r_y^{min} > \widehat{LST}_l(\mathcal {J\,}^S, v_p)$. Therefore, the set $\mathcal {J\,}^I$ must be empty, thereby proving that no job can interfere with $\mathcal {J\,}^S$ and, by Definition 6, $\mathcal {J\,}^S$ is a safe reduction set.

Corollary 1

A job $J_x \in \mathcal {J} \setminus (\mathcal {J\,}^S\cup \mathcal {J\,}^P)$ may interfere with jobs in the set $\mathcal {J\,}^S$ only if either Eq. (3) holds or $J_x \in \mathcal {J\,}^{high} \wedge \exists J_l \in \mathcal {J\,}^S\mid p_x < p_l \wedge r_x^{min} \le \widehat{LST}_l(\mathcal {J\,}^S, v_p)$.

Proof

It is the contra-positive of Lemma 5.

An upper bound $\widehat{LST}_i(\mathcal {J\,}^S, v_p)$ on the start time of any job $J_i \in \mathcal {J\,}^S$ can be computed using Eq. (8) presented in Sect. 4.7.

4.5 Computing $\overline{EFT}$

Lemmas 2–5 require a lower bound $\overline{EFT}(\mathcal {C}(r_i^{max}, v_p), v_p)$ on the finish time of any job in the job set $\mathcal {C}(r_i^{max}, v_p)$.

A lower bound on the EFT of any set of jobs $\mathcal {J\,}^X$ can be computed by scheduling all jobs in $\mathcal {J\,}^X$ as early as possible and assume that they execute for their BCET. Algorithm 2 shows how to obtain this lower bound, i.e., $\overline{EFT}(\mathcal {J\,}^X, v_p)$. Further in Lemma 6, we prove that $\overline{EFT}(\mathcal {J\,}^X, v_p)$ as calculated by Algorithm 2 is indeed a lower bound on the earliest time at which the processor can possibly become available after dispatching the jobs in $\mathcal {J\,}^X$ in any possible execution order following system state $v_p$.

Lemma 6

The set of jobs $\mathcal {J\,}^X$ scheduled after state $v_p$ cannot complete its execution before $\overline{EFT}(\mathcal {J\,}^X, v_p)$ as returned at line 6 of Algorithm 2.

Proof

At line 1 of Algorithm 2, the jobs in $\mathcal {J\,}^X$ are sorted in ascending order of $r^{min}$, and any ties are broken by highest priority. Let $J_k$ denote the $k^{\text {th}}$ job in the ordered set $\mathcal {J\,}^X$, and let $J_k^X = \{J_1, J_2, \ldots , J_k \}$ denote the re-ordered (re-indexed) set of jobs in $\mathcal {J\,}^X$. And finally, let $\overline{EFT}_k$ be the value computed at line 4 of Algorithm 2 after the $k^{\text {th}}$ iteration of the for-loop.

We prove by induction that $\overline{EFT}_k$ is a lower bound on the finish time of all jobs in $J_k^X$ assuming that no job $J_j \in \mathcal {J} {\setminus } (J^P \cup J_k^X)$ executes between the jobs in $J_k^X$. The base case considers the first job $J_1$. Job $J_1$ is the job with the earliest $r^{min}$ in $\mathcal {J\,}^X$, and in case of a tie, the highest-priority one. We prove that line 4 of Algorithm 2 computes a lower bound on the EFT of $J_1$. Since a job cannot start executing before it is released and the processor is available, $\max \{A_1^{min}, r_1^{min}\}$ is a lower bound on the start time of $J_1$. Therefore, $J_1$ cannot finish before $\max \{A_1^{min}, r_1^{min}\} + C_1^{min}$ as computed at line 4 since $C_1^{min}$ is the BCET of $J_1$.

In the induction step, $\overline{EFT}_{k-1}$ is a lower bound on the finish time of the jobs in $\{J_1, \ldots , J_{k-1}\}$ assuming no other job executes between them. We show that $\overline{EFT}_k$ as computed at line 4 of Algorithm 2 is the EFT of all jobs $\{J_1, \ldots , J_k\}$. We divide the proof into two cases depending on whether $J_k$ starts its execution before or after the completion of the jobs in $J_{k-1}^X = \{J_1, \ldots , J_{k-1} \}$.

Case (i): Assume that $J_k$ does not start its execution before the jobs in $J_{k-1}^X$ have finished, namely, it does not start before $\overline{EFT}_{k-1}$. We know that $J_k$ cannot start before $r_k^{min}$ since $J_k$ cannot start before it is released. Thus, $\max \{\overline{EFT}_{k-1}, r_k^{min}\}$ is a lower bound on the start time of $J_k$. Since $C_k^{min}$ is the BCET of $J_k$, if $J_k$ starts executing at $\max \{\overline{EFT}_{k-1}, r_k^{min}\}$ then it cannot finish before $\overline{EFT}_k = \max \{\overline{EFT}_{k-1}, r_k^{min} + C_k^{min}\}$ as computed at line 4. Furthermore, since $J_k$ starts executing after all jobs in $J_{k-1}^X$ completed their own execution, the finish time $\overline{EFT}_k$ of $J_k$ is also a lower bound on the finish time of all the other jobs in $J_k^X = J_{k-1}^X \cup \{J_k\}$.

Case (ii): Assume that $J_k$ starts executing before $\overline{EFT}_{k-1}$. Let $s_k$ be the start time of $J_k$. By assumption, $s_k < \overline{EFT}_{k-1}$. Since $J_k$ cannot start before it is released, $r_k^{min} \le s_k$. We show that $\overline{EFT}_k$ computed as $\overline{EFT}_k = \overline{EFT}_{k-1} + C_k^{min}$ by Algorithm 2 is a lower bound on the finish time of $J_k^X = J_{k-1}^X \cup \{J_k\}$. Since all jobs in $J_{k-1}^X$ have their release before that of $J_k$ by line 1 of Algorithm 2, the processor executes at least $\overline{EFT}_{k-1} - s_k$ time units of workload from the jobs in $J_{k-1}^X$ after $s_k$. Thus, when including $J_k$, the processor must execute at least $\overline{EFT}_{k-1} - s_k + C_k^{min}$ time units of workload of $J_k^X$ after $s_k$. Therefore, the jobs in $J_k^X$ cannot complete before $s_k + \overline{EFT}_{k-1} - s_k + C_k^{min} = \overline{EFT}_{k-1} + C_k^{min}$, which is $\overline{EFT}_k$ as computed at line 4 of Algorithm 2.

Hence, if we apply the inductive step to all jobs in $\mathcal {J\,}^X$, then line 6 of Algorithm 2 returns a lower bound on the earliest time the processor can finish scheduling all jobs in $\mathcal {J\,}^X$.

4.6 Exact finish time intervals of a safe reduction set

If Lemma 5 holds for a job set $\mathcal {J\,}^S$, then $\mathcal {J\,}^S$ is a safe reduction set (denoted by $\mathcal {J\,}^M$ from now on) that satisfies Definition 6. Algorithm 1 thus requires to compute a lower bound (EFT) and upper bound (LFT) on the finish time of all jobs in $\mathcal {J\,}^M$ (line 6 of Algorithm 1). In this section, we explain how to compute exact bounds on the finish time of a safe reduction set $\mathcal {J\,}^M$ where an exact EFT and LFT are defined as follows.

Definition 8

The EFT of a safe reduction set $\mathcal {J\,}^M$ is exact iff the set of jobs $\mathcal {J\,}^M$ cannot complete its execution before EFT and there exists an execution scenario such that all jobs in $\mathcal {J\,}^M$ have completed exactly at EFT.

Definition 9

The LFT of a safe reduction set $\mathcal {J\,}^M$ is exact iff the set of jobs $\mathcal {J\,}^M$ cannot complete its execution later than LFT and there exists an execution scenario such that all jobs in $\mathcal {J\,}^M$ have completed exactly at LFT.

First, we prove using Lemma 7 and Corollary 2 that the bound $\overline{EFT}(\mathcal {J\,}^M, v_p)$ as returned by line 6 of Algorithm 2 is an exact bound on EFT when $\mathcal {J\,}^M$ is a safe reduction set.

Lemma 7

There exists an execution scenario such that all jobs in $\mathcal {J\,}^M$ have completed exactly at $\overline{EFT}(\mathcal {J\,}^M, v_p)$ as returned by line 6 of Algorithm 2.

Proof

If each $J_i \in \mathcal {J\,}^M$ releases at $r_i^{min}$ and executes for exactly $C_i^{min}$ time units and the processor becomes available at $A_1^{min}$, then, the execution of $\mathcal {J\,}^M$ will complete exactly at $\overline{EFT}(\mathcal {J\,}^M, v_p)$ as returned by line 6 of Algorithm 2 since this algorithm practically simulates the schedule of the jobs in $\mathcal {J\,}^M$ under the given execution scenario. Hence, there exists an execution such that all jobs in $\mathcal {J\,}^M$ have completed exactly at $\overline{EFT}(\mathcal {J\,}^M, v_p)$. 

Corollary 2

The $\overline{EFT}(\mathcal {J\,}^M, v_p)$ as returned by line 6 of Algorithm 2 is the exact earliest finish time of $\mathcal {J\,}^M$.

Proof

The set of jobs $\mathcal {J\,}^M$ cannot complete its execution before $\overline{EFT}(\mathcal {J\,}^M, v_p)$ (Lemma 6), and there exists an execution scenario such that the jobs in $\mathcal {J\,}^M$ complete at $\overline{EFT}(\mathcal {J\,}^M, v_p)$ (Lemma 7). Hence, $\overline{EFT}(\mathcal {J\,}^M, v_p)$ is exact.

The LFT of a safe reduction set $\mathcal {J\,}^M$ can be determined by scheduling all jobs as late as possible and by assuming that they execute for their WCET. Algorithm 3 does exactly that, and Lemmas 8, 9 and Corollary 3 prove that the bound $\overline{LFT}(\mathcal {J\,}^M, v_p)$ as returned by line 6 of Algorithm 3 is an exact bound on LFT when $\mathcal {J\,}^M$ is a safe reduction set.

Lemma 8

The set of jobs $\mathcal {J\,}^M$ scheduled after state $v_p$ cannot complete their execution later than $\overline{LFT}(\mathcal {J\,}^M, v_p)$ as returned by line 6 of Algorithm 3.

Proof

At line 1 of Algorithm 3, the jobs in $\mathcal {J\,}^M$ are sorted in ascending order of $r^{max}$, and any ties are broken by highest priority. Let $J_k$ denote the $k^{th}$ job in the ordered set and let $J_k^M = \{J_1, \ldots , J_k \}$ denote the re-indexed set of jobs in $\mathcal {J\,}^M$ sorted by their $r^{max}$ (in line 1 of the algorithm). Finally, let $\overline{LFT}_k$ be the value computed at line 4 of Algorithm 3 after the $k^{th}$ iteration of the for-loop.

We prove by induction that $\overline{LFT}_k$ is an upper bound on the finish time of all jobs in $J_k^M$ assuming that no job $J_j \in \mathcal {J} {\setminus } (J^P \cup J_k^M)$ executes between the jobs in $J_k^M$. The base case considers the first job $J_1$. $J_1$ is the job with the earliest $r^{max}$ in $\mathcal {J\,}^M$, and in case of a tie, the highest priority one. We prove that line 4 of Algorithm 3 computes an upper bound on the LFT of $J_1$. Because the scheduler is work-conserving, a job cannot start later than the time by which it is certainly released and the processor is certainly available. Hence, $\max \{A_1^{max}, r_1^{max}\}$ is an upper bound on the start time of $J_1$. If $J_1$ starts at $\max \{A_1^{max}, r_1^{max}\}$ it cannot finish after $\max \{A_1^{max}, r_1^{max}\} + C_1^{max}$ as computed at line 4 of Algorithm 3 since $C_1^{max}$ is the WCET of $J_1$.

In the induction step, $\overline{LFT}_{k-1}$ is an upper bound on the finish time of the jobs in $\{J_1, \ldots , J_{k-1}\}$ assuming no other job executes between them. We show that $\overline{LFT}_k$ as computed at line 4 of Algorithm 3 is the LFT of all jobs $\{J_1, \ldots , J_k\}$. We divide the proof into two cases depending on whether $J_k$ starts its execution before or after the completion of the jobs in $J_{k-1}^M = \{J_1, \ldots , J_{k-1} \}$.

Case (i): If $J_k$ does not start its execution before the jobs in $J_{k-1}^M$ have finished, then, we know that $\overline{LFT}_{k-1}$ is the latest time at which the processor becomes available to other jobs including $J_k$. We also know that $J_k$ will be released at the latest by time $r_k^{max}$. Hence, an upper bound on the start time of $J_k$ is $\max \{\overline{LFT}_{k-1}, r_k^{max}\}$ because at that time, a work-conserving scheduler must dispatch a job (in this case, $J_k$). Since $C_k^{max}$ is the WCET of $J_k$, if $J_k$ starts executing at $\max \{\overline{LFT}_{k-1}, r_k^{max}\}$ then it cannot finish after $\overline{LFT}_k = \max \{\overline{LFT}_{k-1}, r_k^{max} + C_k^{max}\}$ as computed at line 4. Furthermore, since $J_k$ starts executing after all jobs in $J_{k-1}^M$ completed their own execution, the finish time $\overline{LFT}_k$ of $J_k$ is also an upper bound on the finish time of all the other jobs in $J_k^M = J_{k-1}^M \cup \{J_k\}$.

Case (ii): If $J_k$ starts executing before $\overline{LFT}_{k-1}$, then let $s_k$ be the start time of $J_k$. By assumption, $s_k < \overline{LFT}_{k-1}$. We show that $\overline{LFT}_k$ computed as $\overline{LFT}_k = \overline{LFT}_{k-1} + C_k^{max}$ by Algorithm 3 is an upper bound on the finish time of $J_k^M = J_{k-1}^M \cup \{J_k\}$. Since all jobs in $J_{k-1}^M$ have their latest release ($r^{max}$) before that of $J_k$ by line 1 of Algorithm 3, the processor executes at most $\overline{LFT}_{k-1} - s_k$ time units of workload from the jobs in $J_{k-1}^M$ after $s_k$. Thus, the processor must execute at most $\overline{LFT}_{k-1} - s_k + C_k^{max}$ time units of workload of $J_k^M$ after $s_k$. Therefore, the jobs in $J_k^M$ cannot complete after $s_k + (\overline{LFT}_{k-1} - s_k + C_k^{max}) = \overline{LFT}_{k-1} + C_k^{max}$, which is $\overline{LFT}_k$ as computed at line 4 of Algorithm 3.

Hence, if we apply the inductive step to all jobs in $\mathcal {J\,}^M$, then line 6 of Algorithm 3 returns an upper bound on the latest time the processor can finish scheduling all jobs in $\mathcal {J\,}^M$. 

Lemma 9

There exists an execution scenario such that all jobs in $\mathcal {J\,}^M$ have completed exactly at $\overline{LFT}(\mathcal {J\,}^M, v_p)$ as returned by line 6 of Algorithm 3.

Proof

If each $J_i \in \mathcal {J\,}^M$ releases at $r_i^{max}$ and executes for exactly $C_i^{max}$ time units and the processor becomes available at $A_1^{max}$, then, the execution of $\mathcal {J\,}^M$ will complete exactly at $\overline{LFT}(\mathcal {J\,}^M, v_p)$ as returned by line 6 of Algorithm 3. Hence, there exists an execution such that all jobs in $\mathcal {J\,}^M$ have completed exactly at $\overline{LFT}(\mathcal {J\,}^M, v_p)$.

Corollary 3

The $\overline{LFT}(\mathcal {J\,}^M, v_p)$ as returned by line 6 of Algorithm 3 is the exact latest finish time of $\mathcal {J\,}^M$.

Proof

The set of jobs $\mathcal {J\,}^M$ cannot complete its execution after $\overline{LFT}(\mathcal {J\,}^M, v_p)$ (Lemma 8), and there exists an execution scenario such that the jobs in $\mathcal {J\,}^M$ complete at $\overline{LFT}(\mathcal {J\,}^M, v_p)$ (Lemma 9). Hence, $\overline{LFT}(\mathcal {J\,}^M, v_p)$ is exact.

4.7 Exact schedulability analysis of a safe reduction set

In order to efficiently determine whether a deadline miss may happen for the jobs in $\mathcal {J\,}^M$, we use a sufficient schedulability test on $\mathcal {J\,}^M$. If $\mathcal {J\,}^M$ passes the sufficient test, i.e., it is certainly schedulable, we apply the POR and create a single edge for $\mathcal {J\,}^M$ in the SAG (lines 5 to 7 in Algorithm 1). Otherwise, we do not know whether a deadline miss could happen unless we explore all possible execution orderings of the jobs in $\mathcal {J\,}^M$. Therefore, we reject $\mathcal {J\,}^M$ and let the original SAG analysis explore the schedules that could be generated from these jobs for us (line 10 in Algorithm 1).

The sufficient schedulability test for $\mathcal {J\,}^M$ is defined as

$$\begin{aligned} \forall J_i \in \mathcal {J\,}^M, \widehat{LFT}_{i}(\mathcal {J\,}^M, v_p) \le d_i, \end{aligned}$$

(5)

where $\widehat{LFT}_{i}(\mathcal {J\,}^M, v_p)$ is an upper bound on the finish time of $J_i \in \mathcal {J\,}^M$ when scheduled after state $v_p$.

In order to compute $\widehat{LFT}_{i}(\mathcal {J\,}^M, v_p)$, we need an upper bound on the start time of every job $J_i \in \mathcal {J\,}^M$.

4.7.1 A fixed-point iteration to obtain EFT and LFT bounds

As shown by Davis et al. (2007), for a non-preemptive JLFP scheduling policy, the following execution scenario results in a late start time for any job $J_i$: a lower priority job starts its execution just before $J_i$ is released and, subsequently, all higher-priority jobs interfere with $J_i$.

While the above-mentioned scenario is very pessimistic and often does not happen in practice, assuming that scenario allows us to easily compute an upper bound on the start time of $J_i$ using a fixed-point iteration equation. Note that it is possible to compute a tighter upper bound on $J_i$’s start time. However, it would require exploring more execution scenarios and thus generate more overhead. Consequently, we compute an upper bound $s_i(v_p)$ on the start time of any job $J_i \in \mathcal {J\,}^M(v_p)$ using the following recursive equations and stopping when $s_i^{(k)} = s_i^{(k-1)}$.

$$\begin{aligned} s_i^{(0)}= & {} \max \{A_1^{max}, r_i^{max} - 1 + \max _{\forall J_j \in \mathcal {J\,}^M(v_p)}\{C_j^{max} \mid p_i < p_j \} \} \end{aligned}$$

(6)

$$\begin{aligned} s_i^{(k)}= & {} s_i^{(0)} + \sum _{ \{ J_j \mid J_j \in \mathcal {J\,}^M(v_p) \wedge r_j^{min} \le s_i^{(k-1)} \wedge p_j < p_i\} }{C_j^{max}} \end{aligned}$$

(7)

Figure 7a shows how the fixed-point iteration works on a simple example. In this example, $J_3$ is the job under consideration and $\mathcal {J\,}^M= \{J_1, J_2, J_3, J_4\}$. The initial value of $s_3^{(0)}$ is the maximum between $A_1^{max}$ and the combination of the blocking term (the WCET of the largest low-priority job in $\mathcal {J\,}^M$) plus $r_3^{max} - 1$.

Lemma 10

The fixed-point iteration in Eq. (7) converges.

Proof

$s_i^{(k)}$ increases or remains constant as only non-negative terms are added because $\forall J_j$, $C_j^{max} \ge 0$. Furthermore, $s_i^{(k)}$ increases when there exists $J_j \in \mathcal {J\,}^M(v_p)$ such that $J_j$ has a higher priority than $J_i$ and $s_i^{(k - 2)} < r_j^{min} \le s_i^{(k - 1)}$. If such a $J_j$ does not exist, there is no more job that has a higher priority than $J_i$ and is possibly released at $s_i^{(k - 1)}$ and $s_i^{(k)} = s_i^{(k-1)}$. Therefore, as long as it does not converge, Eq. (7) must add at least one more job from $\mathcal {J\,}^M(v_p)$ at every iteration. Since the number of jobs in $\mathcal {J\,}^M(v_p)$ is finite, the number of iterations by Eq. (7) is upper bounded by $|\mathcal {J\,}^M(v_p)|$. This proves the lemma.

Lemma 11

$J_i \in \mathcal {J\,}^M(v_p)$ starts executing no later than $s_i(v_p)$.

Proof

The proof is by contradiction. Assume that the processor starts executing $J_i~\in ~\mathcal {J\,}^M(v_p)$ later than $s_i(v_p)$. Then, there should either be a larger blocking by a lower-priority job or a larger interference by higher-priority jobs than accounted for by $s_i(v_p)$. We divide the proof into two cases depending on whether there is a larger blocking or interference for $J_i$. We show that there cannot be a larger blocking or interference than what is already included in $s_i(v_p)$.

Case (i): There is a larger blocking for $J_i$. This means either the processor becomes possibly available later than $A_1^{max}$, or there exists a job with a lower priority that can execute for longer than what is used in Eq. (6). The former contradicts the assumption that $A_1^{max}$ is the exact latest time at which the processor becomes possibly available. The latter contradicts the assumptions that a lower-priority job cannot execute for longer than its WCET $C_j^{max}$ (note that Eq. (6) uses the lower-priority job with the largest WCET, so no other job with a higher WCET can block $J_i$).

Case (ii): There is a larger interference for $J_i$. Equation (7) terminates when there is no more higher-priority job that possibly releases at $s_i^{(k - 1)}$. If $J_i$ can start later than $s_i(v_p)$, the jobs currently included in $s_i(v_p)$ can execute longer than their WCET, or there must be a higher-priority job that is released before $J_i$ starts but is not included in $s_i(v_p)$. The former is not possible as $C_j^{max}$ is the WCET of a job $J_j$. The latter means that there is still a $J_j$ with $p_j < p_i$ and $r_j^{min} < s_i(v_p)$. But this contradicts the assumption that Eq. (7) has terminated.

Hence, when Eq. (7) terminates, $s_i^{(k)}$ is the latest time instant the processor may start scheduling $J_i \in \mathcal {J\,}^M$ after $v_p$.

Fig. 7

Examples to show how to obtain the latest finish time of the jobs in a candidate reduction set $\mathcal {J\,}^M= \{J_1, J_2, J_3, J_4\}$ using a a fixed-point iteration method (Eqs. (6) and (7)) and b priority-agnostic simulation-based method (Algorithm 3)

4.7.2 A priority-agnostic simulation method to obtain EFT and LFT bounds

As it can be seen in Fig. 7a, the starting value of the fixed-point iteration method might be larger than a work-conserving JLFP scheduler would allow. The interval shown by the dashed rectangle in Fig. 7a cannot be idle when a work-conserving scheduler is used because the core is certainly available from time $A_1^{max}$ and there are jobs such as $J_1$, $J_2$ and $J_4$ that are certainly released before $A_1^{max}$. Thus, some of these jobs cannot contribute to Eq. (13).

To limit the impact of pessimism in our fixed-point iteration method, we introduce another bound that uses the priority-agnostic simulation-method introduced in Algorithms 2 and 3.

A second upper bound on the start time of $J_i$ is given by $\overline{LFT}(\mathcal {J\,}^M, v_p) - C_i^{max}$, as proven in Lemma 12, where $\overline{LFT}(\mathcal {J\,}^M, v_p)$ is obtained from Algorithms 3.

Lemma 12

$J_i \in \mathcal {J\,}^M(v_p)$ starts executing no later than $\overline{LFT}(\mathcal {J\,}^M, v_p) - C_i^{max}$.

Proof

By contradiction. Assume that the processor starts executing $J_i \in \mathcal {J\,}^M(v_p)$ later than $\overline{LFT}(\mathcal {J\,}^M, v_p) - C_i^{max}$, say at $\overline{LFT}(\mathcal {J\,}^M, v_p) - C_i^{max} + x$, where $x > 0$. According to the definition of $\mathcal {J\,}^M(v_p)$, no job $J_j \in \mathcal {J} {\setminus } (\mathcal {J\,}^M(v_p) \cup \mathcal {J\,}^P)$ can start executing before all jobs in $\mathcal {J\,}^M(v_p)$ finish their execution. Hence, the processor is busy executing jobs in $\mathcal {J\,}^M(v_p) \setminus J_i$ until $\overline{LFT}(\mathcal {J\,}^M, v_p) - C_i^{max} + x$. Consequently, at least one job in $\mathcal {J\,}^M(v_p) {\setminus } J_i$ finishes at $\overline{LFT}(\mathcal {J\,}^M, v_p) - C_i^{max} + x$. Then, $J_i$ starts at $\overline{LFT}(\mathcal {J\,}^M, v_p) - C_i^{max} + x$. If $J_i$ executes for its WCET $C_i^{max}$, it finishes at $\overline{LFT}(\mathcal {J\,}^M, v_p) + x$. This contradicts Corollary 2 that states that $\overline{LFT}(\mathcal {J\,}^M, v_p)$ is the latest time instant the processor may be busy executing jobs in $\mathcal {J\,}^M(v_p)$.

Combining the two upper bounds provided by Lemmas 11 and 12, we get that the latest start time of any job $J_i \in \mathcal {J\,}^M(v_p)$ is upper bounded by:

$$\begin{aligned} \widehat{LST}_i(\mathcal {J\,}^M, v_p) = \min \{s_i(v_p), \overline{LFT}(\mathcal {J\,}^M, v_p) - C_i^{max}\} \end{aligned}$$

(8)

Then, as proven in Lemma 13, the LFT of any job $J_i \in \mathcal {J\,}^M(v_p)$ is upper bounded by

$$\begin{aligned} \widehat{LFT}_{i}(\mathcal {J\,}^M, v_p) = \widehat{LST}_i(\mathcal {J\,}^M, v_p) + C_i^{max} \end{aligned}$$

(9)

Lemma 13

$J_i \in \mathcal {J\,}^M(v_p)$ cannot complete its execution later than $\widehat{LFT}_{i}(\mathcal {J\,}^M, v_p)$ as defined in (9).

Proof

$J_i$ cannot start later than $\widehat{LST}_i(\mathcal {J\,}^M, v_p)$ as it is an upper bound on the latest start time of $J_i$ (by Lemmas 11 and 12). If $J_i$ starts at $\widehat{LST}_i(\mathcal {J\,}^M, v_p)$, it cannot finish later than $\widehat{LST}_i(\mathcal {J\,}^M, v_p) + C_i^{max}$ as $C_i^{max}$ is the WCET of $J_i$.

Lemma 14

No job in $\mathcal {J\,}^M(v_p)$ misses its deadline if Eq. (5) holds.

Proof

Lemma 13 shows that $\widehat{LFT}_{i}(\mathcal {J\,}^M, v_p)$ is an upper bound on the LFT of $J_i \in \mathcal {J\,}^M(v_p)$. Hence, if it is smaller than the deadline of $J_i$, then it is certain that $J_i \in \mathcal {J\,}^M(v_p)$ cannot miss its deadline.

4.8 Computing safe response-time bounds for jobs in a safe reductions set

Section 4.7 already describes how to compute a safe upper bound on the LFT of any job $J_i \in \mathcal {J\,}^M$, so all that remains to derive is a safe lower bound on their EFT. As proven in Lemma 15, the EFT of $J_i \in \mathcal {J\,}^M$ is lower bounded by

$$\begin{aligned} \widehat{EFT}_{i}(\mathcal {J\,}^M, v_p)= \max \{A_1^{min}(v_p), r_i^{min}\} + C_i^{min} \end{aligned}$$

(10)

Lemma 15

$J_i \in \mathcal {J\,}^M(v_p)$ cannot complete its execution before $\widehat{EFT}_{i}(\mathcal {J\,}^M, v_p)$ as defined in Eq. (10).

Proof

$J_i$ cannot start before $r_i^{min}$ as a job cannot start before it is released, and $J_i$ cannot start before $A_1^{min}$ as $A_1^{min}$ is the earliest time at which all jobs before $J_i$ finish. Hence, $\max \{A_1^{min}, r_i^{min}\}$ is a lower bound on the start time of $J_i$. If $J_i$ starts at $\max \{A_1^{min}, r_i^{min}\}$ it cannot finish before $\max \{A_1^{min}, r_i^{min}\} + C_i^{min}$ as $C_i^{min}$ is the BCET of $J_i$.

4.9 Algorithm to construct a safe reduction set

Algorithm 4 shows how to create the safe reduction set $\mathcal {J\,}^M$ for a system state $v_p$. In short, interfering jobs are added to the candidate reduction set $\mathcal {J\,}^S$ until the POR is either accepted because it is safe, or rejected because it fails the sufficient schedulability test. At line 1 of Algorithm 4, $\mathcal {J\,}^S$ is initialized with the direct successors of $v_p$, i.e., successors that the original SAG analysis would naturally add immediately after state $v_p$ according to Definition 2.

4.9.1 Dealing with interfering jobs

Through lines 3–6, the interfering job set $\mathcal {J\,}^I$ is formed. If $\mathcal {J\,}^I$ is empty (line 7), i.e., there are no interfering jobs for $\mathcal {J\,}^S$, the algorithm checks whether $\mathcal {J\,}^S$ passes the sufficient schedulability test (line 8). If so, the POR is safe and $\mathcal {J\,}^S$ is returned as the safe reduction set (line 9). Otherwise, the empty set is returned (line 11) as the POR of $\mathcal {J\,}^S$ is unsafe and therefore rejected. If there are interfering jobs (line 13), a $J_x \in \mathcal {J\,}^I$ is chosen according to input criterion X (line 14) and added to $\mathcal {J\,}^S$ (line 15).

4.9.2 Criteria to expand the candidate reduction set

The order in which interfering jobs are integrated into $\mathcal {J\,}^S$ may affect the composition and success of the candidate reduction set at the end of the algorithm. We use a greedy criterion (denoted by X) to move one job $J_x \in \mathcal {J\,}^I$ from the interfering set $\mathcal {J\,}^I$ to $\mathcal {J\,}^S$. In the experimental section of this paper, we adopted a criterion X that always selects the highest-priority job in $\mathcal {J\,}^I$. After adding $J_x$ to $\mathcal {J\,}^S$ (line 15) the while-loop repeats, either until the POR is accepted (line 9) or rejected (line 11).

Lemma 16

A POR of a safe reduction set $\mathcal {J\,}^M$ as returned by line 9 of Algorithm 4 maintains exact schedulability.

Proof

According to Corollary 2 and 3, $\overline{EFT}(\mathcal {J\,}^M, v_p)$ and $\overline{LFT}(\mathcal {J\,}^M, v_p)$ computed with Algorithms 2 and 3, are exact bounds on the finish time of every job in a safe reduction set $\mathcal {J\,}^M$. Hence, the reduction of $\mathcal {J\,}^M$ to a single scheduling decision will not affect the analysis of the execution of jobs not contained in $\mathcal {J\,}^M$. Furthermore, the reduction will not affect the schedulability analysis of $\mathcal {J\,}^M$ itself because no $J_i \in \mathcal {J\,}^M$ can miss its deadline (Lemma 14). Thus, if the POR of $\mathcal {J\,}^M$ is safe, the schedulability analysis remains exact.

Lemma 17

A POR of a safe reduction set $\mathcal {J\,}^M$ as returned by line 9 of Algorithm 4 maintains safe response-time bounds.

Proof

As the POR of $\mathcal {J\,}^M$ will not affect the analysis of the execution of jobs not contained in $\mathcal {J\,}^M$ (Lemma 16), the response-time bounds of these jobs will remain exact as in the original analysis by Nasri and Brandenburg (2017). For the jobs contained in $\mathcal {J\,}^M$, the EFT and LFT are lower and upper bounds respectively (Lemma 15 and 13 respectively). Therefore, the response-time bounds of jobs in $\mathcal {J\,}^M$ are also safe.

5 Precedence constraints

The POR algorithm presented so far assumes the non-preemptive execution of independent jobs. However, most practical use-cases will have some kind of dependencies between jobs under the form of precedence constraints or data dependencies, which require to execute sets of jobs in specific orders. In this section, we extend the analysis to accommodate more complex systems. Specifically, we adapt POR to analyze limited-preemptive tasks with fixed preemption points, parallel DAG tasks, and job sets with precedence constraints.

We start with introducing the system properties that can be analyzed and follow with our solution.

Limited-preemptive tasks with fixed preemption points. As its name implies, a limited-preemptive task with fixed preemption points implicitly executes non-preemptively but allows to preempt a task at predefined points in its code. More formally, a task $\tau _i$ releases task instances. Each task instance is made of a sequence of jobs (also called segments in the related literature) that must execute in a predefined order. The first job in the sequence can execute as soon as it is released, whilst subsequent jobs in the sequence can start executing as soon as their predecessor job is completed. Jobs execute non-preemptively but the task instance may be preempted between the execution of two of its jobs.

DAG tasks. A DAG task is modelled with a directed-acyclic graph $G_i=(V_i,E_i)$ made of a set of vertices $V_i$ and a set of directed edges $E_i$. Each vertex represents a sub-task to be performed by the task, and each edge connecting two vertices represents a precedence constraint between those sub-tasks. At runtime, a task $\tau _i$ releases task instances made of as many jobs as there are vertices in the graph $G_i$, i.e., it releases one job $J_{i,j}$ for each sub-task $v_{i,j} \in V_i$. We say that a job $J_{i,j}$ is a predecessor of job $J_{i,k}$ if there is an edge connecting vertex $v_{i,j}$ to $v_{i,k}$ in the DAG $G_i$. A job can only start to execute when all its predecessors have completed their execution. Jobs execute non-preemptively, but preemptions can happen between jobs of the same task. Note that a limited-preemptive task with fixed preemption points is a particular case of DAG tasks since a limited-preemptive task can be modelled with a DAG where each vertex has at most one predecessor.

Job sets with precedence constraints. The most generic system model we can accommodate is that of a set of jobs $\mathcal {J}$ with precedence constraints. Each job $J_i \in \mathcal {J}$ has a set of predecessor jobs $pred (J_i)$ that must complete their execution before $J_i$ may start executing. The jobs in $pred (J_i)$ may be released by the same or different tasks as $J_i$ and may have the same or different priorities, arrival times, and deadlines than $J_i$. In other words, jobs with precedence constraints may have completely unrelated timing properties and requirements but must be executed in a specific order to meet the application requirements. Note that there must not be a cycle in the precedence constraints, otherwise the job set will be infeasible by definition.

Note again that both DAG tasks and limited-preemptive tasks with fixed preemption points can be modelled as job sets with precedence constraints. The main difference is that for DAG and limited-preemptive tasks, the jobs in the set $pred (J_i)$ are released by the same task as $J_i$ and thus share the same arrival time and deadline as $J_i$. This is however not required in the generic case of job sets with precedence constraints.

5.1 Additional notations and job set pre-processing

Since job sets with precedence constraints are the most generic system model we can analyze as they encompass both DAG and limited-preemptive tasks, we only discuss job sets with precedence constraints in the rest of this paper.

To model job sets with precedence constraints, we assume that each job $J_i \in \mathcal {J}$ has a set of predecessor jobs $pred (J_i)$. Job $J_i$ may only start executing once all its predecessors have completed.

All jobs that are direct or indirect predecessors of $J_i$, i.e., any job that must complete before $J_i$ starts executing according to the precedence constraints defined between jobs, are called the ancestors of $J_i$. Similarly, all the jobs for which $J_i$ is an ancestor, i.e., all the jobs that can only start executing after the completion of $J_i$ due to precedence constraints, are called the descendants of $J_i$. We denote the set of ancestors and descendants of $J_i$ by $ances (J_i)$ and $desc (J_i)$, respectively.

Importantly, in the rest of this section, we assume that the set of jobs being analyzed by the POR algorithm is pre-processed using Algorithm 5. That is, we assume that the earliest release time of a job $J_i$ is never smaller than that of its ancestors. Similarly, we assume that the latest release time of job $J_i$ is never smaller than that of its ancestors (being direct ancestors or indirect ones, as defined in Sect. 2.1). Note that enforcing such constraint does not limit the applicability of our analysis since a job $J_i$ will never start executing before its ancestors did. Therefore, in all legal execution scenarios that may happen at runtime, the effective release time of a job $J_i$ is never smaller than that of its ancestors.

5.2 Extending the POR analysis to job precedence constraints

As explained in Sect. 4, the POR algorithm first creates a safe reduction set $\mathcal {J\,}^M$ using Algorithm 4. If $\mathcal {J\,}^M$ is not empty, Algorithm 3 computes a safe upper bound $\widehat{LFT}_{i}(\mathcal {J\,}^M, v_p)$ on the the finish time of every job $J_i$ in the reduction set. If $\widehat{LFT}_{i}(\mathcal {J\,}^M, v_p) \le d_i$ for all jobs $J_i \in \mathcal {J\,}^M$, then all jobs in the reduction set meet their deadline and the POR can safely be applied. Algorithm 1 then computes an exact lower bound $\overline{EFT}$ and exact upper bound $\overline{LFT}$ on the finish time of all jobs in $\mathcal {J\,}^M$, and then creates a new state in the schedule abstraction graph using $\overline{EFT}$ and $\overline{LFT}$ as the bounds on the earliest and latest time at which the processor can become available after executing the jobs in $\mathcal {J\,}^M$.

In the rest of this section, we first explain how to compute a safe bound $\widehat{LFT}_{i}(\mathcal {J\,}^M, v_p)$ on the finish time of every job $J_i \in \mathcal {J\,}^M$ when jobs in that set may have precedence constraints (Sect. 5.2.1). We continue with showing that $\overline{EFT}$ and $\overline{LFT}$ as computed by Algorithms 2 and 3 are still exact bounds on the finish time of the whole reduction set $\mathcal {J\,}^M$ (Sect. 5.2.2 ). Finally, we present a revised algorithm to build a safe reduction set $\mathcal {J\,}^M$ (Sect. 5.2.3).

5.2.1 Safe bound on the finish time $\widehat{LFT}_{i}(\mathcal {J\,}^M,v_p)$

As already discussed in Sect. 4.7, since jobs execute non-preemptively, an upper bound on the finish time of a job $J_i$ in the reduction set $\mathcal {J\,}^M(v_p)$ can be computed as

$$\begin{aligned} \widehat{LFT}_{i}(\mathcal {J\,}^M,v_p) = \widehat{LST}_i(\mathcal {J\,}^M,v_p) + C_i^{max} \end{aligned}$$

where $\widehat{LST}_i(\mathcal {J\,}^M,v_p)$ is an upper bound on the time at which $J_i$ start executing.

Two bounds on $\widehat{LST}_i(\mathcal {J\,}^M,v_p)$ were presented in Sect. 4.7.

• The first assumes that a lower-priority job starts its execution just before $J_i$ is released and all higher-priority jobs subsequently interfere with $J_i$.

• The second assumes that $J_i$ is the last job of the reduction set $\mathcal {J\,}^M(v_p)$ to execute.

We show that the first bound is unsafe for jobs with precedence constraints, and the second may be pessimistic. Therefore, we revise both in this section.

First bound on $\widehat{LST}_i(\mathcal {J\,}^M,v_p)$. As just discussed, when jobs have no precedence constraints, a first upper bound on the start time of $J_i$ can be computed by assuming a lower priority job starts executing just before $J_i$ is released, and all jobs with a higher priority than $J_i$ subsequently interfere with $J_i$. This bound was computed with Eqs. (6) and (7) in Sect. 4.7. However, as shown in the example below, it is not anymore the worst-case scenario for jobs with precedence constraints.

Example 1

Consider the case where the job $J_i$ has an ancestor $J_p$ with a lower priority than $J_i$. Assume there is a set of jobs $\mathcal {M}$ with higher priorities than $J_p$ but lower priorities than $J_i$. Assume the jobs in $\mathcal {M}$ are released before $J_p$ starts to execute. According to the supposedly worst-case scenario described above, none of the jobs in $\mathcal {M}$ except one can interfere with $J_i$. However, since $J_i$ cannot start before $J_p$ due to precedence constraints, and because all the jobs in $\mathcal {M}$ can interfere with $J_p$, there may be an execution scenario where the jobs in $\mathcal {M}$ indirectly interfere with $J_i$ through $J_p$. Therefore, the bound computed by Eqs. (6) and (7) are not an upper bound on the start time of $J_i$ under precedence constraints.

The example above shows that jobs that may interfere with the execution of ancestors of $J_i$ may indirectly interfere with $J_i$. To capture that effect, we compute a rectified priority $p_i^*$ for $J_i$ as being the lowest priority among $J_i$ and its ancestors that are also part of the reduction set. That is¹,

$$\begin{aligned} p_i^* = \max \{p_i, \max _0\{p_j \mid J_j \in ( ances (J_i) \cap \mathcal {J\,}^M) \} \}. \end{aligned}$$

(11)

Using the rectified priority $p_i^*$ for $J_i$, a first upper bound $s_i(v_p)$ on the start time $\widehat{LST}_i(\mathcal {J\,}^M,v_p)$ of any job $J_i \in \mathcal {J\,}^M(v_p)$ can then be computed using the following recursive equations.

$$\begin{aligned} s_i^{(0)}= & {} \max \{A_1^{max}, r_i^{max} - 1 + \max _{\forall J_j \in \mathcal {J\,}^M(v_p)}\{C_j^{max} \mid p_i^* < p_j \} \} + \sum _{J_p \in ances (J_i) \cap \mathcal {J\,}^M} C_p^{max} \end{aligned}$$

(12)

$$\begin{aligned} s_i^{(k)}= & {} s_i^{(0)} + \sum _{ \{ J_j \mid J_j \in \mathcal {J\,}^M(v_p) ~\wedge ~ r_j^{min} \le s_i^{(k-1)} \wedge p_j < p_i^*\} }{C_j^{max}} \end{aligned}$$

(13)

Since Eqs. (12) and (13) use the recitified priority $p_i^*$ for $J_i$, all non-completed jobs released before $J_i$ starts executing and with a priority higher than that of $J_i$ or one of its ancestors that did not complete its execution yet, will be considered to be interfering with $J_i$.

Lemma 18

$s_i(v_p)$ as computed by Eqs. (12) and (13) is an upper bound on the latest start time of $J_i \in \mathcal {J\,}^M(v_p)$.

Proof

The proof is by contradiction. Assume that the processor starts executing $J_i~\in ~\mathcal {J\,}^M(v_p)$ later than $s_i(v_p)$. Then, at least one job in $\mathcal {J}\setminus \mathcal {J\,}^P$ must be delaying the start of $J_i$ by more than what is accounted for in $s_i(v_p)$. That extra delay may be caused by lower priority jobs (under the form of blocking), higher-priority jobs (under the form of direct or indirect interference) or by jobs with precedence constraints with $J_i$ (Note that these three sets of jobs account for all jobs in $\mathcal {J}\setminus \mathcal {J\,}^P$). We discuss those three cases and show that none can hold.

Case (i): $J_i$ suffers more blocking. By definition of JLFP scheduling, blocking by a lower priority job may only happen if the blocking job starts executing before $J_i$ is released. Equation (12) considers that the blocking of $J_i$ completes at $\max \{A_1^{max}, r_i^{max} - 1 + \max _{\forall J_j \in \mathcal {J\,}^M(v_p)}\{C_j^{max} \mid p_i^* < p_j \} \}$. If the blocking ends later than what is accounted for in Eq. (12), it means that either the processor becomes possibly available later than $A_1^{max}$, or there exists a job with a lower priority than $J_i$ or one of its ancestors that can execute for longer than what is accounted for in Eq. (6). The former contradicts the assumption that $A_1^{max}$ is the exact latest time at which the processor becomes possibly available. The latter contradicts the assumptions that a lower-priority job cannot execute for longer than its WCET $C_j^{max}$. We also note that by definition of a safe reduction set such as $\mathcal {J\,}^M$, all jobs that may start executing before $J_i$ are in $\mathcal {J\,}^M$. Thus, all lower and higher priority jobs in $\mathcal {J}\setminus \mathcal {J\,}^P$ and may block or interfere with $J_i$ are also in $\mathcal {J\,}^M$.

Case (ii). There is a larger interference by jobs with precedence constraints with $J_i$. Note that only ancestors of $J_i$ can delay $J_i$’s execution since descendants are not ready to execute until $J_i$ completes. Equation (12) assumes that all ancestors of $J_i$ in the reduction set $\mathcal {J\,}^M$ interfere with $J_i$ (i.e., there participation to the interference is $\sum _{J_p \in ances (J_i) \cap \mathcal {J\,}^M} C_p^{max}$). Therefore, if ancestors of $J_i$ interfere more, it either means that an ancestor $J_p$ of $J_i$ executes for larger than $C_p^{max}$ or an ancestor of $J_i$ that is not in $\mathcal {J\,}^M$ may interfere with $J_i$. The former is impossible by our assumption that $C_p^{max}$ is the worst-case execution time of $J_p$. The latter is impossible by our assumption that $\mathcal {J\,}^M$ is a safe reduction set and thus that no job outside of $\mathcal {J\,}^M$ can start executing before all the jobs in $\mathcal {J\,}^M$ complete their own execution, and by the definition of precedence constraints that ancestors of $J_i$ must always execute before $J_i \in \mathcal {J\,}^M$ starts.

Case (iii): There is a larger direct or indirect interference by higher priority jobs on $J_i$. A job $J_h$ can interfere with $J_i$ if it is released before $J_i$ starts executing and it has a higher priority than $J_i$ or one of its non-yet-completed ancestors. Since Eq. (7) considers that all jobs with a priority higher than the rectified priority $p_i^*$ (i.e., the lowest priority among $J_i$ and its non-completed ancestors) that may be released before $J_i$ starts (i.e., $\{ J_j \mid J_j \in \mathcal {J\,}^M(v_p) ~\wedge ~ r_j^{min} \le s_i^{(k-1)} \wedge p_j < p_i^*\}$) interfere with $J_i$ for their WCET, there is no other high-priority job that may possibly interfere with $J_i$.

Hence, when Eq. (7) terminates, $s_i^{(k)}$ is the latest time instant the processor may start executing $J_i \in \mathcal {J\,}^M$ after $v_p$.

Second bound on $\widehat{LST}_i(\mathcal {J\,}^M,v_p)$. In Sect. 4.7, a second upper bound on the latest start time of a job $J_i \in \mathcal {J\,}^M(v_p)$ was computed by assuming that $J_i$ is the last job of the reduction set to execute. However, if a job has descendants in $\mathcal {J\,}^M(v_p)$ then $J_i$ cannot be the last job of $\mathcal {J\,}^M(v_p)$ to execute since, by precedence constraints, its descendants must execute after it. Therefore, a tighter upper bound on the latest start time of $J_i$ is proven in Lemmas 19 and 20.

Lemma 19

$J_i \in \mathcal {J\,}^M(v_p)$ finishes executing no later than

$$\begin{aligned} \overline{LFT}(\mathcal {J\,}^M, v_p) - \sum _{ \{ J_j \mid J_j \in (\mathcal {J\,}^M(v_p) \cap desc (J_i)) \} }{C_j^{max}}. \end{aligned}$$

(14)

Proof

By contradiction, assume $J_i$ finishes executing at $t > \overline{LFT}(\mathcal {J\,}^M, v_p) - \sum _{ \{ J_j \mid J_j \in (\mathcal {J\,}^M(v_p) \cap desc (J_i)) \} }{C_j^{max}}$. Then, there is a legal schedule where the descendants of $J_i$ start executing after t and execute for their WCET. They would then complete at or later than $t+\sum _{ \{ J_j \mid J_j \in (\mathcal {J\,}^M(v_p) \cap desc (J_i)) \} }{C_j^{max}} > \overline{LFT}(\mathcal {J\,}^M, v_p) - \sum _{ \{ J_j \mid J_j \in (\mathcal {J\,}^M(v_p) \cap desc (J_i)) \} }{C_j^{max}} +\sum _{ \{ J_j \mid J_j \in (\mathcal {J\,}^M(v_p) \cap desc (J_i)) \} }{C_j^{max}} = \overline{LFT}(\mathcal {J\,}^M, v_p)$. This contradicts the assumption that $\overline{LFT}(\mathcal {J\,}^M, v_p)$ is an upperbound on the finishing time of all jobs in $J^M$. Thus, $J_i$ must have completed at or before $\overline{LFT}(\mathcal {J\,}^M, v_p) - \sum _{J_j \in J^M \cap desc(J_i)} C_j^{max}$.

Lemma 20

$J_i \in \mathcal {J\,}^M(v_p)$ starts executing no later than

$$\begin{aligned} \overline{LFT}(\mathcal {J\,}^M, v_p) - \sum _{ \{ J_j \mid J_j \in (\mathcal {J\,}^M(v_p) \cap desc (J_i)) \} }{C_j^{max}} - C_i^{max}. \end{aligned}$$

(15)

Proof

By contradiction, assume that $J_i$ starts at time $t>\overline{LFT}(\mathcal {J\,}^M, v_p) - \sum _{ \{ J_j \mid J_j \in (\mathcal {J\,}^M(v_p) \cap desc (J_i)) \} }{C_j^{max}} - C_i^{max}$. Then there is a legal schedule where $J_i$ starts at t and executes for its WCET, thus finishing at $t+C_i^{max} >\overline{LFT}(\mathcal {J\,}^M, v_p) - \sum _{ \{ J_j \mid J_j \in (\mathcal {J\,}^M(v_p) \cap desc (J_i)) \} }{C_j^{max}} - C_i^{max} + C_i^{max} = \overline{LFT}(\mathcal {J\,}^M, v_p) - \sum _{ \{ J_j \mid J_j \in (\mathcal {J\,}^M(v_p) \cap desc (J_i)) \} }{C_j^{max}}$. It contradicts that, according to Lemma 19,

$$\begin{aligned} \overline{LFT}(\mathcal {J\,}^M, v_p) - \sum _{ \{ J_j \mid J_j \in (\mathcal {J\,}^M(v_p) \cap desc (J_i)) \} }{C_j^{max}} \end{aligned}$$

is an upper bound on the finish time of $J_i$. Therefore,

$$\begin{aligned} \overline{LFT}(\mathcal {J\,}^M, v_p) - \sum _{ \{ J_j \mid J_j \in (\mathcal {J\,}^M(v_p) \cap desc (J_i)) \} }{C_j^{max}} - C_i^{max} \end{aligned}$$

must be an upper bound on the start time of $J_i$.

Final bound on $\widehat{LST}_i(\mathcal {J\,}^M,v_p)$. Combining the two bounds proved above, we get the following lemma.

Lemma 21

A job $J_i$ in the reduction set $\mathcal {J\,}^M(v_p)$ cannot start later than

$$\begin{aligned} \widehat{LST}_i(\mathcal {J\,}^M, v_p) = \min \{s_i(v_p), \overline{LFT}(\mathcal {J\,}^M, v_p) - \sum _{ \{ J_j \mid J_j \in (\mathcal {J\,}^M(v_p) \cap desc (J_i)) \} }{C_j^{max}} - C_i^{max}\} \end{aligned}$$

(16)

where $s_i(v_p)$ is computed with the recursive Eqs. (12) and (13).

Proof

Since both $s_i(v_p)$ and $\overline{LFT}(\mathcal {J\,}^M, v_p) - \sum _{ \{ J_j \mid J_j \in (\mathcal {J\,}^M(v_p) \cap desc (J_i)) \} }{C_j^{max}} - C_i^{max}$ are upper bounds on the start time of job $J_i$ (Lemmas 18 and 20), the minimum of the two is also an upper bound one the start time of $J_i$.

5.2.2 Exact bounds on $\overline{EFT}$ and $\overline{LFT}$

When building the schedule abstraction graph, Algorithm 1 computes exact bounds, denoted $\overline{EFT}(\mathcal {J\,}^M, v_p)$ and $\overline{LFT}(\mathcal {J\,}^M, v_p)$, on the earliest and latest time at which a safe reduction set $\mathcal {J\,}^M(v_p)$ may complete its execution. Those bounds are then used to determine when the processor will become available to execute new jobs after those of $\mathcal {J\,}^M(v_p)$. The bounds $\overline{EFT}(\mathcal {J\,}^M, v_p)$ and $\overline{LFT}(\mathcal {J\,}^M, v_p)$ are computed using Algorithms 2 and  3, respectively. It can be proven that those bounds are still exact for jobs with precedence constraints under the assumption that the release time of any job $J_x \in \mathcal {J\,}^M(v_p)$ is never smaller than that of its ancestors. Note that the latter is always true thanks to the job pre-processing step (Algorithm 5) introduced in Sect. 5.1.

Lemma 22

$\overline{EFT}(\mathcal {J\,}^M, v_p)$ computed by Algorithm 2 is the exact earliest finish time of the entire reduction set $\mathcal {J\,}^M$ if

$$\begin{aligned} \forall J_x \in \mathcal {J\,}^M(v_p), ~r_x^{min} \ge \max _0\{r_j^{min} \mid J_j \in ances (J_i) \}. \end{aligned}$$

Proof

The proof is identical to that of Corollary 2. The additional condition is only required to ensure that Algorithm 2 does not let a job $J_x$ execute before its ancestors.

Lemma 23

$\overline{LFT}(\mathcal {J\,}^M, v_p)$ computed by Algorithm 3 is the exact latest finish time of the entire reduction set $\mathcal {J\,}^M$ if

$$\begin{aligned} \forall J_x \in \mathcal {J\,}^M(v_p), ~r_x^{max} \ge \max _0\{r_j^{max} \mid J_j \in ances (J_i) \}. \end{aligned}$$

Proof

The proof is identical to that of Corollary 3. The additional condition is only required to ensure that Algorithm 3 does not let a job $J_x$ execute before its ancestors.

5.2.3 Constructing a safe reduction set

A safe reduction set is constructed by using Algorithm 4. Algorithm 4 repeatedly increases the content of a candidate reduction set by adding jobs that may interfere with the content of the candidate set built at the previous iteration. It stops as soon as there is no job outside of the candidate reduction set that may potentially interfere with the jobs in the candidate reduction set. The candidate reduction set is then considered to be safe.

Algorithm 4 remains the same when jobs have precedence constraints. The only difference lies in how we detect jobs that may potentially interfere with a candidate reduction set $\mathcal {J\,}^S$. We explain how this is done in the rest of this section.

First, we prove a simple property on the content of a safe reduction set when jobs have precedence constraints.

Property 1

All the ancestors of a job $J_i \in \mathcal {J\,}^M(v_p)$ that did not complete their execution yet in system state $v_p$ are also in the safe reduction set $\mathcal {J\,}^M(v_p)$.

Proof

By definition of a safe reduction set, no job that is outside of the safe reduction set and did not complete their execution yet may start executing before all jobs in $\mathcal {J\,}^M(v_p)$ have finished their own execution. Since, by precedence constraints, an ancestor of $J_i$ must start executing before $J_i$, ancestors of $J_i$ that did not complete their execution yet must be in $\mathcal {J\,}^M(v_p)$ for $\mathcal {J\,}^M(v_p)$ to be safe.

We now prove a property on jobs that may interfere with a candidate reduction set.

Lemma 24

A job $J_x \in \mathcal {J} \setminus (\mathcal {J\,}^S\cup \mathcal {J\,}^P)$ can execute between two jobs of a set $\mathcal {J\,}^S$ only if

$$\begin{aligned} ances (J_x) \subseteq (\mathcal {J\,}^S\cup \mathcal {J\,}^P) \wedge \mathcal {J\,}^S\not \subseteq ances (J_x) \end{aligned}$$

(17)

Proof

By precedence constraints, $J_x$ can only start executing when all its ancestors have completed. Hence, to execute between two jobs in $\mathcal {J\,}^S$, the ancestors of $J_x$ must be in $\mathcal {J\,}^S$ or $\mathcal {J\,}^P$ (i.e., the set of jobs that already completed their execution). Additionally, if the jobs in $\mathcal {J\,}^S$ are all predecessors of $J_x$, $J_x$ cannot interfere with $\mathcal {J\,}^S$ since all jobs in $\mathcal {J\,}^S$ must have completed before $J_x$ can start executing. This proves both conditions stated in the lemma.

We now prove that adding only jobs that respect the property stated in Lemma 24 to the reduction set ensures that Property 1 is respected.

Lemma 25

If a job $J_x$ respects Eq. (17), then all ancestors of $J_x$ that did not complete yet are in the candidate reduction set $\mathcal {J\,}^S$.

Proof

Restating the claim, we must prove that if a job $J_x$ respects Eq. (17), then $( ances (J_x) {\setminus } \mathcal {J\,}^P) \subseteq \mathcal {J\,}^S$. By Eq. (17), we have $ances (J_x) \subseteq (\mathcal {J\,}^S\cup \mathcal {J\,}^P)$. Moving $\mathcal {J\,}^P$ from the right-hand-side to the left-hand-side of the $\subseteq$ operator, we have $( ances (J_x) {\setminus } \mathcal {J\,}^P) \subseteq \mathcal {J\,}^S$. This proves the lemma.

We can now use the newly proved constrains Eq. (17) on interfering jobs to restate the conditions on how to check the existence of potentially interfering jobs for a candidate reduction set $\mathcal {J\,}^S$.

Lemma 26

A job $J_x \in \mathcal {J} \setminus (\mathcal {J\,}^S\cup \mathcal {J\,}^P)$ can execute in an idle interval between two jobs of $\mathcal {J\,}^S$ only if Eq. (17) and (3) hold.

Proof

The first condition was proven in Lemma 24 whilst the second was proven in Lemma 4.

The following lemma establishes the conditions by which a job $J_x$ may interfere with $\mathcal {J\,}^S$. Recall that $\mathcal {J\,}^{high}$ is the set of jobs not in $\mathcal {J\,}^S$ that have a higher priority than at least one job in $\mathcal {J\,}^S$ (defined in Eq. (4)).

Lemma 27

A job $J_x \in \mathcal {J} \setminus (\mathcal {J\,}^S\cup \mathcal {J\,}^P)$ may interfere with jobs in the set $\mathcal {J\,}^S$ only if (i) Eq. (17) holds and (ii) either Eq. (3) holds or $J_x \in \mathcal {J\,}^{high} \wedge \exists J_l \in \mathcal {J\,}^S\mid p_x < p_l \wedge r_x^{min} \le \widehat{LST}_l(\mathcal {J\,}^S, v_p)$, where $\mathcal {J\,}^{high}$ is defined in Eq. (4).

Proof

The first condition was proven in Lemma 24 and the second is proven in Corollary 1. 

The proof that the final reduction set returned by Algorithm 4 is safe remains unchanged. It only requires to substitute Corollaries 2 and 3 with Lemmas 22 and 23, respectively, and Lemmas 11 and 12 with Lemmas 18 and 20, respectively.

6 Empirical evaluation

As stated earlier in Sect. 1 and will be discussed later in Sect. 7, the goal of our contribution is to increase the scalability of the original SAG analysis by introducing partial-order reduction rules. Since the SAG analysis is an exact schedulability analysis for non-preemptive job sets (with or without precedence constraints) on a single-core platform, we do not compare our solution, which also maintains the exactness of the original SAG analysis, against existing sufficient tests in the state of the art. A detailed comparison of those methods have already been presented in prior work: by Nasri and Brandenburg (2017) for independent non-preemptive tasks on single-core platforms, by Yalcinkaya et al. (2019b) for limited-preemptive tasks on single and multi-core platforms, and by Nasri et al. (2019) for non-preemptive DAG tasks on multi-core platforms.

The purpose of this section is to provide a thorough assessment of our solution in improving scalability of the SAG analysis. Hence, we conducted empirical experiments to answer the following questions: (i) does POR provide a speedup and state-space reduction over the original SAG implementation by Nasri and Brandenburg (2017) (referred to as ‘original’)? and (ii) how is the worst-case response time affected by the partial-order reduction?

We considered three schedulability analysis problems all focused on periodic tasks with implicit deadline scheduled by a JLFP scheduling policy on a single-core platform. The difference between the three problems lies in the assumption about precedence constraints between task segments. In Sect. 6.1 and 6.2, we focus on independent non-preemptive tasks, in Sect. 6.3.1, we consider limited-preemptive tasks with fixed-preemption points, and in Sect. 6.3.2, we consider DAG tasks (i.e., tasks with multiple segments between which there is a precedence constraint relation that follows a directed-acyclic graph structure).

We derived the set of jobs of all tasks in one hyperperiod and used it as an input for SAG (see more explanations in Sect. 2.3). We define criterion X in Algorithm 4 such that it selects the highest-priority job in $\mathcal {J\,}^I$. In our experiments, we used the fixed-priority scheduling policy with rate-monotonic priority assignment. We performed our POR-based analysis according to Algorithm 1 and compared it to the original SAG analysis of Nasri and Brandenburg (2017) using their implementation (Git 2021). Both analyses were implemented as a single-threaded C++ program.

Fig. 8

Experimental results for performance on synthetic task sets. a Schedulability ratio. b Timeout ratio. c State-reduction ratio. d Speedup. e Exploration front width. f Distribution of normalized WCRT. h Percentiles of state-reduction ratio, speedup, and normalized WCRT. g Scalability in terms of CPU time. i Case study results

Metrics: Our performance metrics are as follows.

• State-reduction ratio is defined as $(1 - N^P / N^{O}) \cdot 100\%$, where $N^P$ and $N^{O}$ are the number of states explored by respectively the POR and the original analyses for an input job set. The closer this ratio is to 100%, the more states have been removed from the state-space by POR in comparison to the original analysis.

• Speedup is the CPU time required by the original analysis to analyze a job set $\mathcal {J}$ divided by the CPU time required by POR to analyze $\mathcal {J}$.

• Normalized WCRT is the WCRT of each task reported by the POR-based analysis divided by the WCRT of the same task reported by the original analysis.

6.1 Case study

We performed a case study using the APP4MC specification of the automotive use case provided at the WATERS 2017 industrial challenge (Hamann et al. 2017). We considered the task set assigned to Core 2 (of Hamann et al. (2017)), which consists of 710 periodic runnables grouped into 7 periodic tasks. We performed two experiments: (i) each task is assumed to be non-preemptive, and (ii) each runnable is assumed to be non-preemptive but preemptions can happen between the execution of runnables of the same or different tasks. As there was no predefined release jitter in the use case specification, we assumed two cases: no jitter, and jitter equal to the largest WCET among runnables. We evaluated the performance using the priorities specified for each period/task in the model specification (Hamann et al. 2017). Using the provided clock speed of 200 MHz resulted in inherently unschedulable task sets because the total utilization is larger than 1. Hence, we assumed the first clock speeds where the task sets were schedulable, namely 400 MHz and 1.2 GHz for experiments (i) and (ii), respectively. The experiments were performed on a cluster with AMD EPYC 7H12 processors clocked at 2.6GHz and 256GB RAM.

Figure 8i shows a summary of the results. In all but one case, POR provided a speedup over the original analysis, either because it finished faster, or the original analysis never finished due to running out of memory (as is the case for the last row of the table). POR is only outperformed by the original analysis when the system has very few tasks that do not have release jitter (first row of the table) because then there are very few branches in the analysis to be reduced by POR. In that case, the overhead of performing POR out-weights the small reduction in state-space. When there are many tasks with release jitter (the last row of the table), the original analysis runs out of memory, whereas POR is able to finish in a matter of seconds (i.e., 14 s). This is because there are many more jobs interfering with each other when there is release jitter, which gives POR more opportunities to create reduction sets. Hence, we see that when there is release jitter, an edge in the graph contains 107 jobs on average, whereas there are only about 2.5 jobs per edge when there is no release jitter. Since there are more jobs per edge, POR produces a significantly smaller state space (351 states with jitter vs. 15,261 states without jitter). In conclusion, this case study shows that POR enables the SAG analysis to scale to large industrial use cases.

6.2 Empirical results for synthetic independent task sets

To evaluate the scalability of POR, we generate random synthetic task sets with n independent periodic tasks and a total utilization of U, we follow the method of Emberson et al. (2010); we generate periods following a log-uniform distribution in the range [10, 100]ms with a granularity of 5ms. We generate n task-utilization values with a total sum of U with RandFixedSum (Stafford 2006). Using periods and task-utilization values, we obtain the WCET of each task. The BCET is set to 0 for all tasks (i.e., we maximize execution-time variation). We assumed a release jitter of 100$\upmu$s for each job of a task in the hyperperiod. We assume rate-monotonic priorities. In the following experiments, we set $U=0.3$ and varied the number of tasks per task set to evaluate the impact of the number of tasks (scalability). Choosing $U=0.3$ ensures generating mostly schedulable task sets which tend to increase the runtime of POR and SAG analyses. Finally, we generated 200 random task sets for each parameter value. The experiments were performed on a cluster with Intel Xeon E5-2690 v3 processors clocked at 2.6GHz and 64GB RAM.

A task set was deemed unschedulable when either an execution scenario containing a deadline miss was encountered, or a timeout of four hours was reached. We continued the analysis until either the end of the hyperperiod or the 4 h timeout was reached. For the performance evaluation, task sets with more than 50,000 jobs per hyperperiod were discarded to limit the runtimes, as otherwise we would not be able to compare our solution against the original SAG that was susceptible to state-space explosions. For the scalability evaluation (Fig. 8g), task sets were limited to 6,000,000 jobs per hyperperiod.

6.2.1 Performance results

Figure 8a shows a large difference between the schedulability ratio of the analyses due to the large number of timeouts after 4 h in the original analysis, as can be seen in Fig. 8b. In these experiments, the POR-based analysis was able to explore the entire state-space within 5.2 s on average. This shows that POR allows task sets with more uncertainties and more tasks to be analyzed before the timeout is reached.

Figure 8c shows that the state-reduction ratio for POR increases with an increase in the number of tasks showing that it becomes more successful on larger task sets because then POR has more opportunities to form bigger reduction sets. The average state-reduction ratio is $98.53\%$, demonstrating that POR is able to remove the vast majority of states from the state-space compared to the original analysis.

Figure 8d shows that POR provides a significant speedup over the original analysis for any number of tasks per task set, with an average speedup of $1.12 \times 10^5$. Figure 8f shows a box plot of the normalized WCRT for task sets for which neither analyses timed out. The whiskers represent the 2nd and 98th percentiles. Observe that the normalized WCRT is very close to 1, with an average of 1.001. This shows that the WCRT reported by our POR-based analysis is only a slight over-approximation of the true WCRT.

Figure 9a demonstrates schedulability of task set with different utilization. In line with increasing utilization, the schedulability ratio of task sets decreased. However, since the original SAG in some task sets reached the 4 h time budget, its schedulability seems to be lower than SAG with POR. Note that if there was no timeout limit, then we would have expected that the POR and original SAG analysis return the same schedulability because both of them are exact schedulability analyses.

Figure 9b shows that increasing the utilization decreases the speedup. This trend could be the direct consequence of decreasing the schedulability ratio in higher utilization, which gives less opportunity to POR to make reduction sets. In spite of this, the POR is still at least 973 times (and 16 times) faster than the original analysis when $U = 50\%$ ($U = 70\%$, respectively).

Figure 9c illustrates that the state-reduction ratio for POR decreases with an increase in task set utilization, meaning that fewer reduction sets will be considered safe in task sets with greater utilization. This is due to the pessimism of the two sufficient methods we used to over-estimate the latest finish time of the jobs in a reduction set. This over-estimation results in rejecting some reduction sets that could actually be safe.

Fig. 9

Experiments on non-preemptive task sets for utilizations $U = 30\%$, $50\%$, and $70\%$. a Schedulability. b Speedup. c State-reduction ratio

6.2.2 Scalability results

Figure 8g shows that the runtime of our analysis increases with the number of jobs per hyperperiod. Although there are some timeouts from $1.5\cdot 10^6$ jobs per hyperperiod onward, the vast majority of task sets are analyzed within four hours. This experiment shows that POR provides a significant increase in the scalability of SAG-based analyses even to task sets with $6\cdot 10^6$ jobs per hyperperiod.

6.3 Precedence constraints

This section evaluates the scalability of our POR solution for job sets with precedence constraints. Section 6.3.1 focuses on limited-preemptive periodic tasks with fixed preemption points and Sect. 6.3.2 focuses on periodic DAG tasks. In both sections, we consider $n=20$ tasks per task set. Note that, as reported in Fig. 8b, even for single-segment independent tasks, the original SAG analysis fails to complete the analysis of more than 40% of the task sets within the time budget of 4 h when there are 20 tasks with release jitter.

In the following experiments (presented in Sects. 6.3.1 and 6.3.2), we generate the parameters of the periodic tasks as in Sect. 6.2. Namely, we draw periods from a log-uniform distribution with a granularity of 5ms from the range [10, 100]ms. We employ the RandFixedSum (Stafford 2006) algorithm to generate task-utilization values with a total sum of U (where the utilization U is set to 30, 50, and 70% in different experiments). We assume a release jitter of 100$\upmu$s for every job.

We discarded task sets having more than 10,000 task instances per hyperperiod for the performance evaluation in order to limit runtimes, as otherwise, we would not have been able to compare our solution with the original SAG. However, when the experiments completed, we eventually realized that even by limiting the number of task instances per hyperperiod, the original SAG analysis times out for most task sets as soon as a task instance has more than one segment for both limited-preemptive tasks and DAG tasks.

6.3.1 Limited-preemptive

In this section, we evaluate the impact of the number of segments on the scalability of our analysis for limited-preemptive tasks. The total WCET assigned to a task is calculated by using the period and task utilization values (i.e., $C_i^{max} = U_i \times T_i$, where $T_i$ is the period and $U_i$ is the utilization of a task $\tau _i$). The BCET is set to 0 for all tasks (i.e., we maximize execution-time variation). In order to generate task segments with a random length and a total sum equal to C, we repeatedly draw a random variable x with a uniform distribution from [0, C], generate a segment with $C^{min} = 0$ and $C^{max} = x$, update $C \leftarrow C - x$, and continue until we either reach the maximum number of segments (in that case, the last segment will be as large as the remained C), or C becomes zero. We performed the experiments on a cluster with AMD Epyc 7601 processors clocked at 2.2GHz and 512GB RAM.

Fig. 10

Experiments on limited-preemptive task sets for utilizations $U = 30\%$, $50\%$, and $70\%$. a–c Schedulability. d–f Number of states. g–i Average CPU time. j–l CPU time. m–o Timeout ratio

Figure 10a–c show the schedulability ratio for different utilization values. According to these figures, there is a considerable difference between the schedulability ratios of the two analyses. Note that we only report a task set to be schedulable by an analysis if the analysis reaches to a conclusive decision within the time budget of four hours. Since the original SAG analysis timed out for most task sets (as it can be seen in Fig. 10m), its reported schedulability is near zero in almost all cases when tasks have two or more segments per task. These results demonstrate that the POR technique allows SAG to scale to much larger task sets (having up to 20 segments per task).

In a further investigation into why the original SAG analysis could not analyze task sets with more than 2 segments per task within the time budget, we realized that the number of states generated by the original analysis becomes uncontrollably large due to the release jitter of the tasks (which is set to 100$\upmu$s for each task). On the one hand, release jitter increases the permissible execution interleaving between the jobs and on the other hand, the narrow range of tasks periods (within [10, 100]ms) tends to increase the number of possible execution scenarios at runtime and hence push the SAG analysis to its limits. To test our hypothesis, we have removed the release jitter from the task sets and observed that task sets which previously timed out could be analyzed within less than 200 s with the original SAG analysis.² We have not reported those results (and did not change our experiment setups) since our aim is to evaluate the performance of POR under harder scenarios such as those with release jitter.

Another observation about Fig. 10a–c is that as the utilization increases (comparing (a) against (c)), the schedulability ratio decreases. Moreover, when tasks have fewer segments (e.g., 1 or 2), the blocking caused by low-priority tasks increases and hence the schedulability reduces. Having more segments means having more opportunities for preemption, which in turn, increases schedulability.

The schedulability drop in Fig. 10c in comparison to (a) and (b) is mainly due to increasing timeouts, as shown in Fig. 10o. These timeouts are the results of having a much larger number of jobs in a hyperperiod and failure of POR in forming safe reduction sets (Fig. 10f and l). This is expected since the main criteria for a safe reduction set is to not observe a deadline miss. However, the two sufficient tests that we used to estimate the latest finish time (LFT) of the jobs in a candidate reduction set are pessimistic and hence may over-estimate the LFT, and therefore result in rejecting the candidate set. If a candidate set is rejected, our solution lets the original SAG analysis generate the next states (recall Fig. 2). This increases the runtime and makes POR less efficient.

Due to lack of conclusive results from the original SAG analysis, we could not obtain the speedup, state-reduction ratio, or normalized WCRT metrics as we did in Sects. 6.2 and 6.1. We, instead, report the number of states (Fig. 10d–f), CPU time (Fig. 10g–i, the average CPU time (Fig. 10j–l, and the timeout ratio (Fig. 10m–o for POR. Note that for the CPU time and the number of states, we have plotted the values as per number of segments in the entire observation window, which in this case is one hyperperiod. We have done this to be able to further distinguish the impact of the input size of the SAG analysis, i.e, the number of ‘jobs’ in an observation window, on the performance of our POR solution. As can be seen in these figures, the job sets input to the SAG analysis include up to 200,000 jobs in their observation window.

As seen in Fig. 10d–f, the number of states generated by POR increases for higher utilization values (for example, while for $U = 30\%$ the number of states was well below $2\times 10^4$, for $U = 70\%$ it reached up to $2\times 10^5$). This matches with the observation that when the utilization increases, POR finds less opportunities to form reduction sets.

Another interesting observation about Fig. 10f is that task sets with fewer segments have a larger number of states. For example, with $U=50\%$, the average number of states with 1 segment is 4338, while for 3 segments it is 1954. This is due to the fact that asserting schedulability of non-preemptive task sets (or task sets with very few preemption points) with higher utilizations requires looking into many more execution scenarios. Task sets that are on the border line between being schedulable and not being schedulable typically require more processing time than those that are not schedulable (and hence their analysis can be stopped as soon as a deadline miss is observed).

It is worth noting that the gray cross marks in Fig. 10e, f (as well as (k) and (l)) belong to task sets that observed a timeout. Figure 10o shows that about 16% of the task sets with two segments timed out before the analysis can reach a conclusive decision. These task sets had a larger number of states.

Figure 10g–i, show the average CPU time of the POR analysis including and excluding task sets that timeouts. These two curves are denoted by POR(TO) and POR, respectively. As expected, with the increase in utilization, the runtime also increases. Similarly, the increase in the number of segments per task increases the runtime too. It is also expected that when including tasks with timeout, the average runtime seems to be larger. Note that since we did not let task sets that observed a timeout complete, the first average value (shown on POR(TO) curve) does not show a realistic picture of the average runtime of the analysis. However, comparing those two curves (average runtime with and without timeouts) allows us to conclude that the SAG analysis with POR is very fast (between a few seconds and two minutes) in most cases ($>90\%$ of the analyzed task sets) when there are up to 10 segments per task, but the average is pulled up by a small number of task sets whose schedulability is difficult to assess.

The large gap between the average runtime at $U=50\%$ and $U=70\%$ is due to the failures of POR to form safe reduction sets which in turn show themselves in the increased number of task sets (about 16%) that could not be analyzed within four hours. Overall, the average runtime is 63 s when $U=30\%$, 139 s when $U=50\%$, and 263 s when $U=70\%$.

Putting Fig. 10g–i along Fig. 10j–l which show the individual runtime of the task sets (including those that timed out) we see that task sets with larger number of segments tend to have larger runtime.

6.3.2 DAG tasks

DAG tasks are generated following the method of Casini et al. (2018). In this method, DAGs with nested fork-joins are generated through recursive expansions of blocks (often called non-terminal nodes or segments) into terminal segments or parallel sub-graphs until (i) a maximum depth of recursion (which limits the number of nested branches), (ii) a maximum length of the critical path, or (iii) a maximum number of segments is reached. In our experiment, we consider that the probability of a segment to fork is 0.8, the maximum number of nested forks is 3, and the maximum critical-path length is 30 segments. Additionally, we assume that the BCET of each segment is 0. In order to assign the WCET, we generate x random integer numbers with the total sum equal to the WCET of the task (obtained from the period and the task utilization generated as explained in Sect. 6.3), where x is the number of segments in the DAG. In this experiment, we varied the maximum number of segments per DAG task. We performed the experiments on a cluster with AMD Rome 7H12 processors clocked at 2.6GHz and 1TB RAM.

Fig. 11

Experiments on DAG task sets for utilizations $U = 30\%$, $50\%$, and $70\%$. a–c Schedulability. d–f Number of states. g–i Average CPU time. j–l CPU time. m–o Timeout ratio

Figure 11a–c show the schedulability ratio for different utilizations. Similar to the experiments in Sect. 6.3.1, there is a major difference between the reported schedulability ratios of the two analyses. This is again caused by the timeouts of the original SAG and not because of the pessimism of one analysis over the other since we know that both analyses are exact in terms of schedulability.

As expected, when there are only a few segments in a DAG task, the schedulability is lower (e.g., for one segment). For the case of two and three segments, we see an increase in the timeout as well as an increase in the CPU time and the number of states of the task sets (putting along Fig. 11f–o together). As explained in Sect. 6.3.1, the border line task sets with few preemption points (or segments) and high utilization tend to be harder to analyze by SAG. The fact that there is a risk of deadline miss reduces the chance of POR to form safe reduction sets and hence the analysis tends to retreat to the original SAG. Accordingly, DAG tasks with 2 segments and $30\%$ utilization have an average of 1500 states, while DAG tasks with $70\%$ utilization have an average of 24,788 states.

Comparing Figs. 10c and 11c (limited preemptive vs. DAG tasks) we see that our POR is more efficient in analyzing DAG tasks than limited preemptive tasks. The reason is that in the presence of multiple successors (segments) that are ready to execute as soon as a predecessor segment completes (in the case of DAG tasks), POR can form larger safe reduction sets (i.e., by combining the independent siblings and hence avoiding to explore the ordering between the siblings). This results in reducing the state space (this is also observable when comparing Figs. 10f and 11f).

As expected, we see that the average CPU time increases with the increase in the number of segments. This is shown in Fig. 11g–i as well as Fig. 11j–l. Another observation about Fig 11i is that the average runtime of the POR solution is larger for task sets with 1 segment than for task sets with 5 segments or more (task sets with 1 segment have an average runtime of 184 s, whereas those with 5 segments have an average runtime of 13 s). This is again due to the fact that asserting schedulability of non-preemptive task sets (or task sets with very few preemption points) in larger utilization values typically results in more failures of POR in forming safe reduction sets. Overall, the average runtime of POR to analyze a DAG task set with 15 segments was 2146 s when $U=30\%$, 2813 s when $U=50\%$, and 4463 s when $U=70\%$.

In conclusion, our results confirm that the POR technique significantly improves the scalability of the SAG analysis. While almost none of the task sets considered in Sects. 6.3.1 and 6.3.2 could be analyzed by the original SAG analysis within the four hours time budget, POR succeed to analyze almost all of them. In case of high-utilization task sets, and particularly for limited preemptive tasks, we see that the POR struggles to find enough safe reduction sets for about 16% of task sets on average (having 2 to 20 segments per task) as shown in Fig. 10c and o.

7 Related work

In this section, we first review the state of the art on the schedulability analysis of non-preemptive and limited-preemptive tasks to motivate why we focus on the SAG analysis (Sect. 7.1) and then summarize related work on partial-order reduction methods to position our POR technique w.r.t. the state of the art (Sect. 7.2). To the best of our knowledge, POR has not been used with any reachability-based schedulability analysis technique, and certainly not with the schedule-abstraction graph technique.

7.1 Schedulability analysis of non-preemptive and limited-preemptive tasks

The general problem of non-preemptive scheduling of a set of jobs with release and due dates has been considered in various research domains including real-time systems, operational management, factory planning and job-shop scheduling just to mention a few. A thorough overview of these problems can be found in the book of Pinedo (2016). These works, however, typically focus on finding an offline (static) schedule that optimizes some objective functions (e.g., maximum tardiness) rather than verifying schedulability of the job set under an existing online scheduling policy.

In the context of real-time systems, prior work has focused on exact schedulability tests for non-preemptive sporadic tasks, where only the minimum inter-arrival time of jobs is known. For example, Jeffay et al. (1991) analyzed non-preemptive EDF and Tindell et al. (1994), George et al. (1996, 2000), and Davis et al. (2007) analyzed non-preemptive FP scheduling policies. As shown previously (Nasri and Fohler 2016; Nasri and Brandenburg 2017), these tests are pessimistic when applied on periodic tasks, and cannot be applied on arbitrary job sets (that may not have a repeatable arrival pattern).

Sun et al. (1997) have introduced three sufficient schedulability tests for non-preemptive FP scheduling and tasks with preemptive and non-preemptive execution segments. Their tests consider both periodic and non-periodic tasks with given offsets (but not with release jitter). These tests carefully characterize the blocking caused by any lower-priority task that could start its execution before the job under analysis. However, since they do not precisely account for the earliest and latest finish times of the lower-priority jobs, the tests cannot reliably filter all impossible cases and hence are not exact (they are pessimistic).

Stigge et al. (2011); Stigge and Yi (2015) proposed a sufficient schedulability test for preemptive and non-preemptive digraph tasks. A digraph task has a set of modes (with different periods or execution times). At runtime, it may change its mode, and thus, execute with a different timing parameters (execution time or period). The schedulability analysis proposed by Stigge and Yi (2015) searches all possible scenarios while gradually pruning the number of test cases that will certainly not lead to a deadline miss. Using this method, experiments were conducted for task sets with up to 20 tasks. This analysis differs from the SAG analysis of Nasri and Brandenburg (2017) in three ways: first, SAG considers a different workload model that incorporates release jitter (which drastically increases the number of possible interleavings between jobs); second, SAG is not based on post-hoc pruning, but rather on the early merging of matching paths; and finally, SAG provides an exact analysis (and not a sufficient test).

Baker and Cirinei (2007) introduced an exact schedulability test for preemptive sporadic tasks scheduled by global EDF. The test uses a finite state machine that models all possible combinations of arrival times and execution sequences. The authors reported that the method can handle tasks with period values chosen from $\{3, 4, 5\}$. Larger period values could not be handled due to an early state-space explosion. Bonifaci and Marchetti-Spaccamela (2010) and Burmyakov et al. (2015, 2022) later improved this technique, however, without substantially altering its practical scalability limitations. The fundamental difference between this approach and the SAG analysis is that SAG explores the admissible orderings between non-preemptive jobs when they are scheduled by a given scheduling policy, while the works of Burmyakov et al. (2015, 2022) are designed for preemptive systems, where a task could potentially be preempted at any time instant. Each such potential preemption results in a new edge and a new state (which could be merged with already visited states). In conclusion, the approach of Burmyakov et al. (2015, 2022) is strongly tied to the the resolution of time unit and encodes the notion of time (e.g., the remained execution time of each task) inside the state. We are not aware of any use of interval-based abstractions in this method to avoid keeping track of distinct remained-execution time values in each system state.

Guan et al. (2007) used a model-checking approach based on timed automata to analyze sporadic tasks under global FP scheduling; their method was shown to scale well only as long as tasks have periods in the range $\{8, 9, \ldots , 20\}$ time units. Along this line of research, Sun and Lipari (2016b) introduced an exact schedulability analysis for preemptive sporadic tasks under global FP scheduling on a multiprocessor using hybrid automata. To improve scalability, they provide a set of sound pruning rules. According to the evaluations reported by Sun and Lipari (2016b), the analysis can handle up to 7 tasks and 4 processors before timing out. Although these works are similar to the SAG analysis in that they seek to explore the space of all possible schedules, they leverage general-purpose formal methods that are known to scale poorly, whereas the SAG analysis has a much narrower, problem-specific solution that scales much better (Nasri and Brandenburg 2017).

Buttazzo et al. (2013) provide a survey on schedulability analyses for limited-preemptive sporadic tasks. For example, Baruah (2005); Bril et al. (2007); Bertogna and Baruah (2010) introduce methods to analyze the schedulability of limited-preemptive tasks with fixed-preemption points. These methods scale well and are based on fixed-point iteration equations that capture the maximum interference and blocking that a job of a task can suffer from other tasks. Despite their high scalability, they are not accurate when applied on periodic tasks.

Serrano et al. (2017) proposed an analysis for limited-preemptive DAG tasks. This analysis, however, was shown to be very pessimistic even when only one core is used (Nasri et al. 2019; Yalcinkaya et al. 2019b). Despite its pessimism in most cases, it was recently shown to also be unsafe by being optimistic in some cases (Mohaqeqi et al. 2022). An analysis for limited-preemptive DAG tasks under partitioned scheduling was proposed by Casini et al. (2018).

Schedule-abstraction graph (SAG) is a recently introduced reachability-based response-time analysis proposed by (Nasri and Brandenburg 2017). It surpasses the scalability limitations of the timed-automata based response-time analyses by at least three orders of magnitude (Yalcinkaya et al. 2019b; Nasri et al. 2019). SAG has been extended to analyze non-preemptive job sets (Nasri et al. 2018) as well as parallel DAG tasks (or job sets with precedence constraints) (Nasri et al. 2019) scheduled by a global JLFP scheduling policy on a multi-core platform. It has also been used to analyze tasks with shared resources that are protected by priority-based and FIFO-based spin-locks (Nogd et al. 2020). and finally, it has been recently extended to analyze moldable gang tasks (Nelissen et al. 2022). However, as we have shown in Sects. 3 and 6, the original SAG analysis suffers from state-space explosion when there are large uncertainties in the release jitter or execution-time of the tasks/jobs.

In our paper, we focus on designing an exact schedulability analysis for non-preemptive job sets with and without precedence constraint by using the SAG analysis as a basis. However, in order to improve the scalability of the original SAG analysis, we introduce partial-order reduction rules to be integrated in the schedule-abstraction graph analysis To the best of our knowledge, there is no work in the state of the art of real-time systems research that has tried applying partial-order reduction for reducing the search space of a reachability-based schedulability analysis.

7.2 Partial-order reduction

Partial-order reduction is a well-known technique for reducing the size of the state space in reachability analyses, model checking (Valmari 1989; Wehrle and Helmert 2012, 2014; Aronis et al. 2018), automated planning (AlKhazraji 2017), and scheduling (Abdeddaım and Niebert 2004). For example, a scheduling problem can be coded as a reachability problem of transition systems, e.g., as time Petri nets (Abdeddaım and Niebert 2004). Then, generating an optimal schedule means finding a shortest path in the reachability graph (where the weight of edges shows the elapsed time) to a state where all work has completed. Similarly, the planning problem requires finding a short (good) path in a large space of decisions (Wehrle and Helmert 2012, 2014). The role of POR is to help cutting out unnecessary searches in the state space without jeopardizing optimality of the final solution. On the other hand, in the context of model-checking problems, the goal of POR is to avoid exploring options/actions/transitions that do not contribute to the verification of a certain property, or have already been explored elsewhere. In this sense, the use of POR in schedulability analysis is similar to the model-checking problems.

In state-based transition systems, POR exploits the mutuality of concurrent transitions that result in the same state regardless of their order of execution. There are three core categories of POR methods: (i) stubborn set methods (Valmari 1989; Peled 1993; Godefroid 1996), (ii) persistent set methods (Godefroid 1996), and (iii) sleep set methods (Godefroid 1996). Later on, these three methods have been combined to create dynamic partial-order reduction techniques (Flanagan and Godefroid 2005a; Aronis et al. 2018) mainly applied to the automatic verification of concurrent software programs.

7.2.1 Stubborn set methods

These methods were initially introduced by Valmari (1989) and used to alleviate the problem of state explosion in Petri Nets. They are known as state-dependent partial-order reduction methods, i.e., when the goal of POR is to prune states from already explored states, even though the states to be pruned are unique and have not been seen before (Wehrle and Helmert 2012, 2014; AlKhazraji 2017). The idea is to prune states that are guaranteed to be uncritical for reaching some desired final states or verifying some properties (e.g., deadlocks) AlKhazraji (2017). The POR technique we used in our work is not based on stubborn set methods because we do not let irrelevant states to be created to begin with.

7.2.2 Persistent set methods

These methods compute a sufficient subset of the set of enabled transitions to be explored in every state (Godefroid 1996). Enabled transitions are selected based on static information available in the state in such a way that transitions that are not selected (but enabled) will not interfere with the execution of transitions that are selected (Flanagan and Godefroid 2005a, b).

This is yet different from what we do in our POR method because we do not leave out jobs that could be dispatched after a given state as we do not know if those jobs could later result in a deadline miss for other jobs. When we find a safe reduction set for a state, that state will only have one outgoing edge which will contain all jobs that could possibly be dispatched at that state plus other jobs that could be dispatched in the future. Furthermore, our safe reduction sets are formed in such as way that no possible execution scenario is missed or ignored when exploring a given state. We think that a POR that is based on the notion of persistent sets would need to argue on why/how a possible dispatch event from a state can be ignored.

7.2.3 Sleep set methods

Sleep sets create a set of transitions that need not be taken anymore from a given state (Godefroid 1996). This set is computed using information given by states previously visited on the same path. Sleep sets reduce the exploration by removing transitions from the graph but not the number of states (which will remain the same) (Aronis et al. 2018). These sets can only be formed for independent enabled transitions, as stated by Goedfroid (Godefroid 1996). The transitions in the SAG, however, are mostly dependent. Consequently, the resulting sleep sets will be empty in almost all states. We believe that the sleep set method does not seem to solve the challenges faced by the reachability-based response-time analyses because they would not even be able to reduce the number of transitions in the graph.

In conclusion, our POR is different from the classic POR techniques developed for state exploration and reachability analysis mainly due to the fact that we cannot eliminate any execution scenario unless we are sure it will not contribute to a deadline miss. Unlike classic techniques, we do not achieve this guarantee by prioritizing the states to be explored (over those that will be left alone or ignored) because in the context of scheduling problem, a deadline miss can happen far in the future and we currently do not have a quick way to identify the absence of it without looking into many scenarios. Moreover, the classic approaches require the assumption that there are independent transitions in the state space, however, as explained earlier, transitions (job-dispatch events) in the response-time analysis are dependent because execution of jobs affect the status of resources, resulting in interference and blocking on the future jobs and hence change their response-time.

For the above reason, we have designed an entirely different way of partial-order reduction. Our solution takes a peek (i.e., quickly looks) at potential future events (job dispatches) to see if it is safe to skip the interleaving of these events and jump forward in time. We archive this goal by repeatedly adding the newly-found interfering jobs to a candidate reduction set until reaching a point where the ordering between the jobs in the set does not impact schedulability any more and no other new job can be added to the set (recall Fig. 2).

8 Conclusion

Summary: In this work, we applied partial-order reduction (POR) to one of the most recent reachability-based response-time analyses called schedule-abstraction graph (SAG). We limit the combinatorial exploration of all scheduling decisions by aggregating them when their order does not impact system’s schedulability. This allows us to improve the scalability of the SAG analysis without jeopardizing its soundness and with barely any added pessimism on the WCRT estimates.

Results and conclusion: Our empirical evaluation shows that our POR was able to reduce the runtime by five orders of magnitude and the number of explored states by 98% compared to the original SAG analysis for non-preemptive tasks. Our solution could analyse a large automotive use case made of hundreds of runnables and tens of thousands of jobs in a matter of seconds when the original analysis failed to finish. Lastly, tests on synthetic task sets showed that our new solution scales to $6\cdot 10^6$ jobs per hyperperiod, whereas the original analysis already fails to finish at $5\cdot 10^4$ jobs per hyperperiod. In case of limited-preemptive and DAG tasks, the original SAG did not scale beyond a few segments per tasks when tasks have release jitter. On the other hand, the POR approach could easily analyze tasks with up to 20 segments in a few minutes. Overall, the average runtime of POR to analyze a task set with 20 limited-preemptive tasks (each having up to 20 segments) was 63 s when $U=30\%$, 139 s when $U=50\%$, and 263 s when $U=70\%$.

These results confirm that POR allows us to analyze significantly more complex task sets (with more tasks, more jobs, and complex precedence constraint relations) than the original analysis and has the potential to be used in industrial design-space exploration tools.

Discussions and future directions: The partial-order reduction approach laid out in this work crucially depends on the availability of information about the release interval (jitter) of jobs in the input job set within an observation window (e.g., during a hyperperiod). This information, which is also required by the schedule-abstraction graph (even without partial-order reduction), is used to identify the candidate reduction set and derive bounds on the earliest and latest finish time of jobs in that set. Therefore, both the current POR approach and its underlying schedule-abstraction graph technique need to be adapted when dealing with sporadic task sets. One way to do so is to construct a (or a set of) job set (with uncertain release times) that encompasses all possible and valid release scenarios of a sporadic task set. In that case, both SAG and POR techniques could be readily applied to analyze the schedulability of sporadic tasks. However, as (i) to the best of our knowledge, there has been no prior work on constructing such job set, and (ii) the inclusion of large uncertainties in the release interval of the jobs would likely result in early state-space explosions even when POR is used, reachability-based schedulability analysis of sporadic tasks may require significant structural changes to the current SAG technique. In the future, we would adapt SAG to analyze whether an arbitrary job of a sporadic task meets its deadline by constructing the largest busy-window before the job starts its execution.

Recent schedule-abstraction techniques (Nasri et al. 2018, 2019; Nelissen et al. 2022) allow analyzing global scheduling policies on multicore platforms. However, the integration of our POR approach to these analyses is not trivial as it requires designing methods to identify interfering jobs in a multicore setup. Our current solutions to finding potential idle intervals, bounding the earliest and latest start times of jobs in a candidate job set, and checking whether a set of interfering jobs is schedulable (steps 3 and 6 of Fig. 2) are dedicated to single-core platforms. In the future, we would extend these steps to systems that have more than one core.

Furthermore, we plan to investigate the possibility of combining our POR technique with other classic POR methods such as dynamic POR.