Abstract
Deterministic timed automata are strictly less expressive than their non-deterministic counterparts, which are again less expressive than those with silent transitions. As a consequence, timed automata are in general non-determinizable. This is unfortunate since deterministic automata play a major role in model-based testing, observability and implementability. However, by bounding the length of the traces in the automaton, effective determinization becomes possible. We propose a novel procedure for bounded determinization of timed automata. The procedure unfolds the automata to bounded trees, removes all silent transitions and determinizes via disjunction of guards. The proposed algorithms are optimized to the bounded setting and thus are more efficient and can handle a larger class of timed automata than the general algorithms. We show how to apply the approach in a fault-based test-case generation method, called model-based mutation testing, that was previously restricted to deterministic timed automata. The approach is implemented in a prototype tool and evaluated on several scientific examples and one industrial case study. To our best knowledge, this is the first implementation of this type of procedure for timed automata.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The design of modern embedded systems often involves the integration of interacting components \(I_1\) and \(I_2\) that realize some requested behavior. Figure 1 illustrates two components \(I_{1}\) and \(I_{2}\) that realize the integrated system I. In early stages of the design, \(I_{1}\) and \(I_{2}\) are high-level and partial models that allow considerable implementation freedom to the designer. In practice, this freedom is reflected in the non-deterministic choices that are intended to be resolved during subsequent design refinement steps. In addition, the composition of two components involves their synchronization on some shared actions. Typically, the actions over which the two components interact are hidden and become unobservable to the user. It follows that the overall specification \(I = I_{1}~||~I_{2}\) can be a non-deterministic partially observable model.
The passage from a high-level model towards an implementation consists of an iteration of refinement steps. In every refinement step, the designer must ensure that the more concrete model \(I'\) restricts the behavior of I (e.g. by resolving some of the non-deterministic choices in I) and does not add new behavior which I does not admit. It follows that the designer has to check, using for instance model checking or model-based testing techniques, whether \(I'\) refines I. When considering non-deterministic partially observable models, the notion of refinement is often based on trace or alternating trace inclusion. In practice, checking whether \(I'\) refines I often requires the determinization of I. In fact, for many problems, such as model-based testing, observability, implementability and language inclusion checking, it is desirable and in certain cases necessary to work with the deterministic model.
Many embedded systems must meet strict real-time requirements. It follows that the timing constraints are needed to be part of the model from the early stages of the design. Timed automata (TA) (Alur and Dill 1994) are a formal modeling language that enables specification of complex real-time systems. The theory of TA has received considerable attention in the past decades and is supported by a number of tools, such as UPPAAL (Bengtsson et al. 1996), IF (Bozga et al. 2002), Kronos (Daws et al. 1996) and RED (Wang 2003). In contrast to the classical automata theory, determinism and observability play a crucial role in the theory of TA. In particular, deterministic TA (DTA) are strictly less expressive than the fully observable non-deterministic TA (NTA) (Alur and Dill 1994; Tripakis 2006; Finkel 2006), whereas the latter are strictly less expressive than TA with silent transitions (eNTA) (Bérard et al. 1998). This strict hierarchy of TA with respect to determinism and observability has an important direct consequence - NTA are not determinizable in general. In addition, due to their complexity, it is rarely the case that exhaustive verification methods are used during the design of modern embedded systems. Lighter and incomplete methods, such as model-based testing (Tretmans 1996) and bounded model checking (Biere et al. 2003) are used in practice, in order to gain confidence in the design-under-test and effectively catch bugs.
In this paper, we propose a procedure for bounded determinization of \(\mathrm {eNTA}\). Given an arbitrary strongly responsive Footnote 1 \(\mathrm {eNTA}\) A and a bound k, our algorithm computes a DTA D(A) in the form of a timed tree, such that every timed trace consisting of at most k observable actions is a trace in A if and only if it is a trace in D(A). It provides the basis for effectively implementing bounded refinement checking and test-case generation procedures.
Our concrete motivation behind determinizing the model was induced by our previous model-based testing approach, called model-based mutation testing Aichernig et al. (2013). The approach aims at building a test suite that covers specific types of possible faults in the model. In the first step, it alters the model according to a set of mutation operators, to create a set of faulty models, called mutants, where each contains one fault. Then it performs a language inclusion check, implemented via SMT-solving, between the original model and each of the mutants. If the two models do not conform to each other, a test case is created, that leads to the first transition that uncovers the fault. This creates one test case for each non-equivalent mutant, and thus covers all faults specified by the set of mutation operators.
The language inclusion check, however, relies on deterministic original models. Thus, for non-deterministic models, we were previously not able to perform the test-case generation. The bounded determinization introduced in this paper works as a pre-processing step for the test generation. It enables the processing of a wider class of models. The restriction to bounded traces does not pose a problem, as testing only considers finite traces.
The proposed algorithms are performed in three steps: (1) we unfold the original automaton into a finite tree and rename the clocks in a way that only needs one clock reset per transition, (2) we remove the silent transitions from the tree, (3) we determinize it. Our determinization procedure results in a TA description which includes diagonal (Bouyer et al. 2005) and disjunctive constraints. Although non-standard, this representation is practical and optimized for the bounded setting—it avoids costly transformation of the TA into its standard form and exploits efficient heuristics in SMT solvers that can directly deal with this type of constraints. In addition, our focus on bounded determinization allows us to consider models, such as TA with loops containing both observable and silent transitions with reset, that could not be determinized otherwise. We implemented the procedure in a prototype tool and evaluated it on several examples. To our best knowledge, this is the first implementation of this type of procedure for timed automata.
Running example The different steps of the algorithms will be illustrated on a running example of a coffee-machine shown in Fig. 2. After inserting a coin, the system heats up for zero to three seconds, followed by a beep-tone indicating its readiness. Alternatively, if there is no coffee or water left, the beep might occur after exactly two seconds, indicating that the refunding process has started and the coin will be returned within four seconds. Heating up and graining the coffee together may only take up to two seconds, indicated by the invariant of the graining location. Then the brewing process starts and finally the machine releases the coffee after one second of brewing. There is no observable signal indicating the transition from graining to brewing, thus this transition is silent.
This article is an extended version of a publication in the proceedings of the 13th International Conference on Formal Modeling and Analysis of Timed Systems (Lorber et al. 2015). The additional content presented in this paper covers a short introduction into model-based mutation testing, which is our motivation behind the determinization, an industrial case study for evaluation, proofs of the theorems and an update of the algorithms, that allows to keep invariants in the final automata.
The rest of the paper is structured as follows: first, we give the basic definitions and notation of TA with silent transitions (Sect. 2). Then we present our practical motivation behind the determinization approach, give a short overview of model-based mutation testing (Sect. 3), and explain why it needs the determinization. Next, we illustrate the first step of our procedure, the bounded-unfolding of the automaton and the renaming of clocks (Sect. 4.1). This is followed by the second step, the removal of silent transitions (Sect. 5) and the final step, our determinization approach (Sect. 6). Section 7 summarizes the complexity of the different steps. In Sect. 8 we evaluate our prototype implementation and in Sect. 9 we address related work. Finally, in Sect. 10 we conclude our work.
2 Timed automata with silent transitions
A timed automaton is an abstract model aiming at capturing the real-time behaviour of systems. It is a finite automaton extended with a set of clocks defined over \(\mathbb {R}_{\ge 0}\), the set of non-negative real numbers. We may represent the timed automaton by a graph whose nodes are called locations. To each location there may be assigned a set of invariants, which are non-negative integer upper bounds on the values of the clocks. While being at a location, all clocks progress at the same rate, but they are not allowed to pass the location invariants. The edges of the graph are called transitions. Each transition may be subject to constraints, called guards, put on clock values in the form of integer inequalities. At each such transition an action occurs and some of the clocks may be reset. The actions take values in some finite domain denoted by \(\Sigma \). Here we are dealing with the class of timed automata with an extended set of actions including also silent actions, denoted by \(\epsilon \). These are internal actions that are non-observable from the outside, and we distinguish them from the actions that are not silent and called observable actions. We call a TA without silent transitions fully-observable.
Let \(\mathcal {X}\) be a finite set of clock variables. A clock valuation \(v(x)\) is a function \(v:\mathcal {X}\rightarrow \mathbb {R}_{\ge 0}\) assigning a real value to every clock \(x\in \mathcal {X}\). We denote by \(\mathcal {V}\) the set of all clock valuations and by \(\mathbf 0 \) the valuation assigning 0 to every clock. For a valuation v and \(d \in \mathbb {R}_{\ge 0}\) we define \(v+d\) to be the valuation \((v+d)(x) = v(x)+d\) for all \( x\in \mathcal {X}\). For a subset \(\mathcal {X}_{rst}\) of \(\mathcal {X}\), we denote by \(v[\mathcal {X}_{rst}]\) the valuation such that for every \(x\in \mathcal {X}_{rst}\), \(v[\mathcal {X}_{rst}](x) = 0\) and for every \(x\in \mathcal {X}\setminus \mathcal {X}_{rst}\), \(v[\mathcal {X}_{rst}](x) = v(x)\). A clock constraint \(\varphi \) is a conjunction of predicates of the form \(x\sim n\), where \(x\in \mathcal {X}\), \(n \in \mathbb {N}\) and \(\sim \ \in \{ <, \le , =, \ge , > \}\). Given a clock valuation v, we write \(v \models \varphi \) when v satisfies \(\varphi \). We give now a formal definition of (non-deterministic) timed automata with silent transitions.
Definition 1
(\(\mathrm {eNTA}\)) A (non-deterministic) timed automaton with silent transitions A is a tuple \((\mathcal {Q}, q_{init}, \Sigma _{\epsilon }, \mathcal {X}, \mathcal {I}, \mathcal {G},\mathcal {T}, \mathcal {Q}_{accept})\), where
-
1.
\(\mathcal {Q}\) is a finite set of locations and \(q_{init} \in \mathcal {Q}\) is the initial location;
-
2.
\(\Sigma _{\epsilon }= \Sigma \cup \{\epsilon \}\) is a finite set of actions, where \(\Sigma \) are the observable actions and \(\epsilon \) represents a silent action, that is a non-observable internal action;
-
3.
\(\mathcal {X}\) is a finite set of clock variables;
-
4.
\(\mathcal {I}: \mathcal {Q}\rightarrow LI\) is a mapping from locations to location invariants, where each location invariant \(li \in LI\) is a conjunction of constraints of the form true, \(x< n\) or \(x\le n\), with \(x\in \mathcal {X}\) and \(n \in \mathbb {N}\);
-
5.
\(\mathcal {G}\) is a set of transition guards, where each guard is a conjunction of constraints of the form \(x\sim n\), where \(x\in \mathcal {X}\), \(\sim \ \in \{<,\le , =,\ge , >\}\) and \(n \in \mathbb {N}\);
-
6.
\(\mathcal {T}\subseteq \mathcal {Q}\times \Sigma _{\epsilon }\times \mathcal {G}\times \mathcal P \left( {\mathcal {X}}\right) \times \mathcal {Q}\) is a finite set of transitions of the form \((q, \alpha , g, \mathcal {X}_{rst}, q')\), where
-
(a)
\(q,q' \in \mathcal {Q}\) are the source and the target locations,
-
(b)
\(\alpha \in \Sigma _{\epsilon }\) is the transition action,
-
(c)
\(g \in \mathcal {G}\) is the transition guard,
-
(d)
\(\mathcal {X}_{rst}\subseteq \mathcal {X}\) is the subset of clocks to be reset;
-
(a)
-
7.
\(\mathcal {Q}_{accept}\subseteq \mathcal {Q}\) is the subset of accepting locations.
Example 1
For the eNTA illustrated in Fig. 2 we have \(\mathcal {Q}= \{q_0, \dots , q_4\}\), \(q_{init} = q_0\), \(\Sigma _{\epsilon }= \{\epsilon , coin , beep , refund , coffee \}\), \(\mathcal {X}= \{x\}\), \(\mathcal {I}(q_0) = true\), \(\mathcal {I}(q_1) = true\), \(\mathcal {I}(q_2) = x<2\), \(\mathcal {I}(q_3) = x \le 1\), \(\mathcal {I}(q_4) = x<4\), \(\mathcal {G}= \{0<x<3, x=2, x<4, 1<x, x=1\}\), \(\mathcal {Q}_{accept}= \{q_0\}\). \(\mathcal {T}\) is the set containing all transitions, e.g. the transition from \(q_2\) to \(q_3\), with \(\alpha = \epsilon \) (thus, it is a silent transition), \(g = 1<x<2\) and \(\mathcal {X}_{rst}= \{x\}\).
The semantics of an \(\mathrm {eNTA}\) A is given by the timed transition system \([[A]] = (S, s_{init}, \mathbb {R}_{\ge 0}, \Sigma _{\epsilon }, T, S_{accept})\), where
-
1.
\(S = \{(q,v) \in \mathcal {Q}\times \mathcal {V}~|~ v \models \mathcal {I}(q) \}\);
-
2.
\( s_{init} = (q_{init},\mathbf 0 )\);
-
3.
\(T \subseteq S \times (\Sigma _{\epsilon }\cup \mathbb {R}_{\ge 0}) \times S\) is the transition relation consisting of timed and discrete transitions such that:
-
(a)
Timed transitions (delay): \(((q,v), d, (q, v+d)) \in T\), where \(d \in \mathbb {R}_{\ge 0}\), if \(v+d \models \mathcal {I}(q)\),
-
(b)
Discrete transitions (jump): \(((q,v), \alpha , (q',v')) \in T\), where \(\alpha \in \Sigma _{\epsilon }\), if there exists a transition \((q, \alpha , g, \mathcal {X}_{rst}, q')\) in \(\mathcal {T}\), such that: (1) \(v \models g\); (2) \(v' = v[\mathcal {X}_{rst}]\) and (3) \(v' \models \mathcal {I}(q')\);
-
(a)
-
4.
\(S_{accept} \subseteq S\) such that \((q,v)\in S_{accept}\) if and only if \(q \in \mathcal {Q}_{accept}\).
A finite well-behaving run \(\rho \) of an \(\mathrm {eNTA}\) A is a finite sequence of alternating timed and discrete transitions, that ends with an observable action, of the form \((q_{0}, v_{0}) \xrightarrow {d_{1}} (q_{0}, v_{0} + d_{1}) \xrightarrow {\tau _{1}} (q_{1}, v_{1}) \xrightarrow {d_{2}} \cdots \xrightarrow {d_{n}} (q_{n-1}, v_{n-1} + d_{n}) \xrightarrow {\tau _{n}} (q_{n}, v_{n})\), where \(q_{0} = q_{init}\), \(v_{0} = \mathbf 0 \), \(\tau _{i} = (q_{i-1}, \alpha _{i}, g_{i}, \mathcal {X}_{rst(i)}, q_{i}) \in \mathcal {T}\) and \(\alpha _i \in \Sigma _{\epsilon }\) for \(i < n\), \(\alpha _n \in \Sigma \). In this paper we consider only finite and well-behaving runs. A run \(\rho \) is accepting if the last location \(q_n\) is accepting. The run \(\rho \) of A induces the timed trace \(\sigma = (t_{1}, \alpha _{1}), (t_{2}, \alpha _{2}), \ldots , (t_{n}, \alpha _{n})\) defined over \(\Sigma _{\epsilon }\), where \(t_{i} = \Sigma _{j=1}^{i} d_i\). From the latter we can extract the observable timed trace, which is obtained by removing from \(\sigma \) all the pairs containing silent actions while taking into account the passage of time. A TA is called deterministic if it does not contain silent transitions and whenever two timed traces are the same then they are induced by the same run. Otherwise, the TA is non-deterministic. The language accepted by an \(\mathrm {eNTA}\) A, denoted \(\mathfrak {L}(A)\), is the set of observable timed traces induced by all accepting runs of A. Note, that the restriction to well-behaving runs is compatible with the definition of the language of the automaton, where silent actions that occur after the last observable action on a finite run are ignored. As a consequence, a location with in-going edges consisting of only silent transitions cannot be an accepting location.
Additionally note, that our determinization process produces a class of timed automata where the definition of guards and invariants is weakened, allowing the disjunction of constraints.
3 Practical motivation
The practical motivation behind our determinization approach comes from the field of model-based testing. In previous work (Aichernig et al. 2013) we developed a fault-based testing approach for timed automata, called model-based mutation testing. One restriction of the approach was the limitation to deterministic and fully observable models. In this section we will first introduce our model-based mutation testing approach, and then briefly illustrate how the determinization developed in this paper removes our restriction.
Model-based testing (Tretmans 2008) was introduced as a pragmatic compromise between the conceptual simplicity of classical testing, and automation and exhaustiveness of model checking. In model-based testing, test suites are automatically generated from a mathematical model of the system-under-test(SUT). The main advantage of this technique is the full test automation that provides effective means to catch errors in the SUT. The aim of model-based testing is to check conformance of the SUT to a given specification, where the SUT is often seen as a “black-box” with unknown internal structure, but observable input/output interface. Model-based testing is commonly combined with some coverage criteria, with the aim to generate test cases that cover most possible use cases of the SUT.
Model-based mutation testing is a specific type of model-based testing, in which faults are deliberately injected into the specification model. This generates a set of faulty models, called mutants, where each contains exactly one fault. The aim of mutation-based testing techniques is to generate test cases that can detect the injected errors. This means that a generated test case shall fail if it is executed on a (deterministic) SUT that implements the faulty model. The power of this testing approach is that it can guarantee the absence of certain specific faults. To generate the test cases, we check for conformance between the original specification model and each of the mutants. If we detect non-conformance, we generate a test case leading directly to the conformance violation, otherwise we consider the mutant to be equivalent. An example for an equivalent mutant would for instance be a mutant adding or removing a clock reset of a clock that is never used in a guard after the reset.
We already presented our model-based mutation testing approach for timed automata (Aichernig et al. 2013), using timed input output conformance (Schmaltz and Tretmans 2008) for the conformance check between the models. The check was expressed as a language inclusion problem, which we solved via SMT-solving. The approach is restricted to deterministic specifications that are fully observable, as it might produce spurious counterexamples for non-deterministic models. The algorithm searches for a location in the specification, where the mutant may perform more outputs than the specification. If such a location is found in a non-deterministic specification, there might still be another location, that can be reached by the same trace and allows the behavior of the mutant. In such a case, we would generate a test case, even though the mutant actually conformed to the specification.
Using the bounded determinization approach presented in this paper, we are able to determinize the specification and the mutants in a preprocessing step. In principle, to remove the spurious counter examples, it would suffice for the original model to be deterministic, while the mutants may contain non-determinism. However, as the conformance check cannot handle silent transitions, at least the silent transitions have to be removed in the mutants as well. As this already includes the unfolding, we also determinize them, to keep the number of transitions in the mutants low. After the determinization, we can safely apply the test-case generation approach to all timed automata, as long as they do not contain loops of silent transitions that reset clocks. In case a mutation introduces such loops, we discard the corresponding mutant from our experiments. Figure 3 illustrates the updated workflow of model-based mutation testing, including the determinization and silent transition removal of the original and the mutated specifications, as a preprocessing step to the conformance check. First we model the correct specification as a non-deterministic timed automata with silent transitons, and mutate it to generate a set of non-deterministic mutants. Then all the automata are determinized and the test-case generator checks whether the mutants conform to the specification or not. In case of non-conformance, we generate test cases, which can than be executed on the SUT. If the SUT conforms to the specification, the test cases will successfully be executed and assign the verdict pass.
Figure 4 shows a possible mutant of the running example, where the coffee machine refunds the money, instead of producing coffee. A timed trace for revealing the mutation would be \((0,coin),(1,beep),(0.5,\epsilon )\), where the specification would expect (1, coffee) in the next step, and the mutant produces (1, refund) instead.
Note that in model-based mutation testing, we consider timed automata with inputs and outputs. Thus, the set of observable actions is split into two disjoint sets of inputs and outputs. For the coffee machine, we consider refund, beep and coffee as outputs, and the coin as an input. However, this is only relevant for the test case generation and will not be considered during the determinization.
4 Preprocessing
4.1 k-Bounded unfolding of timed automata
Given an \(\mathrm {eNTA}\) A which is strongly responsive, its k-prefix language \(\mathfrak {L}_k(A) \subseteq \mathfrak {L}(A)\) is the set of observable timed traces induced by all accepting runs of A
which are of observable length bounded by k. That is,
By unfolding A and cutting it at observable level k, the resulting TA, \(U_k(A)\), satisfies
\(U_k(A)\) is in the form of a finite tree, where each path that starts at the root ends after at most k observable transitions, and we may also further cut A by requiring that all leaves are accepting locations. Note, that if we reach in \(U_k(A)\) a copy of an accepting location q of A by a silent transition then it will not be marked as an accepting location (but another copy might be marked as an accepting location if reached by an observable transition).
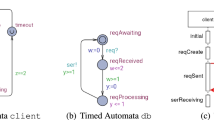
Figure 5a shows the unfolding of the coffee-machine up to observable depth three. The left branch is longer than the right, as it contains a silent transition.
4.2 Renaming the clocks
Every unfolded timed automaton can be expressed by an equivalent timed automaton that resets at most one clock per transition. This known normal form Baier et al. (2009) crucially simplifies the next stages of our algorithm, where we do not need to bother with multiple clock resets in one transition. While this is not a novel contribution of this paper, we will now give some details on the algorithm, to enhance the comprehensibleness of the paper. The basic idea is to substitute the clocks from the original automaton by new clocks, where multiple old clocks reset at the same transition are replaced by the same new clock, as they measure the same time until they are reset again. The substitution of the clocks works in a straightforward way: At each path from the root, at the i-th observable transition, a new clock \(x_i\) is introduced and reset, and if this transition is followed by \(l > 0\) silent transitions then new clocks \(x_{i,0}, \ldots , x_{i,l-1}\) are introduced and reset. A clock x that occurs in a guard is substituted by the new clock that was introduced in the transition where the last reset of x happened, or by \(x_0\) if it was never reset. Let \(\tau _i\) and \(\tau _j\) be two transitions on the same path in the original automaton at observable depths i and j, with \(i<j\). Assume that a clock x that appears in the guard of \(\tau _j\) is reset in the previous transition \(\tau _i\), but is not reset on any of the transitions between \(\tau _i\) and \(\tau _j\). Then, \(x_i\) is introduced and reset at \(\tau _i\) and the original clock variable x is substituted by \(x_i\) in the guard of \(\tau _j\). Clocks in invariants are updated the same way as guards. Figure 5b illustrates the clock renaming applied to the coffee machine. In the guards of the two beep-transitions starting at \(q_1\), x is replaced by \(x_1\), since the last reset of x in the original automaton was at depth one, while in the coffee-transition from \(q_3\) it is replaced by \(x_{2,0}\), as x was reset in the first silent transition after depth two.

The concrete algorithm used for renaming of the clocks is presented in pseudo-code in Algorithm 1. The original clocks are \(x_0, \ldots , x_{n-1}\). Each new clock has either one index (\(l_1\)) in case the transition in which it is reset is observable, or two indices (\(l_1, l_2\)) in case of a silent transition. After the removal of the silent transitions stage we will be left with clocks with a single index and the same clock reset for the same level of the tree. The vector \(X[0..n-1]\) holds the clock substitution list: X[i] refers to the new clock that substitutes the original clock \(x_i\). The set of transitions with source location q is denoted by trans(q).
4.3 Integrating invariants into guards
In this last preprocessing step, we integrate (i.e. conjugate) the location invariants into the guards of all the incoming and outgoing transitions from that location. Since the guards are updated and synchronized during the silent transition removal, this ensures that the constraints of the invariants are also taken into account in that step. The invariants are still kept unchanged in the automaton. Figure 5c shows the integrating of the invariants in the running example, where e.g., the guard of the silent transition was augmented by \(x_1<2\) and the guard of the left beep transition was modified to \(0<x_1<2\). Note that the guard of the coffee transition was not modified, as \(x_{2,0} = 1\) is already more strict than \(x_{2,0} \le 1\). Additionally, the guard of the silent transition was not updated according to the invariant of its target location, since the invariant uses the clock that was reset by the silent transition and thus only influences the coffee transition. As no transition can be traversed if the invariant of its source or target location is not enabled, adding the invariants to the guards does not change the language of the automaton. Due to the fact that a transition can not be traversed if the invariant of the target location is not enabled, the invariants of the target locations need not be incorporated into the guards of a transition for performing the silent transition removal. However, during the determinization we add disjunctive invariants, which are possibly weaker than the original invariants. For this reason we also need to integrate the invariants into the guards of incoming transitions.
5 Removing the silent transitions
In this section we present an algorithm that removes the silent transitions from the \(\mathrm {eNTA}\) A, where A is the automaton obtained by the preprocessing stage in the form of a finite tree with renamed clocks. That is, one clock \(x_0\) is reset at the initial location. Then, at each path from the root, at the i-th observable transition a clock \(x_i\) is reset, and if this transition is followed by \(l > 0\) silent transitions then the clocks \(x_{i,0}, \ldots , x_{i,l-1}\) are reset. In the next observable transition the clock \(x_{i+1}\) is reset, and so on. All these clocks are not reset again. After removing the silent transitions, the new TA, R(A), will have the same one clock reset at all transitions of same level.
We remove the silent transitions one at a time, where at each iteration we remove the first occurrence of a silent transition on some path from the root, until no silent transitions are left (e.g. we can pick a path and remove one-by-one all its silent transitions, then move to another path, and so on).
In order to remove a silent transition we add a new transition that bypasses the silent transition by connecting the location that leads to the source of the silent transition to the location that is the target of the silent transition. This is illustrated in Fig. 6, where the silent transition \(\tau _{s,0}\) from location \(q_s\) to location \(q_{s,0}\) is removed and a bypass is formed from location \(q_{s-1}\) to location \(q_{s,0}\). The case where \(q_s\) is the initial location is simpler, as it does not require building a bypass. We just check the conjunction of constraints on the single reset clock \(x_0\) of the guard of the silent transition, delete the transition and the subtree beneath if the guard defines an empty set, and otherwise delete only the silent transition as described in the workflow below, which leads to the merging of its target location and the initial location.
The removal of the silent transition enforces the update of the transitions’ guards and the locations’ invariants. First we create the guard of the bypass transition. This is done by conjuncting the original guard \(g_s\) of the transition from \(q_{s-1}\) to \(q_s\) with what we call an enabling guard (guard \(eg(\tau _{s,0})\) in Fig. 6). The aim is to guarantee that the bypass could have been followed by the silent transition if the latter would not have been removed. In order to achieve this goal we need to make sure that by the time the bypass is taken the upper bounds of the clocks that appear in the guard \(g_{s,0}\) of the silent transition are not passed, and, moreover, that the clocks appearing in \(g_{s,0}\) are synchronized in such a way that after a possible delay all the constraints of the silent transition guard are satisfied simultaneously.
Since the bypass transition occurs before the silent transition, it is necessary to ensure that after taking the bypass and reaching \(q_{s,0}\) we stay at \(q_{s,0}\) long enough that all lower bound constraints of the silent transition guard are reached. This is done by adding the taken guard to all out-going transitions of \(q_{s,0}\).
The next step is to update the guards and location invariants in all the paths that start at \(q_{s,0}\), the target of the silent transition. These may refer to a clock that was reset during the silent transition (clock \(x_{s,0}\) in Fig. 6). Thus, we may not be able to refer to the exact time of the silent transition (captured by \(x_{s,0}\)), but instead we can refer to the clocks that form the constraints of the silent transition. In addition, we need to synchronize between these added constraints to the future guards and invariants, in such a way that simultaneously they satisfy the same possible reset of the silent transition clock.
Algorithm 2 shows the overall workflow of the silent transition removal.

5.1 Setting a lower bound to the silent transition
We set a lower bound to the silent transition by augmenting the guard \(g_{s,0}\) of \(\tau _{s,0}\) to be \(g'_{s,0} = g_{s,0} \wedge (0 \le x_s)\), where \(x_s\) is the clock that is reset on the transition \(\tau _s\) that precedes the silent transition. This additional constraint per definition always evaluates to true, but it is used in the next step to compute the unary constraints of the enabling guard. The guard of the silent transition in Fig. 5 (c) after setting the lower bound is \(1< x_1 < 2 \wedge 0 \le x_2\).
5.2 Creating a bypass with the enabling guard
The enabling guard \(eg(\tau _{s,0})\) guarantees that each clock’s constraint that was part of the silent transition is satisfied at some non-negative delay and that these constraints are satisfied simultaneously, thus at some point during the bypass transition the silent transition would have been enabled as well. We describe here how the enabling guards are defined for strict inequalities, as shown in the first line of Table 1. The other cases are dealt with similarly, as seen in the next lines of the table, and the constraint \(x_i = n_i\) is treated as \(n_i \le x_i \le n_i\). For each pair of a lower bound constraint \(m_i < x_i\) and an upper bound constraint \(x_j < n_j\) that appear in \(g'_{s,0}\), we form the enabling guard binary constraint \(x_j - x_i < n_j - m_i\).
The last line of Table 1 refers to the special case where the lower bound constraint is \(0 \le x_s\), the constraint, added in the previous step, that involves the new clock \(x_s\) (that is reset on the silent transition). Since at the time of the silent transition the value of \(x_s\) is 0, the inequality \(x_j - x_s < n_j - 0\) simplifies to the unary constraint \(x_j < n_j\), which guarantees that at the time of the bypass \(x_j\) does not pass its upper bound constraint of the silent transition. An example of such a unary constraint is marked in red in the transition from \(q_1\) to \(q_3\) in Fig. 7. The silent transition in the original automaton could not have been enabled if \(x_1\) had already been higher than 2 after the beep-transition, thus the bypass can also only be enabled while \(x_1\) is smaller than 2. The running example does not contain any binary constraints.
Note that the upper bound constraints of the invariant of \(q_s\) were integrated into the guard of the silent transition. Thus, they are also integrated into the enabling guard. Consequently, the bypass will satisfy the constraints of the location invariant. The invariant itself remains unchanged, as it remains active for all traces that pass through \(q_s\), but do not take the silent transition.
To create the bypass, we split the paths through \(q_s\) in the original automaton A into two. Those that do not take the silent transition \(\tau _{s,0}\) continue as before from \(q_{s-1}\) to \(q_s\) and then to some location different from \(q_{s,0}\). The paths that went through \(\tau _{s,0}\) are directed from \(q_{s-1}\) to \(q_{s,0}\) and then continue as before. The bypass \(\tau '_s\) from \(q_{s-1}\) to \(q_{s,0}\) has the same observable actions as those of \(\tau _s\), the same new clock reset \(x_s\), and the guard \(g'_s\) which is the guard \(g_s\) of \(\tau _s\) augmented with the enabling guard \(eg(\tau _{s,0})\) (see Fig. 6). Fig. 7 shows the removal of the silent transition illustrated on the coffee-machine. The transition from \(q_1\) to \(q_{3}\) is the bypass and the transition from \(q_1\) to \(q_2\) is the original transition. Since the silent transition was the only transition leaving \(q_2\), \(q_2\) does not contain any outgoing transitions anymore, once the bypass is generated.
5.3 Adding the taken guard
For each transition from \(q_{s,0}\) to \(q_{s+1}\) we augment its guard \(g_{s+1}\) by forming \(g'_{s+1} = g_{s+1} \wedge tg(\tau _{s,0})\) (see Fig. 6), where \(tg(\tau _{s,0})\) is the taken guard. \(tg(\tau _{s,0})\) is composed of a single constraint: \(0 \le x_{s,0}\), where \(x_{s,0}\) is the clock that is reset at the silent transition \(\tau _{s,0}\). In the next stage of the algorithm of updating the future guards it will be transformed into the conjunction of the lower bound constraints \(m_i < x_i\) or \(m_i \le x_i\) that appear in \(g'_{s,0}\). These constraints make sure that we spend enough time at \(q_{s,0}\) before moving to the next locations, as if we had taken the silent transition. The constraint is also used for synchronization of the future guards in the next step. In Fig. 7, the red-marked part of the guard from transition \(q_{3}\) to \(q_6\) shows the taken guard that has already been updated from \(0 \le x_{2,0}\) to \(1<x_1\).
5.4 Updating the future guards
The removal of the silent transition \(\tau _{s,0}\) enforces updating of the guards in the paths that start at \(q_{s,0}\) and that refer to the clock \(x_{s,0}\), that is reset on the silent transition. The constraints that refer to the other clocks can remain as they are.
The most simple case is when the silent transition guard \(g'_{s,0}\) contains an exact constraint \(x_i = n_i\), because then any future constraint of the form \(x_{s,0} \sim l\) where \(\sim \) is one of the signs \(=\), <, >, \(\le \) or \(\ge \), can be replaced by \(x_i \sim n_i+ l\). In that case we know the exact time of the silent transition, and all other constraints may be ignored. So, let us assume that the silent transition does not contain an exact constraint. The rules for updating the future guards are summarized in Table 2. Note, that an equality constraint \(x_{s,0} = n_{s+j}\) in a future guard may be treated as \(n_{s+j} \le x_{s,0} \le n_{s+j}\).
Let \(g_{s+1}, \ldots , g_{s+p}\) be the ordered list of guards of consecutive transitions \(\tau _{s+1}, \ldots , \tau _{s+p}\) along a path that starts at \(q_{s,0}\). Suppose, for simplicity, that each \(g_{s+j}\) contains constraints that refer to \(x_{s,0}\) (if not - we can ignore \(g_{s+j}\)). Then, if \(g_{s+j}\) contains a constraint \(m_{s+j} < x_{s,0}\) then it is replaced by the conjunction of constraints \(m_i + m_{s+j} < x_i\), for each constraint \(m_i < x_i\) that appears in \(g'_{s,0}\). Similarly, an upper bound constraints \(x_{s,0} < n_{s+j}\) of \(g_{s+j}\) is replaced by the conjunction of constraints \(x_i < n_i + n_{s+j}\), for each constraint \(x_i < n_i\) or \(x_i \le n_i\) of \(g'_{s,0}\). In Fig. 7, one future guard was updated in the transition from \(q_{3}\) to \(q_6\): The original guard of this transition was \(x_{2,0}=1\) (where \(x_{2,0}\) was reset on the silent transition) and the guard of the silent transition was \(1<x_1<2\). Thus, according to the update rules, the updated future guard is \(2<x_1<3\) (written in black), conjuncted with the taken guard (marked in red).
These rules ensure that each future constraint on the clock \(x_{s,0}\) separately conforms to and does not deviate from the possible time range of the silent transition. Yet, we need to satisfy a second condition: that along each path that starts at \(q_{s,0}\) these future occurrences of \(x_{s,0}\) are synchronized. For example, if one constraint is \(x_{s,0} = n\) and another one further on the same path is \(x_{s,0} = n+2\) then there should be a time difference of exactly 2 time units between these events. This is achieved by augmenting the future guards with constraints of the form that appear in Table 3, which refer to each pair of a lower bound and an upper bound constraint on \(x_{s,0}\) in two different transitions. No transition in our running example needs synchronization, hence we use a different example: the upper automaton in Fig. 8 shows one silent transition followed by two observable transitions. Using only the previous update rules when removing the silent transition, the first observable transition might occur between 3 and 4 seconds, and the second one between 5 and 6 seconds. If the first transition occurs after exactly 3.1 seconds and the second one after exactly 5.9 seconds, this would not conform to the original automaton which required exactly 2 seconds between them. Thus, applying the last synchronization rule of Table 3, the constraint \(x_1=4-2\) is conjuncted to the second guard. The lower automaton in Fig. 8 illustrates the synchronization. Note, we do not need a bypass transition here, since the silent transition starts in the initial state.
5.5 Updating the future location invariants
In this last step, we need to update all location invariants that refer to \(x_{s,0}\), the clock that was reset by the silent transition. Consider an invariant li in any location after the silent transition (which might be \(q_{s,0}\), the target location of the silent transition, or any following location). All constraints in li that do not involve \(x_{s,0}\) can remain unchanged, and we can assume that there is only one constraint for each clock, as a stronger upper bound subsumes a weaker one. Thus we only consider the constraint \(x_{s,0} < n\). This constraint is updated the same way as a future guard that refers to \(x_{s,0}\). The upper bounds of the silent transition (\(x_{i} < n_i\)) and the upper bound of the invariant (\(x_{s,0} < n\)) are combined to the new upper bounds \(x_i < n_i+n\). Note that it is not necessary to synchronize updated invariants among each other, as they only contain upper bounds and thus do not interfere with each other. The synchronization of the future guards with the invariants already happened in the last step, as the constraints of the invariants were added to the guards of the following transitions. Figure 7 shows that the invariant of location \(q_3\) was updated from \(x_{2,0} \le 1\) to \(x_1 \le 3\), according to the upper bound \(x_1 < 2\) of the silent transition.
5.6 Removing the silent transition
Finally, we can safely remove the silent transition \(\tau _{s,0}\) from \(q_s\) to \(q_{s,0}\) after forming the bypass from \(q_{s-1}\) to \(q_{s,0}\) with the necessary modifications to the transition guards.
Theorem 1
(Silent Transitions Removal) \(\mathfrak {L}(R(A)) = \mathfrak {L}(A)\).
A proof of the theorem can be found in the appendix.
6 Determinization
Existing determinization algorithms (as e.g. applied in Wang et al. 2014) create the powerset of all transitions to be determinized, and build one transition for each subset in the powerset. We propose an alternative approach, that reduces the amount of locations and transitions in the deterministic automata, by shifting some complexity towards the guards. Our motivation is the use of SMT solvers for model-based test-case generation from timed automata, as described in our first paper on mutation-based test-case generation from timed automata (Aichernig et al. 2013). The larger guards can be directly converted into SMT-LIB formulas, and thus should not pose a problem. The produced automata contain disjunctions, both in the guards and the invariants. While this does not conform to the standard definition of timed automata, in the context of SMT-solving the disjunctions can efficiently be processed and do not hinder test-case generation.
The approach works under the following prerequisites: After the removal of the silent transitions the timed automaton A is in the form of a tree of depth k. At each level i the same new clock \(x_i\) is reset on each of the transitions of that level. This is the only clock reset on this level, and no clock is ever reset again.


The basic idea behind the determinization algorithm is to merge all transitions of the same source location and the same action via disjunction, and to push the decision which of them was actually taken to the following transitions. The postponed decision regarding which transition was actually taken can be solved later on by forming diagonal constraints (as in zones) that are invariants of the time progress, and are conjuncted to immediately following transitions. Note that the distinction between accepting and non-accepting locations increases complexity slightly: the determinization of transitions leading to accepting locations and transitions leading to non-accepting locations can not be done exclusively by disjunction of their guards. We therefore need to add an accepting and a non-accepting location to the deterministic tree, and merge all transitions leading to non-accepting locations and all transitions leading to accepting locations separately. To ensure determinism for these transitions, we conjunct the negated guard of the accepting transition to the guard of the non-accepting transition. Additionally, the location invariants of merged target locations are combined via disjunction.
A pseudo-code description is given in Algorithm 3 and Algorithm 4. Algorithm 3 contains the outline of the algorithm: The determinization is done in several steps applied to every location q with multiple outgoing transitions with the same action (Line 5), starting at the initial location (Line 1). First, we add an accepting and a non-accepting location \(q_ {acc}\), \(q_{\lnot acc}\) that will replace the target locations of the multiple \(\alpha \) transitions (Line 7). Then we perform the merging of these transitions according to Algorithm 4: let \(q_i\) be such a location with multiple \(\alpha \) transitions (Line 1). For each \(\tau _i\) in the \(\alpha \) transitions with guard g from \(q_i\) to \(q'\), let \(g_d\) be the result of subtracting the clock x that is reset on \(\tau _i\) from all clocks that appear in g (Lines 2–5). Next, \(g_d\) is conjuncted to the guards of each transition \(\tau _{i+1}\) that follows \(\tau _i\) and the source location of \(\tau _{i+1}\) is set to either \(q_{acc}\) or \(q_{\lnot acc}\), depending on whether \(q'\) is accepting or not. Transitions leaving \(q_{\lnot acc}\) are additionally copied to \(q_{acc}\), in case the guards of \(\alpha \) transitions overlap. (Lines 7,8). Note that \(g_d\) evaluates to true in every branch below \(\tau _i\) if \(\tau _i\) was enabled, thus the conjunction does not change the language of the automaton. Figure 9a illustrates the conjunction of the modified guards on our running example, marked in red. Note that the determinization did not involve any accepting locations, thus there was no splitting into \(q_{acc}\) and \(q_{\lnot acc}\). Next, all the \(\alpha \)-transitions from q leading to accepting locations are merged into a transition leading to \(q_{acc}\) (Line 19) and all others into a transition leading to \(q_{\lnot acc}\)(Line 20), by disjuncting their guards (Lines 12,15). The guard of the transition leading to \(q_{\lnot acc}\) is conjuncted to the negation of the other guard, to ensure determinism (Line 20). Additionally, in Lines 12 and 15, the location invariants of the different target locations of the merged transitions are combined via disjunction. Finally, all merged \(\tau _i\) and their target locations can be removed (Line 17). Figure 9b shows the determinized coffee-machine. The location \(q_{\lnot acc}\) contains a location invariant that is a disjunction of the invariants from locations \(q_2\), \(q_3\) and \(q_4\) of the non-deterministic tree.
Example 2
Figure 10 shows a non-deterministic timed automaton \(A_{ex}\) and Fig. 11 shows its determinized form \(D(A_{ex})\). The automata illustrate the separation into accepting and non-accepting locations. As there is only one accepting location in \(A_{ex}\), the transition from \(q'_0\) to \(q'_{acc}\) in \(D(A_{ex})\) simply keeps that guard, while the transition from \(q'_0\) to \(q'_{\lnot acc}\) is a disjunction of the guards of the two other non-deterministic transitions, conjuncted with the negation of the guard of the transition to the accepting location. The example also shows the propagation of the diagonal constraints in case of sequences of non-determinism, e.g. in the transition from \(q'_{acc}\) to \(q'_1\): since \(q'_{acc}\) combines the locations \(q_1\) and \(q_3\) from \(A_{ex}\), the two b transitions from \(q_1\) to \(q_4\) and from \(q_3\) to \(q_6\) need to be determinized once more, after being updated via diagonal constraints, resulting in the guard \((x_0 > 3 \wedge x_0-x_1< 2) \vee (x_0<3 \wedge x_0-x_1 < 3) \). The c transition leaving \(q'_{acc}\) does not need to be determinized and thus it does not contain disjunction. It does, however, contain the diagonal constraints that were attached when the a transitions were determinized.
Theorem 2
(Determinization) The determinization algorithm constructs a deterministic timed automaton D(A) such that \(\mathfrak {L}(D(A)) = \mathfrak {L}(A)\).
The proof of the theorem can be found in the appendix.
7 Complexity
Bounded unfolding We unfold the timed automaton A into a tree and cut it when reaching observable level k. Let us assume that the tree is of depth K, \(K \ge k\), and of size \(N = O(d^{K})\), with \(d \ge 1\) representing the approximate out-degree of the vertices in the graph of A. Since the analysis of the SMT solvers for different applications requires the exploration of all the transitions in the unfolded graph of A, the unfolding stage of our algorithm does not necessarily increase the overall time complexity of the algorithm.
Removing silent transitions Our algorithm does not increase the size of the tree since we only substitute the silent transitions by the bypass transitions. We do add, however, constraints. The number of enabling-guard constraints that we add to each bypass transition is of order \(O(K^2)\). Each updated future constraint is of order O(K) (including on-the-fly simplification, so that each clock has at most one lower and one upper bound), and each future transition may be updated at most O(K) times. Hence, the updating step is also of order \(O(K^{2})\), and the complexity of the whole algorithm is \(O(N K^2)\). Note, we do not need to transform the diagonal constraints introduced in the algorithm into unary constraints, nor do they introduce problems in the next algorithm of determinization.
Determinization decreases the size of the unfolded automaton, if non-determinism exists. The complexity gain can be exponential in the number of locations and transitions, but is lost by a proportional larger complexity in the guards.
8 Implementation and experimental results
The algorithms were implemented in Scala (Version 2.10.3) and integrated into the test-case generation tool MoMuT::TAFootnote 2, providing a significant increase in the capabilities of the tool. MoMuT::TA provides model-based mutation testing algorithms for timed automata (Aichernig et al. 2013), using UPPAAL’s (Larsen et al. 1997) XML format as input and output. The determinization algorithm uses the SMT-solver Z3 (Moura and Bjørner 2008) for checking satisfiability of guards. All experiments were run on a MacBook Pro with a 2.53 GHz Intel Core 2 Duo Processor and 4 GB RAM.
The implementation is still a prototype and further optimizations are planned. One already implemented optimization is the “on-the-fly” execution of the presented algorithms, allowing the unfolding, clock renaming, silent transition removal and determinization in one single walk through the tree. The combined algorithm does not suffer from the full exponential blow-up of the explicit unfolding: if the automaton contains a location that can be reached via different traces, yet with the same clock resets, the unfolding splits it into several, separately processed, locations, while the on-the-fly algorithm only needs to process it once.
The following studies compare the numbers of locations and the runtimes of a) the silent transition removal, b) a standard determinization algorithm that works by splitting non-deterministic transitions into several transitions that contain each possible combination of their guards, c) the new determinization algorithm introduced in Sect. 6 and d) its on-the-fly version, where the runtime includes the time for unfolding, silent transition removal and determinization. The runtimes of the determinization do not include the removal of silent transitions.
8.1 Scientific studies
For the current subsection we picked two small examples that were introduced in previous papers on determinization and one example that was previously used for test-case generation.
Study 1 The first example, taken from Diekert et al. (1997), is the timed automaton illustrated in Fig. 12a, where the silent transition cannot be removed, as there is no unbounded observable automaton with the same language. We then added another \(\alpha \)-transition (Fig. 12b), which causes non-determinism after removing the silent transition. The test results are shown in Table 4 (before and after modification).
Study 2 The second example is taken from Baier et al. (2009) and is illustrated in Fig. 12c. We modified the automaton by adding a silent transition (Fig. 12d). Table 5 shows the results of the two determinization approaches.
Study 3 This study is part of a model of an industrial application: it is based on a car alarm system that was already used as an example in our work on model-based mutation testing from timed automata (see Aichernig et al. 2013 for the whole model). In this evaluation, we introduced a silent transition that adds a non-deterministic delay of up to two seconds before the timer of the alarm starts, and our results are given in Table 6. We were able to perform the removal of silent transitions and the guard-oriented determinization up to depth 12, and the location-oriented determinization up to depth 8. The on-the-fly algorithm still only took ten seconds for depth 12. However, it also shows a \(10-\) times increased runtime on depth 12 compared to depth 8.
As expected, the studies confirm that the size of the produced tree and the runtime of the algorithm depends vastly on the input models.
8.2 Industrial case study
In this subsection we present an industrial study, that was provided as a use case by Volvo within the European Artemis Project Crystal.Footnote 3 The use case evolves around an automated speed-limiter (ASL), that limits the actual car speed according to an internally stored value.
The speed limiter can assume three operating states: deactivated, limiting and overridden. In the limiting state the device is active, and overridden means that the user temporarily deactivated it by a kickdown of the gas pedal. In its initial state, the ASL is deactivated.
After receiving any of the inputs preset?, plus? or minus?, the speed limiter switches from deactivated to limiting. There it stays, until the user either turns it off via the off? input, or overrides it via a kickdown?. The kickdown triggers a timed transition back to the limiting state, that is executed within eight to ten seconds, if there was no manual state change in between. This timed transition is a silent transition, thus it is not observable by the user.
The current speed limit is stored internally. It can be modified by three inputs: preset? sets it to a predefined constant value, plus? increases the limit and minus? decreases it. However, plus and minus only change the limit, if the system is limiting, otherwise they only trigger a state change towards limiting.
For the current experiments, we concentrate on the state-change mechanics, neglecting the actual value of the current limit. The only important information is whether the limit is zero, lower than the predefined value that is set by the preset? input, equal to it, or higher. Thus, we applied qualitative abstraction to the limit and encoded these four value ranges in the locations.
Figure 13 gives an impression of the case study. Note that the first column of locations contains the deactivated states, the second column contains the limiting states and the third contains the overridden states. The first row indicates that the current limit is higher than the preset, the second row indicates that it is equal, the third that it is lower and the bottom row indicates that the limit is zero. The figure is a little simplified for presentational purposes: in the real automaton each state has an “on entry”-transition. That is, each state consists of two locations, where all ingoing transitions lead to the first location, and there is an output transition labeled by the name of the state, leading to the second location. For example, there is a limiting! output for the limiting state. All outgoing transitions only leave the second location. These “on entry”-transitions were neglected in the figure to make it more understandable. Additionally, for every location besides \(q_7\) there exists a transition with label preset? leading to \(q_7\), as the preset? input both turns the state to limiting and sets the limit to the predefined value. These transitions were omitted to reduce the amount of crossing and overlaying transitions.
In \(q_{10}\), where the current limit is higher than the preset value, a minus? transition may non-deterministically stay in \(q_{10}\) or lead to \(q_7\), where the current limit equals the preset. The same non-determinism also appears in \(q_4\).
We produced 342 mutants from the original automaton, using the mutation operators described in our paper on model-based mutation testing for timed automata (Aichernig et al. 2013). 40 of these mutants contained loops of silent transitions and were neglected from the following process. The remaining 302 mutants were unfolded to depth ten, together with the original specification. Then the silent transition removal and the determinization were performed on all of them, using the on-the-fly algorithm. The on-the-fly algorithm took an average of 0.2 seconds, with a maximum of 1.0 and a minimum of 0.14 seconds. The unfolded determinized mutants contained an average of 620 locations, with a minimum of 337 and a maximum of 1065 locations. The correct specification contained 606 locations. The different amount of locations is caused by the fact that the mutations change the amount of non-determinism (and thus the amount of merged locations in the trees) of the mutants.
Then we started the test-case generation, which means applying tioco- conformance checks between the determinized mutants and the determinized specifications. The checks took an average of 63.3 seconds, with a minimum of 0.2 and a maximum of 201.9 seconds. In total, the test-case generation took 5.4 hours, and produced 128 test cases. All runtimes are summarized in Table 7, including the quartiles (\(Q_1...Q_3\)).
The results show that the determinization only takes a fraction of the time needed for test-case generation. However, due to the increased amount of locations and transitions in the explicit unfolding, the runtime of the test-case generation was significantly increased, compared to being executed on a deterministic model that was not unfolded. The most efficient way to combine determinizing and test-case generation would most likely be to integrate the test-case generation into the on-the-fly algorithm.
9 Related work
The main inspiration to our work comes from Bérard et al. (1998) and Baier et al. (2009). Bérard et al. 1998 show that silent transitions extend the expressive power of TA and identify a sub-class of eNTA for which silent transitions can be removed. By restricting ourselves to the bounded setting, we can remove silent transitions of all strongly-responsive eNTAs. In addition, our approach for removing silent transitions preserves diagonal constraints in the resulting automaton, thus avoiding a potential exponential blow-up in the size of its representation (see Bouyer et al. 2005 for the practical advantages of preserving diagonal constraints in TA). Baier et al. (2009) propose a procedure for translating \(\mathrm {NTA}\) to infinite DTA trees, and then identify several classes of \(\mathrm {NTA}\) that can be effectively determinized into finite DTA. In contrast to our work, their procedure works on the region graph, which makes it impractical for implementation. In addition, we also allow in our determinization procedure disjunctive constraints which results in a more succint representation that can be directly handled by the bounded model checking tools. While transitions with disjunctive constraints in their guards can be split into multiple transitions containing only conjunctions, this may result in a huge blowup in the number of locations. Both Bérard et al. (1998) and Baier et al. (2009) tackle non-determinism and observabilty in TA from a general theoretical perspective. We adapt the ideas from these papers and propose an effective procedure for the bounded determinization of \(\mathrm {eNTA}\).
There already exist several tools for model-based testing with timed automata:
The UPPAAL tool family contains a series of tools working with timed automata. There are three UPPAAL tools used in the context of testing: UPPAAL Cover (Hessel and Pettersson 2007) generates tests offline and allows the specification of observers to generate tests satisfying pre-defined coverage criteria. Cover required the specification to be deterministic. UPPAAL Tron (Mikucionis et al. 2003) is used for online testing, where inputs and delays are chosen non-deterministically and executed on the system-under-test and the specification simultaneously and all outputs that are received from the system are checked for conformance on the model. UPPAAL Yggdrasil (Kim et al. 2015) is the newest testing tool in the UPPAAL family, allowing offline test-case generation, with the advantage of adding test scripts to transitions, that are added to the tests during generation. The resulting tests can thus be executable scripts or function calls in any desired language. None of the tools in the UPPAAL family performs mutation-based test-case generation. Note that while we model our automata in UPPAAL, the produced automata can not be analysed with UPPAAL anymore, as they contain disjunctions. They can, however, still be opened and viewed.
Wang et al. (2014) use timed automata for language inclusion. Their procedure involves building a tree, renaming the clocks and determinization of the tree. Contrary to our work, they do not restrict themselves to the bounded setting, thus taking the risk that their algorithm does not terminate for some classes of timed automata. Also, they use the “standard” determinization method that involves splitting non-deterministic transitions into a possibly far larger set of deterministic transitions, whereas we join them into one transition.
Krichen and Tripakis (2009) produce deterministic testers for non-deterministic timed automata in the context of model-based testing. They consider only testers using one clock, which is reset upon receiving an input. The testers are sound, but not in general complete and might accept behavior of the system under test that should be rejected. Bertrand et al. (2011) develop a game-based method for determinization of eNTA which generates either a language equivalent DTA when possible, or its approximation otherwise. A similar approach is proposed in Bertrand et al. (2011) in the context of model-based testing, where it is shown that their approximate determinization procedure preserves the tioco relation. In contrast to our approach, which is language preserving up to a bound k, and thus appropriate for bounded model checking algorithms, determinization in the above-mentioned papers introduces a different kind of approximation than ours.
In a recent paper, Aichernig et al. (2016) compared the bounded model-checking approach for test-case generation with symbolic execution. The bounded model-checking required the determinization approach described in this paper as a pre-processing step, while the symbolic execution approch did not. It showed that symbolic execution could deal with the non-determinism more efficiently than the bounded model-checking approch.
10 Conclusion
The bounded setting allows the handling of a larger class of TA and in a more efficient way than in the unbounded setting. The extension from standard unary constraints to diagonal and disjunctive constraints has a practical reason: it is more efficient to let the SMT solvers deal with them than to translate them into standard form. In this paper a novel procedure was presented, which transforms bounded, non-deterministic and partially-observable TA into deterministic and fully-observable TA with diagonal and disjunctive constraints. The procedure includes an algorithm for removing the silent transitions and a determinization algorithm. The performed experiments show that runtimes increase drastically for greater depths. However, the depths needed for test-case generation can be performed in reasonable times. To ensure that all mutations created by our mutation operators can be reached, and eventually be detected by a wrong output, one could calculate the needed depth by the number of steps needed to reach the deepest location in a specification plus the highest number of steps needed to reach an output in any location. For the presented industrial study, these numbers would be 7 and 2, indicating that 9 would be a suitable search depth. It was implemented, tested and integrated into a model-based test generation tool. We applied the tool to an industrial case study and presented the results of both the determinization and the test-case generation.
11 Proofs
11.1 Proof of Theorem 1 [Silent Transitions Removal]
Given a non-deterministic timed automaton with silent transitions A in the form of a finite tree, we need to show that our algorithm of removing the silent transitions results in an equivalent timed automaton, that is, \(\mathfrak {L}(R(A)) = \mathfrak {L}(A)\).
By induction, it suffices to show that if \(A'\) is the result of removing one first silent transition then A and \(A'\) are equivalent: for every timed trace of A there is an equivalent timed trace of \(A'\) and vice versa, in the sense that the corresponding observable timed traces are identical. Note that the removal of a silent transition does not change the form of the guards at the part of the automaton that contains the remaining silent transitions: the introduction of diagonal constraints happens only at the enabling guards, which are observable transitions.
So, let \(\tau _{s,0}\) be a first silent transition on a path \(\gamma \) that starts at the initial location. Let \(\tau _{s,0}\) be from location \(q_s\) to location \(q_{s,0}\), let \(q_{s-1}\) be the location that leads to \(q_s\) and let \(q_{s+1}\) be a location that follows \(q_{s,0}\) on the path. Let \(A'\) be the automaton that results after removing \(\tau \) and performing the steps as in Algorithm 2. Clearly, for every run that does not pass through \(\tau _{s,0}\) there is an identical run in the other automaton. Thus, we restrict ourselves to runs though \(\tau _{s,0}\). We will mostly restrict ourselves to strict inequalities, as the extension to the other cases (strict inequality versus weak inequality or weak inequality versus weak inequality) is straight forward.
11.2 \(\varvec{\mathfrak {L}(A) \subseteq \mathfrak {L}(A')}\)
Let \(\rho \) be a run on A through \(\gamma \). We need to show that there exists a run \(\rho '\) on \(A'\) with the same observable trace as of \(\rho \). The run \(\rho '\) will go through the same locations and transitions as does \(\rho \), except for the part \(q_{s-1}\), \(\tau _s\), \(q_s\), \(\tau _{s,0}\), \(q_{s,0}\) in A which will be replaced by the bypass \(q_{s-1}\), \(\tau '_s\), \(q_{s,0}\) in \(A'\) as in Fig. 6. The times of the transitions will also be the same, except for the silent transition that is missing in \(\rho '\). That is, if \(t_s\), \(t_{s,0}\) and \(t_{s+1}\) are the times of \(\rho \) at the transitions \(\tau _s\), \(\tau _{s,0}\) (the silent transition) and \(\tau _{s+1}\) then the corresponding transitions of \(\rho '\) will take place at \(t_s\) (the time of the bypass) and \(t_{s+1}\).
We first need to show, that the guard of the bypass transition, \(g'_s = g_s \wedge eg(\tau _{s,0})\), is satisfied at time \(t_s\). The enabling guard consists of unary constraints and binary constraints. The unary constraints are simply the upper bound limits of the guard of the silent transition. The time of the bypass \(t_s\) lies before the time of the silent transition \(t_{s,0}\). But since \(\rho \) is a run on A through \(t_{s,0}\), we know that these upper bounds are satisfied at the time of \(t_{s,0}\). Thus, they also have to be satisfied at the time of \(t_s\).
The binary constraints are built by comparing the upper bounds of all clocks with the lower bounds of all other clocks, where \(x_j < n_j\) and \(m_i < x_i\) build the constraint \(n_j - x_j > m_i - x_i\). This constraint ensures, that at time \(t_s\) the delay needed to reach the upper bound of \(x_j\) (which would disable the silent transition), is greater than the delay needed to reach the lower bound of \(x_i\) (which enables the silent transition). As the silent transition is enabled at \(t_{s,0}\), we know that all lower bounds can be reached, without violating any of the upper bounds. Thus, the binary constraints are satisfied.
We have seen that all the constraints of \(eg(\tau _{s,0})\) are satisfied at time \(t_s\) and so the constraint \(g'_s\) of \(\rho '\) is satisfied at \(t_s\) and the transition \(\tau '_s\) can be taken.
The next step is to show that the transition \(\tau _{s+1}\) with guard \(g'_{s+1}\) of \(\rho '\) from location \(q_{s,0}\) to location \(q_{s+1}\), as well as the next transitions \(\tau _{s+j}\), \(j = 2, \ldots , p\), with guards \(g'_{s+j}\) can be taken at the same times \(t_{s+j}\) on which \(\tau _{s+j}\) are taken in \(\rho \) on guards \(g_{s+j}\), \(j = 1, \ldots , p\).
If the silent transition happens to be on an exact time: \(x_i = n_i\) then the update of the future guards that refer to the clock \(x_{s,0}\) that was reset at \(\tau _{s,0}\) is clear: each occurrence of \(x_{s,0}\) is replaced by \(x_i - n_i\), and we are done. So, suppose that there are no exact constraints at the silent transition.
We write the guard \(g'_{s,0}\) of the silent transition \(\tau _{s,0}\) as:
where for some of the clocks \(x_i\) there may be only a lower bound or only an upper bound constraint.
The constraints on \(x_{s,0}\) at the transitions \(\tau _{s+j}\), \(j = 1, \ldots , p\) contain \(0 \le x_{s,0}\) in \(\tau _{s+1}\) and are of the general (strict inequalities) form \(m_{s+j}< x_{s,0} < n_{s+j}\) in \(\tau _{s+j}\). The corresponding updated constraints of \(A'\) at time \(t_{s+j}\), \(j = 1, \ldots , p\), are
First, we need to show that the taken guard \(tg(\tau _{s,0})\) is satisfied at time \(t_{s+1}\). The taken guard is the constraint \(0 \le x_{s,0}\). After the update of the future guards this constraint is replaced by the conjunction of all the lower bound constraints \(m_i < x_i\) of \(g'_{s,0}\). But since these lower bound constraints are satisfied at the time \(t_{s,0}\) of the silent transition (in \(\rho \)) then clearly they are satisfied at \(t_{s+1}\), \(t_{s+1} \ge t_{s,0}\), that is, the updated taken guard \(tg(\tau _{s,0})\) is satisfied in \(\rho '\).
Let us look at the other updated future constraints. Since at the time of the silent transition \(x_{s,0} = 0\) and \(m_i < x_i\) then at time \(t_{s+j}\) when \(m_{s+j} < x_{s,0}\) we have \(m_i +m_{s+j} < x_i\). With a similar argument for the upper bound constraints, we see that the constraints of (4) are satisfied in \(\rho '\).
Also the part of the synchronization rules is clear since it refers to the possible minimum and maximum time difference between every two transitions on which \(x_{s,0}\) occurs, and since the run \(\rho \) goes through these transitions it assures that these constraints can be satisfied. So, for example, the synchronization constraint \(m_{s+j} - n_{s+i}< x_{s+i} < n_{s+j} - m_{s+i}\) that is added to the guard \(g_{s+j}\) of \(\tau _{s+j}\), refers to the time difference \(t_{s+j} - t_{s+i}\) between the transition \(\tau _{s+i}\) and the transition \(\tau _{s+j}\), \(i < j\).
Note that the synchronization with the constraint \(0 \le x_{s,0}\) of \(\tau _{s+1}\) results in adding to \(\tau _{s+j}\), \(j = 1, \ldots , p\) the constraint \(x_{s+1} < n_{s+j}\), that is \(t_{s+j} - t_{s+1} < n_{s+j}\), which clearly is satisfied since \(t_{s+j} - t_{s,0} < n_{s+j}\).
We showed that the observable trace of \(\rho '\) is the same as that of \(\rho \) and this completes the proof of \(\mathfrak {L}(A) \subseteq \mathfrak {L}(A')\).
11.3 \(\varvec{\mathfrak {L}(A') \subseteq \mathfrak {L}(A)}\)
Let \(\rho '\) be a run on \(A'\) going through the bypass \(\tau '_s\). We will show that there exists a run \(\rho \) through \(\tau _{s,0}\) in A with the same observable trace as of \(\rho '\).
The first thing we need to check is that the silent transition \(\tau _{s,0}\) can be taken, given that the enabling guard \(eg(\tau _{s,0})\) is satisfied at time \(t_s\). The unary constraints \(x_j < n_j\) ( \(x_j \le n_j\)) of \(eg(\tau _{s,0})\) guarantee that each of the constraints in the guard \(g'_{s,0}\) of the silent transition \(\tau _{s,0}\) can be satisfied separately at some time that is equal or is later than \(t_s\). Then, in order that all the constraints could be satisfied simultaneously, it suffices to show that the minimum upon the time delays to the upper bound constraints of the clocks appearing in \(g'_{s,0}\) is greater than the maximum upon the time delays to the lower bound constraints in \(g'_{s,0}\) (the ’greater’ should be replaced by ’greater or equal’ in case both the maximum and minimum come from weak inequalities):
But this condition is equivalent to the condition that \(n_j - x_j > m_i - x_i\) at time \(t_s\) for every i, j, which is exactly the conjunction of diagonal constraints
of \(eg(\tau _{s,0})\).
Thus, we know that the silent transition \(\tau _{s,0}\) can be taken in the run \(\rho \) at some time \(t_{s,0}\) after a delay of \(M = \max _{i} (m_i - x_i)\) from \(t_s\) (this delay is not negative since we introduced the constraint \(0 \le x_s\)) and before a delay of \(N = \min _{j} (n_j - x_j)\).
It remains to show that the transitions \(\tau _{s+1}, \ldots , \tau _{s+p}\) on guards \(g_{s+1}, \ldots , g_{s+p}\) of \(\rho \) can be taken at the same times \(t_{s+1}, \ldots , t_{s+p}\) as the corresponding transitions on guards \(g'_{s+1}, \ldots , g'_{s+p}\) are taken in \(\rho '\).
To be more specific, it suffices to prove that there exists \(t_{s,0}\) with the following conditions:
-
1.
\(t_s \le t_{s,0} \le t_{s+1}\);
-
2.
\(g'_{s,0}\) is satisfied at \(t_{s,0}\);
-
3.
the constraints on \(x_{s,0}\) are satisfied at \(t_{s+1}, \ldots , t_{s+p}\), with \(x_{s,0}\) reset at \(t_{s,0}\).
For the second condition the constraints of \(g'_{s,0}\) that should be satisfied at time \(t_{s,0}\) are
Equivalently, at each time \(t_{s+j}\), \(j = 1, \ldots , p\):
or,
For the third condition the constraints on \(x_{s,0}\) that should be satisfied at times \(t_{s+1}, \ldots , t_{s+p}\) are \(m_{s+j}< x_{s,0}(t_{s+j}) < n_{s+j}\) for \(j = 1, \ldots , p\). The constraint here at time \(t_{s+1}\) is \(0 \le x_{s,0}(t_{s+1})\) possibly conjuncted with other constraints (for convenience we wrote all constraints as strict inequalities). This is equivalent to
or
We need to show that the constraints on \(t_{s,0}\) of (9) and (11) do not define an empty set. This condition is equivalent to showing that the set \(S_1\) of the above expressions to the left of \(t_{s,0}\) is smaller than the set \(S_2\) of the expressions to the right of \(t_{s,0}\) (equivalently that the maximum of \(S_1\) is smaller than the minimum of \(S_2\)), where
and
There are two types of expressions in \(S_1\) and two types of expressions in \(S_2\), hence we need to check that the following 4 cases are satisfied.
11.4 Case 1 \(m_i - x_i(t_{s+j}) + t_{s+j} < n_{i'} - x_{i'}(t_{s+j'}) + t_{s+j'}\)
This inequality is equivalent to
or to
The latter is equivalent to
which is (6), the enabling guard \(eg(\tau _{s,0})\) that is satisfied at time \(t_s\) of the run \(\rho '\).
11.5 Case 2 \(m_i - x_i(t_{s+j}) + t_{s+j} < -m_{s+j'} + t_{s+j'}\)
This inequality is equivalent to
The last inequality is no other than one of the left inequalities of (4), which are the updated future constraints in \(A'\) of the reset clock \(x_{s,0}\), and thus are given to be satisfied.
11.6 Case 3 \( -n_{s+j'} + t_{s+j'} < n_i - x_i(t_{s+j}) + t_{s+j} \)
This inequality is equivalent to
But the last inequality is one of the right inequalities of (4), which are the updated future constraints in \(A'\) of the reset clock \(x_{s,0}\), and thus are given to be satisfied.
11.7 Case 4 \( -n_{s+i} + t_{s+i} < -m_{s+j} + t_{s+j} \)
This inequality is equivalent to
The inequality certainly holds when \(i = j\). When \(i < j\) we can write this inequality with the clock \(x_{s+i}\) that is reset at time \(t_{s+i}\) in \(A'\):
But the last inequality can be found in the first row of Table 3 which contains the synchronization constraints of the updated future constraints in \(A'\) of the reset clock \(x_{s,0}\).
Similarly, when \(j < i\) we need to satisfy the inequality
which can be found in the fourth row of Table 3.
We showed that the set of possible time values \(t_{s,0}\) for the silent transition in \(\rho \) is not empty, that is, there is a solution to the set of inequalities (9) and (11) in the indeterminate \(t_{s,0}\) (again, the extension to weak inequalities is straight forward).
To complete the proof it remains to show that the solution for \(t_{s,0}\) satisfies the first condition, that is that \(t_s \le t_{s,0} \le t_{s+1}\). The left inequality \(t_s \le t_{s,0}\) comes from satisfying the inequality \(m_i - x_i(t_{s+j}) + t_{s+j} \le t_{s,0}\) of (9) with \(x_i = x_s\) and \(m_i = m_s = 0\) (it refers to augmenting the silent transition guard with the constraint \(0 \le x_s\)). This inequality is equivalent to \(0 -x_s(t_s) + t_s \le t_{s,0}\) or \(t_s \le t_{s,0}\) since \(x_s\) was reset at time \(t_s\).
The right inequality comes from satisfying the inequality \(t_{s,0} \le -m_{s+1} + t_{s+1}\) of (11) with \(m_{s+1} \ge 0\), that is, \(t_{s,0} \le t_{s+1}\).
11.8 Proof of Theorem 2 [Determinization]
The deterministic property of D(A) follows from the fact that when merging \(\alpha \)-transitions into \(\tau _{acc}\) and \(\tau _{\lnot acc}\) then the guard of \(\tau _{\lnot acc}\) is a conjunction of some guard with the negation of the guard of \(\tau _{acc}\). Hence, different runs will induce different time traces.
When we merge two transitions we also merge their target locations, and all transitions leaving those locations now leave the merged location. The guard of the merged transition is weaker than the individual guards, thus by merging locations of A in D(A) we may only expand the language and conclude that \(\mathfrak {L}(A) \subseteq \mathfrak {L}(D(A))\). The same holds true for the disjunction of two invariants, which also weakens the original invariants. On the other hand, the new diagonal constraints introduced in D(A) and conjuncted to the guards of the following transitions may restrict the language. So, let us examine the new transformed constraints and show that they do not impose additional restrictions. Suppose the guard of transition \(\tau \) contains the constraint \(x \sim n\) and that y is reset on \(\tau \). Then, for any run through \(\tau \), at the time \(t_0\) of \(\tau \), the constraint \(x(t_0) - y(t_0) \sim n\) holds. But also at time \(t_1 > t_0\), the constraint \(x(t_1) - y(t_1) \sim n\) holds since x and y progress at the same rate and are never reset again. Hence, for any run through \(\tau \) in A there exists a corresponding run in D(A) with the same trace because the additional constraints of the form \(x - y \sim n\) that are added to the future guards are satisfied automatically by all runs in D(A) that satisfy the guard of \(\tau \). Thus, it remains \(\mathfrak {L}(A) \subseteq \mathfrak {L}(D(A))\).
To show that the language of D(A) does not contain accepting traces that are not in the language of A, and thus that \(\mathfrak {L}(D(A)) \subseteq \mathfrak {L}(A)\), it suffices to show two parts: First, we need to show, that whenever the merged transition in D(A) is enabled, at least one of the non-deterministic transitions in A is enabled. This is trivially true, as the guard of the merged transition is a disjunction of the guards of the non-deterministic transitions. Second, we show that when a transition in a merged location of D(A) is enabled, then the corresponding original transition in A is enabled. But this is indeed the case, since the diagonal constraints that are attached to these transitions are, as already shown, always enabled when the original transitions in A are reachable, and the rest of the guard is identical in both transitions. As for the invariants, it holds that if the invariant of a merged location l in D(A) is satisfied, then at least on of the invariants of the split locations in A is enabled. Since each transition has the invariants of its target and source locations integrated into its guard, it is ensured that, even though the invariant in D(A) is weaker than each original invariant in A, the transition leading to l and leaving l are only enabled if they satisfy their original invariants.
Notes
In model-based testing, strong responsiveness is the requirement that there are no silent loops, otherwise the tester cannot distinguish between deadlocks and livelocks.
References
Aichernig BK, Lorber F, Ničković D (2013) Time for mutants—model-based mutation testing with timed automata. In: Tests and proofs—7th international conference, TAP 2013, Budapest, Hungary, June 16–20, 2013. Proceedings, pp 20–38
Aichernig BK, Lorber F, Tappler M (2016) Conformance checking of real-time models—symbolic execution vs. bounded model checking. In: Ábrahám E, Bonsangue MM, Johnsen EB (eds) Theory and practice of formal methods—essays dedicated to Frank de Boer on the occasion of his 60th birthday. Lecture Notes in Computer Science, vol 9660. Springer, pp 15–32
Alur R, Dill DL (1994) A theory of timed automata. Theoret Comput Sci 126(2):183–235
Baier C, Bertrand N, Bouyer P, Brihaye T (2009) When are timed automata determinizable? In: Susanne A, Alberto M-S, Yossi M, Sotiris N, Wolfgang T (eds) Automata, languages and programming: 36th international collogquium, ICALP 2009, Rhodes, Greece, July 5–12, 2009, Proceedings, Part II. Springer, Berlin Heidelberg, pp 43–54
Bengtsson J, Larsen K, Larsson F, Pettersson P, Yi W (1996) UPPAAL a tool suite for automatic verification of real-time systems. In: Alur R, Henzinger TA, Sontag ED (eds) Hybrid systems III. Lecture Notes in Computer Science, vol 1066. Springer, Berlin, Heidelberg, pp 232–243
Bérard B, Petit A, Diekert V, Gastin P (1998) Characterization of the expressive power of silent transitions in timed automata. Fundamenta Informaticae 36(2–3):145–182
Bertrand N, Jéron T, Stainer A, Krichen M (2011) Off-line test selection with test purposes for non-deterministic timed automata. In Abdulla PA, Leino KRM (eds) Tools and algorithms for the construction and analysis of systems. Lecture Notes in Computer Science, vol 6605. Springer, Berlin, Heidelberg, pp 96–111
Biere A, Cimatti A, Clarke EM, Strichman O, Zhu Y (2003) Bounded model checking. Adv Comput 58:117–148
Bouyer P, Laroussinie F, Reynier P-A (2005) Diagonal constraints in timed automata: forward analysis of timed systems. In: Paul P, Wang Y (eds) Formal modeling and analysis of timed systems: third international conference, FORMATS 2005, Uppsala, Sweden, September 26–28, 2005, Proceedings. Springer, Berlin, Heidelberg, pp 112–126
Bozga M, Graf S, Mounier L (2002) If-2.0: a validation environment for component-based real-time systems. In: Brinksma E, Larsen KG (eds) Computer aided verification. Lecture Notes in Computer Science, vol 2404. Springer, Berlin, Heidelberg, pp 343–348
Daws C, Olivero A, Tripakis S, Yovine S (1996) The tool Kronos. In: Alur R, Henzinger TA, Sontag ED (eds) Hybrid systems III. Lecture Notes in Computer Science, vol 1066. Springer, Berlin, Heidelberg, pp 208–219
De Moura L, Bjørner N (2008) Z3: an efficient SMT solver. In: Proceedings of the theory and practice of software, 14th international conference on tools and algorithms for the construction and analysis of systems, TACAS’08/ETAPS’08. Springer, pp 337–340
Diekert V, Gastin P, Petit A (1997) Removing epsilon-transitions in timed automata. In: Reischuk R, Morvan M (eds) Proceedings of the 14th annual symposium on theoretical aspects of computer science. Lecture Notes in Computer Science, vol 1200. Springer, pp 583–594
Finkel O (2006) Undecidable problems about timed automata. In: Proceedings of the 4th international conference on formal modeling and analysis of timed systems, FORMATS’06. Springer, pp 187–199
Hessel A, Pettersson P (2007) Cover-a test-case generation tool for timed systems. Testing of software and communicating systems, pp 31–34
Hofmann M (ed) (2011) A game approach to determinize timed automata. Springer, Berlin, Heidelberg
Kim JH, Larsen KG, Nielsen B, Mikucionis M, Olsen P (2015) Formal analysis and testing of real-time automotive systems using UPPAAL tools. In: Núñez M, Güdemann M (eds) Formal methods for industrial critical systems. Lecture Notes in Computer Science, vol 9128. Springer International Publishing, pp 47–61
Krichen M, Tripakis S (2009) Conformance testing for real-time systems. Form Methods Syst Des 34(3):238–304
Larsen KG, Pettersson P, Yi W (1997) UPPAAL in a nutshell. Softw Tools Technol Transf 1(1–2):134–152
Lorber F, Rosenmann A, Nickovic D, Aichernig BK (2015) Bounded determinization of timed automata with silent transitions. In Sankaranarayanan S, Vicario E (eds) Formal modeling and analysis of timed systems—13th international conference, FORMATS 2015, Madrid, Spain, September 2–4, 2015, Proceedings. Lecture Notes in Computer Science, vol 9268. Springer, pp 288–304
Mikucionis M, Nielsen B, Larsen KG (2003) Real-time system testing on-the-fly. In: Sere K, Waldén M (eds) The 15th nordic workshop on programming theory, number 34 in B. Abo Akademi, Department of Computer Science, Finland, October 29–31. Abstracts, pp 36–38
Schmaltz J, Tretmans J (2008) On conformance testing for timed systems. In: Proceedings of the 6th international conference on formal modeling and analysis of timed systems, FORMATS ’08. Springer, pp 250–264
Tretmans J (1996) Test generation with inputs, outputs, and quiescence. In: Margaria T, Steffen B (eds) Tools and algorithms for the construction and analysis of systems: second international workshop, TACAS ’96 Passau, Germany, March 27–29, 1996 Proceedings. Springer, Berlin, Heidelberg, pp 127–146
Tretmans J (2008) Model based testing with labelled transition systems. In: Formal methods and testing, pp 1–38
Tripakis S (2006) Folk theorems on the determinization and minimization of timed automata. Inf Process Lett 99(6):222–226
Wang F (2003) Efficient verification of timed automata with BDD-like data-structures. In: Zuck LD, Attie PC, Cortesi A, Mukhopadhyay S (eds) Verification, model checking, and abstract interpretation. Lecture Notes in Computer Science, vol 2575. Springer Berlin, Heidelberg, pp 189–205
Wang T, Sun J, Liu Y, Wang X, Li S (2014) Are timed automata bad for a specification language? Language inclusion checking for timed automata. In: Ábrahám E, Havelund K (eds) Tools and algorithms for the construction and analysis of systems: 20th international conference, TACAS 2014, Grenoble, France, April 5–13, 2014, Proceedings. Springer, Berlin, Heidelberg, pp 310–325
Acknowledgements
Open access funding provided by Graz University of Technology. The research leading to these results has received funding from the ARTEMIS Joint Undertaking under Grant agreement N\(^{\circ }\) 332830 and from the Austrian Research Promotion Agency (FFG) under Grant agreement N\(^{\circ }\) 838498 for the implementation of the project CRYSTAL, Critical System Engineering Acceleration.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lorber, F., Rosenmann, A., Ničković, D. et al. Bounded determinization of timed automata with silent transitions. Real-Time Syst 53, 291–326 (2017). https://doi.org/10.1007/s11241-017-9271-x
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11241-017-9271-x