On the effectiveness of cache partitioning in hard real-time systems

Abstract

In hard real-time systems, cache partitioning is often suggested as a means of increasing the predictability of caches in pre-emptively scheduled systems: when a task is assigned its own cache partition, inter-task cache eviction is avoided, and timing verification is reduced to the standard worst-case execution time analysis used in non-pre-emptive systems. The downside of cache partitioning is the potential increase in execution times. In this paper, we evaluate cache partitioning for hard real-time systems in terms of overall schedulability. To this end, we examine the sensitivity of (i) task execution times and (ii) pre-emption costs to the size of the cache partition allocated and present a cache partitioning algorithm that is optimal with respect to taskset schedulability. We also devise an alternative algorithm which primarily optimises schedulability but also minimises processor utilization. We evaluate the performance of cache partitioning compared to state-of-the-art pre-emption cost analysis based on benchmark code and on a large number of synthetic tasksets with both fixed priority and EDF scheduling. This allows us to derive general conclusions about the usability of cache partitioning and identify taskset and system parameters that influence the relative effectiveness of cache partitioning. We also examine the improvement in processor utilization obtained using an alternative cache partitioning algorithm, and the tradeoff in terms of increased analysis time.

Extended version

This paper builds upon and extends the ECRTS 2014 paper on Evaluation of Cache Partitioning for Hard Real-Time Systems (Altmeyer et al. 2014) as follows:

• The evaluation now covers both fixed priority and EDF scheduling.

• We examined how the schedulability of a group of tasks sharing a partition depends upon partition size.

• We present an alternative cache partitioning algorithm which both optimises schedulability and minimises processor utilization. We examine the improvement in processor utilization obtained using this algorithm as compared to the original cache partitioning algorithm, and the tradeoff in terms of increased analysis time.

Introduction

Cache partitioning is often suggested as a means of increasing the predictability of caches in pre-emptively scheduled hard real-time systems. The rationale behind this argument is that when a task is assigned its own cache partition, inter-task cache eviction is avoided, and timing verification is reduced to the standard worst-case execution time (WCET) analysis used in non-pre-emptive systems. Cache partitioning comes at a cost. The reduced amount of cache available to each task potentially increases intra-task cache conflicts, trading an increase in (non-pre-emptive) execution times for reduced cache related pre-emption delays (CRPD).

Despite the wealth of publications on cache partitioning for real-time systems, little work has been done on the effectiveness of cache partitioning compared to systems where tasks make unconstrained use of the cache. Pre-emptive multi-tasking systems with unconstrained caches were considered unpredictable. Given recent advances in the analysis of cache related pre-emption delays, we consider this view outdated.

In this paper, we evaluate cache partitioning for hard real-time systems in terms of overall schedulability. To this end, we first determine the sensitivity of task execution times to the size of the available cache partition using application code from real-time benchmarks. Contrary to the implicit assumptions in prior work, the worst-case execution time of a task is not necessarily monotonic in the partition size. We show how the monotonicity property can be re-established using a monotonic upper bound function for the execution times. We then present a cache partitioning algorithm that aims at optimizing taskset schedulability. Under the assumption of monotonic execution times, the algorithm is optimal in the sense that it finds a schedulable cache partitioning whenever one exists. The algorithm is based on a branch-and-bound approach and is agnostic with respect to the schedulability test used, i.e., it is valid for any, sustainable schedulability test (Baruah and Burns 2006) and scheduling algorithm. Further, we introduce an alternative branch-and-bound algorithm which optimizes schedulability as its primary concern and minimizes processor utilization as a secondary concern. This algorithm is optimal under the same conditions, in the sense that it finds a schedulable cache partitioning with the minimum processor utilization whenever a schedulable partitioning exists.

We evaluate the performance of cache partitioning vs. a non-partitioned cache, using state-of-the-art pre-emption cost aware schedulability analysis, based on two different benchmark sets (PapaBench and Mälardalen Benchmark Suite) and on a large number of synthetic tasksets. The evaluation using synthetic tasksets enables us to derive results that are valid in general, and not just for a small selection of use-cases. In addition, we identify how different parameter settings affect the relative performance of the partitioned vs. non-partitioned approaches. We also evaluate the improvement in processor utilization obtained using the alternative cache partitioning algorithm as compared to the original cache partitioning algorithm, and the tradeoff in terms of increased analysis time. Finally, we quantify the error margin introduced by the assumption of monotonic execution times.

We focus on a completely analytical approach, where we compare the schedulability of real-time systems assuming pre-emptive scheduling under either a fixed priority or EDF scheduling policy, with a direct mapped cache. In both cases, partitioned and non-partitioned cache, we rely on bounds on the execution times obtained via WCET analysis, and in the non-partitioned case, also on analytical bounds on the CRPD.

The paper is structured as follows: In Sect. 2, we introduce the required terminology and notation and in Sect. 3 we present the schedulability tests for fixed priority and EDF scheduling. In Sect. 4, we review existing approaches to cache partitioning. Section 5 explains the sensitivity of the worst-case execution times of tasks with respect to the size of their allocated cache partitions. The optimal cache partitioning algorithms are presented in Sect. 6, the results of the case study in Sect. 7 and the evaluation based on synthetic tasksets in Sect. 8. Section 9 concludes with a summary and discussion of future work.

System model, terminology and notation

We consider both fixed priority pre-emptive scheduling and EDF (pre-emptive) scheduling of a set of sporadic tasks (or taskset) on a single processor. Each taskset $\Gamma$ comprises n tasks $\Gamma = \{\tau _1,\ldots ,\tau _n\}$, where n is a positive integer. We assume a discrete time model, where all task parameters are positive integers.

Each task $\tau _i$ is characterized by its bounded worst-case execution time $C_i$ obtained assuming no pre-emption (i.e. not including any cache related pre-emption delays), minimum inter-arrival time or period $T_i$, and relative deadline $D_i$. Each task $\tau _i$ therefore gives rise to a potentially unbounded sequence of invocations or jobs, each of which has an execution time upper bounded by $C_i$, an arrival time at least $T_i$ after the arrival of its previous job, and an absolute deadline that is $D_i$ after its arrival. In an implicit-deadline taskset, all tasks have $D_i = T_i$, in a constrained-deadline taskset, all tasks have $D_i \le T_i$ while in an arbitrary-deadline taskset, task deadlines are independent of their periods. In this paper, we assume constrained deadline tasksets. The tasks are assumed to be independent and so cannot block each other from executing by accessing mutually exclusive shared resources, with the exception of the processor. (We note that this restriction is only made to simplify comparisons between the different approaches, resource sharing can be accounted for by schedulability analysis that incorporates CRPD as shown by Altmeyer et al. 2011, 2012).

The utilization $U_i$, of a task is given by its execution time divided by its period ($U_i = C_i / T_i$). The total utilization U of a taskset is the sum of the utilizations of all of its tasks, i.e.

$$\begin{aligned} U = \sum _i C_i / T_i. \end{aligned}$$

(1)

Static timing analysis

The paper is set in the context of static timing analysis as used for many safety-critical hard real-time applications. This means that we derive the worst-case execution time $C_i$ of each task $\tau _i$ using a static analysis, in our case, the aiT Timing analyzer (Ferdinand and Heckmann 2004).

Static timing analyses offer higher reliability compared to measurement-based approaches, as exhaustive measurements are considered infeasible for modern architectures. The higher confidence in the correctness of the execution time estimates comes at the cost of system restrictions, which must be fulfilled in order to apply static timing analyses. Foremost the restriction to static instead of dynamic memory allocation and write-through data caches.

Pre-emption costs

We now extend the sporadic task model to include pre-emption costs. To this end, we need to explain how pre-emption costs can be derived. To simplify the following explanation and examples, we assume direct-mapped caches.

The additional execution time due to pre-emption is mainly caused by cache eviction: the pre-empting task evicts cache blocks of the pre-empted task that have to be reloaded after the pre-empted task resumes. The additional context switch costs due to the scheduler invocation and a possible pipeline-flush can be upper-bounded by a constant. We assume that these constant costs are already included in $C_i$. Hence, from here on, we use pre-emption cost to refer only to the cost of additional cache reloads due to pre-emption. This cache-related pre-emption delay (CRPD) is bounded by $g \times {\hbox {BRT}}$ where g is an upper bound on the number of cache block reloads due to pre-emption and ${\hbox {BRT}}$ is an upper-bound on the time necessary to reload a memory block in the cache (block reload time).

To analyse the effect of pre-emption on a pre-empted task, Lee et al. (1998) introduced the concept of a useful cache block: A memory block m is called a useful cache block (UCB) at program point $\varvec{\mathcal {P}}$, if (i) m may be cached at $\varvec{\mathcal {P}}$ and (ii) m may be reused at program point $\varvec{\mathcal {Q}}$ that may be reached from $\varvec{\mathcal {P}}$ without eviction of m on this path. In the case of pre-emption at program point $\varvec{\mathcal {P}}$, only the memory blocks that (i) are cached and (ii) will be reused, may cause additional reloads. Hence, the number of UCBs at program point $\varvec{\mathcal {P}}$ gives an upper bound on the number of additional reloads due to a pre-emption at $\varvec{\mathcal {P}}$. The maximum possible pre-emption cost for a task is determined by the program point with the highest number of UCBs. Note that for each subsequent pre-emption, the program point with the next smaller number of UCBs can be considered. Thus, the j-th highest number of UCBs can be counted for the j-th pre-emption. A tighter definition is presented by Altmeyer and Burguière 2009; however, in this paper we need only the basic concept.

The worst-case impact of a pre-empting task is given by the number of cache blocks that the task may evict during its execution. Recall that we consider direct-mapped caches: in this case, loading one block into the cache may result in the eviction of at most one cache block. A memory block accessed during the execution of a pre-empting task is referred to as an evicting cache block (ECB). Accessing an ECB may evict a cache block of a pre-empted task.

In this paper, we represent the sets of ECBs and UCBs as sets of integers with the following meaning:

$$\begin{aligned} s \in {\hbox {UCB}}_i \Leftrightarrow \tau _i \hbox { has a useful cache block in cache-set } s \end{aligned}$$

$$\begin{aligned} s \in {\hbox {ECB}}_i \Leftrightarrow \tau _i \hbox { may evict a cache block in cache-set } s \end{aligned}$$

Separate computation of the pre-emption cost is restricted to architectures without timing anomalies (Lundqvist and Stenström 1999) but is independent of the type of cache used, i.e. data, instruction or unified cache.

In the case of set-associative LRU caches¹, a single cache-set may contain several useful cache blocks. For instance, ${\hbox {UCB}}_1 = \{1,2,2,2,3,4\}$ means that task $\tau _1$ contains 3 UCBs in cache-set 2 and one UCB in each of the cache sets 1, 3 and 4. As one ECB suffices to evict all UCBs of the same cache-set (Burguière et al. 2009), multiple accesses to the same set by the pre-empting task does not need to appear in the set of ECBs. Hence, we keep the set of ECBs as used for direct-mapped caches. A bound on the CRPD in the case of LRU caches due to task $\tau _i$ directly pre-empting $\tau _j$ is thus given by the intersection ${\hbox {UCB}}_j \cap ' {\hbox {ECB}}_i = \{m \vert m \in {\hbox {UCB}}_j: m \in {\hbox {ECB}}_i \}$, where the result is also a multiset that contains each element from ${\hbox {UCB}}_j$ if it is also in ${\hbox {ECB}}_i$. A precise computation of the CRPD in the case of LRU caches is given by Altmeyer et al. (2010). In this paper, we assume direct-mapped caches. Note that all equations provided within this paper are for direct-mapped caches, they are also valid for set-associative LRU caches with the above adaptation to the set-intersection.

Schedulability tests

In this section, we present schedulability tests for fixed-priority scheduling using response time analysis and for EDF scheduling using processor demand analysis. Both analyses are sustainable (Baruah and Burns 2006) in the sense that any taskset that was deemed schedulable by the test remains schedulable if the parameters “improve”, e.g., if the execution times decrease or periods increase.

Fixed priority pre-emptive scheduling

We now recapitulate the exact (sufficient and necessary) schedulability test for fixed priority pre-emptive scheduling of constrained-deadline tasksets based on response time analysis (Audsley et al. 1993; Joseph and Pandya 1986; Davis et al. 2008). Subsequent work on integrating cache related pre-emption delays into schedulability analysis for fixed priority pre-emptive systems is based on this analysis. The basic form given below assumes that pre-emption costs are zero.

We assume that the index i of task $\tau _i$ represents its priority, hence $\tau _1$ has the highest priority, and $\tau _n$ the lowest. We use the notation hp(i) (and lp(i)) to mean the set of tasks with priorities higher than (and lower than) i, and the notation hep(i) (and lep(i)) to mean the set of tasks with priorities higher than or equal to (lower than or equal to) i.

The worst-case response time $R_i$ of a task $\tau _i$ is given by the longest possible time from release of a job of the task until it completes execution. Thus task $\tau _i$ is schedulable if and only if $R_i \le D_i$ , and a taskset is schedulable if and only if all of its tasks are schedulable.

The response time $R_i$ of a task necessarily contains its execution time $C_i$, and in addition, $\tau _i$ may suffer interference and be pre-empted by tasks with higher priority than i. Let $\tau _j$ be such a task. Within the response time $R_i$ of $\tau _i$, task $\tau _j$ executes at most $\left\lceil \frac{R_i}{T_j}\right\rceil$ times, each time for at most $C_j$. Hence, the response time $R_i$ of task $\tau _i$ is given by:

$$\begin{aligned} R_i = C_i + \sum _{\forall j \in \mathrm{hp}(i)} \left\lceil \frac{R_i}{T_j} \right\rceil C_j \end{aligned}$$

(2)

where ${\mathrm{hp}}(i)$ denotes the set of tasks with higher priority than i. The response time $R_i$ of task $\tau _i$ appears on both the left-hand side and the right-hand side of (2). As the right-hand side is a monotonically non-decreasing function of $R_i$, then a solution may be found via fixed-point iteration:

$$\begin{aligned}&R_i^{x+1} = C_i + \sum _{\forall j \in \mathrm{hp}(i)} \left\lceil \frac{R_i^x}{T_j} \right\rceil C_j \end{aligned}$$

(3)

Iteration starts with an initial value, typically $R_i^0 = C_i$, and ends when either $R_i^{x+1} > D_i$ in which case the task is unschedulable, or when $R_i^{x+1} = R_i^x$, in which case the task is schedulable, with a worst-case response time $R_i^{x+1}$. We note that convergence may be speeded up using the techniques described by Davis et al. (2008).

Pre-emption cost aware schedulability test

To integrate pre-emption costs into response time analysis, Busquets-Mataix et al. (1996) extended (2) by adding a term $\gamma _{i,j}$ representing the pre-emption cost of a job of task $\tau _j$ executing during the response time of task $\tau _i$ (with $j \in hp(i)$):

$$\begin{aligned} R_i = C_i + \sum _{\forall j \in \mathrm{hp}(i)} \left\lceil \frac{R_i}{T_j} \right\rceil (C_j + \gamma _{i,j}) \end{aligned}$$

(4)

An alternative approach was taken by Petters and Farber (2001) and later Staschulat et al. (2005), who based their analyses on the following equation:

$$\begin{aligned} R_i = C_i + \sum _{\forall j \in \mathrm{hp}(i)} \left( \left\lceil \frac{R_i}{T_j} \right\rceil C_j + \hat{\gamma }_{i,j} \right) \end{aligned}$$

(5)

The value $\hat{\gamma }_{i,j}$ denotes the pre-emption cost of all jobs of task $\tau _j$ executing during the response time of task $\tau _i$ (again with $j \in hp(i)$). It is given by the $\left\lceil \frac{R_i}{T_j} \right\rceil$-highest pre-emption costs of a job of task $\tau _j$ executing during $R_i$. Although the difference with respect to (4) is subtle, more precise analysis can be obtained by using $\hat{\gamma }_{i,j}$ as a bound on the overall impact of all jobs of $\tau _j$ on the response time $R_i$ instead of a bound on the impact of just one job of $\tau _j$.

We note that when pre-emption costs are considered explicitly, the worst-case scenario is not necessarily given by a synchronous release of all higher priority tasks (Meumeu Yomsi and Sorel 2007) and hence (4) and (5) provide sufficient, but not exact schedulability tests.

Pre-emption cost computation

The value $\gamma _{i,j}$ can be computed in a number of different ways, which are described in detail by Altmeyer et al. (2012), here, we restrict our explanations to the two dominant approaches: ECB-Union and UCB-Union.

UCB-Union Tan and Mooney (2007) analysed the pre-emption cost via an upper bound on the number of useful cache blocks (of all pre-empted tasks) that a pre-empting task $\tau _j$ may evict. As it is only the eviction of useful cache blocks belonging to tasks with equal or higher priority than task $\tau _i$ that may increase the response time of task $\tau _i$, only tasks with intermediate priorities in the set ${\hbox {aff}}(i,j) = {\hbox {hep}}(i) \cap lp(j)$, need be considered.

$$\begin{aligned} \gamma _{i,j}^{\mathrm{UCB-U}}= {\hbox {BRT}}\cdot \left| \left( \bigcup _{k \in {\hbox {aff}}(i,j)} {\hbox {UCB}}_k \right) \cap {\hbox {ECB}}_j \right| \end{aligned}$$

(6)

Here, $\gamma _{i,j}^{\mathrm{UCB-U}}$ represents the worst-case impact a job of task $\tau _j$ can have on all (useful cache blocks of) tasks with lower priority than task $\tau _j$ down to task $\tau _i$. We refer to this approach as UCB-Union.

ECB-Union Instead of considering the precise set of ECBs of a pre-empting task and bounding all possibly affected UCBs (as UCB-Union does), ECB-Union (Altmeyer et al. 2011, 2012) considers the precise number of UCBs of the pre-empted task. It then assumes that the pre-empting task $\tau _j$ has itself already been pre-empted by all tasks with higher priority. This nested pre-emption of the pre-empting task is represented by the union of the ECBs of all tasks with higher or equal priority than task $\tau _j$:

$$\begin{aligned} \gamma _{i,j}^{\mathrm{ECB-U}}= \max _{\forall k \in {\hbox {aff}}(i,j)}\left\{ \left| {\hbox {UCB}}_k \cap \left( \bigcup _{h \in \mathrm{hep}(j)} {\hbox {ECB}}_h \right) \right| \right\} \end{aligned}$$

(7)

The UCB-Union and ECB-Union approaches are incomparable in that there are tasks that may be deemed schedulable using one approach but not the other and vice-versa.

Multiset approaches The UCB-Union and ECB-Union can be lifted to the so-called Multiset approaches to be used within Eq. (5) to account for the $\left\lceil \frac{R_i}{T_j} \right\rceil$-highest pre-emption costs of a job of task $\tau _j$ executing during $R_i$ instead of accounting for the highest pre-emption costs of a job $\left\lceil \frac{R_i}{T_j} \right\rceil$ times. To simplify our equations, we introduce $E_k(R_i)$ to denote the maximum number of jobs of task $\tau _k$ that can execute during response time $R_i$, i.e.:

$$\begin{aligned} E_k(R_i) = \left\lceil \frac{R_i}{T_k} \right\rceil \end{aligned}$$

The pre-emption cost $\gamma _{i,j}^{{\mathrm{ECB-M}}}$ is then computed as follows, recognising the fact that task $\tau _j$ can pre-empt each intermediate task $\tau _k$ at most $E_j(R_k)E_k(R_i)$ times during the response time of task $\tau _i$. We form a multiset M that contains the cost

$$\begin{aligned} \left| {\hbox {UCB}}_k \cap \left( \bigcup _{h \in \mathrm{hp}(j)\cup \{j\}} {\hbox {ECB}}_h \right) \right| \end{aligned}$$

(8)

of $\tau _j$ pre-empting task $\tau _k$ $E_j(R_k)E_k(R_i)$ times, for each task $\tau _k \in {\hbox {aff}}(i,j)$. Hence:

$$\begin{aligned} M = \bigcup _{k \in {\hbox {aff}}(i,j)} \left( \bigcup _{E_j(R_k)E_k(R_i)} \left| {\hbox {UCB}}_k \cap \left( \bigcup _{h \in \mathrm{hp}(j)\cup \{j\}} {\hbox {ECB}}_h \right) \right| \right) \end{aligned}$$

(9)

$\gamma _{i,j}^{{\mathrm{ECB-M}}}$ is then given by the $E_j(R_i)$ largest values in M.

$$\begin{aligned} \gamma ^{\mathrm{ECB-M}}_{i,j} = {\hbox {BRT}}\cdot \sum _{l=1}^{E_j(R_i)} \vert M^l \vert \end{aligned}$$

(10)

where $M^l$ is the l-th largest value in M. We note that by construction, the ECB-Union Multiset approach dominates the ECB-Union approach.

The pre-emption cost $\gamma _{i,j}^{{\mathrm{UCB-M}}}$ is computed as follows, recognising the fact that task $\tau _j$ can pre-empt each intermediate task $\tau _k$ directly or indirectly at most $E_j(R_k)E_k(R_i)$ times during the response time of task $\tau _i$. First, we form a multi-set $M_{i, j}^{{\mathrm{ucb}}}$ containing $E_j(R_k)E_k(R_i)$ copies of the ${\hbox {UCB}}_k$ of each task $k \in {\hbox {aff}}(i,j)$. This multi-set reflects the fact that during the response time $R_i$ of task $\tau _i$, task $\tau _j$ cannot evict a UCB of task $\tau _k$ more than $E_j(R_k)E_k(R_i)$ times. Hence:

$$\begin{aligned} M^{{\mathrm{ucb}}}_{i,j} = \bigcup _{k \in {\hbox {aff}}(i,j)} \left( \bigcup _{E_j(R_k)E_k(R_i)} {\hbox {UCB}}_k \right) \end{aligned}$$

(11)

Next, we form a multi-set $M^{{\mathrm{ecb}}}_j$ containing $E_j(R_i)$ copies of the ${\hbox {ECB}}_j$ of task $\tau _j$ . This multi-set reflects the fact that during the response time $R_i$ of task $\tau _i$, task $\tau _j$ can evict ECBs in the set ${\hbox {ECB}}_j$ at most $E_j (R_i)$ times.

$$\begin{aligned} M^{{\mathrm{ecb}}}_j = \bigcup _{E_j(R_i)}({\hbox {ECB}}_j) \end{aligned}$$

(12)

$\gamma _{i,j}^{{\mathrm{UCB-M}}}$ is then given by the size of the multi-set intersection of $M^{{\mathrm{ecb}}}_j$ and $M^{{\mathrm{ucb}}}_{i,j}$

$$\begin{aligned} \gamma _{i,j}^{{\mathrm{UCB-M}}} = {\hbox {BRT}}\cdot \left| M^{{\mathrm{ucb}}}_{i,j} \cap M^{{\mathrm{ecb}}}_j \right| \end{aligned}$$

(13)

We note that by construction, the UCB-Union Multiset approach dominates the UCB-Union approach.

The UCB-Union Multiset and the ECB-Union Multiset approach are incomparable in that there are tasks that may be deemed schedulable using one approach but not the other and vice-versa. More precise analysis can therefore be achieved by using a combination of both approaches as follows:

$$\begin{aligned} R_i = \min \left( R_i^{{\mathrm{ECB-M}}}, R_i^{{\mathrm{UCB-M}}}\right) \end{aligned}$$

(14)

A detailed description of the pre-emption cost aware schedulability tests can be found in Altmeyer et al. (2012).

EDF scheduling

We now recapitulate the exact (sufficient and necessary) schedulability test for pre-emptive EDF scheduling of sporadic tasksets based on processor demand analysis (Baruah et al. 1990). Subsequent work on integrating cache related pre-emption delays into schedulability analysis for EDF scheduled systems is based on this analysis. The basic form given below assumes that pre-emption costs are zero. Pre-emptive EDF scheduling is optimal among all scheduling algorithms on a uniprocessor (Dertouzos 1974) under the assumption of negligible pre-emption overhead.

A necessary and sufficient schedulability test for EDF and implicit deadlines $(D_i = T_i)$ is given by the processor utilizations (Liu and Layland 1973): a task set is schedulable, iff

$$\begin{aligned} U = \sum _i \frac{C_i}{T_i} \le 1 \end{aligned}$$

(15)

This test is necessary, but not sufficient if $D_i \ne T_i$.

Baruah et al. (1990) introduced the processor demand function h(t), which denotes the maximum execution time requirement of all tasks jobs which have both their arrival times and their deadlines in a contiguous interval of length t. Using this they showed that a taskset is schedulable iff $\forall t > 0, h(t) \le t$ where h(t) is defined as:

$$\begin{aligned} h(t) = \sum _{i=1} \max \left\{ 0,1+ \left\lfloor \frac{t-D_i}{T_i} \right\rfloor \right\} C_i \end{aligned}$$

(16)

As h(t) can only change when t is equal to an absolute deadline, we can restrict the number of values of t that need to be checked. To place an upper bound on t, and so on the number of calculations of h(t), the minimum interval in which it can be guaranteed that an unschedulable taskset will be shown to be unschedulable must be found. For a general taskset with arbitrary deadlines t can be bounded by $L_a$ (George et al. 1996):

$$\begin{aligned} L_a = \max \left\{ D_i, \ldots , D_n, \frac{\sum _{i+1}^n (T_i = D_i) U_i}{1-U} \right\} \end{aligned}$$

(17)

And an alternative bound, $L_b$ given by the length of the synchronous busy period can be used (Ripoll et al. 1996), where $L_b$ is computed using the following equation using fixed point iteration:

$$\begin{aligned} w^{\alpha + 1} = \sum _{i=1}^n \left\lceil \frac{w^\alpha }{T_i} \right\rceil C_i \end{aligned}$$

(18)

There is no direct relationship between $L_a$ and $L_b$, which enables t to be bounded by $L = \min (L_a, L_b)$. Combined with the knowledge that h(t) can only change at an absolute deadline, a taskset is therefore schedulable under EDF iff $U \le 1$ and:

$$\begin{aligned} \forall t \in Q, h(t) \le t \end{aligned}$$

(19)

Where Q is defined as

$$\begin{aligned} Q = \{ d_k \vert d_k = kT_i + D_i \wedge d_k < \min (L_a, L_b), k\in \mathbb {N} \} \end{aligned}$$

(20)

Zhang andBurns (2009) presented the Quick convergence Processor-demand Analysis (QPA) algorithm which exploits the monotonicity of h(t) to reduce the number of required checks.

Pre-emption cost aware schedulability test

In order to account for CRPD using EDF scheduling, Lunniss et al. (2013) include a component $\gamma _{t,j}$ which represents the CRPD associated with a pre-emption by a single job of task $\tau _j$ on jobs of other tasks that are both released and have their deadlines in an interval of length t. Note, unlike its counterpart in CRPD analysis for fixed priority scheduling, $\gamma _{t,j}$ refers to the pre-empting task $\tau _j$ and t, rather than the pre-empting and pre-empted tasks. Including $\gamma _{t,j}$ in (16) a revised equation for h(t) is obtained:

$$\begin{aligned} h(t) = \sum _{i=1} \max \left\{ 0,1+ \left\lfloor \frac{t-D_i}{T_i} \right\rfloor \right\} (C_i + \gamma _{t,j}) \end{aligned}$$

(21)

The set of affected tasks for EDF is based on the relative deadlines of the tasks:

$$\begin{aligned} {\hbox {aff}}(t_j) = \{ \forall \tau _i \vert t \ge D_i > D_j\} \end{aligned}$$

(22)

Task $\tau _j$ can only pre-empt tasks with a larger relative deadline than $D_j$ and only tasks with a relative deadline $D_i$ less than or equal to t need to be accounted for when calculating h(t)

Pre-emption cost computation

The UCB-Union (see Eq. (23)) and ECB-Union (see Eq. (24)) approaches as used for fixed-priorities can be adapted as follows:

$$\begin{aligned} \gamma _{t,j}^{\mathrm{UCB-U}}= {\hbox {BRT}}\cdot \left| \left( \bigcup _{k \in {\hbox {aff}}(t,j)} {\hbox {UCB}}_k \right) \cap {\hbox {ECB}}_j \right| \end{aligned}$$

(23)

and

$$\begin{aligned} \gamma _{t,j}^{\mathrm{ECB-U}}= \max _{\forall k \in {\hbox {aff}}(t,j)}\left\{ \left| {\hbox {UCB}}_k \cap \left( \bigcup _{h \in \mathrm{hep}(j)} {\hbox {ECB}}_h \right) \right| \right\} \end{aligned}$$

(24)

The UCB-Union and ECB-Union approaches are incomparable in that there are tasks that may be deemed schedulable using one approach but not the other and vice-versa.

Similar to Eq. (5) that accounts for the highest n pre-emption costs of a job instead of the highest pre-emption costs of a job n times, we can adapt Eq. (21) as follows

$$\begin{aligned} h(t) = \sum _{i=1} \left( \max \left\{ 0,1+ \left\lfloor \frac{t-D_i}{T_i} \right\rfloor \right\} C_i + \gamma _{t,j} \right) \end{aligned}$$

(25)

and lift the UCB-Union and ECB-Union approaches to their multiset counterparts.

The ECB-Union multiset approach computes the union of all ECBs that may affect a pre-empted task during a pre-emption by task $\tau _j$. It accounts for nested pre-emptions by assuming that task $\tau _j$ has already been pre-empted by all other tasks that may pre-empt it. The first step is to form a multiset $M_{t,j}$ that contains the cost of task $\tau _j$ pre-empting task $\tau _k$ repeated $P_j(D_k)E_k(t)$ times, for each task $\tau _k \in {\hbox {aff}}(t, j)$, where $P_j(D_k)$ denotes the maximum number of jobs of task $\tau _j$ that can pre-empt a single job of task $\tau _k$:

$$\begin{aligned} P_j(D_k) = \max \left( 0,\left\lceil \frac{D_k - D_j}{T_j}\right\rceil \right) \end{aligned}$$

and $E_k(t)$ is defined as

$$\begin{aligned} E_k(t) = \max \left( 0,\left\lfloor \frac{t-D_k}{T_k} \right\rfloor \right) \end{aligned}$$

Hence:

$$\begin{aligned} M = \bigcup _{k \in {\hbox {aff}}(t,j)} \left( \bigcup _{P_j(D_k)E_k(t)} \left| {\hbox {UCB}}_k \cap \left( \bigcup _{h \in \mathrm{hp}(j)\cup \{j\}} {\hbox {ECB}}_h \right) \right| \right) \end{aligned}$$

(26)

$\gamma _{t,j}^{{\mathrm{ECB-M}}}$ is then given by the $E_j(t)$ largest values in M.

$$\begin{aligned} \gamma ^{\mathrm{ECB-M}}_{t,j} = {\hbox {BRT}}\cdot \sum _{l=1}^{E_j(t)} \vert M^l \vert \end{aligned}$$

(27)

The pre-emption cost $\gamma _{t,j}^{{\mathrm{UCB-M}}}$ for EDF scheduling is computed similarly to the UCB-Union Multiset approach for fixed-priority scheduling: Task $\tau _j$ can pre-empt each intermediate task $\tau _k$ directly or indirectly at most $P_j(D_k)E_k(t)$ times within the deadline of task $\tau _i$. First, we form a multi-set $M_{t, j}^{{\mathrm{ucb}}}$ containing $P_j(D_k)E_k(t)$ copies of the ${\hbox {UCB}}_k$ of each task $k \in {\hbox {aff}}(t,j)$ reflecting the fact that within time t, task $\tau _j$ cannot evict a UCB of task $\tau _k$ more than $P_j(D_k)E_k(t)$ times. Hence:

$$\begin{aligned} M^{{\mathrm{ucb}}}_{t,j} = \bigcup _{k \in {\hbox {aff}}(t,j)} \left( \bigcup _{P_j(D_k)E_k(t)} {\hbox {UCB}}_k \right) \end{aligned}$$

(28)

Next, we form a multi-set $M^{{\mathrm{ecb}}}_j$ containing $E_j(t)$ copies of the ${\hbox {ECB}}_j$ of task $\tau _j$. This multi-set reflects the fact that during t, task $\tau _j$ can evict ECBs in the set ${\hbox {ECB}}_j$ at most $E_j(t)$ times.

$$\begin{aligned} M^{{\mathrm{ecb}}}_j = \bigcup _{E_j(t)}({\hbox {ECB}}_j) \end{aligned}$$

(29)

$\gamma _{i,j}^{{\mathrm{UCB-M}}}$ is then given by the size of the multi-set intersection of $M^{{\mathrm{ecb}}}_j$ and $M^{{\mathrm{ucb}}}_{i,j}$

$$\begin{aligned} \gamma _{i,j}^{{\mathrm{UCB-M}}} = {\hbox {BRT}}\cdot \left| M^{{\mathrm{ucb}}}_{i,j} \cap M^{{\mathrm{ecb}}}_j \right| \end{aligned}$$

(30)

We note that the UCB-Union Multiset and the ECB-Union Multiset approach for EDF are also incomparable and hence, a combined approach can be defined as follows:

$$\begin{aligned} h(t) = \min \left( h(t)^{{\mathrm{ECB-M}}}, h(t)^{{\mathrm{UCB-M}}}\right) \end{aligned}$$

(31)

As the multiset approaches effectively inflate the execution time of task $\tau _j$ by the CRPD that it can cause in an interval of length t, the upper bound L, used for calculating the processor demand h(t), must be adjusted. This is achieved by calculating an upper bound on the utilisation due to CRPD that is valid for all intervals of length greater than some value $L_c$. This CRPD utilisation value is then used to inflate the taskset utilisation and thus compute an upper bound $L_d$ on the maximum length of the synchronous busy period. This upper bound is valid provided that it is greater than $L_c$, otherwise the actual maximum length of the busy period may lie somewhere in the interval $[L_d,L_c]$, hence we can use $max(L_c,L_d)$ as a bound. We refer the reader to (Lunniss et al. 2013) for a detailed explanation.

Optimal task layout

The precise cache mapping, i.e., the mapping of memory block to cache sets strongly influences the pre-emption costs. Consider for instance the extreme situation where all tasks are aligned to the first cache-set: Each task will definitely evict cache blocks of another task. If tasks’ code is instead aligned sequentially in the cache, the pre-emption costs are very likely to be smaller. Lunniss et al. (2012) showed how to optimize the task layout with respect to the taskset schedulability and the pre-emption costs. The technique used determines the order in which the code for each task is placed sequentially in memory, without leaving any gaps. Optimizing the task layout does not require any changes to the source code or the compilation and is completely transparent to the user. Only the linker file is adapted. The optimzation changes the addresses of the code and data in the binary, but not the code/data itself, hence an appropriate layout can only improve performance.

Review of cache partitioning for real-time systems

Cache partitioning (Mueller 1995; Plazar et al. 2009) is a technique to reduce or even completely avoid cache-related pre-emption delays, aimed at increasing the predictability of real-time systems. Cache partitioning trades inter-task for intra-task cache conflicts, i.e. it trades off reduced cache-related pre-emption delays against potentially increased worst-case execution times. Partitioning techniques can be implemented either in hardware (Kirk and Strosnider 1990) or in software (Mueller 1995; Plazar et al. 2009). Modern common-off-the-shelf processors may provide native hardware support for partitioning, as for instance the OMAP-L138 DSP from Texas Instruments.² A native software-based solution can be implemented using page coloring (Ye et al. 2014) when virtual memory management is used. If no such support is available, the realization of cache partitioning is more compilcated: Mueller (1995) and later Plazar et al. (2009) proposed a partitioning-aware compiler, asserting that each task only accesses its own cache partition. This comes at the cost of often substantial changes to the code and data layout, which further increases task execution times; however, as no additional hardware is needed, the memory access delays remain unchanged. This is in contrast to hardware-based solutions where an additional mapping layer from code/data to main memory is needed.

Despite the wealth of publications on cache partitioning for real-time systems, little work has been done on evaluating the effects of cache partitioning, and in particular, its effectiveness compared to systems where tasks make unconstrained use of the cache. The previously cited papers either focus on the implementation of cache partitioning (Muller 1995; Plazar et al. 2009; Puaut and Decotigny 2002), or compare partitioned systems with systems without cache (Vera et al. 2007). The rationale behind this limited evaluation is the belief that pre-emptive systems that make unconstrained use of cache are unpredictable. Given recent advances in the analysis of cache related pre-emption delays, this view can now be considered somewhat outdated.

Studies on general usability of cache partitioning have been conducted by Busquets-Mataix and Wellings (1997) (to a limited extent), and more recently by Bui et al. (2008). Busquets-Mataix and Wellings based their evaluation on simplistic models of task execution times and pre-emption costs. The execution time variation was modelled according to Higbee (1990), favouring efficiency over precision, and only delivers rough estimates. The authors also assume that each evicting cache block causes an additional pre-emption cost, which is a very pessimistic assumption (Altmeyer et al. 2012).

Bui et al. (2008) based their evaluation on high-level execution time models (Wolf 1992) to estimate the execution time variation and pre-emption cost overhead. We rely on the results of state-of-the-art static timing analysis (both for the WCET bounds and the pre-emption costs) as used in safety-critical hard real-time systems, which provide firm guarantees.

Since finding an optimal cache partitioning is NP-hard (Bui et al. 2008), previous approaches employed heuristics either to minimize the number of cache misses, or to minimize the processor utilization (Kirk and Strosnider 1990; Busquets-Mataix and Wellings 1997; Bui et al. 2008; Plazar et al. 2009).

The research that we present in this paper differs in the following aspects: As schedulability is the key criterion in verifying the temporal correctness of hard real-time systems, we focus on taskset schedulability as opposed to utilization. A cache partitioning may be schedulable even though the task utilization is not the minimum that could be obtained. Similarly, minimizing the utilization does not necessarily optimize schedulability. We present partitioning algorithms which are optimal under the assumption that the worst-case execution time of each task is monotonic in the size of the partition allocated to that task. We aim at deriving general statements about the usability and efficiency of cache partitioning compared to a non-partitioned cache analysed using state-of-the-art pre-emption cost analyses.

Partition-size sensitivity

Partition-size sensitivity (task level)

In this section, we evaluate the sensitivity of the worst-case execution times of tasks with respect to the size of their allocated cache partitions. The aim of this sensitivity analysis is to form simple yet accurate execution time functions that are parametric in the size of the cache partition allocated to the task. These functions provide the information required by the optimal partitioning algorithm described in Sect. 6.

We perform sensitivity analysis by computing WCET bounds for varying cache partition sizes using static analysis. Based on these values, we can deduce typical variations in execution time depending on the code size of the task and the size of the cache partition allocated to it. The rationale behind this empirical evaluation is twofold: First, we are interested in the behaviour of a set of real examples, and second, we want to use realistic models of execution-time as a function of cache partition size to determine an effective partitioning of the cache between tasks. We note that with hardware support for cache partitioning, partitions are typically restricted to being a power of 2 in size e.g. 8,16,32 cache sets etc.; whereas software methods (Mueller 1995) can support cache partitions of any arbitrary number of sets. In the remainder of the paper, we assume that the number of cache sets in a partition may take any arbitrary value; however, we note that the techniques introduced are easily adapted to the case were partition sizes come from a restricted set of hardware-supported values.

The target architecture is an ARM7 processor³ with direct-mapped cache of size 4 kB with a line size of 16 Bytes (and thus, 256 cache sets), a block reload time of 8 $\upmu$s and a clock rate of 100 MHz. The cache uses a write-through policy to enable a constant block reload time, required for the static timing analysis. The values are derived from an example configuration of the ARM7 as used in previous work (see Altmeyer et al. 2011). As benchmarks, we used PapaBench (Nemer et al. 2006) and the Mälardalen benchmark suite (Gustafsson et al. 2010). We used the aiT Timing analyzer (Ferdinand and Heckmann 2004) to compute WCET bounds, and evaluate the sensitivity of execution time with respect to cache partition size.

Figures 1 and 2 show the normalized WCET bounds for the benchmark tasks with varying cache partition sizes and cache types. Each line denotes the execution time for one benchmark. The y-axis depicts the normalized execution time with the value 1 representing the largest WCET bound (which typically corresponds to the smallest cache partition size i.e. zero). The x-axis depicts the normalized cache partition size with the value 1 representing the code-size/maximum memory usage of the task. Increasing the size of the cache partition beyond the code size/memory footprint does not improve the execution time any further. The graphs are best viewed online in colour.

A perfect data (or instruction) cache means that all data (or instruction) accesses are served instantaneously. Even though this assumption is unrealistic, it removes possible noise and and allows us to fully concentrate on the effects of pre-emption and partitioning. We have also performed experiments with instruction cache but without data cache and also with data cache but without instruction cache. The results are very similar to the evaluation shown for perfect caches, but less accentuated.

Fig. 1

WCETs depending on the cache partition size (PapaBench, see Table 1). a Direct mapped instruction cache, perfect data cache. b Direct mapped data cache, perfect instruction cache

Fig. 2

WCETs depending on the cache partition size (Mälardalen and SCADE Benchmarks, see Table 3). a direct mapped instruction cache, perfect data cache, b direct mapped data cache, perfect instruction cache

We can see that variation in the execution times is stronger in the case of instruction cache compared to data cache. This behaviour is as expected since each instruction results in an instruction cache access, but not necessarily in a data cache access. Similarly, the variation in the execution times is amplified by the assumption of a perfect data/instruction cache. Note we do not assume any implementation cost for cache partitioning. Additional delays to implement cache partitioning only occur if no native support for partitioning is available.

Monotonicity

We observe from Figs. 1 and 2 that the execution time bounds are not necessarily monotonic with respect to the cache partition size.

This counter-intuitive behaviour can be explained by differences in the mapping of memory blocks to the cache sets. Assuming a direct-mapped cache with a line size of 16 bytes and a task that exhibits the following access sequence

$$\begin{aligned} 0x00030 \rightarrow 0x00080 \rightarrow 0x00030 \end{aligned}$$

If we assign this task a cache partition of size 4, memory block 0x00030 maps to set 3 of this partition and 0x00080 maps to set 0. The last access to 0x00030 therefore results in a cache hit. In contrast, in a larger cache partition of size 5, memory blocks 0x00030 and 0x00080 both map to cache set 3 and the last access to 0x00030 is a cache miss. Hence, for this trivial example, the performance with 5 cache sets is worse than that for 4 cache sets.

We note that the assumption of monotonic execution time bounds is both common and often not explicitly stated in work on cache partitioning for real-time systems (Bui et al. 2008; Busquets-Mataix and Wellings 1997; Kirk and Strosnider 1990; Mueller 1995; Plazar et al. 2009).

The impact of these effects is however limited, and so we can replace the actual execution time function with monotonic over/under-approximations without significant loss of precision, as shown in Fig. 3. Here, the basic function (black line) is non-monotonic, while the upper bound (blue line) and the lower bound (red line) are monotonically non-increasing functions of cache partition size. We thus establish monotonicity of the WCET with respect to the cache partition size and can use this property in our approach to partitioning the cache. In Sect. 8.5, we quantify the error introduced by this approximation.

Fig. 3

Over-/underapproximations of the WCET function (statemate benchmark, direct mapped data cache, perfect instruction cache)

Partition-size sensitivity (task group level)

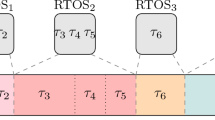
In this section, we examine the sustainability of a group of tasks sharing a cache partition with respect to the partition size. The rational behind a shared cache partition is that a subset of the complete taskset can be grouped together, either to improve performance or to implement spatial isolation between several task groups for safety reasons—as often used in hierarchical scheduling. Optimality of the partitioning algorithm described in Sect. 6 can only be guaranteed for shared cache partitions, if the schedulability tests are sustainable with respect to the size of a cache partition.

In case of a shared cache partition, two opposing factors influence the system’s performance: the execution time bounds and the pre-emption costs. Whereas the execution time bounds typically increase when the size of the assigned cache partition is reduced, the pre-emption costs decrease. A smaller cache results in a higher number of intra-task conflicts and hence, in fewer cache hits without pre-emption. Figure 4 depicts this behaviour. We note that a change in the maximum number of useful cache blocks always co-incides with a change in the execution time bound, whereas a change in the execution time bound does not necessarily imply a change in the maximum number of useful cache blocks. Furthermore under the hardware restrictions assumed in this paper (set-based partitioned, LRU or direct-mapped caches), the impact of the execution time limits the impact of the pre-emption costs: The pre-emption costs can only increase, if the number of cached and re-used memory blocks increases, which means that the execution time decreases. The decrease in the execution time always dominates the increase in the pre-emption costs. When the number of potentially evicted memory blocks increases, then the execution time decreases at least by the time to reload these additional memory blocks times how often these memory blocks need to be reloaded. A large number of pre-emptions will then at most cancel out the decrease in the execution time, but never exceed it.

Fig. 4

WCET and number of UCBs depending on the cache partition size (statemate benchmark, direct mapped data cache, perfect instruction cache)

However, the dominance relation between the execution time bound and the pre-emption costs is not necessarily reflected in these schedulability analyses: The terms $\gamma _{i,j}$ in (4) and $\gamma _{i,j}$ in (21) representing the pre-emption costs–and thus the number of UCBs—may contribute more often to the response time/demand bound than they actually occur in practice. Consequently, the schedulability tests presented in Sect. 3 are not sustainable for taskgroups, even under the assumption of monotonic execution times. This unsustainability of the schedulability tests means that the algorithms described in Sect. 6 would not retain their optimality if extended to the case where groups of tasks share partitions: False negatives are possible in the sense that no feasible shared cache partition is found although one may exist.

Optimal cache partitioning

In this section, we derive an optimal cache partitioning algorithm, which makes use of the monotonic upper bound execution time functions of cache partition size described in the previous section. We assume a direct-mapped cache of size S. A cache partitioning P is a tuple of non-negative integers describing for each task $\tau _i$, the size $p_i$ of its allocated cache partition:

$$\begin{aligned} P = (p_1,p_2,\ldots ,p_n): \underbrace{\mathbb {N} \times \cdots \times \mathbb {N}}_{n} \end{aligned}$$

(32)

We assume that each task has a dedicated cache partition which is not shared with any other tasks (we return to this point in Sect. 9). A cache partitioning is valid, if the total size of the cache partitions does not exceed the overall size S of the cache (i.e. if $\sum _i p_i \le S$).

Schedulability

We are interested in the schedulability of a taskset, as this is the main optimization criterion for hard real-time systems. We therefore say that a cache partitioning algorithm is optimal, iff it finds a cache partitioning whereby the tasks are schedulable, whenever such a partitioning exists. Note that this is different from minimizing the utilization of a taskset, since taskset utilization is only a rough indicator of system schedulability.

To compute an optimal cache partitioning, we use a branch-and-bound approach (see Algorithm 1) which is certain, under the assumption of monotonic execution time functions, to find a feasible cache partitioning if one exists. To this end, we exploit the sustainability of the schedulability test with respect to execution times and the monotonicity of the execution time function with respect to the cache partition size to prune the search space.

The algorithm is implemented using a recursive function checkPartition. This function takes as its input the current task index i, a partially defined partitioning P and the remaining cache size s. The partitioning is defined up to index i and the remaining cache size s is given by S minus the sum of the sizes of the first i partitions i.e. $s = S - \sum _{j=1}^i p_i$.

The initial input to the function is the first task index 1, an arbitrary partitioning P and the overall cache size S. If the last task index is reached, the partitioning is fully defined and the result is determined by the function isSchedulable, which checks the schedulability of the taskset for the defined partitioning. Note, here we employ the basic schedulability tests without pre-emption costs (see Sect. 3) given by (2) and  (16), as the cache partitioning prevents any cache-related pre-emption delays.

In the next step, the algorithm checks taskset schedulability under (a) the optimistic assumption that each not yet specified task partition is of size s and (b) under the pessimistic assumption that each not yet specified task partition is given an equal share of the remaining cache size, i.e., $\left\lfloor s/(n-i+1) \right\rfloor$. This enables effective pruning of the search in the case where (a) schedulability is disproved for any extensions to the current partial partitioning, and early exit in the case (b) schedulability is proven assuming that all further tasks are schedulable with a cache partition of equal size.

The last construct of the algorithm, the while loop, implements the branching. The partition size of cache partition $p_i$ is varied from 0 up to the remaining cache size s and each possible partitioning is evaluated using a recursive function call. This is done using the function nextStep which computes the next partition size for task $\tau _i$. Due to the monotonicity of the execution time functions with respect to cache partition size, nextStep jumps directly to the next partition size where the execution time changes. All intermediate partition sizes with the same execution time can be safely ignored. In the worst-case, up to $n^S$ different cache partitionings must be evaluated, where n is the number of tasks and S the number of cache sets. In practice, the runtime is substantially lower due to early exits and the reduced number of partition sizes which give different execution times. We return to this point in the following section. Further, in the case where hardware support is provided for a limited number of partition sizes, the runtime is further reduced due to the restricted number of partition sizes supported.

Schedulability and minimal utilization

Algorithm 1 can be extended to find a schedulable cache partitioning with the minimum processor utilization (see Algorithm 2). Schedulability is usually the dominating criterion for hard real-time systems but a reduced processor utilization typically reduces the energy consumption and the response times and thus improves the overal performance of the system.

The global variable minUtil is initially set to 1.1 to indicate that no schedulable cache partitioning has been found yet. As soon as the algorithm encounters a schedulable partitioning, the utilization is computed and compared to minUtil (which is updated if necessary).

Algorithm 2 also differs in the abort conditions. We are no longer allowed to stop the algorithm once we have found a schedulable partitioning (see line 9 in Algorithm 1), as only one of the two optimization criteria has at that point been fulfilled. Instead, we can bound the search when the current value of minUtil is less than or equal to the utilization of the cache partitioning where each not yet specified task partition is given the complete remaining size s (see line 16). This step is valid as the processor utilization (1) is monotonically non-decreasing in the tasks’ execution times. Due to the weaker abort-condition of Algorithm 2, a significantly higher number of cache partitionings must be evaluated when a schedulable partitioning exists. When no such partitioning exists, both algorithm consider exactly the same number of partitionings. We evaluate the difference in the average processor utilization and analysis time for the two algorithms in Sect. 7.3.

Case study

In this section, we evaluate the partitioning algorithms based on PapaBench (Nemer et al. 2006), the Mälardalen benchmark suite (Gustafsson et al. 2010) and a set of SCADE⁴ tasks (partially provided by SCADE, partially from our own SCADE models). Besides the effectiveness of the cache partitioning algorithms, we are interested in (i) the precision of the simplified execution time model, (ii) the runtime performance of the algorithms, and (iii) the difference between the two partitioning algorithms with respect to the minimum utilization obtained.

For the case study, the target architecture is an ARM7 processor (with a 4 kB direct-mapped write-through cache, line size of 16 Bytes, 256 cache sets, block reload time 8 $\upmu$s, clock rate of 100 MHz). The execution time bounds were derived using the aiT Timing analyzer (Ferdinand and Heckmann 2004). The values are derived from an example configuration of the ARM7 as used in previous work (see Altmeyer et al. 2011).

Papabench provides two different tasksets (fbw and autopilot) with deadlines and periods (except for the interrupts I4 to I7) (see Tables 1 and 2). With the initial processor frequency of 100 MHz, both tasksets are schedulable both with and without cache partitioning. The other benchmarks only provide code and do not form a meaningful taskset. We therefore randomly selected tasks from (i) Tables 1 and 2, and (ii) Table 3 and 4 (together with execution times, the execution time variations, codes size and UCBs/ECBs).

The remaining task and taskset parameters used in our experiments were randomly generated as follows:

• The default taskset size was 10.

• Task utilizations were generated using the UUnifast (Bini and Buttazzo 2005) algorithm.

• Task periods were set based on the utilization and execution times: $C_i = U_i \cdot T_i$.

• Task deadlines were implicit,⁵ i.e., $D_i = T_i$.

• For fixed priority scheduling, priorities were assigned in Rate Monotonic priority order.

The tasks are indexed and processed by the partioning algorithms in decreasing priority order.

In each experiment the taskset utilization not including pre-emption cost was varied from 0.025 to 0.975 in steps of 0.025. For each utilization value, 1000 tasksets were generated and the schedulability of those tasksets was determined using the cache partitioning algorithms or pre-emption cost aware analysis with either sequential or optimal task layout (Lunniss et al. 2012). We thus compared the results for cache partitioning against those for (i) no partitioning with a sequential task layout, (ii) no partitioning with an optimized task layout, (iii) analysis ignoring pre-emption costs, but assuming that all the tasks shared the cache; (iv) naive cache partitioning with all tasks allocated the same size partition S / n; (v) no cache. The sequential task layout reflects the basic un-optimized cache mapping, i.e., where the code for each task is placed consecutively in memory. In case of unconstrained cache usage, we used the combined multiset approaches for fixed-priority (14) and for EDF scheduling (31) to compute the schedulability of the tasksets.

For fixed priority scheduling, we were able to compute the schedulability of all tasksets (42,000 tasksets per case study) in less than 10 min on a 2.6-GHz Quadcore processor—despite the exponential worst-case behaviour of the cache partitioning algorithm (Algorithm 1). For EDF scheduling, the computation for the same configurations took about 60 min. This shows a more than acceptable analysis time for the partitioning algorithm, with a strong dependency on the runtime of the schedulability test that it uses.

Table 1 Execution times and number of UCBs and ECBs for the PapaBench benchmarks

PapaBench

Most tasks from Tables 1 and  2 have rather short execution times, leading to relatively high pre-emption costs. These tasks are simple, short control tasks with limited computations and data accesses. Figure 5a and c for fixed priorities and Fig.  6a and c for dynamic priorities show the success ratio; the number of tasksets based on Papabench that were schedulable at the various levels of utilization. In the case of instruction caches (Figs. 5b and 6b), optimal partitioning has similar performance to sequential task layout with no partitioning, while optimal task layout with no partitioning results in improved performance. Optimal cache partitioning was only able to improve performance over sequential task layout with no partitioning in a few cases. In the case of data caches(Figs. 5d and 6d), optimal partitioning outperforms optimal task layout with no partitioning. The variation of the execution times in this case is rather low, while the number of UCBs is comparably high. We thus note that the two approaches are incomparable. Almost no tasksets were schedulable with no cache, except for the case of data cache with perfect instruction cache as the impact of the data cache alone is limited.

Table 2 Execution times and number of UCBs and ECBs for the PapaBench benchmarks

Table 3 Mälardalen benchmark suite (M) and SCADE benchmarks (S)

With respect to the scheduling policy, i.e. fixed priority vs. EDF, there was no significant difference in the relative performance of the various approaches. As expected, the schedulability tests for EDF deem consistently more tasksets schedulable (for all approaches) than those for fixed priority scheduling.

Mälardalen and SCADE benchmarks

In contrast to the first case study, the execution times of the tasks from Tables 3 and 4 for the Mälardalen and SCADE Benchmarks are comparably high, and thus the pre-emption costs relatively low. These tasks exhibit a low locality of memory accesses but high amounts of computation. In this case, the low cache related pre-emption delays result in significantly better performance if the cache is not partitioned. Here, cache partitioning was unable to improve performance over the simple sequence task layout with no partitioning, as illustrated in Figs. 7a and 8a. Note that in this case there are no major differences for data and instruction caches, the results of the different approaches are just more (instruction caches) or less (data caches) accentuated.

Table 4 Mälardalen benchmark suite (M) and SCADE benchmarks (S)

Fig. 5

Evaluation of PapaBench benchmarks (fixed priority scheduling). a Number of tasksets deemed schedulable at the different total utilizations (instruction cache with perfect data cache), b number of tasksets deemed schedulable with one approach and not another (instruction cache with perfect data cache), c number of tasksets deemed schedulable at the different total utilizations (data cache with perfect instruction cache), d number of tasksets deemed schedulable with one approach and not another (data cache with perfect instruction cache)

Fig. 6

Evaluation of PapaBench benchmarks (EDF scheduling). a Number of tasksets deemed schedulable at the different total utilizations (instruction cache with perfect data cache), b number of tasksets deemed schedulable with one approach and not another (instruction cache with perfect data cache), c number of tasksets deemed schedulable at the different total utilizations (data cache with perfect instruction cache), d number of tasksets deemed schedulable with one approach and not another (data cache with perfect instruction cache)

Fig. 7

Evaluation of Mälardalen benchmarks (fixed priority scheduling). a Number of tasksets deemed schedulable at the different total utilizations (instruction cache with perfect data cache), b number of tasksets deemed schedulable with one approach and not another (instruction cache with perfect data cache), c number of tasksets deemed schedulable at the different total utilizations (data cache with perfect instruction cache), d number of tasksets deemed schedulable with one approach and not another (data cache with perfect instruction cache)

Fig. 8

Evaluation of Mälardalen benchmarks (EDF scheduling). a Number of tasksets deemed schedulable at the different total utilizations (instruction cache with perfect data cache), b number of tasksets deemed schedulable with one approach and not another (instruction cache with perfect data cache), c number of tasksets deemed schedulable at the different total utilizations (data cache with perfect instruction cache), d number of tasksets deemed schedulable with one approach and not another (data cache with perfect instruction cache)

Utilization versus analysis time

The first cache partitioning algorithm (Algorithm 1) only optimizes for schedulability and ignores the processor utilization. In this section, we evaluate the consequences of this simplified optimization: how much further can the processor utilization be reduced and what is the analysis time needed to compute a schedulable partitioning with minimum utilization. To this end, we compare the results and analysis times of both algorithms presented in Sect. 6, i.e. with and without optimizing minimum processor utilization as a secondary concern.

Fig. 9

Evaluation of the average utilization PapaBench benchmarks (fixed priority scheduling, instruction cache with perfect data cache). a Average utilization of schedulable tasksets per nominal utilization, b total analysis time for 1000 tasksets

Fig. 10

Evaluation of the average utilization PapaBench benchmarks (EDF scheduling, instruction cache with perfect data cache). a Average utilization of schedulable tasksets per nominal utilization, b total analysis time for 1000 tasksets

Fig. 11

Evaluation of the average utilization of Mälardalen benchmarks (fixed priority scheduling, instruction cache with perfect data cache). a Average utilization of schedulable tasksets per nominal utilization, b total analysis time for 1000 tasksets

Fig. 12

Evaluation of the average utilization of Mälardalen benchmarks (EDF scheduling, instruction cache with perfect data cache). a Average utilization of schedulable tasksets per nominal utilization, b total analysis time for 1000 tasksets

The results of this comparison are shown in Figs. 9 and 10 for the PapaBench benchmark suite and in Figs. 11 and 12 for the Mälardalen benchmark suite. Subfigures (a) show the average percentage increase in processor utilization (i.e. with the execution time overhead due to cache partitioning) of schedulable tasksets with respect to the nominal utilization (i.e. without execution time overhead due to cache partitioning). Subfigures (b) show the analysis time for all 1000 tasksets generated per utilization level. The blue line representes the optimal cache paritioning algorithm without optimized utilization (Algorithm 1) and the pink line with optimized utilization (Algorithm 2). We have omitted the results for data cache with perfect instruction cache as they resemble the results for instruction cache with perfect data cache, with a less significant difference.

The minimum utilization of a schedulable cache partitioning is at most $1\,\%$ above the nominal utilization. The average difference of the results of the two algorithms is also limited. Mälardalen benchmarks with instruction cache/perfect data cache—irrespective of the priority assignment—exhibits the largest relative difference in utilization of around $7\,\%$ at a utilization level of 0.8, (i.e. an absolute difference in utilization of less than 0.056). In the case of data caches with perfect instruction cache, the difference is always below $2\,\%$.

In contrast to the processor utilization, the difference in the total analysis time is noticable in all cases, especially if the nominal processor utilization is above 0.8. This indicates that the algorithm to optimize the processor utilization requires a significant amount of time to either find an improved cache partitioning or to show the optimality of the current candidate. We conclude that a small but nevertheless useful improvement in utilization can be obtained using Algorithm 2; however, that this comes at a cost in terms of increased runtime of the analysis.

We note that the average increase in utilization which occurs using Algorithm 1 is similar for both fixed priority and EDF scheduling with the only difference beeing that the increase drops at a lower nominal utilization for fixed-priority scheduling (0.8) than for EDF scheduling (0.85). This is because EDF has a schedulable utilization bound of 1 (much higher than that for fixed priority scheduling), thus a careful tuning of the partition size to achieve a schedulable partitioning is only required at higher nominal utilizations. The reduced difference in the nominal utilization also coincides in both cases (fixed-priority and EDF) with an increase in the analysis time of Algorithm 1.

Note, as both algorithms behave similar in case no schedulable cache partitioning exists, the differences in the analysis time are only due to the optimization of schedulable partitionings.

Synthetic tasksets

We also evaluated the effectiveness of cache partitioning on a large number of synthetic tasksets with varying cache configurations and varying task parameters. Our aim here was to identify those parameters that have a significant influence on the relative effectiveness of cache partitioning versus a non-partitioned cache. The evaluation using randomly generated tasksets enables us to fully control all relevant parameters, which is not possible using the benchmark tasks directly.

The task parameters used in our experiments were randomly generated as follows:

• The default taskset size was 10.

• Task utilizations were generated using the UUnifast (Bini and Buttazzo 2005) algorithm.

• Task periods were generated according to a log-uniform distribution with a factor of 1000 difference between the minimum and maximum possible task period and a minimum period of 5 ms. This represents a spread of task periods from 5 ms to 5 s, thus providing reasonable correspondence with real systems.

• Task execution times were set based on the utilization and period selected: $C_i = U_i \cdot T_i$.

• Task deadlines were implicit

• For fixed priority scheduling, priorities were assigned in Deadline Monotonic priority order.

To model the variation in the execution time, we randomly selected one of the execution time functions from our benchmarks (see Tables 1 and 3 and Figs. 1 and 2). Note that this only affects the variation of the execution time for different partition-sizes and $C_i$ refers to the base execution time when $\tau _i$ can use the complete cache. The tasks are indexed and processed by the partioning algorithms in decreasing priority order.

The following parameters affecting pre-emption costs were also varied, with default values given in parentheses:

• The number of cache-sets ($CS = 256$).

• The block-reload time ($BRT = 8\,\upmu$s)

• The cache usage of each task, and thus, the number of ECBs, were generated using the UUnifast (Bini and Buttazzo 2005) algorithm (for a total cache utilization $CU = \sum _i \vert {\hbox {ECB}}\vert /CS = 4$). UUnifast may produce values larger than 1 which means a task fills the whole cache.

• For each task, the UCBs were generated according to a uniform distribution ranging from 0 to the number of ECBs times a reuse factor: $[0, RF \cdot \vert ECB \vert ]$. The factor RF was used to adapt the assumed reuse of cache-sets to account for different types of real-time applications, for example, from data processing applications with little reuse up to control-based applications with heavy reuse (default $RF =0.3$).

The parameters of the base configuration were chosen according to the actual values observed in the case studies of the PapaBench benchmarks 7.1 and the Mälardalen benchmarks 7.2. The results (Figs. 13 and 14) lie between those of the case studies (Figs. 5a and 7a for fixed priority scheduling, and Figs. 6a and 8a for EDF scheduling respectively).

Overall, cache partitioning and pre-emption cost analysis with a sequential, un-optimized task layout have similar performance; however, we note that there are also a large number of tasksets that can only be scheduled with one of the two approaches, but not with the other. This shows that cache partitioning is a viable alternative in some scenarios and detrimental in others. However, we also observe that the optimal task layout with no partitioning has a clear advantage over optimal partitioning in terms of the number of schedulable tasksets (see Figs. 13b and 14b).

The choice of scheduling policy has a limited influence on the relative performance of the various approaches. Under EDF cache partitioning showed improved performance relative to no partitioning and a sequential task layout, most likely due to the higher imprecision in the cache-aware schedulability test for EDF.

Fig. 13

Evaluation for the base configuration, fixed priority scheduling. a Number of tasksets deemed schedulable at the different total utilizations, b number of tasksets deemed schedulable with one approach and not another

Fig. 14

Evaluation of the base configuration, EDF scheduling. a Number of tasksets deemed schedulable at the different total utilizations, b number of tasksets deemed schedulable with one approach and not another

Exhaustive evaluation of all combinations of cache and taskset configuration parameters is not possible. We therefore fixed all parameters except one and varied the remaining parameter in order to see how performance depends on this value. The parameters we examined were: (i) the pre-emption cost as determined by the block reload time (BRT) and a scaling factor applied to task periods; (ii) the cache utilization, (iii) the number of tasks, and (iv) the cache size.

The graphs show the weighted schedulability measure $W_y(q)$ (Bastoni et al. 2010) for schedulability test y as a function of parameter q. For each value of q, this measure combines data for all of the tasksets $\tau$ generated for all of a set of equally spaced utilization levels. Let $S_y(\tau , q)$ be the binary result (1 or 0) of schedulability test y for a taskset $\tau$ and parameter value q then:

$$\begin{aligned} W_y(q) = \left( \sum _{\forall \tau } u(\tau ) \cdot S_y(\tau , q)\right) / \sum _{\forall \tau } u(\tau ) \end{aligned}$$

(33)

where $u(\tau )$ is the utilization of taskset $\tau$. This weighted schedulability measure reduces what would otherwise be a 3-dimensional plot to 2 dimensions (Bastoni et al. 2010). Weighting the individual schedulability results by taskset utilization reflects the higher value placed on being able to schedule higher utilization tasksets.

Pre-emption costs

Pre-emption costs are determined by several parameters. Among those, the dominant factors are the block reload time (${\hbox {BRT}}$) and the range of task execution times. Figure 15 shows the weighted schedulability measure for different block reload times. In our setting, the break-even point is at a block reload time of about $10 \mu s$. For larger block reload times cache partitioning becomes the more effective approach, while for smaller block reload times a non-partitioned cache is more effective.

Fig. 15

Weighted schedulability measure; varying block reload time from 1 to 20 $\upmu$s (assuming constant worst-case execution times). a Fixed priority scheduling, b EDF scheduling

In Fig. 16, we varied the scaling factor w from 0.5 to 10 and hence the range of task periods given by w[1, 100]ms. Given that the block reload time is constant in this experiment, the ratio of pre-emption costs to taskset utilization decreases as the task periods, deadlines and execution times are all scaled up. A lower scaling factor resembles tasks with shorter execution times (as in Tables 1 and 2), a higher scaling factor resembles tasks with higher execution times and commensurately longer periods (as in Tables 3 and 4).

Fig. 16

Weighted schedulability measure; varying the scale of task periods w[1, 100] from $w=0.5$ to $w=10$. a Fixed priority scheduling, b EDF scheduling

The results indicate that cache partitioning is useful for control-oriented tasks with short execution times and very short periods and thus relatively high pre-emption costs compared to their WCET. When the pre-emption costs are low compared to the WCET, cache partitioning typically does not pay off.

Note that increasing the block reload time typically also leads to increased (non-pre-emptive) execution times. In these experiments, we have fixed the execution times to vary only the relation between pre-emption costs and execution time bounds.

The impact of the scheduling policy, i.e. fixed priority vs. EDF, on the relative performance of the various approaches remains limited.

Cache utilization

The cache utilization determines the ratio between the total code size of all the tasks and the overall cache size. Increasing the cache utilization leads to higher pre-emption costs, and higher execution times in the case of cache partitioning. Cache partitioning; however, suffers less from increased cache utilization as can be seen in Fig. 17a.

Fig. 17

Weighted schedulability measure; varying cache utilization from 0 to 20. a Fixed priority scheduling, b EDF scheduling

The results for the non-partitioned system suffer somewhat from the over-approximation of the UCB/ECB analysis and the pre-emption cost aware response time analysis: This assumes additional cache misses due to pre-emption even though the misses have already been accounted for by a prior pre-emption, providing more pessimistic results at high cache utilization levels.

Number of tasks

We also conducted experiments varying the number of tasks. Note that it is an unrealistic assumption to change the number of tasks without also changing the cache utilization. This would mean the cache usage of each individual task decreasing as more tasks are added to the system. Realistically, cache utilization increases with the number of tasks. Figure 18a shows the results of the evaluation if we increase the number of tasks and the cache utilization, while keeping the per task cache utilization constant.

Fig. 18

Weighted schedulability measure; varying the number of tasks from 2 to 24 with constant ratio of number of tasks to cache usage. a Fixed priority scheduling, b EDF scheduling

Here, we see that the performance of the non-partitioned approach gradually degrades with increasing taskset size due to pessimism in the analysis of a large number of pre-emption levels. We also notice a quicker decline in the case of EDF compared to fixed priority scheduling. This validates our assumption that the relative difference is due to a larger imprecision in the cache-aware schedulability test for EDF.

Cache size

If we only adapt the cache size without changing the relation between the execution time and the pre-emption costs (or the cache utilization), we would penalise the pre-emption cost computation: if there are more cache sets, there are also more UCBs and thus, higher pre-emption costs. The results of the cache partitioning, though, does not change. To avoid this discrimination, we have increased the number of sets, while keeping the relation of cache utilization to cache size (CU / CS) constant. The results are shown in Fig. 19a. For small cache, the partition sizes are very small which leads to high execution times and thus low schedulability for the paritioning approaches. For larger caches, the performance of partitioned and non-partitioned systems converge as the cache utilization decreases.

Fig. 19

Weighted schedulability measure; varying the number of cache sets 64 to 1024 with constant ratio (CU / CS). a Fixed priority scheduling, b EDF scheduling

We note that small caches also lead to a reduced pre-emption overhead as the number of UCBs is upper bounded by the number of sets: The delay of additional cache reloads that would otherwise contribute to the pre-emption overhead is included in the non-pre-emptive execution time bound. The performance of the non-partitioned approaches thus declines from 32 to 128 sets (where the pre-emption overhead is maximal) as we use the task utilization (without pre-emption costs) as the baseline for each experiment.

Precision of the simplified execution-time model

To evaluate the precision of the simplified execution time model, and so obtain a measure of the pessimism introduced in order to obtain monotonicity of execution times, we computed for each taskset an optimal cache partitioning (using Algorithm 1) (i) assuming upper bounds (Fig. 3 blue upper line) and (ii) optimistic lower bounds on the execution times (Fig. 3 red lower line). The difference in the results—the number of tasksets that were deemed schedulable using the lower but not the upper bounds—provides a measure of the imprecision of the simplified execution time model. In the first case study (PapaBench) $0.21\,\%$ of all tasksets were deemed schedulable only using lower bounds, and $1.21\,\%$ (Mälardalen and SCADE) for the second case study. Note that these percentages refer to the uncertainty due to the assumed monotonicity and not due to the cache partitioning algorithm. Also note that this does not necessarily mean that $0.21\,\%$, resp. $1.21\,\%$, of the tasksets have been falsely deemed not schedulable, rather these are upper bounds on the imprecision.

Conclusions and future work

In this paper, we evaluated the relative performance, in terms of taskset schedulability, of partitioning the cache on a per task basis versus allowing all tasks to share the entire cache. Our research contrasts with previous work in this area, in that we used system schedulability as the performance metric, effective techniques for analysis of cache related pre-emption delays, and code from real benchmarks as the foundation of our empirical evaluation.

The main contributions of this paper are as follow:

• Sensitivity analysis of WCET with respect to partition size, showing how the precise WCET bound as a function of the size of the partition can be effectively upper and lower bounded by monotonic functions.

• Sensitivity analysis of the schedulability of groups of tasks with respect to the size of a shared partition, showing that the precise schedulability of the task group is sustainable with respect to the size of the partition whereas the schedulability tests are not sustainable.

• The introduction of optimal algorithm for cache partitioning which finds a schedulable partioning whenever such a partitioning exists. This algorithm makes use of the monotonic WCET functions.

• The introduction of an optimal algorithm for cache partitioning which finds a schedulable partitioning with the minimum processor utilisation whenever a schedulable partitioning exists. This algorithm also makes use of the monotonic WCET functions.

• A thorough evaluation of the relative performance of optimal per task cache partitioning versus no partitioning for static and dynamic priority assignment.

• An evaluation of the trade-off of mininal processor utilization against increased analysis time.

Our results showed that for simple, short control tasks such as those from Papabench, where the pre-emption costs are relatively high compared to the WCET, the performance of partitioned and non-partitioned approaches were similar, with the use of an optimal task layout providing the non-partitioned approach with a small performance advantage. By contrast, tasks from the Mälardalen benchmark suite exhibited lower locality of memory accesses and higher amounts of computation, with larger WCETs compared to the associated cache related pre-emption delays. For tasksets based on this benchmark, the non-partitioned approach (with and without cache layout optimization) outperformed optimal partitioning. These results indicate that in most cases, the increased predictability of a partitioned cache, in terms of eliminating cache related pre-emption delays, does not compensate for the performance degradation in the WCETs.

Our extended evaluation using synthetic benchmark tasksets showed that the key parameters affecting the relative effectiveness of cache partitioning versus no partitioning are: (i) The ratio of pre-emption costs to the overall WCET (partitioning does not pay off when this ratio is small). (ii) The Block Reload Time (partitioning is most effective when the BRT is large increasing pre-emption costs). (iii) Cache utilization (the non-partitioned approach suffers from pessimism at high values of cache utilization). (iv) The number of tasks (with no partitioning the analysis suffers from increasing pessimism in the computation of pre-emption costs as the number of tasks increases). Further, we found that the relative performance of the two approaches was largely unaffected by the number of cache sets. The scheduling policy had a comparably limited impact on the overall results; however, the increased pessimism of the cache-aware schedulability analysis for EDF slightly improved the relative performance of cache partitioning in this case.

Cache partitioning often increases the utilization of the tasksets by allocating each task a partition which is less than the size of the cache, thus inflating the WCET. We found that Algorithm 2 which minimizes utilization as a secondary criterion makes small but useful gains in the average taskset utilization obtained over Algorithm 1 which only optimizes for the primary criteria of schedulability. These gains, however, come at a cost in terms of an increased runtime for the analysis. For high utilization tasksets, the differences in the utilization obtained is small, since few partitionings are schedulable and both algorithms tend towards producing very similar results.

Our evaluation shows that static cache and CRPD analyses are sufficiently precise to justify unconstrained cache usage; Cache partitioning to increase predictability is often not required but instead is detrimental to the provable system performance. Spatial isolation which reduces the certification costs and enables the integration of independently developed system components remains a strong point in favour of cache partitioning.

This paper compares two extremes, either all of the tasks share the entire cache, or every task has an individual cache partition. It is clear that between these two extremes, there is an approach which subsumes and dominates both. This intermediate approach involves allocating groups of tasks to appropriately sized cache partitions, and then controlling the layout of those tasks in memory (Lunniss et al. 2012) to enhance schedulability through a reduction in cache related pre-emption delays within each partition.

The intermediate approach in between cache partitioning and unconstrained cache usage is also fundamental for spatial isolation. Isolation is typically required between groups of tasks constituting a system component, and not in between individual tasks. The CRPD analysis has recently been extended to hierarchical scheduling to implement temporal isolation (Lunniss et al. 2014, 2015), but the integration with cache partitioning, and in particular the optimization of the cache partitioning in this context, to achieve full temporal and spatial isolation is future work.

Recent work by Wang et al. (2015) investigates an alternative intermediate approach where groups of tasks share a partition and also a preemption threshold (Wang and Saksena 1999; Saksena and Wang 2000), hence ensuring that tasks using the same partition cannot preempt each other, thus avoiding CRPD. (Analysis of CRPD has also been integrated into fixed priority scheduling with preemption thresholds assuming that the cache is shared Bril et al. 2014).

Our analysis and evaluation is restricted to a single level of cache. This restriction was necessary to single out the effect of cache partitioning and unconstrained cache usage and to reduce noise due to interferences from other parts of the cache hierarchy. Broadening the view to several cache levels, a combination of the predictability of cache partitioning on one cache level with the performance of unconstrained cache usage on another one is likely to provide optimal performance.