The co-determination decision game with consumption externalities

Abstract

This work aims to investigate the effects of co-determination in a game-theoretic setting by considering network externalities in consumption. The received theoretical literature, so far focused only on standard (non-network) industries, showed that co-determination might emerge as the sub-game perfect Nash equilibrium (SPNE) of a non-cooperative Cournot duopoly, but this outcome generates a prisoner’s dilemma. The present research shows that (positive) network externalities may solve the prisoner’s dilemma and let co-determination become a Pareto-efficient SPNE with homogeneous or heterogeneous products. In a network industry, co-determination becomes a Pareto-superior institution for society, as firms, consumers and workers are better off than under profit maximisation. These results hold for exogenous (homogeneous and heterogeneous) co-determination and endogenous co-determination.

1 Introduction

The present article aims to contribute to the debate on the regulatory policies and institutions concerning the labour market and industrial relations. The main historical labour market institution, which is pervasive in several central European countries is the so-called co-determination, which mixes some characteristics of the competitive labour market and the unionised labour market (e.g., the right to manage and efficient bargaining models). Co-determination—often regulated by law—may also be considered a regulatory tool for harmonising labour relationships and for improving social welfare. However, despite its social harmonising role, from a strict microeconomic approach, the mandatory introduction of co-determination in markets with standard non-network goods cannot represent a Pareto improvement for society. This is because co-determination contributes to enhancing the welfare of workers (trade unions) and consumers, so that both groups are better off, but it also reduces firms’ profitability so that firms are worse off.

By assuming network industries, the present article shows, in a non-cooperative game-theoretic setting, that co-determination can (1) endogenously emerge in the market, i.e., without the need for ad hoc law regulation and enforcement, like previous studies on this issue already showed (e.g., Fanti et al., 2018; Gori & Fanti, 2022; Kraft, 1998, 2001; Kraft et al., 2011), and (2) become a Pareto-superior institution for society. This is because consumption externalities work out by expanding the market demand, in turn, increasing production, consumer surplus, profits and the welfare of workers representatives. The policy implications are clear and far-reaching: mandatory co-determination in network industries is Pareto improving. Indeed, unlike in the previous literature, codetermination can emerge as a Pareto efficient SPNE in a network industry, and as social welfare corresponding to the SPNE when both firms bargain under co-determination, (B,B), is higher than social welfare corresponding to the SPNE when firms are profit maximisers, (PM,PM), the result is twofold: (1) voluntary codetermination is Pareto superior to profit maximisation, (2) if the government chooses to mandatorily introduce codetermination the result for society would be as if it emerged voluntarily and thus society would still get a Pareto superior situation to profit maximisation.

This work then combines two different strands of research belonging to the labour economics and industrial economics literature—co-determination and network externalities—by building on a tractable model describing a strategic competitive framework with quantity-setting firms.

On the one hand, there is increasing attention towards co-determination in several countries of Western Europe. This institution implies, broadly speaking, that employees’ representatives sit on the supervisory board (or similar structures) in large companies. Co-determination is known to be a relevant feature of the German industry (at least since the 1950s), but it is also widespread in other European countries.¹ Its main feature is that employment (production) is jointly determined by owners (or their managers) and workers (or their representatives) in the supervisory board, but the wage is left to be bargained by the federation of firms and the trade unions at the industry level.² More in general, active workers involvement in the firm’s decisions are a crucial element of the European social model.³ Despite this, there is little economic analysis on the effects of co-determination resulting in a gap on the side of policy recipes at the European level: “The practice of board participation and its impact are very hard to gauge, given a general lack of research and evidence.” (Schulten & Zagelmeyer, 1998). However, the number of theoretical and empirical works on the subject is growing.

On theoretical grounds, McCain (1980) represents a pioneering work opening the route to causes for reflections about co-determination, working conditions and labour productivity. Some years later, Kraft (1998) shows—considering a Cournot duopoly with homogeneous products—that profit-maximising firms have the incentive to become bargainers over employment. This in turn implies that co-determination becomes the dominant strategy of the game. However, firms would prefer to have the full power to choose employment (profit maximisation). Then, co-determination emerges as the unique Pareto-inefficient sub-game perfect Nash equilibrium (SPNE) of a non-cooperative co-determination decision game, but firms are entrapped in a prisoner’s dilemma. Subsequently, Kraft (2001) extends his previous work by accounting for a general oligopolistic market and discussing the effects of employment bargaining from both theoretical and empirical perspectives, confirming the existence of a prisoner’s dilemma for a sizable range of the union’s bargaining power. Three other contributions study the effects of R&D activities in codetermined firms. First, Granero (2006)⁴ shows that co-determination could help a firm to increase market share, employment and innovation. Second, Kraft et. al. (2011)⁵ built on a work mixing theoretical and empirical analyses and concluded, by taking the number of patents as a benchmark, that results “do not support the view that co-determination slows down technological progress and reduces innovativity” (Kraft et al., 2011, p. 145). Third, Fanti et. al. (2018) find that the main conclusions of Kraft (1998) and Kraft et al. (2011) may not be robust to a more general setting with horizontal product differentiation. Finally, Fanti & Gori (2019) extend the study of co-determination to a price competition setting with network effects and Gori and Fanti (2022) introduce endogenous co-determination in a Cournot duopoly.

On the side of the empirical evidence, the results of the existing literature on the subject are controversial.⁶ Amongst a few, we recall here that Cable and FitzRoy (1980) find that co-determination positively affects labour productivity, FitzRoy & Kraft (1993) obtain no statistically significant evidence of productivity gains due to co-determination laws, Baums & Frick (1998) study how the behaviour of the German courts during the period 1974–1995 on co-determination issues affects the stock price developments, finding no statistically significant stock market response to court verdicts. More recently, Gorton & Schmid (2004) and FitzRoy & Kraft (2005) respectively pinpoint (1) the negative effect caused by co-determination on the market value of firms, and (2) the positive labour productivity effect of near-parity co-determination, whereas Kraft (2018) considers a model to study empirically the effects of extending co-determination rights on both productivity and bargaining power. He pinpoints no productivity disadvantages of codetermined firms. More generally, increasing co-determination rights appears to be neutral on the side of efficiency. However, it positively affects the bargaining power of labour and modifies the distribution of rents. To sum up, notwithstanding the empirics on co-determination is still a small field and there exist results of opposite signs, co-determination often worsens the performance of firms (productivity, market value, etc.). This is indeed coherent with the theoretical result of the Pareto-inefficiency of the SPNE following the co-determination strategy.

However, a recent authoritative study by Jäger et al. (2021) provides quasi-experimental evidence showing that (mandatory) co-determination has no effects on the wage structure, the labour share, revenues, employment and firm profitability. Then, given the main features of co-determination and the results of Jäger et al. (2021), it seems that co-determination rules lose their effectiveness as devices affecting the behaviour of the firms in the market, possibly being harmful by reducing the labour demand and driving up involuntary unemployment. We can therefore ask whether the theoretical model developed in the present article can capture the key features of co-determination and/or whether there exist significant objective differences between profit maximisation and co-determination. Indeed, one of the goals of this work is to continue giving theoretical support (since Kraft, 1998) to the topic of co-determination by considering firms with market power in a strategic context. In this sense, our contribution should be interpreted to provide a narrative in which co-determination rules are not mandatory, but voluntarily emerge as a device working exactly as the managerial delegation contracts in the models à la Vickers (1985), Fershtman & Judd (1987) and Sklivas (1987), VFJS, in turn, (1) stressing the conditions under which must be applied because it is convenient to firms becoming bargainers under co-determination instead of profit maximisers, and (2) solving the prisoner’s dilemma raised in Kraft (1998), in turn achieving mutually beneficial outcomes. The main difference between a profit-maximising firm and a codetermined firm in the strategic framework adopted here stands about the objective function in the market stage: in the former case, the firm alone chooses production (employment) by maximising profits; in the latter case, the firm chooses production (employment) together the employees’ representatives by maximising a weighted product between profits and the utility function of the firm’s union bargaining unit. From a strategic point of view, this represents a relevant difference, giving rise to an incentive to increase production and reduce profits by opening the route for the emergence of a prisoner’s dilemma. This dilemma can be solved because of the network consumption externalities bringing together Katz & Shapiro (1985) and Kraft (1998), KSK, in the same setting. The implicit assumption behind our model is that each firm can credibly commit to its corporate governance structure in the first stage by bargaining with workers’ representatives, and the co-determination rules are applied as a strategic device (exactly as in the case of managerial firms considering the VFJS modelling setting according to which a firm can credibly commit to its corporate governance structure by strategically hiring a manager in the first stage of a managerial decision game). Each firm, therefore, moves along its reaction function and every choice out of it (including sharing the monopoly output equally, with or without co-determination) does not represent an optimal response to the rival’s choice. Therefore, the commitment power of playing a strategy in a non-cooperative game should be credible (the best reply functions represent the loci of optimal responses), but any other choices out of best replies cannot credibly be implemented with commitment. Unlike the model à la VFJS, co-determination, which can be viewed being part of the agenda of a strategic firm, in a KSK setting can credibly be committed to achieving mutually beneficial outcomes. Some policy implications directly follow. Co-determination can emerge voluntarily in the market and consumers and firms can be better off under co-determination than under profit maximisation; however, the empirical evidence of voluntary co-determination, i.e., in countries in which co-determination is not imposed by law (US for example), is scant so that the fraction of firms with co-determination is negligible. Therefore, our results can be interpreted also in the direction that mandatory co-determination can become a Pareto superior policy from a societal perspective if markets are characterised by network externalities. The present article wants to give the theoretical base to apply this institution efficiently.

Choosing to play the co-determination strategy or the profit maximisation strategy in our non-cooperative game is the same as, for instance, choosing whether to hire a manager as in the VFJS literature, at the early stage of the game. Consequently, the game developed in this article resembles the managerial decision game in which each player credibly chooses to hire or not to hire a manager, and this choice is common knowledge and undeniable. This is a standard assumption of most multi-stage games in the industrial economics literature, e.g., the R&D investment, the managerial decision game, the mode of competition game (Cournot versus Bertrand) and the co-determination decision game. A player’s choice therefore (to play X or to play NX) is always reliable with full commitment. Thus, the choice to collude is not part of this non-cooperative game that indeed follows the structure of any game without binding contracts. To sum up, suppose that a firm can make only two types of binding contracts with their trade union bargaining units: the co-determination contract and no contract (i.e., the profit maximisation contract). Choosing the former implies that the firm will maximise an objective function including a weighted product between profits and its (decentralised) trade union utility, whatever action the competitor takes. Choosing the latter implies that the firm is committing to maximising profits irrespective of the action of the rival. Then, players in two-stage game first simultaneously commit themselves to a type of contract (stage 1) and compete on quantities in the market stage (stage 2), contingent on the chosen types of contracts. The co-determination contract strategy and the no contract strategy do not represent binding contracts for the players but are undeniable due to, e.g., the prohibitive costs of changing the type of contract.

Another pillar of modern economies is represented by network consumption externalities.⁷ These kinds of externalities are of increasing importance and there exists a burgeoning Industrial Organization literature pioneered by Katz & Shapiro (1985) which is growing rapidly. For instance, in an oligopoly context, Hoernig (2012), Bhattacharjee and Pal (2014), and Chirco & Scrimitore (2013) show that the standard results of the managerial delegation literature may change when markets deal with network goods, whereas Fanti and Buccella (2017, 2018) investigate whether and how the network effects may modify the common wisdom regarding the bargaining agenda (between unions and firms) and corporate social responsibility. More recently, Buccella et al. (2022) and Choi & Lim (2022) respectively extend the R&D investment decision game and the commitment decision game to a network industry with linear demand pinpointing the key role of the network strength in determining the SPNE.

Empirical evidence about network effects for industries located in countries with the institution of co-determination (e.g., Germany) also exists. For example, by focusing on the specific case of telecommunications,⁸ Doganoglu and Grzybowski (2007) account for network effects in the German mobile telecommunication market by estimating a system of demand functions for mobile subscribers in Germany (data on mobile subscriptions was collected from the Internet site run by the German regulator—RegTP) from January 1998 to June 2003. They found that network effects played a significant role in the diffusion of mobile services in Germany. More specifically, they conclude that, as a proxy that measures the intensity of the network effect, if the previous period’s total installed base increased by 1%, current period sales would surge on average by 0.69% (which is considered a strong network effect).⁹ Another example is represented by the work of Baraldi (2008) considering 30 OECD countries from 1989 to 2006 to specify and estimate a model of consumer demand for mobile telephone calls aimed at identifying the extent of network externalities. This work shows that also for countries such as Austria and Germany the network effect is significantly large (though smaller than that found by Doganoglu & Grzybowski, 2007), thus confirming that the competition analysis under co-determination in network industries (such as the telecommunications industry) should consider the extent and intensity of network effects.

Given this empirical background, different labour market institutions may affect the consumers’ expectations about the total sales of the (network) goods. Despite the possible theoretical and empirical relevance of positive consumption externalities on market outcomes, the issues related to network goods have been ignored in the literature on co-determined industries. This article aims to fill this gap by providing a theoretical analysis based on a strategic competitive framework with quantity-setting duopoly firms.

The article differentiates between exogenous and endogenous co-determination in a network Cournot duopoly. In the former case, results show that (exogenous) co-determination emerges as a Pareto-efficient SPNE. This, in turn, implies that network goods solve the prisoner’s dilemma raised in Kraft (1998) by letting the co-determination decision game move from a prisoner’s dilemma (there is a conflict between self-interest and mutual benefit of co-determination) to an anti-prisoner’s dilemma or deadlock (no conflict exists between self-interest and mutual benefit of co-determination). This holds in the cases of homogeneous and heterogeneous trade unions or bargaining strength. In the latter case (endogenous co-determination), results extend Gori & Fanti (2022) to a network industry by enriching the spectrum of Nash equilibria that can correspondingly emerge, including the anti-prisoner’s dilemma that cannot be observed in the non-network case.

The rest of the article proceeds as follows. Section 2 builds on a non-cooperative co-determination decision game (exogenous co-determination with homogeneous trade unions or bargaining strength) played in a quantity-setting network duopoly with homogeneous goods. Section 3 extends the model to horizontal product differentiation. Section 4 introduces endogenous co-determination in a network industry by extending Gori and Fanti (2022). Section 5 studies the co-determination decision game (exogenous co-determination) by assuming heterogeneous trade unions. Section 6 concentrates on welfare analysis. Section 7 outlines the main conclusions. The Appendix provides some analytical details.

2 A quantity-setting duopoly with network externalities: the basic set-up

This section aims at studying a Cournot duopoly considering a non-cooperative two-stage co-determination decision game in which in the first, decision-making stage each owner must choose to be either a codetermined or profit maximisation firm (exogenous co-determination with homogeneous bargaining strength), whereas in the second stage, they compete à la Cournot in the product market.

The economy consists of two types of agents, firms and consumers. It is bi-sectorial with a competitive industry producing the numeraire goods $m$ and a duopolistic industry in which firm $i$ and firm $j$ produce horizontally differentiated products of variety $i$ and variety $j$, respectively $\left( {i,j = \{ 1,2\} ,\;i \ne j} \right)$.

Different from the traditional industrial organisation literature (that assumes that a demand for a good is independent of one another), we assume that there are network externalities in consumption. This implies that one person’s demand also depends on the demand of other consumers. The mechanism of network effects considered in the present article work follows the tradition initiated by Katz & Shapiro (1985) so that the surplus that a firm’s client obtains increases (resp. reduces) with the number of other clients of this firm if the network consumption externality is positive (resp. negative).

The issue of network externalities on the side of consumers has become relevant especially due to the tremendous growth of internet-related activities (e.g., online games, telephone and so on). We pinpoint that in what follows we will use the terms “network externality”, “consumption externality” or “network consumption externality” interchangeably. In the words of Katz and Shapiro (1985, p. 424): “… the utility that a given user derives from the good depends upon the number of other users who are in the same “network” as is he or she. The scope of the network that gives rise to the consumption externalities will vary across markets…”.

The model used in the present article directly departs from Katz and Shapiro (1985), which has been the base for more recent contributions on the subject, such as Hoernig (2012), Chirco & Scrimitore (2013), Song & Wang (2017), Buccella et al. (2022) and Choi & Lim (2022), who consider the representative consumer approach with quadratic utility and linear demand in markets with network goods. Following the model proposed by Katz and Shapiro (1985) in the main text of their article (in which firms do not commit to an announced output level), the utility function of consumers (and then their marginal willingness to pay) depends on expected network sizes (network $i$ and network $j$, $i,j = \{ 1,2\}$, $i \ne j$). Consumers choose to buy the product of network $i$ or product of network $j$ before the actual network sizes are known to them. This implies that consumers first form the expectations about the size of networks and then the duopolistic firm $i$ and firm $j$ play a non-cooperative co-determination decision game based on Cournot rivalry. This is done by considering consumers’ expectations as given. Consumers are rational and their expectations are realised in equilibrium.

2.1 Consumption side

There exist identical consumers whose preferences are characterised by the utility function $V = U + m$ (Amir et al., 2017; Dixit, 1979; Singh & Vives, 1984), which is linear in the numeraire good $m$ and

$$ U = q_{i} + q_{j} - \frac{1}{2}\left( {q_{i}^{2} + q_{j}^{2} + 2dq_{i} q_{j} } \right) + n\left[ {q_{i} (y_{i} + dy_{j} ) + q_{j} (y_{j} + dy_{i} )} \right] - \frac{n}{2}\left( {y_{i}^{2} + y_{j}^{2} + 2dy_{i} y_{j} } \right). $$

(1)

where $q_{i}$ and $q_{j}$ the quantities respectively produced by firm $i$ and firm $j$ and $y_{i}$ (resp. $y_{j}$) denotes consumers’ expectations about the network of firm $i$’s (resp. $j$’s) equilibrium total sales, capturing the consumption externality for the size of network $i$ (resp. $j$). In addition, (1) horizontal product differentiation is weighted by parameter $d$. When $d = 1$ (resp. $d \to - 1$) products are perfect substitutes (resp. tend to be perfect complements), whereas $d > 0$ (resp. $d < 0$) reflects the case of imperfect substitutability (resp. imperfect complementarity). The case $d = 0$ implies that each firm behaves as if it were a monopolist for its product; (2) the strength of the network effect is denoted by $- 1 \le n < 1$. The model boils down to the standard non-network case if $n = 0$. When $n > 0$ (resp. $n < 0$) there exists a positive (resp. negative) consumption externality representing the well-known bandwagon (resp. snob) effect generated by the network, for which there exists a positive (resp. negative) feedback loop if the network size increases. We note that the last addendum in (1) is a specific symmetric function of expectations such that for each given consumption vector $(q_{1} ,q_{2} )$ utility is the highest if expectations are correct. The terms $y_{i} + dy_{j}$ and $y_{j} + dy_{i}$ represent the expected effective network size of firm $i$’s consumers and firm $j$’s consumers, respectively.¹⁰

The maximisation of $V$ for $q_{i}$ and $q_{j}$ follows the representative consumer approach with quadratic utility developed by Dixit (1979) and used by Singh & Vives (1984) for product differentiation and then extended to network externalities with rational expectations of consumers by Hoernig (2012), Chirco & Scrimitore (2013), Song & Wang (2017), Buccella et al. (2022), Choi & Lim (2022) and several other articles.¹¹ We pinpoint that Amir et. al. (2017) revisit the microeconomic foundation of the linear demand emerging from quasi-linear preferences with no networks, showing (Remark 13) that the case treated by Singh and Vives (1984) with $- 1 < d < 1$ is correct, but the microeconomic foundation changes slightly when $d = 1$. Then, our model follows and applies the results by Amir et al. (2017, Assumption A.3, Lemma 4, Remark 5 and Remark 6, p. 649) and Choné & Linnemer (2020). The only difference with Amir et al. (2017) is to add a constant to the market size quantitatively changing the threshold income required to have well-defined and invertible linear demands (see Eqs. (2a) and (2b) below), but the qualitative results are the same.

The representative consumer maximises $V = U + m$ subject to the budget constraint $p_{i} q_{i} + p_{j} q_{j} + m = R$, where $p_{i}$ and $p_{j}$ are the marginal willingness to pay for the product of network $i$ and network $j$, respectively, and $R$ is the consumer’s exogenous nominal income. This income is assumed to be high enough to avoid income effects on the demand of $q_{i}$ and $q_{j}$ (i.e., the goods entering non-linearly in $V$). In this regard, the utility function $V$ is quasi-linear in the numeraire good $m$ so that all the related properties about the demand of $m$ and that of $q_{i}$ and $q_{j}$ hold (Amir et al., 2017; Choné & Linnemer, 2020) for any $- 1 < d < 1$.

From (1), the demand for products of both networks is positive (and linear) only when the nominal income is large enough to allow $m > 0$. By avoiding explicitly considering the case of perfect complements $\left( {d = - 1} \right)$, for which the income needed to have positive demands converges to infinity, an interior solution to the consumer problem exists for any positive, finite value of the nominal income $R$ (Amir et al., 2017).

Specifically, the utility function in (1) is a modified version of the utility used by Singh & Vives (1984) allowing to study network effects in the case of homogeneous products $\left( {d = 1} \right)$. This is because the formulation popularised by Hoernig (2012) and used by other scholars in related works is not well defined for the case of perfect substitutability (as is also pointed out by Song & Wang, 2017, Footnote 3, p. 24).

Following Amir et al. (2017) and Buccella et al. (2022), the maximisation of the surplus by the representative consumer gives the linear inverse demands for products of networks $i$ and $j$, which are different though consumers are homogeneous in their evaluation of the network effects, i.e.:

$$ p_{i} = 1 - q_{i} - dq_{j} + n(y_{i} + dy_{j} ). $$

(2a)

and

$$ p_{j} = 1 - q_{j} - dq_{i} + n(y_{j} + dy_{i} ). $$

(2b)

From (2a) and (2b), it is easy to see that network externalities enter additively in the demand function. If the network externality is positive (resp. negative), an increase in the positive (resp. negative) feedback loop of the network effect causes an outward (resp. inward) shift in the demand curve. This externality, therefore, acts as a device that increases (resp. reduces) the market size.

Given the results of the existing literature on co-determination in a strategic competitive Cournot duopoly (Fanti et al., 2018; Kraft, 1998), it would be instructive to begin by considering the effects of network externalities under perfect substitutability $\left( {d = 1} \right)$, studying later the case of product differentiation (Sect. 3). This allows us to bring to light the strict relationship between network externalities and co-determination in determining the market outcome as well as to stress similarities and differences between Kraft (1998) and the present work.

By assuming homogeneous products $\left( {d = 1} \right)$ the inverse demand boils down to:

$$ p_{i} = p_{j} = p = 1 - Q + n(y_{i} + y_{j} ), $$

(3)

where $Q = q_{i} + q_{j}$. To get the expression in (3), the maximisation of the utility function should follow the analysis detailed in Amir et al. (2017, Section 4.2, p. 655), according to which one cannot solve for separate demand functions for $q_{i}$ and $q_{j}$ as they are perfect substitutes. Then, it is sufficient to maximise the consumer surplus for $Q$ and get the expression in (3).

2.2 Production side

The technology used by firm $i$ to produce goods of network $i$ in the duopolistic sector is $q_{i} = L_{i}$, where $L_{i}$ is the labour force (employment). Each firm faces a constant marginal (and average) cost $0 \le w < 1$ representing the wage per unit of labour set in centralised or industry-wide bargaining, which is taken as given by firm $i$ irrespective of profit maximisation or co-determination. Firm $i$’s profits are then usually expressed as $\Pi_{i} = (p - w)q_{i}$.

By following Kraft (1998, 2001), Kraft et al. (2011) and Fanti et al. (2018), we assume that firms are either subject to the rules of co-determination (B) or they are profit maximisers (PM).

Under B, firm $i$’s representatives bargain with the employee representatives over employment but not over wages on the supervisory board (the wage is determined elsewhere). In the words of Kraft et. al. (2011, p. 152): “The starting point […] is the assumption that wages are determined by an exogenous process at industry level, which is consistent with the German institutional setting. Exogenous means not influenced at the individual firm level, as is the case if wages are negotiated at the economy-wide level.”

Therefore, firm $i$ engages in decentralised bargaining with its union-bargaining unit. The bargaining function will be determined and specified later as the product (in the case of asymmetric bargaining power of the two parties) between firm $i$’s profits ($\Pi_{i}$) and the corresponding union $i$’s utility function ($Z_{i}$, which will be defined in Eq. (5)). The bargaining effort over employment will be solved by considering production ($q_{i}$) as the control variable. Employment is eventually determined through the production function.

Under PM, the objective of firm $i$ is to maximise $\Pi_{i}$ for $q_{i}$.

By using the inverse demand in (3), the profits of firm $i$ become:

$$ \Pi_{i} = \left[ {1 - q_{i} - q_{j} + n(y_{i} + y_{j} ) - w} \right]q_{i} . $$

(4)

Each firm-specific union aims at maximising its utility $Z_{i} = (w - w^\circ )L_{i}$, which is increasing in $w$ and $L_{i}$, by choosing employment $L_{i}$, where $w^\circ$ is the reservation (or competitive) wage. Without loss of generality, we set $w^\circ = 0$ henceforth (Kraft, 1998, 2001, 2006). This is also because there is no role for the competitive wage as each firm will pay $w$ irrespective of whether it will act according to strategy B or strategy PM. The utility function $Z_{i}$ resembles the Stone-Geary utility representing rent maximisation where $L_{i}$ is the control variable under co-determination. As $L_{i} = q_{i}$, $Z_{i}$ can be expressed as the wage bill, which is maximised for $q_{i}$:

$$ Z_{i} = wq_{i} . $$

(5)

By assuming the existence of one and only one type of trade union bargaining homogeneously with each firm at a decentralised level over employment, the negotiation process is represented by the Nash bargaining solution between firm $i$ and its union bargaining unit over employment and it is given by ${\rm N}_{i} = \Pi_{i}^{\beta } Z_{i}^{1 - \beta }$. Therefore, by using (4) and (5) the generalised Nash bargaining takes the form¹²:

$$ \mathop {\max }\limits_{{\{ q_{i} \} }} \left\{ [{1 - q_{i} - q_{j} + n(y_{i} + y_{j} ) - w]q_{i} } \right\}^{\beta } (wq_{i} )^{1 - \beta } , $$

(6)

where $0 < \beta \le 1$ is the relative bargaining power of firm $i$, and $0 \le 1 - \beta < 1$ is the relative bargaining power of the decentralised trade union bargaining unit $i$. In this sense, the bargaining effort in (6) is exerted with asymmetric bargaining power between the two parties.

We now clarify the ideas of homogeneous and heterogeneous bargaining decentralised trade unions, and exogenous and endogenous co-determination.

If the bargaining effort is exerted by firms and unions having homogeneous or identical bargaining power, i.e., $1 - \beta_{i} = 1 - \beta_{j} = 1 - \beta$ so that $\beta_{i} = \beta_{j} = \beta$, and further $\beta$ is taken exogenously by each firm, then we refer to the case of exogenous homogeneous co-determination (i.e., there exist trade unions that bargain with the same bargaining strength). This case is outlined in Sect. 2 (homogeneous products) and Sect. 3 (heterogeneous products). The idea of exogenous homogeneous co-determination directly follows Kraft (1998) and the related literature emerging over the course of the years.

If the bargaining effort is exerted by firms and unions having heterogeneous or different bargaining power, i.e., $1 - \beta_{i} \ne 1 - \beta_{j}$ so that $\beta_{i} \ne \beta_{j}$, and further $\beta_{i}$ and $\beta_{j}$ are taken exogenously by firm $i$ and firm $j$, respectively, then we refer to the case of exogenous heterogeneous co-determination (i.e., there exist trade unions that bargain with a different bargaining strength). This case is outlined in Sect. 5. The idea of exogenous heterogeneous co-determination directly follows Fanti & Gori (2019), which however has been developed in a price-setting duopoly context.

If the bargaining effort is heterogeneous and $\beta_{i}$ (resp. $\beta_{j}$) is chosen endogenously by firm $i$ (resp. firm $j$) to maximise profits, then we refer to the case of endogenous co-determination. This case is outlined in Sect. 4. The idea of endogenous co-determination directly follows Gori and Fanti (2022).

By following Kraft (1998) and the literature cited therein, the threat points of the Nash bargaining solution have been set to zero (see also Fershtman, 1985; Bughin, 1995; Booth & Chatterji, 1995). Assuming a threat point different from zero on the side of the unions does not allow closed-form expressions for the control variable. The threat point on the firm side can safely be considered the zero-profit condition.

The firm-union bargaining problem adopted here strictly resembles Kraft (1998) and the subsequent theoretical literature on co-determination (Fanti & Gori, 2019; Fanti et al., 2018; Gori & Fanti, 2022; Kraft, 2001, 2006; Kraft et al., 2011). This literature clarifies that under co-determination the control variable of the two bargaining parties is employment, which can be determined through the choices over production and transformed into labour through the production function. Co-determination is an institution for which every firm and its decentralised union choose employment (i.e., production) by taking the wage as given. The problem stated in (6) is mathematically equivalent to the well-known Nash bargaining solution between firms and unions following the rules of the right-to-manage model, in which the control variable is the wage, or the efficient bargaining model, in which the control variables are wage and employment. This is clarified, e.g., in the analysis of the model of collective bargaining in Booth and Chatterji (1995), Kraft (1998, 2001), Booth (2010) and Cahuc et. al. (2014). More in general, about the use of the asymmetric Nash bargaining solution, we adopt the words of Kraft (2001, p. 546): “The asymmetric Nash solution is more general than the symmetric one as the realistic case of unequal bargaining power is included. On the question of whether the Nash-bargaining solution is appropriate if cooperation is not very probable, Binmore et al. (1986) proved that the simple Nash solution may still be used as the equilibrium outcome of a sequence of non-cooperative moves. Thus, the Nash-bargaining solution has a more general relevance than one might expect at first sight.” On this issue, one can refer to the general analyses of Binmore et al. (1986), Anbarci & Sun (2013) and the references cited therein.

The timing of the events of this two-stage non-cooperative game is the following. At the contract stage (stage 1), each owner must choose to be either a codetermined or profit maximisation firm in a network industry. At the market stage (stage 2), firms either choose output in the case of profit maximisation or bargain it together with its union bargaining unit in the case of co-determination.

As is usual from Katz & Shapiro (1985) and Hoernig (2012), we assume that consumers have rational expectations. Therefore, at stage 2 we impose that $q_{1} = y_{1}$ and $q_{2} = y_{2}$ hold (i.e., expectations are realised) in equilibrium. We proceed with the analysis according to the standard backward induction logic.

2.3 The symmetric subgame in which both firms play B

First, we consider that both firms are codetermined $\left( {\beta < 1} \right)$ so that the output of firm $i$ at stage 2 is chosen by firms and employees’ representatives by maximising Eq. (6) for $q_{i}$. Therefore, the reaction function of the $i$th player is given by:

$$ \frac{{\partial {\rm N}_{i} }}{{\partial q_{i} }} = 0 \Leftrightarrow q_{i} \left( {q_{j} ,y_{i} ,y_{j} } \right) = \frac{{1 - w - q_{j} + n\left( {y_{i} + y_{j} } \right)}}{1 + \beta }, $$

(7)

From (7), an increase in the strength of the network externality shifts the reaction function upwards and then causes an increase in the quantity produced by the firm (the reaction functions are negatively sloped, and goods are strategic substitutes). By using (7) together with the corresponding counterpart of player $j$ and knowing that $y_{i} = q_{i}$ and $y_{j} = q_{j}$, $i,j = \{ 1,2\}$ $\left( {i \ne j} \right)$, we get the equilibrium outcome of firm $i$, that is:

$$ q_{i}^{B/B} = \frac{1 - w}{{2(1 - n) + \beta }}. $$

(8)

Therefore, equilibrium profits are:

$$ \Pi_{i}^{B/B} = \frac{{\beta (1 - w)^{2} }}{{[2(1 - n) + \beta ]^{2} }}. $$

(9)

Straightforward algebra from (8) and (9) shows that an increase in $n$ causes a monotonic increase in the quantity produced by both firms and their profits.

2.4 The symmetric subgame in which both firms play PM

If both firms are profit maximisers $\left( {\beta = 1} \right)$, the equilibrium output and profit of firm $i$ (by imposing the rational expectations conditions on the consumer side) are the following:

$$ q_{i}^{PM/PM} = \frac{1 - w}{{3 - 2n}}, $$

(10)

and

$$ \Pi_{i}^{PM/PM} = \frac{{(1 - w)^{2} }}{{(3 - 2n)^{2} }}. $$

(11)

2.5 The asymmetric subgame in which one firm plays B and the rival PM

Let us now consider the asymmetric case in which firm 1 is codetermined and firm 2 is profit maximiser. At stage 2, firm 1 and its corresponding union bargain unit are involved in bargaining aimed at maximising ${\rm N}_{1}$ for $q_{1}$, whereas firm 2 maximises $\Pi_{2}$ for $q_{2}$. The reaction functions are given by:

$$ \frac{{\partial {\rm N}_{1} }}{{\partial q_{1} }} = 0 \Leftrightarrow q_{1} \left( {q_{2} ,y_{1} ,y_{2} } \right) = \frac{{1 - w - q_{2} + n\left( {y_{1} + y_{2} } \right)}}{1 + \beta }, $$

(12)

and

$$ \frac{{\partial \Pi_{2} }}{{\partial q_{2} }} = 0 \Leftrightarrow q_{2} \left( {q_{1} ,y_{1} ,y_{2} } \right) = \frac{{1 - w - q_{1} + n\left( {y_{1} + y_{2} } \right)}}{2}. $$

(13)

By imposing the conditions $y_{1} = q_{1}$ and $y_{2} = q_{2}$, we easily get:

$$ q_{1}^{B/PM} = \frac{1 - w}{{1 - n + \beta (2 - n)}}, $$

(14)

and

$$ q_{2}^{B/PM} = \frac{\beta (1 - w)}{{1 - n + \beta (2 - n)}}. $$

(15)

Therefore, the equilibrium profits of firm 1 and firm 2 are the following:

$$ \Pi_{1}^{B/PM} = \frac{{\beta (1 - w)^{2} }}{{\left[ {1 - n + \beta (2 - n)} \right]^{2} }}, $$

(16)

and

$$ \Pi_{2}^{B/PM} = \frac{{\beta^{2} (1 - w)^{2} }}{{\left[ {1 - n + \beta (2 - n)} \right]^{2} }}. $$

(17)

2.6 Nash equilibria and discussion

The equilibrium outcomes of the game are summarised in Table 1 (quantities) and Table 2 (profits) according to the strategies available to each player.¹³

Table 1 Equilibrium values of quantities under B and PM (homogeneous products)

Table 2 Payoff matrix (profits) under B and PM (homogeneous products)

We recall that the consumers’ surplus is an increasing function of production. As production is equal to employment, the union’s utility is also an increasing function of the production. Therefore, a simple comparison of the values reported in Table 1 leads to Lemma 1.

Lemma 1

The consumers’ surplus and the workers’ utility are higher when both firms are codetermined than when they are profit maximisers.

Proof

See the Appendix.

Let $n_{a} (\beta ): = \frac{1 - 2\beta - \sqrt \beta }{{1 - \beta }}$, where $0 \le n_{a} (\beta ) < 1$ for any $0 < \beta \le 0.25$ and $n_{a} (\beta ) < 0$ for any $0.25 < \beta \le 1$, be a threshold value of $n$ such that $\Delta_{a} = \Pi_{i}^{B/PM} - \Pi_{i}^{PM/PM} = 0$ for any $i,j = \{ 1,2\} ,\;i \ne j$. This profit differential allows us to check whether firm $i$ has an incentive to deviate from PM to B when the rival is playing PM. Let $n_{c} (\beta ): = 1 - \frac{1}{2}\sqrt \beta$, where $1/2 \le n_{c} (\beta ) < 1$ for any $0 < \beta \le 1$, be a threshold value of $n$ such that $\Delta_{c} = \Pi_{i}^{PM/PM} - \Pi_{i}^{B/B} = 0$ for any $i,j = \{ 1,2\} ,\;i \ne j$. This profit differential allows us to check whether B is dominated by PM for each firm $i$. The shape of $n_{a} (\beta )$ and $n_{c} (\beta )$ is depicted in Fig. 1 in the parameter space $(\beta ,n)$. We note that the threshold $n_{b} (\beta )$ such that $\Delta_{b} = \Pi_{i}^{PM/B} - \Pi_{i}^{B/B} = 0$ for any $i,j = \{ 1,2\} ,\;i \ne j$ is larger than one for any $0 < \beta \le 1$ and then it is not economically meaningful in the parameter space $(\beta ,n)$ when the network-co-determination game is played with homogeneous products. It will become a meaningful threshold in the case of product differentiation as we will see later in this article. This profit differential allows us to check whether firm $i$ has an incentive to deviate from B to PM when the rival is playing B. Then, Lemma 2 and Proposition 1 clarify the outcomes of the game at stage 1, where each owner must choose to be either a codetermined or profit-maximising firm. In this sense, the main aim of the present article—resembling the strategic use of managerial delegation—is to study the conditions for which co-determination can be used as a strategic device by neoclassical firms in network instead of non-network duopolistic industries.

Fig. 1

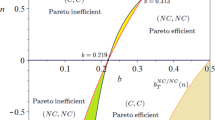
Exogenous (homogeneous) co-determination and network externalities in a quantity-setting duopoly with homogeneous products. Profit differentials in $(\beta ,n)$ space. The solid (resp. dotted) line represents the threshold value $n_{a} (\beta )$ (resp. $n_{c} (\beta )$) such that $\Delta_{a} = 0$ (resp. $\Delta_{c} = 0$). The strength of the network externality allows solving the prisoner’s dilemma of Kraft (1998), which holds only in the parametric space of Pareto inefficiency. The area bounded by the red rectangle represents values of the union bargaining power (ranging from 0.5 to almost 0.7) that are consistent with 1) the Works Constitution Act (Betriebsverfassungsgesetz) issued in 1952 (with small changes since 2004) that introduced 1/3 representation of employees on supervisory boards in all industries with firms employing more than 500 workers, and 2) the Co-determination Act (Mitbestimmungsgesetz) issued in 1976 that introduced 1/2 representation on supervisory boards in all industries with firms employing more than 2000 workers

Lemma 2

If $n < n_{c} (\beta )$ then $\Pi_{i}^{PM/PM} > \Pi_{i}^{B/B}$. If $n > n_{c} (\beta )$ then $\Pi_{i}^{B/B} > \Pi_{i}^{PM/PM}$.

Proof

See the Appendix.

Proposition 1

(1) If $- 1 \le n < n_{a} (\beta )$ then there exist two pure-strategy Nash equilibria given by (B,B) and (PM,PM), and PM payoff dominates B (coordination game). (2) If $n_{a} (\beta ) < n < n_{c} (\beta )$ then (B,B) is the unique Pareto-inefficient¹⁴SPNE (prisoner’s dilemma). (3) If $n_{c} (\beta ) < n < 1$ then (B,B) is the unique Pareto-efficient SPNE (deadlock).

Proof

See the Appendix.

The main result of Proposition 1 is represented by the solution to the prisoner’s dilemma of Kraft (1998). When the strength of the network effect is sufficiently large, (B,B) becomes the unique Pareto-efficient SPNE. In general, the proposition shows the existence of a wide spectrum of equilibrium outcomes in a Kraft-like game played by quantity-setting duopoly firms in a network industry with negative and positive consumption externalities rather than in a standard Cournot (non-network) setting.

We now discuss the mechanisms through which the network effect works in this model. We restrict the discussion to changes in $n$ as the analysis of the mechanics of what happens when $\beta$ varies has been already pointed out in Fanti et al. (2018).

Let us begin the discussion with the case of a non-network industry ($n = 0$). As is clear by looking at the $\beta$-axis in Fig. 1, inthis case our model boils down to Kraft (1998). This means that (B,B) is the unique Pareto-inefficient Nash equilibrium of the game for any $\beta > 0.25$, implying that B is the dominant strategy, and there exist two pure-strategy Nash equilibria when $\beta < 0.25$. We want to stress that in contrast with this, Kraft (1998) stated that “for values of $\beta < 0.25$ profit-maximization is the dominant strategy.” (p. 199). Indeed, there do not exist dominant strategies when $\beta < 0.25$ in a market for homogeneous products (see Fanti et al., 2018). Negative values of $n$ do not modify the qualitative outcomes of Kraft (1998).

Let us now turn to the case of positive values of $n$. We recall that $n$ represents the strength of the network externality on the consumers’ side. Therefore, ceteris paribus, larger values of $n$ cause an increase in the quantity produced by the firms irrespective of whether firms are playing B or PM. This causes an outward shift in the market demand, which in turn contributes to an increase in the market price.¹⁵ Then, an increase in $n$ causes a twofold effect on the profits of each firm. A positive direct effect through the augmented production. A positive indirect effect through the increase in the market price. Both these effects cause an increase in firms’ profits. Therefore, it is important to understand the relative strength of these two effects under PM and B.

As the B firm produces more than the PM firm, the effect of an increase in $n$ on the market demand is to let the price increase more under B rather than under PM. This implies that the outward shift in the market demand in a network-codetermined industry is larger than the outward shift in the market demand in a network profit-maximising industry, i.e., the network effect strengthens the co-determination effect on the production side.

For any given level of bargaining power, $\beta$, players do not have dominant strategies in a non-network industry $\left( {n = 0} \right)$ or in a network industry where the strength of the network effect is sufficiently small $\left( {n < n_{a} (\beta )} \right)$. In this case, each player has the incentive to play the same strategy as the rival (coordination game). As far as the network externality becomes stronger and the market size increases, a codetermined firm increases profits more than its profit-maximising rival. When $n$ belongs to intermediate values $\left( {n < n_{c} (\beta )} \right)$, players have a joint incentive to become profit maximisers, but no one has a unilateral incentive to deviate from co-determination. This is because the codetermined firm greatly increases its profits in the asymmetric subgame. This, in turn, implies that B becomes a dominant strategy, but the result of the game is still a prisoner’s dilemma (Kraft, 1998). However, larger values of $n$ $\left( {n > n_{c} (\beta )} \right)$ allow each player to lose the incentive to be a profit maximiser due to a further increase in profits under B caused by a much stronger consumption externality. This is illustrated in Fig. 1 and clarified in Tables 3, 4, 5, representing payoff matrices (profits) built on by taking $w = 0$, the same level of $\beta$ (0.2) and three different values of $n$ (0.05, 0.35 and 0.8). This is an example of how the network externality can solve the prisoner’s dilemma raised in Kraft (1998) by letting the sub-game perfect Nash equilibrium (B,B) be Pareto-efficient. Of course, if one takes smaller values of the union’s bargaining power in line with the co-determination rules, i.e. values of $\beta$ ranging from 0.5 to 0.6667 (Gorton & Schmid, 2004; Kraft, 1998), as shown in the region bounded by the red lines in Fig. 1, the network-co-determination game has only two possible outcomes where (B,B) emerges as the unique SPNE, one is a prisoner’s dilemma (small values of $n$) and the other is an anti-prisoner’s dilemma or deadlock (large values of $n$).

Table 3 Payoff matrix (profits) under B and PM when $\beta = 0.2$ and $n = 0.05$

Table 4 Payoff matrix (profits) under B and PM when $\beta = 0.2$ and $n = 0.35$

Table 5 Payoff matrix (profits) under B and PM when $\beta = 0.2$ and $n = 0.8$

When no dominant strategies exist in this game, there are multiple Nash equilibria in pure strategies (this holds when the bargaining power of the union is sufficiently high, and the strength of the consumption externality is sufficiently small or null), as also Kraft (1998) pinpointed. This implies that each firm does not have the incentive to deviate from PM when the rival plays PM (indeed, a reduction either in $\beta$ or $n$ reduces profits) and the game from a prisoner’s dilemma becomes a coordination game. To solve the problem of equilibrium selection, we consider that a Nash equilibrium in mixed strategies can be obtained by defining probabilities $x_{1}$ and $1 - x_{1}$ (resp. $x_{2}$ and $1 - x_{2}$) that firm 1 (resp. firm 2) plays either B or PM. The unique mixed-strategy Nash equilibrium is the following:

$$ \begin{aligned} x_{1} = x_{2} = x_{*}^{B/PM} & = \frac{{\Pi_{i}^{B/PM} - \Pi_{i}^{PM/PM} }}{{\left( {\Pi_{i}^{B/PM} - \Pi_{i}^{PM/PM} } \right) + \left( {\Pi_{i}^{PM/B} - \Pi_{i}^{B/B} } \right)}} \\ & = \frac{{\left[ {\beta + 2(1 - n)} \right]^{2} \left[ { - (1 - \beta )n^{2} + 2n(1 - 2\beta ) + 4\beta - 1} \right]}}{{(1 - n)(1 - \beta )\left[ {4(1 + \beta )n^{2} (n - 3) + 3( - \beta^{2} + 3\beta + 4)n + 5\beta^{2} - \beta - 4} \right]}}. \\ \end{aligned} $$

(18)

From (18) it is easy to check that $x_{*}^{B/PM} > 0$ only when $0 \le n < n_{a} (\beta )$ and it is a decreasing function of $\beta$. This probability vanishes when $n = n_{a} (\beta )$ and approaches $1$ when $n_{a} (\beta ) \to 1$, that is when $\beta \to 0$. This is in line with the results summarised in Proposition 1. Equation (18) represents the mixed-strategy Nash equilibrium of the game. The rule that comes from (18) is the following: each firm will choose to play B (resp. PM) as a pure strategy if the rival plays B (resp. PM) with a probability $x > x_{*}^{B/PM}$ (resp. $x < x_{*}^{B/PM}$). The lower $\beta$, the higher the probability of playing PM as a pure strategy. By using the Pareto dominance criterion for the parameter configuration $\beta - n$ represented by the areas where there is a multiplicity of equilibria in pure strategies in Fig. 1,¹⁶ we may conclude that in a network industry with co-determination (PM,PM) Pareto dominates (B,B).

The analysis above allows writing down the following results on the effects of a positive network consumption externality in a codetermined duopoly with homogeneous products.

Result 1

The strength of the network effect is sufficiently small $\left( {n < 1/2} \right)$. The Nash equilibrium (B,B) cannot be Pareto-efficient. An increase in $n$ promotes the emergence of (B,B) as the unique Pareto-inefficient SPNE, as it reduces the parameter space $(\beta ,n)$ with multiplicity of equilibria in pure strategies, where PM is the payoff dominant strategy.

Result 2

The strength of the network effect is sufficiently large ($n > 1/2$). An increase in $n$ promotes the emergence of (B,B) as the unique Pareto-efficient SPNE (deadlock). This holds when $n > n_{c} (\beta )$.

Result 3

When (B,B) is the Pareto-efficient SPNE of the network-co-determination game $\left( {n > n_{c} (\beta )} \right)$, it also represents a Pareto-superior outcome for society. This is because firms (Result 2), consumers and workers (Lemma 1) are better off than in the profit-maximising scenario.

The economic intuition is the following: playing the co-determination strategy has the same strategic effect as the managerial delegation device, i.e., making a credible commitment to a higher output level. As the game is played in strategic substitutes (Cournot), the rival would reduce its market share and profits. Therefore, each rational firm has the interest to play the co-determination contract. However, the rival also chooses the same strategy and then the total quantity produced in the market is higher than if the firms had chosen to be profit maximisers. This, in turn, implies that the price and profits at the SPNE are lower than under the profit maximisation contract. This is the “classical” prisoner's dilemma studied by Kraft (1998) and Fanti et al. (2018). However, in network markets, the increase in quantity due to the consumption externality has a positive effect on the price consumers are willing to pay (network effect). If this effect is sufficiently high, the equilibrium price remains high enough to increase profits even when firms are bargainers under co-determination and the quantities produced are higher than under the profit maximisation contract. This effect indeed allows solving the prisoner’s dilemma.

3 Product differentiation (exogenous co-determination with homogeneous bargaining strength)

This section extends the results of Sect. 2 to the case of horizontal product differentiation $\left( { - 1 < d < 1} \right)$. Therefore, the inverse market demand for product of variety $i$ is expressed by Eqs. (2a, 2b). Tables 6 and 7 summarise the equilibrium values of quantity and profits in this case.

Table 6 Equilibrium values of quantities under B and PM (heterogeneous products)

Table 7 Payoff matrix (profits) under B and PM (heterogeneous products)

Let $n_{a} (\beta ,d)$, $n_{b} (\beta ,d)$ and $n_{c} (\beta ,d): = 1 - \frac{\sqrt \beta }{{1 + d}}$ be three threshold values of $n$ such that $\Delta_{a} = \Pi_{i}^{B/PM} - \Pi_{i}^{PM/PM} = 0$, $\Delta_{b} = \Pi_{i}^{PM/B} - \Pi_{i}^{B/B} = 0$ and $\Delta_{c} = \Pi_{i}^{PM/PM} - \Pi_{i}^{B/B} = 0$ for any $i,j = \{ 1,2\} ,\;i \ne j$, respectively. Then, Lemma 3 and Propositions 2 and 3 clarify the outcomes of the network-co-determination game at stage 1 in the case of heterogeneous products.

Lemma 3

If $n < n_{c} (\beta ,d)$ then $\Pi_{i}^{PM/PM} > \Pi_{i}^{B/B}$. If $n > n_{c} (\beta ,d)$ then $\Pi_{i}^{B/B} > \Pi_{i}^{PM/PM}$. This holds in both cases of product substitutability $\left( {0 < d < 1} \right)$ and product complementarity $- 1 < d < 0$.

Proposition 2

[Product substitutability ($0 < d < 1$)]. (1) If $- 1 < n < n_{b} (\beta ,d)$ then (PM,PM) is the unique Pareto-efficient SPNE (deadlock). (2) If $n_{b} (\beta ,d) < n < n_{a} (\beta ,d)$ then there exist two pure-strategy Nash equilibria given by (B,B) and (PM,PM), and PM payoff dominates B (coordination game). (3) If $n_{a} (\beta ,d) < n < n_{c} (\beta ,d)$ then (B,B) is the unique Pareto-inefficient SPNE (prisoner’s dilemma). (4) If $n_{c} (\beta ,d) < n < 1$ then (B,B) is the unique Pareto-efficient SPNE (deadlock).

Proposition 3

[Product complementarity ($- 1 < d < 0$)]. (1) If $- 1 < n < n_{c} (\beta ,d)$ then (PM,PM) is the unique Pareto-efficient SPNE (deadlock). (2) If $n_{c} (\beta ,d) < n < n_{b} (\beta ,d)$ then (PM,PM) is the unique Pareto-inefficient SPNE (prisoner’s dilemma). (3) If $n_{b} (\beta ,d) < n < n_{a} (\beta ,d)$ then there exist two pure-strategy Nash equilibria given by (B,B) and (PM,PM), and B payoff dominates PM (coordination game). (4) If $n_{a} (\beta ,d) < n < 1$ then (B,B) is the unique Pareto-efficient SPNE (deadlock).

The proof of Lemma 3 and Propositions 2 and 3 follows by applying the same line of reasoning used to show Lemma 2 and Proposition 1. Specifically, Proposition 2 shows that product differentiation allows (PM,PM) to become the unique SPNE, i.e., product differentiation works out against co-determination. This is in line with the results obtained by Fanti et al. (2018). However, the interaction between network externalities and product differentiation can bring to light an interesting (and counterintuitive) outcome. As an increase in both the degree of product differentiation and the strength of the network effect allows firms to increase their profits. Indeed, a reduction in $d$ (increase in the market power) in a network industry can make the profitability of a codetermined firm larger than that of a profit-maximising firm due to the outward shift in the market demand that B promotes compared to PM. In other words, product differentiation strengthens the working of the network effects as a device increasing profits under co-determination. This allows to let (B,B) become the Pareto-efficient outcome of the game for a wider range of values of $\beta$ and $n$.

Proposition 4 shows this result, which is strictly related to Propositions 2 and 3 and also illustrated in Fig. 2 by contrasting Panels (A) and (C), related to product substitutability, plotted for $d = 0.8$ and $d = 0.5$, respectively, and Panels (B) and (D), related to product complementarity, plotted for $d = - 0.8$ and $d = - 0.5$, respectively.

Fig. 2

Exogenous (homogeneous) co-determination and network externalities in a quantity-setting duopoly with heterogeneous products. Profit differentials in $(\beta ,n)$ space. The solid (resp. dashed) [resp. dotted] line represents the threshold value $n_{a} (\beta ,d)$ (resp. $n_{b} (\beta ,d)$) [resp. $n_{c} (\beta ,d)$] such that $\Delta_{a} = 0$ (resp. $\Delta_{b} = 0$) [resp. $\Delta_{c} = 0$]. A $d = 0.8$. B $d = - 0.8$. C $d = 0.5$. D $d = - 0.5$. Amongst other things, the figure shows that an increase in product differentiation ($d \downarrow$) increases the area in which the prisoner’s dilemma of Kraft (1998) is solved. The area bounded by the red rectangle represents values of the union bargaining power (ranging from 0.5 to almost 0.7) that are consistent with 1) the Works Constitution Act (Betriebsverfassungsgesetz) issued in 1952 (with small changes since 2004) that introduced 1/3 representation of employees on supervisory boards in all industries with firms employing more than 500 workers, and 2) the Co-determination Act (Mitbestimmungsgesetz) issued in 1976 that introduced 1/2 representation on supervisory boards in all industries with firms employing more than 2000 workers

Proposition 4

An increase in the degree of product differentiation $\left( {d \downarrow } \right)$ shifts downward the threshold curve $n_{c} (\beta ,d): = 1 - \frac{\sqrt \beta }{{1 + d}}$ in the space $(\beta ,n)$.

Proof

See the Appendix.

4 Endogenous co-determination and network externalities

The results obtained in the previous section allow having some policy recipes (mandatory co-determination versus voluntary co-determination) depending on the values of the main parameters of the problem. However, one of the drawbacks of the proposed approach (following the original idea of Kraft, 1998) is an exogenous degree of co-determination (i.e., the strength with which trade unions negotiate with firms). Unlike this, firms might decide to bargain not with any trade union, but with the trade union exerting a bargaining effort just allowing them to maximise profits. Indeed, in actual economies, there may be distinct types of union bargaining units that should not necessarily be appreciated by the firm as part of the bargaining process. To consider this heterogeneity, this section speculates in this direction and extends the model of exogenous co-determination by assuming that each firm is aware of the union’s attitude at the time of bargaining and then chooses to bargain with a union bargaining unit under co-determination only whether the firm’s bargaining power is the profit-maximising one. In doing this, we assume that the firm has the right to choose the composition of the board of representatives (including or not workers’ representatives) to make production decisions. This amounts to say that firms may choose the optimal union’s bargaining effort by choosing the optimal corresponding number of workers’ representatives to be co-opted within the supervisory board.

A rationale for this approach is that even focusing only on Europe, we can observe significantly different degrees of co-determination in different countries. Consequently, a natural motivation for endogenous co-determination is that, in an international context, firms can choose the country where they produce their brands and therefore hire workers, which in practice allows firms to choose the version of co-determination that arises from local labour relationships.

Let us first assume the existence of a continuum of firm-specific unions differentiated amongst them based on their relative attitude to bargaining $\left( {0 < 1 - \beta_{i} \le 1} \right)$. The research question, which is novel and follows Gori and Fanti (2022), arising in this context is the following. Do firms always prefer to bargain with a trade union with little bargaining power? The answer is not so obvious, and this section aims to show that the strategic interacting effects between the degree of product differentiation and the strength of the network effect may lead a quantity-setting duopoly firm to bargain with a union unit with a sizeable bargaining power, as this choice allows a firm to maximise profits.

The stages of the game change and become the following. At stage 1 (the contract stage), each owner must choose to be either a codetermined or profit-maximising firm. At stage 2 (the union-strength stage) the owner of each firm chooses to bargain with a union bargaining unit only whether its bargaining attitude is exactly the profit-maximising one. At stage 3 (the market stage), firms either choose the quantity in the output market in the case of profit maximisation or bargain it together with unions in the case of co-determination. The game follows the backward induction logic.

We now briefly discuss the key features of a network-co-determination non-cooperative (three-stage) game with quantity competing firms, complete information and endogenous co-determination. Of course, equilibrium outcomes are still those reported in Tables 6 and 7 (Sect. 3) if both firms are profit maximising (PM) so that $\beta_{1} = \beta_{2} = 1$. When both firms are codetermined (B), the Nash bargaining function ${\rm N}_{i} = \Pi_{i}^{\beta } Z_{i}^{1 - \beta }$ modifies to become ${\rm N}_{i} = \Pi_{i}^{{\beta_{i} }} Z_{i}^{{1 - \beta_{i} }}$. Then, firm 1 aims at bargaining with a type-1 union bargaining unit with an effort or bargaining strength $\beta_{1}$ to choose the quantity of product of variety 1. Correspondingly, firm 2 bargains with a type-2 union bargaining unit with an effort or bargaining strength $\beta_{2}$ to produce the quantity of product of variety 2. Then, there will be reaction functions depending on $\beta_{1}$ and $\beta_{2}$ that should be used to compute quantities of firm1 and firm 2, in turn, allowing to compute profits of firm $i$ $\left( {i,j = \{ 1,2\} ,\;i \ne j} \right)$ as follows:

$$ \overline{\Pi }_{i}^{B/B} = \frac{{\beta_{i} (1 - w)^{2} \left[ {(1 - n)(1 - d) + \beta_{j} } \right]^{2} }}{{\left[ {(1 - n)^{2} (1 - d^{2} ) + (1 - n)(\beta_{i} + \beta_{j} ) + \beta_{i} \beta_{j} } \right]^{2} }}. $$

(19)

As each firm chooses to bargain with its union bargaining unit if and only if there exists a profit-maximising bargaining power, we get the following reaction-bargaining-function of firm $i$, that is:

$$ \frac{{\partial \overline{\Pi }_{i}^{B/B} }}{{\partial \beta_{i} }} = 0 \Leftrightarrow \beta_{i} (\beta_{j} ) = \frac{{(1 - n)\left[ {(1 - n)(1 - d^{2} ) + \beta_{j} } \right]}}{{1 - n + \beta_{j} }}. $$

(20)

By using the corresponding counterpart of (20) for firm $j$, one can get the optimal value of firm $i$’s bargaining strength (outcomes are symmetric), that is

$$ \beta_{i}^{*(B/B)} = (1 - n)\sqrt {1 - d^{2} } ,\quad i,j = \{ 1,2\} . $$

(21)

The expression in (21) gives all the couples $(n,d)$ such that the owner maximises profits by choosing to be a bargainer under co-determination and augments the result of Gori and Fanti (2022). The expression in (21) is meaningful if and only if $\beta_{i}^{*(B/B)} \le 1$. This condition implies that

$$ n \ge n_{\beta } (d): = 1 - \frac{1}{{\sqrt {1 - d^{2} } }}, $$

(22)

should hold, otherwise, there would be no economically meaningful profit-maximising value of $\beta_{i}$. Equation (22) tells us that each firm would decide to be codetermined by choosing a profit-maximising bargaining effort if and only if the network externality is strong enough, otherwise it would prefer to be a profit-maximiser. In the case of positive network externalities, the condition in (21) is meaningful for any $0 < n < 1$ and $- 1 \le d < 1$ so that (22) is always fulfilled. In the case of negative network externalities, the condition in (21) is meaningful only whether (22) holds, that is for any $- n_{\beta } (d) < n < 0$ and $- \sqrt 3 /2 < d < \sqrt 3 /2$.

By substituting (21) into (19) for $\beta_{i}$ one gets profits of firm $i$ under optimal co-determination and network externalities, that is

$$ \Pi_{i}^{B/B} = \frac{{(1 - w)^{2} \sqrt {1 - d^{2} } \left( {1 - d + \sqrt {1 - d^{2} } } \right)^{2} }}{{4(1 - n)\left( {1 - d^{2} + \sqrt {1 - d^{2} } } \right)^{2} }}. $$

(23)

When firm 1 is codetermined (B) and firm 2 is profit maximiser (PM), firm 1 bargains with type-1 union bargaining unit with an effort $\beta_{1}$ and firm 2 does not bargain at all $\left( {\beta_{2} = 1} \right)$. Then, by considering quantities and prices as a function of $\beta_{1}$ profits of firm 1 and firm 2 are the following:

$$ \overline{\Pi }_{1}^{B/PM} = \frac{{\beta_{1} (1 - w)^{2} \left[ {1 + (1 - n)(1 - d)} \right]^{2} }}{{\left\{ {(1 - n)\left[ {1 + (1 - n)(1 - d^{2} )} \right] + \beta_{1} (2 - n)} \right\}^{2} }}, $$

(24)

and

$$ \overline{\Pi }_{2}^{B/PM} = \frac{{(1 - w)^{2} \left[ {\beta_{1} + (1 - n)(1 - d)} \right]^{2} }}{{\left\{ {(1 - n)\left[ {1 + (1 - n)(1 - d^{2} )} \right] + \beta_{1} (2 - n)} \right\}^{2} }}. $$

(25)

The profit-maximising bargaining power $\beta_{1}$ is the following:

$$ \frac{{\partial \overline{\Pi }_{1}^{B/PM} }}{{\partial \beta_{1} }} = 0 \Leftrightarrow \beta_{1}^{*(B/PM)} = \frac{{(1 - n)\left[ {1 + (1 - n)(1 - d^{2} )} \right]}}{2 - n}. $$

(26)

In the case of positive network externalities, the condition in (26) implies that $\beta_{1}^{*(B/PM)} \le 1$ for any $0 < n < 1$ and $- 1 < d < 1$. In the case of negative network externalities, the condition in (26) is meaningful only whether $- n_{\beta } (d) < n < 0$ and $- \sqrt 3 /2 < d < \sqrt 3 /2$. By substituting (26) into (24) and (25) for $\beta_{1}$ one gets

$$ \Pi_{1}^{B/PM} = \frac{{(1 - w)^{2} \left[ {1 + (1 - n)(1 - d)} \right]^{2} }}{{4(1 - n)(2 - n)\left[ {1 + (1 - n)(1 - d^{2} )} \right]}}. $$

(27)

and

$$ \Pi_{2}^{B/PM} = \frac{{(1 - w)^{2} \left[ {n + (2 - n)(1 - d) + (1 - n)(2 - d^{2} )} \right]^{2} }}{{4(2 - n)^{2} \left[ {1 + (1 - n)(1 - d^{2} )} \right]^{2} }}. $$

(28)

To sum up, Table 8 summarises the equilibrium outcomes of the optimal bargaining strength in the cases of both symmetric and asymmetric behaviours and Table 9 refers to the corresponding values of firms’ profits (payoff matrix).

Table 8 Endogenous co-determination; equilibrium values of the bargaining strength under B and PM

Table 9 Endogenous co-determination; equilibrium values of profits under B and PM (payoff matrix)

Define $n_{b}^{1} (d) = n_{c}^{1} (d) = 1 - \frac{1}{{\sqrt {1 - d^{2} } }} = n_{\beta } (d)$, and let $n_{b}^{2} (d)$ and $n_{c}^{2} (d)$ be two threshold values of the strength of the network effect such that the corresponding profit differentials $\Delta_{b} = \Pi_{i}^{PM/B} - \Pi_{i}^{B/B} = 0$ and $\Delta_{c} = \Pi_{i}^{PM/PM} - \Pi_{i}^{B/B} = 0$ $\left( {i,j = \{ 1,2\} ,\;i \ne j} \right)$. The shape of $n_{\beta } (d)$, $n_{b}^{2} (d)$ (red line) and $n_{c}^{2} (d)$ (black line) is depicted in Fig. 3 in the parameter space $(n,d)$.¹⁷ The red region in the figure refers to the couples $(n,d)$ corresponding to which every firm does not find it convenient to bargain with its trade union under co-determination. Result 4 classifies the outcomes of the network-co-determination game at stage 1, where each owner must choose to be either a codetermined or profit-maximising firm under endogenous co-determination, for the case of positive consumption externality. The case of negative consumption externality is more difficult to disentangle analytically and economically. To this purpose, the red area in Fig. 3 highlights the unfeasible parameter space of optimal co-determination.

Fig. 3

Endogenous co-determination and network externalities in a quantity-setting duopoly with heterogeneous products. Nash equilibrium outcomes in $(n,d)$ plane. The red (resp. black) solid line represents the threshold value $n_{b}^{2} (d)$ (resp. $n_{c}^{2} (d)$) such that $\Delta_{b} = 0$ (resp. $\Delta_{c} = 0$). The red region represents the unfeasible parameter space of optimal co-determination. Its boundary (black solid line) is given by $n_{\beta } (d) = n_{b}^{1} (d) = n_{c}^{1} (d) = 1 - \frac{1}{{\sqrt {1 - d^{2} } }}$, which applies only for negative values of $n$ and it is meaningful if and only if $1 - \frac{1}{{\sqrt {1 - d^{2} } }} > - 1$, i.e., $- \sqrt 3 /2 < d < \sqrt 3 /2$. The yellow region represents the parameter space of optimal co-determination (corresponding to product substitutability and negative consumption externalities) where (B,B) is the unique Pareto-inefficient SPNE

Result 4

[Positive externality $\left( {0 < n < 1} \right)$ and product substitutability $\left( {0 < d \le 1} \right)$]. Parameter $d$ is low enough. (1) If $1 > n > n_{c}^{2} (d)$ then (B,B) is the unique Pareto-efficient SPNE (deadlock). (2) If $n_{c}^{2} (d) > n > 0$ then (B,B) is the unique Pareto-inefficient SPNE (prisoner’s dilemma). Parameter $d$ is high enough. (3) If $1 > n > n_{b}^{2} (d)$ then (B,B) is the unique Pareto-inefficient SPNE (prisoner’s dilemma). If $n_{b}^{2} (d) > n > 0$ then (B,PM) and (PM,B) are two pure-strategy Nash equilibria of the game (anti-coordination game). [Positive externality $\left( {0 < n < 1} \right)$ and product complementarity $\left( { - 1 < d < 0} \right)$]. The Pareto-inefficient Nash equilibrium is (B,B) and the game is a prisoner’s dilemma for any $0 < n < 1$ and $- 1 < d < 0$.

The main findings emerging from Result 4 and Fig. 3 (positive and negative externalities) under endogenous co-determination are in line with those obtained under exogenous co-determination. The figure shows that the larger the degree of product substitutability and the larger the network effect, the lower the optimal bargaining effort of the firm needed to maximise profits. The red area represents the unfeasible parameter space of optimal co-determination, where firms behave as profit maximisers and co-determination can be applied only through legislation. In all other cases, co-determination can emerge through voluntary agreements (irrespective of the number of employees). When products are substitutes, a voluntary co-determination agreement is efficient when the strength of the network effect is sufficiently large. However, it is possible to have also multiple mixed Nash equilibria corresponding to which only one firm voluntarily chooses to be codetermined. In this case, no one has a dominant strategy and both equilibria are Pareto-efficient. The solution to the game may emerge from the credible disclosure of a player’s will to not play B. Then, the rival will be forced to (be the first to) play B to avoid obtaining a lower pay-off unilaterally.

5 Exogenous co-determination with heterogeneous bargaining strength

To complete the analysis of the network-co-determination game, this section considers the case of exogenous heterogeneous co-determination presented until Sect. 3. The main assumptions that hold here partly follow those presented in Sect. 4. Therefore, under exogenous co-determination with heterogeneous bargaining strength, we assume, unlike Sect. 4, that the firm does not have the right to choose the composition of the board of representatives to make production decisions. This amounts to saying that firms cannot choose the optimal union’s bargaining effort by choosing the optimal corresponding number of workers’ representatives to be co-opted within the supervisory board. Then, like Sects. 2 and 3, each firm takes the bargaining effort as given and then considers the case of exogenous co-determination in a context in which there exists a continuum of firm-specific unions differentiated amongst them based on their relative attitude to bargaining $\left( {0 < 1 - \beta_{i} \le 1} \right)$. The stages of the game, therefore, turn out to be the same as those used to solve the games presented in Sects. 2 and 3.

The payoff matrix is determined by the following equations:

$$ \Pi_{1}^{B/B} = \frac{{\beta_{1} (1 - w)^{2} \left[ {(1 - n)(1 - d) + \beta_{2} } \right]^{2} }}{{\left[ {(1 - n)^{2} (1 - d^{2} ) + (1 - n)(\beta_{1} + \beta_{2} ) + \beta_{1} \beta_{2} } \right]^{2} }}, $$

(29)

$$ \Pi_{2}^{B/B} = \frac{{\beta_{2} (1 - w)^{2} \left[ {(1 - n)(1 - d) + \beta_{1} } \right]^{2} }}{{\left[ {(1 - n)^{2} (1 - d^{2} ) + (1 - n)(\beta_{1} + \beta_{2} ) + \beta_{1} \beta_{2} } \right]^{2} }}, $$

(30)

$$ \Pi_{1}^{PM/PM} = \Pi_{2}^{PM/PM} = \frac{{(1 - w)^{2} }}{{\left[ {1 + (1 - n)(1 + d)} \right]^{2} }}, $$

(31)

$$ \Pi_{1}^{B/PM} = \frac{{\beta_{1} (1 - w)^{2} \left[ {1 + (1 - n)(1 - d)} \right]^{2} }}{{\left\{ {(1 - n)\left[ {1 + (1 - n)(1 - d^{2} )} \right] + \beta_{1} (2 - n)} \right\}^{2} }}, $$

(32)

$$ \Pi_{2}^{B/PM} = \frac{{(1 - w)^{2} \left[ {\beta_{1} + (1 - n)(1 - d)} \right]^{2} }}{{\left\{ {(1 - n)\left[ {1 + (1 - n)(1 - d^{2} )} \right] + \beta_{1} (2 - n)} \right\}^{2} }}, $$

(33)

$$ \Pi_{1}^{PM/B} = \frac{{(1 - w)^{2} \left[ {\beta_{2} + (1 - n)(1 - d)} \right]^{2} }}{{\left\{ {(1 - n)\left[ {1 + (1 - n)(1 - d^{2} )} \right] + \beta_{2} (2 - n)} \right\}^{2} }}, $$

(34)

and

$$ \Pi_{2}^{PM/B} = \frac{{\beta_{2} (1 - w)^{2} \left[ {1 + (1 - n)(1 - d)} \right]^{2} }}{{\left\{ {(1 - n)\left[ {1 + (1 - n)(1 - d^{2} )} \right] + \beta_{2} (2 - n)} \right\}^{2} }}. $$

(35)

Given Eqs. (29)–(31), the outcomes of the network-co-determination game with exogenous co-determination and heterogeneous bargaining strength at stage 1 are summarised in Figs. 4, 5, 6. The figures are depicted in the space $(\beta_{1} ,\beta_{2} )$ for different values of $n$ and $d$, showing the loci of points such that (1) the profit differential of firm 1 $\Delta_{1,a} = \Pi_{1}^{B/PM} - \Pi_{1}^{PM/PM} = 0$, i.e., $\beta_{1,a} (n,d)$, and the profit differential of firm 2 $\Delta_{2,a} = \Pi_{2}^{PM/B} - \Pi_{2}^{PM/PM} = 0$, i.e., $\beta_{2,a} (n,d)$, where $\beta_{1,a} (n,d) = \beta_{2,a} (n,d) = \beta_{a} (n,d) = \frac{{(1 - n)^{2} [1 + (1 - n)(1 - d^{2} )]^{2} }}{{(2 - n)^{2} }}$, and (2) the profit differential of firm 1 $\Delta_{1,b} = \Pi_{1}^{PM/B} - \Pi_{1}^{B/B} = 0$, i.e., $\beta_{1,b} (\beta_{2} ,n,d)$, and the profit differential of firm 2 $\Delta_{2,b} = \Pi_{2}^{B/PM} - \Pi_{2}^{B/B} = 0$, i.e., $\beta_{2,b} (\beta_{1} ,n,d)$, where $\beta_{1,b} (\beta_{2} ,n,d) = \frac{{(1 - n)^{2} [\beta_{2} + (1 - n)(1 - d^{2} )]^{2} }}{{(1 - n + \beta_{2} )^{2} }}$ and $\beta_{2,b} (\beta_{1} ,n,d) = \frac{{(1 - n)^{2} [\beta_{1} + (1 - n)(1 - d^{2} )]^{2} }}{{(1 - n + \beta_{1} )^{2} }}$.

Fig. 4

Exogenous (heterogeneous) co-determination in a non-network quantity-setting duopoly with heterogeneous products. Profit differentials in $(\beta_{1} ,\beta_{2} )$ space for $n = 0$ and $d = 1$ (A), and $d = 0.7$ and $d = - 0.7$ (B). The solid red (resp. black) lines represents the threshold value $\beta_{1,a} (n,d)$ and $\beta_{2,a} (n,d)$ with $\beta_{1,a} (n,d) = \beta_{2,a} (n,d)$ (resp. $\beta_{1,b} (\beta_{2} ,n,d)$ and $\beta_{2,b} (\beta_{1} ,n,d)$) such that $\Delta_{1,a} = 0$ and $\Delta_{2,a} = 0$ (resp. $\Delta_{1,b} = 0$ and $\Delta_{2,b} = 0$)

Fig. 5

Exogenous (heterogeneous) co-determination and positive network externalities in a quantity-setting duopoly with heterogeneous products. Profit differentials in $(\beta_{1} ,\beta_{2} )$ space for $n = 0.5$ and $d = 1$ (A), and $d = 0.7$ and $d = - 0.7$ (B). The solid red (resp. black) lines represents the threshold value $\beta_{1,a} (n,d)$ and $\beta_{2,a} (n,d)$ with $\beta_{1,a} (n,d) = \beta_{2,a} (n,d)$ (resp. $\beta_{1,b} (\beta_{2} ,n,d)$ and $\beta_{2,b} (\beta_{1} ,n,d)$) such that $\Delta_{1,a} = 0$ and $\Delta_{2,a} = 0$ (resp. $\Delta_{1,b} = 0$ and $\Delta_{2,b} = 0$)

Fig. 6

Exogenous (heterogeneous) co-determination and negative network externalities in a quantity-setting duopoly with heterogeneous products. Profit differentials in $(\beta_{1} ,\beta_{2} )$ space for $n = - 0.5$ and $d = 1$ (A), and $d = 0.5$ and $d = - 0.5$ (B). The solid red (resp. black) lines represents the threshold value $\beta_{1,a} (n,d)$ and $\beta_{2,a} (n,d)$ with $\beta_{1,a} (n,d) = \beta_{2,a} (n,d)$ (resp. $\beta_{1,b} (\beta_{2} ,n,d)$ and $\beta_{2,b} (\beta_{1} ,n,d)$) such that $\Delta_{1,a} = 0$ and $\Delta_{2,a} = 0$ (resp. $\Delta_{1,b} = 0$ and $\Delta_{2,b} = 0$)

Figure 4 represents the non-network industry $\left( {n = 0} \right)$ and contrasts the cases of perfect substitutability $\left( {d = 1} \right)$, Panel A, with the cases of imperfect substitutability $\left( {d = 0.7} \right)$ and complementarity $\left( {d = - 0.7} \right)$, Panel B, which are symmetric in the emergence of Nash equilibria. Figure 5 represents a network industry with positive consumption externalities $\left( {n = 0.5} \right)$ and contrasts the cases of perfect substitutability $d = 1$, Panel A, with the cases of imperfect substitutability $\left( {d = 0.7} \right)$ and complementarity $\left( {d = - 0.7} \right)$, Panel B, which are symmetric in the emergence of Nash equilibria. Figure 6 represents a network industry with negative consumption externalities $\left( {n = - 0.5} \right)$ and contrasts the cases of perfect substitutability $d = 1$, Panel A, with the cases of imperfect substitutability $d = 0.5$ and complementarity $\left( {d = - 0.5} \right)$, Panel B, which are symmetric in the emergence of Nash equilibria.

The figures clearly show, as expected from the results of previous sections, that (1) for a given value of the network strength (including the case of non-network industry) product heterogeneity (by increasing the firm’s market power) favours the emergence of (PM,PM) as the unique Nash equilibrium of the game, (2) for a given value of the extent of product differentiation a positive consumption externality (by shifting outward the market demand) favours the emergence of (B,B) as the unique Nash equilibrium of the game, and (3) for a given value of the extent of product differentiation a negative consumption externality (by shifting inward the market demand) favours the emergence of (PM,PM) as the unique Nash equilibrium of the game. In all the cases, a high degree of heterogeneity between the bargaining strength of firm 1 (union 1) and firm 2 (union 2) favours the emergence of asymmetric Nash equilibria in which only one firm chooses to be a codetermined entity. The codetermined firm will be the one in which the union is bargaining with the lower bargaining power. In this case, the firm is incentivised to follow the union’s request to increase employment and production.

6 Welfare analysis

The welfare analysis is conducted by considering the most analytically tractable model, i.e., exogenous homogeneous co-determination. We pinpoint, however, that the results and the rankings presented in this section hold also for the case of exogenous heterogeneous co-determination and endogenous co-determination.

The classical notion of social welfare $\left( W \right)$, which is also the one employed in the pioneering work of Kraft (1998), is $W = CS + PS$, where $CS = \frac{1 - n}{2}\left( {q_{1}^{2} + q_{2}^{2} + 2dq_{1} q_{2} } \right)$ and $PS = \Pi_{1} + \Pi_{2}$. However, as also pinpoint in Kraft (2006), an alternative measure of social welfare, including the utility functions of each trade union, can safely be used (see also Buccella et al., 2023). In this case, therefore, social welfare would be given by $W = CS + PS + Z$, where $Z = Z_{1} + Z_{2}$. For analytical tractability, we employ the simplest definition, but results hold a fortiori by including the utility of the trade unions.

The consumers’ surplus, producers’ surplus and social welfare under (PM,PM) are respectively given by:

$$ CS^{PM/PM} = \frac{{(1 - w)^{2} (1 - n)(1 + d)}}{{\left[ {1 + (1 - n)(1 + d)} \right]^{2} }}, $$

(36)

$$ PS^{PM/PM} = \frac{{2(1 - w)^{2} }}{{\left[ {1 + (1 - n)(1 + d)} \right]^{2} }},$$

(37)

and

$$ W^{PM/PM} = \frac{{(1 - w)^{2} \left[ {2 + (1 - n)(1 + d)} \right]}}{{\left[ {1 + (1 - n)(1 + d)} \right]^{2} }}. $$

(38)

The consumers’ surplus, producers’ surplus and social welfare under (B,B) are respectively given by:

$$ CS^{B/B} = \frac{{(1 - w)^{2} (1 - n)(1 + d)}}{{\left[ {\beta + (1 - n)(1 + d)} \right]^{2} }}, $$

(39)

$$ PS^{B/B} = \frac{{2\beta (1 - w)^{2} }}{{\left[ {\beta + (1 - n)(1 + d)} \right]^{2} }},$$

(40)

and

$$ W^{B/B} = \frac{{(1 - w)^{2} \left[ {2\beta + (1 - n)(1 + d)} \right]}}{{\left[ {\beta + (1 - n)(1 + d)} \right]^{2} }}. $$

(41)

The results emerging from a direct comparison between (36) and (39), (37) and (40), and (38) and (41) are the following: $CS^{B/B} > CS^{PM/PM}$, $PS^{B/B} > PS^{PM/PM}$ if and only if $n > n_{c} (\beta ,d)$, as was already pinpointed in the article, and $W^{B/B} > W^{PM/PM}$.

By also considering the asymmetric case (B,PM) (or (PM,B)) one can show that the ranking $W^{B/B} > W^{B/PM} > W^{PM/PM}$ always holds in all the models of the article.

This definitively implies that mandatory co-determination results in a Pareto superior allocative scenario compared to neoclassical profit maximisation when (B,B) emerges as the unique Pareto-efficient Nash equilibrium of the network-co-determination game played by quantity-setting firms. In this regard, the role of the network effect is relevant as this scenario holds when the (positive) network externality is sufficiently high.

7 Conclusions

The present article extends the strand of research dealing with the institution of co-determination by considering network externality in consumption by considering Katz & Shapiro (1985) and Kraft (1998) in the same setting. Co-determination is an institution that plays a significant role in the protection of workers’ rights and the improvement of working conditions. Amongst other North European countries, it has become relevant in the German industry since at least 1976 (The German Co-determination Act), extending co-determination rules to all industries and firms with more than 2000 employees, by also affecting the designing of German industrial policy.

In modern economies, industries producing goods that generate positive consumption externalities has become relevant (e.g., software, mobile phone) and work in the direction of increasing the quantity available in the market, in turn, also expanding the market size (or reducing it in the case of negative network effects).

The empirical and historical evidence has shown that production decisions/incentives are different between profit maximisation and co-determination. The empirical literature on co-determination has shown that quantity, prices, profits and wages under co-determination are different than under profit maximisation. Specifically, productivity, profits, stock returns, wages and employment adjustment, labour share, bargaining power and other relevant variables on the firm side have been widely analysed by many studies such as Svejnar (1982), FitzRoy & Kraft (1993, 2005), Kraft & Ugarkovic (2006), Gorton & Schmid (2004), Fauver & Fuerst (2006) and Kraft (2018). For instance, Gorton & Schmid (2004, p. 895) pinpoint that co-determination appears “to succeed in altering the objective function of the firm”, Fauver and Fuerst (2006, p. 677) state that “… our analysis suggests that the judicious use of labor representation can increase firm value”, whereas Kraft (2018) finds that co-determination leads to a significant increase in workers’ bargaining power and the distribution of rents. Unlike these studies, Jäger et al. (2021) provide quasi-experimental evidence to show no effects of co-determination on the wage structure, the labour share, revenue, employment or profitability.

The present article shows that network externalities play a relevant role in a strategic competitive quantity-setting duopoly à la Kraft (1998) with codetermined firms. This is because co-determination per se allows firms to produce more than standard profit maximisation and a network externality broadens this effect. Unlike Kraft (1998), who showed that co-determination is a Pareto-inefficient SPNE (prisoner’s dilemma) in a non-network market with homogeneous products, this article identified a solution to the dilemma by letting co-determination become a Pareto-efficient SPNE of a network industry in a quantity-setting duopoly. The result is also extended to the case of horizontal product differentiation. Finally, as co-determination enhances the consumer’s surplus and the workers’ utility, we must emphasise that this institution may represent a Pareto-superior policy in comparison to profit maximisation. Therefore, in network industries co-determination may voluntarily emerge as the endogenous (Pareto-efficient) outcome of a Cournot strategic competitive framework, thus coming not only from legislative rules. Alternatively, mandatory co-determination can become a Pareto superior policy from a societal perspective.

The economic reasons for the main results are clear: as in the previous literature, the key strategic effect of co-determination is that each codetermined firm produces a higher output for any given output of its opponent. The reason is that, due to co-determination, employee representatives are part of each firm’s supervisory board. Formally, this is captured by assuming that co-determination changes the objective function of the firms from conventional profits to a Nash bargaining maximand that is made up of both profits and workers’ labour income. As workers want to increase employment for any given wage, each codetermined firm will have the incentive to increase its output level accordingly. Hence, relative to a situation without co-determination, the codetermined firms will end up producing more output, then the market price will fall, and profits will fall as well. This implies that co-determination will lead to a more competitive outcome. In this context, the novelty of the paper is to explore the impact of network externalities on consumption. The results from the analysis point to these externalities as relevant. The main results suggest that (positive) consumption network externalities can preserve the positive impact of co-determination on consumer surplus but, at the same time, they can also contribute to higher profits. This is because the (positive) externality on the demand side contributes to expanding the market demand and makes consumers willing to pay a higher price.

Results hold for the cases of (1) exogenous homogeneous or heterogeneous co-determination, according to which firms cannot choose the composition of the board of representatives but can bargain with decentralised unions having identical or different bargaining efforts, which is taken as given in the bargaining between the two parties, and (2) endogenous co-determination, according to which firms can choose the composition of the board of representatives (including or not workers’ representatives) by choosing the bargaining effort that maximises its profits and then correspondingly choosing the optimal number of workers’ representative to be co-opted within the supervisory board.

Definitively, in network industries co-determination emerges as an institution that harmonises labour relationships and improves social welfare. To the extent that the network industries are becoming predominant in the economies, “co-determination” may be the “natural” institution of the labour market, which—from a societal point of view—is Pareto-superior to the neoclassical institution. Therefore, the policy implications are obvious and far-reaching. Though the empirical relevance of voluntary co-determination is indeed low, our results do not refer to the case of voluntary co-determination as an institution being observed in the market, but rather that mandatory co-determination results in higher social welfare than profit maximisation. This is because consumers are better due to an increase in output (in turn increasing consumer surplus) and this benefit more than offsets the reduction in the firms’ profits. However, before our work, this institution was considered harmful to firms as it contributed to reducing their profitability. Instead, in markets with positive consumption externalities co-determination can be beneficial also to firms (Pareto-efficient SPNE), in turn, resulting in a win–win solution for society. Consequently, mandatory co-determination may be Pareto superior to profit maximisation.

Thus, co-determination voluntarily emerging in non-network markets from non-cooperative games such as those by Kraft (1998) and Fanti et al. (2018) represents a Pareto-inefficient SPNE for firms. Unlike this, the present article provides the conditions to let it become a Pareto-efficient outcome. Accordingly, our theoretical prediction is that co-determination can be a strategic variable enabling an efficient outcome in network markets. In this sense, our work may offer a future research direction for econometricians to study whether in network markets the presence of voluntary co-determination may be less negligible than in standard non-network markets. The point, therefore, is not that the fraction of firms with voluntary co-determination is negligible but rather that the fraction of firms with voluntary co-determination in network markets is less negligible than in standard non-network markets.

The article complements the analysis of co-determination and price competition in a network industry developed by Fanti & Gori (2019). However, considering the competition (or mode of competition) game played by codetermined firms that choose whether be quantity or price competitors, the outcome that endogenously emerges is always the quantity competition.

The potential future development of this study can follow, e.g., the framework developed by Yang et al. (2015) about manufacturers’ channel structures. In this regard, the theoretical analysis of co-determination in strategic competitive industries is still silent thus representing a promising research agenda.

Appendix

This appendix provides the proofs of some lemmas and propositions.

Proof of Lemma 1. The consumers’ surplus in equilibrium is defined as $CS = \frac{1 - n}{2}\left( {q_{1}^{2} + q_{2}^{2} + 2dq_{1} q_{2} } \right)$. Then under B/B and PM/PM for $d = 1$ one gets $CS^{B/B} = \frac{{2(1 - w)^{2} (1 - n)}}{{\left[ {\beta + 2(1 - n)} \right]^{2} }}$ and $CS^{PM/PM} = \frac{{2(1 - w)^{2} (1 - n)}}{{(3 - 2n)^{2} }}$, so that $CS^{B/B} > CS^{PM/PM}$ for any $0 < \beta < 1$ and $CS^{B/B} = CS^{PM/PM}$ for any $\beta = 1$. The equilibrium workers’ utility in the B/B scenario is $Z^{B/B} = Z_{1}^{B/B} + Z_{2}^{B/B} = w(q_{1}^{B/B} + q_{2}^{B/B} )$. The workers’ utility in the PM/PM scenario is $Z^{PM/PM} = 0$. Then, $Z^{B/B} > Z^{PM/PM}$ always holds.

Proof of Lemma 2. The proof follows by studying the sign of

$$ \Delta_{c} = \frac{{(1 - w)^{2} (1 - \beta )\left[ {4n^{2} - 8n + 4 - \beta } \right]}}{{(3 - 2n)^{2} \left[ {\beta + 2(1 - n)} \right]^{2} }}. $$

If $n < n_{c} (\beta )$ (resp. $n > n_{c} (\beta )$) then $\Delta_{c} > 0$ (resp. $\Delta_{c} < 0$).

Proof of Proposition 1. Profit differentials $\Delta_{a}$ and $\Delta_{b}$ are the following:

$$ \Delta_{a} = \frac{{(1 - w)^{2} (1 - \beta )\left[ { - (1 - \beta )n^{2} + 2n(1 - 2\beta ) + 4\beta - 1} \right]}}{{(3 - 2n)^{2} \left[ {\beta + 2(1 - n)} \right]^{2} }}, $$

and

$$ \Delta_{b} = \frac{{ - (1 - w)^{2} \beta (1 - \beta )\left[ {(1 - \beta )n^{2} - 2n + 1 + \beta + \beta^{2} } \right]}}{{\left[ {1 - n + \beta (2 - n)} \right]^{2} \left[ {\beta + 2(1 - n)} \right]^{2} }} < 0. $$

The sign of $\Delta_{a}$ and $\Delta_{c}$ change depending on the relative size of $\beta$ and $n$. Given Lemma 2, we have that (1) if $- 1 \le n < n_{a} (\beta )$ then $\Delta_{a} < 0$, $\Delta_{b} < 0$ and $\Delta_{c} > 0$, (2) if $n_{a} (\beta ) < n < n_{c} (\beta )$ then $\Delta_{a} > 0$, $\Delta_{b} < 0$ and $\Delta_{c} > 0$, so that B is a dominant strategy for each player, (3) if $n_{c} (\beta ) < n < 1$ then $\Delta_{a} > 0$, $\Delta_{b} < 0$ and $\Delta_{c} < 0$, so that B is a dominant strategy for each player.

Proof of Proposition 4. It is sufficient to note that $n_{c} (\beta ,d)$ is a monotonic increasing function of $d$.