1 Introduction

Ever since the celebrated Gibbard–Satterthwaite theorem (Gibbard, 1973; Satterthwaite, 1975), strategy-proofness (‘non-manipulability’) is one of the focal properties in voting theory. Strategy-proofness requires that truth-telling is a weakly dominant strategy. This is a desirable property for several reasons. One important aspect of strategy-proofness is the robustness that it implies: under a strategy-proof voting rule, every individual has an optimal (i.e. weakly dominant) strategy independently of the behavior of all other voters. In particular, optimal play is robust with respect to the beliefs voters may have about the type and the behavior of the other voters. Following Blin and Satterthwaite (1977), we call this property belief-independence of a voting rule. Strategy-proofness adds to this the requirement that one of the optimal strategies for each voter be truth-telling. Thus, strategy-proofness is formally a strictly stronger condition than belief-independence.

In this paper, we give a number of examples of voting rules (social choice functions) that are belief-independent, but not strategy-proof. However, we also show—much in the spirit of Blin and Satterthwaite (1977)—that belief-independence implies strategy-proofness under a few natural additional conditions, and we present a number of natural sufficient conditions that guarantee the equivalence of belief-independence and strategy-proofness. Our results pertain both to the universal domain and to restricted preference domains. We distinguish two different approaches to restricting preferences in voting theory. First, in what we call the common domain approach, one assumes that both the actual (‘true’) preferences of all voters and the voting rule are restricted to the same subset of preferences; this is in fact the standard approach to considerations of strategy-proofness on restricted domains taken in the literature (see, e.g., Barberà, 2001). On the other hand, and perhaps conceptually more attractive, one may restrict only the actual preferences of voters while keeping the voting rule being defined on the universal domain. We call this the unrestricted message space approach. The important difference is that under the latter assumption, voters can report any preference from the unrestricted domain even when their factual preferences are restricted to a subdomain. While one usually assumes for the common domain approach that the domain restriction is common knowledge, in the unrestricted message space approach one only has to require that the social planner knows the domain restriction. This, arguably, makes the unrestricted message space approach particularly appealing.

In this setup, meaningful (and stronger) definitions of strategy-proofness and belief-independence would require robustness with respect to the reporting of these additional preference orderings. We call the corresponding concepts robust strategy-proofness and robust belief-independence. Again, we (i) give examples demonstrating that the robust versions of strategy-proofness and belief-independence are indeed stronger, and (ii) provide equivalence results under natural additional conditions.

1.1 Relation to the literature

There are quite a few literature dealing with beliefs—in particular in the mechanism design literature—as beliefs play a crucial role when collective decisions are taken under incomplete information. Strategic considerations of the individuals then depend on the actions the other individuals take, and thus on the beliefs on the actions of the other individuals. These actions, on their own, depend on their beliefs. Hence, the strategy choice also depends on an individual’s beliefs about the beliefs of the others. Thus, additionally, they also depend on one’s belief about the belief of the others about the beliefs of the others and so on and so forth. This infinite hierarchy of beliefs was first addressed by Harsanyi (1967/1968), who introduced type spaces to deal with that issue. This idea was later formalized by Mertens and Zamir (1985) and further developed by Bergemann and Morris (2005). In their sophisticated approach, beliefs are implicitly contained in the individual’s type. In this paper, we consider belief-independence as introduced by Blin and Satterthwaite (1977), which is meant to be understood literally: independence of all possible kinds and forms of beliefs via weakly dominant strategies. Blin and Satterthwaite (1977) introduced this condition and provide an impossibility result similar to the theorem of Gibbard (1973) and Satterthwaite (1975). Additionally, they illustrate in how far beliefs might be manipulated in case of non-belief-independent rules. While weaker than strategy-proofness, belief-independence is still a very restrictive condition and one may want to weaken it. The ‘strategically simple mechanisms’ introduced by Börgers and Li (2019), that only depend on first-order beliefs, can be considered a step in that direction but are out of the scope of this work.

In this paper, we are interested in the interplay of the ‘pure’ notions of strategy-proofness and belief-independence; we thus focus on Blin and Satterthwaite’s original and simple concept. Importantly, we approach the problem of comparing strategy-proofness and belief-independence from the perspective of voting theory and not from the perspective of mechanism design. Indeed, by the revelation principle for dominant strategies introduced by Gibbard (1973) (see also Mas-Colell et al., 1995), we know that every belief-independent voting rule can be truthfully implemented in dominant strategies. In the present work, we only consider direct mechanisms and give natural conditions under which belief-independent voting rules can be truthfully implemented by a direct mechanism. Hence, one way of interpreting our results is that we give conditions under which one does not need to resort to the revelation principle to get from a belief-independent to a strategy-proof voting rule.

1.2 Structure of the paper

The paper is organized as follows. Section 2 introduces the general model and the basic definitions, presents the theorem of Blin and Satterthwaite (1977) and gives a result that demonstrates the equivalence of belief-independence and strategy-proofness for sovereign, positive responsive and tops-only voting rules (Proposition 2.9). We also show by means of examples that none of these conditions can be dropped in this result.

Section 3 extends the analysis to two different approaches to restricted preference domains: the common domain approach and the unrestricted message space approach. The common domain approach is the standard approach in the literature restricting all preferences and the domain of the voting rule to the same restricted preference domain for all individuals. In the unrestricted message space approach, the domain of the ‘true’ preference orderings is also restricted to the same restricted preference domain for all voters, but the voting rule is defined on the universal domain and thus—and in contrast to the common domains approach—all preference orderings are feasible as voters’ reports.

For the common domain approach, several examples illustrate the problems that come with generalizing the equivalence result (Proposition 2.9) to restricted preference domains. It is shown that, when adding anonymity and replacing positive responsiveness by unanimity, the equivalence of strategy-proofness and belief-independence is restored on restricted common preference domains (Proposition 3.6).

In the unrestricted message space approach, we adapt the concepts of strategy-proofness and belief-independence to ‘robust’ belief-independence and ‘robust’ strategy-proofness. We provide an equivalence result for strategy-proof and robust strategy-proof voting rules for tops-only rules on minimally rich domains (Proposition 3.12). Moreover, we demonstrate how the equivalence between (robust) strategy-proofness and (robust) belief-independence for the common domain approach can be translated to the unrestricted message space approach (Proposition 3.14). An additional equivalence result is provided for tops-only, positive responsive and neutral rules (Proposition 3.16).

2 Belief-independence and strategy-proofness on the universal domain

2.1 Model

We consider a situation in which a finite set of individuals \(N=\{1,\dots ,n\}\) \((n\ge 2)\) faces a finite set of alternatives \(A=\{a_1,\dots ,a_m\}\) that contains at least three elements. Every individual has linear preferences over the alternatives. The set of all linear preferences over A is denoted by \(\mathcal {P}\) and the preference ordering of individual i by \(\succ _i\ \in \mathcal {P}\). We sometimes write \(\succcurlyeq _i\) instead of \(\succ _i\), note that \(a \,\succcurlyeq _i b\) and \(b \,\succcurlyeq _i a\) together imply that \(a=b\). By \(\tau ^{(k)}(\succ _i)\), we denote the k-th placed alternative within the preference ordering \(\succ _i\) but—to simplify notation—we omit the superscript when denoting the most preferred alternative, i.e., \(\tau ^{(1)}(\succ _i)=\tau (\succ _i)\). A profile of preferences is denoted by \(\succ \ =(\succ _1,\dots ,\succ _n)\in \mathcal {P}^n\). Further, we denote by \(\succ _{-i}\ =(\succ _1,\dots ,\succ _{i-1},\succ _{i+1},\dots ,\succ _n)\in \mathcal {P}^{n-1}\) the profile of preferences excluding the preference ordering of individual i. We examine deterministic voting rules (or social choice functions) \(f:\mathcal {P}^n\rightarrow A\) that map profiles of preferences of the individuals to one alternative in A. We will assume throughout this section that the voting rules satisfy sovereignty, i.e., for all alternatives \(a\in A\) there exists a profile \(\succ \ \in \mathcal {P}^n\) such that \(f(\succ )=a\). This is a natural assumption, as the violation of sovereignty implies that some alternatives are never chosen by the voting rule. In this case, they should not be considered alternatives in the first place.

We assume that all individuals are equipped with beliefs toward the other individuals. In general, beliefs may take a variety of forms. As we focus on the independence of beliefs, we keep beliefs as general as possible. In fact, following Blin and Satterthwaite (1977), we say that a voting rule satisfies belief-independence if every individual possesses a very weakly dominant strategy, i.e., if for every individual there exists one strategy that is always at least as good as any other strategy. This dominance concept is the only dominance concept that we will use in this paper. From now on, to keep the wording simpler, we will omit the ‘very’ when referring to it. Note that this concept varies from the definition of weakly dominant strategies in game theory textbooks, as these require the dominant strategy to be strictly better sometimes.

A weakly dominant strategy is optimal given all possible behavior of the other individuals, and hence independent of whatever belief one might have about the other individuals and moreover independent of the precise shape of the belief. Thus, a weakly dominant strategy really is ‘belief-independent’.

Definition 2.1

A voting rule \(f:\mathcal {P}^n\rightarrow A\) is called belief-independent, if for all \(i\in N\) and all \(\succ _i\ \in \mathcal {P}\) there exists \(\succ _i^\star \ \in \mathcal {P}\) such that

$$\begin{aligned} f\left( \succ _i^\star ,\succ _{-i}\right) \ \succcurlyeq _i\ f\left( \succ '_i,\succ _{-i}\right) \text { for all } \succ _{-i}\ \in \mathcal {P}^{n-1} \text { and all } \succ '_i\ \in \mathcal {P}. \end{aligned}$$

Note that for a belief-independent voting rule, an individual may have several weakly dominant strategies. In this case, all these strategies result in the same outcome (while keeping everything else fixed). As all individuals possess (at least) one weakly dominant strategy, and thus a strategy that is weakly better than all of her other strategies independently of the other individuals’ strategies, it is in particular independent of which of the weakly dominant strategies the other individuals play. Hence, whenever every individual plays one of the weakly dominant strategies, the outcome is the same.

Definition 2.2

A voting rule \(f:\mathcal {P}^n\rightarrow A\) is called strategy-proof, if for all \(i\in N\) and all \(\succ _i,\succ '_i\ \in \mathcal {P}\)

$$\begin{aligned} f\left( \succ _i,\succ _{-i}\right) \ \succcurlyeq _i\ f\left( \succ '_i,\succ _{-i}\right) \text { for all } \succ _{-i}\ \in \mathcal {P}^{n-1}. \end{aligned}$$

It is straightforward to see that belief-independence is directly implied by strategy-proofness of a voting rule, as strategy-proofness requires truth-telling to be a weakly dominant strategy.

On the universal domain, we know by the theorem of Gibbard (1973) and Satterthwaite (1975) that every strategy-proof and sovereign rule is dictatorial. As belief-independence is a weakening of strategy-proofness, this result does not directly translate to belief-independent rules and, in fact, one can find examples of non-dictatorial rules that are belief-independent.

Definition 2.3

A voting rule \(f:\mathcal {P}^n\rightarrow A\) is called dictatorial, if there exists \(i \in N\) such that \(f(\succ _i,\succ _{-i})=\tau (\succ _i)\) for all \(\succ _i\ \in \mathcal {P}\) and all \(\succ _{-i}\ \in \mathcal {P}^{n-1}\).

The following examples illustrate that there are non-dictatorial and belief-independent voting rules.

Example 2.4

Consider the following voting rule:

$$\begin{aligned} f(\succ ):= \left\{ \begin{array}{ll} \tau \left( \succ _1\right) &{} \text {if } \tau ^{(m)}\left( \succ _1\right) =a \\ a &{} \text {else.} \end{array} \right. \end{aligned}$$

Every player possesses a weakly dominant strategy: individual 1 submits her true preference if she likes alternative a the most; else, she submits her true preference but with alternative a moved down to the last (and therefore m-th) position. This ensures that her most preferred alternative is chosen. No other individual influences the outcome, and hence all strategies are weakly dominant strategies. Thus, this voting rule is belief-independent, but not strategy-proof.

Example 2.5

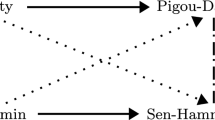
Let \(A=\{a,b,c\}\) and consider the following voting rule:

$$\begin{aligned} f(\succ ):= \left\{ \begin{array}{ll} a &{} \text {if } \tau \left( \succ _1\right) =b \\ b &{} \text {if } \tau \left( \succ _1\right) =c \\ c &{} \text {if } \tau \left( \succ _1\right) =a. \end{array} \right. \end{aligned}$$

Again, all players have weakly dominant strategies. Individual 1 will adjust her submitted preference ordering—and thus deviate from truth-telling—assuring her most preferred alternative to be chosen. Since no other individual influences the outcome, submitting any preference ordering is a weakly dominant strategy for them. As all individuals possess a weakly dominant strategy, this rule is belief-independent. However, as truth-telling is not a weakly dominant strategy for individual 1, f is not strategy-proof.

2.2 Result of Blin and Satterthwaite (1977) and extension

The previous example illustrates a non-dictatorial rule; nevertheless it has a strong dictatorial feel, as there exists one individual who can guarantee her most preferred alternative to be the outcome. To capture this, Blin and Satterthwaite (1977) use a suitable adaption of the definition of dictatorship, which we renamed to dictatorship* to avoid confusion.Footnote 1

Definition 2.6

Let \(f:\mathcal {P}^n\rightarrow A\) be a belief-independent voting rule. Then we call f dictatorial*, if there exists an individual \(i\in N\) such that for all \(\succ _i\ \in \mathcal {P}\) and all \(\succ _{-i}\ \in \mathcal {P}^{n-1}\) there exists \(\succ _i^\star \ \in \mathcal {P}\) with

$$\begin{aligned} f\left( \succ _i^\star ,\succ _{-i}\right) =\tau \left( \succ _i\right) . \end{aligned}$$

With this concept of dictatorship, Blin and Satterthwaite (1977) are able to establish a Gibbard–Satterthwaite-type result for belief-independent voting rules.

Theorem 2.7

(Blin & Satterthwaite, 1977) Let \(f:\mathcal {P}^n\rightarrow A\) be a belief-independent and sovereign voting rule. Then, f is dictatorial*.

The original theorem is even stronger, only assuming an effective range of at least three elements, rather than sovereignty.

In this subsection, we want to further examine the relation between strategy-proofness and belief-independence. It can be seen directly from the definitions that strategy-proofness implies belief-independence. We show that, if we require the voting rule to satisfy some mild and natural conditions, belief-independence also implies strategy-proofness.

Definition 2.8

  • Given preference profiles \(\succ ,\succ '\ \in \mathcal {P}^n\) and an alternative \(a\in A\), we say that a keeps or improves its relative position from \(\succ\) to \(\succ '\), if for all \(b\in A\) and all \(i\in N\): \(a\succ _i b \Rightarrow a \succ '_i b\).

  • A voting rule \(f:\mathcal {P}^n\rightarrow A\) is called positive responsive, if for all \(\succ ,\succ '\ \in \mathcal {P}^n\) and all \(a\in A\):

    $$\begin{aligned} \left\{ \begin{array}{l} f(\succ ) = a,\ \ \succ '\ =\ \succ \text { on } A\setminus \{a\} \ \text { and } a \text { keeps} \\ \text {or improves its relative position from } \succ \text { to } \succ ' \end{array} \right\} \ \Rightarrow \ f\left( \succ '\right) = a . \end{aligned}$$

  • A social choice function \(f:\mathcal {P}^n\rightarrow A\) is called tops-only, if for all preference profiles \(\succ ,\succ '\ \in \mathcal {P}^n\) with \(\tau (\succ _i)=\tau (\succ '_i)\) for all \(i\in N\): \(f(\succ )=f(\succ ')\).

These conditions are not really restrictive. Positive responsiveness is a minimal monotonicity condition, and therefore also known as elementary monotonicity. Tops-onlyness is a property most of the commonly used voting rules share. Moreover, as Chatterji and Sen (2011) find, tops-only and strategy-proof rules are often closely related. The proposition below establishes the equivalence of strategy-proofness and belief-independence given that the voting rule is tops-only and positive responsive.

Proposition 2.9

Let \(f:\mathcal {P}^n\rightarrow A\) be a sovereign voting rule. Then, f is belief-independent, positive responsive and tops-only if and only if f is strategy-proof.

Proof

By Theorem 2.7 we know that f is dictatorial*. Hence there exists \(i\in N\) such that for all \(\succ _i\ \in \mathcal {P}\) and all \(\succ _{-i}\ \in \mathcal {P}^{n-1},\) there exists a \(\succ _i^\star \ \in \mathcal {P}\) such that \(f(\succ _i^\star ,\succ _{-i})=\tau (\succ _i)\). Consider the preference ordering \(\succ '_i\) that (i) coincides with \(\succ _i^\star\) on \(A\setminus \{\tau (\succ _i)\}\) and for which (ii) \(\tau (\succ '_i)=\tau (\succ _i)\). By positive responsiveness, we obtain that \(f(\succ '_i,\succ _{-i})=\tau (\succ _i)\) for all \(\succ _i\ \in \mathcal {P}\) and all \(\succ _{-i}\ \in \mathcal {P}^{n-1}\). As f is tops-only, we have \(f(\succ _i,\succ _{-i})=\tau (\succ _i)\) for all \(\succ _i\ \in \mathcal {P}\) and all \(\succ _{-i}\ \in \mathcal {P}^{n-1}\). Thus, f is dictatorial and thus in particular strategy-proof.

Let f be strategy-proof. Then f is dictatorial and thus positive responsive and tops-only. \(\square\)

The idea of adding positive responsiveness stems from Example 2.5, and the idea of adding tops-onlyness from Example 2.4, as these examples exploit the absence of these conditions. Note that in Proposition 2.9, sovereignty cannot be dropped either as the following example illustrates.

Example 2.10

Let \(A=\{a,b,c\}\) and consider the following voting rule:

$$\begin{aligned} f(\succ ):= \left\{ \begin{array}{ll} a &{} \text {if } \#\left\{ i\in N: \tau \left( \succ _i\right) =a\right\} \ge \#\left\{ i\in N: \tau \left( \succ _i\right) =b\right\} \\ b &{} \text {else.} \end{array} \right. \end{aligned}$$

This rule is belief-independent, but not strategy-proof. If an individual’s top alternative is c, she has an incentive to deviate from truth-telling and vote for a or b, depending on which alternative she prefers of these two. Moreover, this rule is positive responsive and tops-only, but not sovereign.

3 Restricted preference domains

In this chapter, we extend our analysis to restricted preference domains. We use two different approaches to restricted domains and give sufficient conditions for the equivalence of belief-independence and strategy-proofness on restricted domains in both cases. Neither of the two approaches assumes specific domain restrictions. In particular, one can apply them to all known domains that admit strategy-proof voting rules (and, in fact, to all other domains as well). The only assumption made on the structure of the restricted domain \(\mathcal {D}\) is that it is the same for all individuals, which is a standard assumption in the literature.

3.1 Common domain approach

We start with the common domain approach, which is the standard approach in the literature on restricted domains. Here, the preferences, as well as the domain of the voting rule are restricted to a commonly known domain. Formally, we denote a restricted preference domain by \(\mathcal {D}\subset \mathcal {P}\) and consider the case where all individuals \(i\in N\) have preferences \(\succ _i\ \in \mathcal {D}\) in that domain and the voting rule \(f:\mathcal {D}^n\rightarrow A\) is defined on the n-fold cartesian product of that domain only. We adjust the definition of belief-independence by assuming that in \(\mathcal {D},\) every individual has a weakly dominant strategy. The definition of strategy-proofness on \(\mathcal {D}\) requires that truth-telling is a weakly dominant strategy in the domain \(\mathcal {D}\).

Definition 3.1

  • A voting rule \(f:\mathcal {D}^n\rightarrow A\) is called belief-independent on \(\varvec{\mathcal {D}}\), if for all \(i\in N\) and all \(\succ _i\ \in \mathcal {D}\) there exists \(\succ _i^\star \in \mathcal {D}\) such that

    $$\begin{aligned} f\left( \succ _i^\star ,\succ _{-i}\right) \ \succcurlyeq _i \ f\left( \succ '_i,\succ _{-i}\right) \ \text { for all } \succ _{-i}\ \in \mathcal {D}^{n-1},\succ '_i\ \in \mathcal {D}. \end{aligned}$$

  • A voting rule \(f:\mathcal {D}^n\rightarrow A\) is called strategy-proof on \(\varvec{\mathcal {D}}\), if for all \(i\in N\) and all \(\succ _i\ \in \mathcal {D}\)

    $$\begin{aligned} f\left( \succ _i,\succ _{-i}\right) \ \succcurlyeq _i \ f\left( \succ '_i,\succ _{-i}\right) \ \text { for all } \succ _{-i}\ \in \mathcal {D}^{n-1},\succ '_i\ \in \mathcal {D}. \end{aligned}$$

Again, by construction, strategy-proofness on a restricted domain implies belief-independence on that domain. The converse is not true in general as Example 3.2 illustrates. Hence, we look to extend Proposition 2.9 to restricted preference domains. Unfortunately, this turns out to be more subtle than one might expect. The following example considers a rule that is tops-only, positive responsive, sovereign and belief-independent on a restricted preference domain (with separable preferences), but not strategy-proof on that domain.

Example 3.2

Let \(A=\{a,b,c\}\) and consider the (restricted) preference domain \(\mathcal {D}=\{abc,acb,bca,cba\}\) and the following voting rule:

$$\begin{aligned} f(\succ ):= \left\{ \begin{array}{ll} a, &{} \text {if } \tau \left( \succ _2\right) =a ,\\ b, &{} \text {if } \tau \left( \succ _1\right) =b \text { and } \tau \left( \succ _2\right) \in \{b,c\} ,\\ c, &{} \text {if } \tau \left( \succ _1\right) =c \text { and } \tau \left( \succ _2\right) \in \{b,c\}, \\ \tau \left( \succ _2\right) , &{} \text {if } \tau \left( \succ _1\right) =a \text { and } \tau \left( \succ _2\right) \in \{b,c\}. \end{array} \right. \end{aligned}$$

It can be easily seen that this rule is sovereign and tops-only. The voting rule is also positive responsive. To show this we need to go through all possible cases.

Case 1: Let \(f(\succ )=a\).

Then \(\tau (\succ _2)=a\) and in all profiles in which a keeps or improves its relative position, a remains the top alternative of individual 2, thus a remains the outcome.

Case 2: Let \(f(\succ )=b\).

Then (i) \(\tau (\succ _1)=b\) and \(\tau (\succ _2)\in \{b,c\}\) or (ii) \(\tau (\succ _1)=a\) and \(\tau (\succ _2)=b\). In the first case, only individual 2 can change the top alternative to b, which does not change the outcome. In case (ii), individual 1 can change the top alternative to b, resulting in case (i), but still with outcome b.

Case 3: Let \(f(\succ )=c\).

The argument for \(f(\succ )=c\) is analogous to the one for b.

Furthermore, f is belief-independent on \(\mathcal {D}\). Individual 1 can never change the outcome to a, but can decide on whether b or c are chosen, given that individual 2 did not submit a as her top alternative. Hence, individuals 1’s weakly dominant strategy is putting b or c on top of her submitted preference ordering, depending on which alternative she prefers. Individual 2’s weakly dominant strategy is truth-telling as she always likes a the most or the least in all preferences in \(\mathcal {D}\). Hence, if she prefers a,  she gets her best alternative by truth-telling. If she prefers b or c, then by truth-telling she can ensure the outcome to be within b and c, and if individual 2 submits a as her top alternative, she can even determine the outcome. Thus, the voting rule is sovereign, tops-only, positive responsive and belief-independent on \(\mathcal {D},\) but not strategy-proof on \(\mathcal {D}\) as truth-telling is not a weakly dominant strategy for individual 1.

There are further problems that can arise when restricted preference domains are rather small. Then, the condition of positive responsiveness can turn into a vacuous requirement as the following example illustrates.

Example 3.3

Let \(A=\{a,b,c,d\}\) and let \(\mathcal {D}=\{abcd,badc,cbda,dbca\}\). Consider

$$\begin{aligned} f(\succ ):= \left\{ \begin{array}{ll} a, &{} \text {if } \tau (\succ _1)=b \\ b, &{} \text {if } \tau (\succ _1)=c \\ c, &{} \text {if } \tau (\succ _1)=d \\ d &{} \text {else.} \end{array} \right. \end{aligned}$$

This rule is sovereign and tops-only. As all players have a weakly dominant strategy, and as truth-telling is clearly not a weakly dominant strategy for individual 1, this rule is belief-independent on \(\mathcal {D}\), but not strategy-proof on \(\mathcal {D}\). Moreover, for all \(\succ _i\ \in \mathcal {D}\) there exists no \(\succ '_i\ \in \mathcal {D}\setminus \{\succ _i\}\) such that any alternative keeps or improves its relative position from \(\succ _i\) to \(\succ '_i\). Hence any voting rule defined on \(\mathcal {D}\) is positive responsive (on \(\mathcal {D}\)).

The natural hope is that all these problems can be solved, when choosing appropriate preference domains, that are in some sense “well-behaved”. The first candidate that comes to mind is the domain of single-peaked preferences (Black, 1948), which is well studied in the literature and known to have nice properties, e.g., the existence of non-dictatorial and strategy-proof voting rules. Unfortunately, Proposition 2.9 cannot be extended to the domain of single-peaked preferences as the following example demonstrates.

Example 3.4

Let \(A=\{a_1,\dots ,a_m\}\), let n be odd and let \(\mathcal {D}\) be the single-peaked domain with respect to the linear order \(a_1<\dots <a_m\). Denote by \(\textit{lmed}(\succ _{-1})\) the lower median and by \({\textit{umed}}(\succ _{-1})\) the upper median of the top alternatives of the preference profile \(\succ _{-1}\ \in \mathcal {D}^{n-1}\). Note that \(\succ _{-1}\) has an even number of elements. Consider

$$\begin{aligned} f(\succ ):= \left\{ \begin{array}{ll} a_2, &{} \text {if } \textit{lmed}(\succ _{-1})=a_2,\ \textit{umed}\left( \succ _{-1}\right) =a_3,\ \tau \left( \succ _1\right) =a_2 \\ \ {} &{} \\ \textit{umed}\left( \succ _{-1}\right) , &{} \text {else.} \end{array} \right. \end{aligned}$$

It is easy to see that this rule is sovereign and tops-only. Moreover, one can show that f is positively responsive:

Case 1: Let \(f(\succ )=a_j\) for \(j\ne 2\).

Then \(a_j=\textit{umed}(\succ _{-1})\). As f is tops-only, the outcome can only change if an individual submits a different peak. By positive responsiveness, the peak can only change to \(a_j\). If any individual changes her top alternative to \(a_j\), then \(a_j\) remains the upper median and thus the outcome remains unchanged.

Case 2: Let \(f(\succ )=a_2\).

If \(a_2=\text {\textit{umed}}(\succ _{-1})\), then by the same argument we obtain that the outcome does not change when we consider a profile in which \(a_2\) keeps or improves its relative position.

Assume that \(\textit{lmed}(\succ _{-1})=a_2\), \(\textit{umed}(\succ _{-1})=a_3\) and \(\tau (\succ _1)=a_2\). Then, if an individual with top alternative \(a_1\) changes her top alternative to \(a_2\), nothing changes as the lower and the upper median remain the same. If an individual with a top alternative different from \(a_1\) and \(a_2\) changes her top alternative to \(a_2\), the upper median changes to \(a_2\). Thus, the outcome is defined by the second instance in the definition of f. As \(a_2\) corresponds to the new upper median, the outcome remains the same. Hence, f is positive responsive.

Furthermore, f is belief-independent on \(\mathcal {D}\). Individual 1 only influences the outcome in one instance, where she can choose between \(a_2\) and \(a_3\). Assume that this instance is given, i.e., \(\textit{lmed}(\succ _{-1})=a_2\) and \(\textit{umed}(\succ _{-1})=a_3\). Moreover, assume that the top alternative of individual 1 is \(a_1\). Then she prefers \(a_2\) over \(a_3\) as she has single-peaked preferences. However, the outcome will by \(a_3\) unless individual 1 submits \(a_2\) as her top alternative, in which case the outcome will be \(a_2\). Hence, in this case, she has a strict incentive to not submit her true preference ordering. For all other individuals truth-telling is a weakly dominant strategy. Thus, f is belief-independent on \(\mathcal {D}\), but not strategy-proof on \(\mathcal {D}\).

The previous examples illustrate that even for the domain of single-peaked preferences and for a domain of separable preferences, one cannot simply extend Proposition 2.9 to restricted domains without imposing further conditions. Hence, we add anonymity (and unanimity) to establish the equivalence between belief-independence and strategy-proofness on restricted domains.

Definition 3.5

  • For every permutation p of N into itself, denote by \(\succ _p\) the profile \(\succ _p\ = (\succ _{p(i)})_{i\in N}\). We say that a voting rule \(f:\mathcal {D}^n\rightarrow A\) is anonymous, if for all \(\succ \ \in \mathcal {D}^n\) and all p, \(f(\succ _p)=f(\succ )\).

  • A voting rule \(f:\mathcal {D}^n\rightarrow A\) is called unanimous, if for all \(\succ \ =(\succ _1,\dots ,\succ _n)\in \mathcal {D}^n\) with \(\succ _i\ =\ \succ _j\) for all \(i,j\in N\), we have \(f(\succ )=\tau (\succ _1)=\tau (\succ _2)=\dots =\tau (\succ _n)\).

As the previous examples treat individuals differently, we add anonymity, which is sufficient to establish the equivalence. In order to avoid problems with positive responsiveness on sparse preference domains, we replace it with unanimity, a condition that is implied by positive responsiveness, sovereignty and tops-onlyness on sufficiently rich domains.Footnote 2 Note that while we assume sovereignty throughout this paper, it is not needed for the following proposition.

Proposition 3.6

Let \(f:\mathcal {D}^n\rightarrow A\) be a tops-only, unanimous and anonymous voting rule. Then, f is strategy-proof on \(\mathcal {D}\) if and only if f is belief-independent on \(\mathcal {D}\).

Proof

Strategy-proofness on \(\mathcal {D}\) implies belief-independence on \(\mathcal {D}\) by construction. Hence, we only need to show that tops-onlyness, unanimity, anonymity and belief-independence on \(\mathcal {D}\) imply strategy-proofness on \(\mathcal {D}\).

Let \(f:\mathcal {D}^n\rightarrow A\) be a tops-only, unanimous and anonymous voting rule. Assume, by way of contradiction, that f is belief-independent on \(\mathcal {D}\) but not strategy-proof on \(\mathcal {D}\).

Then, there exists \(i\in N, \succ _i\ \in \mathcal {D}\) and \(\succ _i^\star \ \in \mathcal {D}\) such that \(f(\succ _i^\star ,\succ _{-i})\succcurlyeq _i f(\succ '_i,\succ _{-i})\) for all \(\succ '_i\ \in \mathcal {D} ,\succ _{-i}\ \in \mathcal {D}^{n-1}\) and \(f(\succ _i^\star ,\succ '_{-i})\succ _i f(\succ _i,\succ '_{-i})\) for some \(\succ '_{-i}\ \in \mathcal {D}^{n-1}.\) As f is tops-only, we obtain that \(\tau (\succ _i^\star )\ne \tau (\succ _i)\), as otherwise the outcome would be identical when submitting both preference orderings, while keeping everything else fixed.

Consider \(\overline{\succ }_{-i}\in \mathcal {D}^{n-1}\) with \(\overline{\succ }_j=\ \succ _i\) for all \(j\in N\setminus \{i\}\). By unanimity, we obtain \(f(\succ _i,\overline{\succ }_{-i})=\tau (\succ _i),\) and by belief- independence we get \(f(\succ _i^\star ,\overline{\succ }_{-i})=\tau (\succ _i)\).

Consider \(\overline{\succ }'_{-i}\) with \(\overline{\succ }'_j=\overline{\succ }_j\) for all \(j\in N\setminus \{i,k\}\) for some \(k\ne i\) and \(\overline{\succ }'_k=\ \succ _i^\star\).

Anonymity yields \(f(\succ _i,\overline{\succ }'_{-i})=\tau (\succ _i),\) and due to the belief-independence of f we obtain \(f(\succ _i^\star ,\overline{\succ }'_{-i})=\tau (\succ _i)\). We repeat this argument \(n-1\) times, while replacing all preference orderings in \(\overline{\succ }_{-i}\) one by one by \(\succ _i^\star\). With the corresponding preference profile \(\overline{\succ }^{(n-1)}_{-i}\), we obtain \(f(\succ _i,\overline{\succ }^{(n-1)}_{-i})=\tau (\succ _i)\) and \(f(\succ _i^\star ,\overline{\succ }^{(n-1)}_{-i})=\tau (\succ _i)\ne \tau (\succ _i^\star ),\) which contradicts the unanimity of f. \(\square\)

Only dictatorial voting rules satisfy the conditions of Proposition 2.9 and thus these are the only rules that are strategy-proof and belief-independent on the universal domain. Hence, as dictatorial rules are excluded here by anonymity, one might wonder whether there are rules that satisfy all conditions of Proposition 3.6. Such rules exist, as the following example shows.

Example 3.7

Let \(\mathcal {D}\) be the domain of all single-peaked preferences and let f be the median rule (both with respect to the order \(a_1<\dots <a_m\)). This rule is tops-only, unanimous, anonymous and non-dictatorial.

Note that within this section, we did not impose any conditions on the domain \(\mathcal {D}\) itself, other than it being identical for all individuals.

3.2 Unrestricted message space approach

When taking the basic idea of belief-independence seriously, it makes sense to adopt a different approach of restricting preferences. If we want a voting rule to be belief-independent, it should not depend on any possible belief, even if it seems implausible. For example one might believe that other individuals, even with preferences from a commonly known restricted preference domain \(\mathcal {D}\), submit a preference ordering outside of \(\mathcal {D}\). We explicitly want to allow for such beliefs and such behavior, and thus only restrict the domain of the “true” preferences of the individuals, but not the domain of the voting rule, hence explicitly also allowing for preferences outside of \(\mathcal {D}\) to be submitted. We call this the unrestricted message space approach. This approach could be considered closer to reality in at least some instances, as voting rules used in practice usually do not exclude preference orderings from being submitted. Moreover, this approach has the advantage that we do not require the common preference domain to be common knowledge. It is sufficient for the social planner to know the domain restriction. Additionally, if a voting rule is robustly strategy-proof (see Definition 3.9) on some domain \(\mathcal {D'}\), then truth-telling is a weakly dominant strategy for every individual with a truthful preference in \(\mathcal {D'}\). Note that \(\mathcal {D'}\) needs neither to be known to the individual, nor be the actual common preference domain.

We therefore need to adjust the definitions of strategy-proofness and belief-independence to this setup. Strategy-proofness and belief-independence on a preference domain in this setting are stronger conditions than in the previous section, which is why we call strategy-proofness and belief-independence in this setup robust strategy-proofness and robust belief-independence. The idea of robust strategy-proofness, but without the focus on belief-independence, has also been explored recently in Maskin and Dasgupta (2020).Footnote 3

Definition 3.8

  • A voting rule \(f:\mathcal {P}^n\rightarrow A\) is called robustly belief-independent on \(\varvec{\mathcal {D}}\), if for all \(i\in N\) and all \(\succ _i\ \in \mathcal {D}\) there exists \(\succ _i^\star \ \in \mathcal {P}\) such that

    $$\begin{aligned} f\left( \succ _i^\star ,\succ _{-i}\right) \ \succcurlyeq _i \ f\left( \succ '_i,\succ _{-i}\right) \ \text { for all } \ \succ _{-i}\ \in \mathcal {P}^{n-1}, \succ '_i\ \in \mathcal {P}. \end{aligned}$$

Definition 3.9

  • A voting rule \(f:\mathcal {P}^n \rightarrow A\) is robustly strategy-proof on \(\varvec{\mathcal {D}}\), if for all \(i\in N\) and all \(\succ _i \ \in \mathcal {D},\)

    $$\begin{aligned} f\left( \succ _i,\succ _{-i}\right) \ \succcurlyeq _i \ f\left( \succ '_i,\succ _{-i}\right) \ \text { for all } \ \succ _{-i}\ \in \mathcal {P}^{n-1},\succ _i'\ \in \mathcal {P}. \end{aligned}$$

  • It is straightforward to see that robust strategy-proofness on \(\mathcal {D}\) implies robust belief-independence on \(\mathcal {D}\). Moreover, for \(\mathcal {D}=\mathcal {P}\) robust strategy-proofness coincides with strategy-proofness. The following example illustrates that the two concepts are in general not equivalent.

Example 3.10

Let \(\mathcal {D}=\{abc,cba\}\) and consider the following voting rule:

$$\begin{aligned} f(\succ ):= \left\{ \begin{array}{ll} \tau (\succ _1), &{} \text {if } \tau (\succ _1)=\tau (\succ _2) \\ b, &{} \text {if } \tau (\succ _1)=a \text { and }\tau (\succ _2)=c \\ b, &{} \text {if } \tau (\succ _1)=c \text { and }\tau (\succ _2)=a \\ a, &{} \text {else.} \end{array} \right. \end{aligned}$$

If f is restricted to \(\mathcal {D}\), the last case can never occur and no individual has profitable deviations from truth-telling within \(\mathcal {D}\). But there are profitable deviations if all preference orderings are admissible. If the true preference ordering of individual 1 is \(\succ _1\ =(cba)\), then she has a strict incentive to deviate from truth-telling given that individual 2 submits b as her top alternative. Thus, f is strategy-proof on \(\mathcal {D}\) but not robustly strategy-proof on \(\mathcal {D}\).

Even if robust strategy-proofness and strategy-proofness on a restricted preference domain are different conditions in general, they coincide under mild conditions. Whenever a voting rule is tops-only and the preference domain satisfies a minimal richness condition, the two definitions are equivalent.

Definition 3.11

A preference domain \(\mathcal {D}\) is called minimally rich, if for all \(a\in A\) there exists \(\succ _i\ \in \mathcal {D}\) such that \(\tau (\succ _i)=a\).

The following proposition establishes the equivalence between strategy-proofness on \(\mathcal {D}\) and robust strategy-proofness on \(\mathcal {D}\) given these mild conditions. Note that while we assume sovereignty throughout this paper, it is not needed for the following proposition.

Proposition 3.12

Let \(f:\mathcal {P}^n\rightarrow A\) be a tops-only voting rule and let \(\mathcal {D}\) be minimally rich. Then, f is strategy-proof on \(\mathcal {D}\) if and only if f is robustly strategy-proof on \(\mathcal {D}\).

Proof

Robust strategy-proofness on \(\mathcal {D}\) always implies strategy-proofness on \(\mathcal {D}\). Therefore we only need to show that for a minimally rich preference domain \(\mathcal {D}\) and a tops-only social choice function f strategy-proofness on \(\mathcal {D}\) implies robust strategy-proofness on \(\mathcal {D}\).

As \(\mathcal {D}\) is minimally rich, we can find for every preference profile \(\succ _{-i}\ \in \mathcal {P}^{n-1}\) a preference profile \(\overline{\succ }_{-i} \ \in \mathcal {D}^{n-1}\) with \(\tau (\succ _{j})=\tau (\overline{\succ }_{j})\) for all \(j\in N\setminus \{i\}\), and for every preference ordering \(\succ _i \ \in \mathcal {P}\) a corresponding preference ordering \(\overline{\succ }_i \ \in \mathcal {D}\) with \(\tau (\succ _i)=\tau (\overline{\succ }_i)\).

Since f is tops-only the outcome of f does not change when replacing a preference ordering \(\succ _i\) by \(\overline{\succ }_i\) or when replacing a preference profile \(\succ _{-i}\) by \(\overline{\succ }_{-i}\).

Thus, we obtain

$$\begin{aligned} f\left( \succ _i,\succ _{-i}\right) =f\left( \succ _i,\overline{\succ }_{-i}\right) \text { for all }\succ _i \ \in \mathcal {D}, \succ _{-i}\ \in \mathcal {P}^{n-1} \end{aligned}$$
(1)

and

$$\begin{aligned} f\left( \succ '_i,\succ _{-i}\right) =f\left( \overline{\succ }'_i, \overline{\succ }_{-i}\right) \text { for all } \succ '_i \ \in \mathcal {P}, \succ _{-i} \ \in \mathcal {P}^{n-1}. \end{aligned}$$
(2)

As f is strategy-proof on \(\mathcal {D}\), we have

$$\begin{aligned} f\left( \succ _i,\overline{\succ }_{-i}\right) \ \succcurlyeq _i \ f\left( \overline{\succ }'_i, \overline{\succ }_{-i}\right) \end{aligned}$$
(3)

as we ensured that all preferences are in \(\mathcal {D}\) by using \(\overline{\succ }\) instead of \(\succ\). Thus,

$$\begin{aligned} f\left( \succ _i,\succ _{-i}\right) \overset{(1)}{=} f\left( \succ _i,\overline{\succ }_{-i}\right) \ \overset{(3)}{\succcurlyeq _i} \ f\left( \overline{\succ }'_i, \overline{\succ }_{-i}\right) \overset{(2)}{=} f\left( \succ '_i,\succ _{-i}\right) , \end{aligned}$$

for all \(\succ _i \ \in \mathcal {D}, \succ '_i \ \in \mathcal {P}, \succ _{-i}\ \in \mathcal {P}^{n-1}\), which is exactly the condition of robust strategy-proofness. \(\square\)

The conditions of Proposition 3.12 are only sufficient conditions, as for example dictatorship is both strategy-proof and robustly strategy-proof even on non-minimally rich domains. However, Example 3.10 shows that tops-onlyness is a minimal condition in the sense that the equivalence does not hold in general when the condition is dropped.

The following example that is inspired by Barbie et al. (2006) illustrates that the minimal richness of the preference domain is also such a minimal condition.

Example 3.13

Let \(\mathcal {D}=\{abc,bca,cab\}\) and consider the Borda rule. The Borda rule is strategy-proof on \(\mathcal {D}\) as deviations within the domain attribute relatively more points only to the least favorite alternative. Hence, deviations (within \(\mathcal {D}\)) are never profitable. But if all preferences in \(\mathcal {P}\) are admissible as submitted preference orderings, then there are profitable deviations and thus the Borda rule is not robustly strategy-proof on \(\mathcal {D}\).

Example 3.4 can also be used to illustrate that Proposition 2.9 cannot be easily extended in this setup. Thus, we add further conditions that help establish the equivalence of robust strategy-proofness (on \(\mathcal {D}\)) and robust belief-independence (on \(\mathcal {D}\)). We start by adding anonymity like in the previous section and obtain an analogous result.

Proposition 3.14

Let \(f:\mathcal {P}^n\rightarrow A\) be a tops-only, unanimous and anonymous voting rule. Then, f is robustly strategy-proof on \(\mathcal {D}\) if and only if f is robustly belief-independent on \(\mathcal {D}\).

Proof

The proof works similar to the proof of Proposition 3.6 and can be found in the appendix. \(\square\)

Again, the median rule on the domain of single-peaked preferences serves as an example of a non-dictatorial rule that satisfies all conditions of the proposition. By assuring equal treatments of individuals, one obtains the equivalence, the same holds true if one requires alternatives to be treated equally.

Definition 3.15

For every permutation p of A into itself, denote by \(\succ ^p\) the profile \(\succ ^p\ =(\succ _i^p)_{i\in N}\), where \(\succ _i^p(a)=\ \succ _i(p(a))\) for all \(i\in N\) and all \(a\in A\).

A voting rule is called neutral, if for all \(\succ \ \in \mathcal {P}^n\) and all p, \(f(\succ )^p=p^{-1}(f(\succ ))\).

Another advantage of this way of restricting preferences is that the problems that arise with neutrality on restricted domains can be ignored here, as the voting rule is defined on the universal domain.

Proposition 3.16

Let \(f:\mathcal {P}^n\rightarrow A\) be a tops-only, positive responsive and neutral voting rule. Then, f is robustly strategy-proof on \(\mathcal {D}\) if and only if f is robustly belief-independent on \(\mathcal {D}\).

Proof

By definition robust strategy-proofness on \(\mathcal {D}\) implies robust belief-independence on \(\mathcal {D}\).

Let \(f:\mathcal {P}^n\rightarrow A\) be a tops-only, positive responsive and neutral voting rule. Assume, by way of contradiction, that f is robustly belief-independent on \(\mathcal {D}\) but not robustly strategy-proof on \(\mathcal {D}\). Then there exists \(i\in N, \succ _i\ \in \mathcal {D}\) and \(\succ _i^\star \ \in \mathcal {P}\) such that

$$\begin{aligned} f\left( \succ _i^\star ,\succ _{-i}\right) \ \succcurlyeq _i \ f\left( \succ _i,\succ _{-i}\right) \text { for all }\succ _{-i}\ \in \mathcal {P}^{n-1} \end{aligned}$$

and

$$\begin{aligned} f\left( \succ _i^\star ,\succ '_{-i}\right) \ \succ _i \ f\left( \succ _i,\succ '_{-i}\right) \text { for some } \succ '_{-i}\ \in \mathcal {P}^{n-1}. \end{aligned}$$

As f is tops-only, we obtain that \(\tau (\succ _i^\star )\ne \tau (\succ _i)\) as otherwise the outcome would be identical when submitting both preference orderings, while keeping everything else fixed. Then, individual i can never be pivotal between \(\tau (\succ _i^\star )\) and \(\tau (\succ _i)\). If she were pivotal, then there would exist \(\overline{\succ }_{-i}\in \mathcal {P}^{n-1}\) and \(\hat{\succ }_i,\tilde{\succ }_i\in \mathcal {P}\) such that \(f(\hat{\succ }_i,\overline{\succ }_{-i})=\tau (\succ _i^\star )\) and \(f(\tilde{\succ }_i,\overline{\succ }_{-i})=\tau (\succ _i)\).

By positive responsiveness and tops-onlyness we obtain \(f(\succ _i^\star ,\overline{\succ }_{-i})=\tau (\succ _i^\star )\) and \(f(\succ _i,\overline{\succ }_{-i})=\tau (\succ _i)\) which is a contradiction, since \(\succ _i^\star\) weakly dominates \(\succ _i\) by robust belief-independence, thus individual i can never be pivotal between \(\tau (\succ _i^\star )\) and \(\tau (\succ _i)\).

Since individual i is never pivotal between \(\tau (\succ _i^\star )\) and \(\tau (\succ _i)\), we obtain by neutrality that individual i is never pivotal between any two alternatives. But then, \(\succ _i^\star\) cannot weakly dominate \(\succ _i\), and hence we reach a contradiction, which concludes the proof. \(\square\)

A similar result can be deduced for voting rules defined on common domains, but not without imposing some adjacency condition on the preference domain. This result can be found in the appendix. Note that this result (Proposition 4) is the only one within both approaches that requires a specific condition on the restricted preference domain. The only other time that a condition (namely minimally richness) is imposed on the restricted preference domain \(\mathcal {D}\) is in Proposition 3.12 to ensure the equivalence of robust strategy-proofness and strategy-proofness. Thus, this domain condition is only required for the comparison of the different notions of strategy-proofness in the two approaches.

4 Conclusion and summary

In this paper, we revisit the concept of belief-independence originally introduced in Blin and Satterthwaite (1977). We find that, in general, strategy-proofness and belief-independence are not equivalent on the universal domain, but that the equivalence can be restored when imposing the natural conditions of sovereignty, positive responsiveness and tops-onlyness on the social choice function.

We extend the concept of belief-independence and strategy-proofness to restricted domains using two different approaches: the common domain approach and the unrestricted message space approach. The latter is a novel and compelling approach to strategy-proofness on restricted preference domains. We adjust the concept of strategy-proofness to this approach and show that for tops-only rules and minimally rich preference domains, the concept of robust strategy-proofness coincides with the classical notion of strategy-proofness.

Moreover, for both approaches, we obtained that (robust) strategy-proofness and (robust) belief-independence are equivalent for (i) tops-only, unanimous and anonymous and for (ii) tops-only, positive responsive and neutral voting rules, with an additional adjacency condition for common domains in case (ii).