Cournot–Bertrand endogenous behavior in a differentiated oligopoly with entry deterrence

Abstract

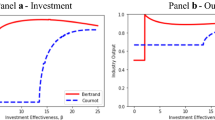
This paper presents a new theoretical justification for the Cournot–Bertrand model to arise in equilibrium when firms have, at the outset, the same cost structure and sell symmetrically differentiated products. The Cournot–Bertrand model assumes some firms compete on price, adjusting their production to meet demand, while others set quantities and let their price adjust until market equilibrium is reached. We show that this may occur endogenously due to the possibility of entry, which may be deterred when some of the incumbents decide to set prices, while others free ride on this behavior and choose quantities.

Appendices

Appendix A

Proof of Lemma 1: Let there be n firms, k of which set quantities with $k\in \left[ 1,n-1\right]$. Without loss of generality let these firms be firm $1,\ldots ,k$. Firms $k+1,\ldots ,n$ set prices. There are such $n-k$ firms.

Aggregating the demand functions (1) for the two types of firms we obtain, respectively, for the firms that set quantities and for the firms that set prices

$$\begin{aligned} P_{k}&=ka-bQ_{k}\left( 1-\gamma \right) -kb\gamma Q\\ P_{n-k}&=(n-k)a-bQ_{n-k}\left( 1-\gamma \right) -(n-k)b\gamma Q \end{aligned}$$

with $P_{k}=\sum _{j=1}^{k}p_{j}$ and $P_{n-k}=\sum _{j=k+1}^{n}p_{j}$ and likewise for quantities. As $Q=Q_{k}+Q_{n-k}$, we have

$$\begin{aligned} P_{k}&=ka-bQ_{k}\left( 1-\gamma \right) -kb\gamma \left( Q_{k} +Q_{n-k}\right) \\ P_{n-k}&=(n-k)a-bQ_{n-k}\left( 1-\gamma \right) -(n-k)b\gamma \left( Q_{k}+Q_{n-k}\right) \end{aligned}$$

or

$$\begin{aligned} Q_{k}&=\frac{ka-P_{k}-kb\gamma Q_{n-k}}{b\left( 1-\gamma +k\gamma \right) }\end{aligned}$$

(7)

$$\begin{aligned} Q_{n-k}&=\frac{(n-k)a-P_{n-k}-(n-k)b\gamma Q_{k}}{b\left( 1-\gamma +(n-k)\gamma \right) } \end{aligned}$$

(8)

Consider one of the quantity setting firms. Its inverse demand is

$$\begin{aligned} p_{i}=a-bq_{i}\left( 1-\gamma \right) -b\gamma \left( Q_{k}+Q_{n-k}\right) \end{aligned}$$

(9)

We want to write this as a function of the quantities of the other quantity setting firms, $Q_{k-i}$, and of the sum of prices of the price setting firms, $P_{n-k}$. Plugging (8) into (9) and simplifying we obtain

$$\begin{aligned} p_{i}=\frac{a\left( 1-\gamma \right) -bq_{i}\left( 1-\gamma \right) \left( \gamma \left( n-k\right) +1\right) +\gamma P_{n-k}-Q_{k-i}b\gamma \left( 1-\gamma \right) }{1-\gamma +\left( n-k\right) \gamma } \end{aligned}$$

(10)

where $Q_{k-i}=Q_{k}-q_{i}$.

Consider now one of the price setting firms. The demand for its product is

$$\begin{aligned} q_{i}=\frac{a-p_{i}-b\gamma \left( Q_{k}+Q_{n-k}\right) }{b\left( 1-\gamma \right) } \end{aligned}$$

(11)

We want to write this as a function of the quantities of the other quantity setting firms, $Q_{k}$, and of the sum of the prices of the other price setting firms, $P_{n-k-i}$. Plugging (8) into (11) and simplifying we obtain

$$\begin{aligned} q_{i}=\frac{a\left( 1-\gamma \right) -p_{i}\left( \gamma \left( n-k-1\right) +1-\gamma \right) +\gamma P_{n-k-i}-b\gamma \left( 1-\gamma \right) Q_{k}}{b\left( 1-\gamma \right) \left( \gamma \left( n-k\right) +1-\gamma \right) } \end{aligned}$$

(12)

where $P_{n-k-i}=\left( P_{n-k}-p_{i}\right)$.

The profit function of the quantity setting firms is then

$$\begin{aligned} \pi _{i}^{Q}&=(p_{i}-c)q_{i}\\&=\left( \frac{a\left( 1-\gamma \right) -bq_{i}\left( 1-\gamma \right) \left( \gamma \left( n-k\right) +1\right) +\gamma \sum _{j=k+1}^{n}p_{j} -\sum _{\begin{array}{c} j=1\\ j\ne i \end{array}}^{k}q_{j}b\gamma \left( 1-\gamma \right) }{1-\gamma +\gamma \left( n-k\right) }-c\right) q_{i} \end{aligned}$$

and the first-order conditions for profit maximization are

$$\begin{aligned} \frac{\partial \pi _{i}^{Q}}{\partial q_{i}}=\frac{a\left( 1-\gamma \right) -2bq_{i}\left( 1-\gamma \right) \left( \gamma \left( n-k\right) +1\right) +\gamma \sum _{j=k+1}^{n}p_{j}-\sum _{\begin{array}{c} j=1\\ j\ne i \end{array}}^{k}q_{j} b\gamma \left( 1-\gamma \right) }{1-\gamma +\gamma \left( n-k\right) }-c=0 \end{aligned}$$

The profit function of the price setting firms is then

$$\begin{aligned} \pi _{i}^{P}&=(p_{i}-c)q_{i}\\&=(p_{i}-c)\frac{a\left( 1-\gamma \right) -p_{i}\left( \gamma \left( n-k-1\right) +1-\gamma \right) +\gamma \sum _{\begin{array}{c} j=k+1\\ j\ne i \end{array} }^{n}p_{j}-b\gamma \left( 1-\gamma \right) \sum _{j=1}^{k}q_{j}}{b\left( 1-\gamma \right) \left( \gamma \left( n-k\right) +1-\gamma \right) } \end{aligned}$$

and the first-order conditions for profit maximization are

$$\begin{aligned} \frac{\partial \pi _{i}^{P}}{\partial p_{i}}&=\frac{a\left( 1-\gamma \right) -p_{i}\left( \gamma \left( n-k-1\right) +1-\gamma \right) +\gamma \sum _{\begin{array}{c} j=k+1\\ j\ne i \end{array}}^{n}p_{j}-b\gamma \left( 1-\gamma \right) \sum _{j=1}^{k}q_{j}}{b\left( 1-\gamma \right) \left( \gamma \left( n-k\right) +1-\gamma \right) }\\&\quad +(p_{i}-c)\frac{-\left( \gamma \left( n-k-1\right) +1-\gamma \right) }{b\left( 1-\gamma \right) \left( \gamma \left( n-k\right) +1-\gamma \right) }=0 \end{aligned}$$

Under symmetry we have $q_{1}=\cdots =q_{k}=q$ and $p_{k+1}=\cdots =p_{n}=p$. Solving the system of first-order conditions with respect to p, q yields:

$$\begin{aligned} p^{P}&=c+\frac{\left( 1-\gamma \right) \left( 2-\gamma +2\gamma \left( n-k\right) \right) }{\left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) \left( n-k\right) \right) }\left( a-c\right) \\ q^{Q}&=\frac{2\left( \gamma \left( n-k\right) +1\right) -3\gamma }{\left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) \left( n-k\right) \right) }\frac{a-c}{b} \end{aligned}$$

Plugging these prices and quantities into (12) and (10) yields the quantity of a price setting firm (say firm $k+1$):

$$\begin{aligned} q_{k+1}=\frac{\left( \gamma \left( n-k-2\right) +1\right) \left( \gamma \left( 2\left( n-k-1\right) +1\right) +2\right) }{\left( \gamma \left( n-k-1\right) +1\right) \left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) \left( n-k\right) \right) }\frac{a-c}{b} \end{aligned}$$

and the price of a quantity setting firm (say firm 1):

$$\begin{aligned} p_{1}=c+\frac{\left( 1-\gamma \right) \left( 2-3\gamma +2\gamma \left( n-k\right) \right) \left( \gamma \left( n-k\right) +1\right) }{\left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) \left( n-k\right) \right) \left( 1-\gamma +\gamma \left( n-k\right) \right) }\left( a-c\right) \end{aligned}$$

It can be showed that the quantities of both types of firms are always positive.

Finally, normalized equilibrium profits (i.e., profits divided by $\frac{\left( a-c\right) ^{2}}{b})$ are

$$\begin{aligned} \pi _{i}^{Q}(n,k)&=(p_{1}-c)q^{Q}\\&=\frac{\left( 1-\gamma \right) \left( \gamma \left( n-k\right) +1\right) }{\left( 1-\gamma +\gamma \left( n-k\right) \right) } \frac{\left( \gamma -2\gamma \left( n-k\right) -2+2\gamma \right) ^{2} }{\left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) \left( n-k\right) \right) ^{2}} \end{aligned}$$

and

$$\begin{aligned} \pi _{i}^{P}(n,k)&=(p^{P}-c)q_{k+1}\\&=\frac{\left( 1-\gamma \right) \left( \gamma \left( n-k-1\right) +1-\gamma \right) }{\left( 1-\gamma +\gamma \left( n-k\right) \right) } \frac{\left( \gamma -2\gamma \left( n-k\right) -2\right) ^{2}}{\left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) \left( n-k\right) \right) ^{2}} \end{aligned}$$

with

$$\begin{aligned} \pi _{i}^{Q}(n,n)=\frac{1}{\left( \gamma \left( n-1\right) +2\right) ^{2}} \end{aligned}$$

and

$$\begin{aligned} \pi _{i}^{P}(n,0)=\frac{\left( 1-\gamma \right) \left( \gamma \left( n-2\right) +1\right) }{\left( \gamma \left( n-1\right) +1\right) \left( -3\gamma +n\gamma +2\right) ^{2}} \end{aligned}$$

Given the equilibrium profits presented above, it is straightforward to check that:

(i) $\pi _{i}^{Q}(n,k)-\pi _{i}^{P}(n,k)>0:$

$$\begin{aligned}&\pi _{i}^{Q}(n,k)-\pi _{i}^{P}(n,k)\\&\quad =\frac{2\gamma ^{3}\left( 1-\gamma \right) }{\left( 1-\gamma +\gamma \left( n-k\right) \right) \left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) \left( n-k\right) \right) ^{2}}>0 \end{aligned}$$

(ii) $\pi _{i}^{Q}(n,k+1)>\pi _{i}^{Q}(n,k).$

Let $k\le n-1$. The result follows from the sign of

$$\begin{aligned}&\frac{\partial \pi _{i}^{Q}(n,k)}{\partial k}=\gamma ^{3}\left( 1-\gamma \right) \left( 2-\gamma +2\gamma \left( n-k-1\right) \right) \\&\quad \times \frac{4k^{2}\gamma ^{2}\left( n+1\right) -2k\gamma \left( 4n+3\gamma -2n\gamma +4n^{2}\gamma -2\right) +\gamma ^{2}\left( 15n-8n^{2}+4n^{3} -9\right) +2\gamma \left( 4n^{2}-8n+9\right) +4\left( n-2\right) }{\left( 1-\gamma +\gamma \left( n-k\right) \right) ^{2}\left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) \left( n-k\right) \right) ^{3}} \end{aligned}$$

This expression has the same sign as the numerator, which is a U-shaped parabola in k minimized at

$$\begin{aligned} k^{*}=\frac{2\left( 2n-1\right) \left( n\gamma +1\right) +3\gamma }{4\gamma \left( n+1\right) } \end{aligned}$$

As $k^{*}>n-1\$if and only if $n>\frac{2-7\gamma }{2\left( 2-\gamma \right) }$, which is always true, we have that the minimum of the numerator occurs at $k=n-1$ and is equal to

$$\begin{aligned} 4\left( 1-\gamma \right) \left( n-2\right) +6\gamma +\gamma ^{2}\left( n+1\right) >0 \end{aligned}$$

Therefore, the derivative is positive.

If $k>n-1$ we have that

$$\begin{aligned}&\pi _{i}^{Q}(n,n)-\pi _{i}^{Q}(n,n-1)\\&\quad =\gamma ^{3}\frac{\left( n-2\right) \left( 4\gamma ^{2}+n\gamma ^{3}+8\right) +24\gamma +\gamma ^{3}+8n\gamma ^{2}-20n\gamma +4n^{2}\gamma \left( 1-\gamma \right) }{\left( \gamma \left( n-1\right) +2\right) ^{2}\left( 4\gamma -2n\gamma +\gamma ^{2}+n\gamma ^{2}-4\right) ^{2}} \end{aligned}$$

The numerator is minimized in n at $n^{*}=\frac{\gamma ^{2}+2-4\gamma }{\gamma \left( \gamma -2\right) }<1$. Therefore, the minimum occurs at $n=2$ and the numerator takes value $\left( 2-2\right) \left( 4\gamma ^{2}+2\gamma ^{3}+8\right) +24\gamma +\gamma ^{3}+8*2\gamma ^{2}-20*2\gamma +4*2^{2}\gamma \left( 1-\gamma \right) =\gamma ^{3}>0.$

(iii) If firms are of the same type, profits decrease with the number of firms

$$\begin{aligned} \frac{\partial \pi _{i}^{Q}(n,n)}{\partial n}&=\frac{-2\gamma }{\left( \gamma \left( n-1\right) +2\right) ^{3}}<0\\ \frac{\partial \pi _{i}^{P}(n,0)}{\partial n}&=-\gamma \left( 1-\gamma \right) \frac{2n^{2}\gamma ^{2}+n\left( 4\gamma -7\gamma ^{2}\right) -8\gamma +7\gamma ^{2}+2}{\left( \gamma \left( n-1\right) +1\right) ^{2}\left( \gamma \left( n-3\right) +2\right) ^{3}}<0 \end{aligned}$$

because $2n^{2}\gamma ^{2}+n\left( 4\gamma -7\gamma ^{2}\right) -8\gamma +7\gamma ^{2}+2$ is increasing in n for $n\ge 2$, and evaluated at $n=2$ is equal to $\gamma ^{2}+2>0.$ In addition

$$\begin{aligned} \pi _{i}^{Q}(n,n)-\pi _{i}^{P}(n,0)=\frac{\gamma ^{3}\left( n-1\right) ^{2}\left( \gamma \left( n-2\right) +2\right) }{\left( \gamma \left( n-1\right) +1\right) \left( \gamma \left( n-3\right) +2\right) ^{2}\left( \gamma \left( n-1\right) +2\right) ^{2}}>0 \end{aligned}$$

(iv) $\pi _{i}^{Q}(n,k)>\pi _{i}^{Q}(n+1,k+1)$ and $\pi _{i} ^{P}(n,k)>\pi _{i}^{P}(n+1,k+1).$

Let the number of price setters be given by g: then $k=\left( n-g\right)$. If $g=0$ the result follows from the fact that if all firms are Cournot competitors profits decrease with the number of firms. If $g\ge 1,$

$$\begin{aligned} \frac{\partial \pi _{i}^{Q}(n,n-g)}{\partial n}&=-\frac{2\gamma \left( 1-\gamma \right) \left( g\gamma +1\right) \left( 2\gamma \left( g-1\right) +2-\gamma \right) ^{3}}{\left( \gamma \left( g-1\right) +1\right) \left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) g\right) ^{3}}<0\\ \frac{\partial \pi _{i}^{P}(n,n-g)}{\partial n}&=-\frac{2\gamma \left( 1-\gamma \right) \left( \gamma \left( g-1\right) +1-\gamma \right) \left( \gamma \left( 2g-1\right) +2\right) ^{2}\left( 2\gamma \left( g-1\right) +2-\gamma \right) }{\left( \gamma \left( g-1\right) +1\right) \left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) g\right) ^{3}}<0 \end{aligned}$$

$\blacksquare$

Proof of Proposition 1:

Parts (a) and (d) are trivial. If the number of firms does not depend on the incumbents’ decision no firm would profit from being a price competitor instead of a quantity competitor.

(b) Assume that $g^{*}(f)=1$. Having $n-1$ quantity setters and one price setter is an equilibrium if any quantity setter does not profit from changing to become a price setter, and the price setter does not profit from changing to become a quantity setter, which will trigger entry.

The first part is implied by

$$\begin{aligned} \pi _{i}^{Q}(n,n-1)>\pi _{i}^{Q}(n,n-2)>\pi _{i}^{P}(n,n-2). \end{aligned}$$

As for the second part, the price setter changing to become a quantity setter, which will trigger entry, is not profitable if

$$\begin{aligned} \pi _{i}^{P}(n,n-1)>\pi _{i}^{Q}(n+1,n+1) \end{aligned}$$

which, with

$$\begin{aligned} \pi _{i}^{Q}(n+1,n+1)&=\frac{1}{\left( \gamma n+2\right) ^{2}}\\ \pi _{i}^{P}(n,n-1)&=\frac{\left( 1-\gamma \right) ^{2}\left( \gamma +2\right) ^{2}}{\left( 4\gamma -2n\gamma +\gamma ^{2}+n\gamma ^{2}-4\right) ^{2}} \end{aligned}$$

is equivalent to

$$\begin{aligned} 1-\frac{\left( 1-\gamma \right) \left( \gamma +4\right) \left( \gamma +2\right) }{\gamma \left( 4-2\gamma -\gamma ^{2}\right) }<n<\frac{2-\gamma }{\gamma ^{2}} \end{aligned}$$

with the first inequality verified trivially.

(c) Assume that $g^{*}(f)>1$.

(i) Having all n firms choosing quantities is a Nash equilibrium (with entry), because no firm profits from changing its decision. If any single firm decides to be a price setter this is not enough to deter entry and the profit of this firm will decrease.

(ii) Having $n-g^{*}(f)$ firms choosing quantities and the remaining $g^{*}(f)$ firms choosing prices is a Nash equilibrium (with no entry) if no firm wants to change its decision.

Any price setter does not want to change its decision (which leads to entry) if and only if

$$\begin{aligned} \pi ^{P}(n,n-g^{*}(f))>\pi ^{Q}(n+1,n-g^{*}(f)+2) \end{aligned}$$

Any quantity setter does not want to change its decision (which leads to no entry) if and only if

$$\begin{aligned} \pi ^{Q}(n,n-g^{*}(f))>\pi ^{P}(n,n-g^{*}(f)-1) \end{aligned}$$

which is always true.

Finally, regardless of the value taken by $g^{*}(f)$, having more than $g^{*}(f)$ firms choosing prices is not an equilibrium as, if one of these firms deviated to become a quantity setter, this would not lead to entry and would be profitable. In addition, having at least one but less than $g^{*}(f)$ firms choosing prices is not also an equilibrium as the deviation to become a quantity setter would still lead to entry and would be profitable.$\blacksquare$

Proof of Corollary 1: For this equilibrium to exist, we need

$$\begin{aligned} \pi ^{Q}(n+1,k+1)&<f<\pi ^{Q}(n+1,k+2)\\ \pi ^{P}(n,k)&>\pi ^{Q}(n+1,k+2) \end{aligned}$$

with $k=\frac{n}{2}$.

The interval in the first condition always exists.

We now move to the second condition, assuming n is even and $k=n/2$ and using

$$\begin{aligned} \pi ^{P}(n,n/2)&=\frac{\left( 1-\gamma \right) \left( \gamma \left( n-4\right) +2\right) \left( \gamma \left( n-1\right) +2\right) ^{2} }{\left( \gamma \left( n-2\right) +2\right) \left( 4+4\gamma \left( n-2\right) +\gamma ^{2}\left( n^{2}-5n+3\right) \right) ^{2}}\\ \pi ^{Q}(n+1,n/2+2)&=\frac{\left( 1-\gamma \right) \left( \gamma \left( n-2\right) +2\right) \left( \gamma \left( n-5\right) +2\right) ^{2} }{\left( \gamma \left( n-4\right) +2\right) \left( 4+2\gamma \left( 2n-5\right) +\gamma ^{2}\left( n^{2}-6n+2\right) \right) ^{2}} \end{aligned}$$

It can be shown that $\pi ^{P}(n,n/2)-\pi ^{Q}(n+1,n/2+2)$ has the same sign as

$$\begin{aligned} g(n,\gamma )&=-\gamma ^{3}\left( -n^{3}+12n^{2}-37n+22\right) +\gamma ^{2}\left( 6n^{2}-44n+62\right) \\&\quad +\gamma \left( 12n-40\right) +8 \end{aligned}$$

for $n\ge 6$.

Both roots of $\frac{\partial g(n,\gamma )}{\partial \gamma }$ with respect to $\gamma$ are negative for $n\ge 8$, so this derivative is always positive and $g(n,\gamma )$ increases with $\gamma$. As $g(n,0)=8>0$ we have that $g(n,0)>0$ for all $\gamma$ if $n\ge 8$.

For the other values of n we proceed case by case. Inequality $\pi ^{P}(n,k)>\pi ^{Q}(n+1,k+2)$ with $k=n/2$ is equivalent to:

(i) if $n=2$: $\gamma <0.78078$ as presented in the numeric example.

(ii) if $n=4$:

$$\begin{aligned} \frac{\left( 1-\gamma \right) \gamma \left( 4\gamma -9\gamma ^{2}-\gamma ^{3}+4\right) \left( 44\gamma +8\gamma ^{2}-27\gamma ^{3}+\gamma ^{4}+16\right) }{4\left( \gamma +1\right) \left( -8\gamma +\gamma ^{2}-4\right) ^{2}\left( -3\gamma +3\gamma ^{2}-2\right) ^{2}}>0 \end{aligned}$$

which holds if and only if $\gamma <0.87067$.

(iii) if $n=6$:

$$\begin{aligned} \frac{\gamma \left( 1-\gamma \right) \left( 2-\gamma \right) \left( 9\gamma +8\gamma ^{2}+2\right) \left( 108\gamma +228\gamma ^{2}+161\gamma ^{3}+28\gamma ^{4}+16\right) }{4\left( \gamma +1\right) \left( 2\gamma +1\right) \left( 16\gamma +9\gamma ^{2}+4\right) ^{2}\left( 7\gamma +\gamma ^{2}+2\right) ^{2}}>0 \end{aligned}$$

which is true for any $\gamma \in \left( 0,1\right) .$

This concludes the proof.$\blacksquare$

Appendix B

In this appendix we detail the three firm example in Sect. 3.2.1 for the case of cost asymmetries.

It is straightforward to show, following the same steps as in the proof of Lemma 1, that in the presence of cost asymmetries the equilibrium profits are given by

$$\begin{aligned} \pi _{i}^{Q}(n,k,Z)&=\frac{\left( 1+\gamma \left( n-k\right) \right) \left( \left( \gamma -1\right) \left( 3\gamma +2k\gamma -2n\gamma -2\right) +Z\gamma \left( n-k\right) \left( 2\gamma +k\gamma -n\gamma -1\right) \right) ^{2}}{\left( 1-\gamma \right) \left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) \left( n-k\right) \right) ^{2}\left( 1-\gamma +\gamma \left( n-k\right) \right) }\\ \pi _{i}^{P}(n,k,Z)&=\frac{\left( 1+\gamma \left( n-k-2\right) \right) \left( \left( 1-\gamma \right) \left( 2-\gamma +2\gamma \left( n-k\right) \right) -Z\left( \begin{array}{c} \gamma \left( k-2n+3\right) +\\ \gamma ^{2}\left( 2n+k\left( k-n-1\right) -1\right) -2 \end{array} \right) \right) ^{2}}{\left( 1-\gamma \right) \left( \left( 2-3\gamma \right) \left( \gamma \left( n-1\right) +2\right) +2\gamma \left( \gamma \left( n-2\right) +2\right) \left( n-k\right) \right) ^{2}\left( 1-\gamma +\gamma \left( n-k\right) \right) } \end{aligned}$$

where $Z=\frac{c(1-\alpha )}{a-c}$ is a normalization of the difference in the marginal costs of quantity setters, c, and price setters, $\alpha c.$

The payoffs involved in Sect. 3 are:

$$\begin{aligned} \pi _{i}^{Q}(3,3,Z)&=\frac{1}{4\left( \gamma +1\right) ^{2}}\\ \pi _{i}^{Q}(3,2,Z)&=\frac{\left( 1-\gamma \right) \left( \gamma +1\right) \left( \gamma +Z\gamma -2\right) ^{2}}{4\left( -\gamma +2\gamma ^{2}-2\right) ^{2}}\\ \pi _{i}^{Q}(3,1,Z)&=\frac{\left( \left( \gamma +2\right) \left( 1-\gamma \right) -2\gamma Z\right) ^{2}\left( 2\gamma +1\right) }{4\left( 1-\gamma \right) \left( \gamma +1\right) \left( \gamma ^{2}-3\gamma -2\right) ^{2}}\\ \pi _{i}^{Q}(2,1,Z)&=\frac{\left( \gamma +1\right) \left( 1-\gamma \right) \left( 2-\gamma \left( Z+1\right) \right) ^{2}}{\left( 3\gamma ^{2}-4\right) ^{2}} \end{aligned}$$

All quantities involved in these cases must be positive, that is, cost differences cannot be too large to ensure positive quantities for all firms involved.

The equilibrium quantities (divided by $\frac{a-c}{b}$) are

$$\begin{aligned} q^{Q}&=\frac{\left( 3\gamma -2\left( \gamma \left( n-k\right) +1\right) \right) \left( 1-\gamma \right) +\gamma \left( n-k\right) \left( \gamma \left( n-k\right) +1-2\gamma \right) Z}{\left( 1-\gamma \right) \left( 2\left( \gamma \left( 2k-3n+4\right) -2\right) +\gamma ^{2}\left( 7n+2kn-2n^{2}-4k-3\right) \right) }\\ q^{P}&=\frac{\left( \begin{array}{c} \left( \gamma \left( n-k-2\right) +1\right) \left( \gamma \left( 2\left( n-k-1\right) +1\right) +2\right) \left( 1-\gamma \right) \\ -\left( \gamma \left( k-2n+3\right) +\gamma ^{2}\left( -k+2n-kn+k^{2} -1\right) -2\right) \left( \gamma \left( n-k-2\right) +1\right) Z \end{array} \right) }{-\left( 1-\gamma \right) \left( \gamma \left( n-k-1\right) +1\right) \left( 2\left( \gamma \left( 2k-3n+4\right) -2\right) +\gamma ^{2}\left( -4k+7n+2kn-2n^{2}-3\right) \right) } \end{aligned}$$

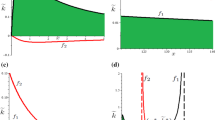
The following table presents the upper and lower bounds on Z, such that all quantities are positive.

	$q^{Q}>0$	$q^{P}>0$
$n=3;k=2$	$Z<\frac{2-\gamma }{\gamma }$	$Z>\frac{\gamma +\gamma ^{2} -2}{\left( \gamma +1\right) (2-\gamma )}$
$n=3;k=1$	$Z<\frac{1}{2}\frac{2-\gamma }{\gamma }-\frac{1}{2}\gamma$	$Z>\frac{1}{2}\left( 3\gamma +2\right) \frac{1-\gamma }{-\gamma +\gamma ^{2}-1}$
$n=2;k=1$	$Z<\frac{2-\gamma }{\gamma }$	$Z>\frac{\gamma +\gamma ^{2} -2}{\left( 2-\gamma ^{2}\right) }$

All these are implied by¹⁵

$$\begin{aligned} \underline{Z_{1}}:=\frac{\gamma +\gamma ^{2}-2}{\left( \gamma +1\right) (2-\gamma )}<Z<\overline{Z_{1}}:=\frac{1}{2}\frac{2-\gamma }{\gamma }-\frac{1}{2}\gamma \end{aligned}$$

This merely states that the cost differences between the two types of firms cannot be too large.

With respect to the preliminary assumption in Sect. 3:

$$\begin{aligned} \pi ^{Q}(3,1,Z)<\pi ^{Q}(3,2,Z)<\pi ^{Q}(3,3,Z)<\pi ^{Q}(2,1,Z) \end{aligned}$$

one needs that $\pi ^{Q}(3,3)<\pi ^{Q}(2,1),$ $\pi _{i}^{Q}(3,2)<\pi _{i} ^{Q}(3,3)$, $\pi _{i}^{Q}(3,1)<\pi _{i}^{Q}(3,2)$, which yield, respectively:

$$\begin{aligned} \text { }Z&<\overline{Z_{2}}:=\frac{2-\gamma }{\gamma }-\frac{\left( 4-3\gamma ^{2}\right) }{2\gamma \sqrt{\left( 1-\gamma \right) \left( \gamma +1\right) ^{3}}}<1\\ Z&>\underline{Z_{2}}:=\frac{2-\gamma }{\gamma }-\frac{\left( \gamma -2\gamma ^{2}+2\right) }{\gamma \sqrt{\left( 1-\gamma \right) \left( \gamma +1\right) ^{3}}}\\ \underline{Z_{3}}&<Z<\overline{Z_{3}} \end{aligned}$$

with

$$\begin{aligned} \underline{Z_{3}}&:=\frac{\left( \gamma -1\right) \left( \begin{array}{c} -28\gamma -18\gamma ^{2}+23\gamma ^{3}+25\gamma ^{4}+2\gamma ^{5}-8\gamma ^{6}-7\gamma ^{7}+\gamma ^{8}-8\\ +\sqrt{2\gamma +1}\left( \gamma +1\right) \left( \gamma ^{2}-3\gamma -2\right) \left( 2\gamma ^{2}-\gamma -2\right) \left( 2-\gamma +\gamma ^{2}\right) \end{array} \right) }{\gamma \left( 36\gamma +7\gamma ^{2}-42\gamma ^{3}-11\gamma ^{4}+8\gamma ^{5}-3\gamma ^{6}+6\gamma ^{7}-\gamma ^{8}+12\right) }\\ \overline{Z_{3}}&:=\frac{\left( \gamma -1\right) \left( \begin{array}{c} -28\gamma -18\gamma ^{2}+23\gamma ^{3}+25\gamma ^{4}+2\gamma ^{5}-8\gamma ^{6}-7\gamma ^{7}+\gamma ^{8}-8\\ -\sqrt{2\gamma +1}\left( \gamma +1\right) \left( \gamma ^{2}-3\gamma -2\right) \left( 2\gamma ^{2}-\gamma -2\right) \left( 2-\gamma +\gamma ^{2}\right) \end{array} \right) }{\gamma \left( 36\gamma +7\gamma ^{2}-42\gamma ^{3}-11\gamma ^{4}+8\gamma ^{5}-3\gamma ^{6}+6\gamma ^{7}-\gamma ^{8}+12\right) } \end{aligned}$$

The first (second) condition imposes that the individual profit in a “pure” Cournot tripoloy is lower (higher) than a quantity setters’ profit when it is competing with a price setter. This is easier to verify if the quantity setter’s cost disadvantage (advantage) is sufficiently low (high). The third condition imposes that the profit of a quantity setter when competing with another quantity setter plus a price setter is higher than when competing with two price setters.

In addition, two more conditions are needed to have an equilibrium with Bertrand-Cournot competition:

(i) $\pi ^{P}(2,1)>\pi ^{Q}(3,3)$, which holds for

$$\begin{aligned} Z>\underline{Z_{4}}:=\gamma \frac{\gamma +2\gamma ^{2}-2}{2\left( \gamma +1\right) \left( 2-\gamma ^{2}\right) } \end{aligned}$$

and;

(ii) $\pi ^{Q}(2,1)>\pi ^{P}(2,0)$, which holds for

$$\begin{aligned} Z<\overline{Z_{4}}:=\frac{\gamma ^{3}}{\left( \gamma +2\right) \left( 2-\gamma ^{2}\right) } \end{aligned}$$

The first condition ensures that it is more profitable to deter entry by being a price setter than to be a quantity setter and allow entry. This is more likely to happen the greater the cost disadvantage of quantity setters. The second condition ensures that the quantity setter in the Cournot–Bertrand duopoly does not want to switch to be a price competitor, which is easier to verify when the quantity setters’ cost disadvantage is small.

Let $\underline{Z}=\max \left\{ \underline{Z_{1}},\underline{Z_{2} },\underline{Z_{3}},\underline{Z_{4}}\right\}$ and $\overline{Z} =\min \left\{ \overline{Z_{1}},\overline{Z_{2}},\overline{Z_{3}} ,\overline{Z_{4}}\right\}$. Figure 2 presents these thresholds and for $\underline{Z}<Z<\overline{Z}$ an equilibrium with Cournot–Bertrand competition exists.