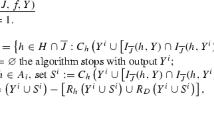Matching with contracts: calculation of the complete set of stable allocations

Abstract

For a many-to-many matching model with contracts, where all the agents have substitutable preferences, we provide an algorithm to compute the full set of stable allocations. This is based on the lattice structure of such set.

Appendix

1.1 A.1 Obtaining the optimal stable allocations and the counterposition of interests

Pepa (2015) developed two symmetric deferred acceptance algorithms called doctors offering algorithm (DOA) and hospitals offering algorithm (HOA), that can be used to obtain the optimal-for-doctors and optimal-for-hospitals stable allocations, respectively, in a many-to-many matching model with contracts, where all the agents have substitutable preferences.

Before transcribing the formal definition of HOA, we need to introduce some notation.

We consider the contracts wanted by their respective doctors under a current allocation and separate such contracts according to the hospital $h\in H$ they appoint. Given $Y\subseteq \mathbf {X}$ and $h\in H$, we define

$$\begin{aligned} I(h,Y)=\left\{ y\in \mathbf {X}_{h}:y\in C_{y_{_{D}}}(Y\cup \{y\})\right\} . \end{aligned}$$

Moreover, we denote

$$\begin{aligned} I(H,Y)=\bigcup \limits _{h\in H}I(h,Y). \end{aligned}$$

Also, we say that an allocation $Y\subseteq \mathbf {X}$ satisfies the inclusion property for hospitals if $Y\subseteq C_{H}\left( I(H,Y)\right) .$ This means that Y is either stable or solely blocked by contracts that hospitals would like to incorporate while retaining all their contracts in Y.

Now, we are ready to describe the HOA. Consider an initial allocation satisfying the Inclusion Property for Hospitals; every doctor is asked about every existing contract (including those contained in the initial allocation), in case the doctor would like to sign such a contract when it is available together with all contracts in that allocation. Then, each hospital selects its favorite set of contracts among those which obtained a positive answer in the previous step (these are the only contracts with real chances of being accepted later by doctors), and offer them to the corresponding doctors. Finally, each doctor accepts the best set of contracts among the received offers. The set of all accepted contracts replaces the initial allocation and the process starts again. The algorithm stops when exactly the same contracts are accepted by doctors in two consecutive iterations. Formally:

The last set of all accepted contracts forms a stable allocation according to Pepa (2015). In that paper, it is shown that for every $i\ge 0,$ the outcome $X^{i+1}$ of applying step 3 in the ith iteration of HOA is individually rational and satisfies the Inclusion Property for Hospitals. Then, HOA stops, because in every iteration, all doctors improve weakly and, given that $X^{i+1}\ne X^{i},$ at least one of them improves strictly.

To prove that the output of HOA is a stable allocation, it is shown that $Z=C_{H}\left( I\left( H,Z\right) \right)$ implies $Z\in S(\mathbf {X})$ for every $Z\subseteq \mathbf {X}$ satisfying the Inclusion Property for Hospitals. Then it is verified that the output of HOA fulfills these requirements.

Remark 16

The formal definition of DOA can be obtained symmetrically by interchanging the roles of doctors and hospitals.

Observe that the empty allocation $\varnothing$ satisfies the inclusion property for hospitals and its symmetric inclusion property for doctors,³ so HOA and DOA converge to stable allocations by starting with $\varnothing$ as input. Let DOA(Y) and HOA(Y) denote the stable allocations obtained by applying DOA and HOA, respectively, with the allocation Y as input. Next, we sketch the proof that $HOA\left( \varnothing \right)$ and $DOA\left( \varnothing \right)$ are the optimal-for-hospital and optimal-for-doctors stable allocations. See Pepa (2015) for details.

First, it is proved the existence of a counterposition of interests relative to Blair’s partial orders between both sides of the market, this is, Y $\succeq _{H}^{B}Z$ if and only if $Z\succeq _{D}^{B}Y$ for any $Y,Z\in S\left( \mathbf {X}\right)$.

Later, it is shown that:

• (i) If Y satisfies the inclusion property for doctors, then $Z\succeq _{H}^{B}Y$ if and only if $Z\succeq _{H}^{B}DOA(Y)$ and

• (ii) If Y satisfies the inclusion property for hospitals, then $Z\succeq _{D}^{B}Y$ if and only if $Z\succeq _{D}^{B}HOA(Y).$

As a consequence, because $Y\succeq _{H}^{B}\varnothing$ and $Y\succeq _{D}^{B}\varnothing$ and the previously mentioned counterposition of interests, it follows that

$$\begin{aligned} HOA\left( \varnothing \right) \succeq _{H}^{B}Y\succeq _{H}^{B}DOA\left( \varnothing \right) \text { and }DOA\left( \varnothing \right) \succeq _{D}^{B}Y\succeq _{D}^{B}HOA\left( \varnothing \right) , \end{aligned}$$

for every stable allocation $Y\subseteq \mathbf {X}.$

Now, observe that $Y\succeq _{D}^{B}Z$ and $Y\succeq _{H}^{B}Z$ imply $Y\succeq _{D}Z$ and $Y\succeq _{H}Z$, respectively, where $\succeq _{D}$ and $\succeq _{H}$ denote the elementary unanimous-for-doctors and unanimous-for-hospitals partial orders.⁴ Therefore

$$\begin{aligned} HOA\left( \varnothing \right) \succeq _{H}Y\succeq _{H}DOA\left( \varnothing \right) \text { and }DOA\left( \varnothing \right) \succeq _{D}Y\succeq _{D}HOA\left( \varnothing \right) . \end{aligned}$$

for every stable allocation $Y\subseteq \mathbf {X}.$

Therefore, $HOA\left( \varnothing \right) =O^{H}$ and $DOA\left( \varnothing \right) =O^{D}.$

1.2 A.2 Lattice structure

Given $Y,Z\in S\left( \mathbf {X}\right)$, consider the binary operations consisting of the application of DOA and HOA starting from the union of both stable allocations:

$$\begin{aligned} Y\vee _{H}Z=DOA(C_{H}\left( Y\cup Z\right) ) \end{aligned}$$

and

$$\begin{aligned} Y\wedge _{H}Z=HOA(C_{D}\left( Y\cup Z\right) ). \end{aligned}$$

The resulting allocations are, respectively, the l.u.b. and the g.l.b. for Z and Y according to $\succeq _{H}^{B}.$ In fact, it can be shown that the operations $\vee _{H}$ and $\wedge _{H}$ are closed in S(X, P) and that:

• (i) $DOA(C_{H}\left( Y\cup Z\right) )\succeq _{H}^{B}Y$ and $DOA(C_{H}\left( Y\cup Z\right) )\succeq _{H}^{B}Z.$

• (ii) If $W\in S\left( \mathbf {X},P\right)$ satisfy $W\succeq _{H}^{B}Y$ and $W\succeq _{H}^{B}Z$, then $W\succeq _{H}^{B}DOA(C_{H}\left( Y\cup Z\right) ).$

• (iii) $Y\succeq _{H}^{B}HOA(C_{D}\left( Y\cup Z\right) )$ and $Z\succeq _{H}^{B}HOA(C_{D}\left( Y\cup Z\right) )$.

• (iv) If $W\in S\left( \mathbf {X},P\right)$ satisfy $Y\succeq _{H}^{B}W$ and $Z\succeq _{H}^{B}W,$ then $HOA(C_{D}\left( Y\cup Z\right) )\succeq _{H}^{B}W.$

See Pepa (2015) for details. Then, according to the definition, $(S( \mathbf {X},P),\succeq _{H}^{B},\vee _{H},\wedge _{H})$ is a lattice.

Symmetrically, we can consider the following operations between two any stable allocations Y and Z:

$$\begin{aligned} Y\vee _{D}Z=HOA(C_{D}\left( Y\cup Z\right) ) \end{aligned}$$

and

$$\begin{aligned} Y\wedge _{D}Z=DOA(C_{H}\left( Y\cup Z\right) ). \end{aligned}$$

By reversing the roles between hospitals and doctors, it can be shown that $(S(\mathbf {X},P),\succeq _{D}^{B},\vee _{D},\wedge _{D})$ is a lattice.

So $S(\mathbf {X})$ is a lattice with respect to Blair’s for hospitals and Blair’s for doctors partial orders; and such lattices are dual.