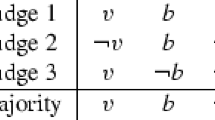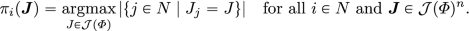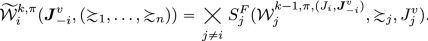1 Introduction

In many instances of their social life, individuals—being members of various groups—need to reach collective decisions by aggregating their private judgments on several issues: from choosing what kind of food to have during a dinner with friends, to reaching an agreement with their colleagues about what policy their company should implement. Judgment aggregation is a formal framework in which such settings are modelled and studied, especially when the issues to be decided upon are logically interconnected (List, 2012; Grossi & Pigozzi, 2014; Endriss, 2016). The aggregation of individual judgments carries further complications when individuals behave strategically, trying to manipulate the collective decision to obtain a better outcome for themselves. These manipulation acts may be achieved by lying, i.e., by reporting a judgment that is different from the individual’s truthful one. This paper focuses on the various levels of reasoning that take place in an individual’s mind prior to making a final decision about which judgment to report, and investigates the manipulability of rules that are used for the aggregation of the multiple judgments of a group. To illustrate the idea, consider the following example.

Example 1

Suppose that in the office of a political party, a decision needs to be taken concerning the opening of a new secretary position. These kinds of issues are typically settled by the leader (Alice) and the deputy (Bob) of the party. But it is also commonly known among all members of the party that both their leader and their deputy only truly want the opening of a new position if they plan to hire a specific person close to them. So, to avoid political tension caused by fights between the party’s two main figures, the established rule is that the position will be announced if and only if exactly one of the two individuals declares in favour of it.

Assume now that the leader wants the position to open (she is trying to have her cousin hired), while the deputy is not interested in the position at the moment and would prefer to have the opening rejected, and this is common knowledge among them. Before reporting her opinion officially, the leader may think that—since the deputy does not want the position—she can be truthful, because she will be the only one in favour of it and thus she will finally be able to hire her cousin (this thought corresponds to level-1 reasoning). However, the leader could also think that—since the deputy knows that she wants the position but he prefers to not have it announced yet—the deputy has an incentive to lie by declaring that he also agrees with the new position, so that the rule prevents it from being announced (this thought of the leader corresponds to level-2 reasoning). In this case, an incentive for the leader to lie is created. But she may think that the deputy has already followed the previous reasoning in his mind, expecting her to lie and therefore making the decision to tell the truth that he does not want the position. Then, it would again be better for the leader to tell the truth as well. Continuing with this reasoning process, Alice and Bob will easily end up applying higher-level reasoning.\(\triangle\)

Already from the example above, we realise that it is not clear how to determine at which level the reasoning process of an individual terminates. Theoretically, the interactive reasoning of the individuals in a group could proceed indefinitely. The question about which level of reasoning can be expected in practice by rational individuals is addressed by behavioral scientists (e.g., Camerer et al., 2004; Costa-Gomes & Crawford, 2006; Costa-Gomes et al., 2001), whose empirical results are often not able to provide a categorical global answer. Despite the limitations that the identification of the exact computational abilities of human beings presents, it is generally accepted that in common real-life strategic situations individuals engage in thinking of at most three levels (Arad & Rubinstein, 2012; Camerer et al., 2004; Stahl & Wilson, 1995). In any case, it is undeniably true that individuals can only reason within finitely many levels.

Thus, in this paper, we focus on finite levels of interactive reasoning. Under this assumption, we explore basic judgment aggregation problems and study the incentives of sophisticated individuals to lie, or in other words, to manipulate the aggregation rule used. We follow the concept of level-k reasoning, first introduced by Nagel (1995) and Stahl and Wilson (1995).Footnote 1 It is usually accepted that manipulation is undesirable in contexts of collective decision-making, since it can drastically distort the collective decision. From this perspective, the main question that we wish to address here is the following.

To what extent can higher-level reasoning protect an aggregation rule from being susceptible to manipulation?

To answer our question, we need to refine the standard framework of strategic manipulation in judgment aggregation (pioneered by Dietrich and List 2007b) and formally account for the notion of higher-level reasoning. Moreover, aiming for a fully fledged model and building on our previous work (Terzopoulou & Endriss, 2019), we incorporate the potential lack of information the individuals may exhibit with respect to the truthful judgments of the other members of their group (note that this was not the case in Example 1, where both individuals had complete information about each other’s judgments). For any type of partial information that may manifest itself in a given scenario, we prove two main results: first, on the positive side, any aggregation rule that is immune to manipulation under first-level reasoning will remain resistant to manipulation under all higher levels of reasoning; that is, higher-level reasoning is never detrimental to a rule’s immunity to manipulation. Second, on the negative side, for any rule that is manipulable under first-level reasoning, it unfortunately never holds that we can find a higher level from which on the rule becomes immune to manipulation; even if there exists a “safe” level in such a case, the immediately next level will still allow for manipulation. Hence, roughly speaking, we conclude that higher-level reasoning cannot guarantee immunity to manipulation.

It is worth stressing here that, as is well-known, preference aggregation can be embedded into judgment aggregation (List & Pettit, 2004; Dietrich & List, 2007a), and notable implications hold regarding our results. In particular, when we talk about “any aggregation rule”, the reader should feel free to think about preference aggregation (and voting) rules as well—our results can be immediately transferred to these domains.Footnote 2

The remainder of this paper is structured as follows. Section 2 discusses previous literature that is pertinent to our work and Sect. 3 illustrates the central ideas, assumptions, and results of this paper by means of examples. Section 4 then recalls the standard formal model of judgment aggregation and introduces our definition of strategic manipulation in the presence of partial information under higher-level reasoning. Our results are presented in Sect. 5, and we conclude in Sect. 6.

2 Related work

Prior work on strategic behaviour in judgment aggregation, initiated by Dietrich and List (2007b) and reviewed by Baumeister et al. (2017), has paid attention exclusively to individuals that are “naïve”, meaning that they consider their own incentives for manipulation, but totally ignore those of their peers. Additionally making the strong assumption that individuals are fully aware of the truthful judgments of the rest of the group (and expect those truthful judgments to be submitted), Dietrich and List proved an influential impossibility theorem, stating that no rule satisfying certain desirable properties can avoid manipulation. However, this impossibility result is known not to hold up when individuals with partial information about the truthful judgments of their peers are taken into account (Terzopoulou & Endriss, 2019).

In spite of not appearing in the literature on judgment aggregation so far, the concern of an individual that her peers may also try to misrepresent their judgments in light of a better outcome has been previously modelled in other fields of social choice theory, like those of preference aggregation and voting.Footnote 3 The idea of modelling sophisticated individuals in a social choice context was introduced by Farquharson (1969). In his pioneering work, he employed the method of iterated elimination of dominated strategies to decide the rational actions of higher-level reasoners, in a game-theoretical interpretation of voting. However, little has been done since then regarding the study of the connections between interactive reasoning and the manipulability of aggregation rules. Applying the tools of epistemic logic, Chopra et al. (2004) design an abstract framework based on knowledge graphs, where the aggregation process is taking place in rounds; in each round, the individuals (represented as nodes in the graph) get signals from a subset of the other individuals (those nodes with which they are connected through edges) about what their truthful preferences are, and decide their next move accordingly. The goal of Chopra et al. is twofold. First, they highlight the role that the elementary assumptions about the information and the reasoning abilities of the individuals play in the classical impossibility theorems of voting. Second, they create a rich logic tailored to the study of strategic voting. But this work provides no concrete results about the manipulability of aggregation rules. The work of Ditmarsch et al. (2013) follows similar lines. These authors call knowledge profile a structure with multiple objects (all possible profiles of preferences of the individuals) and indistinguishability relations over them (denoting the information the individuals hold about the reported profile); they describe several relevant definitions and give emphasis to their model (rather than to results obtained) by discussing specific example cases.

Our model shares plenty of the aspirations of previous works on higher-level reasoning in aggregation settings and directly extends the framework that has earlier been used to capture partial information in (strategic problems of) judgment aggregation (Terzopoulou & Endriss, 2019). In order for such an extension to be successful, many of our underlying intuitions stem from the fields of epistemic game theory (e.g., Perea, 2012) and epistemic logic (e.g., Halpern et al., 2005; Hendricks, 2006).

3 Illustrating the effects of higher-level reasoning

In this section, we illustrate our model informally and prepare the ground for our technical work, relying on the natural setting of Example 1. Note that for everything that follows, the decision-making always takes place in one round—the iterative reasoning only occurs in the individuals’ minds.

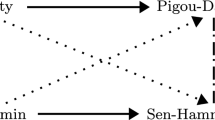
The leader and the deputy of a political party need to express their opinions on whether a new secretary is needed, and the party will announce the position if and only if exactly one of the two individuals reports a positive (yes) judgment on it. It is common knowledge between the two individuals that the leader’s judgment is truthfully in favour of the position, while the deputy’s judgment is not. Also, the preferences of the individuals about the party’s final decision are linked to their truthful judgments, but possibly not in a unique manner. On the one hand, it is very sensible that the leader would strictly prefer the position to be announced, as this is necessary to hire her cousin. On the other hand, the deputy might have a truthful judgment against the position either because he has no interest in it at all (in which case he would be indifferent between any final decision) or because he would like the position to be announced at a later time, when one of his people will also be available to be hired (in which case he would strictly prefer the party to not approve the position at this stage). Suppose the latter holds, we can distinguish three cases, according to the information available to our two individuals (see also Fig. 1).

Case  a: Although the leader knows the deputy’s truthful judgment, she may be unaware of the reason behind it and thus consider possible both cases regarding the deputy’s preferences about the final decision. Then, we can see that in every level of reasoning the deputy will have an incentive to manipulate: when reflecting on their truthful judgments, the leader considers possible that the deputy remains truthful, because she thinks that maybe he does not care about the collective outcome. But if the deputy remains truthful, then the leader does not need to lie. Being afraid to lie with no good reason and risking her reputation, as well as possibly obtaining the opposite outcome to her desirable one, forces the leader to tell the truth at level 1. Now, the deputy, who can follow this reasoning and knows that the leader will tell the truth, manages to achieve his desirable result by lying. Since the leader—no matter her level of reasoning—will never think she can manipulate with no risk involved, the deputy will always have an incentive to do so (see Fig. 1a). We conclude that in this scenario the rule used by the party is susceptible to manipulation under any level of reasoning.

Case b: In an alternative context, the leader may somehow have access to the deputy’s motives behind his opposition to the position (the deputy may for instance have publicly declared that he prefers the position to be announced at a later time). Then, both individuals are certain about the outcome that each of them is trying to achieve. Following an iterative reasoning process analogous to that of Example 1, we see that neither the leader nor the deputy will have an incentive to manipulate when they reason at level 4. Hence, when they both reason at level 4, they will submit their truthful judgments, similarly to level 0 (see Fig. 1b). The sequence of the submitted profiles for higher levels of reasoning will afterwards be repeated. In this case, the rule used by the party is immune to manipulation under any level of reasoning k with \(k\equiv 0\mod 4\).

Case c: Finally, imagine that the members of this particular political party could instead be very secretive, keeping all of their opinions to themselves. In such a case, the leader and the deputy would have no information about each other’s truthful judgments, and as a result they would never manipulate (assuming that they are risk-averse). For instance, the leader, who wants the position to be announced, would not risk to lie and suggest she is against it, because if the deputy (about whom the leader now knows nothing) also expresses a negative judgment, then the position will not open and the leader will be worse off. Figure 1c depicts this scenario.

This example emphasises an important aspect of the research direction we pursue in this paper. It is clear that the preferences of the individuals regarding the collective decision, as well as the knowledge of the group about those preferences, play a principal role with respect to the manipulability of a rule in judgment aggregation, besides the information about the individuals’ truthful judgments. Contrary to classical branches of social choice theory, such as voting theory and preference aggregation, in judgment aggregation there are numerous reasonable ways to generate individual preferences from individual judgments, which implies that the assumptions we make in this respect can be critical for the results we should expect to obtain. Notably, we just saw that when uncertainty about the exact preferences of the others increases, then an aggregation rule can be transformed from being immune to manipulation under some level of reasoning to being manipulable (see level 4 in Fig. 1b versus level 4 in Fig. 1a).

Fig. 1
figure 1

Level 0 represents the truthful judgments of the individuals. In every level of reasoning k, the written judgments are the ones to be submitted when the individuals reason at level k. For the judgments that are in bold, the individuals who hold them have an incentive to manipulate when they reason at the relevant level. To see the incentives for manipulation at level k, we must compare the decision of the party at level \(k-1\) with the truthful judgment of the individual in question. The shaded levels are the ones in which some individual lies

Full size image

4 The model

In this section, we present the standard model of judgment aggregation (List & Pettit, 2002; List & Puppe, 2009; List, 2012; Grossi & Pigozzi, 2014; Endriss, 2016) along with all the relevant notation and terminology we will use in this paper. Then, we introduce the notion of manipulation under partial information and higher-level reasoning.

4.1 Preliminaries

Consider a finite set of individuals \(N=\{1, 2, \ldots , n\}\), with \(n \geqslant 2\), that constitute a group whose judgments are to be aggregated into one collective decision. The issues that the individuals express judgments upon are represented as formulas in classical propositional logic. The domain of decision-making is an agenda, a nonempty set of formulas of the form \(\Phi = \Phi ^+ \cup \{\lnot \varphi \mid \varphi \in \Phi ^+\}\), where the pre-agenda \(\Phi ^+\) consists of non-negated formulas only.

Each individual i accepts a number of formulas in a logically consistent manner, forming her judgment set (or simply judgment) \(J_i\subseteq \Phi\), a consistent subset of the agenda.Footnote 4 We also assume that each individual judges all issues under consideration, i.e., that her judgment set is a complete set (i.e., \(\varphi \in J_i\) or \(\lnot \varphi \in J_i\) for every \(\varphi \in \Phi ^+\)). The set of all consistent and complete subsets of the agenda is denoted as \({\mathcal {J}}(\Phi )\). A profile \(\varvec{J}=(J_1,\ldots ,J_n)\in {\mathcal {J}}(\Phi )^n\) is a vector of all the individual judgment sets, and \(\varvec{J}_{-i}\) stands for the partial profile of judgments of the whole group besides individual i.

An aggregation rule produces a collective decision by combining the individual judgments of the members of a group. Formally, an aggregation rule F is a function that maps every profile of judgments \(\varvec{J} \in {\mathcal {J}}(\Phi )^n\) to a nonempty set of collective judgment sets, i.e., to a nonempty subset of \(2^{\Phi }\), where \(2^\Phi\) is the powerset of \(\Phi\). Thus, there may be a tie between several “best” judgment sets and these judgment sets need not be consistent or complete. When \(F(\varvec{J})\) is always a singleton, that is, when \(F: {\mathcal {J}}(\Phi )^n\rightarrow 2^{\Phi }\), the rule F is called resolute. Throughout this paper, we will work with resolute rules. Whenever resoluteness is not guaranteed, we can enforce it by using some additional tie-breaking rule to resolve the ties between the suggested collective outcomes. A commonly applied such rule is the lexicographic tie-breaking rule, which breaks ties in accordance with some pre-agreed order of the possible collective judgment sets.Footnote 5

For example, a natural aggregation rule is the plurality rule \(F^{{ p}\ell }\), which selects those judgment sets submitted by the largest number of individuals in a given profile. The plurality rule becomes resolute if combined with a suitable tie-breaking rule. It has also played an important role in circumventing a major impossibility theorem by Dietrich and List (2007b) regarding strategyproof judgment aggregation (Terzopoulou & Endriss, 2019).

Another commonsense aggregation rule that is resolute by definition is the propoosition-wise majority rule, according to which a formula belongs to the collective outcome if and only if more than half of the individuals accept it.

Quota rules provide a generalisation of the majority rule, by placing a formula in the outcome if and only if a large enough number of individuals—exceeding a fixed quota—agree with it.

Following a similar idea, the parity rules determine whether a given formula will be part of the collective decision by looking at the parity of the set of individuals that accept it. Although parity rules may look artificial at first, they can be appropriate for several applications. For instance, the rule that the political party in Example 1 endorses is an odd-parity rule.

4.2 First-level strategic manipulation

Individuals that participate in a scenario of collective decision making come with their own truthful judgments as well as with preferred outcomes. But to obtain a better outcome, they may report judgments that are further from their truthful ones. Such manipulation acts directly depend on the individuals’ preferences, the information they hold about their peers, and the level of reasoning in which they engage. We now formalise all the above facets to an individual’s incentive to lie, initially restricting attention to level-1 reasoners, that is, to naïve individuals who think that everyone else (besides themselves) is always truthful.


Preferences. Each individual i is associated with a preference relation \(\succsim _i\), and \(J\succsim _i J'\) means that i (weakly) prefers the collective judgment J to the collective judgment \(J'\). For every i, the relation \(\succsim _i\) is assumed to be

  • reflexive: \(J\succsim _i J\), for all \(J \in 2^{\Phi }\);

  • transitive: \(J\succsim _i J'\) and \(J'\succsim _i J''\) implies \(J\succsim _i J''\), for all \(J, J', J'' \in 2^{\Phi }\);

  • complete: either \(J \succsim _i J'\) or \(J' \succsim _i J\), for all \(J, J' \in 2^{\Phi }\).

We also write \(J\sim _i J'\) if \(J\succsim _i J'\) and \(J'\succsim _i J\), and we denote with \(J\succ _i J'\) the strict component of \(J \succsim _i J'\), i.e., the case where \(J\succsim _i J'\), but not \(J \sim _i J'\).

The preferences of the individuals may be of different types, depending on the context in place. A light assumption that is common in formal models of judgment aggregation (e.g., Dietrich & List, 2007b) suggests that individuals prefer judgments that are “close” to their truthful ones. More specifically, a preference relation \(\succsim _i\) respects closeness to \(J_i\) if, for any J and \(J'\),

$$\begin{aligned} J\cap J_i \supseteq J'\cap J_i \Rightarrow J\succsim _i J' . \end{aligned}$$

For every judgment set \(J_i\), let \(C(J_i)\) be the set of all preference relations \(\succsim _i\) that respect closeness to \(J_i\). Then, \(C= \bigcup _{J_i\in {\mathcal {J}}(\Phi )} C(J_i)\) is the class of closeness-respecting preferences.

Another example of preferences studied in the literature (e.g., Botan et al., 2016; Terzopoulou & Endriss, 2019), that also are closeness-respecting, are Hamming-distance preferences. We define the Hamming distance between two judgment sets J and \(J'\) as \(H(J,J')=|J\setminus J'| + |J'\setminus J|\). For every individual i, the Hamming distance naturally induces a (reflexive, transitive and complete) preference relation \(\succsim _i\) on collective judgments. According to it, individual i prefers exactly those judgments that agree on a greater number of formulas with her truthful judgment \(J_i\). That is,

$$\begin{aligned} H(J, J_i) \leqslant H(J', J_i)\Leftrightarrow J \succsim _i J'. \end{aligned}$$

We denote with \(H(J_i)\) the unique preference relation \({\succsim _i} \subseteq 2^{\Phi }{\times }2^{\Phi }\) that is defined as above, with respect to a fixed judgment set \(J_i\). The family H contains all the Hamming distance preferences \(H(J_i)\), induced by any \(J_i\in {\mathcal {J}}(\Phi )\), i.e., \(H = \bigcup _{J_i\in {\mathcal {J}}(\Phi )} H(J_i)\). Obviously, \(H\subset C\).

More generally, consider a function \(PR\) that assigns to each individual i and judgment set \(J_i\in {\mathcal {J}}(\Phi )\) a non-empty set \(PR (J_i)\) of reflexive, transitive and complete preference relations \(\succsim _i\), which are considered “compatible” with \(J_i\). By a slight abuse of notation, we denote by \(PR\) also the class of preferences constructed by that function: \(PR = \bigcup _{J_i\in {\mathcal {J}}(\Phi )} PR (J_i)\). Examples of such a class are the closeness-respecting and the Hamming-distance preferences.


Information. Among the members of a group that need to reach a collective decision there often is uncertainty about each other’s private truthful judgment. Similarly to preferences, the information that individuals hold in an aggregation scenario may be described by various types. In previous work, we initiated the study of such information types in judgment aggregation, adapting the model of Reijngoud and Endriss (2012) that applies in voting (see Terzopoulou & Endriss, 2019).Footnote 6

In line with this earlier work, we define a judgment information function (JIF) \(\pi :N{\times } {\mathcal {J}}(\Phi )^n\rightarrow {\mathcal {I}}\) as a function mapping individuals and profiles to elements of \({\mathcal {I}}\), which contains all possible pieces of information an individual may hold. For instance, we may consider the following reasonable sets \({\mathcal {I}}\) and JIFs \(\pi\).

  • Full. The full-JIF returns precisely the truthful profile.

    $$\begin{aligned} \pi _i(\varvec{J}) &= \varvec{J} \quad \text {for all}\ i\in N\ \text {and}\ \varvec{J}\in {\mathcal {J}}(\Phi )^n. \end{aligned}$$

  • Plurality. The plurality-JIF returns the judgment set(s) held by the largest number of individuals in the truthful profile.

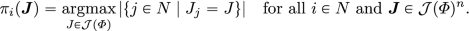
  • Zero. The zero-JIF does not return any information.

    $$\begin{aligned} \pi _i(\varvec{J})& = 0\ \quad \text {for all}\ i\in N\ \text {and}\ \varvec{J}\in {\mathcal {J}}(\Phi )^n. \end{aligned}$$

Having the information expressed by a JIF \(\pi\) and a profile of judgments \(\varvec{J}\), an individual that is a level-1 reasoner (i.e., that assumes everyone else will submit their truthful judgment) considers the following set of (partial) profiles possible to be reported by the group.

$$\begin{aligned} {\mathcal {W}}^{1,\pi , \varvec{J}}_i& = \{\varvec{J}'_{-i} \mid \pi _i(J_i,\varvec{J}'_{-i})=\pi _i(\varvec{J})\} \end{aligned}$$

In other words, \({\mathcal {W}}^{1,\pi , \varvec{J}}_i\) contains all the judgments of the rest of the group that are compatible with individual i’s information and level-1 reasoning.

Incentives for level-1 manipulation.

To formalise the incentives of an individual to manipulate an aggregation rule in our model, let us first define the notion of a best strategy.

Consider an aggregation rule F, a truthful profile \(\varvec{J}=(J_i,\varvec{J}_{-i})\), and an individual \(i\in N\) with preferences \(\succsim _i\) that considers possible the set of (partial) profiles \({\mathcal {W}}\subseteq {\mathcal {J}}(\Phi )^{n-1}\) to be truthfully held by the group. We say that a judgment set \(J\in {\mathcal {J}}(\Phi )\) is undominated in the standard game-theoretical sense, if there is no other judgment set \(J'\) such that the following hold.

  1. 1.

    \(F(J',\varvec{J}'_{-i})\succ _i F(J,\varvec{J}'_{-i})\), for some \(\varvec{J}'_{-i}\in {\mathcal {W}}\);

  2. 2.

    \(F(J',\varvec{J}''_{-i})\succsim _i F(J,\varvec{J}''_{-i})\), for all other \(\varvec{J}'_{-i}\ne \varvec{J}''_{-i}\in {\mathcal {W}}\).

If individual i’s truthful judgment \(J_i\) is undominated, then we assume that being truthful is her unique best strategy.Footnote 7 Otherwise, all the undominated judgment sets can be used by i as her best strategies.

Definition 1

We define the set \(S_i^{F}({\mathcal {W}},\succsim _i,J_i)\) of individual i’s best strategies, when she has preferences \(\succsim _i\), she considers possible partial profiles in the set \({\mathcal {W}}\subseteq {\mathcal {J}}(\Phi )^{n-1}\), and she holds the truthful judgment \(J_i\).

$$\begin{aligned} S_i^{F}({\mathcal {W}},\succsim _i,J_i)= {\left\{ \begin{array}{ll} \{J_i\} &{} \text { if}\ J_i\ \text {is undominated} \\ \{J\in {\mathcal {J}}(\Phi )\mid J \text { is undominated } \} &{} \text { otherwise } \end{array}\right. }. \end{aligned}$$

Following our previous work (Terzopoulou & Endriss, 2019), we now develop a definition of the manipulability of an aggregation rule, relative to a given class of preferences (such as the class of all closeness-respecting preferences) and a type of information (such as plurality information), under the assumption that all individuals are level-1 reasoners. So, when does an individual have an incentive to submit a dishonest judgment in an aggregation problem? We reply: When truthfulness is not a best strategy of that individual.

Definition 2

Consider an aggregation rule F, an individual i holding preferences \(\succsim _i\), a truthful profile \(\varvec{J}=(J_i,\varvec{J}_{-i})\), and a JIF \(\pi\). Individual i has an incentive to \(\varvec{\pi }\)-manipulate under level-1 reasoning in \(\varvec{J}\) if and only if

$$\begin{aligned} S^{F }_i ({\mathcal {W}}_i^{1,\pi ,\varvec{J}},\succsim _i,J_i) \ne \{J_i\}.\end{aligned}$$

If there is a profile \(\varvec{J}\) where at least one individual has an incentive to \(\pi\)-manipulate, then we say that the aggregation rule is \(\pi\)-manipulable.

Definition 3

Consider a JIF \(\pi\). An aggregation rule F is \(\varvec{\pi }\)-manipulable under level-1 reasoning for a class of preferences \(PR\) if there are a profile \(\varvec{J}=(J_i,\varvec{J}_{-i})\in {\mathcal {J}}(\Phi )^n\) and an individual \(i \in N\) holding preferences \({\succsim _i}\in PR (J_i)\) such that i has an incentive to \(\pi\)-manipulate in \(\varvec{J}\).

An aggregation rule F is \(\pi\)-strategyproof for a class of preferences \(PR\) if and only if F is not \(\pi\)-manipulable for \(PR\).

Definition 4

Consider a JIF \(\pi\). An aggregation rule F is \(\varvec{\pi }\)-strategyproof under level-1 reasoning for a class of preferences \(PR\) if, for all individuals \(i \in N\), all truthful profiles \(\varvec{J}=(J_1,\ldots ,J_n) \in {\mathcal {J}}(\Phi )^n\), and all preference relations \({\succsim _i}\in PR (J_i)\),

$$\begin{aligned} S^{F }_i ({\mathcal {W}}_i^{1,\pi ,\varvec{J}},\succsim _i,J_i) = \{J_i\}.\end{aligned}$$

4.3 Higher-level strategic manipulation

In Sect. 4.2, we formalised the level-1 reasoning of individuals in aggregation problems. That is, so far we (as well as the literature to date) have been making the implicit assumption that the only parameter that affects the strategic behavior of the members of a group (except for their preferences) is the information they hold about the truthful judgments of their peers. However, the members of a group are very likely to realise that others may reason strategically too, and thereby choose the best course of action in the light of their own information. This observation brings higher-level reasoning into the picture. We design our general framework along the lines of the level-k reasoning model (Nagel, 1995; Stahl & Wilson, 1995).

Recall that level-1 reasoners only speculate about their own information about the possible truthful judgments of the rest of the group. Now, level-2 reasoners give further thought to the information that the others hold about the truthful profile, while level-k individuals are able to apply exactly k levels of this reasoning operation; they reason about what the other individuals know about what the other individuals know about... what the other individuals know about the truthful judgments of the group. In other words, level-k individuals think that everyone else reasons at level \((k-1)\) and apply their best strategies accordingly.

Information about the information of others. In our model, all the individuals are aware of the type of information that the rest of the group holds, which does not necessarily mean that they know the exact information of the others in a specific aggregation situation, but rather how that information is derived by the truthful profile, whatever that profile may be. More formally, we only assume that the JIF \(\pi\) is common knowledge among the individuals.

The above assumption makes sense in multiple aggregation scenarios. For instance, consider a social network whose structure is known to everyone in it. An example can be the board of a company, consisting of employees from different departments. Suppose that the board has to make a collective decision by aggregating the judgments of its members, and that several meetings in the different departments precede the final reporting of judgments. It is then practicable to assume that everyone knows the truthful opinions of the employees in her own department, and this is common knowledge. However, the individuals cannot know what the truthful opinion of everyone else is, hence they lack the information about what exactly the others know about their colleagues. For the moment, what they know is the type, but not the full content of the group’s information.

As we have already said, apart from the truthful judgment that an individual holds, a key factor of her behaviour in an aggregation situation is her preference relation over the possible collective outcomes. Hence, when examining the interactive reasoning of the members of a group, the assumptions considering the knowledge of the individuals about the preferences of the others is central. In particular, when an individual reasons about the reasoning of another individual, there is a point where she has to wonder about the other individual’s preferences. We will follow a basic intuition here, which prescribes that the preferences of the individuals, in a different manner than their judgments, are not revealed. A safe assumption is only that everyone knows that every individual prefers results that match her own truthful opinion up to a degree. So, we will say that it is common knowledge that the preferences of the group belong to some specific class \(PR\), and in practice this class can usually be taken to be the class C of all preferences that are closeness-respecting. Finally, we will assume that it is common knowledge that nothing more considering the preferences of the individuals is common knowledge.

Making the above formal, given a truthful profile of judgments \(\varvec{J}\) and a JIF \(\pi\), an individual i’s information about the truthful judgments of the rest of the group is given by \(\pi _i(\varvec{J})\). This information induces the set \({\mathcal {W}}^{1,\pi , \varvec{J}}_i\) of (partial) profiles that individual i considers possible to be the truthful ones, or in other words, the different scenarios about the judgments of the group that are compatible with her information and level-1 reasoning. However, after reflecting on the information that her peers hold, individual i may consider different profiles possible to be reported by the individuals.

Incentives for level-k manipulation. In order to locate level-k reasoners’ incentives to lie, we define the set of possible profiles that are compatible with their higher-level reasoning. It may be the case that according to individual i’s level-k reasoning, some other individual, say individual j, has an incentive to manipulate and report an untruthful judgment (following individual j’s level-\((k-1)\) reasoning). Then, individual i will not consider the scenario where individual j is truthful possible anymore; on the contrary, the relevant cases for her will be those where individual j lies. Definition 5 builds inductively on the definitions concerning level-1 reasoning (of Sect. 4.2).

Definition 5

Consider an aggregation rule F, a class of preferences \(PR\), a JIF \(\pi\), and an individual i.

  • Take \({\mathcal {W}}^{1,\pi , \varvec{J}}_i=\{\varvec{J}^1_{-i},\ldots ,\varvec{J}^r_{-i}\}\), an enumeration of the elements in \({\mathcal {W}}^{1,\pi , \varvec{J}}_i\).

  • Suppose we have defined the set of partial profiles \({\mathcal {W}}^{k-1,\pi , \varvec{J}'}_j\) that an individual j considers possible to be submitted by the group, when she engages at level-\((k-1)\) reasoning and the truthful profile is \(\varvec{J}'\).

  • For all partial profiles \(\varvec{J}^v_{-i} \in {\mathcal {W}}^{1,\pi , \varvec{J}}_i\) and for all possible profiles of preference relations \((\succsim _1,\ldots ,\succsim _n)\) in \(PR\), we define a new set of partial profiles \(\widetilde{{\mathcal {W}}}^{k,\pi }_i(\varvec{J}^v_{-i}, (\succsim _1,\ldots ,\succsim _n))\) that individual i considers rational, that is, where her peers reason at level \((k-1)\) and report one of their best strategies when their truthful judgments are in \(\varvec{J}^v_{-i}\). Formally,

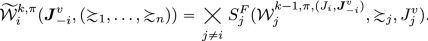
    By taking the union of all the sets of rational partial profiles induced by any partial profile that individual i considers possible to be the truthful one and any combination of preferences in the class \(PR\) for the group, we define

    $$\begin{aligned}{\mathcal {W}}^{k,\pi , \varvec{J}}_i=\bigcup _{v\in {\{1,\ldots ,r\}}}\bigcup _{(\succsim _1,\ldots ,\succsim _n)\in PR ^n} \widetilde{{\mathcal {W}}}^{k,\pi }_i(\varvec{J}^v_{-i},(\succsim _1,\ldots ,\succsim _n)). \end{aligned}$$

The set \({\mathcal {W}}^{k,\pi , \varvec{J}}_i\) contains all partial profiles that are compatible with individual \({\varvec{i}}\)’s level-\({\varvec{k}}\) reasoning.

Example 2

Consider individual \(\ell\) to be the leader of the political party in the example of Sect. 3, and suppose we are in the case where she has full information about the truthful judgment of the deputy (individual d), but she is uncertain about the deputy’s exact preferences (Case (a) of Fig. 1). In level 1, the leader thinks that the deputy will be truthful, reporting \(J_d=\{\lnot p\}\) (where p denotes the opening of the new position). Thus,

$$\begin{aligned}{\mathcal {W}}^{1,\text {full}, \varvec{J}}_\ell = \{J_d\} = \{\{\lnot p\}\}.\end{aligned}$$

In level 2 though, the leader thinks that the deputy will lie given that his preferences suggest so. Let us denote by \(\succsim _d^H\) the preferences of the deputy that are of Hamming-type, and by \(\succsim _d^I\) the preferences that express indifference between the two possible outcomes (in the context of the current example where we have only one issue to decide, closeness respecting preferences can be partitioned to these two types of preferences exactly). Note that under the truth-bias assumption, an individual that is indifferent between the two possible outcomes will remain sincere. Then,

$$\begin{aligned} {\mathcal {W}}^{2,\text {full}, \varvec{J}}_\ell= & {} \bigcup _{\succsim _d \in C} S^{ F}_d ({\mathcal {W}}^{1,\text {full}, (J_\ell ,J_d)}_d,\succsim _d,J_d)\\= & {} S^{ F}_d ({\mathcal {W}}^{1,\text {full}, (J_\ell ,J_d)}_d,\succsim ^H_d,J_d) \quad\, \bigcup S^{ F}_d ({\mathcal {W}}^{1,\text {full}, (J_\ell ,J_d)}_d,\succsim ^I_d,J_d) \\= & {} \{\{ p\}\} \qquad\qquad\qquad\quad \qquad\bigcup \{\{\lnot p\}\} \\= & {} \{\{ p\}, \{\lnot p\}\}.\\ \end{aligned}$$

This means that both possible judgments of the deputy are compatible with the leader’s level-2 reasoning.

Definitions 6 and 7 formalise the notions of manipulability and of strategyproofness of an aggregation rule under level-k reasoning.

Definition 6

An aggregation rule is \(\varvec{\pi }\)-manipulable under level-\({\varvec{k}}\) reasoning for a class of preferences \(PR\) if and only if there are a profile \(\varvec{J}=(J_i,\varvec{J}_{-i})\) and an individual i holding preferences \({\succsim _i}\in PR (J_i)\), such that

$$\begin{aligned}S^{F}_i ({\mathcal {W}}_{i}^{k,\pi ,\varvec{J}},\succsim _i,J_i)\ne \{J_i\} . \end{aligned}$$

An aggregation rule F is \(\pi\)-strategyproof under level-k reasoning if and only if F is not \(\pi\)-manipulable under level-k reasoning.

Definition 7

An aggregation rule is \(\varvec{\pi }\)-strategyproof under level-\({\varvec{k}}\) reasoning for a class of preferences \(PR\) if and only if for all profiles \(\varvec{J}=(J_i,\varvec{J}_{-i})\) and all individuals i holding any preferences \({\succsim _i}\in PR (J_i)\), it holds that

$$\begin{aligned}S^{F}_i ({\mathcal {W}}_{i}^{k,\pi ,\varvec{J}},\succsim _i,J_i)=\{J_i\}. \end{aligned}$$

At this point, a clarification of the terminology is required. The reader has probably realised that so far we have not made any explicit assumption about whether the individuals of the groups that we examine are all reasoning in the same level. To be precise, when we argue that an aggregation rule is susceptible to manipulation under level-k reasoning, what would be more accurate to say is that the aggregation rule is manipulable whenever there is at least one individual in the group who is able to perform level-k reasoning. However, to claim that an aggregation rule is immune to manipulation under level-k reasoning, we have to refer to groups where all the individuals reason at level k. Intuitively, manipulability at a given level can be caused by the reasoning of only one individual reasoning at that level, while strategyproofness requires everyone to be at the same level (or more generally at a level that does not provide incentives for manipulation).

5 Results

In this section, we present our results concerning the manipulabilty of aggregation rules under higher-level reasoning and possibly partial information. Specifically, given any type of information the individuals may hold about the truthful judgments of their peers, we investigate the logical connections between first-level and higher-level reasoning with regard to the strategyproofness of aggregation rules.

Our analysis revolves around two cases: first, we examine aggregation rules that are strategyproof under level-1 reasoning, and second we focus on aggregation rules that are manipulable under level-1 reasoning. In the first case, we establish a very positive fact, namely that—independently of the existing type of (partial) information—all aggregation rules immune to manipulation for level-1 reasoners will also be immune to manipulation for higher-level reasoners (Theorem 1). Said differently, we can guarantee that higher-level reasoning is never damaging with respect to the strategyproofness of an aggregation rule. However, our second finding is a negative result. We show that every aggregation rule that is manipulable under level-1 reasoning is certainly manipulable under level-k reasoning as well, for numbers k that can be arbitrarily large. Specifically, for every such rule, even if we are able to identify a natural number k for which the rule is strategyproof for groups consisting of level-k reasoners, if there is at least one individual who can potentially go one step further and reason at level \((k+1)\), this will cause the manipulability of the rule (Theorem 2).

Theorem 1

Consider a class of preferences \(PR\), an aggregation rule F, and a JIF \(\pi\). If F is \(\pi\)-strategyproof under level-1 reasoning for \(PR\), then F will be \(\pi\)-strategyproof under level-k reasoning for \(PR\), for all \(k \in {\mathbb {N}}\).

Proof

We give a proof by induction. We have that F is immune to \(\pi\)-manipulation under level-1 reasoning, by the hypothesis. Then, suppose that F is immune to \(\pi\)-manipulation under level-\((k-1)\) reasoning. We will show that F is immune to \(\pi\)-manipulation under level-k reasoning.

Consider an arbitrary individual \(i \in N\) and a profile \(\varvec{J} \in {\mathcal {J}}(\Phi )^n\). The set of partial profiles that individual i considers possible after engaging in level-k reasoning when the actual profile is \(\varvec{J}\) is \({\mathcal {W}}^{k,\pi , \varvec{J}}_i\), as defined in Definition 5. But since F is immune to \(\pi\)-manipulation under reasoning at level \(k-1\), it is the case that no individual has an incentive to lie under level-\((k-1)\) reasoning. In other words, this means that the only best strategy of each individual in every possible scenario is her truthful strategy. Specifically, for all \(\varvec{J}'_{-i}\in {\mathcal {W}}^{1,\pi , \varvec{J}}_i\), all individuals j and all preference relations \(\succsim _j\), it holds that

$$\begin{aligned}S^{ F }_j ({\mathcal {W}}^{k-1,\pi , (J_i,\varvec{J}'_{-i})}_j,\succsim _j,J'_j) =\{J'_j\}.\end{aligned}$$

Then, Definition 5 implies that \({\mathcal {W}}^{k,\pi , \varvec{J}}_i={\mathcal {W}}^{1,\pi , \varvec{J}}_i\), as follows:

So, since individual i does not have an incentive to manipulate under level-1 reasoning (we know that by the hypothesis), she will not have an incentive to manipulate under level-k reasoning either. \(\square\)

A strong implication can be derived from Theorem 1, together with a known result stating that every aggregation rule that is strategyproof under full information will remain strategyproof under any type of partial information too (Terzopoulou & Endriss, 2019). More precisely, we now know that it suffices to check the strategyproofness of a rule for the very special case of full information and level-1 reasoning, and we will always be able to generalise a positive result to increased uncertainty and higher levels of reasoning.

Example 3

Dietrich and List (2007b) proved that, for the large class of closeness-respecting preferences, all quota rules are strategyproof under full information and level-1 reasoning. Our result thus shows that quota rules should be regarded as even more powerful: they are thoroughly strategyproof, under any kind of partial information and any level of reasoning.

Theorem 2

Consider a class of preferences \(PR\), an aggregation rule F, and a JIF \(\pi\). If F is \(\pi\)-manipulable for \(PR\) under level-1 reasoning and F is \(\pi\)-strategyproof for \(PR\) under level-k reasoning, then F will be \(\pi\)-manipulable for \(PR\) under level-\((k+1)\) reasoning, for all \(k \in {\mathbb {N}}\).

Proof

Suppose that F is susceptible to \(\pi\)-manipulation under level-1 reasoning and immune to \(\pi\)-manipulation under level-k reasoning for some k. We will show that F is susceptible to \(\pi\)-manipulation under level-\((k+1)\) reasoning. Since F is susceptible to \(\pi\)-manipulation under level-1 reasoning, there are an individual \(i \in N\) and a profile \(\varvec{J} \in {\mathcal {J}}(\Phi )^n\) such that individual i has an incentive to manipulate under level-1 reasoning. Now, the set of partial profiles that individual i considers possible after engaging in level-\((k+1)\) reasoning, when the truthful profile is \(\varvec{J}\), is \({\mathcal {W}}^{1,\pi , \varvec{J}}_i\). But since F is immune to \(\pi\)-manipulation under level-k reasoning, it is the case that no individual has an incentive to lie at level k. In other words, the unique best strategy of each individual in every possible scenario is her truthful strategy. Specifically, for all \(\varvec{J}'_{-i}\in {\mathcal {W}}^{1,\pi , \varvec{J}}_i\), all individuals j and all preference relations \(\succsim _j\), we have that

$$\begin{aligned}S^{F}_j ( {\mathcal {W}}^{k,\pi , (J_i,\varvec{J}'_{-i})}_j,\succsim _j, J'_j) =\{J'_j\}.\end{aligned}$$

Then, Definition 5 implies that \({\mathcal {W}}^{k+1,\pi , \varvec{J}}_i={\mathcal {W}}^{1,\pi , \varvec{J}}_i\), as follows:

Hence, since individual i has an incentive to manipulate under level-1 reasoning, she will have an incentive to manipulate under level-\((k+1)\) reasoning too. \(\square\)

Having an aggregation rule that is manipulable under some type of partial information when the individuals of the group reason at level 1, a desirable result would establish that if all the individuals engaged in reasoning of at least level k for some natural number k, then the rule would become strategyproof. Unfortunately, we proved precisely that this is never the case. Theorem 2 states that if a rule is susceptible to manipulation when the group reasons at level 1, then it can never be strategyproof for two consecutive levels of reasoning. This makes it impossible to argue that higher-level reasoning can prevent manipulation in a global manner.

On the one hand, behavioural experiments only provide evidence that, in strategic problems of real life, people reason within an interval of levels. A common approach is to attempt to obtain a probability distribution over reasoning levels (see for instance the recent work by Penczynski 2016). Hence, every aggregation rule that is manipulable under level-1 reasoning can in practice be considered manipulable under higher levels of reasoning too. Roughly speaking, as convergence to strategyproofness via higher-level speculations is never guaranteed, level-1 reasoning determines whether a rule can be considered manipulable or not (all the above holds independently of the information available to the individuals).

On the other hand, our results can look more positive when viewed within the context of artificial intelligence. For example, within multiagent systems, agents may be programmed to reason at a fixed level—a level that can be chosen by the modeller to be such that strategyproofness is ensured (Shoham & Leyton-Brown, 2009).Footnote 8

Example 4

Let \(F^{{ p}\ell }\) be the plurality rule along with a lexicographic tie-breaking rule and let C be the class of all closeness-respecting preferences. It is not hard to see that \(F^{{ p}\ell }\) is susceptible to plurality-manipulation for C under level-1 reasoning; however, \(F^{pl}\) is immune to plurality-manipulation for C under level-2 reasoning.

Indeed, take an arbitrary individual i, a truthful profile \(\varvec{J}=(J_i,\varvec{J}_{-i})\) with \(F^{{ p}\ell }(\varvec{J})=J\), and a closeness-respecting preference \({\succsim _i}\in C(J_i)\). Suppose that there is a judgment set \(J_i^*\) such that \(F^{{ p}\ell }(J_i^{*},\varvec{J}'_{-i})\succ _i F^{{ p}\ell }(J_i,\varvec{J}'_{-i})\), for some partial profile \(\varvec{J}'_{-i}\in {\mathcal {W}}_{i}^{2,\text {plurality},\varvec{J}}\). By the definitions of the closeness-respecting preferences and the plurality rule, this can only happen if the manipulated outcome is the judgment set \(J_i^*\) and \(J^*_i\succ _i J\). By the definition of the closeness-respecting preferences then, there must exist a formula \(\varphi \in \Phi\) such that \(\varphi \in J_i\cap J_i^*\) and \(\varphi \notin J\). Fix this formula \(\varphi\) and imagine that individual i reasons as follows.

Since she does not know what the other individuals’ truthful opinions are, it is possible for her that some individual j sincerely holds judgment \(J_i^*\). Moreover, it is also possible for her that individual j only cares about formula \(\varphi\) in her truthful judgment, so she holds a closeness-respecting preference relation \(\succsim _j\) such that \(J_i\succ _j J\). But it is common knowledge that judgment J is the collective decision on the truthful profile. Hence, individual j who—according to individual i—engages at level-1 reasoning may try to manipulate the result and be better off by untruthfully reporting \(J_i\). In case \(J_i\) was pivotal in the truthful profile, this manipulation can indeed make it win. On the other hand, if individual i tries to manipulate too, then she will miss the opportunity to see her truthful judgment wining and will be worse off. We conclude that it is risky for individual i to manipulate, so she will avoid doing so.

Finally, an additional theoretical observation may appeal to the reader: The manipulability status of all aggregation rules is characterised by an elegant periodicity. As we saw in Theorem 2, when an aggregation rule is strategyproof under some level k, then all individuals who perform reasoning at level \(k+1\) believe that everyone else will be truthful, so the scenarios they consider possible are exactly the same as the ones compatible with level-1 reasoning. Loosely speaking, this is the reason why after a level k that guarantees strategyproofness, the reasoning of the individuals formally reduces to level 1, and whether or not the rule is manipulable for the next levels \(k+2\), \(k+3\), etc. just depends on levels 2, 3, and so on, respectively. Theorem 3 makes this insight precise.

Theorem 3

Consider a number \(k \in {\mathbb {N}}\), a JIF \(\pi\), a class of preferences \(\textit{PR}\), and an aggregation rule F that is \(\pi\)-strategyproof under level-k reasoning for \(\textit{PR}\). For all \(\ell >k\), there exists an \(x \in \{0,\ldots ,k-1\}\) such that \(\ell \equiv x \mod k\), and it holds that F is \(\pi\)-strategyproof under level-\(\ell\) reasoning if and only if F is \(\pi\)-strategyproof under level-x reasoning.

Proof

Consider an arbitrary \(\ell >k\) and take \(x \in \{0,\ldots ,k-1\}\) such that \(\ell \equiv x \mod k\). To show that the statement holds, it suffices to show that for all individuals \(i \in N\) we have that

$$\begin{aligned}{\mathcal {W}}^{\ell ,\pi , \varvec{J}}_i = {\mathcal {W}}^{x,\pi , \varvec{J}}_i.\end{aligned}$$

We prove this by induction. First, we know from Theorem 2 that \({\mathcal {W}}^{k+1,\pi , \varvec{J}}_i={\mathcal {W}}^{1,\pi , \varvec{J}}_i\) (thus our desideratum holds for \(\ell =k+1\) and \(x=1\)). Then, suppose that \(\ell >k+1\), and that for the level \(\ell -1 >k\) and the number \(x_1\in \{0,\ldots ,k-1\}\) with \(\ell -1 \equiv x_1 \mod k\), it holds that \({\mathcal {W}}^{\ell -1,\pi , \varvec{J}}_i = {\mathcal {W}}^{x_1,\pi , \varvec{J}}_i\).

Note that if \(\ell -1 \equiv x_1 \mod k\) and \(\ell \equiv x \mod k\), then

$$\begin{aligned} x= {\left\{ \begin{array}{ll} x_1+1 &{} \text { when } x_1 < k-1 \\ 0 &{} \text { when } x_1 = k-1 \end{array}\right. }. \end{aligned}$$
(1)

We have that

Now, if \(x_1 < k-1\), then Eq. 1 implies that \({\mathcal {W}}^{\ell ,\pi , \varvec{J}}_i={\mathcal {W}}^{x,\pi , \varvec{J}}_i\). If \(x_1 =k-1\), then \({\mathcal {W}}^{\ell ,\pi , \varvec{J}}_i={\mathcal {W}}^{k,\pi , \varvec{J}}_i={\mathcal {W}}^{0,\pi , \varvec{J}}_i\) (because F is strategyproof under level-k reasoning). Therefore, again by Eq. 1, \({\mathcal {W}}^{\ell ,\pi , \varvec{J}}_i={\mathcal {W}}^{x,\pi , \varvec{J}}_i\), and our proof is concluded. \(\square\)

So, given common knowledge about a JIF \(\pi\) and a class of preferences \(\textit{PR}\), any aggregation rule F belongs to exactly one of the three categories (also illustrated in Table 1):

  1. 1.

    F is strategyproof for level-k reasoning, for all \(k \in {\mathbb {N}}\);

  2. 2.

    F is manipulable for level-k reasoning, for all \(k \in {\mathbb {N}}\);

  3. 3.

    F is strategyproof for level-k reasoning if an only if \(k\equiv 0 \mod r\), where \(r\ne 1\) is some natural number (that depends on F).

Table 1 Manipulability categories of aggregation rules, given common knowledge about a JIF \(\pi\) and a class of preferences \(\textit{PR}\) (“\(\checkmark\)” denotes strategyproofness and “\(\times\)” denotes manipulability)
Full size table

Note that the category to which an aggregation rule F belongs depends directly on the specific JIF \(\pi\) and the class of preferences \(\textit{PR}\). Changing one of these two parameters may radically alter the manipulability status of a rule. For instance, recall the examples we discussed in Sect. 3 about the decision-making between the leader and the deputy of a political party, which was making use of the odd-parity rule. By simply expressing those examples formally, we obtain Example 5.

Example 5

The odd-parity rule is

  • strategyproof for every level k, under zero information and for both the classes of closeness-respecting and of Hamming-distance preferences;

  • manipulable for every level k, under full information and for the class of closeness-respecting preferences;

  • strategyproof for level k if and only if \(k \equiv 0 \mod 4\), under full information and for the class of Hamming-distance preferences.

So, the odd-parity rule can fall into any one of the categories of Table 1, just by changing our assumptions regarding the class of preferences and the information available to the individuals.

6 Conclusion

We have pursued the study of individuals who perform advanced interactive reasoning, that is, individuals who attempt to reason about the strategic reasoning of their peers, within the formal framework of judgment aggregation. We have specifically provided a toolbox to uniformly incorporate partial information and higher-level reasoning into judgment aggregation, thereby enriching the current literature in the area. Our investigation has revolved around one main hope: that individuals who are able to and willing to give deeper thought to the intentions of their peers with respect to manipulation would eventually find it more worthy to remain truthful themselves. Sadly, this hope was disproved. No matter which aggregation rule we may choose to use, if we cannot achieve truthfulness for uncomplicated reasoners of level 1, then there will always be an arbitrarily high level of reasoning for which our rule will still be susceptible to manipulation.

Our analysis brings out numerous directions for further research. First, after having established a general categorisation of all aggregation rules with respect to their manipulability, the natural next step would be to inspect specific rules of interest and possibly characterise the family of information functions in combination with preference relations that render them strategyproof. For instance, we saw that the plurality rule is manipulable for closeness-respecting preferences under plurality information and level-1 reasoning, but it is strategyproof under level-2 reasoning. What about other types of information in combination with different levels of reasoning, or other classes of preferences? And what about other rules, that may be manipulable under exactly the same conditions as the plurality rule? All these are open questions.

Second, even though we are not making any formal claims about complexity theory in this paper, sophisticated speculations about the reasoning of other people in an individual’s environment are undeniably costly with regard to an individual’s time and mental energy. The challenge posed by interactive reasoning is therefore apparent. It is known that computing the final outcome of an aggregation rule (taking certainty over the truthful judgments of the group for granted) is often intractable (Endriss et al., 2012, 2020)—although this is not the case for the rules considered in this paper. Hence, one can imagine the difficulties that an individual would face for more complex rules when she has to compute, not only the outcomes compatible with her information, but also those that the rest of the group may consider possible according to the information each possesses, etc. Many of these difficulties are evident in the simple examples presented in this paper.