Abstract
We consider a proportional-prize contest to forecast future events, and show that, in equilibrium, this mechanism possesses perfect forecasting ability for any group size when the contestants share common knowledge about the probabilities by which future events realize. Data gathered in a laboratory experiment confirm the performance invariance to group size. By contrast, when realization probabilities are not common knowledge, there are some differences across group sizes. The mechanism operates marginally better with three or four compared to two players. However, this effect is mainly driven by players’ behavior rather than by differences in the beliefs they form about the realization probabilities.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Recently several firms have started to offer awards to contestants coming up with the best solutions to different out-of-sample forecasting problems.Footnote 1 Participants in these settings are rewarded based on their performance and can earn significant cash-prizes from their participation. Several recent papers (e.g. Cason et al., 2020; Witkowski et al., 2018; Peeters and Wolk, 2019) show that, in such competitions, mechanisms that award prizes proportional to performance (proportional-prize contests) align incentives better than mechanisms that award the total prize to one winner (winner-take-all contests).
Peeters and Wolk (2019) develop a mechanism, based on the Colonel Blotto game, to elicit subjective forecasts in a group-based manner. In the game, two players independently divide a given amount of resources over possible future events and the prize is shared either among the players in proportion to the amounts they allocated to the realized event or among those that allocated the most resources to this event. While both payoff rules have comparable theoretical properties, the game variation where the prize is shared proportionally shows better performance in their experiment, and it even weakly outperforms a quadratic scoring rule—providing evidence in support for games being a viable alternative to proper scoring rules.
This paper extends the proportional payoff contest in Peeters and Wolk (2019) to settings with more than two players and we show that this mechanism is Bayesian-Nash incentive compatible. That is, for any finite number of participating players, in the unique (symmetric) Nash equilibrium, all players allocate their resources in proportion to the realization probabilities, in case these probabilities are common knowledge to the players. Moreover, we further introduce new treatments in a laboratory experiment where we assess the forecasting performance of this mechanism with groups of three and four players. This allows us to test the robustness of small-group forecasting and contrast the results with those obtained by Peeters and Wolk (2019) for two players. We do this in a setting with and without common knowledge of realization probabilities—the former closely following theoretical predictions, the latter being more relevant for field applications.
In the game, n players independently divide a given amount of resources over possible future events and the prize is shared among the players in proportion to the amounts they allocate to the event that realizes. In our experiment, forecasters compete under this proportional-prize rule over a series of 20 rounds. In each round, each forecaster is endowed with 100 resources that can be freely spent on any of eleven possible linear-ordered future outcomes. At the end of a round, a stochastic process determines the realized outcome, and each forecaster receives a share of the prize in accordance to the relative share of resources allocated to the selected outcome. Players may diverge from allocating their resources in accordance to their beliefs out of strategic considerations, such that elicited forecasts may suffer from strategic distortions. It could, for instance, be that a player does not believe that every competitor behaves according to equilibrium, and if other players diverge from the equilibrium strategy, then it may be optimal to also deviate. The tendency to diverge from the equilibrium strategy in this way is likely stronger with fewer competitors since a player always plays against all other competitors simultaneously. Therefore, the larger the group is, the more likely it is that the ‘average competitor allocation’ is closer to the equilibrium allocation. Another example could be a tendency to anti-coordinate allocations. For instance, players may make high risk bets on one (or a few) of the possible outcomes or players could attempt to divide the outcome space among each other. The tendency to act in this way is also likely to be stronger with fewer forecasters, since it is easier to (anti-)coordinate allocations as well as to divide the outcome space with fewer competitors. To study these effects, we test the mechanism with two, three and four competing forecasters.
Our results show that with common knowledge of realization probabilities, consistent with theoretical predictions, there is no significant effect of group size on the distance between the elicited forecasts (i.e. the distribution of aggregated group allocations) and the true distribution of realization probabilities. When introducing environmental uncertainty, by not informing subjects about the true realization probabilities, we find some evidence that pairs produce worse forecasts than groups of three or four players. There is no significant difference between groups of three and four. The reduction in performance for groups of two relative to larger group sizes is not driven by the accuracy of the beliefs about the true realization probabilities but rather it appears to be driven by pairs displaying a higher level of strategic error of providing too few resources to (extremely) high-probability events. Since we find limited benefits of increasing group size in both information conditions, an optimal implementation of the mechanism does not appear to require the participation of many forecasters. This is of particular importance to field applications where the number of potential forecasters are often limited.
Several recent papers have addressed competitive elicitation from the perspective of scoring rules (e.g. Kilgour and Gerchack, 2004; Pfeifer et al., 2014; Witkowski et al., 2018). Our contribution is to propose and study one such competitive forecasting mechanism that involves only a few forecasters based on the commonly studied Colonel Blotto game. An important insight that we obtain is that when using games to, for instance, aid operational decision-making, in addition to the choice of mechanism, the number of competitors can be an instrumental parameter to optimize, when aiming for good forecasting performance. In many environments, such as corporate settings, relevant information may be dispersed only among a handful of different individuals, and it is, therefore, essential to develop and to further test mechanisms that successfully elicit expectations in an incentive compatible manner under constrained participation.
The impact of the number of competitors on strategic behavior has been addressed experimentally in the context of Tullock contests. Morgan et al. (2012) provide a comprehensive overview in Table 1 in their paper, revealing that expenditure relative to equilibrium level varies highly across experiments, with group size being one of the factors they consider. Furthermore, in a within-subject setting, Anderson and Stafford (2003) expose experimental participants to different conditions that include variations in group size. They find that expenditures relative to equilibrium level are not monotonic in group size, further suggesting that different group sizes may affect competitive pressures. Sheremeta (2011) compares, among other things, one contest between four players to two contests for half the prize with two players. The author finds that individual expenditures, relative to the prize, is lower in the four-player contest. Lim et al. (2014) implement a between-subjects experiment with treatments based on group sizes. They find that, while group size has no effect on individual expenditures on average, expenditures are more dispersed in larger groups. Finally, Brookins and Ryvkin (2014) implement two treatment dimensions in an experiment. The first dimension varies in the effort costs (symmetric with complete information, asymmetric with complete information, and asymmetric with incomplete information) and the second dimension varies the number of competitors (two or four). They do not find differences across the three effort cost variations with two competitors, but report significant differences with four competitors. Fallucchi et al. (2021) report experimental findings with treatments varying in whether the prize is allocated to one individual or shared among multiple individuals, with winning probabilities and shares being proportional to individual expenditures. They implemented these treatments with three and five competitors and find that average individual expenditures are in both situations larger with three competitors, with the winner-take-all setting consistently showing a larger fraction of zero expenditures. Although Tullock contests considered in these papers are different to our Blotto setting with multiple battlefields and costless resources, the evidence reported here reveals that group size can have an important impact on behavior and game outcomes. It is therefore vital to test the robustness of our mechanism by varying the group size. If larger groups perform better, this would inhibit the use of our mechanism when only very few forecasters, such as two, are available.
The paper proceeds as follows. In Sect. 2, we provide the theoretical foundation of our study. Section 3 outlines the experimental design and Sect. 4 presents the results. Section 5 concludes.
2 Theory
Let there be \(n\ge 2\) players who are each endowed with one unit of resource and, being in competition for a prize of a common fixed value V, have to distribute these resources over m possible events \(E_{1},\ldots ,E_{m}\). We denote the distribution of player i by \(\sigma ^{i}=(\sigma ^{i}_{j})_{j=1,\ldots ,m}\) with \(\sigma ^{i}_{j}\ge 0\) for all \(j=1,\ldots ,m\) and \(\sum _{j=1}^{m}\sigma ^{i}_{j}=1\). The share of the prize that each player obtains is fully determined by the realized event and the amount of resources that all players have allocated to this event. If event \(E_{\ell }\) realizes, then each player i receives a share of the prize in proportion to the amount of resources allocated to this event: \(\frac{\sigma ^{i}_{\ell }}{\sum _{k=1}^{n}\sigma ^{k}_{\ell }}\).Footnote 2 So, in case the events \(E_{1},\ldots ,E_{m}\) realize with probabilities \(p_{1},\ldots ,p_{m}\) with \(p_{j}>0\) for all \(j=1,\ldots ,m\) and \(\sum _{j=1}^{m}p_{j}=1\), player i’s expected payoff is given by
in particular, there is no benefit to players of not using some of their resources.
We assume the game properties, including the realization probabilities \((p_{j})_{j=1,\ldots ,m}\), to be common knowledge among the players and assume players to maximize their expected payoff.
Proposition 1
In the unique (symmetric) Nash equilibrium, all players distribute their resources in proportion to the realization probabilities (i.e. \(\sigma ^{i}_{j}=p_{j}\) for all \(j=1,\ldots ,m\) and for all \(i=1,\ldots ,n\)).
Proof
In a Nash equilibrium \({\overline{\sigma }}\), each player i’s resource distribution \({\overline{\sigma }}^{i}\) solves
First, we show that for all players i and all events j, we have \(\sigma ^i_j>0\), such that we can ignore the inequalities in the maximization problem; the equality constraint follows from the resources being of a use-it-or-lose-it type.
Let \(\sigma\) be an equilibrium. First, it is clear that \(\sum _k\sigma ^k_j>0\) for every event j since otherwise all players would benefit from unilaterally moving some of the mass on any other event to event j. Further, for every event j there are at least two players i with \(\sigma ^i_j>0\). If this would not be the case, the only player with mass on event j would benefit from moving some of this mass to any of the other events. From this it follows that \(\sigma ^i_j<\sum _k\sigma ^k_j\) for all players i and all events j. Next, we show that \(\sigma ^i_j>0\) for all players i and all events j.
The change in expected payoff of player i when moving some mass from event j to event \(\ell\) equals
Suppose (by contraposition) that there exists events j and \(\ell\) for which
If for all players i,
then all players with mass on event j (and those do exist in equilibrium) can improve by moving mass from event j to event \(\ell\). If this equation is not satisfied for all players i, then there exists a player i for which
since otherwise
Note that this requires \(\sigma ^i_j>0\), meaning that player i does have mass on event j that can be reallocated. Further, it follows that for player i the change in expected payoff is strictly positive, which contradicts \(\sigma\) being an equilibrium. We can conclude that for all events j and \(\ell\) we have
This means that the change in expected payoff of any player i when moving a small mass from event j to event \(\ell\) equals
Now, suppose there is a player i and an event j for which \(\sigma ^i_j=0\). Then this player would improve his payoff by moving mass from any event \(\ell\) with \(\sigma ^i_{\ell }>0\) (which must exist) to event j. Hence, for all players i and all events j, we have \(\sigma ^i_j>0\). The equilibrium must be interior and we can ignore the inequalities in the maximization problem.
Each player i’s first-order conditions are given by
Since for each pair of different players i and \(i^{\prime }\) the denominators in the respective first-order conditions are identical, for each pair of players i and \(i^{\prime }\), we find
Now, summing over all \(j=1,\ldots ,m\) gives us
such that for each pair of players i and \(i^{\prime }\) we have
Exploiting this symmetry across players, the first-order condition for each player i becomes
Since \(\frac{1}{\lambda ^{i}}\,\frac{n-1}{n^{2}}\) is constant with respect to j, we obtain, for all \(i=1,\ldots ,n\),
This completes the proof.Footnote 3\(\square\)
The proposition implies that, even if the true realization probabilities are unknown to the decision maker who implements the game, equilibrium play will fully reveal these probabilities to her, as long as they are common knowledge to the players. Moreover, this holds for any number of players.
3 Experimental design
Our experimental design implements the setting just described with and without common knowledge of realization probabilities for varying numbers of competing players. In the remainder of this section, we first present the precise decision framework, after which we present the details of our design (including the treatment variations) and all relevant experimental procedures. The experiment uses the same design as in Peeters and Wolk (2019) and extends the treatments with proportional payoffs to more than two players. Therefore, this section largely follows the design section of that paper.
3.1 Setting
Each member of a group of n individuals is asked to allocate 100 units of resources over eleven bins that represent the possible events, as is illustrated in Fig. 1. Next, a chance mechanism determines the bin that is decisive for the individuals’ payoffs. Only the resources that are allocated to this particular bin are relevant for how the total group reward of \(100\,n\) points is shared among the members of the group and individuals receive shares in proportion to the amount of resources allocated to this bin.Footnote 4
The decisive bin is selected by a random process that starts at zero at time \(t=0\) and that terminates once it reaches one of the bounds at either \(+\,\,2.5\) or \(-\,\,2.5\). Alternatively, if neither of the two bounds are crossed before \(t=100\) the process terminates at that point. Each innovation is drawn from a normal distribution with mean zero and a standard deviation equal to 0.2770.Footnote 5 Figure 2 shows one time series generated by this process from the experiment, used in round 11, that led to a termination at the lower bound at time \(t=82\).
The labels above the first ten bins in Fig. 1 represent ranges of termination times; the eleventh bin represents the event that it did not terminate before \(t=100\). The numbers in the bins indicate the probability (rounded to the nearest integer) that the process just described terminates at the respective bin.
3.2 Design and procedures
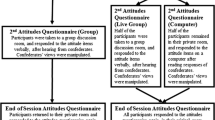
Individuals were randomly assigned into groups which remained unchanged throughout the twenty rounds of the experiment. The experiment started with instructions where subjects were informed about their tasks and the resulting payoff consequences, as described above. Before the first decision round, subjects saw an example time-series animation. This series was generated precisely in the same way and with the same parameters as the time-series in the remainder of the experiment. Next, the allocation task of the experiment began. First, subjects were asked to allocate their resources over the eleven bins representing the different termination times. Second, they were shown the time-series that was used to determine the decisive bin for that round. Finally, after learning which bin was selected, all payoff relevant information was shown to the participants. This included all group members’ allocations to the decisive bin. This sequence of events was repeated twenty times and all participants saw the same time-series in the same order over the course of the experiment.
Our experiment consists of six different treatments which vary in two dimensions. The first dimension is the size of the group (n), within which players compete for the prize (of value \(100\,n\)), that varies from two, three to four. Second, we vary the players’ (common) knowledge about the true realization probabilities. Within this dimension, individuals have full information about these probabilities in the treatment variation ‘Baseline’ that is developed to closely match the ‘common knowledge’ assumptions made in the theoretical model. In the treatment variation ‘Predict’, that is developed in view of possible practical applications, players are not informed about the realization probabilities and only know that the underlying stochastic process is fixed. Throughout the twenty rounds, however, subjects gradually learn more about the chance mechanism determining the decisive bin, and hence the true realization probabilities. Our choice for a time series selecting an event on a linearly ordered domain of events in our design was made to foster this learning process. To control for possible differences in this learning process across different group sizes, in the Predict treatments, after the last decision round, before showing the final time-series animation, we elicited subjects’ beliefs about the true probability distribution by which each bin will be selected as the decisive bin.Footnote 6
The experiments were conducted in the experimental laboratory at Maastricht University in October 2014 and April 2018 for the Predict treatments and in January 2016 and 2017 and April 2018 for the Baseline treatments. We recruited undergraduate students from various disciplines via ORSEE (Greiner, 2015). For both, the Baseline and the Predict treatments, we collected the sequence of twenty allocation decisions for 24, 12, and 9 different groups consisting of, respectively, two, three and four members. Taken together, 240 students participated in the experiment.Footnote 7 All interactions took place anonymously via computer clients that where connected to a central server. The experiments were programmed in z-Tree (Fischbacher, 2007). The instructions are provided in “Appendix C”. Final payment in the experiment was based on the points accumulated over all rounds. A typical session lasted about an hour and the average payoff was about 18 Euros (including 3 Euros show-up fee).Footnote 8
4 Results
In this section, we study the impact of the number of competitors on the elicitation performance of the Blotto game with proportional prize sharing. Here, we measure the elicitation performance by the closeness of the distribution of individual allocations of resources on group level to the real distribution of realization probabilities. In Sect. 4.1, we do so for the Baseline treatment for which we have a clear theoretical prediction. In Sect. 4.2, we proceed with the Predict treatment that captures an information condition that may be more relevant to real-life applications. All across treatment comparisons reported are based on two-sided Mann–Whitney tests with the null hypothesis of equal performance across different group sizes unless noted otherwise.
4.1 Common knowledge of realization probabilities
According to Proposition 1, individuals should distribute their resources in accordance to the true realization probabilities for all group sizes when these realization probabilities are common knowledge, as is the case in the Baseline treatment. Therefore, we do not expect differences in aggregate distributions of resources on group level across group sizes in the Baseline treatment. As a consequence, for all group sizes, we expect the empirical distribution of resources by groups to be equally close to the true realization probabilities. To measure the closeness between group allocations \(\sigma\) and true realization probabilities p, like in Peeters and Wolk (2019), we use the Hellinger distance (Hellinger, 1909):
which takes the maximal value of one in case the supports of the group allocation and the true distribution are disjoint and the minimal value of zero when the two distributions are identical.Footnote 9
Figure 3 shows the evolution of the average Hellinger distance between the distributions of resources aggregated on group-level and the true realization probabilities over time for the different group sizes in the Baseline treatment. The time trend is similar for all three group sizes, with group allocations getting substantially closer to the true realization probabilities in the first three periods, to stabilize from there onwards. Moreover, we observe that the allocations of resources on group level are closer to the true realization probabilities for larger group sizes. However, the test results reported in Table 1 (unadjusted) reveal that the observed differences between group sizes are not significant for any cluster of rounds. Kruskal–Wallis tests confirm there are no significant differences across group size (\(p\ge 0.187\) for all three selections of rounds).
The averages reported in the columns labeled ‘unadjusted’ do not account for the fact that group allocations are averaged over different numbers of individuals for different group sizes. Hellinger distances and statistical differences (or lack thereof) therefore do not properly isolate group performance that can be attributed purely to individual allocation behavior since group averages are taken over a different number of individuals. The columns labeled ‘adjusted’ adjust the average Hellinger distances and test results in an attempt to isolate from such aggregation effects. The column with label ‘\(2\rightarrow 4\)’ presents the average Hellinger distance based on 1000 random pairings of 24 groups of size 2 into 12 groups of size 4, where individual Hellinger distances are calculated based on the average allocation of individuals in these formed groups of size 4. In the column labeled ‘\(4 \rightarrow 2\)’ we select at random, from each group of size 4, two individuals and compute for each of the resulting 9 pairs the Hellinger distance based on the aggregate allocation over the two selected individuals. Again, the table reports the average Hellinger distance after 1000 random draws. While the former procedure leads to a decrease in the Hellinger distance, relative to the unadjusted one for groups of size 2, the latter procedure increases the Hellinger distance relative to the unadjusted one for groups of size 4—supporting the presence of an aggregation effect favoring larger group sizes, and justifying our adjustment. The last two columns labeled ‘\(3\rightarrow 2\)’ and ‘\(4\rightarrow 3\)’ makes the same reduction from larger groups into smaller ones. The treatment comparisons that follow (lower part of the table) compare the treatments after controlling for aggregation effects. The table reports the percentage of times (over 1000 tests; one for each random pairing or draw) the null hypothesis of equal performance across group sizes is rejected using a five percent significance level. Given that we identified no significant differences before the adjustment, and the adjustment brings Hellinger distances closer without reversing the ordering, it is no surprise that none of the tests lead to a rejection of the null hypothesis.
In sum, we conclude that, in line with the theoretical predictions (Proposition 1), the mechanism does not operate substantially different with different group sizes, even after controlling for aggregation effects that typically favor the larger group sizes.
4.2 Absence of (common) knowledge of realization probabilities
Figure 4 replicates Fig. 3 for the Predict treatment. As expected, due to the lack of (common) knowledge of the realization probabilities, the distance to these probabilities is significantly larger in the Predict treatments (Mann–Whitney tests for all nine comparisons give \(p<0.001\)). Similar to the Baseline treatment, group allocations become substantially better over the first three periods. However, unlike in the Baseline treatment, the improvements do not stop there but continue gradually throughout the 20 periods.Footnote 10 This is clearly an effect arising from the fact that subjects have to learn about the realization probabilities in these treatments.
Like in the Baseline treatment, the elicited distribution is farthest away from the true realization probabilities with two competing players. However, this time Kruskal–Wallis tests reveal that there are significant differences across group size (\(p\le 0.006\) for all three selections of rounds). Further inspection of the unadjusted columns in Table 2 reveals that the distance between group allocations and the true distribution is significantly larger for groups of size two relative to having three or four competing players. There is no significant difference between groups of size three and four.
Comparing the unadjusted and adjusted results in Table 2 (where the adjustments are done precisely as in the Baseline condition), we observe that the difference between groups of two and three remains intact and that this effect appears to be robust. Yet, the earlier significant difference between group sizes of two and four does not appear to stem from improved elicitation. Instead, it may be driven by the fact that we aggregate over more individuals with larger groups and thereby ‘reduce’ noise relative to smaller groups.
Unlike in the Baseline treatment where subjects are fully informed about the true realization probabilities ex ante, in the Predict treatment subjects gradually learn about them. Observed differences between groups sizes in the Predict treatment may therefore be (partly) attributable to subjects learning differently, or at a different speed, when interacting with a different number of competitors. To further investigate this possibility, we make use of the subjects’ beliefs about the realization probabilities (\(\beta\)) as reported after the last period of play. Table 3 presents information on the accuracy of subjects’ beliefs across group sizes, where this accuracy is measured by the Hellinger distance (\(H(\beta ,p)\)), and does not provide statistical evidence for individuals learning differently about the true realization probabilities for different group sizes. A Kruskal–Wallis test (\(p= 0.719\)) for differences across group sizes is consistent with the Mann–Whitney U tests reported in the table.
Overall, in absence of initial common knowledge of realization probabilities, the observed differences across group sizes are significant between group sizes of two and three and between groups of two and four. However, when controlling for aggregation effects the significance between two and four disappears, suggesting that it is not driven by improved elicitation. We can, therefore, conclude that there are some differences in performance due to different group sizes within the elicitation game in the Predict treatment. Yet, the source of the observed differences remains unclear and we next investigate possible sources for these differences.
4.3 Risk attitudes
As part of a post-experiment questionnaire we elicit self-reported risk attitudes to test whether subjects’ behavior in the experiment is correlated with such attitudes. Risk attitudes are reported on a scale between one and ten, where a higher score represents more risk-seeking attitudes.Footnote 11 We use this measure to investigate the relationship between risk attitudes and how close to the true realization probabilities individuals distribute their resources.
The first four columns in Table 4 presents regression results for the Baseline and the Predict treatments separately. As dependent variable we select the individual Hellinger distance averaged over all rounds.Footnote 12 Columns labeled ‘(1)’ present the results of a baseline specification where we include group size and risk attitude separately while in the columns labeled ‘(2)’ we also include an interaction term between the two. In all specifications group size is relative to groups of three, and we cluster standard errors on the group level. The relationship that we are most interested in is the one between group size and risk, since any differential effect of risk attitudes with respect to group size could potentially help us explain the performance differentials observed for the Predict treatment in the previous section.
From the first two columns, we see that risk attitude has a significant effect on how close individuals allocate to the true realization probabilities in the Baseline treatment: risk averse individuals allocate closer to the true realization probabilities. Furthermore, the impact of risk attitude is not significantly different across group sizes.
For the Predict treatment, we find a different pattern. Again, as can be concluded from the third column (specification (1)), risk has a similar effect as in the Baseline treatment. However, in the fourth column (specification (2)), we observe that group size has a differential impact on the relation between risk attitude and individual allocations relative to the true realization probabilities. Further inspection reveals that risk attitude is statistically significantly when individuals compete in groups of three but not when competing in groups of size two or four.Footnote 13 Importantly, this effect is not driven by risk attitudes being significantly different across group sizes (Kruskal–Wallis test: \(p=0.885\)).
The results show that while there is a significant effect of risk attitudes on individual allocations in both treatments, there is only a differential effect of risk attitudes with respect to group size in the Predict treatment.Footnote 14 The last two columns in the table repeat the regressions but where the dependent variable is the Hellinger distance between individuals’ reported beliefs and the true realization probabilities (in the predict treatment). While risk attitude has a significant effect for groups of size three (risk averse individuals develop better beliefs about the realization probabilities), there is no such relation for groups of size two and four, nor between groups of size two and four, as our post-regression tests reveal. Hence, risk has a significant effect on behavior, but its effect does not interact with group size. This suggests that the differences across group sizes in Predict are not random but possibly of a strategic nature.
4.4 Strategic errors
We next proceed to investigate whether there are common strategic errors being made in the experiment. As a first step we plot the average number of resources allocated to the different bins in Fig. 5 against the true probability distribution (in gray) when operating in groups of size three. We select two different rounds for this analysis, the first (dashed) and last (solid) round in the Baseline (left plot) and Predict (right plot) treatments. Figures 6 and 7 in Appendix A present similar plots for subjects operating in groups of size two and four. While subjects (on average) clearly improve in how they distribute their resources over the first ten bins, the resources they allocate to the eleventh bin stay far below the true realization probability of 33% for this bin.
Table 5 presents the average number of resources allocated to the eleventh bin in the last round for all treatments and the average reported beliefs on the realization probability of the eleventh bin in the Predict treatments. While the underestimation, as reflected by subjects’ allocations, is significantly worse in the Predict treatment compared to the Baseline treatment, also in the Baseline treatment subjects allocate significantly less to the eleventh bin relative to the true 33% probability. Given that in the Predict treatment the average belief that subjects report about the realization probability of the eleventh bin is significantly below the 33% and that subjects allocate significantly less to this bin relative to their beliefs (see last row in the table), we can conclude that this (persistent) error must be deliberate, or in other words of a strategic nature (including the (higher order) beliefs that are formed in the introspection process).
With regard to the differences across group sizes, we do not find significant differences in the number of resources that subjects allocate to the eleventh bin in the Baseline treatment. For the Predict treatment we do not find subjects reporting different beliefs across the different group sizes. However, we find that, in this treatment, subjects operating in groups of size three allocate significantly more to the eleventh bin than subjects operating in pairs.Footnote 15 This difference is also picked up by the Kruskal–Wallis test for the same comparison, as shown in the rightmost column of Table 5.
The question that naturally follows is whether this difference in behavior towards the last bin drives predictions by groups of three to be better compared to those by groups of two in the Predict treatment. To address this question, we consider the group allocations conditional on their allocations to the first ten bins and compare these to the true realization probabilities conditional on terminating in one of the first ten bins. Table 6 replicates the unadjusted measures reported in Tables 1 and 2 for the Hellinger distances between the resulting conditional distributions.
For the Baseline treatments we can conclude that the earlier observed lack of significance in the performance across group sizes (see Table 1) is not affected by the strategic error related to allocations to the last bin. For the Predict treatments, however, we do no longer find the performance of groups of size three to be significantly better than those of groups of size two. Hence, it is not unlikely that the earlier difference across group sizes (see Table 2) is indeed driven by allocations to the eleventh bin. Since we did not find significant differences in beliefs regarding the eleventh bin across group sizes (see Table 5), the across group size difference reported in Subsection 4.2 may be driven by the systematic strategic error of underallocating resources to high-probability events being sensitive to group size.
5 Conclusion
In this paper, we present and test an elicitation mechanism, practically useful for forecasting purposes, based on the Colonel Blotto game. In our game, the fixed award is shared across the participating players in proportion to the number of resources that they allocated to the realized event. Under the assumption of common knowledge of realization probabilities, we show that there is a unique (symmetric) equilibrium in which players allocate their resources in proportion to their beliefs for any finite number of players.
We implement the mechanism experimentally for various number of players (two, three and four) and in two different information conditions (with and without common knowledge of the realization probabilities). We find that there is no difference in the mechanism’s elicitation performance across different group sizes when realization probabilities are common knowledge ex ante. Though, in absence of common knowledge of the realization probabilities, there are some observed differences across group sizes: the mechanism operates marginally better with three or four compared to two players. This effect is mainly driven by players’ behavior (in particular, the way they act in presence of high-probability events) rather than by differences in the beliefs they form about the realization probabilities.
From the evidence provided here, taken together with the evidence provided in Peeters and Wolk (2019) that a quadratic scoring rule does not perform better than the Blotto mechanism with two players, it becomes evident that groups as small as the ones we consider here can be used to elicit forecasts successfully. Furthermore, using larger groups, while marginally better, may not always significantly improve performance as much as to outweigh the larger cost of using more forecasters. Therefore, overall, our evidence supports the use of small groups in eliciting forecasts. This is particularly relevant for field applications where the number of potential forecasters are limited and the source of uncertainty is not easily controlled or observed. Finally, relevant from a design perspective, the strategic bias identified in relation to high-probability events suggests that an optimal performance of the mechanism can benefit from a careful partitioning of the events.
Notes
Examples include Kaggle (https://www.kaggle.com/) and DrivenData (https://www.drivendata.org).
Note that this is equivalent to interpreting this as the probabilities by which the full prize is allocated to the players.
For the two player situation the strategy profile in the proposition has already been shown to be the unique Nash equilibrium in Friedman (1958). As Friedman (1958) considers unequal amounts of available resources for the two players, it is pretty straight-forward to see that the n-player extension of this equilibrium strategy profile constitutes a Nash equilibrium of the game situation with n players. The uniqueness claim in the proposition is, however, not easily obtained from Friedman (1958). The simpler proof presented here follows Robson (2005) and Peeters and Wolk (2019).
Subjects receive nothing when they did not allocate any resources to the decisive bin, even when others did not do so as well.
We incentivized this task on the individual level using a simple and easy to explain incentive system: we pay a fixed amount for each ‘unit’ of probability mass that is correctly allocated in the termination distribution; that is, subjects received the amount \(\sum _{j=1}^{11} \min \{\beta _{j},p_{j}\}\), where p is the true probability distribution and \(\beta\) is the expressed belief about p.
The data for group sizes of two are also used in Peeters and Wolk (2019), where the proportional payment rule is compared to a winner-takes-all payment rule and a mechanism with individual incentives using a proper scoring rule.
All experiments were conducted with the informed consent of healthy adult subjects who were free to withdraw from participation at any time. Only individuals who voluntarily entered the experiment recruiting database were invited, and informed consent was indicated by electronic acceptance of an invitation to attend an experimental session. The experiments were conducted following the peer-approved procedures established by Maastricht University’s Behavioral and Experimental Economics Laboratory (BEElab). Our study was approved by the BEElab at a public ethics review and project proposal meeting that is mandatory for all scholars wishing to use the BEElab facilities.
To ensure that our findings are not unduly affected by the chosen distance measure, we replicate the main analyses using the Jensen–Shannon divergence in “Appendix B”.
We verify this by running, for each group size separately, a regression of the group-based Hellinger distance on a period counter clustered on the group level. This procedure shows that for all three group sizes there is a negative significant coefficient on period with a p value of at most 0.016. The slope remains negative after including a squared period counter as well. The squared term is positive and significant suggesting that the improvements level-off over time, consistent with the graphical evidence presented in Fig. 4. Regression results are available from the authors upon request.
We follow Dohmen et al. (2011) and ask subjects about their willingness to take risks in general in a non-incentivized manner.
Results are similar when we focus only on the first ten or the last ten rounds.
This effect is also present in our sample when splitting the regressions by group size. Since the results are quantitatively and qualitatively similar we do not report the results here.
One may expect more risk-averse individuals to be more prone to allocate their resources closer to a uniform distribution. We conducted regressions similar to those reported in Table 4, but then for the Hellinger distance relative to the uniform distribution instead of relative to the true realization probabilities. For the Baseline treatment risk attitude is not significant. For the Predict treatment we do find a significant effect: more risk-averse individuals make allocations that indeed are closer to the uniform distribution. However, we do not find differences with respect to group size in this regard.
The reason that the difference between groups of size three and four is not significant is that the difference in means is largely caused by a single individual in the treatment with group size of three who allocated 80 resources to the last bin (while the second-highest allocation is 36). Exclusion of this extreme allocation causes the average allocation to drop from 12.1 to 10.2.
References
Anderson, L. R., & Stafford, S. L. (2003). An experimental analysis of rent seeking under varying competitive conditions. Public Choice, 115, 199–216.
Brookins, P., & Ryvkin, D. (2014). An experimental study of bidding in contests of incomplete information. Experimental Economics, 17, 245–261.
Cason, T. N., Masters, W. A., & Sheremeta, R. M. (2020). Winner-take-all and proportional-prize contests: Theory and experimental results. Journal of Economic Behavior & Organization, 175, 314–327.
Dohmen, T., Falk, A., Huffman, D., Sunde, U., Schupp, J., & Wagner, G. G. (2011). Individual risk attitudes: Measurement, determinants, and behavioral consequences. Journal of the European Economic Association, 9(3), 522–550.
Fallucchi, F., Niederreiter, J., & Riccaboni, M. (2021). Learning and dropout in contests: An experimental approach. Theory and Decision, 90(2), 245–278.
Fischbacher, U. (2007). zTree: Zurich toolbox for ready-made economic experiments. Experimental Economics, 10(2), 171–178.
Friedman, L. (1958). Game-theory models in the allocation of advertising expenditures. Operations Research, 6(5), 699–709.
Greiner, B. (2015). Subject pool recruitment procedures: Organizing experiments with ORSEE. Journal of the Economic Science Association, 1(1), 114–125.
Hellinger, E. (1909). Neue Begründung der Theorie quadratischer Formen von unendlichvielen Veränderlichen. Journal für die reine und angewandte Mathematik, 136, 210–271.
Kilgour, D. M., & Gerchack, Y. (2004). Elicitation of probabilities using competitive scoring rules. Decision Analysis, 1(2), 108–113.
Lim, W., Matros, A., & Turocy, T. (2014). Bounded rationality and group size in Tullock contests: Experimental evidence. Journal of Economic Behavior & Organization, 99, 155–167.
Morgan, J., Orzen, H., & Sefton, M. (2012). Endogenous entry in contests. Economic Theory, 51, 435–463.
Peeters, R., & Wolk, L. (2017). Eliciting interval beliefs: An experimental study. PLoS One, 12(4), e0175163.
Peeters, R., & Wolk, L. (2019). Elicitation of expectations using Colonel Blotto. Experimental Economics, 22(1), 268–288.
Pfeifer, P. E., Grushka-Cockayne, Y., & Lichtendahl, K. C. (2014). The promise of prediction contests. The American Statistician, 68(4), 264–270.
Robson, A. (2005). Multi-item contests. Working paper (2005).
Sheremeta, R. M. (2011). Contest design: An experimental investigation. Economic Inquiry, 49, 573–590.
Witkowski, J., Freeman, R., Wortman Vaughan, J., & Pennock, D.M., & Krause, A. . (2018). Incentive-compatible forecasting competitions. Association for the Advancement of Artificial Intelligence, 2018, 5.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank the participants at the 2018 National Game Theory and Experimental Economics conference in Guangzhou as well as at the 2019 Bayesian Crowd conference in Rotterdam for valuable input on earlier versions of this manuscript. We are particularly thankful to the anonymous reviewers who, via their comments and suggestions, contributed in important ways to the development of the paper.
Appendices
A Additional figures
B Replication using Jensen–Shannon divergence
In this appendix, we replicate the analysis from the main sections using the Jensen–Shannon divergence. To be specific, Fig. 8 and Tables 7, 8 and 9 replicate Figs. 3, 4 and Tables 1, 2 and 3.
where \({\tilde{\sigma }}\) denotes the elicited distribution, p the true distribution, and \(m=\frac{1}{2}(p+{\tilde{\sigma }})\).
C Instructions
1.1 C.1 Predict treatment with two bidders
1.1.1 Welcome
You are about to participate in a session on interactive decision-making. Thank you for agreeing to take part. The session should last about 90 min.
You should already have turned off all your mobile phones, smart phones, mp3 players and any such devices. If not, please do so immediately. These devices must remain switched off throughout the session. Place them in your bag or on the floor besides you. Do not have them in your pocket or on the table in front of you.
The entire session will take place through the computer. You are not allowed to talk or to communicate with other participants in any other way during the session.
You are asked to abide by these rules throughout the session. Should you fail to do so, we will have to exclude you from this (and future) session(s) and you will not receive any compensation for this session.
We will start with a brief instruction period. Please read these instructions carefully. They are identical for all participants in this session with whom you will interact. If you have any questions about these instructions or at any other time during the experiment, then please raise your hand. One of the experimenters will come to answer your question.
1.1.2 Compensation for participation in this session
In addition to the € 3.00 participation fee, what you will earn from this session will depend on your decisions, those of others with whom you interact and chance. In the instructions and all decision tasks that follow, payoffs are reported in Experimental Currency Units (ECUs). At the end of the experiment, the total amount you have earned will be converted into Euros using the following conversion rate:
The payment takes place in cash at the end of the experiment. Your decisions in the experiment will remain anonymous.
1.1.3 Instructions
At the beginning of the experiment all participants are divided in groups of size 2. You will be interacting within this group for the entire session.
This session consists of twenty rounds. Each round you are faced with a decision task and the payoff (in ECU) that you collect in this round depends on the decision you make, that of the other group member, and chance. At the end of the session you are paid according to all payoffs that you gathered during the twenty rounds.
Before the first round starts, you will be shown a realization of a time series from some random process. Figure 9 shows an example of such a time series.
Each round, before you see the time series that is generated for that round, you are asked to allocate an amount of 100 resources over 11 different boxes. See Fig. 10.
In the first round you have to use the red up and down triangles to allocate the resources. In all following rounds, you can use these triangles to adjust your allocation from the previous round.
After you made your decision (and confirmed it), the time series generated for that round will be shown to you. Two things can happen: (1) the time series hits one of the two boundaries (the thick horizontal lines in Figure 1) before time \(t=100\), or (2) the time series does not hit any of the boundaries before time \(t=100\). In the former case (1), one of the first ten boxes are selected; the precise box being determined by the time where it hits one of the boundaries. For example, if the time series hits one of the boundaries at \(t=27\), as is the case in Fig. 9, then the box with label “21–30” is selected (the third box). In the latter case (2), the last box with label “101+” is selected. Hence, regardless of the outcome one out of the eleven boxes will be selected.
It is important to note here that the time series is generated by a statistical software package and is not manipulated for the purpose of this experiment. As all time series shown to you are generated from the same random process, you will gradually become more familiar with the underlying process during the course of the experiment.
Your payoff for a round depends on the box selected, the amount of resources that you allocated to this box and the amount the other group member allocated to this box. There is a fixed payoff for the group of 200 ECU and the amount of resources allocated to the selected box determine the way these 200 ECU are allocated over the group members.
The total group payoff of 200 ECU is shared among the group members in proportion to the amount of resources that were allocated to the selected box. In case you happen to have allocated zero resources to the selected box, you will receive no payoff—even in case the other group member allocated zero resources to this box as well.
After each round, you will learn which box was selected, the amount each of the group members allocated to the box, and your payoff. You will not learn the amounts the other group member allocated to the other ten boxes.
1.2 C.2 Baseline treatments
The instructions of the Baseline treatments were similar to those of the Predict treatments, except for two changes:
-
1.
The sentence “Apart from the realized time series in the previous rounds and the time series shown to you at the beginning (and the one in the figure above), no further information will be given, except that the time series will start at a value of 0 at time \(t=0\).” was taken out.
-
2.
The sentence “As all time series shown to you are generated from the same random process, you will gradually become more familiar with the underlying process during the course of the experiment.” was replaced by “All time series shown to you are generated from the same random process, for which the probabilities that boxes are selected are as given in Fig. 11 (rounded to the nearest whole number).”
1.3 C.3 Treatments with three and four bidders
For the treatments with three and four bidders a plural form was used when referring to the other group members and the size of the prizes were upgraded to 300 and 400, respectively.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Peeters, R., Rao, F. & Wolk, L. Small group forecasting using proportional-prize contests. Theory Decis 92, 293–317 (2022). https://doi.org/10.1007/s11238-021-09825-0
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11238-021-09825-0