Probability weighting for losses and for gains among smallholder farmers in Uganda

Abstract

Probability weighting is a marked feature of decision-making under risk. For poor people in rural areas of developing countries, how probabilities are evaluated matters for livelihoods decisions, especially the probabilities associated with losses. Previous studies of risky choice among poor people in developing countries seldom consider losses and do not offer a refined tracking of the probability-weighting function (PWF). We investigate probability weighting among smallholder farmers in Uganda, separately for losses and for gains, using a method (common consequence ladders) that allows refined tracking of the PWF for a population with low levels of literacy. For losses, we find marked probability weighting near zero, which is in line with evidence found in Western labs. For gains, the absence of probability weighting is remarkable, particularly its absence near 100%. We also find marked differences in probability weighting for traditional farmers which are in line with the observed livelihoods strategies in the study area.

1 Introduction

How do poor people in the rural areas of developing countries, whose livelihoods are subject to the vagaries of nature, thin or absent markets, dysfunctional institutions and erratic governments, evaluate risky prospects? Contrary to a stereotype of what keeps them poor, smallholder farmers in developing countries may exhibit remarkable tolerance of risk, and are considerably less risk averse than typical Western populations (Vieider et al. 2019). In this study, we investigate, for a sample of smallholder farmers from a developing country, not risk aversion as such but a different aspect of decision-making under risk with important implications for livelihoods decisions: probability weighting.

In risky choice decisions, how probabilities are evaluated is crucial. Economists typically think of this as probabilities of outcomes being transformed into decision weights on those outcomes, through some psychologically plausible nonlinear probability-weighting process. Following Allais (1953), violations of the independence axiom of expected utility theory have been observed in a large number of experimental studies, which points to the prevalence of nonlinear probability weighting.¹ The rationale for probability weighting that is currently most commonly invoked is due to prospect theory (Kahneman and Tversky 1979; Tversky and Kahneman 1992). In prospect theory, the so-called “diminishing sensitivity” relative to a reference point is the central organising principle, which governs both the distinct shape of the value function and the shape of the probability weighting function (PWF). In the context of probability weighting, this means that people are less sensitive to changes in probabilities that take place further from a reference probability. For instance, if the reference probability is 0, then weighted probabilities will increase by more when a probability of an outcome changes from 5 to 6% than when it changes from 10 to 11%.

Typically, the reference probabilities 0 and 1 are jointly postulated: the certainty that an outcome will not occur and the certainty that it will occur. Diminishing sensitivity relative to these two reference probabilities produces what Fehr-Duda and Epper (2012, p. 569) call the “famous inverse S”: a PWF that is steep near the reference probabilities of 0 and 100%, and relatively flat in the middle, giving rise to the overweighting of small probabilities and the underweighting of large probabilities (Kahneman and Tversky 1979; Tversky and Kahneman 1992; Wu and Gonzalez 1996; Gonzalez and Wu 1999; Starmer 2000; Takahashi 2011). The inverse S-shaped PWF has been confirmed in the bulk of the large number of experimental studies of probability weighting.² The robustness of this finding suggests that diminishing sensitivity relative to the reference probabilities of 0 and 1 provides a good account of how humans transform probabilities into decision weights.

In this study, we investigated as thoroughly as we deemed feasible the probability-weighting habits of small-scale farmers in a poor country. We were motivated by three considerations. First, these farmers are “experts” on decision-making under risk. Frequent hazards such as droughts, floods, pests, and diseases affect their investments, and getting investment decisions right is a matter of life and death (Fafchamps 2003). To the extent that probability weighting is a bias that experienced decision-makers should be less affected by, nonlinear probability weighting should be less pronounced for such farmers than for typical experimental subjects. Second, most of the experimental literature on nonlinear probability weighting does not obtain a separate PWF for gains and losses; to the best of our knowledge, Vieider et al. (2019) is the only previous experimental study of risky choice in a developing country that obtains a separate PWF for losses. Since hazards are so common in rural areas of developing countries, losses are a frequent occurrence. Knowing the PWF for losses is therefore important, and we investigate it in this study as well as for gains. Third, we were motivated by the intriguing possibility that, in nonstandard subject pools, probability weighting could be very different from that typically found in Western labs. In particular, we wondered whether the all-pervasive nature of risk in the rural areas of developing countries would lead to the emergence of reference probabilities not equal to but somewhere between 0 and 1. If certainty is at best an abstract concept for a population, then perhaps more realistic (historically informed) probabilities would act as referents. If so, then the PWF may no longer resemble an inverse S.

For investigating probability weighting, we designed and implemented common consequence effect tests (Wu and Gonzalez 1998). There are two reasons that we decided to choose this method. The first is that we needed a simple method for a subject pool with low levels of literacy and numeracy (Dave et al. 2010). Humphrey and Verschoor (2004a, 2b) had previously successfully implemented common consequence effect tests in similar subject pools to ours. Based on extensive piloting, we found that we could considerably increase the refinement of these tests while maintaining excellent subject comprehension. Conceptually attractive alternatives such as Van de Kuilen and Wakker (2011)’s midweight method were deemed to be cognitively too demanding for our subject pool. The second is that we needed a method with sufficient tracking ability of the PWF to investigate whether more than two reference probabilities exist (e.g., 0, 1, and one or more others). For that reason, we decided not to make use of functional forms of the PWF, since these rule out a priori plausible shapes influenced by reference probabilities at the extremes as well as in between those extremes of the domain of the PWF (as explained below).

Each subject faced ten choices between two three-outcome lotteries. A pair of lotteries may be thought of as representing a “rung” on a “common consequence ladder”. The rungs are related to each other through an identical manipulation of both lotteries, a so-called common consequence shift. In our case, the manipulation consists in shifting identical probability mass from the worst outcome to the intermediate outcome of both lotteries on one rung, which yields the lotteries on another rung. A preference reversal violates the independence axiom of expected utility theory. Assuming cumulative prospect theory (Tversky and Kahneman 1992), preference reversals permit pronouncements on the relative steepness of the PWF in precisely defined probability intervals.³

Importantly, we implemented two game conditions, in a between-subject design. One condition is in the domain of losses, the other in the domain of gains. In the losses version of the experiment, the best outcome of the three-outcome lotteries is equal to the neutral outcome, so that the intermediate outcome and worst outcome represent losses. In the gains version, the worst outcome is equal to the neutral outcome, so that the intermediate outcome and best outcome represent gains. We established the neutral outcome by giving each subject a voucher 3 weeks before the day of the experimental session in which that subject would participate. The voucher showed the name, address, and portrait photo of the face of the subject, as well as the figure of 8000 shillings prominently displayed. 8000 Ugandan shillings are about twice the median daily wage in the study area, in which waged labour is moreover hard to come by. In a scripted, orally delivered message when the vouchers were handed over, subjects were informed that, depending on the decisions they would be asked to take in three weeks’ time, their final earnings could be higher or lower than 8000 shillings.

By making the figure of 8000 shillings salient in this way, we aimed to establish this amount as a reference point, so that lower amounts would be thought of as losses, and higher amounts as gains. The reason we handed over the vouchers 3 weeks before experimental days was to alleviate concerns about a house-money effect (Thaler and Johnson 1990) through inducing a sense of entitlement to the 8,000 shillings through the passage of time.

In the domain of losses, our investigations focused on probabilities between 0 and 0.8. This is mainly for the sake of realism: investment prospects in which losses are more than 80% likely would not be considered by small-scale farmers in a poor country. We find that probability weighting for losses is pronounced and consistent with diminishing sensitivity relative to the reference probability of 0. Weak evidence is obtained for a second reference probability of 0.5, but we deem it to be insufficient for basing a firm conclusion on.

In the domain of gains, we investigated the curvature of the PWF for probabilities between 0.35 and 1. This is again for realism in that investments that have a success probability lower than 35% would not be contemplated in real life. We find no evidence for probability weighting near the probability of 1, so no evidence that 100% acts as a reference probability relative to which diminishing sensitivity is at work. We do find evidence for a PWF that is relatively flat in the middle, which is consistent with an inverse S shape. However, more striking than that is the overwhelming support for expected utility theory (EUT): 42 out of a total of 45 common consequence steps (comparisons between rungs) are consistent with EUT and only 3 point to nonlinear probability weighting.

When investigating correlates of probability weighting, we find that traditional farmers, those who farm mainly for subsistence and with a minimal reliance on purchased inputs, evaluate probabilities differently from the rest of the sample. Whereas concavity near zero characterises the PWF for the sample as a whole in the domain of losses, convexity does so for traditional farmers. In the domain of gains, whereas linearity of the PWF when approaching 100% characterises the aggregate sample, convexity does so for traditional farmers. We argue in the paper that the contrast between how traditional and nontraditional farmers evaluate probabilities makes sense of the observed difference between them in livelihoods strategies.

The main lesson from our study combines our findings from the domains of losses and gains. In a sample of experienced decision-makers under risk, risky choice in the domain of losses points to pronounced probability weighting that is largely consistent with experimental evidence from Western labs, whereas risky choice in the domain of gains is largely consistent with EUT. Of particular relevance to this special issue, we argue that our results suggest that poor farmers in developing countries should not be seen as shying away from risk but as particularly adept decision-makers under risk (cf. Vieider et al. 2019).

We see the contribution of our study as follows. To begin with, we contribute to the literature on individual risky choice in developing countries. Previous studies have investigated probability weighting (Humphrey and Verschoor 2004a, b; Harrison et al. 2010; Tanaka et al. 2010; Liu 2013; l’Haridon and Vieider 2018; Vieider et al. 2018), but none of these have tracked the PWF with the refinement offered here. Humphrey and Verschoor (2004a, 2004b) use only the probabilities 0, 1/4, 1/2, 3/4, and 1. In other studies of probability weighting in nonstudent samples in developing countries, the parameters of a functional form are estimated as those most likely to generate the experimental data given some assumptions on errors; for instance, Prelec (1998)’s two-parameter functional form of the PWF is estimated both in Harrison et al. (2010) and in Vieider et al. (2018). In the design of Tanaka et al. (2010), which they used in rural Vietnam and Liu (2013) used in rural China, the parameter of Prelec (1998)’s one-parameter functional form of the PWF is instead obtained directly based on a series of paired lottery choices. Shapes with more than one convex or more than one concave area cannot be captured by these functional forms. For that reason, they cannot capture shapes influenced by reference probabilities at the extremes as well as in between those extremes of the domain of the PWF. We deem such shapes plausible in our subject pool; see Sect. 2.2 for further discussion.⁴ Moreover, imposing a functional form may hide linearity of the PWF for ranges of its domain for which decision-makers do not transform probabilities nonlinearly into decision weights. We argue in Sect. 5 that this is a plausible reason for the difference between our findings in the domain of gains and those studies for farmers in developing countries that report finding an inverse S-shaped PWF.

We also contribute to the fairly small literature on probability weighting in the domain of losses (Tversky and Kahneman 1992; Abdellaoui 2000; Abdellaoui et al. 2005; Etchart-Vincent 2004; Abdellaoui et al. 2011). We make a small theoretical contribution by spelling out common consequence conditions for probability weighting in the domain of losses, make a methodological contribution by providing real incentives in the domain of losses without practising deception (cf. Etchart-Vincent and l’Haridon 2011), and expand the evidence base on probability weighting in the domain of losses by investigating it for a nonstandard subject pool.

The paper proceeds as follows. In Sect. 2, we derive our hypotheses in the context of cumulative prospect theory and develop common consequence conditions for testing these hypotheses. Section 3 shows how we implemented these common consequence conditions in our experimental design, and contains details of auxiliary data collection as well as the study area, sampling, and other fieldwork implementation. Section 4 presents descriptive statistics, a balancing test across game conditions, and the univariate and multivariate analyses for testing our hypotheses. Section 5 discusses our main results in terms of the theoretical expectations and the related empirical literature, and concludes.

2 Theory and hypotheses

In this section, we derive from theory the hypotheses to be tested in our experiments, as well as the vehicle for hypothesis testing, so-called common consequence ladders. Our theoretical framework is cumulative prospect theory (CPT) (Tversky and Kahneman 1992), one of the most influential theories of decision-making under uncertainty, which allows precise tests of probability weighting separately in the domains of gains and losses. The tests we derive from CPT consist of a series of choices between paired lotteries, each pair containing a relatively safe lottery and a relatively risky lottery. Each pair in the series is related to every other one through a single manipulation: an identical shift of probability mass between two outcomes, both in the safe lottery and in the risky lottery, a so-called common consequence shift (Wu and Gonzalez 1998). When a common consequence shift leads to a preference reversal (in one pair of lotteries the safe lottery is preferred, in another pair the risky lottery), then evidence has been obtained about the curvature of the probability weighting function (PWF) in a precisely defined interval of probabilities. In what follows, we first present decision weights in cumulative prospect theory, which make use of weighted cumulative probabilities. We next present S-shaped and inverse S-shaped PWFs, as well as the psychological intuitions that underpin them, and the hypotheses for our experimental tests that these give rise to. In the last two subsections, we present common consequence effects, in the domains of gains and losses, respectively. The common consequence conditions for probability weighting obtained in these two subsections form the basis for our experimental design, which constructs common consequence ladders separately in the domains of gains and losses, in a between-subject design.

2.1 Decision weights in cumulative prospect theory

In CPT, individuals maximise a strictly increasing value function $v: X\rightarrow \mathbb {R}$, where X is a set of monetary outcomes, with the neutral outcome denoted as 0, so that gains relative to the neutral outcome are denoted as positive numbers and losses as negative ones. The outcomes $x_{i}$ of uncertain prospect f are arranged in increasing order, $x_{-m},...,x_{0},...,x_{n}$, with $-m$ to $-1$ indexing losses, 0 the neutral outcome, and 1 to n indexing gains. All positive outcomes, encapsulated by $f^{+}$, are multiplied by decision weights $\pi ^{+}(f^{+})=(\pi ^{+}_{0},...,\pi ^{+}_{n})$; all negative outcomes in $f^{-}$ by decision weights $\pi ^{-}(f^{-})=(\pi ^{-}_{-m},...,\pi ^{-}_{0})$. $\pi ^{+}_{0}$ and $\pi ^{-}_{0}$ are in effect redundant, since $v(x_{0})=v(0)=0$.

The value function is additive in gains and losses, so that:

$$\begin{aligned} V(f)=V(f^{+})+V(f^{-})= \displaystyle \sum _{i=0}^{n} \pi ^{+}_{i} v(x_{i})+\displaystyle \sum _{i=-m}^{0} \pi ^{-}_{i} v(x_{i}). \end{aligned}$$

(1)

For risky prospects given by probability distribution $p_{i}$, decision weights are defined by:

$$\begin{aligned}&\pi _{n}^{+}\equiv w^{+}(p_{n}), \end{aligned}$$

(2)

$$\begin{aligned}&\pi _{-m}^{-}\equiv w^{-}(p_{-m}), \end{aligned}$$

(3)

$$\begin{aligned}&\pi _{i}^{+}\equiv w^{+}(p_{i}+...+p_{n})-w^{+}(p_{i+1}+...+p_{n}),\quad 0\le i \le n-1, \end{aligned}$$

(4)

$$\begin{aligned}&\pi _{i}^{-}\equiv w^{-}(p_{-m}+...+p_{i})-w^{-}(p_{-m}+...+p_{i-1}),\quad 1-m\le i \le 0. \end{aligned}$$

(5)

Our interest is in the PWFs $w^{+}$ and $w^{-}$, defined, respectively, for gains and losses.⁵ They convert probabilities $0 \le p_{i} \le 1$ into weighted probabilities $w^{+}(p_{i})$ and $w^{-}(p_{i})$ through strictly increasing functions that satisfy $w^{+}(0)=w^{-}(0)=0$ and $w^{+}(1)=w^{-}(1)=1$.

Expressions 2–5 describe the transformation of weighted probabilities into decision weights. The decision weights on the best gain (expression 2) and worst loss (expression 3) are equal to the weighted probabilities associated with these outcomes. The decision weight on other positive outcomes (expression 4) is equal to the weighted probability that an outcome is at least as high as $x_{i}$, $w^{+}(p_{i}+...+p_{n})$, minus the weighted probability that the outcome is strictly better, $w^{+}(p_{i+1}+...+p_{n})$. The decision weight on negative outcomes other than the worst outcome (expression 5) is defined analogously as the difference between the weighted probability that an outcome is at least as bad as $x_{i}$, $w^{-}(p_{-m}+...+p_{i})$ and the weighted probability that it is strictly worse, $w^{-}(p_{-m}+...+p_{i-1})$.

In Sects. 2.3 and 2.4, we specify decision weights $\pi _{n}^{+}$, $\pi _{i}^{+}$, $\pi _{-m}^{-}$, and $\pi _{i}^{-}$ for three-outcome lotteries, and show how tests for nonlinear probability weighting may be derived from them. However, first, we wish to devote some space to S-shaped and inverse S-shaped PWFs, and the psychological intuitions underpinning these PWFs, since these provide the hypotheses for our experimental tests.

2.2 S-shaped and inverse s-shaped probability weighting functions

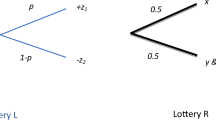
The probability weighting postulated in cumulative prospect theory (Tversky and Kahneman 1992), as it was in original prospect theory (Kahneman and Tversky 1979), is that according to an inverse S-shaped PWF (Fig. 1). The psychological intuition invoked by Kahneman and Tversky is that of “diminishing sensitivity”relative to the reference points of $p^{*}=0$ and $p^{*}=1$, where the superscript * is used to indicate a reference probability. The idea is that changes near these reference probabilities are felt more acutely than changes further away from them: sensitivity to such changes diminishes as they take place further away from these reference points. Therefore, for example, a farmer considering the prospect of an investment in fertiliser would mind more (the value of the prospect would be more affected) if the probability of a loss changes from 5 to 10% than if it changed from 25 to 30%. Likewise, that farmer would mind more if the probability of a gain resulting from the investment dropped from 95 to 90% than if it dropped from 65 to 60%, if she weighted probabilities according to an inverse S-shaped PWF.

Fig. 1

An inverse S-shaped PWF

The bulk of the empirical evidence obtained in Western labs is consistent with an inverse S-shaped PWF, but there are exceptions.⁶ By contrast, the limited evidence available for rural areas of developing countries is sometimes consistent with an inverse S-shaped PWF (Tanaka et al. 2010; Liu 2013; Vieider et al. 2018), and sometimes consistent with an S-shaped PWF (Humphrey and Verschoor 2004a, b).⁷ In S-shaped PWFs (Fig. 2), changes in a middle interval of probabilities are felt more acutely than changes near the end points. Compare for example in Fig. 2 the increase in w(p) of size a when p increases from 0.25 to 0.5 to the increase in w(p) of size b when p increases from 0.75 to 1.0. Therefore, a farmer considering an investment in fertiliser would weight the probability increase of a gain from 50 to 60% more than the increase from 80 to 90%. Similarly, the probability of a loss decreasing from 50 to 40% would matter more than a decrease from 20 to 10% if probabilities are weighted according to an S-shaped PWF.

Fig. 2

An S-shaped PWF

An S-shaped PWF is consistent with a reference probability somewhere in between the extremes of its domain. The psychological intuition underpinning that of a reference probability somewhere in the middle of its domain could be an awareness of the pervasive nature of risk. For instance, if the reference probability is informed by the historical relative frequency of outcomes, then in particularly hazardous environments, in which outcomes seldom occur with probabilities near 0 or 100%, a reference probability (or several reference probabilities) in between these two extremes is plausible.

Diminishing sensitivity relative to reference probability $p^{*}$, $0<p^{*}<1$, would give rise to an S-shaped PWF: convex below $p^{*}$ and concave above $p^{*}$, giving rise to a relatively steep curve in the vicinity of $p^{*}$ and relative flatness near the end points of $p=0$ and $p=1$. In this study, we are interested in whether $0<p^{*}<1$ in a sample of Ugandan farmers. The reason we think this is plausible is that certainty ($p=0$, $p=1$) is at best an abstract concept in the livelihood decisions of these farmers. As detailed in Sect. 4.1, sharp negative income shocks due to harvest failure, droughts, and floods are very common in the study area. If certainty of outcomes is not remotely realistic, then a reference probability $p^{*}$ other than $p^{*}=0$ and $p^{*}=1$, so $0<p^{*}<1$ might be plausible.

We summarise these considerations by spelling out the following four hypotheses, which we test in the paper. An inverse S-shaped PWF gives rise to the first two hypotheses.

Hypothesis 1

The PWF is concave for probabilities $[0,p^{y})$.

Hypothesis 2

The PWF is convex for probabilities $(p^{y},1]$.

Note that theory provides no guidance as to the magnitude of inflection point $p^{y}$; the bulk of the empirical evidence suggests that $p^{y}\approx 1/3$.⁸

By contrast, an S-shaped PWF implies the next two hypotheses.

Hypothesis 3

The PWF is concave for probabilities $(p^{y},1]$.

Hypothesis 4

The PWF is convex for probabilities $[0,p^{y})$.

In these two hypotheses, inflection point $p^{y}$ is also reference probability $p^{*}$, with $0<p^{*}<1$. Again, theory provides no guidance as to its magnitude, so empirical tests should allow for it to lie anywhere in a considerable interval if they are to detect it. We made use of prior evidence on the likelihood of profits and losses, along with some desirable design features, for the specification of the intervals (one for gains and one for losses) within which to search for reference probabilities (see Sect. 3.2).

All four hypotheses are evaluated relative to the null hypothesis of no probability weighting, which implies that the PWF is a straight line connecting $(p,w(p))=(0,0)$ and $(p,w(p))=(1,1)$ The null hypothesis follows from the independence axiom of expected utility theory. We next show how common consequence effects are useful for testing these hypotheses, first for gains and then for losses.

2.3 Common consequence effects in the domain of gains

For deriving conditions for the curvature of the PWF (convex or concave), we make use of common consequence effects. We limit the discussion to three-outcome lotteries, since these feature in our experimental design. The lotteries we consider are of the form $(p_{0},x_{0}; p_{1},x_{1};p_{2},x_{2})$, where $x_{0}$ denotes the neutral outcome and $x_{2}>x_{1}>x_{0}$. For ease of comparison with Wu and Gonzalez (1998), we follow their notation and rewrite $x_{2}\equiv x, x_{1}\equiv y, x_{0}\equiv z; p_{2}\equiv p, p_{1}\equiv q,$ and $p_{0}\equiv r$. The three-outcome lotteries we consider may thus be denoted (p, x; q, y) in which the best outcome x occurs with probability p, the intermediate outcome y with probability q, and the worst (and neutral) outcome z with probability $r=1-p-q$.

In the domain of gains, the value function of CPT for the three-outcome prospects we consider may be written as:

$$\begin{aligned} V(f^{+})=\pi ^{+}_{x}v(x)+\pi ^{+}_{y}v(y)+\pi ^{+}_{z}v(z). \end{aligned}$$

(6)

From expressions 2 and 4, it follows that $\pi ^{+}_{x}=w^{+}(p)$ and $\pi ^{+}_{y}=w^{+}(p+q)-w^{+}(p)$. Since $v(z)=0$, the value function may therefore be rewritten as:

$$\begin{aligned} v=w^{+}(p)v(x)+(w^{+}(p+q)-w^{+}(p))v(y). \end{aligned}$$

(7)

This value function is identical to the one obtained in Wu and Gonzalez (1998), who derive their common consequence conditions in the context of rank-dependent expected utility (RDEU) (Quiggin 1982; Yaari 1987; Segal 1989). In the domain of gains, RDEU is indistinguishable from CPT. However, in the domain of losses, RDEU does not provide separate predictions: it simply ranks outcomes from worst to best and does not consider them relative to a neutral outcome. Following a slightly different approach, we therefore obtain in this subsection identical common consequence conditions for gains to those obtained by Wu and Gonzalez (1998), and derive novel common consequence conditions in the next subsection, for losses.

Consider a choice between safe lottery S (S for safe), characterised by $(p^{'},q^{'})$ and risky lottery R (R for risky), characterised by (p, q). Compared to S, R has a higher probability of the best outcome ($p>p^{'}$) and a higher probability of the worst outcome ($1-p-q>1-p^{'}-q^{'}$). Now, consider a choice between a second pair of lotteries $S_{\epsilon }$ and $R_{\epsilon }$, which are derived from S and R, respectively, by shifting probability mass $\epsilon$ from the worst to the intermediate outcome.⁹$S_{\epsilon }$ is thus characterised by $(p^{'}, q^{'}+\epsilon )$ and $R_{\epsilon }$ by $(p,q+\epsilon )$. A series of binary lottery choices constructed along these lines is known as a common consequence ladder: each lottery choice in the ladder is connected to every other one through a shift of probability mass between the same two outcomes, both in the safe and in the risky lottery. Importantly, outcomes x, y, and z are held constant, so that features of the value function are controlled for in common consequence conditions for the curvature of the PWF.

Nonlinear probability weighting may be inferred from preference reversals upon a common consequence shift. Consider the preference reversal $R\prec S$, while $R_{\epsilon }\succ S_{\epsilon }$, so the safe lottery is preferred before and the risky lottery after common consequence shift $\epsilon$, $\epsilon > 0$. Such a preference reversal is an example of a common consequence effect. The common consequence effect considered here implies that the value of the risky prospect has risen more than the value of the safe prospect as a result of the common consequence shift, or $\Delta v = v_{\epsilon } - v > \Delta v^{'}=v^{'}_{\epsilon }-v^{'}$. For spelling out implications for the curvature of the PWF, we obtain expressions for $\Delta v$ and $\Delta v^{'}$, using Eq. 7. The value of the risky lottery R, so before the common consequence shift, may be rewritten as follows:

$$\begin{aligned} v=w^{+}(p)[v(x)-v(y)]+w^{+}(p+q)v(y). \end{aligned}$$

(8)

Likewise, the value of the risky lottery $R_{\epsilon }$, so after the common consequence shift, is equal to $v_{\epsilon }=w(p)v(x)+(w(p+q+\epsilon )-w(p))v(y)$, which may be rewritten as:

$$\begin{aligned} v_{\epsilon }=w^{+}(p)[v(x)-v(y)]+w^{+}(p+q+\epsilon )v(y). \end{aligned}$$

(9)

The increase in the value of the risky lottery as a result of the common consequence shift may thus be expressed as:

$$\begin{aligned} \Delta v = v_{\epsilon }-v=(w^{+}(p+q+\epsilon )-w^{+}(p+q))v(y). \end{aligned}$$

(10)

Taking similar steps, the increase in the value of the safe lottery brought about by the common consequence shift is equal to:

$$\begin{aligned} \Delta v^{'} = v^{'}_{\epsilon }-v^{'}=(w^{+}(p^{'}+q^{'}+\epsilon )-w^{+}(p^{'}+q^{'}))v(y). \end{aligned}$$

(11)

The preference reversal $R\prec S$ while $R_{\epsilon }\succ S_{\epsilon }$ implies that $\Delta v > \Delta v^{'}$, which by Eqs. 10 and 11 is equivalent to:

$$\begin{aligned} w^{+}(p+q+\epsilon )-w^{+}(p+q)>w^{+}(p^{'}+q^{'}+\epsilon )-w^{+}(p^{'}+q^{'}). \end{aligned}$$

(12)

This inequality may be used to pronounce on the curvature of the PWF for specific intervals of its domain. Consider the interval $[p+q, p^{'}+q^{'}+\epsilon ]$, in which $p+q<p^{'}+q^{'}$ (which we ensure in the experimental design). Strict concavity of $w^{+}(.)$ in interval $[p+q, p^{'}+q^{'}+\epsilon ]$ ensures that inequality 12 holds, since, by the definition of concavity, the PWF is steeper for the interval of probabilities $[p+q,p+q+\epsilon ]$ than for the interval $[p^{'}+q^{'},p^{'}+q^{'}+\epsilon ]$, which lies to the right of the first-mentioned interval. Strict concavity of $w^{+}(.)$ in the interval $[p+q, p^{'}+q^{'}+\epsilon ]$ is thus a sufficient condition for inequality 12 to hold. For it to be a necessary condition, more structure needs to be imposed.¹⁰ Prudently, one should, therefore, limit pronouncements on the curvature of the PWF in the light of preference reversals $R\prec S$, while $R_{\epsilon }\succ S_{\epsilon }$ to stating that evidence has been obtained that the PWF is steeper in the interval $[p+q,p+q+\epsilon ]$ than in the interval $[p^{'}+q^{'},p^{'}+q^{'}+\epsilon ]$, while remaining agnostic about concavity in the entire interval of its domain $[p+q, p^{'}+q^{'}+\epsilon ]$.

Mirroring the steps taken to obtain inequality 12 by reversing the inequality signs in these steps, we may state that the preference reversal $R\succ S$, while $R_{\epsilon }\prec S_{\epsilon }$ implies the following inequality:

$$\begin{aligned} w^{+}(p+q+\epsilon )-w^{+}(p+q)<w^{+}(p^{'}+q^{'}+\epsilon )-w^{+}(p^{'}+q^{'}), \end{aligned}$$

(13)

or that the PWF is steeper in the interval $[p^{'}+q^{'},p^{'}+q^{'}+\epsilon ]$ than in the interval $[p+q,p+q+\epsilon ]$.

2.4 Common consequence effects in the domain of losses

We next derive common consequence conditions for the curvature of the PWF in the domain of losses, in the context of CPT. We consider three-outcome lotteries of the form (p, x; q, y; r, z) in which the worst outcome x occurs with probability p, the intermediate outcome y with probability q, and the neutral outcome z with probability $r=1-p-q$. So now, $x<y<z$ and $v(z)=0$.

In the domain of losses, the value function of such three-outcome lotteries may be written as:

$$\begin{aligned} V(f^{-})=\pi ^{-}_{x}v(x)+\pi ^{-}_{y}v(y)+\pi ^{-}_{z}v(z). \end{aligned}$$

(14)

From expressions 3 and 5, it follows that $\pi ^{-}_{x}=w^{-}(p)$ and $\pi ^{-}_{y}=w^{-}(p+q)-w^{-}(p)$. Since $v(z)=0$:

$$\begin{aligned} v=w^{-}(p)v(x)+(w^{-}(p+q)-w^{-}(p))v(y). \end{aligned}$$

(15)

The problem of obtaining common consequence conditions is thus symmetrical in its starting point to that for gains. However, since $v(x)<0$ and $v(y)<0$, some of the key inequalities reverse. Moreover, the common consequence shifts we consider, from the worst to the intermediate outcome, give rise to changes in the value of prospects that are not symmetrical to such changes in the domain of gains, as will be seen below.

Consider a choice between safe lottery S, ($p^{'},x; q^{'},y)$ and risky lottery R, (p, x; q, y), in which $p^{'}<p$ and $1-p^{'}-q^{'}<1-p-q$, i.e., the probability of the worst outcome occurring and that of the best (neutral) outcome occurring are both lower in S than in R. By construction, $q^{'}>q$.

Our interest is in the curvature of $w^{-}$, which we infer from the absence or presence of preference reversals between various pairs of lotteries that relate to each other through common consequence shifts in the form of a shift of probability mass from the worst to the intermediate outcome. $S_{\epsilon }$ is thus characterised by $(p^{'}-\epsilon , q^{'}+\epsilon )$ and $R_{\epsilon }$ by $(p-\epsilon , q+\epsilon )$.

Consider the preference reversal $R\prec S$ while $R_{\epsilon }\succ S_{\epsilon }$ after the common consequence shift $\epsilon$, $\epsilon >0$.¹¹ As before, this implies that $\Delta v = v_{\epsilon }-v > \Delta v^{'}=v^{'}_{\epsilon }-v^{'}$. For the risky lottery, the common consequence shift implies that:

$$\begin{aligned} v=w^{-}(p)v(x)+(w^{-}(p+q)-w^{-}(p))v(y)=w^{-}(p)[v(x)-v(y)]+w^{-}(p+q)v(y); \end{aligned}$$

(16)

after the common consequence shift becomes:

$$\begin{aligned} v_{\epsilon }=w^{-}(p-\epsilon )v(x)+(w^{-}(p+q)-w^{-}(p-\epsilon ))v(y)=w^{-}(p-\epsilon )[v(x)-v(y)]+w^{-}(p+q)v(y) \end{aligned}$$

(17)

(since $p-\epsilon +q+\epsilon =p+q$). The increase in value of the risky lottery as a result of the common consequence shift may thus be written as:

$$\begin{aligned} \Delta v = v_{\epsilon }-v=[w^{-}(p-\epsilon )-w^{-}(p)][v(x)-v(y)]>0, \end{aligned}$$

(18)

which is strictly positive, since $w^{-}(p-\epsilon )<w^{-}(p)$ and $v(x)<v(y)$.

Analogously, for safe lotteries S and $S_{\epsilon }$:

$$\begin{aligned} \Delta v^{'} = v^{'}_{\epsilon }-v^{'}=[w^{-}(p^{'}-\epsilon )-w^{-}(p^{'})][v(x)-v(y)]>0. \end{aligned}$$

(19)

Preference reversal $R\prec S$ while $R_{\epsilon }\succ S_{\epsilon }$ implies:

$$\begin{aligned} \Delta v> \Delta v^{'} \Leftrightarrow [w^{-}(p-\epsilon )-w^{-}(p)][v(x)-v(y)]>[w^{-}(p^{'}-\epsilon )-w^{-}(p^{'})][v(x)-v(y)]. \end{aligned}$$

(20)

Dividing both sides by $[v(x)-v(y)]<0$ reverses the inequality and gives the following common consequence condition:

$$\begin{aligned} R\prec S, R_{\epsilon }\succ S_{\epsilon } \Rightarrow \Delta v > \Delta v^{'} \Leftrightarrow w^{-}(p-\epsilon )-w^{-}(p)<w^{-}(p^{'}-\epsilon )-w^{-}(p^{'}). \end{aligned}$$

(21)

Since $w^{-}(p-\epsilon )<w^{-}(p)$ and $w^{-}(p^{'}-\epsilon )<w^{-}(p^{'})$, both sides of the inequality are negative. It may therefore be more natural to divide both sides by minus one and write the common consequence condition as follows:

$$\begin{aligned} R\prec S, R_{\epsilon }\succ S_{\epsilon } \Rightarrow \Delta v> \Delta v^{'} \Leftrightarrow w^{-}(p)-w^{-}(p-\epsilon )>w^{-}(p^{'})-w^{-}(p^{'}-\epsilon ). \end{aligned}$$

(22)

In words, the preference reversal implies that the PWF for losses is steeper in the interval of its domain $[p-\epsilon ,p]$ than in $[p^{'}-\epsilon ,p^{'}]$. Since $p^{'}<p$, strict convexity in the interval of its domain $[p^{'}-\epsilon ,p]$ is a sufficient condition for $w^{-}(p)- w^{-}(p-\epsilon )<w^{-}(p^{'})-w^{-}(p^{'}-\epsilon )$ but not a necessary condition (cf. the discussion on the corresponding concavity condition in Sect. 2.3), so we limit our empirical conclusions to the relative steepness of the PWF for interval $[p-\epsilon ,p]$ compared to that of $[p^{'}-\epsilon ,p^{'}]$.

Working through the same logic for the opposite preference reversal yields the mirroring common consequence condition:

$$\begin{aligned} R\succ S, R_{\epsilon }\prec S_{\epsilon } \Rightarrow \Delta v< \Delta v^{'} \Leftrightarrow w^{-}(p)-w^{-}(p-\epsilon )<w^{-}(p^{'})-w^{-}(p^{'}-\epsilon ), \end{aligned}$$

(23)

so that the PWF for losses is steeper in the interval $[p^{'}-\epsilon ,p^{'}]$ than in the interval $[p-\epsilon ,p]$.

We will next show how our experimental design makes use of the common consequence conditions obtained in Sects. 2.3 and 2.4 to test the hypotheses presented in Sect. 2.2.

3 Experimental design, survey, and fieldwork implementation

In this section, we describe our data collection instruments. We first show how we implemented common consequence ladders in a sample with low levels of literacy, present the lottery choices we designed, and provide a rationale for the intervals of probabilities and magnitudes of the common consequence shifts we focused on. Next, we describe the steps we took to establish a neutral outcome in subjects’ minds in the weeks leading up to the experiment, so that gains and losses were meaningful concepts to them when they chose between lotteries. We then present the other key elements of our experimental design: random assignment to either the gains or losses version of the common consequence ladders, and design choices as to the order of the experimental tasks, a simple control for risk aversion, and the random selection of one task for payment. The experiment was complemented with a survey, which we outline in the last subsection, along with details of sample selection and fieldwork implementation.

3.1 Implementing common consequence ladders

Literacy and the ability to translate visual displays on a computer screen into concrete realisations cannot be guaranteed in the study area, so we needed a device for implementing pairwise lottery choices that does not rely on written instructions, and is concrete and simple. Based on extensive piloting, we settled on the following device. Each lottery was represented by twenty coloured counters. So, for example, lottery 6a in the domain of gains (see Table 1) has a 0.4 chance of the neutral outcome, a 0.6 chance of the intermediate outcome, and a 0 chance of the best outcome. This lottery was represented by 8 lilac counters ($8/20=0.4$) and 12 light blue counters. These were vertically set out on a table in single file, so that the 8 lilac counters were neatly arranged at the bottom and the 12 light blue counters on top of those. Underneath that column of counters, 6a was clearly written on a large post-it note stuck to the table. About 40 cm next to the column of counters representing lottery 6a was lottery 6b set out in similar fashion (12 lilac, 1 light blue, and 7 white counters). Figure 3 illustrates these two lotteries.

Fig. 3

An example of a lottery choice problem. Notes: this represents choice problem 6 in the gains condition of the experiment. Subjects were shown that the counters of the lottery they preferred would be put in a bag, from which one counter would be randomly selected. The value of the outcome that counter represents would be their payment. In the gain condition, lilac counters represented 8000 Ugandan shillings, light blue counters 10,000 shillings, and white counters 13,000 shillings

Before they took their decisions, a demonstration was given to subjects of what would happen once they chose one of the two lotteries. All counters representing that lottery would be put in a bag, shuffled thoroughly, and one would be picked out by a volunteer looking the other way. The value of the colour of the counter would be paid out to subjects who had chosen that lottery. We demonstrated this both for the relatively safe (6a) and for the relatively risky lottery (6b).

We ensured that all paired lotteries were spatially sufficiently apart, so that each lottery choice problem would be considered in isolation. For this purpose, we used five large tables arranged in the middle of the experiment room. On one side were set out lottery pairs 1–5, on the other 6–10, with plenty of space left in the middle between the lottery pairs on each side of the table. This arrangement not only encouraged considering each choice in isolation, but also greatly facilitated reversing the order in which lottery choices were presented (see Sect. 3.4).

A control question designed to capture understanding of the essence of the device revealed that subject comprehension was very good: 96% answered it correctly.¹²

3.2 Common consequence ladders implemented

Table 1 presents the common consequence ladder implemented in the domain of gains. The first pair of lotteries (on rung I) constitutes the least attractive choice, the next pair (rung II) the least attractive choice but one, and so forth, until the most attractive choice in terms of expected value of the lotteries (rung X). Each pair consists of a relatively safe and a relatively risky lottery, which subjects face in the form of the number of counters of up to three colours presented in the last three columns. The probability of each outcome is indicated in parentheses.

Table 1 Common consequence ladder (gains)

These ten lottery choice problems were determined as follows. The comparison of choices between rungs allows pronouncing on the relative steepness of the PWF for specific intervals of probabilities. For the horizontal common consequence effects we consider, comparisons are between intervals $[p+q, p+q+\epsilon ]$ and $[p^{'}+q^{'}, p^{'}+q^{'}+\epsilon ]$ with $p^{'}+q^{'}>p+q$ needing to be ensured in the design (see Sect. 2.3).

Consider for example a preference reversal between rung I and rung II. $p+q=0.35$ refers to the probability of either the white or light blue counter being selected in I.R, $p^{'}+q^{'}=0.55$ to the probability of that outcome in I.S, and common consequence shift $\epsilon$ is added to the analogous probabilities in II.S and II.R. A preference reversal therefore indicates the relative steepness of the PWF in probability intervals [0.35, 0.4] compared to [0.55, 0.6]. Following the same logic, comparing rungs V and VI pronounces on the relative steepness of the PWF in intervals [0.55, 0.6] and [0.75, 0.8], rungs IX and X intervals [0.75, 0.8] and [0.95, 1.0], and so forth, for a total number of possible comparisons of $10*9/2=45$ across each combination of rungs.

Such tracking of the PWF for gains is thus limited to part of its domain [0.35, 1.0], which we decided for the sake of realism, avoiding cognitive overload and prioritising more-refined measurement to measurement over the entire domain [0, 1.0]. As to realism, farmers’ investments in fertiliser, improved seeds, and other pertinent agricultural investment goods in Uganda are successful with a probability considerably higher than 0.35 (Verschoor et al. 2016, Table A1, p.147). Avoiding cognitive overload made us decide after piloting that no more than 10 rungs should be implemented and that each lottery should have no more than 20 counters. As to refined measurement, limiting tracking of the PWF to part of its domain [0.35, 1.0] meant that we could set $\epsilon =0.05$ between each two adjacent rungs in the common consequence ladder for gains.

Table 2 Common consequence ladder (losses)

Table 2 presents the common consequence ladder implemented in the domain of losses. Pairs of lotteries are again presented in order from the one with the lowest expected values of S and R on rung I to the one with the highest expected value on rung X. For losses, comparisons across paired lotteries are relevant for the relative steepness of the PWF between probability intervals $[p^{'}-\epsilon ,p^{'}]$ and $[p-\epsilon ,p]$ (see Sect. 2.4).

For example, in lottery I.R, $p=0.8$ and in lottery I.S, $p^{'}=0.7$. When the common consequence shift of size $\epsilon =0.05$ is considered between paired lotteries I and paired lotteries II, then $p^{'}-\epsilon =0.65$ and $p-\epsilon =0.75$. A preference reversal from R to S or S to R between lotteries I and lotteries II thus indicates that the PWF is steeper in one of the two probability intervals [0.65, 0.7] and [0.75, 0.8] than it is in the other.

Following similar logic, comparing choices in V and VI pronounces on the relative steepness of the PWF in intervals [0.3, 0.4] and [0.4, 0.5], comparing choices in IX and X on [0, 0.05] and [0.1, 0.15], and so forth, again for a total possible number of comparisons of $10*9/2=45$.

The tracking of the PWF for losses is thus restricted to part of its domain [0, 0.8]. Considerations of realism, refinement where it matters most, and avoiding cognitive overload have again inspired this design choice. The last two mentioned are similar to those considerations for gains. As to realism, sharp negative income shocks are common in the study area (see Sect. 4.1), which suggests sizeable reference probabilities somewhere in the middle of the PWF’s domain (cf. Sect. 2.2). To reduce the risk of failing to detect reference probabilities, we therefore cast our net somewhat wider than in the domain of gains. Moreover, whereas for gains, it seemed important to close in on certainty at one end of the PWF’s domain (a 100% certain gain); for losses, it seemed important to close in on certainty at the other end (a zero% chance of a loss).

The two common consequence ladders presented here are valid to the extent that we have successfully established in subjects’ minds that $z=8,000$ Ugandan shillings are thought of as the neutral outcome. We next show how we attempted this.

3.3 Establishing the neutral outcome

Three weeks before a subject was scheduled to participate, we gave them a voucher. The voucher contained their name, address, and photo, as well as the figure of 8000 shillings prominently displayed. The following scripted message was read out to participants individually when the voucher was handed over:

On the day of the research workshop you’ll be asked to take some decisions about this money. Depending on the decisions you will be asked to take, you could end up with more than 8000 or with less than 8000 shillings.

During the delivery of the experimental instructions 3 weeks later, the voucher was referred to when the outcome of 8000 shillings was introduced (see online Appendix A, p.8):

Remember, you have already been given a voucher worth 8000 shillings. Therefore, if a white counter is eventually drawn, then you do not earn any extra money, but keep your 8000 shillings.

The vouchers were thus intended to instil a sense of entitlement. Deception was avoided through emphasising that the money could be lost, depending on the decisions subjects were asked to take. To avoid disappointment, an unannounced show-up fee of 5000 shillings was paid after the resolution of the game. The amount of 5000 shillings was the maximum amount that could be lost in the losses condition. Minimum earnings were therefore 8000 shillings, or about twice the median daily wage in the study area. Crucially though, losses could actually be made out of the 8000 shillings mentioned on the voucher, exactly as per the experimental instructions that subjects responded to.¹³

3.4 Other elements of the experimental design

Other elements of the design were as follows. We implemented a simple investment game so as to be able to control for risk aversion, based on the Gneezy and Potters (1997) design. Subjects were endowed with 20 counters, each representing 400 shillings, so 8000 shillings in total. They chose to invest k counters, where $k\in \lbrace 0,1,...,20\rbrace$ for facing the lottery $(0.5, 8000--400k; 0.5, 8000 + 800k)$. In other words, their investment was tripled if successful and lost in its entirety if it failed.¹⁴ The fate of their investment is determined by tossing a coin. We assume a power Constant Relative Risk Aversion (CRRA) utility function over experimental earnings x, which is defined as $U(x)=x^{1-r}/(1-r)$, where r is the coefficient of CRRA. As is conventional, we compute the CRRA coefficient for indifference between investing k and $k-1$, on one hand, and k and $k+1$ on the other, to find the CRRA coefficient range that corresponds with the observed behaviour of investing k. The investment decision was always task 11, so after the 10 lottery choices of the main experiment had taken place.

The random-lottery incentive system was used, so that only one decision was implemented and each of the 11 lottery choices (the decision in the investment game is in effect also a lottery choice) had an equal chance of being played out for real. Subjects were told this before they took their decisions.

The order of the ten paired lottery choices was randomised, both in the gains condition and in the losses condition (see Tables 1 and 2). Moreover, whether a subject faced the sequence of lottery choices 1, 2, ..., 10 or that of 10, 9, ..., 1 was randomly determined.

Two experimental teams were used for delivering the instructions, who were purposively rotated across sessions and game conditions, so that we can control for experimenter effects. The experimental teams are experienced and were intensively trained for 2 weeks, in addition to their involvement in extensive piloting.

Subjects were randomly assigned to either the gains condition or the losses condition of the experiment in a between-subject design.

Experimental instructions were delivered in person, because literacy cannot be guaranteed in the study area. Decision-making was partially private: other subjects were not present but an enumerator recorded choices.

The experimental instructions were translated into Lugisu, the local language of the study area, and back-translated into English to check for inadvertent changes in meanings.

A number of instructions and reassurances were given at the outset to promote orderly, leisurely, and autonomous decision-making; see the experimental instructions in online Appendix A.

3.5 Study area, sample selection, survey, and fieldwork implementation

We selected five sub-counties from a rural area in eastern Uganda: Sironko District and Lower Bulambuli District, which together comprise the former Sironko District. Almost all working adults in the area (95%) are smallholder farmers. The typical farmer grows maize intercropped with beans alongside some cash crops (e.g., coffee) on land that does not exceed 2 acres. Using a multi-stage cluster sampling method, we selected 1803 farmers for a number of risky choice experiments including the ones reported on here. Of the individuals selected for participation, 370 were randomly assigned to the common consequence experiments, 184 of them to the gains condition, and 186 to the losses condition. For a detailed description of the study area and fieldwork implementation, see Verschoor et al. (2016).

Data collection followed the same basic pattern in each sub-county. Three weeks before their relevant experimental session, individuals were visited, reminded about their participation and given the voucher described in Sect. 3.3. In the week before ‘game day’,  we visited all selected participants again to administer a household survey questionnaire, to collect data on basic socio-economic variables, agricultural practises, and the experience of income shocks. The experiment then took place at the end of the week in a central location (usually in a school on a nonschool day); for participants from remote villages, we organised transport.

4 Results

In this section, we present our main results. We first show summary statistics and ascertain whether condition assignment has given rise to inadvertent selection issues. Next, we analyse common consequence effects in the domains of gains and losses, respectively, and derive the shape of the PWFs (one for losses, one for gains) that organise the data. Finally, we present the results of multivariate analysis that searches for correlates of the particularly pronounced nonlinear probability weighting that the univariate analysis has pointed to.

4.1 Sample characteristics

We begin by describing our sample and assess differences on observables between game conditions. Table 3 presents summary statistics and a corresponding balancing test. About 30% of subjects are traditional farmers. We consulted agricultural experts in the study area to define traditional farmers.¹⁵ Traditional farmers grow maize intercropped with beans, with a minimal reliance on bought inputs such as improved seeds, pesticides, and inorganic fertiliser; if they do buy inputs, then this would be limited to purchasing unimproved seeds on local markets. We therefore classified all subjects as traditional farmers who grow only maize and beans and do so without buying improved seeds, pesticides, or fertiliser. All other subjects either buy such inputs or grow cash crops that are more lucrative than maize and beans, but require higher cash outlays (e.g., tomatoes, cabbages, and onions) or both. According to the local experts, traditional farmers avoid initial cash outlays so as not to jeopardise their food security in periods of drought or excessive flooding. This is a recognised motive in development economics (Fafchamps 2003, pp.18ff.).¹⁶

The wealth index presented in the table is the first component of a principal component analysis based on a list of about 30 types of assets that our survey collected information on (this method of constructing a wealth index is due to Filmer and Pritchett (2001)). Risk aversion is measured using the constant relative risk aversion (CRRA) coefficient based on behaviour in the investment game presented in Sect. 3.4.

We asked several questions about income shocks. The way we asked these questions was by inquiring whether respondents had experienced a sharp drop in income in the past 5 years as a result of specified events. 77% had experienced a sharp drop in income resulting from harvest failure, 59% from severe flooding, and 84% from a severe drought. Farmers in the sample are clearly used to frequent sharp income shocks.

Table 3 Summary statistics and balancing test

Most variables in Table 3 are not significantly different between game conditions, but two variables are. One is the wealth index. We think that this should be due to chance, as the random assignment to game condition was rigorously carried out. Game comprehension is the other variable that is significantly different between game conditions: 99% answered the control question correctly in the gains condition and 93% in the losses condition, which is significantly different at the 10% level. This could well be due to the differences between the game versions, with the losses instructions possibly slightly harder to understand. Reassuringly, the omnibus $\chi ^2$-statistic of a test of all coefficients being equal to zero in a logistic regression of condition assignment on the variables presented in the table is insignificant ($\chi ^2=10.8$, $p=.46$), suggesting that inadvertent selection is not a major concern.

Table 4 Summary of behaviour in experiments

Table 4 contains a summary of experimental behaviour. Choosing the risky lottery is somewhat more frequent than the safe one, especially for losses and, within the domain of losses, especially for the lower rungs. In the domain of losses, the gradual lowering of the proportion of risky choices as one moves up the ladder to rung V implies a preponderance of RS switches (choosing risky on a lower rung followed by safe on the higher rung), which hints at the relative steepness of the PWF near $p=0$; we formally test this below. Table 4 also shows that about a third of subjects choose different lotteries on consecutive rungs, which our tests for probability weighting in the next subsection focus on. In the domain of losses, 19.6% of subjects never deviate from their first choice; 13.0% always choose the risky lottery, and 6.5% always safe. In the domain of gains, the corresponding figures are 35.9, 19.0, and 16.8%. On average, experimental subjects switch about three times between consecutive rungs (recall that consecutive rungs were not sequentially presented, since the order in which they were presented to subjects was randomised). In the domain of losses, the mean number of switches between consecutive rungs is 2.9 (Std Dev 2.1), and for gains 2.7 (Std Dev 2.4).

4.2 Tracking the PWF

We next present the choice patterns that the common consequence shifts have given rise to, and show the shapes of the PWFs, one in the domain of losses and one in the domain of gains, that organise the data. Our tests of probability weighting used for tracking the PWF may be construed as tests of the null hypothesis of expected utility theory (EUT) plus noise arising from simple (Fechnerian) errors in decision-making (Hey and Orme 1994). For these tests to be valid, we need to maintain the assumption that erroneous SR switches are not more likely than erroneous RS switches, in any of the comparisons considered between rungs of the common consequence ladder.

Recall that there are two experimental conditions: about half of the subjects are in the gains condition, and the other half are in the losses condition. Each subject makes ten risky choice decisions. In each of the ten decision-making problems, they can choose either the safe (S) or the risky (R) lottery. As is standard in tests for common consequence effects, probability weighting is tested for by comparing decisions in paired problems. There are 45 possible comparisons ($10*9/2$), which all allow tests of probability weighting for specific ranges of probabilities (e.g., whether the probability weighting function is steeper for 0.8–1.0 than it is for 0.4–0.6).

Therefore, we test for probability weighting by focusing on paired problems. Let us consider two decision-making problems, problem 1 and problem 2. An individual decides whether they want S or R in problem 1, and next whether they want S or R in problem 2. There are therefore four possible choice patterns: SS, RR, SR, and RS.

The focus of the analysis (again standard in tests of common consequence effects) is on the proportion of subjects that chooses each of these four possibilities. The null hypothesis is: no probability weighting. In Sect. 2, we showed (in line with standard theory) that this means that if somebody chooses S in one problem, then they should also choose S in the second problem (and vice versa). Likewise, if they choose R in one problem, then they should also choose R in the second problem (and vice versa). The null hypothesis of no probability weighting and no errors requires all choices to be SS or RR.

For testing this, we allow subjects to make mistakes. Therefore, the null hypothesis becomes: apart from mistakes, all choices should be SS or RR. We then make the assumption that mistakes in one direction (SR) are equally likely as mistakes in another direction (RS). For testing for probability weighting, there are several possibilities.

First, we could assume that the lowest of SR and RS is entirely due to mistakes. Using a one-sample binomial test, we can then test whether the higher of RS and SR significantly differs from the lower, the lower being the hypothesized value due to mistakes. This is defensible, but there is an arbitrary element in doing this.

Second, we could do a proportion test for testing whether the proportion of RS is equal to that of SR. However, this requires us to treat SR and RS as coming from two independent samples. That is clearly not correct: they derive from a paired sample (we observe the same subject twice when we consider pairs of decision-making problems).

Third, we could do a sign test. For testing the difference in two variables between paired observations, either a paired t test, or a signed rank test, or a sign test are options. For the first, we need to assume that the difference between the two variables is interval and normally distributed; for the second, we can relax that assumption, but still need to assume that the difference is ordinal; for the third, we need not assume anything about the difference, which seems appropriate here.

Fourth, we could in principle estimate functional forms for the probability weighting and value functions. However, the methodology of common consequence ladders is explicitly designed to avoid estimating value functions (conclusions about probability weighting hold whatever the value function looks like, see Sect. 2). Moreover, an important part of the motivation of the paper is that functional forms are often inadequate and that, therefore, a nonparametric method (such as the one we use) is preferred (see Sect. 1).

We therefore test for probability weighting in paired problems using a sign test. We recode $R = 1$ and $S = 0$, so that $RR = 0$, $SS = 0$, $RS =positive$ and $SR = negative$ (the labels positive and negative are conventions for this test) and test whether observed RS and SR are such that the null hypothesis of their being equally likely to occur can be rejected. Since our priors allow deviations in either direction, we report p values from a two-sided test.

A secondary interest is whether we can reject the null hypothesis that patterns across paired problems are due to chance (driven by noise alone). This amounts to testing whether choices in one problem are independent of choices in the problem it is paired with. We test for this by cross-tabulating choices in paired problems and using a Chi-square test for establishing if there is a relationship between the choices.

For testing diminishing sensitivity relative to the end points, we focus first on rung IX of the common consequence ladder. For losses, this allows us to assess whether the probability weighting function is particularly steep for probabilities between 0.05 and 0.15. We will below also consider the same for the interval 0–0.1, but our primary focus is on an interval near to but not including 0. The reason for this focus is the well-known observation that the probability weighting function is ill-defined near the end points, notwithstanding these end points serving as reference points (Kahneman and Tversky 1979). Focusing on rung IX in the domain of gains allows us to assess whether the PWF is particularly steep for probabilities between 0.75 and 0.95.

In Table 5, we show the choice patterns in the domain of losses for rungs paired with rung IX on the common consequence ladder. As mentioned, there are four possible combinations when two rungs are considered: twice safe (SS), twice risky (RR), first safe then risky (SR), and first risky then safe (RS). SS and RR are consistent with EUT, while SR and RS are not and point to nonlinear probability weighting. Therefore, for example, when choosing between the paired lotteries on rung IX in one decision-making problem and on rung VI in another, 50 subjects chose the safe lottery in each choice problem, 68 the risky lottery both times, 45 chose the safe lottery on rung IX and the risky lottery on rung VI, and 21 chose the risky lottery on rung IX and the safe lottery on rung VI. We first check whether we can reject the notion that such choice patterns are due to “noise alone” by using a Chi-square test for testing the hypothesis that choices in paired problems are independent; this hypothesis is always rejected at the 1% level (Tables 5 and 7).

Using a two-sided sign test, we next test whether SR is significantly different from RS for each of the nine steps involving rung IX. In the example of the step from rung VI to rung IX, the likelihood that SR and RS are due to error is equal to 0.43%; EUT is rejected at the 1% level. As demonstrated in Sect. 2.4, this points to nonlinear probability weighting. The probabilities for which this may be inferred are spelt out in the final column of Table 5. In total, there are six significant common consequence effects: the PWF for losses is less steep for probabilities [0.2, 0.3], [0.3, 0.4], [0.5, 0.6], [0.6, 0.7], [0.65, 0.75], and [0.7, 0.8] than it is for [0.05, 0.15]. Conversely, no evidence is found that the PWF for losses is less steep for [0.05, 0.15] than for any other interval.

We next investigate whether more can be said about the shape of the PWF when considering all possible common consequence effects for losses (Table 6). Of the 45 possible steps between rungs, 10 point to statistically significant probability weighting. Nine of these point to particular steepness of the PWF for probabilities [0, 0.1] and [0.05, 0.15], and are thus all consistent with concavity of the PWF arising from diminishing sensitivity relative to the end point of $p=0$. The tenth significant common consequence effect suggests that the PWF is steeper for [0.4, 0.5] than for [0.7, 0.8], but is only significant at the 10% level. Since there are 45 comparisons, this effect is too weak to base a firm conclusion on.

For losses, we thus find strong evidence for a PWF that is relatively steep near $p=0$. In marked contrast, for gains, we find no evidence that the PWF is relatively steep near $p=1$. There are no significant common consequence effects involving rung IX (Table 7), which allows us to investigate the relative steepness of the PWF for [0.75, 0.95]. Likewise, no evidence is found for the PWF being steeper than elsewhere for the interval [0.8, 1.0] (Table 8).

There is some tentative evidence for the PWF for gains being relatively flat in the middle, which is consistent with an inverse S shape. It is less steep for [0.35, 0.55] than it is for [0.6, 0.8] and [0.7, 0.9] and less steep for [0.45, 0.65] than for [0.7, 0.9] (Table 7). However, the dominant impression for gains is the marked absence of probability weighting.

In sum, probability weighting in the domain of losses is pronounced and points to a relatively steep PWF near $p=0$, which suggests diminishing sensitivity near that probability. This is consistent with an inverse S shape. No strong evidence is found for probability weighting in the domain of gains, but such evidence that is found is also consistent with an inverse S shape.

Table 5 Common consequence effects between rung IX and other rungs (losses)

Table 6 All possible common consequence effects (losses)

Table 7 Common consequence effects between rung IX and other rungs (gains)

Table 8 All possible common consequence effects (gains)

4.3 Multivariate analysis of nonlinear probability weighting

We next report on correlates of probability weighting. We investigated these by classifying subjects according to their choice patterns across the ten rungs of the common consequence ladder (cf. Bleichrodt and Pinto (2000)), and running probit regressions in which the dependent variable is a dummy that captures one category of the classification. In the domain of gains, 35% of subjects are EUT consistent (19% chose always the risky lottery, 16% always safe). We classify the probability weighting of 30% as dominantly convex, because the number of times they chose the risky lottery on the first five rungs exceeds that of the last five rungs. It follows that for them RS switches dominate between rungs corresponding with lower probabilities and rungs corresponding with higher probabilities, i.e., convexity dominates. For mirroring reasons, 20% are classified as exhibiting probability weighting that is dominantly concave, which leaves 15% of subjects unclassified in the domain of gains.

In the domain of losses, 21% of subjects are EUT consistent (14% chose always risky; 7% always safe). For classifying the probability weighters, we ignore rungs V and VI, which capture a relatively flat stretch in the middle of the (aggregate) PWF. Dominant concavity (36% of subjects) is said to occur when the frequency of RS switches between rungs I and IV on one hand and rungs VII–X on the other exceeds that of the frequency of SR switches, and dominant convexity when it is the other way around (28%). As in the domain of gains, 15% of subjects remain unclassified in the domain of losses.

Tables 9 and 10 report marginal effects for a selection of the probit regressions we ran. In the domain of gains, women are less likely than men to be EUT consistent (Table 9). There is also a small effect of the order in which the lottery choice was presented on the likelihood of EUT consistency. In the domain of losses, risk aversion is positively and significantly correlated with EUT consistency, which (not reported in the table) is driven by its significant correlation with the “always safe” choice pattern.

Neither in the domain of gains nor in the domain of losses were any significant correlates found of the choice patterns dominantly convex and dominantly concave. The reason for this could well be that these classifications allow for a wide variety of choice patterns. We therefore zoomed in on probability weighting near the end points of $p=0$ in the domain of losses and $p=1$ in the domain of gains, i.e., comparisons involving rungs IX and X. Recall that, in the domain of gains, we do not find evidence for nonlinear probability weighting near $p=1$ for the sample as a whole (Table 8). By contrast, we find that convexity near $p=1$ is more common among traditional farmers (Table 10). In the domain of losses, for the sample as a whole, we found strong evidence for concavity near $p=0$ (Table 6). By contrast, we find that convexity near $p=0$ is more common among traditional farmers (Table 10). We will reflect on these contrasting findings for traditional and other farmers in Sect. 5.

Table 9 EUT consistent: regression analysis

Table 10 Probability weighting near $p=0$ and $p=1$: regression analysis

5 Discussion and conclusion

Our findings are usefully summarised in terms of our hypotheses (see Sect. 2.2). Hypothesis 1 postulates diminishing sensitivity of the PWF relative to $p^{*}=0$, which we investigated and confirm in the domain of losses. Hypothesis 2 postulates diminishing sensitivity of the PWF relative to $p^{*}=1$, which we investigated but cannot confirm in the domain of gains. Hypotheses 3 and 4 postulate diminishing sensitivity relative to reference probability $p^{*}, 0<p^{*}<1$. Hypothesis 3 states that the PWF is concave for probabilities $(p^{y},1]$. For gains, this is rejected, as those rejections of expected utility theory we find are all consistent with convexity for [0.35, 1]. Moreover, convexity of the PWF approaching $p=1$ is found to be particularly pronounced for traditional farmers. Hypothesis 4 states that the PWF is convex for probabilities $[0,p^{y})$, which we reject for the aggregate sample (as implied by the confirmation of hypothesis 1). However, for traditional farmers, convexity of the PWF near $p^{*}=0$ is more likely than for others.

How do these findings relate to the previous literature, and what do they suggest? The absence of support in the aggregate sample for a reference probability of $p^{*}=1$ in the domain of gains is out of line with the bulk of lab studies in Western countries, as well as with quite a few lab-in-the-field studies in developing countries. The dominant probability weighting found in Western labs finds diminishing sensitivity relative to $p^{*}=1$; see the reviews of the many studies of probability weighting in Wu and Gonzalez (1996, 1998), Prelec (1998), Gonzalez and Wu (1999), Starmer (2000), Sugden (2004), Stott (2006), Van de Kuilen and Wakker (2011), Fehr-Duda and Epper (2012). The evidence on probability weighting in developing countries is more limited. Imposing Prelec (1998)’s one-parameter functional form, Tanaka et al. (2010) find evidence for an inverse S-shaped PWF in a rural sample from Vietnam. Adopting the methodology developed by Tanaka et al. (2010), Liu (2013) also finds evidence for an inverse S-shaped PWF, in a sample of Chinese cotton farmers. Eliciting certainty equivalents of binary lotteries, and estimating parameters of Prelec (1998)’s two-parameter functional form, Vieider et al. (2018) find evidence for an inverse S-shaped PWF for a sample of the general population in rural Ethiopia.¹⁷ An inverse S implies a reference probability of $p^{*}=1$, so we do not find evidence supporting the lab-in-the field studies for developing countries that find this shape of the PWF. One reason for this could be that imposing a functional form for the entire domain of a PWF may suggest probability weighting for certain ranges of probabilities that would not be found if the investigations zoomed in on that range. For example, estimating parameters of one of Prelec (1998)’s PWFs for a sample in which in reality only diminishing sensitivity near $p^{*}=0$ existed and not near $p^{*}=1$ would yield estimates consistent with an inverse S and therefore erroneously suggest convexity near 1.0 (which implies diminishing sensitivity near $p^{*}=1$).

For that reason, we adopted a methodology in this study that enables more-refined tracking of the PWF: common consequence ladders. It is similar to but much more-refined than Humphrey and Verschoor (2004a, 2004b), who, in five rural samples from Ethiopia, Uganda and India find evidence for an S-shaped PWF. (They investigate gains only, not losses.) As in our study, they use common consequence shifts to investigate nonlinear probability weighting. Unlike in our study, the probabilities they consider are limited to 0, 0.25, 0.5, 0.75, and 1. The contrast between their studies and ours is striking, given the similarity in methods (common consequence ladders) and subjects (poor rural farmers, including in Uganda). They find that the PWF for gains is steep for the middle range of probabilities (in the vicinity of 0.5), whereas we find that it is flat for that range. A hypothesis for explaining the difference is that their particular selection of probabilities made the one in the middle, 0.5, prominent so that it became a reference probability. A reference probability of $p^{*}=0.5$ gives rise to an S-shaped PWF, so one that is particularly steep for the middle range of probabilities. This hypothesis may be worth testing in future research.

The reference probability of $p^{*}=0$ that we find in the domain of losses is consistent with the literature on probability weighting that included losses, all conducted in Western labs (Tversky and Kahneman 1992; Abdellaoui 2000; Etchart-Vincent 2004; Abdellaoui et al. 2005). The weak evidence we find for an additional reference probability of $p^{*} = 0.5$ in the domain of losses is at odds with that literature. The evidence is not strong enough to base a firm conclusion on, so may require a higher powered test.

Our findings are plausible in the context of livelihoods strategies of farmers in the rural areas of developing countries. These areas are characterised by frequent shocks that threaten livelihoods, such as droughts, pests and diseases, and so forth (Fafchamps 2003). Our study area is no exception (see Sect. 4.1). These shocks notwithstanding, farmers in our study area do invest: 65% of farmers buy fertiliser for the growing of their crops; 31% grow cash crops, despite great income volatility and sizeable probabilities of investment losses (Verschoor et al. 2016, p.140). Persistent probability weighting for a farmer who invests every agricultural season would be surprising, since it causes profits to be lower than they could have been. In other words, probability weighting is a bias that an experienced decision-maker under risk is unlikely to indulge in. Our finding of a marked absence of probability weighting in the domain of gains is consistent with this insight. So is our finding that such probability weighting persists among traditional farmers, who are not in the habit of investing.

The pronounced probability weighting we find in the domain of losses is striking in the light of its marked absence in the domain of gains. We find strong evidence for concavity of the PWF that is consistent with diminishing sensitivity relative to $p^{*}=0$. To help interpret this, it is helpful to appreciate the reality of agricultural investment in the study area. The inability to recoup an investment may spell the end of the road for smallholder farmers, since Centenary Rural Development Bank (the main source of agricultural credit in the area) may claim a farmer’s land. A nonzero probability that an agricultural investment results in a loss is therefore a very serious matter. Finding diminishing sensitivity relative to $p^{*}=0$ in the domain of losses (i.e., caring particularly when the probability of a loss starts to deviate from zero) is therefore less surprising than diminishing sensitivity relative to $p^{*}=1$ in the domain of gains would have been for experienced decision-makers under risk. The contrasting finding for traditional farmers is again telling. For them, we find convexity, not concavity, of the PWF for small probabilities. These farmers are not in the habit of investing, so this finding is not likely to reflect their attitudes towards losses that may result from agricultural investment. It may well reflect a more general attitude to uncertainty that stems from farming in a particularly hazardous environment. Every few years a drought will strike, or pests and diseases will destroy the harvest. A probability of zero of no losses is therefore an abstract concept, which may help to explain that small probabilities are treated as not that dissimilar from zero and hence the relative flatness of the PWF in the vicinity of zero.

To conclude, in this study, we investigated the probability weighting habits of farmers from eastern Uganda. Previous studies of risky choice in developing countries have not separately investigated probability weighting for losses, but some studies for Western labs have. We find evidence of a reference probability of 0 in the domain of losses. A reference probability of 0 is consistent with an inverse S-shaped probability weighting function. In that respect, our findings are similar to the bulk of the evidence from Western labs. We do not find evidence for a reference probability of 1 in the domain of gains (apart from for traditional farmers, about one third of our sample). In that respect, our findings are at odds with most evidence from Western labs as well as with earlier studies of probability weighting in developing countries. We interpret this as evidence for experience of risky choice diminishing the tendency to transform probabilities nonlinearly into decision weights, although less so in the domain of losses.