Does time inconsistency differ between gain and loss? An intra-personal comparison using a non-parametric elicitation method

Abstract

Several studies on time preference have found time inconsistency in both gain and loss preferences. However, the relationship between the two within the same person remains unclear; that is, does an individual who demonstrates time inconsistency for gain outcomes do so for losses as well? This paper reports on individuals’ time inconsistency for gains and losses in a laboratory setting. To obtain a precise comparison of individuals’ time inconsistency for gains and losses, we used Rohde’s “DI (decreasing impatience)-index” (Manag Sci 65(4):1700–1716, 2018) and measured the level of time inconsistency, rather than merely identifying whether TI was present. This index represents how strongly a person exhibits present bias, and easily extends to the comparison between gain and loss preferences within the same person. Further, it allows the experiment to test for so-called future bias, which has been a focus area in recent time inconsistency literature. It is elicited through a non-parametric method, which avoids any specification errors in the analysis. Our findings are as follows: first, we found future bias in preferences for not only gains but also losses, and we confirmed that this tendency is consistent with previous findings on preferences for gains. Second, a positive correlation between time inconsistency for gains and losses was found at the individual level. Indeed, we could not find a significant difference between the two in most cases.

1 Introduction

It is common knowledge that people occasionally make time-inconsistent decisions; that is, they change their previous decisions without situational changes for both gains and losses outcomes. For example, we may incur additional costs to accelerate the delivery of a new television (gain) or knowingly delay the payment of a debt (loss) simply because time passes. Deviations from previous plans (both acceleration and procrastination) occur in many of our daily decisions, including saving, dieting, and even going to the gym.

To understand such time inconsistency (TI), many researchers have studied present bias, in which people exhibit less patience for outcomes that are in the near future. For example, present bias is exhibited when an individual prefers to receive 105 dollars after 13 months rather than 100 dollars after 12 months (we describe this as $(105,13\,\,{\text {m}})\succ (100,12\,\,{\text {m}})$), but he or she prefers 100–105 when the delay decreases by 12 months, i.e., $(100,0\,\,{\text {m}})\succ (105,1\,\,{\text {m}})$. Then suppose that the person decides between $(100,12\,\,{\text {m}})$ and $(105,13\,\,{\text {m}})$ today, but after 12 months he or she will reconsider that decision. If the individual has the same time preference today as 12 months from now, he or she will choose the larger option (105) today, but will select the one that pays sooner (100) 12 months from now. That is, the individual will choose $(105,13\,\,{\text {m}})$ over $(100,12\,\,{\text {m}})$ today, but he or she will prefer $(100,0\,\,{\text {m}})$ to $(105,1\,\,{\text {m}})$ in 12 months. This means that the person exhibiting present bias has a time-inconsistent preference (for acceleration and procrastination for gains and losses, respectively). There are increasing number of studies that find people have this sort of time-inconsistent preference for both delayed gains and delayed losses (for a review, see Frederick et al. 2002).¹

This paper proposes an intra-personal relationship between the biases for gains and losses. When people have time-inconsistent preferences for gains and losses, the question naturally arises whether the individual’s TI for gains and losses are related to each other. Does an individual who exhibits present bias for gains manifest a similar bias for losses, or are such tendencies independent of each other? We conducted a laboratory experiment and measured the level of TI when the participants chose future gains and when they chose future losses.

To measure the level of TI in a comparative way, we used the DI (decreasing impatience)-index proposed by Rohde (2018). This index represents how strongly a participant exhibits present bias (i.e., the participant’s degree of TI), and it easily extends to the comparison between preferences for gains and losses within the same person. Rohde showed that the DI-index is free from the level of impatience and the utility curvature, which are two important confounds in measurement of TI.

Moreover, the DI-index allows not only present bias but also its inverse, future bias. While most studies on TI have traditionally focused on present bias, its inverse has begun receiving research attention in the last decade. Recent studies have empirically shown that the frequency of present and future bias is affected by the temporal conditions of delayed gains. In other words, the same person exhibits different directions of TI for temporarily different alternatives. However, although losses are associated with many interesting TI phenomena (procrastination), no study has empirically observed future bias for losses. In our setting, present and future biases are observed as having positive and negative DI indices, respectively (a zero DI-index implies time consistency)—depending on the temporal conditions of the alternatives—and gains and losses, respectively.

Our contributions are as follows. First, we observed future bias not only for gains but also for losses. The frequency of losses was consistent with previous findings on gain preference. In the classification of discount functions on loss domain, only 20% of observations, at the most, follow hyperbolic discounting, and no observations follow exponential discounting. However, the generalized class of hyperbolic discounting that allows future bias (called inverse S-shaped discounting, ISD) explains 51–66% of observations. In addition, the same tendency holds in gain preferences; exponential and hyperbolic discounting explain, respectively, 4% and 21% of observations, at the most, whereas ISD explains 57–77%.

Second, we found a strong relationship between TI levels for gains and losses within the same person. The correlation between TI levels for gains and losses was relatively high, and positive, in every condition; in addition, they did not significantly differ from each other in most cases. While differences in impatience levels (the discount rates) for gains and losses have been discussed in the literature (called gain–loss asymmetry), our results clearly indicate that TI levels for gains and losses are strongly related: an individual who exhibited strong present bias for losses also did so for gains.

The rest of this paper is constructed as follows. Section 2 reviews the TI literature. Section 3 describes our experiment and explains how we measure TI and compare TI levels. Section 4 provides the results. Section 5 discusses our findings and the experimental limitations. Section 6 concludes the paper.

2 Time inconsistency

2.1 Basic model

Let $X=\mathbb {R}$ be a set of outcomes and $T=\mathbb {R_+}$ be a set of time periods (days). We assume that individuals have a time preference $\succsim$ over $X\times T$, which is a continuous weak order. Each element (x, t) of $X\times T$ denotes a delayed outcome, “receiving outcome x at time t.” We also assume this preference is strictly monotonic and strictly impatient; both assumptions are required to construct a valid measure of TI later.² The preferences for gains $\succsim _+$ and losses $\succsim _-$ are subsets of $\succsim$ on $X_+\times T$ and $X_-\times T$, where $X_+$ and $X_-$ are sets of gains and losses. For each individual, we assume a reference point of 0, that is, $X_+=\mathbb {R_+}$. Finally, we define the indifference $\sim$ and the strict relation $\succ$ in a manner commonly done in the literature.

To describe intertemporal choices, the discounted utility model is useful

$$\begin{aligned} DU(x,t) = D(t)u(x) \end{aligned}$$

with $D(t)=\exp {(-\int _0^t r(\tau )d\tau )}$, where r(t) is a discount rate and D(t) and u(x) are discount and utility functions, respectively. When we assume constant discounting (i.e., $r(t)\equiv r$), it becomes the exponential discounting utility model, which is the standard model in the literature.

The important property of exponential discounting is this; for all (x, s), $(y,s+d)$ with $d>0$, $(x,s)\sim (y,s+d)$ implies $(x,s^\prime ) \sim (y,s^\prime +d)$ for any $s^\prime <s$. In other words, this says that intertemporal choices will not change when the delay decreases. Since the alternatives of the former indifference will coincide with those of the latter after $s-s^\prime$ days, that person will never change his or her first decision after $s-s^\prime$ days if the time preference at $s-s^\prime$ does not differ from the preference today (time invariance), that is, the preference is time consistent. We assume time invariance throughout this paper, as many theoretical and empirical studies have done (see footnote 1 and Halevy 2015).

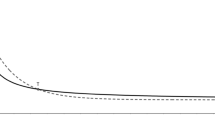
Many empirical studies have reported violations of this property. The traditional one is called present bias, in which people exhibit less patience when the delay decreases, i.e., for some (x, s),  $(y,s+d)$ and $s^\prime$, $(y,s+d)\succ _+ (x,s)$ but $(x,s^\prime )\succ _+(y,s^\prime +d)$ (for $\succsim _-$, the two relations are reversed). Such a person will choose the larger later outcome (LL) y today but will change his or her decision to the smaller sooner one (SS) x after $s-s^\prime$ days (and will choose opposite alternatives for future losses). To explain present bias, researchers have generalized the exponential discounting model to hyperbolic discounting, in which r(t) is decreasing in t. When r(t) is decreasing, people exhibit present bias whenever the delay decreases because $\frac{D(t+d)}{D(t)}$ is increasing in t (panel a in Fig. 1). Many functional specifications in this class are suggested and used in the literature, for example, the generalized hyperbolic discounting (GHD) of Loewenstein and Prelec (1992) and quasi-hyperbolic discounting of Laibson (1997). A review is provided by Frederick et al. (2002).

Fig. 1

Discount functions and exhibited TI. Suppose an individual is indifferent between SS and LL ($(\text {SS},s)\sim (\text {LL},s+d)$). Panel a shows hyperbolic discounting (red) with exponential discounting (black). The red curve becomes flat faster than the black curve (because r(t) is decreasing in hyperbolic discounting). That is, the increase in the discount factor of SS is much faster than that of LL when the delay decreases (from right to left in the figure). Thus, SS becomes relatively more appealing than LL, and present bias is always exhibited. On the other hand, under ISD, which is displayed in panels b and c, the increase in the discount factor of SS might be faster than that of LL at first, as under hyperbolic discounting (on the convex part of D(t)), but this relation is turned back when the delay decreases more (on the concave part). Thus, for SS and LL, with sufficiently small d, and when the delay decreases enough to become close to the present $(s^{\prime \prime })$, future bias can be exhibited (see panel b). Otherwise, since the delay does not decreases enough to become close to the concave domain ($s^\prime$ in panels b and c), or since d is sufficiently large to bury the turned back relation ($s^{\prime \prime }$ in panel c), only present bias is exhibited

2.2 The direction of TI and ISD

However, recent empirical studies have suggested that people exhibit not only present bias but sometimes its inverse, future bias. They reported that, at least for some intertemporal choices, people tended to exhibit weaker impatience when the delay decreases. For example, Sayman and Öncüler (2009) found that 15 out of 38 participants exhibited $(7,1)\succ _+ (10,3)$ but $(10,2)\succ _+ (7,0)$. That is, their participants became more patient when the delay decreases by 1 day for (7, 1) and (10, 3).³

To capture this empirical tendency, the generalized class of discounting, called inverse S-shaped discounting (ISD), is provided (see Sayman and Öncüler 2009; Takeuchi 2011). This is specified by r(t), which is increasing for a smaller period and then decreasing in t (the concave domain in Fig. 1 displays this former period). Then, although hyperbolic discounting expects only present bias for any choice, ISD also allows future bias for specific choice. Figure 1 describes TI in ISD. Because impatience increases between now and the near future, and decreases otherwise, future bias occurs only for future alternatives with a short waiting time, and only when the delay is sufficiently short ($s^{\prime \prime }$ in panel b). Otherwise, present bias may occur ($s^\prime$ in panel b and $s^\prime$ and $s^{\prime \prime }$ in panel c). In particular, when d is sufficiently large, only present bias occurs (panel c), just as under hyperbolic discounting (panel a). More details are provided in the note below the figure. The important note here is that ISD predicts different TI directions (present and future biases) depending on the temporal conditions of the alternatives faced, s, d, and the new delay $s^\prime$.

2.3 Related literature

Both present and future biases for gains are reported in many studies. Thaler (1981) and many others have observed present bias or a decreasing of the imputed discount rate, which indicates present bias. In addition, several studies have found future bias for gains. For example, similar to the 15 participants of Sayman and Öncüler (2009), 362 of 550 observations in Takeuchi (2011) also exhibited future bias. Even in the health domain, future bias has been reported in lab experiments (e.g., Attema and Lipman 2018; Bleichrodt et al. 2016).

The dependency of TI direction on temporal condition was also confirmed. Sayman and Öncüler (2009) concluded that future bias was frequently observed only when s and d were small enough, for example, though 15 of the 38 exhibited future bias for $s=1$ and $d=2$, only 3 exhibited future bias when $s=7$ and $d=7$. The median and classification analyses in Attema et al. (2010) suggested that subjects were increasingly impatient for the near future but not for the far future (sequence III and steps 2–5 in other sequences in their paper). Based on a functional specification, a good performance by ISD in terms of data fitting has also been reported (Takeuchi 2011; Abdellaoui et al. 2013a).

Regarding TI for losses, Benzion et al. (1989) and Thaler (1981) reported non-constant discounting (i.e., TI) under the linear utility assumption, and Abdellaoui et al. (2013a) found a decreasing impatient preference under non-linear utility. However, while Abdellaoui et al. also pointed out the importance of future bias for losses through parameter estimations, no study has, as of yet, directly examined it. This paper proposes a more direct examination of future bias, not only the domain of gains but in that of losses as well.

There are studies that look at the difference between gain and loss preferences in terms of the degree of impatience (discount rate) and utility curvature. For the former, Benzion et al. (1989) and Thaler (1981) reported that delayed gains were more heavily discounted than delayed losses. The latter has still not well studied in the time preference literature, but it has been studied well in a risk preference context (e.g., Booij et al. 2010). This paper focuses on the difference in the degree of TI. As Rohde (2018) explained, the DI-index is free from the impatience level and utility curvature, thus our study properly examines the relationship between TI for gains and losses.

Abdellaoui et al. (2013a) were focused on all three of those relationships. They estimated the parameters of utility curvature, degree of impatience, and TI level for gains and losses, respectively. They, respectively, found a fair and strong relationship for the first two components between the gain and loss preferences. In contrast, the TI levels for gains and losses were not correlated with each other, and the TI for losses was significantly stronger than that for gains in their analysis. However, they measured the degree of TI by the parameter $\alpha$ of the GHD function, and the GHD specification allowed for the existence of only present biases, not future ones, so their measurement of TI could be biased. Moreover, they used parametric functions to capture all three components, which is, of course, a non-negligibly strong requirement on the specification. We measure TI while allowing future bias and avoiding specification errors on functions.

In closing this section, it is worth pointing out the difference in procedure between this study and other specification-free studies of TI (e.g., Attema et al. 2010; Takeuchi 2011; Rohde 2018). These studies conducted a variety of experiments, but all of them were constructed with tasks that asked about delay lengths that make two intertemporal alternatives indifferent (see stage 2 in Sect. 3.2 for an example). On the other hand, Rohde (2010) provided another type of procedure, which works by combining two different tasks; one asking about money size and the other is asking about delay length (see stages 1 and 2 in Sect. 3.2). Due to the different targets of the tasks, this procedure has a potential problem called scale compatibility (Tversky et al. 1988). However, the latter type can control d, which plays a crucial role in determining the direction of TI, as well as s and $s^\prime$, whereas the former cannot do this. We are interested in future bias; thus, we adopted the latter. Since most previous studies have used the former to prioritize minimizing the compatibility problem, to the best of our knowledge, this study is the first to measure (and/or identify) TI that controls d in the non-parametric design. The available results, with limited data that might minimize the compatibility problem, are provided in Sect. 5.2.

3 Experiment

3.1 Compatible measure of TI

In this section, we describe the DI-index and our experimental procedure. Let us fix the outcome x of SS, and two delays s and $s^\prime$, such that $s^\prime <s$. Recall, present (future) bias for gains is obtained when $(y,s+d)\succsim _+ (\prec _-) (x,s)$, but $(x,s^\prime ) \succ _+ (\prec _-) (y,s^\prime +d)$ with $s^\prime <s$. To measure the degree of TI, we need two indifferences:

$$\begin{aligned} (x,s) \sim (y,s+d) \quad \quad \quad \text { and } \quad \quad \quad (x,s^\prime ) \sim (y,s^\prime +d^\prime ). \end{aligned}$$

(1)

When $d^\prime$ is smaller than d and $\succsim$ satisfies impatience, we can easily verify that the person will exhibit present bias for (x, s) and $(y,s+d)$ when the delay decreases $s-s^\prime$, and vice versa (this is independent from the sign of the outcomes). Likewise, when $d^\prime$ is larger than d, he or she will exhibit future bias. The DI-index by Rohde (2018) is defined as

$$\begin{aligned} {\text {DI}} =\frac{d -d^\prime }{d^\prime (s-s^\prime )}. \end{aligned}$$

As Rohde (2018) demonstrated, it is clear that ${\text {DI}}>0$ implies present bias and ${\text {DI}}<0$ implies future bias. Indeed, she showed that this index is a comparable measure across participants and is an approximate measure of Prelec’s measure of decreasing impatience. That is,

$$\begin{aligned} P(t) =-\frac{\bigl [ \ln D(t) \bigr ]^{\prime \prime }}{\bigl [ \ln D(t) \bigr ]^\prime }, \end{aligned}$$

which is a Pratt–Arrow method of measuring convexity provided by Prelec (2004). We briefly describe in what sense the degree of TI is compared. Suppose, we have the above indifferences of two individuals, say i and j, and thus ${\text {DI}}_i$ and ${\text {DI}}_j$. If individual i exhibits present bias for his or her (x, s) and $(y_i,s+d)$ when the delay decreases to $s^\prime$, this present bias can be compensated by accelerating LL $y_i$ by $d-d_i^\prime$ days. This is also the same for individual j when accelerating by $d-d_j^\prime$. We say that i exhibits stronger present bias than j when the acceleration of LL by $d-d_j^\prime$ is enough to compensate for j’s present bias but not for i’s. In other words, i’s present bias is stronger than j’s when i’s present bias is harder to compensate for than j’s. This happens if, and only if, $d_i^\prime <d_j^\prime$, which holds if, and only if, ${\text {DI}}_i>{\text {DI}}_j$.

This comparison can be easily extended to compare the TI for gains and losses in the same person. We say $\succsim _+$ exhibits stronger present bias than $\succsim _-$ when compensating for the present bias is harder for gains than for losses. That is, based on the obtained indifference pair (1) with x and $-x$, respectively, $\succsim _+$ exhibits stronger present bias than $\succsim _-$ when $d^\prime _+<d^\prime _-$, and it holds if, and only if, ${\text {DI}}_+>{\text {DI}}_-$.

3.2 Design and procedure

The experimental procedure is conducted in two parts. In the first part (stage 1), we elicit the first indifference in (1) by asking y with various s and d. In other words, we ask about participants willingness-to-accept (WTA) an additional delay of d. We set x at 10,000 yen. The following is an example of the task:

Please input a number (X) that would make you feel that B is as good as A.

• A: Receiving 10,000 yen in 92 days.

• B: Receiving X yen in 99 days.

We provided such tasks with $s= 92$ and 183 (around 3 and 6 months, respectively) and $d =7$ and 35 (1 and 5 weeks, respectively); there were four tasks in total. We also provided those four tasks with regard to preference for losses, by replacing the words “good” and “receiving” with “not good” and “paying.”

In the second part (stage 2), the second indifference in (1) was elicited. Now, we asked about $t^\prime$, such that $(x,s^\prime )\sim (y,t^\prime )$, where y is a parameter that is obtained in stage 1. Then $d^\prime$ is derived by $t^\prime - s^\prime$, where we call this $d^\prime$ the willingness-to-wait (WTW) for improved outcome y. We set $s^\prime$ at 1, 8, and 29, which are roughly a day, a week, and a month, respectively. Questions were asked about $t^\prime$ for each of four different values of y together with $s^\prime =1$, and then with $s^\prime =8$ and 35, respectively. We randomly ordered the tasks on the list in each phase. The tasks for losses were given in the same way.

We give an example here. Suppose someone answered 11,000 to the task above in stage 1, i.e., we obtained $(10{,}000, 92) \sim _+ (11{,}000,99)$. Then, in stage 2, this person is asked:

Please input a number (X) that would make you feel that B is as good as A.

• A: Receiving 10,000 yen in 1 day.

• B: Receiving 11,000 yen in X days.

We note here that y is not a common parameter, but it varies across participants and across different signs. When the number 3 is filled into the blank, that person’s $d^\prime$ is found to be 2. Then we can calculate the DI-index, which is about 0.03, and thus we can say that this person exhibited present bias with a strength of ${\text {DI}}_+=0.03$. Obviously, those analyses are dependent on the temporal condition, the size of parameters s, d, and $s^\prime$. Likewise, suppose we elicited an indifference pair (1), such that $(-10{,}000,92)\sim _-(-10{,}500,99)$ and $(-10{,}000,1)\sim _-(-10{,}500,4)$, from the same person. ${\text {DI}}_-$ is now around 0.01, and thus, we can conclude that this person exhibited a stronger present bias for gains than for losses.

We set a total of 32 tasks, of which 8 were about WTA (4 each for gains and losses) and 24 about WTW (12 each for gains and losses). To control for the order effect, we divided the subjects into two groups, and gave each group a series of tasks, progressing from losses to gains (for one group) and from gains to losses (for the other group) during the two stages ($n = 57$ and 52). Prior to answering the task questions, the subjects were given two training tasks.

3.3 Elicitation method

We used matching-based elicitation in every task. There is extensive literature on the advantages of matching and choice tasks to elicit decision-making behavior (e.g., Bostic et al. 1990), and both methods coexist, especially in time preference studies. For example, Abdellaoui et al. (2013a) and Sayman and Öncüler (2009) used a choice task, which is sometimes recommended in other literature strands, such as risk preference. We used matching-based elicitation because the choice task provides too coarse a grid point, which is not appropriate for an experiment with a non-parametric elicitation. In fact, because of this, most non-parametric studies use matching-based elicitation.⁴ Moreover, although a matching task may bias the participant’s responses, we do not think that the results were conditional on our elicitation method, that is, such biases did not seriously harm our findings. We will discuss this point in Sect. 5.2. We note here that this elicitation method also helps subjects to maintain concentration despite of the huge number of tasks. To aid their decision-making and ease in the process, we allowed each subject access to a calculator and a calendar printed with the date and number of days discussed in the experiment.

4 Results

4.1 Participants

We conducted a 1-day experiment with 109 students from various departments in Waseda University on January 23, 2017. The subjects were recruited using the university’s online portal and asked to visit our experimental laboratory any time during the day to participate in the study. Of the participants, 69 were male and 40 were female. Most of them (78 participants) were 20–24 years old, 28 were under 19, and 3 were 25–29. Fifteen participants studied natural science, and 94 studied social science or general arts; 7 students studied economics. The largest number of subjects (28 participants) studied literature. The tasks included choices of losses and, thus, were all hypothetical. Subjects received 800 yen (more than 7 US dollars) as a participation fee, which was reasonable since most subjects took about 15–45 min to complete the experiment. The instructions and tasks were given on a computer screen.

4.2 Analysis

4.2.1 Descriptions

Table 1 summarizes the responses. We eliminated one participant (subject ID 42) owing to unreliable answers.⁵ As a result, the total number of observations for ${\text {DI}}$ is $24\times 108$. We included all data for the two ordered groups and corrected certain answers for the following analysis.⁶ For the analysis, we need to assume the set of preference conditions (weak order, continuity, monotonicity and impatience), so only observations that satisfied these conditions were used. This resulted in 2002 observations of the $24 \times 108$.⁷

Table 1 Descriptive statistics of participants’ answers

From this table, we see that our participants’ WTA (which is y) for a 7-day delay in receiving 10,000 after 92 days was 10,722 on average, i.e., participants were indifferent between receiving 10,000 in 92 days and receiving 10,722 in 99 days, on average. The annual discount rate under linear utility was $3600\%$, which was quite high, but this is usual for choices between alternatives with small d (e.g., Kirby 1997. A review is provided in Frederick et al. 2002). The average WTW (which is $d^\prime$) in the first line was 5.35, which could roughly mean that our participants were indifferent between (10, 000, 1) and $(10{,}722,1+5.35)$, as long as we remember that 10,722 was not the exact choice parameter in this stage but its average. The point here is that, on average, the participants exhibited present bias. This is because their WTW was less than 7 days, which indicates $(10{,}000, 92)\sim (10{,}722, 99)$ but $(10{,}000, 1)\succ (10{,}722,8)$. An individual with this preference should have an incentive to change his or her decision from y to x after 91 days.

Figure 2 shows the distribution of DI-index under each temporal condition. The median of the DI-index is always positive, which indicates that the dominant pattern of TI is present bias, not only for gains but for losses as well. Yet, a unignorable number of observations showed future bias. Table 2 describes the ratios of participants who exhibited future bias (i.e., ${\text {DI}}<0$). We found about 20% of observations showed future bias when $d=7$, and 10% when $d=35$. The frequency of future bias was slightly higher for losses than for gains.

Fig. 2

Box plot of ${\text {DI}}$ in each condition. Note: Each subfigure corresponds to the value (s, d) (and thus the first indifference in (1)). The number on the x-axis in each subfigure represents $s^\prime$. Outside values are not displayed for a clear description

Table 2 Ratios of participants who exhibited future bias in each condition

4.2.2 Intra-personal relationship between TI for gains and losses

The results about an intra-personal relationship between TI for gains and losses are reported in Table 3.⁸ This table reports correlations between $\hbox {DI}^+$ and $\hbox {DI}^-$ and the results of the test of difference between the two with respect to the temporal conditions. Spearman’s correlation $\rho$ was positive and relatively high in every condition. Moreover, ${\text {DI}}_-$ did not significantly differ from ${\text {DI}}_+$ in most conditions (sign rank test; the results are stated in Table 3)⁹, although the parameter $y_-$ in the second stage significantly differed from $y_+$ (sign rank test; p-values are 0.02, 0.00, 0.00, and 0.00 in conditions $(s,d)=(92,7)$, (183, 7), (92, 35), and (183, 35), respectively). Thus, we conclude that people’s TIs for gains and losses are strongly related.¹⁰

Table 3 Comparison of test statistics for TIs between gains and losses

4.2.3 Dynamics of impatience and discount functions

Throughout the procedure, we have four indifferences for each y obtained in stage 1:

$$\begin{aligned} \begin{aligned}&\text { (Stage 1) }&\, \, (x,s)\sim&(y,s+d),&\\&\text { (Stage 2) }&\, \, (x,29)\sim&(y,29+d^\prime _{29}),&\\&\text { (Stage 2) }&\, \, (x,8)\sim&(y,8+d^\prime _8)&\text { and } \\&\text { (Stage 2) }&\, \, (x,1)\sim&(y,1+d^\prime _1).&\end{aligned} \end{aligned}$$

(2)

d and $d^\prime$s indicate how participants’ impatience changes over time (as delay decreases), so we display the mean of $d^\prime$ and d with respect to the delay $s^\prime$ and s in Fig. 3. The dynamic change in impatience is almost consistent with ISD, on average. In the figure, $d^\prime$ on each line corresponds to the same y, which is derived under s, d, and the sign of outcomes. From panel (a), the average d and $d^\prime$ for $y_+$ of $(s,d)=(92, 35)$ decreases when the delay decreases from 92 to 29 days and from 29 to 8 days, but then it increases from 8 to 1. In most cases, except for loss with $d=7$, $d^\prime$ decreases first and then increases when the delay decreases.¹¹ On average, as the delay decreases, our participants become impatient first, but once the delay becomes sufficiently small they then become patient, which is a main characteristic of ISD.

Fig. 3

Average d and $d^\prime$ with respect to a delay shift from the far future to the present

On the other hand, other alternative discount functions do not fit our observation very well. We rejected exponential discounting because the hypothesis that $d^\prime$ is constant and coincides with d is rejected statistically (the Kruskal–Wallis test; the p-values are $<0.01$ under every condition of (s, d) for both gains and losses).¹² Indeed, hyperbolic discounting requires that $d^\prime$ monotonically decreases over time, but the figure does not show this tendency.

Table 4 Classification of discounting classes

To consider the explanatory power of discount functions, we classified our participants into discount classes. The classification rules we used are reflected in the property of the discount function we introduced in Sect. 2: $d^\prime$ must be constant under exponential discounting, decreasing under hyperbolic discounting, and first decreasing then increasing under ISD as the delay decreases (see Table 5 in the appendix for more details). Table 4 presents the result of this classification. As seen in the table, almost no observations follow exponential discounting, and only 20%, at the most, are classified under hyperbolic discounting. However, ISD explains 50–77% of observations in every condition. This suggests that we need to apply ISD to validate the explanation.

5 Discussion

5.1 The source of TI

TI has sometimes been explained in the literature as a distortion of individuals’ time perception. Kim and Zauberman (2009), for instance, showed that a preference could be time inconsistent even when a person is constantly impatient, but his or her time perception follows Stevens’ power law, which is not linear. In their model, people perceive a delay of one day differently from a day later and from a year later. While Kim and Zauberman (2009) considered only present bias as TI, Takeuchi (2011) suggested that future bias could also be explained when people perceive the very close future as almost the “present” (which he called extended present). With such a perception, an individual will stop discounting two alternatives once both come into “present” as time passes; thus, he or she exhibits future bias.

Our result on the intra-personal TI relationship is consistent with this explanation of TI. We found no persuasive evidence of differences between TI for gains and losses. This implies that people’s TI tendencies may be common for both delayed gains and delayed losses. This relationship would be natural when we consider time perception as a source of TI. When the wait times for future gains and future losses are the same, the perceived length of time itself should be independent of the sign of the outcomes, though its evaluation (how much they dislike waiting so long) may not be. That is because time perception relates to time length, and time length is only a physical matter (not associated with the sign of the outcome). If this is the case, the sign of the outcome may affect the evaluation of the outcome (e.g., loss aversion and the effect of the sign on the utility curve) and of the delay (effect of the sign on the discount rate), but not TI itself. This intuition is shared by Loewenstein and Prelec (1992), who reconstructed the sign difference of the imputed discount rate by assuming the utility of prospect theory.

Another explanation of the source of TI is potential risk in the future. The future is not always predictable, and future events (receiving or paying) are not certain (e.g., one may die before receiving). This risk changes over time for both SS and LL, so people may change their previous decisions at a later time.¹³ However, our finding of no difference between ${\text {DI}}_+$ and ${\text {DI}}_-$ may not match this explanation well because the potential risks should have differed between gains and losses in our experiment. Some risks, like the possibility of death in the future, might be common for both gains and losses, but these were possibly too small and ignorable (the time horizon was one-half of a year). Other risks, such as financial problems or breaking of promises by the experimenter, should be much larger, and are basically only relevant to gains, not losses. That is, the probability of not realizing gains must be much larger than that of not incurring losses, and the degree of TI varies accordingly. Our results did not exhibit this tendency. One may argue that potential risk truly affects TI, and the finding of no difference between ${\text {DI}}_+$ and ${\text {DI}}_-$ was only due to the hypothetical setting of our experiment. If all events were hypothetical, the risk of realization would not be a concern, and one would not sufficiently consider potential risk. If this is the case, however, one cannot explain why TI (present bias and future bias) was observed so frequently, even in the hypothetical setting, because a no-risk situation is needed to drive time-consistent behaviors.

Our result of a positive correlation between TI for gains and losses was contrary to the finding of Abdellaoui et al. (2013a). Initially, we thought that their result was distorted by an error in their measurement $\alpha$ of the GHD function, because it did not allow for future biases. However, our experiment reported a positive correlation even between $\alpha _+$ and $\alpha _-$ (see Appendix A.7), so this contrary result was apparently due to a different reason, possibly the variation in choice in the experiments or the specification error in the utility function.¹⁴ Indeed, the contrary result could also be attributed to differences in the length of time.

While delays of alternatives varied from 3 months to 5 years in the experiment by Abdellaoui et al., those in the present study ranged from a day to about 50 days, with the latest alternative being 218 days. Considering this difference, we may expect that TI for gains and losses may be correlated only when both delay and wait time are sufficiently short, and not otherwise (similar to the directions of TI in ISD). Since some researchers have stated that time preference depends on the time horizon (Ebert and Prelec 2007; Read 2001), this hypothesis may not be an uncommon one. If this is the case, the source of TI may also differ when the choice involves a long or short time horizon. It is surely important to know how people perceive wait times to understand how they evaluate delays and why time-inconsistent behavior occurs. We leave the exploration of the switches in TI from short- to long-term horizons to further research.

5.2 Experimental strengths and limitations

As we noted in 1, our result is free from any specification errors. We do not specify any curvature of the utility function, loss aversion, or sign-dependency evaluation. What we need to assume to compare TI levels are standard preference conditions: weak order, continuity, (strict) monotonicity, and (strict) impatience. Moreover, our study avoids the potential effect of the existence of immediate alternatives in the choice set. Most studies of future bias set $s=0$; however, immediacy may practically have a special impact, i.e., receiving a good “today” may be much different from receiving a good on “the day” when the experiment is carried out (e.g., difference in transaction costs; see Coller and Williams 1999 for evidence). Existence of an immediate alternative may cause some discontinuity on intertemporal choices, which is, however, not our main research target. Therefore, we set positive front-end delay (more than a day) in our experiment to control for this effect. Thus, we confirmed the existence of future bias and the validity of ISD without the impact of immediacy.

However, despite the generality and validity of our results, this study and its results are not free from limitations. The first, and most important, limitation is a scale compatibility problem. We asked our participants about both money size and delay length and combined the answers. It is, however, well known in the risk preference literature that results depend on the target of the task; i.e., the certainty equivalent (asking outcome to be equivalent) and probability equivalent (asking probability to be indifferent) are not consistent with each other (Hershey and Schoemaker 1985).¹⁵ This problem is still not clearly investigated in the time preference literature as far as we know, but our DI-index may potentially be distorted because it may be constructed by two different responses that used different decision processes. Our analysis of the intra-personal relationship of TI requires combining those two types of tasks and thus we cannot confirm this relationship without this potential problem in this experiment. On the other hand, it is worth pointing out that the validity of ISD still holds, even when we focus only on the data from time-asking tasks (the last three indifferences in (2) to minimize the problem. Future bias was observed more frequently, and the same classification in Sect. 4.2.3 on the limited data suggests that 10.3%, 37.4%, and 83.8% of participants are classified as EXP, HD, and ISD, respectively.

Second, some participants did not conform to monotonicity, impatience, or transitivity (see footnote 7). Since these conditions are fundamental in utility theory, and are needed to guarantee the correspondence between the DI-index and degree of TI, such violations should be considered. Although violation of impatience is not commonly observed in the literature, it is by no means rare. Negative discounting (i.e., preferring a delayed outcome) is mostly found for health, not monetary outcomes (e.g., Ganiats et al. 2000), but Warner and Pleeter (2001) reported that many older officers might exhibit zero or negative discounting for money. Prelec and Loewenstein (1998) also found debt aversion, that is, a tendency to pay even before consumption.¹⁶ Some studies have also reported violations of transitivity (e.g., Roelofsma and Read (2000)).

On the other hand, violations of strict monotonicity are more serious. Those participants answered $t^\prime$, which coincided with $s^\prime$ in stage 2 (i.e., WTW was 0). Since we use money as the outcome, strict monotonicity should hold. However, our participants might have thought that the set T is $\mathbb {N}$ and not $\mathbb {R}_+$. If this is the case, answering $d=0$ does not imply a direct violation of monotonicity; rather, it only means the participants felt $d=1$ was too much. Actually, only one participant answered an unnatural number in the second stage (e.g., $(10{,}000,8)\sim (13{,}000,10.1)$). However, basically, WTW is difficult to interpret with an unnatural number (e.g., what did an individual mean by 8 / 7 days of WTW). This may be one of the practical problems of matching-based experiments, especially if the length of time is asked. We end this discussion noting that our results did not change appreciably when we included observations that satisfied monotonicity, but not strict monotonicity.¹⁷

Lastly, the use of matching-based elicitation might bias participants’ responses. In the decision-making literature, it is known that responses through matching-task elicitations are or may be biased (e.g., the anchoring effect and inconsistency of the choice). We tried to minimize such biases in the experiment, but probably not to a sufficient level. In addition, matching tasks sometimes lead to responses that are not based on serious thinking. In fact, several participants in our experiment might be guilty of this¹⁸ Of course, such potential biases can be avoided through the use of choice tasks, in exchange for giving up the fine grid points of preference relations and fine bridges between the responses in the two stages.

However, we do not think that our elicitation method harmed all our results, because our observations are essentially not much different from those of previous studies that used choice-based elicitation. The finding of future bias and its tendency across temporal conditions are nearly consistent with Sayman and Öncüler (2009). Even the high imputed discount rate was consistent with studies on time preference with small temporal differences, as mentioned in Sect. 4.2.1. In addition, one well-controlled result was provided by Bleichrodt et al. (2016). They replicated the experiment by Attema et al. (2010), in which respondents were asked their WTW through a choice-based matching task, and found the same behavior. This indicates that WTW may not be affected by the elicitation method. Of course, although none of these facts is a direct proof that the matching task did not harm the results, they indirectly validate our observations and results. Thus, we believe that the results would not change if we used a choice task in the experiment.

6 Concluding remarks

We found the intra-personal relationship between TI for gains and losses, and obtained degrees of TI in a laboratory setting under various temporal gain and loss conditions without functional specifications. Our first finding is that participants exhibited not only present bias but also future bias, even for losses. The dynamic change in impatience was consistent with previous findings, and the explanatory power of ISD was much better than that of exponential and hyperbolic discounting.

The second finding is that the degrees of TI for gains and losses were positively correlated to each other, and not significantly different. That is, regardless of how impatient people are, their TI tendency for gains and losses are positively related (and may not be different).

The results of our study suggest that people may have a common (or similar) TI system for gains and losses. This is possibly consistent with the existing explanation that TI is caused by a distorted perception of the time dimension. Indeed, the source of TI may also differ between time horizons in the near and far future. Our results offer a key to discovering the source of TI; that is, how people perceive the future plays a crucial role in TI.

Appendices

Appendix A: Intra-personal relationship between estimated $\alpha _+$ and $\alpha _-$ of GHD

Whereas we found negative evidence for most common discount functions, including GHD (see footnote 10), numerous studies, including Abdellaoui et al. (2013a), have measured TI assuming a GHD function. Thus, we also adopted $\alpha$ of GHD here as a measure and estimated the parameters $\alpha _+$ and $\alpha _-$ of GHD using a non-linear least-square method. As we stated, we have indifference pair (1) for each condition $(s,d,s^\prime )$, where $s^\prime <s$. Under the discounted utility model of intertemporal choice, we have

$$\begin{aligned} D(s)u(x)=D(s+d)u(y) \quad \text { and } \quad D(s^\prime )u(x) =D(s^\prime +d^\prime )u(y), \end{aligned}$$

so that

$$\begin{aligned} d^\prime = D^{-1}\Bigl (\frac{D(s^\prime )}{D(s)} D(s+d)\Bigr ) -s^\prime . \end{aligned}$$

(3)

Assume D is GHD function $D(t)=(1+\alpha t)^{-\frac{\beta }{\alpha }}$ where $\alpha$ represents the degree of deviation from the exponential discounting. Then under those specifications, $d^\prime$ obtained in stage 2 must satisfy

$$\begin{aligned} d^\prime = \frac{1}{\alpha }\Bigl [\frac{1+\alpha s^\prime }{1+\alpha s}\Bigl (1+\alpha (s+d)\Bigr )-1\Bigr ]-s^\prime . \end{aligned}$$

(4)

We should note here that even if we assumed a parametric specification for discounting, the present experiment would be free from specifications on the utility function u because the two intertemporal choices contain the same outcomes, x and y, and thus u(.) is canceled out in Eq. (3). Thus, still utility curvature cannot affect our $\alpha$.

According to Eq. (4), parameter $\beta$ of GHD, and thus the value of function D(t), cannot be estimated in the present study. Takeuchi (2011) proposed estimating them by deriving the ratio of utility $\frac{u(x)}{u(y)}$ from risk preferences in an expected utility model. However, the expected utility specification for risk preference is not reasonable (e.g., Kahneman and Tversky 1979). In addition, the implicit assumption that the utility functions for risk and time are identical may lead to bias (see Abdellaoui et al. 2013b; Andreoni and Sprenger 2012). Since this study focuses on TI, and not the degree of time discounting, we do not follow this method.

For the pooled data, the best-fit estimates of $\alpha _+$ and $\alpha _-$ are 4.30 and 2.57, respectively, implying that time preference deviates from exponential discounting more for gains than for losses. At the individual level, the medians of $\alpha _+$ and $\alpha _-$ are 8.07 (87 subjects) and 4.62 (78 subjects), respectively, considering that certain subjects could not be analyzed because their observations that satisfied our assumptions were too few or the estimator was rather large ($\ge 10^{35}$). These parameters demonstrate a positive correlation (Spearman’s $\rho = 0.64$, $p = 0.00$) and no significant difference (sign rank test; $p = 0.31$) for subjects whose parameters could be fully estimated (75 subjects). The mean values for these subjects are considerably large because some of the subjects reported a high $\alpha$.

Appendix B: Classification rules in Sect. 4.2.3

See Table 5.

Table 5 Classification Table