Abstract
We obtain rich measures of the risk preferences of a sample of Vietnamese farmers, and revisit the link between risk preferences and economic well-being. Far from being particularly risk averse, our farmers are on average risk neutral and, thus, more risk tolerant than typical Western subject populations. This generalises recent findings indicating that students in poorer countries are more risk tolerant than students in richer countries to a general population sample. Risk aversion is, furthermore, negatively correlated with income within our sample, but does not correlate with wealth. This also casts doubt on high levels of risk aversion causing failure to adopt new technologies, which we discuss.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Development economists have long discussed the link between poverty and risk aversion. On the one hand, people in developing countries in general have been depicted as very risk averse (see, e.g., Haushofer and Fehr 2014, for a recent literature review). Such risk aversion may then lead to the perpetuation of poverty, by inducing suboptimal, risk-averse behavior (Liu 2012; Liu and Huang 2013). The evidence on both counts is, however, less than uniform. On the one hand, the supposed correlation between risk preferences and economic well-being cannot always be replicated (see, e.g., Cardenas and Carpenter 2013). On the other, tasks used to measure risk preferences in the developing world are often specifically designed to pick up pronounced risk aversion, and, thus, make the findings difficult to compare to preferences measured in developed countries using different elicitation tasks. In the presence of random switching, such measurement tasks will, furthermore, systematically over-estimate risk aversion (Vieider 2018).
In this paper, we take a fresh look at the relation between risk preferences and economic well-being. We obtain a rich set of experimental measures of risk preferences for a randomly selected, geographically confined group of farmers in Vietnam. The measures are obtained using certainty equivalents, which are easy to understand and administer. They also allow us to compare the results to a large number of experiments that have used the same type of tasks in the West (e.g., Abdellaoui et al. 2011; Fehr-Duda and Epper 2012), and to recent comparative data across a large number of countries obtained with students (Vieider et al. 2015). The richness of the data allows us to separate preferences from noise using structural models, while at the same time, we can back up the findings with nonparametric data. Using a geographically confined and uniform sample allows us to obtain good and comparable income measures, which are not confounded by other differences across subject groups or geographical regions.
We show that—far from conforming to the stereotype of extreme risk aversion—our Vietnamese farmers are on average risk neutral (although preferences change systematically across task characteristics). Comparing their risk preferences to data obtained with other subject populations using the same experimental tasks to put the findings in perspective, we conclude that Vietnamese farmers are significantly less risk averse than American students, which serve but as an example of other student populations in the West. We also find the Vietnamese farmers to be slightly more risk averse than Vietnamese students. Once again, this finding is consistent with previous findings from the West, with for instance Fehr-Duda and Epper (2012) finding Swiss students to be less risk averse than the Swiss general population using tasks similar to ours.
The evidence we present is also highly consistent with recent findings of students in poorer countries being more risk tolerant than students in richer countries (Rieger et al. 2014; Vieider et al. 2015), and, thus, extends the finding from students to a general population sample. At the same time, we find a strong negative correlation between risk aversion and income amongst farmers (while finding no correlation with other measures of well-being, such as wealth). The evidence here presented, thus, fits the narrative of a risk–income paradox presented by Bouchouicha and Vieider (2017), whereby risk aversion decreases with income within countries, but increases with national income between countries.
The experimental evidence here presented needs to be reconciled with the observed real-world behavior of farmers in poor countries. There is indeed considerable evidence that farmers employ risk-averse strategies in their real decisions. For instance, Rosenzweig and Binswanger (1993) famously described the use of risk-averse income smoothing strategies by poor farmers in India, and Jayachandran (2006) showed that the poorest often sell their labour at a considerable risk premium rather than employing it more fruitfully on their own farms. This type of evidence, however, does not lend itself to comparison with Western populations, which generally have much lower risk exposure—over-insuring even modest risks is all too common in the West (Sydnor 2010). Indeed, many elements other than the small stake risk preferences measured in experiments may play a role in such decisions (we will return to this point in the discussion).
This paper proceeds as follows. Section 2 describes our subject pool, the measurement tasks, and the general setup of the experiment. Section 3 introduces the theoretical setup and discusses the econometric specifications used. Section 4 presents the results. Section 5 discusses the results and concludes the paper.
2 Experimental setup
We recruited 207 farmers in the Vietnamese villages Phu Hiep, Phu Loi and Phu Quoi in An Giang province, close to the border with Cambodia alongside the Tien river. The villages were chosen at random amongst a number of locations where we could obtain the backing of the local party authorities. No systematic selection effects are likely to be caused by this—we will discuss this point more at length below. The households were randomly chosen from a complete population list of the three villages. Using repeated visits and trying to make appointments in case household heads were absent in the first visit, we achieved a 100% participation rate of our target population. This means that our sample is representative of the village reality of Southern Vietnam, although we cannot claim representativeness outside of this specific subject pool.
The median household in our sample has an income of 9.9 m Dong per capita per year. This corresponds to $1.32 per capita per day for the median households in current exchange rates at the time of the experiment, and to $2.89 in purchasing power parity (PPP; calculated using World Bank data for 2011). The corresponding means are $2.26 (sd 3.38) and $4.95 (sd 7.39), respectively. About 24% of our subjects fall below the official poverty line of the Vietnamese government.Footnote 1 Income was measured by asking farmers about different categories of income (e.g., income from farming, animals husbandry and aquaculture, from labour, leased land, remittances, etc.) and then aggregating across those categories (the full questionnaire is reported in the supplementary materials). Since most farmers in the region produce for the market, and since we ran our experiments not too long after the main harvest season, the information was relatively recent and, hence, easy to remember. Given the importance of income for our study, we also compare our sample to the corresponding figures for comparable population groups, as obtained from the Vietnamese statistical office (http://www.gso.gov.vn). The income per capita of our farmers is indeed not significantly different from the one of the rural population in Vietnam at large (\(t(198)=-\,1.01, p=0.312\), two-sided t test).
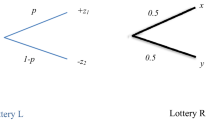
We elicit certainty equivalents (CEs) to measure risk preferences. CEs provide a rich amount of information, are easy to explain to subjects, and the sure amounts of money to be used in the elicitation are naturally limited between the lower and upper amount of the prospect. They are also flexible enough to allow for the detection of risk-seeking as well as risk-neutral and risk-averse behavior. This makes them well suited to estimate structural models of decision-making (Abdellaoui et al. 2011; Bruhin et al. 2010; Tversky and Kahneman 1992). Overall, we elicited 44 CEs per subject. The tasks used for the elicitation procedure were chosen so as to allow for the estimation of multi-parameter models, and were tested in extensive pilots with students before being deployed in the field. Table 1 provides an overview of the decision tasks, and Fig. 1 shows an example of a choice list. Prospects are described in the format (p : x; y), where p is the probability of obtaining x, and y obtains with a complementary probability \(1-p\), \(|x|>|y|\). Outcomes are shown in thousands of Dongs (8000 Dong = 1 Euro in PPP). Losses were deducted from an endowment equivalent to the highest potential loss, given conditional on playing the loss part of the experiment. The highest loss is smaller to the largest gain. This was necessary to limit financial exposure, since all subjects who were randomly selected to play the loss part were given an endowment equal to the highest possible loss. In addition to the prospects over gains and losses, we used one mixed prospect, which is necessary to obtain a measure of loss aversion. In this case, we obtained the value z* which satisfies the indifference \(0\sim (1/2:160;-\,z)\), where z varied in a choice list from 160,000 to 16,000 Dong.Footnote 2
Gains were administered before losses, which took part from an endowment (see Etchart-Vincent and L’Haridon 2011, for evidence that it does not matter whether losses take place from an endowment or are real). We also had prospects with unknown or vague probabilities that will not be analyzed here, and which were always presented in block after the risky prospects. The prospects were presented to subjects in a fixed order, whereby first 50–50 prospects were presented in order of ascending expected value, and then the remaining prospects were presented in order of increasing probability. The fixed order was kept so as to make the task less cognitively demanding for subjects, since in the fixed ordering, only one element would change from one decision task to the next, which could be easily pointed out by the enumerator. To test whether such a fixed ordering of tasks might influence decisions, we ran a large-scale pilot at Ho-Chi-Minh-City University involving 330 subjects. The pilot revealed no differences between the fixed ordering used here and a random ordering (results available upon request).
CEs were elicited in individual interviews by a team of 18 enumerators. The enumerators were extensively trained before going to the field, and had acquired experience by running the same experiment with students. They were, furthermore, supervised in the field by one of the authors. The actual experiment was preceded by a careful explanation of the decision tasks involved. The subjects were told that they would face choices between amounts of money that could be obtained for sure and risky allocations, in which different amounts would obtain with some probabilities indicated next to them. They then learned that the interview would consist in a number of such tasks that would differ in the amounts they offered as well as the likelihood with which these amounts were obtained. At the end, one of the tasks would be extracted at random, and one of the lines in which they had indicated a choice between a sure amount and the prospect would be played for real money (the standard procedure in this sort of task: Abdellaoui et al. 2011; Baltussen et al. 2012; Bruhin et al. 2010; Choi et al. 2007). Losses were only introduced once all the gain prospects had been played. Small breaks were taken between the different parts of the elicitation procedure.
Once a subject had understood the general structure, he was presented as an example of a decision task for risky gains. The enumerator then explained why for a safe amount equal to the lower amount in the prospect, he would likely prefer to take the prospect. Equivalently, once the sure amount reached the highest amount to be won in the prospect, the subject would be explained that he would most likely prefer the sure amount. This would lead naturally to a point at which a subject should switch from the prospect to the sure amount. At which amount this would happen would be purely up to the subjects’s preference. Most subjects understood this very quickly. If subjects wanted to switch multiple times, enumerators were instructed to simply record such choices. This, however, never happened.
Since all farmers were literate, they were shown the lottery depiction and the amounts involved on the interview sheet. Every time a major change occurred in the decision tasks (e.g., a change in probabilities or outcomes, or from gains to losses), the enumerator pointed out the change and gave additional explanations of what this would involve. In the course of the explanation, farmers were also shown bags containing numbered ping pong balls that would be used for the random extraction, and were encouraged to examine their contents. This served to make the decision problems more tangible and concrete.
The prospects concerned payoffs between 0 and 320,000 Dong (in the mixed prospect, including the endowment), which were added to a fixed participation payment of 8000 Dong (these payoffs are the PPP-equivalent of the payoffs used by Vieider et al. 2015; see Vieider 2012, for evidence that small stake variations potentially caused by local differences in PPP do not impact estimated risk preferences). These are substantial sums, with the expected payoff from participation corresponding to about 6 days’ per capita income of the median household, and the highest prize to over 10 days. This indicates a general tendency by which PPP conversions used for developing countries underestimate the amounts used if one were to employ income instead of prices as a gauge. Notice how, given the well-established finding of risk aversion increasing in stakes (Binswanger 1980; Fehr-Duda et al. 2010; Holt and Laury 2002; Kachelmeier and Shehata 1992; Santos-Pinto et al. 2009), this tends to bias our findings against risk tolerance. Notice also that the payoffs we offer are at least as high as most of the payoffs offered in similar studies in developing countries (for instance, Attanasio et al. 2012, have average payoffs of about $2, corresponding to about 1 day’s pay; Yesuf and Bluffstone 2009 have an average payoff of about 3 days of pay).
The overall quality of our data is reasonably good, although there are also significant levels of noise. About 25% of our subjects violated first-order stochastic dominance at least once for gains, and about 31% for losses.Footnote 3 This is only slightly higher than violation rates observed with student samples from the West. Abdellaoui et al. (2013) found about 20% of subjects to violate stochastic dominance in a laboratory experiment with students in the Netherlands using individual interviews. Overall violations relative to total number of CEs in our farmer data amount to only about 3.0% for gains, and to 4.3% for losses.
3 Theory and econometrics
3.1 Theoretical setup
The results presented in this paper are stable to using most major theories, including expected utility theory (EUT) and prospect theory (PT). The main modelling approach in the paper is motivated by obtaining the highest possible descriptive accuracy, conditional on keeping the analysis tractable from an empirical point of view. We will adopt a reference-dependent modelling approach throughout. Such an approach is an integral part of prospect theory (Kahneman and Tversky 1979). It was first proposed for expected utility by Markowitz (1952), in an attempt to accommodate the observation of lottery and insurance purchase by the same person, and has by now been widely adopted into expected utility models in both theory and empirical analysis (Diecidue and van de Ven 2008; Kőszegi and Rabin 2007; Sugden 2003; von Gaudecker et al. 2011).Footnote 4 The elicitation tasks are designed in such a way as to fix the reference point to zero—see L’Haridon and Vieider (2018) for a more detailed discussion.
We will start by representing our preferences through a PT model. We describe decisions for binary prospects. For outcomes that fall purely into one domain, i.e., \(x>y\ge 0\) or \(0\ge y>x\), we can represent the utility of a prospect \(\xi _i\), \(U(\xi _i)\), as follows:
whereby the probability weighting function w(p) is a strictly increasing function that maps probabilities into decision weights, and which satisfies \(w(0)=0\) and \(w(1)=1\); the superscript j indicates the decision domain and can take the values \(+\) for gains and − for losses; and v(.) represents a utility or value function which indicates preferences over outcomes, with a fixed point such that \(v(0)=0\), and \(v(x)=-v(-x)\) if \(x<0\). Contrary to expected utility models, utility curvature in the full PT model cannot be automatically equated with risk preferences, since the latter are determined jointly by the utility function and the weighting function (Schmidt and Zank 2008). For mixed prospects, where \(x>0>y\), the utility of the prospect can be represented as:
In our experimental tasks, we elicit certainty equivalents, such that by definition \(ce\sim (x,p;y)\), where \(\sim \) indicates indifference. We can represent the certainty equivalents estimated according to the model just presented as follows:
To specify the model set out above, we need to determine the functional forms to be used. We start by assuming utility to be piecewise linear:
where the parameter \(\lambda \) indicates loss aversion, generally represented as a kink in the utility function at the origin (Abdellaoui et al. 2007; Köbberling and Wakker 2005).
Simplifying our model by assuming utility to be piecewise linear has several advantages in our setup, which we belief more than outweigh potential drawbacks. Yaari (1987) powerfully made the point that representing risk preferences through subjective probability transformations is just as legitimate as representing them through outcome transformations, and may be more psychologically accurate for small stakes. Our model is then the natural extension of Yaari’s dual theory to reference-dependent models (see Schmidt and Zank 2007, for an axiomatization of this model). Most importantly, this assumption allows us to directly compare subject pools in terms of their risk preferences. This is much more difficult using a full prospect theory model, given issues of collinearity between utility and weighting functions, which may both reflect risk preferences under prospect theory (Zeisberger et al. 2012). The obvious cost of our simplification is that we largely ignore any variation taking place over different stake levels. This variation is, however, modest in our data, and most interesting patterns with our stake levels typically emerge over the probability dimension (Fehr-Duda and Epper 2012; Prelec 1998). Most importantly, none of the results presented below depend on the linear probability assumption (see Appendix A for a stability analysis using the full PT model).
For probability weighting, we adopt the 2-parameter weighting function proposed by Prelec (1998). (Other functional forms from the two-parameter family deliver similar results. One-parameter forms are, on the other hand, not well suited to describe our data, for reasons that will become apparent below):
For \(\beta =1\), this function conveniently simplifies to the 1-parameter function proposed by Prelec, which has a fixed point at \(1/e\simeq 0.368\), and which has been developed to fit typical aggregate data from the West.Footnote 5 In terms of interpretation, \(\beta \) is a parameter that governs mostly the elevation of the weighting function, with higher values indicating a lower function. Since this indicates the weight assigned to the best outcome for gains, and the weight assigned to the worst outcome for losses, a higher value of \(\beta \) indicates increased probabilistic pessimism for gains, and increased probabilistic optimism for losses. Since we assume utility to be linear, we can directly interpret this parameter to indicate risk aversion for gains, and risk seeking for losses on average over the probability spectrum. For \(\alpha =1\), the parameter indeed represents standard risk aversion, with \(\beta \ge 1\) indicating risk aversion and \(\beta \le 1\) risk seeking. The parameter \(\alpha \) governs the slope of the probability weighting function, with \(\alpha =1\) indicating linearity of the weighting function (the EUT case), and \(\alpha <1\) representing the typical case of probabilistic insentivity.
3.2 Stochastic modeling and econometric specification
The model considered so far is fully deterministic, assuming that subjects know their preferences perfectly well and execute them without making mistakes. It also assumes that we can capture such preferences perfectly in our model. Both assumptions seem untenable, especially in a development setting such as ours. We, thus, abandon this restrictive assumption and introduce an explicit stochastic structure. Given our setup, the certainty equivalent of a given prospect i we observe, \(ce_i\) will, thus, be equal to the certainty equivalent for the same prospect calculated from our model, \(\hat{ce}_i\), plus some error term, or \(ce_i=\hat{ce}_i+\epsilon _i\). We assume this error to be normally distributed, \(\epsilon _i\sim (0,\sigma _i^2)\), which allows for the errors to be serially correlated (see Train 2009). We can now express the probability density function \(\psi (.)\) for a given subject n as follows
where \(\phi \) is the standard normal density function, and \(\theta =\{\lambda ,\alpha ^j,\beta ^j,\}\) indicates the vector of parameters to be estimated. The subscript n to the parameter vector \(\theta \) indicates that we will let the parameters depend linearly on the observable characteristics of decision makers, such that \(\hat{\theta }=\hat{\theta }_k+\beta X\), where \(\hat{\theta }_k\) is a vector of constants and X represents a matrix of observable characteristics of the decision maker.Footnote 6 Finally, \(\sigma \) indicates a so-called Fechner error (Hey and Orme 1994). The subscripts emphasize that we are allowing for three different types of heteroscedasticity, whereby n indicates as usual the observable characteristics of the decision maker, j indicates the decision domain (gains vs. losses), and i indicates that we allow the error term to depend on the specific prospect, or rather, on the difference between the high and low outcome in the prospect, such that \(\sigma _i=\sigma |x_i-y_i|\) (see Bruhin et al. 2010). For mixed prospects, we adopt the error term for losses, since only losses vary in the mixed choice list.
These parameters can now be estimated by maximum likelihood procedures. To obtain the overall likelihood function, we need to take the product of the density functions above across prospects and decision makers:
where \(\theta \) is the vector of parameters to be estimated such as to maximize the likelihood function. Taking logs, we obtain the following log-likelihood function:
We estimate this log-likelihood function in Stata using the Broyden–Fletcher–Goldfarb–Shanno optimization algorithm. Errors are always clustered at the subject level.
4 Results
4.1 Risk-preference comparison
Table 2 shows a regression comparing the parameter estimates for farmers to those of American and Vietnamese students. The student data were obtained using the same experimental tasks as the ones used with the farmers and stakes are the same in terms of PPP. The American student data are borrowed from L’Haridon and Vieider (2018), who amongst other things report parameter estimates for the same model for students across 30 countries, and are meant to relate our current data to the results of that paper.Footnote 7 In this sense, American students are meant to proxy for Western populations more in general—a point to which we will return shortly.
The regression controls for the sex of the respondent to address concerns that differences may be driven by gender effects that are often found for risk (Croson and Gneezy 2009), but the differences found are stable to dropping the demographic controls. Adding additional controls is difficult, as the control variables obtained for the student and farmer subject pools are generally not comparable. An exception to this is age. However, given that all our students are very young compared to the farmer sample, adding age results in high degrees of collinearity with the student dummies. We find that women are less sensitive to probabilistic change for both gains and losses, as well as less risk tolerant for losses. This is in line with the results reported by L’Haridon and Vieider (2018), who find a gender effect mostly on probabilistic sensitivity using a sample of almost 3000 students from 30 countries.
We find both student groups to be significantly more sensitive to probabilistic change than farmers, as indicated by the larger \(\alpha \) parameter. This holds for both gains and losses, and is consistent with the interpretation of the sensitivity parameter as a proxy for rationality or numeracy (Tversky and Wakker 1995; Wakker 2010). Students also show less noise in their decisions compared to the farmers. The farmers are slightly (but not significantly) less risk tolerant than Vietnamese students for gains, as indicated by the negative coefficient for the \(\beta ^+\) parameter. The farmers are, however, significantly more risk tolerant than the American students for both gains and losses (see Fig. 2). Indeed, American students exhibit decision patterns as they have typically been estimated in the West (see again L’Haridon and Vieider 2018), with a \(\beta ^+\) parameter slightly larger than one.Footnote 8 For loss aversion, we find again that our farmers are intermediate between the two student populations, although none of the differences are significant.
Figure 4 shows the three risk-preference functions for gains together with the non-parametric data points (for losses see supplementary materials).Footnote 9 The estimated functions can be seen to trace the nonparametric data closely. The risk-preference function for farmers is more elevated than the one of the American students up to and including \(p=\nicefrac {5}{8}\), and becomes very similar and somewhat lower for the two highest probability levels, respectively. Compared to Vietnamese students, the risk-preference functions are very similar up to at least \(p=\nicefrac {3}{8}\), after which the two functions start to diverge, as reflected in the farmers’ lower probabilistic sensitivity.
The comparison results may appear surprising, given a large number of studies showing risk aversion as the prevalent pattern in decisions under risk (we will discuss this point further below). To investigate the stability of these findings—and to be able to discuss average risk preferences over all choices with one simple measure—we now take the risk premium, given by EV\(\,-\,\)CE, averaged over all gain prospects (in PPP Euros; PPP US Dollars obtain by multiplication with 1.2).Footnote 10 We here concentrate on gains—an equivalent analysis for losses is shown in the supplementary materials. Farmers have a significantly lower risk premium than American students (\(z=-2.07\), \(p=0.039\), two-sided Mann–Whitney test), and a (non-significantly) larger risk premium than Vietnamese students (\(z=1.54, p=0.123\)). While American students are significantly risk averse (\(z=4.67, p<0.001\); two-sided Wilcoxon signed-rank test), the farmers are on average risk neutral (\(z=0.23\), \(p=0.815\)), and Vietnamese students are on average risk seeking (\(z=-2.38, p=0.017\)). These findings are in no way unique to American students, whom we use as a typical exponent of Western subject pools. L’Haridon and Vieider (2018) indeed show a strong positive correlation between risk aversion and GDP per capita using students subject pools from 30 different countries over a wide range of income levels, and Vieider et al. (2018) report results for a general population sample from Ethiopia that is consistent with the evidence obtained for students.
4.2 Risk preferences and economic well-being
So far, we have only considered aggregate preferences. The next step will be to look into individual characteristics and their correlation with risk preferences. In particular, we are interested in income, as well as measures of wealth. Table 3 shows the results of a regression of risk preferences on income per capita, education, and the age of the respondent (z-values are used for age, education, and income; using discrete categories for education does not change our results). Our subject pool is reduced to 197 subjects, since for the remaining subjects one of the observable characteristics is not reported.
We start by looking at the elevation of the risk preference function. For both gains and losses, we find risk tolerance to increase in income, as indicated by the negative coefficient for \(\beta ^+\) and the positive coefficient for \(\beta ^-\) (since for losses we transform probabilities attached to the worst outcome, following the going convention; see Wakker 2010). Loss aversion is also found to decrease in income. Probabilistic sensitivity for both gains and losses decreases with age. Given that probabilistic sensitivity is often taken to be an indicator of rationality or cognitive ability, this corresponds well to what we would expect. Also, the result corresponds closely to the results reported by L’Haridon and Vieider (2018), who find sensitivity to decrease in age and increase in grade point average. It is also in general agreement with findings by Choi et al. (2014), who found violations of rationality principles to increase with age and decrease with education and income (the latter effect is not significant in our data). Loss aversion is also found to increase in education. This is contrary to the findings of Gächter et al. (2010), but in agreement with the findings by von Gaudecker et al. (2011).
An important issue is whether our findings are indeed driven by income, and not by wealth. To capture wealth levels, we use the first two components from a principal component analysis into which all variables capturing wealth in our data set are entered, such as size and type of house, access to running water, sanitation facilities, motorcycles owned, ownership of TV or fridge, etc. (Filmer and Pritchett 2001). Table 4 reproduces the results from Table 3 controlling for these wealth indicators.Footnote 11 The wealth controls do not show any significant effects. This goes against the traditional assumption of risk aversion decreasing in wealth. The effect of income, however, only results reinforced from the introduction of wealth controls.
We, thus, find clear evidence of a negative correlation between risk aversion and income in our data. Such a negative correlation has frequently been reported in Western population samples (e.g., Dohmen et al. 2011; Donkers et al. 2001; Hopland et al. 2016), although sometimes it has been found only for a subset of the risk-preference measures used (for instance, von Gaudecker et al. 2011, and Booij et al. (2010) both only found the effect for loss aversion in representative Dutch samples, but not for utility curvature over gains), and at least one study found an effect going in the opposite direction (Harrison et al. 2007). A similar negative relationship with income or income proxies and risk aversion has also been found repeatedly in developing countries (Liebenehm and Waibel 2014; Vieider et al. 2018; Yesuf and Bluffstone 2009). Other studies, especially in developing countries, have not found any correlation between risk preferences and measures of well-being (Binswanger 1980; Cardenas and Carpenter 2013).
5 Discussion and conclusion
The results presented in this paper break radically with some assumptions on risk preferences of rural populations in developing countries. Far from finding high levels of risk aversion amongst poor farmers, we find farmers in Vietnam to be quite risk tolerant in comparison to typical Western populations. Taken together with international comparisons based on student samples (Rieger et al. 2014; Vieider et al. 2015), and with results from other general population samples of poor countries (Vieider et al. 2018), the results here presented provide increasingly solid evidence of a systematic negative relationship between risk tolerance and GDP per capita between countries. We have furthermore shown a clear increase in risk tolerance with income within the farmer sample itself, while risk preferences were found to be uncorrelated with wealth. This may indeed show one of the reasons why past studies especially in developing countries have not always found a correlation with measures of well-being.
Given how strong the relationship with income is, it seems unlikely that other factors would constitute a better explanation for these aggregate risk preferences. In particular, we do not think that our data can be explained in any way by noise or systematic error. While answering randomly on our choice lists would produce risk neutrality on average, the choice patterns we find are clearly not random. Indeed, purely random choice would result in much higher frequency of violations of first-order stochastic dominance than the ones we found, and would be picked up mostly by the error term.
For the development literature, the high level of risk tolerance we find at the aggregate level poses the issue of what may hold back technology adoption on the farm. To the extent that preferences cannot be blamed for this, we may look at other factors that hinder adoption. Feder (1980) observed how “risk and risk-aversion have been used to explain differences in input use and the relative rate of adoption of modern technologies by farmers of different sizes. But different patterns of behaviour are observed in different regions, and thus the impact of risk and risk-aversion needs to be examined in relation to other factors and constraints [...]” (p. 263). This conclusion is reinforced in some of the recent literature. Karlan et al. (2012) present results suggesting that it is the sheer amount of risk exposure that makes investments unprofitable in some cases. Mobarak and Rosenzweig (2012) present evidence that risk taking in production goes up once farmers are sheltered from the worst risks through insurance. This suggests that risk-averse coping behavior may be driven by external constraints, rather than or in addition to individual preferences (Feder et al. 1985). This obviously does not preclude an effect of individual risk attitudes on the relative likelihood of a farmer to adopt new technology. This issue is, however, beyond the scope of this paper.
The high levels of risk tolerance we find seem to contrast with a large part of the existing development literature. This may at least in part be due to the popularity enjoyed amongst development economists by choice list that are systematically distorted in the direction of risk aversion. For instance, the task developed by Binswanger (1980) remains hugely popular in development economics because of its simplicity (Attanasio et al. 2012; Bauer et al. 2012; Giné et al. 2008; Yesuf and Bluffstone 2009). While it may be perfectly adequate to detect within-sample differences, it is capped at risk neutrality, thus making it impossible to register risk seeking behavior. In the presence of noise registering in terms of random choices, it will, thus, result in a drastic overestimation of risk aversion (Vieider 2018).
Our results are also quite different from the ones obtained by Tanaka et al. (2010) in the same area of southern Vietnam. Once again, this may be due to the asymmetric choice lists employed by the latter. The case of risk neutrality, which in their model would obtain for linear utility in combination with linear probability weights, obtains in their model when subjects switch around the middle of list 1, but at the very first question in list 2 (list 3 is used only to determine loss aversion). The relation of risk aversion to each step in the choice list is, furthermore, highly nonlinear, so that each step beyond the point of risk neutrality results in increasingly large steps in terms of estimated risk aversion. Just like the Binswanger task, the elicitation tasks are very unlikely to result in the detection of risk-seeking behavior in the presence of noise, with noise counted systematically towards risk aversion. Clearly, there are also other differences in both elicitation and estimation that might drive the differences in our findings. More direct comparative evidence on risk elicitation tasks is need to disentangle the influence of different factors.
Notes
The poverty line applied here is based on “Decision of the Prime Minister 9/2011/QD-TTG: Promulgating standards of poor households, poor households to apply for stage from 2011 to 2015”, in which the poverty line for rural areas is 400,000 Dong per capita per month and for urban areas, it is 500,000 Dong per capita per month.
The choice tasks (though not the instructions, this experiment being run in individual interviews) and payoffs were the same as the ones used by Vieider et al. (2015) in experiments with students across 30 countries. For an overview of the tasks, see the instructions available for download in various languages at http://www.ferdinandvieider.com/instructions.html.
Violations of first-order stochastic dominance are not transparent in our experiment. They could occur for instance, if a CE for a given prospect (p : x; y) is larger than a CE for another prospect (\(p+\epsilon : x; y\)) or a prospect (\(p: x + \epsilon ; y\)), where \(\epsilon >0\), and \(x>y\).
We refer to these models as models of ‘expected utility’ inasmuch as they still transform outcomes into utilities and then take the expectation of these utilities. The main difference with (original) EUT is that reference-dependent models define utility over changes in wealth, while the original model defined utility over total wealth.
The one-parameter formulation was, for instance, adopted by Tanaka et al. (2010) to investigate risk preferences in Vietnam. We will discuss their results in more detail below.
We always carry out the regression within the overall maximim likelihood model. A possible alternative is to estimate the parameters at the individual level, and then to separately regress these parameters on the characteristics of the decision makers. We deem such an approach less suitable for our purposes, both because estimations at the individual level are based on relatively few data points and may result in outliers, and because it is not clear how to treat the standard errors in separate regressions of parameters that result from one and the same estimation procedure.
The data for American students were obained using sessions instead of individual interviews. For Vietnamese students, we obtained the data partially in interviews using identical procedures as for farmers, partially in sessions. We pool the data since we did not find any differences between the two methods (except for loss aversion, which is found to be lower in the interview condition; see Vieider 2009, for a potential explanation). A regression showing this is reported in the supplementary materials.
For the prospect theory formulation shown in the appendix, \(\beta ^+=1\) cannot be rejected for American students, so that the function reduces to its one-parameter formulation. This estimate is, thus, at the lower end in terms of risk aversion of the range of estimates obtained in Western countries—see Booij et al. (2010) for an overview.
The non-parametric data are made comparable to the parametric estimates by normlization of the certainty equivalent, \(\frac{\mathrm{CE}-y}{x-y}\), which are then plotted against the probability of winning the prize x.
Notice how using a normalised risk premium, \(\frac{{\text {EV}}-{\text {CE}}}{\text {EV}}\) attributes more weight to small-probability prospects relative to large-probability prospects, thus distorting the picture. Nonetheless, all our results are even stronger under this definition, as the largest differences are observed for small to moderate probability prospects.
Wealth is positively correlated with income, as one might expect. However, the correlations of our income measure with the first principal component of wealth is relatively modest at \(r=0.31\).
References
Abdellaoui, M., Baillon, A., Placido, L., & Wakker, P. P. (2011). The rich domain of uncertainty: Source functions and their experimental implementation. American Economic Review, 101, 695–723.
Abdellaoui, M., Bleichrodt, H., L’Haridon, O., & Van Dolder, D. (2013). Source-dependence of utility and loss aversion: A critical test of ambiguity models. University of Rennes 1 working paper.
Abdellaoui, M., Bleichrodt, H., & Paraschiv, C. (2007). Loss aversion under prospect theory: A parameter-free measurement. Management Science, 53(10), 1659–1674.
Attanasio, O., Barr, A., Cardenas, J. C., Genicot, G., & Meghir, C. (2012). Risk pooling, risk preferences, and social network. American Economic Journal: Applied Economics, 4(2), 134–167.
Baltussen, G., Post, T., van den Assem, M. J., & Wakker, P. P. (2012). Random incentive systems in a dynamic choice experiment. Experimental Economics, 15(3), 418–443.
Bauer, M., Chytilová, J., & Morduch, J. (2012). Behavioral foundations of microcredit: experimental and survey evidence from rural India. The American Economic Review, 102(2), 1118–1139.
Binswanger, H. P. (1980). Attitudes toward risk: Experimental measurement in rural India. American Journal of Agricultural Economics, 62(3), 395–407.
Booij, A. S., van Praag, B. M. S., & van de Kuilen, G. (2010). A parametric analysis of prospect theory’s functionals for the general population. Theory and Decision, 68(1–2), 115–148.
Bouchouicha, R., & Vieider, F. M. (2017). Growth, entrepreneurship, and risk tolerance: A risk-income paradox. University of Reading working paper
Bruhin, A., Fehr-Duda, H., & Epper, T. (2010). Risk and rationality: Uncovering heterogeneity in probability distortion. Econometrica, 78(4), 1375–1412.
Cardenas, J. C., & Carpenter, J. (2013). Risk attitudes and economic well-being in Latin America. Journal of Development Economics, 103, 52–61.
Choi, S., Fisman, R., Gale, D., & Kariv, S. (2007). Consistency and heterogeneity of individual behavior under uncertainty. The American Economic Review, 97(5), 1921–1938.
Choi, S., Kariv, S., Müller, W., & Silverman, D. (2014). Who is (more) rational? American Economic Review, 104(6), 1518–1550.
Croson, R., & Gneezy, U. (2009). Gender differences in preferences. Journal of Economic Literature, 47(2), 1–27.
Diecidue, E., & van de Ven, J. (2008). Aspiration level, probability of success and failure, and expected utility. International Economic Review, 49(2), 683–700.
Dohmen, T., Falk, A., Huffman, D., Sunde, U., Schupp, J., & Wagner, G. G. (2011). Individual risk attitudes: Measurement, determinants, and behavioral consequences. Journal of the European Economic Association, 9(3), 522–550.
Donkers, B., Melenberg, B., & Van Soest, A. (2001). Estimating risk attitudes using lotteries: A large sample approach. Journal of Risk and Uncertainty, 22(2), 165–95.
Etchart-Vincent, N., & L’Haridon, O. (2011). Monetary incentives in the loss domain and behavior toward risk: An experimental comparison of three reward schemes inclusing real losses. Journal of Risk and Uncertainty, 42, 61–83.
Feder, G. (1980). Farm size, risk aversion, and the adoption of new technology under uncertainty. Oxford Economic Papers, 32(2), 263–282.
Feder, G., Just, R. E., & Zilberman, D. (1985). Adoption of agricultural innovations in developing countries: A survey. Economic Development and Cultural Change, 33(2), 255–298.
Fehr-Duda, H., Bruhin, A., Epper, T. F., & Schubert, R. (2010). Rationality on the rise: Why relative risk aversion increases with stake size. Journal of Risk and Uncertainty, 40(2), 147–180.
Fehr-Duda, H., & Epper, T. (2012). Probability and risk: Foundations and economic implications of probability-dependent risk preferences. Annual Review of Economics, 4(1), 567–593.
Filmer, D., & Pritchett, L. H. (2001). Estimating wealth effects without expenditure data—Or tears: An application to educational enrollments in states of India. Demography, 38(1), 115–132.
Gächter, S., Johnson, E., & Herrmann, A. (2010). Individual-level loss aversion in riskless and risky choices. Technical report 2010–20, CeDEx discussion paper series.
Giné, X., Townsend, R., & Vickery, J. (2008). Patterns of rainfall insurance participation in rural India. World Bank Economic Review, 22, 539–566.
Harrison, G. W., Lau, M. I., & Rutström, E. E. (2007). Estimating risk attitudes in Denmark: A field experiment. Scandinavian Journal of Economics, 109, 341–368.
Haushofer, J., & Fehr, E. (2014). On the psychology of poverty. Science, 344(6186), 862–867.
Hey, J. D., & Orme, C. (1994). Investigating generalizations of expected utility theory using experimental data. Econometrica, 62(6), 1291–1326.
Holt, C. A., & Laury, S. K. (2002). Risk aversion and incentive effects. American Economic Review, 92(5), 1644–1655.
Hopland, A. O., Matsen, E., & Strøm, B. (2016). Income and choice under risk. Journal of Behavioral and Experimental Finance, 12, 55–64.
Jayachandran, S. (2006). Selling labor low: Wage responses to productivity shocks in developing countries. Journal of Political Economy, 114(3), 538–575.
Kachelmeier, S. J., & Shehata, M. (1992). Examining riskpreferences under high monetary incentives: Experimental evidence from the People’s Republic ofChina. American Economic Review, 82(5), 1120–1141.
Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47(2), 263–291.
Karlan, D., Osei, R. D., Osei-Akoto, I., & Udry, C. (2012). Agricultural decisions after relaxing credit and risk constraints. Working paper 18463, National Bureau of Economic Research, October.
Köbberling, V., & Wakker, P. P. (2005). An index of loss aversion. Journal of Economic Theory, 122(1), 119–131.
Kőszegi, B., & Rabin, M. (2007). Reference-dependent risk attitudes. The American Economic Review, 97(4), 1047–1073.
L’Haridon, O., & Vieider, F. M. (2018). All over the map: A worldwide comparison of risk preferences. Quantitative Economics (in press).
Liebenehm, S., & Waibel, H. (2014). Simultaneous estimation of risk and time preferences among small-scale farmers in West Africa. American Journal of Agricultural Economics, 96, 1420–1438.
Liu, E. M. (2012). Time to change what to sow: Risk preferences and technology adoption decisions of cotton farmers in China. Review of Economics and Statistics, 95(4), 1386–1403.
Liu, E. M., & Huang, J. K. (2013). Risk preferences and pesticide use by cotton farmers in China. Journal of Development Economics, 103, 202–215.
Markowitz, H. (1952). The utility of wealth. Journal of Political Economy, 60(2), 151–158.
Mobarak, A. M., & Rosenzweig, M. R. (2012). Selling formal insurance to the informally insured. Yale Economics Department working paper no. 97.
Pahlke, J., Strasser, S., & Vieider, F. M. (2012). Risk-taking for others under accountability. Economics Letters, 114(1), 102–105.
Prelec, D. (1998). The probability weighting function. Econometrica, 66, 497–527.
Rieger, M. O., Wang, M., & Hens, T. (2014). Risk preferences around the world. Management Science, 61(3), 637–648.
Rosenzweig, M. R., & Binswanger, H. P. (1993). Wealth, weather risk, and the composition and profitability of agricultural investments. Economic Journal, 103(January), 56–78.
Santos-Pinto, L.S., Astebro, T., & Mata, J. (2009). Preference for skew in lotteries: Evidence from the laboratory. MPRA paper.
Schmidt, U., & Zank, H. (2007). Linear cumulative prospect theory with applications to portfolio selection and insurance demand. Decisions in Economics and Finance, 30(1), 1–18.
Schmidt, U., & Zank, H. (2008). Risk aversion in cumulative prospect theory. Management Science, 54(1), 208–216.
Sugden, R. (2003). Reference-dependent subjective expected utility. Journal of Economic Theory, 111(2), 172–191.
Sydnor, J. (2010). (Over)insuring modest risks. American Economic Journal: Applied Economics, 2(4), 177–199.
Tanaka, T., Camerer, C. F., & Nguyen, Q. (2010). Risk and time preferences: Linking experimental and household survey data from Vietnam. American Economic Review, 100(1), 557–571.
Train, K. (2009). Discrete choice methods with simulation. Cambridge: Cambridge University Press.
Tversky, A., & Kahneman, D. (1992). Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty, 5, 297–323.
Tversky, A., & Wakker, P. P. (1995). Risk attitudes and decision weights. Econometrica, 63(6), 1255–1280.
Vieider, F. M. (2009). The effect of accountability on loss aversion. Acta Psychologica, 132(1), 96–101.
Vieider, F. M. (2012). Moderate stake variations for risk and uncertainty, gains and losses: Methodological implications for comparative studies. Economics Letters, 117, 718–721.
Vieider, F. M. (2018). Certainty preference, random choice, and loss aversion: A comment on “Violence and risk preference: Experimental evidence from afghanistan”. American Economic Review, 108(8), 2366–2382.
Vieider, F. M., Beyene, A., Bluffstone, R. A., Dissanayake, S., Gebreegziabher, Z., Martinsson, P., et al. (2018). Measuring risk preferences in rural Ethiopia. Economic Development and Cultural Change, 66(3), 417–446.
Vieider, F. M., Lefebvre, M., Bouchouicha, R., Chmura, T., Hakimov, R., Krawczyk, M., et al. (2015). Common components of risk and uncertainty attitudes across contexts and domains: Evidence from 30 countries. Journal of the European Economic Association, 13(3), 421–452.
von Gaudecker, H.-M., van Soest, A., & Wengström, E. (2011). Heterogeneity in risky choice behaviour in a broad population. American Economic Review, 101(2), 664–694.
Wakker, P. P. (2010). Prospect theory for risk and ambiguity. Cambridge: Cambridge University Press.
Yaari, M. E. (1987). The dual theory of choice under risk. Econometrica, 55(1), 95–115.
Yesuf, M., & Bluffstone, R. A. (2009). Poverty, risk aversion, and path dependence in low-income countries: Experimental evidence from Ethiopia. American Journal of Agricultural Economics, 91(4), 1022–1037.
Zeisberger, S., Vrecko, D., & Langer, T. (2012). Measuring the time stability of prospect theory preferences. Theory and Decision, 72(3), 359–386.
Author information
Authors and Affiliations
Corresponding author
Additional information
This study was financed by EEPSEA. We are grateful to Jack Knetsch, Maarten Voors, Christoph Rheinberger, and Peter Wakker for helpful comments. All errors remain ours alone.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendix: Subject pool comparison under PT
Appendix: Subject pool comparison under PT
Table 5 shows the subject pool comparison using the full PT model, using a domain-specific power utility function. Utility for gains can be seen to be slightly convex for our farmers, an effect that is marginally significant (\(\chi ^2(1)=3.63\), \(p=0.057\)). Utility is more convex for Vietnamese students and linear for American students, although neither of the two differences is statistically significant. To examine the results in terms of risk preferences, however, we must consider them jointly with the results on probability weighting. Both student populations are significantly more probabilistically sensitive than the farmers. American students are also marginally significantly more pessimistic than the farmers, as indicated by the higher value of \(\beta ^+\). However, the difference between farmers and American students on utility curvature and the elevation of the probability weighting function jointly is highly significant (\(\chi ^2(1)=15.59, p<0.001\)). While Vietnamese farmers show significant probabilistic optimism (\(\chi ^2(1)=4.13, p=0.042\), rejecting \(\beta ^+=1\)), for American students we cannot reject the hypothesis that \(\beta ^+=1\) (\(\chi ^2(1)=0.27, p=0.605\)), which corresponds to typical findings from the West. The results for losses are similar and will not be discussed further.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Vieider, F.M., Martinsson, P., Nam, P.K. et al. Risk preferences and development revisited. Theory Decis 86, 1–21 (2019). https://doi.org/10.1007/s11238-018-9674-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11238-018-9674-8