Abstract
We investigate the limits of communication and leadership in avoiding coordination failure in minimum effort games. Our environment is challenging, with low benefits of coordination relative to the effort cost. We consider two leader types: cheap-talk leader-communicators who suggest an effort level, and first-mover leaders who lead by example. Both types of leadership have some ability to increase effort in groups with no history, but are insufficient in groups with a history of low effort. Using the strategy method for followers’ responses, we attribute the persistence of coordination failure to the presence of followers who do not follow the leader.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Coordination problems arise in many organizations. There are often complementarities between members’ choices, and these complementarities can lead to multiple stable outcomes. Organizations may be successful in coordinating on a good outcome, or they may become trapped in an inefficient situation even though better outcomes are also potentially stable.
Few coordination problems are as stark as those arising in the minimum effort game (also called weakest-link game), analyzed first in Huyck et al. (1990). In this game, a player’s payoff depends, in addition to the player’s own choice, on the minimum choice in the group.Footnote 1 This game is a coordination game with multiple Pareto-ranked equilibria: any situation where all players make the same effort is a Nash equilibrium, but equilibria with a higher effort level have greater payoffs for all players.
Huyck et al. (1990) find that failure to coordinate on the efficient outcome in the minimum effort game is common in the laboratory. They point out that this coordination failure is due to the effects of strategic uncertainty: players do not choose the efficient action because they cannot be sure that all others will choose it.Footnote 2 These findings have been confirmed by later studies (see Camerer 2003 Chapter 7; Devetag and Ortmann 2007, for an overview). A typical pattern of behavior found in minimum effort game experiments is that initially many subjects choose high levels of effort, but after several rounds the majority choose a low effort.Footnote 3
Coordination failure in a minimum effort game could be prevented if the game is modified from the beginning, possibly avoiding the decline of effort choices to a low level. For example, Blume and Ortmann (2007) find that pre-play communication significantly increases efficiency relative to the baseline treatment with no communication.Footnote 4 Cartwright et al. (2013) let one of the players “lead-by-example” by choosing effort before the other players. This arrangement increases effort in some groups, although not many groups reached the maximum possible effort. Sahin et al. (2015) compare the effects of communication and leading-by-example and find that both modifications lead to an increased group effort in the minimum effort game, and the magnitude of the increase is similar in both cases.Footnote 5
Although the above studies found that coordination failure can be prevented in the minimum effort game by introducing various extensions, how robust is this result? Does it depend on the particular parametrization of the minimum effort game? And what if a group has already played the game and converged to low effort? Can modifying the game restore coordination on a higher effort after a history of being trapped in an inefficient equilibrium? After all, most organizations have existed for a period of time and a mechanism that works with zero-experience groups might not work with groups that already have a history. For example, a device that is successful in a new company might not work in restructuring an old one.
In this paper, we look at a more challenging minimum effort game parametrization, introduced by Brandts and Cooper (2006) in the context of their “turnaround game”. For this environment, which typically leads to coordination failure in the absence of further modifications, we focus on two leadership mechanisms similar to the ones discussed above. One mechanism involves cheap-talk (CT) one-way pre-play communication, where one of the group members acts as a leader by suggesting an effort level; after observing the suggestion, all players choose an effort level simultaneously. The second mechanism entails a first-mover (FM) leader that leads by example. One player chooses an effort level prior to his followers, who observe this choice and then choose their own effort simultaneously. We subject these mechanisms to a stringent test by looking at their ability to restore higher effort after a history of coordination failure, and we compare the results of this test with their ability to prevent coordination failure in groups without history.
Both CT and FM mechanisms are expected to help players to coordinate on a more efficient equilibrium since in both cases the leader’s suggestion or choice may act as a focal point. In addition, in the leading-by-example case, observing the leader’s effort reduces the strategic uncertainty faced by the followers. On the other hand, commiting to a choice is more risky for the leader than making a non-binding suggestion. Which mechanism is more successful overall is not clear a priori. A novel aspect of our experiment is to elicit responses of followers to all possible suggestions or choices by the leader using the strategy method. This allows us to analyze followers’ behavior more systematically by classifying their strategies into types. In this way we can measure how their responsiveness to the leader’s choice in the two mechanisms changes over time. In addition, we are able to conduct a counterfactual analysis of the consequences of alternative choices by the leaders.
Our interest is whether in our tough environment, the leadership mechanisms can prevent or overcome coordination failure (without changing the payoff structure of the game).Footnote 6 In our experiment, leaders are chosen randomly,Footnote 7 and the leader-communicator in our cheap-talk mechanism can only suggest an effort level rather than send a more complicated message.Footnote 8 Our implementations of the leadership mechanisms are thus minimal as they do not require extended messages or (potentially costly) elections to determine the leader. By using a challenging environment (especially after a history of coordination failure) and minimal implementations of the mechanisms, we explore the limits of what these mechanisms can achieve.
After having confirmed that coordination failure happens in our tough environment without a mechanism present, we find, contrary to most of the previous studies, that this history of coordination failure is a powerful attractor, and the leadership mechanisms fail to provide a means to overcome it in the long run. The environment is too challenging for the mechanisms to be effective. Nevertheless, shortly after the introduction of the mechanisms, average effort is higher as some subjects do attempt to make use of the mechanisms. Even without a history of coordination failure, both types of leadership have only a limited ability to prevent it in our environment, with only about 30–40% of the groups having their minimum effort above the lowest level.
Given the relatively poor performance of the mechanisms in terms of escaping from and even preventing coordination failure, what are the reasons for this? Is it due to an ineffective leadership or to the reluctance of other players to follow? We find that followers do follow the leader’s suggestion or choice to some extent (more in the first-mover case than in the cheap-talk one, and more without a history of coordination failure) but there is a sizable minority that always chooses the lowest possible effort. We also find that not all leaders dare to choose a high effort (even after having suggested it); hence, both leaders and followers can be blamed for the poor performance to some degree. Using the data from the strategy method, we find that even if leaders had chosen a higher effort, they would not have increased their payoff. The presence in a group of just one player who is not responsive to the leader’s suggestion or choice makes it impossible to avoid coordination failure, as it is then individually rational for the leader and for any of the followers to choose the lowest possible effort.
The remainder of the paper is organized as follows. Section 2 provides a general background on the minimum effort game and a discussion of possible effects of the leadership mechanisms. Section 3 describes the experimental design and hypotheses. The results of the experiment are discussed in Sects. 4 and 5 concludes.
2 Effects of leadership in the minimum effort game
2.1 The minimum effort game
In the minimum effort game, there are n players. Player i’s strategy is denoted by \(x_{i}\in X_{i}\subseteq \mathbf {R_{+}}\), where \(X_{i}\) is a finite set. Players’ strategies can be interpreted as effort levels. The payoff function of player i is
where a, b, c are exogenous constants with \(b>c>0\).
Any strategy profile in which all players in the group choose the same effort is a Nash equilibrium. A unilateral increase in \(x_{i}\) incurs a cost without changing the minimum. A unilateral decrease in \(x_{i}\) reduces the minimum; the effect of this reduction outweighs the saving on cost since \(b>c\). The multiple Nash equilibria in the game can be Pareto-ranked according to the players’ choice: any equilibrium with a higher choice Pareto-dominates any equilibrium with a lower choice.
Every player choosing the highest possible effort is the payoff-dominant equilibrium and thus it would be selected by Harsanyi and Selten’s (1988) primary selection criterion. However, choosing a high effort is risky because a player may incur a large cost if the group’s minimum effort happens to be low. There is a conflict between the Pareto-efficiency property of everybody choosing the highest possible effort and the insurance value for an individual player of choosing the lowest effort. The lower uncertainty associated with the choice of a lower effort is related to Harsanyi and Selten’s (1988) secondary risk-dominance selection criterion. One generalization of this criterion to n-player potential games (of which the minimum effort game is an example) is maximization of the potential function (Monderer and Shapley 1996; Goeree and Holt 2005). In the minimum effort game, maximization of the potential selects coordination on the highest effort level if \(n<b/c\) and on the lowest effort level if \(n>b/c\).Footnote 9
2.2 Effects of leadership
In a game with multiple equilibria, players’ beliefs about the strategies of the other players are important for equilibrium selection. We will discuss how our two leadership mechanisms, while not altering the payoff function of the game, can affect players’ beliefs and therefore possibly change their behavior allowing coordination on a different equilibrium. In our experiment, we have three types of games based on the payoff function above but differing in the dynamic structure. The baseline game is the simultaneous game, where all players make their choices at the same time. The other two games correspond to our mechanisms. Recall that in the cheap-talk (CT) mechanism, an exogenously chosen leader-communicator sends a message from the set \(X_{i}\) of possible effort levels. This message is interpreted as a suggestion to the players. The message is seen by all players; then all players (the leader and the \(n-1\) followers) choose an effort level simultaneously. In the first-mover (FM) mechanism an exogenously chosen leader makes a choice first. The other \(n-1\) players (followers) observe this choice and then make their choices simultaneously.
Cartwright et al. (2013), who discuss only the game corresponding to our FM game, offer two reasons why leadership may increase the minimum effort in the group. First, the leader’s choice may act as a focal point that facilitates coordination. Second, the leader’s choice reduces the strategic uncertainty faced by the followers, who are now effectively playing a coordination game with \(n-1\) players. Both effects are present in our FM game but only the focality effect is present in our CT game. We discuss the differences between the games below; a more formal analysis can be found in our working paper Dong et al. (2015).
Let L denote the suggestion (in CT) or choice (in FM) by the leader. First, in a given mechanism, suppose players believe that a higher L induces (stochastically) higher choices by the followers. Consider a player that would choose effort level \(\hat{k}\) in the simultaneous game. If this player is selected to be the leader, it cannot be optimal to set L strictly less than \(\hat{k}\). This is because of the focality effect: setting \(L=\hat{k}\) pulls up the effort of players who would have chosen an effort below \(\hat{k}\) (it can also pull down the effort of players who would have chosen an effort above \(\hat{k}\), but only down to \(\hat{k}\) itself). Thus, in FM the leader will choose L (which is the effort choice) not lower than \(\hat{k}\). In CT, the leader is not restricted to choose an effort equal to his/her own suggestion L. In this case the leader would find it optimal to suggest the highest possible L but not necessarily follow it.Footnote 10 The leader’s actual effort in CT still would not be below \(\hat{k}\) because the focality effect of the highest possible L cannot lead to an effort lower than \(\hat{k}\) being optimal. Since the leader does not decrease the effort (compared with the choice in the simultaneous game) and other players either match this choice or increase their effort towards it, in a group as a whole the minimum effort cannot be lower with a leadership mechanism than with simultaneous play.
Second, the focality effect is likely to be stronger in the FM game, where the leader is committed to the announced effort level, than in the CT game, where the leader can still make a different choice. Then the choices made by followers in response to a given L should be at least as high in FM as in CT. Due to greater focality in FM, one could expect that leaders would choose a higher effort in FM than in CT. Despite this intuition, it may be optimal for a leader to choose a higher effort in CT than in FM. Suppose that a high L shifts beliefs towards a medium level of effort by followers, whereas a medium L keeps beliefs low. Then the leader in FM would find it optimal to choose a low level of effort. The leader in CT may find it optimal to send a high L and then choose a medium effort level. Therefore we do not have an unambiguous prediction for the comparison between minimum group efforts in CT and in FM.
3 Experimental procedures and hypotheses
3.1 Experimental design
We use the parametrization of the minimum effort game introduced in Brandts and Cooper (2006). There are four players and five effort levels, \(x_{i}\in \{0,10,20,30,40\}\). Player i ’s payoff is given by
Table 1 shows the corresponding payoff matrix. This payoff matrix with five Pareto-ranked equilibria along the main diagonal was used by Brandts and Cooper (2006, 2007), Hamman et al. (2007) and Brandts et al. (2015). It is an economical way of “inducing” coordination failure by making \(n\gg b/c\) with a relatively small number of players, \(n=4\).Footnote 11
The main part of the experiment consists of two blocks of ten rounds (see Table 2).Footnote 12 In each round, a group of participants play either the baseline game or one of the mechanisms, according to Table 2. The group composition remains fixed for the entire experiment. We divide experimental sessions according to the type of leadership mechanism and according to the timing of the introduction of the mechanism. Both mechanisms involve a randomly selected player (a leader) acting before others at the beginning of each round.Footnote 13 In our CT treatments, the leader suggests a number; after seeing this number all players (including the leader) simultaneously choose their effort level.Footnote 14 In the FM treatments, the leader makes an effort choice before the rest of the group. Having observed the leader’s choice, the other players (the followers) make their effort choice simultaneously.
We consider two scenarios for the timing of the introduction of the mechanisms. In Restore sessions, the mechanism is introduced in the second block, after the group has played the baseline minimum effort game for ten rounds. This simulates an attempt to turn around an existing organization that has (likely) experienced coordination failure. In Prevent sessions, the order of the blocks is reversed: a group starts with a randomly assigned leader for ten rounds and then plays another block of ten rounds without a leader. We also run a control treatment in which the baseline game is played in all rounds.
At the end of each round, subjects are shown the group minimum effort from the current round and the effort levels selected by all subjects. These efforts are sorted from highest to lowest, so they cannot be traced to individual group members. The feedback format is similar to the one used by Brandts and Cooper (2006).
In the mechanisms, we use the strategy method to elicit followers’ decisions. Specifically, we ask followers to enter an effort choice for each possible suggestion (in CT) or effort choice (in FM) of the leader. In this way we are able to collect data on followers’ complete strategies rather than only on the choices in response to the actual suggestion/choice of the leader. With these strategies, we are able to test hypotheses about the followers’ responses to different suggestions/choices of the leader and conduct a counterfactual analysis of group effort for different leader’s choices.Footnote 15 For leaders, we elicited their (point) beliefs about the minimum effort of the followers in response to their actual suggestion or choice; leaders got 20 points if their prediction was correct.
The experimental sessions were conducted in the CeDEx laboratory at the University of Nottingham, UK. The experiment was computerized using z-Tree (Fischbacher 2007) and subjects were recruited with ORSEE (Greiner 2015). Our sample consisted of 252 student participants from various fields of study in 13 sessions with 16–20 participants per session. We ensured the recruited subjects had not participated in a similar experiment (i.e., in a minimum effort game or a public goods game) before. At the beginning of a session, subjects were seated at a computer terminal in a cubicle. An experimenter read the instructions aloud in front of all the participants. Subjects received the relevant instructions only at the beginning of each block. As in Brandts and Cooper (2006) and subsequent papers on the turnaround game, the instructions were framed in a corporate context where the four players in the group are referred to as “employees” and are told that they are working for a “firm”. We used “employee X” and “employee Y” to represent the leader and the follower roles, where applicable. Before the beginning of a block, subjects were required to answer several quiz questions regarding the payoff function and procedure details. At the end of a session, subjects were paid in private the amount they earned. The quiz, 20 rounds of decision-making, and the questionnaire lasted approximately one hour and subjects earned on average £9.63 (equivalent to $14.64 at the time of the experiment).
3.2 Hypotheses
Based on our discussion of possible leadership effects in Sect. 2, we formulate the following hypotheses.Footnote 16 As we argued, the minimum effort in a group cannot be lower with a leader than if the players were choosing simultaneously. Therefore,
Hypothesis 1
The minimum group effort is higher in CT and FM than in Baseline.
The history of the group is likely to affect players’ beliefs. It can be expected that beliefs are more pessimistic if the mechanism is introduced after experiencing a common history of coordination failure. Our Restore sessions are designed to induce coordination failure, thus beliefs are likely to be more pessimistic in Restore. If beliefs are more pessimistic, then the chosen effort is likely to be lower.
Hypothesis 2
The minimum group effort is lower in Restore than in Prevent, holding the treatment (CT or FM) constant.
The previous hypotheses, although formulated on the aggregate level of the group, are based on individual behavior. Our strategy method design is well suited to test hypotheses about the contingent strategies of the followers. We argued in Sect. 2 that followers’ strategies would be more responsive to the leader’s suggestion/choice in FM than in CT. It is also natural to expect the followers to be more responsive in Prevent than in Restore.
Hypothesis 3
For a given suggestion/choice of the leader, the effort choices of the followers are higher in FM than in CT, and they are higher in Prevent than in Restore.
Since a leader has an incentive to suggest the highest possible effort in CT, but not necessarily to choose it in FM (or indeed in CT),
Hypothesis 4
The suggestion of leaders in CT is higher than the choice of leaders in FM.
This hypothesis is based on the assumption that in CT it is not costly for a leader to suggest an effort different from the one he/she intends to choose. In repeated interactions, not following one’s own suggestion would have the cost of reducing the focality effect of it. Even in the one-shot game, leaders may have a disutility from not following their own suggestion (lie aversion, see Ellingsen and Johannesson 2004) or from letting other players down (guilt aversion, Battigalli and Dufwenberg 2007). In all these cases, leaders may decide to suggest the effort they are actually going to choose. Thus, because followers are more likely to follow leaders in FM, some CT leaders may suggest (and choose) a lower effort than they would have done in FM.
Nevertheless, even if we assume that leaders must follow their own suggestion in CT, it cannot be optimal to suggest (and therefore do) less than what a player would have chosen in the simultaneous game. The actual effort choice of the leader in both treatments should be above the choices in Baseline.
Hypothesis 5
The effort choice of leaders in CT and FM is higher than in Baseline.
4 Results
We first present an overview of group outcomes in our treatments. We then look at the individual behavior of the subjects and try to determine what role is played by leaders and followers during the coordination process.
4.1 Group effort and coordination with and without leadership
In the analysis below, first we look at whether the mechanisms were successful in the toughest environment, i.e., after a history of coordination failure in Restore sessions. Then we look at their performance in preventing coordination failure (Prevent sessions). Finally, we discuss how the timing of the introduction of the mechanisms influenced overall payoffs.
4.1.1 Trying to overcome coordination failure
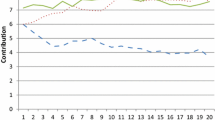
For the Restore sessions, a low effort level is a necessary condition to analyze the effectiveness of leadership in overcoming coordination failure. We consider as coordination failure the situation in which the minimum effort in a group is zero. During the first ten rounds in Control and Restore sessions there is a clear trend towards lower effort levels, as seen in Fig. 1, and the minimum effort is zero in round ten in 32 out of 35 groups.Footnote 17 There is no significant difference between CT, FM and Control treatments in these ten rounds, reflecting the identical setup across those treatments.
The results from the first block in Restore and Control sessions confirm the findings in the previous literature (Brandts and Cooper 2006, 2007; Hamman et al. 2007; Brandts et al. 2015). Coordination failure after ten rounds is not surprising if one realizes how tough the environment is. The cost of not being the minimum-effort player is high compared with the benefits of coordination on the most efficient equilibrium. A player who chooses effort 40 instead of 0 gains 40 if all other players choose 40 as well, but loses 200 if any of the other players chooses 0.
In the analysis below, we focus on the 32 groups in which coordination failure occurred. Starting from round 11, groups in Restore sessions face a mechanism (either CT or FM). One can expect that players would increase their effort in round 11 compared to round 10. Indeed, 48 out of 108 subjects increase their effort in round 11. The average effort level in round 11 is 14.26 in Restore sessions with a history of coordination failure (13.04 in CT and 15.58 in FM). Figure 2 shows the distribution of choices in round 11 and the average payoff obtained for each choice in these groups.
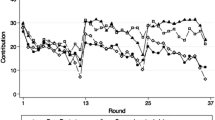
With a leadership mechanism, group average efforts are significantly higher in round 11 than in round 10 (p value of the two-sided Wilcoxon matched pairs sign-rank test <0.001). Group minimum efforts increase only slightly though, and the right panel in Fig. 2 shows that players choosing lower efforts had higher payoffs. Thus, it is not surprising that this increase in average effort is short-lived: Fig. 3 shows a clear decrease in effort during the second block. All groups that were trapped in coordination failure in round 10 also experience itin round 20 (the three groups that coordinated on a non-zero effort level in the first ten rounds continued to coordinate on the same level for the rest of the experiment). As can be seen from the figure, there are no clear differences between CT and FM treatments and statistical tests confirm this (in round-by-round comparisons of group average or minimum efforts, p values of the two-sided Wilcoxon–Mann–Whitney rank-sum tests are >0.1 for all rounds except for average effort in round 15 where \(p=0.028\)).
The increase in effort in round 11 may come partly from a restart effect, as often happens in similar experiments (Brandts and Cooper 2006; Hamman et al. 2007; Le Lec et al. 2014). There is a visible restart effect in Control treatment in Fig. 3 but it is much smaller than in CT and FM treatments; thus, the increase in effort after the mechanism is introduced appears to go beyond the restart effect. Although non-parametric tests are not powerful enough to detect this difference, regressing individual efforts in round 11 on the dummy that takes value 1 if a mechanism is present find that the coefficient on the dummy variable is positive and statistically significant (\(p=0.033\) in an ordered probit regression with standard errors clustered on the group level, controlling for individual effort in round 1).
Result 1
After a history of coordination failure, the mechanisms increase individual effort in the short run but not in the long run. They do not have a significant effect on group minimum effort.
We conclude that the strong form of hypothesis 1 (that mechanisms strictly increase minimum effort) is not confirmed after a history of coordination failure. Could our mechanisms have prevented coordination failure if they were available from the start? The next subsection looks at this question.
4.1.2 Preventing coordination failure
We saw in the previous subsection that neither of the leadership mechanisms was successful in overcoming coordination failure. In our Prevent sessions, one of the mechanisms is present from round 1, thus the first block in those sessions allows the analysis of the effectiveness of communication and leading-by-example in avoiding coordination failure.
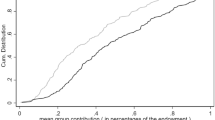
The left panel of Fig. 4 displays the distribution of choices in the first round of the simultaneous game (our Control and Restore sessions). Similarly, the left panels of Fig. 5 do the same separately for CT and FM mechanisms in our Prevent sessions and for leaders and followers. As can be seen in the figures, choices in round 1 are quite variable. The average effort in the first round in Control and Restore sessions is 20.14. The average effort of the leaders in round 1 is 21.43 in both CT and FM Prevent treatments; the average effort of the followers is 25.24 in the CT treatment and 19.76 in the FM treatment. The distribution of leaders’ efforts, pooled over CT and FM treatments, does not differ significantly from the distribution of first-round choices in Control and Restore treatments (p value of the one-sided rank-sum test is 0.363). Thus, the mechanisms do not per se lead to higher efforts in round 1. However, since followers’ efforts are correlated with their group leader’s effort, the average minimum effort across groups is higher in Prevent sessions than in Control and Restore sessions (10.71 in Prevent vs 5.14 in Control and Restore). As we see below, this has a significant effect for the evolution of play in subsequent rounds.
The right panel of Fig. 4 shows that in round 1 of Control and Restore sessions players who chose lower efforts got on average a higher payoff. From the right panels of Fig. 5, in round 1 of Prevent sessions average payoffs still tend to decline with effort but sometimes a higher effort leads to a higher payoff. The possibility of getting a higher payoff by choosing a higher effort arises because of the correlation of the choices of the followers.
Note that the average effort of the followers in round 1 is higher in CT than in FM, while the average effort of the leaders is the same in both treatments. Recall that in CT treatments leaders could choose an effort different from the number they suggested; in fact, the average suggestion in CT in round 1 (which was 30.00) was higher than the average effort by the leaders (21.43). Since followers mostly matched the suggestion, this resulted in a higher average effort by followers in CT. The “deceptive” behavior of leaders is, of course, likely to lead to a decrease of effort in the future in their group.
The evolution of average and minimum group efforts over the first 10 rounds in Prevent sessions, separately for CT and FM treatments, can be seen in Fig. 6. There is no significant difference between the mechanisms (minimum p value of the two-sided rank-sum tests on average or minimum group effort is 0.180 in round-by-round comparisons). As in Restore sessions, average effort declines over time, although average minimum effort increases in some rounds. By round 10, there are 9 out of 28 groups with a positive minimum group effort in our Prevent sessions (4 out of 14 groups in CT and 5 out of 14 in FM). Although this proportion of groups with non-zero effort is not very high, recall that only 3 out of 35 groups in Control and Restore sessions had a positive minimum effort in round 10. Comparing pooled CT and FM data for rounds 1 to 10 with the simultaneous game, there is a significant difference in average group effort in each round after round 4 (all p values for the one-sided rank-sum tests <0.05). The average minimum effort in Prevent sessions is stable around 10 and is significantly higher than in Control and Restore sessions for each round after round 2 (for all these rounds \(p<0.05\)). As Cartwright et al. (2013) and Sahin et al. (2015) found in more favorable parameterizations of the minimum effort game, we also observe that CT and FM mechanisms have some ability to raise average and minimum effort.
Do the effects of the mechanisms persist after the mechanism is removed? One can expect that because of an equilibrium lock-in, most subjects would choose the same effort in round 11 as in round 10. Nevertheless, some subjects may increase their effort due to the restart effect mentioned earlier; other subjects may reduce their effort due to beliefs being affected by the removal of the mechanism. In our experiment, more subjects increased their effort than reduced it; the overall effect was that the average effort increased from round 10 to round 11 but the average group minimum effort went down. Of the 9 groups that achieved a non-zero minimum effort in round 10, only 6 groups still have a positive minimum effort in round 11. Thus the removal of the correlation device (leader’s suggestion/choice) has an immediate effect on the ability to avoid zero minimum effort in some groups. By round 20, only 5 groups still maintain a minimum effort above zero. Efforts in rounds 12–20 of Prevent sessions are not significantly different from those of rounds 2–10 in Control and Restore (i.e., comparing round 2 in Restore with round 12 in Prevent etc.; the smallest p value of two-sided rank-sum tests is 0.136).
Result 2
The leadership mechanisms have some ability to prevent coordination failure but there is no lasting effect after the mechanisms are removed.
4.1.3 Timing of the mechanisms and welfare
The rules of the second block of the Restore sessions are the same as those of the first block of the Prevent sessions; the only difference is the history of coordination failure in Restore sessions (although not all groups experienced it). Pooling the two mechanisms (CT and FM) together, both average and minimum effort levels are noticeably higher in the first block of Prevent sessions compared with the second block of Restore sessions, as Fig. 7 shows. Non-parametric tests confirm that both average and minimum efforts are significantly higher in the first block of Prevent sessions compared with the second block of Restore sessions (i.e. comparing round 2 in Prevent with round 12 in Restore etc.) after round 2 (p values of the one-sided rank-sum round-by-round tests are <0.05). This confirms our hypothesis 2.
Result 3
The leadership mechanisms are more effective if introduced early.
For the comparison between rounds 1 in Prevent and 11 in Restore, the difference in group average and minimum efforts is less noticeable in Fig. 7, and non-parametric tests are only marginally significant for the minimum group effort (\(p=0.055\) for the one-sided test). The analysis of individual strategies presented in the next section will help us understand the dynamics that make this difference significant in later rounds.
As discussed in the previous subsections, the mechanisms have a positive effect on individual effort. However, since the average minimum effort remains relatively flat in each treatment, within a treatment a higher average effort means that there is more mis-coordination. Because of the high cost of mis-coordination in our environment, a higher average effort resulted in a lower average payoff. This can be seen in Fig. 7, which, along with the average and minimum effort levels, shows the average payoff (on a different scale) in each treatment over time.
Across treatments, the group payoffs, averaged over all twenty rounds, are not significantly different between Prevent and Restore sessions (p value of the two-sided rank-sum test is 0.797). These payoffs, pooled over Prevent and Restore sessions, also do not differ significantly from those of groups in the Control session (in Control, groups had an average payoff 182.9 across all rounds; in the other groups the average payoff was 191.2). Thus the mechanisms have no significant effect on group average payoffs. Note also that the average payoffs are below 200, the payoff that any player could guarantee by choosing effort 0; in fact, the difference of average payoff from 200 is significant (p value of the two-sided sign-rank test based on all 63 groups is <0.001).
4.2 Individual behavior
One innovative aspect of our design is the use of the strategy method to elicit followers’ contingent strategies. Followers were asked to state an effort level for each possible choice (suggestion in CT treatment and actual effort in FM treatment) of the leader. In this section we analyze the strategies of the followers, the choices of the leaders, and perform a counterfactual analysis to address the question of whether the responsibility for coordination failure lies with the leader or with the followers.
4.2.1 Followers’ strategies
Figure 8 shows the followers’ strategies in each of the mechanisms for each round of the leader-follower block (rounds 1–10 in Prevent and rounds 11–20 in Restore). Each bar represents the frequency of a certain choice by the followers in a certain round, given the leaders’ suggestion or choice. For example, the leftmost bar in the bottom-left corner of panel (a) of the figure indicates that about 30% of the followers would choose 0 effort in round 11 (round 1 of the leader-follower setup in Restore) if the leader suggested 40; the rightmost bar in the same corner shows that about 75% of the followers would choose 0 effort in round 20 if the leader suggested 40.
As can be seen in the figure, the most common strategies were either to match the leader’s suggestion or choice (the bars on the diagonal of each panel) or to choose zero effort irrespective of the leader’s suggestion or choice (the bars in the left column of each panel).Footnote 18 We define the Match+ strategy as a strategy in which a follower chooses at leastFootnote 19 L for all effort levels L that the leader might suggest or choose. Always-zero (All0) is a strategy where a follower chooses zero regardless of what the leader might suggest or choose.
Figure 9 condenses the information in Fig. 8 to show the evolution of these two strategies. Initially, Match+ is more frequent than All0. However, in all treatments, the play of the All0 strategy increases over time. The play of the Match+ strategy generally decreases over time except in the FM-Prevent treatment where it stays roughly constant. The reason behind this change in the use of the All0 and Match+ strategies is that the Match+ strategy is effective only if all three followers adopt it (if at least one other follower uses the All0 strategy and the leader suggests or chooses a non-zero effort level, the Match+ strategy hurts the follower who uses it).
From our discussion in Sect. 2, followers are expected to shift their effort towards the leader’s suggestion/choice, compared with the distribution of choices in the simultaneous game, and more so in FM than in CT. For any given suggestion/choice of the leader, we find no significant difference in followers’ choices between CT and FM in round 1 of Prevent sessions, but the pooled distribution of follower’s choices in CT and FM is significantly higher than the distribution of choices in the simultaneous game.Footnote 20 Similarly, for Restore sessions, in groups with coordination failure in round 10, there is no significant difference between CT and FM followers’ choices in round 11, but these (pooled) choices are significantly higher than the choices in round 11 of the Control session. Thus the followers’ strategies are consistent with the mechanisms having a focality effect in the first round.
Followers are also expected to be more responsive to the leader’s suggestion/choice in Prevent sessions compared with Restore sessions. In order to include this comparison, since the choices of the followers in a group are not independent after round 1, we take, for a given suggestion/choice of the leader, the average choice of the followers in the same group over all ten rounds as a measure of responsiveness of the followers in this group. This gives us, for each treatment (CT-Restore, CT-Prevent, FM-Restore, FM-Prevent), as many independent observations as there are groups in the treatment. With this measure, for each possible suggestion/choice of the leader, we are able to reject the hypothesis that there are no differences between the four treatments (maximum p value of the Kruskal–Wallis tests is 0.022). When we pool CT and FM treatments and compare Restore with Prevent sessions, we find a significantly higher responsiveness in Prevent sessions (the largest p value of the one-sided tests is 0.006). When we pool Restore and Prevent sessions and compare CT with FM, the responsiveness in FM is also significantly higher than in CT (the largest p value of the one-sided tests is 0.038). Thus we find support for our hypothesis 3.
Table 3 reports the results of mixed-effects multi-level (levels being group and individual) regressions of followers’ choices on treatment dummies, separately for period 1 in Prevent (and period 11 in Restore), and for all other periods. In the regressions we also include the leader’s (hypothetical) suggestion/choice, the history of the group represented by the minimum effort in the previous round, and a time trend.
The leader’s suggestion/choice variable is highly significant, as expected, and the coefficients in the linear regressions show that, for a unit increase in leader’s effort, followers increase their effort on average only by 0.58 in round 1 and by 0.39 in rounds 2–10, confirming that they do not match the leader’s suggestion/choice perfectly. The regressions also confirm that there are significant differences between CT-Restore and CT-Prevent in round 1 (round 11 in Restore). In the other rounds there is a significant difference between CT-Restore and CT-Prevent, and CT-Prevent and FM-Prevent treatments, again confirming that in Restore sessions followers’ choices are lower than in Prevent sessions, as well as that in CT treatment choices are lower than in FM treatment. In addition to the leader’s suggestion/choice and treatment dummies, group history is important, and there is also a significant downward trend not explained by the other variables.
Result 4
On average, followers match a leader’s increase in effort only partially. For a given suggestion/choice of the leader, the effort choices of the followers are higher in FM than in CT, and they are higher in Prevent than in Restore.
The regressions reported in Table 3 find little difference between FM-Restore and FM-Prevent treatments in rounds 1 and 11, and indeed from Fig. 9 the proportion of Match+ strategy in FM-Restore in round 11 is actually higher than in FM-Prevent in round 1. How did the significant difference between FM-Restore and FM-Prevent nevertheless developed? To understand this, we introduce a variable measuring the number of other subjects in the group whose effort was observed to be 0. This variable can take values between 0 (if the leader chose a positive effort and the other followers made a positive effort in response to this) and 3 (if all three others, including the leader, chose 0 effort). The idea is that subjects may become discouraged from choosing positive effort, and thus start playing the All0 strategy, if they see that many in their group chose zero effort.
Table 4 presents the results of mixed-effects multi-level probit regressions for the FM treatment in which the dependent variables are the indicator variables whether a strategy employed by a follower was All0 or Match+. For rounds 1 and 11, the Restore/Prevent dummy by itself does not have explanatory power. The variable measuring the observed number of zero effort choices of others is statistically significant explanation of the probability of choosing strategies All0 (positively) and Match+ (negatively), when also controlling for the choice of these strategies in the previous period, both in rounds 2 and 12 only, and for all rounds between 2–10 and 12–20.
As we will see in the next subsection, leaders’ choices of effort were not significantly different between FM-Restore and FM-Prevent in rounds 1 and 11. The regressions thus show that the small initial difference in the frequency of All0 strategy, and thus in observing how many others in the group chose zero effort, is amplified over time leading to the differences between FM-Restore and FM-Prevent observed in later rounds.
4.2.2 Leaders’ choices
In our FM treatment, leaders simply choose effort; in CT treatment leaders also suggest a number that is seen by their followers but they could choose an effort different from the suggested number. In all treatments, leaders also state their beliefs about what they expect the minimum effort of the followers to be. Figure 10 shows average leaders’ effort choices, suggestions and beliefs in each round, together with the average group minimum effort in the round.
Recall that from our discussion in Sect. 2 we could not make an unambiguous prediction about whether leaders would choose a higher effort in CT or in FM. The two-sided rank-sum tests on leader’s effort choices find no differences between CT and FM treatments, either in round 1 of Prevent, round 11 of Restore, or averaging each leader’s choices over all ten rounds of a mechanism. Pooling CT and FM together and comparing the averages of leaders’ effort choices in the ten rounds of the mechanisms, we find that leaders in Prevent choose a significantly higher effort than in Restore (p value of the one-sided rank-sum test is 0.042).
According to hypothesis 5, we expect leaders’ effort to be higher than the effort of players in the simultaneous game. Although leaders’ efforts in round 1 of Prevent sessions are not significantly above those in round 1 of the simultaneous game (Restore and Control sessions), the one-sided rank-sum test on the average efforts over ten rounds (averaging all players in a group in the simultaneous game) finds that efforts by leaders are marginally significantly higher (p value is 0.075). In Restore sessions, leaders’ effort in round 11 in groups with a history of coordination failure is significantly higher than efforts in the simultaneous game in the Control treatment (p value of the one-sided rank-sum test is 0.014). This provides some evidence in support of the hypothesis.
Figure 10 shows that, while beliefs, actions and minimum effort become very close in all treatments after a few rounds, average suggestions in CT treatments are higher than average actions for almost all rounds, especially in Prevent sessions. While a majority of leader-communicators’ decisions coincide with the suggestion, a sizable minority of effort choices by a leader when the suggestion was not zero is below the suggested number (around 44% in both Restore and Prevent). In Prevent sessions, the suggestions of leaders in CT are significantly higher than the choices of leaders in FM (p values of the one-sided rank-sum tests are 0.066 for round 1 and 0.022 for averages over rounds 1–10); in Restore sessions, there is no significant difference. Interestingly, the average actual effort of leaders in CT-Prevent is lower than that of the followers (14.79 vs 16.76), implying that the leaders followed their own suggestion (on average 22.64) even less than their followers did, though this difference in effort is not significant.
To get more insight into leaders’ decisions, we use regression analysis. Unlike followers, leaders did not have a suggestion or choice of another player to base their decisions on; the amount of information they have available is similar to that of players in the simultaneous game. We therefore combine leaders’ effort choices with those of players that did not experience a leadership mechanism (rounds 1–10 in Restore and Control sessions and rounds 11–20 in Control session in our experiment). In the first two columns of Table 5 we report the results of mixed-effects multi-level linear regressions of effort choices on treatment dummies, group history and a time trend.Footnote 21
The regressions confirm that there is little difference in leaders’ efforts across treatments; they also do not find a significant difference in efforts between the first ten rounds of the simultaneous game and the leaders’ efforts in Prevent. The signs of the coefficients show that leaders’ efforts were not below the choices in the simultaneous games. The only significant difference is that the efforts in the second ten rounds of the simultaneous game are lower than the efforts of the leaders. The history of the group, summarized by the minimum effort in the previous round, plays a role in the effort choice of the leader, and there is a downward trend.
The last two columns in Table 5 regress leaders’ suggestions (in CT) or effort choices (in FM) on treatment dummies and the other variables. Although in rounds 1 and 11 the difference is only marginally significant, over all ten rounds of the mechanisms the suggestions of the leaders in CT-Prevent are found to be significantly higher than the leaders’ efforts in FM-Prevent, while there is little difference for the other treatments. Since the efforts of the leaders are not significantly different across treatments, this confirms the previous evidence that in CT leaders often put a higher suggestion than the effort they choose.Footnote 22
Result 5
Efforts of leaders are similar in the two leadership mechanisms, and only marginally higher than the efforts of players in the simultaneous game. In CT-Prevent treatment, leaders, similarly to their followers, do not follow their own suggestion to the full extent.
4.2.3 Coordination failure: leader’s or followers’ responsibility?
Knowing followers’ strategies, we can see if it would have been possible for leaders to achieve a higher group effort by unilaterally changing their choice. We find that if the leader had chosen a different effort level (and corresponding suggestion in CT), the minimum effort in 22 out of 58 groups would have increased in the first round of the leader-follower setup (i.e. round 11 in Restore sessions and round 1 in Prevent sessions). There are, however, also many cases where the leader’s effort is higher than the minimum effort of the followers (29 out of 58 groups).Footnote 23
Given the distribution of the followers’ choices, we ask what the expected payoff for leaders would be from choosing various effort levels (in FM) or suggesting various numbers and following them (in CT). The leader’s expected payoff is calculated as follows: using followers’ choices collected by the strategy method, we determine the distribution of the minimum effort of three randomly selected followers for each possible choice of the leader, and use this distribution to find the leader’s expected payoff for each choice. We also do this for the followers, calculating expected payoffs a follower would get from following various possible choices or suggestions of the leader. For this, we take into account the probability distribution for the choices of the other two followers in the group, randomly chosen from the observed population of followers. Figure 11 shows the leader’s and a follower’s expected payoffs calculated in this way.
The two left panels in the figure are for the leaders. Even though there are some treatment differences, zero effort is the optimal choice in all treatments. The two right panels are for the followers. The payoffs of followers are calculated for cases in which the leader would choose (in FM) or suggest and choose (in CT) the given effort level and the follower would follow that leader’s choice. For all effort levels higher than 0, the expected payoffs are lower than the payoff 200 that a player could guarantee by always choosing 0. What the figure thus shows is that fully following the leader’s suggestion/choice is not optimal even for a risk-neutral follower (and even if CT leaders always followed their own suggestion).Footnote 24 The uncertainty arising from the decisions of only two (rather than three as for the leader) other followers in a group is still sufficiently high, so that the expected payoff of a follower is lower than 200. The payoffs in Fig. 11 are based on the first round of the leader-follower setup. Given that the strategies of the followers become less responsive over time, in subsequent rounds effort 0 remains the optimal choice.
Result 6
Given the population distribution of followers’ choices, neither the leader nor a follower would individually be better off in expected terms in the first round of the mechanisms by choosing an effort other than 0.
The main blame for this observation lies with followers: the proportion of them playing the All0 strategy is too high for any positive effort to be profitable. Leaders are also partially to blame though: their persistent failure to follow their own suggestion in CT may be a reason why not all followers follow the leader’s suggestion, and in many groups a different leader’s choice could have increased the minimum effort. Overall, it is a collective failure: players could not unilaterally have increased their expected payoff by choosing a higher effort, thus it was individually rational to choose the safe option of zero effort.
5 Conclusion
We analyzed the effects of two leadership mechanisms (pre-play communication and leading-by-example) in a tough parametrization of the minimum effort game, both with and without history of coordination failure. Unlike most of the literature (e.g., Blume and Ortmann 2007; Cartwright et al. 2013; Sahin et al. 2015, in different environments), we found that in this challenging setting the mechanisms failed to overcome coordination failure and had only limited effectiveness in preventing it. The mechanisms had some effect in the short run as some players attempted to choose a higher effort but in the long run most players fell back to the lowest possible effort. These results therefore delineate the limits of the mechanisms for preventing and overcoming coordination failure. Our mechanisms involve a rather minimal implementation: our leaders are randomly chosen and communication consists of a single number (interpreted as a suggestion of effort); thus it appears necessary to have more complicated mechanisms to enable players to avoid coordination failure in this game.
In both leadership mechanisms, a substantial proportion of followers chose the effort level corresponding to the leader’s suggestion or choice. However, in each treatment, there was a considerable number of followers who, instead of following the leader, always chose zero effort, irrespective of the suggestion or choice of the leader. Since the outcome depends on the minimum effort in the group, the presence of even one such player often led to the group effort falling back to the lowest level in the long run. Given the non-negligible proportion of such players, the expected payoff of both leaders and followers would be maximized by choosing zero effort. Thus the mechanisms’ failure can be attributed to a large extent to non-responsive followers in our environment.
Notwithstanding the non-responsiveness of some players, the data from the strategy method show that followers followed the leader more in the first-mover treatment than in the cheap-talk treatment. Moving first seems to bestow a greater legitimacy on a leader than simply making a suggestion; indeed, even the leaders themselves did not always follow their own suggestion. However, committing to a high effort is risky in our game and the efforts of first-mover leaders were lower than the suggestions of cheap-talk leaders. The signals sent by leaders were different in the two mechanisms, and followers reacted to them differently, but the combination of leaders’ suggestions or choices and followers’ reaction to them led on aggregate to similar results in both mechanisms.
Notes
Examples of such situations include the classical stag-hunt game (Rousseau 1755), and, more modernly, writing joint reports with several sections where completion of the report requires all sections to be completed (Weber et al. 2001) and airline departures, where for a plane to be able to depart several separate tasks must be completed (Knez and Simester 2001).
Huyck et al. (1990) distinguish two possibilities for players failing to coordinate on the efficient equilibrium: playing a Pareto-dominated equilibrium instead or not playing an equilibrium at all. They use the term coordination failure to refer to the first situation.
The prevalence of coordination failure is higher if the benefits from coordinating on a higher effort are low relative to the cost of effort; coordination failure is also more likely with more players (Devetag and Ortmann 2007).
There are several studies on the use of financial incentives, possibly together with communication, to overcome coordination failure (Brandts and Cooper 2006, 2007; Hamman et al. 2007; Brandts et al. 2015). Increasing the benefits of coordination is found to improve efficiency, albeit to a lesser degree than communication. Efficiency is also found to increase once post-play monetary punishment is introduced (Le Lec et al. 2014).
Free-form communication by a leader is found to shift group effort upward in Brandts et al. (2015).
If we interpret the suggestion as a statement of the leader’s intention to play, the highest possible L is not self-signaling, since the leader has an incentive to shift the followers’ beliefs upwards for other intended effort choices as well (a message is self-signaling if the sender wants to send it if and only if it is true, see Farrell and Rabin 1996).
Note that the game has a particularly low ratio of benefits b from coordinating on a higher effort to cost c of effort.
In Restore sessions, there was a third block consisting of ten more rounds of the baseline setup. Since the participants were not informed about how many blocks there would be in the experiment and the instructions for the next block were given only at the beginning of each block, there should be no effect on the first two blocks in the sessions.
Once selected, the identity of the leader remains fixed for the entire block of 10 rounds. Leaders are also fixed for the entire block in Brandts and Cooper (2007), Sahin et al. (2015) and Brandts et al. (2015). Pogrebna et al. (2011) and Cartwright et al. (2013) select a leader separately for each round.
In the instructions, we specified that for the leader “the choice ... is the one used to calculate the points, and it could be different from the suggested number”.
Experimental results with the strategy method usually do not differ much from results with the direct response method (see Brandts and Charness 2011, and Fischbacher et al. 2012). We ran two sessions (CT-Restore and FM-Prevent) using the direct response method and confirmed that results are not significantly different.
In the experiment, we have repeated interactions rather than a one-shot game. There is no obvious reason why the focality effects of leadership would not apply with repeated interactions. Also, subjects may have preferences different from the risk-neutral own-payoff-oriented preferences assumed in the discussion. However, risk aversion is expected to exacerbate the difference in focality between CT and FM due to the reduced strategic uncertainty. Reciprocity motives would also tend to favor focality in FM.
14 out of 15 groups in CT, 13 out of 15 in FM, and all 5 groups in Control.
Note that followers do not choose zero more often after a higher suggestion/choice of the leader and their non-zero choices match the leader’s choice. Thus their efforts are (stochastically) higher after a higher suggestion/choice by the leader, as conjectured in Sect. 2.
Choosing an effort above what the leader chooses or suggests might seem irrational but may be done either in expectation that the leader will actually choose a high rather than a low effort (thus what the follower chooses for a low effort of the leader is irrelevant), or in order to “teach” the leader the virtue of choosing a high effort.
If the leader’s suggestion/choice is 40, the distributions can be directly compared. For other suggestions/choices (for example, \(L=30\)), we look only at the distribution of choices in the simultaneous game that do not exceed L.
An ordered probit specification produces similar significance results.
Pogrebna et al. (2011) find a similar result in a voluntary contribution game setting. Actual contributions of cheap-talk leaders and first movers are similar, but announcements by cheap-talk leaders are significantly above their actual contribution.
Note that a low minimum group effort could be both leader’s and followers’ fault. For example, suppose that the minimum of the followers’ effort is zero except in the case in which the leader chooses 40. If the leader chooses 20, the group minimum is zero while at the same time the leader could have chosen 40 and the whole group would coordinate on the efficient effort of 40.
We also calculated expected payoffs of leaders in CT from choosing efforts different from the suggested one and of followers (in all treatments) from partially following the leader (e.g. choosing 10 after the leader suggests/chooses 30). All expected payoffs were below 200.
References
Battigalli, P., & Dufwenberg, M. (2007). Guilt in games. American Economic Review, 97, 170–176.
Blume, A., & Ortmann, A. (2007). The effects of costless pre-play communication: Experimental evidence from games with Pareto-ranked equilibria. Journal of Economic Theory, 132, 274–290.
Brandts, J., & Charness, G. (2011). The strategy versus the direct-response method: A first survey of experimental comparisons. Experimental Economics, 14, 375–398.
Brandts, J., & Cooper, D. J. (2006). A change would do you good.. An experimental study on how to overcome coordination failure in organizations. American Economic Review, 96, 669–693.
Brandts, J., & Cooper, D. J. (2007). It’s what you say, not what you pay: An experimental study of manager-employee relationships in overcoming coordination failure. Journal of the European Economic Association, 5, 1223–1268.
Brandts, J., Cooper, D. J., & Weber, R. A. (2015). Legitimacy, communication, and leadership in the turnaround game. Management Science, 61, 2627–2645.
Camerer, C. F. (2003). Behavioral Game Theory: Experiments in Strategic Interaction. Princeton: Princeton University Press.
Cartwright, E., Gillet, J., & van Vugt, M. (2013). Leadership by example in the weak-link game. Economic Inquiry, 51, 2028–2043.
Chaudhuri, A., Schotter, A., & Sopher, B. (2009). Talking ourselves to efficiency: Coordination in inter-generational minimum effort games with private, almost common and common knowledge of advice. Economic Journal, 119, 91–122.
Chen, R., & Chen, Y. (2011). The potential of social identity for equilibrium selection. American Economic Review, 101, 2562–2589.
Devetag, G., & Ortmann, A. (2007). When and why? A critical survey on coordination failure in the laboratory. Experimental Economics, 10, 331–344.
Dong, L., Montero, M., & Possajennikov, A. (2015). Communication, leadership and coordination failure. Available at SSRN. doi:10.2139/ssrn.2655861.
Dugar, S. (2010). Nonmonetary sanctions and rewards in an experimental coordination game. Journal of Economic Behavior and Organization, 73, 377–386.
Ellingsen, T., & Johannesson, M. (2004). Promises, threats and fairness. Economic Journal, 114, 397–420.
Farrell, J., & Rabin, M. (1996). Cheap talk. Journal of Economic Perspectives, 10, 103–118.
Fischbacher, U. (2007). z-Tree: Zurich toolbox for ready-made economic experiments. Experimental Economics, 10, 171–178.
Fischbacher, U., Gächter, S., & Quercia, S. (2012). The behavioral validity of the strategy method in public good experiments. Journal of Economic Psychology, 33, 897–913.
Goeree, J. K., & Holt, C. A. (2005). An experimental study of costly coordination. Games and Economic Behavior, 51, 349–364.
Greiner, B. (2015). Subject pool recruitment procedures: organizing experiments with ORSEE. Journal of the Economic Science Association, 1, 114–125.
Hamman, J., Rick, S., & Weber, R. A. (2007). Solving coordination failure with all-or-none group-level incentives. Experimental Economics, 10, 285–303.
Harsanyi, J. C., & Selten, R. (1988). A General Theory of Equilibrium Selection in Games. Cambridge: MIT Press.
Knez, M., & Simester, D. (2001). Firm-wide incentives and mutual monitoring at Continental Airlines. Journal of Labor Economics, 19, 743–772.
Kriss, P. H., Blume, A., & Weber, R. A. (2016). Coordination with decentralized costly communication. Journal of Economic Behavior and Organization, 130, 225–241.
Le Lec, F., Rydval, O., & Matthey, A. (2014). Efficiency and punishment in a coordination game: Voluntary sanctions in the minimum effort game. CERGE-EI working paper 526.
Manzini, P., Sadrieh, A., & Vriend, N. J. (2009). On smiles, winks and handshakes as coordination devices. Economic Journal, 119, 826–854.
Monderer, D., & Shapley, L. S. (1996). Potential games. Games and Economic Behavior, 14, 124–143.
Pogrebna, G., Krantz, D. H., Schade, C., & Keser, C. (2011). Words versus actions as a means to influence cooperation in social dilemma situations. Theory and Decision, 71, 473–502.
Préget, R., Nguyen-Van, P., & Willinger, M. (2016). Who are the voluntary leaders? Experimental evidence from a sequential contribution game. Theory and Decision, 81, 581–599.
Rousseau, J.-J. (1755). Discours sur l’ origine et les fondemens de l’ inégalité parmi les hommes. Marc-Michel Rey, Holland. English translation: A Discourse upon the Origin and Foundation of the Inequality among Mankind. Dodsley, London, 1761.
Sahin, S. G., Eckel, C., & Komai, M. (2015). An experimental study of leadership institutions in collective action games. Journal of the Economic Science Association, 1, 100–113.
Van Huyck, J. B., Battalio, R. C., & Beil, R. O. (1990). Tacit coordination games, strategic uncertainty, and coordination failure. American Economic Review, 80, 234–248.
Weber, R., Camerer, C., Rottenstreich, Y., & Knez, M. (2001). The illusion of leadership: Misattribution of cause in coordination games. Organization Science, 12, 582–598.
Author information
Authors and Affiliations
Corresponding author
Additional information
The authors would like to thank the Centre for Decision Research and Experimental Economics (CeDEx) at the University of Nottingham for financial support.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Dong, L., Montero, M. & Possajennikov, A. Communication, leadership and coordination failure. Theory Decis 84, 557–584 (2018). https://doi.org/10.1007/s11238-017-9617-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11238-017-9617-9