Abstract
Maximum-likelihood updating (MLU) is a well-known approach for extending static ambiguity sensitive preferences to dynamic set-ups. This paper develops an example in which MLU induces an ambiguity averse maxmin expected utility (MEU) decision-maker to (1) prefer a bet on an ambiguous over a risky urn and (2) be more willing to bet on the ambiguous urn compared to an (ambiguity neutral) subjective expected utility (SEU) decision-maker. This is challenging, since prior to observing (symmetric) draws from the urns, the MEU decision-maker (in line with the usual notion of ambiguity aversion) actually preferred the risky over the ambiguous bet and was less willing to bet on the ambiguous urn than the SEU decision-maker. The identified switch in betting preferences is not due to a violation of dynamic consistency or consequentialism. Rather, it results from MLU’s selection of extreme priors, causing a violation of the stability of set inclusion over the course of the updating process.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The best-known and dominant approach for decision-making under uncertainty is subjective expected utility (SEU, Savage 1954), relying on (the formation of) a unique probability distribution. Based on descriptive (Ellsberg 1961; Camerer and Weber 1992) and normative considerations (Gilboa et al. 2008; Gilboa 2009), there have been attempts to find alternative decision rules reflecting sensitivity to ambiguity, i.e., decision set-ups in which probabilities are not known. Typical approaches are based on non-additive probabilities, also known as “capacities” (Schmeidler 1989; Eichberger and Kelsey 1999; Chateauneuf et al. 2007), and multiple priors (Gilboa and Schmeidler 1989; Ghirardato et al. 2004; Klibanoff et al. 2005; Maccheroni et al. 2006).
Dynamic extensions of these static ambiguity sensitive preferences are needed, since “almost all potential applications of interest in economics involve some dynamic element. Furthermore, static expected-utility theory comes equipped with a natural, essentially “built-in” theory of updating and dynamic choice; it is quite natural to ask whether existing theories of ambiguity also allow a similarly convenient and effective analysis of dynamic behaviour” (Siniscalchi 2009). The natural updating theory of SEU preferences Siniscalchi (2009) refers to is Savage’s axiom P2, best-known as the “sure thing principle”. This axiom is the basis of Bayesian updating and the obvious way to define conditional preferences given an event E. Models with ambiguity sensitive preferences, however, drop P2, thus precluding this canonical extension to dynamic environments.
Two competing approaches for updating ambiguity sensitive preferences have been suggested (cf. Machina and Siniscalchi 2014). The first is full Bayesian updating with a simple interpretation for multiple prior models: all priors in the relevant set are updated prior-by-prior according to Bayes rule. Full Bayesian updating, going back to contributions by Fagin and Halpern (1991) and Jaffray (1992), was axiomatized for general capacities by Eichberger et al. (2007) and for maxmin preferences by Pires (2002) and Epstein and Schneider (2003). The second updating approach corresponds to the Dempster–Shafer rule for capacities (Dempster 1967; Shafer 1976) and takes, for multiple prior models, the form of maximum-likelihood updating (MLU) (Gilboa and Schmeidler 1993): Bayesian updating is applied only to those priors with maximal likelihood given the observed event.
This paper contributes to the debate about these update rules. Its main contribution is to design and analyse a simple example to demonstrate that MLU suffers from unintuitive characteristics. The example revolves around two urns with unknown composition. The composition in the first urn is determined via a fair mechanism like a coin toss (“risk”), while the decision-maker has no information about the mechanism that determined the second urn’s composition (“ambiguity”). In this standard set-up, an ambiguity averse decision-maker lacking experience with both urns typically (1) prefers bets on the risky over the ambiguous urn and (2) is less willing to bet on the ambiguous urn than a subjective expected utility decision-maker. The problematic feature of this example reveals is that, upon observing a draw from either urn, MLU can reverse both (1) and (2) despite the fact that the information provided by the draws was symmetric across urns and agents.
It is well known that intertemporal ambiguity sensitive preferences tend to be in tension with standard rationality requirements. For ambiguity sensitive preferences, it is not possible to maintain consequentialism (preferences conditional on event E do not depend on the unrealized part of the decision-tree \(E^C\)), dynamic consistency (no reversals in preferences once event E actually happened), and full generality in the representation of ambiguity attitudes at the same time (Ghirardato 2002; Al-Najjar and Weinstein 2009; Siniscalchi 2009, 2011; Dominiak et al. 2012). Accordingly, some dynamic axiomatizations of ambiguity sensitive preferences give up consequentialism (Machina 1989; Hanany and Klibanoff 2007; Eichberger and Kelsey 1996), others dynamic consistency (Pires 2002; Eichberger et al. 2007; Siniscalchi 2011), or determine the conditions under which non-SEU preferences fulfil both dynamic consistency and consequentialism (Sarin and Wakker 1998; Epstein and Schneider 2003; Eichberger et al. 2005).
It is crucial that the switch in betting preferences identified in this paper is rooted neither in dynamic inconsistency nor a violation of consequentialism. To clarify this, the paper adopts the framework of Epstein and Schneider (2007) which respects dynamic consistency as well as consequentialism.Footnote 1 The other reason to follow Epstein and Schneider (2007) is their explicit use of MLU. Concrete, they adopt the generalized and less extreme MLU, already suggested by Gilboa and Schmeidler (1993), in which also priors that only “epsilon maximise the likelihood function” are updated. This paper demonstrates that MLU, both in the strict and the generalized form, gives rise to the switch in betting preferences surrounding risky and ambiguous urns. The deeper reason is that MLU does not respect set inclusion stability over the course of the updating process.
The paper proceeds as follows. Section 2 presents the simple example in which ex-ante and ex-post betting preferences are surprisingly unaligned. Section 3 presents the underlying framework of learning under ambiguity, a simplified version of Epstein and Schneider (2007). Thus equipped, Sect. 4 will revisit the example to understand the deeper reason for the switch in betting preferences. Section 5 concludes.
2 Guiding example
2.1 Betting on urns with unknown composition
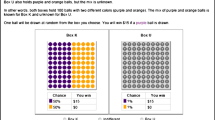
The example presented in this section revolves around the two urns depicted in Fig. 1. Both urns contain exactly three balls. Apart from a white and a black ball, each urn contains a third ball that is either black or white. The composition of either urn, which does not change over the course of the experiment, is unknown to the decision-maker. The key difference between both urns is that the decision-maker knows that the colour of the third ball in the ‘risky’ urn R has been determined via an equiprobable mechanism, e.g., a fair coin. For the ambiguous urn A, however, there is no information about the mechanism that determined the colour of the third ball.
In every period and for each urn, one ball is drawn and then put back (sampling with replacement). The repeated observations enable the decision-maker to learn about the composition of the urns. The objects of choice are simple binary bets of the form \(x_{\mathrm {Colour}}^{\mathrm {Urn}}y\) on the colour of the next ball drawn. The bet \({1}_{B}^{A} 0 \), for instance, is based on the colour of the ball drawn from urn A and involves a payment of 1 $ if the ball is black, and 0 $ otherwise.Footnote 2
2.2 Two decision rules
The decision criterion for evaluating bets on urn R is quite straightforward. The standard Bayesian approach is to start with a prior belief that assigns equal probability to both composition scenarios and then repeatedly update this prior belief upon observing more and more draws. Bets are ranked according to expected payoffs based on the current belief.Footnote 3 For urn A, the uniform prior distribution lacks the clear ‘objective’ justification. We compare decision-makers following two prominent approaches in light of ambiguity. The first decision-maker maximises subjective expected utility (SEU, Savage 1954), which involves the formation of a unique (subjective) initial prior (in the absence of further information typically the uniform distribution) about the composition of urn A that is used to rank bets according to the associated expected payoffs. The natural dynamic extension of SEU is standard Bayesian updating. The second decision-maker maximises maxmin expected utility (MEU, Gilboa and Schmeidler 1989). In contrast to SEU, MEU preferences involve a set of beliefs, and bets are ranked according to minimal expected payoffs. The dynamic extension of MEU preferences employed here is MLU as axiomatized by Gilboa and Schmeidler (1993) and used in Epstein and Schneider (2007). The updating process will be explained in detail in Sect. 3.
We compare betting preferences along two dimensions. First, for each decision-maker separately, we will compare whether the decision-maker prefers a bet on the risky or the ambiguous urn. Second, for each urn separately, we will compare the willingness to bet (expressed as certainty equivalents) of both decision-makers.
2.3 Surprising choices
Assume that the decision-makers are currently characterized by the following belief structure. For urn R, both decision-makers assign the probability 2 / 3 to the scenario that the unknown ball is black. Let this also to be the SEU decision-maker’s assessment of urn A, for instance, because she held the same initial prior and observed the same history of draws. In contrast, the MEU decision-maker’s belief structure regarding urn A is assumed to be quite different; her set of beliefs has a tendency towards the two-black-one-white scenario in the sense that this scenario’s probability ranges from 3 / 4 to 1. In particular, this set of beliefs does not contain the ‘weaker’ 2 / 3, currently held by the SEU decision-maker.
It is a simple task to determine the preferences over the standard bets on a black ball, \({1}_{B}^{R} 0\) and \({1}_{B}^{A} 0\), that result from this belief configuration. Since her beliefs coincide, the SEU decision-maker is indifferent between betting on the risky and the ambiguous urn. In contrast, the MEU decision-maker strictly prefers a bet on the ambiguous urn A over the same bet on urn R. For urn R, as their beliefs coincide, the SEU and MEU decision-makers have the same willingness to bet on the next ball being black, expressed as a same certainty equivalent. For urn A, however, the MEU decision-maker is more willing to bet than her SEU counterpart.
This is unusual. Ambiguity aversion in general and MEU in particular are typically associated with a preference for risky rather than ambiguous situations. However, to be clear, neither the MEU decision-maker’s preference for the ambiguous over the risky urn nor the higher certainty equivalent (as compared to the SEU decision-maker’s) stands in internal conflict with the axioms of ambiguity aversion. Actually, the MEU decision-maker is ambiguity averse given her beliefs: she evaluates the bet \({1}_{B}^{A} 0\) based on her worst belief, here 3 / 4. The reason for the untypical betting preferences is that this worst belief is still more ‘optimistic’ than her belief about urn R and the SEU decision-maker’s assessment of urn A. In summary, we should not regard the MEU decision-maker’s inclination to bets on the ambiguous urn as problematic per se; it may simply be that she received more conclusive evidence for the scenario that the unknown ball in urn A is black.
What, however, actually makes this example surprising and noteworthy is that this is not the case. Rather, the information both decision-makers received about both urns was fully symmetric. Initially, the level of information was symmetric in the sense that both decision-makers had not observed any draw from either urn. And, indeed, at this ex-ante stage—and in accordance with usual notions of ambiguity averse behaviour—the MEU decision-maker strictly preferred a bet on urn R over urn A and was less willing to bet on urn A than the SEU decision-maker. Then, again preserving symmetry across agents and urns, both decision-makers observed the draw of one black ball from either urn. This information led to the ex-post configuration of beliefs and associated unusual betting preferences described above. Table 1 summarises the example.
To understand why this symmetric information had the potential to induce such unintuitive switch in betting preferences, it is needed to have a closer look at the framework behind the example and in particular the maximum-likelihood updating process. This is the focus of the subsequent Sect. 3. Thus equipped, we can revisit the example in Sect. 4.
3 Dynamic MEU preferences with maximum-likelihood updating
The framework to verify the switch in betting preferences identified in the previous section is a simplified version of Epstein and Schneider (2007). In particular, the two urns presented above are reduced versions of the scenarios in Epstein and Schneider (2007).
3.1 Fundamentals
The ratio of black balls in the urn is the unknown parameter \(\theta \) with possible values in the parameter space \(\Theta =\left\{ 1/3 , 2/3 \right\} \). The period state space is \(S_t=S=\left\{ B , W\right\} \), identical for all times. We denote by \(s_t \in S\) the colour observed by the agent at time t. An agent’s information at time t is the history \(s^t= \left( s_1 , \ldots , s_t \right) \). The natural full state space is \(S^\infty \).
The evaluation criterion for choices about bets on urn R is straightforward. Starting with the uniform prior \(\mu _0 = (1/2,1/2)\) over the parameter space \(\Theta =\left\{ 1/3 , 2/3 \right\} \), the decision-maker uses Bayesian updating to process the information provided by the observed signal history \(s^t\) to a posterior \(\mu _t\). This posterior, in turn, is directly associated with a ‘one-step ahead belief’ \(p_t (\cdot ) = \int _\Theta l(\cdot | \theta ) \mathrm{d} \mu _t (\theta )\) on S about the colour of the next ball. Here, \(l(\cdot | \theta )\) is the likelihood of a draw \(s\in S\) given a composition of the urn \(\theta \), i.e., \(l(s=B | \theta ) = \theta \) and \(l(s=W | \theta ) = 1- \theta \). To rank different bets, the decision-maker compares expected payoffs. For instance, the expected payoff \(\pi \) of bet \({x}_{B}^{R} y \) given the one-step ahead belief \(p_t(\cdot )\) is
There are different decision criteria for bets on urn A. The SEU decision-maker forms a unique prior about the composition of the urn and then follows the standard Bayesian updating procedure, so that the decision rule coincides with that in (1). In the absence of any observations, the uniform distribution is a plausible prior and the betting behaviour regarding urn R and urn A indistinguishable. In contrast to SEU, the intertemporal MEU decision-maker initially holds a set of priors \(\mathcal {M}_0\) that is, upon arrival of new information, updated to a set of posteriors \(\mathcal {M}_t\). This updating process is characterized by MLU; the next subsection explains this process in detail. The set of posteriors \(\mathcal {M}_t\) is, in turn, associated with a set of ‘one-step ahead beliefs’ \(\mathcal {P}_t(s^t) = \left\{ p_t (\cdot ) = \int _\Theta l(\cdot | \theta ) \mathrm{d} \mu _t (\theta ) \ : \mu _t \in \mathcal {M}_t(s^t)\right\} \) on S about the colour of the next ball. The MEU decision-maker ranks bets according to maxmin expected utility. Given \(\mathcal {P}_t(s^t)\), the maxmin expected payoff of bet \({x}_{B}^{A} y\) is
Note that the model presented here is much simpler than the framework of Epstein and Schneider (2007). Here, the decision task is structurally the same at all points in time. In particular, past choices in no way restrict the remaining decision-tree. In addition, the current choices do not impact the ‘informativeness’ of the next ball drawn; there is no room for experimentation and similar considerations of giving up short-term payoffs for long-term information benefits (see, for instance, Moscarini and Smith 2001). Every decision just focuses on the colour of the next ball and has to be made solely based on what the decision-maker has learned about the composition of the urn. In particular, discounting does not play a role and can be ignored.
3.2 Maximum-likelihood updating
This subsection describes the process of updating the set of priors \(\mathcal {M}_0\) to the set of posteriors \(\mathcal {M}_t\) by MLU. It proves useful to define the plausibility of a prior \(\mu _0\in \mathcal {M}_0\) given the data \(s^t=(s_1 , \ldots , s_t)\) by
We use the generalization of MLU presented in Epstein and Schneider (2007) and already suggested in the classical paper (Gilboa and Schmeidler 1993). Generalized MLU with parameter \(\alpha \in (0 , 1]\) only updates priors with \(\alpha \)-maximal plausibility given the signal history \(s^t\). Concrete, the set of posteriors \(\mathcal {M}_t(s^t)\) is the priorwise update of the set of admissible priors:
The strict MLU is the case \(\alpha =1\) in which only priors with maximal plausibility are updated. In contrast, full Bayesian updating is the corner case \(\alpha =0\)—explicitly not included in the present paper and in Epstein and Schneider (2007)—in which all priors are updated unconditionally. The example presented in Sect. 2 and revisited in Sect. 4 is characterized by \(\alpha =4/5\).
4 The example revisited
This section demonstrates that the surprising and unintuitive betting behaviour identified in Sect. 2 is a direct consequence of MLU.
4.1 Ex-ante choices
The example presented in Sect. 2 is based on the following plausible assumptions about the ex-ante belief structure. For urn R, it is natural that initially both decision-makers assign equal weights to the two scenarios \(\theta =1/3\) and \(\theta =2/3\). Formally, they hold the initial prior \(\mu _0=(1/2,1/2)\) over the parameter space \(\Theta =\left\{ 1/3 , 2/3 \right\} \). In line with the principle of insufficient reason, this is also the prior that the SEU decision-maker holds regarding urn A before receiving any information about its composition. In contrast, the MEU decision-maker is assumed to initially hold the full prior set \(\mathcal {M}_0= \left\{ (\nu ,1-\nu ) \ \vert \ 0 \le \nu \le 1 \right\} \).
This belief configuration directly leads to the following ex-ante betting preferences. The SEU decision-maker is, irrespective of the bet, indifferent between betting on urn R and urn A as \(p_0(s=B)=1/2\cdot 1/3 + 1/2 \cdot 2/3 = 1/2\) in any case. As a consequence, the certainty equivalent of the standard bet on black is \(\mathrm {CE^{{SEU}{}}}({1}_{B}^{R} 0) = \mathrm {CE^{{SEU}{}}}({1}_{B}^{A} 0) = 1/2\). In contrast, the MEU decision-maker bases here decisions on the worst prior in \(\mathcal {M}_0\). For a bet on black, this is the prior (1, 0) that puts maximal weight on the scenario with only one black ball in the urn, \(\theta =1/3\). Accordingly, the relevant \(p_0 \in \Delta (S)\) for evaluating expected payoffs is \(1 \cdot 1/3 + 0 \cdot 2/3 = 1/3\), so that \(\mathrm {CE^{{MEU}{}}}({1}_{B}^{A} 0) = 1/3\), while \(\mathrm {CE^{{MEU}{}}}({1}_{B}^{R} 0) = 1/2\). In the decision set-up before observing the first draw from the urns, the MEU decision-maker strictly prefers to bet on the risky urn R, in particular \({1}_{B}^{A} 0 \prec ^{MEU}{} {1}_{B}^{R} 0\), and her certainty equivalent for bets on urn A is smaller than SEU’s, \(\mathrm {CE^{{MEU}{}}}({1}_{B}^{A} 0) < \mathrm {CE^{{SEU}{}}}({1}_{B}^{A} 0)\) (cf. Table 1). This is in line with the usual notion of ambiguity aversion.
4.2 Ex-post choices
We now turn to the situation in which the decision-makers have observed the draw of a black ball from both urns. For urn R, on which both decision-makers agree, standard Bayesian updating
transforms the prior \(\mu _0=(1/2,1/2)\) to \(\mu _1=(1/3,2/3)\), reflecting the increased subjective probability for the scenario that the unknown ball is black. This is also how the SEU decision-maker interprets the black draw from urn A. As a result, the SEU decision-maker is still indifferent between betting on urn R and urn A; in addition, the certainty equivalent of a bet on urn R is assessed equally by both decision-makers (cf. Table 1).
The MEU decision-maker naturally has a different take on Urn A. To recapitulate the procedure explained in Sect. 3.2, the first task is to find the most plausible theory \(\mu _0 \in \mathcal {M}_0\). This is (0, 1). The plausibility of this theory, cf. (3), is 2 / 3. With \(\alpha = 4/5\), the MEU decision-maker rejects all theories with a plausibility less than \(4/5 \cdot 2/3\) and thus keeps the set \(\mathfrak {M}_0(s) = \left\{ (\nu ,1-\nu ) \ | \ 0 \le \nu \le 2/5 \right\} \). Finally, this set is updated to \(\mathcal {M}_1^\alpha (s) = \left\{ (\nu , 1-\nu ) \ \vert \ 0 \le \nu \le 1/4\right\} \). Note that this is the set that induced the surprising choices identified in Sect. 2. As demonstrated there, \({1}_{B}^{A} 0 \succ ^{MEU}{} {1}_{B}^{R} 0\) and \(\mathrm {CE^{{MEU}{}}}({1}_{B}^{A} 0) > \mathrm {CE^{{SEU}{}}}({1}_{B}^{A} 0)\). This is a switch to the ex-ante configuration and noteworthy insofar as the information that caused this switch was symmetric across urns and decision-makers.
Another way to illustrate the surprising behaviour is to compare two different MEU decision-makers. Besides the MEU decision-maker starting with the full prior set \(\mathcal {M}_0= \left\{ (\nu ,1-\nu ) \ \vert \ 0 \le \nu \le 1 \right\} \), consider a second decision-maker MEU\('\) with a smaller prior set, \(\mathcal {M}_0' = \left\{ (\nu ,1-\nu ) \ \vert \ 1/4 \le \nu \le 3/4 \right\} \).Footnote 4 Not surprisingly, ex-ante MEU\('\) is less pessimistic in the sense that the certainty equivalent \(\mathrm {CE^{{MEU}'}}({1}_{B}^{A} 0) = 5/12 > 1/3 = \mathrm {CE^{{MEU}{}}}({1}_{B}^{A} 0)\) is larger. Having observed the black ball being drawn from urn A and equipped with the same rejection parameter \(\alpha =4/5\), she keeps the set \(\mathfrak {M}_0(s) = \left\{ (\nu ,1-\nu ) \ | \ 1/4 \le \nu \le 3/5 \right\} \) and hence transforms her beliefs to the set of posteriors \({\mathcal {M}_1^\alpha }' (s) = \left\{ (\nu , 1-\nu ) \ \vert \ 1/7 \le \nu \le 3/7 \right\} \). This results in a certainty equivalent \(\mathrm {CE^{{MEU}'}}({1}_{B}^{A} 0) = 4/7\), now smaller than \(\mathrm {CE^{{MEU}{}}}({1}_{B}^{A} 0) = 3/4\). The initially less pessimistic MEU\('\) decision-maker has turned more pessimistic than her MEU counterpart upon observing the same signal.
4.3 The cause of the switch
This raises the question about the origin of the switch just presented, both in the comparison of SEU and MEU as well as MEU\('\) and MEU.Footnote 5 One explanation might be that the unintuitive betting preferences after updating occur, because the intertemporal formalization of MEU fails to ensure ambiguity aversion. However, this is not the case. Given her beliefs, the MEU decision-maker is, in fact, ambiguity averse. Through the \(\min \)-operator in (2), she is ambiguity averse by construction.
Another possible narrative for the switch is dynamic inconsistency. One may tend to think—even more so as dynamic inconsistency is a typical deviation from standard rationality assumptions with ambiguity averse preferences—that the decision-maker initially prefers bets on the risky urn, but cannot sustain, for whatever reason, this preference over time. Yet, this narrative does not apply here. The decision-makers actually do not make any plans for future choices and only have preferences over the very next bet. And even if their current choices depended on future plans, dynamic consistency would be ensured, because it is written into the recursively defined framework of Epstein and Schneider (2007).
The actual reason for the switch in betting preferences is the belief dynamics under MLU, in particular MLU’s focus on ‘extreme’ priors. This gets most obvious in the comparison of the two maxmin decision-maker MEU and MEU\('\) in the last subsection: what the ‘more pessimistic’ decision-maker MEU with the full prior set identifies as the most likely prior after observing one black ball is certainty that the urn consists of one white and two black balls. For making the point stark, we can focus on strict MLU, \(\alpha =1\), and see that this ‘certainty’ is in fact the only posterior the MEU decision-maker bases her decision on. In contrast, the ‘less pessimistic’ decision-maker MEU\('\) with a smaller prior set cannot regard certainty regarding the composition of the urn as the most likely prior, simply because this extreme case was not a prior to begin with. In summary, the property MLU violates is set inclusion stability of the set of beliefs over the learning process:
Whenever the implication in (6) is violated, there is room for a switch in betting behaviour of some sort to occur. Full Bayesian updating, i.e., the corner case \(\alpha =0\) in the above setting, however, trivially respects (6).
4.4 The general case
One may argue that the switch in betting preferences can be avoided by adequately choosing the rejection parameter \(\alpha \). In fact, any \(\alpha < 3/4\) would, at least at \(t=1\), prevent the example’s switch in preferences. It thus seems in principle possible to restrict \(\alpha \) to innocent values.
The Appendix, however, demonstrates that this is not the case. For every \(\alpha > 0\), there is a setting similar to that considered in the example for which such a disconnect in the behaviour of the MEU decision-maker occurs. The proof involves a generalization of urn R and urn A with more than three balls and constructs a signal history that gives rise to the rejection of the uniform distribution, SEU’s initial prior, and thus a violation of (6). See the Appendix for details. Overall, this demonstrates that MLU will always be prone to some switch in betting preferences.
5 Concluding discussion
Ambiguity sensitive preferences play—in theory and applications as well as for descriptive and prescriptive reasons—an increasing role in economics. Unlike subjective expected utility (SEU), there is no canonical way to extend static ambiguity sensitive preferences to dynamic settings. The two main competing approaches for this extension are full Bayesian updating and maximum-likelihood updating (MLU). This paper has made a contribution to the debate about these updating rules by demonstrating that the latter involves unintuitive ramifications. MLU induces an ambiguity averse maxmin expected utility (MEU) decision-maker to prefer bets on urns with unknown over urns with known composition and to have a higher inclination to bet on the ambiguous urn than her SEU counterpart, despite the absence of any asymmetries in information across urns and agents that might have caused this switch.
The paper has further demonstrated that neither a violation of dynamic consistency nor that of consequentialism—typical sources for deviations from standard rationality when extending ambiguity averse preferences to dynamic settings—is the source of this surprising switch. Rather, the paper has uncovered that MLU favours ‘extreme’ priors and hence does not preserve set inclusion stability of prior and posterior sets. Moreover, it has demonstrated that adopting a less strict MLU is not able to preclude the switch in betting preferences, irrespective of how moderate the rejection criterion is.
The choice to base the example on the framework of Epstein and Schneider (2007) was motivated by convenience and to ensure dynamic consistency right from the start. However, the findings of this paper extend to a broader set of models. It immediately extends to uncertainty averse capacities, as these can be expressed with multiple priors. However, the problematic switch in betting preferences is not restricted to ambiguity averse preferences and may thus occur both in alternative multiple prior models and for general capacities. An ambiguity loving \(\max \)–\(\max \) decision-maker, for example, can be expected to be surprisingly reluctant to bet on black upon having observed the draw of one white ball. The upshot here is that MLU has broad repercussions through its effect on the belief dynamics.
The findings of this paper are relevant for various reasons. In a normative dimension, it is hard to argue why a decision-maker that initially was more cautious in her description of the probabilistic environment, and accordingly less willing to expose herself to ambiguity, should change this and, upon observing information, become more willing to bet on this ambiguous source of uncertainty, both relative to a risky counterpart and relative to an SEU decision-maker. Accordingly, all economic applications that intend to model intertemporal ambiguity averse preferences ought to be aware of the unintuitive implications which MLU may have on their results. The obvious alternative is to rely on full Bayesian updating. To ensure learning with the set of posteriors converging to the true parameter, it is just needed to avoid that the initial prior set contains ‘certainty’ priors that are immune to re-evaluation. In a positive dimension, the findings of this paper raise the empirical question whether choices of decision-makers are compatible or in conflict with the stability of set inclusion of beliefs. In a similar direction, recent experimental evidence shows that some individuals prefer ambiguous over risky bets, especially for unlikely events and losses (Trautmann and Kuilen 2015). This is interpreted as ambiguity seeking. The present paper shows that such ambiguity seeking behaviour can be compatible with ambiguity aversion given specific beliefs, hence adding a further dimension to the recent debate on ambiguity attitudes, in particular in dynamic settings.
Notes
The price for ensuring dynamic consistency and consequentialism at the same time is a restriction in acts and ambiguity sensitive preferences that can be modeled within the framework. The simple example used in this paper is not affected by this restriction.
Due to \(x_B y = y_W x\), we here and in the following restrict to bets on black.
For simplicity, we assume throughout the paper risk-neutral decision-makers with \(u(x)=x\).
The symmetry around 1 / 2 can be regarded as the multiple prior analogue of the principle of insufficient reason.
SEU is the special case of MEU\('\) with \(\mathcal {M}_0'=\left\{ (1/2,1/2) \right\} \).
An alternative generalization would be that of k independent coin flips. The uniform choice, however, is more intuitive and technically simpler.
References
Al-Najjar, N. I., & Weinstein, J. (2009). The ambiguity aversion literature: A critical assessment. Economics and Philosophy, 25(03), 249–284.
Camerer, C., & Weber, M. (1992). Recent developments in modeling preferences: Uncertainty and ambiguity. Journal of Risk and Uncertainty, 5(4), 325–370.
Chateauneuf, A., Eichberger, J., & Grant, S. (2007). Choice under uncertainty with the best and worst in mind: Neo-additive capacities. Journal of Economic Theory, 137(1), 538–567.
Dempster, A. P. (1967). Upper and lower probabilities induced by a multivalued mapping. The Annals of Mathematical Statistics, 38(2), 325–339.
Dominiak, A., Duersch, P., & Lefort, J.-P. (2012). A dynamic Ellsberg urn experiment. Games and Economic Behavior, 75(2), 625–638.
Eichberger, J., & Kelsey, D. (1996). Uncertainty aversion and dynamic consistency. International Economic Review, 37(3), 625–640.
Eichberger, J., & Kelsey, D. (1999). E-capacities and the Ellsberg paradox. Theory and Decision, 46(2), 107–138.
Eichberger, J., Grant, S., & Kelsey, D. (2005). CEU preferences and dynamic consistency. Mathematical Social Sciences, 49(2), 143–151.
Eichberger, J., Grant, S., & Kelsey, D. (2007). Updating Choquet beliefs. Journal of Mathematical Economics, 43(78), 888–899.
Ellsberg, D. (1961). Risk, ambiguity, and the Savage axioms. The Quarterly Journal of Economics 75, 643–669.
Epstein, L. G., & Schneider, M. (2003). Recursive multiple-priors. Journal of Economic Theory, 113(1), 1–31.
Epstein, L. G., & Schneider, M. (2007). Learning under ambiguity. The Review of Economic Studies, 74(4), 1275–1303.
Fagin, R., Halpern, J.Y. (1991). A new approach to updating beliefs. In: Bonissone, P. P., Henrion, M., Kanal L. N., Lemmer, J. (Eds), Uncertainty in Artificial Intelligence (Vol. VI, pp. 347–374). Elsevier.
Ghirardato, P. (2002). Revisiting Savage in a conditional world. Economic Theory, 20(1), 83–92.
Ghirardato, P., Maccheroni, F., & Marinacci, M. (2004). Differentiating ambiguity and ambiguity attitude. Journal of Economic Theory, 118(2), 133–173.
Gilboa, I. (2009). Theory of decision under uncertainty (Vol. 1). Cambridge: Cambridge University Press.
Gilboa, I., & Schmeidler, D. (1989). Maxmin expected utility with non-unique prior. Journal of Mathematical Economics, 18(2), 141–153.
Gilboa, I., & Schmeidler, D. (1993). Updating ambiguous beliefs. Journal of Economic Theory, 59(1), 33–49.
Gilboa, I., Postlewaite, A. W., & Schmeidler, D. (2008). Probability and uncertainty in economic modeling. The Journal of Economic Perspectives, 22(3), 173–188.
Hanany, E., & Klibanoff, P. (2007). Updating preferences with multiple priors. Theoretical Economics, 2(3), 261–298.
Jaffray, J.-Y. (1992). Bayesian updating and belief functions. IEEE Transactions on Systems, Man and Cybernetics, 22(5), 1144–1152.
Klibanoff, P., Marinacci, M., & Mukerji, S. (2005). A smooth model of decision making under ambiguity. Econometrica, 73(6), 1849–1892.
Maccheroni, F., Marinacci, M., & Rustichini, A. (2006). Ambiguity aversion. Robustness, and the Variational Representation of Preferences, Econometrica, 74(6), 1447–1498.
Machina, M. J. (1989). Dynamic consistency and non-expected utility models of choice under uncertainty. Journal of Economic Literature, 27(4), 1622–1668.
Machina, M. J., & Siniscalchi, M. (2014). Chapter 13—Ambiguity and ambiguity aversion. In M. M. A. K. Viscusi (Ed.), Handbook of the Economics of Risk and Uncertainty (Vol. 1, pp. 729–807). Amsterdam: North-Holland.
Moscarini, G., & Smith, L. (2001). The optimal level of experimentation. Econometrica, 69(6), 1629–1644.
Pires, C. P. (2002). A rule for updating ambiguous beliefs. Theory and Decision, 53(2), 137–152.
Sarin, R., & Wakker, P. P. (1998). Dynamic choice and nonexpected utility. Journal of Risk and Uncertainty, 17(2), 87–120.
Savage, L. J. (1954). The foundations of statistics. New York: Wiley.
Schmeidler, D. (1989). Subjective probability and expected utility without additivity. Econometrica, 57(3), 571–587.
Shafer, G. (1976). A mathematical theory of evidence (Vol. 1). Princeton: Princeton University Press.
Siniscalchi, M. (2009). Two out of three ain’t bad: A comment on “the ambiguity aversion literature: A critical assessment”. Economics and Philosophy, 25(Special Issue 03), 335–356.
Siniscalchi, M. (2011). Dynamic choice under ambiguity. Theoretical Economics, 6(3), 379–421.
Trautmann, S. T., & van de Kuilen, G. (2015). Ambiguity attitudes. In G. Keren & G. Wu (Eds.), Blackwell Handbook of Judgement and Decision Making (Vol. 1). New York: Wiley-Blackwell.
Acknowledgements
I thank the editors and two anonymous referees for their helpful suggestions. Support from the German Research Foundation, Grant no. GO 1604/2 and HE 7551/1-1, is gratefully acknowledged. I am grateful to Jürgen Eichberger for his valuable suggestions that led to the current version and thank Boris Wiesenfarth, Timo Goeschl, and Tobias Pfrommer for the discussions in the early stages of this paper.
Author information
Authors and Affiliations
Corresponding author
Appendix: The general result
Appendix: The general result
In line with the example in the main text, this appendix focuses on two decision-makers, the MEU decision-maker with the full prior set \(\mathcal {M}_0=\Delta (\Theta )\), and an alternative decision-maker MEU\('\) with a smaller prior set \(\mathcal {M}_0' \subset \mathcal {M}_0\). The SEU decision-maker following the principle of insufficient reason is the special case of MEU\('\) with \(\mathcal {M}_0\) being the singleton containing just the uniform distribution.
To show that no rejection parameter \(0 < \alpha \le 1\) can prevent a switch in betting preferences, the strategy in this appendix is to prove that for any \(\alpha \), there is a pair of urns similar to urn R and urn A and a signal history \(s^t\) for which \(\mathcal {M}_t' \not \subset \mathcal {M}_t\), hence violating (6). For this purpose, we start by generalizing the setting from urns with three balls to arbitrary symmetric settings. Then, we construct, for given rejection parameter \(\alpha \), a suited urn and signal, such that \(\mathcal {M}_t' \not \subset \mathcal {M}_t\).
The generalized urn R and urn A, denoted by \(U_R(n,k)\) and \(U_A(n,k)\), respectively, have exactly \(2n+k\) balls. It is known that n balls are black, n balls are white, and each of the remaining k balls can either be black or white. As will become clear in what follows, the urns in the example in the main text correspond to the case \(n=k=1\). To generalize the three balls in urn example, we assume that the number of black balls within the k unknown balls in urn \(U_R(n,k)\) is uniformly distributed.Footnote 6 The urn \(U_A(n,k)\) is basically the same, but without information about the distribution of the k unknown balls. In either case, the parameter set is \(\Theta = \left\{ n/(2n+k) , \ldots , (n+k)/(2n+k)\right\} \) with \(\theta \in \Theta \) being the true fraction of black balls in the urn, unknown to the decision-maker. The period state space is again S with the full state space \(S^\infty \). The likelihood functions are fully specified by \(l(s=B | \theta ) = \theta \).
As mentioned above, let \(\mathcal {M}_0=\Delta (\Theta )\) be the full prior set. For \(\mathcal {M}_0'\), it is convenient to consider symmetric sets around the uniform distribution:
By construction, all these sets contain the uniform distribution. The full set of priors \(\Delta (\Theta )\) is the special case \(\Delta _{\epsilon }^{(k)}\) with \(\epsilon =0\), and for \(\epsilon \rightarrow 1/(k+1)\), the set collapses to a singleton with the uniform distribution as the only element. Clearly, \(\Delta _{\epsilon '}^{(k)} \subset \Delta _{\epsilon }^{(k)}\) if \(\epsilon '>\epsilon \). We now have the toolkit at hand to formulate and prove the main result.
Proposition A.1
Let \(0 < \alpha \le 1\) be a rejection parameter. Let \(\mathcal {M}_0=\Delta (\Theta )\) and \(\mathcal {M}_0' = \Delta _{\epsilon }^{(k)}\) with \(0< \epsilon < \alpha /2\). Then, there are generalized urns \(U_R(n,k)\) and \(U_A(n,k)\) characterized by \((n,k) \in \mathbb {N}^2\) and a signal history \(s^t\), such that \({\mathcal {M}_t^\alpha }' \not \subset \mathcal {M}_t^\alpha \).
Proof
We even construct the stronger \({\mathcal {M}_t^\alpha }' \cap \mathcal {M}_t^\alpha = \emptyset \). Without loss of generality, consider the bet \(1_B 0\). Accordingly, the suited signal history will be constructed by repeated observations of black balls, \(s^t= \left( B , \ldots , B \right) \). For \(\mathcal {M}_0=\Delta (\Theta )\) and \(\mathcal {M}_0'= \Delta _{\epsilon }^{(k)}\), the maximal plausible prior after observing only black signals is \((0, \ldots , 1)\) and \((\epsilon , \ldots , \epsilon , 1 - k \epsilon )\), respectively. The condition \({\mathcal {M}_t^\alpha }' \cap \mathcal {M}_t^\alpha = \emptyset \) is equivalent with MEU rejecting the most plausible prior held by MEU\('\). This condition, after multiplying with \((2n+k)^t\), reads
which is, by dividing by \((n+k)^t\), equivalent with
There is a \(t=t(n,k)\), such that \(\left( (n+i)/(n+k)\right) ^t < 1/k\) for all \(0 \le i \le k-1\). A sufficient condition for (9) is thus \(\epsilon + 1-k \epsilon < \alpha \), equivalent with
The choice \(\hat{k}:=\lfloor 1 + \frac{1-\alpha }{\epsilon } \rfloor + 1\) does the job. The initial restriction \(\epsilon < \alpha / 2\) makes sure that \(\epsilon < 1 / (\hat{k} + 1)\) and is hence feasible, cf. (7). \(\square \)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Heyen, D. Ambiguity aversion under maximum-likelihood updating. Theory Decis 84, 373–386 (2018). https://doi.org/10.1007/s11238-017-9611-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11238-017-9611-2