A robust resolution of Newcomb’s paradox

Abstract

Newcomb’s problem is viewed as a dynamic game with an agent and a superior being as players. Depending on whether or not a risk-neutral agent’s confidence in the superior being, as measured by a subjective probability assigned to the move order, exceeds a threshold or not, one obtains the one-box outcome or the two-box outcome, respectively. The findings are extended to an agent with arbitrary increasing utility, featuring in general two thresholds. All solutions require only minimal assumptions about the being’s payoffs, and the being is always sure to predict the agent’s choice in equilibrium. The relevant Nash equilibria are subgame-perfect, except for risk-seeking agents where for intermediate beliefs, the being may be unable to ensure perfect prediction without relying on noncredible threats. Lastly, analogies of Newcomb’s problem to the commitment problem on a continuum are discussed.

1 Introduction

Suppose a “superior being” claims to be able to predict an agent’s action and, conditional on this prediction, influence his payoffs in a simple game of choice. In this game, there are two boxes, labelled I and II. Box I is transparent and contains a positive monetary reward r. Box II is opaque and, unbeknownst to the agent, the being puts in it either a monetary reward R (where $R>r$) or no reward at all. The reward in box I remains untouched. The agent faces the choice of either taking both boxes or taking only box II; his payoff consists of the rewards in the boxes he takes. The being claims that box II will contain R if and only if the agent takes only box II. What should a rational agent do?

This problem, devised by William A. Newcomb in 1960 (Gardner 1973) and published by Nozick (1969), is now referred to as Newcomb’s paradox because for both of the agent’s feasible actions a priori reasonable justifications have been advanced (see also Gardner 1974). Taking both boxes (the “two-box strategy”) seems plausible because of the following dominance argument: no matter what box II contains, adding the reward of box I increases the agent’s payoff. Taking only box II (the “one-box strategy”) may be plausible because a superior being by simulating the agent’s decision process could anticipate the two-box strategy, which would therefore lead to no reward in box II and thus a payoff of r, which in turn is less than the reward R the agent could earn by only taking box II. Lastly, to discourage randomization on the part of the agent, the being claims to put no reward in box II whenever the agent’s choice emanates from a mixed strategy, i.e., a randomization over his two pure strategies (Nozick 1969, pp. 115/143, endnote 1).

In this paper, we resolve Newcomb’s paradox using game theory based on a belief the agent should reasonably form about the structure of the game, specifically about the probability p that the being is informed about the agent’s action before placing the reward. We first consider a risk-neutral agent. Depending on whether the belief probability exceeds a certain threshold or not, the agent will prefer either the one-box strategy or the two-box strategy. If the being can observe this belief, then by anticipating the agent’s choice the being can ensure perfect prediction on the equilibrium path, where, perhaps somewhat unexpectedly, an agent who thinks ex-post intervention of the being unlikely, ends up with the low reward r in the unique Nash equilibrium of the game. If the belief p belongs to the agent’s private information, then the being can devise a mechanism that leads to full information revelation, guarantees perfect prediction, and implements the (first-best) one-box strategy, given the two additional assumptions that the agent’s belief is always strictly positive and that the agent believes the being may be able to inflict a negative payoff to discourage deviations which therefore never occur in equilibrium. If the agent is not risk-neutral, his optimal decisions are generally described by two different thresholds, corresponding to whether, in equilibrium, R ends up in box II or not, should the being move first. Still, the being can solve Newcomb’s problem with zero prediction error in equilibrium unless the agent is risk-seeking. Faced with a risk-seeking agent of intermediate belief, the being cannot maintain a zero prediction error in equilibrium without relying on noncredible threats.

1.1 Literature

Nozick (1969) formulates Newcomb’s paradox and links it to decision theory without offering a resolution; he leans towards the two-box strategy on account of the “dominance principle” which he also defends in later discussions (Nozick 1993, 1997). In the first account of the problem, rewards are set to $r=\$1{,}000$ and $R=\$1$ million, and these amounts have been largely maintained in the subsequent literature. Bar-Hillel and Margalit (1972) argue for the one-box strategy, stating that the “dominance principle looses its appeal when applied to situations where the states of the world (...) are affected by the decision maker’s actions” (p. 297). Their solution invokes game theory where the being acts in order to maximize the probability of being correct. However, they assume this probability is given exogenously, which makes it generally inconsistent with the proposed equilibrium of the game. Schlesinger (1974) points out that the one-box strategy might be interpreted as backward causation, questioning the possibility of free will, which he considers in turn inherently unpredictable.¹ He then attempts to rationalize the two-box strategy based on the agent’s following a well-meaning observer’s imaginary advice. Benditt and Ross (1976), Locke (1978) and Horgan (1981) give largely intuitive counterarguments. Sorenson (1983) and, more recently, Burgess (2004) defend the two-box strategy by separating in time the agent’s conclusion about the contents of box II and the eventual possibility of revising his decision to also take box I. Horwich (1985) argues for the “evidential principle” and thus the one-box strategy because “the choiceworthiness of an act depends solely upon its likelihood of being associated with desirable events” (p. 432), so the agent should maximize expected utility rather than following “causal decision theory” which relies on the additional assumption that his “act might be a cause of the desired outcome” (ibid.). The counterargument by Sobel (1988) invokes the possible endogeneity of the probability that the being predicts the agent’s action correctly, for the agent a priori cannot “be sure that he cannot falsfify the prediction whatever it is” (p. 20).

In the early discussions of Newcomb’s paradox, the being’s accuracy in predicting the agent’s choice is justified by past observations of this predictive performance. Schlesinger (1974) argues that no amount of inductive evidence is able to increase the agent’s confidence in the being’s prediction performance. Brams (1975) discusses some analogies to the prisoner’s dilemma game,² which are again predicated upon assuming an exogenous probability of the being’s correctly predicting the agent’s choice which generally turns out to be inconsistent with the pure-strategy equilibrium.³ The viewpoint in this paper is different, in that the being can in the end perfectly forecast the agent’s choice, simply based on a robust assumption of common knowledge about the game that is being played (Lewis (1969); Aumann 1976; Brandenburger 1992). No performance data on repeated versions of the game or alternative justification of the superior being’s predictive abilities are required other than the ability to determine the equilibrium of a game, which is then realized based on rational expectations (Muth 1961) on the part of the agent and the being.

1.2 Applications

Frydman et al. (1982) and Broome (1989) point out that the problem of a government committing to a policy which tries to implement measures contingent on agents’ actions taken under the policy may be akin to Newcomb’s problem. Indeed, when the agents anticipate the implemented policy measures, their actions may tend to undo the effect of these measures. Broome (1989) explains this using the example of monetary policy, where expanding the money supply leads to increased employment (ranked best) as long as this measure is unexpected, and otherwise to inflation (ranked third-best). If, on the other hand, the government does not expand the money supply, then provided an expansion is expected, it leads to a recession (ranked worst) and otherwise to no change at all (ranked second-best). As a result, assuming rational expectations on the part of the agents, the best the government can do is to obtain inflation, corresponding to the third-best outcome. As Frydman et al. (1982) point out, this dilemma relates to a problem discussed in a seminal paper by Kydland and Prescott (1977) where a government seeks to find an optimal dynamic policy. Because it cannot commit to its future actions, any time-consistent policy [which it has an incentive to adhere to at any future time; see Weber (2011), p. 191] is suboptimal compared to what could be achieved with full commitment, when agents believe that the initially announced policy remains unchanged.

Sugden (1991) points out that in dynamic games actions can be time-inconsistent, even though commitment may at the outset be in a player’s best interest. He compares Newcomb’s paradox to the “toxin” puzzle, where a player is promised a large reward based on his current intention to drink a nonlethal toxin after having received the reward. More importantly, Sugden (1991) also notes that in games, other players’ actions are generally endogenous and cannot, in principle, be viewed as mere lotteries. Hence, a player’s strategic choice is not reduced to a mere decision problem in the tradition of Savage (1954). For Newcomb’s problem, we show that because of rational expectations the probability of the being’s making correct predictions is endogenously determined in equilibrium and must be 100 % (except for one special case), provided the being, in the absence of other pursuits, has just the slightest interest in making correct predictions.

2 Results for a risk-neutral agent

A risk-neutral agent A and a superior being B play a dynamic prediction game $\mathcal G$ over the times $t\in \{1,1.5,2\}$.⁴ There are two boxes, I and II, where box I is transparent and box II is opaque. At the end of the game, box I contains an amount $r>0$ and box II contains an amount in ${\mathcal X} = \{0,R\}$, with $R>r$, which is under B’s control. An extensive-form representation of $\mathcal G$ is given in Fig. 1; some equivalent implementations of this game are discussed in Remark 2.

Fig. 1

Extensive-form representation of the dynamic game $\mathcal G$, for $p\in [0,1]$

• At time $t=1$, the being chooses an amount $x_1\in {\mathcal X}$ to be placed in box II, and tells the agent that $x_1=R$ if and only if A’s choice (at time $t=1.5$) will be to take only box II, with probability 1.

• At time $t=1.5$, without having observed B’s action in the previous period, the agent decides to either take both boxes or to take box II alone. Allowing for randomization between the two possibilities, let $a\in {\mathcal A} = [0,1]$ denote the agent’s chosen probability with which to take both boxes. Thus, with probability a the agent ends up with box I in addition to box II. When pondering his decision the agent believes that with probability $p\in [0,1]$, the being can in the next period observe A’s strategy a and revise the amount placed in box II.

• At time $t=2$, with probability p (according to A’s beliefs) B replaces $x_1$ by an amount $x_2(a)\in {\mathcal X}$ in box II, contingent on A’s strategy a. Otherwise, with probability $1-p$, the amount $x_1$ remains in box II. Immediately thereafter, both players’ payoffs are realized. A’s payoff consists of the combined contents of the boxes he has taken at $t=1.5$. B’s payoff is negative (say, equal to $-1$) if the chosen actions are inconsistent with the statement at $t=1$ and zero otherwise. That is, B’s payoff is negative if $x_2(a)\ne \mathbf{1}_{\{a=0\}}R$, and it is zero otherwise.

To summarize, A’s strategy consists of the number $a\in {\mathcal A}$ which describes the probability with which he ends up with box I in addition to box II. B’s strategy consists of the tuple $x=(x_1,x_2(\cdot ))$, where $x_1\in {\mathcal X}$ is a number in $\{0,R\}$ and $x_2:{\mathcal A}\rightarrow {\mathcal X}$ is a function. The agent’s belief p is common knowledge.⁵ At the end of the game, A’s payoff is the combined contents of all boxes, and B’s payoff is negative whenever $x_1\ne a$ and zero otherwise.⁶ The agent’s expected payoff is

$$\begin{aligned} \pi (a,x,p) = (1-p)\left[ a r + x_1\right] + p\left[ a r + x_2(a) \right] . \end{aligned}$$

(1)

The three-period dynamic game of incomplete information just described encapsulates Newcomb’s problem in its standard form. As solution concept we use a subgame-perfect Nash equilibrium (Selten 1965).⁷

Remark 1

(Does $\mathcal G$ represent the Newcomb problem?) The main differences between the standard exposition of the Newcomb problem and the above game-theoretic formulation is that in $\mathcal G$ the payoffs for the being and the beliefs for the agent are made explicit. Regarding the former, our conclusions depend only on the assumption that B’s payoffs are negative whenever its prediction is incorrect with positive probability. As far as A’s beliefs are concerned, they constitute in fact the “secret ingredient” which allows a resolution of the paradox. The agent’s beliefs imply the being’s ability to commit to the rules of the game.⁸ Its value has nothing to do with B’s predictive accuracy of at least 99.9 % in the standard narrative (see also Appendix 1). In fact, on the equilibrium path of $\mathcal G$ the being’s predictive accuracy is 100 %, independent of p. The formulation of Newcomb’s paradox as a dynamic game of the form $\mathcal G$ recasts the problem effectively as a commitment problem (see, e.g., Weber 2014) where the degree of B’s commitment is determined by A’s beliefs.

Remark 2

(Alternative versions of $\mathcal G$) (i) By collapsing the periods $t=1$ and $t=1.5$ in $\mathcal G$ into a single period at $t=1$, the resulting two-period game $\hat{\mathcal G}$ consists of a simultaneous-move stage game at time $t=1$, followed by B’s decision at time $t=2$. Because in $\mathcal G$ the agent is at time $t=1.5$ unaware of B’s initial choice, the game $\hat{\mathcal G}$ is equivalent to $\mathcal G$. (ii) Conceptually, one can interpret the last period of $\mathcal G$ as a device that with probability p ensures the reward in box II is R if and only if $a=0$, and with probability $1-p$ does nothing. However, while such a device would produce outcome equivalence with the unique subgame-perfect Nash equilibrium of $\mathcal G$, the resulting one-person game (against a machine) would not deliver a plausible explanation for the incentive compatibility of the equilibrium with the being’s objectives. Instead, by hard-wiring B’s equilibrium strategy, this interpretation merely illustrates the fact that unilateral deviations from A’s equilibrium strategy are not in the agent’s best interest. (iii) It is also possible to delete the first period in $\mathcal G$ and think of B’s occurring as one of two types, the first being able to condition its action on A’s action, and the second moving without knowledge of A’s action. In that setting, the agent’s common-knowledge prior belief about the distribution of B’s types is described by p. In that interpretation of the game, the corresponding Bayes-Nash equilibrium would specify B’s strategy at time $t=2$ as a mapping from types to actions, analogous to the branches before the last decision nodes in Fig. 1. (iv) To avoid an extensive form where the belief probability p is relevant for six different events, it is also possible to introduce Nature as a player that at time 0 randomizes over two possible move orders,⁹ which induces the belief probability p.

Taking into account that the being explicitly discourages randomization by the agent (Nozick 1969, pp. 115/143), one obtains¹⁰

$$\begin{aligned} a\in (0,1) \Rightarrow x_2(a) = 0. \end{aligned}$$

(2)

As a result, the agent can never strictly prefer randomization [when $a\in (0,1)$] to a pure strategy (when $a\in \{0,1\}$). In order to exclude noncredible threats,¹¹ we limit attention to subgame-perfect Nash equilibria, which can be found via backward induction, starting in the last period (which contains the only proper subgame of $\mathcal G$).

At time $t=2$, to avoid the possibility of a negative payoff, B has no choice but to set

$$\begin{aligned} x_2(0)=R \quad \text{ and } \quad x_2(1)=0. \end{aligned}$$

(3)

Combining Eqs. (2) and (3), B’s only possible choice at time $t=2$ is

$$\begin{aligned} x_2(a) = \left\{ \begin{array}{ll} R, &{} \quad \text{ if } a = 0,\\ 0, &{} \quad \text{ otherwise }\!. \end{array}\right. \end{aligned}$$

(4)

This corresponds to a forcing strategy, which rewards only perfect compliance by the agent using the strongest possible incentive scheme, independent of p.

At time $t=1.5$, the agent chooses a to maximize his expected payoff in Eq. (1). Taking into account Eq. (4), for all $a\in (0,1)$ it is

$$\begin{aligned} \pi (1,x,p) - \pi (a,x,p) =(1-a)r > 0, \end{aligned}$$

so taking both boxes always strictly dominates any nondegenerate mixed strategy the agent might consider, independent of p. Furthermore,

$$\begin{aligned} \pi (0,x,p)\ge \pi (1,x,p) \end{aligned}$$

if and only if

$$\begin{aligned} p\ge {q} = \frac{r}{R}. \end{aligned}$$

Hence, as a function of his belief p the agent’s equilibrium strategy is

$$\begin{aligned} a(p) \in \left\{ \begin{array}{ll} 1, &{} \quad \text{ if } p < {q},\\ 0, &{} \quad \text{ otherwise }\!. \end{array}\right. \end{aligned}$$

(5)

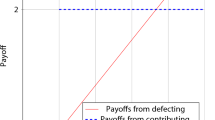
The agent’s choice depends only on the sign of ${q}-p$; it is independent of $x_1$.¹² The dashed black lines in Fig. 2 show A’s payoffs as a function of his belief p, for the two possible actions of B at time 1 (corresponding to $x_1\in \{0,R\}$), respectively. The upper envelope of each strategy (shaded in grey) shows A’s payoffs given his equilibrium strategy in Eq. (5), for both of B’s possible time-1 actions.

Fig. 2

Risk-neutral agent’s expected payoff, for $p\in [0,1]$

At time $t=1$, the being uses the common knowledge about the agent’s belief p [and A’s action a(p) as specified in Eq. (5)] to achieve a nonnegative payoff, by setting

$$\begin{aligned} x_1(p) = \left\{ \begin{array}{ll} R, &{} \quad \text{ if } p > {q},\\ 0, &{} \quad \text{ otherwise }\!. \end{array}\right. \end{aligned}$$

(6)

Thus if $p\ge {q}$, the being can implement $a=0$. As already noted, the agent’s choice will not depend on $x_1$. Yet, the being can guarantee a perfect prediction by choosing $x_1=R$. If $p<{q}$, it is better for the agent to take both boxes, i.e., to choose $a=0$. Hence, the being chooses $x_1=0$, and $x_2(\cdot )$ applies to out-of-equilibrium behavior as well. The solid black line in Fig. 2 depicts A’s resulting equilibrium payoff.

Proposition 1

For any risk-neutral agent with belief $p\in [0,1]$, there is a unique subgame-perfect Nash equilibrium (SPNE) (a(p), x(p)), specified by Eqs. (4)–(6). In this equilibrium, the being makes perfect predictions, and the agent selects the two-box strategy if and only if $p<{q}$.

Proof

By backward induction $x_2(a)$ in Eq. (4) is B’s unique response at $t=2$ to any of A’s feasible actions $a\in {\mathcal A}$ at $t=1.5$. Anticipating this response, A’s unique optimal action (taking into account footnote 12) is given in Eq. (5). Thus, choosing $x_1$ as in Eq. (6) is B’s only way to guarantee a perfect prediction (and thus a nonnegative payoff) in equilibrium.$\square$

Consider the agent’s expected payoff $\pi ^*(p)\equiv \pi (a(p),(x_1(p),x_2(a(p))),p)$ in equilibrium (also shown in Fig. 2). For $p<{q}$, the agent ends up with the low payoff r, analogous to the prisoner’s dilemma solutions. The equilibrium in Proposition 1 does not rely on detailed assumptions about the being’s payoffs, other than that B should have a preference for making correct predictions; in particular, no assumption inconsistent with the general narrative of Newcomb’s problem is made. For $p\ge {q}$, the agent enjoys the sure payoff R, higher than any solution proposed thus far, except for the cooperative supergame solution in the repeated prisoner’s dilemma.

3 Results for an agent with arbitrary risk attitude

The setting of the last section is generalized to an agent with an increasing utility function for money $u(\cdot )$, which represents preferences that are locally nonsatiated. So far, Newcomb’s problem has not been considered for agents with a nonneutral risk attitude.¹³ Without loss of generality one can select a cardinal representation of the agent’s preferences such that ¹⁴

$$\begin{aligned} u(0) = 0 \quad \text{ and } \quad u(R) = 1; \end{aligned}$$

(7)

this simplifies some of the discussion below. The agent’s expected utility becomes

$$\begin{aligned} \bar{u}(a,x,p) = (1-p)u(ar + x_1) + p u(ar+x_2(a)), \end{aligned}$$

(8)

for any $a\in {\mathcal A}$ and $x=(x_1,x_2(\cdot ))$ as specified in Sect. 2. Using the arguments in Sect. 2, Eqs. (2)–(3) continue to hold. Hence, at time $t=2$ the being sets $x_2(\cdot )$ as in Eq. (4).

Fig. 3

Expected payoffs when agent is risk-averse (a) or risk-seeking (b), for $p\in [0,1]$

At time $t=1.5$, when maximizing his expected utility in Eq. (8), the agent cares about the value of $x_1$. For $x_1=0$, the agent’s optimal action is

$$\begin{aligned} a_0(p) = \left\{ \begin{array}{ll} 1, &{}\quad \text{ if } p<{q}_0, \\ 0, &{}\quad \text{ otherwise }\!; \end{array}\right. \end{aligned}$$

(9)

the decision threshold in that case is given by

$$\begin{aligned} {q}_0 = \frac{u(r)-u(0)}{u(R)-u(0)} = u(r)\in (0,1). \end{aligned}$$

Similarly, if $x_1=R$, the agent’s optimal action becomes

$$\begin{aligned} a_1(p) = \left\{ \begin{array}{ll} 1, &{}\quad \text{ if } p<{q}_1, \\ 0, &{}\quad \text{ otherwise, } \end{array}\right. \end{aligned}$$

(10)

with corresponding decision threshold

$$\begin{aligned} {q}_1 = \frac{u(r+R)-u(R)}{u(r+R)-u(r)} = \frac{u(r+R)-1}{u(r+R)-u(r)}\in (0,1). \end{aligned}$$

Fig. 3 shows the agent’s expected utility and optimal actions for different utility functions; the line types follow the same logic as in Fig. 2. If $x_1(p)\in \{0,R\}$ can be chosen in such a way that A’s optimal action is

$$\begin{aligned} a(p) = 1-(x_1(p)/R), \end{aligned}$$

(11)

then B is guaranteed a perfect prediction [in conjunction with Eq. (4)], and thus a nonnegative payoff. Otherwise a perfect prediction is not possible given the said specification of $x_2(\cdot )$ in Eq. (4), which was obtained via backward induction. We now show that the existence of a subgame-perfect Nash equilibrium with perfect prediction, where

$$\begin{aligned} x_1(p) = \left\{ \begin{array}{ll} R, &{}\quad \text{ if } p > {q}_1,\\ 0, &{}\quad \text{ otherwise }\!, \end{array}\right. \end{aligned}$$

(12)

depends on the relative magnitudes of the decision thresholds ${q}_0$ and ${q}_1$.

Proposition 2

Consider an agent with belief $p\in [0,1]$ and arbitrary risk attitude.

• (i) If ${q}_1\le {q}_0$, then there is a unique subgame-perfect Nash equilibrium (a(p), x(p)), specified by Eqs. (4),(11) and (12).

• (ii) If ${q}_0<{q}_1$ and $p\notin ({q}_0,{q}_1)$, then there is a unique pure-strategy Nash equilibrium specified as in part (i).

• (iii) If ${q}_0<p<{q}_1$, then there is a unique pure-strategy Nash equilibrium. In this equilibrium with $a(p)=1$ and $x(p)=0$, the being relies on the noncredible threat of never placing the reward, even when it could be placed contingent on the agent’s choice.

Proof

(i) Assume ${q}_1\le {q}_0$. If B sets $x_1(p)=0$ for $p<{q}_1$ and $x_1(p)=R$ for $p\ge {q}_1$, then by Eq. (9) it is $a(p)=a_0(p)=0$ for $p<{q}_1$. By Eq. (10) it is $a(p)=a_1(p) = 1$ for $p\ge {q}_1$. Moreover, since $a_1(p)=a_0(p)=0$ for $p<{q}_1$, we obtain A’s optimal action at time $t=1.5$,

$$\begin{aligned} a(p) = a_1(p), \end{aligned}$$

for all $p\in [0,1]$. Lastly, at time $t=1$ anticipating a(p) and $x_2(a(p))$, the being expects a nonnegative payoff and would therefore not want to deviate, so Eqs. (4), (11) and (12) specify indeed an SPNE. This equilibrium is unique, since a(p) and $x_2(\cdot )$ are unique, analogous to the proof of Proposition 1 and any deviation by B at $t=1$ leads to a violation of Eq. (11) and thus to an expected negative payoff due to possibly imperfect prediction. (ii) Assume ${q}_0<{q}_1$ and $p\notin ({q}_0,{q}_1)$. If $p<{q}_0$ (resp. $p\ge {q}_1$), then A’s optimal action is $a_0(p)=1$ (resp. $a_1(p)=0$). Hence, we obtain $a(p)=a_1(p)$ as in part (i) and therefore the existence of a unique SPNE with the same specifications as before, for these extreme beliefs $p\notin ({q}_0,{q}_1)$. (iii) Assume ${q}_0<p<{q}_1$. If $x_1(p)=0$, then A’s optimal action is $a(p)=a_0(p) = 0$ which violates Eq. (9). Otherwise, if $x_1(p)=R$, then A’s optimal action $a(p) = a_1(p) = 1$ again violates Eq. (9). Hence, no matter what B’s allocational choice at time $t=1$, there is a positive probability of an incorrect prediction, resulting in a negative expected payoff. To improve the probability $1-p$ of failing to choose a correct allocation using pure strategies, the being would want to randomize in equilibrium, eliminating thus the possibility of a pure-strategy SPNE. On the other hand, a pure-strategy subgame-imperfect Nash equilibrium does exist, with B choosing $x(p)=0$, i.e., the allocation $x_t=0$ for $t\in \{1,2\}$, to which the agent finds it (weakly) optimal to respond with $a(p)=0$, which satisfies Eq. (11) and thus ensures a perfect prediction. B’s threat of an unconditional zero allocation is not credible, because were the agent to deviate and take only box II ($a=0$), then B would find it beneficial to respond with $x_2=R$ in order to avoid an allocation error.$\square$

The critical condition ${q}_1\le {q}_0$ in Proposition 2 is equivalent to ¹⁵

$$\begin{aligned} u(r+R) - u(R) \le u(r)- u(0). \end{aligned}$$

(13)

In other words, the utility difference from owning the additional reward r does not go up when the default reward increases from 0 to R. Since $u(0)=0$ by Eq. (7), this holds for all $r,R\ge 0$ if and only if the utility is subadditive, so $u(r+R)\le u(r)+u(R)$. A sufficient condition for inequality (13) to hold is that u is concave, i.e., the agent is risk-averse. In the special case where the agent is risk-neutral, the thresholds are identical, ${q}_0={q}_1={q}$, and the same results as in Sect. 2 obtain. When the agent is risk-seeking, that is, his utility function is strictly convex, the inequality (13) becomes false for all positive r, R with $r<R$, that is ${q}_1>{q}_0$, which according to part (iii) of Proposition 2 implies a region of beliefs for which a pure-strategy SPNE does not exist. The expected equilibrium utility, $\bar{u}^*(p) = \bar{u}(a(p),(x_1(p),x_2(a(p))),p)$ together with the agent’s optimal actions are shown in Fig. 3a for the “risk-averse” case where ${q}_0>{q}_1$ and in Fig. 3b for the “risk-seeking” case where ${q}_1>{q}_0$ (where the dashed bold line in the shaded area indicates the support of payoffs in a mixed-strategy equilibrium).

4 Discussion

Beginning with Nozick (1969) the discussion of Newcomb’s problem has centered on trying to adjudicate which of two alternative views of the world is correct, a deterministic (“causal”) framework in which future outcomes are fully deductible from past states or an indeterministic (“evidentiary”) framework in which future outcomes cannot be predicted with certainty and depend inductively on past states.¹⁶ Depending on which of the two is chosen, solutions to the problem were proposed via a dominance argument (supporting the two-box strategy) or an expected-utility-maximization argument (supporting the one-box strategy), respectively, with no possible resolution between these two solutions. Gardner (1973) noted a third approach by Immanuel Kant which “accepts both sides as being equally true but incommensurable ways of viewing human behavior” (p. 104). In physics, a version of this third approach was formulated by Niels Bohr in his “principle of complementarity” which states, roughly speaking, that reality must depend on the observer (Bohr 1958/1961; Plotnitsky 2012).

Much in the same way as Bohr’s complementarity principle, our proposed solution depends on the agent, specifically his beliefs in the being’s ability to commit. And the being, knowing these beliefs, will react to them. For an agent who thinks it unlikely that the being can condition the content of box II on his action, the two-box strategy prevails, essentially because of dominance. On the other hand, an agent who thinks that the being is likely to condition the content of box II on his own action, prefers the one-box strategy. In this context, the parameter p can also be viewed as continuously indexing the being’s ability to commit to an allocation at time $t=1$, from $p=0$ for full commitment to $p=1$ for no commitment. At the ends of the spectrum one obtains the two-box outcome (at low reward r) and the one-box outcome (at high reward R), respectively. For intermediate values of p, the being’s perceived ability depends on the agent’s perception of reality, in particular his risk preference. In this interpretation, Newcomb’s problem is related to commitment measured on a continuum because an initial action may at least be partially revocable (Henkel 2002; Weber 2014).¹⁷ Instead of a belief, the parameter p then indexes an objective ability by the being to revise the earlier allocation after the agent selected his strategy. In either interpretation, as in the Coase problem (see footnote 17), the agent benefits from the other party’s inability to commit. As much as the being lacks the ability to commit, the agent’s own action becomes influential in determining the final payoffs of the game.

The solution to Newcomb’s problem presented in Sects. 2 and 3 is robust in the sense that almost no assumptions were made about the being’s intentions, other than a preference for making correct predictions.¹⁸ The being also does not need very complex distributional assumptions about the agent’s potential preferences other than the decision threshold q (resp. ${q}_1$ in the case with general risk attitude; see Sect. 3). Even if the being operates in the complete absence of any information about the agent (see Appendix 1), there is a high chance, given the small ${q} = r/R = 0.001$ (using the standard numbers), that the being’s decisions would lead to correct predictions, exactly as in the usual narrative of Newcomb’s problem.

Appendix 1: Asymmetric information

Suppose that information about a risk-neutral agent’s belief is private, or equivalently, that the being faces a population of different agents with beliefs $\theta \in \Theta = {[}{\underline{\theta }},\bar{\theta }{]}$, where $0\le {\underline{\theta }}\le \bar{\theta }\le 1$. B encounters one of these agents at random.¹⁹ From the preceding analysis we have seen that what matters for the agent’s binary decision is whether his beliefs are above or below the threshold ${q}=r/R$.  Hence, when designing a mechanism $({\mathcal M},\xi )$ to reveal the agent’s information, B can restrict attention to a binary message space ${\mathcal M} = \{L,H\}$, where L is a message that (if truthful) indicates a low type ($p<{q}$), and H is a message that (if truthful) indicates a high type ($p\ge {q}$). For each action-message tuple $(a,m)\in {\mathcal A}\times {\mathcal M}$, the being chooses the allocation $\xi (a,m) = (\xi _1(m),\xi _2(a,m))$. To minimize the prediction error on the equilibrium path, B does not randomize allocations, so $\xi (a,m)\in \{(0,0),(\nu ,R),(R,\nu ),(R,R)\}$ for all $(a,m)\in {\mathcal A}\times {\mathcal M}$, where $\nu$ is a real number to be determined below. Analogous to the equilibrium concept chosen in the main text, we limit attention to perfect Bayesian Nash equilibria.

Proposition 3

When the information about the belief $p=\theta$ is private to the agent and ${\underline{\theta }}>0$, there is a revelation mechanism under which the agent does not object to reporting his beliefs truthfully and the being makes no mistakes.

Proof

Given a mechanism $({\mathcal M},\xi )$, let $(\alpha ,\mu )$ with $\alpha :\Theta \rightarrow {\mathcal A}$ and $\mu :\Theta \rightarrow {\mathcal M}$ be the agent’s strategy. Then

$$\begin{aligned} (\alpha (\theta ),\mu (\theta ))\in \arg \max _{(a,m)\in {\mathcal A}\times {\mathcal M}} \left\{ a r + (1-\theta )\xi _1(m) + \theta \xi _2(a,m)\right\} . \end{aligned}$$

To avoid mistakes, B has no choice but to discourage $a\in (0,1)$ by leaving box II empty, that is $\xi _2(a,m)=0$ irrespective of m; therefore randomization is never optimal for the agent. Consider an allocation function $\xi = (\xi _1,\xi _2)$ with $\xi _1:{\mathcal M}\rightarrow {\mathbb R}$ and $\xi _2:{\mathcal A}\times {\mathcal M}\rightarrow {\mathbb R}$ with

$$\begin{aligned} \xi _1(L) = \xi _1(H) = R, \end{aligned}$$

(14)

and

$$\begin{aligned} \xi _2(a,m) = \left\{ \begin{array}{ll} R, &{}\quad \text{ if } a = 0,\\ \nu , &{}\quad \text{ if } (a,m) = (1,L),\\ 0, &{}\quad \text{ otherwise }\!, \end{array}\right. \end{aligned}$$

(15)

where the real number $\nu$ is determined below. We know for $\theta <{q}$ the agent prefers (1, L) and for $\theta \ge {q}$ he prefers (0, H) in the set of deterministic actions (a, m) in $\{(0,L),(1,L),(0,R),(1,R)\}$. That is, any agent reports truthfully whether his belief is above or below the threshold and otherwise chooses the one-box strategy.

• 1. $\theta \in [{q},\bar{\theta }]$: The agent prefers (0, H) to (1, H), since by Eqs. (14)–(15):

  $$\begin{aligned} (1-\theta )\xi _1(H) + \theta \xi _2(0,H)= & {} R > (1-\theta )R \nonumber \\= & {} (1-\theta )\xi _1(H) + \theta \xi _2(1,H). \end{aligned}$$

  (16)

  Furthermore, (0, H) is (weakly) preferred to (0, L) since either action yields a sure payoff of R. Lastly, (0, H) is also preferred to (1, L) because

  $$\begin{aligned} (1-\theta )\xi _1(H) + \theta \xi _2(0,H)= & {} R \ge r + (1-\theta )\xi _1(L) + \theta \xi _2(1,L)\nonumber \\= & {} r + (1-\theta )R + \theta \xi _2(1,L), \end{aligned}$$

  for all $\theta \ge {q} = r/R$, which is equivalent to $\xi _2(1,L)\le 0$.

• 2. $\theta \in [{\underline{\theta }},{q})$: By Eqs. (14)–(15) the agent prefers (0, L) to (1, L) and to (1, H) if and only if

  $$\begin{aligned} R\ge r + (1-\theta )R + \theta \nu . \end{aligned}$$

  This inequality is satisfied for all $\theta \in [{\underline{\theta }},{q})$ if B sets

  $$\begin{aligned} \nu \equiv R - \frac{r}{{\underline{\theta }}} = -\left( \frac{{q}}{{\underline{\theta }}}-1\right) R. \end{aligned}$$

  Finally, the agent (weakly) prefers (0, L) to (0, H), for he is guaranteed a certain payoff of R.

This concludes our proof. $\square$

The mechanism specified in Proposition 3 depends on the being’s ability to deter the agent from deviations with negative payoffs. The being therefore needs to be able to credibly threaten the agent, saying something to the effect that if B gets to choose at time $t=2$ and finds that $a\ne x_1 = 0$, then box II is likely to “explode” when the agent opens it. Without this threat, the only other possibility for the being is to revert to the Nash equilibrium where B never puts any reward in box II, relying on the noncredible threat discussed at the end of the proof of Proposition 2.

When the agent has a general risk attitude, B is left with a similar dichotomy and thus needs to decide whether case (iii) in Proposition 2 applies or not. If negative payoffs can be implemented, then a mechanism analogous to the one in Proposition 3 can be found. Otherwise, B needs to form beliefs about the population of agents. For example, if in the risk-neutral case, agents’ types (beliefs) are uniformly distributed on $\Theta =[0,1]$, then for ${q}=0.001$ the being in the equilibrium specified in Proposition 1, assuming $p\ge {q}$, would make a correct prediction 99.9 % of the time, consistent with the standard narrative of Newcomb’s problem. Note also that in our resolution of Newcomb’s problem, the agent does not need to make any assumptions (other than the structure of the game, which we have tacitly assumed to be common knowledge), but rather just act according to his beliefs.