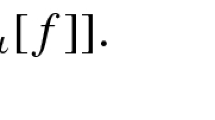Choquet expected utility with affine capacities

Abstract

This paper studies decisions under ambiguity when attention is paid to extreme outcomes. In a purely subjective framework, we propose an axiomatic characterization of affine capacities, which are Choquet capacities consisting in an affine transformation of a subjective probability. Our main axiom restricts the well-known Savage’s Sure-Thing Principle to a change in a common intermediate outcome. The representation result is then an affine combination of the expected utility of the valued act and its maximal and minimal utilities.

Appendix 1: Proofs

Without any essential loss of generality, we assume that the utility function U is normalized such that $U(M)=1$ and $U(0)=0$. Since the utility U is continuous, its range is the interval [0, 1].

Chateauneuf et al. (2007) lists some properties of essential events when there exist at least three pairwise disjoint essential events (property 4 is omitted since it is not explicitly used in our proofs).

1.1 Properties of essential events

Property 1

$E\in \Sigma ^*$ implies $E^c\in \Sigma ^*$.

Property 2

There exists a partition $A_1,\ldots ,A_3$ of S such that $A_i\in \Sigma ^*$ for any $i=1,2,3$.

Property 3

Let $A_1,\ldots ,A_3 \in \Sigma ^*$ be pairwise disjoints events, then $A_i \cup A_j \in \Sigma ^*$ for any $i,j=1,\ldots ,3$.

1.2 Proof of Theorem 1

Proof of Lemma 1

Part A $\mathrm{(i)}\Rightarrow \mathrm{(ii)}$. Properties A and D follow from the definition of an affine capacity.

Part B $\mathrm{(ii)}\Rightarrow \mathrm{(i)}$. Lemma 3 of Eichberger et al. (2012) shows that if property D is satisfied by a capacity $\nu$ satisfying property A, then $\nu$ is a GNAC. To show that $\nu$ is an affine capacity, it remains to show that property D directly implies that the probability $\pi$ is congruent with $\mathcal {N}$. Let E be an essential event and N be a null event. If $\nu$ is a GNAC satisfying property D, we have $\nu (E\cup N)=\nu (E)$ if and only if $a+b[\pi (E)+\pi (N)]=a+b\pi (E)$ if and only if $\pi (N)=0$. Furthermore, $\pi (N^c)=1$ by additivity and normalization of $\pi$, with $\pi (N\cup N^c)=1$. Hence, $\pi$ is congruent with $\mathcal {N}$ and $\nu$ is an affine capacity.

Proof of Lemma 2

Part A $\mathrm{(i)}\Rightarrow \mathrm{(ii)}$.

By Lemma 2 of Eichberger et al. (2012), Axiom 1 implies that for any $E\in \Sigma$ and any $N\in \mathcal {N}$ such that $E\cap N=\emptyset$, we have $\nu (E\cup N)=\nu (E)$. Hence, $\nu$ satisfies property D. Furthermore, $\mathcal {N}$ is an ideal: CEU implies (i) $\emptyset \in \mathcal {N}$, (ii) $A\in \mathcal {N}$ implies $B\in \mathcal {N}$ for any $B\subset A$; property D with $E\in \mathcal {N}$ implies (iii) $A\in \mathcal {N}$ and $B\in \mathcal {N}$ implies $A\cup B\in \mathcal {N}$.

It remains to show that $\nu$ is congruent with $\mathcal {N}$.⁴ Suppose, per absurdum, $A\in \mathcal {N}$ and $\nu (A^c) < 1$. Since $A\cup A^c=S$ and $\mathcal {N}$ is an ideal, we cannot have $A^c \in \mathcal {N}$. Hence, $A^c \in \Sigma ^*$ so property D implies $1=\nu (S)=\nu (A \cup A^c)=\nu (A^c)$ which contradicts $A^c \in \Sigma ^*$. Therefore, $A \in \mathcal {N}$ implies $\nu (A)=0$ and $\nu (A^c)=1$.

Part B $\mathrm{(ii)}\Rightarrow \mathrm{(i)}$. Let A be an event, $\mathcal {N}$ be a null event and x, y, z be any three outcomes such that $x\succ y \succ z$. Under CEU, the act $f\equiv y_Nx_Az$ is valued as:

$$\begin{aligned} E(U\circ f\vert \nu )=U(z)[1-\nu (A\cup N)]+U(y)[\nu (A\cup N)-\nu (A)]+U(x)\nu (A) \end{aligned}$$

If $A\in \Sigma ^*$, property D implies $\nu (A\cup N)=\nu (A)$ and then $f\sim x_Az$. If $A\in \mathcal {N}$, we also have $\nu (A\cup N)=0$ since $\mathcal {N}$ is an ideal (hence, $A\cup N \in \mathcal {N}$) and then $f \sim x_Az$. Finally, when $A\in \mathcal {U}$, $\nu (A\cup N)=\nu (A)=1$ implies $f \sim x_Az$.

Proof of Lemma 3

Part A $\mathrm{(i)}\Rightarrow \mathrm{(ii)}$. Let n be the number of pairwise disjoint essential events. We have two cases to treat, depending on if $n=3$ or $n>3$, to prove that property A holds, since $B\cap F\ne \emptyset$ with $B\cup G\in \Sigma ^*$ and $F\cup G\in \Sigma ^*$ implies $B=F$ in the former case.

Case 1: $n=3$. When there are only three pairwise disjoint essential events, property 2 implies that there exists a partition $E_1,E_2,E_3$ of S, such that $E_i\in \Sigma ^*$ for any $i=1,2,3$, and property 3 implies $E_i \cup E_j \in \Sigma ^*$ for any $i,j=1,2,3$. Let $E=E_i\cup E_j$. We have to prove that

$$\begin{aligned} \nu (E_i\cup G)-\nu (E_i)=\nu (E_j\cup G)-\nu (E_j) \end{aligned}$$

(3)

for any $i,j=1,2,3$ and any essential event $G=E^c$. We know that G is an essential event by property 1. Let $f_E x\equiv (x_i,E_j;x,G;x_j,E_j)$ and $g_E x\equiv (y_i,E_i;x,G;y_j,E_j)$, with $x_i\succ x \succ x_j$ and $y_j\succ x \succ y_i$, such that $f_E x\sim g_Ex$.

Let $y\in X$ such that $x_i\succ y \succ x_j$ and $y_j\succ y \succ y_i$. By continuity, one can find y such that $y\succ x$ or $x\succ y$. Axiom 2 then implies $f_E x\sim g_E x$ if and only if $f_Ey \sim g_E y$. Under CEU, these two indifference imply

$$\begin{aligned} E(U\circ f_Ex \vert \nu )-E(U\circ f_Ey \vert \nu )=E(U\circ g_Ex \vert \nu )-E(U\circ g_Ey\vert \nu ) \end{aligned}$$

which is equivalent to Eq. (3), hence property A holds for $B=E_i$, $F=E_j$ and $G=S\backslash (E_i\cup E_j)$. If $\mathcal {N}$ contains null event(s) other than the empty set $\{\emptyset \}$, there may be one or several partitions of S other than $E_1,E_2,E_3$. Under property D, property A is automatically satisfied on these partitions hence it holds on $\Sigma ^*$. Otherwise the same argument could be used to prove that property A holds for any partition of three essential events.

Case 2: $n>3$.

By property 2, if there exist four essential disjoint events, then there exists a partition $A_1,\ldots ,A_n,G$ of S such that $n\ge 3$ and $A_i\in \Sigma ^*$. By property 1, $A_n \in \Sigma ^*$ implies $A_n ^c=\cup _{i=1}^{n-1} A_i \cup G \in \Sigma ^*$. Let

$$\begin{aligned} f\equiv (x_1,A_1;\ldots ;\,x_i,A_i;\,x,G;\,x_i,A_{i+1};\ldots ;\,x_n,A_n) \end{aligned}$$

and

$$\begin{aligned} g\equiv (y_1,A_1;\ldots ;\,y_i,A_i;\,x,G;\,y_{i+1},A_{i+1};\ldots ;\,y_n,A_n), \end{aligned}$$

where

$$\begin{aligned} x_1 \succ x_2 \succsim \cdots \succsim x_i \succ x \succsim x_{i+1} \succsim \cdots \succ x_n \end{aligned}$$

and

$$\begin{aligned} y_1\succ y_2 \succsim \cdots \succsim y_i \succ x \succsim y_{i+1} \succsim \cdots \succ y_n, \end{aligned}$$

be such that $f\sim g$. By EOS, $f\sim g$ if and only if $y_Gf \sim y_G g$, where $\{x_{i-1},y_{i}\} \succ y \succ x_i$. By continuity of CEU preferences, such an outcome $y\in X$ may be found. Under CEU, these two indifference imply

$$\begin{aligned} E(U\circ y_G f\vert \nu )-E(U\circ f\vert \nu ) =E(U\circ y_G g\vert \nu ) - E(U\circ g\vert \nu ) \end{aligned}$$

which is equivalent to

$$\begin{aligned} \nu (A_1 \cup \ldots \cup A_i \cup G)-\nu (A_1\cup \ldots \cup A_i) = \nu (A_1\cup \ldots \cup A_{i-1}\cup G)-\nu (A_1\cup \ldots \cup A_{i-1}) \end{aligned}$$

(4)

for any $i=2,\ldots ,n-1$. Since this equation holds for any $f,g\in \mathcal {A}$, hence for any partition $A_1,\ldots ,A_n,G$ of S such that $n\ge 3$ and $A_1,\ldots ,A_n,G \in \Sigma ^*$, property A holds on $\Sigma ^*$.

Part B $\mathrm{(ii)}\Rightarrow \mathrm{(i)}$. Since $\succsim$ satisfies Axiom 1, Lemma 2 implies that $\nu$ satisfies property D, $\nu$ is congruent with $\mathcal {N}$ and $\mathcal {N}$ is an ideal. Therefore, by Lemma 1, $\nu$ is an affine capacity and $\succsim$ is represented by Eq. 2.

We prove that $\succsim$ satisfies $f_Ez\succsim g_Ez$ if and only if $f_Ez'\succsim g_Ez'$ for any non-null event E, any two acts $f,g\in \mathcal {A}$ and any two outcomes $z,z' \in X$ such that for $x,x'\in f(E)$ and $y,y'\in g(E)$, we have $f^{-1}(x),f^{-1}(x'),g^{-1}(y),g^{-1}(y')\in \Sigma ^*$ and $\{x,y\} \succ \{z,z'\} \succ \{x',y'\}$.

Under representation 2, $f_E z \succsim g_E z$ if and only if:

$$\begin{aligned}&a \max \{U\circ f_E z:f_E z^{-1}(x)\notin \mathcal {N}\} +b \left[ E(U\circ f_E z\vert \pi (.\cap E)) +\pi (E^c)U(z)\right] \\&\qquad +(1-a-b) \min \{U\circ f_E z:f_E z^{-1}(x)\notin \mathcal {N}\} \\&\quad \ge a \max \{U\circ g_E z:g_E z^{-1}(x)\notin \mathcal {N}\} +b \left[ E(U\circ g_E z\vert \pi (.\cap E)) +\pi (E^c)U(z)\right] \\&\qquad +(1-a-b) \min \{U\circ g_E z:g_E z^{-1}(x)\notin \mathcal {N}\} \end{aligned}$$

which is equivalent to

$$\begin{aligned}&a \max \{U\circ f_E z':f_E z'^{-1}(x)\notin \mathcal {N}\} +b \left[ E(U\circ f_E z'\vert \pi (.\cap E)) +\pi (E^c)U(z')\right] \\&\qquad +(1-a-b) \min \{U\circ f_E z':f_E z'^{-1}(x)\notin \mathcal {N}\} \\&\quad \ge a \max \{U\circ g_Ez':g_E z'^{-1}(x)\notin \mathcal {N}\} +b \left[ E(U\circ g_Ez'\vert \pi (.\cap E)) +\pi (E^c)U(z')\right] \\&\qquad +(1-a-b) \min \{U\circ g_E z':g_E z'^{-1}(x)\notin \mathcal {N}\} \end{aligned}$$

which holds if and only if $f_E z'\succsim g_E z'$.